Dynamics of terminal fraying–peeling and hydrogen bonds dictates the sequential vs. cooperative melting pathways of nanoscale DNA and PNA triplexes†
Sandip
Mandal
 a,
Krishna N.
Ganesh
b and
Prabal K.
Maiti
a,
Krishna N.
Ganesh
b and
Prabal K.
Maiti
 *a
*a
aCenter for Condensed Matter Theory, Department of Physics, Indian Institute of Science, Bangalore 560012, India. E-mail: maiti@iisc.ac.in; sandipmandal@iisc.ac.in; Fax: +91-80-2360-2602; Tel: +91-80-2293-2865
bJawaharlal Nehru Center for Advanced Scientific Research (JNCASR), Jakkur, Bengaluru 560064, India. E-mail: kn.ganesh@jncasr.ac.in
First published on 21st June 2024
Abstract
Peptide nucleic acids (PNAs) are charge-neutral synthetic DNA/RNA analogues. In many aspects of biology and biotechnology, the details of DNA and PNA melting reaction coordinates are crucial, and their associative/dissociative details remain inadequately understood. In the current study, we have attempted to gain insights into comparative melting pathways and binding affinity of iso-sequences of an 18-mer PNA–DNA–PNA triplex and the analogous DNA–DNA–DNA triplex, and DNA–DNA and PNA–DNA duplexes. It is intriguing that while the DNA–DNA–DNA triplex melts in two sequential steps, the PNA–DNA–PNA triplex melts in a single step and the mechanistic aspects for this difference are still not clear. We report an all-atom molecular dynamics simulation of both complexes in the temperature range of 300 to 500 K with 20 K intervals. Based on the trajectory analysis, we provide evidence that the association and dissociation are dictated by the differences in fraying–peeling effects from either terminus to the center in a zipper pattern among the PNA–DNA–PNA triplex and DNA–DNA–DNA triplexes. These are shown to be governed by the different characteristics of H-bonding, RMSD, and Free Energy Landscape (FEL) as analyzed by PCA, leading to the DNA–DNA–DNA triplex exhibiting sequential melting, while the PNA–DNA–PNA triplex shows cooperative melting of the whole fragment in a single-step. The PNA–DNA–PNA triplex base pairs are thermodynamically more stable than the DNA–DNA–DNA triplex, with the binding affinity of PNA–TFO to the PNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DNA duplex being higher than that of DNA–TFO to the DNA
DNA duplex being higher than that of DNA–TFO to the DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DNA duplex. The investigation of the association/dissociation of PNA–TFO to the PNA–DNA duplex has relevance and importance in the emerging effective applications of oligonucleotide therapy.
DNA duplex. The investigation of the association/dissociation of PNA–TFO to the PNA–DNA duplex has relevance and importance in the emerging effective applications of oligonucleotide therapy.
1. Introduction
PNAs are uncharged synthetic molecules that potentially mimic natural nucleic acids DNA/RNA.1 The PNA backbone consists of repeating N-(2-aminoethyl)-glycine(aeg) units connected by peptide bonds by replacing the negatively charged sugar–phosphate backbone of DNA/RNA. Overall, the pseudo-peptide backbone of PNA is achiral to which natural bases adenine, thymine, guanine, and cytosine are attached as side chains via a methyl carbonyl linker. The first PNA–DNA duplex structure was observed by Nielsen, Buchardt, Egholm and Berg in 1991. PNA is among the most efficient molecules for targeting DNA/RNA hybridization2,3 out of the various derivatives and analogs proposed for this scope. PNA can block the transcription of genomic DNA (antigene) and prevent mRNA translation (antisense) to proteins that cause different diseases.4PNA has caught researchers’ interest in various therapeutic applications, such as antisense therapy, gene editing and diagnostics,5,6 all of which involve its hybridization with complementary DNA/RNA. Therefore, understanding the mechanism of the association/dissociation process of PNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DNA duplexes and triplexes at an atomistic scale is most relevant for developing effective PNA-based therapeutic and diagnostic applications. Previous simulation studies on the DNA duplex proposed that three states are involved in DNA duplex melting: searching, fraying, and peeling of the complementary strands.7–10 The natural DNA duplexes or triplexes are less stable in vivo as they are susceptible to the action of endo/exonucleases. In contrast, PNA
DNA duplexes and triplexes at an atomistic scale is most relevant for developing effective PNA-based therapeutic and diagnostic applications. Previous simulation studies on the DNA duplex proposed that three states are involved in DNA duplex melting: searching, fraying, and peeling of the complementary strands.7–10 The natural DNA duplexes or triplexes are less stable in vivo as they are susceptible to the action of endo/exonucleases. In contrast, PNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DNA duplexes are stable to both proteases and exo/endonucleases.11 As exonucleases act from the 3′/5′-terminus, an interesting question is how the molecular dynamics of 3′/5′-termini are different in PNA
DNA duplexes are stable to both proteases and exo/endonucleases.11 As exonucleases act from the 3′/5′-terminus, an interesting question is how the molecular dynamics of 3′/5′-termini are different in PNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DNA and DNA
DNA and DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
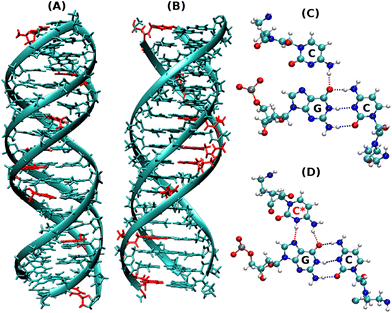
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DNA duplexes and the derived triplexes. The two strands at the termini in DNA duplexes are known to breathe making H-bonding weaker at termini12 and exhibit a temperature-dependent fraying peeling effect. With this question in mind, we intended to examine the comparative mechanisms of the melting (association/dissociation) pathway of the DNA–DNA–DNA (DNA triplex, Fig. 1A) and PNA–DNA–PNA (PNA triplex, Fig. 1B) triplexes as a function of temperature and understand the mechanistic differences in the dynamics of strands involved in DNA and PNA triplexes.
DNA duplexes and the derived triplexes. The two strands at the termini in DNA duplexes are known to breathe making H-bonding weaker at termini12 and exhibit a temperature-dependent fraying peeling effect. With this question in mind, we intended to examine the comparative mechanisms of the melting (association/dissociation) pathway of the DNA–DNA–DNA (DNA triplex, Fig. 1A) and PNA–DNA–PNA (PNA triplex, Fig. 1B) triplexes as a function of temperature and understand the mechanistic differences in the dynamics of strands involved in DNA and PNA triplexes.
To fully understand the PNA melting pathways, it is important to know how different factors contribute to the thermodynamic stability of PNA-involving structures. Hydrogen bonding, electrostatic attraction, hydrophobic charge neutral backbone, strong binding affinity, etc., are the key forces that keep the PNA triplex structures intact at higher temperatures as in DNA triplexes. PNA structures can be melted using various physical and chemical perturbations.13 Thermal stress is a widely used technique for studying the conformational changes of biomolecules. Though a plethora of experimental studies on DNA thermal denaturation exist, these experiments cannot capture microscopic mechanistic changes in the biophysical process. In this context, computational methods would play a complementary role since computer simulations can use moderate to high temperatures to accelerate the unfolding processes that lead to conformational transitions from the triplex to duplex and then to single strands.
PNA forms a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex with DNA to generate the PNA–DNA–PNA triplex,1–3 in which the second PNA strand is the triplex-forming oligonucleotides (TFOs) binding in the major groove of the double helix through Hoogsteen hydrogen bonds to the PNA–DNA WC duplex. PNA
1 complex with DNA to generate the PNA–DNA–PNA triplex,1–3 in which the second PNA strand is the triplex-forming oligonucleotides (TFOs) binding in the major groove of the double helix through Hoogsteen hydrogen bonds to the PNA–DNA WC duplex. PNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DNA duplexes are generally more stable thermally than only DNA/RNA-containing duplexes.2,3 Furthermore, the stability of PNA
DNA duplexes are generally more stable thermally than only DNA/RNA-containing duplexes.2,3 Furthermore, the stability of PNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DNA complexes is unaffected by changes in the salt concentration since the PNA backbone is charge-neutral unlike the polyanionic backbones in DNA
DNA complexes is unaffected by changes in the salt concentration since the PNA backbone is charge-neutral unlike the polyanionic backbones in DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DNA duplexes. At low ionic strength, the stability of DNA–DNA duplexes is reduced due to insufficient neutralization of interstrand charge repulsion. Furthermore, the polyamide backbone in PNA protects it from enzymatic degradation by proteases and nucleases since they are neither peptides nor nucleic acids.4,11
DNA duplexes. At low ionic strength, the stability of DNA–DNA duplexes is reduced due to insufficient neutralization of interstrand charge repulsion. Furthermore, the polyamide backbone in PNA protects it from enzymatic degradation by proteases and nucleases since they are neither peptides nor nucleic acids.4,11
Some MD simulation studies9,13 have shown temperature-induced melting of short 10-mer PNA–PNA, PNA–RNA, and RNA–RNA duplexes. Earlier, we reported force-induced melting of DNA and RNA duplexes using the pulling and unzipping protocol.14,15 Our simulation showed different melting versus emergence of S-form under different pulling protocols.16 A recent simulation work by Chhetri et al.17 through analysis of their molecular mechanical properties showed that PNA-involved duplexes are more flexible and have lower persistence length than analogous pure DNA/RNA duplexes.
Our present work includes both non-protonated and protonated cytosine residues (Fig. 1C and D) on the PNA/DNA TFO strands of the triplex to investigate the specific effects of protonation on the melting behaviour, thermal stability, and binding affinity of the triplexes. The non-protonated DNA triplexes are less stable due to repulsion between anionic charges of the two strands, but C-protonated triplexes are relatively more stable18–20 due to their increased positive charges at N3 positions of cytosine residues, resulting in electrostatic attraction between strands and also cytosine N3 protonation gives rise to the formation of an extra hydrogen bond between the middle strand and the TFO strand. Interestingly, the PNA-containing triplex and duplex13 do not show a terminal fraying–peeling effect, unlike pure DNA duplexes and triplexes. Terminal fraying is the rapid dynamics of hydrogen bonds holding the bases at the terminus, without breaking or complete separation of strands. This is the first step before strand separation, initiated at the terminus. The H-bonds holding the bases are weaker at the terminus, due to a “breathing” effect of H-bonds. With an increase in temperature, this results in a peeling effect, with the third strand separating out slowly. Since HG H-bonds are weaker than WC H-bonds, fraying and peeling in the DNA triplex occur initially with the third strand bound by weaker HG base pairing. Since H-bonds are stronger with PNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DNA duplexes, the HG strand in the PNA–DNA–PNA triplex is also strong, thus minimizing the fraying–peeling effects.
DNA duplexes, the HG strand in the PNA–DNA–PNA triplex is also strong, thus minimizing the fraying–peeling effects.
This may have consequences on the sequential breaking of H-bonds between bases in the PNA duplex and triplex to result in cooperative melting phenomena, wherein most of the base pairs melt near a critical temperature, termed melting temperature. There are many theoretical and experimental studies on DNA duplex melting,21–26 but to date, no simulation studies are available on temperature-induced PNA–DNA–PNA triplex melting. Our present work provides hitherto unobserved molecular behaviour of PNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DNA duplexes and triplexes that give insights into their nanoscale unique melting pathways.
DNA duplexes and triplexes that give insights into their nanoscale unique melting pathways.
2. Methods
2.1. Modeling and simulation details
In this work, we have investigated 18 base triple long PNA–DNA–PNA and DNA–DNA–DNA triplexes with non-protonated and protonated cytosine residues in the TFO strand and their conjugate duplexes for comparison. The initial structure of the 18-mer PNA–DNA–PNA and DNA–DNA–DNA triplexes, the conjugate DNA–DNA and PNA–DNA duplexes of the same sequence were generated using the in-house NAB27 code of AmberTools21.28–30 End-capping of an acetyl (COCH3) group and an amide (NH2) group was done to the PNA's N-terminus and C-terminus, respectively, using the xLEAP module of AMBER20.28 The chosen sequence corresponds to a crystal structure,31 which consisted of a purine strand of DNA in the middle and two complementary pyrimidine strands of PNA. The sequences and other details of all the systems are listed in Table 1.| System | Sequence (18 bp) | Buffer |
|---|---|---|
| DNA–DNA–DNA | 5′-CTTCTTCTCCTCTTCTTC-3′ | 20 Å |
| 3′-GAAGAAGAGGAGAAGAAG-5′ | ||
| 5′-CTTCTTCTCCTCTTCTTC-3′ | ||
| PNA–DNA–PNA | Nter-CTTCTTCTCCTCTTCTTC-Cter | 20 Å |
| 5′-GAAGAAGAGGAGAAGAAG-3′ | ||
| Cter-CTTCTTCTCCTCTTCTTC-Nter | ||
| DNA–DNA | 3′-CTTCTTCTCCTCTTCTTC-3′ | 20 Å |
| 5′-GAAGAAGAGGAGAAGAAG-5′ | ||
| PNA–DNA | Nter-CTTCTTCTCCTCTTCTTC-Cter | 20 Å |
| 5′-GAAGAAGAGGAGAAGAAG-3′ |
We have used a force field developed by Maciej Jasinski et al.32 to describe the bonded and non-bonded interaction of PNA atoms and leaprc.DNA.OL15 for DNA atoms.33,34 Partial charges (RESP)35 for the protonated cytosine residue were generated using Gaussian0936 with the basis set 6-31G* and BL3YP functional. The nucleic acid molecules were then solvated in a cubic box with a buffer length of 20 Å using the TIP3P water model.37,38 As a result, all atoms of the nucleic acid molecule will be 20 Å apart from the edge of the simulation box. All the systems were neutralized by adding an appropriate number of Na+ counter ions to mimic physiological conditions. The interaction of ions with DNA, PNA and water is described using the Joung–Chetham ion parameter set.39 Following that, the energy of the solvated systems was minimized using the steepest descent method for the first 4000 steps, followed by the conjugate gradient method for the next 6000 steps. All of the solute atoms were held fixed by a harmonic potential with a force constant of 500 kcal mol−1 Å−2 so that ions and water molecules can redistribute themselves from their initial ordered configuration to remove the bad contacts between atoms. The positional restraining of nucleic acid atoms was subsequently reduced from 500 kcal mol−1 Å−2 to 5 kcal mol−1 Å−2 in five consecutive stages and finally equilibrated with no restraints.
The systems were then gradually heated in four steps: first, from 10 to 50 K for 6000 MD steps, then, from 50 to 100 K for 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps, then from 100 to 200 K for 10
000 steps, then from 100 to 200 K for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps, from 200 to 300 K for 10
000 steps, from 200 to 300 K for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps and finally at 300 K for another 12
000 steps and finally at 300 K for another 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MD steps. Positional restraints were applied to the heavy atoms of the solute during heating with a force constant of 20 kcal mol−1 Å−2. After heating, the systems were equilibrated for 5 ns in an NPT ensemble with a Berendsen weak coupling method40,41 to adjust the box size with a target pressure of 1 bar. Periodic boundary conditions (PBCs) were used in all three dimensions to intimate bulk solvents. All bonds involving hydrogens were constrained using the Shake algorithm.42,43 This allowed us to use an integration time step of 2 fs. The long-range electrostatic interactions were treated using the Particle Mesh Ewald method44 with a real space cutoff of 10 Å. For the short-range VDW interaction, we have used the same cutoff distance. Following equilibration, the systems were simulated using a Langevin thermostat45,46 with a coupling constant of 1 ps for 200 ns in the NVT ensemble at 300 K.
000 MD steps. Positional restraints were applied to the heavy atoms of the solute during heating with a force constant of 20 kcal mol−1 Å−2. After heating, the systems were equilibrated for 5 ns in an NPT ensemble with a Berendsen weak coupling method40,41 to adjust the box size with a target pressure of 1 bar. Periodic boundary conditions (PBCs) were used in all three dimensions to intimate bulk solvents. All bonds involving hydrogens were constrained using the Shake algorithm.42,43 This allowed us to use an integration time step of 2 fs. The long-range electrostatic interactions were treated using the Particle Mesh Ewald method44 with a real space cutoff of 10 Å. For the short-range VDW interaction, we have used the same cutoff distance. Following equilibration, the systems were simulated using a Langevin thermostat45,46 with a coupling constant of 1 ps for 200 ns in the NVT ensemble at 300 K.
The systems were then simulated at elevated temperatures to study the melting profile using a sequential heating protocol in which the final configuration from the previous temperature run was used as the input to the next higher temperature. Then, the systems were heated from an equilibrated structure to reach different target temperatures. Each step consisted of a 50 ps simulation time with restraints imposed on the nucleic acid atoms with a force constant of 20 kcal mol−1 Å−2. After reaching the target temperature, further equilibration was carried out using the previous protocol, with NVT production runs of 200 ns. The temperature was increased with 20 K increments from 300 to 500 k. Similar simulation methodologies at ambient temperatures have been implemented in some of the previous studies.14,17,47–51
Three sets of statistically independent simulations are carried out with different random seed values for the correct averaging of the calculated properties from the all-atom simulation to ensure that our conclusions are reliable and reproducible. All three runs showed consistent trends and converged towards similar results (RMSD, H-bonds, final structures, etc.) for both DNA–DNA–DNA and PNA–DNA–PNA triplexes. Therefore, we decided to perform MMGBSA and PCA calculations using data from one of the runs only. In addition, we simulated 18 base pair DNA–DNA–DNA and PNA–DNA–PNA triplexes with all TAT base triples to find the effect of the absence of protonated cytosine and sequence dependence; all the details of the TAT triplexes are shown in Fig. S1–S3 and Tables 1–3 in the ESI.† All our trajectories are analyzed with the Visual Molecular Dynamics (VMD),52 CPPTRAJ53 for modelling and the analysis of molecular systems. Xmgrace tool and Python Matpltlib54 libraries were also used to visualize the data and export the figures.
2.2. Binding free energy calculations
Kollman et al. developed the MM–GBSA technique55,56 based on MD simulation of the receptor–ligand complex; it is a popular method for estimating the free energy of ligand binding to receptor sites. The binding free energy estimates the binding affinity and thermodynamic stability of the third strands (TFOs) to its DNA–DNA or PNA–DNA duplex counterpart. The binding free energy of these structures was calculated using the molecular mechanics generalized Born surface area (MMGBSA)56–60 method of AMBER2028 code. The binding free energy of a molecule calculated using the MMGBSA method is the sum of average molecular potential energy, solvation energy and the entropic term TS. The change in binding free energies between two strands of nucleic acids is the difference between these energy terms as given in eqn (1) and (2) of each of the individual strands.| ΔGbinding = ΔEMM + ΔEsolvation − TΔS | (1) |
| ΔEMM = ΔEbonded + ΔEvdW + ΔEelec | (2) |
The binding free energy of a ligand (DNA/PNA TFO) to its receptor (DNA–DNA or PNA–DNA duplex) is the difference in free energy of the ligand and receptor to their complex counterpart as given in eqn (3)
| ΔGbinding = ΔGligand + ΔGreceptor − ΔGcomplex. | (3) |
We used a single trajectory technique for the MMGBSA calculation. In the single-trajectory approach, we assume conformations of each PNA/DNA strand in the duplex or triplex are the same as free DNA/PNA strands in solution, which means that ΔEbonded = 0. The validity of the approach was tested from the MD simulation trajectory in the article by Goodman et al.61
2.3. Free energy landscape (FEL) calculations
The non-hydrogen atoms were chosen from the simulation trajectory to perform Principal Component Analysis (PCA) in each system.62 PCA yields dominant motions, implying conformational alterations of structures in the conformational phase space. Only the first few eigenvectors describe sub-conformational changes in triplex and duplex structures. Eqn (4)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 63,64 estimates Gibbs free energy from the projection population of the first two eigenvectors derived from PCA using the Cpptraj module of AmberTools21 from AMBER20.28 The complex stability is assessed using relative energy minima, with the lower free energy of the complex representing higher conformational stability.
63,64 estimates Gibbs free energy from the projection population of the first two eigenvectors derived from PCA using the Cpptraj module of AmberTools21 from AMBER20.28 The complex stability is assessed using relative energy minima, with the lower free energy of the complex representing higher conformational stability.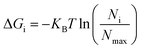 | (4) |
3. Results and discussion
3.1. Root-mean-square-deviation (RMSD)
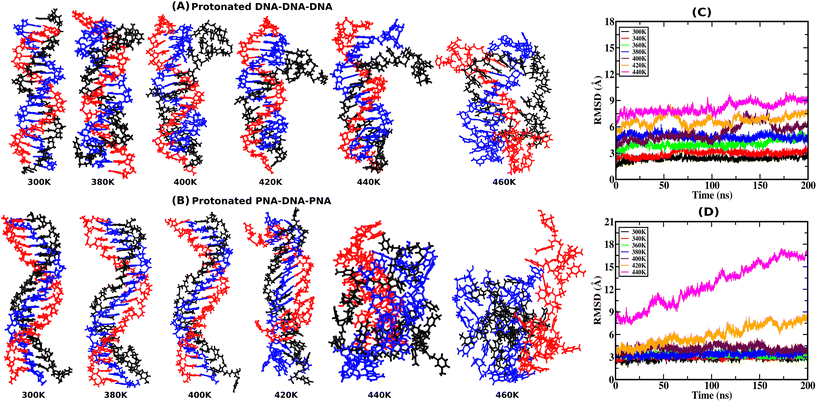
RMSD provides atomistic insights into structural stability and conformational changes from the 200 ns-long simulation trajectory of the protonated triplex structures. Instantaneous snapshots of final structures from one of the three independent simulation trajectories are shown in Fig. 2(A and B) at ambient and elevated temperatures for protonated triplexes. The final snapshots from the other two simulation runs are added in the ESI, in Fig. S4 and S5.† RMSD was calculated by comparing the positions of all non-hydrogen atoms in the MD trajectory to that in a reference (initial energy minimized) structure at ambient and elevated temperatures. Lower RMSD values with plateaus imply that the structures are very stable and do not undergo major conformational changes during the simulation, even at elevated temperatures up to 360 K for the DNA triplex and 400 K for the PNA triplex, respectively, as shown in Fig. 2(C and D). A significant increase in RMSD values near certain temperatures suggests conformational changes or structural disturbances. At lower temperatures (300 K), RMSD reaches close to 3 Å after the first 5 ns, indicating that PNA/DNA triplexes remain closer to their native configurations. Because of its flexibility, PNA–TFO occupies a favourable position in the major groove of the PNA–DNA duplex during dynamics, resulting in a more stable PNA triplex than the DNA triplex. RMSDs of the PNA–DNA–PNA triplex increase dramatically from 420 K onwards, suggesting the cooperative melting nature of the PNA triplex at higher temperatures, as shown in Fig. 2D. The RMSD of the DNA triplex reaches close to 4 Å after the first 5 ns at 360 K, which suggests terminal fraying. After sufficient simulation time, DNA triplexes at 360 K and higher temperatures tend to form different non-canonical conformations, leading to the eventual separation of DNA–TFO from the duplex. The RMSD of the DNA triplex increases sequentially from the start of the simulations from 360 K onwards, as shown in Fig. 2C. However, the RMSDs of the PNA triplexes are generally steady close to 2.5–3.5 Å up to a 400 K temperature. Stable RMSD values indicate that the PNA triplex, unlike the DNA triplex, does not undergo significant structural changes for temperatures up to 400 K. Their RMSD suddenly increases to a higher value from 420 K onwards, suggesting that the PNA triplex melts cooperatively in a one-step process at a higher temperature, as opposed to the DNA triplex's sequential terminal melting. The time-averaged RMSD values from all three independent runs are listed in Table 4 in the ESI.†3.2. Hydrogen bond analysis with temperature
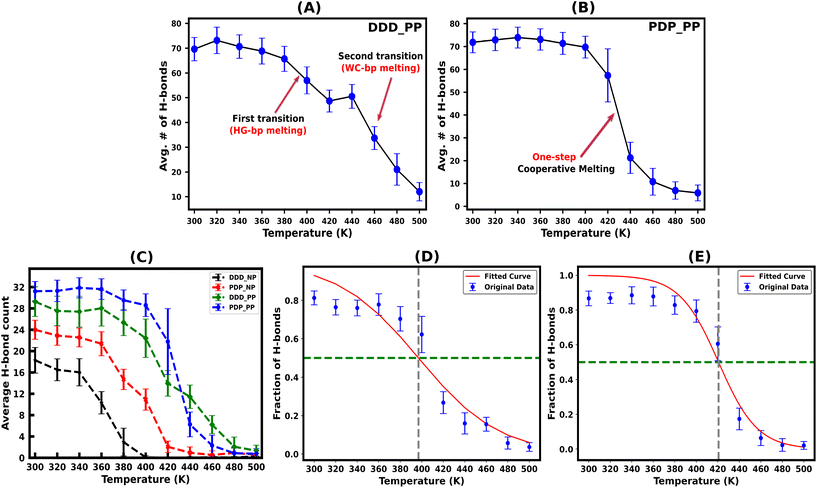
Hydrogen bonds are the primary forces, holding the Watson–Crick (WC) and Hoogsteen (HG) base pairs in duplex and triplex nucleic acid structures, respectively. During the melting transition, the initial rupture of the weaker HG hydrogen bond destabilizes triplex structures. The average number of total (WC + HG) hydrogen bonds for both protonated and non-protonated DNA and PNA triplexes, obtained from the simulation trajectory using a distance cut-off of 3.5 Å and an angle cut-off of 120° as recommended by IUPAC,50,65 are shown in Fig. 3(A–C). The charge-neutral peptide backbone of PNA–TFO is more flexible than DNA–TFO; as a result, PNA–TFO fits into the major groove of the PNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DNA duplex with greater binding affinity than DNA–TFO in the DNA
DNA duplex with greater binding affinity than DNA–TFO in the DNA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DNA duplex.
DNA duplex.
The protonated PNA triplex shows a slightly higher number of stable hydrogen bonds, closely approximating the initial structure at ambient and higher temperatures up to 400 K. On the other hand, even at ambient temperature (300 K), the protonated DNA triplex exhibits well-known terminal frayed-peeling effects in a stochastic back-and-forth pattern, which propagates towards the centre in a zipper-like fashion with the increase in temperature. This leads to the separation of the DNA–TFO strand as the first step of sequential melting. Our trajectory analysis reveals that the PNA-containing triplex lacking the terminal fraying–peeling effect melts cooperatively in a one-step process near melting temperature, while the DNA triplex melts sequentially from termini to the center in two steps, with the third strand separating first (DNA–TFO strand), followed by the corresponding WC duplex melting (Fig. 3A and B). The two-step sequential melting is prominent in the non-protonated A–T rich DNA triplex with A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T base pairs held by only two H-bonds and the absence of a positively charged cytosine residue in the TFO strand (Fig. S6, ESI†).
T base pairs held by only two H-bonds and the absence of a positively charged cytosine residue in the TFO strand (Fig. S6, ESI†).
Our work shows that most hydrogen bonds in the protonated PNA triplex have a sharp melting transition with less fluctuation near the melting temperature (Fig. 3B), implying that the more stable PNA triplex melts cooperatively. The remaining portion of the discussion will focus on the protonated triplex results because non-protonated triplexes are highly unstable, as has also been observed experimentally for DNA triplexes.18,66–68
We subsequently investigated the fraction of HG hydrogen bonds (f) as a function of temperature (T) for the protonated triplexes. The resulting melting curves indicated two-state melting transitions between the folded and melted states of the TFO strands. The two-state melting transitions were modelled for TFOs using a logistic function13 as shown in Fig. 3(D and E), presented in eqn (5):
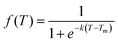 | (5) |
| Melting temp. | DNA–DNA–DNA | PNA–DNA–PNA |
|---|---|---|
| T m [f(Tm) = 0.5] [K] | 396.68 | 420.69 |
| T m (ΔG = 0) [K] | 364.50 | 425.65 |
3.3. Binding free energy
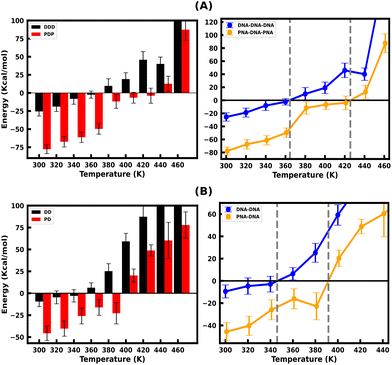
Since the DNA and PNA triplex melting process is primarily a thermal energy-driven process, we examined the thermodynamic properties to quantify the thermal stability of triplexes and also the binding affinity of TFOs to their WC duplex counterpart. The comparison between the binding free energies of separated strands and intact triplexes or duplexes (Fig. S7, ESI†) also established an association between the binding free energy and thermal melting. The binding affinity of DNA–TFO and PNA–TFO at ambient and elevated temperatures also reflects how thermal stability is related to the melting of nucleic acid structures. This analysis, in turn, can shed some light on the thermodynamics of the melting process.We performed MMGBSA analysis of the intact and melted triplex and duplex structures using the last 100 ns of the 200 ns long simulation trajectory to calculate the binding free energy ΔGbinding at different temperatures. For the binding energy calculation, the triplex is treated as a complex, the PNA–DNA or DNA–DNA WC duplex is treated as a receptor, and the third strand (DNA–TFO or PNA–TFO) is treated as a ligand. Thus, the binding affinities of DNA–TFO and PNA–TFO to the WC duplexes with HG base pairing were estimated and are listed in Tables 3 and 4.
| Component | DNA–DNA–DNA | PNA–DNA–PNA |
|---|---|---|
| van der Waals | −183.3922 (9.59) | −200.9966 (8.05) |
| Electrostatic | 4043.6857 (60.67) | −2770.8970 (39.81) |
| Generalized Born | −3919.1861 (56.42) | 2755.5958 (38.08) |
| Surface | −18.3963 (0.59) | −17.2203 (0.51) |
| ΔGgas | 3860.2935 (57.51) | −2971.8936 (38.98) |
| ΔGSolvation | −3937.5825 (56.54) | 2738.3755 (38.05) |
| ΔGBinding | −25.53 (6.46) | −77.74 (6.10) |
| Temperature (K) | DNA–DNA–DNA | PNA–DNA–PNA |
|---|---|---|
| 300 | −25.53 (6.46) | −77.74 (6.10) |
| 320 | −18.85 (6.86) | −67.37 (7.36) |
| 340 | −8.11 (7.52) | −61.23 (7.13) |
| 360 | −2.39 (4.91) | −49.64 (7.28) |
| 380 | 9.74 (9.79) | −11.76 (11.51) |
| 400 | 19.08 (8.82) | −6.58 (7.50) |
| 420 | 45.85 (11.10) | −3.85 (10.49) |
| 440 | 40.04 (9.51) | 12.69 (10.04) |
| 460 | 192.37 (21.45) | 87.36 (14.46) |
The binding free energy of protonated PNA–TFO to the PNA–DNA duplex is −77.74 kcal mol−1 at 300 K, while that of protonated DNA–TFO to the DNA–DNA duplex is −25.53 kcal mol−1, indicating that the protonated PNA triplex is energetically more favourable (stable) than the DNA triplex. The details of the MMGBSA energy components at 300 K are listed in Table 3, which shows significant electrostatic repulsion for the negatively charged DNA–TFO strand and strong electrostatic attraction for the charge neutral PNA–TFO strand. Thus, the PNA–TFO binds to the PNA–DNA duplex in a sequence-specific manner to create a strong triplex due to its higher structural flexibility, charge-neutral backbone, and stronger stacking interactions with non-neighbouring bases.69 The positive binding free energy (less triplex stability) of the DNA–TFO in a protonated DNA triplex at higher temperatures of 380 K and above is due to the repulsion between polyanionic charges on DNA strands as shown in Table 4. The stability of the DNA–TFO may be affected by the protonation state of the cytosine bases involved in HG base pairing. In non-protonated triplexes, the electrostatic repulsion between the negatively charged phosphate backbone and the overall negative charge density makes it less favourable from 300 K onwards, with lower triplex stabilisation. The base protonation also seems to influence the specificity and strength of hydrogen bonding between the bases in the triplex by adding one extra hydrogen bond at the N3 position of cytosine residues.
These results suggest that the protonated PNA–TFO has higher binding affinity at ambient and elevated temperatures, which means that PNA–TFO has increased stability during the interaction with the WC duplex, whereas the lower binding affinity of the DNA–TFO at ambient and elevated temperatures suggests that the triplex formation with DNA–TFO is thermodynamically not as favourable to form a DNA triplex, as that of PNA–TFO to form a PNA triplex.
Fig. 4(A and B) depicts the binding free energy (ΔGbinding) as a function of the simulation temperature, allowing the extraction of melting temperatures Tm based on the condition of ΔGbinding = 0 for the protonated TFOs and Watson–Crick duplexes of the same sequence. Table 2 shows the calculated melting temperature (Tm) using eqn (5) and the ΔGbinding = 0 condition, indicating the order of thermal stability of the protonated triplexes is PNA–DNA–PNA > DNA–DNA–DNA.
The non-protonated DNA–TFO does not bind with the DNA–DNA WC duplex counterpart to create a stable DNA triplex at ambient and elevated temperatures, while PNA–TFO generates a relatively stable triplex even in non-protonated form (only at lower temperatures). In addition to unfavourable electrostatic repulsion between negatively charged DNA strands, the structural conformation of nucleotides is another key cause of triplex destabilization. Nucleic acids (PNAs) with electrically neutral backbones instead of negatively charged backbones effectively overcome this constraint. The absence of the sugar ring in PNA strands makes it a better choice for overcoming this destabilization constraint.
3.4. Principal component analysis
Principal Component Analysis (PCA) is used to assess the atomic motions of molecules by reducing the large number of degrees of freedom. PCA constructs a covariance matrix for PC analysis using a time series of cartesian atom coordinates. The eigenvectors are primary components or modes; they define the melting properties of the triplex structures, while the eigenvalues provide details on the deformability of structures along these motions. The first few principal components typically span 90% of the MD trajectory in reduced dimensional space (Fig. S8(A–D), ESI†). Hence, we consider only the first five principal components to visualise the protonated DNA and PNA triplex's structural changes during the sequential and cooperative melting process with increasing temperature.The normalized projection population histograms along the first five principal components for the protonated DNA and PNA triplexes are shown in Fig. S9(A and B), ESI,† respectively. The first principal component (PC1), with a bimodal probability distribution and wider span along the principal component projection, describes most of the significant conformational changes sequentially of the protonated DNA triplex structures from 360 K onwards during the melting process. The other higher-order components (PC2, PC3, PC4, and PC5) show unimodal probability distributions, indicate smaller conformational changes, and are considered as constrained motion due to their very low contribution. On the other hand, the protonated PNA triplex exhibits a wider span along PC1's projection only near the melting temperature (∼420 K), and at lower temperatures of up to 400 K, they maintain stable triplex structures with unimodal probability distributions and narrow span along the projection. Hence, the prevailing mode of motion demonstrates that PNA triplexes dissociate in a single step, compared to the sequential dissociation of DNA triplexes.
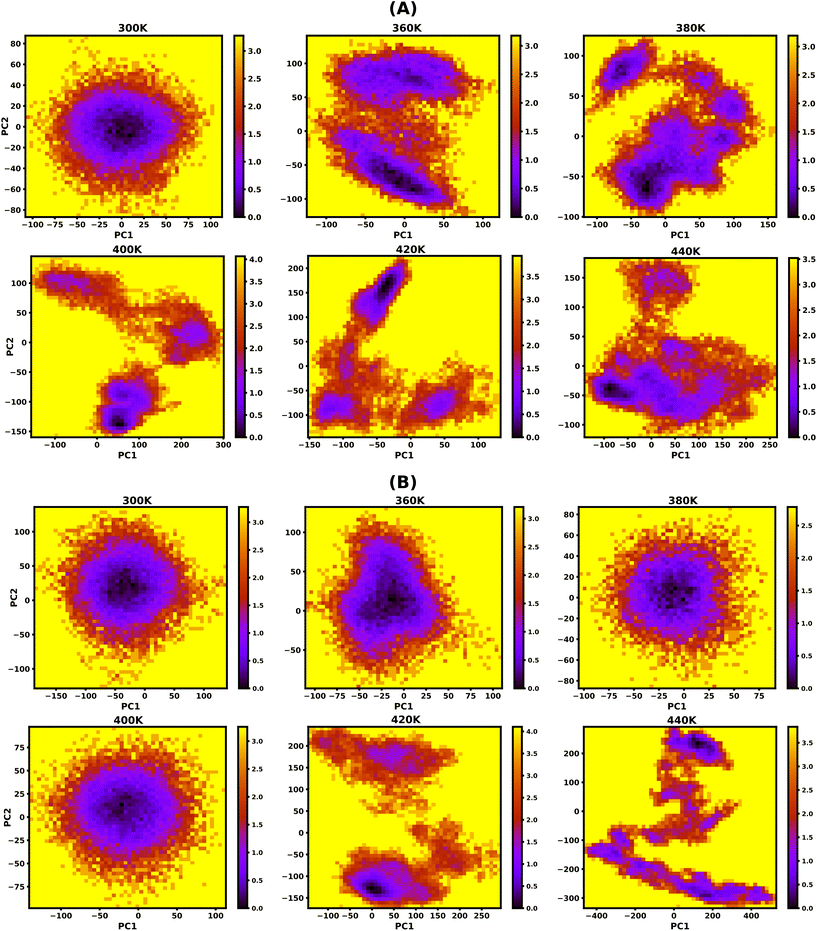
3.5. Free energy landscape (FEL)
To study the effect of temperature on conformational stability and denaturation, Gibbs's free energy landscape (FEL) was evaluated using PC1 and PC2 eigenvectors from PCA using the last 100 ns of the 200 ns long simulation trajectory. The degree of dispersion of the global and local energy minima in the FEL plots clearly shows the sequential and cooperative melting nature of the protonated DNA and PNA triplexes. The existence of several local energy minima in tiny patches in the conformational space of the DNA triplex, from 360 K onwards, indicates significant sequential dissociation from both terminals as shown in Fig. 5A. On the other hand, a compact global energy minimum basin is observed for the protonated PNA triplex up to 400 K, displayed by deep violet, as shown in Fig. 5B, indicating intact PNA triplex structures. This observation also supports our previous findings from the hydrogen bond, RMSD, and PCA analyses, which demonstrate the PNA triplex structures are extremely stable up to 400 K. The protonated PNA triplex also shows multiple metastable local energy minima with tiny patches only near melting temperature (∼420 K), which explores a wider range of conformational space, indicating their single-step cooperative melting as shown in Fig. 5B.3.6. Stiffness
At temperature T, the bending stiffness (Si) corresponds to the ith principal components given using eqn (6).17,70 We observed that stiffness from PCA of DNA and PNA triplexes show different denaturation patterns. The dissociation characteristics of the structures are directly shown by the first principal component eigenvalues (Fig. S10(A–D), ESI†). For the protonated DNA and PNA triplex, the eigenvalues and stiffness of the first three principal components at different temperatures are listed in Tables 5 and 6, respectively.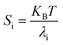 | (6) |
| Modes | Temp. (K) | Eig. value (λi) (Å2) | Stiffness (Si) (10−4 kcal mol−1 Å2) | Temp. (K) | Eig. value (λi) (Å2) | Stiffness (Si) (10−4 kcal mol−1 Å2) |
|---|---|---|---|---|---|---|
| I | 300 | 581.51 | 10.25 | 400 | 881.70 | 9.01 |
| II | 425.26 | 14.01 | 700.90 | 11.34 | ||
| III | 165.04 | 36.12 | 427.64 | 18.58 | ||
| I | 360 | 497.65 | 14.37 | 420 | 1102.35 | 7.57 |
| II | 489.55 | 14.61 | 798.53 | 10.75 | ||
| III | 182.96 | 39.06 | 636.88 | 13.10 | ||
| I | 380 | 773.14 | 9.76 | 440 | 1023.18 | 8.54 |
| II | 478.40 | 15.78 | 743.07 | 11.76 | ||
| III | 320.19 | 23.58 | 491.89 | 17.77 |
| Modes | Temp. (K) | Eig. value (λi) (Å2) | Stiffness (Si) (10−4 kcal mol−1 Å2) | Temp. (K) | Eig. value (λi) (Å2) | Stiffness (Si) (10−4 kcal mol−1 Å2) |
|---|---|---|---|---|---|---|
| I | 300 | 1011.18 | 5.89 | 400 | 638.84 | 12.44 |
| II | 640.30 | 9.31 | 433.15 | 18.35 | ||
| III | 463.32 | 12.86 | 344.12 | 23.09 | ||
| I | 360 | 620.77 | 11.52 | 420 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 991.01 991.01 |
0.75 |
| II | 393.20 | 18.19 | 2062.56 | 4.04 | ||
| III | 278.59 | 25.67 | 1825.03 | 4.57 | ||
| I | 380 | 962.32 | 7.84 | 440 | 59![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 281.38 281.38 |
0.14 |
| II | 405.59 | 18.61 | 7422.97 | 1.17 | ||
| III | 348.10 | 21.69 | 5949.91 | 1.46 |
The protonated PNA triplex's stiffness drops dramatically to an extremely low value near melting temperature (∼420 K), indicating that the PNA triplex will adopt unstable conformations and cause cooperative melting in a single step because of its charge-neutral and hydrophobic backbone. On the other hand, the protonated DNA triplex maintains stiffer structures during the terminal fraying–peeling and sequential dissociation processes because of the repulsion from the negatively charged backbones, which prevents the stiffness of the DNA triplexes from decreasing to an abnormally low value with an increase in temperature.
4. Conclusion
The temperature-dependent melting pathway and thermodynamic stability of the 18-base pair protonated and non-protonated DNA–DNA–DNA and PNA–DNA–PNA triplexes, as well as the 18-mer DNA–DNA and PNA–DNA duplexes of the same sequence, were investigated using molecular dynamics simulations based on a recently developed PNA force field32 for few hundreds of ns at ambient and elevated temperatures.This provided important insights into the conformational dynamics and local behavior of nucleic acid structures during melting by a thorough analysis of the binding free energy, hydrogen bond, RMSD, PCA, FEL and temperature profiles. The temperature-induced MD simulation of the PNA triplexes is reported here for the first time. The trend of sequential melting of DNA–TFO in the DNA triplex versus cooperative melting of PNA–TFO in the PNA triplex is revealed by the analysis of the simulation trajectory and two-state melting transition model. At temperatures above 360 K, our structural study reveals that the DNA triplex melts sequentially from termini to center in a zipper-like pattern. At temperatures above 420 K, the PNA triplex melts as a complete fragment with a sharp melting transition in a cooperative melting process. Thus, our findings help decipher the local melting of PNA–TFO triplexes, which are important in understanding and tuning the bio-relevant functional properties (diagnostic and hybridization) for the application of PNA as biosensors and molecular hybridization probes, and in the distant future as antisense and antigene agents.
It is shown that 44% protonated cytosine residues in the pyrimidine-rich TFO strand preferentially attach to the major groove of the corresponding duplex and become thermally more stable compared to their non-protonated counterpart. This suggests that the more flexible and charge-neutral PNA–TFO attaches to PNA–DNA duplexes with high affinity to construct stable PNA triplexes. The PNA triplex melts as a whole fragment in one step near the melting temperature (cooperative melting). On the other hand, the DNA triplex, being stiffer and less stable due to its negatively charged backbone, melts with a fraying–peeling effect from the terminus to the center sequentially in a zipper-like pattern at lower temperatures than the PNA triplex.
For assessing the correct ability of the charge-neutral PNA strands to interact with charged DNA strands in PNA–DNA–PNA triplexes, the degrees of freedom of individual strands must be understood. Specifically, the base sequence, functionalization with various moieties, and backbone flexibility are important for binding/denaturation with the intended target. According to a recent study, the unmodified ssPNA strand does not adopt conformations that facilitate hybridization with nucleic acid strands.71 Verona and co-workers found that the backbone-modified ssPNA structure has a stable helical conformation and can easily attach to DNA/RNA target strands, supporting findings from experiments also.71 Their study reveals a fine balance between entropy effects and the enthalpy contribution produced by intra-strand base stacking, which leads the sequence to fold chaotically for single-stranded PNAs. Regarding the conformational freedom of a PNA strand, the unmodified ssPNA (used in our work) and the modified ssPNA exhibit significantly different sequential and non-sequential base stackings. In particular, low sequential stacking between the bases is a characteristic of ssPNA, which assumes preferably folded conditions. On the other hand, backbone-modified ssPNA exhibits a greater stable conformation through sequential base stacking to produce helical conformations. In the future, it will be interesting to investigate the J, L, and R modifications of PNA bases in place of protonated cytosine to see how they affect binding selectivity with DNA/RNA strands and the triplex melting behaviour.72 The above explanation supports our hypothesis that the unmodified PNA strand is substantially more flexible and has a lower helical propensity than DNA strands. As a result, after the PNA–DNA–PNA triplex melts in a single step (sharp decrease in H-bonds), the individual strands quickly form compact globular structures due to non-sequential (between non-neighbouring intra-strand bases) base stacking interactions and hydrophobic backbones of PNA strands. This could be the possible reason that their final structure resembles shape deformations without melting.
While the major objective of this work was to investigate the origin of sequential melting of DNA triplexes and cooperative single-step melting of PNA triplexes, the study has also provided the atomic details of the third strand TFO's thermal stability, melting mechanism, and binding affinities. The present work has led to a better understanding of the melting mechanism of PNA-derived duplexes and triplexes and the origin of their thermodynamic stability. It may help in developing more physical and realistic approaches to designing PNA-based nanostructures and biotechnological applications.73,74 PNA or DNA triplexes can produce complex nanostructures with programmable forms and sizes. Very recently, new analogs of PNA termed bimodal/janus PNAs have been reported,75–77 which can bind to two different complementary DNA/RNA sequences generating polyplexes composed of fused double duplexes75 and triplex of duplexes,76,77 which show a synergistic enhancement of thermal stabilities of both duplexes and triplexes. Such dual enhancement of stabilities involves intricate interactions between the duplex and triplex components. The present work is a precursor to understanding and developing models for the melting behavior of such fused polyplexes and derived complex nanostructures. The ultimate goal is to understand the behavior and dynamics of interactions in more intricate self-assembly and disassembly of nanostructures toward their applications for constructing nucleic acid based functional nanodevices.78–83
Data availability
The simulation data used in this study are available in the Zenodo database in ref – https://doi.org/10.5281/zenodo.11222188.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are thankful to Dr Khadka B. Chhetri and Dr Supriyo Naskar for their valuable suggestions. S. M. acknowledges the SRF fellowship from the CSIR, India. We thank the DAE, India, for the financial support. We also thank SERB, India, IRHPA (No. IPA/2020/000034), for funding.References
- P. E. Nielsen, M. Egholm, R. H. Berg and O. Buchardt, Science, 1991, 254, 1497–1500 CrossRef CAS PubMed.
- P. E. Nielsen, Peptide nucleic acids: protocols and applications, Garland Science, 2004 Search PubMed.
- M. Egholm, O. Buchardt, L. Christensen, C. Behrens, S. M. Freier, D. A. Driver, R. H. Berg, S. K. Kim, B. Norden and P. E. Nielsen, Nature, 1993, 365, 566–568 CrossRef CAS PubMed.
- K. E. Lundin, L. Good, R. Strömberg, A. Gräslund and C. E. Smith, Adv. Genet., 2006, 56, 1–51 CAS.
- J. Saarbach, P. M. Sabale and N. Winssinger, Curr. Opin. Chem. Biol., 2019, 52, 112–124 CrossRef CAS PubMed.
- V. MacLelland, M. Kravitz and A. Gupta, Mol. Ther.–Nucleic Acids, 2023, 35, 102086 CrossRef PubMed.
- K.-Y. Wong and B. M. Pettitt, Biophys. J., 2008, 95, 5618–5626 CrossRef CAS PubMed.
- A. Perez and M. Orozco, Angew. Chem., Int. Ed., 2010, 49, 4805–4808 CrossRef CAS PubMed.
- S. Kundu, S. Mukherjee and D. Bhattacharyya, J. Biosci., 2012, 37, 445–455 CrossRef CAS PubMed.
- M. Zgarbová, M. Otyepka, J. Šponer, F. Lankaš and P. Jurečka, J. Chem. Theory Comput., 2014, 10, 3177–3189 CrossRef PubMed.
- V. V. Demidov, V. N. Potaman, M. Frank-Kamenetskil, M. Egholm, O. Buchard, S. H. Sönnichsen and P. E. Nlelsen, Biochem. Pharmacol., 1994, 48, 1310–1313 CrossRef CAS PubMed.
- W. Saenger and W. Saenger, Principles of nucleic acid structure, 1984, pp. 9–28 Search PubMed.
- M. Jasinski, J. Miszkiewicz, M. Feig and J. Trylska, J. Phys. Chem. B, 2019, 123, 8168–8177 CrossRef CAS PubMed.
- M. Santosh and P. K. Maiti, J. Phys.: Condens. Matter, 2008, 21, 034113 CrossRef PubMed.
- A. Aggarwal, S. Bag and P. K. Maiti, Phys. Chem. Chem. Phys., 2018, 20, 28920–28928 RSC.
- A. Garai, S. Mogurampelly, S. Bag and P. K. Maiti, J. Chem. Phys., 2017, 147, 225102 CrossRef PubMed.
- K. B. Chhetri, A. Sharma, S. Naskar and P. K. Maiti, Nanoscale, 2022, 14, 6620–6635 RSC.
- M. Dalla Pozza, A. Abdullrahman, C. J. Cardin, G. Gasser and J. P. Hall, Chem. Sci., 2022, 13, 10193–10215 RSC.
- C. E. Carr, R. Ganugula, R. Shikiya, A. M. Soto and L. A. Marky, Biochimie, 2018, 146, 156–165 CrossRef CAS PubMed.
- C. C. Hardin, M. Corregan, B. A. Brown and L. N. Frederick, Biochemistry, 1993, 32, 5870–5880 CrossRef CAS PubMed.
- I. Rouzina and V. A. Bloomfield, Biophys. J., 2001, 80, 894–900 CrossRef CAS PubMed.
- J. A. Bueren-Calabuig, C. Giraudon, C. M. Galmarini, J. M. Egly and F. Gago, Nucleic Acids Res., 2011, 39, 8248–8257 CrossRef CAS PubMed.
- C. Schildkraut and S. Lifson, Biopolymers, 1965, 3, 195–208 CrossRef CAS PubMed.
- C. J. Wienken, P. Baaske, S. Duhr and D. Braun, Nucleic Acids Res., 2011, 39, e52–e52 CrossRef CAS PubMed.
- J. G. Duguid, V. A. Bloomfield, J. M. Benevides and G. Thomas, Biophys. J., 1996, 71, 3350–3360 CrossRef CAS PubMed.
- E. A. Galburt, E. Tomko, W. Stump and A. R. Manzano, Biophys. Chem., 2014, 187, 23–28 CrossRef PubMed.
- T. J. Macke and D. A. Case, Modeling unusual nucleic acid structures, 1998 Search PubMed.
- D. A. Case, H. M. Aktulga, K. Belfon, I. Ben-Shalom, S. R. Brozell, D. S. Cerutti, T. E. Cheatham III, V. W. D. Cruzeiro, T. A. Darden and R. E. Duke, et al., Amber 2021, University of California, San Francisco, 2021 Search PubMed.
- R. Salomon-Ferrer, D. Case and R. Walker, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 198–210 CAS.
- T. E. Cheatham III and D. A. Case, Biopolymers, 2013, 99, 969–977 CrossRef PubMed.
- L. Betts, J. A. Josey, J. M. Veal and S. R. Jordan, Science, 1995, 270, 1838–1841 CrossRef CAS PubMed.
- M. Jasinski, M. Feig and J. Trylska, J. Chem. Theory Comput., 2018, 14, 3603–3620 CrossRef CAS PubMed.
- A. Pérez, I. Marchán, D. Svozil, J. Sponer, T. E. Cheatham III, C. A. Laughton and M. Orozco, Biophys. J., 2007, 92, 3817–3829 CrossRef PubMed.
- M. Zgarbová, J. Sponer, M. Otyepka, T. E. Cheatham III, R. Galindo-Murillo and P. Jurecka, J. Chem. Theory Comput., 2015, 11, 5723–5736 CrossRef PubMed.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280 CrossRef CAS.
- M. Caricato, J. Hiscocks and M. J. Frisch, Gaussian 09: IOps Reference, 2009 Search PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- P. Mark and L. Nilsson, J. Phys. Chem. A, 2001, 105, 9954–9960 CrossRef CAS.
- I. S. Joung and T. E. Chetham III, J. Phys. Chem. B, 2008, 112, 9020–9041 CrossRef CAS PubMed.
- H. J. Berendsen, J. V. Postma, W. F. Van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- P. Hünenberger, C. Holm and K. Kremer, Adv. Polym. Sci., 2005, 173, 105–149 CrossRef.
- V. Kräutler, W. F. Van Gunsteren and P. H. Hünenberger, J. Comput. Chem., 2001, 22, 501–508 CrossRef.
- J.-P. Ryckaert, G. Ciccotti and H. J. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- R. L. Davidchack, R. Handel and M. Tretyakov, J. Chem. Phys., 2009, 130, 234101 CrossRef PubMed.
- W. F. Van Gunsteren and H. J. Berendsen, Mol. Simul., 1988, 1, 173–185 CrossRef.
- R. Singh, K. Kansara, S. Mandal, R. Varshney, S. Gupt, A. Kumar, P. K. Maiti and D. Bhatia, bioRxiv, 2023, 2023–2009 Search PubMed.
- P. Kumbhakar, I. D. Jana, S. Basu, S. Mandal, S. Banerjee, S. Roy, C. C. Gowda, A. Chakraborty, A. Pramanik and P. Lahiri, et al. , Phys. Chem. Chem. Phys., 2023, 25, 17143–17153 RSC.
- S. Naskar, H. Joshi, B. Chakraborty, N. C. Seeman and P. K. Maiti, Nanoscale, 2019, 11, 14863–14878 RSC.
- S. Naskar, M. Gosika, H. Joshi and P. K. Maiti, J. Phys. Chem. C, 2019, 123, 9461–9470 CrossRef CAS.
- H. Joshi, A. Kaushik, N. C. Seeman and P. K. Maiti, ACS Nano, 2016, 10, 7780–7791 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- D. R. Roe and T. E. Cheatham III, J. Chem. Theory Comput., 2013, 9, 3084–3095 CrossRef CAS PubMed.
- J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95 Search PubMed.
- P. A. Kollman, I. Massova, C. Reyes, B. Kuhn, S. Huo, L. Chong, M. Lee, T. Lee, Y. Duan and W. Wang, et al. , Acc. Chem. Res., 2000, 33, 889–897 CrossRef CAS PubMed.
- J. Srinivasan, T. E. Cheatham, P. Cieplak, P. A. Kollman and D. A. Case, J. Am. Chem. Soc., 1998, 120, 9401–9409 CrossRef CAS.
- H. Gohlke and D. A. Case, J. Comput. Chem., 2004, 25, 238–250 CrossRef CAS PubMed.
- M. S. Lee, F. R. Salsbury Jr and C. L. Brooks III, J. Chem. Phys., 2002, 116, 10606–10614 CrossRef CAS.
- M. S. Lee, M. Feig, F. R. Salsbury Jr and C. L. Brooks III, J. Comput. Chem., 2003, 24, 1348–1356 CrossRef CAS PubMed.
- D. Sitkoff, K. A. Sharp and B. Honig, J. Phys. Chem., 1994, 98, 1978–1988 CrossRef CAS.
- J. Goodman, D. Attwood, J. Kiely, P. Coladas Mato and R. Luxton, J. Phys. Chem. B, 2022, 126, 9528–9538 CrossRef CAS PubMed.
- H. Abdi, L. J. Williams and D. Valentin, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 5, 149–179 CrossRef.
- H. Frauenfelder, S. G. Sligar and P. G. Wolynes, Science, 1991, 254, 1598–1603 CrossRef CAS PubMed.
- M. F. Sk, R. Roy, N. A. Jonniya, S. Poddar and P. Kar, J. Biomol. Struct. Dyn., 2021, 39, 3649–3661 CrossRef CAS PubMed.
- E. Arunan, G. R. Desiraju, R. A. Klein, J. Sadlej, S. Scheiner, I. Alkorta, D. C. Clary, R. H. Crabtree, J. J. Dannenberg and P. Hobza, et al. , Pure Appl. Chem., 2011, 83, 1637–1641 CrossRef CAS.
- L. Petraccone, E. Erra, C. A. Mattia, V. Fedullo, G. Barone and C. Giancola, Biophys. Chem., 2004, 110, 73–81 CrossRef CAS PubMed.
- J. Volker and H. H. Klump, Biochemistry, 1994, 33, 13502–13508 CrossRef CAS PubMed.
- B. J. Boehm, C. Whidborne, A. L. Button, T. L. Pukala and D. M. Huang, Phys. Chem. Chem. Phys., 2018, 20, 14013–14023 RSC.
- T. Pienko, A. J. Wierzba, M. Wojciechowska, D. Gryko and J. Trylska, J. Phys. Chem. B, 2017, 121, 2968–2979 CrossRef CAS PubMed.
- A. Perez, A. Noy, F. Lankas, F. J. Luque and M. Orozco, Nucleic Acids Res., 2004, 32, 6144–6151 CrossRef CAS PubMed.
- M. D. Verona, V. Verdolino, F. Palazzesi and R. Corradini, Sci. Rep., 2017, 7, 42799 CrossRef CAS PubMed.
- X. Zhan, L. Deng and G. Chen, Biopolymers, 2022, 113, e23476 CrossRef CAS PubMed.
- S. Sarkar, Biopolymers, 2024, 115, e23567 CrossRef CAS PubMed.
- K. R. Singh, P. Sridevi and R. P. Singh, Eng. Rep., 2020, 2, e12238 CrossRef CAS PubMed.
- M. K. Gupta, B. R. Madhanagopal, D. Datta and K. N. Ganesh, Org. Lett., 2020, 22, 5255–5260 CrossRef CAS PubMed.
- P. Bhingardeve, B. R. Madhanagopal and K. N. Ganesh, J. Org. Chem., 2020, 85, 13680–13693 CrossRef CAS PubMed.
- M. K. Gupta, B. R. Madhanagopal and K. N. Ganesh, J. Org. Chem., 2020, 86, 414–428 CrossRef PubMed.
- X. Chen, B. Yan and G. Yao, Nanotechnology, 2023, 34, 172002 CrossRef PubMed.
- U. Singh, V. Morya, B. Datta, C. Ghoroi and D. Bhatia, Front. Chem., 2021, 9, 704234 CrossRef CAS PubMed.
- M. Vinther and J. Kjems, New J. Phys., 2016, 18, 085005 CrossRef.
- M. Qi, P. Shi, X. Zhang, S. Cui, Y. Liu, S. Zhou and Q. Zhang, RSC Adv., 2023, 13, 9864–9870 RSC.
- T. Li, D. Ackermann, A. M. Hall and M. Famulok, J. Am. Chem. Soc., 2012, 134, 3508–3516 CrossRef CAS PubMed.
- Y. Zhao, A. R. Chandrasekaran, D. A. Rusling, K. Woloszyn, Y. Hao, C. Hernandez, S. Vecchioni, Y. P. Ohayon, C. Mao and N. C. Seeman, et al. , J. Am. Chem. Soc., 2023, 145, 3599–3605 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr01104j |
| This journal is © The Royal Society of Chemistry 2024 |