Evidence of carrier diffusion between emission states in CdSe/ZnS core–shell quantum dots: a comprehensive investigation combining fluorescence lifetime correlation spectroscopy (FLCS) and single dot photoluminescence studies

Abstract

Investigation of carrier dynamics in CdSe/ZnS core–shell quantum dots (QDs) is performed using fluorescence-lifetime-correlation-spectroscopy (FLCS) and single-dot PL blinking studies. The origin of an emitted photon from a QD in an FLCS study is assigned to either an exciton state or trap state based on its excited state lifetime (τ_fl). Subsequently, two intrastate autocorrelation functions (ACFs) representing the exciton and trap states and one cross-correlation function (CCF) coupling these two states are constructed. Interestingly, the timescales of carrier diffusion (τ_R) show striking similarities across all three correlation functions, which further correlate with τ_R of the conventional FCS. However, ACFs notably deviate from the CCF in their μs progression patterns, with the latter showing growth, whereas the former ones display decay. This implies inter-state carrier diffusions leading to the QD blinking. Further study of single particle PL blinking on a surface-immobilized QD indicates shallow trap states near the band edge cause the blinking at low excitation power, while trion recombination becomes an additional contributing factor at higher pump power. Overall, the results highlight not only an excellent correlation between these two techniques but also the potential of our approach for achieving an accurate and comprehensive understanding of carrier dynamics in CdSe/ZnS QDs.

---

Introduction

The CdSe/ZnS core–shell quantum dot (QD) stands out as a pivotal member of the semiconductor nanocrystal family, extensively employed across diverse domains.^1–7 These QDs comprise a cadmium selenide (CdSe) core for efficient light absorption and emission and a zinc sulfide (ZnS) shell for enhancing PL efficiency by mitigating surface defects.⁴ The core–shell configuration not only boosts the optical characteristics of QDs but also acts as a protective barrier against oxidation and photodegradation, thereby extending the excited state lifespan of the QDs.^9,10 Like other quantum-confined semiconductor materials, CdSe/ZnS QDs have diverse applications, including cell imaging, light-emitting diodes (LEDs), photovoltaics, and quantum dot-based displays.^1,3,11,12 All these applications benefit from their tuneable emission wavelengths, high photoluminescence quantum yields (PLQYs), and remarkable photostability.

Despite having several promising optoelectrical and material properties, QDs encounter challenges due to trap induced PL blinking, hindering their practical deployment in display and related applications.^13–18 Several approaches, such as surface treatments, modifications in synthesis pathways, heteroatom doping, and interface engineering, have demonstrated a significant reduction in trap states.^17,19–22 However, these methods have not yet succeeded in producing completely defect-free QDs, since they still experience shallow traps near the band edge. These states facilitate efficient non-radiative band-edge carrier (NBC) recombination well before forming a second exciton. NBC blinking is common in QDs.^{13,15,23–25} Deep trap states within QDs result in the prolonged entrapment of carriers, subsequently leading to the charging of QDs. Upon subsequent photoexcitation, the charged QDs convert into trions, which relax either through radiative recombination or through fast non-radiative Auger recombination, with the former occurring at a rate constant (2k_r) twice faster than the radiative recombination rate (k_r) of neutral exciton.^{13,15,24–26} Blinking caused by trion recombination is referred to as “AC blinking”. Previous studies demonstrated that QDs could experience both NBC and AC blinking simultaneously.^13,24,27 Further studies, particularly involving the excitation of QDs with energies surpassing the band-gap threshold, reveal a new phenomenon called non-radiative hot carrier (HC) recombination that may occur alongside NBC and AC recombinations within the same QD.^23,27,28 These findings represent a significant advancement in understanding of different types of blinking phenomena observed in QDs, however, they all share a commonality in being linked to trap states. Thus, achieving a comprehensive understanding of the mechanisms of trap-state-induced carrier recombination in QDs is essential for expanding their applications in photovoltaics and optoelectronics.

In this study, we employed several non-invasive single molecule-based techniques to investigate the recombination mechanisms occurring in CdSe/ZnS QDs, which are responsible for the blinking at various timescales. Two widely accepted single-particle PL techniques are actively being considered for studying QDs: (i) single-particle blinking study of surface-immobilized QD, and (ii) FCS study of QD in the solution phase. Although the latter technique represents measurements from a small ensemble of particles (∼nM concentrations), it can still offer evidence of sample heterogeneity and distribution of characteristic time constant.^29–39 Single-particle blinking studies are conventionally performed by embedding individual QDs in a polymer matrix with only a limited scope of retaining their surface state integrity because of the inevitable influences of QD-surface interactions.¹³ This would definitely hinder the realization of the intrinsic PL properties of QDs. Single particle blinking study of surface-immobilized QD also suffers from low throughput data collection. To this front, FCS is considered to be more advantageous because it is a solution phase study and compatible with high throughput data collection. Despite the numerous advantages of FCS, there have been only a limited number of studies on QD blinking using this technique.^29–31 Other than high throughput and absence of unwanted interactions, FCS also offers better temporal resolution (<0.1 μs) compared to one (∼10 ms) in a single dot blinking study on a surface-immobilized QD. The temporal resolution of later is limited by the binning time (≥1 ms) of the PL intensity trajectory.^25,40,41 All these factors render FCS a promising technique for studying carrier dynamics.

FCS analyzes intensity fluctuations within an extremely small (<1 femtoliter) excitation volume, enabling the detection of timescales associated with the processes accountable for PL fluctuations.^42,43 While conventional FCS is capable of capturing timescales related to a number of phenomena such as diffusion, structural changes, triplet kinetics and molecular recognitions, it lacks the ability to determine the number of emission centers contributing to an FCS curve, even if they possess different lifetimes and thereby unable to provide several crucial information related to the interstate carrier dynamics.⁴² On the other hand, FLCS offers the capability to distinguish between two or more emission centers within a QD that have different PL lifetimes (τ_fl), even if their PL peak positions are similar.^30,44–50 This ultimately offers a thorough understanding of the blinking behaviors of individual emission centers related to the exciton (long τ_fl) and trap states (short τ_fl) through the analyses of their ACFs.³¹ Additionally, FLCS allows for the simultaneous detection of the trajectory of carrier dynamics involving multiple emission states by analyzing interstate CCF.³¹ The present study reveals that the growth feature (anti-correlation) in CCF between exciton and trap states serves as direct evidence of carrier diffusion between the respective states, leading to the quenching of one state at the cost of gaining PL intensity of the other state. Conventional FCS studies can't provide such a distinct evidence of carrier migration from one state to another. Additional investigation into the blinking behavior of surface-immobilized QD reveals that shallow trap states near the band edge cause blinking at low excitation power, whereas, at higher pump intensity, trion recombination emerges as an additional contributing factor.

Results and discussion

CdSe/ZnS core–shell QDs with a diameter of approximately 8 nm (as depicted in the TEM image in Fig. 1a) and a photoluminescence quantum yield (PLQY) of approximately 60% were obtained from Merck (product number 748056). The QD sample was dispersed in octadecene (ODE) through mild sonication. The absorption spectrum displays the first excitonic peak at ∼532 nm, while the PL peak is observed at ∼537 nm (Fig. 1b). Additional characterizations using X-ray diffraction spectroscopy (XRD), dynamic light scattering (DLS), and Fourier-transform infrared spectroscopy (FTIR), are available in the ESI [Fig. S1–S3†]. The findings of the above studies align well with prior studies.^6–8,51,52

Fig. 1 (a) HRTEM image of CdSe/ZnS QDs, inset shows the particle size distribution. (b) Absorption (dashed line) and PL (solid line, λ_ex ∼450 nm) spectra of CdSe/ZnS QDs dispersed in octadecene (ODE). (c) The excited state PL lifetime profile (grey curve, simultaneously recorded during FLCS) of CdSe/ZnS QDs is resolved into two decay profiles representing trap state (blue) and exciton state (green). The inset shows intrastate autocorrelation functions (ACFs) of the exciton (long τ_fl, green) and trap (short τ_fl, blue) states along with the interstate cross-correlation function (CCF) between the exciton and trap states (blue-green line). FLCS utilizes TCSPC to separate FCS contributions of trap and exciton states based on the lifetimes of the detected photons. The core of this technique lies in the statistical isolation of distinct intensity contributions carried out at the single photon level. FLCS serves as a lifetime analogy to multicolor FCS, offering numerous additional benefits.

In conventional FCS, only the macroscopic arrival times (τ, with ns precision) of each recorded photons with respect to the start pulse are registered. Conventional FCS provides valuable insights into diffusion, triplet kinetics, molecular interactions, carrier dynamics, or other processes causing PL fluctuations at μs-to-ms timescale.^42,43 However, FLCS expands on this by additionally recording the microscopic delay times (t, with ps precision) of the recorded photons with respect to the previous sub-ns excitation pulse.^44–50 Since the FCS curves are plotted as a function of τ (macroscopic arrival time), henceforth, we would recognize this timescale as the FCS scale. Conversely, the microscopic delay times (t) utilized for constructing the TCSPC histogram vary among different emission centers and are recorded on a lifetime scale. The ACF and CCF are calculated from various arrival timescales (τ and t) of detected photons. If a nanocrystal contains two emission states, both contributing to the PL, the resultant FCS curve is not a linear combination but instead a complicated superposition of both. Separation of FCS contributions first involves the determination of statistical origins of the detected photons, followed by the formulation of statistical filters that lead to the separation of intensity contributions. Once separated, the formations of ACFs and CCF are straightforward. Further details on the FLCS, construction of the CCF and ACF can be found elsewhere.⁴⁴

Fig. 1c illustrates resolving the conventional FCS curve of QDs into two intrastate ACFs related to the exciton and trap states and one interstate CCF coupling these two states. The key to this entire separation process in FLCS lies in different lifetimes of the exciton (∼8.9 ns) and trap (∼1.9 ns) states, respectively. The statistical distribution of microscopic arrival times of detected photons at low excitation power (∼0.02 kW cm⁻²) fits nicely to a bi-exponential decay function, with characteristic timescales of ∼8.9 ns (exciton) and ∼1.9 ns (trap), respectively. As the pump power increases from ∼0.02 kW cm⁻² to ∼0.2 kW cm⁻², the contribution of the trap state lifetime (∼1.9 ns) rises from ∼49% to ∼57%, implying efficient trapping of charge carriers at an elevated pump intensity. ACFs and CCF display similarities, including their dynamical timescales of carrier diffusion (τ_R) and translational diffusion of QDs (τ_D), with the exception of their correlation patterns at μs time regime. ACFs demonstrate a decay pattern, whereas CCF exhibits growth or anti-correlation (Fig. 1c). The growth feature in CCF unequivocally confirms the strong coupling between the exciton and the trap states, where the population (or PL intensity) increases in one state at the cost of sacrificing the PL intensity of the other state (Fig. 2a and b). Thus, our FLCS study allows direct tracking of the carrier diffusion in QDs through the examinations of intrastate ACFs and interstate CCF. These analyses additionally offer substantiation for carrier migration at the μs timescale as the underlying mechanism of QD blinking.

Fig. 2 (a) Schematics of PL intensity traces of exciton (long τ_fl, green) and trap (short τ_fl, blue) states of a QD. Over time, if the PL fluctuation patterns of the two emission centers (exciton and trap) correlate in a reverse manner, an anti-correlation or growth feature would be observed in CCF. (b) Schematics of ACFs of exciton (green) and trap (blue) states, along with inter-state CCF (blue-green line) with growth feature, correlating with PL blinking depicted in (a). Since both emission centers belong to the same QD, later time decay (ms regime) of all three correlation functions follows similar timescales (τ_D) decided by QD diffusion. Also, the μs evolution timescale of all three correlation curves would match since this timescale (τ_R) is decided by trapping (k₁) and de-trapping (k₂) rates of charge carrier; τ_R = (k₁ + k₂)⁻¹. (a and b) are schematic representations, not showing any real data. (c and d) ACFs and CCF of CdSe/ZnS QDs at low (c) and high (d) excitation power (real data). The inset shows the CCF of the main figure to realize the growth feature by zooming the y-axis.

PL lifetime profiles at both the excitation powers fit satisfactorily to a bi-exponential decay function with characteristic timescales of ∼1.9 ns and 8.9 ns, respectively (Fig. 1c). A larger contribution of exciton state (∼8.9 ns) is observed at lower pump intensity (∼0.02 kW cm⁻²). Correlating with previous studies, we assigned the faster component (∼1.9 ns) to trion or trap state-mediated recombination, whereas the longer component to radiative recombination of exciton.^31,53 The ACFs of the trap state with ∼1.9 ns lifetime component [G(τ)_1.9×1.9] and the exciton state with ∼8.9 ns component [G(τ)_8.9×8.9], as well as the CCF between trap and exciton state [G(τ)_1.9×8.9], at low (∼0.02 kW cm⁻²) and high (∼0.2 kW cm⁻²) excitation powers are illustrated in Fig. 2c and d. These ACFs and CCF fit nicely to the following analytical fitting function (eqn (1)), which combines two blinking phenomena. The initial part [G_R(τ)] accounts for the blinking stemming from carrier trapping (rate constant k₁) and de-trapping (rate constant k₂) at characteristic timescale of τ_R [=1/(k₁ + k₂)], whereas the latter part [G_D(τ)] represents the blinking as a result of translational diffusion of the QDs across the excitation volume.³¹

where,and

G_D(τ) = (1 + τ/τ_D)⁻¹(1 + τ/k²τ_D)^−1/2 (3)

where A in eqn (1) is the average number of QDs in the excitation volume.³¹ In eqn (2), while g_1.9×1.9 (and g_8.9×8.9) = k₂/k₁ (and k₁/k₂), g_1.9×8.9 = −1. τ_R [=1/(k₁ + k₂)] represents the characteristic timescale of blinking induced by carrier trapping/de-trapping, where the stretching exponent β (0 ≤ β ≤ 1) accounts for the energy distribution of the trap states.^31,53,54β shows a distinctive shift to a lower value at high pump intensity, pointing toward the dispersive nature of the trap states, presumably due to the participation of trion recombination at a high excitation power (Table 1).^31,54 In eqn (3), τ_D represents the characteristic timescale of translational diffusion of QDs across the excitation volume, whose aspect ratio is described by k (∼4). k represents the ratio of the longitudinal radius (ω_z) to the transverse radius (ω_xy) of the excitation volume.⁴³ The above fitting model has previously been employed to fit FCS curves of metal chalcogenides and, very recently, in perovskite nanocrystals.^31,52 Also, Hof and colleagues utilized the same model to fit the ACFs and CCFs of their FLCS study of DNA condensation.⁴⁵ Excitation volume was calibrated through an FCS study of an organic dye molecule (rhodamine 6g) whose diffusion constant is known.³⁶ In our study with CdSe/ZnS QDs, we noted that the decay pattern is evident in the initial correlation (μs regime) of ACFs. However, in the case of CCF, a consistent growth feature is observed regardless of the pump intensity (Fig. 2c and d). Furthermore, the timescale of carrier dynamics (τ_R) observed in any of the ACFs aligns well with that of the other ACF, and both the timescales correlate further with the τ_R of CCF under the same excitation power (Fig. 2c and d, Table 1). These observations provide direct evidence of carrier diffusion from one state to another, causing the PL blinking in QD, wherein the carrier diffusion timescale is represented by τ_R. The τ_R becomes faster from 150 μs to ≤100 μs as the pump power increases from ∼0.02 kW cm⁻² to ∼0.2 kW cm⁻² due to the involvement of an additional recombination channel, presumably trion mediated (Fig. 2c and d, Table 1). Also, the stretching exponent (β), which accounts for the distribution of τ_R, reduces as the excitation power increases (Table 1). This observation is evident in both the ACFs and CCF, which is attributed to the charge carrier trapping by dispersive trap states with distributed energies.^31,54 Analysis of correlation functions at long delay time renders diffusion timescale (τ_D) of QDs, traversing across the excitation profile. Table 1 collected the τ_Ds from the fitting of correlation functions (ACFs and CCF) by eqn (1). We noted similar τ_Ds from all three correlation functions (ACFs and CCF) of FLCS, which is indeed due to the presence of both the states (trap and exciton) within the same QD. The diffusion timescales of both states, as reflected in their ACFs, are controlled by the diffusion of QD, where these states originate. It is pertinent to mention here that τ_R and τ_D of conventional FCS match with those of the ACFs and CCF (Table 1). One might raise doubts regarding the practical utility of FLCS in our investigation, considering that classical FCS can also furnish timescales of carrier dynamics and particle diffusion. However, here we argue that FLCS offers valuable insights into the trapping mechanism, enriching our understanding beyond what FCS can provide. FLCS offers advantages over FCS by not only distinguishing between emissive centers with different lifetimes but also by determining the relative patterns of their emissions (whether it's correlative, anti-correlative, or non-correlative). The observed growth feature in the CCF indeed validates the anti-correlative nature of the emissions from exciton and trap states. This phenomenon suggests that an increase in PL intensity in one state occurs at the expense of a decrease in intensity in the other state (Fig. 2a).

Table 1 Optimal FCS parameters derived from fitting correlation functions with eqn (1), at low (∼0.02 kW cm⁻²) and high (∼0.2 kW cm⁻²) excitation powers. Conventional FCS curves were fitted with the same fitting function used for the fitting of exciton ACF [i.e., G_8.9×8.9(τ)]. The reported values are the averages of three consecutive measurements, with the sample replaced with a fresh one between each measurement. Deviations in the FCS parameters were less than 10% from their respective means in any measurement

Correlations	τ D (ms) [low/high power]	τ b (μs) [low/high power]	β [low/high power]	g [low/high power]	Fraction of time spent in trap state [k1/(k1 + k2)] [low/high power]
Conventional FCS	3.0/3.9	150/100	0.20/0.11	0.5/2.5	0.33/0.71
FLCS-ACF (8.9 × 8.9 ns)	3.0/4.0	150/100	0.29/0.18	0.5/2.5	0.33/0.71
FLCS-ACF (1.9 × 1.9 ns)	3.2/3.8	150/90	0.13/0.50	2.0/0.4	0.33/0.71
FLCS-CCF (8.9 × 1.9 ns)	3.2/4.0	150/90	0.08/0.06	−1/−1

---

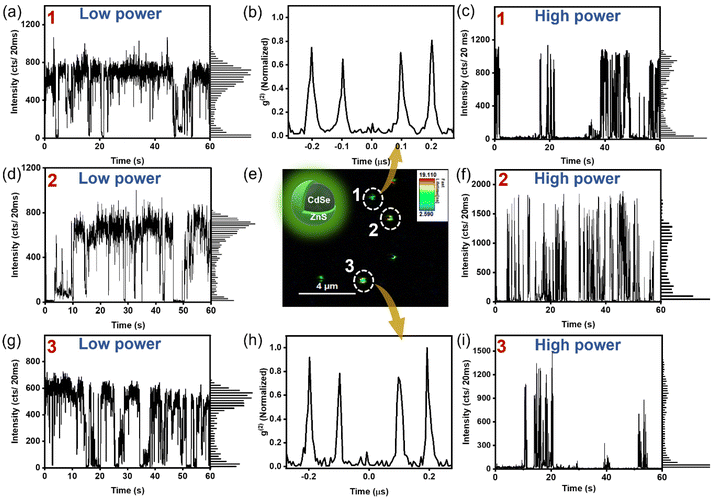
Next, we investigated the PL intensity trajectories of individual QDs embedded in a PMMA matrix (Fig. 3). Through dot-to-dot analysis, we were able to elucidate the distinct characteristics of carrier dynamics by mitigating the influence of ensemble averaging. Single-dot measurements were conducted using confocal microscopy. Our single-dot blinking investigation has provided insights into the origin of trap states and the associated carrier dynamics. Furthermore, the results of the single-dot study qualitatively correlate with FLCS study. The first step of the single dot blinking investigation involves spin-coating an extensively diluted QD sample onto a coverslip. This diluted sample was prepared by dispersing QDs in a solution containing toluene and 1% (w/v) poly(methyl methacrylate) (PMMA). Fig. 3e illustrates the fluorescence lifetime imaging (FLIM) recorded on a small portion of the coverslip, displaying diffraction-limited spots (or dots) separated by considerable distances from each other. To confirm that each dot in the scan image represents a single QD rather than a cluster of multiple QDs, we performed a second-order photon anti-bunching study on the individual dots, which revealed sub-Poissonian photon statistics (Fig. 3b and h). Photon anti-bunching or sub-Poissonian photon statistics can be observed when photons are emitted one after another from a single emission source. Indeed, our anti-bunching study can be utilized to corroborate individual dots in scan image comprising a single QD (Fig. 3e). A pulse laser emitting at ∼422 nm with a repetition rate of ∼10 MHz was used to excite the individual dots, and PL intensity trajectories were recorded for a sufficiently long time (60 seconds) (Fig. 3 left and right panels). Simultaneously, arrival times of photons relative to the excitation pulse were recorded using TCSPC for statistical analysis of the excited state lifetime. Single-dot measurements were replicated across 70–80 dots to provide a more accurate analysis of the observed phenomenon without any biases stemming from analyzing a randomly selected QD. Fig. 3 depicts the data of a few randomly selected representatives of PL intensity traces along with the statistical distribution of intensity states at different excitation powers. Intensity histograms reveal a bimodal distribution comprising high-intensity ON states and weakly intense OFF states. The OFF-state fraction was found to increase with increasing pump intensity. This observation is attributed to trion recombination at high pump intensity, as evidenced by the nearly twofold increase in the radiative recombination rate (2k_r) of the OFF state at high pump intensity compared to the recombination rate (k_r) of the ON state. This will be discussed in more detail in the subsequent paragraphs.

Fig. 3 The figures at the left (a, d and g) and right (c, f and i) panels depict the PL intensity trajectories of three individual QDs under low (2 W cm⁻²) and high (20 W cm⁻²) pump powers. The statistical distributions of intensity states are depicted along the right y-axis of the figures on the left and right panels, showing a larger OFF state fraction at elevated pump intensity. Individual figures in the left and right panels are marked with a number identifying the particle in the lifetime scan image (e) whose PL trajectory data has been shown. (b and h) Second-order cross-correlation functions [g²(τ)] recorded in pulse mode demonstrate that the emitted photons from individual dots in (e) exhibit sub-Poissonian statistics. This indicates that each dot observed in the lifetime scan image corresponds to a single QD.

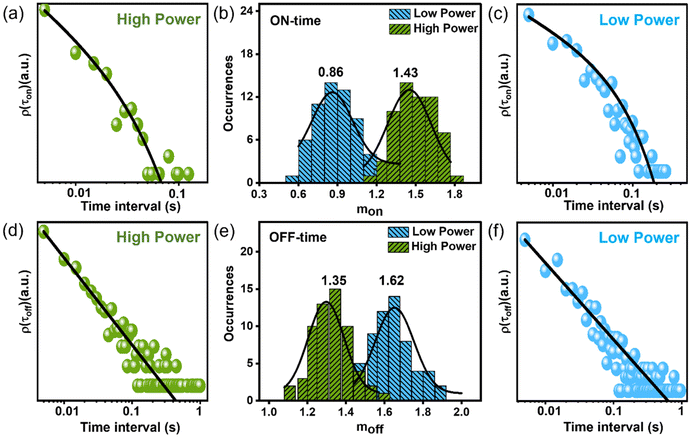
The OFF states in the PL trajectory that cause blinking predominantly stem from carrier trapping. Although several mechanisms are reported for QD blinking contingent upon the materials involved and the pump intensity, they all share a commonality in being linked to trap states. Thus, we examined the statistical distribution of OFF and ON states with varying durations for individual QDs, represented by ρ(τ_off) and ρ(τ_on), respectively (Fig. 4). To delineate the ON and OFF events in a PL intensity trace, a threshold line was positioned between the average ON and OFF intensities. Intensity states above the threshold are considered to be ON events, whereas those below the threshold are considered to be OFF states. The probability distribution of OFF-time durations [ρ(τ_off)] follows a power-law kinetics, ρ(τ_off) ∝ τ^−m_off, whereas the probability distribution of ON-time durations [ρ(τ_on)] follows a truncated power-law kinetics, . The power-law exponents m_off and m_on here indicate the relative rates of charge de-trapping and trapping in a single QD.¹⁵ The exponential cut-off time (τ_C) in the ON time distribution [ρ(τ_on)] is crucial as it provides information on the photoionization probability [ρ_ion] of the QD, given that ρ_ion is proportional to 1/τ_C.²⁵ Certainly, we did observe this truncation behavior of ρ(τ_on) plot, a signature of photo charging (Fig. S4†).

Fig. 4 (a and c) The probability distribution plots of ON time durations of a QD at low (∼2 W cm⁻², c) and high (∼20 W cm⁻², a) excitation powers. (d and f) Similar plots for OFF time durations at low (∼2 W cm⁻², f) and high (∼20 W cm⁻², d) excitation powers. (b) Probability histograms of the ON time power law exponents (m_on) recorded over 60–70 particles at low and high powers. (e) Same plots for m_off at two different powers. The mean values are mentioned above each distribution. As the pump intensity increases relative charge trapping rate (m_on) rate increases (b), whereas the relative charge de-trapping rate (m_off) decreases (e), implying more efficient charge trapping at high power.

Fig. 4b and e show the probability histograms of m_on and m_off, which are based on measurements from 60–70 individual QDs. As the pump intensity increases, the relative trapping rate (m_on) speeds up, whereas the relative de-trapping rate (m_off) slows down. This observation indicates that charge carriers are effectively trapped at high excitation power. A similar observation was also noted in the FCS study, as discussed previously. Possible models elucidating the power-dependent PL blinking of QD include (i) fluctuation of tunneling barrier with time in the pathway of carrier diffusion, where trapping occurs through tunneling of the carrier from the QD core to the external trap states.²⁸ Excitation power here changes the PL blinking by changing the time-dependent accessibility of trap states by modulating the barrier height. Model (ii) relies on photo-charging of QDs leading to trion states where efficient Auger recombination causes the OFF state.²⁵ The duration of the OFF state is decided by the lifetime of the carrier in the trap state. These models explain the power-law distribution of OFF-durations considering a distribution of relative distances of trap states from the core.²⁸ Other existing models propose the involvement of hot carrier trapping and NBC recombination in the blinking process, as previously discussed. In most cases, with increasing excitation power, a greater number of recombination phenomena participate in the blinking. As a result, the cause of blinking in our QD remains uncertain, whether it can be due to the fluctuation of the tunneling barrier, the activating and deactivating of trap states, or the distribution of the density of static trap states.^28,55 However, analyzing the power dependency on ρ_ion (α1/τ_c) reveals a super-linear dependence on excitation power, implying Auger ionization plays a crucial role in the blinking of our QDs (Fig. S4†). We observed that 1/τ_c is superlinear in excitation power (i.e., ρ_ion ∝ I_P^1.2), implying nonlinear (Auger ionization) and linear processes may contribute to the photo charging of our QDs (Fig. S4†).^25,56–58

To illuminate the underlying mechanism of blinking in our QDs, conducting a correlation study between PL intensity and lifetime utilizing time-tagged TCSPC study at the single-particle level is essential. This study reveals a strong interdependence between these two quantities, which is more prominent in a fluorescence-lifetime-intensity-distribution (FLID) map (Fig. 5).^13,18,25,41 In the FLID map, the likelihood of the dot occupying a specific state in the “I_PL − τ_PL space” is represented by a color gradient, with red indicating higher probability and shifting to blue as the probability decreases. The FLID trajectory, connecting various probability states, provides valuable insights into the underlying mechanism of QD blinking.^15,23 FLID mappings are carried out at two different powers on a set of 30–35 particles to prevent any biases that may arise from analyzing a randomly chosen QD. Subsequently, the blinking data of a particle showing the highest resemblances with other particles recorded at the same excitation power are examined further, and used for the FLID plot (Fig. 5 and S5†). The ON and OFF intensity states in a PL intensity trajectory arise from carrier recombination at the exciton state and trap state (Fig. 5a and d). These two states are clearly visible in the low-power FLID map (Fig. 5b and S6–S8†). While the ON state involves the radiative recombination of a single exciton, the OFF state encompasses several non-radiative recombination pathways along with radiative.^13,25,41

Fig. 5 (a and d) PL intensity and lifetime trajectories, recorded on the same QD at low (a) and high (d) excitation powers. A clear correlation between lifetime and intensity trajectories was observed, implying trion and/or NBC recombination. (c and f) Excited state lifetime profiles of the OFF (blue) and ON (green) states were obtained by analyzing the emissions with intensities indicated by the blue (OFF) and green (ON) slabs in the upper panels of (a) (for (c)) and (d) (for (f)). (b and e) Fluorescence lifetime intensity distribution (FLID) maps presented in false color at low (b) and high (e) excitation powers, obtained from analyzing intensity and lifetime trajectories in (a) (low power) and (d) (high power), respectively. The shift from blue to red indicates a rising probability of a specific state occurring within the I_PL − τ_PL space. See Fig. S5† for similar plots from other particles.

Since no vertical broadening is evident in none of the FLID plots, hot carrier trapping is ruled out (Fig. 5b and e).⁴⁰ Vertical broadening is generally caused by the trapping of above band-edge carriers to trap states nearby before relaxing to the band-edge state. In such a scenario, PL intensity reduces drastically without affecting the lifetime. This vertical blinking phenomenon is often referred to as B-type blinking, as illustrated by the middle figures in Scheme 1.⁴⁰ To shed light on the darker species in FLID, we applied the lifetime-intensity scaling method, widely reported in the literature.^13,18,25,41 As mentioned earlier, considering that the brightest state in FLID is persuasive solely to the radiative recombination of the single exciton, we can deduce the ratio of radiative rates (k_r,off/k_r,on) between the dark (OFF) and bright (ON) states.¹³ This deduction would be made under the assumption that the intensities (I) of the corresponding states in the blinking trajectory are proportional to their PL quantum yields (PLQYs). Hence, the radiative recombination rate (k_r) would be proportional to PLQY/τ (or I/τ). When this relationship is applied to both ON (green slab) and OFF (blue slab) intensity states of blinking trajectory, one can obtain the relative radiative rates of ON (k_r,on) and OFF (k_r,off) states (Fig. 5a and d). The scaling factor η, representing the ratio of radiative recombination rates of OFF and ON states (k_r,off/k_r,on), provides valuable insights into the darker species. This understanding aids in distinguishing the nature of the OFF states, determining whether they are charged species prone to efficient Auger recombination or quenched neutral species (eqn (4)).

Scheme 1 Various possible PL blinking mechanisms in a QD (upper panel), along with their corresponding appearance patterns on the FLID map (vertical figures in the lower panel). Nonradiative processes are denoted by red arrows, while radiative processes are depicted with green arrows.

In the above equation, I_on (or I_off) represents ON (or OFF) state intensity which is determined by averaging the emission intensity within the green (or blue) vertical slab in the PL intensity trajectory (Fig. 5a and d).¹³ Likewise, τ_on (or τ_off) denotes the lifetime of the ON (or OFF) state's PL, which is determined by fitting the PL decay profile of the ON state to an exponential decay function (as illustrated in Fig. 5c and f). The decay profile of the ON (or OFF) state is derived from the photons collected from the green (or blue) vertical slabs of the PL intensity trajectory, as depicted in Fig. 5a and d. Scaling factor η with value unity implies that the OFF state is a neutral species caused by the NBC recombination. This form of recombination arises from the short-lived shallow trap states located near the band edge, a phenomenon commonly seen in QDs and various other semiconductor materials.^28,40,59,60 NBC blinking involves an interplay between constant radiative recombination rate and fluctuating nonradiative recombination rate, leading to a linear relationship between intensity and lifetime, shown by a white dotted line in the FLID map (Fig. 5b and e). In our case, the blinking phenomenon observed in QDs under low excitation power is solely induced by band-edge carrier trapping and de-trapping, which is referred to as NBC or C-type blinking (Fig. 5a). The pathway of charge trapping in NBC recombination and its manifestation in FLID map is illustrated by the vertical figures on the right side of Scheme 1.¹⁵ As mentioned earlier, NBC blinking is caused by the shallow trap states near the band-edge and can be confirmed by calculating η. This value can be derived by analyzing the low-power PL blinking trajectory using eqn (4) (Fig. 5a). We derived the intensities of ON (I_on ∼701/20 ms) and OFF (I_off ∼84/20 ms) states after subtracting the background intensity (∼8/20 ms) from the apparent ON and OFF state intensities of PL intensity trajectory at low excitation power (Fig. 5a). The lifetimes of ON (τ_on ∼15.6 ns) and OFF (τ_off ∼2.2 ns) states are also derived from the same blinking trajectory (Fig. 5a), analyzing the emissions from the highest (green slab) and lowest (blue slab) intensity regimes. PL intensity decay curves are depicted in Fig. 5c. Plugging all these values into eqn (4) results in η ∼ 0.85, which is close to unity, as expected for NBC or C-type blinking, and is further confirmed by the linear trajectory observed in the FLID map (Fig. 5b).

However, a similar calculation of η for the high-power blinking trajectory reveals the involvement of an additional recombination channel, predominantly trion-mediated Auger recombination (Fig. 5d–f). For trion recombination, η would be 2, and the corresponding blinking is recognized as type-A blinking (Scheme 1). The curved trajectory of the FLID map indicates type-A blinking (Fig. 5e). In contrast to the single exponential lifetime profile observed for the OFF-state at low excitation power, the OFF-state lifetime at high excitation power comprises two components (τ^fast_off ∼ 0.6 ns and τ^slow_off ∼ 2.1 ns) (Fig. 5f). η was calculated separately for these two components, with I_on (∼1200/20 ms), I_off (∼130/20 ms), I_background (∼8/20 ms), and τ_on (∼14 ns) being common parameters. With the faster lifetime component (∼0.6 ns) of the OFF state, our calculated value of η (∼2.5) lies close to 2, suggesting trion recombination.¹³ A slightly higher value of η than the expected one is likely due to the use of an overestimated I_off, which includes contributions from another lifetime component (∼2.1 ns) that is difficult to separate. On the other hand, the longer lifetime component (∼2.1 ns) of the OFF state yields η ∼ 0.72, which is close to unity, implying NBC or C-type recombination. Thus, it is evident that at low excitation power, only type-C or NBC blinking is present in our QDs. However, at an elevated pump intensity, trion-mediated type-A blinking participates alongside type-C blinking. This assertion can be further supported by examining the trajectory of the FLID maps depicted in Fig. 5b and e. At low power, FLID trajectory shows a linear diagonal relationship (dotted white line), while at high power, an additional curved trajectory (solid white line) emerges alongside the linear one as a result of trion recombination (Fig. 5b and e). In none of the excitation powers, the PL intensity trajectory demonstrates hot carrier recombination or B-type blinking.

Our subsequent efforts to investigate the relationship between QD blinking and defect state density enabled us to analyze the FLID patterns of QDs while varying the number of defect states.^23,25,76 This study was performed by enhancing defect states through the gradual photodegradation of QDs via UV irradiation. The colloidal suspension of QDs in hexane was exposed to intense UV light for an extended period (∼5 h), leading to partial photodegradation, as evidenced by a gradual decline in PLQY (Fig. S6†). UV irradiation causes long-lived deep trap states in QDs, where photoexcited charge carriers become easily trapped for long time, leading to photocharging of QDs.²⁵ Upon excitation to these charged QDs, they transform into trions, where carriers efficiently recombine through Auger processes.^23,25,76 Fig. S7–S9† displays the FLID maps of QDs subjected to varying durations of UV exposure. The FLID pattern of QDs not exposed to UV follows a linear relationship between intensity and lifetime, represented by a diagonal trajectory.^23,25,76 In contrast, UV-exposed QDs show an additional FLID pattern with a curved trajectory, indicative of trion recombination, which becomes more pronounced with increased UV exposure.^23,25 Therefore, we conclude that a higher density of defect states leads to the dominance of trion blinking over NBC blinking.

Conclusions

In summary, a thorough examination of carrier dynamics in a model QD system by FLCS and single particle blinking reveals several striking observations. (i) FLCS study provided evidence of carrier diffusion contributing to QD blinking. The anti-correlation feature in the μs regime of CCF is indeed a remarkable finding, suggesting a decrease in PL of exciton state at the expense of an increase in PL of the trap state, and vice versa. Thus, our FLCS study demonstrates a direct evidence of carrier diffusion, such an observation is relatively uncommon in the existing literature. Our FLCS study established further a reduced stretching exponent (β) and faster timescale of carrier dynamics (τ_R) at an elevated pump intensity, implying efficient carrier trapping by dispersive trap states with distributed energies at high pump intensity. Unfortunately, our FLCS study was unable to clarify the true nature of the trap states and their mechanistic involvements in blinking at different excitation powers. Analysis of our single dot PL data confirms that the origin of faster τ_R and dispersive trap states at high power is indeed linked to an additional relaxation channel caused by the trion recombination. At a low excitation power, only the short-lived band edge trap states participate in the blinking, which is less dispersive in nature, and also, the associated timescale of blinking here is relatively slower since it involves recombination between two oppositely charged species. However, for trion recombination at high pump intensity, one hole can recombine either of the two electrons (negative trion) or one electron with two holes (positive trion) with a much faster timescale because of the higher recombination probability. Also, unlike NBC recombination, trion recombination involves long-lived deep trap states that are highly dispersive in nature and stem from the internal structural defect of QDs.^60–63 Thus, the single dot PL blinking analyses nicely explain the origins of reduced β and faster τ_R, observed in the FCS study of QDs at higher excitation power. Moving forward, our future plans include conducting a more in-depth analysis of charge carrier dynamics. We aim to utilize ultrafast time-resolved techniques to provide a comprehensive understanding of carrier dynamics across all timescales.^64–75

Data availability

The data supporting this article have been included in the ESI† and main manuscript. Constructions of FLCS, anti-bunching curves, PL intensity trajectory, distributions of ON and OFF times, FLIDs and subsequent fittings were performed using SymPhoTime 64 software developed by PicoQuant. Details of this software can be found at https://www.picoquant.com/dl_datasheets/SymPhoTime64_brochure.pdf.

Conflicts of interest

There are no conflicts to declare.

References

1. D. A. Hines and P. V. Kamat, ACS Appl. Mater. Interfaces, 2014, 6, 3041–3057.
2. H. Zhu, N. Song and T. Lian, J. Am. Chem. Soc., 2010, 132, 15038–15045.
3. S. Kundu and A. Patra, Chem. Rev., 2017, 117, 712–757.
4. B.-O. Dabbousi, J. Rodriguez-Viejo, F.-V. Mikulec, J. R. Heine, H. Mattoussi, R. Ober, K.-F. Jensen and M. G. Bawendi, J. Phys. Chem. B, 1997, 101, 9463–9475.
5. G. Ba, Y. Yang, F. Huang, J. Wang, Y. Lu, J. Li, C. Cheng, M. Sui and J. Tian, Nano Lett., 2024, 24, 4454–4461.
6. S. Koley, M. R. Panda and S. Ghosh, J. Phys. Chem. C, 2016, 120, 13456–13465.
7. K. Bharadwaj, S. Koley, S. Jana and S. Ghosh, Chem. – Asian J., 2018, 13, 3296–3303.
8. P. Singhal and H. N. Ghosh, J. Phys. Chem. C, 2018, 122, 17586–17600.
9. E. Zenkevich, A. Stupak, C. Göhler, C. Krasselt and C. von Borczyskowski, ACS Nano, 2015, 9, 2886–2903.
10. Y.-S. Park, J. Lim, N. S. Makarov and V. I. Klimov, Nano Lett., 2017, 17, 5607–5613.
11. H. Moon, C. Lee, W. Lee, J. Kim and H. Chae, Adv. Mater., 2019, 31, 1804294.
12. Y. Shu, X. Lin, H. Qin, Z. Hu, Y. Jin and X. Peng, Angew. Chem., Int. Ed., 2020, 59, 22312–22323.
13. M. K. Panda, D. Acharjee, A. B. Mahato and S. Ghosh, Small, 2024, 20, 2311559.
14. K. Mishra, M. Barai and S. Ghosh, J. Phys. Chem. C, 2022, 126, 16905–16918.
15. T. Kim, S. I. Jung, S. Ham, H. Chung and D. Kim, Small, 2019, 15, 1900355.
16. N. Pathoor, A. Halder, A. Mukherjee, J. Mahato, S. K. Sarkar and A. Chowdhury, Angew. Chem., 2018, 130, 11777–11781.
17. E. M. Thomas, S. Ghimire, R. Kohara, A. N. Anil, K.-I. Yuyama, Y. Takano, K. G. Thomas and V. Biju, ACS Nano, 2018, 12, 9060–9069.
18. E. M. Thomas, N. Pradhan and K. G. Thomas, ACS Energy Lett., 2022, 7, 2856–2863.
19. Y. Lee, D. Y. Jo, T. Kim, J. H. Jo, J. Park, H. Yang and D. Kim, ACS Appl. Mater. Interfaces, 2022, 14, 12479–12487.
20. S. Paul and A. Samanta, J. Phys. Chem. Lett., 2022, 13, 5742–5750.
21. C. T. Yuan, P. Yu and J. Tang, Appl. Phys. Lett., 2009, 94, 243108.
22. Y. L. He, J. Chen, R. M. Liu, Y. L. Weng, C. Zhang, Y. M. Kuang, X. J. Wang, L. J. Guo and X. Ran, ACS Appl. Mater. Interfaces, 2022, 14, 12901–12910.
23. C. T. Trinh, D. N. Minh, K. J. Ahn, Y. Kang and K.-G. Lee, Sci. Rep., 2020, 10, 2172.
24. W. Fu, J. Yin, H. Cao, Z. Zhou, J. Zhang, J. Fu, J. H. Warner, C. Wang, X. Jia, G. N. Greaves and A. K. Cheetham, Adv. Mater., 2023, 35, 2304074.
25. Y.-S. Park, S. Guo, N. S. Makarov and V. I. Klimov, ACS Nano, 2015, 9, 10386–10393.
26. S. Mandal, S. Mukherjee, C. K. De, D. Roy, S. Ghosh and P. K. Mandal, J. Phys. Chem. Lett., 2020, 11, 1702–1707.
27. T. Ahmed, S. Seth and A. Samanta, ACS Nano, 2019, 13, 13537–13544.
28. A. A. Cordones and S. R. Leone, Chem. Soc. Rev., 2013, 42, 3209–3221.
29. S. Doose, J. M. Tsay, F. Pinaud and S. Weiss, Anal. Chem., 2005, 77, 2235–2242.
30. P. K. Singha, T. Kistwal and A. Datta, J. Phys. Chem. Lett., 2023, 14, 4289–4296.
31. A. Das, K. Mishra and S. Ghosh, J. Phys. Chem. Lett., 2021, 12, 5413–5422.
32. D. Acharjee, A. Das, M. K. Panda, M. Barai and S. Ghosh, Nano Lett., 2023, 23, 1946–1953.
33. K. Mishra, A. Das and S. Ghosh, J. Phys. Chem. C, 2020, 124, 24115–24125.
34. S. Dey, U. Mandal, A. Adhikari, S. Ghosh and K. Bhattacharyya, Hydrogen Bonding Transfer Excited State, 2010, 1, 159–174.
35. S. Ghosh, A. Adhikari, S. Sen Mojumdar and K. Bhattacharyya, J. Phys. Chem. B, 2010, 114, 5736–5741.
36. S. Ghosh, U. Mandal, A. Adhikari and K. Bhattacharyya, Chem. – Asian J., 2009, 4, 948–954.
37. A. Das, D. Acharjee, M. K. Panda, A. B. Mahato and S. Ghosh, J. Phys. Chem. Lett., 2023, 14, 3953–3960.
38. S. Bhattacharyya, S. Prashanthi, P. R. Bangal and A. Patra, J. Phys. Chem. C, 2013, 117, 26750–26759.
39. S. Kundu, A. Chowdhury, S. Nandi, K. Bhattacharyya and A. Patra, Chem. Sci., 2021, 12, 5874–5882.
40. C. Galland, Y. Ghosh, A. Steinbrück, M. Sykora, J. A. Hollingsworth, V. I. Klimov and H. Htoon, Nature, 2011, 479, 203–207.
41. G. Yuan, D. E. Gómez, N. Kirkwood, K. Boldt and P. Mulvaney, ACS Nano, 2018, 12, 3397–3405.
42. T. Wohland, S. Maiti and R. Macháň, An Introduction to Fluorescence Correlation Spectroscopy, IOP Publishing, Bristol, U.K., 2020. pp. 247–250.
43. P. Schwille and E. Haustein, Fluorescence Correlation Spectroscopy. In A tutorial for the Biophysics Textbook Online (BTOL), Biophysical Society, Rockville, MD, 2002, pp. 10–25.
44. P. Kapusta, R. Machań, A. Benda and M. Hof, Int. J. Mol. Sci., 2012, 13, 12890–12910.
45. J. Humpolíckova, A. Benda, J. Sýkora, R. Machań, T. Kral, B. Gasinska, J. Enderlein and M. Hof, Biophys. J., 2008, 94, L17–L19.
46. A. Ghosh, S. Isbaner, M. Veiga-Gutierrez, I. Gregor, J. Enderlein and N. Karedla, J. Phys. Chem. Lett., 2017, 8, 6022–6028.
47. J. Chen and J. Irudayaraj, Anal. Chem., 2010, 82, 6415–6421.
48. K. Ishii and T. Tahara, J. Phys. Chem. B, 2010, 114, 12383–12391.
49. I. Gregor and J. Enderlein, Photochem. Photobiol. Sci., 2007, 6, 13–18.
50. A. Orte, M. J. Ruedas-Rama, J. M. Paredes, L. Crovetto and J. M. Alvarez-Pez, Langmuir, 2011, 27, 12792–12799.
51. T. Mokari and U. Banin, Chem. Mater., 2003, 15, 3955–3960.
52. R. K. Ratnesh and M. S. Mehata, Spectrochim. Acta, Part A, 2017, 179, 201–210.
53. S. Paul, G. Kishore and A. Samanta, J. Phys. Chem. C, 2023, 127, 10207–10214.
54. S. Seth, N. Mondal, S. Patra and A. Samanta, J. Phys. Chem. Lett., 2016, 7, 266–271.
55. I. Y. Eremchev, A. O. Tarasevich, J. Li, A. V. Naumov and I. G. Scheblykin, Adv. Opt. Mater., 2021, 9, 2001596.
56. M. Kuno, D. P. Fromm, S. T. Johnson, A. Gallagher and D. J. Nesbitt, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 125304.
57. S. Wang, C. Querner, T. Emmons, M. Drndic and C. H. Crouch, J. Phys. Chem. B, 2006, 110, 23221–23227.
58. F. D. Stefani, W. Knoll, M. Kreiter, X. Zhong and M. Y. Han, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 125304.
59. M. Nirmal, B. O. Dabbousi, M. G. Bawendi, J. J. Macklint, J. K. Trautmant, T. D. Harrist and L. E. Brus, Nature, 1996, 383, 802–804.
60. M. Abdellah, K. J. Karki, N. Lenngren, K. Zheng, T. Pascher, A. Yartsev and T. Pullerits, J. Phys. Chem. C, 2014, 118, 21682–21686.
61. J. Meng, Z. Lan, M. Abdellah, B. Yang, S. Mossin, M. Liang, M. Naumova, Q. Shi, S. L. Gutierrez Alvarez, Y. Liu, W. Lin, I. E. Castelli, S. E. Canton, T. Pullerits and K. Zheng, J. Phys. Chem. Lett., 2020, 11, 3705–3711.
62. S. Chatterjee, M. Ghosal, K. Tiwari and P. Sen, J. Phys. Chem. Lett., 2021, 12, 546–551.
63. S. Kundu, M. Ghosh and N. Sarkar, Langmuir, 2021, 37, 9281–9301.
64. U. Mandal, S. Ghosh, S. Dey, A. Adhikari and K. Bhattacharyya, J. Chem. Phys., 2008, 128, 164505–164510.
65. S. Koley and S. Ghosh, Phys. Chem. Chem. Phys., 2016, 18, 24830–24834.
66. S. K. Mondal, S. Ghosh, K. Sahu, P. Sen and K. Bhattacharyya, J. Chem. Sci., 2007, 119, 71–76.
67. U. Mandal, S. Ghosh, G. Mitra, A. Adhikari, S. Dey and K. Bhattacharyya, Chem. – Asian J., 2008, 3, 1430–1434.
68. D. Acharjee, A. B. Mahato, A. Das and S. Ghosh, J. Phys. Chem. C, 2023, 127, 19643–19650.
69. K. Mishra, D. Acharjee, A. Das and S. Ghosh, J. Phys. Chem. B, 2021, 125, 11017–11025.
70. S. Ghosh, U. Mandal, A. Adhikari, S. Dey and K. Bhattacharyya, Int. Rev. Phys. Chem., 2007, 26, 421–448.
71. A. Adhikari, S. Dey, U. Mandal, D. K. Das, S. Ghosh and K. Bhattacharyya, J. Phys. Chem. B, 2008, 112, 3575–3580.
72. G. Bounos, S. Ghosh, A. K. Lee, K. N. Plunkett, K. H. DuBay, J. C. Bolinger, R. Zhang, R. A. Friesner, C. Nuckolls, D. R. Reichman and P. F. Barbara, J. Am. Chem. Soc., 2011, 133, 10155–10160.
73. K. Bharadwaj, H. Choudhary, S. Hazra and S. Ghosh, ChemPhysChem, 2020, 21, 415–422.
74. S. Chakrabarty, H. Kaur, T. Pal, S. Kar, S. Ghosh and S. Ghosh, RSC Adv., 2014, 4, 35531–35540.
75. S. Ghosh, K. Sahu, S. K. Mondal, P. Sen and K. Bhattacharyya, J. Chem. Phys., 2006, 125, 054509.
76. M. K. Panda, D. Acharjee, N. Nandi, S. Koley and S. Ghosh, Chem. – Eur. J., 2024, e202401938,  DOI:10.1002/chem.202401938.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr02221a

---