Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding the nanoscale phenomena of nucleation and crystal growth in electrodeposition
Jiancheng
Lin
 a,
Mohamed
Kilani
a,
Mohamed
Kilani
 a,
Mahroo
Baharfar
a,
Ren
Wang
a,
Mahroo
Baharfar
a,
Ren
Wang
 a and
Guangzhao
Mao
a and
Guangzhao
Mao
 *ab
*ab
aSchool of Chemical Engineering, University of New South Wales (UNSW Sydney), Sydney, New South Wales 2052, Australia. E-mail: guangzhao.mao@unsw.edu.au
bSchool of Engineering, Institute for Materials and Processes, The University of Edinburgh, Robert Stevenson Road, Edinburgh, EH9 3FB, UK
First published on 7th October 2024
Abstract
Electrodeposition is used at the industrial scale to make coatings, membranes, and composites. With better understanding of the nanoscale phenomena associated with the early stage of the process, electrodeposition has potential to be adopted by manufacturers of energy storage devices, advanced electrode materials, fuel cells, carbon dioxide capturing technologies, and advanced sensing electronics. The ability to conduct precise electrochemical measurements using cyclic voltammetry, chronoamperometry, and chronopotentiometry in addition to control of precursor composition and concentration makes electrocrystallization an attractive method to investigate nucleation and early-stage crystal growth. In this article, we review recent findings of nucleation and crystal growth behaviors at the nanoscale, paying close attention to those that deviate from the classical theories in various electrodeposition systems. The review affirms electrodeposition as a valuable method both for gaining new insights into nucleation and crystallization on surfaces and as a low-cost scalable technology for the manufacturing of advanced materials and devices.
Introduction
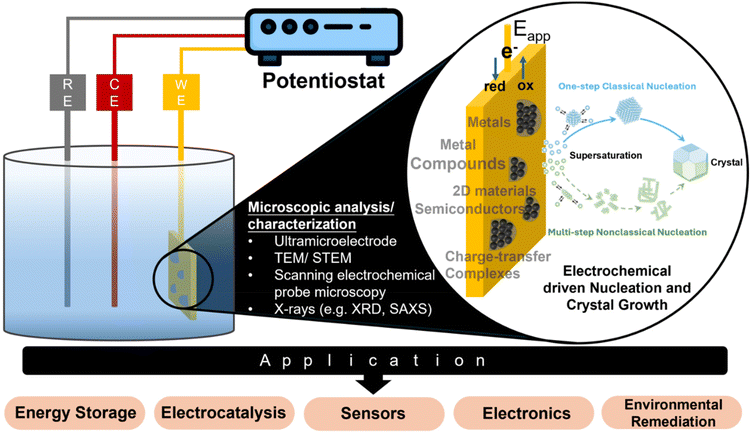
Electrodeposition is a widely used industrial process for depositing monolayers, thin films, and thick coatings onto conductive substrates for electroplating applications.1–3 The typical electrodeposition setup consists of a working electrode (WE), a counter electrode (CE), and a reference electrode (RE) (Fig. 1). Electrocrystallization refers to the formation of stable nuclei, achieved through the electroreduction of metal ion precursors or the electrooxidation of other precursor types on the surface of the working electrode. The electrocrystallization process involves nucleation, followed by addition of atoms, molecules, or other monomeric building blocks to the nuclei to facilitate the growth of thin films or 3D crystals, known as crystal growth.4 While the term “electrodeposition” is commonly used in application-focused contexts, and “electrocrystallization” is more often associated with fundamental studies of nucleation and crystal growth, the two terms are frequently used interchangeably. This is because electrodeposited coatings are often crystalline in nature. One can find industrial relevance of electrocrystallization beyond electroplating. For example, in energy storage devices, uncontrolled electrocrystallization of metal anodes, during repeated cycles of charge and discharge, results in significant degradation of device performance.5 The catalytic performance of electrocatalysts is often shape- or surface morphology-dependent, and electrocrystallization offers control over these properties.6 Electrocrystallization is also a promising lower energy alternative for synthesizing functional materials, which find applications in a wide range of industries.7–10Table 1 provides a comparative summary of electrodeposition versus non-electrochemical processes for direct synthesis or deposition of different materials.| Technique | Advantages | Disadvantages | Material type | Dimension | Ref. |
|---|---|---|---|---|---|
| Electrodeposition | Cost effective, simple process set-up, relatively easy to scale up, ambient condition process, wide variety of deposits by choosing the right precursors and conditions, one-step synthesis and assembly is possible | Requires conductive surface for growth, which can limit device configuration, can have low crystallinity and requires post treatment, unapplicable to insulating materials | Metal | 0D, 3D | 15–17 |
| Metal compound, e.g., oxides, hydroxides, dichalcogenides, nitride | 0D, 1D, 2D, 3D | 10 and 18–21 | |||
| Metal–organic framework | 3D | 22 and 23 | |||
| Charge-transfer complex | 1D | 24 and 25 | |||
| Polymer | 2D | 26 | |||
| Chemical vapor deposition (CVD), e.g., metal organic, plasma enhanced, atomic layer deposition | Controllable thickness for 2D structures, scalable to some extent, high quality and conformity 2D crystal | High vacuum and temperature needed for the process, high capital and operational cost, suitable substrate needed for growth of high-quality crystals, gaseous precursor can be dangerous to handle, slow deposition rate, requires specialized trained personnel for operation | Metal compounds, e.g., oxide, dichalcogenides, carbide | 1D, 2D | 27–30 |
| Metal–organic framework | 2D | 31 and 32 | |||
| III–V compound | 1D, 2D | 33–35 | |||
| Polymer | 2D | 36 | |||
| Physical vapor deposition (PVD), e.g., e-beam, sputtering, pulsed laser, molecular beam epitaxy | Wafer-scale deposition is possible, may require lower operating temperature than CVD | High vacuum and temperature needed for the process, high capital and operational cost, slow deposition rate, requires specialized trained personnel for operation, specific substrate is necessary for highly crystalline product, poorer crystallinity or smaller grain size as compared to CVD | Metal compounds, e.g., oxides, dichalcogenides | 2D | 37 and 38 |
| Solution-based chemical methods, e.g., hydrothermal, solvothermal, sol–gel, hot-injection, solvent evaporation | Some solution-based process does not require specific specialized equipment, compatible with conventional chemical reactor, can achieve morphological change by simply altering reaction conditions | Process time can be very long, up to several hours for the case of hydrothermal method, precise control over reaction rate can be challenging, often involve two-step: synthesis and assembly – difficult to scale | Metal compounds, e.g., halides, oxides | 0D, 2D | 39–41 |
| Charge-transfer complex | 1D, 2D | 42 |
Fig. 1 outlines in situ analytical techniques for advancing the microscopic understanding of the electrocrystallization processes and its impact on real-world applications, which will be described in detail in the section on “Experimental Techniques for Electrochemical Nucleation and Growth”. The microscopic picture of nucleation and crystal growth, at the nanoscale or even atomic scale, continues to evolve, facilitated by advances in experimental and modeling tools. Due to the growing importance of electrodeposition in cutting-edge technologies such as battery technology, fuel cells, electrocatalysis, sensors, wearable electronics, and environmental remediation, this review fills a gap in current literature by putting together latest findings that have contributed significantly to our understanding of electrochemical nucleation and growth down to the single-nanoparticle level. We include electrodeposition of nonmetals including charge-transfer complexes (CTCs), metal organic frameworks (MOFs), mineral salts, and metal oxides, which are not typically discussed with metal electrodeposition. We benefit from earlier reviews and perspectives on aspects of electrochemical nucleation and crystal growth.11–14
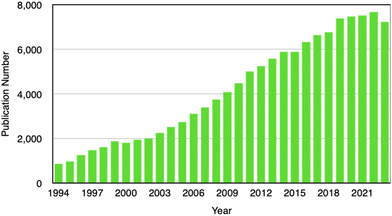
Our literature survey shows that Li electrodeposition and dendrite formation have continuously been of interest to researchers because of the relevance in mitigating battery degradation. Others delve into the challenge in controlling electrodeposition for catalysis, sensing, wearable electronics, and environmental applications. A search on the Web of Science using keywords including “electroplating”, “electrodeposition”, “electrochemical deposition”, “electrocrystallization”, and “electrochemical crystallization” indicates a sustained interest in this field (Fig. 2). Despite the increasing importance of electrodeposition in cutting-edge technologies such as battery technology, fuel cells, electrocatalysis, sensors, wearable electronics, and environmental remediation, to our best knowledge there are no recent reviews on nanoscale understanding of electrodeposition. This review therefore fills this significant gap by putting together latest findings that have contributed to our understanding of electrochemical nucleation and growth down to the single-entity level. In-depth understanding of the electrodeposition process will enable precise control of nanostructure formation and enable wide adoption of electrodeposition by manufacturers of energy storage devices, advanced electrode materials, fuel cells, carbon dioxide capturing technologies, and advanced sensing devices. A better understanding of nucleation and initial crystal growth will lead to the realization of desirable and reproducible functional properties in electrodeposited thin films, coatings, devices, and systems.
Classical and nonclassical nucleation and crystal growth theories for electrodeposition
Classical theories
The electrocrystallization process can be described by the classical nucleation theory with the primary driving force being the electrochemical overpotential, η, which is defined as the difference between the applied potential and the equilibrium potential at zero current. According to the classical nucleation theory, the formation of a nucleus is a one-step process, wherein atom-by-atom assembly, driven by density fluctuations, culminates in the attainment of the critical nucleus size, rcritical, positioned at the peak of the free-energy nucleation barrier (the Gibbs free energy for nucleation), ΔGnucleation. Once this critical point is reached, a microscopic nucleus becomes stable and grows in size while maintaining the same crystalline packing structure and chemical composition. The solid arrows in Fig. 3a illustrate the nucleation pathway in accordance with the classical nucleation theory and the solid curve in Fig. 3b shows the corresponding single energy barrier.43 The Gibbs free energy, ΔG, for a spherical nucleus of radius r is determined by the sum of a bulk free energy term, ΔGbulk, and a surface free energy term, ΔGsurf, as follows.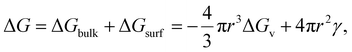 | (1) |
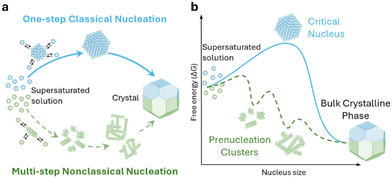 | ||
| Fig. 3 Schematic representation of classical vs. multi-step nucleation mechanisms for (a) the formation of crystals from supersaturated solutions and (b) their corresponding energy barriers: a single barrier in classical nucleation (solid blue curve), a multi-step barrier model for nonclassical nucleation (dashed green curve) and associated prenucleation clusters. Redrawn from ref. 43. | ||
Now specific to electrocrystallization, ΔGv varies with η according to the following equation:11
| ΔGv = zF|η|/Vm, | (2) |
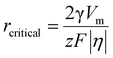 | (3) |
The number of atoms in the critical nucleus, Ncritical, is related to rcritical and proportional to γ3/|η|3:
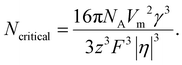 | (4) |
Here, NA is the Avogadro's number.
In the classical nucleation theory, the nucleation rate, J (number of nuclei formed per area per second), varies with η as follows.
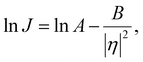 | (5) |
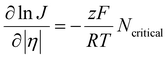 | (6) |
Here, R is the gas constant and T is the temperature. An alternative model to the classical nucleation theory that describes electrochemical nucleation is the atomistic model developed by Milchev et al.44,45 Similarly, the atomistic model describes the nucleation process being atom-by-atom addition and predicts a critical number of atoms for a thermodynamically stable nucleus to form. The difference is that the atomistic model takes into account of the energy associated with the interaction between individual atoms and their interactions with the electrode surface, instead of the interfacial energy of the nucleus.46–48
If electrodeposition is limited by diffusion, nucleation can be defined as instantaneous or progressive. If the number of nuclei remains the same (N = N0) from the start of the potential step in potentiostatic electrodeposition, then it is instantaneous nucleation. If N increases with time, t, then it is progressive nucleation. The Scharifker–Hills model has been widely used for analyzing the current–time curves in potentiostatic electrodeposition of metals:49–54
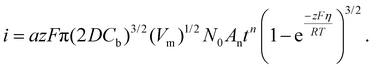 | (7) |
Taking into account of the electrochemical reaction (charge transfer) step at the solution/electrode interface, Fletcher derived the following equation for the current–time behavior in electrodeposition of hemispherical metal nuclei of radius r (the Fletcher model):58
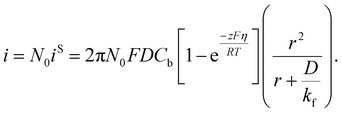 | (8) |
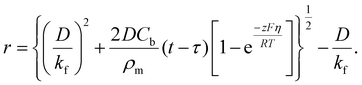 | (9) |
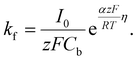 | (10) |
Here, iS is the current for a single nucleus formation, N0 is the number of isolated nuclei formed instantaneously, ρm is the molar density, I0 is the exchange current density determined by the Tafel plot,59α is the charge-transfer coefficient, τ is the nucleation induction time, and the rate constant of the deposition reaction, kf, is given by eqn (10). Building on these works, models were developed to better describe the current–time transient during the early stage of electrodeposition in the mixed reaction-diffusion control regime.60,61 Regardless, these models enabled the determination of J and Ncritical based on the current–time transient.
Crystal growth according to the classical theories progresses by incremental addition of atoms (or molecules), resulting in the replication of unit cells in the growing crystal, with no accompanying structural changes. Crystal growth is described by the Frank–van der Merwe 1D growth, 2D monolayer growth, or Volmer–Weber 3D island growth mechanisms.62 In general, strong adatom and surface interactions favor 2D growth while weak interactions favor 3D island growth. Under equilibrium conditions, the shape (morphology) of the single crystal is dictated by the minimization of total Gibbs surface free energy, as prescribed by the Wulff theorem.63 With increasing chemical potential driving force (e.g., higher η), the surface integration of atoms changes from the spiral 1D growth mechanism to 2D growth mechanism where atoms attach to kinks and steps on the bulk crystal surface and the rough growth mechanism associated with spherulitic, fractal, and dendritic patterns. Fractal (dendritic) growth, particularly relevant for Li batteries, can be described by diffusion-limited aggregation assuming irreversible adatom sticking upon initial contact with the crystal surface.64,65
The key steps in 2D electrodeposition are: (1) bulk diffusion, which involves atoms and molecules moving from solution to the electrode surface as adatoms; (2) charge transfer, which involves the transfer of charge at the electrode surface; (3) surface diffusion, which involves atoms or molecules moving along the electrode surface with the surface diffusion rate determined from logarithmic density of 3D islands vs. 1/T plot; and (4) transfer from adatom to step or kink position, which is defined by the transition of atoms or molecules from their initial adatom position to either a step or kink position on the crystalline surface.11 Moreover, the Winand diagram has been used as an empirical guide to predict crystal morphology based on i (normalized by the diffusion-limiting i) and the inhibition intensity.66 Inhibition refers to any factor that slows down surface reactions, such as adsorbed species requiring displacement by primary metal cations at the electrode surface. According to the Winand diagram, the combination of low i and slow surface reaction results in higher degree of order in the electrodeposited thin films.
For the 3D growth of a single particle, the crystal growth rate of a spherical particle of radius r can be expressed by eqn (11)–(13) depending on the nature of the rate-limiting step.67 If diffusion is the rate-limiting step, the crystal growth rate can be derived from Fick's first law:
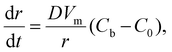 | (11) |
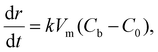 | (12) |
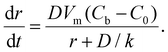 | (13) |
In electrocrystallization, the growth rate varies with η. In the case of a reaction-limited system, the growth rate of a hemispherical nucleus on an electrode surface is described as following:68
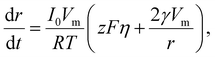 | (14) |
Nonclassical theories
Classical nucleation and crystal growth theories remain valuable in interpreting CV, chronoamperometry, and chronopotentiometry data. Not surprisingly, with new experimental and simulation tools, studies have revealed complex, dynamic, and multistep processes69–77 that cannot be solely described by the classical theories. Electrocrystallization being a sub-field of crystallization systems has contributed to this accumulating body of evidence of nonclassical behaviors, which are exhibited by diverse material types. Fig. 3 highlights the differences between classical and nonclassical theories wherein nonclassical nucleation displays complex, dynamic, multistep nucleation pathways (green arrows, Fig. 2a) and multiple nucleation energy barriers (green dashed curves, Fig. 2b). Intermediate clusters with nanostructures different from both the mother phase and the new crystalline phase have been observed in metals,78–82 inorganic compounds such as tungsten carbide,83 zinc oxide,84 iron oxide,85 cerium oxide,86 zeolite,87–92 sodium chloride,93 calcium carbonate,94–97 calcium phosphate,98 calcium sulfate,99 and calcium hydroxide,100 organic molecules,101,102 metal–organic frameworks (MOFs),103 and large colloidal particles and proteins.104–107 Nonclassical nucleation theories introduce the concept of prenucleation clusters (PNCs) as stable building blocks108–113 as opposed to individual atom/molecule building blocks in classical theories. Depending on the material, PNCs can be an aggregation of atoms, ions or molecules with size ranging from a few nanometers down to a few angstroms.95Crystal growth through particle aggregation and coalescence has also been observed.114 In zeolite crystallization, a wide range of crystal growth pathways have been identified including monomer-by-monomer, oligomers, gel-like islands, amorphous nanoparticles, colloidal assembly, and oriented attachment.87 We want to point out that electrocrystallization models to explain nonclassical behaviors observed in electrodeposition use the same concepts of nanocluster surface diffusion and aggregation, orientated attachment, and recrystallization13,115–120 as those in zeolite crystallization. The concept of a nanocluster building block was utilized in the formulation of the generalized electrochemical aggregative growth mechanism for metal electrodeposition on low-energy surfaces (Fig. 4).13 The nanoclusters with self-limiting growth are similar in concept to the PNCs found in many nonelectrochemical crystallization systems.108–113 According to the aggregative growth model, nanocluster surface diffusion is explained by adatom dissolution and re-adsorption process, i.e., the higher the mobile adatom concentration on the nanocluster, the higher the surface diffusion coefficient of the nanocluster. The surface diffusion coefficient increases with increasing η. The rates of nanocluster coalescence and recrystallization also increase with increasing η. A major deviation from the classical picture is in the interpretation of the current–time transients in the induction period of metal electrodeposition. The induction time in the chronoamperometric data according to the electrochemical aggregative growth mechanism is related to aggregate–nucleation events rather than to the standard nucleation process. The crystal growth pathways are η dependent. This aggregative growth phenomenon during the early stages of electrodeposition highlights the risk that values of J and Ncritical calculated using the classical model may deviate significantly from the experimental results through in situ surface analysis.12
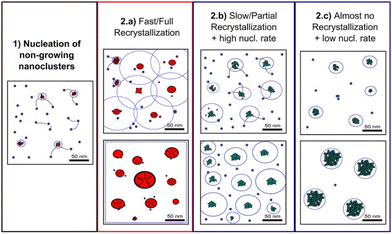 | ||
| Fig. 4 Schematic diagram showing the different crystallization stages of the generalized electrochemical aggregative growth mechanism. Dots represent the nongrowing nanoclusters and blue circles around the aggregates represent their nucleation exclusion zones. Black stripes within a particle represent defects. Reprinted with permission from ref. 13. Copyright 2013 American Chemical Society. | ||
Variations to the classical Volmer–Weber 3D island growth model based on nanocluster aggregation have been proposed by the Unwin group.117 The nanocluster aggregation rate constant, kAGG, can be extracted from the experimental chronoamperometric curves. The nanocluster nucleation rate, kN, and the nucleus dissolution rate, kD, can be expressed as following:
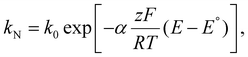 | (15) |
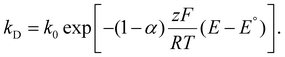 | (16) |
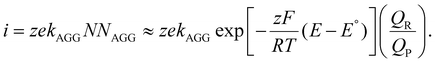 | (17) |
Here, N is the number of isolated nanoclusters, NAGG is the number of aggregated nanoclusters, QR is total charge passed in an i–t transient, and QR is the charge passed per nanocluster. kAGG varies with η.
Other nonclassical crystal growth mechanisms include oriented attachment121–126 and Ostwald ripening growth.127,128 The oriented growth model assumes that nanoclusters with short-range orders can directly attach to each other or to larger crystals. For example, CaSO4·2H2O undergoes a three-stage crystal growth process:126 (1) homogeneous precipitation of nanocrystalline hemihydrate bassanite below its predicted solubility, (2) self-assembly of bassanite into elongated aggregates co-oriented along their c axis, and (3) transformation into dihydrate gypsum. This oriented attachment has recently been observed in the electrocrystallization of the charge-transfer complex (CTC) cobalt tetracyanoquinodimethane complex (Co-TCNQ).25 For the Ostwald ripening growth, the Lifshitz–Slyozov–Wagner (LSW) theory is used to describe the crystal growth kinetics of a spherical particle with radius r a follows.129,130
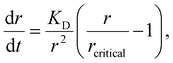 | (18) |
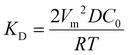 and
and 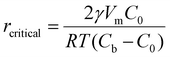 . It is noted that the dynamic nature of nanoclusters in nonclassical crystallization make them very different from the static building blocks in the well-studied colloidal crystallization.
. It is noted that the dynamic nature of nanoclusters in nonclassical crystallization make them very different from the static building blocks in the well-studied colloidal crystallization.
Our literature review of electrodeposition identifies many instances that deviate from the classical behaviors, which will be discussed in detail in the last part of the paper. While theoretical treatments of nucleation and crystal growth in electrodeposition remain limited, we foresee future development to be significantly aided by advances in nanomaterials characterization tools with increasing spatiotemporal resolutions. New method development for the characterization of electrochemical nucleation and early-stage crystal growth will be highlighted in the next section.
Experimental techniques for electrochemical nucleation and growth
Traditional electrochemical measurements such as chronoamperometry and CV are used both for electrodeposition and electroanalysis of the electrodeposition process. In galvanostatic electrodeposition, the current is kept constant to achieve uniform deposited nanoparticle size. In potentiostatic electrodeposition, a constant potential is applied for a period of time and the current vs. time data are collected. The current–time measurements correspond to average behaviors of large ensembles at the macroscopic level. Therefore, more advanced techniques are needed for the investigation of nanoscale phenomena in electrodeposition.The ultramicroelectrode technique
To gain microscopic understanding of electrodeposition, the ultramicroelectrode technique has been developed.131–141 Ultramicroelectrodes, by definition, are electrodes with dimeter smaller than 25 μm. With innovative experimental setups and advanced fabrication tools, sub-micron and nanoelectrodes of smaller than 500 nm are also made possible.48,142,143 We recently reviewed the application of ultramicroelectrodes for the study of electrocrystallization of diverse materials.132 The ultramicroelectrode technique exhibits major advantages over bulk electrodes due to their small size enabling steady-state measurements with ultra-sensitivity down to the single entity. These advantages make ultramicroelectrodes ideally suited for fundamental studies of early-stage electrodeposition of both metallic and nonmetallic materials. Electrocrystallization experiments carried out with ultramicroelectrodes could further reveal the limitations of the classical nucleation theory and enable the development of new theories for understanding and controlling electrodeposition. Combining the ultramicroelectrode technique with advanced imaging instrumentation allows simultaneous chronoamperometric or chronopotentiometric experimentation and real-time characterization of nanoparticle formation and elucidate the nano/atomic-scale phenomena associated with electrodeposition.Here we review microscopic and X-ray methods that have been used to capture nucleation and crystal growth events at the single-entity level, typically at or smaller than nanoscale, most relevant to electrodeposition. An excellent review on in situ kinetic observations of crystal nucleation and growth has been provided by Li and Deepak.131 We keep this part brief by focusing on aspects of the methods that are most relevant for the monitoring of the electrochemical process. Table 2 summarizes the various techniques, principles, and applications in electrodeposition.
| Technique | Advantages | Disadvantages | Applications in electrodeposition | Ref. |
|---|---|---|---|---|
| TEM/STEM | High resolution within atomic to micro range, possibility of structural, morphological, and phase characterization | Challenges in electron beam focusing across liquid electrolyte, the effect of electron beam on structures and electrolyte, limited probing area, electrochemical data might be impacted by using a thin layer of electrolyte | Observation of lithiation/delithiation in Si terminals, characterization of crystal nucleation and growth during electrocrystallization | 144–154 |
| SEPM | Real-time observation of morphological, topographical, and electrochemical features | Lower resolution compared to TEM and STEM, the possible effect of mechanical forces on structures, probe effect | Versatile technique for observation of in situ electrocrystallization, monitoring electrocatalytic reactions in real time, imaging electrochemical activity of nanostructures, monitoring electrode surface dynamics | 155–157 |
| XRD/SAXS | Non-destructive, large probing area, provides crystallographic information | Poor signal-to-noise ratio in case of limited amount of sample, insensitivity to intermediate amorphous structures | Monitoring catalytic interfaces during catalysis, real-time observation of crystallization (non-classical nucleation in particular) | 81 and 158 |
Liquid-cell transmission electron microscopy (LCTEM) and scanning transmission electron microscopy (STEM)
Electrochemical LCTEM (EC-LCTEM) and STEM utilizing electrochemical liquid cells are powerful tools for real-time monitoring of nucleation and early-stage crystal growth in electrodeposition.144–154An essential component for EC-LCTEM is a liquid cell that can accommodate both the electrochemical reaction on the working electrode and TEM imaging. Radisic et al. in 2006 reported one of the earliest LCTEM studies of electrocrystallization of Cu with simultaneous chronoamperometry and TEM data capture.146 A 1–2 μm thick electrochemical cell was constructed to enclose the electrolytic solution between two Si3N4 windows, one of which contained a micropatterned Au working electrode. The Au ultramicroelectrode was connected to the leads that were connected to an electrochemical workstation to perform electrodeposition and electroanalytical measurements. In 2014, Unocic et al. introduced a microfluidic electrochemical liquid cell design for STEM imaging, diffraction, and spectroscopy.150 The microfluidic electrochemical liquid cell has a three-electrode configuration with glassy carbon (GC) and Pt microband electrodes. The electrochemical cell design was further improved by using a thin nanofluidic channel TEM liquid sample holder with two Si3N4 windows and a metal-coated microchip serving as the working electrode.144 Multiple ultramicroelectrodes can be built into the same liquid cell holder so that multiple experiments can be performed on the same microchip, and the ultramicroelectrode geometry can be varied to control the assembly of nanostructures.148 To mitigate systematic errors in electrochemical measurements inside a TEM liquid cell Fahrenkrug et al. provided design criteria for TEM liquid cells used in conjunction with electrochemical measurements.144
LCTEM and STEM studies of electrodeposition will be described in detail in the following section. Here, we highlight a few recent examples of their use in capturing atomic-level evidence of non-classical nature in nonelectrochemical crystallization systems. The purpose of including these examples is to forecast the potential use of LCTEM and STEM for electrocrystallization studies.
Low-dose LCTEM was used to monitor the transition of dispersed Au nanoprisms to an Au superlattice at the single-particle level.82 Combining real-time particle tracking with Monte Carlo simulations, a nonclassical nucleation pathway involving a dense, amorphous intermediate was identified. In another study, aberration-corrected TEM captured a nonclassical nucleation process in which Au crystal nucleates via reversible structural fluctuations between disordered and crystalline states at atomic spatial resolution and millisecond temporal resolution.80 This study cleverly used the energy of the electron beam to initiate Au recrystallization from preformed Au nanoribbons to enable real-time monitoring of Au crystallization at the single-atom resolution.
LCTEM has played a critical role in confirming the existence of PNCs in crystallization of inorganic compounds such as NaCl93,159 and CaCO3.109 Several precursors, such as amorphous calcium carbonate (ACC), prenucleation crystals, and embryos, have been captured by LCTEM in CaCO3 nucleation.160 The study found that among 150 prenucleation crystals, only one exceeded Ncritical (∼104 molecules). The lifetime of the prenucleation crystals was independent of their size, which implies the existence of several different prenucleation polymorphs. An important recent work on nucleation and early-stage crystallization was reported by Nakamuro et al. utilizing in situ LCTEM to monitor NaCl crystallization confined to a vibrating carbon nanotube cone.93 In the narrow apex of the carbon nanotube, a transient NaCl nanocluster was repeatedly found to fluctuate between amorphous and semi-ordered states with a sudden appearance of a crystalline nucleus (Fig. 5). LCTEM images revealed a two-step nucleation mechanism that involves multiple nonproductive semi-ordered nanoclusters before the final crystalline nanocluster. After reaching stable nucleation, classical homoepitaxial crystal growth was found to take place stochastically in the vibrating carbon nanotube in NaCl crystallization.
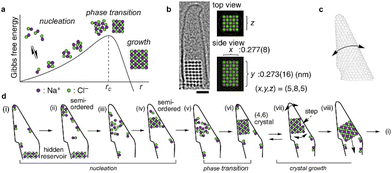 | ||
| Fig. 5 Nucleation and growth of a NaCl nanocrystal in a vibrating carbon nanotube. (a) Schematic energy diagram of NaCl crystallization according to the classical nucleation theory. (b) LCTEM image of a NaCl nanocrystal. Scale bar = 1 nm. (c) Schematic drawing of the vibrating conical carbon nanotube. (d) Schematic diagram of fluctuating PNCs prior to stable nucleation confirming a two-step nucleation mechanism and subsequent classical homoepitaxial crystal growth. Reprinted with permission from ref. 93. Copyright, 2021 The Authors under CC-BY-NC-ND license, published by American Chemical Society. | ||
Scanning electrochemical probe microscopy (SEPM) techniques
SEPM techniques are a family of scanning-based instruments including scanning electrochemical microscopy (SECM), scanning ion conductance microscopy (SICM), electrochemical scanning tunneling microscopy (ECSTM), electrochemical atomic force microscopy (ECAFM), and scanning electrochemical cell microscopy (SECCM). These techniques have been comprehensively described by Santana Santos et al. in the context of electrocatalysis.155 Here we briefly describe features relevant to electrodeposition in SEPM techniques together with electrochemical atomic force microscopy (ECAFM).SECM utilizes ultramicroelectrodes as scanning probes for electrochemical characterization of surfaces.161–163 First reported in 1989 by Bard et al.161 the scanning ultramicroelectrode probe moves above a substrate surface in an electrolytic solution enclosed in an electrochemical liquid cell. The electrodeposition process can be monitored in the collection mode by the probe either held at a constant potential or operated during CV scans. Electrodeposition can also be monitored by the tip current change in the feedback mode. The conductive probe allows imaging of contact currents and electrochemical currents in addition to topographical imaging. The spatial resolution of SECM is limited by the size and geometry of the ultramicroelectrode scanning probe.
A technique related to SECM is ECAFM, which offers improved spatial resolution to SECM by combining liquid-cell AFM (LCAFM) with a sharp but nonconductive probe and a three-electrode electrochemical cell. ECAFM and ECSTM, connectively known as electrochemical scanning probe microscopy (ECSPM), enable in situ measurements of electrodeposition on conductive sample surfaces.156 An earlier ECSTM investigation focused on the electrodeposition and dissolution of Ag at the HOPG working electrode.164 The electrical circuit was made of a four-electrode cell in a bipotentiostat mode so that the electrochemical current at a constant potential could be monitored simultaneously with the tunneling current between the STM tip and the sample/working electrode surface. ECSTM captured a single Ag nanoparticle whose morphology is consistent with the 3D island crystal growth mechanism. More recently, ECAFM has been used to simultaneously characterize the size and electrochemical properties of individual Pt nanoparticles on Si though an electroless plating process.157 While STM offers atomic resolution it also has more stringent requirements such as sample conductivity required to generate the tunneling current. In contrast, ECAFM is more versatile, only requiring the sample to be connected to an external potentiostat. Development of commercial high-speed ECSPM will further enable measurements of fast nucleation and crystal growth phenomena at the electrode surface.165 Like all scanning probe techniques effects of the probe need to be considered in interpreting electrodeposition data.
SICM utilizes a nano-sized electrolyte-filled glass pipette as a scanning probe.166–168 In the original nonmodulated mode, ion current is generated by applying a constant potential bias between an electrode inserted into the electrolyte in the pipette and the reference electrode in the bath electrolyte outside the pipette. A topographical image is obtained while the probe scans over the surface through a feedback mechanism similar to that of AFM. More advanced modes have been developed including modulated, pulse, hopping, and hybrid modes.167 SECCM improves on the SICM technique by employing a mobile meniscus containing the electrolytic solution in contact with a working electrode surface. Combined with SEM, TEM, AFM, Raman spectroscopy, and electron backscatter diffraction (EBSD), precise knowledge of the size of the electrochemical cell formed between the nanopipette meniscus and the surface can be obtained.169–173 The Unwin group developed the nonclassical nucleation–aggregative growth–detachment model118 based on the data from their SECCM studies and will be described in more details below.
X-ray methods
In situ small angle X-ray scattering (SAXS), X-ray absorption spectroscopy (XAS), and high-energy X-ray diffraction (HE-XRD) have played a role in capturing nonclassical nucleation pathways such as those involving PNCs in chemical reduction synthesis of Au nanoparticles.81 X-ray methods combined with local imaging probes discussed above are often required to solve complex surface structures during electrodeposition.X-ray diffraction (XRD) is an essential tool for crystal structure determination. For nucleation and early-stage crystal growth in electrodeposition, surface X-ray diffraction (SXRD) or grazing-incidence XRD combined with synchrotron can resolve atomic layer structures of a crystal as well as species near the electrolyte/electrode interface on the solution side such as the Stern layer.158 X-rays scattered at a sharp surface form crystal truncation rods whose intensities can be modelled to yield dynamic information on surface structures such as chemical bond length, adlayer ordering, and surface restructuring when operated in situ. In an in situ SXRD study of Pt electrochemistry, an electrochemical cell was constructed with electrolyte droplet in a capillary in contact with a working electrode to limit the electroactive area of study (improving the quality of CV),174 reminiscent of SECCM. Other advanced XRD methods include energy dispersive SXRD, high-energy SXRD, transmission SXRD, and coherent surface X-ray scattering.158
In situ X-ray can also be combined with spectroscopies such as Raman spectroscopy and molecular dynamics (MD) simulations to further determine the chemical structure of deposited species during nucleation and crystal growth.159,175
Next, we delve into individual studies that shed new lights on electrochemical nucleation and early-stage crystal growth of diverse materials starting with the most studied class of materials – metals.
Electrodeposition of elemental metals and semiconductors
As can be seen from the following discussion, our understanding of early-stage electrodeposition remains largely obtained from studies of metal deposition to this date.Au
Nonclassical nucleation and crystal growth have been captured by STEM at the single-atom resolution for Au electrodeposition. Atomic resolution was achieved by combining identical location-STEM with repeated electrodepositions and ex situ STEM imaging of the same area.120 During early-stage (0–30 ms) of Au electrodeposition on a boron-doped diamond (BDD) working electrode, STEM images show that isolated Au atoms aggregate into either disordered nanoclusters or ordered nanoparticles in response to an applied potential (Fig. 6). Neighboring nanoclusters were shown to interact with each other, and the disordered nanoclusters were consumed by a nearby nanoparticle via a cluster disintegration process. The growth of the nanoparticles does not follow the Ostwald ripening mechanism; instead, the growth occurs by the addition of atoms from neighboring nanoclusters through surface diffusion and direct reduction of Au ions to Au atoms at the nanoparticle surface. Considering disordered Au nanocluster intermediates also been captured during electron beam-induced Au nucleation on graphene,80 we see a common nucleation pathway between electrochemically-driven and non-electrochemically-driven nucleation of Au nanocrystals. Interestingly, the same study120 also captured stable single Au atoms on the BDD electrode, which has important implications for single atom-based applications such as electrocatalysis and magnetism.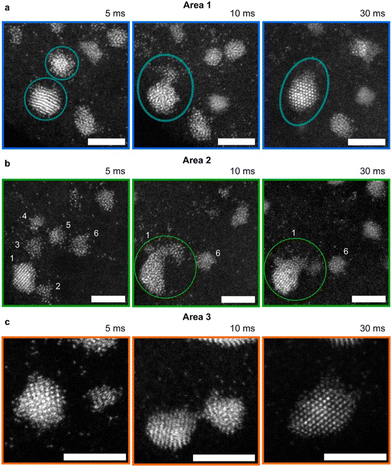 | ||
| Fig. 6 STEM images of Au nanoclusters and dynamic interactions with Au nanoparticles during electrodeposition. (a–c) Au nanocluster and nanoparticle interactions during Au electrodeposition in three different areas at growth times of 5, 10, and 30 ms. The electrodeposition potential is −0.5 V vs. SCE. Au nanoclusters disintegrate to provide atoms to a neighboring crystalline nanoparticle. The nanoparticle becomes disordered first and then ordered due to recrystallization. Scale bar = 3 nm. Reproduced from ref. 120 with permission from the American Chemical Society. | ||
Ag
The Unwin group pioneered the use of SECCM for the study of metal electrodeposition and established a nonclassical nucleation–aggregative growth–detachment mechanism.118 As in microelectrodes, SECCM enables the steady-state characterization of a small number of nucleation events by confining the electrolyte/electrode interface to micrometer size with a nanoscale pipette. The current–time traces obtained by SECCM show discrete current peaks (Fig. 7A), which correspond to Ag nanoparticles of diameter 30 nm. The i–t traces show that Ag nanoparticles repeatedly nucleate and detach from the HOPG surface. They found discrepancy in nanoparticle nucleation density between the results from the Scharifker–Hills calculations (eqn (7)) and those from ex situ AFM. They then proposed a nucleation–aggressive growth–detachment mechanism for metal electrodeposition (Fig. 7B). According to this mechanism, multiple critical Ag nuclei nucleate on the HOPG electrode. As the nuclei grow into nanoparticles, the Ag+ ion concentration becomes depleted, and the growth becomes diffusion limited. At the same time, to minimize surface tension, mobile nuclei aggregate to form nanoparticles. Once the growing nanoparticle reaches a critical size, it detaches from the electrode surface. Subsequently the Ag+ ion concentration is replenished by bulk diffusion to repeat the nucleation–aggregative growth–detachment cycle. This mechanism is applicable to metal electrodeposition on a dissimilar substrate surface with weak deposit/substrate interactions. In heterogeneous nucleation without the electrochemical driving force, nucleation is promoted by favorable interfacial energy terms to give rise to strong deposit/substrate interactions at near equilibrium conditions. The strong interfacial interactions reduce nucleus mobility and likelihood of detachment from the substrate surface.Cu
Electrodeposition and dissolution of Cu in acidic electrolytes are relevant to the microelectronics industry. As early as 1992, the initial stage of Cu deposition on Au single-crystal electrodes was studied by in situ ECSTM.176 It was determined that Cu forms a monolayer in underpotential deposition and small clusters in overpotential deposition. The study by Radisic et al. in 2006 with combined LCTEM and chronoamperometry yielded findings that are consistent with the classical 3D island growth model.146 The study concluded that Cu electrodeposition follows first-order kinetics and 3D diffusion-limited growth. More recently, EC-LCTEM imaging of Cu electrodeposition was carried out on a W–Au ultramicroelectrode.148 Time-lapse TEM images during linear sweep voltammetry were obtained. After Cu grains first nucleated on the small area of exposed W before nucleating on the Au patch, and they grew larger at more negative potentials. In this case, multiple nucleation sites were found on the W–Au ultramicroelectrode. TEM imaging conducted during a CV sweep shows dendritic crystal growth.High-speed ECAFM has been used to study Cu electrodeposition.177,178 Nucleation and growth of multilayer Cu islands were observed within seconds after applying the potential step, which grew rapidly. The shape evolution was analyzed quantitatively by determining the island diameter vs. growth time. Here, a change in the growth law was attributed to the transition from hemispherical to planar diffusion. In addition, the experiments revealed a strong increase in the nucleation density with increasing η. Unlike the cases for Au and Ag, these results for Cu electrodeposition do not deviate from classical considerations under a combined reaction and mass transport control.
Pt
Electrodeposition of Pt nanoparticles for catalysis applications has several advantages over other synthesis methods including high purity of products (without surfactants or additives), low cost, and ease of morphological control. For example, the competing effects of diffusion limitation vs. electrokinetic limitation have been used to vary Pt nanoparticle morphology during pulsed electrodeposition.179 However, studies focused on the electrocatalytic activities of Pt nanoparticles often lack quantitative information on Pt nucleation and crystal growth rates and mechanisms. Here we highlight recent advances in method development to obtain atomic level understanding of Pt electrodeposition and rate measurements.Jacobse et al. provided insights on the surface roughening process of Pt(111) when subjected to repeated oxidation–reduction cycles (ORCs), by linking, for the first-time, electrochemical measurements to structural information obtained from in situ high-resolution ECSTM.180 Two growth regimes were identified: (1) the nucleation and early growth regime where nano-islands nucleate and grow laterally; and (2) the late growth regime where the nano-islands coalesce and the growth becomes predominately in the height direction. Interestingly, no correlation between the roughness of the surface and the electrochemical signal was observed during the earlier regime while a linear correlation was observed during the later regime. The reason for the nano-islands not contributing to the electrochemical signal during the nucleation and early-growth regime remains unclear. Nonetheless, this approach enables a quantitative correlation between electrochemical characterization and STM data in Pt electrodeposition.
A novel investigation was conducted by the Dick group, which combined water-in-oil emulsion with the ultramicroelectrode technique to allow observations of the electrodeposition of a single Pt nanoparticle on a 10 μm Pt ultramicroelectrode.140 Nanodroplets of an aqueous/glycerol solution containing PtCl62− precursor ions were dispersed in tetrabutylammonium perchlorate (TBAP) and 1,2-dichloroethane (DCE) by ultrasonication. Upon nanodroplet collision with the electrode, the precursor ion was reduced to Pt metal in a four-electron process (Fig. 8A). The small droplet volume ensures rapid precursor ion depletion and permits the observation of reaction-controlled electrodeposition of individual Pt nanoparticles. The current–time traces at low η exhibit a parabolic rising edge, proportional to t2, consistent with electrokinetically controlled crystal growth. The current–time traces at high η exhibit an edge that is proportional to t1/2, indicative of diffusion-controlled crystal growth (Fig. 8B and C). This is the first time the crystal growth rate constant was accurately determined for Pt electrodeposition to be 0.003 cm s−1 from analysis of numerous current–time curves of individual Pt nanoparticle formation events. This method holds potential for measuring kinetic and mass-transfer rates of nanoscale electrodeposition of a broad range of materials and systems.
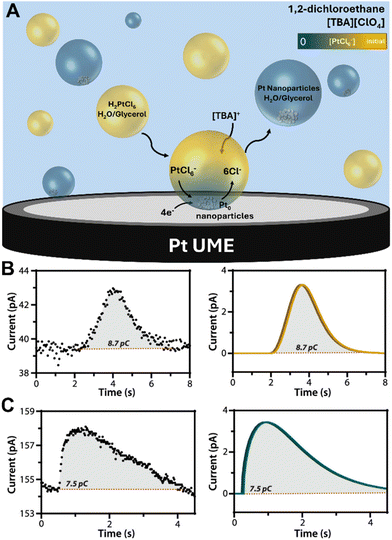 | ||
Fig. 8 (A) Schematic representation of Pt nanoparticle electrodeposition on a Pt ultramicroelectrode by the single nanodroplet method. (Bottom) experimental and simulated amperometric response of (B) electrokinetic-controlled electrodeposition at low η (0.3 V vs. Ag/AgCl), showing a rising edge proportional to t2 and (C) diffusion-controlled electrodeposition at high η (0.0 V vs. Ag/AgCl), showing a rising edge proportional to t1/2. The nanodroplet consists of 50 mM chloroplatinate in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 water/glycerol suspended in 0.1 M TBAP + DCE. Reproduced from ref. 140 with permission from the American Chemical Society. 1 water/glycerol suspended in 0.1 M TBAP + DCE. Reproduced from ref. 140 with permission from the American Chemical Society. | ||
The Bard group studied electrodeposition of isolated Pt atoms and nanoclusters (9-atom cluster) on a Bi ultramicroelectrode and characterized the deposited nanostructure by the electrochemical hydrogen evolution reaction (HER).181,182 By combining ultralow concentration of H2PtCl6 in water and the ultramicroelectrode technique a single Pt atom deposition was detected by CV via HER electrocatalytic amplification. A minimum diffusion-limiting current of 55 pA in the steady-state voltammograms points to the presence of a single Pt atom on Bi. This result has important implications for emerging single-atom catalysis. Individual nanoclusters with radii less than 1 nm and Pt nanoparticles of 1–10 nm in size were also studied for their electrocatalytic activity. The HER kinetics were found to increase with Pt nanoparticle radius until reaching a plateau at ∼4 nm.
Pd
Pd nanostructures have applications in hydrogen production from the electrochemical water splitting reaction and hydrogen storage.183,184 An earlier LCTEM study focused on the understanding of the growth mechanisms of the dendritic nanostructure (DNS) formed during Pd electrodeposition.185 The electrodeposition in this study was mimicked by electron irradiation-induced crystallization. A single nucleation center was created at the liquid–solid interface of the Si3N4 membrane using an electron probe, followed by the growth of dendritic branches. TEM images show many discrete single-crystalline Pd nanoclusters in close proximity to the edge of the growing DNS. In situ and ex situ STEM characterization revealed two mechanisms responsible for the formation of Pd DNS: diffusion-limited aggregation (DLA) of nanoclusters and direct atomic deposition. They suggested that direct atomic deposition has a major role in facilitating the DLA of nanoclusters at the edge of the DNS. Direct atomic deposition also resulted in increasing density of branches towards the center of the DNS. A greater degree of dendritic growth was also observed in a thin layer of liquid within the membrane due to limited diffusivity of the precursor, which was not observed in a thicker precursor liquid layer. We note that direct atomic deposition on existing nuclei was also observed in Au electrodeposition on the BDD electrode.120Macpherson, Unwin, and coworkers pioneered the use of nanopipettes for the study of metal electrodeposition. They used the microcapillary electrochemical cell to study Pd nanoparticle electrodeposition on single walled carbon nanotubes (SWNTs).186 The nanostructures were characterized by current–time tracing and ex situ AFM and field-emission SEM (FESEM) imaging. At low deposition η values (10–50 mV), nucleation takes place preferentially at defect sites on the SWNTs. This feature can potentially be used to identify defect sites on the SWNTs and their chemical nature. At high η, Pd growth takes place on non-defected regions of the SWNT, referred to as random nucleation. The nanoparticle density was found to vary little during electrodeposition on SWNTs, which indicates that Pd nanoparticle nucleation occurs at sub-ms timescale. The experimentally determined nanoparticle size distributions by AFM and FESEM imaging were found to match the calculated sizes from the Scharifker–Hills model (eqn (7)) fit to the current–time traces.
A more recent work by the Unwin group studied Pd electrodeposition directly on a carbon-coated TEM grid from a nanodroplet (avoiding the materials transfer step in a typical TEM experiment).117 A double potential step chronoamperometry method was used to jump the applied potential back and forth from a base potential where no reaction occurs. TEM analysis shows a majority of deposited Pd nanoparticles to be 1–2 nm in diameter. Moreover the results are consistent with the nucleation and aggregative growth model for metal electrodeposition (Fig. 3).13 The first step involves the reversible nucleation and dissolution of discrete nanoparticles. The second step involves the attainment of a critical size after which point nanoparticles aggregate to grow larger. They reported quantitative measurements of aggregate rate constants at 3 different potentials:
| kagg (0.05 V) = (7.89 ± 0.01) × 104 s−1 |
| kagg (0.035 V) = (9.57 ± 0.03) × 104 s−1 |
| kagg (0.025 V) = (8.11 ± 0.02) × 104 s−1 |
The solvent effect on Pd electrodeposition was studied by the McPherson group by changing the mole fractions of water and acetonitrile (MeCN).187Ex situ FESEM and STEM imaging of electrodeposited Pd was carried out on BDD electrodes. From the shift in the potential necessary to initiate Pd deposition, it was determined that the process is kinetically more favorable in the presence of water. Water molecules bind to the acetate ligands and free up the Pd cation for solvation by MeCN and electrodeposition. For equal volumes of water and MeCN, electrodeposited Pd was in the forms of single atoms, amorphous atom clusters, monocrystalline nanoparticles, defected nanoparticles, and more complex nanostructures with the latter three comprising 96% of all morphologies. The defected and elongated nanostructures were attributed to nearby nanoparticle coalescence or possibly to Ostwald ripening. But no evidence of aggregation prior to coalesce was observed. In MeCN rich solution, precursors to Pd nucleation including Pd atoms and amorphous atom clusters were observed similar to those observed in Au electrodeposition.120 The solvation effect of metal precursor ions on electrodeposition warrants more attention in order to fully understand and control electrocrystallization.
Zn
Zn electrodeposition plays a role in the reversibility of energy storage in secondary/rechargeable batteries because Zn possesses desirable properties such as high theoretical capacity, low electrochemical potential, high abundance, and low toxicity, along with its intrinsic safety.188 The Archer group has recently accomplished epitaxial electrodeposition of Zn thin films on graphene as a basis for rechargeable Zn batteries.189 In another attempt to promote dense Zn electrodeposition and to prevent dendrite formation, the classical nucleation theory of Ncritical dependence on γ and η (eqn (4)) was applied by using trimethyl phosphate to reduce γ and increase η.190 Previously, the dendrite growth kinetics in Zn electrodeposition under potentiostatic mode have been established.191 If the growth is dominated by activation/kinetic-limited growth, Zn dendrite growth has a linear relationship with time. If the growth is diffusion limited, the growth mode follows an exponential law with time.Instead of coating the electrode with thin films to promote epitaxial growth of Zn, Shen et al. explored the use of co-solvents such as cyclic tetramethylene sulfone to promote uniform distribution of adsorbed Zn2+ precursor ions.192 Cyclic tetramethylene sulfone molecules preferentially adsorb on the Zn (0001) face compared to water and form oriented dipole arrays, where the low electron density and large steric hindrance slows down Zn2+ adsorption on the electrode surface. This effectively reduces the reaction rate and was shown to improve Zn battery cycle stability. This study provides another example of using co-solvents to control electrodeposition kinetics.
Li et al. applied in situ ECTEM to study early-stage Zn electrodeposition on Au working electrodes.193 The applied potential vs. time traces in galvanostatic electrodeposition captured a nucleation η spike at the beginning followed by a η plateau corresponding to continued growth of Zn dendrites. The ECTEM results are consistent with the classical picture for Zn electrodeposition in a two-stage process, nucleation followed by crystal growth. In stage one, the metastable Zn nanoclusters fluctuate between deposition and dissolution. In stage two, η decreases to a plateau value with stable Zn nucleus growth.
In another recent work, ECAFM captured the initial Zn deposition on polycrystalline Cu electrodes.194 It was determined that preexisting CuO particles on the Cu surface act as nucleation sites for Zn electrodeposition. To better follow and capture the onset of Zn deposition with successively applied small changes in potential, AFM images were recorded at an increased scan rate. The deposited Zn was found to dissolve after reducing the anodic potential with a morphological change from the triangular growth to a rounded shape and was redeposited again after increasing the anodic potential. The results show a reversible Zn deposition process with no significant deviation from classical crystal growth models.
Li
Li appears to be the most studied metal in electrodeposition due to its importance as anode materials for high-energy-density batteries.195 A key issue is the growth stability in Li metal electrodeposition.196 Chen et al. has recently reviewed the nucleation and crystal growth aspects as they relate to the solid-electrolyte interphase (SEI) formation in Li-ion batteries and highlighted the key mechanisms:197 (1) the heterogeneous model describes the heterogeneous nucleation and early growth behavior; (2) the surface diffusion model demonstrates that the Li has an inherent tendency for 1D growth due to the high surface diffusion barrier; (3) the crystallography model reveals the preferential crystallographic orientation in Li deposits; (4) the space charge model emphasizes the impact of Li ion distribution on the reaction activity of different sites; and (5) the Li-SEI model correlates the Li nucleation and deposition behaviors with the SEI function. The heterogeneous model essentially applies the classical nucleation and crystal growth theories for the purpose of preventing Li dendrite formation detrimental to battery cyclability. The surface diffusion model focuses on reducing the surface diffusion barrier and enhancing surface migration to promote uniform Li deposition.198 The crystallography model predicts Li dendrite/whisker morphology based on surface energy minimization stemming from the classical Wulff theorem. The space charge model describes Li dendrite growth based on diffusion limitation.199 During Li electroplating at a fast rate, the concentration of Li ions declines to create a Li ion depletion zone on the surface of the anode and induces a space charge, resulting in the dendrite growth. Finally, the SEI model considers the effect of an initial SEI formation on the subsequent nucleation and crystal growth in Li electrodeposition. All these factors need to be considered to prevent SEI formation.SICM has been used to study lithiation on Sn/Cu films.200 Prior to the lithiation, surface roughness determined from the topographical image of the as-deposited Sn/Cu film matched well with the ion current image, indicating that variations in the ion current were due to the thickness variations in the thin film. Following the lithiation, local areas on the sample displayed an increase in topography attributed to the decomposition of the Li-containing electrolyte at the Sn/Cu film surface. An increase in current at a tall topographical feature and a drop in current around the peripheral regions was attributed to the SEI formation, which obstructs the flow of ions to the underlying Sn/Cu film while inducing a higher rate of lithiation at the protruding area. Tall features in the topographical map sometimes showed decreased ion current, which was attributed to the SEI film blocking the current flow in the Sn electrode.
Ex situ SEM was used to monitor the nucleation of Li metal on Cu substrates by the Cui group and the data were described by the classical nucleation theory.201 The Li nucleus size was found to be proportional to the 1/η (eqn (3)) and the number density of nuclei was proportional to η3. By applying the new knowledge, the researchers achieved improved Li deposit uniformity and particle density, desirable attributes for high-performance Li metal batteries. The authors concluded that more potentiostatic experiments are necessary for understanding Li nucleation mechanism.
In situ ECTEM and STEM have been used by several groups to study Li electrodeposition.202–205 Mehdi et al. applied HAADF-STEM to study Li deposition and dissolution at the interface between the Pt working ultramicroelectrode and the electrolyte solution during 3 charge and discharge cycles of the operando battery cell built into the STEM.205 The primary finding is the existence of hysteresis in Li electrodeposition. The Unocic group applied in situ STEM to directly visualize the early stages of SEI growth and Li electrodeposition on a 30–50 nm thick GC working electrode.202,203 The STEM images show that Li nucleates at the edge of the GC electrode and grows perpendicular to the electrode surface. Li deposits do not have the classical fractal shape exhibited by other metals during dendritic growth. Rather Li deposits tend to be clusters of globular objects. It was shown that Li grows in bursts – after the initial growth to a critical diameter of 400–500 nm a second nucleation burst follows. The globular nucleus shape was also captured by Kushima et al. in an in situ ECTEM study of Li nucleation and early growth on patterned Au electrodes.204 The TEM images show distinct stages in Li electrodeposition: (1) spherical nuclei emerge at the surface of the Au electrode with their size increasing with t1/2 indicating diffusion-limited growth; (2) the growth of Li whiskers at the SEI pushes the initial deposits away from the electrode surface suggesting preferential Li deposition at the Li/Au interface; (3) thickening of the SEI decreases Li metal crystal growth rate; and (4) kink formation on the whisker divides it into two segments under accumulated stress due to the SEI (SEI fracture). A crystal growth model for Li electrodeposition was derived by Thirumalraj et al. by considering both 3D diffusion-controlled instantaneous nucleation and electrolyte decomposition due to the SEI fracture.206 The equation allows the extraction of important kinetic parameters such as diffusion coefficient, number of nucleation sites, and rate constant of the electrolyte decomposition due to SEI fracture during Li electrodeposition by fitting the equation to the experimental current–transient curves.
In a final example of Li electrodeposition, an operando reflection interference microscope (RIM) was applied for real-time imaging of the entire Li nucleation dynamics at the single nanoparticle level (Fig. 9).207 Li electrodeposition starts with progressive nucleation and then changes into instantaneous nucleation. The RIM images show inhomogeneity of the surface electrochemical environment, which impacts Li nucleation and growth on the Cu electrode. The electrode surface heterogeneity causes local variation in η, which varies with the nucleus size (Fig. 9A). In the first 75 s of deposition, nuclei emerge randomly on the sample surface (Fig. 9B). With further deposition from 75 s to 140 s, the surface electrochemical heterogeneity is reduced to promote more uniform growth of the Li thin film (Fig. 9C and D).
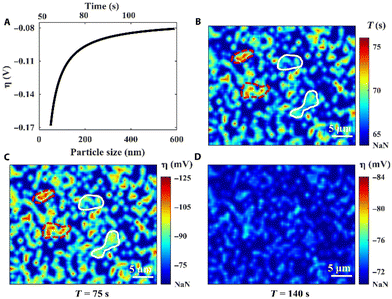 | ||
| Fig. 9 Localized overpotential mapping by RIM. (A) Proof-of-concept curve fitting correlates η with the nucleus size. (B) The nuclei formation time map. (C) The overall η map at the deposition time of 75 s. (D) The overall η map at the deposition time of 140 s. “NaN” represents the region without nuclei. Reproduced from ref. 207 with permission. Copyright, 2021, under CC-BY license, published by Science Advances. | ||
Ge
There are very few studies on single element deposition beyond metals. However, we did find an article by Cheek et al. on electrodeposition of semiconducting Ge nanowires.208 In the study, nanodroplets of liquid metal Ga and In were used to initiate the electrochemical reduction of dissolved GeO2 precursors and the growth of Ge nanowires. A modified liquid–liquid–solid growth mechanism of nanowires was applied for the understanding of the nanowire growth. The liquid metal nanodroplets are treated both as the precursor reservoir and an ultramicroelectrode. The Ge nanowire growth in this study occurs at far-from-thermodynamic equilibrium with supersaturation values of 104 prior to nucleation. The process was further complicated by the effect of electron beam irradiation during in situ LCTEM experimentation. In situ TEM images show that the nucleation of Ge nanowires is determined by the capping ligand coverage on the liquid metal surface. The initial Ge nuclei exhibited an ill-defined curvy shape, different from the final crystal morphology.Electrodeposition of compounds and complexes
In this section we review recent studies on nucleation and early-stage growth of electrodeposition of inorganic and organic compounds. Historically, knowledge of nucleation and crystal growth mechanisms has played an important role in the development of anodized alumina materials. Early studies of porous anodized alumina films have attributed the nucleation and growth of hexagonal cell networks to the grain boundaries on the Al working electrode surface.209 While the number of studies on nonmetallic materials is much fewer than that on metal electrodeposition, it is interesting to point out similarities in nucleation and crystal growth behaviors among diverse material types. Here, we will start with metal oxides and metal sulfides followed by CaCO3, MOFs, and CTCs.ZnO
A major observation in electrodeposition of semiconductive compound materials such as ZnO is that it is heavily influenced by the properties of the working electrode materials. For example, in the study of ZnO electrodeposition on graphene electrodes for solar cell applications, it was found that ZnO electrodeposition was strongly influenced by the graphene conductivity.210 A thicker or annealed graphene film with higher conductivity produced more hydroxide ions for the preferred 1D growth, in the [001] direction, of ZnO wurtzite structure. The degree of crystallinity was determined by XRD, SEM, and HR-TEM.Electron beam-induced precipitation of ZnO from solution mimics the electrodeposition of ZnO in terms of the crystal growth pathway.211 ZnO particles after nucleation were found to aggregate and grow anisotropically without coalescence according to the in situ TEM investigation.
Tay et al. developed an in situ three-electrode cell capable of in situ monitoring of the nanostructure during electrodeposition with a transmission X-ray microscope.212 A electrochemical liquid cell was designed for simultaneous electrodeposition and synchrotron X-ray imaging. The cell has a bulk volume of 30 ml, larger than the typical TEM liquid cells, and tapers to a width of 2 mm at the bottom where the X-ray beam can pass through two Kapton windows. One window was coated with 10 nm Au as the working electrode. Pt was used as the counter electrode and Ag/AgCl microelectrode was used as the reference electrode. X-ray absorption images were recorded at intervals of 2.2 s during ZnO electrodeposition. Nanorods were found at 5 mM Zn(NO3)2 and nanoplates were produced at 50 mM Zn(NO3)2 at an applied potential of −0.97 V or −0.75 V. The nucleation phase was indicated by an initial current density peak at 25 s for nanorod formation and 90 s for nanoplate formation. Imaging blurring in the X-ray absorption near edge structure (XANES) images suggests the existence of precipitated ZnO particles near the electrode surface in the solution phase (Fig. 10). The presence of swirling, smeared-out particles is prominent in Fig. 9a–d during the first 200 s of electrodeposition and remains visible in the latter time period of 332–336 s (Fig. 9n–p). This X-ray technique provides information on the particle structure in the solution phase, which cannot be easily obtained by in situ ECTEM or SEPM. This information would be useful to obtain a complete picture of the dynamic nature in electrodeposition, for example, confirming the detachment step in nucleation–aggregative growth–detachment,118 a growth pathway likely to occur in many electrodeposition systems with weak deposit/substrate interfaces. The spatial resolution of the XANES technique is at the micrometer scale, which presents a limitation of this method for the study of early-stage crystallization.
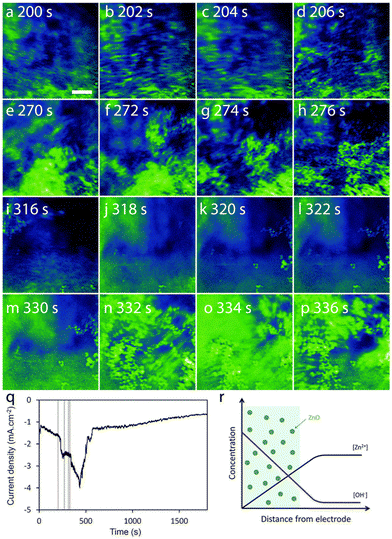 | ||
| Fig. 10 (a–p) The sequence of absorption images that captured every 2.2 s, is organized into 4 time periods: ∼200 s (a–d), 270 s (e–h), 315 s (i–l), and 330 s (m–p). Scale bar = 5 μm. (q) Current density vs. deposition time curve with vertical lines corresponding to the 4 time periods under concentration of Zn(NO3)2 is 50 mM. The deposition potential is −0.75 V. (r) A schematic representation focuses on the area near the working electrode, showing regions (colored green) where ZnO precipitation occurs due to the supersaturation of ZnO. Reproduced from ref. 212 with permission from Royal Society of Chemistry. | ||
Fe2O3 and Fe3O4
Tschulik et al. reported novel electrocrystallization methods, namely cathodic and anodic particle coulometry, to transform between Fe2O3 and Fe3O4 and for determining the size of nanoparticles.213 The electrochemical behavior of Fe3O4 nanoparticles was scrutinized under cathodic conditions (CPC) at −0.9 V vs. SCE and the charge associated with the reduction of Fe(III) to Fe(II) was measured; while in anodic conditions (APC) at 0.75 V, the charge involved in the oxidation from Fe(II) to Fe(III) was quantified. Both CPC and APC methods were validated through >1000 recorded spikes for CPC and ∼450 for APC. These methods can potentially be tailored for a wider range of metal oxides and other redox active materials.Hauwiller et al. applied real-time EC-LCTEM to study the nucleation and dendritic growth of iron oxide.214 Nucleation was initiated by electron beam illumination, a process resembling electrodeposition. The nanoclusters grew to 4–6 nm in diameter and then changed into nano-dendrites due to supersaturation-induced growth instability. Ex situ energy dispersive X-ray spectroscopy (EDS) elemental maps revealed that the as-grown nanostructure was amorphous, and it transformed into crystalline Fe2O3/Fe3O4 under prolonged electron beam irradiation. This work investigated further the dendritic growth mechanism. The growth was diffusion limited. The dendritic tip curvature was found to be in a linear relationship with the growth rate as predicted by the theory.215 The tip splitting can also be explained by the established analytical model. The growing tip was found to impact the growth of a neighboring tip in close proximity due to precursor depletion. This paper established a strong correlation between fractal growth of iron oxide nano-dendrites and the morphological evolution predicted by the classical crystal growth theories.
Composite coatings of metal oxides can also be made by electrodeposition in direct current, pulsed direct current, pulsed reverse current, potentiostatic, and pulsed potentiostatic modes to improve coating performance.216,217 But the literature on metal oxide composite electrodeposition is largely on the empirical side without mechanistic understanding of the complex process. This area warrants further fundamental research.
CaCO3
Chemically induced nucleation of CaCO3 has been studied extensively and contributed to the establishment of PNCs in nonclassical nucleation theories.94–97 There are few studies of electrochemically induced nucleation of CaCO3 though PNCs may likely exist in the electrochemical system. We found an earlier study by Devos et al. that looked into the effect of Mg2+ on the electrocrystallization of CaCO3.218 The CaCO3 electrodeposition was initiated by applying a cathodic potential of 1 V (vs. SCE) at the working electrode in the so called "accelerating scaling method". Mg2+ was shown to have an inhibitory effect on the nucleation process of CaCO3. Their conclusion has implications for scale and corrosion prevention. We can adapt the accelerating scaling method for future studies of CaCO3 electrodeposition pathways and mechanisms.More recently a nanoelectrode study was conducted by Blount et al. for the understanding of the nucleation and growth of ionic crystals with CaCO3 as a model system.219 The experiment was carried out on Pt nanoelectrodes in an aqueous solution of NaHCO3 and Ca2+. Pt nanoelectrodes with radii less than 100 nm were fabricated by a bench-top method originally developed by the White group.143 CaCO3 precipitation was initiated by electroreduction of water to create a higher local pH near the electrode surface. The excess OH− converted HCO3− into CO32− and produced a local supersaturation sufficiently high for CaCO3 nucleation. A sudden cathodic current drop in the voltammogram signaled the nucleation and growth of nonconductive CaCO3 on the electrode surface, which blocks the electroactive surface area of the electrode. It is interesting to note that the authors attributed the noisy residual current to the dynamic attachment and detachment of the nucleated CaCO3 crystals, which may share the same origin as Ag electrodeposition on HOPG of the nucleation–aggregative growth–detachment mechanism.118 The characteristic peak current was used to quantify the supersaturation ratio required for nucleation based on the classical nucleation theory. The supersaturation ratio, 220–420, was used to calculate the nucleation energy for CaCO3, 12–14 kJ mol−1.
Metal sulfides
CdS nanowires with lengths up to 1 μm and diameters as small as 9 nm were electrochemically deposited directly into the pores of anodic Al2O3 films from an electrolyte containing Cd2+ and S in dimethyl sulfoxide.220 While we did not find more recent studies to further illuminating the nucleation and crystal growth mechanisms in CdS electrodeposition; we did, however, came across a recent work by Robinson and White on electrochemical synthesis of Ag2S.221 The chemical conversion of Ag to Ag2S in the presence of bisulfide ions (HS−) in aqueous solution was used as a model system to study electrochemical metal–semiconductor transformations at the single nanoparticle level. For every Ag nanoparticle colliding with the Au ultramicroelectrode, the current first increased rapidly, followed by a slower nonlinear increase to reach a current peak, and then the current decayed until a sudden sharp decrease to the baseline, signaling the termination of the reaction. This current–time behavior is different from previous studies of nanoparticle collisions with microelectrodes. The slow current decay signals a progressive Ag2S nucleation mechanism as predicted by eqn (7) for progressive nucleation in which the number of nuclei increases with time. The reaction terminated after ∼80% of the Ag in the particle transformed into Ag2S. The termination was attributed to a disruption of the intermetallic contact between the Ag core and Au electrode due to the formation of an electronically insulating Ag2S interphase. The total charge passed for each event can be accurately calculated from the integration of the current spikes.Transition metal dichalcogenides
TMDCs are semiconducting two-dimensional (2D) materials with molecular formula of M–X2, where M is a transition metal atom, such as Mo or W and X being a chalcogen atom such S, Se or Te.222 Crystalline TMDCs are of significant interest due to their electronic and optoelectronic properties. The existing fabrication method of 2D crystalline TMDCs includes exfoliation, sputtering, thermal decomposition, pulsed laser deposition, and chemical vapor deposition (CVD). Among them, CVD or metal–organic CVD (MOCVD) is the most promising method for up scaling. However, all these methods have limitations that prevent producing large scale fabrication of uniform thin films with controllable thinness. Furthermore, some of these processes require high vacuum, which is energy intensive and difficult to scale. Although electrodeposition of 2D TMDCs has not be widely explored it is potentially a simpler method for large scale fabrication of 2D TMDC materials.MoS2 is the one of the most widely explored 2D TMDCs for electrodeposition. Many synthesis methods have been proposed, including the use of different working electrode material, aqueous vs. non-aqueous syste.223–225 Recently, the Kees de Groot group demonstrated the electrodeposition of thin MoS2 layers on a graphene working electrode in a nonaqueous environment, using a three-electrode system.18 The group modified an existing technique and achieved highly anisotropic lateral growth of MoS2 from TiN microelectrode over an insulating surface. In this work, the flat planar graphene working electrode was replaced with TiN sandwiched between two SiO2 layers.226 However, in both cases, the as-deposited film is amorphous and required annealing to achieve crystallinity. Our literature survey found a lack of mechanistic studies of the electrodeposition process, which could be a key to achieve high crystallinity 2D film via electrodeposition.
MOFs
MOFs exhibit tunable pore size, metal center, and functional linkers suitable for a wide range of applications such as sensors, catalysis, electronic devices, and membranes.227,228 MOFs can be electrodeposited using either an anodic or a cathodic process.229,230 The anodic process involves the anodic dissolution (corrosion) of the substrate into metal ions for subsequent MOF deposition. The cathodic deposition requires a pH increase near the working electrode via the reduction of pro-bases and the deprotonation of the linkers. The deprotonated organic ligands react with metal cations in the solution to form MOFs. Supersaturation was shown to play a key role in controlling the crystal morphology of MOFs during electrodeposition.231 A complex solid–solid transformation process was hypothesized for cathodic electrodeposition of MOFs involving an intermediate layered phase.232ECAFM was used to monitor the in situ anodic Cu dissolution and deposition of Cu-MOF HKUST-1 (composed of Cu2+ cations and 1,3,5-benzenetricarboxylic acid (BTC) ligands).233 The real-time imaging together with in situ EC Raman spectroscopy confirmed a previous hypothesis of a 4-step process in Cu-MOF nucleation and crystal growth.234 Firstly, a critical Cu2+ concentration is necessary to initiate Cu-MOF nucleation. Nucleation occurs at defects on the roughened electrode surface. Then the nuclei grow through the classical 3D island mechanism. After the third intergrowth step, the Cu-MOF crystals detach from the electrode surface due to prolonged metal substrate corrosion. No Cu2O or amorphous nucleation intermediates103,235 were observed in this study.
A precursor ion layer was found to promote the nucleation and growth Co-MOF crystals on carbon fiber cloth in cathodic electrodeposition.236 The self-assembled Co2+ ions at the negative potential on the electrode induce the nucleation and growth of Co-MOF in 3D rodlike crystal bundles. The nucleation was found to start from defects on the Co coating. The nucleated crystals grow through the 3D island growth mechanism to several microns and then merge into a continuous layer.
CTCs
CTCs have recently emerged as promising sensing, ferroelectric, piezoelectric, and photothermal materials.237–239 CTCs are composed of electron-donating and electron-accepting pairs exemplified by the most famous tetrathiafulvalene and 7,7′,8,8′-tetracyano-p-quinodimethane complex (TTF-TCNQ).240 The conductivity of CTCs arises from the delocalized electrons and holes along the segregated stacks of free radicals of donors and acceptors. Fig. 11 lists commonly studied CTC electron donors and acceptors. Hundreds of different kinds of CTC nanocrystals can be grown by either non-electrochemical, solubility-based methods or electrochemical methods. For example, nanocrystals of perylene-TCNQ were synthesized by rapid precipitation induced by rapid addition of a miscible non-solvent.241 However, this method produced a mixture of co-crystal stoichiometries as well as crystals of pure perylene and TCNQ. In contrast, electrocrystallization offers control of nucleation, growth, morphology, and stoichiometry of CTC crystals for device applications.Ward has defined the basic steps in CTC electrocrystallization:242
(1) Electrochemical reaction: The process begins with the electrochemical reduction or oxidation of redox-active precursors at the electrode surface.
(2) Formation of ion pairs and clusters: Following the electrochemical reaction, the generated species interact with counterions present in the solution to form ion pairs. These ion pairs can further aggregate into larger clusters, setting the stage for nucleation.
(3) Nucleation: Nucleation occurs when the clusters reach a critical size and configuration, allowing for the stable formation of a new crystalline phase. This critical size is influenced by the local supersaturation and electrochemical conditions such as the applied current density and potential.
(4) Crystal growth: The crystal grows by further deposition of ion pairs onto the existing nuclei. Growth tends to occur preferentially along specific crystallographic directions depending on the molecular and ionic arrangements, driven by the local electrochemical and intermolecular interactions, such as π–π stacking.
(5) Morphological development: The morphology of the crystals and rate of growth can be significantly affected by the electrochemical conditions, such as the current density, electrode potential, and the presence of impurities, leading to different crystal shapes and sizes.
TTF-Br nanocrystals with width of 30–600 nm and aspect ratios of 20 or higher were electrochemically synthesized on Pt nanoparticle seeds by Favier et al.243 The Pt nanoparticles imposed a nanoconfinement effect on the TTF-Br crystal morphology in which the width of the nucleated TTF-Br crystals varied linearly with the Pt nanoparticle diameter to which TTF-Br is attached. A paper by Mas-Torrent and Hadley demonstrated the electrochemical growth of 1–2 μm long and 200 nm wide TTF-Br microcrystals on microfabricated Au electrodes.244 Ren et al. made significant contributions on the understanding on controlled CTC micro/nanowire electrodeposition on carbon nanotubes.245 They synthesized 12 CTC types of CTC micro/nanowires with combinations of the donors and acceptors shown in Fig. 11. Compared to CTC grown on bulk Au electrodes, CTCs grown on carbon nanotube nanoelectrodes are longer in length and smaller in diameter indicating a nanoconfinement effect imposed by the carbon nanotubes. The CTC morphology was shown to be dependent on the intrinsic structure and properties of the CTCs. CTC crystals based on TCNQ are smaller in diameter than CTC crystals containing TTF, TMTSF, and ET.
Beyond TTF- and TCNQ-based molecular complexes, electrocrystallization of linear chain complexes was studied by Wysocka et al. by electrooxidation of [IrCl2(CO)2]− in dichloromethane containing different tetra(alkyl)ammonium cations (TAA+) on Au working electrodes.246 The experimental chronoamperometric curves were fitted with eqn (7) to determine the nucleation and growth kinetics. Values of the exponent n and the constant K were found to depend on the type of nucleation (instantaneous or progressive) and growth (1D, 2D, or 3D) mechanisms.49–51 The linear double logarithmic fit with a slope close to 1 indicated progressive nucleation followed by 1D growth of needlelike microcrystals. Additional kinetic parameters can be extracted using the following equation:
| I = nFAL2kt, | (19) |
Our group has been exploring seed-mediated electrocrystallization as a solution to nanosensor manufacturing by directly synthesizing CTC nanowire sensors in a controlled manner on sensor substrates. This stems from an original discovery made by Mao et al. that nanoparticles of monolayer-protected CdSe and Au are effective seeds for the nucleation of 1D nanorods in solution crystallization via solvent evaporation.247,248 The small nanoparticle seed size (or radius of curvature) was hypothesized to be responsible for the confined nucleation and growth of the molecular crystals.248,249 Subsequently, this hypothesis has been validated in different crystallization systems using compounds including aliphatic carboxylic acids, TTF-Br, and Krogmann's salts.247–252 Electrochemical methods have been used for TTF-Br and Krogmann's salt crystallization on Au nanoparticle seeds and microelectrode patterns.
We further examined the nucleation and growth mechanisms of TTF-Br in nanoconfinement using Pt microdisk electrodes.253 The current increases linearly with time due to the increasing electroactive area upon conductive TTF-Br microwire growth. The linear growth of the CTC microwires on the Pt microdisk electrode enables precise control of the microwire length for device fabrication. In addition, this work demonstrated the use of ultramicroelectrodes in controlling the aspect ratio, orientation, and number of CTC microwire crystals, all are desirable features for scaling up chemiresistive gas sensor technology based on CTC electrodeposition on patterned micro/nanoelectrodes. Currently there are no other methods that enable the control of all these features except with predefined templates.
Recently we demonstrated precise control of TTF-Br electrodeposition on lithographic electrode patterns by varying the shape of the electrodes.24 Triangular shaped Au patterns with tip angles of 5°, 30°, and 90°, and thickness of 5–500 nm were made by photolithography. The electrode geometry was shown to have a strong effect on crystal growth rates. SECM imaging shows TTF-Br to nucleate randomly along the edge of the Au electrode initially. At a later time, crystals near the electrode tip grew more at the expense of the ones away from the tip, which was explained by 3D finite element simulations of the diffusion flux near a triangular tip. The simulation results and the experimental data matched each other, they collectively demonstrate that sharp electrode patterns are more effective in promoting 1D crystal growth of CTCs and their precise placement across source and drain electrodes for making chemiresistive gas sensors. Another interesting finding of this work is the existence of transient PNCs as indicated by multiple small current spikes in the induction period of the current–time transients at a low TTF concentration (Fig. 12a–b(i–iv)) on Au microdisk electrodes. The current peak height, ip, offers an estimate of the corresponding PNC radius, r:254
| ip = 2πzFDcr. | (20) |
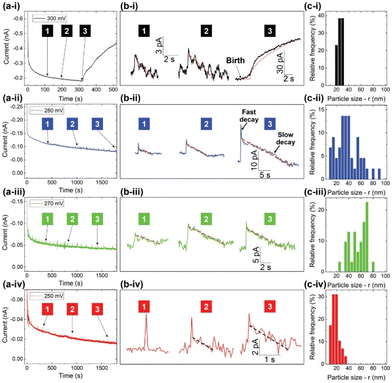 | ||
| Fig. 12 (a) The current–time transients of TTF-Br electrodeposition at 300, 280, 270, and 250 mV, respectively, on the Au microdisk electrode in 0.1 mM TTF and 20 mM TBAB MeCN solution. (b) The magnified views from (a) showing individual current spikes represented by solid lines, alongside fits corresponding to zero-order kinetics represented by dashed lines. (c) The nanocluster size histograms at different applied potentials. Reproduced from ref. 24 with permission from John Wiley and Sons. | ||
The PNC particle size histograms based on eqn (20) are shown in Fig. 11c. Measurements of the largest PNC size provided a lower bound of rcritical to be 29 nm at 300 mV and 75–89 nm at 270–280 mV. This is among the first reports of PNCs in CTC electrodeposition.
In addition to applying electrodeposition for the understanding of nucleation, CTC electrochemistry has also been also revealed a nonclassical crystal growth mechanism in Co-TCNQ electrodeposition on a ultramicroelectrode.25 The presence of Co in the otherwise organic solid enabled us to examine the nanostructure of Co-TCNQ crystals by HR-TEM, which shows distinct crystalline domains with sizes in the range of only a few nanometers. These domains feature lattice fringes arranged along a preferred direction – the long axis of the Co-TCNQ crystal. This system this resembles closely the oriented attachment crystallization pathway observed in nonelectrochemical systems.121–126 Density function theory (DFT) calculations suggest that under high electric fields, the (100) facet of Co-TCNQ can become sufficiently energetic to be the preferential growth facet. A preferred attachment of crystallites in the long axis (π–π stacking) direction of the Co-TCNQ crystal may therefore be the result of applied potential-induced surface energy change.
We have demonstrated the gas sensing capabilities of electrodeposited TTF-Br, Co-TCNQ, and Krogmann's salt nanowires on microelectrode patterns to be effective chemiresistive gas nanosensors for ammonia, nitrogen dioxide, and other gases.25,251,255 We therefore advocate for the use of electrodeposition as a platform technology for precise deposition and assembly of conductive and semiconductive nanowires into electronics for gas sensing and potentially other optoelectronic applications.
Conclusions
Electrochemical science and engineering are experiencing significant growth due to their enabling role in making functional materials, thin films, and devices to address major global challenges in energy, environment, and health. Electrodeposition has several advantages over other synthesis methods including high purity of products (without surfactants or additives), low cost, ease of morphological control, and scalability. Thorough understanding of the electrodeposition process at nano or atomic scale is critical for precise control of nanostructure formation in the industry-scale manufacturing of energy storage devices, advanced electrode materials, fuel cells, carbon dioxide capturing equipment, and sensors. Here, we provided a comprehensive, but not exhaustive, review of the recent progress in the understand of nucleation specifically in electrodeposition and the advances in in situ characterization of nucleation and crystal growth in electrodeposition of different classes of material.In this review, both classical and nonclassical nucleation and crystal growth theories are discussed as they apply to electrochemical systems. The classical nucleation theory provides a knowledge foundation for defining and controlling important parameters such as the critical nucleus size, the number of atoms/molecules in the critical nucleus, and the nucleation rate as a function of the applied overpotential. The Scharifker–Hills model remains valid for the interpretation of current–time behaviors in metal electrodeposition. Classical crystal growth mechanisms include the Frank–van der Merwe 1D growth, 2D monolayer growth, and Volmer–Weber 3D island growth mechanisms have been presented. The relationship between the crystal growth rate of a hemispherical nucleus on an electrode surface as a function of the applied overpotential during electrodeposition is described. At the same time, more evidence emerges of discrete nanoclusters acting as the primary building blocks in electrochemical nucleation. The role of nanocluster building blocks in electrocrystallization is explained both by the generalized electrochemical aggregative growth model and the nucleation–aggregative growth–detachment mechanism. Electrocrystallization is made more complicated by the dynamic nature of the nanoclusters, which can undergo surface diffusion, aggregation, merging, disintegration, and detachment, and reattachment. We expect to see exciting research in further understanding the dynamic nature of electrocrystallization due to rapid advances in both experimental and computational methods with ever-improving sophistication and spatiotemporal resolutions. Research topics for further investigation include multiple nucleation sites overlapping each other, crystal growth after the nucleation stage, electrodeposition of materials beyond elemental metals and multiscale computational method to model the electrochemical driven nucleation and crystal growth processes. Recent work on charge-transfer complexes shows evidence of prenucleation clusters and oriented attachment during their electrochemical crystal growth. Further research may unveil electrocrystallization phenomena and underlying mechanisms already been observed in nonelectrochemical systems such as calcium carbonate and zeolite crystallization or completely new phenomena specific to the electrochemical process. With regard to the decades long debate of classical vs. nonclassical nucleation theory, future studies can attempt to reconcile these two theories. We should not rule out the possibility that, similar to nonelectrochemical systems, the pathway for nucleation is condition dependent.
We reviewed advanced characterization methods that are applicable for the study of electrodeposition. They include high-resolution transmission electron microscopy, various electrochemical scanning probe microscopy methods, and X-ray diffraction and scattering methods. Many of the advanced imaging methods utilize ultramicroelectrodes and patterned nanoelectrodes for simultaneous electrochemical experimentation and real-time imaging of nanoparticle formation during electrodeposition at a precise location. There have been significant advances in method development that extend the capability of the ultramicroelectrode technique significantly by integrating different technologies such as nanopipettes, nanofluidics, liquid metal nanodroplets, microemulsion, and nanoparticle electrocatalysis. This review highlighted significant advances using these new methods to capture electrodeposition structures and dynamics at an unprecedented resolution – down to the single-atom size. For the study of fast electrodeposition kinetics, further development of high-speed cameras and data acquisition specifically for electrochemical systems will be necessary. Further advancement in characterization instruments to achieve higher temporal and spatial resolution, with less stringent sample preparation requirements will no doubt offer deeper insight into the fundamental of nucleation and crystal growth in electrodeposition. It is interesting to note that stable single atoms have been observed in Au, Pt, and Pd electrodeposition on certain electrode surfaces and thus paving the way for single atom electrocatalytic and magnetic applications. Our survey of recent publications did not discover substantial new work on nucleation and crystal growth mechanisms of electrodeposited 2D crystalline materials, e.g., II–V or III–V semiconductors, transition metal chalcogenides, etc. Future studies should explore the microscopic understanding of electrochemically driven nucleation and crystal growth of 2D thin film materials to overcome the problem of poor crystallinity. This may lead to exciting new discoveries and offer opportunity for less energy intensive, simpler, and more scalable synthesis methods for device manufacturing.
The precise control over the morphology, nucleation density, and growth rate remains a major challenge for device manufacturing. This has prevented real-world applications of electrodeposition in microelectronics and optoelectronics, and hindered the advancement of technologies where controlled electrocrystallization is essential. In conclusion, there have been significant advances with many future opportunities to unveil the mysteries of electrochemical nucleation and growth of functional crystals of diverse chemical nature.
Data availability
The data that support the findings of this study are available on request from the corresponding author.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge funding support from the Asian Office of Aerospace Research and Development under award number FA2386-20-1-4077 and Australian Research Council (ARC) under award numbers IH210100040 and IH210100048.References
- M. Stelter and H. Bombach, Adv. Eng. Mater., 2004, 6, 558–562 CrossRef CAS.
- R. Winand, Electrochim. Acta, 1994, 39, 1091–1105 CrossRef CAS.
- C. R. K. Rao and D. C. Trivedi, Coord. Chem. Rev., 2005, 249, 613–631 CrossRef CAS.
- B. R. Scharifker and J. Mostany, Encyclopedia of Electrochemistry, 2007, DOI:10.1002/9783527610426.bard020503.
- W. Du, J. Yan, C. Cao and C. C. Li, Energy Storage Mater., 2022, 52, 329–354 CrossRef.
- A. Mariella Babu and A. Varghese, J. Electroanal. Chem., 2023, 937, 117417 CrossRef CAS.
- M. B. Kale, R. A. Borse, A. Gomaa Abdelkader Mohamed and Y. Wang, Adv. Funct. Mater., 2021, 31, 2101313 CrossRef CAS.
- M. Al-Katrib, L. Perrin, L. Flandin and E. Planes, Adv. Mater. Technol., 2023, 8, 2300964 CrossRef CAS.
- H. Siddiqui, N. Singh, P. Naidu, K. Bhavani Srinivas Rao, S. Gupta, A. Kumar Srivastava, M. S. Santosh, S. Natarajan, S. Kumar, L. F. Dumée and S. Rtimi, Mater. Today, 2023, 70, 161–192 CrossRef CAS.
- A. Neira-Carrillo, T. Zegers Arce and M. Yazdani-Pedram, ACS Omega, 2024, 9, 17045–17053 CAS.
- W. Plieth, Electrochemistry for Materials Science, Elsevier, Amsterdam, 2008 Search PubMed.
- J. Ustarroz, Curr. Opin. Electrochem., 2020, 19, 144–152 CrossRef CAS.
- J. Ustarroz, J. A. Hammons, T. Altantzis, A. Hubin, S. Bals and H. Terryn, J. Am. Chem. Soc., 2013, 135, 11550–11561 CrossRef CAS.
- V. Tsakova, J. Solid State Electrochem., 2020, 24, 2183–2185 CrossRef CAS.
- T. Dhara, D. Sarkar, S. Chakraborty, P. P. Mukherjee and S. DasGupta, J. Phys. Chem. C, 2024, 128, 10650–10659 CrossRef CAS.
- Y. Shi, W.-M. Huang, J. Li, Y. Zhou, Z.-Q. Li, Y.-C. Yin and X.-H. Xia, Nat. Commun., 2020, 11, 4558 CrossRef CAS.
- Z. Shen, J. Mao, G. Yu, W. Zhang, S. Mao, W. Zhong, H. Cheng, J. Guo, J. Zhang and Y. Lu, Angew. Chem., Int. Ed., 2023, 62, e202218452 CrossRef CAS PubMed.
- Y. J. Noori, S. Thomas, S. Ramadan, D. E. Smith, V. K. Greenacre, N. Abdelazim, Y. Han, R. Beanland, A. L. Hector, N. Klein, G. Reid, P. N. Bartlett and C. H. Kees de Groot, ACS Appl. Mater. Interfaces, 2020, 12, 49786–49794 CrossRef CAS.
- H. C. Lim, E. Park, I.-S. Shin and J.-I. Hong, Bull. Korean Chem. Soc., 2020, 41, 358–361 CrossRef CAS.
- E. Çepni and T. Öznülüer Özer, J. Energy Storage, 2022, 45, 103678 CrossRef.
- A. I. Ali, E. Omotoso, J. M. Nel and W. E. Meyer, Semicond. Sci. Technol., 2023, 38, 045005 CrossRef.
- D. B. Bailmare, B. V. Malozyomov and A. D. Deshmukh, Commun. Chem., 2024, 7, 178 CrossRef CAS.
- S. Xie, W. Monnens, K. Wan, W. Zhang, W. Guo, M. Xu, I. F. J. Vankelecom, X. Zhang and J. Fransaer, Angew. Chem., Int. Ed., 2021, 60, 24950–24957 CrossRef CAS.
- M. Kilani, M. Ahmed, M. Mayyas, Y. Wang, K. Kalantar-Zadeh and G. Mao, Small Methods, 2023, 7, 2201198 CrossRef CAS.
- J. Lin, M. Kilani, M. Baharfar, J. Tang, J. Zheng, P. V. Kumar, K. Kalantar-Zadeh and G. Mao, ChemElectroChem, 2024, 11, e202300826 CrossRef CAS.
- C. Garcia-Cabezon, C. Salvo-Comino, C. Garcia-Hernandez, M. L. Rodriguez-Mendez and F. Martin-Pedrosa, Surf. Coat. Technol., 2020, 403, 126395 CrossRef CAS.
- J. Li, S. Wang, Q. Jiang, H. Qian, S. Hu, H. Kang, C. Chen, X. Zhan, A. Yu, S. Zhao, Y. Zhang, Z. Chen, Y. Sui, S. Qiao, G. Yu, S. Peng, Z. Jin and X. Liu, Small, 2021, 17, 2100743 CrossRef CAS.
- P. Yang, D. Wang, X. Zhao, W. Quan, Q. Jiang, X. Li, B. Tang, J. Hu, L. Zhu, S. Pan, Y. Shi, Y. Huan, F. Cui, S. Qiao, Q. Chen, Z. Liu, X. Zou and Y. Zhang, Nat. Commun., 2022, 13, 3238 CrossRef CAS PubMed.
- D. Wang, C. Zhou, A. S. Filatov, W. Cho, F. Lagunas, M. Wang, S. Vaikuntanathan, C. Liu, R. F. Klie and D. V. Talapin, Science, 2023, 379, 1242–1247 CrossRef CAS PubMed.
- S. H. Lee, B. Lee, B. J. Kim, B. J. Jeong, S. Cho, H. E. Jang, H. H. Cho, J.-H. Lee, J.-H. Park, H. K. Yu and J.-Y. Choi, ACS Sens., 2022, 7, 1912–1918 CrossRef CAS PubMed.
- F. J. Claire, M. A. Solomos, J. Kim, G. Wang, M. A. Siegler, M. F. Crommie and T. J. Kempa, Nat. Commun., 2020, 11, 5524 CrossRef CAS.
- M. Choe, J. Y. Koo, I. Park, H. Ohtsu, J. H. Shim, H. C. Choi and S. S. Park, J. Am. Chem. Soc., 2022, 144, 16726–16731 CrossRef CAS PubMed.
- T.-A. Chen, C.-P. Chuu, C.-C. Tseng, C.-K. Wen, H. S. P. Wong, S. Pan, R. Li, T.-A. Chao, W.-C. Chueh, Y. Zhang, Q. Fu, B. I. Yakobson, W.-H. Chang and L.-J. Li, Nature, 2020, 579, 219–223 CrossRef CAS.
- Y. Yin, Y. Guo, D. Liu, C. Miao, F. Liu, X. Zhuang, Y. Tan, F. Chen and Z.-x. Yang, Adv. Opt. Mater., 2022, 10, 2102291 CrossRef CAS.
- Q. Luo, R. Yuan, Y.-L. Hu and D. Wang, Appl. Surf. Sci., 2021, 537, 147930 CrossRef CAS.
- M. Golda-Cepa, K. Engvall, M. Hakkarainen and A. Kotarba, Prog. Org. Coat., 2020, 140, 105493 CrossRef CAS.
- Y. Xia, D. Ding, K. Xiao, J. Zhang, S. Xu, D. He, X. Yue, Q. Rao, X. Wang, S. Ding, G. Gao, H. Xue, Y. Wang, M. Yuan, W. Ho, D.-K. Ki, H. Xu, X. Cui, C. Jin and M. Xie, Nat. Sci., 2023, 3, 20220059 CrossRef CAS.
- I. u. Haq, J. Jacob, K. Mehboob, K. Mahmood, A. Ali, N. Amin, S. Ikram, S. Hussain, Y. Feng and F. Ashraf, Phys. B, 2021, 606, 412569 CrossRef CAS.
- J. Kim, A. T. John, H. Li, C.-Y. Huang, Y. Chi, P. R. Anandan, K. Murugappan, J. Tang, C.-H. Lin, L. Hu, K. Kalantar-Zadeh, A. Tricoli, D. Chu and T. Wu, Small Methods, 2024, 8, 2300417 CrossRef CAS PubMed.
- J. Kim, L. Hu, H. Chen, X. Guan, P. R. Anandan, F. Li, J. Tang, C.-H. Lin, K. Kalantar-Zadeh, A. Tricoli and T. Wu, ACS Mater. Lett., 2020, 2, 1368–1374 CrossRef CAS.
- D. Kim and J.-Y. Leem, Sci. Rep., 2021, 11, 382 CrossRef CAS PubMed.
- B. Wu, M.-P. Zhuo, S. Chen, Y. Su, Y.-J. Yu, J.-Z. Fan, Z.-S. Wang and X.-D. Wang, Adv. Opt. Mater., 2023, 11, 2202895 CrossRef CAS.
- A. R. Lauer, M. A. Durán-Olivencia, A. Fernandez-Martinez and A. E. S. Van Driessche, Faraday Discuss., 2022, 235, 95–108 RSC.
- A. Milchev and S. Stoyanov, J. Electroanal. Chem. Interf. Electrochem., 1976, 72, 33–43 CrossRef CAS.
- A. Milchev, Nanoscale, 2016, 8, 13867–13872 RSC.
- A. Milchev, ChemTexts, 2016, 2, 4 CrossRef.
- A. Milchev, ChemTexts, 2016, 2, 2 CrossRef.
- N. J. Vitti, P. Majumdar and H. S. White, Langmuir, 2023, 39, 1173–1180 CrossRef CAS.
- M. Abyaneh and M. Fleischmann, J. Electroanal. Chem. Interf. Electrochem., 1981, 119, 197–208 CrossRef CAS.
- G. Gunawardena, G. Hills, I. Montenegro and B. Scharifker, J. Electroanal. Chem. Interf. Electrochem., 1982, 138, 225–239 CrossRef CAS.
- G. J. Hills, D. J. Schiffrin and J. Thompson, Electrochim. Acta, 1974, 19, 671–680 CrossRef CAS.
- B. Scharifker and G. Hills, Electrochim. Acta, 1983, 28, 879–889 CrossRef CAS.
- B. Scharifker and G. Hills, J. Electroanal. Chem. Interf. Electrochem., 1981, 130, 81–97 CrossRef CAS.
- M. E. Hyde and R. G. Compton, J. Electroanal. Chem., 2003, 549, 1–12 CrossRef CAS.
- V. A. Isaev, O. V. Grishenkova and Y. P. Zaykov, RSC Adv., 2020, 10, 6979–6984 RSC.
- A. Gupta and C. Srivastava, Langmuir, 2020, 36, 7824–7834 CrossRef CAS PubMed.
- M. H. Mamme, C. Köhn, J. Deconinck and J. Ustarroz, Nanoscale, 2018, 10, 7194–7209 RSC.
- S. Fletcher, J. Chem. Soc., Faraday Trans. 1, 1983, 79, 467–479 RSC.
- K. H. Lim, S. Park and J.-I. Yun, J. Electrochem. Soc., 2015, 162, E334 CrossRef CAS.
- A. Milchev and T. Zapryanova, Electrochim. Acta, 2006, 51, 2926–2933 CrossRef CAS.
- P. Altimari and F. Pagnanelli, Electrochim. Acta, 2016, 205, 113–117 CrossRef CAS.
- A. D. Randolph and M. A. Larson, in Theory of Particulate Processes, ed. A. D. Randolph and M. A. Larson, Academic Press, 2nd edn, 1988, pp. 109–134, DOI:10.1016/B978-0-12-579652-1.50011-9.
- G. Wulff, Z. Kristallogr. - Cryst. Mater., 1901, 34, 449–530 CrossRef CAS.
- T. A. Witten and L. M. Sander, Phys. Rev. Lett., 1981, 47, 1400–1403 CrossRef CAS.
- T. A. Witten and L. M. Sander, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27, 5686–5697 CrossRef.
- R. Winand, J. Appl. Electrochem., 1991, 21, 377–385 CrossRef CAS.
- N. T. K. Thanh, N. Maclean and S. Mahiddine, Chem. Rev., 2014, 114, 7610–7630 CrossRef CAS PubMed.
- D. R. Ely and R. E. García, J. Electrochem. Soc., 2013, 160, A662 CrossRef CAS.
- J. F. Lutsko, J. Chem. Phys., 2012, 136, 034509 CrossRef.
- A. Russo, S. P. Perez, M. A. Durán-Olivencia, P. Yatsyshin, J. Carrillo and S. Kalliadasis, A Finite-Volume Method for Fluctuating Dynamical Density Functional Theory, 2019 Search PubMed.
- J. F. Lutsko, Sci. Adv., 2019, 5, eaav7399 CrossRef CAS PubMed.
- P. G. Vekilov, Cryst. Growth Des., 2010, 10, 5007–5019 CrossRef CAS PubMed.
- D. Gebauer, P. Raiteri, J. Gale and H. Cölfen, Am. J. Sci., 2018, 318, 969–988 CrossRef CAS.
- J. De Yoreo, Nat. Mater., 2013, 12, 284–285 CrossRef CAS PubMed.
- P. G. Vekilov, Nanoscale, 2010, 2, 2346–2357 RSC.
- D. Erdemir, A. Y. Lee and A. S. Myerson, Acc. Chem. Res., 2009, 42, 621–629 CrossRef CAS.
- S. Karthika, T. K. Radhakrishnan and P. Kalaichelvi, Cryst. Growth Des., 2016, 16, 6663–6681 CrossRef CAS.
- J. Li, Y. Li, Q. Li, Z. Wang and F. Leonard Deepak, Nanoscale Horiz., 2019, 4, 1302–1309 RSC.
- J. Li, Z. Wang and F. L. Deepak, ACS Nano, 2017, 11, 5590–5597 CrossRef CAS PubMed.
- S. Jeon, T. Heo, S.-Y. Hwang, J. Ciston, K. C. Bustillo, B. W. Reed, J. Ham, S. Kang, S. Kim, J. Lim, K. Lim, J. S. Kim, M.-H. Kang, R. S. Bloom, S. Hong, K. Kim, A. Zettl, W. Y. Kim, P. Ercius, J. Park and W. C. Lee, Science, 2021, 371, 498–503 CrossRef CAS.
- R. K. Ramamoorthy, E. Yildirim, E. Barba, P. Roblin, J. A. Vargas, L.-M. Lacroix, I. Rodriguez-Ruiz, P. Decorse, V. Petkov, S. Teychené and G. Viau, Nanoscale, 2020, 12, 16173–16188 RSC.
- Z. Ou, Z. Wang, B. Luo, E. Luijten and Q. Chen, Nat. Mater., 2020, 19, 450–455 CrossRef CAS.
- L. Fei, X. Gan, S. M. Ng, H. Wang, M. Xu, W. Lu, Y. Zhou, C. W. Leung, C.-L. Mak and Y. Wang, ACS Nano, 2019, 13, 681–688 CrossRef CAS.
- M. M. J. van Rijt, B. M. Oosterlaken, R. R. M. Joosten, L. E. A. Wijkhuijs, P. H. H. Bomans, H. Friedrich and G. de With, CrystEngComm, 2020, 22, 5854–5861 RSC.
- J. Baumgartner, A. Dey, P. H. H. Bomans, C. Le Coadou, P. Fratzl, N. A. J. M. Sommerdijk and D. Faivre, Nat. Mater., 2013, 12, 310–314 CrossRef CAS PubMed.
- Z. Li, D. Piankova, Y. Yang, Y. Kumagai, H. Zschiesche, M. Jonsson, N. V. Tarakina and I. L. Soroka, Angew. Chem., Int. Ed., 2022, 61, e202112204 CrossRef CAS.
- D. Parmar, Z. Niu, Y. Liang, H. Dai and J. D. Rimer, Faraday Discuss., 2022, 235, 322–342 RSC.
- M. Kumar, M. K. Choudhary and J. D. Rimer, Nat. Commun., 2018, 9, 2129 CrossRef.
- K. N. Bozhilov, T. T. Le, Z. Qin, T. Terlier, A. Palčić, J. D. Rimer and V. Valtchev, Sci. Adv., 2021, 7, eabg0454 CrossRef CAS PubMed.
- M. K. Choudhary, M. Kumar and J. D. Rimer, Angew. Chem., Int. Ed., 2019, 58, 15712–15716 CrossRef CAS PubMed.
- M. Kumar, H. Luo, Y. Román-Leshkov and J. D. Rimer, J. Am. Chem. Soc., 2015, 137, 13007–13017 CrossRef CAS PubMed.
- R. Bai, M. T. Navarro, Y. Song, T. Zhang, Y. Zou, Z. Feng, P. Zhang, A. Corma and J. Yu, Chem. Sci., 2020, 11, 12341–12349 RSC.
- T. Nakamuro, M. Sakakibara, H. Nada, K. Harano and E. Nakamura, J. Am. Chem. Soc., 2021, 143, 1763–1767 CrossRef CAS PubMed.
- M. H. Nielsen, S. Aloni and J. J. De Yoreo, Science, 2014, 345, 1158–1162 CrossRef CAS.
- D. Gebauer and H. Cölfen, Nano Today, 2011, 6, 564–584 CrossRef CAS.
- Y. Xu, K. C. H. Tijssen, P. H. H. Bomans, A. Akiva, H. Friedrich, A. P. M. Kentgens and N. Sommerdijk, Nat. Commun., 2018, 9, 2582 CrossRef.
- S. Sun, D. M. Chevrier, P. Zhang, D. Gebauer and H. Cölfen, Angew. Chem., Int. Ed., 2016, 55, 12206–12209 CrossRef CAS PubMed.
- W. J. E. M. Habraken, J. Tao, L. J. Brylka, H. Friedrich, L. Bertinetti, A. S. Schenk, A. Verch, V. Dmitrovic, P. H. H. Bomans, P. M. Frederik, J. Laven, P. van der Schoot, B. Aichmayer, G. de With, J. J. DeYoreo and N. A. J. M. Sommerdijk, Nat. Commun., 2013, 4, 1507 CrossRef.
- T. M. Stawski, A. E. S. van Driessche, M. Ossorio, J. Diego Rodriguez-Blanco, R. Besselink and L. G. Benning, Nat. Commun., 2016, 7, 11177 CrossRef CAS.
- C. Rodriguez-Navarro, A. Burgos-Cara, F. D. Lorenzo, E. Ruiz-Agudo and K. Elert, Cryst. Growth Des., 2020, 20, 4418–4432 CrossRef CAS.
- B. A. Garetz, J. Matic and A. S. Myerson, Phys. Rev. Lett., 2002, 89, 175501 CrossRef PubMed.
- P. E. Bonnett, K. J. Carpenter, S. Dawson and R. J. Davey, Chem. Commun., 2003, 698–699, 10.1039/B212062C.
- A. F. Ogata, A. M. Rakowski, B. P. Carpenter, D. A. Fishman, J. G. Merham, P. J. Hurst and J. P. Patterson, J. Am. Chem. Soc., 2020, 142, 1433–1442 CrossRef CAS PubMed.
- Z. Ou, Z. Wang, B. Luo, E. Luijten and Q. Chen, Nat. Mater., 2020, 19, 450–455 CrossRef CAS PubMed.
- T. H. Zhang and X. Y. Liu, Angew. Chem., Int. Ed., 2009, 48, 1308–1312 CrossRef CAS PubMed.
- P. R. ten Wolde and D. Frenkel, Science, 1997, 277, 1975–1978 CrossRef CAS PubMed.
- L. Houben, H. Weissman, S. G. Wolf and B. Rybtchinski, Nature, 2020, 579, 540–543 CrossRef CAS PubMed.
- J. T. Avaro, S. L. P. Wolf, K. Hauser and D. Gebauer, Angew. Chem., Int. Ed., 2020, 59, 6155–6159 CrossRef CAS PubMed.
- D. Gebauer, A. Völkel and H. Cölfen, Science, 2008, 322, 1819–1822 CrossRef CAS PubMed.
- R. Demichelis, P. Raiteri, J. D. Gale, D. Quigley and D. Gebauer, Nat. Commun., 2011, 2, 590 CrossRef PubMed.
- F. Sebastiani, S. L. P. Wolf, B. Born, T. Q. Luong, H. Cölfen, D. Gebauer and M. Havenith, Angew. Chem., Int. Ed., 2017, 56, 490–495 CrossRef CAS PubMed.
- J. Scheck, B. Wu, M. Drechsler, R. Rosenberg, A. E. S. Van Driessche, T. M. Stawski and D. Gebauer, J. Phys. Chem. Lett., 2016, 7, 3123–3130 CrossRef CAS PubMed.
- D. Zahn, ChemPhysChem, 2015, 16, 2069–2075 CrossRef CAS PubMed.
- H. Zheng, R. K. Smith, Y.-w. Jun, C. Kisielowski, U. Dahmen and A. P. Alivisatos, Science, 2009, 324, 1309–1312 CrossRef CAS PubMed.
- J. Ustarroz, T. Altantzis, J. A. Hammons, A. Hubin, S. Bals and H. Terryn, Chem. Mater., 2014, 26, 2396–2406 CrossRef CAS.
- J. Ustarroz, X. Ke, A. Hubin, S. Bals and H. Terryn, J. Phys. Chem. C, 2012, 116, 2322–2329 CrossRef CAS.
- Y.-R. Kim, S. C. S. Lai, K. McKelvey, G. Zhang, D. Perry, T. S. Miller and P. R. Unwin, J. Phys. Chem. C, 2015, 119, 17389–17397 CrossRef CAS.
- S. C. S. Lai, R. A. Lazenby, P. M. Kirkman and P. R. Unwin, Chem. Sci., 2015, 6, 1126–1138 RSC.
- R. L. Harniman, D. Plana, G. H. Carter, K. A. Bradley, M. J. Miles and D. J. Fermín, Nat. Commun., 2017, 8, 971 CrossRef PubMed.
- H. E. M. Hussein, R. J. Maurer, H. Amari, J. J. P. Peters, L. Meng, R. Beanland, M. E. Newton and J. V. Macpherson, ACS Nano, 2018, 12, 7388–7396 CrossRef CAS PubMed.
- J. J. De Yoreo, P. U. P. A. Gilbert, N. A. J. M. Sommerdijk, R. L. Penn, S. Whitelam, D. Joester, H. Zhang, J. D. Rimer, A. Navrotsky, J. F. Banfield, A. F. Wallace, F. M. Michel, F. C. Meldrum, H. Cölfen and P. M. Dove, Science, 2015, 349, aaa6760 CrossRef PubMed.
- M. Niederberger and H. Cölfen, Phys. Chem. Chem. Phys., 2006, 8, 3271–3287 RSC.
- D. Li, M. H. Nielsen, J. R. I. Lee, C. Frandsen, J. F. Banfield and J. J. De Yoreo, Science, 2012, 336, 1014–1018 CrossRef CAS PubMed.
- G. Mirabello, A. Ianiro, P. H. H. Bomans, T. Yoda, A. Arakaki, H. Friedrich, G. de With and N. A. J. M. Sommerdijk, Nat. Mater., 2020, 19, 391–396 CrossRef CAS PubMed.
- H. Su, P. H. H. Bomans, H. Friedrich, Y. Xu and N. Sommerdijk, J. Phys. Chem. C, 2021, 125, 1143–1149 CrossRef CAS.
- A. E. Van Driessche, L. G. Benning, J. D. Rodriguez-Blanco, M. Ossorio, P. Bots and J. M. García-Ruiz, Science, 2012, 336, 69–72 CrossRef CAS PubMed.
- C. Wagner, Z. Elektrochem., 1961, 65, 581–591 CrossRef CAS.
- I. M. Lifshitz and V. V. Slyozov, J. Phys. Chem. Solids, 1961, 19, 35–50 CrossRef.
- M. D. Clark, S. K. Kumar, J. S. Owen and E. M. Chan, Nano Lett., 2011, 11, 1976–1980 CrossRef CAS PubMed.
- M. Kahlweit, Adv. Colloid Interface Sci., 1975, 5, 1–35 CrossRef CAS.
- J. Li and F. L. Deepak, Chem. Rev., 2022, 122, 16911–16982 CrossRef CAS PubMed.
- G. Mao, M. Kilani and M. Ahmed, J. Electrochem. Soc., 2022, 169, 022505 CrossRef CAS.
- J. Velmurugan, J.-M. Noël, W. Nogala and M. V. Mirkin, Chem. Sci., 2012, 3, 3307–3314 RSC.
- J. Velmurugan, J.-M. Noël and M. V. Mirkin, Chem. Sci., 2014, 5, 189–194 RSC.
- S. Chen and A. Kucernak, J. Phys. Chem. B, 2003, 107, 8392–8402 CrossRef CAS.
- S. Chen and A. Kucernak, Electrochem. Commun., 2002, 4, 80–85 CrossRef CAS.
- V. Brasiliense, J. Clausmeyer, A. L. Dauphin, J.-M. Noël, P. Berto, G. Tessier, W. Schuhmann and F. Kanoufi, Angew. Chem., Int. Ed., 2017, 56, 10598–10601 CrossRef CAS PubMed.
- J. Clausmeyer, J. Masa, E. Ventosa, D. Öhl and W. Schuhmann, Chem. Commun., 2016, 52, 2408–2411 RSC.
- K. Huang, J. Clausmeyer, L. Luo, K. Jarvis and R. M. Crooks, Faraday Discuss., 2018, 210, 267–280 RSC.
- M. W. Glasscott, C. M. Hill and J. E. Dick, J. Phys. Chem. C, 2020, 124, 14380–14389 CrossRef CAS.
- C. G. Zoski, Electroanalysis, 2002, 14, 1041–1051 CrossRef CAS.
- K. Lim, S. Goines, M. Deng, H. McCormick, P. J. Kauffmann and J. E. Dick, Analyst, 2023, 148, 2992–3001 RSC.
- B. Zhang, J. Galusha, P. G. Shiozawa, G. Wang, A. J. Bergren, R. M. Jones, R. J. White, E. N. Ervin, C. C. Cauley and H. S. White, Anal. Chem., 2007, 79, 4778–4787 CrossRef CAS PubMed.
- E. Fahrenkrug, D. H. Alsem, N. Salmon and S. Maldonado, J. Electrochem. Soc., 2017, 164, H358 CrossRef CAS.
- X. H. Liu, J. W. Wang, S. Huang, F. Fan, X. Huang, Y. Liu, S. Krylyuk, J. Yoo, S. A. Dayeh, A. V. Davydov, S. X. Mao, S. T. Picraux, S. Zhang, J. Li, T. Zhu and J. Y. Huang, Nat. Nanotechnol., 2012, 7, 749–756 CrossRef CAS PubMed.
- A. Radisic, P. M. Vereecken, J. B. Hannon, P. C. Searson and F. M. Ross, Nano Lett., 2006, 6, 238–242 CrossRef CAS PubMed.
- M. Gu, L. R. Parent, B. L. Mehdi, R. R. Unocic, M. T. McDowell, R. L. Sacci, W. Xu, J. G. Connell, P. Xu, P. Abellan, X. Chen, Y. Zhang, D. E. Perea, J. E. Evans, L. J. Lauhon, J.-G. Zhang, J. Liu, N. D. Browning, Y. Cui, I. Arslan and C.-M. Wang, Nano Lett., 2013, 13, 6106–6112 CrossRef CAS PubMed.
- A. J. Leenheer, J. P. Sullivan, M. J. Shaw and C. T. Harris, J. Microelectromech. Syst., 2015, 24, 1061–1068 CAS.
- E. R. White, S. B. Singer, V. Augustyn, W. A. Hubbard, M. Mecklenburg, B. Dunn and B. C. Regan, ACS Nano, 2012, 6, 6308–6317 CrossRef CAS PubMed.
- R. R. Unocic, R. L. Sacci, G. M. Brown, G. M. Veith, N. J. Dudney, K. L. More, F. S. Walden II, D. S. Gardiner, J. Damiano and D. P. Nackashi, Microsc. Microanal., 2014, 20, 452–461 CrossRef CAS PubMed.
- C.-M. Wang, J. Mater. Res., 2015, 30, 326–339 CrossRef CAS.
- M. J. Williamson, R. M. Tromp, P. M. Vereecken, R. Hull and F. M. Ross, Nat. Mater., 2003, 2, 532–536 CrossRef CAS PubMed.
- Z. Fan, L. Zhang, D. Baumann, L. Mei, Y. Yao, X. Duan, Y. Shi, J. Huang, Y. Huang and X. Duan, Adv. Mater., 2019, 31, 1900608 CrossRef PubMed.
- R. Yang, L. Mei, Y. Fan, Q. Zhang, H.-G. Liao, J. Yang, J. Li and Z. Zeng, Nat. Protoc., 2023, 18, 555–578 CrossRef CAS PubMed.
- C. Santana Santos, B. N. Jaato, I. Sanjuán, W. Schuhmann and C. Andronescu, Chem. Rev., 2023, 123, 4972–5019 CrossRef CAS PubMed.
- A. A. Gewirth and B. K. Niece, Chem. Rev., 1997, 97, 1129–1162 CrossRef CAS PubMed.
- J. Jiang, Z. Huang, C. Xiang, R. Poddar, H.-J. Lewerenz, K. M. Papadantonakis, N. S. Lewis and B. S. Brunschwig, ChemSusChem, 2017, 10, 4657–4663 CrossRef CAS PubMed.
- G. S. Harlow, E. Lundgren and M. Escudero-Escribano, Curr. Opin. Electrochem., 2020, 23, 162–173 CrossRef CAS.
- H. Hwang, Y. C. Cho, S. Lee, Y.-H. Lee, S. Kim, Y. Kim, W. Jo, P. Duchstein, D. Zahn and G. W. Lee, Chem. Sci., 2021, 12, 179–187 RSC.
- Y. Kimura, H. Katsuno and T. Yamazaki, Faraday Discuss., 2022, 235, 81–94 RSC.
- A. J. Bard, F. R. F. Fan, J. Kwak and O. Lev, Anal. Chem., 1989, 61, 132–138 CrossRef CAS.
- A. Schulte and W. Schuhmann, Angew. Chem., Int. Ed., 2007, 46, 8760–8777 CrossRef CAS PubMed.
- T. Kai, C. G. Zoski and A. J. Bard, Chem. Commun., 2018, 54, 1934–1947 RSC.
- K. Itaya and E. Tomita, Surf. Sci., 1988, 201, L507–L512 CrossRef CAS.
- O. M. Magnussen, Chem. – Eur. J., 2019, 25, 12865–12883 CrossRef CAS PubMed.
- M. Kang, D. Perry, C. L. Bentley, G. West, A. Page and P. R. Unwin, ACS Nano, 2017, 11, 9525–9535 CrossRef CAS PubMed.
- C. Zhu, K. Huang, N. P. Siepser and L. A. Baker, Chem. Rev., 2021, 121, 11726–11768 CrossRef CAS PubMed.
- P. K. Hansma, B. Drake, O. Marti, S. A. Gould and C. B. Prater, Science, 1989, 243, 641–643 CrossRef CAS PubMed.
- C. L. Bentley, M. Kang, F. M. Maddar, F. Li, M. Walker, J. Zhang and P. R. Unwin, Chem. Sci., 2017, 8, 6583–6593 RSC.
- N. Ebejer, A. G. Güell, S. C. S. Lai, K. McKelvey, M. E. Snowden and P. R. Unwin, Annu. Rev. Anal. Chem., 2013, 6, 329–351 CrossRef CAS PubMed.
- N. Ebejer, M. Schnippering, A. W. Colburn, M. A. Edwards and P. R. Unwin, Anal. Chem., 2010, 82, 9141–9145 CrossRef CAS PubMed.
- O. J. Wahab, M. Kang and P. R. Unwin, Curr. Opin. Electrochem., 2020, 22, 120–128 CrossRef CAS.
- D. Martín-Yerga, P. R. Unwin, D. Valavanis and X. Xu, Curr. Opin. Electrochem., 2023, 42, 101405 CrossRef.
- M. Escudero-Escribano, A. F. Pedersen, E. T. Ulrikkeholm, K. D. Jensen, M. H. Hansen, J. Rossmeisl, I. E. L. Stephens and I. Chorkendorff, Chem. – Eur. J., 2018, 24, 12280–12290 CrossRef CAS PubMed.
- O. Urquidi, J. Brazard, N. LeMessurier, L. Simine and T. B. M. Adachi, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2122990119 CrossRef CAS PubMed.
- N. Batina, T. Will and D. M. Kolb, Faraday Discuss., 1992, 94, 93–106 RSC.
- T. Yoshioka, H. Matsushima and M. Ueda, Electrochem. Commun., 2018, 92, 29–32 CrossRef CAS.
- T. Yoshioka, H. Matsushima and M. Ueda, Electrochim. Acta, 2019, 302, 422–427 CrossRef CAS.
- J. Liu, C. Zhong, X. Du, Y. Wu, P. Xu, J. Liu and W. Hu, Electrochim. Acta, 2013, 100, 164–170 CrossRef CAS.
- L. Jacobse, Y.-F. Huang, M. T. M. Koper and M. J. Rost, Nat. Mater., 2018, 17, 277–282 CrossRef CAS PubMed.
- M. Zhou, J. E. Dick and A. J. Bard, J. Am. Chem. Soc., 2017, 139, 17677–17682 CrossRef CAS PubMed.
- M. Zhou, S. Bao and A. J. Bard, J. Am. Chem. Soc., 2019, 141, 7327–7332 CrossRef CAS PubMed.
- F. Favier, E. C. Walter, M. P. Zach, T. Benter and R. M. Penner, Science, 2001, 293, 2227–2231 CrossRef CAS PubMed.
- E. Antolini, Energy Environ. Sci., 2009, 2, 915–931 RSC.
- G. Zhu, Y. Jiang, F. Lin, H. Zhang, C. Jin, J. Yuan, D. Yang and Z. Zhang, Chem. Commun., 2014, 50, 9447–9450 RSC.
- T. M. Day, P. R. Unwin and J. V. Macpherson, Nano Lett., 2007, 7, 51–57 CrossRef CAS PubMed.
- H. E. M. Hussein, H. Amari, B. G. Breeze, R. Beanland and J. V. Macpherson, Nanoscale, 2020, 12, 21757–21769 RSC.
- F. Wang, O. Borodin, T. Gao, X. Fan, W. Sun, F. Han, A. Faraone, J. A. Dura, K. Xu and C. Wang, Nat. Mater., 2018, 17, 543–549 CrossRef CAS PubMed.
- J. Zheng, Q. Zhao, T. Tang, J. Yin, C. D. Quilty, G. D. Renderos, X. Liu, Y. Deng, L. Wang, D. C. Bock, C. Jaye, D. Zhang, E. S. Takeuchi, K. J. Takeuchi, A. C. Marschilok and L. A. Archer, Science, 2019, 366, 645–648 CrossRef CAS PubMed.
- X. Luo, M. Zhou, Z. Luo, T. Shi, L. Li, X. Xie, Y. Sun, X. Cao, M. Long, S. Liang and G. Fang, Energy Storage Mater., 2023, 57, 628–638 CrossRef.
- J. W. Diggle, A. R. Despic and J. O. M. Bockris, J. Electrochem. Soc., 1969, 116, 1503 CrossRef CAS.
- Z. Shen, J. Mao, G. Yu, W. Zhang, S. Mao, W. Zhong, H. Cheng, J. Guo, J. Zhang and Y. Lu, Angew. Chem., Int. Ed., 2023, 62, e202218452 CrossRef CAS PubMed.
- M. Li, L. Ran and R. Knibbe, J. Phys. Chem. Lett., 2021, 12, 913–918 CrossRef CAS PubMed.
- S. Neupane, A. Valencia-Ramírez, P. Losada-Pérez and F. U. Renner, Phys. Status Solidi A, 2021, 218, 2100470 CrossRef CAS.
- M. S. Whittingham, Proc. IEEE, 2012, 100, 1518–1534 CAS.
- M. D. Tikekar, L. A. Archer and D. L. Koch, Sci. Adv., 2016, 2, e1600320 CrossRef PubMed.
- X.-R. Chen, B.-C. Zhao, C. Yan and Q. Zhang, Adv. Mater., 2021, 33, 2004128 CrossRef CAS PubMed.
- E. A. Brener, J. Cryst. Growth, 1990, 99, 165–170 CrossRef CAS.
- J. N. Chazalviel, Phys. Rev. A, 1990, 42, 7355–7367 CrossRef CAS PubMed.
- L. Y. Beaulieu, S. D. Beattie, T. D. Hatchard and J. R. Dahn, J. Electrochem. Soc., 2003, 150, A419 CrossRef CAS.
- A. Pei, G. Zheng, F. Shi, Y. Li and Y. Cui, Nano Lett., 2017, 17, 1132–1139 CrossRef CAS PubMed.
- R. L. Sacci, J. M. Black, N. Balke, N. J. Dudney, K. L. More and R. R. Unocic, Nano Lett., 2015, 15, 2011–2018 CrossRef CAS PubMed.
- R. L. Sacci, N. J. Dudney, K. L. More, L. R. Parent, I. Arslan, N. D. Browning and R. R. Unocic, Chem. Commun., 2014, 50, 2104–2107 RSC.
- A. Kushima, K. P. So, C. Su, P. Bai, N. Kuriyama, T. Maebashi, Y. Fujiwara, M. Z. Bazant and J. Li, Nano Energy, 2017, 32, 271–279 CrossRef CAS.
- B. L. Mehdi, J. Qian, E. Nasybulin, C. Park, D. A. Welch, R. Faller, H. Mehta, W. A. Henderson, W. Xu, C. M. Wang, J. E. Evans, J. Liu, J. G. Zhang, K. T. Mueller and N. D. Browning, Nano Lett., 2015, 15, 2168–2173 CrossRef CAS PubMed.
- B. Thirumalraj, T. T. Hagos, C.-J. Huang, M. A. Teshager, J.-H. Cheng, W.-N. Su and B.-J. Hwang, J. Am. Chem. Soc., 2019, 141, 18612–18623 CrossRef CAS PubMed.
- G. Feng, Y. Shi, H. Jia, S. Risal, X. Yang, P. Ruchhoeft, W.-C. Shih, Z. Fan, W. Xu and X. Shan, Sci. Adv., 2023, 9, eadg6813 CrossRef CAS PubMed.
- Q. Cheek, E. Fahrenkrug, S. Hlynchuk, D. H. Alsem, N. J. Salmon and S. Maldonado, ACS Nano, 2020, 14, 2869–2879 CrossRef CAS PubMed.
- G. E. Thompson, R. C. Furneaux, G. C. Wood, J. A. Richardson and J. S. Goode, Nature, 1978, 272, 433–435 CrossRef CAS.
- Z. Yin, S. Wu, X. Zhou, X. Huang, Q. Zhang, F. Boey and H. Zhang, Small, 2010, 6, 307–312 CrossRef CAS PubMed.
- Y. Liu, K. Tai and S. J. Dillon, Chem. Mater., 2013, 25, 2927–2933 CrossRef CAS.
- S. E. R. Tay, A. E. Goode, J. Nelson Weker, A. A. Cruickshank, S. Heutz, A. E. Porter, M. P. Ryan and M. F. Toney, Nanoscale, 2016, 8, 1849–1853 RSC.
- K. Tschulik, B. Haddou, D. Omanović, N. V. Rees and R. G. Compton, Nano Res., 2013, 6, 836–841 CrossRef CAS.
- M. R. Hauwiller, X. Zhang, W.-I. Liang, C.-H. Chiu, Q. Zhang, W. Zheng, C. Ophus, E. M. Chan, C. Czarnik, M. Pan, F. M. Ross, W.-W. Wu, Y.-H. Chu, M. Asta, P. W. Voorhees, A. P. Alivisatos and H. Zheng, Nano Lett., 2018, 18, 6427–6433 CrossRef CAS PubMed.
- G. Ivantsov, Dokl. Akad. Nauk. S.S.S.R., 1947, 58, p. 567 Search PubMed.
- F. C. Walsh, S. Wang and N. Zhou, Curr. Opin. Electrochem., 2020, 20, 8–19 CrossRef CAS.
- S. Pinate, P. Leisner and C. Zanella, J. Electrochem. Soc., 2019, 166, D804 CrossRef CAS.
- O. Devos, S. Jakab, C. Gabrielli, S. Joiret, B. Tribollet and S. Picart, J. Cryst. Growth, 2009, 311, 4334–4342 CrossRef CAS.
- B. Blount, K. Kilner, H. Hu, D. Gohmann, E. Gordon, Y. Wang and H. Ren, J. Phys. Chem. C, 2020, 124, 17413–17417 CrossRef CAS.
- D. Routkevitch, T. Bigioni, M. Moskovits and J. M. Xu, J. Phys. Chem., 1996, 100, 14037–14047 CrossRef CAS.
- D. A. Robinson and H. S. White, Nano Lett., 2019, 19, 5612–5619 CrossRef CAS PubMed.
- S. Manzeli, D. Ovchinnikov, D. Pasquier, O. V. Yazyev and A. Kis, Nat. Rev. Mater., 2017, 2, 17033 CrossRef CAS.
- X. Wan, K. Chen, Z. Chen, F. Xie, X. Zeng, W. Xie, J. Chen and J. Xu, Adv. Funct. Mater., 2017, 27, 1603998 CrossRef.
- S. Thomas, D. E. Smith, V. K. Greenacre, Y. J. Noori, A. L. Hector, C. H. d. Groot, G. Reid and P. N. Bartlett, J. Electrochem. Soc., 2020, 167, 106511 CrossRef CAS.
- S. Murugesan, A. Akkineni, B. P. Chou, M. S. Glaz, D. A. Vanden Bout and K. J. Stevenson, ACS Nano, 2013, 7, 8199–8205 CrossRef CAS PubMed.
- N. M. Abdelazim, Y. J. Noori, S. Thomas, V. K. Greenacre, Y. Han, D. E. Smith, G. Piana, N. Zhelev, A. L. Hector, R. Beanland, G. Reid, P. N. Bartlett and C. H. de Groot, Adv. Electron. Mater., 2021, 7, 2100419 CrossRef CAS.
- O. M. Yaghi, G. Li and H. Li, Nature, 1995, 378, 703–706 CrossRef CAS.
- A. Bétard and R. A. Fischer, Chem. Rev., 2012, 112, 1055–1083 CrossRef PubMed.
- X. Zhang, K. Wan, P. Subramanian, M. Xu, J. Luo and J. Fransaer, J. Mater. Chem. A, 2020, 8, 7569–7587 RSC.
- H. Al-Kutubi, J. Gascon, E. J. R. Sudhölter and L. Rassaei, ChemElectroChem, 2015, 2, 462–474 CrossRef CAS.
- W. Guo, W. Zhang, N. Han, S. Xie, Z. Zhou, W. Monnens, O. Martinez Mora, Z. Xue, X. Zhang, X. Zhang and J. Fransaer, Chem. – Eur. J., 2023, 29, e202302338 CrossRef CAS PubMed.
- M. Li and M. Dincă, Chem. Mater., 2015, 27, 3203–3206 CrossRef CAS.
- S. D. Worrall, M. A. Bissett, M. P. Attfield and R. A. W. Dryfe, CrystEngComm, 2018, 20, 4421–4427 RSC.
- N. Campagnol, T. R. C. Van Assche, M. Li, L. Stappers, M. Dincă, J. F. M. Denayer, K. Binnemans, D. E. De Vos and J. Fransaer, J. Mater. Chem. A, 2016, 4, 3914–3925 RSC.
- P. Schäfer, M. A. van der Veen and K. F. Domke, Chem. Commun., 2016, 52, 4722–4725 RSC.
- Y. Han, J. Cui, Y. Yu, Y. Chao, D. Li, C. Wang and G. G. Wallace, ChemSusChem, 2022, 15, e202200644 CrossRef CAS PubMed.
- A. Jana, S. Bähring, M. Ishida, S. Goeb, D. Canevet, M. Salle, J. Jeppesen and J. Sessler, Chem. Soc. Rev., 2018, 47, 5614–5645 RSC.
- W. Wang, L. Luo, P. Sheng, J. Zhang and Q. Zhang, Chemistry, 2021, 27, 464–490 CrossRef CAS PubMed.
- Y. Wang, L. Sun, C. Wang, F. Yang, X. Ren, X. Zhang, H. Dong and W. Hu, Chem. Soc. Rev., 2019, 48, 1492–1530 RSC.
- J. Ferraris, D. O. Cowan, V. Walatka and J. H. Perlstein, J. Am. Chem. Soc., 1973, 95, 948–949 CrossRef CAS.
- T. Li, S. Melis, C. Bagade, A. Khatib, R. Kosarzycki, G. Maglieri, X. Zhang and E. Van Keuren, J. Nanopart. Res., 2019, 21, 147 CrossRef.
- M. D. Ward, in Supramolecular Architecture, American Chemical Society, 1992, vol. 499, ch. 17, pp. 231–243 Search PubMed.
- F. Favier, H. Liu and R. M. Penner, Adv. Mater., 2001, 13, 1567–1570 CrossRef CAS.
- M. Mas-Torrent and P. Hadley, Small, 2005, 1, 806–808 CrossRef CAS PubMed.
- L. Ren, X. Xian, K. Yan, L. Fu, Y. Liu, S. Chen and Z. Liu, Adv. Funct. Mater., 2010, 20, 1209–1223 CrossRef CAS.
- M. Wysocka, K. Winkler, J. R. Stork and A. L. Balch, Chem. Mater., 2004, 16, 771–780 CrossRef CAS.
- D. Chen, R. Wang, I. Arachchige, G. Mao and S. L. Brock, J. Am. Chem. Soc., 2004, 126, 16290–16291 CrossRef CAS PubMed.
- S. X. Wang, L. Li and G. Z. Mao, J. Phys. Chem. C, 2012, 116, 5492–5498 CrossRef CAS.
- R. M. Wang, L. Li, I. Arachchige, S. Ganguly, S. L. Brock and G. Z. Mao, ACS Nano, 2010, 4, 6687–6696 CrossRef CAS PubMed.
- D. Gunasekera, M. Kilani, X. Yu, Q. Chen, G. Mao and L. Luo, J. Electrochem. Soc., 2019, 166, H63–H69 CrossRef CAS.
- P. Jahanian, X. Yu, M. Kilani and G. Mao, Mater. Res. Lett., 2017, 5, 569–576 CrossRef CAS.
- L. Li, P. Jahanian and G. Mao, J. Phys. Chem. C, 2014, 118, 18771–18782 CrossRef CAS.
- D. Gunasekera, M. Kilani, X. Yu, Q. Chen, G. Mao and L. Luo, J. Electrochem. Soc., 2019, 166, H63–H69 CrossRef CAS.
- X. Xiao, F. R. Fan, J. Zhou and A. J. Bard, J. Am. Chem. Soc., 2008, 130, 16669–16677 CrossRef CAS PubMed.
- X. Yu, M. Kilani, A. Siddiqui and G. Mao, Adv. Mater. Technol., 2020, 5, 2000554 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |