Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Controlled synthesis and characterization of porous silicon nanoparticles for dynamic nuclear polarization†
Gevin
von Witte
 ab,
Aaron
Himmler
b,
Viivi
Hyppönen
c,
Jiri
Jäntti
ab,
Aaron
Himmler
b,
Viivi
Hyppönen
c,
Jiri
Jäntti
 d,
Mohammed M.
Albannay
a,
Jani O.
Moilanen
d,
Mohammed M.
Albannay
a,
Jani O.
Moilanen
 e,
Matthias
Ernst
e,
Matthias
Ernst
 b,
Vesa-Pekka
Lehto
b,
Vesa-Pekka
Lehto
 d,
Joakim
Riikonen
d,
Sebastian
Kozerke
a,
Mikko I.
Kettunen‡
c and
Konstantin
Tamarov‡
d,
Joakim
Riikonen
d,
Sebastian
Kozerke
a,
Mikko I.
Kettunen‡
c and
Konstantin
Tamarov‡
 *d
*d
aInstitute for Biomedical Engineering, University and ETH Zurich, Zurich, Switzerland
bInstitute of Molecular Physical Science, ETH Zurich, Zurich, Switzerland
cKuopio Biomedical Imaging Unit, A.I. Virtanen Institute, University of Eastern Finland, Kuopio, Finland
dDepartment of Technical Physics, University of Eastern Finland, Kuopio, Finland. E-mail: konstantin.tamarov@uef.fi
eDepartment of Chemistry, Nanoscience Center, University of Jyväskylä, Jyväskylä, Finland
First published on 18th September 2024
Abstract
Si nanoparticles (NPs) have been actively developed as a hyperpolarized magnetic resonance imaging (MRI) contrast agent with an imaging window close to one hour. However, the progress in the development of NPs has been hampered by the incomplete understanding of their structural properties that correspond to efficient hyperpolarization buildup and long polarization decays. In this work we study dynamic nuclear polarization (DNP) of single crystal porous Si (PSi) NPs with defined doping densities ranging from nominally undoped to highly doped with boron or phosphorus. To develop such PSi NPs we perform low-load metal-assisted catalytic etching for electronic grade Si powder followed by thermal oxidation to form the dangling bonds in the Si/SiO2 interface, the Pb centers. Pb centers are the endogenous source of the unpaired electron spins necessary for DNP. The controlled fabrication and oxidation procedures allow us to thoroughly investigate the impact of the magnetic field, temperature and doping on the DNP process. We argue that the buildup and decay rate constants are independent of size of Si crystals between approximately 10 and 60 nm. Instead, the rates are limited by the polarization transfer across the nuclear spin diffusion barrier determined by the large hyperfine shift of the central 29Si nuclei of the Pb centers. The size-independent rates are then weakly affected by the doping degree for low and moderately doped Si although slight doping is required to achieve the highest polarization. Thus, we find the room temperature relaxation of low boron doped PSi NPs reaching 75 ± 3 minutes and nuclear polarization levels exceeding ∼6% when polarized at 6.7 T and 1.4 K. Our study thus establishes solid grounds for further development of Si NPs as hyperpolarized contrast agents.
1 Introduction
Magnetic resonance imaging (MRI) is a non-invasive versatile technique that can provide anatomical images with either sub-millimeter spatial1 or milliseconds temporal2 resolution. Applying recent advances in artificial intelligence based image reconstruction and enhancement methods,3 low field MRI has recently reached real world adoption even in the mobile setting.4 MRI, however, is inherently insensitive at room temperature due to low thermal polarization of nuclei, which complicates the observation of nuclei other than 1H. Detecting low-abundant nuclei, such as 13C, 15N or 29Si, brings additional versatility to MRI allowing to e.g., image tumor metabolism,5 locally detect pH,6,7 detect Si particles in vivo during prolonged time window.8–10 Porous Si nanoparticles (NPs) hold particular promise due to their biocompatibility and numerous treatment modalities.11To detect Si NPs in an MRI scanner, their 29Si nuclei require hyperpolarization i.e., a polarization significantly beyond thermal equilibrium at body temperature. A mature method to hyperpolarize various nuclei in the solid state is dynamic nuclear polarization (DNP).12 DNP requires the presence of polarized unpaired electronic spins, whose polarization is subsequently transferred to hyperfine (HF) coupled nuclei by (near-) resonant microwave (MW) irradiation.
In Si, the unbound electrons required for DNP can originate from substitutional donor dopant atoms, such as group V (P, As, Sb, Bi) or group VI (S) atoms, which carry one or more donor electrons. As each dopant carries extra electron(s), the majority carriers are negatively charged electrons and Si is named n-type. Spins of electrons bound to 31P donors have been widely used to polarize 29Si nuclear spins and to study polarization dynamics in bulk Si samples with different 29Si and 31P content.13–16 With the variation of 31P and 29Si content, well resolved solid effect (SE),13,15,16 differential SE13 and Overhauser effect (OE)14–16 DNP mechanisms of 29Si hyperpolarization have been identified. More sophisticated protocols, such as resonant polarization transfer from polarized 31P to 29Si nuclei,17 have been demonstrated.
If Si is doped with group III atoms, in particular boron, each dopant atom binds an electron leaving a hole in the valence band. The majority carriers are the positively charged holes and the Si is called p-type. Hole states in the valence band from the p-orbitals as opposed to the s-orbitals of electrons in the conduction band. The need to satisfy the 3-fold degeneracy of the p-orbital results in the splitting of the valence band into heavy and light hole bands.18 The degeneracy of these bands combined with the dopant atom-induced local random stresses broadens the electron paramagnetic resonance (EPR) spectrum making it hard to observe in B-doped Si unless uniaxial strain is applied.19–21 Strained single crystal Si![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B has been used to study the integrated solid effect.20
B has been used to study the integrated solid effect.20
Another source of electron spins are defect sites found in amorphous Si,22 oxidized Si surfaces23–25 and elemental Si particles.8,9,26 Such defect sites are characterized by a broken Si bond with an unpaired electron mostly localized on the central Si atom.25 When the defect is located at the Si/SiO2 interface, it is called the Pb center.23–25Pb centers and Pb-like centers in amorphous Si have been used to hyperpolarize various Si particles and apply them as background-free contrast agents for MRI.8,27 The long hyperpolarization decay times (τdec) of Si particles around ∼40 min at room temperature offered extended imaging time windows compared to about 30 s in 13C molecules6 or 145 s (15 min) in nanodiamonds (microdiamonds).28 In diamonds, the substitutional nitrogen defects in the particle's bulk (often called C or P1 center) are responsible for DNP while surface dangling bonds commonly cause strong relaxation. The surface dangling bonds thus are detrimental for nanodiamonds with high surface-to-bulk ratio leading to lower polarization levels and faster relaxation compared to microdiamonds.29 This is different from the case in Si with the Pb centers located on the interface to the naturally forming surface oxide which allows the hyperpolarization of 50 nm particles with identical enhancements compared to μm-sized particles.26
Despite the demonstrated high nuclear polarization and long nuclear τdec relaxation times at room temperature26,30 in bulk Si particles, the proposed slow spin diffusion fails to explain the similar τdec in micro- and nanoparticles. The diversity of fabrication methods further complicates the identification of the structural properties, their comparison between different particles and influence on τdec. In this study, we apply a top-down fabrication approach31,32 to produce porous silicon nanoparticles (PSi NPs, sometimes denoted as nanobeads) with a high surface area from doping controlled, single crystal Si wafers. The role of the high surface area is twofold. First, it enables the controlled formation of a relatively large number of endogenous Pb centers to drive the DNP process. To the best of our knowledge, previous attempts to hyperpolarize PSi NPs required the use of external radicals for DNP to be efficient10 complicating possible MRI applications of those NPs. Second, the large surface area combines good biocompatibility with a well understood diverse chemistry for (targeted) nanocarrier capabilities11 making the developed PSi NPs suitable both for imaging and drug delivery.11 Herein, we prove that endogenous Pb centers in PSi NPs are capable of providing DNP enhancements similar to state-of-the-art bulk particles.26 Furthermore, we demonstrate that PSi nanoparticles from slightly doped Si wafers can achieve room temperature hyperpolarization decay times exceeding one hour and 29Si polarization levels around 6%.
2 Methods
2.1 Silicon
Previous studies on the DNP of Si NPs relied on either commercially available9,26,30,37 or on in-house bottom-up fabrication approaches.10,30,38,39 In contrast, we selected single crystal Si wafers as the starting material to precisely control crystallinity and doping level (Table 1). Specifically, we used electronics grade single crystal (100) silicon wafers of different doping (Okmetic Oy, Finland). The samples were denoted according to the doping type and doping density. Doping type was indicated by P (positive) and N (negative) letters for boron and phosphorus doping, respectively. The doping density ranged from 4 × 1018 cm−3 for P++ and N++ porous Si (PSi) NPs down to less than 1012 cm−3 for the nominally undoped wafer (UW). The doping density was below the insulator-to-metal transition for all Si wafers considered. In addition to wafers, we prepared PSi NPs from a relatively cheaper commercially available polycrystalline (1–10) μm Silgrain Supreme MC10 SB powder (Elkem Silicon Products, Norway) with known concentration of impurities (MC10 sample): the purity of the powder was 99.997% determined by the supplier, where the main impurities were Fe (14 ppm), Al (6 ppm), Ca (3 ppm), Ti (1 ppm), B (<1 ppm), and P (<1 ppm).| Abbreviation | Resistivity (Ω cm) | Dopant | Doping densitya (cm−3) | Average dopant distanceb (nm) |
|---|---|---|---|---|
| a Dopant densities were calculated using Caughey–Thomas expression33 for electron and hole mobilities. Effective Bohr radii are 1.3 (3.8) and 2.1 nm for heavy (light) holes and electrons in B doped and P doped Si, respectively. The effective Bohr radius of the P electron assumes the pancake-like wavefunction ansatz proposed by Kohn and Luttinger.34 b Average distance between the dopant atoms was calculated from their density using the random probability distribution in three dimensions.36 c Powder from single crystal (100) wafers, Okmetic. d Elkem Silicon Products. | ||||
| P++c | 0.0186 | Boron | 4 × 1018 | 3.49 |
| P+c | 0.105 | Boron | 3 × 1017 | 8.27 |
| Pc | 25 | Boron | 5 × 1014 | 69.8 |
| UWc | >5000 | Boron | <1012 | >554 |
| Nc | 19.7 | Phosphorus | 2.3 × 1014 | 90.4 |
| N+c | 1.15 | Phosphorus | 3 × 1015 | 38.4 |
| N++c | 0.0144 | Phosphorus | 3 × 1018 | 3.84 |
| MC10d | Metallurgical grade powder, polycrystalline, 99.997% purity. Impurities: Al, Fe, Ca, Ti | |||
Dopant type of the Si wafers was verified by hot point probe method.40 Specific resistivity was calculated using a MATLAB (The MathWorks, Inc., USA) script using wafer thickness and resistivity measured with a four-point probe (Jandel Engineering Ltd, UK) connected to a Cropico DO5000 microhmmeter (Seaward Electronics Ltd, UK).40 The dopant concentrations were estimated by comparing the measured specific resistivities with the ones calculated using Caughey–Thomas expression33 from electron and hole mobilities at 300 K assuming full ionization of dopant atoms. The average distances between dopant atoms were calculated from the doping densities using the probability density function to find the atom at a distance r.36 Assuming the uniform random distribution of the dopant atoms, the average distance is 〈r〉 ≈ 0.554·Nc−⅓, where Nc is the density of atoms. The equivalent Bohr radii for acceptors were estimated using the expression derived from the hydrogen atom-like model of donor (acceptor): aA = εrm0/meff·a0, where a0 is the Bohr radius of hydrogen atom, εr is the relative dielectric permittivity of Si, m0 is the electron mass, and meff is the effective mass of a hole. For the donors, a more precise value of the electron's effective Bohr radius is given by the geometric mean aD = a⅓∥a⅔⊥ ≈ 2.087 nm, where a∥ ≈ 1.44 nm and a⊥ ≈ 2.51 nm are the two radii of the pancake-like wavefunction ansatz for the electron ground state proposed by Kohn and Luttinger.34,35 The information about Si types and abbreviations used in the text are summarized in Table 1.
2.2 Porous Si powders
(10–25) μm powders were prepared by ball-milling Si wafers using Fritsch Pulverisette 7 Premium Line (Fritsch GmbH, Germany). Obtained powders were washed in 3 wt% aqueous H2O2 by sonicating them for 1 h in an ultrasound bath.32 Such washing removes possible surface contaminations and ensures reproducibility. The powders were then dried and used to produce porous Si by low-load metal-assisted catalytic etching (LL-MACE) as reported before.31,32 The protocol was scaled up to perform etching of 2 g Si powder batches. Briefly, 2 g of Si powder was first dispersed in 30 ml of acetic acid (Ph. Eur., VWR Chemicals) inside of a 50 ml PTFE dish by 5 min sonication. Then, 30 ml of hydrogen fluoride (HF, 30–40%, Merck) was added, and the dish was placed in a water bath on a heat plate under stirring. Next, Au NPs were nucleated on Si powder surfaces using a syringe pump injection of 8.334 ml (= 50 μmol) of 0.006 M Au3+ ion solution, which was prepared by dissolving HAuCl4·3H2O (99.99%, Alfa Aesar, Thermo Fisher GmbH) in water. Injection rate was 333.3 μl min−1; after it was completed, Si powder suspension was stirred for 5 min more to complete the nucleation of Au3+ NPs. The temperature of the water bath was kept at about 39 °C to retain the temperature of the suspension in the range of (51–53) °C during etching. The etching was performed by injecting H2O2/H2O solution using the syringe pump at a rate of 133.3 μl min−1 (injection time equals to 90 min). The H2O2 volume (35 wt%, Acros Organics, Thermo Fisher GmbH) in the solution was selected to match the H2O2/Si molar ratio of 1.03. The open end of the plastic tube going from the syringe was immersed into the suspension with Si particles.After the etching finished, porous Si particles were washed in Büchner-style funnel on a 55 mm diameter Grade 2 WhatmanRRR filter. After the etching solution was removed, porous Si particles were washed three times on the filter using deionized water. Next, about 10 ml of n-pentane (≥99%, VWR Chemicals) was poured on the filter with porous powder and it was allowed to dry for a few min under the fume hood. N-Pentane reduced the surface tension of water inside the pores and prevented the collapse of porous structure during the final drying which was completed overnight in an oven at 65 °C. Obtained microscale PSi powders were then stored in glass vials.
2.3 Surface oxidation and preparation of nanoparticles
After LL-MACE surfaces of PSi powders were hydrogen terminated (Fig. S3 and S4, ESI†). Localized electronic defects (Pb centers) formed at the Si/SiO2 interface during thermal oxidation of PSi particles. This approach gives the highest number of Pb defects among other methods.41 Thermal oxidation was done for 2 hours in NaberTherm R50/500/12 tube furnace (Nabertherm GmbH) at 345 °C in air.41Thermally oxidized PSi powders were then milled into NPs using a dedicated system.42 About 400 mg of a PSi powder was placed into a 4 ml glass vial which was subsequently filled with 1 mm ZrO2 milling balls. The milling was then performed in 5 min cycles at 900 rpm to avoid overheating and leaks. After each cycle, pressure was released from the vials. Typically, 10 cycles were enough to obtain PSi NPs with most of the particles below 200 nm in hydrodynamic diameter (Fig. 1b and S1, ESI†).
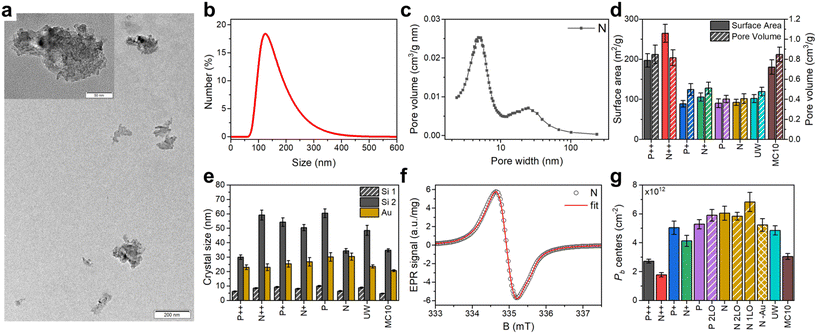 | ||
| Fig. 1 Characterization of PSi NPs. (a) Typical transmission electron microscopy image of PSi NPs dried out of suspension; the inset shows the high magnification view. (b) Hydrodynamic size distribution of the N PSi NPs in water suspension. (c) Pore size distribution of N Si powder after LL-MACE. (d) Specific surface areas and pore volumes obtained from N2 sorption measurements of Si powders after LL-MACE. (e) Crystalline sizes of Au NPs and pore sizes in PSi NPs calculated from X-ray powder diffraction spectra. (f) Electron paramagnetic resonance spectrum of N PSi NPs. The experimental data (black circles) was fitted (red lines) using trigonal P(111)b and isotropic Pisob centers (details see text and section S2.4, ESI†). (g) Pb defect density of PSi NPs formed by thermal oxidation (no label), thermal and two-step liquid-phase oxidation (2LO label), thermal and one-step liquid-phase oxidation (1LO label), and oxidation induced by Au dissolving solution (–Au label). | ||
In addition to thermal oxidation, two-step liquid-phase oxidation (oxidation in H2O2/NH4OH solution followed by oxidation in H2O2/HCl solution),41 or one-step (only H2O2/HCl solution) was performed for thermally oxidized PSi NPs (i.e., after milling of thermally oxidized PSi powders, details in ESI†). Liquid-phase oxidation removed the remaining hydrogen in −OySiHx groups (Fig. S3 and S4, ESI†) as well as induced additional backbond oxidation. Liquid-phase oxidation was tested because it would be needed in future surface modification with PEG molecules to prolong the systemic circulation time and enabling the use of the PSi NPs e.g., as MR imaging agents.43
2.4 Au removal
The absence of Au NPs influence on the DNP was confirmed with the N sample. Au NPs were dissolved using the KI/I2 gold etchant for the porous Si powder after LL-MACE. Gold etchant solution was prepared by dissolving 6.08 g of KI and 1.51 g of I2 in 30 ml of 5 M HCl. Use of HCl as solvent demonstrated better Au dissolution compared to water. To dissolve Au NPs, about 250 mg of N powder after LL-MACE was dispersed in 3 ml of ethanol to wet the hydrophobic surfaces. Then, 15 ml of gold etchant was slowly added to the Si powder suspension. Particles were then stirred for 2 h at 75 °C. Au amount before and after the dissolution was measured using a home build portable XRF setup44 and calculated using the calibration standards prepared with Au deposition step of LL-MACE. Finally, particles were washed 3 times with water in a Büchner-style funnel, wetted with n-pentane and dried in an oven as above. Then the powder was milled to NPs and denoted as N–Au.2.5 Characterization
Morphology of PSi NPs was examined by transmission electron microscopy (JEOL JEM-2100F, JEOL Ltd). A 2.5 μl drop of suspension diluted in ethanol to a concentration of 20 μg ml−1 was dried on 400 mesh Cu holey carbon grid (Agar Scientific Ltd) and the grid was examined in the instrument. Hydrodynamic sizes of PSi NP were measured using dynamic light scattering (Zetasizer Nano ZS, Malvern Panalytical Ltd) after redispersion in water at 0.1 mg ml−1 concentration.Specific surface area, specific pore volume and pore size distributions of PSi powders after LL-MACE were characterized by N2 sorption (Tristar II, Micromeritics Instrument Corp.). Specific surface areas were calculated from the linear part of adsorption isotherm using Brunauer–Emmett–Teller theory. Specific pore volumes were obtained from the total adsorbed amount at relative pressure of 0.97. Pore size distributions were calculated from desorption isotherm using Barrett–Joyner–Halenda model.
Pore sizes and sizes of catalytic Au NPs were further measured with X-ray powder diffraction (XRD, D8 Discover, Bruker Corp.). Powders were placed on a zero-background holder and scanned in (25–60)° two-theta angle range with step size of 0.0057° and time per step of 0.205 s. Crystalline sizes of two Si phases and one Au phase were then calculated with Rietvield refinement method using TOPAS® 4.6 software (section S2.3, ESI†). The sizes calculated from the Si peak broadenings corresponded to the two pore sizes according to the Babinet's principle in single crystals.45
Surface chemical species and Pb centers formed by oxidation were studied with Fourier-transform infrared spectroscopy (FTIR, Thermo Nicolet iS50, ThermoFisher Scientific Corp.) and electron paramagnetic resonance spectroscopy (EPR, Magnettech MiniScope MS5000, Bruker Corp.). In FTIR, KBr tablets with dried PSi NPs were measured in transmission mode (Sec. S2.2, ESI†). For EPR measurements, the first 7 mm of an EPR tube were filled with dried PSi NP powder. The tube was placed in the spectrometer at the same height for each measurement with the following parameters: (1) B0 = 336 mT, Bscan0 = 15.5 mT, Bmodulation0 = 0.2 mT, tscan = 60 s, MW attenuation 25 dB and gain 10 for the full spectra; (2) B0 = 336 mT, Bscan0 = 35 mT, Bmodulation0 = 0.7 mT, tscan = 60 s averaged 3 times, MW attenuation 15 dB and gain 500 to resolve hyperfine peaks. To calculate the concentration of Pb centers and the g-factor, a standard 2,2,6,6-tetramethylpiperidinyloxyl (TEMPO) radical (99%, Sigma-Aldrich) sample with known number of paramagnetic centers and g-factors was used. EPR spectra were fitted using EasySpin 5.2.35 by simulating solid-state continuous-wave powder spectra using a combination of anisotropic P(111)b and isotropic Pisob centers. g-Factor strain, hyperfine coupling and Voigtian line broadening were included (section S2.4, ESI†).46
2.6 Dynamic nuclear polarization
Hyperpolarization of PSi NPs was studied using three different polarizer designs: SpinAligner (Polarize ApS) operating at 3.35 T or 6.7 T and a base temperature of 1.4 K as well as with two home-built setups with 3.34 and 7 T (ref. 47–49) with both operating at a base temperature of 3.4 K. About 100 mg of dried PSi NP powder was packed into a polymer sample container for measurements with the SpinAligner compared to (50–60) mg for the home-built set-ups. Microwave radiation was delivered through a waveguide elbow to directly irradiate the sample. The microwave irradiation9,26 was frequency modulated in all polarizers. Magnetic field strength, temperature, microwave power W, frequency modulation bandwidth ΔνMW and frequency of modulation νMW are summarized in Table 2.| B 0, T | T, K | W , mW | ΔνFM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b, MHz b, MHz |
ν
FM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c, kHz c, kHz |
|---|---|---|---|---|
| a Microwave power. b Frequency modulation bandwidth. c Frequency of the modulation. d Silver-plating the waveguide approximately doubled the MW power reaching the sample49 for the nominal 200 mW output of the source. | ||||
| 3.34 | 3.4 | 200 | ∼150 | 1 |
| 3.35 | 1.4 | 80 | 100 | 1 |
| 6.7 | 1.4 | 30 | 200 | 3 |
| 7 | 3.4 | 200d | 300 | 10 |
To monitor the 29Si signal, a flip angle of ∼2.8° was used in the SpinAligner with varied time intervals between the measurements. Flip angles of ∼1.5° each 20 min at 3.34 T and ∼6.9° every 6 to 10 min at 7 T were used. Obtained data was analyzed using MATLAB scripts, where either the real part of the time-domain free induction decay (FID) was fitted with an exponential ansatz or the real part after fast Fourier transform (FFT) in the frequency-domain was fitted with pseudo-Voigt functions. Polarization enhancements and absolute polarization values were calculated from the thermal equilibrium signal taken in the hyperpolarization conditions after 72 h of polarization with microwave irradiation switched off for the 6.7 T (1.4 K) measurements (section S3.1, ESI†). For the 3.34 and 7 T (3.4 K) measurements, the thermal equilibrium signal at 300 K of a fully 29Si isotope labeled sample (Isoflex, Russia) was measured and adjusted for temperature upon calculation of enhancements and absolute polarization in the DNP experiments. Both the polarization buildup data and the relaxation data was corrected for the perturbations by the monitoring RF pulses50 (except for the 3.34 T due to the small flip angle used and difficulties in measuring such small flip angles with high relative accuracy).
2.7 Correlation analysis
Correlation analysis was performed using the Matlab corrcoef() function. The data supplied to the function consisted of sample characterization data (Fig. 1), EPR data obtained from fitting (Tables S1 and S2, ESI†), DNP data obtained from fitting and the rate-equation model (Fig. 3 and S26, ESI†).3 Results
The applied fabrication procedure (Methods section) results in irregular shaped PSi NPs with average particle sizes of (150 ± 65) nm (Fig. 1a and b). Additional milling and centrifugal selection could further reduce particle sizes if required for a specific (biological or medical) application (section S2.1, ESI†). The porous structure with two distinct pore sizes was formed during the Au-catalyzed LL-MACE (Fig. 1c). Etch track pores (>10 nm) were produced by Au NPs boring into Si, while tortuous pores (<10 nm) were formed by hole escape from space-charge layers to distant Si surfaces.31,32 This porosity resulted in a high surface area and a high number of surface Pb centers after oxidation (Fig. 1d and g). X-ray powder diffraction (Fig. 1e and section S5, ESI†) showed Si peaks with distinct superimposed peak profiles. Typically, the peak broadening of small crystals is dependent on the crystallite size but the porous nature of the PSi NPs complicates the picture. Since the Si particles are single crystals before etching (except for the MC10 sample) and preserve the crystallinity during the etching, the pores also give a contribution to the peak broadening according to the Babinet's principlecite.45 Therefore, three distinct contributions to the peak broadening would be expected for the PSi NPs caused by the crystallite size, population of wide etch track pores and the population of narrow tortuous pores. It was not possible to reliably fit the data with three peak profiles but instead fit with two profiles was done. The narrower peak profiles ((30–60) nm bars) were attributed to the etch track pores and the broadening from the small crystal size, while the wider ones ((5–10) nm bars) were due to tortuous pores penetrating the large crystals (Fig. 1e).31,32 The wide and narrow XRD peaks were on the order of the corresponding pore sizes measured by N2 sorption and depicted in Fig. 1c.The subsequent thermal oxidation (Methods and section S2.2, ESI†) stabilized the H-terminated surface of freshly etched samples simultaneously making them hydrophilic. The created core–shell structure of PSi NPs thus consisted of the crystalline cores of pore walls (bulk) with a thin oxide shell (surface). The lattice constant mismatch between the Si and SiO2 led to the formation of paramagnetic centers in the Si/SiO2 interface.
Electron paramagnetic resonance (EPR) spectra (Fig. 1f, discussion of Pb centers below and section S2.4, ESI†) showed the presence of two typical paramagnetic centers found on oxidized (porous) Si surfaces: (i) trigonal P(111)b centers with axial symmetry similar to defects found in oxidized planar (111) and porous Si surfaces (g∥ = 2.00185, g⊥ = 2.0081)25,51,52 and (ii) isotropic Pisob defects commonly observed in oxidized porous Si (g = 2.0055).51,53–57 EasySpin58 was used to simulate the experimental EPR spectra to obtain the relative weights of the P(111)b and Pisob centers in our samples (section S2.4, ESI†). The simulations gave typical weights of (10–20)% for the P(111)b and (80–90)% for the Pisob defects. It was expected that Pisob is the dominant defect center due to the random nature of pore formation in LL-MACE and thermal oxidation in air. Hyperfine (HF) interaction with the central 29Si was also observed (section S2.4, ESI†) and measured to be in the range of A = (325–431) MHz, which coincided well with A∥ = 210 MHz and A⊥ = 417 MHz for the planar P(111)b center.52 The number of all types of Pb centers per unit area and per mass varied between (1.8–6.8) × 1012 cm−2 (Fig. 1g) and (4.4–6.3) × 1015 mg−1, respectively (section S2.4, ESI†). These values corresponded to the fraction of total Pb centers per silicon interface atoms of f ≡ [Pb]/Na = (0.23–0.87)% (where Na = 7.83 × 1014 cm−2 is the density of lattice sites in the (111) plane). The average distance between the Pb centers was then calculated from the concentration per unit area using the nearest neighbors distribution36 derived for the 2D case. The average distances varied between 1.9 nm (N 1LO PSi NPs) and 3.7 nm (N++ PSi NPs). Correspondingly, the maximum dipolar interaction between electron spins of Pb centers ranges from 1.0 to 7.4 MHz if a uniform surface distribution of Pb centers is assumed.
We performed DNP NMR hyperpolarization and relaxation studies at four different conditions (3.34 T and 7 T at 3.4 K, 3.35 T and 6.7 T at 1.4 K, Table 2) with only selected samples evaluated at all the experimental conditions. The measured DNP profiles followed the symmetry of the EPR spectrum with the positive and negative DNP lobes located at a similar distance to the central zero crossing of the DNP enhancement (section S3.3, ESI†). The zero crossing of the DNP enhancement coincided with the center of the EPR line in agreement with previous works with endogenous defects in Si.26,30
29Si polarization buildup data at 6.7 T (1.4 K) for the thermally oxidized PSi NPs with various dopants are depicted in Fig. 2. The data was corrected for the perturbations by the monitoring RF pulses.50 We confirmed that the algorithm correctly recovered the genuine buildup dynamics from high sampling rate data in Fig. 2 using a low sampling rate of 30 min for the P sample (Fig. S17, ESI†). The one-compartment model underlying the RF correction assumes a mono-exponential buildup and decay dynamics50 as observed in all our samples and experimental conditions (section S3.3, ESI†).
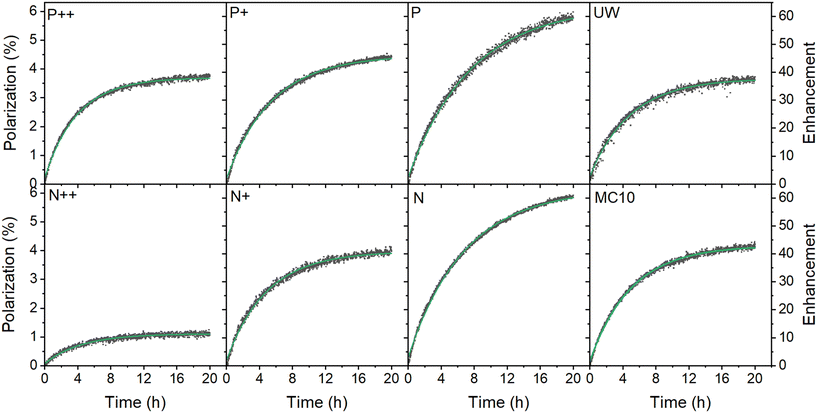 | ||
| Fig. 2 Dynamic nuclear polarization of thermally oxidized PSi NPs with different dopants after correcting for perturbation by the RF pulses50 (dark squares) and single exponential fit (green lines) at 6.7 T and 1.4 K. The microwave frequency was set to 187.82 GHz with a 150 MHz modulation bandwidth, 3 kHz modulation frequency and 30 mW microwave output power. The enhancement is relative to the thermal polarization of 29Si nuclear at the polarization buildup conditions. For the characteristics of the various samples, see Table 1. | ||
The polarization buildup (at 6.7 T and 1.4 K) depended on the doping degree. The lowest polarization was found for the highly doped P++ and N++ samples but with significant difference between them despite the similar doping level of the starting Si powder (Table 1). With the decrease of doping density, the gained polarization levels tended to equalize between different doping types (P+ and N+ PSi NPs). Interestingly, the nominally undoped UW PSi NPs did not show the highest absolute 29Si polarization; the highest polarization levels were obtained for lightly doped P and N samples. Moreover, the relatively impure polycrystalline MC10 PSi NPs showed slightly better DNP polarization and similar buildup times than moderately doped P+ and N+ samples. Such polycrystalline grades could thus be a cheaper alternative to electronics grade sample with sufficiently good DNP properties.
The DNP characteristics changed significantly at 3.34 T and 3.4 K (Fig. 3 and S18, ESI†). The polarization buildup times (Fig. 3c) for all the samples almost halved compared to 6.7 T (1.4 K). The observed enhancements (Fig. 3b) were significantly higher at 3.34 T especially for the low B doped PSi NPs compared to the 6.7 T data. The n-type samples demonstrated only moderate enhancement increases with the N sample showing even lower enhancement than at 6.7 T. Despite the higher enhancements at 3.34 T, the estimated absolute 29Si polarization was still higher at 6.7 T (1.4 K) compared to 3.34 T (3.4 K) (Fig. 2, 3a and S18, ESI†) due to the higher thermal nuclear polarization.
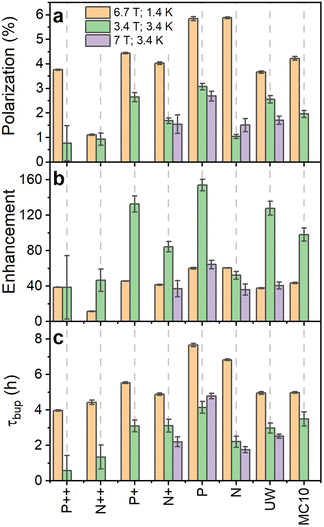 | ||
| Fig. 3 Comparison of 29Si nuclear polarization (a), enhancement over the thermal signal (b) and polarization buildup time (c) for PSi NPs at 6.7 T (1.4 K) (orange bars) as well as 3.34 T (3.4 K) (green bars) and 7 T (3.4 K) (violet bars). Temperature decrease or increase of magnetic field strength increase the thermal nuclear polarization used to calculate the enhancement from the nuclear polarization. The polarization, enhancement and buildup time are corrected for perturbations by the RF pulses.50 MW frequency modulation was employed in all the experiments. | ||
In order to clarify the influence of the experimental conditions on DNP, we performed selected measurements at 7 T (3.4 K) to discriminate between field and temperature dependent changes (Fig. 3 and S19, ESI†). The decreased polarization for the N PSi NPs clearly followed the same trend as at 3.34 T while the absolute enhancement values and buildup times for P and UW samples were close to the 6.7 T data. The similarities for P and UW samples were even more striking provided the MW power was 30 mW at 6.7 T compared to 200 mW at 7 T. We then verified at 7 T (3.4 K) that 200 mW and 20 mW provided similar enhancements at 7 T making the comparison between 6.7 T and 7 T possible despite the large difference in MW power (Fig. S22, ESI†). We, therefore, conclude that temperature plays the crucial role in DNP performance of n-type PSi NPs, while it has less influence on the p-type samples. The temperature dependence for p-type samples was further investigated at 3.35 T (1.4 K) (Fig. S23, ESI†). We found a significant decrease of enhancement levels compared to the other conditions with minor differences between P and P++ PSi NPs.
In addition to the thermal oxidation used to create Pb centers on differently doped PSi NPs, we applied liquid oxidation41 to the P and N PSi NPs. Liquid oxidation reduced the number of surface hydrogen in –SiyHx-Si–H and –O3SiH surface groups (section S2.2, ESI†), which is an important step towards an improved surface coating for biomedical applications.43 We note that liquid oxidation affected the p- and n-type Si samples differently (section S2.2, ESI†). The same is true for the measurements with different DNP conditions (Fig. 4 and Fig. S18, S20, S21, ESI†): for the P sample, enhancement dropped significantly at 6.7 T (1.4 K) and 3.34 T (3.4 K). Contrary to the P sample, liquid oxidation of the N sample increased the enhancement about 1.4 times at 3.34 T (3.4 K), while at 6.7 T (1.4 K) the enhancement decreased. The polarization build up times were affected in a more consistent manner (Fig. 4b): for all the samples and liquid oxidations, the buildup times shortened to (0.5–0.7) times the buildup time of the thermally oxidized N or P PSi NPs. Future studies might explore the influence of oxidation, doping, and DNP conditions on the DNP via Pb centers further.
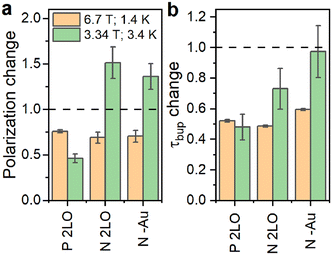 | ||
| Fig. 4 Relative change of the 29Si steady-state polarization (enhancement) (a) and polarization build up time (b) due to oxidations for P and N samples. The 2LO oxidation indicates the two-step liquid oxidation (section S1.1, ESI†) performed after the thermal oxidation. For the N–Au, oxidation emerged during the Au removal after LL-MACE (Experimental section). The dashed line indicates no change i.e., the same measured value compared to thermally oxidized samples. The absolute values are in Fig. S21, ESI.† | ||
Finally, we verified that the presence of Au NPs left in PSi NPs after LL-MACE had little impact on DNP performance. For verification, we applied an iodine-based Au etchant to the N PSi NPs directly after LL-MACE (no thermal oxidation). The Au dissolution resulted in decrease of Au content from 0.37% for N PSi NPs to 0.02% for N–Au PSi NPs as measured by XRF. Since the Au etchant is a strong oxidative solution, the dissolution process also oxidized the PSi NP surfaces which are hydrogen terminated and hydrophobic after LL-MACE. For N PSi NPs, the etchant-induced oxidation had similar effects as liquid oxidation (Fig. 4).
After collecting the DNP data for the various samples at 3.34 T and 6.7 T, we selected the P, UW and N samples for room temperature relaxation measurements (Fig. S25, ESI†). For this, the samples were hyperpolarized at 3.34 T (3.4 K) for around 20 h and subsequently transferred (dry, tightly packed sample container) to the nearby temperature-controlled (300 K) 7 T setup. At room temperature, the differences between the decay times τdec of the selected samples diminished compared to liquid helium temperatures (Table S3, ESI†). Nevertheless, a smaller τdec for the N sample compared to the P and UW samples was observed. The hyperpolarized decay times at room temperatures of the P and UW samples were around 70 min (Table 3).
| Abbreviation | τ dec, min |
|---|---|
| P | 75 ± 3 |
| UW | 67 ± 8 |
| N | 52 ± 5 |
4 Discussion
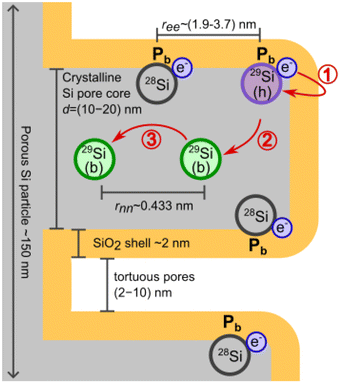
The following discussion is organised along Fig. 5, which sketches the relevant length scales and the proposed polarization pathway in the PSi NPs. The Pb centers at the interface between the surface oxide shell and the crystalline silicon core provide the unbound electrons required for DNP. Thus, understanding DNP in PSi NPs requires a basic understanding of Pb centers, which will be provided in section 4.1.To achieve a hyperpolarized nuclear state, the high thermal electron polarization is transferred via hyperfine (HF) coupling to 29Si nuclei of a Pb center located on the interface between the bulk pore walls and oxide shell (step 1 of hyperpolarization buildup sketched in Fig. 5). The HF coupling shifts the resonance frequency of the Pb nuclear spins rendering it difficult to observe these spins with NMR (hypershifted spins59). The hypershifted spins have a resonance frequency (energy) discrepancy to the bulk nuclear spins in the pore walls (visible by NMR). The frequency discrepancy suppresses the nuclear spin diffusion between the hypershifted and bulk spins (step 2 in Fig. 5) making the step to be the time limiting as further argued below in section 4.2. Between the bulk 29Si in the pore wall cores, nuclear spin diffusion (nSD) spreads the nuclear hyperpolarization throughout the crystalline pore wall cores (step 3 in Fig. 5). The discussion of the different steps is then extended to the hyperpolarization decay in section 4.3. Finally, the effects of different samples and experimental conditions are discussed in section 4.4.
4.1 P b centers
In section S2.5, ESI,† we concisely review existing literature on the interfacial Pb centers in Si/SiO2. Based on this review, the measured EPR spectra are fitted with two types of Pb centers: (i) a P(111)b center with trigonal symmetry and (ii) Pisob with spatially isotropic g-factor. If a Pbcenter has a 29Si nucleus at its central site, it possesses a Fermi-contact (isotropic) hyperfine coupling of several hundred MHz (A∥ = 210 MHz; A⊥ = 417 MHz) to the unbound electron owing to the localized Pb electron's wavefunction. The next nearest neighboring 29Si atoms have hyperfine (HF) coupling of a few tens of MHz.25 Si nuclei further away from the Pb center are assumed to be mostly coupled via dipolar HF interactions to the electron and to other Si nuclei. In naturally abundant Si with 4.7% 29Si, only a fraction of Pb centers has a HF coupling exceeding tens of MHz and only 4.7% will have HF couplings exceeding hundreds of MHz.The HF couplings of hundreds of MHz split the EPR line into three lines: a strong central EPR line of Pb centers with non-magnetic Si nuclei and weak HF doublet of the 4.7% of Pb centers with a 29Si nucleus at its central site. In our experiments, the doublet outer lines are shifted by roughly ±Aave/2 = ±(A⊥ + A∥)/4 ≈ ±162 MHz with respect to the central electron line in a good agreement with the literature (section S2.5†). Each of the three lines is anisotropically broadened due to g-factor strain in the irregular Si/SiO2 interface, which leads to a full electron line consisting of three connected EPR lines (mI = −½, 0, ½). Taken together, the anisotropic line broadening provided by the HF interaction and the g-factor strain (together >300 MHz) is larger than the nuclear Larmor frequency ω0n (between 28 and 60 MHz).
From the fitted Pb signal (Fig. 1d and Table S1, ESI†) and the measured surface area (Fig. 1d), the estimated average distance between the Pb centers assuming their uniform distribution is ree = (1.9–3.7) nm. This distance gives the estimated electron dipolar coupling Dee on the order of Dee = (1.0–7.4) MHz. The electron dipolar coupling is about (1–10) times lower than the homogeneous line broadening (Table S2, ESI†) which might indicate a non-uniform distribution and with that larger electronic couplings. The estimated electron dipolar coupling values Dee are strong enough to induce mutual electron spin flip-flops within the EPR line.60
The summarized EPR data satisfies the three main conditions for the triple spin (2 electron spins and 1 nuclear spin) family of DNP mechanisms. First, the dipolar interaction is strong enough within the EPR line to result in electron–electron flip-flops. Second, the EPR line is broader than the nuclear Larmor frequency at all the experimental conditions. Third, part of the electron spins in Pb centers are HF coupled to 29Si nuclei. Following the ongoing theoretical efforts to understand triple spin flips in DNP,60–66 we refrain ourselves from going into the specific variants, such as cross effect or thermal mixing DNP. We highlight that Dee values in our samples support cross effect DNP according to recent quantum mechanical simulations.60 Finally, we also note the results from previous study of nominally undoped Si microparticles, in which the decay of nuclear hyperpolarization was explained through triple spin flips,67 emphasizing the importance of triple spin flips in the Si/SiO2 interface.
4.2 Rate limiting step for the polarization buildup
To achieve the polarization levels up to a few percent, the polarization needs to penetrate from the surface nuclei into the pore wall cores of the PSi NPs for which we invoke the concept of nuclear spin diffusion (nSD).12,68 The dipolar interaction between nuclei induces nuclear spin flip-flops—a zero-quantum (ZQ) process with no net change of the total magnetic quantum number. This ZQ process causes an effective spatial transport of magnetization that can be described by a diffusion equation if a nuclear polarization gradient is present in the sample.The nSD constant in Si was previously approximated with Ddiff ≈ a2/(cT2n), where c = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13 or c = 50,69a is the average distance between 29Si nuclei in a cubic lattice and T2n is a measure for the inhomogeneous single quantum (SQ) line width in the spectra. In the approximation of Ddiff in ref. 69, it was implicitly assumed that the experimentally measured SQ Hahn echo decay characterized by T′2n ≈ 5.6 ms (ref. 70) characterizes also the width of the ZQ line, which is relevant for nSD. In ref. 13, the decay constant of the FID
13 or c = 50,69a is the average distance between 29Si nuclei in a cubic lattice and T2n is a measure for the inhomogeneous single quantum (SQ) line width in the spectra. In the approximation of Ddiff in ref. 69, it was implicitly assumed that the experimentally measured SQ Hahn echo decay characterized by T′2n ≈ 5.6 ms (ref. 70) characterizes also the width of the ZQ line, which is relevant for nSD. In ref. 13, the decay constant of the FID 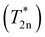 was assumed to characterize the width of the ZQ line.13 We note that all of these decay time constants are not relaxation times in the strict sense of stochastic processes that lead to decoherence. Nonetheless, both approaches lead to similar nSD coefficients of Ddiff ≈ 0.5–1.7 nm2 s−1. Therefore, for the polarization to diffuse from the surface into the pore wall cores rwall/2, a time scale of only ∼8 s or ∼140 s (τdiff = 〈(rwall/2)2〉/6Ddiff) is required for the tortuous or etch track pores, respectively (Fig. 1c and e). These time scales are orders of magnitude shorter than the liquid helium build-up times of hours (Fig. 2 and section S3.3, ESI†) or the room temperature decay times of around one hour (Table 3 and Fig. S25, ESI†). Hence, we conclude that the nuclear spin diffusion (step 3 of the hyperpolarization buildup in Fig. 5) is not limiting the hyperpolarization process.
was assumed to characterize the width of the ZQ line.13 We note that all of these decay time constants are not relaxation times in the strict sense of stochastic processes that lead to decoherence. Nonetheless, both approaches lead to similar nSD coefficients of Ddiff ≈ 0.5–1.7 nm2 s−1. Therefore, for the polarization to diffuse from the surface into the pore wall cores rwall/2, a time scale of only ∼8 s or ∼140 s (τdiff = 〈(rwall/2)2〉/6Ddiff) is required for the tortuous or etch track pores, respectively (Fig. 1c and e). These time scales are orders of magnitude shorter than the liquid helium build-up times of hours (Fig. 2 and section S3.3, ESI†) or the room temperature decay times of around one hour (Table 3 and Fig. S25, ESI†). Hence, we conclude that the nuclear spin diffusion (step 3 of the hyperpolarization buildup in Fig. 5) is not limiting the hyperpolarization process.
The EPR spectrum extrapolated to the DNP field strength of 3.34 T or 6.7 T consists of three lines (Fig. 6): the central line for Pb with 28Si nuclei is surrounded by the two HF-split lines for mI = ±1/2 whose shape is the same as of the central line. The DNP profiles show two DNP peaks of positive and negative enhancements with nearly equal amplitude and width (Fig. 6 and S13, ESI†). If MW modulation is applied, the extrema of the DNP enhancement in our samples coincide with the frequencies of the HF-split mI = ±1/2 doublet in the EPR spectrum (Fig. 6b and c). Switching off MW modulation (Fig. 6a) narrows the DNP profile while retaining its featureless shape with its width far exceeding the nuclear Larmor frequency (ω0n (3.34 T) ≈ 28 MHz).
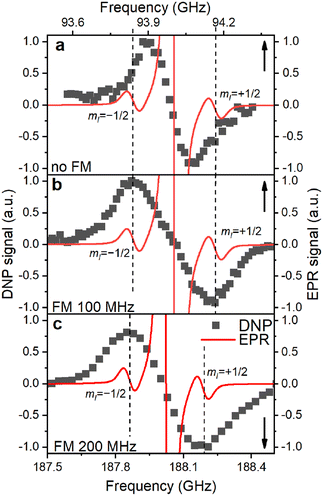 | ||
| Fig. 6 Overlay of the simulated EPR and experimental DNP spectra for the P sample at (a) 3.35 T, 1.4 K without MW modulation (frequency modulation – FM), (b) 3.35 T, 1.4 K with 100 MHz MW modulation and (c) 6.7 T, 1.4 K with 200 MHz MW modulation. The DNP and EPR spectra are normalized separately in each panel. EPR spectrum is the frequency-swept spectrum simulated using the model obtained from the experimental data fitting (Fig. 1f, section S2.4, ESI†). EPR spectrum consists of the central 28Si manifold (clipped) and two hyperfine-split manifolds for Pb centers with 29Si nuclei (mI = ±1/2, dashed lines). The upwards and downwards arrows indicate the X axis for each graph. | ||
In DNP, the strength of the HF interaction between electron and nuclear spins determines the polarization transfer rate constant, which is proportional to the square of the HF coupling matrix element. Owing to the large HF constant between the Pb electron and the central Si atom (A∥ = 210 MHz; A⊥ = 417 MHz), the DNP of these nuclei should be efficient and fast (step 1 of the hyperpolarization buildup in Fig. 5). Already for nearest neighbors (A2n ≈ 42 MHz (ref. 25)) 29Si nuclei the roughly ten times lower HF coupling would lead to an approximately hundred-fold lower polarization transfer rate compared to the central 29Si, which outweighs the higher number of nearest neighbor lattice sites (between 1.5 and 3 depending on the location of a Pb center). MW modulation further improves the DNP likely through recruiting more electrons and shifts the positive and negative enhancements apart when applied9,26,71 as observed in Fig. 6a and b. Interestingly, we found the optimal MW modulation bandwidth to be 100 MHz and 200 MHz at 3.35 T and 6.7 T, respectively. These bandwidths make the maximum positive and negative DNP enhancements to coincide with the mI = ±1/2 EPR manifolds. We interpret this coincidence as indication for the electron-nuclear polarization transfer pathway occurring preferentially through Pb centers with 29Si central nuclei and not through the backbonded nearest neighbor 29Si. The increased transfer efficiency to the central 29Si can be understood by the up to ten times larger HF coupling compared to other possible locations of 29Si and amplified by the polarization transfer rate scaling approximately with the HF coupling squared.
Taken together, both the polarization of the central Pb29Si and the nuclear spin diffusion throughout pore walls (steps 1 and 3 of the hyperpolarization buildup in Fig. 5) are relatively fast processes compared to the measured buildup and decay times at all the DNP conditions (Fig. 2 and section S3.3, ESI†). In order to explain the long polarization buildup and decays we shall recall that there are 29Si nuclei with remarkably strong HF interaction—the central and backbonded Pb nuclei. Between these strongly hypershifted 29Si spins and the bulk spins exists a large shift in frequency/energy, which is further enhanced due to the sparsity of 29Si in the naturally abundant PSi NPs. Such frequency shifts suppress nuclear flip-flop transitions and create a so called spin diffusion barrier.12,68 The transfer from the hypershifted nuclear spins to the bulk 29Si is, therefore, restrained, making it the rate limiting step in the DNP buildup.
For the nuclear polarization to diffuse across the spin diffusion barrier, the electrons need to modify the effective nuclear-nuclear spin interactions.72–80 Specifically, a coherent electron-nuclear four-spin flip-flop process79,80 can be consistent with low temperatures employed in our experiments. The electron-nuclear four-spin flip-flops are very similar to triple spin flips involving an electronic flip-flop and nuclear spin flip but the nuclear spin flip is replaced by a nuclear dipolar flip-flop.79 The transition matrix element of the electron-nuclear four-spin flip-flops is proportional to the electronic and nuclear dipolar couplings. Thus, a higher nuclear isotope abundance increases the rate of electron-nuclear four-spin flip-flops by increasing the nuclear dipolar couplings (due to the decrease of the average internuclear distances). A higher electron-nuclear four-spin flip-flop rate leads to a faster spin transport from the hypershifted to bulk spins (step 2 in Fig. 5).
Another possible explanation for the long buildup time invokes the polarization transfer towards weakly HF-coupled spins. In this case, distant 29Si nuclei are polarized directly by the dipolar coupling to a Pb electron spin. The direct polarization transfer hypothesis, however, possess a few flaws. First, this process has a low probability since the HF coupling between a Pb electron and a distant 29Si nucleus rapidly vanishes with the distance between them. For example, for a nuclei located at a distance of three lattice constants, the HF interaction is ∼3.5 kHz, yielding low rates of direct polarization transfer. Such a low polarization transfer rate might be too slow for the observed buildup times and enhancements. Second, even a frequency difference of ∼3.5 kHz is large compared to natural abundance SQ NMR line width of around 100 Hz.13 Assuming that the SQ line is a good approximation for the ZQ line mediating nSD, the spectral density of energy conserving ZQ flip-flops vanishes when the ZQ line width is much smaller than the energy difference between the nuclei81 as in this case by the given HF couplings. Hence, nSD would still be suppressed by the HF couplings and would require an electron spin to alter the spin diffusion locally similar to the polarization transfer occurring at the strongly HF coupled nuclei.72–80 Third, the direct polarization transfer fails to explain the mI = ±1/2 DNP enhancements and zero DNP for the central EPR peak (Fig. 6).
We highlight that 95.3% of the Pb centers have magnetically inactive 28Si or 30Si central nuclei. Therefore, in addition to the low probability of transfer from the central 29Si to the distanced bulk, only 4.7% of Pb contribute to the hyperpolarization buildup if the polarization transfer flows through the central nuclei. According to the sample characterization data, a typical PSi NP of 150 nm size, 55% porosity (0.55 cm3 g−1 pore volume) and 100 m2 g−1 surface area contains on average 2.3 × 106 29Si nuclei and 1.3 × 104Pb centers (Fig. 1b–g). Therefore, a straightforward but incorrect calculation yields the number of 29Si to be polarized by one Pb center equal to ∼180—a common value for partially deuterated water glycerol mixtures (DNP juice).82 However, the number of 29Si nuclei that are central to the Pb electrons is only 4.7% of the total number of nuclei. This leads to around 3800 nuclei to be polarized per DNP-active Pb center, a much lower value than in typical DNP samples.
4.3 Rate limiting step for the polarization decay
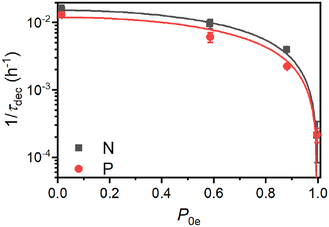
The polarization decay in Si particles with endogenous electronic centers has been commonly considered to be limited by nSD from bulk 29Si to the 29Si in the core–shell interface.8,37,67 The arguments of low electron polarization at room temperature and orders of magnitude lower T1e and T2e than at DNP conditions further supported the hypothesis of nSD limiting relaxation. Although these arguments seem to be a reasonable for μm-sized Si particles, they are hardly applicable to our case of PSi NPs or to other types of Si NPs26,30,38,83 with crystalline cores on the order of 20 nm. If nSD is the rate limiting step for the relaxation in our samples, the polarization decay time τdec at room temperature should be tens of seconds at the slowest, according to the estimated Ddiff ≈ 0.5–1.7 nm2 s−1. Unless this estimation is orders of magnitude incorrect, which is unlikely, nSD fails to explain the room temperature relaxation times in nanoscale Si.Fig. 7 depicts the dependence of nuclear hyperpolarization decay rates τdec−1 on the thermal electron polarization P0e at the given experimental conditions. The τdec−1 follows a 1 − P20e scaling indicating that the nuclear relaxation appears to be governed by paramagnetic effects.12,84
We note that naturally abundant 160 nm (ref. 38) and 50 nm (ref. 9 and 26) non-porous Si NPs as well as the porous particles in this work all give similar room temperature relaxation times of around 50 min. Such a similar relaxation time across particles and the dependence on the 29Si abundance might indicate that even at room temperature the nuclear relaxation is governed by the same process as at the DNP conditions, i.e., by the electron modified nSD across the spin diffusion barrier with fast relaxation of hypershifted 29Si spins. The observed 1 − P20e scaling (Fig. 7) would in this case not describe the paramagnetic relaxation itself but the actual spin transport via electron-nuclear four-spin flip-flops.79 Electron-nuclear four-spin flip-flops have a similar mechanism as triple spin flips causing indirect paramagnetic relaxation12 because both mechanisms involve an electron dipolar flip-flop, which provides energy for a nuclear excitation e.g., a nuclear spin flip for triple spin flips and a nuclear flip-flop for electron-nuclear four-spin flip-flops. Therefore, both triple spin and four-spin flip-flops can be considered to have the same scaling with electron polarization, which for paramagnetic relaxation follows 1 − P20e dependence.12
Alternatively, the averaging of the HF couplings in combination with slow paramagnetic relaxation could explain the long room temperature relaxation times. Both interpretations would be in good agreement with isotope enrichment experiments38 which found a 3-fold decrease in τdec (from 48 to 17 minutes) upon increasing the 29Si abundance from 4.7% to 15%. The higher isotope abundance results in larger nuclear dipolar couplings and reduced frequency differences for nuclei close to the electron which would increase the transport of polarization across the spin diffusion barrier. Additionally, more Pb centers with a central 29Si results in a larger fraction of Pb centers with large (averaged) HF couplings which increases nuclear relaxation.
A major open question concerning the proposed rate limiting step of the room temperature decay is the lack of knowledge of the electron relaxation times with respect to the nuclear Larmor frequency ω0n. If the relaxation rate is much smaller than ω0n, the HF couplings are not averaged and the situation is similar to low temperature DNP conditions. For much faster relaxation rates than ω0n, the thermal electron polarization of 1.6% at room temperature and 7 T leads to (pseudo-)contact shifts due to the partially averaged HF couplings.85–88 Even in this averaged case the (pseudo-)contact shift is expected to be large compared to the nuclear dipolar couplings mediating the nSD.
4.4 Samples and experimental conditions
Above we discussed that DNP likely originates from triple spin flips which require strong HF coupling of the involved electrons to the central 29Si nuclei of Pb centers for a fast polarization transfer between them. This is followed by a slow transfer from this central, strongly hypershifted nucleus to the bulk nuclei, followed by fast spin diffusion in the bulk. For the decay, the inverse process happens with paramagnetic relaxation instead of triple spin flip DNP. Similar to the buildup, the decay time appears to be governed by the hyperpolarization transfer from the bulk to the strongly hypershifted 29Si nuclei. Since both the buildup and the decay involve a single rate limiting step, a mono-exponential hyperpolarization dynamics50 is expected and found experimentally (Fig. 2, section S3.3, ESI†).For a mono-exponential hyperpolarization dynamics, the buildup time, steady-state polarization and thermal electron polarization can be used to define hyperpolarization injection and decay rate constants during buildup,50 which we briefly summarize below and in more detail in section S3.4, ESI.† With these rate constants, it is possible to quantify the nuclear relaxation during buildup and compare it to the rate with which hyperpolarization is created.
In the rate-equation model, the buildup time τbup depends on two competing processes: the nuclear polarization injection with rate constant kW and the nuclear relaxation with rate constant kbupR. Together with the thermal electron polarization P0e, we can describe the buildup as:50
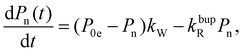 | (1a) |
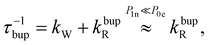 | (1b) |
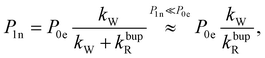 | (1c) |
Fig. 8 compares the DNP injection and relaxation rates during buildup and decay at 6.7 T, 1.4 K. The rates at other conditions and a more detailed discussion of these are given in section S3.4, ESI† with the main results summarized below. The relaxation rates during the buildup are an order of magnitude larger than the injection rates and, hence, govern the buildup time. The imbalance between buildup and relaxation rates results in moderate steady-state polarization (and enhancements) compared to 1H or 13C enhancements under similar conditions (ref. 89 and references therein for state-of-the-art enhancements). DNP injection appears rather uniform across the samples while the relaxation rates show a variation between samples. Thus, differences between samples mostly originate from different relaxation properties. Furthermore, the DNP injection shows a less pronounced dependence on the experimental conditions than the relaxation rates (Fig. S26, ESI† and discussion thereof). However, suppressing the relaxation with lower temperatures (1.4 K instead of 3.4 K) shows at best only a modest improvement because relaxation enhancement by MW irradiation89 becomes more pronounced as evident by the much higher relaxation rates during buildup (kbupR) compared to decay (kdecR) as shown in Fig. 8. Reduction of this relaxation enhancement e.g., by higher fields, lower temperatures or shortening of electronic relaxation times,89 offers the possibility of higher enhancements and polarization levels.
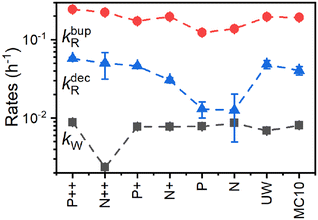 | ||
| Fig. 8 Polarization buildup (dark squares and red circles) and decay (blue triangles) rates (eqn (1a)–(1c)) for the PSi NPs with different doping and oxidation. The data was acquired at 6.7 T, 1.4 K. Lines are a guide for the eye. | ||
By performing the correlation analysis, we further connect the structural properties of PSi NPs, Pb centers and hyperpolarization. The nuclear hyperpolarization at 6.7 T, 1.4 K (Fig. 2) is nearly independent from the number of Pb centers (Fig. 1g) expressed by a correlation coefficient of 0.04 across all samples but correlates (0.44) with the interface density of the Pb centers (number of Pb defects divided by the specific surface area, Fig. 1d and g). The density of Pb centers correlates strongly negatively across all the samples with the specific surface area (coefficient equals to −0.9) because the increase of surface area does not lead to the proportional increase of the number of Pb centers (Fig. 1d and g). Such an independence of the number of Pb centers suggests existence of a limit for their formation at least for the oxidation methods applied here. A more detailed discussion of the correlation analysis can be found in section S3.4, ESI.†
Before concluding, we want to highlight specific aspects of the investigated PSi NPs. First, the ability to create nuclear hyperpolarization in PSi NP appears exceptionally robust due to the core–shell nature of the particles with the paramagnetic centers protected from the environment. Specifically, the Pb centers form at the interface between the crystalline pore wall cores and the oxide shell. Hence, the Pb centers as well as the nuclear hyperpolarization are largely shielded from everything outside each particle e.g., different particle coating or solution media.83 This is exemplified by the inertness to the presence of the catalytic Au NPs in PSi NPs: removing the Au NPs used as an etching catalyst shows no clear effect on the hyperpolarization process and the observed changes are in line with other additional oxidation steps (Fig. 4). This suggests that the pores in PSi NPs with their large surface area available for coating could be used for loading with additional substances to add further diagnostic or therapy capabilities.
Second, the nuclear hyperpolarization in the bulk seems to be inert with respect to a wide range of bulk defects and their densities: both boron and phosphorous doping with densities up to ∼1016 cm−3 show similar high polarization levels (Fig. 2 and 3). Furthermore, the light doping of ∼5 × 1014 cm−3 is superior compared to the most pure UW sample. The increase of doping level to the order of 1018 cm−3 becomes detrimental for achievable hyperpolarization levels due to the onset of the wavefunction overlap of the dopants. At room temperature, high densities of thermally excited mobile charge carriers from shallow dopants strongly increase the nuclear relaxation.67 The least pure MC10 sample possesses various different dopants, with energy levels often deep in the bandgap of Si and thus with narrow defect wave functions, which makes DNP performance of MC10 sample very similar to the best electronic wafer grade samples. Such a stable polarization process is important if other, especially bottom-up manufacturing techniques should be employed as these offer a reduced control over the bulk purity compared to the top-down approach of the current work.
5 Conclusion
We employed low-load metal assisted catalytic etching (LL-MACE)31,32 to fabricate a variety of porous Si NPs from electronic grade single crystal Si wafers. This top-down fabrication approach allowed us to vary dopant type and density while achieving nearly identical surface properties and crystallinity in all the NPs. A separate oxidation step led to the formation of electronic Pb centers with similar structure and surface density for all the types of PSi NPs. This resulted in the successful and similar DNP injection in all samples with the polarization differences mostly ascribed to relaxation. The robustness of the hyperpolarization process to different shallow dopant concentrations and metallurgical grade Si samples containing deep dopants enables and justifies the use of a wide range of manufacturing methods with eventually poor control over the bulk composition e.g., bottom-up synthesis methods. The highest steady-state polarization levels were achieved with lightly (∼1014 cm−3) phosphorous or boron-doped samples. Measurements at 7 T (3.4 K) and 3.35 T (1.4 and 3.4 K) gave lower polarization levels than the 6% achieved at 6.7 T, 1.4 K. Room temperature decay times of the studied samples exceeded one hour—the longest hyperpolarization decay time obtained so far in Si NPs to our knowledge although slightly longer saturation-recovery T1 times (102 ± 10) min have been reported for 21 nm (comparable to pore walls in the present work) particles.90The gained insights about Pb centers enabled us to shed light on the polarization transfer from the electron spins to 29Si. Owing to the core–shell nature of the PSi NPs with the Pb centers at the interface between the pore wall cores and oxide shell, nuclear spin diffusion is required to transport the hyperpolarization across the sample. The central 29Si nuclei of the Pb centers with hyperfine couplings around 300 MHz are predominantly hyperpolarized by DNP. The large difference in frequency compared to the bulk 29Si spins seems to cause a slow transport of polarization from the central Pb29Si nuclei towards the bulk, which causes the long buildup and relaxation times in the presence of fast bulk spin diffusion. Isotope labelling may improve the transport across the spin diffusion barrier and, therefore, improve the NMR signal through the increased enhancement and number of magnetically active spins. The disadvantages of isotope labelling are high sample cost and shortened room temperature decay times. The described hyperpolarization process could be translated to create other slowly relaxing NPs with sizes down to possibly 10 nm. For this, three properties of (Si) NPs appear essential: (i) a low bulk relaxation, (ii) DNP on the outer surfaces of the particles and (iii) a slow transport from the bulk to the surface e.g., a strongly localized wavefunction of a surface paramagnetic center with large hyperfine coupling compared to the nuclear line width.
Author contributions
Conceptualization: G. v. W., M. E., J. R., V. P. L., S. K., M. I. K., K. T. Data curation: G. v. W., V. H., M. I. K., K. T. Methodology: G. v. W., A. H., M. M. A., M. E., M. I. K., K. T. Formal analysis: G. v. W., K. T. Investigation: G. v. W., A. H., V. H., J. J., J. O. M., S. K., M. I. K., K. T. Funding acquisition: M. E., J. R., V. P. L., S. K., M. I. K., K. T. Resources: J. O. M., M. E., S. K., V. P. L., M. I. K. Writing – original draft: K. T., G. v. W. Writing – review and editing: G. v. W, M. E., J. R., S. K., M. I. K., K. T. All authors approved the draft.Data availability
All the data and analysis scripts for this article are available at ETH Library at https://doi.org/10.3929/ethz-b-000679152.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work was supported by Research Council of Finland (grant no. 314551, 331371, 322006, 338733 and Flagship of Advanced Mathematics for Sensing Imaging and Modelling grant 358944), ETH Zürich and the Schweizerischer Nationalfonds zur Förderung der Wissenschaftlichen Forschung (grant no. 200020_188988 and 200020_219375), Finnish Cultural Foundation (North Savo regional fund) and Saastamoinen Foundation. The microscopy studies were performed using the facilities of SIB Labs, Laboratory of Microscopy at the University of Eastern Finland. Part of the work was carried out with the support of Kuopio Biomedical Imaging Unit, University of Eastern Finland, Kuopio, Finland (part of Biocenter Kuopio, Finnish Biomedical Imaging Node, and EuroBioImaging). Silicon was provided by Elkem Silicon Products (Elkem ASA, Norway) and Okmetic (Okmetik Oy, Finland). We thank the anonymous reviewers for improving the manuscript.References
- S. O. Dumoulin, A. Fracasso, W. van der Zwaag, J. C. Siero and N. Petridou, NeuroImage, 2018, 168, 345–357 CrossRef PubMed.
- Z. Zhong, K. Sun, G. Dan, Q. Luo and X. J. Zhou, Magn. Reson. Med., 2021, 86, 3166–3174 CrossRef PubMed.
- J. D. Rudie, T. Gleason, M. J. Barkovich, D. M. Wilson, A. Shankaranarayanan, T. Zhang, L. Wang, E. Gong, G. Zaharchuk and J. E. Villanueva-Meyer, Radiology, 2022, 4, e210059 Search PubMed.
- S. C. L. Deoni, P. Medeiros, A. T. Deoni, P. Burton, J. Beauchemin, V. D’Sa, E. Boskamp, S. By, C. McNulty, W. Mileski, B. E. Welch and M. Huentelman, Sci. Rep., 2022, 12, 5690 CrossRef CAS PubMed.
- S. E. Day, M. I. Kettunen, F. A. Gallagher, D.-E. Hu, M. Lerche, J. Wolber, K. Golman, J. H. Ardenkjaer-Larsen and K. M. Brindle, Nat. Med., 2007, 13, 1382–1387 CrossRef CAS PubMed.
- F. A. Gallagher, M. I. Kettunen, S. E. Day, D.-E. Hu, J. H. Ardenkjær-Larsen, R. Zandt, P. R. Jensen, M. Karlsson, K. Golman, M. H. Lerche and K. M. Brindle, Nature, 2008, 453, 940–943 CrossRef CAS PubMed.
- W. Jiang, L. Lumata, W. Chen, S. Zhang, Z. Kovacs, A. D. Sherry and C. Khemtong, Sci. Rep., 2015, 5, 9104 CrossRef PubMed.
- M. C. Cassidy, H. R. Chan, B. D. Ross, P. K. Bhattacharya and C. M. Marcus, Nat. Nanotechnol., 2013, 8, 363–368 CrossRef CAS PubMed.
- G. Kwiatkowski, F. Jähnig, J. Steinhauser, P. Wespi, M. Ernst and S. Kozerke, Sci. Rep., 2017, 7, 7946 CrossRef PubMed.
- H. Seo, I. Choi, N. Whiting, J. Hu, Q. S. Luu, S. Pudakalakatti, C. McCowan, Y. Kim, N. Zacharias, S. Lee, P. Bhattacharya and Y. Lee, ChemPhysChem, 2018, 19, 2143–2147 CrossRef CAS PubMed.
- H. Santos, Porous silicon for biomedical applications, Woodhead Publishing, 2nd edn, 2021 Search PubMed.
- W. T. Wenckebach, Essentials of Dynamic Nuclear Polarisation, Spindrift Publications, 2016 Search PubMed.
- H. Hayashi, T. Itahashi, K. M. Itoh, L. S. Vlasenko and M. P. Vlasenko, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 1–10 Search PubMed.
- A. E. Dementyev, D. G. Cory and C. Ramanathan, J. Chem. Phys., 2011, 134, 154511 CrossRef PubMed.
- J. Järvinen, D. Zvezdov, J. Ahokas, S. Sheludyakov, O. Vainio, L. Lehtonen, S. Vasiliev, Y. Fujii, S. Mitsudo, T. Mizusaki, M. Gwak, S. Lee, S. Lee and L. Vlasenko, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 2–5 CrossRef.
- J. Järvinen, D. Zvezdov, J. Ahokas, S. Sheludiakov, L. Lehtonen, S. Vasiliev, L. Vlasenko, Y. Ishikawa and Y. Fujii, Phys. Chem. Chem. Phys., 2020, 22, 10227–10237 RSC.
- P. Dluhy, J. Z. Salvail, K. Saeedi, M. L. Thewalt and S. Simmons, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 1–5 CrossRef.
- J. M. Luttinger, Phys. Rev., 1956, 102, 1030–1041 CrossRef CAS.
- G. Feher, J. C. Hensel and E. A. Gere, Phys. Rev. Lett., 1960, 5, 309–311 CrossRef CAS.
- A. Henstra, P. Dirksen and W. T. Wenckebach, Phys. Lett. A, 1988, 134, 134–136 CrossRef CAS.
- P. Dirksen, A. Henstra and W. T. Wenckebach, J. Phys.: Condens. Matter, 1989, 1, 8535–8541 CrossRef CAS.
- M. Stutzmann and D. K. Biegelsen, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 9834–9840 CrossRef CAS PubMed.
- E. H. Poindexter, G. J. Gerardi, M. E. Rueckel, P. J. Caplan, N. M. Johnson and D. K. Biegelsen, J. Appl. Phys., 1984, 56, 2844–2849 CrossRef CAS.
- A. Stesmans, Z. Phys. Chem., 1987, 151, 191–209 CrossRef CAS PubMed.
- K. L. Brower, Semicond. Sci. Technol., 1989, 4, 970–979 CrossRef CAS.
- G. Kwiatkowski, Y. Polyhach, F. Jähnig, T. Shiroka, F. H. L. Starsich, M. Ernst and S. Kozerke, J. Phys. Chem. C, 2018, 122, 25668–25680 CrossRef CAS.
- N. Whiting, J. Hu, N. M. Zacharias, G. L. R. Lokesh, D. E. Volk, D. G. Menter, R. Rupaimoole, R. Previs, A. K. Sood and P. Bhattacharya, J. Med. Imaging, 2016, 3, 036001 CrossRef PubMed.
- G. Kwiatkowski, F. Jähnig, J. Steinhauser, P. Wespi, M. Ernst and S. Kozerke, J. Magn. Reson., 2018, 286, 42–51 CrossRef CAS PubMed.
- T. Boele, D. E. Waddington, T. Gaebel, E. Rej, A. Hasija, L. J. Brown, D. R. McCamey and D. J. Reilly, Phys. Rev. B, 2020, 101, 1–11 CrossRef.
- T. M. Atkins, M. C. Cassidy, M. Lee, S. Ganguly, C. M. Marcus and S. M. Kauzlarich, ACS Nano, 2013, 7, 1609–1617 CrossRef CAS PubMed.
- K. Tamarov, J. D. Swanson, B. A. Unger, K. W. Kolasinski, A. T. Ernst, M. Aindow, V.-P. Lehto and J. Riikonen, ACS Appl. Mater. Interfaces, 2020, 12, 4787–4796 CrossRef CAS PubMed.
- K. Tamarov, R. Kiviluoto, J. Swanson, B. Unger, A. Ernst, M. Aindow, J. Riikonen, V.-P. Lehto and K. Kolasinski, ACS Appl. Mater. Interfaces, 2020, 12, 48969–48981 CrossRef CAS PubMed.
- D. B. M. Klaassen, Solid-State Electron., 1992, 35, 961–967 CrossRef CAS.
- W. Kohn and J. M. Luttinger, Phys. Rev., 1955, 98(4), 915–923 CrossRef CAS.
- B. Koiller, X. Hu, S. Das Sarma and B. Koiller, Phys. Rev. Lett., 2002, 88, 4 Search PubMed.
- S. Chandrasekhar, Rev. Mod. Phys., 1943, 15, 1–89 CrossRef.
- J. W. Aptekar, M. C. Cassidy, A. C. Johnson, R. A. Barton, M. Lee, A. C. Ogier, C. Vo, M. N. Anahtar, Y. Ren, S. N. Bhatia, C. Ramanathan, D. G. Cory, A. L. Hill, R. W. Mair, M. S. Rosen, R. L. Walsworth and C. M. Marcus, ACS Nano, 2009, 3, 4003–4008 CrossRef CAS PubMed.
- J. Kim, D. Jo, S.-H. Yang, C.-G. Joo, N. Whiting, S. Pudakalakatti, H. Seo, H. Y. Son, S.-J. Min, P. Bhattacharya, Y.-M. Huh, J. H. Shim and Y. Lee, ACS Appl. Mater. Interfaces, 2021, 13, 56923–56930 CrossRef CAS PubMed.
- J. Hu, N. Whiting and P. Bhattacharya, J. Phys. Chem. C, 2018, 122, 10575–10581 CrossRef CAS.
- M. J. Sailor, Porous silicon in practice: preparation, characterization and applications, Wiley-VCH Verlag GmbH & Co. KGaA, 2012, p. 262 Search PubMed.
- J. Riikonen, M. Salomäki, J. Van Wonderen, M. Kemell, W. Xu, O. Korhonen, M. Ritala, F. MacMillan, J. Salonen and V. P. Lehto, Langmuir, 2012, 28, 10573–10583 CrossRef CAS PubMed.
- T. Nissinen, T. Ikonen, M. Lama, J. Riikonen and V.-P. Lehto, Powder Technol., 2016, 288, 360–365 CrossRef CAS.
- T. Nissinen, S. Näkki, H. Laakso, D. Kučiauskas, A. Kaupinis, M. I. Kettunen, T. Liimatainen, M. Hyvönen, M. Valius, O. Gröhn and V. P. Lehto, ACS Appl. Mater. Interfaces, 2016, 8, 32723–32731 CrossRef CAS PubMed.
- T. E. Tiihonen, T. J. Nissinen, P. A. Turhanen, J. J. Vepsäläinen, J. Riikonen and V. P. Lehto, Anal. Chem., 2022, 94, 11739–11744 CrossRef CAS PubMed.
- M. Born and E. Wolf, Principles of Optics, Cambridge University Press, 60th edn, 2019 Search PubMed.
- E. A. Konstantinova, Handbook of Porous Silicon, Springer International Publishing, 2nd edn, 2018, pp. 627–654 Search PubMed.
- M. Batel, A. Däpp, A. Hunkeler, B. H. Meier, S. Kozerke and M. Ernst, Phys. Chem. Chem. Phys., 2014, 16, 21407–21416 RSC.
- F. Jähnig, A. Himmler, G. Kwiatkowski, A. Däpp, A. Hunkeler, S. Kozerke and M. Ernst, J. Magn. Reson., 2019, 303, 91–104 CrossRef PubMed.
- A. Himmler, M. M. Albannay, G. von Witte, S. Kozerke and M. Ernst, Magn. Reson., 2022, 3, 203–209 CrossRef CAS PubMed.
- G. von Witte, M. Ernst and S. Kozerke, Magn. Reson., 2023, 1–16 CAS.
- H. J. Von Bardeleben, M. Schoisswohl and J. L. Cantin, Colloids Surf., A, 1996, 115, 277–289 CrossRef CAS.
- A. Stesmans and V. V. Afanas'ev, J. Appl. Phys., 1998, 83, 2449–2457 CrossRef CAS.
- E. H. Poindexter and P. J. Caplan, Prog. Surf. Sci., 1983, 14, 201–294 CrossRef CAS.
- F. C. Rong, J. F. Harvey, E. H. Poindexter and G. J. Gerardi, Appl. Phys. Lett., 1993, 63, 920–922 CrossRef CAS.
- H. J. von Bardeleben, M. Chamarro, A. Grosman, V. Morazzani, C. Ortega, J. Siejka and S. Rigo, J. Lumin., 1993, 57, 39–43 CrossRef CAS.
- H. J. Von Bardeleben, D. Stievenard, A. Grosman, C. Ortega and J. Siejka, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 10899–10902 Search PubMed.
- R. Laiho, L. S. Vlasenko, M. M. Afanasiev and M. P. Vlasenko, J. Appl. Phys., 1994, 76, 4290–4293 CrossRef CAS.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- Z. Pang, K. Sheberstov, B. A. Rodin, J. Lumsden, U. Banerjee, D. Abergel, G. Bodenhausen and K. Tan, ChemRxiv, 2024, preprint, 1–20, DOI:10.26434/chemrxiv-2024-zr8zv.
- K. Kundu, A. Feintuch and S. Vega, J. Phys. Chem. Lett., 2019, 10, 1769–1778 CrossRef CAS PubMed.
- W. T. Wenckebach, J. Magn. Reson., 2019, 299, 124–134 CrossRef CAS PubMed.
- W. T. Wenckebach, J. Magn. Reson., 2019, 299, 151–167 Search PubMed.
- W. T. Wenckebach, Appl. Magn. Reson., 2021, 52, 731–748 Search PubMed.
- W. T. Wenckebach, A. Capozzi, S. Patel and J. H. Ardenkjær-Larsen, J. Magn. Reson., 2021, 327, 106982 CrossRef CAS PubMed.
- W. T. Wenckebach and Y. Quan, J. Magn. Reson., 2021, 326, 106948 CrossRef CAS PubMed.
- W. Wenckebach and S. Cox, J. Magn. Reson., 2023, 348, 107375 CrossRef CAS PubMed.
- M. Lee, M. C. Cassidy, C. Ramanathan and C. M. Marcus, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 33–35 Search PubMed.
- N. Bloembergen, Physica, 1949, 15, 386–426 CrossRef CAS.
- A. E. Dementyev, D. G. Cory and C. Ramanathan, Phys. Rev. Lett., 2008, 100, 127601 CrossRef CAS PubMed.
- E. Dementyev, D. Li, K. MacLean and E. Barrett, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 1–4 CrossRef.
- Y. Hovav, A. Feintuch, S. Vega and D. Goldfarb, J. Magn. Reson., 2014, 238, 94–105 CrossRef CAS PubMed.
- E. P. Horvitz, Phys. Rev. B: Solid State, 1971, 3, 2868–2872 CrossRef.
- L. L. Buishvili, M. D. Zviadadze and B. D. Mikaberidze, Zh. Eksp. Teor. Fiz., 1975, 69, 1077–1079 Search PubMed.
- K. K. Sabirov, Phys. Status Solidi B, 1979, 91, 735–739 CrossRef.
- V. A. Atsarkin and V. V. Demidov, Zh. Eksp. Teor. Fiz., 1980, 79, 1438–1450 CAS.
- J. J. Wittmann, M. Eckardt, W. Harneit and B. Corzilius, Phys. Chem. Chem. Phys., 2018, 20, 11418–11429 RSC.
- Q. Stern, S. F. Cousin, F. Mentink-Vigier, A. C. Pinon, S. J. Elliott, O. Cala and S. Jannin, Sci. Adv., 2021, 7, 1–13 Search PubMed.
- A. Chessari, S. F. Cousin, S. Jannin and Q. Stern, Phys. Rev. B, 2023, 107, 224429 CrossRef CAS.
- G. von Witte, S. Kozerke and M. Ernst, Two-electron two-nucleus effective Hamiltonian and the spin diffusion barrier, arXiv, 2024, preprint, arXiv:2407.10319, DOI:10.48550/arXiv.2407.10319.
- V. S. Redrouthu, M. Mannai, L. Taha, W. Zia, S. V. Sadasivan, R. Jabbour and A. Equbal, Overcoming Nuclear Spin Diffusion Barrier in DNP via Electron-Electron Flip-Flop, 2024, DOI:10.26434/chemrxiv-2024-kt7xx.
- M. Ernst and B. H. Meier, Studies in Physical and Theoretical Chemistry, Elsevier, 1998, vol. 84, pp. 83–121 Search PubMed.
- N. A. Prisco, A. C. Pinon, L. Emsley and B. F. Chmelka, Phys. Chem. Chem. Phys., 2021, 23, 1006–1020 RSC.
- G. Kwiatkowski, G. von Witte, A. Däpp, J. Kocic, B. Hattendorf, M. Ernst and S. Kozerke, Magn. Reson. Med., 2024, 1–10 CAS.
- A. Abragam and M. Goldman, Nuclear Magnetism: Order and Disorder, Oxford University Press, 1982 Search PubMed.
- N. Bloembergen and W. C. Dickinson, Phys. Rev., 1950, 79, 179–180 CrossRef CAS.
- I. Bertini, C. Luchinat and G. Parigi, Prog. Nucl. Magn. Reson. Spectrosc., 2002, 40, 249–273 CrossRef CAS.
- G. Parigi, E. Ravera and C. Luchinat, Prog. Nucl. Magn. Reson. Spectrosc., 2019, 114–115, 211–236 CrossRef CAS PubMed.
- A. J. Pell, G. Pintacuda and C. P. Grey, Prog. Nucl. Magn. Reson. Spectrosc., 2019, 111, 1–271 CrossRef CAS PubMed.
- G. Von Witte, A. Himmler, S. Kozerke and M. Ernst, Phys. Chem. Chem. Phys., 2024, 26, 9578–9585 RSC.
- A. N. Thiessen, M. Ha, R. W. Hooper, H. Yu, A. O. Oliynyk, J. G. Veinot and V. K. Michaelis, Chem. Mater., 2019, 31, 678–688 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: FTIR, XRPD, EPR characterization data for all the samples as well as the additional DNP data including DNP sweep spectra, polarization buildup and decay data, rate constants for various experimental conditions. See DOI: https://doi.org/10.1039/d4nr02603a |
| ‡ Joint senior authorship. |
| This journal is © The Royal Society of Chemistry 2024 |