Tuning the product selectivity of single-atom catalysts for CO₂ reduction beyond CO formation by orbital engineering

Abstract

Electrochemical CO₂ reduction (CO₂R) is one of the promising strategies for developing sustainable energy resources. Single-atom catalysts (SACs) have emerged as efficient catalysts for CO₂R. However, the efficiency of SACs for the formation of reduction products beyond two-step CO formation is low due to the lower binding strength of the CO intermediate. In this study, we present an orbital engineering strategy based on density functional theory calculations and the fragment molecular orbital approach to tune product selectivity for the CO₂R reaction on macrocycle based molecular catalysts (porphyrin and phthalocyanine) and extended SACs (graphene and covalent organic frameworks) with Fe, Co, and Ni dopants. The introduction of neutral axial ligands such as imidazole, pyridine, and trimethyl phosphine to the metal dopants enhances the binding affinity of the CO intermediate. The stability of the catalysts is investigated through the thermodynamic binding energy of the axial ligands and ab initio molecular dynamics simulations (AIMD). The grand canonical potential method is used to determine the reaction free energy values. Using a unified activity volcano plot based on the reaction free energy values, we investigated the catalytic activity and product selectivity at an applied potential of −0.8 V vs. SHE and a pH of 6.8. We found that with the imidazole and pyridine axial ligands, the selectivity of Fe-doped SACs towards the formation of the methanol product is improved. The activity volcano plot for these SACs shows a similar activity to that of the Cu (211) surface. The catalytic activity is found to be directly proportional to the sigma-donating ability of the axial ligands.

---

1 Introduction

The electrochemical CO₂ reduction (CO₂R) reaction is an efficient method for the valorization of CO₂ into value-added chemicals and fuels.^1–3 At a comparable reduction potential, several single and multi-carbon-derived products could be generated. CO is the simplest reduction product, requiring a two-step proton-coupled electron transfer (PCET) pathway.^4,5 However, the production of carbon derivatives beyond the two-step reduction process would be more desirable. Among the several products that are obtained with the further reduction of the CO intermediate, methane and methanol are of prime importance as substitutions for fossil fuels,⁶ particularly due to their high energy density, compatible storage and transportation strategies.

Several technological limitations have been found to bring additional challenges toward making this process suitable for industrial-scale utilization. The chemical inertness of CO₂ resulting in the need for a high electrochemical energy input for activating the C–O bond is one of the prime challenges. Furthermore, the H₂ evolution reaction (HER) could be competitive under a reductive potential and acidic environment. Therefore, catalysts are required to reduce the energy barrier for CO₂R and improve product selectivity.

Among the different catalysts, noble metal surfaces such as those of Au and Ag have been identified as having high activity for CO₂ to CO production and for suppressing the HER activity.^4,7 The copper (Cu) surface shows a unique activity for producing carbon-derived products beyond CO (alcohols and higher C_n products).^8–13 Although it allows for the formation of more than two-step reduction products, the product selectivity and the faradaic efficiency for methane or methanol formation are considerably lower. In addition, high overpotential values (≥1 V) are needed to achieve carbon-derived products beyond CO.^14–17

Recently, single-atom catalysts (SACs) have emerged as a promising new form of catalyst for CO₂R reactions^18–24 and the oxygen reduction reaction (ORR).^25–29 These catalysts involve doping single transition metals onto a conductive supporting surface. Among the different classes of supporting materials, molecular macrocyclic ligands such as porphyrin and phthalocyanines have been found to be an optimum choice. The assembly of these molecular catalysts using different organic and inorganic linkers enables the synthesis of supramolecular frameworks, allowing applications in both homogeneous and heterogeneous catalysis.^30–33 Furthermore, various post-synthetic modifications in the primary and secondary coordination environment around the metal atoms provide a great opportunity to precisely modulate their electronic structure and tune their catalytic activity.^34–40 For example, secondary sphere modification at meso-positions with a local proton donor and cationic moiety in porphyrin-based catalysts has been found to enhance activity for CO₂ to CO formation.^30,34

While SACs show promising activity for CO₂ to CO formation and suppressing the competitive HER, the design principles for achieving post-CO reduction (CH₃OH and CH₄) products have remained less explored. Inspired by natural enzymes (heme,⁴¹ Cytochrome P450,⁴² and heme peroxidase⁴³), axial ligation strategies for porphyrin-based metal centers have been observed to activate substrates selectively towards the specific reaction products. In recent studies, cobalt phthalocyanine-based (Co@pth) complexes have been synthesized with Py (pyridine) and IMD (imidazole) as the axial ligands.⁴⁴ Tethering nitrogen-based ligands to the axial positions of cobalt phthalocyanine complexes has been found to increase CO₂ to CO reduction activity.^45,46

In this study, we show an axial ligation strategy with porphyrin and phthalocyanine-based SACs to tune the product selectivity and activity towards the formation of post-CO reduction products. In addition to these molecular catalysts, the CO₂R catalytic activity was investigated in graphene-based SACs and extended two-dimensional porphyrin-based supramolecular structures doped with transition metals and attached axial ligands. Using first-principles-based computational methods and grand-canonical potential free energy calculations,^47–50 we characterized the preferred binding site motifs of the CO₂R intermediates favoring the specific reaction products. With fragment molecular orbital overlap studies, we analyzed the frontier molecular orbital interactions between the catalysts and the adsorbed reaction intermediates. This led us to rationalize the general selectivity trend of SACs towards favoring the formation of different CO₂R products. We show that by engineering the orbital overlap principles and local electronic structures via the axial ligation, the binding strength of different CO₂R intermediates and product selectivity could be effectively tuned. Using unified micro-kinetic models developed based on thermodynamic free energy calculations and Bell–Evans–Polanyi (BEP) relations, we analyzed the catalytic activity and product selectivity with respect to the Cu (211) surface. We found that Fe-doped SACs with axial ligands could show comparable activity to the Cu (211) surface towards the formation of post-CO reduction products.

2 Results and discussion

2.1 Identifying the stability of SACs with different axial ligands

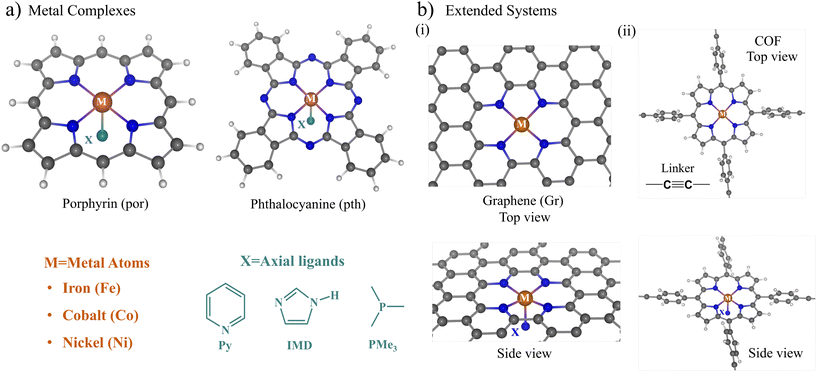
Fig. 1a and b show a schematic representation of the catalyst structures considered in this study. As the supporting materials, we used molecular macrocyclic ligands and 2D extended systems. The porphyrin and phthalocyanine moieties (Fig. 1a) were considered as the molecular macrocyclic ligands for embedding the metal dopants (iron (Fe), cobalt (Co), and nickel (Ni)). On the other hand, to build extended SACs, we doped the nitrogenated graphene surface with two-carbon-atom vacancy defects and a porphyrin-based two-dimensional covalent organic framework (COF), as shown in Fig. 1b(i) and (ii) respectively. The tetraphenyl porphyrin (TPP) units linked via acetylene linkers were used to build the 2D-COF.

Fig. 1 (a) Schematic representation of macrocyclic complexes porphyrin and phthalocyanine (M@por and M@pth) considered in this study. Here, M indicates 3d transition metals Fe, Co and Ni, and X indicates the neutral axial ligands imidazole (IMD), pyridine (Py), and trimethyl phosphine (PMe₃). (b) (i) and (ii) illustrate the top and side views of extended graphene (Gr) and tetraphenyl porphyrin (TPP) with an acetylene linker-based covalent organic framework (COF), respectively.

The ligand (X) attached to the metal (M) atom represents the axial ligand. We chose neutral nitrogen-coordinating ligands, such as imidazole (IMD) and pyridine (Py), and a phosphorus-coordinating ligand, trimethyl phosphine (PMe₃), to bind to the axial position X. The choice of these axial ligands is based upon some recent experiments,^44–46 where the stability and synthetic routes to Co-doped porphyrin and phthalocyanine were explored with imidazole (IMD) and pyridine (Py) as the axial ligands. Secondly, these axial ligands attached to metal–porphyrin units are present as active centers in several biomolecules, mediating numerous biochemical redox reactions.^41–43 As the metal dopants, we chose the late 3d transition metals Fe, Co, and Ni due to their multiple redox-active states and better complexing stability with the porphyrin and phthalocyanine moieties. The metal atoms show a penta-coordination geometry with the four surrounding N atoms present on the catalyst plane and an axial ligand oriented perpendicular to the catalyst plane (Fig. 1(a) and (b)). The metal center shows a distorted square pyramidal geometry, with the metal atom distorted slightly away from the catalyst plane towards the axial ligand.

The metal–macrocyclic structures with axial ligands are denoted using the symbol M@cy-X, where M denotes the metal dopant, X is the axial ligand, and cy stands for the macrocyclic units (porphyrin and phthalocyanine) and extended systems (graphene and COF). We use the shorthand notation por for porphyrin and pth for phthalocyanine. M@Gr/COF represents the extended system of graphene (Gr) and tetraphenyl porphyrin-based COF, respectively. For example, the Fe- and Co-porphyrin with imidazole ligands are denoted as Fe@por-IMD and Co@por-IMD, respectively.

To understand the binding strength of the axial ligands to the molecular catalysts and the extended SACs, we calculated the binding energies, as shown in Table 1.

Table 1 The calculated binding energies (in eV) of the different axial ligands (X) to the different SACs (M@cy). The free energy calculation is ΔE = ΔE^DFT_M@cy-X − ΔE^DFT_M@cy − E^DFT_X. Here, ΔE^DFT_M@cy-X represents the electronic energy of a metal catalyst with axial ligands, ΔE^DFT_M@cy is the electronic energy of a metal catalyst, and E^DFT_X represents the electronic energy of the axial ligand. The binding energies are found to be exothermic, indicating the considerable stability of these catalysts

Complex	Porphyrin			Phthalocyanine
Metals	Py	IMD	PMe3	Py	IMD	PMe3
Fe	−1.383	−1.573	−1.877	−1.345	−1.590	−1.791
Co	−0.770*	−0.974*	−0.898	−1.065*	−1.271*	−1.192
Ni	−0.794	−1.030	−0.926	−0.571	−0.818	−0.467

---

Complex	Graphene			COF
Metals	Py	IMD	PMe3	Py	IMD	PMe3
The values indicated with an asterisk (*) symbol are experimentally known.^44–46,51
Fe	−1.043*	−1.244	−1.637	−1.39	−1.587	−1.931
Co	−0.85	−1.077	−1.062	−0.840	−1.047	−1.001
Ni	−0.390	−0.577	−0.463	−0.713	−0.968	−0.939

---

The ligand binding free energy values show that these axial ligands form stable complexes with both molecular and extended systems. The ligand binding energies are found to be exothermic for all the cases. The axial ligands with the Fe@por/pth complexes (corresponding to molecular catalysts) show the maximum exothermicity in the binding energies. Co and Ni@por complexes show binding energies within the range of −0.8 to −1 eV for all three axial ligands. However, with phthalocyanine complexes, the axial ligand binding energies are slightly more exothermic for the Co complex compared to the Ni@pth complex.

The graphene-based SACs and 2D COF structures with different metal dopants show a similar trend in the binding strength of the axial ligands to that observed for the metalloporphyrin and phthalocyanine moieties. We observed the highest exothermicity in ligand binding in the case of Fe-doped SACs.

The values marked with an asterisk symbol in Table 1 correspond to Co@por/pth-IMD and Co@por/pth-Py complexes and Fe@Gr-Py, which have recently been synthesized and studied for CO₂R to CO formation.^45,46,51 It is to be noted that the binding energy values of the axial ligands to SACs studied here are comparable to those of the experimentally known Co@por/pth-IMD and Co@por/pth-Py. Therefore, by carefully controlling the experimental conditions and selection of preferred precursors, axial ligation to the different support materials could be successfully achieved with all the axial ligands considered here.

Axial coordination to the macrocyclic complexes and graphene-doped SACs has been achieved experimentally in recent studies.^45,46,51 To account for the thermodynamic stability of 2D-COFs with the axial ligands, we performed ab initio molecular dynamics (AIMD) simulations at three different temperatures, namely 400 K, 500 K, and 800 K, over a timescale of up to 10 ps. We found that the axially ligated 2D-COFs show considerable stability up to 400 K. Section X and Fig. S8–S11 in the ESI† show the initial and final structures obtained during the AIMD simulations and the alternations in the metal–ligand bond distances. We did not observe considerable changes in the metal–ligand bond lengths during the AIMD simulations. At 500 K and 800 K, the axial ligands were found to detach after 4 ps. The experimental axial ligation strategies were mostly performed in a temperature range from 320 to 350 K.^26,45,46,51 Therefore, we believe that the metal-doped COF SACs explored here have good thermodynamic stability and are viable candidates for synthesis.

2.2 Axial ligands influence the adsorption energies of CO₂R intermediates: a *H vs. *CO classification plot

Having determined the thermodynamic stability of the catalysts, next, we analyze the product selectivity for the CO₂R reaction. Using the binding energies of the *H and *CO intermediates on the catalyst surfaces, we classified the possible selectivity to different CO₂R products following the classification approach introduced by Bagger et al.⁵²Fig. 2(a) and (b) show the *H and *CO binding energies (ΔE_*H and ΔE_*CO, respectively) on the molecular catalysts (M@por and M@pth) and extended SACs (M@Gr and M@COF), respectively, with and without the axial ligands. The black solid circles represent the binding energies on the (111) surfaces of Pt, Pd, Cu, Au, and Ag. The binding energies of M@por and M@pth are denoted using circular and square markers in different color shades, whereas diamond and triangular markers denote the binding energies for M@Gr and M@COF, respectively. The color scheme used to denote the metal dopants is given in Fig. 2(a) and (b) inset.

Fig. 2 (a) and (b) show the product classification plots based on *H (x-axis) and *CO (y-axis) intermediate binding energies (ΔE_*H and ΔE_*CO, respectively) on the molecular catalysts and extended systems with and without the axial ligands. The horizontal and vertical grey lines represent the thermodynamic free energy for adsorbed and non-adsorbed CO and H (ΔG_*CO = 0 and ΔG_*H = 0, respectively). The black solid circles represent the corresponding binding energies on the transition metal (111) surfaces. The markers (Fe: orange, Co: pink and Ni: green) used to define the binding energies of the SACs with different metals and axial ligands are given in the bottom inset of the plot. While comparing binding energies with transition metal (111) surfaces, Fe-doped molecular complexes (porphyrin and phthalocyanine) and extended systems (graphene and COF) with different axial ligands show comparable binding energies as Cu (111) surfaces.

The ΔE_*H values for both molecular and extended SACs with and without the axial ligands were endothermic compared to Pd and Pt surfaces. This suggests a low selectivity for the HER. For the molecular macrocyclic complexes, the *CO binding affinity without the axial ligands is comparable to that for Au (111) and Ag (111) surfaces. Fe- and Co-doped macrocyclic complexes show binding energies varying from −0.11 to 0.05 eV. Ni@por and Ni@pth complexes show slightly weaker binding affinities compared to Fe- and Co-doped complexes (within the range of 0.35–0.39 eV). Therefore, CO will be the major product for CO₂R on both the porphyrin and phthalocyanine complexes without the axial ligands with Fe and Co dopants. Our results are consistent with the previous theoretical and experimental studies,^44,45,53 where Co- and Fe-based porphyrin and phthalocyanine complexes are reported to be superior catalysts for the formation of CO₂ to CO reduction products.

On attaching the axial ligands to these molecular catalysts, we found considerable variation in the CO binding affinity depending upon the metal dopants. The Fe-doped metallocyclic complexes show an exothermic binding affinity comparable with that of the Cu (111) surface (binding energy range between −0.11 and −0.94 eV). On the other hand, for Co- and Ni-doped metallocyclic complexes, the binding energies of *CO either remain the same or get slightly destabilized compared to those obtained before attaching the axial ligands.

The metal-doped graphene SACs and COFs show a trend in the *CO vs. *H intermediate binding energies matching those of the macrocyclic complexes (por and pth). The binding energies of *CO on Fe@Gr and Fe@COF with the axial ligands show a similarity to those on the Cu (111) surface. The ΔG_*CO intermediate binding energies are within the range of −0.42 to −0.95 eV. Co- and Ni-doped graphene and COFs with and without axial ligands show weaker CO binding affinity (ΔG_*CO is endothermic), varying within the range of 0.3–0.8 eV.

This indicates that axial ligation to both the Fe-doped metallocyclic complexes and Fe-doped extended SACs could allow the formation of reduction products beyond CO formation. However, Co- and Ni-doped SACs exhibit good activity for CO₂ to CO formation.

To understand the varying binding strength of CO on these catalysts, we investigated the orbital overlap interactions between the metal and the adsorbed CO using the fragment molecular orbital approach in the next section.

2.3 Metal–CO bonding analysis in CO-adsorbed metallocyclic complexes

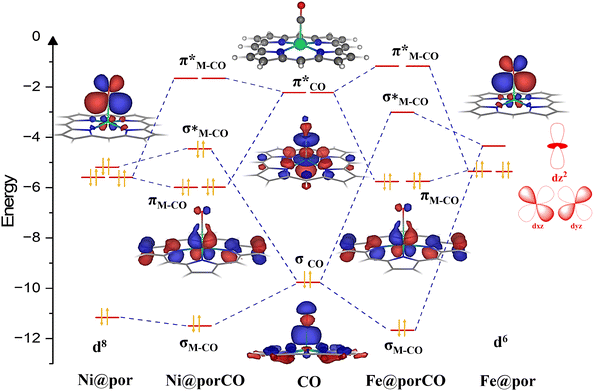
To build frontier molecular orbitals of metal complexes (active site), spin-polarized calculations were performed for metal-doped porphyrins. The calculation details are given in section IX of the ESI.† A comparative orbital interaction diagram for Fe@por and Ni@por without the axial ligand is shown in Fig. 3. The corresponding orbitals involved in the formation of the metal–CO bonds are only shown in the figure.

Fig. 3 Comparative orbital interaction diagram of Fe@por (right) and Ni@por (left) with the CO intermediate. The M–CO intermediate shows a distorted square pyramidal geometry. The HOMO (σ) and LUMO (π*) of CO interact with the metal d-orbitals of the catalysts. In Fe@por, Fe has a d⁶ configuration, and electrons occupy only the bonding molecular orbitals of the M–CO complex. On the other hand, in Ni@por, Ni is in the d⁸ configuration. The excess electrons occupy the anti-bonding molecular orbitals of the M–CO complex. This reduces the stability of the M–CO complex and increases the endothermicity of the CO binding energy. The corresponding molecular orbitals are also shown here.

The metal–macrocyclic complexes show a distorted square .02wplanar symmetry with the metal atoms occupying a position slightly above the plane of the macro-cyclic ring. CO binds to the metals via the donation of electrons from one of the frontier lone pair (σ) orbitals to the metal d_z² orbital (σ_CO → d_z²(M)) as well as π acceptance to the degenerate vacant orbitals from the filled metal d_xz and d_yz orbitals . Due to the differing electron counts in the valence metal d-orbitals, the electronic configuration dramatically varies from Fe@por to Ni@por complexes (Fig. 3). For Fe@por, the d_z² orbital is unoccupied, whereas d_xz and d_yz molecular orbitals are occupied. For Ni@por, we found that both d_z² and degenerate d_xz and d_yz are filled up. CO binding to Ni@por is repulsive compared to Fe@por since the interaction between the filled d_z² orbitals on Ni and the filled σ_CO orbitals leads to the occupation of both the bonding and anti-bonding Ni–CO σ bonds (left panel of Fig. 3). This not only reduces the binding strength of CO on Ni@por but also slightly increases the metal–CO bond distance for Ni (1.97 Å) in comparison with Fe@por (1.71 Å). A similar repulsive interaction between CO and the Co@por complex is observed due to the partial filling of the d_z² orbital. This is evident from the increase in the metal–CO bond length (1.93 Å) compared to Fe@por. The detailed catalyst structural information is provided for the SACs in ESI sections VII and VIII.†

While the orbital interaction diagram in Fig. 3 gives a qualitative overview of the M–CO orbital overlap, a quantitative understanding has been obtained using bonding energy decomposition analysis (BEDA), detailed in section IX of the ESI.† BEDA was performed for the M–CO bond in M@por-CO complexes, with M corresponding to Fe, Co, and Ni. The bonding analysis shows that electrostatic interaction, Pauli repulsion energy, and orbital interaction energies between the metal energy states and CO MOs play important roles in stabilizing the M–CO intermediate. Among these energy terms, the orbital interaction energy is found to be the dominating factor in increasing the stability of the M–CO intermediate on Fe@por compared to Co@por and Ni@por. The repulsive interaction, possibly due to the presence of excess electrons in the antibonding M–CO orbitals, increases the Pauli repulsive interactions and reduces the binding strength of CO on both Co@por and Ni@por catalysts.

To account for the effect of the axial ligand on CO binding affinity, an interaction diagram for CO adsorbed on Fe@por with the imidazole axial ligand is shown in Fig. 4. The metal–CO complex with the axial ligands (X = IMD, Py, and PMe₃) adopts a distorted octahedral structure. The presence of the axial ligand introduces a push effect to the metal center, which results in the restoration of the planar arrangement of the metal atom to the macrocyclic plane. This allows the re-hybridization of the metal p_z orbital with the d_z² orbital to form two p–d hybrid orbitals before binding to the σ_CO orbital. The interaction diagram in Fig. 4 shows that CO forms a σ bond with one of these p–d hybrid orbitals (σ_M-IMD). The other p–d orbital is bound to the axial ligand.

Fig. 4 The MO interaction diagram of Fe@por-IMD with the CO intermediate. The attachment of the axial ligand results in the re-hybridization of metal d_z² orbital with the metal p_z orbital, leading to the formation of two p–d hybrid orbitals. One of the p–d hybrid orbitals overlaps with the CO σ orbital, and the other binds to the axial ligand. Therefore, an octahedral geometry is attained, which satisfies the 18-electron count. The corresponding bonding M–CO MOs are shown in the right panel.

Comparing the orbital interactions of Fe@por-IMD vs. Fe@por with CO, we found that the addition of the axial ligands helps satisfy the 18-electron count of the metal complexes. This provides extra stability to the metal–CO bond. A similar interaction is observed with the other axial ligands shown in Fig. S7 in the ESI.† It is to be noted that the attachment of the axial ligands is not found to be beneficial for the Co and Ni@por/pth complexes. Co and Ni porphyrin and phthalocyanine complexes with the axial ligands show endothermic binding energies for CO. Eighteen electron counts are satisfactory for both systems with the addition of the axial ligands. However, due to the presence of excess electrons in the valence d-orbitals of Co (d⁷) and Ni (d⁸) compared to Fe (d⁶), these complexes show repulsive interactions with CO MOs. The excess electrons present in Co or Ni@por/pth will populate the anti-bonding M–CO orbitals, leading to a decrease in the M–CO binding affinity and an increase in the M–CO bond length. A similar metal–ligand binding environment of M@Gr and M@COF systems would result in similar orbital interactions. Therefore, the CO binding energies on these catalyst surfaces follow a similar trend to that of the metal–macrocyclic complexes with and without the axial ligands.

2.4 The Gibbs free energy reaction pathways for the CO₂R reaction

While the binding energies of the *H and *CO intermediates as the descriptors could enable us to classify the selectivity of the catalysts, they do not allow us to characterize the activity of the catalysts. On both the Fe-doped molecular and extended SACs with axially coordinated Py, IMD, and PMe₃ ligands, the formation of reduction products beyond CO might be possible due to the increase in the stabilization of the *CO intermediate. We determined the binding energies of the different CO₂R intermediates on these complexes with and without the axial ligands to characterize the favorable CO₂R reaction pathways.

Inspired by the previous studies of the CO₂R reaction on SACs, we considered a proton-coupled electron transfer (PCET) mechanism for each of the reduction steps.^8,31,54 The binding free energies of the hydrogen intermediate on the Fe-doped SACs with and without the axial ligands are found to vary within the range of 0.5–1.3 eV at zero applied potential, with a few exceptions for Py and IMD as the axial ligands. Table S4 in the ESI† shows the ΔG_*H values for the SACs. However, in a recent experimental study,^51,55 Fe-doped graphene with Py as the axial ligand has been found to show low efficiency for the HER. Therefore, we did not consider the possibility of the HER on the catalyst surfaces in the present study.

Fig. 5(a) shows the electrochemical CO₂ reduction pathway considered here. Using the grand canonical potential approach for free energy calculations, we determined the reaction free energy values, under different applied potentials. Section II in the ESI† presents the computation details for the constant potential free energy calculations.^47–50 The reduction intermediate could show different binding motifs on the active site. We calculated the relative stability of all the binding motifs for each intermediate. Considering the preferable motifs, the free energy diagrams (FEDs) for Fe@Gr and Fe@COF with and without the IMD axial ligand are shown in Fig. 5(b) and (c), respectively. The reaction free energies (ΔG) at zero applied potential are shown with blue and orange lines for Fe@Gr and Fe@Gr-IMD, respectively. The FEDs under a reduction potential of −0.8 V vs. SHE and a pH of 6.8 for these complexes are respectively represented by black and red lines. The FEDs of Fe@Gr and Fe@COF with the other axial ligands are shown in Fig. S4 in the ESI.† The FEDs of the molecular catalysts are shown in Fig. S6 in the ESI.†

Fig. 5 (a) The proposed electrochemical CO₂R reaction pathways considered in this study for DFT calculations. The electrochemical steps from 0 to 8 represent the eight-step PCET mechanism. The less stable reaction intermediates at each step are shown in a light-shaded color, whereas the most stable intermediates obtained in the calculations are shown in prominent shades. (b) and (c) The free energy diagram (FED) for CO₂R to different products for Fe@Gr and Fe@COF without and with IMD as the axial ligand, respectively. The FEDs at zero applied potential are shown with blue and orange lines for Fe@Gr/COF and Fe@Gr/COF-IMD, respectively, whereas the FEDs under a reduction potential of −0.8 V vs. SHE and at a pH of 6.8 are illustrated by black and red lines. The reaction free energy values are calculated following the grand canonical potential method (GCP). The details of the computational procedures are given in the ESI (sections I and II†). Fe@Gr/COF preferentially stabilizes the M–CO intermediate (step 2) on attaching the axial ligand.

The formation free energy of the *CHO intermediate from *CO plays a critical role in determining the selectivity towards the formation of the reduction products beyond the CO intermediate.^8,54 Among the several reaction intermediates, the *CO to *CHO step is known to be a potential determining step (PDS) for the electrochemical CO₂R to CH₃OH or CH₄. Involving the formation of several reaction intermediates, a six-step PCET mechanism is followed for the methanol pathway, whereas an eight-step PCET mechanism is followed for methane formation.

In Fig. 5(b), without the axial ligand on Fe@Gr at zero applied potential, the *COOH formation step is observed with the highest endothermicity. Following the *COOH formation, the reaction free energy is found to be nearly exothermic for all intermediates. On Fe@Gr, CO desorption is found to be slightly more favorable compared to the formation of the *CHO intermediate. The energy difference between *CO to CO desorption and *CO to *CHO formation is 0.35 eV.

With IMD as the axial ligand at zero applied potential, the M–CO intermediate dramatically stabilizes by around 0.7 eV. The other intermediate steps are also found to be stabilized in comparison with Fe@Gr. However, it varies within the range of 0.2–0.6 eV. The highest stability observed for the *CO intermediate increases the endothermicity in ΔG for CO desorption from *CO. In the absence of an applied potential, both CO desorption and *CHO formation are found to be equally favorable. Therefore, the expected selectivity will be lower towards the formation of the reduction products beyond CO.

On applying a potential of −0.8 V vs. SHE on Fe@Gr, the energy difference between CO desorption (ΔG_CO↑) and *CHO (ΔG_*CHO) formation reduces (black lines in the FED). Both ΔG_CO↑ and *CHO formation show equal preference. The desorption of CO reduces the possibility of forming other C₁ products. However, with IMD as the ligand, we observed a reversal in stability for *CHO (ΔG_*CHO) formation in comparison with CO desorption. On Fe@Gr-IMD, ΔG_CO↑ is endothermic to ΔG_*CHO by 0.6 eV. Therefore, the selectivity for *CHO will be higher compared to CO desorption.

Under the applied potential, for Fe@Gr, the protonation of CO₂ to the *COOH intermediate is the PDS, and the following reaction steps beyond CO intermediates are found to be exothermic. We see a change in the reaction selectivity for Fe@Gr-IMD with respect to Fe@Gr. The PDS is found to be the *CO to *CHO formation.

Among the different C₁ products beyond the two-step CO formation, the reaction free energy differences ΔG_CH3OH and ΔG_CH4↑+*O (*CH₂OH → CH₃OH and *CH₂OH → CH_4↑ + *O, respectively) critically determine the selectivity between methane and methanol formation. The higher exothermicity for ΔG_CH3OH will favor the formation of methanol, whereas for methane formation, ΔG_CH4↑+*O should be more exothermic. The calculated free energies for Fe@Gr with and without the applied potential show a greater exothermicity for ΔG_CH3OH (by around 0.5 eV). With IMD as the axial ligand, the reaction free energy difference between ΔG_CH3OH and ΔG_CH4↑+*O reduces. Under an applied potential of −0.8 V vs. SHE, CH₃OH formation is found to be thermodynamically more favorable than G_CH4↑+*O. However, both steps are exothermic and the reaction free energy difference is less (0.3 eV). Hence, the simultaneous formation of CH₃OH and CH₄ could be possible. Since these products (CH₃OH and CH₄) are heterogeneous, the separation process will be feasible.

A similar trend in reaction selectivity is observed for Fe@COF with the axial IMD ligand (Fig. 5(c)). Under −0.8 V vs. SHE, the preference for *CHO (ΔG_*CHO) formation considerably increases compared to CO desorption (ΔG_CO↑). The energy difference between CH₃OH and CH₄ formation shows a slight preference for methanol as the major product.

It is evident that the free energy differences between the intermediates in the third (ΔG_CO↑ − ΔG_*CHO) and the sixth PCET steps (ΔG_CH3OH − ΔG_CH4↑+*O) mainly dictate the product selectivity. Table 2 summarizes ΔG differences at −0.8 V vs. SHE and 6.8 pH with and without the axial ligands for Fe@Gr and Fe@COF. We determined the potential determining steps based upon the reaction free energy value with the highest endothermicity as given in column 5 of Table 2. Comparing the ΔG values for these steps for Fe@Gr and Fe@COF with Py and IMD as axial ligands, methanol formation at the sixth PCET shows a slightly greater preference. However, with PMe₃ as the axial ligand, the free energy differences between CO desorption and *CHO formation are much less for Fe@Gr and Fe@COF. Although a considerable exothermicity for CH₃OH formation is observed with PMe₃ as the axial ligand compared to the CH₄ pathway, the preference for the CO product at −0.8 V vs. SHE will be high due to the comparable energy difference between ΔG_CO↑ and ΔG_*CHO. With a higher applied reductive potential, the CO desorption will be less favorable, and therefore, the selectivity towards methanol formation will be high. Fig. S4, S5 and Table S1 in the ESI† show this possibility for Fe@Gr and Fe@COF with PMe₃ at −0.8 V and −1 V vs. SHE and pH 6.8.

Table 2 The reaction free energy difference of the third and sixth PCET steps (in eV) of the proposed mechanism (Fig. 5a), the product selectivity and the potential determining step (PDS) at −0.8 V vs. SHE and 6.8 pH are shown here for Fe@Gr/COF with the different axial ligands (IMD, Py and PMe₃). The energy difference for the third and sixth PCETs is found to influence the product selectivity of the catalysts mainly. The greater the endothermicity of the third step, the greater the preference will be for post-CO product formation. On the other hand, an increase in exothermicity for the sixth step will favor the selectivity towards CH₃OH formation as the major product

Complexes	ΔGCO↑ − ΔG*CHO	ΔGCH3OH − ΔGCH4↑+*O	Major products	PDS(RDS)
Fe@Gr
Fe@Gr	0.05	−0.54	CO	*COOH (*COOH)
Fe@Gr-IMD	0.45	−0.29	CH3OH	*CHO (*CHO)
Fe@Gr-Py	0.51	−0.27	CH3OH	*CHO (*CHO)
Fe@Gr-PMe3	0.06	−0.59	CO	*CHO (*CHO)
Fe@COF
Fe@COF	0.15	−0.69	CO	*COOH (*COOH)
Fe@COF-IMD	0.26	−0.43	CH3OH	*CHO (*CHO)
Fe@COF-Py	0.33	−0.43	CH3OH	*CHO (*CHO)
Fe@COF-PMe3	0.09	−0.65	CO	*CHO (*CHO)

---

Fig. S6 in the ESI† shows the FEDs for Fe@por and Fe@pth complexes with and without the axial ligands at zero and −0.8 V vs. SHE applied potential. With IMD and Py as the axial ligands for Fe@por, the formation of products beyond the CO step is found to be more favorable. However, for Fe@por-PMe₃ and Fe@pth with all the axial ligands at −0.8 V vs. SHE, CO desorption and CHO* formation have similar preferences. This indicates that CO is the thermodynamically preferable product for these catalysts. With high negative reductive potentials, we expect good selectivity for Fe@por and Fe@pth with these axial ligands beyond CO product formation. The free energy values for these complexes at −1 V vs. SHE given in the ESI (Tables S2 and S3†) show these possibilities.

2.5 Activity volcano plot

Using the potential-dependent reaction free energies of the different intermediates, here we present an activity volcano plot of these catalysts towards methanol/methane formation. The mean-field microkinetic model was developed using the thermodynamic free energies of *CHO and *CO as the reaction descriptors, as in ref. 10, 56–60. The kinetic barriers were estimated following the Bell–Evans–Polanyi (BEP) relations. Further details of the microkinetic models and the computational techniques are discussed in section IV of the ESI.†

Fig. 6 shows the unified activity volcano plot at −0.8 V vs. SHE and 6.8 pH. The choice of pH is made based on the recent experimental studies, where buffer conditions are found to be an advantage for CO₂R reactions on metal-doped macrocyclic catalysts.^61–63 The black circles represent the activity of the (211) metal surfaces. The Fe@Gr and Fe@COF SACs with and without the axial ligands are shown with brown diamond and triangular markers. The color scheme is further explained in Fig. 6. The activity is shown on the logarithmic scale relative to the Cu (211) surface.

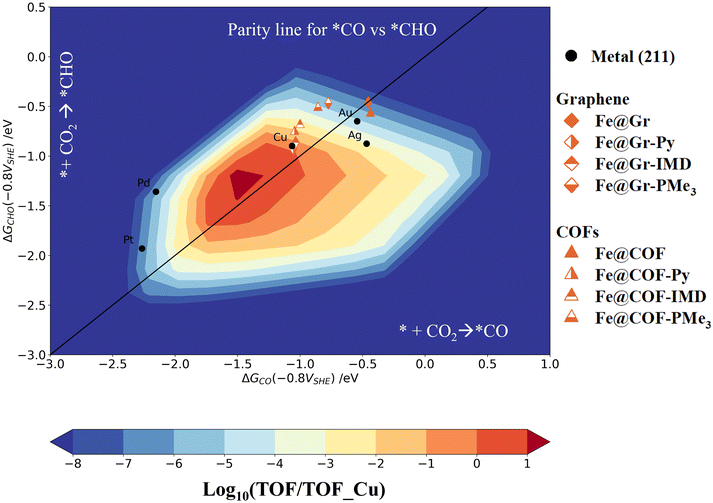Fig. 6 Unified activity volcano plot for CO₂ → CH₃OH/CH₄ formation, plotted using the free energies of *CO and *CHO intermediates as the activity descriptors at an applied potential of −0.8 V vs. SHE and pH of 6.8. The Fe@Gr/COF catalysts with and without axial ligands are represented using different markers, as shown in the right inset of Fig. 6. The catalytic activity is shown on a logarithmic scale with respect to the Cu (211) surface. The black circles represent the activity of the 211 surfaces of Pt, Pd, Au, Ag, and Cu. The parity line denoted by a black solid line indicates the preference for PDS between the * + CO₂ → *CO and * + CO₂ → CHO intermediates. The activity with respect to the Cu (211) surface increases on moving from blue to red regions. Without the axial ligands, both Fe@Gr and Fe@COF show similar activity to that of the Au (211) surface. With the different axial ligands, the SACs show activity comparable to that of Cu (211) surfaces.

We used the potential dependent reactivity descriptor G_max(η) at an applied potential of −0.8 V vs. SHE to determine the rate-determining steps (RDS).^64–67 Using the reaction free energies of the elementary steps, G_max(η) allows us to characterize the reaction steps potentially contributing towards determining the reaction kinetics. Section V in the ESI† presents the calculation details for G_max(η) and the corresponding highest free energy span values for Fe@Gr and Fe@COF with and without the axial ligands at −0.8 vs. SHE and pH 6.8. We found that for most of the SACs, either *COOH or *CHO formation is the contributing step towards the RDS. Based on this, we chose two reaction steps (* + CO₂ → *CO and * + CO₂ → *CHO) as the activity descriptors. The black solid line shows the parity plot between these two reaction steps in Fig. 6.

Without the axial ligands, both Fe@Gr and Fe@COF show similar activity trends to those of the Au (211) surface. The low binding energy of the *CO intermediate will favor the formation of the CO product as observed in several recent studies.^{2,21,34–39,44–46} For Fe@Gr and Fe@COF with IMD and Py as the axial ligands, we observed a similar trend in activity to that of the Cu (211) surface. With PMe₃ as the axial ligand, the SACs show slightly low activity but are better than the Au(211) and Ag (211) surfaces.

While comparing the overall activity of SACs with axial ligands, we found that the sigma donor strength of the neutral axial ligands increases the catalyst activity and selectivity. The donor strength reduces from IMD to PMe₃, with Py being intermediate (IMD > Py > PMe₃). The CO binding strength at zero applied potential on the SACs shows a similar reducing trend from IMD to PMe₃ on attaching the axial ligand. Depending upon the σ donating activity of these axial ligands, the *CO intermediate achieves specific stability, thereby influencing both the activity and the selectivity of CO₂R products. However, with the applied potential, *CO is found to be slightly stabilized with Py as the axial ligand compared to IMD.

3 Conclusion

The porphyrin- and phthalocyanine-based SACs show good activity for CO₂R to CO production. However, the formation of reduction products beyond CO is more desirable for industrial-scale applications and value-added chemical synthesis. In this study, we analyzed the electronic properties and catalytic activity of porphyrin- and phthalocyanine-based SACs with Fe, Co, and Ni metal dopants for CO₂R reactions using density functional theory calculations. Using neutral ligands such as imidazole (IMD), pyridine (Py), and trimethyl phosphine (PMe₃) attached at the axial positions to the metal dopants, we present an axial ligation strategy to tune the product selectivity towards the formation of post-CO products. In addition to molecular macrocyclic ligands as the support materials, we explored the activity of metal-doped defective graphene surfaces and a covalent organic framework system composed of tetra-phenyl porphyrin (TPP) with acetylene linkers. Based on the orbital engineering method, orbital overlap principles and free energy calculations of the reaction intermediates, we characterized the determining factors for tuning the catalyst activity and product selectivity.

The binding free energy values of the axial ligands to the SACs indicate that these axial ligands form stable complexes. To characterize the catalytic activity and product selectivity, we performed binding energy calculations for the different reaction intermediates. Using the binding energies of *CO and *H intermediates, we classified the SACs with or without the axial ligands with reference to the transition metal (111) surfaces for different CO₂R products. The introduction of the axial ligands is found to stabilize the *CO intermediates on Fe-based SACs. On the other hand, Co- and Ni-based catalysts with and without the axial ligands are found to show great similarity to Ag (111) and Au (111) surfaces. The classification results show that Fe-based SACs with the axial ligands might be capable of yielding CO₂R products beyond CO.

We performed an orbital interaction analysis and bonding energy decomposition analysis (BEDA) to understand the improved binding affinity of CO intermediates on Fe-based macrocyclic frameworks with axial ligands in comparison with the Co- and Ni-based macrocyclic catalysts. The orbital interactions show that Fe-doped SACs satisfy the 18-electron count in the presence of the attached axial ligands. Deviation from the 18-electron count in both the Co and Ni SACs reduces the binding affinity of CO. The excess valence electrons on the Co- and Ni-based SACs populate the anti-bonding molecular orbitals, leading to an increase in the metal–CO bond length and a reduction in the binding affinity.

The CO₂R free energy pathways were determined to analyze the reaction mechanism. Using the PCET steps and the grand-canonical potential simulations, we calculated the binding energies of the different reaction intermediates. The differential ΔG values for the intermediates in the third (ΔG_CO↑ − ΔG_*CHO) and sixth PCET steps (ΔG_CH3OH − ΔG_CH4↑+*O) are found to mainly determine product selectivity. At an applied potential of −0.8 V vs. SHE and pH 6.8, for Fe@Gr and Fe@COF with the IMD and Py axial ligands, the formation of the CH₃OH product is found to be thermodynamically more preferable. However, with the PMe₃ axial ligand, CO production is found to be the preferred pathway. A unified activity volcano plot for methanol and methane formation has been developed based on the binding free energy values of the *CO and *CHO intermediates as the activity descriptors. Comparing the specific activity of Fe@Gr and Fe@COF with transition metal (211) surfaces, we found different activity trends depending upon the attached axial ligand. Without the axial ligands, the activity trend is similar to that of the Au (211) surface, while with IMD and Py axial ligands, both Fe@Gr and Fe@COF show activities similar to that of the Cu (211) surface. We found a similar preferential selectivity with the macrocyclic complexes as the support materials and with Py and IMD as the axial ligands.

We believe that our study will help in developing catalyst design principles for SACs for tuning product selectivity, particularly for the formation of the products beyond the two-step CO production. The SACs explored in this study could serve as precursors for the synthesis of heterogeneous catalysts. These electrocatalysts could scale up the formation of post-CO products (CH₃OH and CH₄) with high efficiency.

Data availability

Basic calculation details are available in the ESI.† Detailed data for current research findings and studies are available from the corresponding author upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

V. M. and N. K. acknowledge the Shiv Nadar Foundation and the Shiv Nadar Institution of Eminence for financial support and computing infrastructure.

References

1. Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, eaad4998.
2. B. Zhang and L. Sun, Chem. Soc. Rev., 2019, 48, 2216–2264.
3. M. Zhang, K. Zhang, X. Ai, X. Liang, Q. Zhang, H. Chen and X. Zou, Chin. J. Catal., 2022, 43, 2987–3018.
4. K. C. Poon, W. Y. Wan, H. Su and H. Sato, RSC Adv., 2022, 12, 22703–22721.
5. Z. Sun, T. Ma, H. Tao, Q. Fan and B. Han, Chem, 2017, 3, 560–587.
6. S. Nitopi, E. Bertheussen, S. B. Scott, X. Liu, A. K. Engstfeld, S. Horch, B. Seger, I. E. Stephens, K. Chan and C. Hahn, et al. , Chem. Rev., 2019, 119, 7610–7672.
7. Y. Pei, H. Zhong and F. Jin, Energy Environ. Sci., 2021, 9, 1012–1032.
8. A. A. Peterson, F. Abild-Pedersen, F. Studt, J. Rossmeisl and J. K. Nørskov, Energy Environ. Sci., 2010, 3, 1311–1315.
9. Z. Weng, J. Jiang, Y. Wu, Z. Wu, X. Guo, K. L. Materna, W. Liu, V. S. Batista, G. W. Brudvig and H. Wang, J. Am. Chem. Soc., 2016, 138, 8076–8079.
10. X. Liu, J. Xiao, H. Peng, X. Hong, K. Chan and J. K. Nørskov, Nat. Commun., 2017, 8, 15438.
11. S. Nitopi, E. Bertheussen, S. B. Scott, X. Liu, A. K. Engstfeld, S. Horch, B. Seger, I. E. L. Stephens, K. Chan, C. Hahn, J. K. Nørskov, T. F. Jaramillo and I. Chorkendorff, Chem. Rev., 2019, 119, 7610–7672.
12. F. Chang, M. Xiao, R. Miao, Y. Liu, M. Ren, Z. Jia, D. Han, Y. Yuan, Z. Bai and L. Yang, Electrochem. Energy Rev., 2022, 5(4), 1–35.
13. A. Xu, S.-F. Hung, A. Cao, Z. Wang, N. Karmodak, J. E. Huang, Y. Yan, A. Sedighian Rasouli, A. Ozden and F.-Y. Wu, et al. , Nat. Catal., 2022, 5, 1081–1088.
14. X.-Q. Wang, Q. Chen, Y.-J. Zhou, H.-M. Li, J.-W. Fu and M. Liu, Adv. Energy Mater., 2022, 1, 100023.
15. J. Gong, J. Li, C. Liu, F. Wei, J. Yin, W. Li, L. Xiao, G. Wang, J. Lu and L. Zhuang, Chin. J. Catal., 2022, 43, 3101–3106.
16. S. Liu, B. Zhang, L. Zhang and J. Sun, J. Energy Chem., 2022, 71, 63–82.
17. J. F. D. Brito, K. Irikura, C. M. Terzi, S. Nakagaki and M. V. B. Zanoni, J. CO2 Util., 2020, 41, 101261.
18. F. Stephanopoulos and N. Commu, Nat. Commun., 2021, 12, 5884.
19. N. Cheng, L. Zhang, K. Doyle-Davis and X. Sun, Electrochem. Energy Rev., 2019, 2, 539–573.
20. W. Ren and C. Zhao, Nat. Sci., 2020, 7, 7–9.
21. N. Karmodak, S. Vijay, G. Kastlunger and K. Chan, ACS Catal., 2022, 12, 4818–4824.
22. J. Wu, H. Shi, K. Li and X. Guo, Curr. Opin. Chem. Eng., 2023, 40, 100923.
23. C. Li, W. Ju, S. Vijay, J. Timoshenko, K. Mou, D. A. Cullen, J. Yang, X. Wang, P. Pachfule and S. Brückner, et al. , Angew. Chem., 2022, 134, e202114707.
24. S. Vijay, W. Ju, S. Brückner, S.-C. Tsang, P. Strasser and K. Chan, Nat. Catal., 2021, 4, 1024–1031.
25. N. Karmodak and O. Andreussi, J. Phys. Chem. C, 2021, 125, 10397–10405.
26. L. Zhang, N. Jin, Y. Yang, X.-Y. Miao, H. Wang, J. Luo and L. Han, Nano-Micro Lett., 2023, 15, 228.
27. Z. Kang, X. Wang, D. Wang, B. Bai, Y. Zhao, X. Xiang, B. Zhang and H. Shang, Nanoscale, 2023, 15, 9605–9634.
28. Y. Yan, H. Cheng, Z. Qu, R. Yu, F. Liu, Q. Ma, S. Zhao, H. Hu, Y. Cheng and C. Yang, et al. , J. Mater. Chem., 2021, 9, 19489–19507.
29. N. Karmodak and J. K. Nørskov, Angew. Chem., Int. Ed., 2023, 62, e202311113.
30. B. Zhang and L. Sun, Chem. Soc. Rev., 2019, 48, 2216–2264.
31. J.-H. Liu, L.-M. Yang and E. Ganz, ACS Sustainable Chem. Eng., 2018, 6, 15494–15502.
32. D.-H. Nam, P. De Luna, A. Rosas-Hernández, A. Thevenon, F. Li, T. Agapie, J. C. Peters, O. Shekhah, M. Eddaoudi and E. H. Sargent, Nat. Mater., 2020, 19, 266–276.
33. H. S. Whang, J. Lim, M. S. Choi, J. Lee and H. Lee, BMC Chem., 2019, 1, 1–19.
34. P. Gotico, Z. Halime and A. Aukauloo, Dalton Trans., 2020, 49, 2381–2396.
35. E. Boutin and M. Robert, Trends Chem., 2021, 3, 359–372.
36. R. Zhang and J. J. Warren, ChemSusChem, 2021, 14, 293–302.
37. Z. Liang, H.-Y. Wang, H. Zheng, W. Zhang and R. Cao, Chem. Soc. Rev., 2021, 50, 2540–2581.
38. S. Amanullah, P. Saha and A. Dey, ChemComm, 2022, 58, 5808–5828.
39. E. Nikoloudakis, I. López-Duarte, G. Charalambidis, K. Ladomenou, M. Ince and A. G. Coutsolelos, Chem. Soc. Rev., 2022, 51, 6965–7045.
40. S. Kumar, J. Koh, R. Srivastava and D. K. Gupta, Nano-catalysts for Energy Applications, CRC Press, 2021, pp. 45–65.
41. X. Huang and J. T. Groves, Chem. Rev., 2018, 118, 2491–2553.
42. H. Suzuki, K. Inabe, Y. Shirakawa, N. Umezawa, N. Kato and T. Higuchi, Inorg. Chem., 2017, 56, 4245–4248.
43. P. C. Moody and E. L. Raven, Acc. Chem. Res., 2018, 51, 427–435.
44. L.-L. Shi, M. Li, B. You and R.-Z. Liao, Inorg. Chem., 2022, 61, 16549–16564.
45. H. Kang, A. Staples-West, A. Washington, C. Turchiano, A. Cooksy, J. Huang and J. Gu, ChemCatChem, 2023, 15, e202300576.
46. K. E. Rivera Cruz, Y. Liu, T. L. Soucy, P. M. Zimmerman and C. C. L. McCrory, ACS Catal., 2021, 11, 13203–13216.
47. M. M. Melander, M. J. Kuisma, T. E. K. Christensen and K. Honkala, J. Chem. Phys., 2019, 150, 1–23.
48. J. D. Goodpaster, A. T. Bell and M. Head-Gordon, J. Phys. Chem. Lett., 2016, 7, 1471–1477.
49. N. G. Hörmann, O. Andreussi and N. Marzari, J. Chem. Phys., 2019, 150, 1–19.
50. J. A. Gauthier, C. F. Dickens, H. H. Heenen, S. Vijay, S. Ringe and K. Chan, J. Chem. Theory Comput., 2019, 15, 6895–6906.
51. S. C. Sarma, J. Barrio, A. Bagger, A. Pedersen, M. Gong, H. Luo, M. Wang, S. Favero, C.-X. Zhao and Q. Zhang, et al., Adv. Funct. Mater., 2023, 33, 2302468.
52. A. Bagger, W. Ju, A. S. Varela, P. Strasser and J. Rossmeisl, ChemPhysChem, 2017, 18, 3266–3273.
53. S. Gu, A. N. Marianov, Y. Zhu and Y. Jiang, J. Energy Chem., 2021, 55, 219–227.
54. X. Liu, J. Xiao, H. Peng, X. Hong, K. Chan and J. K. Nørskov, Nat. Commun., 2017, 8, 15438.
55. K. S. Exner, Angew. Chem., 2020, 132, 10320–10324.
56. H. Li, S. Kelly, D. Guevarra, Z. Wang, Y. Wang, J. A. Haber, M. Anand, G. K. K. Gunasooriya, C. S. Abraham and S. Vijay, et al. , Nat. Catal., 2021, 4, 463–468.
57. H. Wan, A. W. Jensen, M. Escudero-Escribano and J. Rossmeisl, ACS Catal., 2020, 10, 5979–5989.
58. H. A. Hansen, V. Viswanathan and J. K. Nørskov, J. Phys. Chem. C, 2014, 118, 6706–6718.
59. A. J. Medford, C. Shi, M. J. Hoffmann, A. C. Lausche, S. R. Fitzgibbon, T. Bligaard and J. K. Nørskov, Catal. Lett., 2015, 145, 794–807.
60. V. M., S. Singh, F. Bononi, O. Andreussi and N. Karmodak, J. Chem. Phys., 2023, 159, 111001.
61. R. Khakpour, D. Lindberg, K. Laasonen and M. Busch, ChemCatChem, 2023, 15, e202201671.
62. R. Khakpour, K. Laasonen and M. Busch, Electrochim. Acta, 2023, 442, 141784.
63. R. Khakpour, K. Farshadfar, S.-T. Dong, B. Lassalle-Kaiser, K. Laasonen and M. Busch, J. Phys. Chem. C, 2024, 128, 5867–5877.
64. K. S. Exner and H. Over, Acc. Chem. Res., 2017, 50, 1240–1247.
65. K. S. Exner, ChemCatChem, 2019, 11, 3234–3241.
66. K. S. Exner, ACS Catal., 2020, 10, 12607–12617.
67. S. Razzaq and K. S. Exner, ACS Catal., 2023, 13, 1740–1758.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr02650k

---