Theoretical investigation of tautomerism of 2- and 4-pyridones: origin, substituent and solvent effects

Abstract

Computational investigation at the BHandHLYP/6-311+G(d,p) level of theory of the gas-phase tautomerism of 2- and 4-pyridones confirmed the slight prevalence of lactim in the case of the former, but its dominance in the case of the latter, as shown previously. Examination of aromaticity by using HOMA, EDDB, NBOdel, NICS and AICD led to the conclusion that tautomerization of 4-pyridone results in greater aromaticity gain. It is also driven by the Pauli repulsion relief, which was revealed by the tautomerization energy decomposition analysis. By contrast, in the case of 2-pyridone, lactim is favoured by orbital and electrostatic interactions and disfavoured by the Pauli repulsion. Aromaticity gain in this case is smaller. The position of the tautomeric equilibrium can be modulated by substituent inductive effects (Cl and F), inductive and resonance effects (NH₂ and NO₂), hydrogen bonding (NO₂), and medium polarity, the increase of which increases lactam population.

---

Introduction

Tautomerism is the dynamic equilibrium between two structures that differ in the position of one atom or a functional group and distribution of electron density.¹ The position of such equilibrium in a particular compound depends on its aggregation state, solvent, concentration and temperature, and can strongly affect its physical, chemical and biological properties. The common type of tautomerism involves migration of the hydrogen atom and is known as prototropic tautomerism covering, for example, keto–enol, amine–imine, amide–imide and lactam–lactim equilibria.

The stable amide function is extremely important for biological processes as it constitutes the backbone of proteins. By using a simple model compound, Kashid et al. have demonstrated that amide tautomerization can be triggered by divalent cations, which can affect protein biological functions.² The rather elusive higher energy imide form (Fig. 1), postulated to be involved in the formation of stable molecules in prebiotic Earth, was synthesized and spectroscopically characterized, recently.³ The high-energy imide form may also be involved in protein reactions.⁴

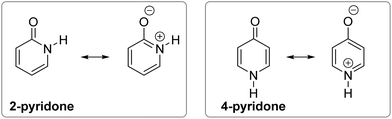
Fig. 1 Position of tautomeric equilibrium in simple amides, 2-pyridone and 4-pyridone in the gas phase.

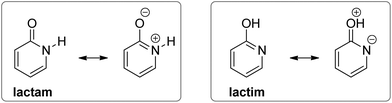
However, when an amide function is part of a cyclic conjugated system, lactam can equilibrate with lactim, or lactim can be the exclusive tautomeric form. For example, 2-pyridone is just slightly less stable than 2-hydroxypyridine in the gas phase,^5,6 whereas 4-hydroxypyridine is the only detectable form^5,7 (Fig. 1). These equilibria shift towards the lactam with increase in solvent polarity^5,8 and in the solid state,⁹ which can be ascribed to better solvation of the lactam having a larger dipole moment and to molecular association via hydrogen bonding. All these interactions are absent in the gas phase, leaving intramolecular effects to determine the tautomeric equilibria, which, in the case of pyridones, could be considered as aromaticity driven.^1,10 But, why is 4-hydroxy pyridine the only tautomer of 4-pyridone, whereas the isomeric 2-pyridone exists as a mixture of lactam and lactim with a ratio of 1 : 2.8?¹¹

The following explanations have been given. The aromatic resonance structure of 4-pyridone involves greater charge separation compared with 2-pyridone (Fig. 2) so that the lactam form is less favoured in this compound.¹² However, both compounds were predicted to have a similar degree of aromaticity on the basis of aromatic stabilization energies¹³ and I₆ index,¹⁴ though the HOMA index characterizes 4-pyridone as less aromatic.¹⁰ According to the dipole–dipole interaction model, the interaction energy is much more favourable in 2-pyridone in which the C=O and N–H bond dipoles are almost anti-parallel, whereas in 4-pyridone they are exactly parallel.^7b In a later work, the relationship between tautomerism and electron delocalization in hydroxyazines was found to be more complex than in aminoazines and two factors were suggested to influence tautomeric equilibrium of pyridones: aromaticity and stability of oxo groups.¹⁵

Fig. 2 Aromatic resonance structures of 2-pyridone and 4-pyridone.

The tautomeric equilibrium of pyridones can be altered by ring substitution. Experimental and theoretical results showed that chlorine atom in the 6-position of the 2-pyridone ring pushes the equilibrium towards the lactim form, both in the gas phase and in solution.¹⁶ Shifting the chlorine atom to the 5-, 4- and 3-positions decreases the lactim/lactam ratio in the order 6 > 5 > 4 > 3.¹⁷ A similar trend was found computationally and experimentally for the amino-substituent, though in this case, only 5- and 6-substituted 2-pyridones showed tautomerization to the lactim in solution.^16c,18 Experimental and theoretical analysis of tautomerism of 3- and 5-nitro-2-pyridone showed the dominance of the lactam form in the solid state and in solution.^16d,19 In the case of 4-pyridone in solution, an electronegative substituent, such as chlorine, and electron-withdrawing groups, such as aldehyde and ester, favour the lactim tautomer when placed at position 2.^16a,20 However, little effect on the tautomeric equilibrium of 4-pyridone was observed for substituents at position 3 (NH₂, Cl and NO₂).^16a,19d,21

The substituent inductive effect was recognized as the most important factor to determine the tautomeric equilibria of 2- and 4-pyridones, affecting the acidity of the N–H and O–H bonds,^16a,d,17a or stabilizing either the lactam (3-substitution) or the lactim (5- and 6-substitution) charge-separated resonance forms (Fig. 3).^17a,c Additionally, the mesomeric effect of the chlorine atom was invoked to explain the difference in population of tautomeric forms for the 5-chloro/6-chloro and 3-chloro/4-chloro derivatives of 2-pyridone: within each pair, the 5- and 3-position is para- and ortho-related, respectively, to the OH group of the lactim so that chlorine substitution at that position stabilizes the keto group (lactam form).^17b

Fig. 3 Resonance structures of lactam and lactim forms of 2-pyridone.

Prototropic tautomerism frequently occurs in chemical and biological systems, influencing their properties and functions. For example, a transient formation of the minor tautomer of nucleic acid bases during DNA replication leads to spontaneous mutations.²² The mode of action of antiviral nucleoside analogues is based on their ability to adopt a greater population of minor tautomeric forms, thus inducing mutations in the viral genome.^22,23 Because of its simple structure and similarity to nucleic acid bases (thymine, cytosine and uracil) the 2-pyridone/2-hydroxypyridine pair is considered as a prototype system to study lactam/lactim tautomerization.²⁴ 2-Pyridone is also a constituent of many biologically active natural products and pharmaceuticals,²⁵ DNA base analogue,²⁶ an important building block in synthesis²⁷ and shows the potential to direct molecular association by formation of hydrogen bonds.²⁸ The 4-pyridone structure can also be found in biologically active compounds,²⁹ in synthetic building blocks³⁰ and self-assembling building blocks, forming hydrogen bonds with extraordinary stability.³¹

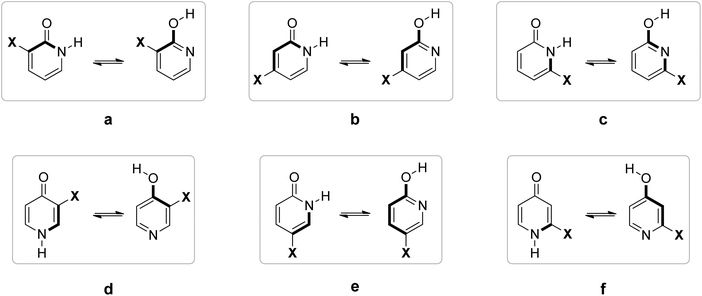
Herein, we present results of our computational work performed with the aim to get a deeper understanding of pyridone tautomerism, and substituent and solvent effects on it. As substituents, we have chosen the already studied chlorine atom,^16,17 the less studied amino^16c,d,18,21 and nitro^16d,19,21 groups, and unexplored fluorine atom which is an important bioisostere of hydrogen atom.³² The choice of substituents also includes the most important combination of inductive (I) and resonance (R) effects: −I and −R (NO₂), −I and +R with predominant induction (F and Cl) and −I and +R with predominant resonance effect (NH₂).

Choice of computational method

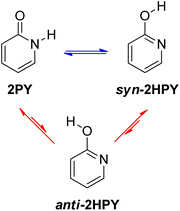
Examination of 2-pyridone (2PY) tautomerism represents a great challenge for theoretical chemists because of the small gas-phase energy difference between the lactam and lactim forms. Results are sensitive to method and basis set.^6d,24,33 At the beginning of our work, we optimized two tautomers of 2-pyridone by using one pure DFT functional and five hybrid DFT functionals, all in combination with the Pople's 6-311+G(d,p) basis set.³⁴ The following functionals were used: BLYP^35a,b (pure), B3LYP³⁵ (20% exact Hartree–Fock (HF) exchange), the long-range corrected CAM-B3LYP³⁶ (19% HF exchange at short range and 65% HF exchange at long range), the long-range corrected wB97XD³⁷ (22% HF exchange at short range and 100% HF exchange at long range) also having empirical dispersion correction, BHandHLYP³⁸ (50% HF exchange) and M06-2X³⁹ (54% HF exchange). The optimizations were followed by frequency calculations, done at the same level of theory, to show that the obtained stationary point on the potential energy surface (PES) was a minimum (no imaginary frequency(ies)) and to obtain Gibbs free energies, which are reported throughout the manuscript.

The lactim form, 2-hydroxypyridine (2HPY), can have two conformations: syn, in which the hydroxyl hydrogen atom is oriented toward the ring nitrogen atom (Fig. 4, syn-2HPY) and anti, with the hydroxyl hydrogen atom pointing away from the ring nitrogen atom (Fig. 4, anti-2HPY). Only the syn-conformation was detected experimentally^6c and is believed to be stabilized by intramolecular hydrogen bonding.⁴⁰ The CH tautomers have very high energy¹⁵ and are not considered here. Calculated relative Gibbs free energies for the 2HPY forms in Fig. 4 are listed in Table 1. As can be seen, only M06-2X and BHandHLYP correctly predicted the lower energy of the syn-lactim form of 2-pyridone. It appears that the percentage of the HF exchange is an important factor influencing computational prediction of tautomer energies of 2PY. In the previous comparison of density functional calculations with the Hartree–Fock ones the same effect was noticed.^24a Due to its high energy, correctly predicted by all functionals (ΔG_anti–syn = 5.1–5.5 kcal mol⁻¹), anti-2HPY is not considered in the discussion on gas-phase tautomerism.

Fig. 4 Tautomeric equilibria of 2-pyridone.

Table 1 Calculated relative Gibbs free energies (kcal mol⁻¹) of syn- and anti-2-hydroxypyridines by using different functionals and 6-311+G(d,p) basis set

Conformer	BLYP	B3LYP	CAM-B3LYP	wB97XD	BHandHLYP	M06-2X	Exp.
a Ref. 6a. b Ref. 6b. c Ref. 6d and 11.
syn-2HP	2.3	0.9	0.3	0.8	−0.6	−1.4	−0.8^a, −0.58^b, −0.69^c
anti-2HP	7.4	6.1	5.8	6.0	4.9	3.9	Not detected

---

The increase of the basis set to 6-311++G(d,p) in combination with the M06-2X functional had no effect on the obtained relative energies.

The best agreement with experimental values of −0.8 kcal mol⁻¹,^6a −0.58 ± 0.08 kcal mol⁻¹ (ref. 6b) and −0.69 ± 0.12 kcal mol⁻¹ (ref. 6d and 11) was achieved with the BHandHLYP. The same functional also provided molecular geometries in excellent agreement with experimental ones, and was therefore chosen for further calculations (experimental and calculated bond lengths are collected in Table S1† and correlation between calculated and experimental data is shown in Fig. S1 in the ESI†).

Computational details

On the basis of the results of the previous section, all calculations were done at the BHandHLYP/6-311+G(d,p) level of theory. Gaussian 09 ⁴¹ was used for geometry optimizations and frequency calculations. All structures were characterized as minima on the PES. Solvent effects were included as the integral equation formalism polarizable continuum model (IEFPCM)⁴² with the following solvents: tetrahydrofuran (THF, ε = 7.4257), dimethyl sulfoxide (DMSO, ε = 46.826) and water (ε = 78.3553).

Aromaticity was studied by employing the harmonic oscillator model of aromaticity (HOMA),⁴³ electron density of delocalized bonds (EDDB),⁴⁴ nucleus-independent chemical shift (NICS),⁴⁵ anisotropy of the induced current density (AICD)⁴⁶ and natural bond orbitals deletion (NBOdel) analysis.⁴⁷ The HOMA⁴³ measures deviations from optimal bond lengths of an aromatic molecule. It equals 1 when system is aromatic and is close to zero when system is nonaromatic. The HOMA values were obtained by using the Multiwfn program⁴⁸ and 1.388/1.334 Å as an optimal CC/CN bond length and value of 257.7/93.52 for the empirical constant α.^43c The EDDB⁴⁴ quantifies the number of delocalized electrons in the whole molecule, within a cycle (EDDB_P) and along a particular path in a molecule. To study aromaticity we used the EDDB_P within the RunEDDB software⁴⁹ and NBO 6.0 ⁵⁰ linked to the Gaussian 09 software. The NICS⁴⁵ is the negative of magnetic shielding of a point near a molecule. For aromaticity studies, points in the ring center or 1 Å above/below it are often used and values are denoted as NICS(0) and NICS(1), respectively. Negative NICS values denote aromaticity, those close to zero nonaromaticity and positive ones antiaromaticity. The NICS_zz-scan⁵¹ is more reliable than a single NICS value. In this method, NICS values are calculated for points which are located along a line going perpendicularly from the ring center usually up to 4 Å away. In this way, possible wrong conclusions due to the, sometimes observed, height dependence of NICS values are eliminated.⁵² The scans were calculated by using the Aroma 1.0 program package⁵³ and points were separated by 0.1 Å from each other. The values were calculated with the gauge-independent atomic orbital (GIAO) method⁵⁴ and contained only the π-electron contributions to the out-of-plane component of magnetic shielding tensor, which is relevant for aromaticity studies.⁵⁵ The π-electron contribution to shielding values was obtained by employing the σ-only method.⁵⁶ The NICS(1.5), which is also given in the manuscript, was extracted from the NICS-scan data. The AICD⁴⁶ gives information about electron delocalization in molecules. Current densities were calculated with the continuous set of gauge transformations (CSGT) method⁵⁷ and were visualized with POV-Ray, v.3.7.⁵⁸ The NBOdel⁴⁷ calculates delocalization energy as a difference between the total molecular energy and energy when certain delocalizations are disabled. For aromaticity study of pyridones and hydroxypyridines, the π-electron delocalization was disabled by deletion of all π*-orbitals.⁵⁹

The origin of bonding interactions was studied by performing the localized molecular orbitals energy decomposition analysis (LMO-EDA)⁶⁰ implemented in the Gamess program.⁶¹ Details of the analysis are described in the Results and discussion section, Tautomerism of 2-pyridone and 4-pyridone subsection.

Results and discussion

Tautomerism of 2-pyridone and 4-pyridone

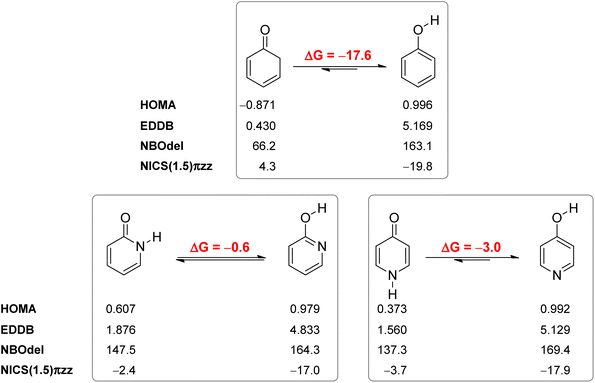
Our calculated Gibbs free energy for tautomeric equilibrium of 4-pyridone (4PY) in gas phase amounts −3.0 kcal mol⁻¹ and is in good agreement with the experimental result that this compound is at least 95% in the lactim form.^7a Calculated bond lengths of 4PY are also in nice agreement with experimental ones, which are obtained by X-ray analysis so that some deviations are expected (experimental and calculated bond lengths are collected in Table S2† and correlation between calculated and experimental data is shown in Fig. S2 in the ESI†). In the case of 4-hydroxypyridine tautomer, there is only one conformational form for the OH group rotation due to the ring symmetry. In addition, the calculated Gibbs free energy for the tautomeric equilibrium of cyclohexa-2,4-dienone, ΔG = −17.6 kcal mol⁻¹, is also in good agreement with the previously determined, ΔG = −15.0 kcal mol⁻¹.¹

Whereas the tautomeric equilibrium of cyclohexa-2,4-dienone is fully shifted toward the aromatic phenol, in the case of 4PY ΔG is smaller (in absolute value) and much smaller in the case of 2PY (Fig. 5). The reason for this could be the ring conjugation already present in 2PY¹ and 4PY, but disrupted in cyclohexa-2,4-dienone by the methylene group. To quantify conjugation, we calculated aromaticity indices belonging to all four recommended types: structural (HOMA), electronic (EDDB_P), magnetic (NICS_πzz) and energetic (NBOdel), as described in the Computational details section. Their values are given in Fig. 5. Additionally, we present NICS_πzz-scan results (Fig. 6) and AICD plots (Fig. 7; a higher resolution figure is given as Fig. S3 in the ESI†) for the two pyridones. The HOMA, EDDB_P and NBOdel all agree that 2PY is more aromatic than 4PY, whereas the NICS(1.5) tells the opposite. In fact, the NICS_πzz-scans predict greater aromaticity of 4PY, even though they show large height dependence up to 1.1 Å (which is the reason why NICS(1.5) data are given in Fig. 5). No such variations are observed for the aromatic lactim forms. We note that the calculated NICS reflects the magnitude of magnetic shielding coming from the π-electron density, which is not necessarily cyclically delocalized, as defined by aromaticity. The AICD plots indicate moderate diatropicity of both compounds which should be the case since they contain 6π electrons in the ring, taking into account polarization of carbonyl group. However, these diatropic ring currents seem to be somewhat interrupted at the carbonyl carbon atom of 4PY (Fig. 7 and S3†), which could be a consequence of mainly one-directional π-electron delocalization from nitrogen atom to carbonyl group in this compound, but more cyclic delocalization in 2PY. Therefore, on the basis of the presented data, we conclude that 2PY is more aromatic than 4PY, although the degree of their aromaticity is small (HOMA and NBOdel). According to NICS and EDDB they can even be classified as non-aromatic.

Fig. 5 Calculated, BHandHLYP/6-311+G(d,p), gas-phase Gibbs free energies (kcal mol⁻¹) for tautomeric equilibria of cyclohexa-2,4-dienone, 2-pyridone and 4-pyridone, and calculated aromaticity descriptors, HOMA, EDDB_P (e), NBOdel (kcal mol⁻¹) and NICS(1.5)_πzz (ppm).

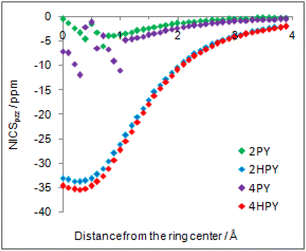Fig. 6 NICS_πzz-scans of 2-pyridone (2PY), syn-2-hydroxypyridine (2HPY), 4-pyridone (4PY) and 4-hydroxypyridine (4HPY) in the direction from the ring center up to 4 Å away.

Fig. 7 AICD plots of 2-pyridone (2PY), syn-2-hydroxypyridine (2HPY), 4-pyridone (4PY) and 4-hydroxypyridine (4HPY) at an isovalue of 0.05 a.u. Clockwise circulation is diatropic and counterclockwise circulation is paratropic.

All calculated indices and NICS_πzz-scans agree that 4HPY is slightly more aromatic than 2HPY. Therefore, there is larger aromaticity gain upon tautomerization of 4PY, which could be the reason for its existence almost solely as lactim in the gas phase. An even greater gain in aromaticity and more negative Gibbs free energy can be seen for cyclohexa-2,4-dienone. The difference in aromaticity between 2PY and 2HPY is smaller, which may be the reason for the presence of both forms in tautomeric equilibrium, slightly shifted towards the more aromatic 2HPY. Previous experimental and theoretical work has shown that benzannelated 2-pyridone exists exclusively as lactam or lactim depending on the fusion position^6d (Fig. 8). It is apparent that aromaticity gain upon tautomerization to lactim is large in the case of 3-isoquinolinone, but it should be smaller in the case 1-isoquinolinone and 2-quinolinone compared with 2-pyridone. The latter effect was explained by an extended π-electron delocalization over the whole molecule when benzene is bound to 2-pyridone, which stabilizes the lactam tautomer.^6d

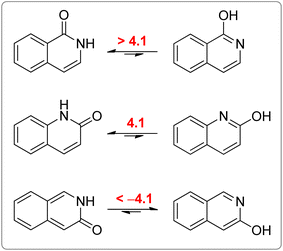Fig. 8 Gibbs free energies (kcal mol⁻¹) for lactam–lactim tautomeric equilibria of 1-isoquinolinone, 2-quinolinone and 3-isoquinolinone, taken from ref. 6d.

Although aromaticity certainly plays a role in tautomeric equilibria, pyridones are only weakly aromatic or non-aromatic, as already mentioned. Therefore, we also investigated whether other effects also contribute to the observed population of tautomers of the studied compounds.

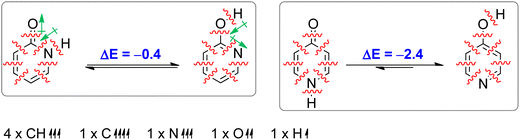
Aromaticity is a stabilizing effect coming from cyclic π-electron delocalization. In order to identify other effects we performed an isomerization (tautomerization) energy decomposition analysis (IEDA).⁶² In this analysis, we decomposed the bonding energy (ΔE_bond) of CC, CN, NH and C=O bonds of lactam forms and CC, CN, CO and OH bonds of lactim forms into deformation energy (ΔE_def) and interaction energy (ΔE_int) by decomposing each molecule into eight atoms/fragments taken in such an electronic state that each atom/fragment can interact with its neighbours: four CH units in quartet state, one C atom in quintet state, one N atom in quartet state, one O atom in triplet state and one H atom in doublet state (Table 2). The ΔE_def is the energy needed to deform each fragment (only CH bonds in this case) from its equilibrium geometry to the geometry it has in a molecule. As can be seen, this energy is small and does not contribute to tautomerization energy. ΔE_int was further decomposed into electrostatic interaction energy (ΔE_elstat), Pauli repulsion energy (ΔE_Pauli, steric hindrance), orbital interaction energy (ΔE_oi) and dispersion energy (ΔE_disp). The change in ΔE_disp upon tautomerization is very small (−0.4 kcal mol⁻¹ and −0.2 kcal mol⁻¹ in the case of 2PY and 4PY, respectively) and does not much affect tautomeric equilibria.

Table 2 Tautomerization energy decomposition analysis of 2- and 4-pyridones. Values are in kcal mol^−1 a

	2PY	2HPY	2PY → 2HPY	4PY	4HPY	4PY → 4HPY
a ΔEelstat = electrostatic energy, ΔEPauli = Pauli repulsion energy, ΔEoi = orbital interaction energy, ΔEdisp = dispersion energy, ΔEint = interaction energy (the sum of the previous four energies), ΔEdef = deformation energy, ΔEbond = bonding energy, ΔEtaut = tautomerization energy. Values in bold are contributions to tautomerization energy.
ΔEelstat	−1841.6	−1888.8	−47.2	−1846.8	−1840.1	6.7
ΔEPauli	2818.2	2920.1	101.9	2826.1	2784.1	−42.1
ΔEoi	−1786.4	−1841.2	−54.8	−1779.8	−1746.6	33.2
ΔEdisp	−332.2	−332.6	−0.4	−331.9	−332.1	−0.2
ΔEint	−1142.1	−1142.5	−0.4	−1132.4	−1134.8	−2.4
ΔEdef	0.2	0.2	0.0	0.2	0.2	0.0
ΔEbond/ΔEtaut	−1141.9	−1142.3	−0.4	−1132.2	−1134.6	−2.4

---

2HPY is favoured by ΔE_oi and ΔE_elstat, and almost equally disfavoured by ΔE_Pauli, which results in small negative tautomerization energy (ΔE_taut), curiously determined by the value of ΔE_disp. The larger orbital interactions can be ascribed to the strengthening of ring bonds due to the increased aromaticity and formation of a slightly stronger O–H bond vs. N–H bond in lactam (ΔE_dissociation = 100.3 kcal mol⁻¹ and 99.8 kcal mol⁻¹, respectively, calculated at the BHandHLYP/6-311+G(d,p) level). The more favourable electrostatic energy of lactim can partly be explained by the smaller distance between the anti-oriented H → O and C → N bond dipoles vs. C → O and H → N bond dipoles in lactam (figure in Table 2): 1.339 Å (the C O distance in 2HPY) vs. 1.390 (the C N distance in 2PY) and 2.248 (the H N distance in 2HPY) vs. 2.421 (the H O distance in 2PY). As the most important cause for increased Pauli repulsion in lactim form we single out the repulsion between the sp²-hybridized nitrogen lone pair and the C–O bond vs. p-type lone pair and C=O bond in lactam.

The last two mentioned interactions are absent in 4HPY ⁶³ so that tautomerization of 4PY results in less favourable ΔE_elstat and decreased Pauli repulsion (Table 2). Curiously, decrease in the Pauli repulsion is the only term responsible for 4PY existing in the lactim form, according to IEDA. Even though aromaticity is significantly increased upon 4PY tautomerization, all orbital interactions become weaker. This contrasts with the result for 2PY and our comprehension of aromaticity. To explain this observation we decomposed ring bonding energy of all four tautomers. The results are shown in Table S3 in the ESI† and point to the conclusion that aromaticity increase does not always increase orbital interactions.⁶⁴ We explain it in the following way. In 2PY, there is already cyclic delocalization of π-electrons (Fig. 9) which is increased upon tautomerization, thus strengthening orbital interactions of all ring bonds. In 4PY, however, π-electron delocalization is one-directional, from nitrogen atom to carbonyl group via the two strong C=C double bonds. The change in the topology of π-electron delocalization to the cyclic one weakens the two double bonds by formation of a delocalized system in which all six bonds possess partial double-bond character. The result is the weakening of ring bonds in total. To check this, we performed EDA of the two double bonds of 2PY/2HPY and 4PY/4HPY as shown in Table S4 in the ESI.† As we assumed, the results show increase in orbital interactions in the case of 2PY → 2HPY, but significant decrease in the case of 4PY → 4HPY.

Fig. 9 Cyclic and one-directional π-electron delocalization in 2-pyridone (2PY) and 4-pyridone (4PY).

Hence, tautomerization of 4PY is driven by an increase in aromaticity and a relief in Pauli repulsion. We attribute this relief to the change of the nitrogen lone pair from the p-type, interacting with the π-electrons of the neighbouring double bonds, to the sp²-type which lacks this kind of interaction and also the interaction with the C–O bond. The same change in the case of 2PY, as a consequence of tautomerization, results in increased Pauli repulsion due to the adjacent C–O bond, but orbital interactions and electrostatic attraction are strengthened. Since both kinds of stabilizing interaction are also present in the lactam form (cyclic delocalization and attraction between the C → O and H → N bond dipoles), but are smaller in magnitude, the lactam form is more populated in tautomeric equilibrium of 2PY compared with that of 4PY. For the latter, the two strong C=C double bonds exert two opposite effects: they stabilize the lactam form by orbital interactions, but, more than this, destabilize it by interacting with the same spin electrons of the nitrogen lone pair, shifting the equilibrium towards the lactim.

Substituent effect on tautomeric equilibrium of 2-pyridone and 4-pyridone

As already discussed, 2HPY can have two conformations with respect to the OH group rotation. For all studied derivatives, the syn-form is energetically preferred, except for 3-nitro-2-hydroxypyridine in which intramolecular hydrogen bond stabilizes the anti-form and makes it highly preferred in tautomeric equilibrium (see Fig. 10 for structures and Table S5† for relative energies). This kind of isomerism also appears in substituted 4HPY, where hydroxy hydrogen atom is at the same side as the substituent in syn-conformation and at the opposite side in anti-conformation (Fig. 10). In the case of 2-substituted 4HPY the energy difference between these two forms is small (less than 0.4 kcal mol⁻¹), but in the case of 3-substituted 4HPY the syn-form is more preferred due to the H → O and C → X (X = substituent) bond dipoles attraction and intramolecular hydrogen bond in the case of NO₂ and NH₂ groups (Fig. 10 and Table S5†). This stabilization is especially pronounced for F, Cl and NO₂, for which lactim is much more preferred than for the parent compound. In the case of NH₂, the equilibrium is shifted to lactim, but less than for 4PY.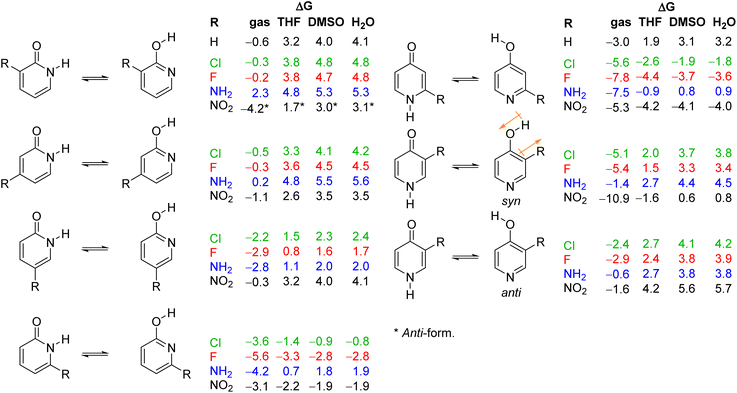

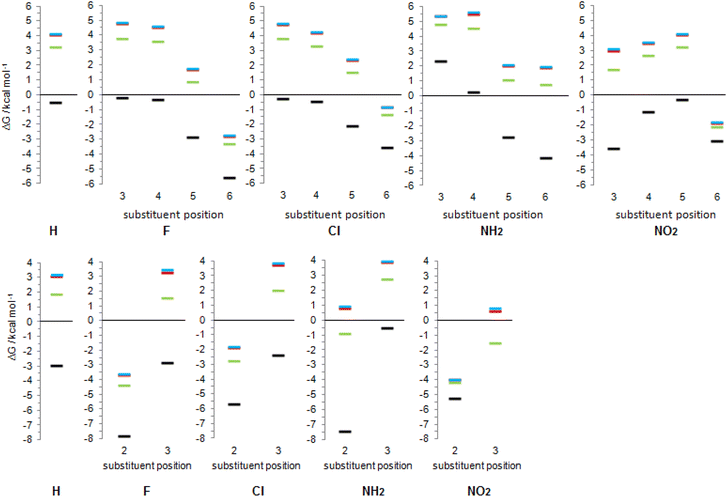
Fig. 10 Gibbs free energies for tautomeric equilibria of (substituted) 2-pyridone and (substituted) 4-pyridone in gas phase and in solvents, calculated at the BHandHLYP/6-311+G(d,p) level of theory.

In the following discussion, with the aim of understanding substituent effects on tautomeric equilibria, we use the less stable anti-forms of 3-substituted 4HPY and syn-isomer of 3-nitro-2-hydroxypyridine and compare them with other derivatives which do not possess such OH/substituent stabilizing interaction.

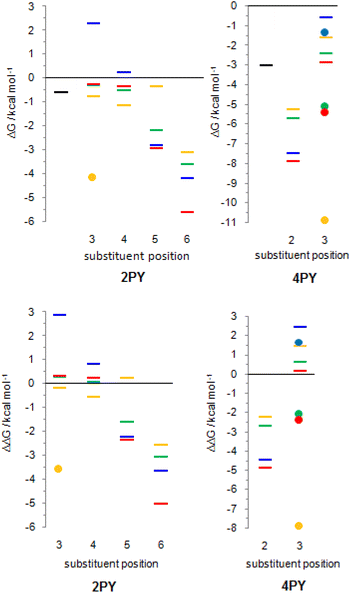
The employed level of theory provided tautomerization energies of chloro-substituted 2PY in correct order as observed previously¹⁷ (Fig. 10 and 11, upper part, and Table S5†), and the obtained values nicely agree with experimental values,^17c calc./exp. (kcal mol⁻¹): 3Cl-2PY −0.3/−0.3, 4Cl-2PY −0.5/−0.5, 5Cl-2PY −2.2/−2.0 and 6Cl-2PY −3.6/−2.7. Therefore, the population of lactim decreases in the order 6 > 5 > 4 > 3. Additionally, calculated bond lengths of 6-chloro-2-hydroxypyridine (6Cl-2HPY) are in good agreement with those obtained by X-ray analysis^24a (Table S6 and Fig. S4†). Since experimental values correspond to solid state, some deviations are expected. Our calculations predicted the same order of tautomerization energies for amino-substituted 2PY, although in this case negative values were obtained only for 5- and 6-substitution (Fig. 10 and 11, upper part, and Table S5†). This also agrees with previous predictions.^16c,18 Calculated tautomerization energies for fluoro-substituted 2PY follow the same order (6 > 5 > 4 > 3) and all equilibria are predicted to be shifted towards the lactim form, which is also the case for all nitro-substituted 2PY. However, in the case of NO₂, the trend is somewhat different: the population of lactim increases when moving from position 3 to position 4 (not taking into account the hydrogen-bonded anti 3-nitro derivative) and then to position 6. 5-Nitro-2-pyridone is predicted to have the smallest lactim population among the nitro-derivatives. For all 4PY derivatives, the equilibrium is predicted to be shifted towards lactim, whose population decreases in the order 2 > 3, again not taking into account the hydrogen-bonded syn 3-nitro derivative (Fig. 10 and 11, upper part, and Table S5†).

Fig. 11 Upper part: relative Gibbs free energies of lactim forms of substituted 2-pyridone (2PY) and substituted 4-pyridone (4PY) in the gas phase; x-axis shows substituent position within the ring; black colour – no substituent, red colour – fluorine as a substituent; green colour – chlorine as a substituent; blue colour – amino group as a substituent; yellow colour – nitro group as a substituent. Lower part: tautomerization energy of 2-hydroxypyridine and 4-hydroxypyridine is set as reference value, ΔΔG = 0 kcal mol⁻¹. Circles represent anti/syn forms of 2HPY/4HPY with respect to the rotation of the OH group, which are characterized by the direct OH/substituent stabilizing interaction.

The effect of substituent on tautomeric equilibria is shown in the lower part of Fig. 11 where tautomerization energies of 2PY and 4PY are set as reference values (isomers that have direct OH/substituent stabilizing interaction are represented by the circles). The following general trends can be observed. (1) Substituent at position 2 of 4PY and positions 6 and 5 of 2PY shifts the equilibrium more towards the lactim form in the order F > NH₂ > Cl > NO₂, with the exception of 5-nitro-2-pyridone where the substituent shifts the equilibrium just slightly more towards the lactam. The effect is more pronounced for position 6 than position 5 in 2PY. (2) Substituent at positions 3 and 4 of 2PY increases the population of lactam tautomer in the order NH₂ > F > Cl. The effect is more pronounced for position 3 than position 4. The NO₂ increases population of lactim when placed at positions 3 and 4 of 2PY and the effect is greater for position 4. The effect is actually small for halogen atoms and NO₂ (in position 3). Similar behaviour can be seen for anti 3-substituted 4PY: the population of lactam is increased for all substituents and this effect is small for halogen atoms.

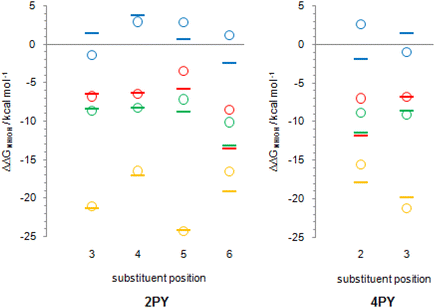
Tautomerization energy reflects the relative acidity of N–H and O–H bonds. Increase of N–H bond acidity favours the lactim form, whereas increase of O–H bond acidity favours the lactam form. To get information on substituent effect on the acidity of these bonds, we calculated Gibbs free energy for equilibrium involving proton transfer to one water molecule, in gas phase. Table S5† lists the calculated values and values relative to unsubstituted pyridones. Relative values (substituent effects) are also shown as Fig. 12 (only data for isomers that do not have the direct OH/substituent stabilizing interaction are shown). By combining these data with the known inductive and resonance effects of substituents we give some explanations for substituent effect on the tautomeric equilibrium of 2- and 4-pyridones.

Fig. 12 The N–H bond (dashes) and O–H bond (circles) acidity relative to unsubstituted pyridones: red colour – fluorine as a substituent; green colour – chlorine as a substituent; blue colour – amino group as a substituent; yellow colour – nitro group as a substituent.

First of all, while Cl, F and NO₂ increase the acidity of both bonds at any position in the ring, NH₂ group tends to decrease it. This can be explained by anion stabilization by −I effect of halogen atoms, −I and −R effects of NO₂, which increases acidity the most, but slight destabilization due to the combination of −I and +R effects of NH₂, where the latter dominates.

Fig. 12 shows that F and Cl when present at positions 3 and 4 of 2PY/2HPY and position 3 of 4PY/4HPY increase acidity of both N–H and O–H bonds by a very similar magnitude. Acidity increase for position 3 of both compounds is also similar and is slightly greater than for position 4 of 2PY/2HPY. The NO₂ at position 3 of 2PY/2HPY also increases the acidity of both N–H and O–H bonds by a very similar magnitude, but at position 4 it increases the acidity of the N–H bond slightly more than the acidity of the O–H bond. The NH₂ at position 3 of 2PY/2HPY and 4PY/4HPY increases the acidity of the O–H bond, but decreases the acidity of the N–H bond by almost the same amount in both pyridones. In position 4 of 2PY/2HPY it decreases the acidity of both bonds, slightly less for the O–H than the N–H bond. In the case of both positions, 3 in 2PY/2HPY and 4PY/4HPY, and 4 in 2PY/2HPY, the substituent is at equal distance from the nitrogen and oxygen atoms: two-bond distance for position 3 (Fig. 13a and d) and three-bond distance for position 4 (Fig. 13b). The results of Fig. 12 and Table S5† suggest that F and Cl act dominantly by their inductive effect, increasing almost equally the acidity of both N–H and O–H bonds. The net result is the negligible change of the position of tautomeric equilibria of 3-fluoro(chloro)-2-pyridone and 4-fluoro(chloro)-2-pyridone relative to 2PY. The same is true for NO₂ at position 3 of 2PY/2HPY, where it acts mainly by its inductive effect due to its tilting away from the plane of the ring by dipole repulsion from the adjacent C=O/C–O bond. However, at position 4, its resonance effect also comes into play so that it increases the acidity of the para-related N–H bond slightly more than the acidity of the meta-related O–H bond, shifting the equilibrium slightly toward lactim (Fig. 10 and 11). The resonance effect is also important for the NH₂ group. Lactam tautomers are less aromatic and, thus, more prone to substituent resonance effects. Therefore, the increase of electron density at the C2 and C6 atoms of 3-substituted pyridones reduces electron-withdrawing power of the nitrogen atom, which reduces the N–H bond acidity (Fig. 12 and Table S5†). As a result, the lactam population increases (Fig. 10 and 11). At position 4 of 2PY, the NH₂ group increases electron density at the para-related nitrogen atom, which reduces the acidity of the N–H bond somewhat more than the acidity of the O–H bond. As a result, the tautomeric equilibrium is slightly shifted towards lactam (Fig. 11).

Fig. 13 Distance between substituent and nitrogen/oxygen atom of lactam/lactim form. Bonds which separate substituent and N/O atoms are shown as thick bonds.

A substituent at position 5 of 2PY/2HPY is closer to the nitrogen atom (two-bond distance vs. four-bond distance to the oxygen atom, Fig. 13e), so that it experiences a stronger inductive effect that increases the acidity of the N–H bond more than that of the O–H bond. However, the relative acidity of the two bonds is similar for F and NH₂, and larger than that when Cl is substituent. This is not consistent with the strength of the substituent inductive effect, so that the nitrogen resonance effect should be invoked: the increase of π-electron density at the para-related carbon atom (C2) of 2HPY reduces oxygen electron-withdrawal from the O–H bond, which slightly reduces its acidity and increases the difference in the acidity of the N–H and O–H bonds. However, we mentioned before that lactam is more prone to substituent effects than the more aromatic lactim, so it can be expected that the increase of electron density ortho to the nitrogen atom should decrease the N–H bond acidity, too. According to the results (Fig. 12), this effect seems to be outweighed by the inductive effect due to the substituent proximity. In the case of NO₂, the increase in the acidity of the N–H and O–H bonds relative to 2PY/2HPY is the same (Fig. 12). The greater distance from the oxygen atom is now compensated by the −R effect of the substituent and the adjacent ring nitrogen atom, whose electronegativity is increased by the presence of the NO₂ at the two-bond distance from it. As a result, NO₂ at position 5 has a slight effect on the tautomeric equilibrium of 2PY (Fig. 10 and 11).

Position 6 of 2PY/2HPY and position 2 of 4PY/4HPY is closest to the nitrogen atom (one-bond distance vs. three-bond distance to the oxygen atom, Fig. 13c and f). This results in the largest increase of the N–H bond acidity by induction for all but the NO₂ group. The latter increases the acidity of the N–H bond more when placed at positions 3 and 5 of 2PY and position 3 of 4PY, despite the greater distance from the nitrogen atom (two-bond distance, Fig. 13). This finding can be interpreted by the stabilization of the N–H bond of 6-nitro-2-pyridone and 2-nitro-4-pyridone due to the formation of intramolecular hydrogen bonding, which reduces its acidity. Therefore, the induction and hydrogen bond stabilization act in opposite directions, resulting in NO₂ shifting the equilibrium toward lactim the least among all substituents studied. The results in Fig. 12 show that the relative acidity of the N–H and O–H bonds in 6-substituted 2PY/2HPY is similar when Cl and NH₂ are substituents and smaller than that when F is the substituent, but greater than for the 6-nitro derivative. This can be explained by induction and, additionally, the hydrogen bond effect in the case of NO₂, as discussed above. However, in 4PY/4HPY the effect of NH₂ is closer to the effect of F, indicating involvement of the resonance effect. We ascribe it to the enhancement of amino nitrogen atom's electronegativity due to the conjugation of its lone pair with the π-electron system of the ring.

In the previous study, the chlorine inductive effect was found as dominant in determining the core electron ionization potential (IP) of nitrogen atom, N(1s), in chlorinated 2HPY, whereas it was postulated that both induction and resonance affect N(1s) IP in chlorinated 2PY.^17c The substituent-N/O distance dependence was also invoked previously to explain the effect of chlorination of 4PY on tautomeric equilibrium.^16a

Solvent effect on tautomeric equilibrium of (substituted) 2-pyridone and (substituted) 4-pyridone

Since most processes occur in solution, we calculated tautomerization Gibbs free energies by including three solvents: weakly polar tetrahydrofuran (THF), polar aprotic dimethyl sulfoxide (DMSO) and polar protic water. The obtained values are given in Fig. 10, and the results are also presented graphically as Fig. 14. Our computational predictions agree with all previous observations that transfer of a molecule from the gas phase in a solvent increases the population of the lactam form having greater dipole moment. The more polar the solvent, the greater is the lactam population, which is the result of better solvation of the more polar isomer. Though, in a few cases, our calculations predict substituted anti-2HPY to have a larger dipole moment than the lactam form.

Fig. 14 Solvent effects on tautomeric equilibrium of (substituted) 2-pyridones (upper part) and (substituted) 4-pyridones (lower part): x-axis shows substituent position within the ring, y-axis shows relative Gibbs free energies of lactim forms, black colour – in gas phase, green colour – in THF, red colour – in DMSO, blue colour – in water. The gas-phase value of 3-NO₂4PY (−10.9) is below the scale shown.

In all solvents, syn-conformation of (substituted) 2HPY is energetically preferred, except 3-nitro derivative whose anti-form has lower energy, as already discussed above. In the case of 2-substituted 4HPY the two conformations have almost the same energy, while in the case of 3-substituted 4HPY their energy differs, and data for both forms are included in Fig. 10, but only for more stable forms in Fig. 14.

Calculated data predict that 2PY would exist almost exclusively as lactam in all three solvents, which is also the case for 4PY in DMSO and water. In THF, lactam will equilibrate with a certain amount of lactim (ΔG = 1.9 kcal mol⁻¹). In all solvents, 3- and 4-substituted 2PY have large positive tautomerization energies and will be present as lactams (only 3-nitro-2-pyridone has smaller ΔG = 1.7 kcal mol⁻¹ in THF and is predicted to have a certain amount of lactim). The same will happen with 3-substituted 4PY (F, Cl, NH₂) in polar solvents, DMSO and water, but in the weakly polar THF an equilibrium shifted toward the lactam is predicted. In the case of 3-nitro-4-pyridone, calculations predict lactam as the main isomer in polar solvents, but lactim in THF. Lactam is the main (F, Cl, NH₂), or the sole isomer (NO₂) in the case of 5-substituted 2PY and 6-amino-2-pyridone, while lactim is the dominant species in the case of other 6-substituted 2PY. According to calculations, 2-fluoro and 2-nitro-4-pyridone exist exclusively as lactim in all solvents studied, while in the case of 2-chloro derivative lactim would be the main isomer in tautomeric equilibrium. For 2-amino-4-pyridone, calculations predict an equilibrium shifted towards lactim in THF and towards lactam in DMSO and water.

The results presented in Fig. 14 show a general trend of solvent effect on the tautomeric equilibria of 2PY and 4PY and its derivatives: the lactam population increases with increasing solvent polarity. The direction of the equilibrium also depends on substituent effect. Our calculations predict that the lactam may predominate for all derivatives except those with large negative gas-phase tautomerization energies, such as 6-fluoro/chloro/nitro-2-pyridone and 2-fluoro/chloro/nitro-4-pyridone.

Conclusions

In this work, we computationally studied the tautomerism of 2- and 4-pyridone, and their derivatives having a single substituent (Cl, NH₂, F and NO₂) at different positions in the ring. Since tautomers are structurally different, they show different chemical, biological and physical properties so that knowledge about the position of equilibrium and factors determining it is of great importance.

Based on the results of this work, the well-known difference in the gas-phase tautomeric equilibria of 2PY, existing as a mixture of lactam and lactim in ∼1 : 3 ratio, and 4PY existing as lactim, can be attributed to the greater aromaticity gain upon tautomerization of the latter. This can be interpreted as a consequence of the already cyclic delocalization of π-electrons in 2PY, but one-directional in 4PY, from nitrogen atom to carbonyl group. In addition, tautomerization of 4PY leads to the relief of Pauli repulsion between the nitrogen lone pair and π-electrons of the double bonds, while tautomerization of 2PY increases Pauli repulsion, attributed to the sp²-type nitrogen lone pair and the adjacent C–O bond interaction (absent in 4HPY), but enhances orbital interactions (aromaticity) and electrostatic interactions (mainly attributed to H → O and C → N bond dipole attraction). Since both kinds of stabilizing interaction are also present in lactam (somewhat weaker cyclic delocalization and also weaker H → N and C → O bond dipole attraction), 2-pyridone contains both tautomers in equilibrium.

Tautomeric equilibrium can be altered by ring substitution (F, Cl, NH₂ and NO₂): it can be shifted more to the lactim (2-substituted 4PY and 6-substituted 2PY, 3- and 4-nitro-2-pyridone, 3-substituted 4PY and 5-substituted 2PY, except 3-amino-4-pyridone and 5-nitro-2-pyridone), or more to the lactam (3-amino-4-pyridone, 3- and 4-amino-2-pyridone). Tautomerism is almost unaltered in the case of 3- and 4-fluoro(chloro)-2-pyridone and 5-nitro-2-pyridone. It is concluded that halogen atoms modulate tautomerization energy by their inductive effect, or by H → O/C → X dipole–dipole attraction in 3-substituted 4PY. For the nitro group, induction, resonance and hydrogen bonding are all important, and only the first two effects in the case of the amino group.

Increase of medium polarity shifts the tautomeric equilibrium toward the more polar lactam. Only 6-fluoro/chloro/nitro-2-pyridone and 2-fluoro/chloro/nitro-4-pyridone will have lactim as dominant species in all solvents studied (THF, DMSO and water).

We hope that the results of this work will add new knowledge to the already studied unsubstituted and chloro-substituted pyridones and give useful predictions and explanations for the less studied amino, nitro and fluoro derivatives.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the Ministry of Science, Technological Development and Innovation of the Republic of Serbia, contract number: 451-03-47/2023-01/200168.

References

1. Tautomerism: Methods and Theories, ed. L. Antonov, Wiley-VCH, Verlag GmbH & Co. KGaA, 2014.
2. S. M. Kashid, R. K. Singh, H. Kwon, Y. S. Kim, A. Mukherjee and S. Bagchi, Arresting an Unusual Amide Tautomer Using Divalent Cations, J. Phys. Chem. B, 2019, 123, 8419–8424.
3. A. Mardyukov, F. Keul and P. R. Schreiner, Preparation and characterization of the enol of acetamide: 1-aminoethenol, a high-energy prebiotic molecule, Chem. Sci., 2020, 11, 12358–12363.
4. B. L. Grigorenko, M. G. Khrenova and A. V. Nemukhin, Amide–imide tautomerization in the glutamine side chain in enzymatic and photochemical reactions in proteins, Phys. Chem. Chem. Phys., 2018, 20, 23827–23836.
5. (a) P. Beak, F. S. Fry, Jr., J. Lee and F. Steele, Equilibration Studies. Protomeric Equilibria of 2- and 4-Hydroxypyridines, 2- and 4-Hydroxypyrimidines, 2- and 4-Mercaptopyridines, and Structurally Related Compounds in the Gas Phase, J. Am. Chem. Soc., 1976, 98, 171–179; (b) P. Beak, Energies and Alkylations of Tautomeric Heterocyclic Compounds: Old Problems − New Answers, Acc. Chem. Res., 1977, 10, 186–192.
6. (a) D. H. Aue, L. D. Betowski, W. R. Davidson, M. T. Bowers, P. Beak and J. Lee, Gas phase Basicities of Amides and Imidates. Estimation of Protomeric Equilibrium Constants by the Basicity Method in the Gas Phase, J. Am. Chem. Soc., 1979, 101, 1361–1368; (b) R. S. Brown, A. Tse and J. C. Vederas, J. Am. Chem. Soc., 1980, 102, 1174–1176; (c) L. D. Hatherley, R. D. Brown, P. D. Godfrey, A. P. Pierlot, W. Caminati, D. Damiani, S. Melandri and L. B. Favero, Gas phase Tautomeric Equilibrium of 2-Pyridinone and 2-Hydroxypyridine by Microwave Spectroscopy, J. Phys. Chem., 1993, 97, 46–51; (d) A. Gerega, L. Lapinski, M. J. Nowak, A. Furmanchuk and J. Leszczynski, Systematic Effect of Benzo-Annelation on Oxo-Hydroxy Tautomerism of Heterocyclic Compounds. Experimental Matrix-Isolation and Theoretical Study, J. Phys. Chem. A, 2007, 111, 4934–4943.
7. (a) M. J. Cook, S. El-Abaddy and A. R. Katritzky, Photoelectron Spectra of Hydroxy- and Mercapto-pyridines and Models of Fixed Structure, J. Chem. Soc., Perkin Trans. 2, 1977, 1652–1656; (b) R. Sanchez, B. M. Giuliano, S. Melandri and W. Caminati, Tautomeric equilibrium and hydroxyl group internal rotation in 4-hydroxypyridine, Phys. Chem. Lett., 2006, 425, 6–9.
8. (a) P. Beak, J. B. Covington and S. G. Smith, Structural Studies of Tautomeric Systems: the Importance of Association for 2-Hydroxypyridine-2-Pyridone and 2-Mercaptopyridine-2-Thiopyridone, J. Am. Chem. Soc., 1976, 98, 8284–8286; (b) J. Frank and A. R. Katritzky, Tautomeric Pyridines. Part XV. Pyridone-Hydroxypyridine Equilibria in Solvents of Differing Polarity, J. Chem. Soc., Perkin Trans. 2, 1976, 1428–1431; (c) M. M. Karelson, A. R. Katritzky, M. Szafran and M. C. Zerner, Quantitative Predictions of Tautomeric Equilibria for 2-, 3-, and 4-Substituted Pyridines in both the Gas Phase and Aqueous Solution: Combination of AMI with Reaction Field Theory, J. Org. Chem., 1989, 54, 6030–6034; (d) J. Gao and L. Shao, Polarization Effects on the Tautomeric Equilibria of 2- and 4-Hydroxypyridine in Aqueous and Organic Solution, J. Phys. Chem., 1994, 98, 13772–13779; (e) J. Wang and R. J. Boyd, Tautomeric Equilibria of Hydroxypyridines in Different Solvents: An ab Initio Study, J. Phys. Chem., 1996, 100, 16141–16146; (f) P. I. Nagy, G. Alagona and C. Ghio, Theoretical Investigation of Tautomeric Equilibria for Isonicotinic Acid, 4-Pyridone, and Acetylacetone in Vacuo and in Solution, J. Chem. Theory Comput., 2007, 3, 1249–1266; (g) C. S. Peng and A. Tokmakoff, Identification of Lactam–Lactim Tautomers of Aromatic Heterocycles in Aqueous Solution Using 2D IR Spectroscopy, J. Phys. Chem. Lett., 2012, 3, 3302–3306.
9. (a) A. Tyl, M. Nowak and J. Kusz, Two polymorphs of anhydrous 4-pyridone at 100 K, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2008, 64, o661–o664; (b) T. L. Motley, D. G. Allis and T. M. Korter, Investigation of crystalline 2-pyridone using terahertz spectroscopy and solid-state density functional theory, Chem. Phys. Lett., 2009, 478, 166–171; (c) H. T. Flakus and A. Tyl, Electron-induced phase transition in hydrogen-bonded anhydrous solid state 4-pyridone, Vib. Spectrosc., 2012, 63, 440–450.
10. E. D. Raczyńska, W. Kosińska, B. Ośmiałowski and R. Gawinecki, Tautomeric Equilibria in Relation to Pi-Electron Delocalization, Chem. Rev., 2005, 105, 3561–3612.
11. M. C. Nowak, L. Lapinski, J. Fulara, A. Les and L. Adamowicz, Matrix Isolation IR Spectroscopy of Tautomeric Systems and Its Theoretical Interpretation. 2-Hydroxypyridine/2(1H)-Pyridinone, J. Phys. Chem., 1992, 96, 1562–1569.
12. N. Bodor, M. J. S. Dewar and A. J. Harget, Ground States of Conjugated Molecules. XIX. Tautomerism of Heteroaromatic Hydroxy and Amino Derivatives and Nucleotide Bases, J. Am. Chem. Soc., 1970, 92, 2929–2936.
13. (a) M. J. Cook, A. R. Katritzky, P. Linda and R. D. Tack, Quantitative Measure of the Aromatic Stabilization Energy of 2-Pyridone and Related Compounds, J. Chem. Soc. D, 1971, 510–511; (b) M. J. Cook, A. R. Katritzky, P. Linda and R. D. Tack, Aromaticity and Tautomerism. Part 1. The Aromatic Resonance Energy of 2-Pyridone and the Related Thione, Methide, and lmine, J. Chem. Soc., Perkin Trans. 2, 1972, 1295–1301; (c) M. J. Cook, A. R. Katritzky, P. Linda and R. D. Tack, Aromaticity and Tautomerism. Part II. The 4-Pyridone, 2-Quinolone, and 1-isoquinolone Series, J. Chem. Soc., Perkin Trans. 2, 1973, 1080–1086.
14. A. R. Katritzky, M. Szafran, N. Malhotra, S. U. Chaudry and E. Anders, Aromaticity as a Quantitative Concept. Part V. A Comparison of Semiempirical Methods for the Calculation of Molecular Geometries of Heteroaromatic Compoundsand Application of the AM1 and MNDO Methods to the Calculations of Bird's Aromaticity Indices, Tetrahedron Comput. Methodol., 1990, 3, 247–269.
15. E. D. Raczyńska, Electron delocalization and relative stabilities for the favored and rare tautomers of hydroxyazines in the gas phase – A comparison with aminoazines, Comput. Theor. Chem., 2014, 1042, 8–15.
16. (a) A. R. Katritzky, J. D. Rowe and S. K. Roy, Potentially Tautomeric Pyridines. Part IX. The Effect of Chlorine Substituents on Pyridone-Hydroxypyridine Tautomerism, J. Chem. Soc. B, 1967, 758–761; (b) O. G. Parchment, I. H. Hillier and D. V. S. Green, A Theoretical Study of the Protomeric Equilibrium of 6-Chloro-2-hydroxypyridine in the Gas Phase and in Solution, J. Chem. Soc., Perkin Trans. 2, 1991, 799–802; (c) J. C. Facelli, A. M. Orendt, R. H. Contreras, M. F. Tufró and D. G. de Kowalewski, Ab Initio and ¹⁷O NMR Studies of the Substituent Effects on the Tautomeric Equilibrium in 6-X-1H-2-Pyrldones, J. Phys. Chem., 1992, 96, 7895–7898; (d) L. Forlani, G. Cristoni, C. Boga, P. E. Todesco, E. Del Vecchio, S. Selva and M. Monari, Reinvestigation of the tautomerism of some substituted 2-hydroxypyridines, ARKIVOC, 2002, xi, 198–215.
17. (a) S. S. T. King, W. L. Dilling and N. B. Tefertiller, An Infrared Study of the Tautomerism of Chlorinated 2-Pyridinols Isolated in an Argon Matrix, Tetrahedron, 1972, 28, 5859–5863; (b) C. Calabrese, A. Maris, I. Uriarte, E. J. Cocinero and S. Melandri, Effects of Chlorination on the Tautomeric Equilibrium of 2-Hydroxypyridine: Experiment and Theory, Chem. – Eur. J., 2017, 23, 3595–3604; (c) S. Melandri, L. Evangelisti, S. Canola, H. Sa'adeh, C. Calabrese, M. Coreno, C. Grazioli, K. C. Prince, F. Negri and A. Maris, Chlorination and tautomerism: a computational and UPS/XPS study of 2-hydroxypyridine ⇌ 2-pyridone equilibrium, Phys. Chem. Chem. Phys., 2020, 22, 13440–13455.
18. A. Fujimoto and K. Inuzuka, The Lactam-Lactim Tautomerization of Monoamino-Substituted 2-Pyridinols in Tetrahydrofuran, Bull. Chem. Soc. Jpn., 1990, 63, 2292–2299.
19. (a) E. Spinner and J. C. B. White, Spectral and Ionisation Constant Studies of Substituted 2-Hydroxypyridines (1,2-Dihydro-2-oxopyridines), J. Chem. Soc. B, 1966, 991–995; (b) J. T. Gerig and J. D. Reinheimer, NMR Studies of Substituted Pyridines, Org. Magn. Reson., 1969, 1, 239–247; (c) R. Hilal and Sh. El-Basil, Electronic Spectra and Tautomeric Equilibria of Some Substituted 5-Nitropyridines, Z. Phys. Chem., 1981, 262, 162–168; (d) E. Kolehmainen, K. Laihia, D. Rasała and R. Gawinecki, ¹H, ¹³C and ¹⁷O NMR Study of Substituted Nitropyridines, Magn. Reson. Chem., 1991, 29, 878–884; (e) T. A. Mohamed, I. A. Shaaban, U. A. Soliman and W. M. Zoghaib, 2-Hydroxy-5-nitropyridine and 5-nitro-2-pyridone: Tautomerism, infrared, Raman, and NMR spectral interpretations, normal coordinate analysis, and DFT calculations, J. Chin. Chem. Soc., 2021, 68, 1863–1879.
20. H. Besso, K. Imafuku and H. Matsumura, Tautomerism of 4-Pyridones, Bull. Chem. Soc. Jpn., 1977, 50, 710–712.
21. R. A. Jones and B. D. Roney, Tautomeric Equilibrium Constants for 3-Amino- and 3-Nitro-4-pyridone, J. Chem. Soc. B, 1967, 84–85.
22. B. I. Fedeles, D. Li and V. Singh, Structural Insights Into Tautomeric Dynamics in Nucleic Acids and in Antiviral Nucleoside Analogs, Front. Mol. Biosci., 2022, 8, 823253.
23. D. Li, B. I. Fedeles, V. Singh, C. S. Peng, K. J. Silvestre, A. K. Simi, J. H. Simpson, A. Tokmakoff and J. M. Essigmann, Tautomerism provides a molecular explanation for the mutagenic properties of the anti-HIV nucleoside 5-aza-5,6-dihydro-2′-deoxycytidine, Proc. Natl. Acad. Sci. U. S. A., 2014, E3252–E3259.
24. (a) A. R. Carvalho, Tautomeric Equilibria Revisited: proton-tautomerism in solvent and the fundamentals of molecular stability prediction, ChemRxiv, 2019, preprint,  DOI:10.26434/chemrxiv.7699952.v3; (b) S. A. Hejazi, O. I. Osman, A. O. Alyoubi, S. G. Aziz and R. H. Hilal, The Thermodynamic and Kinetic Properties of 2-Hydroxypyridine/2-Pyridone Tautomerization: A Theoretical and Computational Revisit, Int. J. Mol. Sci., 2016, 17, 1893.
25. (a) S. Sangwan, N. Yadav, R. Kumar, S. Chauhan, V. Dhanda, P. Walia and A. Duhan, A score years’ update in the synthesis and biological evaluation of medicinally important 2-pyridones, Eur. J. Med. Chem., 2022, 232, 114199; (b) S. Lin, C. Liu, X. Zhao, X. Han, X. Li, Y. Ye and Z. Li, Recent Advances of Pyridinone in Medicinal Chemistry, Front. Chem., 2022, 10, 869860.
26. (a) S. Hoshika, N. A. Leal, M. J. Kim, M. S. Kim, N. B. Karalkar, H. J. Kim, A. M. Bates, N. E. Watkins, Jr., H. A. SantaLucia, A. J. Meyer, S. DasGupta, J. A. Piccirilli, A. D. Ellington, J. SantaLucia Jr., M. M. Georgiadis and S. A. Benner, Hachimoji DNA and RNA: A genetic system with eight building blocks, Science, 2019, 363, 884–887; (b) N. G. J. Richards and M. M. Georgiadis, Toward an Expanded Genome: Structural and Computational Characterization of an Artificially Expanded Genetic Information System, Acc. Chem. Res., 2017, 50, 1375–1382.
27. J. G. Sośnicki and T. J. Idzik, Pyridones – Powerful Precursors for the Synthesis of Alkaloids, Their Derivatives, and Alkaloid-Inspired Compounds, Synthesis, 2019, 3369–3396.
28. (a) M. Mohan, T. Maris and A. Duong, Building coordination polymers using dipyridone ligands, CrystEngComm, 2020, 22, 441–447; (b) M. Mohan, M. Essalhi, S. Zaye, L. K. Rana, T. Maris and A. Duong, Hydrogen Bond Patterns of Dipyridone and Bis(Hydroxypyridinium) Cations, ACS Omega, 2021, 6, 35649–35656.
29. (a) J. M. Bueno, E. Herreros, I. Angulo-Barturen, S. Ferrer, J. M. Fiandor, F. J. Gamo, D. Gargallo-Viola and G. Derimanov, Exploration of 4(1H)-pyridones as a novel family of potent antimalarial inhibitors of the plasmodial cytochrome bc1, Future Med. Chem., 2012, 4, 2311–2323; (b) A. S. Asakawa and R. Manetsch, A Comprehensive Review of 4(1H)-Quinolones and 4(1H)-Pyridones for the Development of an Effective Antimalarial, IntechOpen, 2021,  DOI:10.5772/intechopen.97084.
30. (a) X. Gao, R. P. Singh and E. J. Corey, Enantioselective Synthesis of a Chiral C3-Symmetric Bridgehead Amine, Org. Lett., 2010, 12, 1812–1814; (b) T. Burckhardt, K. Harms and U. Koert, Total Synthesis of Lodopyridone, Org. Lett., 2012, 14, 4674–4677; (c) W. Shao, Y. Wang, Z.-P. Yang, X. Zhang and S.-L. You, Efficient Synthesis of N-Alkylated 4-Pyridones by Copper-Catalyzed Intermolecular Asymmetric Propargylic Amination, Chem. – Asian J., 2018, 13, 1103–1107.
31. (a) Y.-f. Chen and J. J. Dannenberg, Cooperative 4-Pyridone H-Bonds with Extraordinary Stability. A DFT Molecular Orbital Study, J. Am. Chem. Soc., 2006, 128, 8100–8101; (b) M. Anand, I. Fernández, H. F. Schaefer III and J. I.-C. Wu, Hydrogen Bond-Aromaticity Cooperativity in Self-Assembling 4-Pyridone Chains, J. Comput. Chem., 2016, 37, 59–63.
32. (a) N. A. Meanwell, The Influence of Bioisosteres in Drug Design: Tactical Applications to Address Developability Problems, Top. Med. Chem., 2015, 9, 283–382; (b) N. A. Meanwell, Fluorine and Fluorinated Motifs in the Design and Application of Bioisosteres for Drug Design, J. Med. Chem., 2018, 61, 5822–5880.
33. G. Galstyan and E.-W. Knapp, Computations of 36 Tautomer/Isomer Equilibria of Different Lactams, J. Phys. Chem. A, 2012, 116, 6885–6893.
34. J. B. Foresman and A. Frisch, Exploring Chemistry with Electronic Structure Methods, Gaussian, Inc., 1996.
35. (a) A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A, 1988, 38, 3098–3100; (b) C. Lee, W. Yang and R. G. Parr, Development of the Colic-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789; (c) A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652.
36. T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57.
37. J. D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
38. A. D. Becke, A new mixing of Hartree-Fock and local density-functional theories, J. Chem. Phys., 1993, 98, 1372–1377.
39. Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120, 215–241.
40. D. R. Borst, J. R. Roscioli and D. W. Pratt, High-Resolution Electronic Spectra of 2-Hydroxy and 2-Aminopyridine. Perturbing Effects of the Nitrogen Atom in the Aromatic Ring, J. Phys. Chem. A, 2002, 106, 4022–4027.
41. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (Revision D.01), Gaussian, Inc., Wallingford, CT, 2013.
42. J. Tomasi, B. Mennucci and R. Cammi, Quantum Mechanical Continuum Solvation Models, Chem. Rev., 2005, 105, 2999–3093.
43. (a) J. Kruszewski and T. M. Krygowski, Definition of Aromaticity Basing on the Harmonic Oscillator Model, Tetrahedron Lett., 1972, 3839–3842; (b) T. M. Krygowski and M. K. Cyrański, Structural Aspects of Aromaticity, Chem. Rev., 2001, 101, 1385–1419; (c) T. M. Krygowski, H. Szatylowicz, O. A. Stasyuk, J. Dominikowska and M. Palusiak, Aromaticity from the Viewpoint of Molecular Geometry: Application to Planar Systems, Chem. Rev., 2014, 114, 6383–6422.
44. (a) D. W. Szczepanik, M. Andrzejak, K. Dyduch, E. Żak, M. Makowski, G. Mazur and J. Mrozek, A Uniform Approach to the Description of Multicenter Bonding, Phys. Chem. Chem. Phys., 2014, 16, 20514–20523; (b) D. W. Szczepanik, A New Perspective on Quantifying Electron Localization and Delocalization in Molecular Systems, Comput. Theor. Chem., 2016, 1080, 33–37; (c) D. W. Szczepanik, M. Andrzejak, J. Dominikowska, B. Pawełek, T. M. Krygowski, H. Szatylowicz and M. Solà, The Electron Density of Delocalized Bonds (EDDB) Applied for Quantifying Aromaticity, Phys. Chem. Chem. Phys., 2017, 19, 28970–28981; (d) D. W. Szczepanik and M. Solà, The Electron Density of Delocalized Bonds (EDDBs) as a Measure of Local and Global Aromaticity, in Aromaticity. Modern Computational Methods and Applications, ed. I. Fernandez, Elsevier Inc., 2021, pp. 259–284.
45. (a) P. von Ragué Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. van Eikema Hommes, Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe, J. Am. Chem. Soc., 1996, 118, 6317–6318; (b) P. von Ragué Schleyer, H. Jiao, N. J. R. van Eikema Hommes, V. G. Malkin and O. L. Malkina, An Evaluation of the Aromaticity of Inorganic Rings: Refined Evidence from Magnetic Properties, J. Am. Chem. Soc., 1997, 119, 12669–12670; (c) Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. von Ragué Schleyer, Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion, Chem. Rev., 2005, 105, 3842–3888; (d) H. Fallah-Bagher-Shaidaei, C. S. Wannere, C. Corminboeuf, R. Puchta and P. von Ragué Schleyer, Which NICS Aromaticity Index for Planar π Rings Is Best?, Org. Lett., 2006, 8, 863–866; (e) R. Gershoni-Poranne and A. Stanger, Magnetic Criteria of Aromaticity, Chem. Soc. Rev., 2015, 44, 6597–6615; (f) A. Stanger, NICS – Past and Present, Eur. J. Org. Chem., 2020, 3120–3127.
46. (a) R. Herges and D. Geuenich, Delocalization of Electrons in Molecules, J. Phys. Chem. A, 2001, 105, 3214–3220; (b) D. Geuenich, K. Hess, F. Köhler and R. Herges, Anisotropy of the Induced Current Density (ACID), a General Method To Quantify and Visualize Electronic Delocalization, Chem. Rev., 2005, 105, 3758–3772.
47. (a) E. D. Glendening, C. R. Landis and F. Weinhold, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 1–42; (b) F. Weinhold and C. R. Landis, Discovering Chemistry with Natural Bond Orbitals, John Wiley & Sons, Inc., 2012.
48. T. Lu and F. Chen, Multiwfn: A Multifunctional Wavefunction Analyzer, J. Comput. Chem., 2012, 33, 580–592.
49. D. W. Szczepanik, https://www.eddb.pl/runeddb/, accessed July 8, 2021.
50. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO 6.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2013.
51. A. Stanger, Nucleus-Independent Chemical Shifts (NICS): Distance Dependence and Revised Criteria for Aromaticity and Antiaromaticity, J. Org. Chem., 2006, 71, 883–893.
52. A. Stanger, Reexamination of NICS_π,zz: Height Dependence, Off-Center Values, and Integration, J. Phys. Chem. A, 2019, 123, 3922–3927.
53. A. Rahalkar and A. Stanger, Aroma, https://chemistry.technion.ac.il/members/amnon-stanger/, accessed January 30, 2020.
54. (a) R. Ditchfeld, Self-Consistent Perturbation Theory of Diamagnetism. 1. Gauge-Invariant LCAO Method for N.M.R. Chemical Shifts, Mol. Phys., 1974, 27, 789–807; (b) K. Wolinski, J. F. Hinton and P. Pulay, Efficient Implementation of the Gauge-Independent Atomic Orbital Method for NMR Chemical Shift Calculations, J. Am. Chem. Soc., 1990, 112, 8251–8260.
55. (a) R. G. Viglione, R. Zanassi and P. Lazzeretti, Are Ring Currents Still Useful to Rationalize the Benzene Proton Magnetic Shielding?, Org. Lett., 2004, 6, 2265–2267; (b) P. Lazzeretti, Assessment of Aromaticity via Molecular Response Properties, Phys. Chem. Chem. Phys., 2004, 6, 217–223.
56. A. Stanger, Obtaining Relative Induced Ring Currents Quantitatively from NICS, J. Org. Chem., 2010, 75, 2281–2288.
57. T. A. Keith and R. F. W. Bader, Calculation of magnetic response properties using a continuous set of gauge transformations, Chem. Phys. Lett., 1993, 210, 223–231.
58. C. Cason, T. Froehlich and C. Lipka, POV-Ray 3.7.0.msvc10.win64, Persistence of Vision Raytracer Pty. Ltd., © 1991–2013.
59. F. Weinhold and E. D. Glendening, NBO 6.0 Program Manual, Copyright 1996–2015 Board of Regents of the University of Wisconsin System on behalf of the Theoretical Chemistry Institute.
60. P. Su and H. Li, J. Chem. Phys., 2009, 131, 014102.
61. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. J. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, Jr., J. Comput. Chem., 1993, 14, 1347–1363 , Gamess 2013-R1 version was used in this work.
62. (a) M. El-Hamdi, W. Tiznado, J. Poater and M. Solá, An Analysis of the Isomerization Energies of 1,2-/1,3-Diazacyclobutadiene, Pyrazole/Imidazole, and Pyridazine/Pyrimidinewith the Turn-Upside-Down Approach, J. Org. Chem., 2011, 76, 8913–8921; (b) M. Contreras, E. Osorio, F. Ferraro, G. Puga, K. J. Donald, J. G. Harrison, G. Merino and W. Tiznado, Isomerization Energy Decomposition Analysis for Highly Ionic Systems: Case Study of Starlike E₅Li₇⁺ Clusters, Chem. – Eur. J., 2013, 19, 2305–2310; (c) M. Baranac-Stojanović, Aromaticity and Stability of Azaborines, Chem. – Eur. J., 2014, 20, 16558–16565; (d) M. Baranac-Stojanović, 4π-Electron B–N Monocycles: Stability and (Anti)aromaticity, Eur. J. Org. Chem., 2017, 5163–5169.
63. In 4HPY, the H → O and the two C → N bond dipoles are farther away and less favourably oriented than in 2HPY.
64. A detailed analysis showing that π-electrons prefer to be localized is presented in the following ref.: S. C. A. H. Pierrefixe and F. M. Bickelhaupt, Aromaticity: Molecular-Orbital Picture of an Intuitive Concept, Chem. – Eur. J., 2007, 13, 6321–6328.

---

Footnote

† Electronic supplementary information (ESI) available: Comparison of calculated and experimental bond lengths of 2-pyridone, syn-2-hydroxypyridine, 4-pyridone and 6-chloro-2-hydroxypyridine (Tables S1, S2 and S6, Fig. S1, S2 and S4); AICD plots of 2- and 4-pyridone, 2- and 4-hydroxypyridine; results of energy decomposition analysis of ring bonds and double bonds of 2- and 4-pyridone, 2- and 4-hydroxypyridine; absolute energies and x, y, z coordinates of the gas-phase optimized structures at the BHandHLYP/6-311+G(d,p) level of theory. See DOI: https://doi.org/10.1039/d3ob01588b

---