Open Access Article
Open Access ArticleNeutral rhodol-based dyes expressing localization in mitochondria†
Ilaria
Ferraboschi‡
 a,
Juraj
Ovčar‡
bc,
Kateryna V.
Vygranenko
d,
Shupei
Yu
e,
Alfonso
Minervino
a,
Juraj
Ovčar‡
bc,
Kateryna V.
Vygranenko
d,
Shupei
Yu
e,
Alfonso
Minervino
 e,
Antoni
Wrzosek
f,
Adam
Szewczyk
f,
Riccardo
Rozza
c,
Alessandra
Magistrato
c,
Kevin D.
Belfield
e,
Antoni
Wrzosek
f,
Adam
Szewczyk
f,
Riccardo
Rozza
c,
Alessandra
Magistrato
c,
Kevin D.
Belfield
 e,
Daniel T.
Gryko
e,
Daniel T.
Gryko
 d,
Luca
Grisanti
d,
Luca
Grisanti
 *bc and
Cristina
Sissa
*bc and
Cristina
Sissa
 *a
*a
aDepartment of Chemistry, Life Sciences and Environmental Sustainability, University of Parma, 43124 Parma, Italy. E-mail: cristina.sissa@unipr.it
bRuđer Bošković Institute, Bijenička cesta 54, 10000 Zagreb, Croatia. E-mail: grisanti@iom.cnr.it
cNational Research Council – Materials Foundry Institute (CNR-IOM) c/o SISSA (International School for Advanced Studies), Via Bonomea 265, 34136 Trieste, Italy
dInstitute of Organic Chemistry, Polish Academy of Sciences, Kasprzaka 44/52, 01-224 Warsaw, Poland
eDepartment of Chemistry and Environmental Science, College of Science and Liberal Arts, New Jersey Institute of Technology, Newark, New Jersey 07102, USA
fNencki Institute of Experimental Biology of Polish Academy of Sciences, Pasteura 3, 02-093 Warsaw, Poland
First published on 28th May 2024
Abstract
Neutral rhodol-based red emitters are shown to efficiently localize in mitochondria, as demonstrated by confocal microscopy and co-localization studies. A simple model is proposed to explain the localization mechanism of neutral molecules. The model takes into account the strong coupling between the molecular dipole moment and the electric field of the inner mitochondrial membrane.
Mitochondria are organelles found in the cytoplasm of most eukaryotic cells. Mitochondrial dysfunction has been shown to have far-reaching consequences, being implicated as a major contributing factor in the development of various diseases.1 Monitoring mitochondrial morphology and dynamics via fluorescent probes (trackers) can reveal valuable information on cell functioning,2 allowing for the development of disease treatment strategies based on understanding mitochondrial dysfunction and its pathological implications at the molecular level.3
The vast majority of commercially available mitochondria trackers are positively charged,4–6 exploiting the electrochemical potential difference ΔμH+ generated across the mitochondrial inner membrane as a result of a proton gradient established by the respiratory chain.7 In contrast to cationic trackers, there have been far fewer reports of neutral tracking probes5,8–17 despite several significant advantages neutral trackers offer over charged ones; e.g., their accumulation in mitochondria does not lead to membrane depolarization,13,15 allowing for the investigation of mitochondrial morphology in a minimally perturbed environment. The efficiency of cationic trackers is heavily dependent on the mitochondrial membrane potential,5,18 leading to an inability to label dysfunctional mitochondria18 or mitochondria with membrane potentials temporarily altered by normal biological processes.18,19 It has been shown that common cationic trackers may stain organelles other than mitochondria, such as lysosomes, due to their own membrane potential.19,20 It is also known that the mitochondrial inner membranes intrinsically possess low ion permeability,21,22 requiring additional considerations in the design of cationic trackers.
Generally, the physical mechanisms of the localization of neutral molecules in mitochondria are not fully understood. The lack of understanding of the physical processes underpinning mitochondrial localization of neutral trackers from a fundamental point of view is detrimental to the formulation of improved strategies for rational design of novel trackers, as well as to the integrity of the interpretations of mitochondrial tracking experiments.
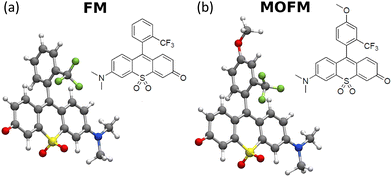
In this paper, by performing confocal microscopy experiments and co-localization studies with a commercial mitochondrial tracker, we demonstrate that the red-fluorescent rhodol-based dyes FM and MOFM (Fig. 1) function as efficient neutral mitochondral trackers. In addition, we propose a physical mechanism governing mitochondrial localization of neutral polar molecules.
FM and MOFM were previously synthesized by some of us as efficient red emitters.23 The two molecules share the same sulfone-rhodol backbone, while the substituted upper ring confers stability. Based on density functional theory (DFT) simulations (computational details reported in sect. S1†), the two aromatic groups are almost perpendicular to each other (see Fig. 1 and Tables S2 and S3†), suggesting negligible conjugation between the two units. Spectroscopic characterization was already available,23 and here it is extended to include cell culture medium and PBS (Fig. S5; technical details in sect. S2†). The results show a marked positive solvatochromism, suggesting that (i) both the ground and the first excited states are polar, (ii) the permanent dipole moment of the first excited state is larger than the ground state dipole moment, and (iii) the low-energy transition has a charge transfer character.
The excitation anisotropy of FM and MOFM in glycerol (Fig. S6†) has a constant value of 0.4 within the broad excitation band, confirming that only one excited state is involved in this transition and that the same excited state is responsible for absorption and emission. To further investigate excited states of FM and MOFM, we measured two-photon absorption (2PA) spectra in DCM (Fig. S7†). 2PA spectra of both compounds overlap very well with one-photon absorption which is a further confirmation of their dipolar nature.24 They exhibit similar values of the 2PA cross section σ (σFMλmax = 120 GM and σλmaxMOFM = 110 GM), showing that both molecules are suitable candidates for two-photon microscopy experiments.
DFT and time-dependent density functional theory (TDDFT) simulations in implicit solvents provide important information on the orientation of dipole moments (Tables S2 and S3†): the transition dipole moment from the ground state S0 to the first excited state S1 is oriented along the long axis of the 3-ring moieties, while the ground-state dipole moment forms an angle of approximately 30° with respect to it. TDDFT results (Tables S4 and S5†) correctly reproduce the experimental solvatochromism with a bright first transition (with a HOMO–LUMO dominance; see molecular orbitals in Fig. S3 and S4†), while S0 → S2 appears to be a dark transition with a n → π* character. Interestingly, the behaviour is different in vacuum and S1 and S2 are reversed.
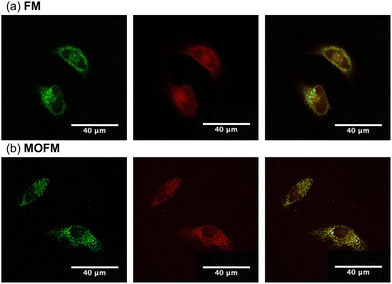
To assess the propensity of the compounds to selectively localize in mitochondria, we conducted experiments on HeLa cells stained with FM and MOFM. Measurements of cell viability (Fig. S9†) after 24 hours of incubation show that the compounds become toxic for the cells at concentrations above 1 μM. In order to reduce the effect of toxicity in further experiments, we performed measurements after incubating cells for 30 min using a concentration of 1.5 μM. Owing to the excellent optical properties of both FM and MOFM in terms of fluorescence quantum yield and molar extinction coefficient, the effects of toxicity can be mitigated by keeping the concentration at 1 μM or lower and adjusting the excitation power and/or detector gains to maintain high quality images. Images of HeLa cells stained with FM and MOFM (Fig. S10†) confirm the uptake of dyes, as is further evidenced by the red emission from the incubated cells (Fig. S8†). The images of HeLa cells incubated with FM and MOFM indicate that the dyes localize in some organelles. Therefore, we investigated co-localization of FM and MOFM with MitoTracker™ Green25 (MTG), a commercially available dye (Fig. 2). The Pearson correlation coefficients (PCCs), calculated from the resulting images, are PCCFM = 0.79 and PCCMOFM = 0.89, showing that both compounds selectively localize inside mitochondria, with MOFM having a stronger localization tendency compared to FM. While the PCC of MOFM is so high that we deem co-localization experiments in other organelles unnecessary, for FM we investigated possible localization in lysosomes by performing a co-localization experiment of FM and Lysotracker Green (Fig. S11†): the resulting PCC is 0.6, confirming a low degree localization within these organelles.
While for cationic trackers the physical localization mechanism is well understood, reports of neutral mitochondrial trackers often remain unclear or silent on their localization mechanism (sect. S5 and S6†). Here we propose a mechanism based on the electrostatic interaction between a neutral polar molecule and the inner mitochondrial membrane. A discussion of further reasonable mitochondrial localization mechanisms for neutral molecules is given in sect. S6;† however, we determined that they do not apply to the dyes presented in this work.
The interior of the inner mitochondrial membrane can be modeled as a phospholipid bilayer of palmitoyl-oleyl-phosphatidylcholine (POPC), while the intermembrane space and the mitochondrial matrix are considered aqueous solutions.26–28 The total electrostatic potential of a one-dimensional inner mitochondrial membrane is then given by:
| Φ(x, ΔΨNP) = ΦP(x, ΔΨNP) + ΦW(x, ΔΨNP) | (1) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) direction from the phospholipid bilayer (i.e. x → −∞) and the mitochondrial matrix being located in the +
direction from the phospholipid bilayer (i.e. x → −∞) and the mitochondrial matrix being located in the +![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) direction (x → +∞). The obtained fitted curves are shown on Fig. S12,† with the explicit functional forms and the fitted parameters given in sect. S7.†
direction (x → +∞). The obtained fitted curves are shown on Fig. S12,† with the explicit functional forms and the fitted parameters given in sect. S7.†
As can be seen from Fig. S13,† the calculated electric field across the membrane indeed exhibits significant variation on the length scale of FM and MOFM (≈10 Å), allowing for a net electrostatic force on the polar molecules. We consider a model in which we represent a molecule as a collection of N rigidly connected particles with respective masses mi and partial charges qi. The equations of motion for these particles in a spatially varying one-dimensional electric field 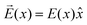 are:
are:
| miẍi = qiE(xi) | (2) |
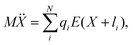 | (3) |
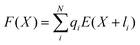 .
.
In a stationary state, the molecule will be oriented in such a way that the dipole moment 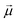 is aligned with
is aligned with 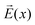 . Let us fix {l1…lN}, so that the dipole moment is parallel to the x-axis, i.e.
. Let us fix {l1…lN}, so that the dipole moment is parallel to the x-axis, i.e.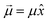 . Then, the respective electrostatic potential energies Ep±(x) for the two configurations with the dipole moment being (anti)parallel to the x-axis are simply:
. Then, the respective electrostatic potential energies Ep±(x) for the two configurations with the dipole moment being (anti)parallel to the x-axis are simply:
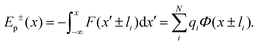 | (4) |
Note that x in eqn (4) denotes the position of the molecular center of mass. To obtain the ionic point charges qi, we calculate Mulliken charges from the ground state electronic density obtained by DFT optimizations of FM and MOFM in vacuum and water. We test different environments as it is not trivial to determine which is the most representative environment of the relevant realistic physical system.30 It is known that the center of the inner mitochondrial membrane is non-polar, with the value of the relative permittivity being ε ≈ 2, while the relative permittivity of the aqueous solutions representing the intermembrane space and the mitochondrial matrix is ε ≈ 80.28,30,31
From Table 1, we can see that the dipole moments calculated using Mulliken charges agree well with the dipole moments calculated directly from the electronic density obtained using DFT. Furthermore, we note that both molecules have large dipole moments and are highly polarizable. The large dipole moment is a result of donor and acceptor groups connected at the two ends of the conjugated molecular unit, similarly to push–pull molecules.
| Molecule | Solvent | μ ρ | μ M | E b + | E b − |
|---|---|---|---|---|---|
| FM | Vacuum | 12.346 | 13.253 | −347 | −326 |
| Water | 22.918 | 23.084 | −598 | −561 | |
| MOFM | Vacuum | 12.638 | 13.716 | −353 | −332 |
| Water | 23.211 | 23.492 | −606 | −570 |
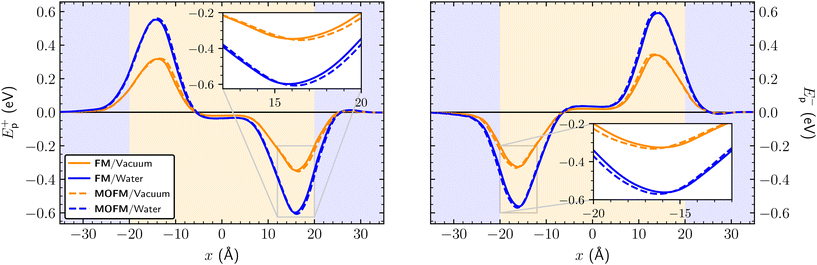
The electrostatic potential energies calculated as per eqn (4), using Mulliken charges obtained in different solvents and using ΔΨNP = −0.15 V, are shown on Fig. 3, with the binding energies Eb± (minimal values of Ep±(x)) being listed in Table 1. We find that two binding sites at x ≈ ± 16 Å exist for both FM and MOFM. These positions are found within the phospholipid bilayer, as the lipid heads are located at x ≈ ± 20 Å.29 Both binding sites are stable with respect to molecular rotations (Fig. S14†). From Table 1, we observe that the binding energy of the site near the mitochondrial matrix (Eb+) is consistently lower than the one of the site near the intermembrane space (Eb−). This asymmetry in the binding energies between the two sites stems from the polarization of the POPC and water subsystems due to ΔΨNP. Notably, we find that all calculated binding energies for MOFM are lower than the corresponding ones for FM, consistent with the experimental observation that MOFM has a larger tendency to localize in mitochondria compared to FM. Because of the difficulty in determining the most appropriate ionic charges (see discussion above), we consider the binding energies calculated using Mulliken charges obtained in vacuum (water) to represent the upper (lower) bound of the real electrostatic binding energy; however, we note that, due to the large solvatochromism of the considered molecules, the similarity in the measured emission spectra of MOFM in PBS (ε ≈ 79) and cells (Fig. S8†) indicates that the relevant physical environment could be best approximated by water.
To calculate the total binding energy, it is necessary to account for all molecule–membrane interactions other than the electrostatic one (e.g. hydrophobic, van der Waals, steric and specific chemical interactions). This is difficult to achieve without the use of more complex methods, i.e., a detailed study of molecular permeation through the inner mitochondrial membrane. We elect to leave this task to a future investigation and instead offer a qualitative assessment of the aforementioned factors. Using a simple lipophilicity model,32 we obtain log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P = 3 for both FM and MOFM, meaning that both molecules are significantly hydrophobic. This further enhances localization to the POPC bilayer.27,28 Steric and other factors have been shown to be of secondary importance in modeling hydrophobic ion interactions with membranes30 and are unlikely to hinder localization within the POPC bilayer, especially considering the large electrostatic binding energy, high lipophilicity and the comparatively small size of FM and MOFM with respect to some of the larger lipophilic mitochondria trackers.4–6
P = 3 for both FM and MOFM, meaning that both molecules are significantly hydrophobic. This further enhances localization to the POPC bilayer.27,28 Steric and other factors have been shown to be of secondary importance in modeling hydrophobic ion interactions with membranes30 and are unlikely to hinder localization within the POPC bilayer, especially considering the large electrostatic binding energy, high lipophilicity and the comparatively small size of FM and MOFM with respect to some of the larger lipophilic mitochondria trackers.4–6
Finally, we estimated the ratio of the concentrations of FM and MOFM localized in mitochondria. Due to the structural similarity of the considered molecules, we assume that the total binding energies of the two molecules significantly differ only in the electrostatic contribution. We can then use the following expression to approximate the ratio of concentrations of localized molecules:
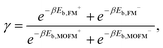 | (5) |
To further deepen our investigation, a computational investigation of a more specific localization scenario was attempted (sect. S8†). In general, the possibility that these dyes, once in the inner mitochondrial space, interact with specific sites (proteins) may deserve further investigations.
In this work, we reported on new red emitter neutral mitochondrial trackers constituted by substituted rhodol-based structures. Both FM and MOFM show specific mitochondrial localization, co-localizing with MTG to a very high degree, comparable to both cationic33,34 and neutral14 novel mitochondrial trackers. Moreover, FM and MOFM are red emitters that exhibit high fluorescence quantum yields and large extinction coefficients. This makes them suitable for use as fluorescent probes in bio-imaging at very low concentrations.23
Our combined experimental and computational study made it possible to suggest that the electrostatic interaction between molecular dipole moment and the electric field present at the inner mitochondrial membrane is responsible for the selective localization mechanism. By providing a straightforward and physically transparent model for the localization mechanism, we have made a significant step forward towards rational design of novel neutral mitochondrial trackers and understanding their localization in mitochondria.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 101007804-Micro4Nano. IF benefited from a PhD fellowship financed by PON R&I 2014–2020 (FSEREACT EU fundings). IF and CS also benefited from the equipment and framework of the COMP-HUB and COMP-R Initiatives, funded by the ‘Departments of Excellence’ program of the Italian Ministry for University and Research (MIUR, 2018–2022 and MUR, 2023–2027).References
- Y. Li, Y. Ma, Q.-Y. Dang, X.-R. Fan, C.-T. Han, S.-Z. Xu and P.-Y. Li, Life Sci., 2022, 306, 120834 CrossRef CAS PubMed.
- M. Karbowski and R. Youle, Cell Death Differ., 2003, 10, 870–880 CrossRef CAS PubMed.
- S. R. Pieczenik and J. Neustadt, Exp. Mol. Pathol., 2007, 83, 84–92 CrossRef CAS PubMed.
- H. Crawford, M. Dimitriadi, J. Bassin, M. T. Cook, T. F. Abelha and J. Calvo-Castro, Chem. – Eur. J., 2022, 28, e202202366 CrossRef CAS PubMed.
- B. A. Neto, J. R. Corrêa and R. G. Silva, RSC Adv., 2013, 3, 5291–5301 RSC.
- X. Zhang, Q. Sun, Z. Huang, L. Huang and Y. Xiao, J. Mater. Chem. B, 2019, 7, 2749–2758 RSC.
- D. G. Nicholls, Essays Biochem., 2010, 47, 25–35 CrossRef CAS PubMed.
- J. Jose, A. Loudet, Y. Ueno, R. Barhoumi, R. C. Burghardt and K. Burgess, Org. Biomol. Chem., 2010, 8, 2052–2059 RSC.
- B. A. D. Neto, J. R. Corrêa, P. H. Carvalho, D. C. Santos, B. C. Guido, C. C. Gatto, H. C. de Oliveira, M. Fasciotti, M. N. Eberlin and E. N. d. Silva Jr, J. Braz. Chem. Soc., 2012, 23, 770–781 CrossRef CAS.
- T. Gayathri, S. Karnewar, S. Kotamraju and S. P. Singh, ACS Med. Chem. Lett., 2018, 9, 618–622 CrossRef CAS PubMed.
- H. Yao, G. Wei, Y. Liu, H. Yao, Z. Zhu, W. Ye, X. Wu, J. Xu and S. Xu, ACS Med. Chem. Lett., 2018, 9, 1030–1034 CrossRef CAS PubMed.
- P. E. Kesavan, V. Pandey, M. K. Raza, S. Mori and I. Gupta, Bioorg. Chem., 2019, 91, 103139 CrossRef CAS PubMed.
- Y. Wang, B. Xu, R. Sun, Y.-J. Xu and J.-F. Ge, J. Mater. Chem. B, 2020, 8, 7466–7474 RSC.
- Á. Ramos-Torres, E. Avellanal-Zaballa, F. García-Garrido, A. B. Fernández-Martínez, A. Prieto-Castaneda, A. R. Agarrabeitia, J. Bañuelos, I. García-Moreno, F.-J. Lucio-Cazana and M. J. Ortiz, Chem. Commun., 2021, 57, 5318–5321 RSC.
- W. Ma, B. Xu, R. Sun, Y.-J. Xu and J.-F. Ge, J. Mater. Chem. B, 2021, 9, 2524–2531 RSC.
- B. Roy, M. C. Reddy, G. P. Jose, F. C. Niemeyer, J. Voskuhl and P. Hazra, J. Phys. Chem. Lett., 2021, 12, 1162–1168 CrossRef CAS PubMed.
- H. G. Agrawal, P. S. Giri, P. Meena, S. N. Rath and A. K. Mishra, ACS Med. Chem. Lett., 2023, 14, 1857–1862 CrossRef CAS PubMed.
- K. Neikirk, A. G. Marshall, B. Kula, N. Smith, S. LeBlanc and A. Hinton Jr, Eur. J. Cell Biol., 2023, 102, 151371 CrossRef CAS PubMed.
- F. Dong, M. Zhu, F. Zheng and C. Fu, FEBS J., 2022, 289, 262–278 CrossRef CAS PubMed.
- P. E. Klier, R. Roo and E. W. Miller, Curr. Opin. Chem. Biol., 2022, 71, 102203 CrossRef CAS PubMed.
- P. Bernardi, Physiol. Rev., 1999, 79, 1127–1155 CrossRef CAS PubMed.
- J. J. Lemasters, J. Gastroenterol. Hepatol., 2007, 22, S31–S37 CrossRef CAS PubMed.
- K. V. Vygranenko, Y. M. Poronik, A. Wrzosek, A. Szewczyk and D. T. Gryko, Chem. Commun., 2021, 57, 7782–7785 RSC.
- F. Terenziani, C. Katan, E. Badaeva, S. Tretiak and M. Blanchard-Desce, Adv. Mater., 2008, 20, 4641–4678 CrossRef CAS.
- A. D. Presley, K. M. Fuller and E. A. Arriaga, J. Chromatogr. B: Anal. Technol. Biomed. Life Sci., 2003, 793, 141–150 CrossRef CAS PubMed.
- B. Ketterer, B. Neumcke and P. Läuger,
![[J with combining low line]](https://www.rsc.org/images/entities/char_004a_0332.gif) .
. ![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif)
![[e with combining low line]](https://www.rsc.org/images/entities/char_0065_0332.gif)
![[m with combining low line]](https://www.rsc.org/images/entities/char_006d_0332.gif)
![[b with combining low line]](https://www.rsc.org/images/entities/char_0062_0332.gif)
![[r with combining low line]](https://www.rsc.org/images/entities/char_0072_0332.gif) .
. ![[B with combining low line]](https://www.rsc.org/images/entities/char_0042_0332.gif)
![[i with combining low line]](https://www.rsc.org/images/entities/char_0069_0332.gif)
![[o with combining low line]](https://www.rsc.org/images/entities/char_006f_0332.gif)
![[l with combining low line]](https://www.rsc.org/images/entities/char_006c_0332.gif) ., 1971, 5, 225–245 CAS.
., 1971, 5, 225–245 CAS. - R. F. Flewelling and W. L. Hubbell, Biophys. J., 1986, 49, 531–540 CrossRef CAS PubMed.
- M. F. Ross, G. Kelso, F. H. Blaikie, A. M. James, H. M. Cocheme, A. Filipovska, T. Da Ros, T. Hurd, R. A. Smith and M. P. Murphy, Biochemistry (Moscow), 2005, 70, 222–230 CrossRef CAS PubMed.
- L. Delemotte and M. Tarek,
![[J with combining low line]](https://www.rsc.org/images/entities/char_004a_0332.gif) .
. ![[M with combining low line]](https://www.rsc.org/images/entities/char_004d_0332.gif)
![[e with combining low line]](https://www.rsc.org/images/entities/char_0065_0332.gif)
![[m with combining low line]](https://www.rsc.org/images/entities/char_006d_0332.gif)
![[b with combining low line]](https://www.rsc.org/images/entities/char_0062_0332.gif)
![[r with combining low line]](https://www.rsc.org/images/entities/char_0072_0332.gif) .
. ![[B with combining low line]](https://www.rsc.org/images/entities/char_0042_0332.gif)
![[i with combining low line]](https://www.rsc.org/images/entities/char_0069_0332.gif)
![[o with combining low line]](https://www.rsc.org/images/entities/char_006f_0332.gif)
![[l with combining low line]](https://www.rsc.org/images/entities/char_006c_0332.gif) ., 2012, 245, 531–543 CAS.
., 2012, 245, 531–543 CAS. - R. F. Flewelling and W. L. Hubbell, Biophys. J., 1986, 49, 541–552 CrossRef CAS PubMed.
- B. H. Honig, W. L. Hubbell and R. F. Flewelling, Annu. Rev. Biophys. Biophys. Chem., 1986, 15, 163–193 CrossRef CAS PubMed.
- R. Mannhold, G. I. Poda, C. Ostermann and I. V. Tetko, J. Pharm. Sci., 2009, 98, 861–893 CrossRef CAS PubMed.
- X. Song, N. Li, C. Wang and Y. Xiao, J. Mater. Chem. B, 2017, 5, 360–368 RSC.
- T. Gao, H. He, R. Huang, M. Zheng, F.-F. Wang, Y.-J. Hu, F.-L. Jiang and Y. Liu, Dyes Pigm., 2017, 141, 530–535 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Theoretical and experimental methods; DFT and TDDFT analysis of ground and first-excited states; detailed spectroscopic characterization; cell viability and images of incubated cells; overview of mitochondrial localization mechanisms; fluorescence correlation spectroscopy and time-correlated single photon counting in HeLa cells; molecular dynamics and docking simulations. See DOI: https://doi.org/10.1039/d4ob00252k |
| ‡ These authors are equal contributors to this work and designated as co-first authors. |
| This journal is © The Royal Society of Chemistry 2024 |