Selective recognition between aromatics and aliphatics by cage-shaped borates supported by a machine learning approach

Abstract

Selective recognition between hydrocarbon moieties is a longstanding issue. Although we developed a π-pocket Lewis acid catalyst with high selectivity for aromatic aldehydes over aliphatic ones, a general strategy for catalyst design remains elusive. As an approach that transfers the molecular recognition based on multiple cooperative non-covalent interactions within the π-pocket to a rational catalyst design, herein, we demonstrate Lewis acid catalysts showing improved selectivity through the support of an ensemble algorithm with random forest, Ada Boost, and XG Boost as a machine learning (ML) approach. Using 7963 explanatory variables extracted from model hetero-Diels–Alder reactions, the ensemble algorithm predicted the chemoselectivity of unlearned catalysts. Experiments confirmed the prediction. The proposed catalyst shows the highest selective recognition, reminiscing enzymatic catalytic activity. Additionally, a SHapley Additive exPlanations (SHAP) method suggested that the selectivity originates from the polarizability and three-dimensional size of the catalyst. This insight leads to rational design guidelines for Lewis acid catalysts with dispersion forces.

---

Introduction

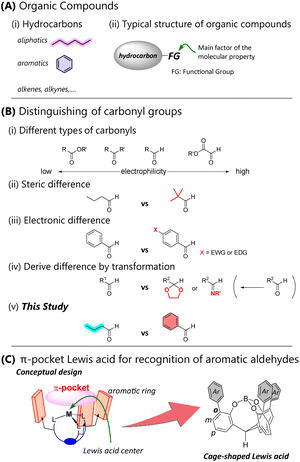
Hydrocarbons, which are composed of carbon and hydrogen atoms, are centerpiece skeletons of various molecules (Fig. 1A-i). The carbon framework and arrangement of carbon–carbon bonds govern the molecular properties. Hydrocarbons are mainly divided into aliphatic and aromatic compounds. These groups exhibit distinct characteristics, particularly in terms of their physical properties and reactivity. In organic compounds, heteroatoms are often introduced as functional groups into the hydrocarbon moieties. These functional groups contribute significantly to the overall properties of organic compounds (Fig. 1A-ii). Most organic compounds, except for simple hydrocarbons, are highly influenced by functional groups composed primarily of heteroatoms rather than the CH-built hydrocarbon moieties. When a carbonyl compound serves as a functional group, the reactivity depends on the substitution mode around the carbonyl carbon. Selective recognition between different carbonyls can be achieved by distinguishing them according to the order of reactivity. For example, Fig. 1B-i depicts the reactivity by electrophilicity: ester < ketone < aldehyde < glyoxylate.^1,2 Syntheses of organic molecules are designed using the difference in reactivity for selective bond formation. However, if the functional groups are the same (e.g., formyl groups in Fig. 1B-ii and iii), the hydrocarbon moieties must be distinguished. Hydrocarbon moieties with extremely different steric hindrance or electronic properties are easy to distinguish because chemical transformation of a functional group such as protection or modification changes the reactivity (Fig. 1B-iv).

Fig. 1 (A) Classification of organic compounds. (B) Distinguishing carbonyl groups based on the difference in reactivity in several ways. (C) Our concept to design a cage-shaped Lewis acid with a π-pocket to recognize aromatic aldehydes.

Distinguishing between aliphatic and aromatic aldehydes remains a longstanding issue because attaining selectivity can be a direct synthetic method for complicated molecules. Aliphatics and aromatics exhibit different properties. However, when aliphatic and aromatic moieties contain the same functional group, the properties of the functional group contribute strongly. Consequently, it is almost impossible for molecular catalysts to distinguish between them. Since aliphatics and aromatics are both hydrocarbons, their polarities are the same unless there is a noticeable difference in steric factors (Fig. 1B-v). Our research aims to develop catalysts that discriminate between aliphatic and aromatic aldehydes because Lewis acid mediated electrophilic reactions of carbonyls are the most fundamental and important reactions for carbon–carbon bond formation in the construction of many useful molecules. We realized a catalyst that selectively recognizes aromatic aldehydes by forming an aromatic π-pocket shaped skeleton around the Lewis acid site, which attracts carbonyl groups (Fig. 1C). A cage-shaped triphenolic ligand has established its effectiveness in controlling the Lewis acidity of a boron^3,4 or an aluminum atom.⁵ The decoration of the ligand framework endows the cage-shaped catalyst with tailored Lewis acidity,^6–9 chirality,¹⁰ and photoactivation.^11,12 In some cases, the π-pocket catalyst shows high selectivity for aromatic aldehydes compared to aliphatic ones.⁸ However, a general strategy for catalyst design has yet to be established. Although we speculate that the π-pocket moiety has affinity for aromatic compounds due to the π–π or CH–π interaction, the details remain unclear. Numerous experiments confirm a correlation between the catalyst structure and the selectivity, but conventional knowledge such as the steric or electrostatic environment of the π-pocket cannot explain this correlation. This may be because molecular recognition is defined by multiple cooperative non-covalent interactions within the π-pocket.⁹

Herein, we propose a new cage-shaped borate catalyst showing improved selectivity for aromatic compounds through the support of machine learning (ML). Recent advances in ML applications to organic synthetic chemistry^13–17 have significantly contributed to the predictions of yields and selectivity,^13,18 sequential searches for optimal reaction conditions,^19–21 and reverse structure searches for catalysts, ligands, or transient states,^{14,15,22–24} design of asymmetric catalysts,^25–33 predictions of site-selectivity for C–H functionalization catalyzed by a pocket-shaped Rh complex,³⁴ and estimations of the substrate specificity of enzymes.³⁵ Although these studies employed various algorithms, including linear algorithms (e.g., multivariate linear regression, Lasso,³⁶ Ridge,³⁷ and PLS³⁸), non-linear non-tree-based algorithms (e.g., GP,³⁹ MLP,⁴⁰ and SVR⁴¹) and non-linear tree-based algorithms (e.g., DT,⁴² RF,⁴³ and XGB⁴⁴), they all used individual algorithms to construct comprehensive models. In contrast, we propose an ensemble of algorithms to achieve stable and small root mean squared error for unlearned data (QRMSE) of the predicted selectivity. Our ensemble algorithm combines multiple non-linear tree-based algorithms with RF,⁴³ AB,⁴⁵ and XGB.⁴⁴ Since the underlying patterns and relationships in multiple chemical factors of the π-pocket catalyst should be analyzed and explored by data-driven methods, the application of ML may provide insight to design the π-pocket. If a high-performance model can be constructed to represent the relationships, it could predict the performance of new structured catalysts or existing catalysts under new reaction conditions. Furthermore, it may extract factors contributing to catalyst performance. Such information will not only elucidate reaction mechanisms but also aid in inverse analysis of catalyst structures to achieve the required performance.

Results and discussion

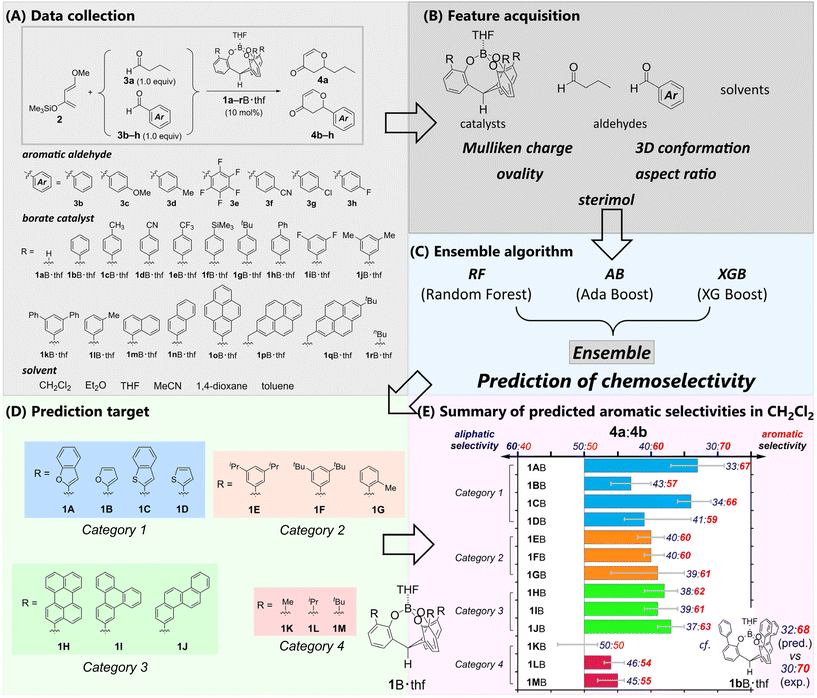
To propose suitable ML algorithms, we used the competitive hetero-Diels–Alder reactions of Danishefsky's diene 2 with an equimolar mixture of butanal 3a and benzaldehyde derivatives 3b–h catalyzed by cage-shaped Lewis acids⁴1a–rB·thf as model reaction systems (Fig. 2A, also see Fig. S1,† which depicts all the molecular structures of the described catalysts). There were 7963 explanatory variables for ML, including ordinary chemical descriptors generated from SMILES⁴⁶ by alvaDesc,⁴⁷ Mulliken charge, 3D conformation, ovality (real surface area/minimum surface area), aspect ratio, and sterimol⁴⁸ of each aldehyde, catalyst, and solvent (Fig. 2B and Fig. S12†). Cross-validation was conducted to compare different types of algorithms (Fig. S13–S17†). The cross-validation showed that neither individual algorithms nor combinations of two algorithms achieved a small QRMSE for all catalysts (Fig. S13 and S14†). Therefore, we applied an ensemble algorithm with RF,⁴³ AB,⁴⁵ and XGB⁴⁴ to propose the predicted selectivity (Fig. 2C). The ML approach based on an ensemble algorithm has attracted attention in other chemical fields.^49,50 Our ensemble algorithm gave a stable and small QRMSE for all catalysts and predicted the mean, maximum, and minimum values with the lowest mean and smaller deviation. The maximum and minimum values can be interpreted as an optimistic and pessimistic expectation, respectively. By employing the proposed algorithm, the selectivities of 13 new and not-yet-synthesized catalysts 1A–MB·thf were predicted (Fig. 2D). The various and unexplored π-pocket environments will provide insight into the nature of the chemoselectivity.

Fig. 2 Workflow from parameter generation and statistical modeling to prediction of chemoselectivity. (A) Summary of the datasets of the competitive reactions between 3a and 3b–h catalyzed by 1a–rB·thf for machine learning (ML). (B) Extraction of the explanatory variables for ML. (C) Proposed ensemble algorithm. (D) Target unlearned borate catalysts. (E) Predicted aromatic selectivity in CH₂Cl₂ from catalyst 1AB to catalyst 1MB. Bars show the predicted ensemble mean aromatic selectivity. Error bars indicate the ensemble minimum to ensemble maximum aromatic selectivity. As a reference, the predicted values of 1bB estimated by the algorithm as well as the experimental ones are shown.

To briefly describe the π-pocket environment, we divided these catalysts into four categories based on the components of their π-pocket. Category 1 (1AB–1DB) has π-pockets composed of heteroaromatics. Category 2 (1EB–1GB) possesses alkylated aryl groups. The π-pockets of category 3 (1HB–1JB) are built by polycyclic aromatic hydrocarbons. In category 4 (1KB–1MB), the aromatic moieties of the π-pockets are replaced with alkyl groups. The predictions indicated the importance of the aromatic moieties in the π-pocket (Fig. 2E, also see Fig. S19 and Table S21†). Catalysts in category 4 (1KB–1MB) showed little or no selectivity. The other catalysts in categories 1, 2, and 3 were predicted to show preferred selectivity for the aromatic aldehyde 3b. The catalysts in categories 2 (1EB–1GB) and 3 (1HB–1JB) exhibited moderate selectivities for 3b, and the small differences in selectivity were estimated for each borate. In contrast, the catalysts in category 1 demonstrated that the benzo-fusion into the heterole moieties effectively improved the predicted selectivity. Although the catalyst with a π-pocket consisting of a simple furan (1BB) or thiophene (1DB) showed poor selectivity (4a/4b = 43 : 57 (for 1BB) or 41 : 59 (for 1DB)), the predicted selectivity was enhanced for 1AB (4a/4b = 33 : 67) or 1CB (4a/4b = 34 : 66) due to the benzo-fusions to the heterole moieties. Minor structural changes can significantly improve the selectivity. Our curiosity regarding the prediction as well as the high synthetic accessibility of the catalysts in category 1 prompted us to experimentally investigate their selective recognition of aromatic aldehydes. In particular, complex 1AB, which has a π-pocket composed of 2-benzofuryl moieties, had the highest predicted selectivity and the narrowest range between the maximum and minimum prediction (Fig. 2D). Consequently, complex 1AB·thf was determined to be a viable experimental target (Table S21†).

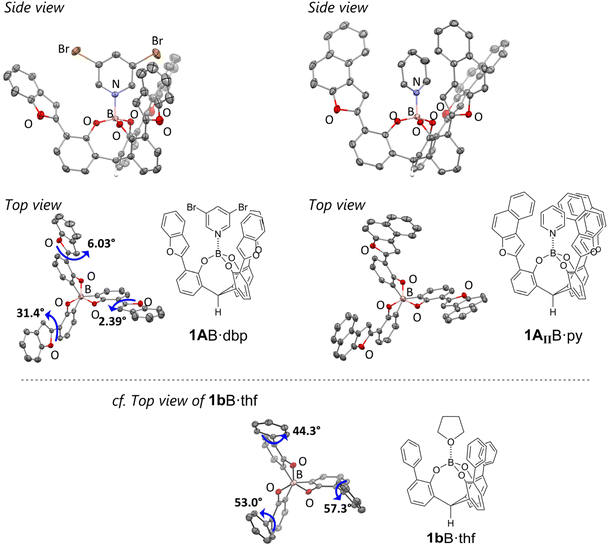
The cage-shaped boron complexes with the π-pocket composed of 2-benzofuryl moieties 1AB·L (L = tetrahydrofuran (thf), pyridine (py), or 3,5-dibromopyridine (dbp)) were synthesized according to our previous synthetic procedures (Scheme S1†).⁹ To compare the chemoselectivity of 1AB·L, complex 1BB·thf, which has a π-pocket composed of 2-furyl moieties, and several modified cage-shaped borates 1A_I–A_IVB·L with 2-benzofuryl-based π-pockets were also synthesized (Scheme S1†). All cage-shaped borates were fully characterized by ¹H, ¹³C, and ¹¹B NMR spectroscopy. The ORTEP drawings indicated that the three 2-benzofuryl groups effectively built a C₃-symmetric π-pocket around the boron center (Fig. 3). One significant difference in the geometry between 1AB and 1bB is the dihedral angle of the component aryl group of the π-pocket against the phenoxy moiety. The large angle (ave. 51.5°) of the phenyl group in 1bB·thf led to a twisted biaryl substructure,⁹ whereas the small angle (ave. 13.3°) of the 2-benzofuryl group in 1AB·dbp led to a coplanarized biaryl substructure. The observed difference is attributed to the presence or absence of steric hindrance due to the hydrogen atoms at the ortho-positions in each biaryl substructure. The ligand-exchange rate of the cage-shaped borates investigated by ¹H NMR measurements provided further information about the effect of the 2-benzofuryl-based π-pocket on the catalytic activity. Dimethylaminopyridine (DMAP) complexes of 1AB were dissolved in pyridine-d₅, and the ligand dissociation rate was measured during the ligand exchange from DMAP to pyridine. Table S1† summarizes the results. The kinetic analysis gave activation parameters of 1AB: ΔG^‡(293 K) = 29.1 kcal mol⁻¹, ΔH^‡ = 29.5 kcal mol⁻¹, ΔS^‡ = 1.46 cal K⁻¹ mol⁻¹, and k = 1.23 × 10⁻⁹ s⁻¹. The observed parameters are similar to those of 1bB: ΔG^‡(293 K) = 29.0 kcal mol⁻¹, ΔH^‡ = 31.2 kcal mol⁻¹, ΔS^‡ = 7.52 cal K⁻¹ mol⁻¹, and k = 1.16 × 10⁻⁹ s⁻¹,⁷ suggesting that the catalytic turnover efficiency does not significantly differ between 1AB and 1bB.

Fig. 3 ORTEP drawings of cage-shaped borates 1AB·dbp, 1A_IIB·py, and 1bB·thf with 50% probability ellipsoids. Some hydrogen atoms are omitted for clarity. In the top view, the ligated ligand (3,5-dibromopyridine (dbp), pyridine (py), and THF (thf)) on the boron center is omitted.

Borates 1AB·thf, 1BB·thf, and 1A_I–A_IVB·thf were applied as Lewis acid catalysts in competitive hetero-Diels–Alder reactions between 3a and various aromatic aldehydes 3b–f with diene 2. The adduct yields (4a + 4b–f) are listed in Table S2 in the ESI.† These borates sufficiently catalyzed all the reactions to give the corresponding adducts in acceptable yields.

Next, we compared the chemoselectivity for 3b–3f with that for 3a (Fig. 4). The ML-predicted borate 1AB·thf demonstrated chemoselectivity for benzaldehyde 3b over that of butanal 3a to give the corresponding adducts (4a/4b) in a ratio of 26 : 74 (purple bar in Fig. 4). This is improved selectivity compared to that of conventional o-phenylated 1bB·thf (4a/4b = 30 : 70, blue bar in Fig. 4).^8,9 Catalyst 1BB·thf, which ML predicted to have poor selectivity, experimentally showed sluggish selectivity (4a/4b = 46 : 54, pink bar in Fig. 4), confirming the importance of benzo-fusions to the furan moieties. Modified catalyst 1A_IB·thf, in which a methyl group was introduced at the 3-position of the 2-benzofuryl group of 1AB, had lower selectivity for 3b than for 3a (4a/4b = 34 : 66, green bar in Fig. 4), implying that the introduced methyl groups into the 2-benzofuryl group shrink the π-pocket and inhibit the substrate uptake. Borate 1A_II–A_IVB·thf with a π-pocket constructed by π-extended naphthofuryl groups exhibited comparable chemoselectivity for 3b and 3a to 1AB·thf (Fig. 4A). For benzaldehyde derivatives bearing an electron-donating group (3c and 3d, Fig. 4B and C), ML-predicted borate 1AB·thf showed improved chemoselectivity for aromatic aldehydes over that for 3a, relative to the catalytic system of 1bB·thf. Notably, the competitive reaction catalyzed by 1AB·thf between butanal 3a and anisaldehyde 3c, which exhibited relatively low reactivity due to the electron-donating group, showed slightly enhanced chemoselectivity (4a/4c = 45 : 55) compared to that catalyzed by 1bB·thf (4a/4c = 49 : 51). Even allowing for experimental error, the slightly enhanced chemoselectivity for 4c was a common trend in the series of catalysts with a furan-based π-pocket (1AB·thf, 1BB·thf and 1A_II–A_IVB·thf). Our previous report⁹ showed such a better combination of the π-pocket and aromatic aldehyde, and the investigation of the details of the origin was continued. For the competitive reaction between aromatic aldehydes bearing electron-withdrawing groups (3e and 3f, Fig. 4D and E) and butanal 3a catalyzed by 1AB·thf and 1A_II–A_IVB·thf, higher selectivity for aromatic aldehydes over that for 3a was generally observed. The highest selectivities for 3f (4a/4f = 9 : 91–7 : 93) achieved with 1AB·thf and 1A_II–A_IVB·thf were comparable to our previously reported results.⁹

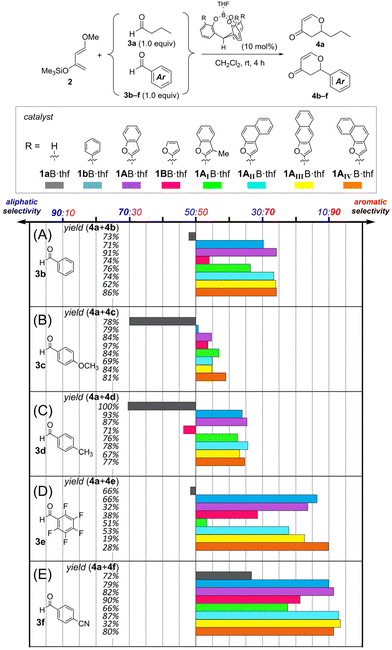Fig. 4 Observed chemoselectivity and total yield (4a + 4b–4f) in the competitive hetero-Diels–Alder reactions of 3a and various benzaldehyde derivatives 3b–f. rt = 25 °C.

Theoretical calculations provided insight into the higher chemoselectivity assisted by ML-predicted borate 1AB. Fig. S8† summarizes the computational results of the reaction mechanisms for the hetero-Diels–Alder reactions of 2 with 3a/b catalyzed by borate 1AB·thf. Like our catalytic reaction of 1bB·thf,⁹ the hetero-Diels–Alder reaction can be divided into three steps: (1) preorganization (reactants → IM1 → IM2) to form the inclusion complex 1AB·3⊃2, which takes up the substrates into the π-pocket, (2) C–C bond formation (IM2 → TS1 → IM3) between 2 and 3 in the π-pocket, and (3) subsequent C–O bond formation (IM3 → TS2 → products) to afford the adduct–borate complex 1AB·5. Although step 3 is the rate-determining step as it shows the highest activation energy at TS2 (ΔG^‡(3a) = 8.8 kcal mol⁻¹ and ΔG^‡(3b) = 9.6 kcal mol⁻¹), the observed chemoselectivity is hard to explain using the difference between the activation energies of 3a and 3b. This implies that step 3 with low and similar activation energies barely participates in the chemoselectivity caused by the π-pocket of 1AB. The situation is identical to that of our previous study.⁹ Alternatively, we found a significant difference in the stabilization energy (ΔE_S) for the inclusion complex 1AB·3⊃2 in the preorganization step. For reactions catalyzed by 1bB and 1AB, the stabilization energy of the inclusion complex with 3b was always larger than that with 3a.⁹ However, the energy difference in ΔE_S between 3a and 3b (ΔΔE_S = |ΔE_S(3b) − ΔE_S(3a)|) was larger in the catalytic system of 1AB (ΔΔE_S = 6.6 kcal mol⁻¹) than that in 1bB (ΔΔE_S = 5.5 kcal mol⁻¹).⁹ The enhanced stabilization in the inclusion complex 1AB·3b⊃2 was attributed to the large dispersion energy. Among the compared systems 1AB·3a⊃2, 1bB·3a⊃2, and 1bB·3b⊃2, the inclusion complex 1AB·3b⊃2 had the largest dispersion energy calculated at the B3LYP-D3(BJ)/6-31G** level⁵¹ (Table 1). From the NCI plots,^52,53 a slightly larger NCI area was demonstrated in the π-pocket of 1AB·3b⊃2 (Fig. S10 and S11†). Notably, borate 1AB was proposed by the ML based on structural and electronic factors of the related borates themselves and not those of the inclusion complex with the substrates. Hence, our established algorithm may be extended to predict the essential intermediates in the preorganization step that determine the chemoselectivity driven by the π-pocket concept.

Table 1 Summary of the stabilization energy (ΔE_S) in the reactions catalyzed by 1AB and 1bB

Entry	Inclusion complex	ΔES/kcal mol^−1	Dispersion energy^a/kcal mol^−1
a Grimme's D3 dispersion correction with Becke–Johnson (BJ) damping calculated at the B3LYP/6-31G**//ωB97XD/def2svp level.
1	1AB·3a⊃2	−11.6	−203.6
2	1AB·3b⊃2	−18.2	−215.6
3^9	1bB·3a⊃2	−24.8	−188.9
4^9	1bB·3b⊃2	−30.3	−198.4

---

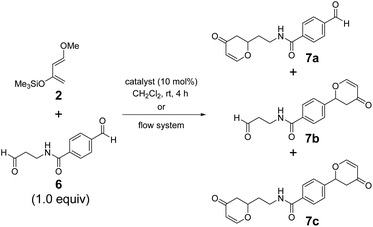
The chemoselectivity of borate 1AB·thf was significantly highlighted in the intramolecular recognition of aromatic moieties. We investigated hetero-Diels–Alder reactions of 2 with dialdehyde 6, where the aromatic and aliphatic carbonyl groups were separated by an amide group spacer, as model systems (Table 2). The reaction of dialdehyde 6 prepared from a β-alanine derivative with 2 showed higher selectivity. Borate 1AB·thf successfully recognized the aromatic moiety of 6 and exhibited excellent selectivity under the standard conditions (7a/7b/7c = 8 : 82 : 10, entry 1). Our previous borates 1aB·thf and 1bB·thf did not achieve the result of 1AB·thf. Instead, they showed a poor ratio of the products (7a/7b/7c = 39 : 22 : 39 (1aB·thf, entry 3) and 20 : 58 : 22 (1bB·thf, entry 4)). Conventional Lewis acids did not show catalytic activity or the desired selectivity (entries 5–7). The ratio of the products given by 1AB·thf under the standard conditions improved to 7a/7b/7c = 8 : 90 : 2 (entry 2) when using the flow system.⁹ Although aldehyde 6 contained a secondary amide group, which can act as a strong anchor toward the Lewis acidic center, borate 1AB remarkably recognized the aromatic moiety in 6. The behavior of 1AB is reminiscent of a certain kind of enzymatic catalytic activity based on selective molecular recognition.^54,55 Hence, 1AB holds promise as a catalyst for late-stage functionalization of complex biomolecules bearing various functional groups.

Table 2 Intramolecular recognition of the aromatic carbonyl group of 6^a

Entry	Catalyst	Condition	Yield/% (7a + 7b + 7c)	Ratio 7a/7b/7c
a rt = 25 °C.
1	1AB·thf	Batch	62	8/82/10
2	1AB·thf	Flow system	25	8/90/2
3	1aB·thf	Batch	47	39/22/39
4	1bB·thf	Batch	72	20/58/22
5	BF3·Et2O	Batch	7	34/65/1
6	TiCl4	Batch	17	81/9/10
7	SnCl4	Batch	16	49/14/37

---

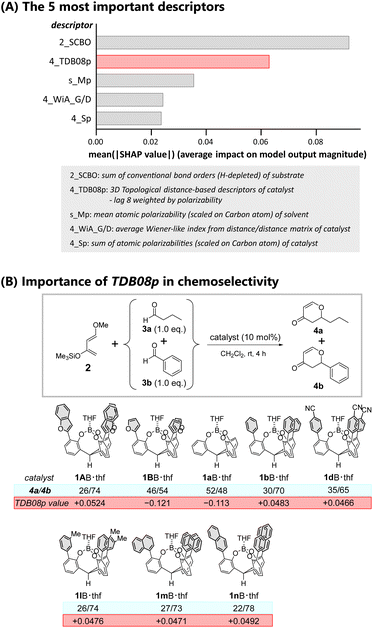
Further analysis of the ML-proposed predictions rationalized the observed highest performance of catalyst 1AB. We evaluated the contribution of each of the employed molecular descriptors to the predicted chemoselectivity using a Shapley Additive exPlanations (SHAP) method. The SHAP method was introduced in cooperative game theory to assess the contribution of each feature.⁵⁶Fig. 5A summarizes the top five extracted molecular descriptors (also see Fig. S22†). The top two molecular descriptors (2_SCBO and 4_TDB08p) contributed significantly to the predicted chemoselectivity, while the other variables had a modest contribution. Herein 2_SCBO (sum of conventional bond orders (H-depleted)) corresponds to the three-dimensional size of a substrate weighted by the number of composed covalent bonds, while 4_TDB08p (three-dimensional topological distance-based descriptors – lag 8 weighted by polarizability) corresponds to the three-dimensional size of a catalyst weighted by its molecular polarizability. 2_SCBO decisively influenced the chemoselectivity. The selectivity for aromatic aldehydes with substituents and fewer hydrogen atoms such as pentafluorobenzaldehyde 3e and 4-cyanobenzaldehyde 3f was high compared to that for butanal 3a. Among the employed aldehydes, the increase in the conventional bond order is intuitively associated with the lower LUMO levels of the carbonyl, promoting selective hetero-Diels–Alder reactions.

Fig. 5 (A) The five most important descriptors of the mean absolute SHAP value. (B) Correlation between the observed chemoselectivity (4a/4b) and the value of TDB08p for selected catalysts. rt = 25 °C.

Although the large SCBO contribution of the substrate to the predicted chemoselectivity was expected, the contribution of the TDB08p of the catalyst is truly thought provoking. We previously noted that catalysts possessing a π-pocket constructed by meta-substituted phenyl (1lB) or 1-(1mB)/2-naphthyl (1nB) moieties showed higher selectivity for aromatic aldehydes than catalysts with a π-pocket constructed by para-substituted (1c–hB, and their π-extended analogues 1o–qB) or 3,5-disubstituted (1i–kB) aromatic moieties. Considering the importance of polarizability in characterizing the molecular descriptor TDB08p, the lower symmetric substituent patterns of the π-pocket should sustain the averaged molecular polarizability of the catalyst, realizing high selectivity for aromatic aldehydes. Fig. 5B clearly shows the correlation. Catalysts 1lB, 1mB, and 1nB with positive TDB08p values larger than that of 1dB possessing para-cyano groups showed enhanced chemoselectivities. For the predicted reactions catalyzed by 1AB·thf and 1BB·thf in CH₂Cl₂, Table S22† provides further evidence of the importance of the contribution of TDB08p. The TDB08p value of 1AB·thf (+0.0524) is the most positive among all catalysts. In contrast, the value of 1BB·thf (−0.121) suggests an enduring negative effect on selectivity. The DFT calculations also supported the difference in molecular polarizability between 1AB and 1BB (1AB: 5.01 Debye; 1BB: 2.48 Debye).

A π-extended aromatic moiety with large polarizability is advantageous to promote non-covalent interactions within the π-pocket space in the reaction step. Notably, understanding the molecular structure–property relationship with the aid of the ML-based insight elucidated the previously unidentified origin of the chemoselectivity of the π-pocket. The size and polarizability of the π-pocket are crucial to determine the relationship. These findings provide insight to design π-pockets as molecular recognition sites.

Conclusions

In summary, we introduce an ML algorithm to predict the chemoselective activation of the carbonyl group through the π-pocket structure of a cage-shaped borate. Our algorithm successfully predicted the structure of the Lewis acid catalyst showing high selectivity. According to the ML predictions, we synthesized and characterized cage-shaped borate 1AB possessing a π-pocket constructed by three 2-benzofuryl groups. The fundamental properties of 1AB such as Lewis acidity and catalytic turnover efficiency are similar to those of our conventional borate 1bB, which has a π-pocket constructed by three phenyl groups. However, borate 1AB more effectively stabilizes the taken up substrates in its π-pocket due to the significant dispersion interactions. Consequently, 1AB realizes higher chemoselectivity for aromatic aldehydes than for butanal in the inter- and intramolecular competitive hetero-Diels–Alder reactions.

The present study not only introduces new borate-based Lewis acid catalysts with π-pocket cavities but also highlights the importance of weak and multiple dispersion forces working within aromatic cavities. The combination of the experimental studies with the DFT calculations, the ML approach, and the SHAP analysis proposed an essential factor for the Lewis acid catalyst showing peculiar selectivity driven by the π-pocket: molecular polarizability. We believe that this strategy, assisted by the ML approach, broadens the design of other catalysts exhibiting selectivity based on dispersion forces, which enables distinguishing between carbon frameworks and a direct synthetic methodology for useful organic molecules.

Author contributions

All authors discussed the results and commented on the manuscript. M. Y. conceived the project and played a critical role in discussions of the experimental design, project direction, experiments and results, and preparation of the manuscript. Y. T. designed and carried out the experiments. A. K. acquired and analysed the X-ray crystallographic data and performed quantum chemical calculations. I. Y. and K. T. performed the ML and analysed the obtained data. M. K., S. T., and R. K. interpreted the ML investigations and wrote the discussion on the ML. Y. T., A. K., K. T., and M. Y. wrote the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the MEXT Grant-in-Aid for Transformative Research Areas (A) “Digitalization-driven Transformative Organic Synthesis (Digi-TOS)” (JP21H05212 [MY], JP21H05222 [KT], JP21H05217 [ST and MK], and JP21H05221 [RK]), by JST CREST (JPMJCR20R3 [MY]), and by the Japan Society for the Promotion of Science (JP23K17845 [MY], JP23H01950 [AK], and JP23KJ1437 [YT]). A. K. also thanks the “Condensed Conjugation” (JP23H04028 [AK]). We acknowledge the Analytical Instrumentation Facility, Graduate School of Engineering, Osaka University.

References

1. H. Miyabe and Y. Takemoto, in Comprehensive Organic Synthesis, ed. P. Knochel, Elsevier, Amsterdam, 2nd edn, 2014, pp. 751–769.
2. M. B. Smith, March's Advanced Organic Chemistry: Reactions, Mechanisms, and Structure, Wiley, 8th edn, 2020.
3. M. Yasuda, S. Yoshioka, S. Yamasaki, T. Somyo, K. Chiba and A. Baba, Org. Lett., 2006, 8, 761–764.
4. M. Yasuda, S. Yoshioka, H. Nakajima, K. Chiba and A. Baba, Org. Lett., 2008, 10, 929–932.
5. D. Tanaka, Y. Kadonaga, Y. Manabe, K. Fukase, S. Sasaya, H. Maruyama, S. Nishimura, M. Yanagihara, A. Konishi and M. Yasuda, J. Am. Chem. Soc., 2019, 141, 17466–17471.
6. A. Konishi, K. Nakaoka, H. Nakajima, K. Chiba, A. Baba and M. Yasuda, Chem. – Eur. J., 2017, 23, 5219–5223.
7. M. Yasuda, H. Nakajima, R. Takeda, S. Yoshioka, S. Yamasaki, K. Chiba and A. Baba, Chem. – Eur. J., 2011, 17, 3856–3867.
8. H. Nakajima, M. Yasuda, R. Takeda and A. Baba, Angew. Chem., Int. Ed., 2012, 51, 3867–3870.
9. D. Tanaka, Y. Tsutsui, A. Konishi, K. Nakaoka, H. Nakajima, A. Baba, K. Chiba and M. Yasuda, Chem. – Eur. J., 2020, 26, 15023–15034.
10. A. Konishi, K. Nakaoka, H. Maruyama, H. Nakajima, T. Eguchi, A. Baba and M. Yasuda, Chem. – Eur. J., 2017, 23, 1273–1277.
11. A. Konishi, R. Yasunaga, K. Chiba and M. Yasuda, Chem. Commun., 2016, 52, 3348–3351.
12. Y. Tsutsui, D. Tanaka, Y. Manabe, Y. Ikinaga, K. Yano, K. Fukase, A. Konishi and M. Yasuda, Chem. – Eur. J., 2022, 28, e202202284.
13. A. M. Żurański, J. I. Martinez Alvarado, B. J. Shields and A. G. Doyle, Acc. Chem. Res., 2021, 54, 1856–1865.
14. D. J. Durand and N. Fey, Acc. Chem. Res., 2021, 54, 837–848.
15. J. M. Crawford, C. Kingston, F. D. Toste and M. S. Sigman, Acc. Chem. Res., 2021, 54, 3136–3148.
16. K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555.
17. P. Raccuglia, K. C. Elbert, P. D. F. Adler, C. Falk, M. B. Wenny, A. Mollo, M. Zeller, S. A. Friedler, J. Schrier and A. J. Norquist, Nature, 2016, 533, 73–76.
18. D. T. Ahneman, J. G. Estrada, S. Lin, S. D. Dreher and A. G. Doyle, Science, 2018, 360, 186–190.
19. Y. Amar, A. M. Schweidtmann, P. Deutsch, L. Cao and A. Lapkin, Chem. Sci., 2019, 10, 6697–6706.
20. M. Kondo, H. D. P. Wathsala, M. Sako, Y. Hanatani, K. Ishikawa, S. Hara, T. Takaai, T. Washio, S. Takizawa and H. Sasai, Chem. Commun., 2020, 56, 1259–1262.
21. M. I. Jeraal, S. Sung and A. A. Lapkin, Chem.: Methods, 2021, 1, 71–77.
22. M. Moskal, W. Beker, S. Szymkuć and B. A. Grzybowski, Angew. Chem., Int. Ed., 2021, 60, 15230–15235.
23. N. Noto, A. Yada, T. Yanai and S. Saito, Angew. Chem., Int. Ed., 2023, 62, e202219107.
24. S. Akita, J.-Y. Guo, F. W. Seidel, M. S. Sigman and K. Nozaki, Organometallics, 2022, 41, 3185–3196.
25. S. Zhao, T. Gensch, B. Murray, Z. L. Niemeyer, M. S. Sigman and M. R. Biscoe, Science, 2018, 362, 670–674.
26. J. P. Reid and M. S. Sigman, Nature, 2019, 571, 343–348.
27. A. F. Zahrt, J. J. Henle, B. T. Rose, Y. Wang, W. T. Darrow and S. E. Denmark, Science, 2019, 363, eaau5631.
28. S. Yamaguchi and M. Sodeoka, Bull. Chem. Soc. Jpn., 2019, 92, 1701–1706.
29. N. I. Rinehart, A. F. Zahrt, J. J. Henle and S. E. Denmark, Acc. Chem. Res., 2021, 54, 2041–2054.
30. J. Werth and M. S. Sigman, ACS Catal., 2021, 11, 3916–3922.
31. H. Chen, S. Yamaguchi, Y. Morita, H. Nakao, X. Zhai, Y. Shimizu, H. Mitsunuma and M. Kanai, Cell Rep. Phys. Sci., 2021, 2, 100679.
32. E. Miller, B. K. Mai, J. A. Read, W. C. Bell, J. S. Derrick, P. Liu and F. D. Toste, ACS Catal., 2022, 12, 12369–12385.
33. E. Y. Xu, J. Werth, C. B. Roos, A. J. Bendelsmith, M. S. Sigman and R. R. Knowles, J. Am. Chem. Soc., 2022, 144, 18948–18958.
34. R. C. Cammarota, W. Liu, J. Bacsa, H. M. L. Davies and M. S. Sigman, J. Am. Chem. Soc., 2022, 144, 1881–1898.
35. S. L. Robinson, M. D. Smith, J. E. Richman, K. G. Aukema and L. P. Wackett, Synth. Biol., 2020, 5, ysaa004.
36. G. James, D. Witten, T. Hastie and R. Tibshirani, An Introduction to Statistical Learning, Springer New York, New York, NY, 2013, vol. 103.
37. A. E. Hoerl and R. W. Kennard, Technometrics, 1970, 12, 55–67.
38. S. Wold, J. Trygg, A. Berglund and H. Antti, Chemom. Intell. Lab. Syst., 2001, 58, 131–150.
39. C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, The MIT Press, 2006.
40. J. C. Platt, Adv. Large Margin Classif., 1999, 10, 61–74.
41. G. E. Hinton, Artif. Intell., 1989, 40, 185–234.
42. L. Breiman, J. H. Friedman, R. A. Olshen and C. J. Stone, Classification And Regression Trees, Routledge, 2017.
43. L. Breiman, Mach. Learn., 2001, 45, 5–32.
44. T. Chen and C. Guestrin, in Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Association for Computing Machinery, New York, NY, USA, 2016, pp. 785–794.
45. Y. Freund and R. E. Schapire, in Computational Learning Theory, ed. P. Vitányi, Springer Berlin Heidelberg, Berlin, Heidelberg, 1995, pp. 23–37.
46. D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36.
47. alvaDesc, https://www.affinity-science.com/alvadesc/.
48. A. Verloop, W. Hoogenstraaten and J. Tipker, in Drug Design, ed. E. J. Ariëns, Academic Press, Amsterdam, 1976, vol. 11, pp. 165–207.
49. P. Hu, Z. Jiao, Z. Zhang and Q. Wang, Ind. Eng. Chem. Res., 2021, 60, 11627–11635.
50. J. M. Schmitt, J. M. Baumann and M. M. Morgen, Pharm. Res., 2022, 39, 3223–3239.
51. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
52. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
53. J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632.
54. D. Fiedler, D. H. Leung, R. G. Bergman and K. N. Raymond, Acc. Chem. Res., 2005, 38, 349–358.
55. Z. Zhang and P. R. Schreiner, Chem. Soc. Rev., 2009, 38, 1187.
56. S. M. Lundberg and S.-I. Lee, in Proceedings of 31st Conference in Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 2017.

---

Footnote

† Electronic supplementary information (ESI) available: Synthetic procedures, and spectroscopic, computational, and machine learning data. CCDC 2297702 (1AB·dbp) and 2297703 (1A_IIB·py). For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4ob00408f

---