Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Computational methods for investigating organic radical species
Tim
Renningholtz
a,
Ethan R. X.
Lim
a,
Michael J.
James
 *a and
Cristina
Trujillo
*a and
Cristina
Trujillo
 *ab
*ab
aThe University of Manchester, Oxford Road, Manchester, M13 9PL, UK. E-mail: michael.james@manchester.ac.uk; cristina.trujillodelvalle@manchester.ac.uk
bTBSI – School of Chemistry, The University of Dublin, Trinity College, D02 R590 Dublin 2, Ireland
First published on 2nd July 2024
Abstract
Computational analysis of organic radical species presents significant challenges. This study compares the efficacy of various DFT and wavefunction methods in predicting radical stabilisation energies, bond dissociation energies, and redox potentials for organic radicals. The hybrid meta-GGA M062X-D3(0), and the range-separated hybrids ωB97M-V and ωB97M-D3(BJ) emerged as the most reliable functionals, consistently providing accurate predictions across different basis sets including 6-311G**, cc-pVTZ, and def2-TZVP.
1 Introduction
Computational chemistry is routinely used to help rationalise and provide insight into the reactivity of organic radical species.1–8 In the field of organic chemistry, experimentalists are increasingly eager to accurately model and assess the thermodynamic feasibility of organic radical reactions (as illustrated in Fig. 1). These reactions involve molecules containing unpaired electrons, adding a layer of complexity to their study. However, there are conflicting reports regarding the suitability of common methods to study such open-shell species.9 Computationally demanding wavefunction-based methods, which are normally highly reliable for closed-sell systems, often suffer from complications regarding spin contamination.10 Therefore, less computationally expensive DFT methods are often employed due to their greater speed and resilience to spin contamination. However, determining the most suitable methods for describing radical species, particularly when employing basis sets with lower computational costs, can be challenging, especially for those new to the field.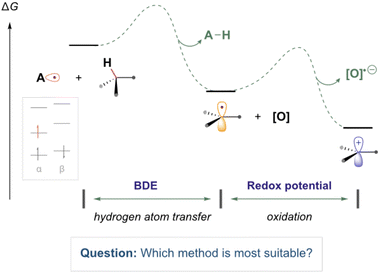 | ||
| Fig. 1 An illustrative reaction process containing common reaction steps of relevance to this work (electron transfer and hydrogen atom transfer). | ||
One solution to this problem may be to avoid traditional approaches entirely and instead apply machine learning (ML) techniques to predict the outcomes of quantum mechanical calculations. Indeed, while this field is still in its infancy, a few pioneering papers have begun to explore the utility of ML to predict properties related to radical species, such as bond dissociation energies (BDEs).11–17 Although not the primary focus of this paper, the potential of ML within the context of organic radical chemistry should be acknowledged.
Turning our attention to quantum computational methods, we sought to examine the performance of selected computational methods and basis sets in the context of organic synthetic chemistry. A total of 12 different DFT functionals and three basis sets were evaluated to find the best methods to reliably calculate radical stabilisation energies (RSEs), BDEs and redox potentials. These properties were selected due to their significance in characterising both neutral and ionic radical species, ensuring a broad analysis of radical behaviour.
The DFT functionals selected for this study were chosen based on their prevalent use in organic chemistry,18 those which performed best in the GMTKN55 dataset,19 and to evenly cover each rung of Jacob's ladder (see Table 1). Jacob's ladder is a commonly used concept in computational chemistry to classify density functional approximations (DFAs) based on the terms included in the exchange–correlation functional.20 Additional terms are included at each rung (see Table 1), which are thought to improve the accuracy of the functional, while increasing the computational cost. In this study, we focus only on the three highest rungs, since lower rung functionals are rarely used for modelling molecular systems.
| Rung | Functional | Component |
|---|---|---|
| Rung 5: Double hybrids | DSD-PBEP86, ωB97X-2 | Non-local MP2 correlation |
| Rung 4: Global and range-separated hybrids | ωB97M, CAM-B3LYP, B3LYP, B3LYP, M062X, PBE0 | Non-local Fock exchange |
| Rung 3: Meta-GGA | B97M, M06L | Gradients of the electron density and kinetic energy |
While Goerigk et al.21 and Najibi and Goerigk22 describe benchmarks against the GMTKN55 dataset, which covers many different types of reactivity and properties, some properties or conclusions might be only marginally relevant to experimental researchers looking to solely study radical species. However, these benchmarks provide the foundation of general guidelines such as the use of dispersion correction schemes for DFAs.
In addition, recent studies by Nie, Zhang and co-workers highlighted the importance of dispersion corrections to accurately calculate the BDEs of X–NO2 bonds.23 Therefore, dispersion corrections were included for all functionals (see Fig. 2), as demonstrated by Goerigk, Grimme, and co-workers with the GMTKN55 benchmark dataset.21
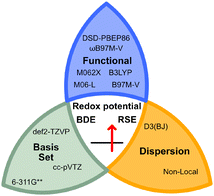 | ||
| Fig. 2 Selection of the benchmarked functionals, basis sets, and dispersion corrections used in this study. The studied properties are highlighted in the centre of the knot. | ||
The “gold standard” CCSD(T) and CCSD methods were chosen for wavefunction-based methods. Considering that most MP2 methods are known to suffer from severe spin contamination, the orbital-optimised spin component-scaled MP2 (OO-RI-SCS-MP2) method developed by Neese and co-workers was selected as this approach was shown to effectively eliminate spin contamination from the wavefunction.24
The accuracy of a chosen computational method is inherently influenced by the basis set used. Therefore, we evaluated the performance of three moderately-sized and commonly used basis sets for each method. These included the 6-311G** Pople,25,26 cc-pVTZ Dunning,27,28 and def2-TZVP Ahlrichs basis sets.29
It is important to emphasise that, while the conclusions drawn from this study are significant, they should not be regarded as universally applicable. However, we aim for this work to serve as a valuable resource and reference for researchers studying organic radical species, offering insights and guidance in navigating the complexities of computational methodologies in this field.
2 Computational methods
All quantum chemical calculations were performed using ORCA 5.0.4,30 which was interfaced with xtb31 6.6.1 for executing GFN2-xTB32 calculations. The investigated methods are comprised of twelve density functional approximations with either non-local33,34 or atom-pairwise35,36 treatment of dispersion interactions, and three wavefunction-based methods. The methods were invoked with the following keywords RI-DSD-PBEP86 NL,37 RI-wB97X-238 D3BJ,39 wB97M-V,40 wB97M-D3BJ,22 CAM-B3LYP41 D3BJ,42 B3LYP43,44 D3BJ,35 B3LYP43,44 NL34, M062X45 D3ZERO,42 PBE046 D3BJ,36 B97M-V,47 B97M-D3BJ,22,47 M06L48 D3ZERO,42 OO-RI-SCS-MP2,24,49 CCSD,50,51 CCSD(T).51 The dispersion parameters for the ωB97X-2 functional were taken from Mehta et al.,39 while the ORCA default parameters were used for all other methods. Dispersion corrections were applied non self-consistently to the final energy. The respective Coulomb-fitting auxiliary basis sets (AuxJ) were used according to the ORCA default settings.29,52 The resolution of identity (RI) approximation with the respective auxiliary basis sets (AuxC) was used for the MP2-based correlated methods.52–54 If no suitable auxiliary basis set was available (e.g. for 6-311G**), either the AutoAux keyword was invoked or no RI approximation was used with the NORI keyword. Frequency calculations and thermostatistical corrections were performed within the quasi-rigid rotor harmonic oscillator approximation.2.1 Radical stabilisation energy
Radical stabilisation energies constitute a measure of the stability of a radical species relative to a reference radical, typically the methyl radical (˙CH3):| ˙CH3 + R–H → CH4 + R˙ | (1) |
The radical R˙ is more stable than the methyl radical, if the reaction is exothermic. Therefore, the RSE is an indicator of the stabilising or destabilising effect of the substituent R on the radical species and is often employed to estimate the reactivity and formation of organic radical species.11
The performance of each method and the three different basis sets was evaluated on the RSE43 dataset, which is a subset of the GMTKN55 database.21,24 This dataset comprises carbon-centred radicals adjacent to various electron-donating (EDG) and electron-withdrawing (EWG) groups. The RSE43 geometries had been generated with B3LYP/TZVP,24 and additional geometries were generated by re-optimising these geometries with B3LYP-D3(BJ)/def2-TZVP, and GFN2-xTB for this benchmark. Electronic single-point energies were compared with published reference values obtained using the W1-F12 protocol with B3LYP/TZVP geometries.21,55 All systems were treated with the unrestricted formalism. The radical stabilisation energy relative to the methyl radical (˙CH3) were calculated based on the homodesmotic reaction as defined in eqn (1).
| RSE = E(CH4) + E(R˙) − (E(˙CH3) + E(R–H)) | (2) |
The deviation of the calculated RSE (RSEcalc) from the reference value (RSEref) is calculated as
| ΔRSE = RSEcalc − RSEref | (3) |
Hence, the RSE is overestimated if ΔRSE > 0, and underestimated if ΔRSE < 0.
2.2 Bond dissociation energy
The performance of each method was also evaluated against a dataset comprised of 43 experimentally reported BDE values,56 including C–H, N–H, O–H, and C–N bonds adjacent to both EDG and EWG groups. For wavefunction-based methods, all species were described with the unrestricted formalism. For DFT methods, only open-shell species were described with the unrestricted formalism. Geometries were generated with B3LYP-D3(BJ)/def2-TZVP and vibrational frequency calculations were performed at the same level (T = 298.15 K; ideal gas p = 1 bar) to confirm that the obtained geometries were local minima and to calculate thermochemistry corrections. Electronic single-point calculations were performed on these geometries using the selected method and these energies were converted into enthalpies using the B3LYP-D3(BJ)/def2-TZVP corrections. The DEFGRID3 keyword was added to the input of all BDE calculations. BDEs were calculated based on three reaction classes:| BDE = ΔH°(R˙) + ΔH°(˙H) − ΔH°(R–H) | (4) |
| BDE = ΔH°(R˙) + ΔH°(˙NO) − ΔH°(R–NO) | (5) |
| BDE = ΔH°(R˙) + ΔH°(˙NO2) − ΔH°(R–NO2) | (6) |
2.3 Redox potentials
The OROP dataset, a sub-dataset of the OROP313 benchmark dataset, was used to assess the performance of DFT methods to reproduce experimental redox potentials of small to medium-sized organic molecules (5–82 atoms).57 This dataset consists of 193 one-electron transfer systems in their oxidised and reduced form. Wavefunction-based methods were not assessed in this benchmark due to resource restraints.Redox potentials were determined following the workflow outlined by Neugebauer et al.:57 (i) obtain optimised geometries for oxidised and reduced species; (ii) harmonic frequency analysis for thermostatistical corrections; (iii) single point energy calculations; and (iv) correcting for solvation energies.
The initial geometries for the oxidised and reduced species were obtained from the original work,57 and were reoptimised using B97-3c58 composite method and the GFN2-xTB semi-empirical for consistency reasons. Additionally, the published B97-3c geometries were reoptimised with B3LYP-D3(BJ)/def2-TZVP. Thermostatistical corrections were obtained with each of the three methods at room temperature (T = 298.15 K; ideal gas p = 1 bar) using the Freq keyword, and the NumFreq True setting in case of GFN2-xTB. The minima were confirmed by the absence of imaginary frequencies greater than 10 i cm−1.
Single-point energies were obtained for each functional using the def2-TZVP, 6-311G**, and cc-PVTZ basis sets. Those systems containing iodine were only evaluated using the def2-TZVP basis set since the other two basis sets do not describe iodine basis functions. The solvation model based on density (SMD)59 was employed in the single point calculations to obtain corrections for the solvation energy for each benchmark method, using acetonitrile or dimethylformamide (DMF) as solvent. Those species with an odd number of electrons were treated using the unrestricted scheme, while those with even numbers of electrons were treated using the restricted formalism. Redox potentials were calculated from the free energies 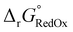 and the absolute potential of the reference electrode
and the absolute potential of the reference electrode 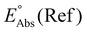 using the Nernst equation:
using the Nernst equation:
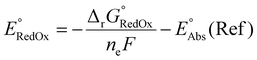 | (7) |
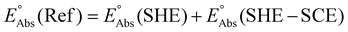 | (8) |
The free energy 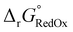 was obtained by applying the thermostatistical
was obtained by applying the thermostatistical 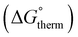 and solvation energy corrections
and solvation energy corrections 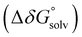 to the adiabatic ionisation potential (IP):
to the adiabatic ionisation potential (IP):
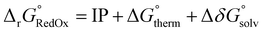 | (9) |
The absolute reference potential was adapted from the primary sources which use the saturated calomel electrode (SCE) as their experimental and computational reference.60,61
3 Results and discussion
3.1 Bond strengths – neutral radicals
Our investigations began by examining the ability of the selected methods to accurately describe bond strengths, as these values are often fundamental to the design of new synthetic reactions. Considering how the prediction and interpretation of experimental findings is a major goal of computational chemistry, it was deemed pertinent to analyse data sets based on both theoretical and experimental data. Accordingly, two datasets were selected, both aimed at characterising the strength of a particular bond:(i) The established RSE43 dataset comprises 43 radical stabilisation energies.21
(ii) A new dataset based on 43 experimentally determined BDE values.56 Importantly, previous studies in this area highlighted that DFT methods might struggle to describe systems with lone-pair–radical (three-electron) interactions,9 so the dataset was selected with a bias towards such systems.
To evaluate the descriptive capabilities of the different methods under study, reliance was placed on various statistical metrics, including the Mean Absolute Error (MAE) and Mean Error (ME), which were calculated based on reported experimental or computational reference values. These metrics offer valuable insights into the accuracy and precision of computational predictions, facilitating comparison of the different methodologies.
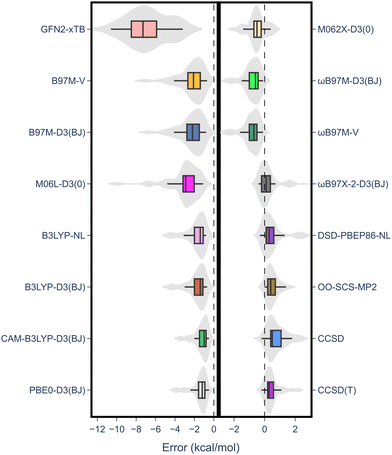
The results from the RSE43 dataset are depicted in Fig. 3. The wavefunction-based methods exhibited the lowest MAEs, indicating their superior accuracy in predicting RSEs. The density functionals, on the other hand, generally showed overall higher MAEs compared to wavefunction-based methods, with notable exceptions. The double-hybrid functional ωB97X-2-D3(BJ) was one of the most accurate among the different functionals covered, with errors below 1 kcal mol−1. Furthermore, the hybrid meta-GGA functional M062X-D3(0) demonstrated a notably low MAE. M062X-D3(0) therefore provides a favourable compromise between accuracy and computational cost, making it an attractive choice for practical applications. The range-separated hybrids also performed generally well, except for CAM-B3LYP-D3(BJ). Global hybrid functionals performed poorly, except as noted for M062X-D3(0). The least accurate functionals belong to the third rung of Jacob's ladder, meta-GGA, which exhibited the highest MAEs consistently. The performance of the semi-empirical GFN2-xTB method was also briefly assessed, but the errors were significant. Interestingly, the different approaches for treating dispersion did not significantly impact the results and no clear pattern emerged regarding one type of dispersion correction being superior to another.
 | ||
| Fig. 3 MAE values for all methods under study against the RSE43 dataset. The reference values were obtained using the W1-F12 composite method.21 | ||
Notably, there was a discernible trend regarding basis sets. Specifically, for both DFT and wave-function-based methods, def2-TZVP consistently outperformed the other two sets. In contrast, the smaller 6-311G** Pople basis set performed worse across the board, except for the M06L-D3(0) meta-GGA functional. Thus, to gain further insight into the performance of each method, the error distribution using the def2-TZVP basis set was investigated (Fig. 4). Here, errors ranged from −12 to 2 kcal mol−1. From this analysis, it became evident that density functionals tended to underestimate the RSE, while single-reference-based dynamic correlation methods such as MP2 or CC, seemed to overestimate the RSE. Additionally, outliers are observed within the dataset, appearing as either mild or hard outliers, depending on their deviation from the mean of the distribution. These outliers originate predominantly from systems presenting unsaturations. In summary, while methods such as M062X-D3(0) and B3LYP-D3(BJ)/NL exhibit relatively few mild outliers, the presence of hard outliers is mainly attributed to DSD-PBEP86-NL. As expected, GFN2-xTB demonstrates the highest error distribution.
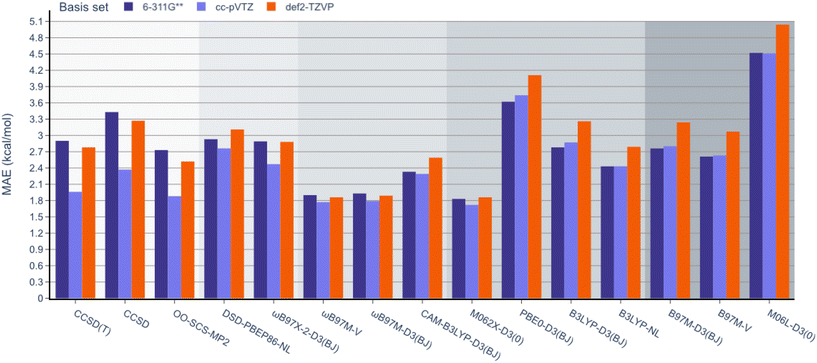
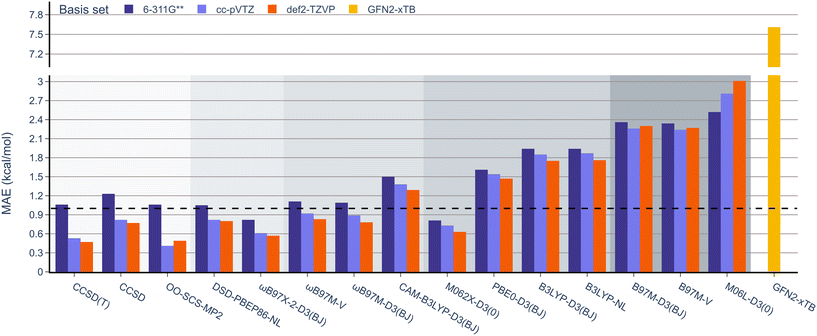
Next, unlike the gradual decrease in MAE observed when climbing the rungs of Jacob's ladder for the RSE43 dataset, results from the experimental BDE dataset were far more varied (Fig. 5). Here, the hybrid meta-GGA functional M062X-D3(0) and range-separated hybrids ωB97M-V and ωB97M-D3(BJ) displayed the smallest MAEs and outperformed the three wavefunction-based methods. The double-hybrid functionals performed comparably to the global hybrid and meta-GGA functionals—excluding PBE0-D3(BJ) and M06L-D3(0), respectively.
Interestingly, single-reference-based dynamic correlation methods, MP2 and CC, performed noticeably better with the cc-pVTZ basis set, which is perhaps unsurprising, as the correlation-consistent basis sets are often used in post-HF calculations. To further study the importance of the basis set in these calculations, the BDE dataset was reanalysed using the larger 6-311G(3df,3pd), cc-pVQZ Dunning, and def2-QZVP basis sets for the top performing M062X-D3(0) functional (Table 2). The MAE values were reduced from 1.83 to 1.66 kcal mol−1 by adding more polarisation functions to the 6-311G Pople basis sets (entries 1 and 2). However, the larger cc-pVTZ and cc-pVQZ Dunning basis sets gave very similar results (1.72 and 1.74 kcal mol−1, respectively, entries 3 and 4). Finally, increasing the Ahlrichs basis set from triple to quadruple zeta slightly reduced the MAE from 1.86 to 1.79 kcal mol−1 (entries 5 and 6). It is important to note that these values are all very close to the typical uncertainty ranges of the reported experimental data, so further increasing the size of the basis set is unlikely to improve the accuracy of these results.
| Entry | Basis set | MAE (kcal mol−1) |
|---|---|---|
| 1 | 6-311G** | 1.83 |
| 2 | 6-311G(3df,3pd) | 1.66 |
| 3 | cc-pVTZ | 1.72 |
| 4 | cc-pVQZ | 1.74 |
| 5 | def2-TZVP | 1.86 |
| 6 | def2-QZVP | 1.79 |
3.2 Redox potentials – ionic radicals
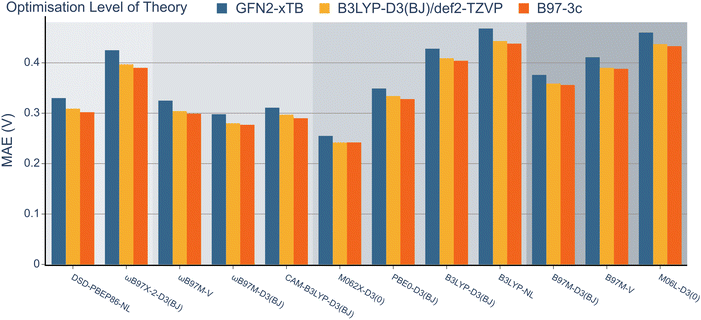
Having explored the description of neutral organic radicals, our attention turned toward ionic radical species. To achieve this, redox potentials from the OROP dataset were identified as excellent properties to benchmark the selected methods.First, to investigate the impact of the geometry optimisation method, geometries from the OROP dataset were reoptimised using the B97-3c composite method, semi-empirical GFN2-xTB, and B3LYP-D3(BJ). Redox potentials were then calculated using each set of geometries and the 12 density functional methods with the def2-TZVP basis set (Fig. 6, note that wavefunction-based methods were omitted due to resource restraints). The differences between each geometry optimisation method were minimal and the MAE values obtained for all functionals remained within the range of 0.2 to 0.5 V. The GFN2-xTB geometry optimisation method consistently exhibited the highest MAE value for each method, while the B97-3c method consistently resulted in the lowest MAE values throughout. However, the B97-3c and B3LYP-D3(BJ) methods often resulted in nearly identical MAE values. Consequently, both the composite method and B3LYP-D3(BJ) appear to offer accurate structures within a comparable range, although it should be noted that frequency calculations are less computationally expensive for B97-3c.
Next, the effect of the basis set was examined as in the previous section (Fig. 7). Pleasingly, the mean absolute errors (MAEs) consistently remained below 1.0 V in all cases. On examination of different functionals, M062x-D3(0) exhibited the lowest MAE, followed by the range-separated hybrids. Interestingly, similar to the BDE analysis, the double hybrids did not noticeably outperform the range-separated hybrids. Except for PBE0-D3(BJ), both B3LYP-D3(BJ) and B3LYP-NL global hybrids performed slightly worse than meta-GGA functionals.
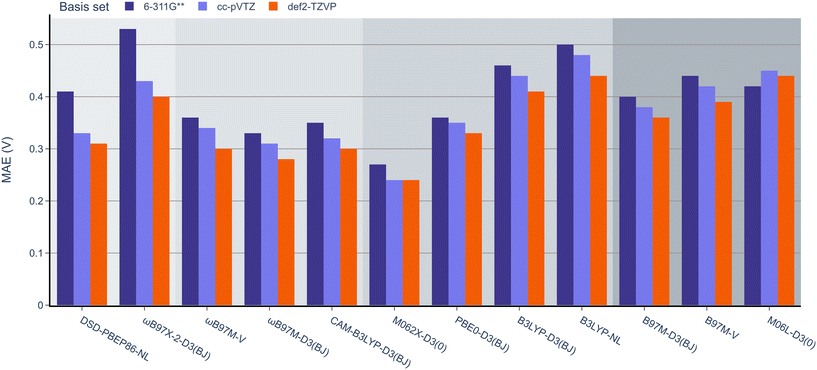 | ||
| Fig. 7 MAE values for B3LYP-D3(BJ) def2-TZVP geometries and 12 DFT functionals with the 6-311G**, def2-TZVP, and cc-pVTZ basis sets against the experimental OROP dataset. | ||
When examining the effect of the different basis sets, the same trend noted for the RSE-43 dataset was observed. Specifically, def2-TZVP resulted in the lowest MAEs for each method, while 6-311G** resulted in the highest errors, most notably for the double hybrids.
When comparing the different dispersion schemes used, it can be noted that the atom-pairwise dispersion correction yields lower errors than the non-local dispersion model for the same functional (see Fig. 6 and 7). On average, the MAE for the D3(BJ) corrected ωB97M and B3LYP functionals using the def2-TZVP basis set is 0.03 V (≈0.7 kcal mol−1) lower than for the same functionals using the non-local dispersion model. We attribute the influence of the dispersion model on the MAE to the larger systems in this dataset. The BDE and RSE43 datasets contain only small molecules (up to 30 atoms), for which either dispersion model seems to be accurate.
4 Conclusions
This benchmarking study enables selected DFT and wavefunction methods to be compared for their ability to describe organic radical species through the prediction of RSEs, BDEs, and redox potentials. For the prediction of RSEs, the hybrid meta-GGA functional M062X-D3(0) was notable for its low MAEs, which were comparable to much more computationally expensive wavefunction and double-hybrid methods. For the prediction of experimentally determined BDEs and redox potentials, the hybrid meta-GGA functional M062X-D3(0) exhibited the lowest MAEs of all methods studied. Consistent with recent studies,12,13,62,63 it appears that M062X-D3(0) represents an excellent and resource-efficient starting point for calculating the electronic energies and thermodynamic properties of organic radical species. After M062X-D3(0), the range-separated hybrids ωB97M-V and ωB97M-D3(BJ) also performed strongly for the prediction of RSEs, BDEs, and redox potentials. It is also important to note that the MAEs for these three recommended functionals were quite consistent regardless of the chosen basis set, which reinforces confidence in the robustness of these methods.While barrier heights/activation energies have not been studied in this work, the performance of M062X-D3(0), ωB97M-V, and ωB97M-D3(BJ) has already been tested against other relevant data sets. For example, in the BH76 barrier-height test set, the mean absolute deviation (MAD) values for M062X-D3(0), ωB97M-V, and ωB97M-D3(BJ) were 2.34, 1.60, and 1.41 kcal mol−1, respectively.21,22 Collectively, these findings suggest that these functionals may be reliably employed to model full reaction profiles and explore potential reaction mechanisms.
In conclusion, it is important to stress that the recommended functionals will not provide a perfect universal answer for every problem, but they may serve as valuable starting points for the investigation of organic radical species.
Author contributions
Conceptualisation, supervision and writing – M. J. J., C. T.; investigation, methodology, and visualisation – T. R., E. R. X. L.; all authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
T. R. thanks The University of Manchester for the PhD studentship. E. R. X. L. thanks the EPSRC Centre for Doctoral Training in Integrated Catalysis (EPSRC grant: EP/S023755/1) for a PhD Studentship. For the purpose of Open Access, the author has applied a CC BY public copyright licence to any Author Accepted Manuscript version arising from this submission. The authors acknowledge the assistance provided by Research IT and the use of the Computational Shared Facility at The University of Manchester.References
- I. Iribarren, M. R. Garcia and C. Trujillo, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1616 CAS.
- S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009 CrossRef CAS PubMed.
- A. G. Collar, C. Trujillo and S. J. Connon, Chem. – Eur. J., 2019, 25, 7270–7274 CrossRef CAS.
- D. A. Strassfeld, R. F. Algera, Z. K. Wickens and E. N. Jacobsen, J. Am. Chem. Soc., 2021, 143, 9585–9594 CrossRef CAS PubMed.
- A. Shoja and J. P. Reid, J. Am. Chem. Soc., 2021, 143, 7209–7215 CrossRef CAS.
- C. L. Jarvis, J. S. Hirschi, M. J. Vetticatt and D. Seidel, Angew. Chem., Int. Ed., 2017, 56, 2670–2674 CrossRef CAS.
- P. H.-Y. Cheong, C. Y. Legault, J. M. Um, N. Çelebi Ölçüm and K. N. Houk, Chem. Rev., 2011, 111, 5042–5137 CrossRef CAS PubMed.
- Y.-h. Lam, M. N. Grayson, M. C. Holland, A. Simon and K. N. Houk, Acc. Chem. Res., 2016, 49, 750–762 CrossRef CAS.
- E. I. Izgorodina, D. R. B. Brittain, J. L. Hodgson, E. H. Krenske, C. Y. Lin, M. Namazian and M. L. Coote, J. Phys. Chem. A, 2007, 111, 10754–10768 CrossRef CAS.
- A. S. Menon and L. Radom, J. Phys. Chem. A, 2008, 112, 13225–13230 CrossRef CAS PubMed.
- S. Sowndarya S. V., P. C. St. John and R. S. Paton, Chem. Sci., 2021, 12, 13158–13166 RSC.
- S. Sowndarya S. V., J. N. Law, C. E. Tripp, D. Duplyakin, E. Skordilis, D. Biagioni, R. S. Paton and P. C. St. John, Nat. Mach. Intell., 2022, 4, 720–730 CrossRef.
- P. C. St. John, Y. Guan, Y. Kim, S. Kim and R. S. Paton, Nat. Commun., 2020, 11, 2328 CrossRef.
- M. Nakajima and T. Nemoto, Sci. Rep., 2021, 11, 20207 CrossRef CAS PubMed.
- L.-C. Yang, X. Li, S.-Q. Zhang and X. Hong, Org. Chem. Front., 2021, 8, 6187–6195 RSC.
- M. Tavakoli, Y. T. T. Chiu, P. Baldi, A. M. Carlton and D. Van Vranken, J. Chem. Inf. Model., 2023, 63, 1114–1123 CrossRef CAS PubMed.
- J. Lu, H. Zhang, J. Yu, D. Shan, J. Qi, J. Chen, H. Song and M. Yang, J. Chem. Inf. Model., 2021, 61, 4259–4265 CrossRef CAS.
- J. L. Borioni, M. Puiatti, D. M. A. Vera and A. B. Pierini, Phys. Chem. Chem. Phys., 2017, 19, 9189–9198 RSC.
- L. Goerigk, Advanced Electronic Structure Methods in Computational Quantum Chemistry, 2024, pp. 78–93 Search PubMed.
- J. P. Perdew and K. Schmidt, AIP Conf. Proc., 2001, 577, 1–20 CrossRef CAS.
- L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215 RSC.
- A. Najibi and L. Goerigk, J. Chem. Theory Comput., 2018, 14, 5725–5738 CrossRef CAS PubMed.
- J. Liu, X. He, Y. Xiong, F. Nie and C. Zhang, Def. Technol., 2023, 22, 144–155 CrossRef.
- F. Neese, T. Schwabe, S. Kossmann, B. Schirmer and S. Grimme, J. Chem. Theory Comput., 2009, 5, 3060–3073 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1493 CAS.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS.
- O. A. Vydrov and T. V. Voorhis, J. Chem. Phys., 2010, 133, 244103 CrossRef PubMed.
- W. Hujo and S. Grimme, J. Chem. Theory Comput., 2011, 7, 3866–3871 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- S. Kozuch and J. M. L. Martin, Phys. Chem. Chem. Phys., 2011, 13, 20104–20107 RSC.
- J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2009, 131, 174105 CrossRef PubMed.
- N. Mehta, M. Casanova-Páez and L. Goerigk, Phys. Chem. Chem. Phys., 2018, 20, 23175–23194 RSC.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2016, 144, 214110 CrossRef.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CAS.
- L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688 RSC.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2015, 142, 074111 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef.
- S. Grimme, J. Chem. Phys., 2003, 118, 9095–9102 CrossRef CAS.
- T. D. Crawford and H. F. Schaefer III, in An Introduction to Coupled Cluster Theory for Computational Chemists, John Wiley & Sons, Ltd, 2000, pp. 33–136 Search PubMed.
- R. J. Bartlett and M. Musiał, Rev. Mod. Phys., 2007, 79, 291–352 CrossRef CAS.
- G. L. Stoychev, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2017, 13, 554–562 CrossRef CAS PubMed.
- F. Weigend, A. Köhn and C. Hättig, J. Chem. Phys., 2002, 116, 3175–3183 CrossRef CAS.
- A. Hellweg, C. Hättig, S. Höfener and W. Klopper, Theor. Chem. Acc., 2007, 117, 587–597 Search PubMed.
- A. Karton and J. M. L. Martin, J. Chem. Phys., 2012, 136, 124114 CrossRef PubMed.
- Y.-R. Luo, Comprehensive Handbook of Chemical Bond Energies, CRC Press, 1st edn, 2007 Search PubMed.
- H. Neugebauer, F. Bohle, M. Bursch, A. Hansen and S. Grimme, J. Phys. Chem. A, 2020, 124, 7166–7176 CrossRef CAS PubMed.
- J. G. Brandenburg, C. Bannwarth, A. Hansen and S. Grimme, J. Chem. Phys., 2018, 148, 064104 CrossRef PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS.
- M.-H. Baik and R. A. Friesner, J. Phys. Chem. A, 2002, 106, 7407–7412 CrossRef CAS.
- H. Roth, N. Romero and D. Nicewicz, Synlett, 2015, 714–723 Search PubMed.
- I. Y. Zhang, J. Wu, Y. Luo and X. Xu, J. Comput. Chem., 2011, 32, 1824–1838 CrossRef CAS.
- G. L. C. de Souza and K. A. Peterson, J. Phys. Chem. A, 2021, 125, 198–208 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |