Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electrostatically hindered diffusion for predictable release of encapsulated cationic antimicrobials†
Viktor
Eriksson
 a,
Erik
Nygren
b,
Romain
Bordes
a,
Erik
Nygren
b,
Romain
Bordes
 a,
Lars
Evenäs
a,
Lars
Evenäs
 a and
Markus
Andersson Trojer
a and
Markus
Andersson Trojer
 *ac
*ac
aDepartment of Chemistry and Chemical Engineering, Chalmers University of Technology, Gothenburg, Sweden
bDepartment of Bioeconomy and Health, RISE Research Institutes of Sweden, Gothenburg, Sweden
cDepartment of Materials and Production, RISE Research Institutes of Sweden, Mölndal, Sweden. E-mail: markus.andersson-trojer@ri.se
First published on 19th February 2024
Abstract
A common challenge in infection control is uncontrolled and unpredictable rapid release of antimicrobials – with ramifications on antimicrobial resistance (AMR) development and pollution – that makes it difficult to determine appropriate dosage levels and treatment times. An important class of antimicrobials is surface-active cationic substances, whose charge can be exploited for manipulating both their encapsulation and controlled release. As a proof of concept, the cationic antimicrobial octenidine dihydrochloride (OCT) was encapsulated in a microcapsule matrix of poly(D,L-lactide-co-glycolide) (PLGA) bearing anionic carboxylate end groups. The strong PLGA–OCT interaction was verified by infrared spectroscopy and by comparing the release of OCT to its uptake into empty microcapsules. By expanding a Fickian diffusion model, the binding event was estimated to result in a 10-fold reduction in effective diffusivity resulting in a sustained release maintained for several months. Using this model, the impacts of temperature and release medium solubilizers were globally examined to improve predictability. By exceeding the glass transition temperature of hydrated PLGA, the diffusional release was significantly faster at 37 °C with a diffusivity 200 times that at room temperature. The addition of solubilizers increased the OCT partitioning towards the aqueous phase without affecting its diffusivity.
1. Introduction
One of the main factors leading to non-healing chronic wounds is related to bacterial colonization in the wound bed, which can be prevented through the use of topical antibiotics.1 With the emergence and increasing prevalence of resistance to common antibiotics in bacteria,2 alternatives to the classical antibiotics are desired. The amphiphilic and cationic octenidine dihydrochloride (OCT) has been developed as a promising alternative to other topical antiseptics in the last decades.3 For several common both Gram-positive and Gram-negative bacteria, minimum inhibitory concentrations (MICs) of OCT on the order of milligrams per liter have been reported.4 This illustrates its broad-spectrum antimicrobial activity through disruption of the microbial cell envelope.5A key factor for a successful antimicrobial treatment is the administration of the drug in and to the wound site. For most topical treatments, the antimicrobial is applied in the form of an ointment/cream or as an impregnation of a wound dressing. This leads to (1) an initial fast and excessive release of the antimicrobial followed by the release of low doses for a longer period of time, (2) a subsequent rapid loss of antimicrobial functionality, and (3) patient suffering since more frequent changes of the wound dressings are required. Yet an additional serious ramification is that the uncontrolled release of antimicrobials is a driver for antimicrobial resistance (AMR) development since it is well established that administration of antimicrobials at low concentrations below the MIC over time leads to resistant strains.6
To circumvent these problems and enable long-term efficacy, a controlled and continuously sustained release of OCT to the wound is consequently desired. Such sustained release has been given significant attention in pharmaceutical settings where microcapsule formulations have been developed for a sustained release of both small organic drugs as well as larger biomolecules.7–9 These microcapsules act as a rate-limiting barrier for release, relying either on the restricted diffusivity of the active inside the capsules,10 erosion of the microcapsule matrix, or a combination of both.11 We have previously shown that microcapsules can be incorporated into a multitude of different biobased polysaccharide fibers, to yield a macroscopic controlled release material/dressing for use in e.g. wound care.12 From these materials, the release was exclusively determined by the microcapsules.10 Restricted diffusivity is controlled by factors such as the porosity of the microcapsule matrix whereas the erosion is affected by the surrounding media (pH, temperature). More importantly in the case of the cationic OCT, restricted diffusivity is also affected by specific interactions between the matrix and active.13
The encapsulation and subsequent release of OCT has previously only been studied for a limited selection of delivery vehicles, such as mesoporous silica nanoparticles14 and polylactide-based micro- or nanocapsules.15,16 Regarding the latter, the encapsulation of OCT into polylactide-based capsules was hypothesized to be dependent on electrostatic interactions between cationic OCT and anionic carboxylate end groups of the polylactides.15,16 This hypothesis has never been verified, nor has the potential influence of this electrostatic interaction on the sustained release of OCT been studied and quantified.
We have therefore in this work encapsulated OCT into poly(D,L-lactide-co-glycolide) (PLGA) microcapsules bearing anionic end groups to study and model the influence of the electrostatic interaction on both encapsulation and release. To control and predict the release behavior, it is crucial that the most important release parameters can be incorporated into and tested against a model based on diffusional behavior. We have therefore evaluated the effect of temperature (i) and the external release medium composition (ii) as described below. Most importantly, we have extended our model based on Fickian diffusion, whose analytical solution to a spherical geometry (microcapsule) has been derived by Crank,17 to additionally encompass (iii) the hypothesized electrostatic interaction between OCT and PLGA and its influence on the hindered diffusion of the former.
(i) The microcapsule structure is temperature dependent due to the low PLGA glass transition temperature (Tg) of around 30 °C in its hydrated state.18 This should therefore affect the diffusivity of OCT within the microcapsules, and thereby its release rate. With the focus on pharmaceutical formulations in the literature, release measurements are usually performed at physiological temperatures (37 °C) and reports on the effects of temperature are therefore limited.19,20 We have consequently performed release measurements at both ambient (22 °C) and physiological temperatures to understand how temperature fluctuations could affect the release rate.
(ii) The external release medium is a less studied factor that nonetheless is important for release predictability. In complex biological media, amphiphilic proteins, polysaccharides, or phospholipids can usually be found which all could have solubilizing properties. Here, we have therefore varied the affinity of OCT to the release medium in a controlled manner through the addition of a nonionic surfactant (Brij® L23) as a model solubilizer at varying concentrations.
(iii) Finally, we confirm the electrostatic interaction's influence on the encapsulation and how the binding constant correlates with the hindered diffusion (evaluated as an effect of both (i) temperature and (ii) solubilizing agent). By complementing the release measurements with studies on the uptake of OCT into empty microcapsules – where a diffusivity unaffected by the binding event is observed – we have quantified the impact of hindered diffusion, here expressed as an effective diffusion coefficient.
2. Experimental
Brij® L23, chloroform (≥99.8%), dichloromethane (≥99.9%), hydrochloric acid (37%), and tris(hydroxymethyl)amino-methane (TRIS, ≥99.8%) were purchased from Sigma-Aldrich. Ethanol (99.5%) was purchased from Solveco, octenidine dihydrochloride (OCT, 97%) was from AmBeed, poly(D,L-lactic-co-glycolic acid) (PLGA, 70% lactic acid, IV 0.2 dl g−1, ≈10 kDa, acid terminated) was from Polysciences, poly(vinyl alcohol) (PVA, 100 kDa, 95% hydrolyzed) was from Acros Organics. All chemicals were used as received and without further purification. Water of Milli-Q quality (resistivity ≥18 MΩ cm) was used for all aqueous solutions.2.1. Microcapsule formulation
The microcapsules used in this work were formulated according to a solvent evaporation procedure previously described in detail.10 In short, PLGA (and OCT corresponding to up to 10 wt% of the final microcapsule when applicable) was dissolved in dichloromethane. This organic phase was then added slowly to an aqueous phase containing 1 wt% PVA as a stabilizer during high-speed shearing at 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm using a Kinematica Polytron PT3100D immersion disperser equipped with a PT-DA07/2EC-F101 dispersing aggregate in a 5 ml round bottom flask with a side neck. After 30 minutes of homogenization, the emulsion was diluted with an additional equal volume of the aqueous phase and left under gentle magnetic stirring (400 rpm) in a 20 ml glass vial for evaporation of the volatile solvent overnight. The formed suspensions of monolithic microcapsules (2 wt% solids) were characterized by microscopy immediately after formulation and then stored at −20 °C for subsequent studies, to minimize PLGA degradation.
000 rpm using a Kinematica Polytron PT3100D immersion disperser equipped with a PT-DA07/2EC-F101 dispersing aggregate in a 5 ml round bottom flask with a side neck. After 30 minutes of homogenization, the emulsion was diluted with an additional equal volume of the aqueous phase and left under gentle magnetic stirring (400 rpm) in a 20 ml glass vial for evaporation of the volatile solvent overnight. The formed suspensions of monolithic microcapsules (2 wt% solids) were characterized by microscopy immediately after formulation and then stored at −20 °C for subsequent studies, to minimize PLGA degradation.
2.2. Microscopy
Optical characterization of the microspheres was performed using a Zeiss Axio Imager Z2 m microscope. Images were acquired using both Brightfield and Differential Interference Contrast (DIC) techniques. Brightfield micrographs were used for determining the size distribution of the microspheres21 (see ESI†).2.3. Infrared spectroscopy
Samples for infrared spectroscopy were prepared by dissolving PLGA and/or OCT in chloroform at a total concentration of 5 wt%. This solution was then spread onto thin 22 × 22 mm glass slides and left overnight for the solvent to fully evaporate at ambient conditions in a fume hood.Infrared spectra were recorded on a PerkinElmer Frontier FTIR spectrometer in Attenuated Total Reflectance (ATR) mode using a Pike Technologies GladiATR diamond crystal. Samples were recorded with an optical range of 4000 to 400 cm−1 at a resolution of 2 cm−1 and cut between 2600 and 1900 cm−1. 32 scans were collected and averaged.
2.4. Release measurements
Release measurements were in all cases carried out in aqueous 10 mM TRIS-buffered suspensions at pH 7.4. The nonionic surfactant Brij® L23 (CMC = 0.01 wt%, HLB = 17) was also added to the release systems at concentrations of 0, 0.5, or 6 wt% to evaluate the effect of altering the partitioning of OCT between microcapsules and release medium. The release measurements were performed by adding a volume of the formulated microcapsule suspension (loaded with 5 wt% OCT) to a larger volume of aqueous release medium under gentle magnetic stirring (150 rpm) at either ambient (22 °C) or elevated (37 °C) temperature. Measurements at 37 °C were performed by placing the samples in a Stuart SI60D incubator. At given times, 1.5 ml aliquots were taken out from the release medium and centrifuged at 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000g for up to four minutes. The concentration of released OCT in the supernatant was determined by measuring the absorbance at 281 nm with UV-visible spectrophotometry using an HP 8453 spectrophotometer. The total loading in the microcapsules was determined by extraction in a 1
000g for up to four minutes. The concentration of released OCT in the supernatant was determined by measuring the absorbance at 281 nm with UV-visible spectrophotometry using an HP 8453 spectrophotometer. The total loading in the microcapsules was determined by extraction in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 mixture of the release medium and ethanol. The samples were centrifuged, and concentrations were determined spectrophotometrically after at least 12 hours of extraction.
3 mixture of the release medium and ethanol. The samples were centrifuged, and concentrations were determined spectrophotometrically after at least 12 hours of extraction.
Time-dependent sorption measurements were carried out in an analogue manner. A sorption medium was created where OCT (20 mg L−1) was dissolved in TRIS-buffered solutions with up to 6 wt% nonionic surfactant. After being left overnight for complete dissolution, a 1.5 ml aliquot was taken out for determining the total amount of OCT in the aqueous phase. A small volume of empty microcapsules, i.e. pure PLGA microcapsules containing no OCT, was then added to the sorption medium and the OCT concentration in the aqueous phase was determined in analogue to the release measurements described above.
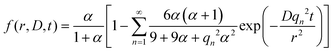 | (1) |
Here, D is the effective diffusion coefficient, r is the microcapsule radius, and t is the time. The coefficient α is related to the partitioning of the active between the microcapsules and surrounding aqueous phase during release and is given by
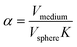 | (2) |
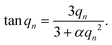 | (3) |
The formulated microcapsules are polydisperse, following a size distribution P(r) where a lognormal size distribution typically describes the polydispersity well.10,21 To account for this polydispersity, the fractional release must be weighted and normalized according to
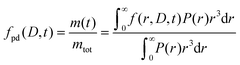 | (4) |
Burst effects are normally seen in the release from microcapsule formulations.11,23 Here, a fraction pb is making up the burst release which is assumed to follow a zero-order release (due to lack of experimental data) during a short time of burst tb, taken as the time until the first experimental data point. The fraction f0 describes any non-encapsulated active present in the aqueous phase at equilibrium after formulation.
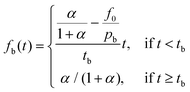 | (5) |
Eqn (1)–(5) can consequently be combined to yield a final expression (frelease(D,t)) for the overall observed release,
| frelease(D,t) = f0 + pbfb(t) + (1 − pb)fpd(D,t). | (6) |
Upon transferring the microcapsules to the release medium, the partitioning of active between microcapsule and continuous phase is displaced which induces a flux of active out from the microcapsules. Starting at the initially free fraction f0, this leads to a burst release, polydispersity-weighted diffusion-controlled release, and degradation-controlled release at successively longer times. The degradation contributions to the final part of the release data has been described in detail in the ESI.† The fits of experimental data to the models were performed by nonlinear regression in MATLAB R2021b (MathWorks).
3. Results and discussion
3.1. Octenidine encapsulation and the acid–base interaction
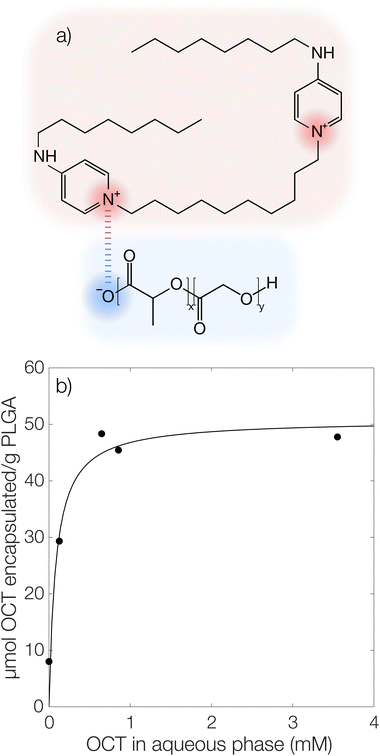
It has previously been hypothesized that there is an interaction between cationic OCT and anionic carboxylate end groups in biodegradable polyesters (Fig. 1a) where an increased concentration of end groups (lower Mw or branched polymer chains) yields greater encapsulation efficiencies.15,16The encapsulated amount of OCT as a function of its equilibrium concentration in the continuous aqueous phase of the suspension immediately after formulation with a varying OCT loading is shown in Fig. 1b, where the experimental data points correspond to loadings between 0.5 and 10 wt% OCT (8 and 160 μmol g−1 PLGA) in the microcapsules. See Fig. S3 in the ESI† for the corresponding data expressed based on the OCT loading during formulation. As can be seen from Fig. 1b, the encapsulated fraction did not follow a simple partition coefficient where an increased loading during formulation results in a proportionally increased encapsulated amount. Instead, a plateau was observed at higher loadings. This could be described by a Langmuir adsorption isotherm, eqn (7), by considering the carboxylate end groups in the PLGA as sorption sites for OCT.
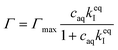 | (7) |
Here, Γmax is the concentration of available sorption sites in the polymer matrix and keqI is the equilibrium constant for binding interaction, given by the Langmuir adsorption model which describes the bound fraction of active (Γ) as a function of the equilibrium concentration caq in the surrounding aqueous phase.
From the data, a binding constant of 12 mM−1 and a maximum binding capacity of 51 μmol OCT g−1 PLGA (3.2 wt%) were fitted. Any additional OCT loaded beyond this limit was simply present in the aqueous phase during formulation due to all available sorption sites in the PLGA matrix being occupied. For comparison, the carboxylic acid end group content in the PLGA was determined to be 168 μmol g−1 (Fig. S1 in the ESI†). Thus, between one and two thirds of the available sorption sites were utilized for binding OCT – based on whether one or two of the cationic sites on OCT bind to PLGA. Adding to this, a significant decrease in encapsulation efficiency was found when changing from the acid-terminated PLGA used here to one being ester-terminated (Fig. S3 in the ESI†). It should be noted that there was still a small amount of encapsulated OCT in the ester-terminated PLGA where no end group interactions are possible. This was likely a result of either hydrophobic interactions or a kinetic entrapment of OCT within the PLGA matrix upon solvent evaporation.
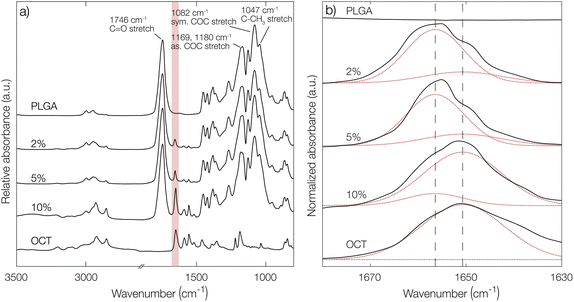
To further confirm the indications of strong PLGA–OCT interaction, infrared spectra of PLGA–OCT thin films were recorded as shown in Fig. 2. Selected PLGA bands were assigned, in good agreement with Vey et al.24 Upon mixing PLGA and OCT, the absorption band of OCT at 1651 cm−1 was gradually blue-shifted to 1656 cm−1 due to the interaction between the electron-donating carboxylate end groups of PLGA and the positively charged OCT (shown schematically in Fig. 1a). There are two resonance structures of OCT where the charge is located either on the pyridinium or imine nitrogen. The observed absorption band at 1651 cm−1 was here assigned to the pyridinium C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N stretch,25–27 in good agreement with Mainka et al.28 who suggested that a majority of the charge is located at this position. Hence, the interaction was at the pyridinium nitrogen (as shown in Fig. 1a) and not the adjacent imine. The observed frequency shift in OCT should have also similarly been observed in the carbonyl stretch frequency of the terminal carboxylates of PLGA. This could not be detected in the spectra, but it is worth noting that only about 1% of the bonds giving rise to absorption in the carbonyl region come from the carboxylates, with the rest being ester groups (1746 cm−1) along the PLGA backbone. Hence, this minor change may not be visible in the spectra.
N stretch,25–27 in good agreement with Mainka et al.28 who suggested that a majority of the charge is located at this position. Hence, the interaction was at the pyridinium nitrogen (as shown in Fig. 1a) and not the adjacent imine. The observed frequency shift in OCT should have also similarly been observed in the carbonyl stretch frequency of the terminal carboxylates of PLGA. This could not be detected in the spectra, but it is worth noting that only about 1% of the bonds giving rise to absorption in the carbonyl region come from the carboxylates, with the rest being ester groups (1746 cm−1) along the PLGA backbone. Hence, this minor change may not be visible in the spectra.
From deconvolutions of the absorption bands in Fig. 2b (shown in more detail in Fig. S4 in the ESI†), the fraction of bound and unbound OCT in the PLGA films could be estimated. By increasing the loading from 2% to 10%, a decrease in bound OCT from 86% to 13% could be observed (Table S2 in the ESI†). This was in good agreement with the encapsulation yield, where a maximum loading of around 3% was found.
3.2. Release measurements
In this section, the effect of temperature and release medium, respectively, on the release of OCT from the PLGA microcapsules is investigated. Moreover, to complement conventional release studies, sorption tests were carried out to further understand the effects of the specific interactions on the release rate. In Table 1 all fitted diffusion coefficients, burst fractions, and calculated bound fractions from diffusivity data (see section 3.3) where applicable are presented. The partition coefficients are reported in the ESI (Table S3†) and only discussed qualitatively, due to large uncertainties.| Brij® L23 fraction (%) | D release (m2 s−1) | Burst fraction | D sorption (m2 s−1) | k I |
|---|---|---|---|---|
| 22 °C | ||||
| 0 | — | — | (4.1 ± 1.7) × 10−19 | — |
| 0.5 | (5.0 ± 6.0) × 10−20 | 0.14 ± 0.04 | 0.12 ± 0.16 | |
| 6 | 0.15 ± 0.04 | |||
| 37 °C | ||||
| 0 | (1.0 ± 0.9) × 10−17 | 0 ± 0.05 | (7.7 ± 2.1) × 10−17 | 0.13 ± 0.12 |
| 0.5 | 0.15 ± 0.05 | |||
| 6 | 0.18 ± 0.05 | |||
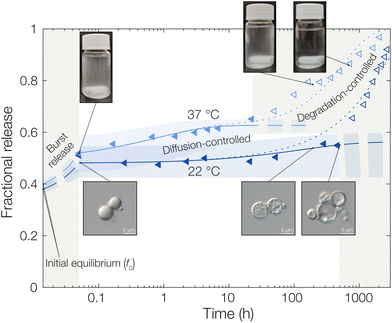
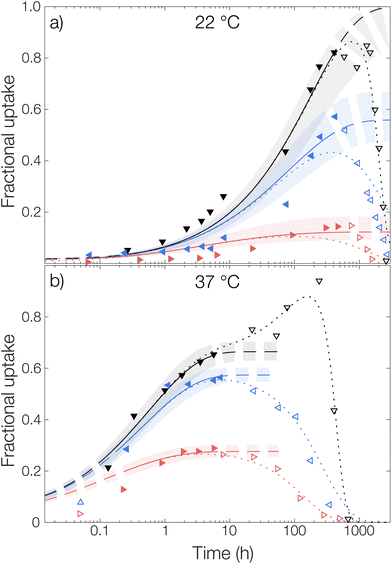
Starting with the burst release in the measured data, a burst release of approximately 20% was observed, independent of temperature. This was likely caused by releasing OCT that was not encapsulated but only adsorbed onto the microcapsule surfaces. At 37 °C, the observed diffusivity of OCT in the PLGA matrix was much higher compared to that at 22 °C, leading to a significantly increased release rate. This was found by fitting eqn (6) to the experimental data where an effective diffusion coefficient approximately 200 times greater was found, compared to the one at 22 °C (see Table 1). This strong temperature effect can most likely be connected to the physical state of the PLGA matrix. The glass transition temperature (Tg) of hydrated PLGA is approximately 30 °C.18 At 37 °C, the amorphous PLGA matrix is consequently in its rubbery state and considerably more swelled with water compared to its state at room temperature. The degradation onset was also significantly earlier in time, and its timeframe shorter, at elevated temperatures29 which could be seen by the time it took until the diffusion equation no longer described the experimental data. At 22 °C the release was following the diffusion model for the first two weeks (400 hours), whereas the release at 37 °C only followed the model for the first day. After this, degradation became so significant that the simplistic model of constant effective diffusivity in a homogeneous sphere no longer was valid. In this final regime, the release data could be described by appropriate degradation rate equations, presented in the ESI.†
For the initially monolithic OCT-loaded PLGA microcapsules, an increase in internal porosity of the microcapsules was observed over time in the release medium (micrographs in Fig. 3).30,31 This behavior was observed at both temperatures studied, although at different time scales due to the temperature-dependent degradation kinetics of PLGA. Additionally, significant swelling of the microcapsules over time has previously been reported,32 and a combination of these two factors likely caused the deviations from diffusion control in the degradation-controlled regime. To complement the microscopic evolution of the microcapsules in the release suspension over time, the macroscopic appearances of the suspensions were followed over time (see photos in Fig. 3). Over time, the suspensions went from opaque – indicating the presence of microcapsules that scatter light – to completely transparent when all spheres had fully degraded and disintegrated. The observed degradation time frame was also in good correlation with the release profiles in Fig. 3, which further confirmed the strong PLGA–OCT interaction. It was not until the PLGA had been degraded sufficiently to become soluble in the aqueous phase that the majority of OCT also was released into the surrounding aqueous phase.
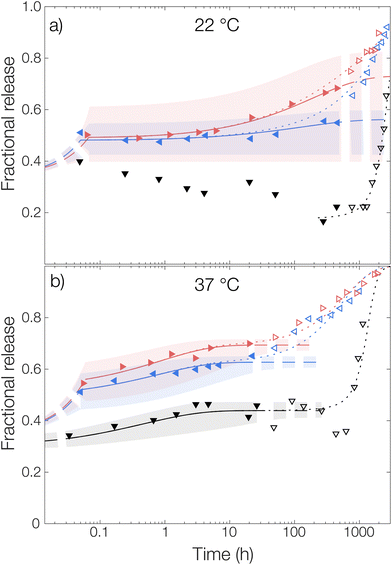
For the measurement without any solubilizing surfactant at 22 °C, a decrease in the released amount of OCT over time could be observed as shown in Fig. 4, meaning that there rather was sorption into the microcapsules than release from them. Clearly, the transfer of the microcapsules from the crude formulated suspension to the TRIS-buffered release medium resulted in the partitioning of OCT becoming more shifted towards the microcapsules despite an approximate 100-fold dilution. However, this could be explained by the effect of the dispersant PVA. The 1 wt% PVA solution is required during formulation to stabilize the formed emulsion, and later also the microcapsule suspension, but it likely also helped to solubilize some of the OCT in the aqueous phase. It should be noted here that sink conditions should have been maintained even in the TRIS buffer on its own since the concentration in the release medium was at least 400 times below the saturation concentration. It was not until after about 40 days (1000 hours), when a significant fraction of the PLGA had begun degrading, that the majority of the OCT was beginning to release from the microcapsules. At 37 °C, this shift in partitioning toward the microcapsules was not observed. Instead, about 15% of the total loading was released following a diffusive process. This was likely due to the increased solubility in the aqueous phase with an increasing temperature being enough to counteract the decrease in solubility caused by the dilution of PVA.
The partition coefficient for OCT between the microcapsule and the aqueous phase was shown to be highly dependent on the addition of nonionic surfactant. This effect was especially pronounced at 22 °C which can be observed in Fig. 4 by inspecting the fitted plateau values at long times (dashed lines) according to eqn (6). It should be noted that the uncertainty of the fitted partition coefficient (ESI, Table S3†) was rather large due to the interference by PLGA degradation kinetics at longer times. However, the trends – with a shift in the partitioning coefficient towards the aqueous phase upon increasing the surfactant concentration – are clear.
One should note that the surfactant can affect the release in more than one way. In addition to the solubilizing effect that drives the partitioning of OCT towards the aqueous phase, surfactants have been reported to swell PLGA matrices which consequently would affect the release kinetics33 similar to the effect associated with increasing the temperature above Tg. However, diffusivities of the same magnitude were observed for all experimental data sets within the same temperature, as shown by the individually fitted diffusion coefficients in Table S3 in the ESI.† It was therefore concluded that the release medium composition only affected the partitioning and burst release, and not the diffusivity or by extension the release rate. Because of this, the diffusivities in Fig. 4 were also fitted globally to one value for each temperature studied to improve accuracy. In the same global fitting routine, the burst fraction and partition coefficient were fitted individually to each measurement series. Regression analyses with all parameters fitted individually to each measurement set are shown in Fig. S7 in the ESI.† Although no release was seen into the TRIS buffer at 22 °C and hence no release model could be fitted, it could be seen that the addition of increasing amounts of Brij® L23 only affected the partition coefficient for OCT between microcapsule and aqueous phase. The diffusivity through the polymer matrix was not affected, meaning that no – or a minimal amount of – surfactant penetrated the microcapsules to plasticize and modify their swelling behavior.
Without solubilizing Brij® L23 in the release medium, no burst release was observed. Here, the OCT present in the aqueous phase at the start of the release measurement originated from dissolved OCT at equilibrium after formulation. For the Brij® L23-containing release media, a burst release of about 20% was, however, seen for both 0.5 wt% and 6 wt% Brij® L23.
Microcapsules without loading were added to an aqueous phase where OCT had been dissolved and the uptake into the capsules was followed over time, see Fig. 5. Similar to the release experiments, the experimental data were fitted globally to eqn (6). However, in contrast to the release measurements, the burst release pb was set to zero. Individual fits of the diffusion equation to each data set are shown in Fig. S8 in the ESI.† Starting with the diffusivity, the same trend as for the release measurements in Fig. 4 was observed, where significantly faster sorption was observed at 37 °C compared to that at 22 °C.
The same trend was also seen in the partitioning of OCT between the microcapsules and the aqueous phase. The partitioning was the most shifted towards the aqueous phase for 6 wt% Brij® L23, where the fractional uptake at the final fitted plateau was almost 0.2 and 0.3 at 22 °C and 37 °C, respectively. This value can be compared to that from the release measurements, where the corresponding fractional release in the same release medium was around 0.7 at both temperatures. Hence, there was an excellent agreement in terms of partition coefficients between the sorption and release data. However, as can be seen in Table 1, the fitted diffusion coefficients were approximately one order of magnitude larger for the sorption measurements. The cause of this difference relates to the different starting conditions mentioned above and is discussed in detail in the next section.
Regarding the sorption in the release medium without added surfactant, an almost complete uptake of all OCT was seen at 22 °C. This further verified that there was a strong PLGA–OCT interaction causing the OCT to partition into the microcapsules, despite fulfilling the traditional sink conditions. It also explained the observed release data in Fig. 4 where no release could be observed from the microcapsules without added solubilizing surfactant at 22 °C.
For the microcapsule degradation kinetics, a similar critical degradation time as for the release measurements could also be observed in the sorption studies. Until this critical degradation point, OCT was taken up by the spheres as explained well by Fickian diffusion. After this, OCT started being released back into the aqueous phase again as significant degradation occurred inside the microcapsules. When comparing this critical time between sorption and release studies, there was a good agreement with it being around two weeks at 22 °C and one day at 37 °C.
3.3. The effective diffusion coefficient and the equilibrium binding constant
If we consider the diffusion of an active in a polymer matrix, the observed diffusion coefficient is most often a composite quantity that depends on several different parameters – such as macroporosity, microporosity (e.g. free volume), tortuosity – and not only the unobstructed diffusivity D0.13 The observed diffusion coefficient is then often termed the effective diffusion coefficient, Deff, and can be expressed as a function of the relevant contributions. One such contribution that can be introduced into Deff is specific interactions between the active and the polymer matrix. If the interaction is strong, such as ionic interaction, only the free non-bound fraction kI of actives is available for diffusion and Deff can be expressed as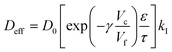 | (8) |
| kI = (keqI (Γmax − Γ(c0)) + 1)−1 | (9) |
Here, Γmax − Γ(c0) is the concentration of available sorption sites in the polymer matrix and keqI is the equilibrium constant for binding, given by the Langmuir adsorption model in eqn (7) and c0 is the total concentration of OCT in the microcapsule. However, as the encapsulated amount is limited by the binding event, c0 will always be lower than Γmax. In this limit, the concentration dependence of available sorption sites can be neglected and eqn (9) can be reduced to the much simpler eqn (10) as a good approximation of kI.
| kI = (keqIΓmax + 1)−1 | (10) |
The full derivation and motivation of this expression for the free fraction kI is given in the ESI.† The free fraction of OCT that diffuses freely and by extension the equilibrium constant for binding can consequently be estimated by two independent measurements: (i) by comparing the diffusivity from sorption and release measurements (eqn (8)), or (ii) via a Langmuir isotherm (eqn (9)).
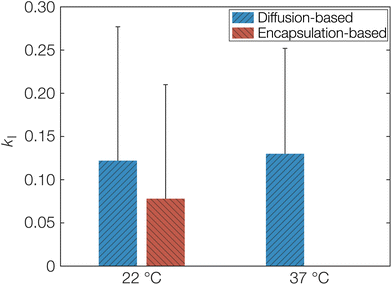
As a first estimation of kI and by extension keqI, we can make use of the different starting conditions for the release and sorption measurements as discussed above. The sorption measurements correspond to diffusion only affected by porosity and tortuosity in eqn (8) since OCT diffuses freely until the molecule encounters a free carboxylate end group. On the other hand, the release measurements correspond to Deff as explained above. The calculated kI, obtained directly from fitted diffusion coefficients can be seen in Table 1. This can be compared to the value calculated from the fitted Langmuir isotherm in Fig. 1, which from an equilibrium constant for binding (keqI) of 12 mM−1 was calculated as 0.08. The latter encapsulation-based determination of kI was only performed at 22 °C. Determining this value at 37 °C would require formulating the microcapsules at 37 °C. Due to the low boiling point of dichloromethane (39.6 °C), its evaporation at elevated temperature would likely be too rapid, meaning that the binding event would not reach its equilibrium. It should also be noted here that the units of the binding constant had to be converted so that it was based on the volume of the microcapsules instead of the volume of the aqueous phase. Similarly, it was also necessary to express the concentration of sorption sites on a volume basis, resulting in a keqI of 0.2 mM−1. As seen, the calculated kI from the adsorption isotherm was indeed in good agreement with the values based on diffusivity as shown graphically in Fig. 6. Hence, this agreement corroborates the proposed model based on a strong specific acid–base interaction between OCT and the carboxylate end groups of PLGA that is responsible for both the reduced effective diffusion coefficient and the observed Langmuir-like encapsulation isotherm. The error bars in Fig. 6 may appear large, as a result of the propagating error for calculations based on several fitted parameters. However, for the diffusion coefficients, larger changes on the order of magnitudes are typically only interesting in the context of release or sorption profiles.
The fitted effective diffusion coefficients for OCT in PLGA microcapsules can also be compared to the effective diffusivity of pyrene – a hydrophobic model substance without specific interactions with PLGA – from similar PLGA microcapsules previously studied by us.10 For pyrene, the fitted effective diffusivity in release studies was approximately two orders of magnitude higher at ambient temperature, compared to OCT in analogous release studies. Hence, this was closer to and within the same order of magnitude as the OCT diffusivity observed in the sorption studies in this work. This further illustrates the significant effect that the presence or absence of specific interaction between the active and PLGA matrix can have.
4. Conclusions
In this work, the encapsulation and sustained release of the antimicrobial octenidine (OCT) from PLGA microcapsules have been systematically investigated at relevant physiological conditions and analyzed within a theoretical framework for hindered diffusion. The release profile could be divided into three distinct regimes; (1) an initial burst release followed by (2) slow diffusive release through the PLGA polymer and (3) a final faster release determined by the hydrolytic degradation of the microcapsule.The release of OCT was further analyzed as a function of temperature and solubilizing agents. The temperature can vary significantly depending on the application, e.g., a medical device surface (room temperature) or a wound or an implant inside the body (33–37 °C). A significantly faster release was seen at 37 °C, which is above the glass transition temperature of hydrated PLGA (30 °C), as compared with that at room temperature. For short times, this was mainly due to an increased OCT diffusivity through the polymer matrix, as shown using diffusion models. At longer times, it was instead due to faster PLGA degradation at elevated temperature, as indicated by the time at which the diffusion model started deviating from experimental data.
The effect of solubilizing agents – such as amphiphilic proteins, polysaccharides, phospholipids, etc., in wound exudates, interstitial fluid, or bacterial biofilms – on the release of OCT was investigated using a nonionic surfactant as a model compound. Despite being a highly efficient solubilizer, this mainly affected the partitioning between the microcapsule and release medium. The OCT diffusivity was not affected, meaning that the microcapsules would retain their barrier properties regardless of whether the release medium contained solubilizing agents or not. It was however remarkable that without a solubilizer the partitioning was highly shifted towards the microcapsules despite a notable solubility of OCT in the release medium and fulfillment of conventional sink conditions. Both the observed release profiles with a degradation-controlled release at long times as well as the high partitioning towards the microcapsules could be explained by a strong specific interaction between OCT and PLGA. Upon encapsulation, a strongly interacting complex was formed which led to a hindered OCT diffusion in subsequent release studies. This was verified experimentally by infrared spectroscopy, as well as by comparing sorption to and release from microcapsules.
Given the antimicrobial efficacy of OCT, applications in for instance wound dressings are easily conceived. We have previously10 verified the biocompatibility of microcapsule-loaded nonwoven fiber materials. Additionally, we have previously shown the rate-limiting properties of microcapsules embedded in nonwoven fiber materials – and that the fiber material itself only to a very minor extent affects the release rate. Hence, results shown here for microcapsules in aqueous suspension would likely be transferrable to wound dressings based on fiber materials containing embedded microcapsules as well. Depending on the type of dressing, its temperature may vary which in turn could influence the OCT release rate as shown here. A separate publication where microencapsulated OCT enables a sustained antimicrobial efficacy in a wound dressing prototype is currently under preparation by us. Finally, since there is a plethora of commercially relevant drugs, biocides, and antimicrobials bearing cationic charges – all of which should display similarities with respect to encapsulation and release from polylactide-based microcapsules – this further widens the applicability of these results.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The Swedish Research Council FORMAS (2018 – 02284) and Vinnova (2017–04693) are acknowledged for funding.References
- T. A. Mustoe, K. O'shaughnessy and O. Kloeters, Plast. Reconstr. Surg., 2006, 117, 35S–41S CrossRef CAS PubMed.
- H. D. Marston, D. M. Dixon, J. M. Knisely, T. N. Palmore and A. S. Fauci, J. Am. Med. Assoc., 2016, 316, 1193–1204 CrossRef CAS PubMed.
- N.-O. Hübner, J. Siebert and A. Kramer, Skin Pharmacol. Physiol., 2010, 23, 244–258 CrossRef PubMed.
- T. Koburger, N.-O. Hübner, M. Braun, J. Siebert and A. Kramer, J. Antimicrob. Chemother., 2010, 65, 1712–1719 CrossRef CAS.
- N. Malanovic, A. Ön, G. Pabst, A. Zellner and K. Lohner, Int. J. Antimicrob. Agents, 2020, 56, 106146 CrossRef CAS.
- E. Gullberg, S. Cao, O. G. Berg, C. Ilbäck, L. Sandegren, D. Hughes and D. I. Andersson, PLoS Pathog., 2011, 7, e1002158 CrossRef CAS.
- R. Bodmeier and H. Chen, J. Controlled Release, 1989, 10, 167–175 CrossRef CAS.
- B. S. Zolnik and D. J. Burgess, J. Controlled Release, 2008, 127, 137–145 CrossRef CAS PubMed.
- Y. Capan, G. Jiang, S. Giovagnoli, K.-H. Na and P. P. DeLuca, AAPS PharmSciTech, 2003, 4, 147–156 CrossRef.
- V. Eriksson, J. Mistral, T. Yang Nilsson, M. Andersson Trojer and L. Evenäs, J. Mater. Chem. B, 2023, 11, 2693–2699 RSC.
- S. Fredenberg, M. Wahlgren, M. Reslow and A. Axelsson, Int. J. Pharm., 2011, 415, 34–52 CrossRef CAS.
- H. Ulmefors, T. Yang Nilsson, V. Eriksson, G. Eriksson, L. Evenäs and M. Andersson Trojer, Macromol. Mater. Eng., 2022, 307, 2200110 CrossRef CAS.
- M. Andersson Trojer, L. Nordstierna, J. Bergek, H. Blanck, K. Holmberg and M. Nydén, Adv. Colloid Interface Sci., 2015, 222, 18–43 CrossRef CAS PubMed.
- C. A. Stewart, Y. Finer and B. D. Hatton, Sci. Rep., 2018, 8, 895 CrossRef PubMed.
- A. Klaue, M. Maraldi, C. Piviali, D. Moscatelli and M. Morbidelli, Eur. Polym. J., 2020, 138, 109987 CrossRef CAS.
- M. Maraldi, A. Guida, M. Sponchioni and D. Moscatelli, Macromol. Mater. Eng., 2021, 306, 2000592 CrossRef CAS.
- J. Crank, The mathematics of diffusion, Oxford university press, 1979 Search PubMed.
- P. Blasi, S. S. D'Souza, F. Selmin and P. P. DeLuca, J. Controlled Release, 2005, 108, 1–9 CrossRef CAS.
- K. Park, A. Otte, F. Sharifi, J. Garner, S. Skidmore, H. Park, Y. K. Jhon, B. Qin and Y. Wang, Mol. Pharm., 2020, 18, 18–32 CrossRef PubMed.
- G. Liu and K. McEnnis, Polymers, 2022, 14, 993 CrossRef CAS PubMed.
- V. Eriksson, M. A. Trojer, S. Vavra, M. Hulander and L. Nordstierna, J. Colloid Interface Sci., 2020, 579, 645–653 CrossRef CAS PubMed.
- M. A. Trojer, L. Nordstierna, M. Nordin, M. Nydén and K. Holmberg, Phys. Chem. Chem. Phys., 2013, 15, 17727–17741 RSC.
- X. Huang and C. S. Brazel, J. Controlled Release, 2001, 73, 121–136 CrossRef CAS PubMed.
- E. Vey, C. Rodger, J. Booth, M. Claybourn, A. F. Miller and A. Saiani, Polym. Degrad. Stab., 2011, 96, 1882–1889 CrossRef CAS.
- K. M. Marzec, A. Jaworska, K. Malek, A. Kaczor and M. Baranska, J. Raman Spectrosc., 2013, 44, 155–165 CrossRef CAS.
- G. R. Clark, G. L. Shaw, P. W. J. Surman, M. J. Taylor and D. Steele, J. Chem. Soc., Faraday Trans., 1994, 90, 3139–3144 RSC.
- G. Socrates, Infrared and Raman characteristic group frequencies: tables and charts, John Wiley & Sons, 2004 Search PubMed.
- D. L. Mainka, J. Schwarz and U. Girreser, ARKIVOC, 2020, 2020, 287–298 Search PubMed.
- M. Dunne, O. I. Corrigan and Z. Ramtoola, Biomaterials, 2000, 21, 1659–1668 CrossRef CAS PubMed.
- D. Klose, F. Siepmann, K. Elkharraz and J. Siepmann, Int. J. Pharm., 2008, 354, 95–103 CrossRef CAS PubMed.
- J. Siepmann, K. Elkharraz, F. Siepmann and D. Klose, Biomacromolecules, 2005, 6, 2312–2319 CrossRef CAS PubMed.
- C. E. Rapier, K. J. Shea and A. P. Lee, Sci. Rep., 2021, 11, 14512 CrossRef CAS.
- C. Wischke and S. P. Schwendeman, Int. J. Pharm., 2008, 364, 298–327 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3pm00025g |
| This journal is © The Royal Society of Chemistry 2024 |