 Open Access Article
Open Access ArticleEvaluation of drug release from polymeric nanoparticles in simulated saliva and gastric media by asymmetric flow field–flow fractionation (AF4)†
Haoran
Wu
 a,
Alaia
Homawoo
b,
Saba
Shariati
c,
Carlos E.
Astete
a,
Alaia
Homawoo
b,
Saba
Shariati
c,
Carlos E.
Astete
 d,
Debora F.
Rodrigues
d,
Debora F.
Rodrigues
 a,
Cristina M.
Sabliov
d,
Elham H.
Fini
c and
Stacey M.
Louie
a,
Cristina M.
Sabliov
d,
Elham H.
Fini
c and
Stacey M.
Louie
 *a
*a
aDepartment of Civil & Environmental Engineering, University of Houston, Houston, TX 77004, USA. E-mail: slouie@uh.edu; Tel: +(713)-743-8646
bDepartment of Electrical & Computer Engineering, University of Houston, Houston, TX 77004, USA
cSchool of Sustainable Engineering and the Built Environment, Arizona State University, Tempe, AZ 85287, USA
dDepartment of Biological & Agricultural Engineering, Louisiana State University, Baton Rouge, LA 70803, USA
First published on 3rd September 2024
Abstract
Nanocarriers for oral drug delivery will encounter various biochemical environments throughout the digestive tract, which could induce different drug release behaviors. Conventional drug release assays can provide total drug release rates but have limited capability to identify drug release mechanisms in complex samples. The objective of this study is to compare the rates and mechanisms for release of an antibiotic, enrofloxacin, from poly(lactic-co-glycolic acid) (PLGA) nanoparticles in simulated saliva and simulated gastric fluid (SGF) by combining drug release profiling using asymmetric flow field–flow fractionation (AF4) with physical release models and density functional theory (DFT) analyses. At 30 °C, similar release profiles were observed in media with near-neutral pH, represented by saliva and phosphate buffered saline (PBS) as a comparative medium, whereas antibiotic release was accelerated in SGF. However, negligible drug release was observed in SGF at room temperature (below the glass transition temperature of the nanoparticles). Enzymatic proteins in the media did not significantly influence the release rates. The advanced AF4 analyses of the drug distribution and release profiles affirmed negligible drug–protein interactions in the media and provided evidence that accelerated release in SGF was attributed to enhanced radial diffusion rates of entrapped drug through the nanoparticles, rather than particle erosion or shrinking. DFT modeling further demonstrated that changes in the charge state of the enrofloxacin and carboxylated PLGA result in diminished drug–polymer interactions upon SGF intrusion into the nanoparticles. Altogether, this study demonstrates the benefits of integrated experimental and modeling analyses to understand drug release mechanisms.
1. Introduction
Polymeric nanoparticles (NPs) are well-known and promising materials for drug delivery. Benefits of nanodelivery include reduced cell toxicity and side effects, enhanced targeting to diseased sites, controlled drug release, and improved drug biodistribution, which ultimately result in better drug bioaccessibility and bioavailability.1–3 The U.S. Food and Drug Administration (FDA) has established analysis of NP drug release profiles as a key required metric to characterize the NPs and predict their drug delivery performance.4 However, drug release rates can be significantly impacted by environmental changes experienced by the NPs after administration, which may include shifts in temperature or pH and exposure to biomolecules.5,6 Hence, it is crucial to evaluate drug release profiles across all relevant environmental conditions. Furthermore, identifying the fundamental mechanisms for changes in release will enable researchers to better predict the behavior of the NPs in biological environments and design improved nanocarriers.This research evaluates poly (lactic-co-glycolic acid) (PLGA) NPs as a drug delivery carrier for enrofloxacin, a fluoroquinolone antibiotic of particular interest for treatment of gastrointestinal infections, as evaluated in our prior work for porcine livestock applications.7,8 For gastrointestinal treatment, orally delivered drugs are first exposed to saliva in the mouth and esophagus, then acidic gastric fluid in the stomach, and finally intestinal fluid in the small and large intestines. Ideally, the nanocarrier should robustly retain the drug through the changing pH conditions of the mouth and stomach, in order to deliver it to the target site of infection in the intestine. In addition, saliva and gastric fluid contain enzymatic proteins, such as amylase or pepsin, respectively, that could interact or react with the drug-loaded NPs.
Nanocarrier drug release profiles are most typically evaluated in a dialysis experiment, with the nanoparticles placed inside the dialysis bag and with drug-free media in the outer reservoir.9–13 Samples are collected in either the reservoir to quantify released drug, or from the dialysis bag to quantify entrapped drug after digesting the NPs. However, dialysis lag time can introduce errors in the release rate analyses.14,15 Furthermore, only total drug is quantified in either the retentate or dialysate, with no information acquired on the properties of the NPs themselves or the drug distribution across various sizes of NPs or biomolecules in the sample.
Our prior research developed and applied a multi-detector asymmetric flow field–flow fractionation (AF4) method to evaluate the release of enrofloxacin and other fluorescent compounds from PLGA NPs in phosphate buffered saline (PBS) at varying temperatures.15,16 The AF4 provided size separation of the nanoparticles and other species in the samples. Coupling the AF4 separation with online dynamic light scattering (DLS), ultraviolet (UV) absorbance, total organic carbon (TOC), and fluorescence detection (FLD) enabled size-resolved analysis of drug loading directly on the NPs within ≈100 min of sample collection.15,16 The AF4 method also provided comprehensive information on size distribution, concentration, and drug loading for nanocarriers.15,16 Hence, the AF4 approach overcomes the dialysis lag and lack of drug distribution information in dialysis-based drug release assays. AF4 is now becoming an established technique to evaluate a variety of nanocarriers, including nanospheres, nanocapsules, solid lipid nanoparticles, liposomes, polymersomes, and micelles, as discussed in the review article by Bian et al.17 and summarized in the ESI Table S1.† However, AF4 is most typically used for physical characterization of the nanocarrier size or structure. Only approximately half of the summarized studies probed the chemical composition or drug loading using online UV,18–26 fluorescence,27–30 or γ-ray detectors31 (ESI Table S1†). To our knowledge, aside from our prior research,15,16 only one study by de Oliveira et al.27 has applied multi-detector AF4 to quantitatively monitor drug release or transfer kinetics. Hence, a research gap remains in exploring the full range of possible applications of AF4 to probe nanocarriers.
The main objectives of this study are to evaluate and compare the rates and mechanisms of enrofloxacin release from PLGA NPs in simulated saliva (pH 6.8) and simulated gastric fluid (SGF, pH 2.5) by employing multi-detector AF4 characterization of the NPs during the release experiments. Release in the simulated saliva or SGF was tested with or without protein (amylase in saliva or pepsin in SGF) at different temperatures (20 °C or 30 °C) and compared to phosphate buffered saline media (PBS, pH 7.4) to assess the role of proteins, the glass transition of the PLGA NPs, and the pH of the media, respectively, on the release rates. Modeling analysis of the drug release profiles from AF4 was employed to better understand the release mechanisms (e.g., diffusion versus erosion), and density functional theory (DFT) modeling was further used to support the proposed mechanisms for changes in release behavior across the various media.
2. Experimental
2.1 Nanocarrier materials and synthesis
The enrofloxacin-loaded PLGA nanoparticles (“PLGA-Enro NPs”) were prepared using PLGA (50% lactide/50% glycolide, molecular weight of 38 to 54 kDa, Resomer RG504H), Tween 80, poly(vinyl alcohol) (PVA) (molecular weight of 31 to 50 kDa), and trehalose, all purchased from Sigma Aldrich (St Louis, MO, USA). The enrofloxacin was supplied by Alfa Aesar (Ward Hill, MA, USA). The Tween 80 surfactant and PVA polymer are used to impart colloidal stability to the NPs, and the trehalose is used as a cryoprotectant. The PLGA-Enro NPs were synthesized in triplicate batches using the emulsion evaporation method, followed by lyophilization, as described in our prior publication.15 Details of the synthesis are provided in the ESI section S2.† The final composition of the lyopholized PLGA-Enro NP powder was PLGA (17.7 wt%), enrofloxacin (1.6 wt%), Tween 80 (23 wt%), PVA (7.57 wt%), and trehalose (50 wt%). The enrofloxacin entrapment efficiency was 6%. Suspensions were freshly prepared from the powder for all following experiments.2.2. Release media materials and preparation
Drug release experiments were conducted in five different media: PBS (pH 7.4 ± 0.1), simulated saliva with or without 0.5 g L−1 of amylase (pH 6.8 ± 0.1), or SGF with or without 3.2 g L−1 of pepsin (pH 2.5 ± 0.1). Protein concentrations were selected following a prior study using simulated saliva and gastric fluid.32 The compositions and ionic strengths of all media are provided in ESI Table S2.† The pH for SGF was selected to better simulate the porcine stomach, with pH ranging from 1.2 to 4 at fasted state and generally higher than human gastric fluids.33 The pH for all media were adjusted using 0.1 M HCl or 0.1 M NaOH.The media that contained proteins (i.e., simulated saliva with amylase, and SGF with pepsin) showed incomplete protein dissolution. To remove undissolved protein, the media were first held under the desired temperature for the release experiments (30 °C) for ≈4 hours, then filtered through a 0.22 μm polyethersulfone bottle-top vacuum filter (250 mL capacity, Corning, NY, USA) to collect the filtrate. The remaining protein concentrations were measured by batch total organic carbon (TOC) analysis (Sievers M9 SEC, Suez Water Technologies, Trevose, PA, USA) using the method reported in the ESI section S4.† The resulting concentrations were (0.40 ± 0.02) g L−1 of amylase in the simulated saliva and (2.16 ± 0.11) g L−1 of pepsin in the SGF.
2.3. Drug release experiments
Drug release experiments were conducted in simulated saliva and SGF, with or without their corresponding enzymatic proteins, at (30 ± 1) °C, which is near the glass transition temperature, Tg, of ≈33 °C (onset and offset temperatures of 29 °C and 38 °C, respectively) that was measured for the synthesized PLGA-Enro NPs.15 This temperature was selected to achieve a relatively slow release to compare the different media. Raising the temperature to the physiological temperature of 37 °C (above Tg) resulted in the same trends comparing the different media, but nearly all of the entrapped enrofloxacin released within 8 h (ESI Fig. S1†), which results in higher uncertainty in fitting release rate constants and identifying significant differences between media. Drug release was also compared to that in PBS at (30 ± 1) °C to better understand the role of the pH of the medium, as well as in SGF without pepsin at room temperature, i.e., (20 ± 1) °C, to better understand the role of temperature and the polymer glass transition.In the release experiments, 120 mL of each release medium was prepared in an amber bottle and preheated to the desired temperature overnight with stirring at 400 rpm. Then, PLGA-Enro NPs were dispersed in an aliquot of the preheated media at a concentration of 15 g L−1 of the total lyophilized powder (or 2.65 g L−1 as PLGA) and bath sonicated for 10 seconds (Branson 1800 CPXH, Emerson, St Louis, MO, USA). A 1 mL SpectraPor Float-A-Lyzer G2 cellulose ester dialysis bag with a molecular weight cut-off (MWCO) of 100 kDa (Repligen, Waltham, MA) was prewashed following the manufacturer's instructions. 1 mL of the PLGA-Enro NP suspension was pipetted into the device, which was then placed into the preheated release media. Eight time points were evaluated at (0, 2, 4, 6, 8, 24, 32, and 48) h, with 20 μL of NP suspension collected from within the dialysis device and added to 280 μL of blank media in an HPLC vial to dilute the NP concentration to 1 g L−1 as total mass (or 0.18 g L−1 as PLGA). Samples were evaluated following the methods described hereafter. Each experiment was replicated three times using each of three different batches of PLGA-Enro NPs.
2.4. Batch DLS and zeta potential measurements
Batch dynamic light scattering (DLS) and electrophoretic light scattering (ELS) measurements were performed using a Zetasizer Nano ZS instrument (Malvern Panalytical Inc., Malvern, UK) to evaluate particle size and zeta potential, respectively. Samples collected from the release experiments were measured at 0 h and 48 h. For batch DLS measurements, the sample was diluted from 15 g L−1 to 1 g L−1 (as total powder) using the blank drug release media, and 0.5 mL of sample was loaded into a semi-micro poly(methyl methacrylate) cuvette. The z-average hydrodynamic diameter (dz) was reported. For zeta potential measurements, the NPs were diluted to 1 g L−1 (as total powder) into deionized water. 1 mL of sample was added into a folded zeta capillary cell (DTS 1070, Malvern), and measurements were conducted with an applied voltage of 40 V. The dilution into deionized water and voltage setting were both chosen to mitigate corrosion of the gold electrode cells.34 The Smoluchowski model was applied to convert electrophoretic mobility to zeta potential. Five measurement replicates were collected per sample for both DLS and ELS. Triplicate samples were collected using the three different batches of synthesized NPs.2.5. Multi-detector AF4 method
Samples collected at all eight time points from 0 h to 48 h were analyzed by multi-detector AF4 to evaluate size distributions and quantify drug release. An Eclipse AF4 module (Wyatt Technology, Santa Barbara, CA, USA) was integrated with a 1290 Infinity HPLC system (Agilent Technologies, Santa Clara, CA, USA) comprising a binary pump, degasser, and autosampler. Sodium sulfate decahydrate (0.15 mM Na2SO4·10H2O, ACS grade >99%, Fisher Scientific, Fair Lawn, NJ, USA) was used as the mobile phase for all AF4 measurements. The AF4 separation was performed on a short channel equipped with a wide spacer (350 μm spacer height) and 10 kDa regenerated cellulose (RC) ultrafiltration membrane as the accumulation wall, which was die-cut from a sheet membrane (Ultracel PLCGC, MilliporeSigma, St Louis, MO, USA). The sample injection volume was 50 μL. The separation parameters for the AF4 method were optimized in our previous study15 and are reported in ESI section S6 and Table S3.† The total run duration was 100 min. The AF4 was coupled with multiple online detectors: an Agilent 1260 Infinity UV-Vis diode array detector (DAD) set to monitor extinction at 400 nm wavelength for the PLGA NPs; an Agilent 1260 Infinity fluorescence detector (FLD) at excitation and emission wavelengths of 280 nm and 420 nm corresponding to the enrofloxacin fluorescence with photomultiplier tube (PMT) gain of 13; Wyatt DAWN HELEOS II multi-angle light scattering (MALS) and dynamic light scattering (DLS) detectors, with the DLS detector collecting measurements over a 2 s duration at 140° scattering angle; Wyatt Optilab T-rEX differential refractive index (dRI) detector; and M9-SEC total organic carbon (TOC) detector (Suez, Trevose, PA, USA) in online turbo mode with acid and oxidizer flow rates of 2 μL min−1 and 4 μL min−1, respectively. It is noted that the dRI data were not used because of their sensitivity to flowrate changes during the AF4 run.15,162.6. Evaluation of bulk drug release using multi-detector AF4 analysis
Bulk drug release (i.e., total release from the entire NP population) was analyzed by integrating the AF4 peak areas recorded by each concentration detector across the NP peak. The UV signal was used to represent NP concentrations, and the FLD signal for drug concentrations. The UV signals were normalized to the maximum NP peak height when presenting chromatographic profiles. To evaluate bulk drug release, FLD peak areas were first normalized to the UV peak area. This peak area ratio is representative of the drug loading, i.e., FLD/UV∝(drug mass)/(PLGA mass). The normalization also corrects for any differences in sample recovery from the AF4 channel between samples. Then, the FLD/UV peak area ratio at each release time point was normalized to that for the 0 h time point to determine the fraction of drug remaining (C/C0).The experimental drug release data were primarily fitted with the radial diffusion release model presented in eqn (1):35
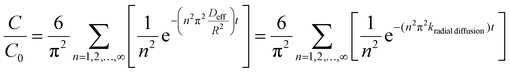 | (1) |
2.7. Evaluation of size-resolved drug release using multi-detector AF4 analysis
Eqn (1) above implies that for radial diffusion, the lumped release rate constant k should vary with particle size proportionally to R−2, assuming a constant value for D. To test this hypothesis, drug release profiles were evaluated at each chromatographic time point (i.e. each particle size) from the AF4 analysis. A MATLAB code was written to process the data. First, AF4 data for the UV, FLD, and DLS detectors were imported. The DLS provided the measured particle size over the AF4 chromatogram. The possibility for elution time shifts between measurements due to AF4 membrane fouling, along with noise in the measured size data, were considered when comparing samples. To correct for elution time shifts and smooth the data, a linear relationship was fitted through the online DLS size vs. elution time results. The fitted line was used to estimate a range of elution times corresponding to each particle radius across the FWHM of the MALS 90° detector peak in 1 nm particle size intervals for each sample. The FLD/UV signal was computed at every chromatographic time point and averaged across the elution time interval to determine drug loading for each 1 nm particle size bin. Finally, the drug loading in each size bin was normalized to the corresponding drug loading for the initial particles (collected at 0 h) to compute a release profile (C/C0versus t) for each size of particle in the population. After processing the data for each individual experiment, the size-resolved release profiles were averaged across the triplicated experiments. Finally, the radial diffusion model (eqn (1)) was fitted to determine a best-fit value for kradial diffusion at each individual particle size, truncating the infinite summation at n = 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. MATLAB has better computational efficiency than Excel, and the higher n value results in lower computational error. The model fitting was performed utilizing the MATLAB fminsearch function to minimize the SSE between the modeled and experimental data. 95% confidence intervals on the fitted values of kradial diffusion for each particle size were evaluated by identifying the minimum and maximum values of kradial diffusion that satisfy the criterion in eqn (2):37
000. MATLAB has better computational efficiency than Excel, and the higher n value results in lower computational error. The model fitting was performed utilizing the MATLAB fminsearch function to minimize the SSE between the modeled and experimental data. 95% confidence intervals on the fitted values of kradial diffusion for each particle size were evaluated by identifying the minimum and maximum values of kradial diffusion that satisfy the criterion in eqn (2):37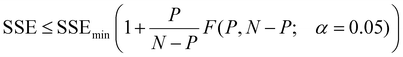 | (2) |
2.8. DFT modeling of drug–polymer interactions
The drug–polymer interactions between enrofloxacin and PLGA were investigated using DFT at the acidic pH conditions of the SGF. DFT modeling in the near-neutral pH conditions relevant to PBS and saliva was presented in our prior publication.16 In short, a PLGA random copolymer with chain length of 10, 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 lactide
50 lactide![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glycolide ratio, and carboxylic acid terminal group was used. The charge states of enrofloxacin at pH 2.5 were predicted using MarvinSketch v. 24.1.1 (ChemAxon, Budapest, Hungary).
glycolide ratio, and carboxylic acid terminal group was used. The charge states of enrofloxacin at pH 2.5 were predicted using MarvinSketch v. 24.1.1 (ChemAxon, Budapest, Hungary).
The DFT calculations were performed using the Dmol3 module38 implemented in the Accelrys Materials Studio program package (Version 7). All geometries were optimized using Perdew–Burke–Ernzerhof (PBE)39 exchange–correlation functional with Grimme's dispersion correction40 (PBE-D) and all-electron double-numerical polarized basis set (DNP). Optimizations were performed with the convergence criteria of 2.0 × 10−5 Hartree, 4.0 × 10−3 Hartree per Å, and 5.0 × 10−3 Å for energy, maximum force, and displacement, respectively. Calculations were performed in solvent medium, and conductor-like screening model (COSMO)41,42 was used to account for solvent effects considering water as the solvent. Binding energies (Ebind) were computed using eqn (3), where Ecomplex is the total energy of the interacting complex, and Efragments is the total energy of the fragments, i.e., PLGA and enrofloxacin.
 | (3) |
3. Results and discussion
3.1. Nanoparticle size, zeta potential, and drug loading under varied drug release conditions
The mean particle size and zeta potential of the PLGA-Enro NPs were evaluated by batch DLS and batch ELS, respectively, at the beginning (0 h) and end (48 h) of each drug release experiment. The zeta potential was near zero in PBS and SGF with or without pepsin and slightly negative (≈−12 mV) in simulated saliva with or without amylase (ESI Fig. S2†). The more negative zeta potential in the saliva can be attributable to the lower ionic strength relative to PBS and SGF, resulting in less charge screening. Weak acid groups on the carboxylated PLGA would also become protonated (neutral) in SGF. After 48 h, no significant change in zeta potential was observed in PBS or SGF, and only a small change in simulated saliva to ≈−9 mV.At the initial time point of dispersion in the media, the particles showed a z-average diameter, dz, of (216 ± 15) nm as the mean ± standard deviation across all replicates in all media (n = 18 samples for 3 replicates and 6 experiment conditions), with no significant differences among the various media. It is noted that the standard deviation includes variability in the size of three separately synthesized batches of particles. When comparing the change in particle size for each individual sample over the duration of the drug release experiments, the z-average particle diameter decreased by (18 ± 4) nm and (19 ± 3) nm in SGF media (with or without pepsin, respectively, with n = 3 replicates per sample) after being held at 30 °C from 0 h to 48 h (Fig. 1(a)). Statistical analysis (Tukey's HSD test) also indicated that the size decreases in the SGF release experiments at 30 °C were significantly different (95% confidence) compared to the experiments conducted in the other media or the SGF at 20 °C (Fig. 1(a)).
AF4 measurements were also applied to evaluate the NP size distributions. The PLGA-Enro NPs were measured at eight time points during the release experiments from 0 h to 48 h, with the AF4-UV detector at 400 nm providing the NP response and the AF4-DLS detector providing z-average hydrodynamic radius (Rh) measurements. Although the online TOC detector can also be used as a NP mass detector,16 it is sensitive to dissolved macromolecules, including PVA surfactant in the NP formulation and proteins in the media, which were not baseline resolved from the NP peaks (ESI Fig. S3†), resulting in higher uncertainty in the NP peak integration.
Fig. 2(a, c, and e) provides the UV chromatograms and online DLS measurements for samples held at 30 °C in PBS, simulated saliva without proteins, and SGF without proteins, respectively. ESI Fig. S4(a, c, and e)† provides the data for simulated saliva with amylase (30 °C), SGF with pepsin (30 °C), and SGF without pepsin (20 °C), respectively. Online DLS sizes were evaluated across the FWHM of the 90° static light scattering signal. In general, larger particles eluted later from the AF4 channel, with the measured size increasing linearly with elution time, as expected from AF4 separation theory.43 The NP diameters ranged from ≈140 nm to 220 nm across the FWHM at the initial time point (0 h) under all conditions, and the dz at the UV peak maximum was (183 ± 11) nm (n = 18 samples) at 0 h. The average size measured by AF4-DLS was smaller compared to the batch DLS measurement of (216 ± 15) nm. This result is typical, considering that the light scattering contribution from large particles is disproportionately higher than that from small particles. Hence, batch DLS measurements on polydisperse samples are biased toward larger sizes in the distribution. Evaluating the AF4-DLS measurements of particle size over the duration of the release experiments (Fig. 1(b)), similar trends were observed as in the batch DLS over 48 h. In SGF, the dz at the UV peak maximum decreased by (14 ± 3) nm and (11 ± 6) nm in SGF at 30 °C without and with pepsin, respectively. Correspondingly, the minimum and maximum values of dz across the FWHM of the overall particle size distribution shifted to smaller diameters (≈120 nm and 210 nm, respectively). In contrast, the AF4-DLS sizes remained approximately stable in the other conditions (Fig. 1(b)). Possible mechanisms for the size decrease in SGF and implications for the drug release are discussed in the following sections.
3.2. Drug release in simulated biological media with varied pH, proteins, and temperature
The drug release rate is one of the most important factors to characterize when evaluating a nanocarrier's suitability for its desired purpose, e.g. slow or controlled release. Evaluations of nanocarriers for oral drug delivery are complicated by the fact that the release rate can be affected by many factors, such as the pH of the release media, temperature, or presence of proteins in the media. Here, the AF4-FLD measurement enables the PLGA-Enro NPs collected during the drug release experiments to be directly evaluated for the loading and release of the fluorescent enrofloxacin compound. Fig. 2(b, d, and f) shows representative fluorescent chromatograms for experiments in the three different media without proteins at 30 °C: PBS (pH 7.4), simulated saliva (pH 6.8), or SGF (pH 2.5). Fig. S3(b, d, and f)† shows the other conditions tested, i.e., simulated saliva with amylase (30 °C), SGF with pepsin (30 °C), or SGF without pepsin (20 °C). Here, enrofloxacin release was primarily evaluated at a temperature of 30 °C based on our prior work showing slow release in PBS at this temperature. This temperature is near the Tg of the PLGA-Enro NPs, which was measured as 33 °C by differential scanning calorimetry (with onset and offset points of 29 °C and 38 °C, respectively).15 Lower temperatures (i.e., room temperature) resulted in negligible release over 48 h, whereas higher temperatures (37 °C) resulted in rapid release within 4 h, so the intermediate temperature allows the best opportunity for changes in release rate to be compared between different pH or with versus without proteins.The overall fraction of drug loading remaining in the bulk NP population, C/C0, was determined at each release time point (0 h, 2 h, etc.) using the integrated fluorescence and UV peak areas from the AF4 chromatograms, as described in section 2.7. The right axis of Fig. 2(b, d, and f) also provides a visual representation of the size-resolved loading analysis, which is discussed later in section 3.3. Release profiles are plotted in Fig. 3(a) using the integrated peak area analysis for the overall fraction of the mass of drug released (Mreleased/Mtotal). Fig. 3 also shows the fitting of the experimental data to a radial diffusion model (eqn (1)). Fitted release rate constants (kradial diffusion) are presented in Fig. 3(b) as the mean ± standard deviation on the fits for independent release experiments in triplicate, along with the drug diffusion coefficients, Deff, which were estimated as Deff = kradial diffusionR2 using the mean size measured by AF4-DLS on each sample. ESI Table S4† also presents the 95% confidence intervals on the best-fit parameter values from the triplicated experiments.
Release occurred in all three media without proteins at 30 °C. The slowest release was observed in PBS (pH 7.4). Slightly faster release occurred in simulated saliva (pH 6.8), although the difference was not significant relative to PBS at a 95% confidence level. However, significantly accelerated release was observed in SGF (pH 2.5) compared to PBS or simulated saliva. Given this difference in release rates, the enrofloxacin was almost completely released in SGF at 30 °C within 48 h (97% ± 2% release), but not in PBS or simulated saliva (72% ± 13% or 83% ± 1% release, respectively). Potential mechanisms for the faster release in SGF are investigated in depth in section 3.3.
The drug release process of nanocarriers in gastrointestinal media may be affected by other factors, such as the presence of different types of proteins. The formation of a protein corona, as well as drug binding to dissolved proteins, can affect the drug release,44–47 although not all nanocarriers exhibit significant changes in release rates in the presence of proteins.45 Here, the potential influence of enzymatic proteins, i.e. amylase in the simulated saliva or pepsin in the SGF, was evaluated at 30 °C (Fig. 3). Although a small increase and decrease in the enrofloxacin release rate was observed with amylase or pepsin, respectively, the release rates were not significantly different from the same media without proteins at a 95% confidence level. These results suggest that the protein has minimal interactions with the drug-loaded NPs (e.g., the protein does not adsorb onto the NP surface or enter into the NPs), as well as minimal influence on the drug solubility in the media (e.g. by complexing or absorbing released drug). Drug–protein interactions in solution were evaluated by the fluorescence signal of the AF4 void peak (ESI Fig. S5†), where the proteins elute in the measurements. The results did not show any enhancement or extended residence of enrofloxacin fluorescence in the void peak for samples containing PLGA-Enro NPs in the protein-containing media, relative to either protein-free media or control samples of the protein itself (without enrofloxacin). Hence, the results corroborate the lack of drug–protein interactions.
Finally, the combined role of temperature and pH was evaluated for SGF by comparing release at 30 °C and room temperature (≈20 °C) (Fig. 3). As noted above, enrofloxacin release from the PLGA nanoparticles in PBS was previously observed to be highly temperature dependent over the range of temperatures spanning the Tg of the enrofloxacin-loaded nanoparticles, which was measured as 33 °C.15 As the temperature approaches and crosses Tg, the polymeric structure transitions from glassy to rubbery. Drug release was significantly slower in SGF at room temperature compared to 30 °C, implying that intrusion of the acidic SGF solvent into the PLGA NPs at the rubbery transition is required for the accelerated drug release to occur. This observation is consistent with the enrofloxacin being entrapped within the particles, as opposed to residing on the surface of the particles.
3.3. Potential mechanisms for accelerated drug release from NPs in SGF
The trend in observed release rates with decreasing pH suggests that acidic conditions accelerate the enrofloxacin release rate. However, acidic pH could induce accelerated drug release via several potential mechanisms, including (1) inducing chemical degradation of PLGA, leading to particle erosion and accompanying drug loss, (2) changing polymer–polymer interactions by changing the protonation state of the COOH-terminated PLGA, leading to physical changes in the particle structure (i.e., the size decrease observed above), and (3) changing the aqueous drug solubility and/or drug–polymer interactions by changing the protonation state of the weak acid/base groups of the enrofloxacin and the PLGA, leading to higher dissolution and reduced adsorptive interactions of the entrapped drug. A combination of experimental and modeling analyses was used to distinguish the most important mechanism.For the enrofloxacin-loaded PLGA nanoparticles evaluated here, we evaluated the possibility of other release mechanisms besides radial diffusion by release modeling analysis (Fig. 4(a)). A first-order kinetic model was tested as a common model fitting approach (ESI eqn (S1)†), although we expected its assumptions of release from a well-mixed pool of drug in the particles would not apply for the entrapped enrofloxacin. Indeed, the first-order model was not able to predict the declining release rate at long times, when drug nearer the center of the particles must travel a longer distance to be released. An “outside-in” surface erosion model was also evaluated, which assumes that the particle mass erosion rate is proportional to the surface area exposed to solution, and the drug loss rate is proportional to the particle mass loss (ESI eqn (S2)†).35 For SGF at 30 °C, the surface erosion model also overestimates drug loss at longer times (>8 h), suggesting that surface erosion is not significant (Fig. 4(a)). With regards to “inside-out” bulk erosion, the timescale of our experiments (48 h) is shorter than the release durations tested by Zolnik and Burgess (14 d and 40 d),49 and we did not observe particle fragmentation (i.e., the AF4 chromatograms do not show the appearance of any new, smaller particle populations). Although it is not possible to completely rule out any erosion in the interior of the particles, these results all suggest that erosion was not the dominant mechanism for the accelerated release of enrofloxacin in SGF.
A reduction in particle size could potentially result in faster drug release by radial diffusion because the drug would have a shorter distance to travel to exit the polymer matrix. Here, the degree of shrinking observed was relatively small (≈10% of the initial particle diameter) and would likely not result in such large change in release rate observed for SGF compared to the other media at 30 °C. To more rigorously assess the influence of size, the AF4 data were processed to evaluate size-resolved release rates across the entire chromatogram representing the size distribution of each sample, as described in section 2.8. This analysis is presented in Fig. 4(b). The radial diffusion model (eqn (1)) predicts that the release rates (kradial diffusion) should be linearly proportional to 1/R2, with the slope corresponding to the diffusion coefficient. For the experimental data, the relationships are not perfectly linear, suggesting a somewhat stronger dependence on R. This deviation from the model could be attributable to experimental error; for example, the online AF4-DLS measurements may incur greater error for larger (slower diffusing) particles where particle motion by advection in the flow-through measurement becomes more significant relative to the diffusive motion used for the DLS analysis.53 Alternatively, the deviations could derive from imperfect assumptions of constant matrix properties in the radial diffusion model. For example, the PLGA first needs to undergo the glassy/rubbery transition with solvent intrusion into the matrix for the SGF or other media to interact with the entrapped drug, but the kinetics of heat transfer and solvent intrusion into particles are not represented in the model. The kinetics of these processes would be more rapid for smaller particles. Lyophilization of PLGA NPs with cryoprotectants, particularly trehalose as used here, has also been reported to induce pore formation.54 Because the trehalose addition and lyophilization steps were performed after the NP synthesis, pore formation can be expected to occur closer to the surface of the particle and affect a greater proportion of the volume of smaller NPs, which would also result in the release rate trends showing stronger than 1/R2 dependence.
In any case, comparing across the media types, we first observe that the overall release rates, kradial diffusion, as well as the apparent diffusion coefficient (i.e., the slope of the kradial diffusionvs. 1/R2 plot) increase slightly from PBS to simulated saliva and significantly to SGF (Fig. 4(b)), corroborating the bulk release analysis (Fig. 3(a)). More notably, the size-resolved analysis affirms that the small shift in particle size distribution in SGF cannot fully explain the more rapid release. We would expect all three of the size-resolved release profiles to overlay on a single line with the same drug diffusion coefficient if the drug were releasing purely by diffusion, the PLGA matrix properties (e.g. glassy/rubbery state) were the same for all media at the same temperature (30 °C), and the more rapid release were caused by the shrinking size alone (resulting in a shorter drug diffusion path through the particle). However, the results clearly show a more rapid apparent diffusion rate of drug in SGF compared to the other media at each individual particle size. Hence, another phenomenon beyond either diffusion or particle shrinking must be involved.
DFT modeling was used to simulate the interactions between enrofloxacin and carboxyl-terminated PLGA in the various media pH. The results provide detailed information for the strength and the type of possible intermolecular interactions. As discussed above, carboxylated PLGA has a pKa of 3.85,52 so it is protonated in SGF but deprotonated in simulated saliva and PBS. The two conditions at near neutral pH were evaluated in our prior publication, i.e. zwitterionic and anionic enrofloxacin interacting with deprotonated PLGA. The maximum binding energy was –19.8 kcal mol−1 for anionic enrofloxacin and –18.0 kcal mol−1 for zwitterionic enrofloxacin, consistent with slightly stronger adsorptive interactions (and hence slower release) observed in PBS compared to simulated saliva. Here, we present results for the intermolecular interactions between protonated PLGA and the cationic enrofloxacin molecule in aqueous medium representing SGF. The geometries of individual fragments or interacting complexes were fully optimized using an implicit continuum solvation model, COSMO. Different orientations were considered for interactions of PLGA with enrofloxacin cation. Binding energies of the interactions were evaluated using eqn (3). Fig. 5 shows the optimized geometries of interacting complexes and their corresponding binding energies.
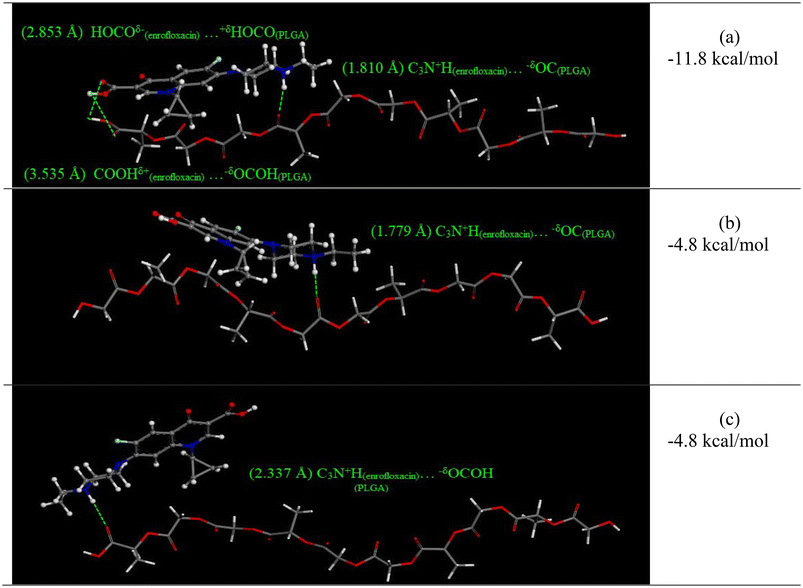 | ||
| Fig. 5 The optimized geometries for the enrofloxacin-PLGA interactions and their corresponding binding energies for cationic enrofloxacin interacting with protonated (neutral) carboxylated PLGA in three configurations (a, b, and c). Density functional theory (DFT) modeling of the zwitterionic and anionic enrofloxacin interacting with deprotonated PLGA are presented in our prior publication.16 | ||
For the enrofloxacin cation-PLGA interaction, a maximum binding energy of −11.8 kcal mol−1 was obtained for a configuration in which three hydrogen bonds were formed between the fragments (Fig. 5(a)). A stronger hydrogen bond (1.810 Å) was formed between the C3N+H functional group of enrofloxacin cation and a carbonyl group in the backbone of PLGA. Two hydrogen bonds with longer distances were formed between the carboxylic acid groups of enrofloxacin and PLGA. These distances were 2.853 Å for the HOCOδ−(enrofloxacin)⋯+δHOCO(PLGA) interaction and 3.535 Å for the COOHδ+(enrofloxacin)⋯−δOCOH(PLGA) interaction.
An interacting complex in which only a hydrogen bond (1.779 Å) was formed between the C3N+H functional group of enrofloxacin cation and a carbonyl group in the backbone of PLGA (C3N+H(enrofloxacin)⋯−δOC(PLGA)) had the binding energy of only −4.8 kcal mol−1 (Fig. 5(b)). Another configuration with only a hydrogen bond between the C3N+H functional group of enrofloxacin cation and the terminal carboxylic acid of PLGA had the same bonding energy of −4.8 kcal mol−1 (Fig. 5(c)).
Overall, all binding energies for the cationic enrofloxacin interacting with protonated PLGA in SGF were weaker (i.e., less negative) than for the zwitterionic and anionic enrofloxacin interacting with deprotonated PLGA in simulated saliva or PBS. The differences in binding energy correspond well with the observed trends in release rate and effective diffusion coefficient. Together with the experimental observations and size-resolved release analyses, the DFT results provide strong evidence that the most significant mechanism for accelerated drug release in SGF was intrusion of acidic media into the PLGA particles, leading to changes in the charge state of the drug and polymer, and hence changes in the adsorptive drug–polymer interactions.
It is highlighted that the conventional radial diffusion model (eqn (1)) assumes diffusion through a homogeneous matrix and does not account for adsorptive interactions. As discussed previously, if there were only changes to the polymer matrix due to temperature (e.g. the glass transition) and the PLGA were a nonporous matrix, the diffusion coefficient should theoretically not depend on the external solvent. However, the results here suggest that the drug is releasing with aqueous solvent that intrudes and moves through pores in the PLGA matrix, and that adsorptive interactions are responsible for the changes in release rates. This adsorption process is considered in eqn (1) by denoting an effective or apparent diffusion coefficient, Deff, which represents the true diffusion coefficient divided by a retardation factor representing the drug partitioning (adsorption) between the PLGA and aqueous phases.
4. Conclusions
This study demonstrates the application of multi-detector AF4 to directly probe the release of an entrapped antibiotic drug, enrofloxacin, from PLGA nanoparticles in three biological media at different pH or temperature, and the utilization of advanced modeling analyses of the size-resolved release rates from AF4 along with DFT modeling to identify the mechanisms for accelerated or unchanged antibiotic drug release rates, as depected in the schematic in Fig. 6. To summarize, a change in PLGA state from glassy to rubbery near the Tg is first necessary for any release to occur. When the temperature is near Tg, changes in pH from neutral (simulated saliva or PBS) to acidic (SGF) induce substantially accelerated enrofloxacin release. Despite a change in particle size in SGF, modeling analyses of the drug release data did not support erosion or particle shrinking as significant mechanisms causing the accelerated release. Rather, the primary mechanism for the accelerated release was determined to be a reduction in drug–polymer binding energy because of the change in enrofloxacin charge state in SGF, resulting in faster release of the entrapped drug by radial diffusion. Finally, proteins did not significantly influence the release of the entrapped drug, as they were likely unable to enter the PLGA pores and did not show any drug interactions in solution.For future work, more complex matrices such as simulated intestinal fluids will be studied, utilizing the AF4 method as a powerful tool to separate the NPs from other nano-sized matrix components, such as bile micelles, while simultaneously quantifying NP concentration, size distribution, active ingredient loading and release, and drug transfer. Different drug–polymer combinations should also be evaluated that may have alternative release mechanisms. For example, the burst release of hydrophobic drugs from the surface of the nanoparticles may be more significantly influenced by media proteins. In addition, nanocarriers synthesized as a truly homogeneous, pure polymer matrix free of pores would be a useful model system to affirm that drug release by true diffusion follows the 1/R2 dependence, as expected in the radial diffusion model. Overall, this study highlights mechanisms for triggered active ingredient release and methods to identify these mechanisms, which can help in further design of the nanocarriers for effective drug delivery in gastrointestinal systems.
Author contributions
H. Wu: investigation, formal analysis, data curation, visualization, writing – original draft; A. Homawoo: software, writing – original draft; S. Shariati: formal analysis, writing – original draft; C. Astete: materials, writing – review and editing; D. F. Rodrigues: funding acquisition, writing – review and editing; C. M. Sabliov: funding acquisition, writing – review and editing; E. H. Fini: writing – original draft, writing – review and editing; S.M. Louie: conceptualization, data curation, software, visualization, writing – original draft, writing – review and editing, funding acquisition, project administration, supervision.Data availability
The data supporting this article have been included as part of the ESI.† Spreadsheets and Matlab code for the model fitting are also freely available from the Texas Data Repository.36Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge Dr Sheyda Shakiba for method development applied in this research, Dr William G. Rixey for insightful comments on the release model, and Marfua Mowla for draft manuscript comments. This material is based upon work supported by the U.S. Department of Agriculture under Grant No. 2018-67022-27969 (PSGT#17545), National Institute of Standards and Technology (NIST) Standards Services Curricula Development (SSCD) Cooperative Agreement No. 70NANB22H206, FMC New Investigator Award, Texas Hazardous Waste Research Center Grant No. 110UHH0080H, and Texas Ecolab (Braun & Gresham).References
- B. Begines, T. Ortiz, M. Pérez-Aranda, G. Martínez, M. Merinero, F. Argüelles-Arias and A. Alcudia, Nanomaterials, 2020, 10, 1403, DOI:10.3390/nano10071403.
- K. M. El-Say and H. S. El-Sawy, Int. J. Pharm., 2017, 528, 675–691, DOI:10.1016/j.ijpharm.2017.06.052.
- S. Sur, A. Rathore, V. Dave, K. R. Reddy, R. S. Chouhan and V. Sadhu, Nano-Struct. Nano-Objects, 2019, 20, 100397, DOI:10.1016/j.nanoso.2019.100397.
- U.S. Department of Health and, Human Services Food and Drug Administration (FDA), Drug Products, Including Biological Products, that Contain Nanomaterials: Guidance for Industry, Center for Drug Evaluation and Research Report FDA-2017-D-0759, Food and Drug Administration, Silver Spring, MD, USA, 2022 Search PubMed.
- M. Bruneau, S. Bennici, J. Brendle, P. Dutournie, L. Limousy and S. Pluchon, J. Controlled Release, 2019, 294, 355–371, DOI:10.1016/j.jconrel.2018.12.038.
- M. A. Aghdam, R. Bagheri, J. Mosafer, B. Baradaran, M. Hashemzaei, A. Baghbanzadeh, M. de la Guardia and A. Mokhtarzadeh, J. Controlled Release, 2019, 315, 1–22, DOI:10.1016/j.jconrel.2019.09.018.
- S. Paudel, C. Cerbu, C. E. Astete, S. M. Louie, C. Sabliov and D. F. Rodrigues, ACS Appl. Nano Mater., 2019, 2, 5035–5043, DOI:10.1021/acsanm.9b00970.
- S. Paudel, J. Peña-Bahamonde, S. Shakiba, C. E. Astete, S. M. Louie, C. M. Sabliov and D. F. Rodrigues, J. Hazard. Mater., 2021, 414, 125454, DOI:10.1016/j.jhazmat.2021.125454.
- Y. Zambito, E. Pedreschi and G. Di Colo, Int. J. Pharm., 2012, 434, 28–34, DOI:10.1016/j.ijpharm.2012.05.020.
- S. Modi and B. D. Anderson, Mol. Pharmaceutics, 2013, 10, 3076–3089, DOI:10.1021/mp400154a.
- G. Moreno-Bautista and K. C. Tam, Colloids Surf., A, 2011, 389, 299–303, DOI:10.1016/j.colsurfa.2011.07.032.
- Y. Zhou, C. He, K. Chen, J. Ni, Y. Cai, X. Guo and X. Y. Wu, J. Controlled Release, 2016, 243, 11–20, DOI:10.1016/j.jconrel.2016.09.031.
- E. Leo, R. Cameroni and F. Forni, Int. J. Pharm., 1999, 180, 23–30, DOI:10.1016/S0378-5173(98)00401-3.
- M. Yu, W. Yuan, D. Li, A. Schwendeman and S. P. Schwendeman, J. Controlled Release, 2019, 315, 23–30, DOI:10.1016/j.jconrel.2019.09.016.
- S. Shakiba, C. E. Astete, R. Cueto, D. F. Rodrigues, C. M. Sabliov and S. M. Louie, J. Controlled Release, 2021, 338, 410–421, DOI:10.1016/j.jconrel.2021.08.041.
- S. Shakiba, S. Shariati, H. Wu, C. E. Astete, R. Cueto, E. H. Fini, D. F. Rodrigues, C. M. Sabliov and S. M. Louie, J. Controlled Release, 2022, 352, 485–496, DOI:10.1016/j.jconrel.2022.10.034.
- J. Bian, N. Gobalasingham, A. Purchel and J. Lin, Molecules, 2023, 28, 4169, DOI:10.3390/molecules28104169.
- S. Boye, N. Polikarpov, D. Appelhans and A. Lederer, J. Chromatogr. A, 2010, 1217, 4841–4849, DOI:10.1016/j.chroma.2010.05.036.
- J. Ehrhart, A.-F. Mingotaud and F. Violleau, J. Chromatogr. A, 2011, 1218, 4249–4256, DOI:10.1016/j.chroma.2011.01.048.
- W. Fraunhofer, G. Winter and C. Coester, Anal. Chem., 2004, 76, 1909–1920, DOI:10.1021/ac0353031.
- M. A. Graewert, C. Wilhelmy, T. Bacic, J. Schumacher, C. Blanchet, F. Meier, R. Drexel, R. Welz, B. Kolb, K. Bartels, T. Nawroth, T. Klein, D. Svergun, P. Langguth and H. Haas, Sci. Rep., 2023, 13, 15764, DOI:10.1038/s41598-023-42274-z.
- A. Hinna, F. Steiniger, S. Hupfeld, M. Brandl and J. Kuntsche, Anal. Bioanal. Chem., 2014, 406, 7827–7839, DOI:10.1007/s00216-014-7643-9.
- A. H. Hinna, S. Hupfeld, J. Kuntsche, A. Bauer-Brandl and M. Brandl, J. Controlled Release, 2016, 232, 228–237, DOI:10.1016/j.jconrel.2016.04.031.
- M. Palinske, U. L. Muza, S. Moreno, D. Appelhans, S. Boye, R. Schweins and A. Lederer, Macromol. Chem. Phys., 2023, 224, 2200300, DOI:10.1002/macp.202200300.
- K. Sztandera, M. Gorzkiewicz, X. Wang, S. Boye, D. Appelhans and B. Klajnert-Maculewicz, Colloids Surf., B, 2022, 217, 112662, DOI:10.1016/j.colsurfb.2022.112662.
- J. Wankar, F. Bonvicini, G. Benkovics, V. Marassi, M. Malanga, E. Fenyvesi, G. A. Gentilomi, P. Reschiglian, B. Roda and I. Manet, Mol. Pharmaceutics, 2018, 15, 3823–3836, DOI:10.1021/acs.molpharmaceut.8b0032.
- M. A. de Oliveira, G. Pound-Lana, P. Capelari-Oliveira, T. G. Pontífice, S. E. D. Silva, M. G. C. Machado, B. B. Postacchini and V. C. F. Mosqueira, J. Chromatogr. A, 2021, 1641, 461959, DOI:10.1016/j.chroma.2021.461959.
- S. Hester, K. B. Ferenz, A. Adick, C. Kakalias, D. Mulac, S. Azhdari and K. Langer, Int. J. Pharm., 2023, 646, 123454, DOI:10.1016/j.ijpharm.2023.123454.
- M. G. C. Machado, G. Pound-Lana, M. A. de Oliveira, E. G. Lanna, M. C. P. Fialho, A. C. F. de Brito, A. P. M. Barboza, R. D. d. O. Aguiar-Soares and V. C. F. Mosqueira, Drug Delivery Transl. Res., 2020, 10, 1626–1643, DOI:10.1007/s13346-020-00812-6.
- A. Moquin, J. Ji, K. Neibert, F. M. Winnik and D. Maysinger, ACS Omega, 2018, 3, 13882–13893, DOI:10.1021/acsomega.8b02311.
- S. Huclier-Markai, A. Grivaud-Le Du, E. N′tsiba, G. Montavon, M. Mougin-Degraef and J. Barbet, J. Chromatogr. A, 2018, 1573, 107–114, DOI:10.1016/j.chroma.2018.08.065.
- A. U. Khan, Z. Xu, X. Qian, A. Hong, Q. Tang, T. Zeng, M. Kah and L. Li, J. Hazard. Mater., 2021, 401, 123406, DOI:10.1016/j.jhazmat.2020.123406.
- L. J. Henze, N. J. Koehl, J. P. O’Shea, E. S. Kostewicz, R. Holm and B. T. Griffin, J. Pharm. Pharmacol., 2018, 71, 581–602, DOI:10.1111/jphp.12912.
- J. D. Clogston and A. Vermilya, NCL Method PCC-2: Measuring Zeta Potential of Nanoparticles, Nanotechnology Characterization Laboratory (NCL), Frederick, MD, 2020 Search PubMed.
- J.-M. Vergnaud, Controlled Drug Release of Oral Dosage Forms, Ellis Horwood, New York, NY, 1993 Search PubMed.
- H. Wu, A. Homawoo and S. M. Louie, Data and Model Fitting for Evaluation of Drug Release from Polymeric Nanoparticles in Simulated Saliva and Gastric Media by Asymmetric Flow Field–Flow Fractionation (AF4), Texas Data Repository, 2024. DOI:10.18738/T8/SQ3EQ4.
- D. M. Bates and D. G. Watts, Nonlinear Regression Analysis and Its Applications, Jon Wiley & Sons, New York, NY, 1988 Search PubMed.
- B. Delley, J. Chem. Phys., 2000, 113, 7756–7764, DOI:10.1063/1.1316015.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868, DOI:10.1103/PhysRevLett.77.3865.
- S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228, DOI:10.1002/wcms.30.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805, 10.1039/P29930000799.
- J. Andzelm, C. Kölmel and A. Klamt, J. Chem. Phys., 1995, 103, 9312–9320, DOI:10.1063/1.469990.
- M. E. Schimpf, K. Caldwell and J. C. Giddings, Field-Flow Fractionation Handbook, John Wiley & Sons, New York, NY, 2000 Search PubMed.
- H. Li, Y. Wang, Q. Tang, D. Yin, C. Tang, E. He, L. Zou and Q. Peng, Acta Biomater., 2021, 129, 57–72, DOI:10.1016/j.actbio.2021.05.019.
- S. Behzadi, V. Serpooshan, R. Sakhtianchi, B. Müller, K. Landfester, D. Crespy and M. Mahmoudi, Colloids Surf., B, 2014, 123, 143–149, DOI:10.1016/j.colsurfb.2014.09.009.
- G. Berrecoso, J. Crecente-Campo and M. J. Alonso, Drug Delivery Transl. Res., 2020, 10, 730–750, DOI:10.1007/s13346-020-00745-0.
- R. Cai and C. Chen, Adv. Mater., 2019, 31, 1805740, DOI:10.1002/adma.201805740.
- S. J. Siegel, J. B. Kahn, K. Metzger, K. I. Winey, K. Werner and N. Dan, Eur. J. Pharm. Biopharm., 2006, 64, 287–293, DOI:10.1016/j.ejpb.2006.06.009.
- B. S. Zolnik and D. J. Burgess, J. Controlled Release, 2007, 122, 338–344, DOI:10.1016/j.jconrel.2007.05.034.
- C. Yuan, S. Jin, J. Wei, J. Huang, C. Liu, X. Lei, Y. Zuo, J. Li and Y. Li, J. Mater. Chem. B, 2021, 9, 5861–5868, 10.1039/D1TB00734C.
- C. E. Rapier, K. J. Shea and A. P. Lee, Sci. Rep., 2021, 11, 14512, DOI:10.1038/s41598-021-93785-6.
- M. L. Houchin, S. A. Neuenswander and E. M. Topp, J. Controlled Release, 2007, 117, 413–420, DOI:10.1016/j.jconrel.2006.11.023.
- ISO, Nanotechnologies—Analysis of nanoobjects using asymmetrical-flow and centrifugal field-flow fractionation, Report ISO/TS 21362:2018, ISO, Geneva, Switzerland, 2018 Search PubMed.
- P. Fonte, S. Soares, A. Costa, J. C. Andrade, V. Seabra, S. Reis and B. Sarmento, Biomatter, 2012, 2, 329–339, DOI:10.4161/biom.23246.
- M. Lizondo, M. Pons, M. Gallardo and J. Estelrich, J. Pharm. Biomed. Anal., 1997, 15, 1845–1849, DOI:10.1016/S0731-7085(96)02033-X.
- S. Kalepu and V. Nekkanti, Acta Pharm. Sin. B, 2015, 5, 442–453, DOI:10.1016/j.apsb.2015.07.003.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4pm00175c |
| This journal is © The Royal Society of Chemistry 2024 |





