Folding mass spectra: how to deal with the signal to noise 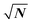 dilemma†
dilemma†
Tanja
Junkers
 * and
Iyomali
Abeysekera
* and
Iyomali
Abeysekera
Polymer Reaction Design Group, School of Chemistry, Monash University, 17 Rainforest Walk, Clayton VIC 3800, Australia. E-mail: tanja.junkers@monash.edu
First published on 21st November 2023
Abstract
A method to exploit the periodic information stored in polymer mass spectra for increasing the obtainable S/N ratio is presented. This method allows ‘folding’ of a spectrum into a single monomer repeat unit. The advantages of this procedure are an improved S/N, automatic averaging of all peaks for a better quantitative analysis of individual polymer end groups and an overall gain in time resolution for in situ experiments. The Python code for the processing of data is described and provided.
Time is Money, or so they say. In scientific research this simple rule may indeed also apply, but when it comes to gathering research data the better rule is often Time is Resolution. The more time a researcher spends on acquisition of a measurement signal, the better the signal to noise ratio (S/N) will become. Statistically, the relation is simple and the S/N will improve with the square root of the number of obtained measurements that can be co-added to form an integrated result.1 In cases where single measurement scans always take the same amount of time, the √N can also be expressed as √t, the square root of measurement time. Researchers use this relation practically constantly to accommodate for limited sensitivity of instruments. For example, NMR spectra are typically co-added over 16 scans for regular proton spectra to obtain a better S/N and to resolve also smaller peaks in the spectrum. Since the improvement of the S/N goes with the square root of number of scans, this improvement comes with a distinct onus. While using 4 scans results in doubling of the signal quality, one already needs 16 for the next doubling, then 64, 256, 1021, 4096, 16
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384, etc. for the following improvements. Depending on the worth of the experiment, or the desperation of the researcher, the time commitment becomes a crucial trade-off for signal quality. Hence, Time is Resolution.
384, etc. for the following improvements. Depending on the worth of the experiment, or the desperation of the researcher, the time commitment becomes a crucial trade-off for signal quality. Hence, Time is Resolution.
Especially with the increasing automation of reactions and the online monitoring that is connected with this development, this is a significant issue.2 In online monitoring, longer acquisition times result in a loss of time-resolution on the reaction axis.3 Thus, online monitors often accept lower signal resolution in order to increase information in the time domain. The same is true for analysing samples in LC-MS, where the LC dimension dictates the speed with which the MS measurement must be carried out.4,5
If a high time resolution is required, the only thing researchers can do is to accept the S/N that results from the instrument itself. Of course, advances in technology come with a constant improvement on this front, and often more expensive instruments will deliver a better S/N.
While the trade-off between time and resolution is obvious, it isn't always the end of the story. In here, we discuss a methodology that is specific to polymer characterization via mass spectrometry, which allows the increase of spectral resolution without omitting any time resolution. In this method, we make use of a specific, almost trivial, feature of mass spectra of polymers. Polymers consist of repeating units, and thus their mass spectra and the information contained therein are periodic.6 While this is again an obvious fact, to the best of our knowledge this is not systematically exploited to increase the S/N of the spectra.
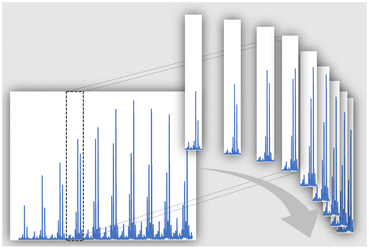
We propose to fold polymer mass spectra over the m/z range according to the monoisotopic monomer mass. In this way, the periodic information of the spectrum is accumulated into a single repeat unit cell of the spectrum, and the S/N will increase with the square root of repeat units visible in the spectrum. Fig. 1 depicts the principle. Practically the spectrum is divided into repeat unit cells, which are then co-added as if they were individual scans of the spectrum. At the same time, this feature averages out effects of different end groups resulting in a variation of relative ionization propensity over the whole spectrum. In other words, folding of the mass spectra simplifies the quantification of end groups, a task often carried out in polymer chemistry, either in synthesis or kinetic investigations.
Before looking at the procedure we devised for folding of spectra, it is useful to have a closer look at the increase in S/N with the number of scans. Modern mass spectrometers feature excellent S/N ratios and sensitivities. Still, especially for detection of low abundance peaks resolution and prolonged data acquisition are often required. In routine measurements, low abundance side products are likely to be missed if not enough care is taken. Hence, to visualize the effects of data acquisition we focus on small peaks, as this is where our method of spectrum folding will be most impactful. Fig. 2 shows a isotopic peak pattern found in a spectrum of poly(methyl acrylate), pMA, synthesized via atom transfer radical polymerization/single electron transfer polymerization (SET).7Fig. 3 shows the entire spectrum of the sample that was used in Fig. 2. The different plots depict the above discussed change in S/N with increasing the number of co-added single scans. With only 2 single scans, the peak series is visible, yet poorly resolved and it is difficult to determine a clear peak maximum for mass assignment. Also, absolute intensities are difficult to assess due to random spikes being visible in the spectrum. With 32 scans, and hence an S/N that is improved by √16 = 4, the peak is much better resolved and the peak shape is generally less noise distorted, even if still a crooked peak shape is observed (see insets for magnification of the peak shapes). While the improvement from 2 to 32 scans is substantial, the plot also shows that a mere doubling of scans isn't as impactful (relative improvement of a factor of √2 = 1.42). When comparing 2 with 4 scans, and 16 with 32, an improvement is visible, but by far not as pronounced.
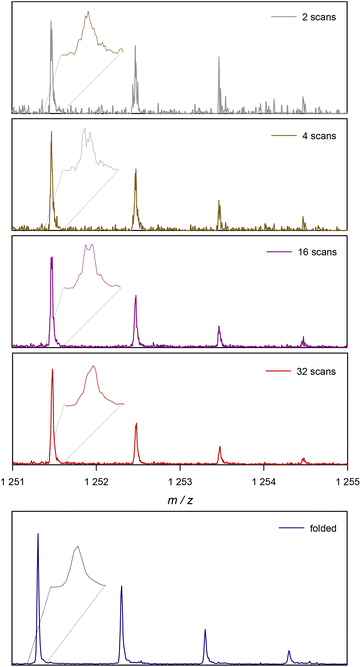 | ||
| Fig. 2 Example of the change in a single ionized species in ESI-MS with the number of scans. At the bottom the result of the proposed folding method is depicted for the same experimental data. | ||
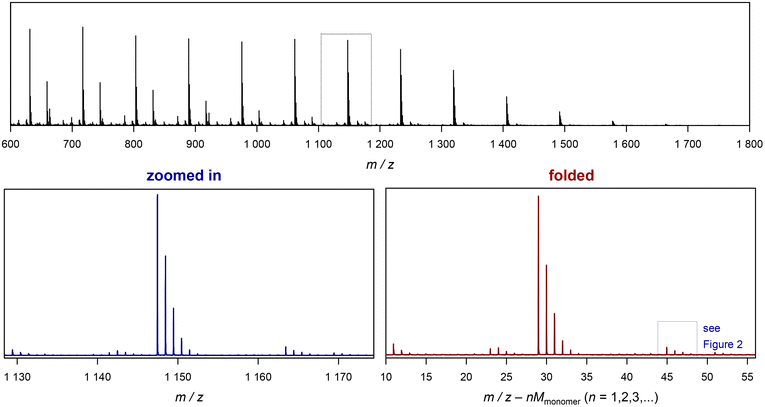 | ||
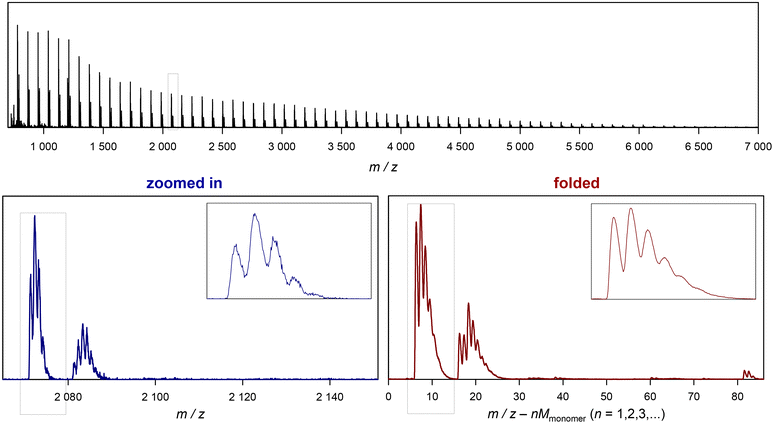
| Fig. 3 Example of folding a whole spectrum, on the example of SET-derived pMA. The top depicts the full ESI-MS raw spectrum. The bottom left shows the zoomed in image of the spectrum, and the bottom right depicts the corresponding folded spectrum. The blue dotted cage marks the peak depicted in Fig. 2. | ||
The added benefit of folding the spectrum is also depicted in Fig. 2. At the bottom, the same peak pattern is depicted for the folded spectrum of 32 scans. The procedure is discussed in the following, but one can already observe that a peak shape becomes visible that is much closer to a Gaussian distribution, underpinning the much higher quality in resolution that is instantaneously reached. Additionally, noise levels are much lower in the background of the spectrum. To avoid confusion, the folded spectrum and the 32-scan peak are both based on exactly the same data and no mathematical noise reduction method such as a spline was applied.
For the folding of spectra, we used a python code to process the peaks automatically.8 In here, we provide two different codes; one is a Jupyter notebook that allows users to process their data. The other is a code of a python function that carries out only the core task of folding. The first provides user convenience, and the latter is useful for researchers who want to implement the procedure into their own python workflow.
A piece of crucial information that is required for the procedure is the exact monoisotopic mass of the monomer repeat unit. This needs to be very exact, as already small deviations cause blurring of the residual folded spectrum. We thus make use of the rdkit library to process the SMILES code of the monomer to calculate the exact mass automatically.9
The python function is called via:
| folded\_data = fold\_massspec(min, max, mw, data) |
The function requires certain input variables, that is, the raw data to be processed (data) and the monoisotopic monomer mass (mw). It should be noted that the input data need to have the form of pandas.DataFrame, with two columns, in which the first contains the m/z values and the second the respective intensities. The sample code (see the ESI† or github) shows how to create such a variable from loading a csv raw data file. min and max define the m/z range that will be considered for the folding. All data above or below that range will be discarded from the original raw data. It should be noted that the function recalculated the min value automatically to match the nearest multiple of the monoisotopic monomer mass within the selected range. The function returns the folded spectrum.
The Jupyter notebook provides some more convenience. As mentioned, the mw variable is calculated automatically from the SMILES code of the monomer that is entered and the min and max variables are prompted after the raw data mass spectrum is plotted for visual examination. Further, after folding the data, more processing of the folded spectrum is carried out, and an automatic peak picking is performed. The notebook will create a plot of the folded spectrum and indicate single and double charged species found in the spectrum (above a defined intensity threshold). It should be noted that the general benefit of folding applies to both single charged and multiple charged species, and an example of the generated output can be found in the ESI.† It further creates a list of these automatically detected peaks (note that the success of this detection depends on the quality and complexity of the spectra) and saves this list automatically together with the folded spectrum in a csv file in the same folder as selected to load the input data from. An example of such conversion from raw data to the folded spectrum is shown in Fig. 3. The difference between the zoomed in section and the folded spectrum may seem to be not large, yet the further noise reduction is significant if the aim of the measurement is quantification of species rather than a mere assignment of species. Also, very low abundance species that are almost undiscernible in the zoomed in spectrum become much more clearly visible in the folded spectrum (see the ESI† for examples).
Before discussing further examples of S/N increase, it is worthwhile to look at the x-axis of the plot in Fig. 3, and what it represents. As discussed, the shown folded spectrum is the result of overlapping the data precisely from each monomer repeat unit in the original spectrum. This procedure does not only increase S/N, but also averages all peaks out with respect to their abundance. It is not uncommon to observe that certain species in a polymer spectrum ionize slightly differently, hence the mass-biased distribution appearing in the mass spectrum shows different overall shapes. This makes quantification of end groups somewhat difficult, as a comparison between single individual repeat units would yield a different result. The folding automatically levels this difference, allowing for a better and faster comparison of individual peaks, and indeed without folding, extensive analysis had to be performed before to reach a similar result.10–12 While the folding certainly averages over mass bias effects, it must, however, still be noted that the result will despite its general improvement still not be fully quantitative in the stricter sense as long as larger ionization biases of end groups cannot be ruled out.
The x axis in the folded spectrum itself represents the m/z found in the spectrum, from which all monomer units have been subtracted. While this might be confusing on first glance, it carries a convenience since for the calculation of theoretical masses of species no number of monomer units in the chain needs to be assumed or accounted for. All mass calculations can be made directly on the associated ion and the end groups or the defect in the polymer chain. Also, since isotope abundancies are also averaged out, peak patterns become often easier to interpret. We hope that researchers can get used to the presentation of the folded spectrum, in our experience it simplifies calculations significantly.
Several more examples of folded spectra compared to their zoomed in repeat units are given in the ESI.†Fig. 4 gives an important example of application of the procedure to MALDI data. In there, the spectrum of a poly(N,N-dimethyl acrylamide), pDMA, sample synthesized via reversible addition fragmentation chain transfer polymerization (RAFT) is shown.13 MALDI spectroscopy often allows covering a broader m/z range than ESI instruments, but suffers from less resolution. Hence, the folding is here an even more impactful procedure. The direct comparison between zoomed in and folded spectra shows that the folded spectrum is not only smoother and less noise-distorted, it also allows resolution of more isotopes in the peak pattern. Further, a peak series becomes clearly visible which in the zoomed in spectrum is virtually invisible, showing that the folding method does not only lead to an improvement of peak patterns, but also allows for identification of side products that otherwise might be missed. For this particular example, almost 50 repeat units in the spectrum were folded, leading to a potential improvement of a factor of 6–7. When analysing the S/N ratio for the folded and unfolded spectra, an improvement of about a factor 5 is found, hence generally in good agreement with theory. That the improvement of S/N is in reality somewhat below the theoretically expected value stems from folding of repeat units that are similar in noise levels, yet dissimilar in signal intensity (due to the apparent bell-shaped distribution of peaks observed experimentally). Thus, low intensity signal repeat units will contribute somewhat less to the S/N improvement. Yet, it should be noted that folding low intensity units still improves the noise level and does add to the signal, hence accounting also for those repeat units found at the edge of the mass spec distribution still contributes to an overall improvement of S/N.
Overall, the presented method is thus a simple, yet powerful tool to increase the mass resolution of mass spectra. It can be used in general mass spectrum analysis, but will unfold its complete potential in cases where co-adding of a significant number of spectra is not possible to increase the signal to noise ratio. This is of particular interest for LC-MS application of polymers or in online monitoring of polymer reactions. The code we provide can be used directly towards both applications.
Author contributions
TJ: conceptualization, writing first draft and editing, software development, and data curation; IA: manuscript editing and measuring of mass spectra.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful for the provision of MALDI spectra by Richard Whitfield and Athina Anastasaki.References
- https://en.wikipedia.org/wiki/Signal-to-noise_ratio .
- J. Haven and T. Junkers, Eur. J. Org. Chem., 2017, 6474–6482 CrossRef CAS.
- J. J. Haven, N. Zaquen, M. Rubens and T. Junkers, Macromol. React., 2017, 1700016 CrossRef.
- E. Uliyanchenko, S. van der Wal and P. J. Schoenmakers, Polym. Chem., 2012, 3, 2313–2335 RSC.
- K. Jovic, T. Nitsche, C. Lang, J. P. Blinco, K. De Bruycker and C. Barner-Kowollik, Polym. Chem., 2019, 10, 3241–3256 RSC.
- T. Gruendling, S. Weidner, J. Falkenhagen and C. Barner-Kowollik, Polym. Chem., 2010, 1, 599–617 RSC.
- D. Konkolewicz, Y. Wang, M. Zhong, P. Krys, A. A. Isse, A. Gennaro and K. Matyjaszewski, Macromolecules, 2013, 46(22), 8749–8772 CrossRef CAS.
- K. A. Tanemura, D. Sierra-Costa and K. M. Merz Jr., Python for Chemists, American Chemical Society, 2022. DOI:10.1021/acsinfocus.7e5030.
- A. P. Bento, A. Hersey, E. Félix, G. Landrum, A. Gaulton, F. Atkinson, L. J. Bellis, M. De Veij and A. R. Leach, J. Cheminf., 2020, 12, 51 CAS.
- K. De Bruycker, T. Krappitz and C. Barner-Kowollik, ACS Macro Lett., 2018, 7, 1443–1447 CrossRef CAS.
- T. Gruendling, W. Wallace, C. Barner-Kowollik, C. Guttman and A. Kearsley, Automated data processing and quantification in polymer mass spectrometry in Mass spectrometry in polymer chemistry, ed. S. Weidner, T. Gruendling, J. Falkenhagen and C. Barner-Kowollik, Wiley, Germany, 2012, pp. 237–280 Search PubMed.
- S. P. S. Koo, T. Junkers and C. Barner-Kowollik, Macromolecules, 2009, 42, 62–69 CrossRef CAS.
- J. Chiefari, Y. K. Chong, F. Ercole, J. Krstina, J. Jeffery, T. P. T. Le, R. T. A. Mayadunne, G. F. Meijs, C. Moad, G. Moad, E. Rizzardo and S. H. Thang, Macromolecules, 1998, 31, 5559–5562 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Installation guide and the Python code of the presented procedures, and further examples of folded spectra and their increase in resolution. See DOI: https://doi.org/10.1039/d3py01174g |
| This journal is © The Royal Society of Chemistry 2024 |