Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Quantum spin coherence and electron spin distribution channels in vanadyl-containing lantern complexes†
Manuel
Imperato‡
 ab,
Alessio
Nicolini‡
ab,
Alessio
Nicolini‡
 a,
Marco
Borsari
a,
Marco
Borsari
 a,
Matteo
Briganti
a,
Matteo
Briganti
 c,
Mario
Chiesa
c,
Mario
Chiesa
 d,
Yu-Kai
Liao
d,
Yu-Kai
Liao
 d,
Antonio
Ranieri
d,
Antonio
Ranieri
 e,
Arsen
Raza
e,
Arsen
Raza
 c,
Enrico
Salvadori
c,
Enrico
Salvadori
 d,
Lorenzo
Sorace
d,
Lorenzo
Sorace
 c and
Andrea
Cornia
c and
Andrea
Cornia
 *a
*a
aDipartimento di Scienze Chimiche e Geologiche e UdR INSTM, Università degli Studi di Modena e Reggio Emilia, via G. Campi 103, 41125 Modena, Italy. E-mail: acornia@unimore.it
bDipartimento di Scienze Fisiche, Informatiche e Matematiche, Università degli Studi di Modena e Reggio Emilia, via G. Campi 213/A, 41125 Modena, Italy
cDipartimento di Chimica “Ugo Schiff” e UdR INSTM, Università degli Studi di Firenze, via della Lastruccia 3, 50019 Sesto Fiorentino, FI, Italy
dDipartimento di Chimica e NIS Centre, Università degli Studi di Torino, via P. Giuria 7, 10125 Torino, Italy
eDipartimento di Scienze della Vita, Università degli Studi di Modena e Reggio Emilia, via G. Campi 103, 41125 Modena, Italy
First published on 3rd November 2023
Abstract
We herein investigate the heterobimetallic lantern complexes [PtVO(SOCR)4] as charge neutral electronic qubits based on vanadyl complexes (S = 1/2) with nuclear spin-free donor atoms. The derivatives with R = Me (1) and Ph (2) give highly resolved X-band EPR spectra in frozen CH2Cl2/toluene solution, which evidence the usual hyperfine coupling with the 51V nucleus (I = 7/2) and an additional superhyperfine interaction with the I = 1/2 nucleus of the 195Pt isotope (natural abundance ca. 34%). DFT calculations ascribe the spin density delocalization on the Pt2+ ion to a combination of π and δ pathways, with the former representing the predominant channel. Spin relaxation measurements in frozen CD2Cl2/toluene-d8 solution between 90 and 10 K yield Tm values (1–6 μs in 1 and 2–11 μs in 2) which compare favorably with those of known vanadyl-based qubits in similar matrices. Coherent spin manipulations indeed prove possible at 70 K, as shown by the observation of Rabi oscillations in nutation experiments. The results indicate that the heavy Group 10 metal ion is not detrimental to the coherence properties of the vanadyl moiety and that Pt–VO lanterns can be used as robust spin-coherent building blocks in materials science and quantum technologies.
Introduction
In the past 15 years, paramagnetic molecular complexes have been actively investigated as promising platforms for implementing quantum technologies.1–4 This followed the discovery that the coherence time of their electronic spin, Tm (i.e., the lifetime of the spin superposition state), can be long enough to allow spin manipulation by using pulsed magnetic resonance techniques.5 Compared to other investigated architectures, the molecular approach provides the possibility of fine-tuning the chemical and physical properties of the qubit by rational chemical design.6–8 In addition to allowing control over the sources of spin decoherence, this permits engineering the inter-spin interactions necessary to build universal quantum gates9–13 and endowing molecules with the features necessary for their controlled organization on a surface.14–17Among the molecules investigated as potential spin qubits, those containing the vanadyl ion (VO2+) have been reported to show almost invariably good coherence times18–23 which persist up to room temperature.19,24,25 Furthermore, thanks to the I = 7/2 nuclear spin of 51V, whose natural abundance (NA) is as high as 99.75%, vanadium(IV) complexes can also be operated as nuclear qudits with an electronic spin ancilla.26–28
Lantern complexes, also known as paddlewheel structures, are among the most versatile and robust building blocks in metal–organic chemistry. Their application potential covers catalysis, biomedical sciences, molecular recognition, and the assembly of molecular frameworks.29–33 Depending on the presence of either three or four bridging ligands (typically carboxylates34), they come in two main variants: trigonal and tetragonal, and often contain metal–metal bonds.35,36 The choice of the constituent metal ions is virtually limitless and has afforded a multitude of homo- and heterobimetallic variants. Examples of paramagnetic paddlewheels are numerous,37,38 but those incorporating vanadyl ions are comparatively rare. Available examples are limited to heterobimetallic species containing a heavy metal ion like Pd2+ or Pt2+ and (N,S), (N,O), or (O,S) bridging ligands like pyridine-2-thiolates,39 2-pyridonates,40 and monothiocarboxylates.41 These ligands coordinate following hard–soft Lewis acid–base principles,42 that is, any O donor is bonded to VO2+, whereas any S donor coordinates the Group 10 metal ion.
We herein investigate monothiocarboxylato-bridged lanterns [PtVO(SOCR)4] with R = Me (1) and Ph (2)41 as a new class of qubits exhibiting a combination of attractive features, which are otherwise separately present in different families of molecular spin qubits: (i) the V4+ ion is only coordinated by O donors, which are virtually nuclear spin-free; (ii) the ligand's skeleton comprises only S, C, and H atoms, and the nuclear spins are primarily embedded in the latter; (iii) the chemical structure can afford fourfold molecular symmetry, thereby simplifying the magnetic and spectroscopic responses; (iv) these lanterns are neutral and potentially processable materials, e.g. by vapor phase methods, and the PtS4 moiety may act as a decoupling layer between the VO2+ complex and a surface; (v) the superhyperfine interaction of the unpaired electron with the nucleus of 195Pt (I = 1/2, NA = 33.83%) may allow for the direct measurement of the degree of spin delocalization on the PtS4 moiety.
We find that the highly resolved X-band EPR spectra exhibited by these complexes in frozen solution allow for the accurate measurement of the superhyperfine coupling with 195Pt, in addition to the usual hyperfine interaction with the 51V nucleus. We then use DFT calculations to ascertain the origin of the superhyperfine coupling with 195Pt. Quantum spin coherence is detected by pulsed EPR spectroscopy up to 90 K, and coherent spin manipulations at 70 K are demonstrated by the Rabi oscillations observed in nutation experiments.
Results and discussion
Compounds 1 and 2·CH2Cl2 were prepared in pure crystalline form as described by Doerrer et al.41 Note that 2·CH2Cl2 loses lattice solvent rapidly, so that the actual composition of dry samples is 2·xCH2Cl2 with x < 1 (see the ESI†). However, for the sake of simplicity, the compound will be indicated as 2·CH2Cl2 throughout. Characterization data in the solid state by combustion analysis, single-crystal X-ray diffraction, and IR spectroscopy were found to be consistent with those reported by the above authors (see the ESI†).The structure of the lantern complexes in 1 and 2·CH2Cl2, as obtained by single-crystal X-ray diffraction at 100 K, is depicted in Fig. 1 (ellipsoid plots are available in Fig. S1†). The two metal centers are at 2.8635(6) Å and 2.7823(10) Å from each other, respectively. All O donors are bonded to the V4+ ion, which achieves a square-pyramidal coordination geometry, whereas the four S donors provide a square-planar environment around the Pt2+ ion. The crystallographic molecular symmetry is only C1, but the two paddlewheels approach fourfold symmetry quite closely in the solid state. Importantly, they assemble into dimers (V⋯V = 8.9–9.0 Å), although with a different interaction mode in the two compounds (Fig. S2†). In 1, two approximately coaxial and pseudo-staggered molecules form a C2-symmetric dimer via a metallophilic Pt⋯Pt interaction [3.1747(4) Å, S–Pt⋯Pt–S = 32.2–33.1°]. On the other hand, paddlewheel dimers in 2·CH2Cl2 are centrosymmetric and comprise two offset molecules interacting through a pair of Pt⋯S contacts [3.1266(14) Å]. It must be noted that a Pt–VO paddlewheel compound supported by 4-methylpyridine-2-thiolates assembles into one-dimensional chains via V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯Pt contacts rather than forming dimers.39
O⋯Pt contacts rather than forming dimers.39
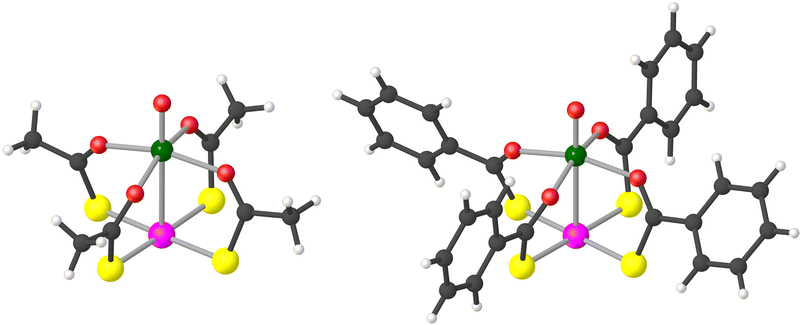 | ||
Fig. 1 Molecular structure of paddlewheel complexes in 1 (left) and 2·CH2Cl2 (right). Color code: dark gray = C, light gray = H, red = O, yellow = S, green = V, and pink = Pt. Selected distances and angles: V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O = 1.58–1.59 Å, V–O = 1.99–2.02 Å, O O = 1.58–1.59 Å, V–O = 1.99–2.02 Å, O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) V–O = 98.1–99.3°, O–V–O = 87.9–90.9°, Pt–S = 2.32 Å, and S–Pt–S = 88.8–90.9°. The line connecting V and Pt does not represent a chemical bond.41 V–O = 98.1–99.3°, O–V–O = 87.9–90.9°, Pt–S = 2.32 Å, and S–Pt–S = 88.8–90.9°. The line connecting V and Pt does not represent a chemical bond.41 | ||
We first extended to 2·CH2Cl2 the magnetic characterization in the solid state, reported in ref. 41 only for 1. The high-temperature value of χMT, where χM is the magnetic susceptibility per mole of vanadyl units and T is temperature, is 0.365 emu K mol−1 and agrees with the expectations for isolated S = 1/2 centers with g slightly smaller than 2.00 (0.368 emu K mol−1 for g = 1.98) (Fig. S6†). The χMT product decreases significantly upon cooling below 30 K, suggesting the presence of weak antiferromagnetic coupling between vanadyl ions. In Fig. S6†, we also present isothermal molar magnetization vs. field data for 2·CH2Cl2 at three different temperatures (1.9, 2.5, and 4.5 K). At the lowest temperature, the highest measured magnetization value is close to 1.0 μB per vanadyl moiety. A simultaneous fit of these magnetization and susceptibility data was performed using spin Hamiltonian (SH)43Ĥ = JŜ1·![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ŝ2 + gμB(Ŝ1 + Ŝ2)·B with S1 = S2 = 1/2 and expressing the calculated values per vanadyl moiety. When g was fixed at 1.975, a value typical of vanadyl complexes, J = 0.644(2) cm−1 was obtained as best-fit value (Fig. S6†).44 A significantly stronger antiferromagnetic interaction (J = 4.70 cm−1) was reported for 1.41
Ŝ2 + gμB(Ŝ1 + Ŝ2)·B with S1 = S2 = 1/2 and expressing the calculated values per vanadyl moiety. When g was fixed at 1.975, a value typical of vanadyl complexes, J = 0.644(2) cm−1 was obtained as best-fit value (Fig. S6†).44 A significantly stronger antiferromagnetic interaction (J = 4.70 cm−1) was reported for 1.41
Finally, since vanadyl complexes often display slow relaxation of magnetization in applied fields, we also performed alternating-current magnetic susceptibility measurements on both compounds (see the ESI and Fig. S7†). However, we did not observe any imaginary component of the susceptibility, indicating that the observed antiferromagnetic coupling hampers slow relaxation of magnetization in the solid state.
As first observed by Doerrer et al.,41 the V⋯V distances between adjacent molecular pairs in the crystal are as short as 4.89 Å in 1 and 4.77 Å in 2·CH2Cl2. Therefore, the involved superexchange coupling pathway is not necessarily intra-dimer in nature. DFT calculations were thus performed to determine the electronic structure of individual paddlewheels and unveil the mechanism of magnetic interaction among them in the solid state (see the ESI†). Single paddlewheels feature significant spin delocalization from V4+ to Pt2+via δ and π interactions (Fig. 2). The δ interaction occurs directly through space and arises from an efficient overlap between the 3dxy and 5dxy orbitals of V and Pt, respectively. The π interaction is mediated by the π system of the monothiocarboxylato ligands, whose O 2pπ and S 3pπ orbitals efficiently interact with the 3dxy and 5dxy orbitals of V and Pt, respectively. The resulting Löwdin spin density on Pt is 0.014 e− in 1 and 0.011 e− in 2. These values exceed those found on monothiocarboxylato O atoms directly bonded to V4+ and are consistent with the superhyperfine interaction with 195Pt observed in the EPR spectra (vide infra).
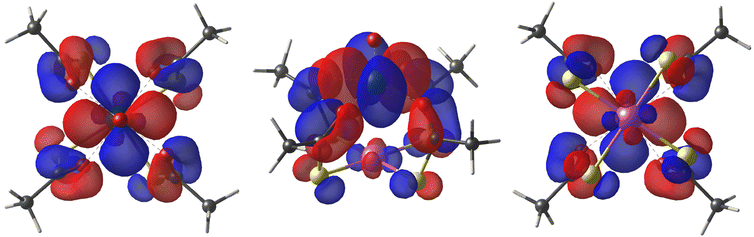 | ||
| Fig. 2 Top, side, and bottom views of the DFT-computed singly occupied quasi-restricted orbital (QRO) of 1. The isosurface value is set to 0.013 e−a0−3 (an additional plot at 0.05 e−a0−3 is available in Fig. S10†). The color code is the same as in Fig. 1. | ||
Further calculations on dimer models within the broken symmetry (BS) approach showed that intra-dimer coupling in 1 is antiferromagnetic with J = 6.55 cm−1, whereas inter-dimer interaction is much weaker (−0.290 cm−1). A much smaller antiferromagnetic interaction is predicted within the dimers of 2·CH2Cl2 (J = 0.466 cm−1), again surpassing in magnitude inter-dimer coupling (0.130 cm−1). A comparison with the experimental J values (4.70 cm−1 in 141 and 0.64 cm−1 in 2·CH2Cl2) indicates that intra-dimer interaction is the leading coupling mechanism in both compounds. Furthermore, calculations reproduce well the smaller J value measured in thiobenzoato derivative 2·CH2Cl2. Since the extent of spin delocalization on Pt is comparable in the two compounds, we ascribe the observed trend to geometrical factors. In 1, the neighboring Pt2+ ions are indeed only 3.175 Å apart from each other and lie along the pseudo-C4 axis of the dimer. The significant deviation of the average S–Pt⋯Pt–S dihedral angle (32.6°) from the staggered value (45°) then allows for some overlap between the magnetic orbitals of the two paddlewheels through the Pt 5dxy component. However, the two neighboring Pt2+ ions in 2·CH2Cl2 are not on the same axis but are engaged in Pt⋯S contacts, which results in a much weaker interaction.
The behavior of 1 and 2 in organic solvents was studied by a manifold of techniques before EPR experiments. The authors of ref. 41 quote room-temperature μeff values measured by the Evans method as a proof of the occurrence of monomeric complexes in CD2Cl2. We contend that these values would be insensitive to the weak superexchange coupling observed within molecular pairs, as evidenced by the solid-state magnetic susceptibility measured at room temperature. Direct estimation of molecular weight (MW) in solution was then attempted by 1H NMR diffusion ordered spectroscopy (DOSY), whose successful application to paramagnetic compounds of first-row transition metals has only recently been demonstrated.45 While 1 yielded featureless 1H NMR spectra in CD2Cl2, 2 afforded one well-resolved resonance assigned to the p-Ar protons (δ = 8.50 ppm, Δν½ = 89 Hz), which proved usable for a 1H NMR DOSY experiment (Fig. S3 and S4†). A procedure based on external calibration curves (ECCs, see the ESI for details†) afforded MW = 560 ± 170, 630 ± 200, or 620 ± 280 g mol−1 depending on the particular ECC used (Table S1†).45,46 Considering that the DOSY technique tends to underestimate the MW of solutes with high molecular densities,45,47 the results provide a strong indication that 2 is monomeric in CD2Cl2 (expected MW = 810.7 g mol−1).
Cyclic voltammetry was also performed on 1 mM solutions of 1 and 2 in CH2Cl2 at −23 °C (Fig. S5†). Both paddlewheels show a well-defined, quasi-reversible one-electron reduction/oxidation process at a formal potential E°′ = −1.737 V in 1 and −1.506 V in 2 (vs. Fc+/Fc). The thiobenzoato derivative 2 displays an additional cathodic signal at a more negative potential, lacking the anodic counterpart, which is indicative of an irreversible reduction process. The peak currents of all the signals are proportional to the square root of the potential scan rate, indicating diffusion-controlled electron transfer processes. The above-quoted formal potential value correlates well with the energy of the LUMO (−1.813 eV in 1 and −2.116 eV in 2), which provides the electron affinity within the Koopmans’ theorem (after sign reversal). Therefore, the larger reduction potential observed for 1 agrees with its computed lower electron affinity.
To gain additional insight into this redox process, one-electron reduced 1 (1−) was simulated by DFT and its structure was optimized in a vacuum. The paddlewheel structure is perfectly preserved upon reduction, and the final geometry is almost superimposable on the neutral one. More interestingly, the extra-electron is located on the 5dx2−y2 orbital of Pt, while the occupation of the 3d orbitals of V is unmodified. This 5dx2−y2 orbital shows an extensive delocalization on S atoms (Fig. S12†), as expected from its antibonding character, and some electron density is also present on V. Therefore, the reduction process leaves the V center unaffected, and a biradical species is formed with Pt showing +1 oxidation state.
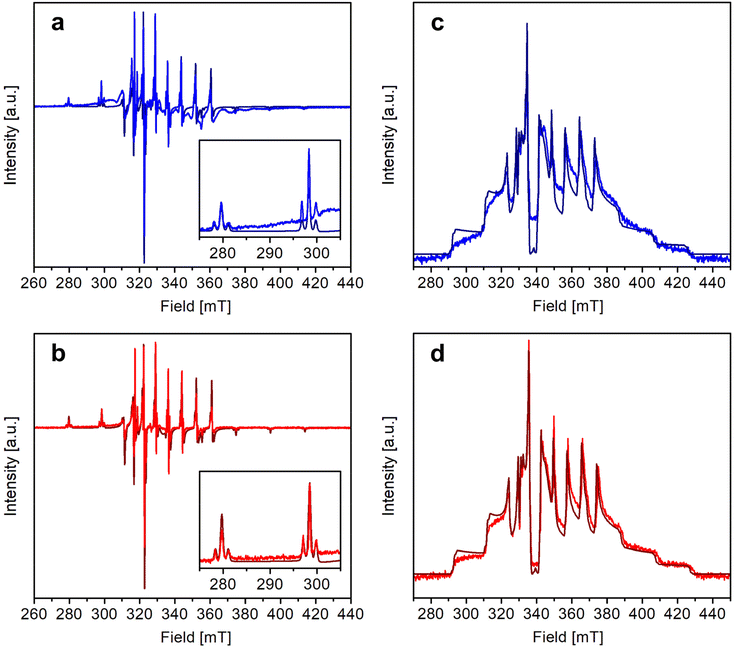
The X-band continuous wave (CW)- and electron spin echo (ESE)-detected EPR spectra of 1 and 2 were recorded in CH2Cl2/toluene or CD2Cl2/toluene-d8 (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v) frozen solution at 1–4 mM vanadyl concentration. The experimental spectra, shown in Fig. 3, are typical of isolated axial vanadyl moieties (S = 1/2), the broad background observed in the CW spectra of 1 being attributable to residual clustered species (expanded views of the spectra are available in Fig. S8†). The spectra are dominated by the anisotropic hyperfine coupling of the electron spin with the nuclear spin of 51V (I = 7/2), which splits each resonance, affording an eight-line pattern. Interestingly, the very narrow linewidth of the CW-EPR spectra allows us to clearly distinguish the further splitting of the signals due to the superhyperfine coupling with the nuclear spin of 195Pt (I = 1/2, NA = 33.83%), which produces satellite signals on either side of the main EPR lines. A superhyperfine coupling with Pt, although partly obscured by the broad linewidth of the spectrum, was previously reported in S = 1/2 paddlewheel [ClPtNi(OH2)(SOCPh)4].48 However, to the best of our knowledge, its observation in molecules containing VO2+ is unprecedented.
1 v/v) frozen solution at 1–4 mM vanadyl concentration. The experimental spectra, shown in Fig. 3, are typical of isolated axial vanadyl moieties (S = 1/2), the broad background observed in the CW spectra of 1 being attributable to residual clustered species (expanded views of the spectra are available in Fig. S8†). The spectra are dominated by the anisotropic hyperfine coupling of the electron spin with the nuclear spin of 51V (I = 7/2), which splits each resonance, affording an eight-line pattern. Interestingly, the very narrow linewidth of the CW-EPR spectra allows us to clearly distinguish the further splitting of the signals due to the superhyperfine coupling with the nuclear spin of 195Pt (I = 1/2, NA = 33.83%), which produces satellite signals on either side of the main EPR lines. A superhyperfine coupling with Pt, although partly obscured by the broad linewidth of the spectrum, was previously reported in S = 1/2 paddlewheel [ClPtNi(OH2)(SOCPh)4].48 However, to the best of our knowledge, its observation in molecules containing VO2+ is unprecedented.
Following this interpretation, all experimental spectra were simulated49 using the SH in eqn (1):
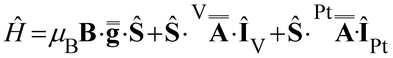 | (1) |
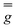 matrix and the hyperfine
matrix and the hyperfine 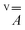 and
and 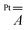 tensors were assumed to be axial and collinear. The SH parameters that provide the best simulation of the experimental CW-EPR spectra are gathered in Table 1 and the corresponding calculated spectra are shown in Fig. 3 and Fig. S8.† The principal components of
tensors were assumed to be axial and collinear. The SH parameters that provide the best simulation of the experimental CW-EPR spectra are gathered in Table 1 and the corresponding calculated spectra are shown in Fig. 3 and Fig. S8.† The principal components of 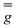 and
and 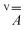 are fully consistent with those of other axial vanadyl complexes, with the unpaired electron mainly localized in the 3dxy orbital.18 It is worth stressing that the two complexes have very close SH parameters, further indicating that their structure is similar and that the structural differences observed in the crystalline state are mostly lost in frozen solution.
are fully consistent with those of other axial vanadyl complexes, with the unpaired electron mainly localized in the 3dxy orbital.18 It is worth stressing that the two complexes have very close SH parameters, further indicating that their structure is similar and that the structural differences observed in the crystalline state are mostly lost in frozen solution.
| 1 | 2 | |||
|---|---|---|---|---|
| EPR | DFT | EPR | DFT | |
a ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V,PtAx,y,z values are given in MHz. Experimental V,PtAx,y,z parameters are absolute values. V,PtAx,y,z values are given in MHz. Experimental V,PtAx,y,z parameters are absolute values.
|
||||
| g x,y | 1.991(1) | 1.991 | 1.990(1) | 1.988, 1.991 |
| g z | 1.9350(5) | 1.950 | 1.9338(3) | 1.952 |
| V A x,y | 196.0(5) | −268.33 | 197.0(5) | −262.310, −265.532 |
| V A z | 517.5(3) | −594.06 | 518.5(3) | −587.888 |
| Pt A x,y | 47(2) | −14.332, −14.247 | 42(2) | −11.596, −12.625 |
| Pt A z | 80.0(5) | −41.741 | 74.0(5) | −36.856 |
In particular, the quality of the simulations shows that any rhombic distortion is below experimental resolution and that both complexes approach axial symmetry. The spectra also firmly exclude intermolecular magnetic couplings comparable to those detected in the solid state (J ∼ 1–5 cm−1) and prove that 1 and 2 exist as monomers in organic solution. As the most significant difference between the two derivatives, the superhyperfine coupling with 195Pt is slightly larger in 1 than in 2 [PtAz = 80.0(5) vs. 74.0(5) MHz; PtAx,y = 47(2) vs. 42(2) MHz]. These values correspond however to a similar spin density delocalized on Pt, which is estimated to be of the order of 2.7% for both complexes (see the ESI†).
The SH parameters were simulated by DFT on the isolated molecules optimized in a vacuum (see the ESI†). The values so obtained are in fair agreement with those extracted from EPR spectra (Table 1).
The hyperfine coupling is slightly overestimated for V and underestimated for Pt, but the overall trend is nicely reproduced. A larger rhombicity is computed for 2, whose optimized structure exhibits a more pronounced deviation from C4 symmetry. The superhyperfine coupling with 195Pt is correctly predicted to be larger for 1 than for 2. To gain insight into the origin of this trend, in Table S5† we present the computed contributions to the 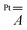 tensor. The modulation mainly arises from a reduced Fermi contact term, and this happens notwithstanding the shorter Pt⋯V distance in the optimized structure of 2 (Table S4†). Moreover, when the optimized structure of 2 is modified by replacing Ph with Me substituents, the computed superhyperfine coupling with Pt is practically unaffected. This shows that the smaller Fermi contact term in 2 is due to different geometrical parameters rather than to the electron-withdrawing effect of the Ph substituents. Specifically, the average V–O⋯S–Pt dihedral angle varies from 22.7° in 1 to 24.7° in 2 (Table S4†). These values are somewhat larger than those observed in the solid state (17.1 and 22.5°, respectively) but exhibit the same trend in the two derivatives. The larger dihedral angles of the thiobenzoato derivative then reduce the spin delocalization (vide supra) through π bonding, which would be maximized for dihedral angles close to zero. The importance of the π interaction through the ligands is further confirmed by model 1δ, where the π channel is switched off and the two metals can communicate only via δ interaction (see the ESI and Fig. S11†). The computed Fermi contact contribution to
tensor. The modulation mainly arises from a reduced Fermi contact term, and this happens notwithstanding the shorter Pt⋯V distance in the optimized structure of 2 (Table S4†). Moreover, when the optimized structure of 2 is modified by replacing Ph with Me substituents, the computed superhyperfine coupling with Pt is practically unaffected. This shows that the smaller Fermi contact term in 2 is due to different geometrical parameters rather than to the electron-withdrawing effect of the Ph substituents. Specifically, the average V–O⋯S–Pt dihedral angle varies from 22.7° in 1 to 24.7° in 2 (Table S4†). These values are somewhat larger than those observed in the solid state (17.1 and 22.5°, respectively) but exhibit the same trend in the two derivatives. The larger dihedral angles of the thiobenzoato derivative then reduce the spin delocalization (vide supra) through π bonding, which would be maximized for dihedral angles close to zero. The importance of the π interaction through the ligands is further confirmed by model 1δ, where the π channel is switched off and the two metals can communicate only via δ interaction (see the ESI and Fig. S11†). The computed Fermi contact contribution to 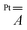 is reduced (in absolute value) from 19.843 MHz in 1 to 5.638 MHz in 1δ (Table S5†). We infer that the δ interaction accounts for roughly one-third of the spin delocalization on the Pt2+ ion, while the main channel is the π interaction through the thioacetato ligands.
is reduced (in absolute value) from 19.843 MHz in 1 to 5.638 MHz in 1δ (Table S5†). We infer that the δ interaction accounts for roughly one-third of the spin delocalization on the Pt2+ ion, while the main channel is the π interaction through the thioacetato ligands.
Finally, DFT calculations indicate that the large anisotropy of the 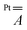 tensor mainly arises from the spin–orbit interaction of the Pt2+ ion, while the dipolar component plays a minor role (Table S5†).
tensor mainly arises from the spin–orbit interaction of the Pt2+ ion, while the dipolar component plays a minor role (Table S5†).
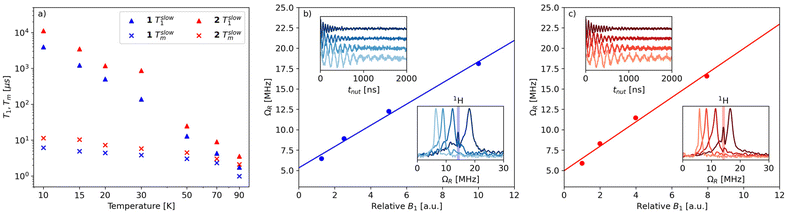
The spin relaxation properties of 1 and 2 were studied by pulsed-EPR spectroscopy at X-band frequency. Temperature-dependent inversion recovery and echo decay experiments were used to determine the spin–lattice relaxation time (T1) and the coherence time (Tm), respectively, in the temperature interval between 10 and 90 K (Fig. 4a). The samples were dissolved in deuterated solvents and measured as frozen solutions at a magnetic field setting corresponding to the maximum intensity of ESE-detected EPR spectrum (Fig. 3c and d). T1 and Tm values were extracted by fitting the experimental inversion recovery and echo decay traces, respectively (Fig. S9† and Table S2†).
The temperature dependence of Tm for 1 (Fig. 4a) is modest between 10 K and 70 K, with values in the range 6–2 μs and a drop at 90 K (Tm = 1 μs). Complex 2 displays slightly longer relaxation times than 1, with values in the range 11–2 μs between 10 K and 90 K. We note that the sudden decrease in Tm observed in 1 at 90 K is consistent with the discontinuity displayed by complexes [Cu(Et2dtc)2] and [Cu(Et2dtp)2] in the temperature range 85–130 K, which was attributed to the effect of methyl rotations (Et2dtc− = diethyldithiocarbamate, Et2dtp− = diethyldithiophosphate).50 Moreover, phenyl substituents in a similar complex, [Cu(Ph2dtp)2] (Ph2dtp− = diphenyldithiophosphate), were shown to affect Tm in a higher temperature range (120–250 K).50
The Tm values of 1 and 2 compare favorably with those of known vanadyl-based qubits in frozen solutions, which are typically in the 1–20 μs range and strongly depend on the presence of protonated solvents.18,20–23,28Tm values of 4–6 μs were reported in protonated solvents,20 while Tm can reach up to 20 μs in deuterated solvents.21–23 An exceptionally long Tm (>100 μs) was reported for bis-dithiolene vanadyl complexes in SO2, a nuclear spin-free solvent.21 This comparison indicates that the orbital overlap between V and Pt is not detrimental to the coherence properties of the vanadyl complex, despite the large spin–orbit coupling constant of Pt (almost fourty times larger than the corresponding value for V).51
To demonstrate the possibility of coherent spin manipulations, i.e., placing the spins in any arbitrary superposition of states, nutation experiments were performed at different microwave powers at 70 K. Rabi oscillations were clearly observed with the expected linear dependence of the Rabi frequency (ΩR) as a function of the microwave attenuation (Fig. 4b and c).
For both samples, the electronic spin–lattice relaxation time T1 was measured in the 10–90 K temperature range. Fig. 4a shows the slow component of the bi-exponential fit, which is usually taken to represent the spin–lattice relaxation (T1). The fast component, associated with spectral diffusion effects (i.e., excitation bandwidth smaller than the spectral width), is not considered.
Similar to Tm, a longer T1 was observed for 2, with a maximum value of ca. 11 ms at 10 K and the lowest value of 4 μs at 90 K. T1/Tm data were however not recorded above 90 K because of the echo intensity decay related to the onset of molecular libration as the melting point of the solvent is approached. The temperature dependence of T1 could be modelled considering a direct mechanism of relaxation at low temperatures and a local vibrational mode responsible for high-temperature relaxation,26,52 according to eqn (2):
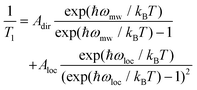 | (2) |
The first term in eqn (2) represents the direct mode (ωmw is the microwave frequency, with ωmw/2π = 9.74 GHz), while the second term accounts for a Raman process promoted by an optical mode of frequency ωloc, which represents an average of the effective vibrations. This model fairly reproduces the temperature dependence of T1 for both samples, providing a mean frequency with ħωloc = 109 cm−1 and 177 cm−1 for 1 and 2, respectively (Fig. 5 and Table S3†). While these values are in line with estimates recently reported for other vanadium-based molecular qubits,26 lower vibrational modes in the order of tens of cm−1 have been identified as drivers of the longitudinal relaxation in similar systems.26,53
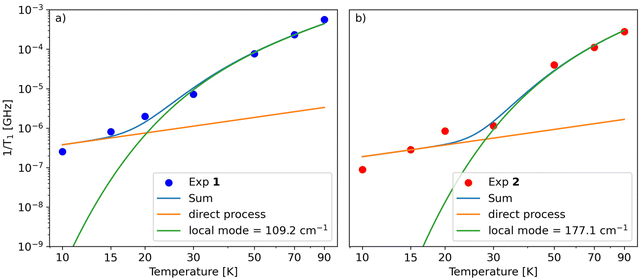 | ||
| Fig. 5 Fit of the dependence of T1vs. temperature for 1 (a) and 2 (b) using eqn (2). | ||
A theoretical analysis of the normal vibration modes of 1 and 2 lends considerable support to the above results (Tables S6 and S7†). Consistent with the average values obtained from the fitting, normal modes that affect the coordination sphere of V4+ are expected at frequencies below 200 cm−1 in both compounds, with the lowest around 60–70 cm−1.54 However, another key parameter is the symmetry of the normal vibration modes, which determines the magnitude of the spin-phonon coupling, as demonstrated elsewhere.55–57 For complexes with C4 symmetry, the normal modes belonging to the totally symmetric irreducible representation are the ones exerting the largest coupling and governing the spin–lattice relaxation.56 Although the two paddlewheels only have approximate C4 symmetry, by inspection of displacement vectors in the first coordination sphere it is straightforward to individuate those modes that would be totally symmetric in exact C4 symmetry. This analysis showed the presence of totally symmetric vibrations located at 104 cm−1 in 1 and at 171 cm−1 in 2, i.e. very close to the values resulting from the fitting (Tables S6, S7 and Fig. S13†). Although the effect of the solvent was not included in the DFT simulation, the agreement is remarkably good and shows again the predictive power of such a chemically intuitive approach. Moreover, in both cases, large contributions to the modes arise from the oxygen atoms in the first coordination sphere, as expected, but also from the methyl and phenyl groups. This feature could suggest a fine-tuning of the relaxation properties by acting on the substituents of the monothiocarboxylato ligands.
Conclusions
Lantern complexes containing VO2+ and Pt2+ ions bridged by monothiocarboxylates, [PtVO(SOCR)4], are a new family of electrically neutral molecular qubits where the paramagnetic vanadyl ion (S = 1/2) is situated in a uniaxial coordination environment with nuclear spin-free donors. The hyperfine interaction with the 51V nucleus (I = 7/2) is accompanied by a further measurable superhyperfine coupling with the fraction of 195Pt nuclei (I = 1/2) precisely located on the fourfold molecular axis. This additional interaction is triggered by the nonnegligible spin density transferred to the Pt2+ ion via π and δ pathways over a V⋯Pt distance of 2.8–2.9 Å. As a result, the 195Pt-51V isotopomer contains one electronic qubit (S = 1/2) coupled with a nuclear qudit (I = 7/2) and with a nuclear qubit (I = 1/2). Rewardingly, the spin coherence properties in frozen organic solution compete with those of the best-known vanadyl-based qubits, with Tm values reaching up to 11 μs for the derivative with R = Ph embedded in a CD2Cl2/toluene-d8 matrix at 10 K. The possibility of a coherent manipulation of the electronic spin was indeed demonstrated by the observation of Rabi oscillations in nutation experiments.The Group 10 metal ion and its square-planar coordination geometry offer attractive perspectives for functionalization and processing. The assembly of paddlewheels into dimers in the solid state through either metallophilic interactions or Pt⋯S contacts indicates a significant tendency of the heavy metal ion to engage in additional bonding interactions. For instance, the flat and electronically “soft” PtS4 moiety may offer a viable route to chemisorb these lanterns on metal surfaces. The fixed Pt⋯V distance of 2.8–2.9 Å is expected to ensure a weak electronic coupling between the VO2+ ion and the surface, with no need for a decoupling layer. Furthermore, unlike with VOPc58,59 and titanium sandwich compounds,60 paddlewheel molecules are expected to adopt a unique orientation on the surface, namely with the V![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vector pointing away from the surface. Attempts in this direction are underway in our laboratories.
O vector pointing away from the surface. Attempts in this direction are underway in our laboratories.
Author contributions
Manuel Imperato: investigation, validation, visualization, and writing – review & editing. Alessio Nicolini: formal analysis, investigation, validation, visualization, and writing – review & editing. Marco Borsari: formal analysis, investigation, validation, and writing – review & editing. Matteo Briganti: data curation, formal analysis, investigation, software, visualization, and writing – review & editing. Mario Chiesa: data curation, formal analysis, funding acquisition, resources, visualization, and writing – review & editing. Yu-Kai Liao: investigation and writing – review & editing. Antonio Ranieri: data curation, formal analysis, investigation, validation, visualization, and writing – review & editing. Arsen Raza: formal analysis, investigation, validation, visualization, and writing – review & editing. Enrico Salvadori: writing – review & editing. Lorenzo Sorace: data curation, formal analysis, investigation, resources, validation, visualization, and writing – review & editing. Andrea Cornia: conceptualization, funding acquisition, methodology, project administration, resources, supervision, and writing – original draft.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Italian Ministry of University and Research under the program Dipartimenti di Eccellenza 2023-2027 through projects DICUS 2.0 (Department of Chemistry “Ugo Schiff”, University of Florence) and CH4.0 (Department of Chemistry, University of Turin), as well as through PRIN project Q-CHISS (no. 2017CR5WCH) and PNRR project PE0000023-NQSTI. We also acknowledge financing by the European Union's Horizon 2020 research and innovation Programme through the FET-OPEN project FATMOLS (no. 862893), and by the European Research Council through the ERC SYNERGY project CASTLE (no. 101071533).References
- F. Troiani and M. Affronte, Molecular spins for quantum information technologies, Chem. Soc. Rev., 2011, 40, 3119–3129 RSC.
- G. Aromí, D. Aguilà, P. Gamez, F. Luis and O. Roubeau, Design of magnetic coordination complexes for quantum computing, Chem. Soc. Rev., 2012, 41, 537–546 RSC.
- M. Atzori and R. Sessoli, The Second Quantum Revolution: Role and Challenges of Molecular Chemistry, J. Am. Chem. Soc., 2019, 141, 11339–11352 CrossRef CAS PubMed.
- M. R. Wasielewski, M. D. E. Forbes, N. L. Frank, K. Kowalski, G. D. Scholes, J. Yuen-Zhou, M. A. Baldo, D. E. Freedman, R. H. Goldsmith, T. Goodson, M. L. Kirk, J. K. McCusker, J. P. Ogilvie, D. A. Shultz, S. Stoll and K. B. Whaley, Exploiting chemistry and molecular systems for quantum information science, Nat. Rev. Chem., 2020, 4, 490–504 CrossRef CAS PubMed.
- A. Ardavan, O. Rival, J. J. L. Morton, S. J. Blundell, A. M. Tyryshkin, G. A. Timco and R. E. P. Winpenny, Will Spin-Relaxation Times in Molecular Magnets Permit Quantum Information Processing?, Phys. Rev. Lett., 2007, 98, 057201 CrossRef PubMed.
- C. J. Wedge, G. A. Timco, E. T. Spielberg, R. E. George, F. Tuna, S. Rigby, E. J. L. McInnes, R. E. P. Winpenny, S. J. Blundell and A. Ardavan, Chemical Engineering of Molecular Qubits, Phys. Rev. Lett., 2012, 108, 107204 CrossRef CAS PubMed.
- M. J. Graham, J. M. Zadrozny, M. S. Fataftah and D. E. Freedman, Forging Solid-State Qubit Design Principles in a Molecular Furnace, Chem. Mater., 2017, 29, 1885–1897 CrossRef CAS.
- S. L. Bayliss, D. W. Laorenza, P. J. Mintun, B. D. Kovos, D. E. Freedman and D. D. Awschalom, Optically addressable molecular spins for quantum information processing, Science, 2020, 370, 1309–1312 CrossRef CAS PubMed.
- D. Aguilà, L. A. Barrios, V. Velasco, O. Roubeau, A. Repollés, P. J. Alonso, J. Sesé, S. J. Teat, F. Luis and G. Aromí, Heterodimetallic [LnLn′] Lanthanide Complexes: Toward a Chemical Design of Two-Qubit Molecular Spin Quantum Gates, J. Am. Chem. Soc., 2014, 136, 14215–14222 CrossRef PubMed.
- S. von Kugelgen, M. D. Krzyaniak, M. Gu, D. Puggioni, J. M. Rondinelli, M. R. Wasielewski and D. E. Freedman, Spectral Addressability in a Modular Two Qubit System, J. Am. Chem. Soc., 2021, 143, 8069–8077 CrossRef CAS PubMed.
- S. Nakazawa, S. Nishida, T. Ise, T. Yoshino, N. Mori, R. D. Rahimi, K. Sato, Y. Morita, K. Toyota, D. Shiomi, M. Kitagawa, H. Hara, P. Carl, P. Höfer and T. Takui, A Synthetic Two-Spin Quantum Bit: g-Engineered Exchange-Coupled Biradical Designed for Controlled-NOT Gate Operations, Angew. Chem., Int. Ed., 2012, 51, 9860–9864 CrossRef CAS PubMed.
- A. Ardavan, A. M. Bowen, A. Fernandez, A. J. Fielding, D. Kaminski, F. Moro, C. A. Muryn, M. D. Wise, A. Ruggi, E. J. L. McInnes, K. Severin, G. A. Timco, C. R. Timmel, F. Tuna, G. F. S. Whitehead and R. E. P. Winpenny, Engineering coherent interactions in molecular nanomagnet dimers, npj Quantum Inf., 2015, 1, 15012 CrossRef.
- D. Ranieri, F. Santanni, A. Privitera, A. Albino, E. Salvadori, M. Chiesa, F. Totti, L. Sorace and R. Sessoli, An exchange coupled meso–meso linked vanadyl porphyrin dimer for quantum information processing, Chem. Sci., 2023, 14, 61–69 RSC.
- A. Urtizberea, E. Natividad, P. J. Alonso, L. Pérez-Martínez, M. A. Andrés, I. Gascón, I. Gimeno, F. Luis and O. Roubeau, Vanadyl spin qubit 2D arrays and their integration on superconducting resonators, Mater. Horiz., 2020, 7, 885–897 RSC.
- K. Noh, L. Colazzo, C. Urdaniz, J. Lee, D. Krylov, P. Devi, A. Doll, A. J. Heinrich, C. Wolf, F. Donati and Y. Bae, Template-directed 2D nanopatterning of S = 1/2 molecular spins, Nanoscale Horiz., 2023, 8, 624–631 RSC.
- L. Poggini, A. Lunghi, A. Collauto, A. Barbon, L. Armelao, A. Magnani, A. Caneschi, F. Totti, L. Sorace and M. Mannini, Chemisorption of nitronyl–nitroxide radicals on gold surface: an assessment of morphology, exchange interaction and decoherence time, Nanoscale, 2021, 13, 7613–7621 RSC.
- L. Tesi, F. Stemmler, M. Winkler, S. S. Y. Liu, S. Das, X. Sun, M. Zharnikov, S. Ludwigs and J. van Slageren, Modular Approach to Creating Functionalized Surface Arrays of Molecular Qubits, Adv. Mater., 2023, 35, 2208998 CrossRef CAS PubMed.
- L. Tesi, E. Lucaccini, I. Cimatti, M. Perfetti, M. Mannini, M. Atzori, E. Morra, M. Chiesa, A. Caneschi, L. Sorace and R. Sessoli, Quantum coherence in a processable vanadyl complex: new tools for the search of molecular spin qubits, Chem. Sci., 2016, 7, 2074–2083 RSC.
- M. Atzori, E. Morra, L. Tesi, A. Albino, M. Chiesa, L. Sorace and R. Sessoli, Quantum Coherence Times Enhancement in Vanadium(IV)-based Potential Molecular Qubits: the Key Role of the Vanadyl Moiety, J. Am. Chem. Soc., 2016, 138, 11234–11244 CrossRef CAS PubMed.
- M. Atzori, S. Benci, E. Morra, L. Tesi, M. Chiesa, R. Torre, L. Sorace and R. Sessoli, Structural Effects on the Spin Dynamics of Potential Molecular Qubits, Inorg. Chem., 2018, 57, 731–740 CrossRef CAS PubMed.
- C.-J. Yu, M. J. Graham, J. M. Zadrozny, J. Niklas, M. D. Krzyaniak, M. R. Wasielewski, O. G. Poluektov and D. E. Freedman, Long Coherence Times in Nuclear Spin-Free Vanadyl Qubits, J. Am. Chem. Soc., 2016, 138, 14678–14685 CrossRef CAS PubMed.
- M. J. Graham, C.-J. Yu, M. D. Krzyaniak, M. R. Wasielewski and D. E. Freedman, Synthetic Approach To Determine the Effect of Nuclear Spin Distance on Electronic Spin Decoherence, J. Am. Chem. Soc., 2017, 139, 3196–3201 CrossRef CAS PubMed.
- K. Bader, M. Winkler and J. van Slageren, Tuning of molecular qubits: very long coherence and spin–lattice relaxation times, Chem. Commun., 2016, 52, 3623–3626 RSC.
- M. Atzori, L. Tesi, E. Morra, M. Chiesa, L. Sorace and R. Sessoli, Room-Temperature Quantum Coherence and Rabi Oscillations in Vanadyl Phthalocyanine: Toward Multifunctional Molecular Spin Qubits, J. Am. Chem. Soc., 2016, 138, 2154–2157 CrossRef CAS PubMed.
- T. Yamabayashi, M. Atzori, L. Tesi, G. Cosquer, F. Santanni, M.-E. Boulon, E. Morra, S. Benci, R. Torre, M. Chiesa, L. Sorace, R. Sessoli and M. Yamashita, Scaling Up Electronic Spin Qubits into a Three-Dimensional Metal–Organic Framework, J. Am. Chem. Soc., 2018, 140, 12090–12101 CrossRef CAS PubMed.
- M. Atzori, E. Garlatti, G. Allodi, S. Chicco, A. Chiesa, A. Albino, R. De Renzi, E. Salvadori, M. Chiesa, S. Carretta and L. Sorace, Radiofrequency to Microwave Coherent Manipulation of an Organometallic Electronic Spin Qubit Coupled to a Nuclear Qudit, Inorg. Chem., 2021, 60, 11273–11286 CrossRef CAS PubMed.
- S. Chicco, A. Chiesa, G. Allodi, E. Garlatti, M. Atzori, L. Sorace, R. De Renzi, R. Sessoli and S. Carretta, Controlled coherent dynamics of [VO(TPP)], a prototype molecular nuclear qudit with an electronic ancilla, Chem. Sci., 2021, 12, 12046–12055 RSC.
- I. Gimeno, A. Urtizberea, J. Román-Roche, D. Zueco, A. Camón, P. J. Alonso, O. Roubeau and F. Luis, Broad-band spectroscopy of a vanadyl porphyrin: a model electronuclear spin qudit, Chem. Sci., 2021, 12, 5621–5630 RSC.
- R. Hrdina, Dirhodium(II,II) Paddlewheel Complexes, Eur. J. Inorg. Chem., 2021, 2021, 501–528 CrossRef CAS.
- H. Miyasaka, Charge Manipulation in Metal–Organic Frameworks: Toward Designer Functional Molecular Materials, Bull. Chem. Soc. Jpn., 2021, 94, 2929–2955 CrossRef CAS.
- Y. Yan, S. Yang, A. J. Blake and M. Schröder, Studies on Metal–Organic Frameworks of Cu(II) with Isophthalate Linkers for Hydrogen Storage, Acc. Chem. Res., 2014, 47, 296–307 CrossRef CAS PubMed.
- M. Köberl, M. Cokoja, W. A. Herrmann and F. E. Kühn, From molecules to materials: Molecular paddle-wheel synthons of macromolecules, cage compounds and metal–organic frameworks, Dalton Trans., 2011, 40, 6834–6859 RSC.
- B. Chen, S. Xiang and G. Qian, Metal−Organic Frameworks with Functional Pores for Recognition of Small Molecules, Acc. Chem. Res., 2010, 43, 1115–1124 CrossRef CAS PubMed.
- M. A. S. Aquino, Recent developments in the synthesis and properties of diruthenium tetracarboxylates, Coord. Chem. Rev., 2004, 248, 1025–1045 CrossRef CAS.
- C. A. Murillo, The δ Bond and Trigonal Paddlewheels Before the Dawn of the Quintuple Bond, Comments Inorg. Chem., 2015, 35, 39–58 CrossRef CAS.
- J. P. Krogman and C. M. Thomas, Metal–metal multiple bonding in C3-symmetric bimetallic complexes of the first row transition metals, Chem. Commun., 2014, 50, 5115–5127 RSC.
- E. A. Hillard, Paramagnetism in Metal-Metal Bonded Paddlewheel Complexes, Curr. Inorg. Chem., 2013, 3, 112–143 CrossRef CAS.
- J. A. Chipman and J. F. Berry, Paramagnetic Metal–Metal Bonded Heterometallic Complexes, Chem. Rev., 2020, 120, 2409–2447 CrossRef CAS PubMed.
- K. Kitano, R. Tanaka, T. Kimura, T. Tsuda, S. Shimizu, H. Takagi, T. Nishioka, D. Shiomi, A. Ichimura, I. Kinoshita, K. Isobe and S. Ooi, Lantern-type dinuclear CrIIIPtII and VIVPtII complexes bridged by pyridine-2-thiolate. Synthesis and characterization, J. Chem. Soc., Dalton Trans., 2000, 995–1000 RSC.
- Y. Funahashi, T. Kamimura, M. Mizutani, Y. Wasada-Tsutsui, M. Sakai, H. Yashiro, T. Ozawa, K. Jitsukawa and H. Masuda, Micro-Columnar Crystals with (-O=V-Pd-)n Infinite Chain Structures Assembled by Hetero-Dinuclear Metal Complexes, Adv. Mater. Res., 2006, 11–12, 273–276 CAS.
- S. A. Beach, J. L. Guillet, S. P. Lagueux, M. Perfetti, B. N. Livesay, M. P. Shores, J. W. Bacon, A. L. Rheingold, P. L. Arnold and L. H. Doerrer, Heterotrimetallic {LnOVPt} complexes with antiferromagnetic Ln–V coupling and magnetic memory, Chem. Commun., 2020, 56, 11062–11065 RSC.
- S. A. Beach and L. H. Doerrer, Heterobimetallic Lantern Complexes and Their Novel Structural and Magnetic Properties, Acc. Chem. Res., 2018, 51, 1063–1072 CrossRef CAS PubMed.
- O. Kahn, Molecular Magnetism, VCH-Verlag, Weinheim, 1993 Search PubMed.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS PubMed.
- M. P. Crockett, H. Zhang, C. M. Thomas and J. A. Byers, Adding diffusion ordered NMR spectroscopy (DOSY) to the arsenal for characterizing paramagnetic complexes, Chem. Commun., 2019, 55, 14426–14429 RSC.
- S. Bachmann, R. Neufeld, M. Dzemski and D. Stalke, New External Calibration Curves (ECCs) for the Estimation of Molecular Weights in Various Common NMR Solvents, Chem. – Eur. J., 2016, 22, 8462–8465 CrossRef CAS PubMed.
- A.-K. Kreyenschmidt, S. Bachmann, T. Niklas and D. Stalke, Molecular Weight Estimation of Molecules Incorporating Heavier Elements from van-der-Waals Corrected ECC-DOSY, ChemistrySelect, 2017, 2, 6957–6960 CrossRef CAS.
- M. Gennari, G. Givaja, O. Castillo, L. Hermosilla, C. J. Gómez-García, C. Duboc, A. Lledós, R. Mas-Ballesté and F. Zamora, On the Road to MM′X Polymers: Redox Properties of Heterometallic Ni⋯Pt Paddlewheel Complexes, Inorg. Chem., 2014, 53, 10553–10562 CrossRef CAS PubMed.
- S. Stoll and A. Schweiger, EasySpin, a comprehensive software package for spectral simulation and analysis in EPR, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- J.-L. Du, G. R. Eaton and S. S. Eaton, Effect of molecular motion on electron spin phase memory times for copper(II) complexes in doped solids, Appl. Magn. Reson., 1994, 6, 373–378 CrossRef CAS.
- S. Koseki, N. Matsunaga, T. Asada, M. W. Schmidt and M. S. Gordon, Spin–Orbit Coupling Constants in Atoms and Ions of Transition Elements: Comparison of Effective Core Potentials, Model Core Potentials, and All-Electron Methods, J. Phys. Chem. A, 2019, 123, 2325–2339 CrossRef CAS PubMed.
- A. Lunghi and S. Sanvito, The Limit of Spin Lifetime in Solid-State Electronic Spins, J. Phys. Chem. Lett., 2020, 11, 6273–6278 CrossRef CAS PubMed.
- F. Santanni, M. Briganti, G. Serrano, E. Salvadori, A. Veneri, C. Batistoni, S. F. Russi, S. Menichetti, M. Mannini, M. Chiesa, L. Sorace and R. Sessoli, VdW Mediated Strong Magnetic Exchange Interactions in Chains of Hydrogen-Free Sublimable Molecular Qubits, JACS Au, 2023, 3, 1250–1262 CrossRef CAS PubMed.
- A. Albino, S. Benci, M. Atzori, L. Chelazzi, S. Ciattini, A. Taschin, P. Bartolini, A. Lunghi, R. Righini, R. Torre, F. Totti and R. Sessoli, Temperature Dependence of Spin–Phonon Coupling in [VO(acac)2]: A Computational and Spectroscopic Study, J. Phys. Chem. C, 2021, 125, 22100–22110 CrossRef CAS PubMed.
- R. Mirzoyan and R. G. Hadt, The dynamic ligand field of a molecular qubit: decoherence through spin–phonon coupling, Phys. Chem. Chem. Phys., 2020, 22, 11249–11265 RSC.
- N. P. Kazmierczak, R. Mirzoyan and R. G. Hadt, The Impact of Ligand Field Symmetry on Molecular Qubit Coherence, J. Am. Chem. Soc., 2021, 143, 17305–17315 CrossRef CAS PubMed.
- F. Santanni, A. Albino, M. Atzori, D. Ranieri, E. Salvadori, M. Chiesa, A. Lunghi, A. Bencini, L. Sorace, F. Totti and R. Sessoli, Probing Vibrational Symmetry Effects and Nuclear Spin Economy Principles in Molecular Spin Qubits, Inorg. Chem., 2021, 60, 140–151 CrossRef CAS PubMed.
- L. Malavolti, M. Briganti, M. Hänze, G. Serrano, I. Cimatti, G. McMurtrie, E. Otero, P. Ohresser, F. Totti, M. Mannini, R. Sessoli and S. Loth, Tunable Spin–Superconductor Coupling of Spin 1/2 Vanadyl Phthalocyanine Molecules, Nano Lett., 2018, 18, 7955–7961 CrossRef CAS PubMed.
- T. Niu, J. Zhang and W. Chen, Molecular Ordering and Dipole Alignment of Vanadyl Phthalocyanine Monolayer on Metals: The Effects of Interfacial Interactions, J. Phys. Chem. C, 2014, 118, 4151–4159 CrossRef CAS.
- M. Briganti, G. Serrano, L. Poggini, A. L. Sorrentino, B. Cortigiani, L. C. de Camargo, J. F. Soares, A. Motta, A. Caneschi, M. Mannini, F. Totti and R. Sessoli, Mixed-Sandwich Titanium(III) Qubits on Au(111): Electron Delocalization Ruled by Molecular Packing, Nano Lett., 2022, 22, 8626–8632 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental procedures with general methods, synthesis, and basic characterization data for 1 and 2·CH2Cl2, additional structural diagrams (Fig. S1 and S2), further details on NMR spectroscopy (Fig. S3 and S4 and Table S1), additional electrochemical data (Fig. S5), details on magnetic measurements (Fig. S6 and S7) and on EPR spectroscopy (Fig. S8 and S9 and Tables S2 and S3), computational procedures (Fig. S10–S13 and Tables S4–S7), and cartesian atomic coordinates of the DFT optimized structures of 1, 2, and 1−. See DOI: https://doi.org/10.1039/d3qi01806g |
| ‡ These authors contributed equally to this work. |
| This journal is © the Partner Organisations 2024 |