Conformationally enforced planarization of bis[1]benzothieno[1,4]thiazines: a rational design of redox-active fluorophores with increased radical cation stability

Abstract

A DFT-based approach guides the rational design of the substance class of anti–anti-bis[1]benzothieno[1,4]thiazines (BBTTs) bearing N-aryl substituents, previously generated as enhanced phenothiazine congeners, based upon the assumption that a minimization of the intrinsic butterfly folding in favor of a more planarized BBTT structure allows for better electronic tuning. Therefore, an intramolecular conformational restriction imposed by a sterically demanding ortho(,ortho′)-substitution pattern on N-aryl moieties is envisioned to provide this planarization of the BBTT's backbone, in solution and in the crystal solid state. Calculations of BBTT's minimum structures with variable N-aryl substitution as well as relaxed geometry PES scans assessing the energy barriers of the intramolecular restriction were carried out, identifying anti–anti-N-ortho,ortho′-disubstituted-phenyl-BBTTs as promising target structures. Synthetically, cyclizing Buchwald–Hartwig aminations starting from brominated sulfanes followed by subsequent functionalizations through organometallic catalysis and reagents pave the way to a substance library of the proposed BBTTs. Extensive structural analysis via X-ray diffraction reveals the molecular structures as well as the superordinate crystal packing patterns. NICS (nucleus-independent chemical shift) calculations indicate that strongly planarized BBTTs reveal a paratropic ring current and, therefore, an anti-aromatic character of their central 1,4-thiazine core. Comprehensive investigations of their optoelectronic properties by cyclic voltammetry, spectroelectrochemistry, and UV/vis absorption and emission spectroscopy shed light on the electronic structure, supported by aid of (TD)-DFT calculations. A broader range of their first redox potentials E^0/+1₀, larger semiquinone formation constants in comparison to para-N-aryl substituted BBTTs causing an increased radical cation stability, and a distinct tunability of their luminescence characteristics render ortho(,ortho′)-substituted BBTTs as highly functional strong donor moieties for future application in various fields.

---

Introduction

Organic electronics are commercially and technologically gaining dominance, for instance by the implementation of organic light emitting diodes (OLEDs), organic field effect transistors (OFETs), or organic photovoltaics (OPVs).¹ Their functional principle is based on organic semiconductors (OSCs) as active parts, characterized by the electronic properties of their expanded π-conjugated systems.² This mainly relies on the molecule's electronic structure, which is often fine-tunable by rational design whereby the desired properties can be achieved.^2a In this spirit, we aim to further refine the substance class of bis[1]benzothieno[1,4]thiazines (BBTT) (Fig. 1).

Fig. 1 Concept of the rational design of anti–anti-BBTTs to enforced conformational planarization through variation of the N-aryl substituent.

BBTTs were previously conceptualized as enhanced phenothiazine (PTZ) congeners by a formal double thieno expansion.³ Especially BBTTs’ anti–anti-regioisomers reveal fine-tunable, significantly lowered first oxidation potentials with a high radical cation stability and intense emission.⁴ For overcoming the inherent 4n-π-antiaromaticity of the central 1,4-thiazine, conjugated BBTTs generally, like their PTZ congeners, adopt a butterfly-like structure. Folding along the S,N-axis of the 1,4-thiazine core places N-substituents either in an N-intra (pseudo equatorial) or N-extra (pseudo axial) conformation.

Therefore, it is particularly impressive that anti–anti-BBTTs are outstandingly the first anellated 1,4-thiazines exhibiting antiaromatic character due to planarization in the crystalline solid state.^4a,c Subsequently, BBTTs as strong donors can be seen as enhanced substitutes for PTZ as an interesting potential OSC. Here, we present the rational design of enforced conformationally enhanced planarization of BBTTs by the N-aryl substituent, from computation over synthesis of a compound library and structural characterization in the solid state to electronic properties in the electronic ground and excited states.

Results and discussion

DFT-supported rational design

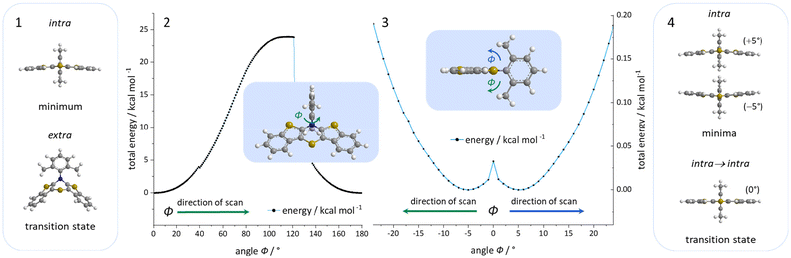
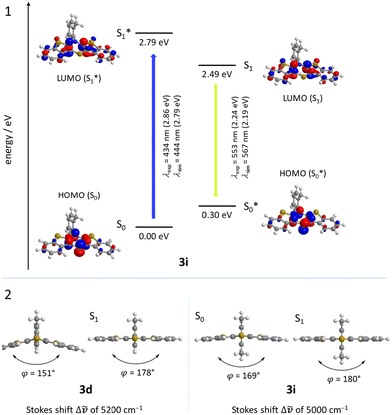
For enhancing the planarization in solution, as observed in the crystalline solid state, folding of the butterfly structure needs to be suppressed. This enforced planarization should promote π–π-stacking and enhance the antiaromatic character of BBTTs even in solution. Hence, the rational design commences with controlling BBTT's conformation as the promising variable. A DFT-based approach is taken aspiring an underlying intramolecular restriction of BBTT's scaffold. Since all known BBTTs planarized in the crystalline solid state bear an N-phenyl moiety, often substituted in the para-position, those were chosen as a starting point. From here on, a computational screen for minimum geometries by varying the N-aryl moiety with different methyl decorations is launched (Fig. 2). A modified constitution by an ortho,ortho′-decoration of the N-aryl results in a pronounced sterically restricted BBTT's backbone inducing an increase in planarization (B3LYP/6-311++G**, IEFPCM CH₂Cl₂).⁵ All postulated geometries reveal BBTTs adopting an N-intra conformation, thus the N-aryl substituents are orthogonally twisted with respect to the BBTTs’ scaffolds. The concept is further supported by employing a relaxed geometry potential energy surface scan (PES scan) of N-aryls torsion exemplarily for anti–anti-N-ortho,ortho′-dimethylphenyl-BBTT 3i (Fig. 3).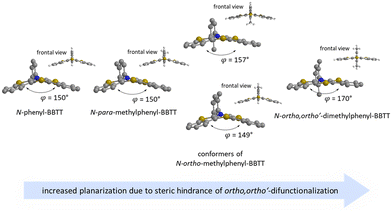

Fig. 2 Visualization of sterically restricted BBTTs due to the introduction of sterically demanding ortho,ortho′-substitution pattern (B3LYP/6-311++G**, IEFPCM CH₂Cl₂).

Fig. 3 Visualization of the relaxed geometry PES scans of N-inversion (2) and ring inversion (3) of N-aryls by the angle Φ of 3i (B3LYP/6-311G**, IEFPCM CH₂Cl₂). Most relevant minimum and transition state geometries of the relaxed geometry PES scan of N-inversion (1) and ring inversion (4) (B3LYP/6-311G**, IEFPCM CH₂Cl₂).

This forces a conformational change from the N-intra conformer (minimum geometry) to the N-extra conformer (B3LYP/6-311G**, IEFPCM CH₂Cl₂). The resulting N-extra conformer does not appear as a second local minimum, but rather as a transition state between both N-intra conformers. The energy barrier in SCF energy as well as the difference in Gibbs free energy amount to 24.0 and 28.3 kcal mol⁻¹, indicating a free rotation at room temperature to be unlikely. Therefore, the significantly more folded N-extra conformation should be suppressed. Determination of the equilibrium constant K_{intra→extra} to 1.90 × 10⁻²¹via Gibbs free energy difference quantifies this, resulting in a Boltzmann distribution of N-intra and N-extra conformer of 100 : 0 at 298 K. Furthermore, a change of conformation could also occur by ring inversion via a planar transition state. This can also be approximated by a relaxed geometry PES scan (B3LYP/6-311G**, IEFPCM CH₂Cl₂). Contrary to expectations no conformational change between N-intra and N-extra conformer arises. Instead an N-intra-intra equilibration occurs, which is particularly interesting for a heterogenic ortho,ortho′-substitution pattern. Significantly lower energy barriers in SCF energy and Gibbs free energy of <1 and 1.63 kcal mol⁻¹ indicate a free ring inversion at 298 K to be anticipated. The ratio of the N-intra conformer to the respective transition state can be determined to 94 : 6 via the equilibrium constant K_intrats of 6.37 × 10⁻².

Modular synthesis

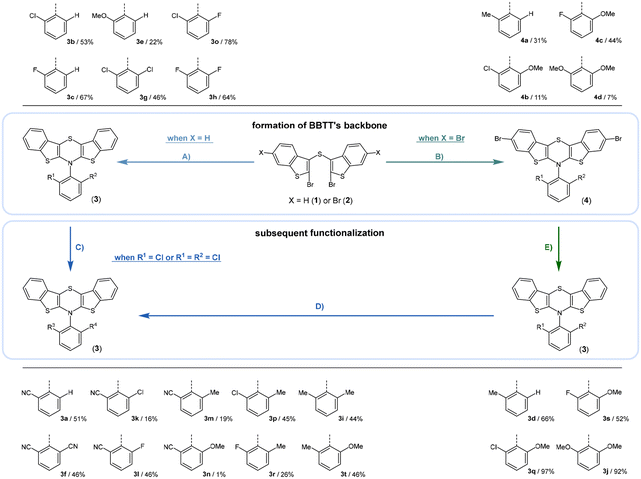
Synthesis follows up on our reliable established route to anellated 1,4-thiazines such as dithieno[1,4]thiazines (DTTs) and BBTTs via Buchwald–Hartwig amination.^3,4b,6 This previous concept has been adapted for the synthesis of sterically restricted anti–anti-BBTTs 3 using the dibrominated sulfane 1 and, in this case, respective ortho(,ortho′)-disubstituted anilines (Scheme 1). Whilst the previously employed ligand DPPF was only successfully applicable for ortho-substituted anilines,^4b for ortho,ortho′-disubstituted anilines the adaption with XantPhos as a ligand results in a breakthrough to satisfactory yields. Upon the sterically more demanding ortho(,ortho′)-substitution pattern efficiency of the coupling still overall dropped in favor of the intramolecular reductive C–C-coupling of the starting material, resulting in dibenzo[d,d′]thieno[3,2-b′;4,5-b′]dithiophene.⁷ At the same time the functional group tolerance is significantly lower. Whilst the ortho-substituted anilines transform to the desired products, the ortho,ortho′-disubstituted anilines only couple efficiently when halogenated anilines are selected. For establishing a broad substance library with a spectrum of electron donating to electron accepting substituents, alternative ways of functionalization need to be explored. On the one hand, synthesis of anti–anti-3,9-dibrominated BBTTs 4via Buchwald–Hartwig amination, starting from the respective tetrabrominated sulfane 2 with BINAP as a ligand, transforms electron-rich anilines. Following this up by a sequence of bromine-lithium exchange with ⁿBuLi and quenching with methanol reliably yields the desired products 3 with a plain BBTT's scaffold.^4a On the other hand, activation of C–Cl bonds on BBTTs with chlorinated N-aryl moieties can be established. The NHC-Pd-catalyst Peppsi™-IPr reliably promotes cyanation as well as Kumada coupling with a Grignard reagent. Since the synthesis of 3a with directly employing ortho-cyanoaniline was previously known to result in a poor yield of 5%, the herein-reported two-step synthesis with an overall yield of 27% can be seen as an improved and more reliable alternative.^4b

Scheme 1 Modular synthesis of sterically restricted BBTTs 3 yielding a functionalization with electron accepting to electron donating substituents in the ortho or ortho,ortho′-position of the N-aryl moiety: (A) ortho(,ortho′)-disubstituted aniline (1.00 equiv.), Pd(dba)₂ (5.00–7.50 mol%), DPPF or XantPhos (10.0–15.0 mol%), NaO^tBu (3.00 equiv.), 110 °C in toluene; (B) ortho(,ortho′)-aniline (1.00 equiv.), Pd(dba)₂ (3.00–5.00 mol%), BINAP (5.00–10.0 mol%), NaO^tBu (3.00 equiv.), 110 °C in toluene; (C) MeMgCl (1.20–2.40 equiv.), PEPPSI-IPr (10.0–15.0 mol%), 60 °C in THF; (D) K₄[Fe(CN)₆]·3H₂O (0.250–5.00 equiv.), PEPPSI-IPr (5.00–20.0 mol%), Na₂CO₃ (2.50–5.00 equiv.), 160 °C in DMF; (E) (I) ⁿBuLi (2.40 equiv.), TMEDA (2.40 equiv.), −78 °C in THF and (II) methanol (10.0 equiv.), −78–22 °C in THF.

Crystal data – molecular structure and underlying crystal packing patterns

Most herein-synthesized BBTTs 3 and 4 were extensively characterized by X-ray diffraction experiments elucidating BBTT's molecular structures (Fig. 4). They are hereafter best quantified by their S,N-folding, torsion, and S–N–C_aryl angles (see ESI: Chapter S3.1‡). All BBTTs adopt an N-intra conformation with an almost orthogonally twisted N-aryl moiety with respect to the BBTT's backbone, resulting torsion angles of ∼0°. S,N-folding angles fall in a range from 146 to 180°, whilst S–N–C_aryl-angles rise from 141° to a complete extension of the N-aryl moiety to the S,N-axis with 180°. Compared to their computational minimum geometries overall a strong induced planarization of BBTTs’ backbone upon crystallization is apparent (B3LYP/6-311++G**). The presence of two molecules per asymmetric unit for 3, as for 3e, 3f, and 3r, generally seems to lead to a more pronounced butterfly structure. In addition, 3f is found with three different polymorphs, showing the overall most folded structure even if there is only a single molecule in the asymmetric unit.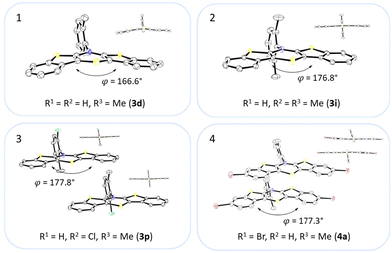

Fig. 4 Molecular structures of 3d (1), 3i (2), 3p (3) and 4a (4). The thermal ellipsoids are set at a 50% probability level while all hydrogen atoms are omitted for clarity.

The BBTTs 3o, 3p, 3r, and 4b with a heterogenic substitution pattern reveal cocrystallization of both possible N-intra conformers. This indicates that the DFT predicted N-intra-intra equilibration of conformation in solution is present. The computationally obtained difference of Gibbs free energy ΔG of the N-intra conformers can be extrapolated. By calculating the corresponding equilibrium constant K, the relative ratio of both N-intra conformers to each other can be determined. Furthermore, the planar transition state of ring inversion is computed for 3a–e and all homogenously substituted derivatives 3f, 3g, 3h, 3i, 3j, and 4d, opening up for extraction of the rate constant k of this N-intra-intra equilibration. The small free activation energies ΔG^‡_A below 2.0 kcal mol⁻¹ and resultingly high rate constants k in the order of 10¹¹–10¹² s⁻¹ suggest, that a substantial free ring inversion is very likely (see ESI: Chapter S4.2‡). Measured NMR spectra prove this experimentally by displaying only a single set of signals. In order to possibly gain an understanding of the induced planarization in the crystalline state, the crystal packing patterns superimposed on the individual molecule's geometry are examined in more detail (see ESI: Chapter S3.2‡). A structurally similar crystal packing pattern is found for the derivatives with only one molecule per asymmetric unit and an ortho-substitution pattern (3a–d) excepted 3c, a homogeneous ortho,ortho′-substitution pattern (3f, 3g, 3h, 3i, 3j), and also for the heterogeneously substituted derivatives 3p and 3t. The single molecules form staircase-like structures with an overlap of approximately a half of the BBTTs’ backbones. For structures 3a and 3g–3j, a larger overlap results solely from the offset of the individual molecules in a self-defined y-axis, whereas for 3b, 3d and 3f the overlap is reduced by additional offset in the self-defined x-ordinate. The molecules of one staircase are aligned in the same direction, which means that the N-aryl moieties all face the same side. These superordinate staircase-like structures are usually not consistently aligned parallel across the entire crystal but are rather twisted with respect to each other. The degree of twisting depends on the compound. Only for molecule 3j a parallel orientation of the staircase-like substructures relative to each other is adopted. This places the BBTTs’ backbones as well as the 90°-twisted N-aryl moieties each in alignment. The crystal packing patterns of 4a, 4b, and 4d do not significantly differ in their degree of planarization despite the varying number of molecules per asymmetric unit, unlike those of BBTTs 3. With their maximized folding angles and S–N–C_aryl-angles of up to 180° 3,9-dibrominated BBTTs 4 even outshine BBTTs 3 by achieving full planarization. They also exhibit a half-sided overlap of the BBTTs’ backbones with only offset in the self-defined y-axis. This overlap is maximized by the two bromine atoms extending the BBTT's backbone causing a stronger planarization. The N-aryl moieties of the individual molecules are again oriented in the same direction. The staircase-like substructures are not twisted relative to each other but arranged alternately parallel as for 3j. To better illustrate the arrangement with regards to the twisting of the staircase-like substructures relative to one another, the structure of compounds 3d, 3i, and 4a are exemplarily compared in Fig. 5.

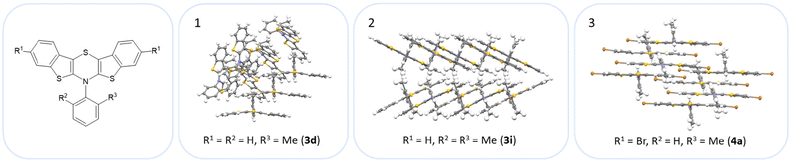Fig. 5 Illustration of the twisting of the staircase-like substructures using the example of 3d (1), 3i (2) and 4a (3).

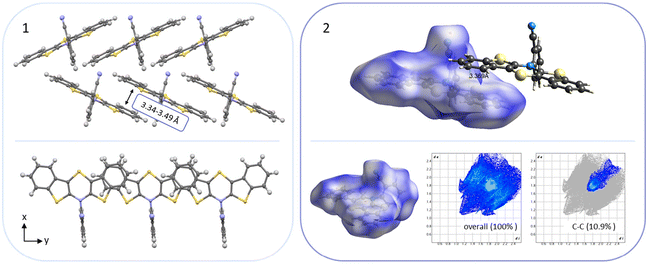
For all above-described crystal packing patterns the intermolecular distance of the planarized BBTTs’ backbones of two individual molecules is ∼3.38 to 4.13 Å. This lies just around the van der Waals radii of two carbon atoms with 3.40 Å.⁸ Only for structure 3a an even stronger proximity of the BBTT scaffolds occurs with values of 3.34 to 3.49 Å, resulting in the beginning of π–π-stacking (Fig. 6). The shortest C–C contact of 3.369 Å arises between two carbon atoms of the anellated benzenes of neighboring BBTT's backbones. Corresponding Hirshfeld surface analysis also depicts this, especially the C–C contact coded for in red. The corresponding fingerprint diagrams reflect this by their light blue areas in the range from 1.8–2.0 d_i to 1.8–2.0 d_e.⁹ Resultingly, the planar geometry and the extent of the intermolecular proximity of the BBTTs’ single molecules can be positively assessed with regard to a possible application as an OSC. Material science knows that a sufficient electronic coupling arises from intermolecular distances of around 3.4 to 4.0 Å, as a basis for potential charge carrier mobility.¹⁰ Comparable thiophene-acene based materials with intermolecular distances of around 3.52 and 3.56 Å show decent charge carrier mobility.¹¹ The remaining derivatives of 3 show no consistent packing patterns. The still quite planarized derivatives 3o and 3n with folding angles of 165° at least show the presence of a substructure, described herein as a pair-like arrangement. The individual molecules are rotated by 180° relative to each other, whereby their N-aryl moieties are oriented in opposite directions. At the same time, the BBTT's scaffolds overlap again halfway. A similar pair-like arrangement, but with a stronger overlap, could be identified for the para-aryl congeners with a pronounced planarization in their molecular structure.^4c

Fig. 6 (1) Section of the crystal packing pattern of anti–anti-N-ortho-cyanophenyl-BBTT 3a. (2) Graphical depiction of the shortest C–C-contact between two BBTT single molecules of one staircase-like substructure as well as the Hirshfeld surface with their respective fingerprint diagrams.

Antiaromaticity

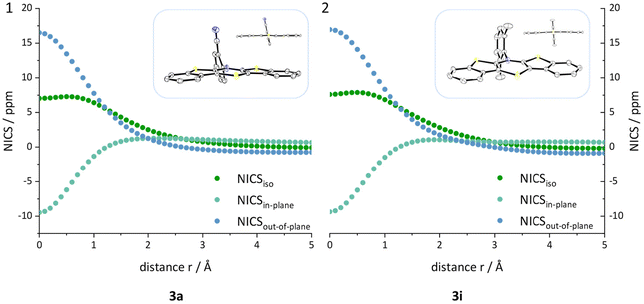
An investigation whether the herein presented planarized BBTTs also exhibit antiaromaticity of the central 1,4-thiazine has to be scrutinized. BBTTs with folding angles over 177° can be analyzed by the well-established DFT-procedure of computing nuclear independent chemical shifts (NICS) using the crystal data's geometry as an input (B3LYP/6-311+G**).¹² Therefore, BBTTs 3a, 3g, 3p, 3h, 3i, 4a, 4b, and 4d are examined by placing ghost atoms in the center and 1 Å above and below the plane, of each respective ring, providing the NICS_iso(0) and NICS_iso(+1/−1) values of interest. The outcome clearly reveals diatropic ring currents for the ring systems of the fused benzo[b]thiophenes and thus, as expected, indicates their aromaticity. The central 1,4-thiazine rings, however, each exhibit a paratropic ring current, which suggests that those rings are antiaromatic. This is further supported by an in-depth analysis, in which the NICS_iso value, divided into its underlying NICS_in-plane and NICS_out-of-plane contributions, is calculated. The ghost atoms are hence placed starting from in the centroid to 5 Å above the 1,4-thiazine ring. The plotted curves, e.g. see Fig. 7, clearly indicate that the 1,4-thiazine rings are not nonaromatic but rather possess considerable antiaromatic character (see ESI: Chapter S3.3‡).

Fig. 7 NICS_iso, NICS_in-plane and NICS_out-of-plane values plotted against the distance r of the ghost atom from the center of the 1,4-thiazine as well as the underlying crystal structure geometry exemplarily for 3a (1) and 3i (2) (B3LYP/6-311+G**).

Optoelectronic properties and electronic structure

The optoelectronic properties of BBTTs 3 are assessed via cyclic voltammetry for the ground state and UV/vis absorption and emission spectroscopy for the excited state elucidating the electronic structure (Table 1). Spectroelectrochemistry is used to generate the oxidized species and to characterize their UV/vis absorption behavior. A deeper insight is gained by accompanying computational studies employing Gaussian 09 for (TD-)DFT-calculations.¹³

Table 1 Electrochemical and photophysical properties of BBTTs 3 and 4 (redox potentials E₀ (vs. Fc/Fc⁺ = 0.00 V) and UV/vis data recorded in CH₂Cl₂, 298 K)

	E ^0/+10,^a mV (E^0/+10,^b mV)	E ^+1/+20,^a mV (E^+1/+20,^b mV)	K Sem	λ abs,sol, nm (ε, 10^3 L mol^−1 cm^−1)	λ em,sol.,^c nm (Δ[small nu, Greek, tilde], cm^−1/Φ/τ,^d ns/kr, s^−1/knr, s^−1)	λ abs,pow,^e nm	λ em,pow,^e nm (Φ)
a Redox potentials obtained by extrapolation of data with v = 100, 250, 500, and 1000 mV s^−1 to v = 0.00 mV s^−1. b Redox potentials at v = 100 mV s^−1. c λ exc. = λabs,max,sol. d Lifetime τ measured at λexc = 448.8 nm. e Powder samples measured.
	115 (119)	895 (906)	1.65 × 10^13	233 (44.3), 309 (6.2), 411 (2.9)	519, 543 (5900/0.00/n.d./n.d./n.d.)	417	620 (0.00)
	20 (33)	828 (840)	4.42 × 10^13	235 (54.2), 263 (25.1, sh), 314 (10.2), 423 (3.6)	519, 540 (5100/0.06/3.31/1.81 × 10^7/2.84 × 10^8)	420	546 (0.04)
	49 (58)	848 (865)	3.44 × 10^13	234 (49.5), 267 (20.8, sh), 282 (13.3, sh), 315 (7.4), 418 (3.1)	515 (sh), 539 (5400/0.20/8.67/2.31 × 10^7/9.23 × 10^7)	422	543 (0.36)
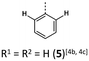
	−22 (−18)	734 (742)	7.61 × 10^12	236 (46.3), 268 (19.4, sh), 321 (7.6), 425 (3.5)	526, 548 (5300/0.16/9.18/1.74 × 10^7/9.15 × 10^7)	414	567 (0.09)
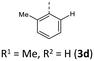
	−29 (−23)	766 (771)	2.92 × 10^13	234 (50.3), 269 (21.1, sh), 316 (9.0), 429 (4.0)	525, 551 (5200/0.24/10.6/2.27 × 10^7/7.20 × 10^7)	433	582 (0.06)
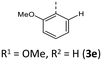
	−69 (−63)	748 (761)	6.97 × 10^13	232 (65.3), 270 (27.6), 318 (10.3), 425 (4.7)	521, 547 (5200/0.22/10.3/2.13 × 10^7 /7.55 × 10^7)	429	551 (0.09)
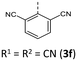
	261 (256)	1066 (1073)	4.41 × 10^13	232 (67.3), 251 (33.0, sh), 260 (25.9, sh), 300 (12.0, sh), 411 (2.5)	—	410	—
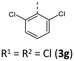
	83 (93)	926 (951)	1.92 × 10^14	230 (57.5), 264 (24.7, sh), 310 (8.8), 420 (3.4)	509, 536 (sh) (5200/0.00/n.d./n.d./n.d.)	440	—
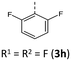
	139 (143)	946 (982)	4.81 × 10^13	234 (49.5), 265 (21.5, sh), 279 (14.9, sh), 309 (8.2), 413 (3.3)	511 (sh), 529 (5300/0.00/n.d./n.d./n.d.)	418	532 (0.01)
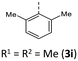
	−46 (−35)	819 (835)	4.57 × 10^14	233 (52.8), 269 (22.9), 316 (8.5), 434 (4.4)	524, 553 (5000/0.27/11.2/2.42 × 10^7/6.53 × 10^7)	439	562 (0.18)
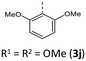
	−97 (−89)	789 (787)	1.05 × 10^15	236 (53.4), 270 (22.6, sh), 315 (11.1), 429 (3.6)	518, 544 (4900/0.33/10.5/3.13 × 10^7/6.36 × 10^7)	438	588 (0.18)
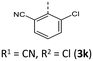
	156 (156)	1014 (1019)	3.47 × 10^14	231 (73.6), 250 (35.9, sh), 279 (18.5, sh), 315 (9.3, sh), 413 (3.3)	—	414	—
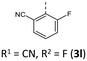
	182 (185)	1006 (1014)	9.12 × 10^13	231 (60.9), 248 (36.3, sh), 277 (17.8, sh), 316 (7.6, sh), 412 (2.9)	—	416	—
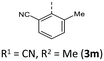
	100 (102)	952 (956)	2.72 × 10^14	231 (58.2), 268 (21.3, sh), 308 (7.9), 419 (3.3)	—	427	—
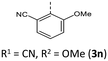
	66 (81)	925 (948)	3.61 × 10^14	232 (62.0), 267 (22.6, sh), 304 (15.0), 413 (3.9)	—	420	—
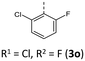
	108 (111)	940 (954)	1.24 × 10^14	233 (40.7), 265 (17.8, sh), 282 (10.9, sh), 308 (6.9), 413 (2.90)	511 (sh), 525 (5200/0.00/n.d./n.d./n.d.)	420	534 (0.00)
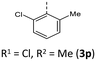
	28 (31)	882 (894)	2.90 × 10^14	234 (57.0), 271 (23.5), 316 (8.1), 433 (4.1)	516, 544 (4700/0.16/7.23/2.21 × 10^7/1.16 × 10^8)	431	552 (0.09)
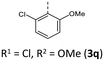
	7 (6)	871 (874)	4.48 × 10^14	233 (56.7), 267 (24.4), 310 (8.7), 423 (4.0)	513, 539 (5100/0.03/8.92/3.36 × 10^6/1.09 × 10^8)	425	544 (0.02)
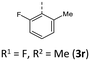
	51 (56)	875 (893)	9.16 × 10^13	233 (45.0), 269 (18.7, sh), 282 (12.9, sh), 312 (7.1), 424 (3.2)	515, 541 (5100/0.19/10.7/1.77 × 10^7/7.55 × 10^7)	431	543 (0.05)
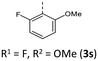
	12 (15)	860 (873)	2.35 × 10^14	233 (57.4), 269 (24.8), 312 (8.9), 416 (4.0)	515 (sh), 535 (5300/0.11/7.00/1.57 × 10^7/1.27 × 10^8)	425	575 (0.12)
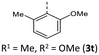
	−61 (−56)	804 (818)	4.59 × 10^14	234 (97.1), 271 (43.6), 312 (15.2), 430 (7.7)	519, 549 (5000/0.33/11.2/2.94 × 10^7/5.98 × 10^7)	433	554 (0.28)

---

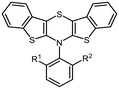
All cyclic voltammograms (CVs) of BBTTs 3 reveal a three-stage redox system of Weitz type with two clearly separated redox processes,¹⁴ which are caused by consecutive one-electron transitions with Nernstian reversibility (Fig. 8).

Fig. 8 (1) CVs of BBTTs of 3m, 3p, 3r, 3i, and 3t (CVs recorded in CH₂Cl₂, T = 298 K, 0.1 M [ⁿBu₄N][PF₆], v = 100 mV s⁻¹, Pt-working- und counter electrode, Ag/AgCl(3 M)-reference electrode, referenced with decamethylferrocene (DMFc)/DMFc⁺, potential vs. Fc/Fc⁺ = 0.00 V). (2) Minimum geometries of BBTTs 3d and 3i as well as their corresponding radical cations 3d˙⁺ and 3i˙⁺ ((u)B3LYP/6-311++G**, IEFPCM CH₂Cl₂) and illustration of the increase in the radical stability.

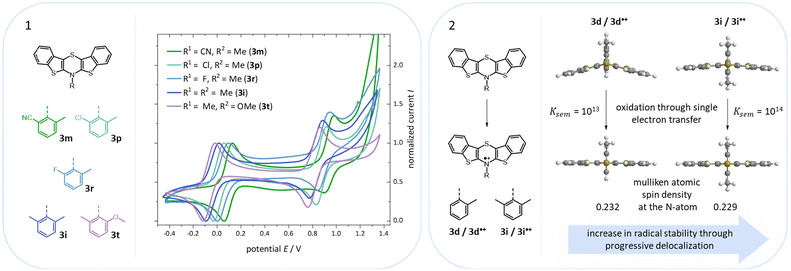
According to their electronic nature, electron donating substituents shift the first redox potential E^0/+1₀ to lower potentials, whereas electron accepting substituents shift the redox potential anodically in comparison to the plain BBTT 5. Compared to their para-congeners the first redox potentials E^0/+1₀ generally appear in the same range, but ortho-substituents show a stronger influence on the shift of the redox potentials E.^4b,c This can be explained by an increase of the inductive and mesomeric substituent effects when considering a shortening of the bond length between the carbon atom and the fused substituent. This results as a consequence of the constitutional change from para- to ortho-substitution as supported computationally (B3LYP/6-311++G**). And this further accounts for the unexpected larger anodic shift caused by the fluorine over the chlorine substitution, since halogens are the only substituents inheriting a dominant inductive effect.¹⁵ Upon bond contraction the inductive effect of fluorine, due to the more pronounced electronegativity,¹⁶ becomes significantly more dominant than for chlorine. This rationalizes the overall stronger shifted potentials. The second redox potentials E^+1/+2₀ of 3 also demonstrate the same dependency of the potential shift to the electronic nature of the substituent. At the same time these are overall progressively anodically shifted along with increasing steric congestion due to a change from para-^4c to ortho- and to ortho,ortho′-substitution pattern. These anodic shifts fall within the order of ∼70 mV for each constitutional change. Due to this consistency, prediction of the redox potentials E^0/+1₀ and E^+1/+2₀ of anti–anti-N-ortho,ortho′-disubstituted phenyl-BBTTs 3f–t by their ortho-analogues 3a–e is possible (see ESI: Chapter S4.4.2‡). To the absolute redox potential E₀ of the plain anti–anti-N-phenyl BBTT 5 are added the two differences in redox potentials ΔE of the ortho-derivatives 3a–e bearing the substituents of interest to the redox potential E of 5 as increments. Linear regression analysis with the experimentally determined redox potentials yields very satisfactory regression coefficients (r² = 0.992 and 0.973). This indicates a consistent and therefore intrinsic effect of the introduction of both ortho-substituents on the electronic structure, even though the geometric structure is mainly affected by the introduction of the second ortho-substituent. The anodic shift of the second redox potentials E^+1/+2₀ furthermore consequently leads to enlarged semiquinone formation constants K_sem.^14a Those fall in orders of magnitude of 10¹³ for ortho- and up to 10¹³–10¹⁵ for ortho,ortho′-derivatives. Their para-congeners show lower values of K_sem with 10¹¹–10¹³.^4a,c This unambiguously points out an increase in relative thermodynamic stability of the formed radical cations by the progressively sterically more demanding substitution patterns. The increasing radical stabilization is additionally supported computationally by the manifestation of a stronger delocalization of the unpaired electron for the radical cations (uB3LYP/6-311++G**). Whilst visualization of the spin density distribution does not clearly illustrate this directly, the Mulliken atomic spin densities support this rationale. In accordance with the constitutional changes overall decreasing values on the central 1,4-thiazine core occur, while the values for the carbon atoms of the anellated benzo rings increase (see ESI: Chapter 4.2‡). Quantum chemistry also allows for calculation of the first redox potentials E^0/+1₀ accounting for properties of native and oxidized species at the same time. The method is based on the free energy cycle, employing the thermodynamic data provided by calculation of BBTT's minimum geometries of the native species and the oxidized radical cation in gas phase and under SMD variation for computing ΔG of solvation ((u)B3LYP/6-311++G**, see ESI: Chapter 4.4.1‡).¹⁷ The best correlations of the experimental and theoretical first redox potentials E^0/+1₀ originate when, in case of a heterogenic substitution pattern, both possible theoretical N-intra conformation's first redox potentials E^0/+1_0,cal. are incorporated. Therefore, their relative ratio is calculated by their difference in Gibbs free enthalpies ΔG (B3LYP/6-311++G**). Overall, this leads to a good fit of the experimental to the computational data (r² = 0.951).

Spectroelectrochemistry

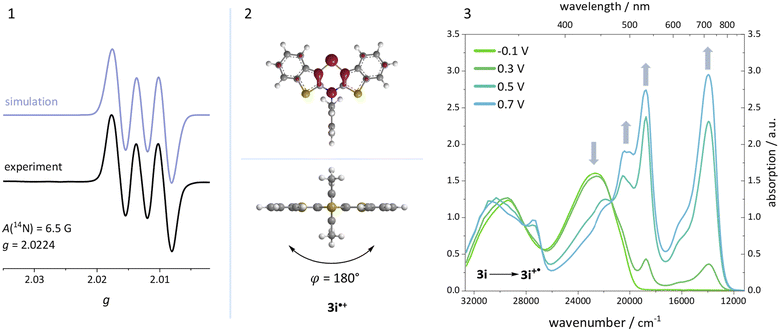
Additionally, a spectroelectrochemical measurement has been carried out on anti–anti-N-ortho,ortho′-dimethylphenyl BBTT 3i. This reliably generates the corresponding radical cation 3i˙⁺ by in situ oxidation through a steady increase of the applied potential (Fig. 9).^4d,19

Fig. 9 (1) EPR spectrum of radical cation 3i˙⁺ (recorded in CH₂Cl₂, T = 298 K, g-factor referenced to external Mn²⁺ in ZnS). (2) Visualization of the spin density distribution (B3LYP/6-311++G**, IEFPCM CH₂Cl₂, isosurface value 0.06 a.u.) and minimum geometry of 3i˙⁺. (3) Spectroelectrochemical measurement of 3i to 3i˙⁺ (recorded in CH₂Cl₂, c = 5 × 10⁻³ M, T = 298 K, electrolyte 0.1 M [ⁿBu₄N][PF₆]; Pt-working electrode, GC-counter electrode and Ag-wire pseudo-reference electrode).

The occurrence of distinct isosbestic points in the UV/vis absorption spectra indicates, that the oxidation to the radical cation proceeds without accumulation of intermediates. The pronounced bathochromic shift of the absorption bands upon oxidation indicates a significant change in the electronic structure. This arises from the major geometry changes upon oxidation, leading the BBTT's butterfly structure of 3i to fully planarize resulting the BBTT's backbone of 3i˙⁺ to reveal a S,N-folding angle of 180°. This allows for an accompanied strong delocalization of the unpaired electron. The stability of 3i˙⁺ over the time scale of this experiment (∼30 min) underpins the high thermodynamic radical stability, also with a significant kinetic persistence. The X-band EPR spectrum in CH₂Cl₂ at room temperature proves the paramagnetic character. It presents a hyperfine coupling pattern of three equidistant lines, reflecting the coupling of the electron spin of the unpaired electron to the nuclear spin of the nitrogen nucleus (I(¹⁴N) = 1).¹⁸ Furthermore, the g-factor of 2.0224 indicates the predominant localization of the unpaired electron on the nitrogen atom. Furthermore, lowering the applied potential successfully leads to the corresponding reduction to 3i. The attempt to generate the corresponding dication in situ fails as a consequence of side reactions. This can be identified by the absence of newly appearing bathochromic bands and isosbestic points as well as an increase in intensity in the hypsochromic region (see ESI: Chapter 4.5‡). In contrast to the corresponding dications of their para-BBTTs, the dication 3i²⁺ lacks the necessary persistence under the experimental conditions.^4d

UV/vis absorption and emission spectroscopy

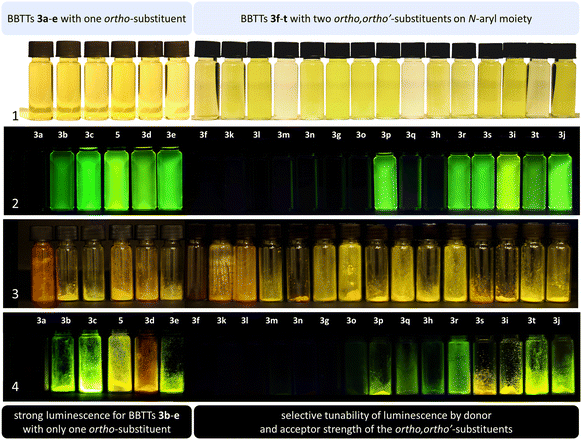
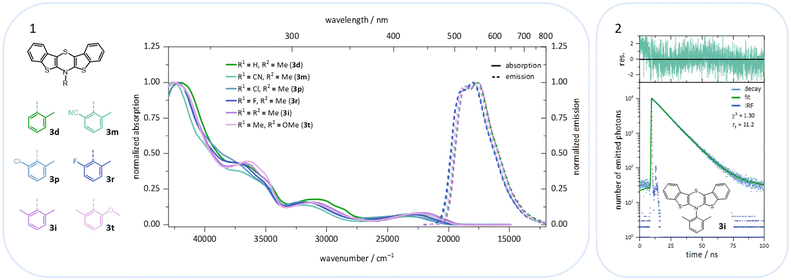
BBTTs 3 have been examined by UV/vis absorption and emission spectroscopy, since some of the yellowish to orange compounds display emission in solution and in the solid state (Fig. 10). All BBTTs 3 reveal similar positions of the absorption and emission maxima despite a variation of functionalization (Fig. 11).

Fig. 10 Solutions of BBTTs 3 and 5 in CH₂Cl₂ (T = 298 K, c = 10^–4 M) at daylight (1) and under UV light (366 nm) (2). Powders of BBTTs 3 and 5 (T = 298 K) at daylight (3) and under UV light (366 nm) (4).

Fig. 11 (1) UV/vis absorption and emission spectra of BBTTs 3 in solution (recorded in CH₂Cl₂, T = 298 K, c = 10⁻⁵ to 10⁻⁷ M). (2) Lifetime data measured by TCSPC experiments exemplarily given for 3i.

TD-DFT calculations allow for a deeper understanding by assignment of the bands to their underlying transitions (PBE1PBE/6-311++G**).²⁰ Therefore, exemplarily for BBTTs 3f–3t the derivatives with a homogenic substitution pattern have been chosen. In the case of 3a–e with two non-identical N-intra conformers, the thermodynamically favored one is considered (see ESI: Chapter 5.2‡).

Calculations nicely underline the four experimentally seen dominant absorption bands. They reproduce their relative dropping intensities and extinction coefficients along the decreasing wavenumber by declining oscillator strengths well. The longest wavelength absorption bands occur overall at around 430 nm, indicating to originate from HOMO → LUMO transitions for mostly all derivatives. Only for nitrile-bearing BBTTs the transitions arise from the HOMO into orbitals energetically higher than the LUMO. The consideration of DFT-computed Kohn–Sham frontier molecular orbitals suggests a plausible reason for the independency of the position of the absorption and emission bands from the substituent pattern. They reveal no coefficient density on the ortho-substituents of the N-aryls (Fig. 12). The transitions also show negligible charge transfer character, due to only a small shift of the coefficient density from the sole location on the central 1,4-thiazine (HOMO) to the delocalization over the whole BBTT's backbone (LUMO) (see ESI: Chapter 5.2‡).

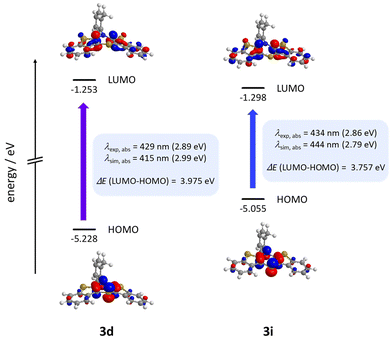Fig. 12 Selected Kohn–Sham frontier orbitals and their energies and the S₀–S₁*-transition of 3d and 3i (PBE1PBE/6-311++G**, IEFPCM CH₂Cl₂, isosurface value at 0.05 a.u.).

The emission bands emerge at around 550 nm, excluding most nitrile-substituted BBTTs due to their indiscernible emission properties. They are best reproduced by TD-DFT calculations of the first singlet excited state (S₁), indicating the emission to be fluorescence (Fig. 13). Fluorescence is experimentally proven by lifetime measurements via time-correlated single photon counting (TCSPC) experiments. They reveal a dependency of the lifetime τ on an electron donating substituent, yielding the highest lifetimes τ up to 11.2 (3i) (Fig. 11 and 2), 11.2 (3t), and 10.5 ns (3j) in solution. Additionally, the fluorescence quantum yields Φ also display the same qualitative trend amounting up to 0.27 (3i), 0.33 (3t), and 0.33 (3j) in solution and 0.18 (3i), 0.28 (3t), and 0.18 (3j) in solid state for donor substituted BBTTs. From fluorescence quantum yields Φ and lifetimes τ, radiative rate constants k_r in a range from 3.36 × 10⁶ to 3.13 × 10⁷ s⁻¹ and non-radiative rate constants k_nr in a range from 5.98 × 10⁷ to 2.84 × 10⁸ s⁻¹ can be deduced. Consequently, it is found that non-radiative processes depopulate the excited state faster than radiative processes for all compounds. The examination of the spectroscopic data also allows for further discussion of the intended suppression of the butterfly structure. Therefore, the Stokes shifts Δ[small nu, Greek, tilde] are taken into consideration. These range between 5100 to 5900 cm⁻¹ for the ortho-derivatives, and are thus comparable to their para-congeners.^4c The ortho,ortho′-derivatives, on the other hand, show overall diminished Stokes shifts Δ[small nu, Greek, tilde] of 4700 to 5300 cm⁻¹. Considering that solvation effects have no significant influence on the absorption and emission maxima, and that the geometries of the vibrationally relaxed S₁-states of BBTTs 3 reveal uniformly planarized BBTT scaffolds with folding angles of ∼180°, the Stokes shifts Δ[small nu, Greek, tilde] correlate with the extent of folding in the S₀-ground state. Consequently, the comparatively small Stokes shifts Δ[small nu, Greek, tilde] of 3f–3t account for smaller structural changes upon photonic excitation. This clearly advocates for stronger planarized S₀-ground state geometries of the BBTTs 3f–t bearing ortho,ortho′-disubstituted N-aryl moieties. The experimental observations reproduce overall well the computationally founded assumption that DFT calculated minimum geometries provide a good approximation of the conformation in solution.

Fig. 13 (1) TD-DFT calculated Jabłoński diagram of BBTT 3i with the associated Kohn–Sham frontier orbitals of the S₀–S₁*-transition and S₀*–S₁-transition. (2) Vibrational relaxed minimum S₀- and S₁-geometries of 3d and 3i indicated with their S,N-folding angles Φ and Stokes shifts Δ[small nu, Greek, tilde] (PBE1PBE/6-311++G**, IEFPCM CH₂Cl₂, isosurface value 0.05 a.u.).

Conclusion

The computationally founded concept to force formally antiaromatic BBTTs into a planarized conformation by introduction of a sterically restricting ortho,ortho′-substitution pattern on the N-aryl moiety can be synthetically successfully implemented by palladium-catalyzed cross-coupling methods. A substance library with a broad variety of electron donating to electron accepting substituents is readily obtained. X-ray analyses reveal the sole adoption of the N-intra conformation for BBTTs’ molecular structures. The comparison to DFT-minimum geometries moreover indicates an overall induced planarization of BBTTs in the crystalline state. Maximized S,N-folding angles and S–N–C_aryl-angles up to almost 180° for compounds 3a–t and 4a and up to a full planarization for compounds 4b and 4d manifest. Therefore, examination of planarized BBTTs with NICS calculations clearly supports a considerable antiaromaticity of the central 1,4-thiazine. The superordinate crystal packing patterns furthermore mainly depict staircase-like substructures consisting of half-side overlapped BBTTs’ backbones with intermolecular C–C distances as low as 3.369 Å. Cyclic voltammetry depicts tunable and low first redox potentials E^0/+1₀ at around −100 to 250 mV. The semiquinone formation constants K_sem indicate pronounced radical cation stabilities of BBTTs 3, that unambiguously exceed their para-analogues upon the change of constitution to ortho-substituents of around two orders of magnitude. This arises from an increased delocalization of the radicals over the BBTTs’ planarized backbones. This is substantiated by DFT calculations of the Mulliken atomic spin density as well as the strongly bathochromically shifted absorption bands of the in situ generated radical cation by spectroelectrochemistry. Photophysical studies of native compounds reveal intensive emission at around 550 nm upon photonic excitation with fluorescence quantum yields Φ of up to 0.33 and lifetimes τ in the range of 3–11 ns. The decreased Stokes shifts Δ[small nu, Greek, tilde] of ortho,ortho′-derivatives compared to their para- and ortho-analogues hint at a successful sterically induced enlargement of the S,N-folding angles in the S₀-ground state Therefore, the concept of conformationally planarized BBTTs by the reduction of the butterfly folding holds even true in solution. The experiments are furthermore plausibly rationalized by (TD-)DFT calculations corroborating the electronic structure. In summary, synthesized BBTTs can be considered as strong donor moieties, being reversible redox chromophores and tunable luminophores. Especially BBTTs with the ortho,ortho′-substitution pattern outshine their para-congeners. The imposed steric strain seems to enforce planarization of BBTTs, in the crystalline solid state as well as in solution. Furthermore, this modification promises a broader tunability of the redox potentials E₀ as well as an increased impeccable radical cation stability. It also implements a selective tunability of the emission properties from intense to elusive fluorescence. Ultimately, due to their favorable properties, these BBTT donors present potential for a further development leading to highly interesting more electron-rich substitutes for phenothiazines, especially for organo-electronic applications.

Data availability

The data supporting this article have been included as part of the ESI.‡

Crystallographic data: deposition numbers CCDC 2346002 (for 3a), 2345988 (for 3b), 2345990 (for 3c), 2345982 (for 3d), 2345989 (for 3e), 2345999 (for 3f (polymorph I)), 2345994 (for 3f (polymorph II)), 2345996 (for 3f (polymorph III)), 2335542 (for 3g), 2335553 (for 3h), 2345957 (for 3i), 2345956 (for 3j), 2345983 (for 3k), 2345987 (for 3l), 2345959 (for 3m), 2345998 (for 3n), 2345948 (for 3o), 2345958 (for 3p), 2345985 (for 3r), 2345992 (for 3t), 2345944 (for 4a), 2346000 (for 4b), and 2345986 (for 4d) contain the supplementary crystallographic data for this paper.‡ These data are provided free of charge by the joint Cambridge Crystallographic Data Centre and Fachinformationszentrum Karlsruhe Access Structures service.

Conflicts of interest

There are no conflicts to declare.

References

1. S. Ahmad, Organic semiconductors for device applications: current trends and future prospects, J. Polym. Eng., 2014, 34, 279–338.
2. (a) Q. Zhang, W. Hu, H. Sirringhaus and K. Müllen, Recent Progress in Emerging Organic Semiconductors, Adv. Mater., 2022, 34, 2108701; (b) Y. Shirota and H. Kageyama, Chem. Rev., 2007, 107, 953; (c) Functional Organic Materials – Synthesis, Strategies, and Applications, ed. T. J. J. Müller and U. H. F. Bunz, Wiley-VCH, Weinheim, 2007.
3. H. R. V. Berens and T. J. J. Müller, S,N-Heteropentacenes – Syntheses of Electron-Rich Anellated Pentacycles, Org. Mater., 2021, 3, 155–167.
4. (a) H. R. V. Berens, K. Mohammad, G. J. Reiss and T. J. J. Müller, 3,9-Disubstituted Bis[1]benzothieno[3,2-b;2′,3′-e,][1,4]thiazines with Low Oxidation Potentials and Enhanced Emission, J. Org. Chem., 2021, 86, 8000–8014; (b) A. P. W. Schneeweis, S. T. Hauer, D. A. Lopez, B. von Dressler, G. J. Reiss and T. J. J. Müller, Game of Isomers: Bifurcation in the Catalytic Formation of Bis[1]benzothieno[1,4]thiazines with Conformation-Dependent Electronic Properties, J. Org. Chem., 2019, 84, 5582–5595; (c) A. P. W. Schneeweis, S. T. Hauer, G. J. Reiss and T. J. J. Müller, Bis[1]benzothieno[1,4]thiazines: Planarity, Enhanced Redox Activity and Luminescence by Thieno-Expansion of Phenothiazine, Chem. – Eur. J., 2019, 25, 3582–3590; (d) S. T. Hauer, A. P. W. Schneeweis, S. D. Waniek, L. P. Sorge, K. Heinze and T. J. J. Müller, Radical cations and dications of bis[1]benzothieno[1,4]thiazine isomers, Org. Chem. Front., 2021, 8, 5744–5755.
5. (a) A. D. Becke, Density-Functional Thermochemistry. III. The Role of Exact Exchange, J. Chem. Phys., 1993, 98, 5648–5652; (b) C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789; (c) R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, Self–consistent molecular orbital methods. XX. A basis set for correlated wave functions, J. Chem. Phys., 1980, 72, 650–654; (d) A. D. McLean and G. S. Chandler, Contracted Gaussian basis sets for molecular calculations. I. Second row atoms, Z=11-18, J. Chem. Phys., 1980, 72, 5639–5648; (e) M. J. Frisch, J. A. Pople and J. S. Binkley, Self-consistent molecular orbital methods 25. Supplementary functions for Gaussian basis sets, J. Chem. Phys., 1984, 80, 3265–3269; (f) T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, Efficient diffuse function-augmented basis sets for anion calculations. III.† The 3-21+G basis set for first-row elements, Li–F, J. Comput. Chem., 1983, 4, 294–301; (g) G. Scalmani and M. J. Frisch, Continuous surface charge polarizable continuum models of solvation. I. General formalism, J. Chem. Phys., 2010, 132, 114110.
6. (a) L. May and T. J. J. Müller, Dithieno[1,4]thiazines and Bis[1]benzothieno[1,4]thiazines—Organometallic Synthesis and Functionalization of Electron Density Enriched Congeners of Phenothiazine, Molecules, 2020, 25, 2180; (b) C. Dostert, C. Wanstrath, W. Frank and T. J. J. Müller, 4H-Dithieno[2,3-b: 3′,2′-e,][1,4]thiazines – synthesis and electronic properties of a novel class of electron rich redox systems, Chem. Commun., 2012, 48, 7271–7273; (c) L. May and T. J. J. Müller, Electron-Rich Phenothiazine Congeners and Beyond: Synthesis and Electronic Properties of Isomeric Dithieno[1,4]thiazines, Chem. – Eur. J., 2020, 26, 12111–12118.
7. The byproduct dibenzo[d,d′]thieno[3,2b′;4,5-b′]dithiophene is assigned by its ¹H and ¹³C NMR spectra and its mass spectrum (see ESI, chpt. 1.2.6.1‡).
8. M. Mantina, A. C. Chamberlin, R. Valero, C. J. Cramer and D. G. Truhlar, Consistent van der Waals Radii for the Whole Main Group, J. Phys. Chem. A, 2009, 113, 5806–5812.
9. P. R. Spackman, M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, D. Jayatilaka and M. A. Spackman, CrystalExplorer: a program for Hirshfeld surface analysis, visualization and quantitative analysis of molecular crystals, J. Appl. Crystallogr., 2021, 54, 1006–1011.
10. V. Coropceanu, J. Cornil, D. A. da Silva Filho, Y. Olivier, R. Silbey and J.-L. Brédas, Charge Transport in Organic Semiconductors, Chem. Rev., 2007, 107, 926–952.
11. K. Takimiya, S. Shinamura, I. Osaka and E. Miyazaki, Thienoacene-Based Organic Semiconductors, Adv. Mater., 2011, 23, 4347–4370.
12. (a) Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. v. R. Schleyer, Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion, Chem. Rev., 2005, 105, 3842–3888; (b) A. Stanger, Nucleus-Independent Chemical Shifts (NICS): Distance Dependence and Revised Criteria for Aromaticity and Antiaromaticity, J. Org. Chem., 2006, 71, 883–893.
13. (a) M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian Inc., Wallingford CT, 2016; (b) E. Runge and E. K. U. Gross, Density-Functional Theory for Time-Dependent Systems, Phys. Rev. Lett., 1984, 52, 997–1000; (c) R. Bauernschmitt and R. Ahlrichs, Treatment of electronic excitations within the adiabatic approximation of time dependent density functional theory, Chem. Phys. Lett., 1996, 256, 454–464.
14. (a) K. Deuchert and S. Hünig, Multistage Organic Redox Systems – A General Structural Principle, Angew. Chem., Int. Ed. Engl., 1978, 17, 875–886; (b) K. Nakasuji, New multi-stage redox systems and new organic molecular metals, Pure Appl. Chem., 1990, 62, 477–482; (c) K. Takahashi, Conjugation-extended ring assemblies with central heterocycles – New multistage redox systems, Pure Appl. Chem., 1993, 65, 127–134.
15. D. T. Clark, J. N. Murrell and J. M. Tedder, The magnitudes and signs of the inductive and mesomeric effects of the halogens, J. Chem. Soc., 1963, 1250–1253.
16. L. C. Allen, Electronegativity is the average one-electron energy of the valence-shell electrons in ground-state free atoms, J. Am. Chem. Soc., 1989, 111, 9003–9014.
17. (a) A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113, 6378–6396; (b) Y. Fu, L. Liu, H.-Z. Yu, Y.-M. Wang and Q.-X. Guo, Quantum-Chemical Predictions of Absolute Standard Redox Potentials of Diverse Organic Molecules and Free Radicals in Acetonitrile, J. Am. Chem. Soc., 2005, 127, 7227–7234.
18. S. Stoll and A. Schweiger, EasySpin, a comprehensive software package for spectral simulation and analysis in EPR, J. Magn. Reson., 2006, 178, 42–55.
19. (a) A. P. W. Schneeweis, A. Neidlinger, G. J. Reiss, W. Frank, K. Heinze and T. J. J. Müller, Radical cation and dication of a 4H-dithieno[2,3-b: 3′,2′-e,][1,4]-thiazine, Org. Chem. Front., 2017, 4, 839–846; (b) F. L. Rupérez, J. C. Conesa and J. Soria, Electron spin resonance study of the influence of the nitrogen substituent on the conformation and spin density distribution of phenothiazine derivatives, J. Chem. Soc., Perkin Trans. 2, 1986, 391–395.
20. C. Adamo and V. Barone, Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model, J. Chem. Phys., 1999, 110, 6158–6170.

---

Footnotes

† Dedicated to Prof. Dr. Frank Würthner on the occasion of his 60th birthday.

‡ Electronic supplementary information (ESI) available. CCDC 2346002, 2345988, 2345990, 2345982, 2345989, 2345999, 2345994, 2345996, 2335542, 2335553, 2345957, 2345956, 2345983, 2345987, 2345959, 2345998, 2345948, 2345958, 2345985, 2345992, 2345944, 2346000 and 2345986. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4qo01155d

---