Open Access Article
Open Access ArticleSuccessful removal of fluoride from aqueous environment using Al(OH)3@AC: column studies and breakthrough curve modeling
S. Bakhtaab,
Z. Sadaouia,
N. Bouazizi b,
B. Samirb,
J. Cosmeb,
O. Allaloua,
F. Le Derfb and
J. Vieillard
b,
B. Samirb,
J. Cosmeb,
O. Allaloua,
F. Le Derfb and
J. Vieillard *b
*b
aLaboratory of Reaction Engineering, Faculty of Mechanical and Processes Engineering, University of Sciences and Technology Houari-Boumediene, BP No. 32, El Alia, Bab Ezzouar, 16111 Algiers, Algeria
bNormandie Univ, UNIROUEN, INSA Rouen, CNRS, COBRA (UMR 6014), 27000 Evreux, France. E-mail: soumia.bakhta64@gmail.com
First published on 2nd January 2024
Abstract
In this study, we discuss the removal of fluoride from water through column adsorption methods using Al(OH)3@AC as a functional granular activated carbon. The height of the bed, fluoride concentration, and flow rate are the experimental factors used to obtain the breakthrough curves. As the flow rate increased, the breakthrough and saturation times decreased. The analysis of simplified column models, such as the Adams–Bohart, Thomas, and Yoon–Nelson models, revealed that the Clark model best described the adsorption process when fitting the experimental data. The obtained breakthrough curves agreed with the corresponding experimental data. The highest capacity for adsorption obtained during the column procedure was found to be 41.84 mg g−1 with a bed height of 3 cm, an initial fluoride concentration of 10 mg L−1 and a flow rate of 7.5 mL min−1.
1. Introduction
Water contamination due to population increase and industrial activity is one of the most challenging issues to researchers because it continuously threatens human health and the environment. It has been found that pollutants, such as nitrate ions, pharmaceutical products, nitrophenol and trace metals, in water sources cause serious problems in human health, the ecosystem and the environment.1–5 Contamination by anionic pollutants, especially fluorides, in drinking water is a universal problem in this era. This pollutant is recognized as the most dangerous inorganic pollutant.When fluoride is present in drinking water within desirable limits, it promotes the formation, maintenance and health of teeth and bones. However, the consumption of water containing a concentration of fluorides higher than the maximum allowable concentration (1.5 mg L−1) leads to several health problems, including osteoporosis, kidney damage, bone deformation, inactivation of the reproductive organs, nerve and muscle degeneration, skeletal fluorosis and more.
Given the health risks mentioned above, it is essential to treat water contaminated with fluorides in order to bring them back to recommended limits. Defluorination is an effective and applicable method to reduce the concentration of F− in drinking water. The main defluorination methods used worldwide are adsorption,6 coagulation/precipitation,7 electrodialysis,8 ion exchange,7 reverse osmosis and nanofiltration.9 These methods include advanced advantages and disadvantages, using different concepts with different effects.
Adsorption is one of the most interesting methods for the elimination of fluoride ions (F−) due to its high effectiveness and limited cost.10,11 Various inorganic materials have been used for the removal of F−, like metal oxide-based materials, carbonaceous materials, soils, clay minerals, and polymer- and biopolymer-based materials.12–16 Of the above materials, porous carbon is a promising candidate for adsorption processes due to its ecological friendliness, high adsorption and low cost.17,18 Carbonaceous materials are an interesting adsorbent that can be used for pollutant removal from water.19–21 However, most types of porous carbons, such as activated carbon, showed a visible decrease in efficiency after the first cycle. The adsorption process explained that the surface functionality is reduced due to its low chemical stability, resulting in the leaching of material, waste and associated costs.22,23 Herein, the adsorption capacity of activated carbon is determined by the modification strategy, aiming to optimize the surface properties and thus the adsorptive character.24 Recently, industries have tried to apply inorganic adsorbents to adsorb fluoride.
More recently, for applications, adsorption procedures using batches for continuous treatments has been very useful in this regard.25–29 Nevertheless, a dynamic adsorption system is recommended for full application in water depollution, because of its simple operation and stability.25,30 In addition, the adsorption of liquid media under continuous flow is considered a non-linear pathway that can be tailored via breakthrough curve.31–33 Herein, the properties of breakthrough curves are determined on the bases of column parameters flow rate, adsorbate quantity, pH, temperature and adsorbent weight.25,32–35 It has been demonstrated that the adsorption process can change significantly from the adsorbent–adsorbate configuration in packed-bed columns. Accordingly, it was shown that modeling of breakthrough analysis for liquid adsorption is highly desirable for water purification in full concreate applications.35 For this, the key factor of the breakthrough analysis modeling steps is the close fitting and prediction of adsorption properties while exploring the experimental results. However, correlation with the adsorption phenomena in packed-bed columns is hard in the laboratory setting compared to modeling in batch methods due to the quantity of elements in the adsorbent and liquid media for dynamic systems. Here, the fittings of the adsorption process are obtained from the mass transfer mechanisms, kinetics and thermodynamics of adsorption.31 Numerous models have been employed for the fitting of breakthrough curve analysis performed in a dynamic adsorption pathway. For the fitting models, it has been established that the Adams–Bohart,36 Thomas,37 Clark,38 Yan,39 and Yoon–Nelson40 models are the most useful for the control of breakthrough curves in dynamic adsorption.26,30,31 The above models are based on analytical equations, which require low computational time for analysis processing. Additionally, these models are popular for fitting adsorption data in dynamic water depollution due to their simple form and performance.
In this work, a functional granular adsorbent based on Al(OH)3@AC was prepared via the simple incorporation of aluminum particles into activated carbon. The granular adsorbent Al(OH)3@AC was used to fabricate a system based on a glass column for continuous removal of fluoride ions as hazardous materials in water. The performance evaluation was obtained via investigation of the flow rate, the fluoride amount and the bed height. To explain the adsorption mechanism, different methods, including the Thomas, Adams–Bohart, Yoon–Nelson, and Clark models, were used. Based on the results, the adsorption mechanism is proposed.
2. Methods and materials
2.1. Materials preparation
In all the experiments, granular activated carbon from date stems was functionalized according to our previous method.32 The chemicals Al(NO3)3·9H2O, NaF (99%) and HCl/NaOH were purchased from Alfa Aesar (Germany), Merck (Germany) and Sigma-Aldrich (USA), respectively. Ultrapure water with resistivity ≥18 MΩ cm was obtained from a Milli-Q system. The specific fluoride ion electrode ISE27F (Cole Parmer, USA) was used to determine the fluoride concentration.In our previously published paper,32 we developed different approaches in parallel. Each process was simple. In order to improve the performance of the material produced (AC) and increase its adsorption capacity from practically zero, we introduced aluminum in various forms through the incorporation of Al(OH)3 compounds and aluminum nanoparticles (Al°) and the grafting of 3-aminopropyltriethoxysilane (APTES)-Al0 and OH-aminopropyltriethoxysilane (APTES)-Al0. All prepared adsorbents were tested for the adsorption of fluorides and the results showed that AC-Al(OH)3 has the best removal efficiency compared to the other adsorbents tested. The fixation of aluminum hydroxide on the surface of AC was achieved by an inexpensive method. Firstly, the activated carbon made from date stems was dispersed in water as a solvent under ultrasonication for 20 minutes. Then, the aqueous solution containing the activated carbon was mixed with the aluminum solution with continuous stirring. A dose of NaOH was added to the mixture in order to adjust the pH to 11 and again the mixture was stirred for 4 h to obtain the hydroxide phase (Al(OH)3). The final material was filtered and washed with ultrapure water. The resulting activated carbon, referenced as AC-Al(OH)3, was dried at 80 °C overnight.32
The fluoride ion content was determined using a selective electrode. The specific ISE27F ion fluoride electrode used in our work is combined with a pH/potential electrode with an integrated millivoltmeter or an ionometer calibrated to directly give the fluoride concentration. The samples were mixed with total ionic strength adjuster buffer (TISAB). This solution makes it possible to maintain the ionic force constant, keep the free fluoride ions in solution and regulate the pH so that the latter is around 5 and therefore the fluoride ions will be in the ionic state and detectable.
2.2. Material characterization
The characteristics and properties of the adsorbent prepared based on activated carbon (Al(OH)3@AC) were presented in our previously published paper.322.3. Fixed column studies
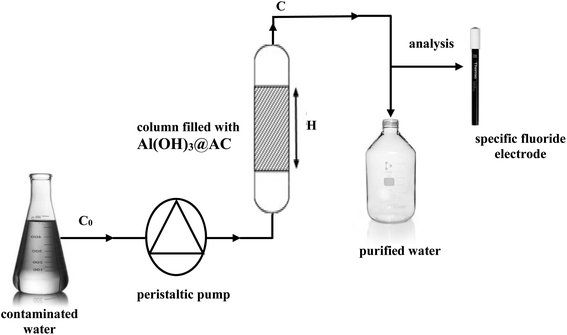
A continuous fixed-bed column was used to test the performance of the granular functional activated carbon in simultaneous fluoride elimination (Scheme 1). The experimental apparatus consisted of a Pyrex glass jacketed column with an external diameter of 18 mm, an interior diameter of 10 mm, and a length of 0.25 m. Nonwoven glass was fixed at the column bottom and then the desired quantity of functional activated carbon was added to the column to reach various bed masses. The fluoride polluted water was pumped downwards through the bed at a stable and continuous flow rate using a peristaltic pump (Ismatec® IPC, Coleman). The obtained aqueous phases were collected and filtered for measurement of the remaining amount of fluoride. Thereby, the breakthrough curves were obtained and fitted according to the following models.2.4. Studies of the breakthrough curves
To study the patterns for dynamic adsorption of pollutants over column systems, various theoretical models were used. The necessary parameters to establish operation and dynamic response are the time for breakthrough appearance and the form of the breakthrough curve.(i) The Thomas model uses the theory of Langmuir kinetics for adsorption–desorption, promoting suppressional dispersion. It was obtained via a simple derivation using the assumption that the force of the derivation rate could fit second order reversible reaction kinetics. According to this model, described by eqn (1), the constant separation factor and its favorable or unfavorable isotherms can be estimated.37 This model was employed to remove F− ions from aluminum basic materials.41
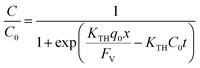 | (1) |
(ii) The Adams–Bohart model was derived from the mathematical relation described by Ce/C0 and t under permanent flow configuration (eqn (2)). The proposed model was focalized from the theory of the surface reaction. It estimates that equilibrium cannot be reached instantly. According to the results obtained by this model, a simple approach to visualize adsorption over columns, its validity is localized in the concentration range of Ce < 0.5C0.36,42
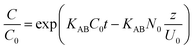 | (2) |
(iii) The Yoon–Nelson model was established via the changes and mechanism involved over the adsorption and breakthrough caused by the statistical data of the adsorbate.40,43 This model is simpler for clear investigation compared to the Adams–Bohart model, as it is not limited by the details of adsorbate characteristics, the type of adsorbent, or the physical properties of the adsorption bed.44 The empirical equation used in this model may reduce the error brought on by using the first established model, Thomas, especially at the beginning and end of the period on the breakthrough curve.39
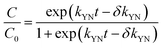 | (3) |
(iv) Clark's model is based on the mass transfer equation accompanied by the Freundlich model to determine the constants such as KF and 1/n. Clark's model resulted in the following equation
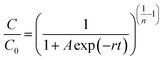 | (4) |
The regeneration of the adsorbent bed in dynamic mode is very important for larger scale applications.45 In our previous article, we carried out a study on the desorption of fluoride from Al(OH)3@AC in batch mode, using different chemical desorption agents, of which NaOH (0.01 M) solution proved the most effective desorption agent among the different chemical agents tested.17 Thus, NaOH was also used in this study of desorption in dynamic mode. For the experiment, the Al(OH)3@AC bed was saturated in a column at 22 °C with an initial fluoride solution (c = 10 mg L−1, pH = 6.15), a flow rate of 7.5 mL min−1 and a bed height of 3 cm. Once the activated carbon bed was saturated, we sent ultrapure water to the column to eliminate traces of the fluoride solution, then NaOH solution (0.01 M) at the same flow rate (7.5 mL min−1). The fluoride concentration was monitored at the column outlet (Scheme 1).
3. Results and discussion
The study was conducted to determine the breakthrough curves and describe the process based on the system's different operating parameters, notably the flow rate, the height of the bed of Al(OH)3@AC and the initial concentration of fluoride.3.1. Influence of bed height
The unremoved fluoride over the column was investigated in three different bed heights: 1, 2 and 3 cm. Measurements were performed via a fixed amount (10 mg L−1) of fluoride in liquid solution under a permanent and stable flow rate of 7.5 mL min−1.Fig. 1a illustrates the breakthrough curves obtained at various heights of activated carbon beds and the different operating parameters of the column are given in Table 1.
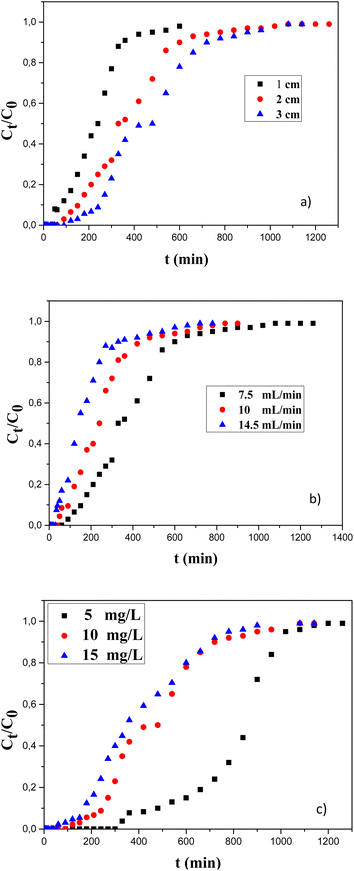 | ||
| Fig. 1 Effect of (a) bed height, (b) flow rate and (c) initial fluoride concentration on breakthrough curves of fluoride adsorption on Al(OH)3@AC in the column system. | ||
| H (cm) | Breakthrough time (tb) (min) | Saturation time (ts) (min) | Breakthrough volume (VP) (mL) | Saturation volume (VS) (mL) | Adsorbed quantity (mads mg) | Yield (R) (%) | Adsorption capacity q (mg g−1) |
|---|---|---|---|---|---|---|---|
| 1 | 40 | 480 | 300 | 3600 | 17.11 | 37.45 | 22.82 |
| 2 | 90 | 780 | 675 | 5850 | 28.01 | 47.88 | 28.01 |
| 3 | 150 | 900 | 1125 | 6750 | 34.62 | 51.28 | 30.10 |
The data clearly show that increasing the bed height, or in this instance the adsorbent dose, induces an increase in breakthrough and saturation times. For bed heights of 1 to 3 cm, the fluoride adsorption capacity rises from 22.82 mg g−1 to 30.1 mg g−1. This result can be explained by a longer residence time corresponding to a higher dose of activated carbon, which improves the fluoride adsorption. Similar results were found by S. Mohan et al.,38 who explained their results by noting that the number of active sites increased with the height of the bed. For the rest of the study, the height of AC-Al(OH)3 which gives the longest saturation time is retained, i.e. 3 cm.
3.2. Influence of flow rate
In continuous mode water treatment, the flow rate is an essential factor. Thus, the flow rates of 7.5, 11 and 14.5 mL min−1 were examined. The other operating parameters were kept constant: the initial fluoride concentration = 10 mg L−1, the height of the fixed bed = 3 cm and the pH of the solution = 6.15. The obtained results are illustrated in Fig. 1b and the different operating parameters of the bed column are given in Table 2.| QV (mL min−1) | Breakthrough time (tb) (min) | Saturation time (ts) (min) | Breakthrough volume (VP) (mL) | Saturation volume (VS) (mL) | Adsorbed quantity (mads mg) | Yield (R) (%) | Adsorption capacity q (mg g−1) |
|---|---|---|---|---|---|---|---|
| 7.5 | 90 | 780 | 675 | 5850 | 28.01 | 47.88 | 28.01 |
| 11 | 50 | 660 | 550 | 7260 | 27.62 | 38.05 | 27.62 |
| 14.5 | 30 | 540 | 435 | 7830 | 24.20 | 30.90 | 22.24 |
In these results, a reduction in the breakthrough and saturation times occurs when the volume flow rate is increased. At a higher flow rate, column saturation is quickly reached and the breakthrough curve becomes steeper (Fig. 1b).
This faster saturation of the bed column is due to the time spent by the solute in the column, which is insufficient for achieving equilibrium, explaining the decrease in adsorption capacity. Clearly, as the flow rate is raised, the time spent in the column by the fluoride molecules decreases, decreasing the contact between the solid and liquid phases and, as a result, the exchange rate. In their recent work, N. Chen and collaborators demonstrated that the time to breakthrough reduced as the flow rate increased.46 They attributed this result to a reduction in the duration of time that fluorides spent in interaction with the adsorbent; thus, the fluoride ions did not have sufficient time to diffuse into the adsorbent pores and left the column before equilibrium was reached. R. Mohan and collaborators obtained the same results.47 The reduction in the contact time causes a reduction in the adsorption capacity. In addition to this, the porosity and pore size of adsorbents is one of the main factors in adsorption. The porosity of AC-Al(OH)3 is high. It consists of 74% mesopores and 26% micropores.32 It is widely known that the more porous the sorbent, the longer the contact time required to fully use its adsorptive ability. Therefore, the impact of flow rate on the sorbent's efficacy is typically greater the higher its microporosity. The volume flow retained for the rest of the study is 7.5 mL min−1.
3.3. Influence of initial concentration
The initial concentration is an essential parameter that allows comprehension of the adsorption behavior. Fig. 1c presents the fluoride concentration over the breakthrough curves. As expected, a rise in F− concentration led to an observable decrease in the breakthrough time. This can be attributed mostly to the higher quantity of fluoride ions introduced into the column per unit time when increasing the initial fluoride concentration. In addition, the low concentration gradient causes slow diffusion produced by a decrease in the transport coefficient, which in turn results in a decrease in the mass transfer coefficient. Thus, higher initial fluoride concentrations lead to greater driving force for mass transfer and the saturation of the bed of the adsorbent is reached more quickly, which leads to a reduction in the breakthrough time (Table 3). The results of the current study are consistent with those published by M. Talbat et al.48| [F−]0 (mg L−1) | Breakthrough time (tb) (min) | Saturation time (ts) (min) | Breakthrough volume (VP) (mL) | Saturation volume (VS) (mL) | Adsorbed quantity (mads) (mg) | Yield (R) (%) | Adsorption capacity q (mg g−1) |
|---|---|---|---|---|---|---|---|
| 5 | 330 | 1020 | 1575 | 5850 | 29.78 | 77.85 | 25.89 |
| 10 | 150 | 900 | 1125 | 6750 | 34.62 | 51.28 | 30.10 |
| 15 | 120 | 780 | 900 | 5850 | 48.12 | 36.20 | 41.84 |
4. Data modelling
The studies of the adsorption phenomenon, kinetics and breakthrough data are necessary to check the efficacy of this continuous fixed bed column for dynamic water treatment. For this, various theoretical models were used to present the breakthrough curves. In the sections that follow, the results obtained allowed the modeling of the breakthrough curves using classic kinetic models such as the Thomas, Adams–Bohart, Yoon–Nelson and Clark models (original Pro 9.064 BIT software).4.1. Thomas model
The Thomas model estimates that the forces of intraparticle diffusion are the same as the axial liquid film concentration over the material's surface.49 The breakthrough curves presented in Fig. 2 were obtained for various flow rates, bed heights and fluorine amounts and then fitted with a nonlinear relation of the Thomas model (eqn (1)). The constant data calculated using this model are listed in Table 4.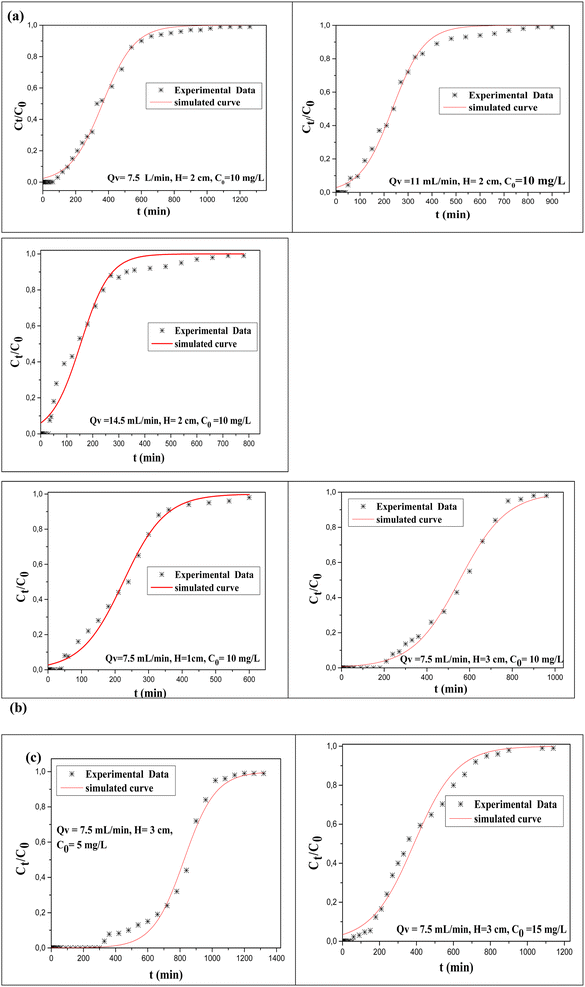 | ||
| Fig. 2 Experimental and calculated breakthrough curves obtained from Thomas model for different (a) flow rates, (b) bed heights, and (c) initial fluoride concentrations. | ||
| Parameters | KTH 10−4 (mL min−1 mg−1) | q0 (mg g−1) | R2 |
|---|---|---|---|
| Flow rate (mL min−1) | |||
| 7.5 | 1.22 | 27.24 | 0.994 |
| 10 | 1.18 | 22.00 | 0.992 |
| 14.5 | 1.02 | 17.66 | 0.986 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Bed height (cm) | |||
| 1 | 3.2 | 17.98 | 0.994 |
| 2 | 1.22 | 25.23 | 0.992 |
| 3 | 1.01 | 30.87 | 0.996 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Initial concentration of fluorides (mg L−1) | |||
| 5 | 2.1 | 25.10 | 0.989 |
| 10 | 1.01 | 27.87 | 0.990 |
| 15 | 2.4 | 30.20 | 0.985 |
The results obtained from this model showed a correlation coefficient near 1 (R2 > 0.98). This can be attributed to the fluoride adsorption process over Al(OH)3@AC, which involves both chemical interactions and the diffusion of F− ions within the adsorbent particles. The obtained KTh demonstrated that the removal rate of fluoride ions decreased with the increase of the flow rate and the amount of fluorine. However, when the height of the bed was raised, the rate of fluoride adsorption decreased. This is explained by the rise in derivation force over the adsorbate/adsorbent during the dynamic removal. In addition, this behavior resulted in an increase of the mass transfer rate while the initial amount and the flow rate increase. Consequently, the diffusion forces and axial dispersion rise with an increased bed height. This was supported by the decrease of KTh.49,50 The removal uptake of F− ions was obtained via the application of the Thomas model, in which the capacity decreases with an increase in flow rate and rises with increases in initial concentration and bed height (Table 4).
This was associated with increased diffusion forces at a high initial quantity of F−, resulting in an increase of fluoride uptake capacity. However, the mass transfer driving forces and resident time for the adsorbate increased with increases in bed height over the column. This trend is not the same for the flow rate effects, where a reduction was obtained for the adsorbent/adsorbate, resulting in a lower capacity.51 The calculated Thomas maximum adsorption capacity for AC-Al(OH)3 was 30.2 mg g−1, which is considerably higher than the adsorption capacities found in the literature (Table 5).
| Parameters | KAB 10−4 (L mg−1 min−1) | N0 (mg L−1) | R2 |
|---|---|---|---|
| Flow rate (mL min−1) | |||
| 7.5 | 1.22 | 26.83 | 0.958 |
| 11 | 2.82 | 24.12 | 0.913 |
| 14.5 | 3.12 | 19.33 | 0.921 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Bed height (cm) | |||
| 1 | 2.18 | 24.45 | 0.925 |
| 2 | 1.22 | 27.4 | 0.958 |
| 3 | 1.09 | 32.8 | 0.929 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Initial concentration of fluoride (mg L−1) | |||
| 5 | 1.98 | 23.87 | 0.961 |
| 10 | 1.09 | 29.56 | 0.958 |
| 15 | 0.98 | 38.45 | 0.958 |
4.2. Adams–Bohart model
The Adams–Bohart model forecasts breakthrough curves during the initial adsorption phase, supposing that the initial amount of fluorine ions and the remaining amount are directly proportional to the number of pollutants removed. According to the results from the Adams–Bohart model, N0 values increased with flow rate but dropped as the bed height rose (Fig. 3).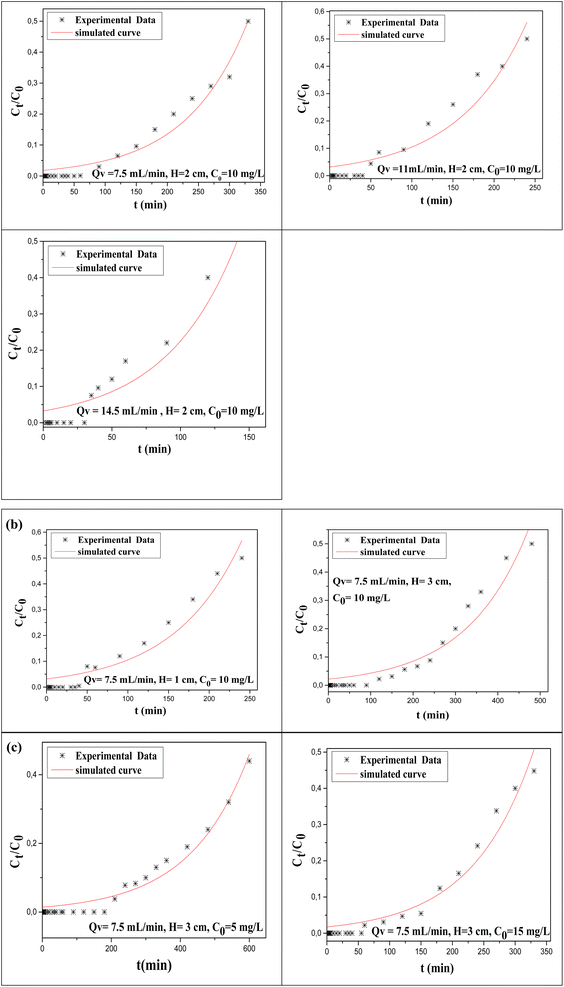 | ||
| Fig. 3 Experimental and calculated breakthrough curves obtained from the Adams–Bohart model for different (a) flow rates, (b) bed heights and (c) initial concentrations. | ||
As shown in Table 5, the KAB constant drops with a rise in all parameters. It established that adsorption uptake was 33 mg g−1 and reached a maximum at 5 cm bed depth, 10 mg L−1 of fluoride concentration, and a flow rate of 5 mL min−1.
As the bed height increased from 1 to 3 cm, the bed uptake rose. The results are explained by the key role of the functionalization of the activated carbon, resulting in sufficient active sites in Al(OH)3@AC. Increasing the flow rate caused an increased amount of F− to stick to Al(OH)3@AC in the fixed column, decreasing the bed capacity. The findings showed that KAB and N0 are inversely related and the condition is controlled by the external mass transfer over the initial phase of adsorption.55 Importantly, measurements of N0 and KAB describe their values, which are related to the system variables and are similar to the results obtained by Ajmani et al.56 Furthermore, the experimental data corresponded well to the Adams–Bohart model with an R2 greater than 0.95 in a majority of cases (Table 5). The No values rose with the flow rate but declined as the bed height increased. Following the same trends, KAB was reduced as the flow rate rose and raised as bed height increased.
4.3. Yoon–Nelson model
The model established by Yoon–Nelson assumes that the rate of adsorption for each adsobate is proportional to the adsorption capacity of the adsorbate and the rate of adsorbate breakthrough over the sorbent.56 The nonlinear regression was accomplished by plotting Ct/C0 versus the time, as seen in Fig. 4.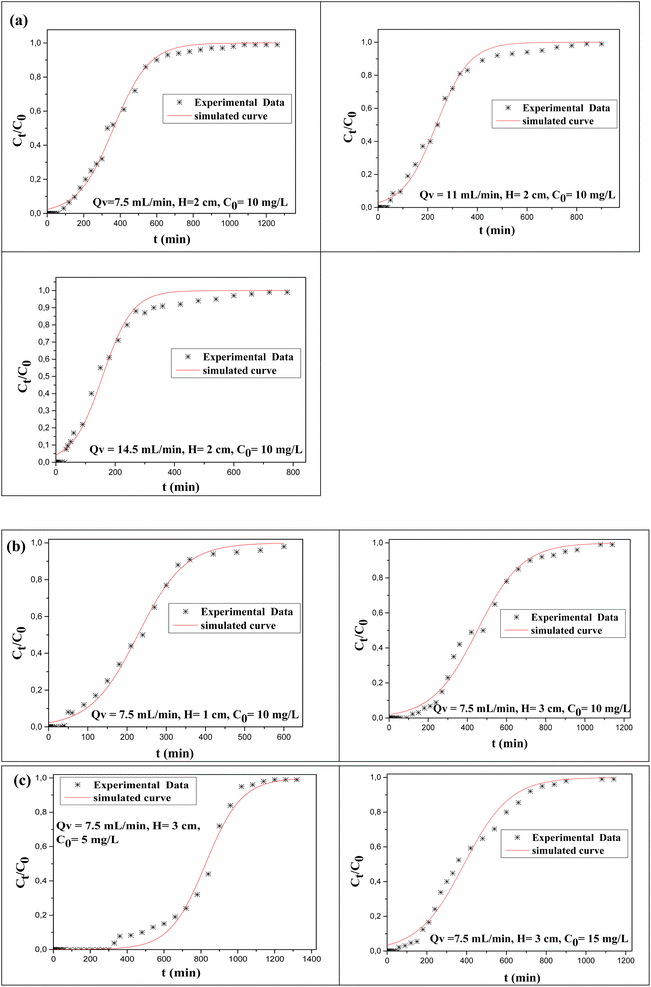 | ||
| Fig. 4 Breakthrough, experimental and calculated curves obtained from the Yoon–Nelson model for different (a) flow rates, (b) bed heights, and (c) initial concentrations. | ||
Table 6 shows the KYN and calculated time values.
| Parameters | KYN (min−1) | τ (min) | R2 |
|---|---|---|---|
| Flow rate (mL min−1) | |||
| 7.5 | 1.02 × 10−2 | 363 | 0.995 |
| 11 | 1.50 × 10−2 | 235 | 0.992 |
| 14.5 | 1.98 × 10−2 | 157 | 0.953 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Bed height (cm) | |||
| 1 | 1.66 × 10−2 | 228 | 0.994 |
| 2 | 1.02 × 10−2 | 363 | 0.995 |
| 3 | 0.87 × 10−2 | 451 | 0.990 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Initial concentration of fluoride (mg L−1) | |||
| 5 | 1.02 × 10−2 | 585 | 0.989 |
| 10 | 0.87 × 10−2 | 451 | 0.990 |
| 15 | 0.87 × 10−2 | 387 | 0.985 |
It was observed that τ values reduced as the solution flow rate increased, but rose as bed height increased. Here, the increase of τ was explained by the greater bed height providing a high number of activated functional sites which require more time to accomplish a 50% adsorbate breakthrough. In contrast, a reduction in τ with the initial amount of F− is associated with less time needed to reach a 50% breakthrough because more fluoride ions are easily available for the available active sites. Likewise, as the flow rises, the τ values decrease and this can be attributed to the fact that F− is supplied to the free activated sites faster than at low flow rates. Furthermore, the KYN rose as the flow rate and F− concentration increased, which was in good agreement with data obtained previously.56 Herein, the model analysis over the nonlinear regression measurements is summarized in Table 6 and R2 values up to 0.98 are obtained in most cases. Importantly, the Yoon–Nelson model fit the experimental values correctly.
4.4. Clark model
Clark created this model to demonstrate the kinetics of a fixed bed adsorption system based on the combination of mass transfer and Freundlich isotherm. The calculated values of the Clark parameters are reported in Table 7 and the associated curves are shown in Fig. 5.| Parameters | A | r (mg L−1 min−1) | n | R2 |
|---|---|---|---|---|
| Flow rate (mL min−1) | ||||
| 7.5 | 39.44 | 6.40 × 10−3 | 1.99 | 0.997 |
| 10 | 25.12 | 9.12 × 10−3 | 1.01 | 0.997 |
| 14.5 | 15.67 | 9.35 × 10−3 | 1.54 | 0.9997 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Bed height (cm) | ||||
| 1 | 27 | 1.34 × 10−3 | 1.53 | 0.995 |
| 2 | 39.44 | 6.40 × 10−3 | 1.99 | 0.997 |
| 3 | 45.32 | 5.62 × 10−3 | 1.97 | 0.995 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Initial concentration of fluoride (mg L−1) | ||||
| 5 | 25.34 | 2.18 × 10−3 | 4.65 | 0.995 |
| 10 | 32.45 | 5.62 × 10−3 | 1.97 | 0.996 |
| 15 | 77.423 | 4.82 × 10−3 | 1.68 | 0.997 |
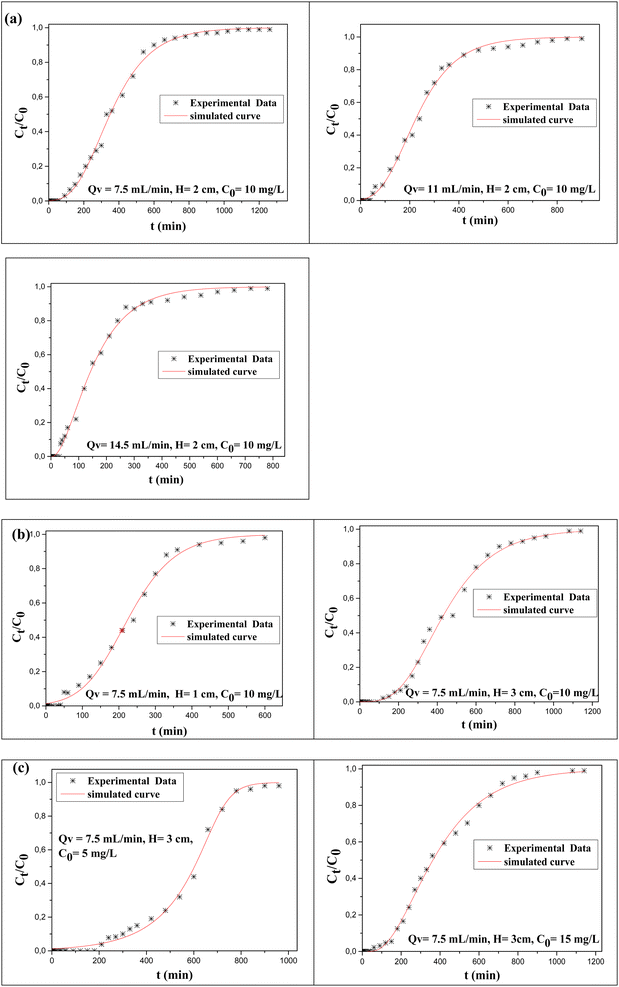 | ||
| Fig. 5 Breakthrough, experimental and calculated curves obtained from the Clark model for different (a) flow rates, (b) bed heights, and (c) initial concentrations. | ||
With an increase in the adsorbate flow rate, the value of the Clark constant (r) rises. For the Freundlich isotherm, it was observed that the constant “n” is higher than 1, indicating that adsorption is favorable. In conclusion, the results obtained from the Clark model showed that a lesser flow rate is efficient for maximizing Al(OH)3@AC adsorption. In this regard, it will be important to study the regeneration over the adsorbent to confirm the above results. The results (Fig. 5) show that the experimental and obtained breakthrough curves are in good agreement.
5. Fluoride desorption tests in dynamic mode
We monitored the number of fluorides at the column outlet over time. The results obtained are presented in Fig. 6.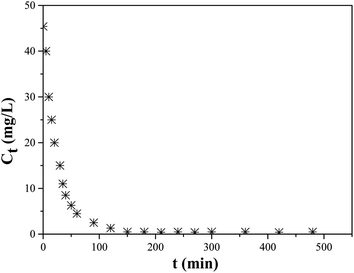 | ||
| Fig. 6 Evolution of the concentration of fluoride at the outlet of the column as a function of time. [NaOH] = 0.01 mol L−1, bed height = 3 cm, flow rate = 7.5 mL min−1, T = 22 °C. | ||
According to the results shown in Fig. 6, we observe rapid desorption during the first hour of contact which then gradually decreases until reaching equilibrium, estimated at a concentration of 0.5 mg L−1 of fluorides after 150 min of desorption with a desorption yield of 75% as determined using the following equations.
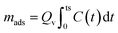 | (5) |
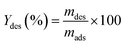 | (6) |
6. Regeneration–reuse of the adsorbent
To evaluate the performance of regenerated Al(OH)3@AC, a continuous adsorption test was performed under optimal operating conditions. The results obtained are illustrated in Fig. 7. According to the results, the breakthrough time goes from 170 min for the first use of the activated carbon bed to 100 min after its regeneration. We see the same trend for the saturation time, which goes from 900 min during the first use to 780 min after regeneration. In addition, the fluoride adsorption yields obtained are 51.21% during the first use and 45.55% after regeneration. These results are promising and further confirm the fluoride removal performance of the produced Al(OH)3@AC activated carbon.7. Conclusions
The dynamic adsorption of fluoride over Al(OH)3@AC was investigated in a continuous fixed bed column to provide theoretical and technological information to expand the industrial scale application of Al(OH)3@AC. The results of the continuous mode study are encouraging and show that a number of parameters such as feed flow, fixed bed height and initial fluoride concentration influence the breakthrough curves. Indeed, the maximum adsorption capacity calculated by the Thomas model (qTh) of 30.20 mg g−1 was obtained for a feed flow rate of 7.5 mg L−1, a bed height of 3 cm and an initial fluoride concentration of 15 mg L−1. Concerning the applicability of existing kinetic models, the results of the fitting of experimental data showed that the Thomas, Yoon–Nelson and Clark models satisfactorily describe the experimental data of the adsorption of fluorides on AC-Al(OH)3 and, to a lesser extent, the Bohart–Adams model, as it describes only the starting phase of the dynamic process of the column system. The breakthrough curves were determined based on the optimization investigations, taking into account bed heights, flow rates, and initial fluoride concentrations. In conclusion, Al(OH)3@AC has significant commercial application potential since it can safely and continuously remove F− pollutants from water using a fixed-bed column.Conflicts of interest
There are no relevant financial or non-financial interests to declare for the authors.Acknowledgements
This work was financially supported by University of Rouen Normandy, INSA Rouen Normandy, the Centre National de la Recherche Scientifique (CNRS), European Regional Development Fund (ERDF), Labex SynOrg (ANR-11-LABX-0029), Carnot Institut I2C, the graduate school for research Xl-Chem (ANR-18-EURE-0020 XL CHEM), and by Region Normandie and the Evreux Portes de Normandie. The authors thank the Algerian Ministry of Higher Education and scientific Research for their offer of the PNE scholarship that allowed to finance the scientific training in France.References
- H. Che, Y. Li, S. Zhang, W. Chen, X. Tian, C. Yang, L. Lu, Z. Zhou and Y. Nie, A portable logic detector based on Eu-MOF for multi-target, on-site, visual detection of Eu3+ and fluoride in groundwater, Sens. Actuators, B, 2020, 324, 128641 CrossRef CAS.
- M. Zamani, M. Aghajanzadeh, H. Molavi, H. Danafar and A. Shojaei, Thermally Oxidized Nanodiamond: An Effective Sorbent for Separation of Methotrexate from Aqueous Media: Synthesis, Characterization, In Vivo and In Vitro Biocompatibility Study, J. Inorg. Organomet. Polym. Mater., 2019, 29, 701–709 CrossRef CAS.
- M. Raeiszadeh, A. Hakimian, A. Shojaei and H. Molavi, Nanodiamond-filled chitosan as an efficient adsorbent for anionic dye removal from aqueous solutions, J. Environ. Chem. Eng., 2018, 6, 3283–3294 CrossRef CAS.
- H. Molavi, H. Moghimi and R. A. Taheri, Zr-Based MOFs with High Drug Loading for Adsorption Removal of Anti-Cancer Drugs: A Potential Drug Storage, Appl. Organomet. Chem., 2020, 34, e5549 CrossRef CAS.
- Z. Fallah, E. N. Zare, M. Ghomi, F. Ahmadijokani, M. Amini, M. Tajbakhsh, M. Arjmand, G. Sharma, H. Ali, A. Ahmad, P. Makvandi, E. Lichtfouse, M. Sillanpää and R. S. Varma, Toxicity and remediation of pharmaceuticals and pesticides using metal oxides and carbon nanomaterials, Chemosphere, 2021, 275, 130055 CrossRef CAS PubMed.
- X. Borgohain, A. Boruah, G. K. Sarma and M. H. Rashid, Rapid and extremely high adsorption performance of porous MgO nanostructures for fluoride removal from water, J. Mol. Liq., 2020, 305, 112799 CrossRef CAS.
- S. S. Waghmare and T. Arfin, Fluoride removal from water by various techniques: review, Int. J. Innov. Sci. Eng. Technol., 2015, 2, 560 Search PubMed.
- D. Clímaco Patrocínio, C. C. Neves Kunrath, M. A. Siqueira Rodrigues, T. Benvenuti and F. Dani Rico Amado, Concentration effect and operational parameters on electrodialysis reversal efficiency applied for fluoride removal in groundwater, J. Environ. Chem. Eng., 2019, 7, 103491 CrossRef.
- J. Shen, B. S. Richards and A. I. Schäfer, Renewable energy powered membrane technology: case study of St. Dorcas borehole in Tanzania demonstrating fluoride removal via nanofiltration/reverse osmosis, Sep. Purif. Technol., 2016, 170, 445–452 CrossRef CAS.
- C. Guan, X. Lv, Z. Han, C. Chen, Z. Xu and Q. Liu, The adsorption enhancement of graphene for fluorine and chlorine from water, Appl. Surf. Sci., 2020, 516, 146157 CrossRef CAS.
- Z. H. Khan, M. Gao, W. Qiu and Z. Song, Properties and adsorption mechanism of magnetic biochar modified with molybdenum disulfide for cadmium in aqueous solution, Chemosphere, 2020, 255, 126995 CrossRef CAS PubMed.
- I. Ali, Z. A. Alothman and M. M. Sanagi, Green Synthesis of Iron Nano-Impregnated Adsorbent for Fast Removal of Fluoride from Water, J. Mol. Liq., 2015, 211, 457–465 CrossRef CAS.
- Q. Zhang, S. Bolisetty, Y. Cao, S. Handschin, J. Adamcik, Q. Peng and R. Mezzenga, Selective and Efficient Removal of Fluoride from Water: In Situ Engineered Amyloid Fibril/ZrO2 Hybrid Membranes, Angew. Chem., Int. Ed., 2019, 58, 6012–6016 CrossRef CAS PubMed.
- L. Xu, X. Gao, Z. Li and C. Gao, Removal of fluoride by nature diatomite from high-fluorine water: an appropriate pretreatment for nanofiltration process, Desalination, 2015, 369, 97–104 CrossRef CAS.
- R. Mondal, S. Pal, D. V. Bhalani, V. Bhadja, U. Chatterjee and S. K. Jewrajka, Preparation of polyvinylidene fluoride blend anion exchange membranes via non-solvent induced phase inversion for desalination and fluoride removal, Desalination, 2018, 445, 85–94 CrossRef CAS.
- S. Raghav and D. Kumar, Comparative kinetics and thermodynamic studies of fluoride adsorption by two novel synthesized biopolymer composites, Carbohydr. Polym., 2019, 203, 430–440 CrossRef CAS PubMed.
- S. Bakhta, Z. Sadaoui, U. Lassi, H. Romar, R. Kupila and J. Vieillard, Performances of metals modified activated carbons for fluoride removal from aqueous solutions, Chem. Phys. Lett., 2020, 754, 137705 CrossRef CAS.
- S. Bakhta, Z. Sadaoui, N. Bouazizi, B. Samir, O. Allalou, C. Devouge-Boyer, M. Mignot and J. Vieillard, Functional activated carbon: from synthesis to groundwater fluoride removal, RSC Adv., 2022, 12, 2332–2348 RSC.
- K. Everaert, J. Baeyens and C. Creemers, Adsorption of dioxins and furans from flue gases in an entrained flow or fixed/moving bed reactor, J. Chem. Technol. Biotechnol., 2003, 78, 213–219 CrossRef CAS.
- X.-J. Zhou, A. Buekens, X.-D. Li, M.-J. Ni and K.-F. Cen, Adsorption of polychlorinated dibenzo-p-dioxins/dibenzofurans on activated carbon from hexane, Chemosphere, 2016, 144, 1264–1269 CrossRef CAS PubMed.
- J. Vieillard, N. Bouazizi, P. N. Fotsing, B. Samir, K. Raguillet, J. Cosme, C. A. Serhal, M. Mignot, M. S. Bette, P. Auger, G. L. Dotto and F. Le Derf, Herbs carbonization and activation for fast sorption of nitrate ions: a new challenge for a full treatment of groundwater pollution, Environ. Sci. Pollut. Res. Int., 2023, 30, 82637–82646 CrossRef CAS PubMed.
- J. G. Bell, X. Zhao, Y. Uygur and K. M. Thomas, Adsorption of Chloroaromatic Models for Dioxins on Porous Carbons: The Influence of Adsorbate Structure and Surface Functional Groups on Surface Interactions and Adsorption Kinetics, J. Phys. Chem. C, 2011, 115, 2776–2789 CrossRef CAS.
- V. X. Nascimento, C. Schnorr, S. F. Lütke, M. C. F. Da Silva, F. Machado Machado, P. S. Thue, C. Lima É, J. Vieillard, L. F. O. Silva and G. L. Dotto, Adsorptive Features of Magnetic Activated Carbons Prepared by a One-Step Process towards Brilliant Blue Dye, Mol., 2023, 28, 1821 CrossRef CAS PubMed.
- D. Zhou, D. Li, A. Li, M. Qi, D. Cui, H. Wang and H. Wei, Activated carbons prepared via reflux-microwave-assisted activation approach with high adsorption capability for methylene blue, J. Environ. Chem. Eng., 2021, 9, 104671 CrossRef CAS.
- W. J. Weber, Adsorption processes, Pure Appl. Chem., 1974, 37, 375–392 CrossRef CAS.
- Z. Xu, J.-G. Cai and B.-C. Pan, Mathematically modeling fixed-bed adsorption in aqueous systems, J. Zhejiang Univ., Sci., A, 2013, 14, 155–176 CrossRef CAS.
- L. Liu, Z. Yang, W. Yang, W. Jiang, Q. Liao, M. Si and F. Zhao, Ferrihydrite transformation impacted by coprecipitation of lignin: inhibition or facilitation?, J. Environ. Sci., 2024, 139, 23–33 CrossRef PubMed.
- W. Yang, Y. Zhang, J. Zheng, L. Liu, M. Si, Q. Liao, Z. Yang and F. Zhao, Migration of spent grain-modified colloidal ferrihydrite: implications for the in situ stabilization of arsenic, lead, and cadmium in co-contaminated soil, Chemosphere, 2023, 344, 140310 CrossRef CAS PubMed.
- F. He, Z. Yang, F. Zhao, E. Repo, W. Yang, Q. Liao, M. Si, B. Zou and Z. Lin, Unveiling the dual roles of the intercalation of [MoS4]2− clusters in boosting heavy metal capture by Ca–Al layered double hydroxide, Environ. Sci.: Nano, 2023, 10, 190–202 RSC.
- L. Lv, Y. Zhang, K. Wang, A. K. Ray and X. S. Zhao, Modeling of the adsorption breakthrough behaviors of Pb2+ in a fixed bed of ETS-10 adsorbent, J. Colloid Interface Sci., 2008, 325, 57–63 CrossRef CAS PubMed.
- K. H. Chu, Improved fixed bed models for metal biosorption, Chem. Eng. J., 2004, 97, 233–239 CrossRef CAS.
- I. A. Aguayo-Villarreal, A. Bonilla-Petriciolet, V. Hernández-Montoya, M. A. Montes-Morán and H. E. Reynel-Avila, Batch and column studies of Zn2+ removal from aqueous solution using chicken feathers as sorbents, Chem. Eng. J., 2011, 167, 67–76 CrossRef CAS.
- R. Tovar-Gómez, M. R. Moreno-Virgen, J. A. Dena-Aguilar, V. Hernández-Montoya, A. Bonilla-Petriciolet and M. A. Montes-Morán, Modeling of fixed-bed adsorption of fluoride on bone char using a hybrid neural network approach, Chem. Eng. J., 2013, 228, 1098–1109 CrossRef.
- L. Cavas, Z. Karabay, H. Alyuruk, H. Doğan and G. K. Demir, Thomas and artificial neural network models for the fixed-bed adsorption of methylene blue by a beach waste Posidonia oceanica (L.) dead leaves, Chem. Eng. J., 2011, 171, 557–562 CrossRef CAS.
- C. E. D. A. Padilha, C. A. D. A. Padilha, D. F. D. S. Souza, J. A. D. Oliveira, G. R. D. Macedo and E. S. D. Santos, Prediction of rhamnolipid breakthrough curves on activated carbon and Amberlite XAD-2 using Artificial Neural Network and Group Method Data Handling models, J. Mol. Liq., 2015, 206, 293–299 CrossRef CAS.
- G. S. Bohart and E. Q. Adams, Some aspects of the behavior of charcoal with respect to chlorine, J. Am. Chem. Soc., 1920, 42, 523–544 CrossRef.
- H. C. Thomas, Heterogeneous Ion Exchange in a Flowing System, J. Am. Chem. Soc., 1944, 66, 1664–1666 CrossRef CAS.
- R. M. Clark, Evaluating the cost and performance of field-scale granular activated carbon systems, Environ. Sci. Technol., 1987, 21, 573–580 CrossRef CAS PubMed.
- G. Yan, T. Viraraghavan and M. Chen, A New Model for Heavy Metal Removal in a Biosorption Column, Adsorpt. Sci. Technol., 2001, 19, 25–43 CrossRef CAS.
- Y. H. Yoon and J. H. Nelson, Application of Gas Adsorption Kinetics I. A Theoretical Model for Respirator Cartridge Service Life, Am. Ind. Hyg. Assoc. J., 1984, 45, 509–516 CrossRef CAS PubMed.
- J. J. García-Sánchez, M. Solache-Ríos, V. Martínez-Miranda and C. Solís Morelos, Removal of fluoride ions from drinking water and fluoride solutions by aluminum modified iron oxides in a column system, J. Colloid Interface Sci., 2013, 407, 410–415 CrossRef PubMed.
- R. Han, L. Zou, X. Zhao, Y. Xu, F. Xu, Y. Li and Y. Wang, Characterization and properties of iron oxide-coated zeolite as adsorbent for removal of copper(II) from solution in fixed bed column, Chem. Eng. J., 2009, 149, 123–131 CrossRef CAS.
- S. R. Pilli, V. V. Goud and K. Mohanty, Biosorption of Cr(VI) on immobilized Hydrilla verticillata in a continuous up-flow packed bed: prediction of kinetic parameters and breakthrough curves, Desalin. Water Treat., 2012, 50, 115–124 CrossRef CAS.
- Z. Aksu and F. Gönen, Biosorption of phenol by immobilized activated sludge in a continuous packed bed: prediction of breakthrough curves, Process Biochem., 2004, 39, 599–613 CrossRef CAS.
- L. Liu, Z. Yang, F. Zhao, Z. Chai, W. Yang, H. Xiang, Q. Liao, M. Si and Z. Lin, Manganese doping of hematite enhancing oxidation and bidentate-binuclear complexation during As(III) remediation: experiments and DFT calculation, Chem. Eng. J., 2023, 471, 144758 CrossRef CAS.
- N. Chen, Z. Zhang, C. Feng, M. Li, R. Chen and N. Sugiura, Investigations on the batch and fixed-bed column performance of fluoride adsorption by Kanuma mud, Desalination, 2011, 268, 76–82 CrossRef CAS.
- S. Mohan, D. K. Singh, V. Kumar and S. H. Hasan, Effective removal of Fluoride ions by rGO/ZrO2 nanocomposite from aqueous solution: fixed bed column adsorption modelling and its adsorption mechanism, J. Fluorine Chem., 2017, 194, 40–50 CrossRef CAS.
- M. Talat, S. Mohan, V. Dixit, D. K. Singh, S. H. Hasan and O. N. Srivastava, Effective removal of fluoride from water by coconut husk activated carbon in fixed bed column: experimental and breakthrough curves analysis, Groundw. Sustain. Dev., 2018, 7, 48–55 CrossRef.
- A. Ghosh, S. Chakrabarti and U. C. Ghosh, Fixed-bed column performance of Mn-incorporated iron(III) oxide nanoparticle agglomerates on As(III) removal from the spiked groundwater in lab bench scale, Chem. Eng. J., 2014, 248, 18–26 CrossRef CAS.
- B. Ramavandi, S. Farjadfard and M. Ardjmand, Mitigation of orange II dye from simulated and actual wastewater using bimetallic chitosan particles: continuous flow fixed-bed reactor, J. Environ. Chem. Eng., 2014, 2, 1776–1784 CrossRef CAS.
- K. Z. Setshedi, M. Bhaumik, M. S. Onyango and A. Maity, Breakthrough studies for Cr(VI) sorption from aqueous solution using exfoliated polypyrrole-organically modified montmorillonite clay nanocomposite, J. Ind. Eng. Chem., 2014, 20, 2208–2216 CrossRef CAS.
- T. Nur, P. Loganathan, T. C. Nguyen, S. Vigneswaran, G. Singh and J. Kandasamy, Batch and column adsorption and desorption of fluoride using hydrous ferric oxide: solution chemistry and modeling, Chem. Eng. J., 2014, 247, 93–102 CrossRef CAS.
- A. Teutli-Sequeira, M. Solache-Ríos, V. Martínez-Miranda and I. Linares-Hernández, Behavior of Fluoride Removal by Aluminum Modified Zeolitic Tuff and Hematite in Column Systems and the Thermodynamic Parameters of the Process, Water, Air, & Soil Pollution, 2015, 226, 239 Search PubMed.
- Y. Ye, J. Yang, W. Jiang, J. Kang, Y. Hu, H. H. Ngo, W. Guo and Y. Liu, Fluoride removal from water using a magnesia-pullulan composite in a continuous fixed-bed column, J. Environ. Manage., 2018, 206, 929–937 CrossRef CAS PubMed.
- C. E. Choong, M. Kim, S. Yoon, G. Lee and C. M. Park, Mesoporous La/Mg/Si-incorporated palm shell activated carbon for the highly efficient removal of aluminum and fluoride from water, J. Taiwan Inst. Chem. Eng., 2018, 93, 306–314 CrossRef CAS.
- A. Ajmani, C. Patra, S. Subbiah and S. Narayanasamy, Packed bed column studies of hexavalent chromium adsorption by zinc chloride activated carbon synthesized from Phanera vahlii fruit biomass, J. Environ. Chem. Eng., 2020, 8, 103825 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |