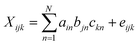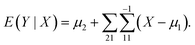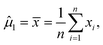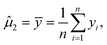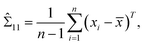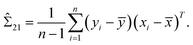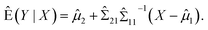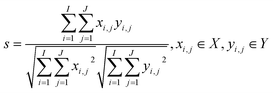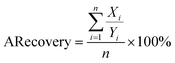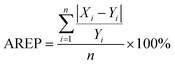Open Access Article
Open Access ArticleDetermination of phenolic compounds in water using a multivariate statistical analysis method combined with three-dimensional fluorescence spectroscopy
Wei Zhu ab,
Ruifang Yang
ab,
Ruifang Yang *b,
Nanjing Zhao*b,
Gaofang Yinb and
Jianguo Liub
*b,
Nanjing Zhao*b,
Gaofang Yinb and
Jianguo Liub
aUniversity of Science and Technology of China, Hefei, 230026, China
bKey Laboratory of Environmental Optics and Technology, Anhui Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Hefei, 230031, China. E-mail: rfyang@aiofm.ac.cn; njzhao@aiofm.ac.cn
First published on 10th January 2024
Abstract
Phenolic compounds are toxic chemical pollutants present in water. Three-dimensional fluorescence spectroscopy analysis is an effective and rapid method for real-time phenol monitoring in aquatic environments. However, similar chemical structures of phenols result in highly overlapping three-dimensional fluorescence spectra. Therefore, it is extremely difficult to analyze and quantify the concentration of components in a mixture system that includes two or more phenolic compounds. In this article, we study the mixed phenol system containing phenol, o-cresol, p-cresol, m-cresol, catechol, and resorcinol combined with excitation-emission matrix (EEM) fluorescence data. A multivariate statistical method called best linear unbiased prediction (BLUP) is proposed to analyze the spectra with the aim to achieve quantitative results and a trilinear decomposition algorithm called parallel factor analysis (PARAFAC) was used for comparison. Two experiments with different calibration samples were set to validate the effectiveness of BLUP through recovery, ARecovery (Average Recovery), AREP (Average Relative Error of Prediction), and RMSE (Root Mean Square Error). Overall, the average recovery of each component in experiment 1 and experiment 2 ranged from 95.91% to 111.62% and 82.91% to 129.02%, respectively. Based on the results of the experiments, the concentration of phenolic compounds in water can be quantitatively determined by combining three-dimensional fluorescence spectroscopy with the BLUP method.
1. Introduction
Water is necessary for humans, but with industrial development, water pollution has become a serious problem.1 Phenolic compounds are toxic pollutants widely distributed in industrial wastewater and have adverse effects on the ecological environment and human health.2,3 Therefore, it is crucial to develop and improve methods for monitoring and identifying them in natural and urban water systems.Chemical analysis, gas chromatography (GC), gas chromatography-mass spectrometry (GC-MS), and high-performance liquid chromatography (HPLC) are some of the classical methods that can be used to determine phenolic compounds.4–8 However, because of the time-consuming process of handling chemical reagents and pretreatment of the experiment, these techniques do not perform very well in terms of real-time monitoring. To solve this issue, three-way fluorescence spectra are used, along with excitation-emission matrix (EEM) fluorescence data. Spectral information, high sensitivity, and low detection limits make it an effective technique for monitoring water pollutants.9–12
In recent years, many mathematical algorithms have been applied and improved to process three-dimensional fluorescence spectra.13–15 The trilinear decomposition algorithm is one type of these algorithms. A typical algorithm called parallel factor analysis (PARAFAC) has been used most commonly for dealing with EEM fluorescence data.16,17 On the premise that the signal-to-noise ratio is appropriate and the number of components is estimated correctly, PARAFAC usually performs well in the separation and reduction of the three-dimensional fluorescence spectra of each component in a mixture system.18,19 The largest advantage of PARAFAC is the uniqueness of decomposition under the condition that the dataset is linear in three directions. However, PARAFAC may not be able to obtain accurate concentrations for each compound when the three-dimensional fluorescence spectra overlap seriously, as in the case of the six phenolic compounds quantitatively studied in this article. It is therefore important to explore various methods to estimate concentrations more precisely in such situations.
Multivariate statistical analysis is a comprehensive analysis method developed from classical statistical analysis. It can be used to analyze the statistical patterns of multiple objects and indicators when they are interrelated. Multivariate statistical analysis includes multiple regression analyses, cluster analysis, factor analysis, and Canonical correlation analysis. Best linear unbiased prediction (BLUP) is a prediction analysis method in multivariate statistical analysis. It is a valuable method for analyzing prediction since the corresponding predictor is the most optimal among the classes of linear and unbiased predictors. BLUP has been widely used in various fields, such as life testing and genetic connectedness in genetic statistics .20,21 It is useful for simplifying prediction calculations in some cases and constructing large-sample approximate predictors for scale and location–scale parameter distributions.22,23
In this study, we apply BLUP to the EEM data. In two different experiments, BLUP quantitative identification is used to identify 5/6 phenols directly from fluorescence excitation-emission matrices (EEMs). The results show that BLUP can provide accurate results for phenols with severe spectral overlap at different calibration set ratios.
2. Theory
2.1 PARAFAC algorithm
The trilinear model, also known as the PARAFAC model, was first developed by Carroll, Chang,24 and Harshman25 in 1970, and named CANDECOMP and PARAFA. Subsequently, the PARAFAC model attracted increasing attention. It is useful to deal with excitation-emission matrix (EEM) fluorescence data with the PARAFAC algorithm. The structural model is as follows:26Here i = 1, 2…, I; j = 1, 2…, J; k = 1, 2…, K; N means the number of components. Ain and bjn represent the (I,n) and (j,n) elements of excitation matrix A (I × N) and emission matrix B (J × N), respectively. ckn is the (k,n) element of relative concentration matrix C (K × N). eijk is the element of a three-dimensional residual matrix E.
2.2 Best linear unbiased prediction
In the statistical regression analysis, suppose that X and Y are p-dimensional and q-dimensional random variables. Here, X represents the EEFM (Excitation Emission Fluorescence Matrix) data and Y represents the concentration of each component, both X and Y matrices are stretched into a vector before processing the data. If we want to predict Y based on X, then a good predictor is E(Y|X), that is, the conditional expectation of Y given X. In particular, if the joint distribution of X and Y is normal, i.e.,
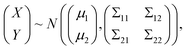 | (1) |
For model (1), the conditional expectation of Y is given by:27
In fact, this predictor is the best linear unbiased predictor (BLUP) under the normality assumption.
Note that μ1, μ2, Σ11, and Σ21 are all unknown in practice, so it is necessary to estimate them based on the sample data. Suppose that the sample 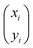 , i = 1,2,…,n are drawn from the population
, i = 1,2,…,n are drawn from the population 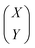 , then the maximum likelihood estimators of the parameters are,
, then the maximum likelihood estimators of the parameters are,
Thus, we can use the following to predict Y, that is,
3. Experimental and measurements
The phenol, o-cresol, m-cresol, p-cresol, catechol, and resorcinol used in these experiments were analytically pure (AR) and purchased from Aladdin. Each stocking solution was prepared by dissolving 500 mg of the corresponding phenolic compounds in deionized water in 500 mL brown volumetric flasks at low temperatures and protected from light. The working solutions are made by diluting the stock solutions proportionally when carrying out the experiments. Excitation-emission matrix fluorescence data were collected using a Hitachi F-7000 three-dimensional fluorescence spectrometer.In this work, we prepared two experiments to determine the calculation accuracy of the BLUP compared with PARAFAC. In experiment 1, the calibration set comprised 9 samples which were mixed with phenol, o-cresol, p-cresol, catechol, and resorcinol in deionized water. Similar to the calibration set, the test set contained different concentration ratios of 5 phenols. All the concentration ratios of 5 phenols in the calibration and test sets are shown in Table 1.
| Calibration set | Test set | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Phenol | o-Cresol | p-Cresol | Catechol | Resorcinol | Phenol | o-Cresol | p-Cresol | Catechol | Resorcinol | ||
| 1 | 0.08 | 0.16 | 0.40 | 0.56 | 0.64 | 1 | 0.10 | 0.64 | 0.10 | 0.30 | 0.20 |
| 2 | 0.16 | 0.32 | 0.08 | 0.40 | 0.56 | 2 | 0.50 | 0.30 | 0.38 | 0.44 | 0.30 |
| 3 | 0.24 | 0.48 | 0.48 | 0.24 | 0.48 | 3 | 0.32 | 0.70 | 0.40 | 0.70 | 0.40 |
| 4 | 0.32 | 0.64 | 0.16 | 0.08 | 0.40 | 4 | 0.72 | 0.60 | 0.18 | 0.62 | 0.70 |
| 5 | 0.40 | 0.08 | 0.56 | 0.64 | 0.32 | 5 | 0.08 | 0.56 | 0.56 | 0.10 | 0.60 |
| 6 | 0.48 | 0.24 | 0.24 | 0.48 | 0.24 | 6 | 0.20 | 0.26 | 0.70 | 0.08 | 0.50 |
| 7 | 0.56 | 0.40 | 0.64 | 0.32 | 0.16 | 7 | 0.60 | 0.10 | 0.22 | 0.50 | 0.10 |
| 8 | 0.64 | 0.56 | 0.32 | 0.16 | 0.08 | 8 | 0.64 | 0.50 | 0.44 | 0.60 | 0.46 |
| 9 | 0.72 | 0.72 | 0.72 | 0.72 | 0.72 | 9 | 0.48 | 0.48 | 0.30 | 0.72 | 0.68 |
| 10 | 0.24 | 0.36 | 0.60 | 0.20 | 0.34 | ||||||
In experiment 2, a calibration set of 21 samples was built from six 2-component mixed samples, four 3-component mixed samples, six 4-component mixed samples, and five 5-component mixed samples. The test set is also a mixed system, but all ten samples contain 6 phenols. The purpose of conducting experiment 2 was to test the situation in which more similar component was added and fewer components were mixed in the calibration set. Table 2 and Table 3 list the concentration values of 6 phenols in the calibration and test samples.
| Calibration set | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Phenol | o-Cresol | m-Cresol | p-Cresol | Catechol | Resorcinol | Phenol | o-Cresol | m-Cresol | p-Cresol | Catechol | Resorcinol | ||
| 1 | 0.8 | 1.5 | 0 | 0 | 0 | 0 | 12 | 0 | 1 | 0.7 | 0.5 | 0 | 0 |
| 2 | 0 | 0.6 | 1.1 | 0 | 0 | 0 | 13 | 0.5 | 0.4 | 0.6 | 0.4 | 0.24 | 0 |
| 3 | 0 | 0 | 1.6 | 0.8 | 0 | 0 | 14 | 0.7 | 0 | 0 | 0.7 | 0.4 | 2.2 |
| 4 | 0 | 0 | 0 | 1.2 | 2 | 0 | 15 | 0 | 0.8 | 0.5 | 0 | 0 | 0.7 |
| 5 | 0 | 0 | 0 | 0 | 1.8 | 2.4 | 16 | 0 | 0.6 | 0 | 1.5 | 1 | 0 |
| 6 | 1.5 | 0 | 0 | 0 | 0 | 1.8 | 17 | 0.16 | 0.7 | 0.16 | 0.3 | 1.2 | 0 |
| 7 | 1 | 1.2 | 0.4 | 0 | 0 | 0 | 18 | 0.9 | 0 | 1.1 | 0.9 | 0.9 | 0.16 |
| 8 | 0 | 0.5 | 0.8 | 0.6 | 0 | 0 | 19 | 1.1 | 0.5 | 0 | 0.16 | 0.5 | 0.9 |
| 9 | 0 | 0 | 1 | 1 | 1.5 | 0 | 20 | 0.3 | 0.3 | 0.8 | 0 | 0.7 | 0.3 |
| 10 | 0.6 | 0 | 0 | 0 | 2.6 | 2 | 21 | 0.8 | 0.9 | 0.3 | 0.6 | 0 | 0.6 |
| 11 | 0.4 | 1 | 0.7 | 0.5 | 0 | 0 | |||||||
| Test set | ||||||
|---|---|---|---|---|---|---|
| Phenol | o-Cresol | m-Cresol | p-Cresol | Catechol | Resorcinol | |
| 1 | 0.64 | 0.64 | 0.66 | 0.24 | 0.6 | 0.4 |
| 2 | 0.5 | 0.3 | 0.32 | 0.38 | 1 | 1 |
| 3 | 0.44 | 0.7 | 0.4 | 0.4 | 0.7 | 1.2 |
| 4 | 0.72 | 0.6 | 0.48 | 0.2 | 0.9 | 0.7 |
| 5 | 0.4 | 0.56 | 0.72 | 0.56 | 0.5 | 0.6 |
| 6 | 0.2 | 0.26 | 0.44 | 0.7 | 1.4 | 0.5 |
| 7 | 0.6 | 0.2 | 0.2 | 0.5 | 1.2 | 1.1 |
| 8 | 0.36 | 0.5 | 0.7 | 0.44 | 0.66 | 1.3 |
| 9 | 0.48 | 0.48 | 0.36 | 0.3 | 0.84 | 1.5 |
| 10 | 0.26 | 0.36 | 0.52 | 0.6 | 1.6 | 0.8 |
4. Results and discussion
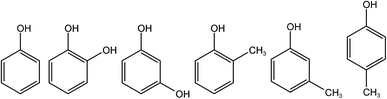
Phenol, o-cresol, m-cresol, p-cresol, catechol, and resorcinol have similar chemical structures, as shown in Fig. 1. Although the positions of the phenolic hydroxyl and methyl groups connected to the benzene ring are different, the conjugated structure of the benzene ring leads to similar fluorescence peaks. Therefore, their three-dimensional fluorescence spectra overlap significantly (Fig. 2). Taking the similarity into account, the similarity factors were calculated using the following formula:Here, X and Y are the EEM data of the two phenolic components, xij, yij are the elements of the matrix X, Y corresponding to the intensity in i-th excitation and j-th emission. The similarity factors obtained from the 6 phenolic components EEM data ranged from 0.7417 to 0.9851 listed in Table 4. So, it is difficult to analyze serious-overlap EEM data and quantitatively determine the concentration of each component.
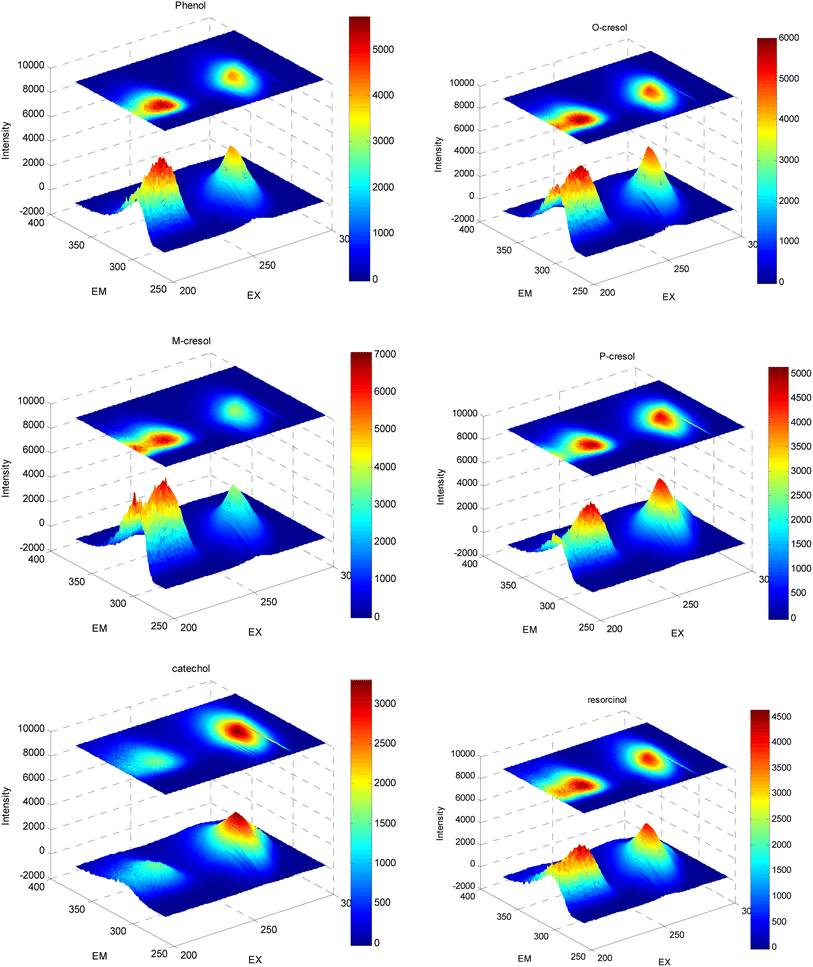 | ||
| Fig. 2 Three-dimensional fluorescence spectra combined with contour plots of six phenolic compounds. | ||
| Phenol | o-Cresol | p-Cresol | Catechol | Resorcinol | m-Cresol | |
|---|---|---|---|---|---|---|
| Phenol | 1 | 0.9728 | 0.8027 | 0.7417 | 0.8761 | 0.9512 |
| o-Cresol | — | 1 | 0.8633 | 0.8302 | 0.9517 | 0.9851 |
| p-Cresol | — | — | 1 | 0.9288 | 0.9127 | 0.8404 |
| Catechol | — | — | — | 1 | 0.9133 | 0.7882 |
| Resorcinol | — | — | — | — | 1 | 0.9485 |
| m-Cresol | — | — | — | — | — | 1 |
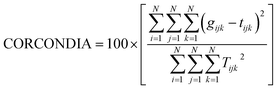
In these experiments, CORCONDIA (core consistency diagnostic) was used as an efficient and useful method to calculate the component numbers. It can determine the number of factors through the value of the core consistency coefficient:
In experiment 1, the value of the core consistency coefficient is above 50%, corresponding to five components, and drops to 5.24% when the number is increased from 5 to 6. Therefore, five components are suggested to be the correct estimation constituents in experiment 1. In the same way, 6 is determined as the suitable component number in experiment 2.
After the number of components is determined, the next step is to use algorithms with appropriate parameters to calculate the concentrations of each component in test samples. Two sets of twenty test samples containing five phenolic compounds in experiment 1 and six phenolic compounds in experiment 2 are quantitatively calculated by BLUP and PARAFAC. ARecovery (Average Recovery), AREP (Average Relative Error of Prediction), and RMSE (Root Mean Square Error) are the four indicators of the calculation results.
Here Xi means the calculated concentration of the i-th sample, Yi means the actual concentration of the i-th sample, n means the total number of all test samples.
Considering the different construction of the calibration sets, two experiments are discussed separately.
4.1 Experiment 1
For a more intuitive comparison between the calculated and actual concentrations, we created 5 line-symbol plots (Fig. 3) corresponding to five phenolic compounds to show the results obtained by BLUP and PARAFAC. The distance from the calculated symbols to the actual ones represents the accuracy of the results, and the fluctuation degree of the line chart represents the stability of the results.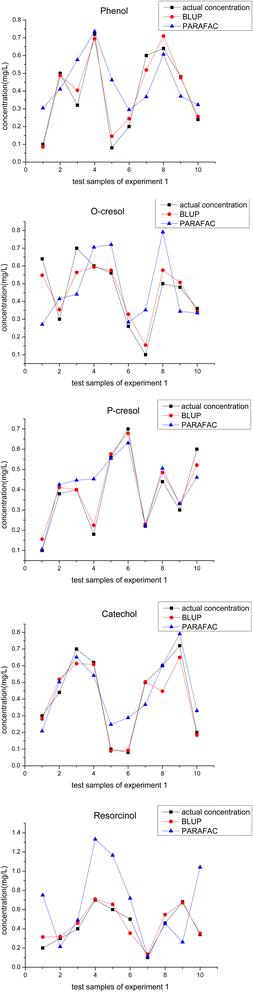 | ||
| Fig. 3 The calculated concentration using BLUP, PARAFAC algorithm, and the actual concentration of 5 phenolic components in all test samples in experiment 1. | ||
As for the quantitative results of phenol, BLUP performed better than PARAFAC in most test samples except samples 4 and 8. Although the recovery rates calculated by BLUP for samples 4 and 8 are not as accurate as those obtained by PARAFAC, they could still reach 96.42% for sample 4 and 110.92% for sample 8. Similar to phenol, there were no more than two samples in which the PARAFAC algorithm was superior to BLUP for calculating o-cresol, p-cresol, and resorcinol. These test samples are sample 6 in o-cresol, sample 5 in p-cresol, and sample 7, 8 in resorcinol, and their corresponding recovery rates were 126.19%, 102.89%, 135.7%, and 118.91%, respectively. The calculation results for catechol were relatively poorer than those for the other 4 phenolic compounds using the BLUP in experiment 1. There were three samples: sample 2, sample 3, and sample 8. Quantitative analysis revealed that BLUP is worse than PARAFAC. The respective recovery rates were 117.79%, 87.61%, and 74.52%, but the calculated concentration was not too far from the actual one.
As can be seen in Fig. 3, overall, BLUP performs better than PARAFAC, irrespective of the accuracy or the stability of results according to the fitness degree between the calculation lines and the actual lines in these plots. This conclusion can also be supported by the data in Table 5, in which average recovery and AREP represent the accuracy of the overall calculation results and RMSE represents the degree of discretization of data. It can be seen in Table 5, that the average recovery rates of all 5 phenolic compounds were closer to 100%, and the values of the average AREP and RMSE were also smaller when using the BLUP algorithm.
| BLUP | PARAFAC | BLUP | PARAFAC | |
|---|---|---|---|---|
| Phenol | p-Cresol | |||
| ARecovery/% | 111.31 | 176.14 | 108.22 | 117.31 |
| AREP/% | 18.38 | 93.06 | 16.14 | 24.12 |
| RMSE/mgL−1 | 0.0512 | 0.1856 | 0.0668 | 0.1040 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| o-Cresol | Catechol | |||
| ARecovery/% | 110.11 | 127.28 | 95.91 | 141.96 |
| AREP/% | 13.33 | 53.32 | 10.88 | 57.31 |
| RMSE/mgL−1 | 0.0401 | 0.2052 | 0.0656 | 0.1119 |
| BLUP | PARAFAC | |
|---|---|---|
| Resorcinol | ||
| ARecovery/% | 111.62 | 165.14 |
| AREP/% | 17.69 | 83.52 |
| RMSE/mgL−1 | 0.0708 | 0.4184 |
4.2 Experiment 2
In experiment 2, another phenolic compound called m-cresol was added. Including the 5 components in experiment 1, the three-dimensional fluorescence spectra of 6 phenolic compounds overlap in a more serious manner, leading to a much more complex mixture system. Different from experiment 1, the composition of the calibration samples in experiment 2 changes from complete mixing to partial mixing, such as 2-components mixing, 3-components mixing, etc. With the addition of m-cresol and the different composition forms for constructing the calibration set, we aimed to test the prediction performance of BLUP in such a situation.As can be seen in Fig. 4, there are only 3 dots that are closer to the actual dots using PARAFAC than using BLUP out of the total 60 dots, and sample 7 of phenol, sample 6 of o-cresol and sample 4 of m-cresol correspond to these three dots. Based on BLUP, their recovery rates were 101.62%, 72.62%, and 75.5%, within the acceptable ranges. The fluctuation range of the recovery rates of each component was also calculated to show the prediction performance of BLUP in experiment 2. For phenol, the recovery ranged from 101.62% to 157.77%; for o-cresol, the recovery ranged from 72.62% to 121.9%%; for m-cresol, recovery ranged from 72.25% to 92.72%; for p-cresol, recovery ranged from 98.02% to 121.9%; for catechol, recovery ranged from 80.71% to 111.8%; for resorcinol, recovery ranged from 95.55% to 120.7%.
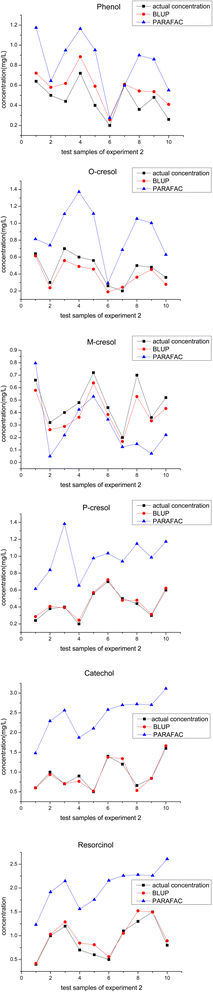 | ||
| Fig. 4 Calculated concentrations using BLUP, PARAFAC algorithm, and actual concentration of 6 phenolic components in all the test samples from experiment 2. | ||
As can be seen in Table 6, BLUP quantitatively calculates better than PARAFAC in terms of average recovery, average REP, and RMSE. Combined with Table 6, the difference between these three indicators the above between BLUP and PARAFAC increases rapidly as the component of the mixture system and composition of the calibration set change from experiment 1 to experiment 2. Meanwhile, it is noteworthy that the accuracy of quantitative calculation results using BLUP in experiment 2 is not significantly affected in such an environment according to the values of average recovery, average REP, and RMSE.
| BLUP | PARAFAC | BLUP | PARAFAC | |
|---|---|---|---|---|
| Phenol | o-Cresol | |||
| ARecovery/% | 129.02 | 180.62 | 85.65 | 200.94 |
| AREP/% | 29.03 | 77.13 | 18.73 | 103.88 |
| RMSE/mgL−1 | 0.1308 | 0.3989 | 0.0899 | 0.4672 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| m-Cresol | p-Cresol | |||
| ARecovery/% | 82.91 | 57.67 | 106.47 | 244.45 |
| AREP/% | 17.09 | 45.22 | 7.70 | 149.89 |
| RMSE/mgL−1 | 0.0920 | 0.2562 | 0.0287 | 0.5747 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Catechol | Resorcinol | |||
| ARecovery/% | 97.75 | 280.90 | 110.64 | 248.28 |
| AREP/% | 6.31 | 190.49 | 11.59 | 139.63 |
| RMSE/mgL−1 | 0.0799 | 1.5195 | 0.1176 | 1.1577 |
5. Conclusions
In this work, the BLUP method was applied to analyze the three-dimensional fluorescence spectra with a severe overlap of phenols in a water environment and quantitatively calculate the concentration of each component. The PARAFAC algorithm was also used for comparison. Two experiments were set with a different construction of the calibration set and a different number of phenolic components. In experiment 1, the average recovery rates of 5 phenols ranged from 95.91% to 111.62% with BLUP and 117.31% to 176.14% utilizing PARAFAC. In experiment 2, the average recovery rates of 6 phenols ranged from 82.91% to 129.02% with BLUP and 57.67% to 280.90% using PARAFAC. The calculation results confirmed that BLUP performs well in quantitatively predicting the concentration of each phenolic component. Furthermore, with less-mixed compositions and similar components added to the calibration samples, BLUP was still calculated precisely, showing prediction accuracy and stability.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Key Research and Development Plan (2022YFC3700902, 2017YFF0108402), the Natural Science Foundation of China (61805255), and the Instrument and Equipment Function Development Program of the Chinese Academy of Science (E03HBF11291).References
- L. W. Canter, and R. C. Knox, Ground Water Pollution Control, Lewis Publishers, 2020 Search PubMed.
- M. L. Davi and F. Gnudi, Phenolic compounds in surface water, Water Res., 1999, 33(14), 3213–3219 CrossRef CAS.
- V. Pasqualini, C. Robles and S. Garzino, et al., Phenolic compounds content in Pinus halepensis Mill. needles: a bioindicator of air pollution, Chemosphere, 2003, 52(1), 239–248 CrossRef CAS PubMed.
- M. Ikawa, T. D. Schaper, C. A. Dollard and J. J. Sansner, Utilization of Folin-Ciocalteu phenol reagent for the detection of certain nitrogen compounds, J. Agric. Food Chem., 2003, 51(7), 1811–1815 CrossRef CAS PubMed.
- F. Zhou, X. Li and Z. Zeng, Determination of phenolic compounds in wastewater samples using a novel fiber by solid-phase microextraction coupled to gas chromatography, Anal. Chim. Acta, 2005, 538(1–2), 63–70 CrossRef CAS.
- M. B. Helen, et al., Antification of 4-ethylphenol in belgian style beers by gas chromatography-mass spectrometry, J. Undergrad. Chem. Res., 2013, 12(1), 4–6 Search PubMed.
- M. Saraji and M. Bakhshi, Determination of phenols in water samples by single-drop microextraction followed by in-syringe derivatization and gas chromatography–mass spectrometric detection, J. Chromatogr. A, 2005, 1098(1–2), 30–37 CrossRef CAS PubMed.
- A. Sun, J. Li and R. Liu, High-performance liquid chromatographic determination of phenolic compounds in natural water coupled with on-line flow injection membrane extraction-preconcentration, J. Sep. Sci., 2006, 29(7), 995–1000 CrossRef CAS PubMed.
- C. M. Romero, et al., Compositional tracking of dissolved organic matter in semiarid wheat-based cropping systems using fluorescence EEMs-PARAFAC and absorbance spectroscopy, J. Arid Environ., 2019, 167(AUG), 34–42 CrossRef.
- K. Bengraine and T. F. Marhaba, Predicting organic loading in natural water using spectral fluorescent signatures, J. Hazard. Mater., 2004, 108(3), 207–211 CrossRef CAS PubMed.
- H. Wang, Y. Zhang and X. Xiao, Quantification of polycyclic aromatic hydrocarbons in water: a comparative study based on three-dimensional excitation-emission matrix fluorescence, Anal. Sci., 2010, 26(12), 1271 CrossRef CAS PubMed.
- H.-Bo Wang, Yu-J. Zhang, X. Xiao, Y. Shao-Hui and W.-Q. Liu, Application of excitation–emission matrix fluorescence combined with second-order calibration algorithm for the determination of five polycyclic aromatic hydrocarbons simultaneously in drinking water, Anal. Methods, 2011, 3, 688–695 RSC.
- J. H. Jiang, H. L. Wu and Z. P. Chen, et al., Coupled vectors resolution method for chemometric calibration with three-way data [J], Anal. Chem., 1999,(19), 71 Search PubMed.
- K. Kumar and A. K. Mishra, Simultaneous quantification of dilute aqueous solutions of certain polycyclic aromatic hydrocarbons (PAHs) with significant fluorescent spectral overlap using total synchronous fluorescence spectroscopy (TSFS) and N-PLS, unfolded-PLS and MCR-ALS analysis, Anal. Methods, 2011, 3(11), 2616–2624 RSC.
- R. Yang, N. Zhao and X. Xiao, et al., Blind separation of fluorescence spectra using sparse non-negative matrix factorization on right hand factor, J. Chemom., 2015, 29(8), 442–447, DOI:10.1002/cem.2723.
- R. Bro, PARAFAC. Tutorial and applications, Chemom. Intell. Lab. Syst., 1997, 38(2), 149–171 CrossRef CAS.
- P. Paatero, Construction and analysis of degenerate PARAFAC models, J. Chemom., 2000, 14(3), 285–299 CrossRef CAS.
- K. R. Murphy, C. A. Stedmon, D. Graeber and R. Bro, Fluorescence spectroscopy and multi-way techniques. PARAFAC, Anal. Methods, 2013, 5(23), 6557–6566 RSC.
- H. A. L. Kiers and A. K. Smilde, Some theoretical results on second-order calibration methods for data with and without rank overlap, J. Chemom., 1995, 9(3), 179–195 CrossRef CAS.
- D. Necip and N. Balakrishnan, A useful property of best linear unbiased predictors with applications to life-testing, Am. Stat., 1997, 51(1), 22–28 Search PubMed.
- H. P. Yu, M. L. Spangler, R. M. Lewis and G. Morota, Do stronger measures of genomic connectedness enhance prediction accuracies across management units, J. Anim. Sci., 2018, 96(11), 4490–4500 Search PubMed.
- H. P. Yu, M. L. Spangler, R. M. Lewis and G. Morota, Do stronger measures of genomic connectedness enhance prediction accuracies across management units?, J. Anim. Sci., 2018, 96(11), 4490–4500 Search PubMed.
- M. Satoh, An alternative derivation method of mixed model equations from best linear unbiased prediction (BLUP) and restricted BLUP of breeding values not using maximum likelihood, Anim. Sci. J., 2018, 89(6), 876–879 CrossRef PubMed.
- J. D. Carroll and J. J. Chang, Analysis of individual differences in multidimensional scaling via an N-way generalization of “Eckart-Young” decomposition, Psychometrika, 1970, 35(3), 283–319 CrossRef.
- J. Saurina, S. Hemandez-Cassou and R. Tauler, Multivariate curve resolution and trilinear decomposition methods in the analysis of stopped-flow kinetic data for binary amino acid mixtures, Anal. Chem., 1997, 69(13), 2329–2336 CrossRef CAS PubMed.
- R. Bro, Multi-Way Analysis in the Food Industry. Models, Algorithms, and Applications, Ethical Theory Moral Pract., 1998, 6(2), 231–235 Search PubMed.
- T. W. Anderson, An Introduction to Multivariate Statistical Analysis, John Wiley & Son, New York, 2nd edn, 1984 Search PubMed.
| This journal is © The Royal Society of Chemistry 2024 |