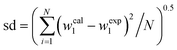DOI:
10.1039/D3RA07066B
(Paper)
RSC Adv., 2024,
14, 12349-12359
Harnessing the power of natural deep eutectic solvents (choline chloride/sucrose) and polypropylene glycol in the formation of aqueous biphasic systems and the application of these systems in drug extraction†
Received
17th October 2023
, Accepted 2nd April 2024
First published on 17th April 2024
Abstract
In recent times, there has been considerable interest in utilizing aqueous biphasic systems (ABSs) containing natural deep eutectic solvents (NADESs) for the extraction of various substances. In this study, we focused on investigating the phase behavior of ABSs composed of poly(propylene) glycol 400 and NADESs (specifically, choline chloride/sucrose with molar ratios of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). By analyzing the compositions of tie-lines, it was observed that these ABSs, which consist of four components, exhibit characteristics similar to ternary systems. To examine the influence of molar ratios on phase separation, the binodal model was applied to the obtained binodal data. The NRTL and UNIQUAC models were employed to establish correlations for the tie-lines. Moreover, we examined the extraction capabilities of the aforementioned ABSs for three commonly used drugs: diclofenac potassium, acetaminophen, and salicylic acid. To assess the efficiency of extraction, partition coefficients and extraction efficiencies were calculated for each drug. The results revealed that the extraction efficiency of these drugs into the polymer-rich top phase is dependent on their hydrophobicity. Furthermore, we employed the Diamond–Hsu equation, along with its modified version, to establish correlations between the experimental partition coefficients of the drugs and NADES overall concentrations.
1). By analyzing the compositions of tie-lines, it was observed that these ABSs, which consist of four components, exhibit characteristics similar to ternary systems. To examine the influence of molar ratios on phase separation, the binodal model was applied to the obtained binodal data. The NRTL and UNIQUAC models were employed to establish correlations for the tie-lines. Moreover, we examined the extraction capabilities of the aforementioned ABSs for three commonly used drugs: diclofenac potassium, acetaminophen, and salicylic acid. To assess the efficiency of extraction, partition coefficients and extraction efficiencies were calculated for each drug. The results revealed that the extraction efficiency of these drugs into the polymer-rich top phase is dependent on their hydrophobicity. Furthermore, we employed the Diamond–Hsu equation, along with its modified version, to establish correlations between the experimental partition coefficients of the drugs and NADES overall concentrations.
1. Introduction
Aqueous biphasic systems (ABSs) are widely used in various biotechnological applications due to their ability to separate biomolecules such as enzymes and proteins.1,2 ABSs offer a cleaner and more sustainable alternative to traditional organic-water solvent extraction systems. Recently, deep eutectic solvents (DESs) have been employed to create ABSs for biomolecule extraction.3–6 DESs are a type of liquid solvent that was introduced in 2003.7 They are formed by combining and heating at least two starting chemicals, resulting in the formation of hydrogen bonds between a hydrogen-bond donor (HBD) and a hydrogen-bond acceptor (HBA). These DESs exhibit substantially lower melting points than their individual constituents. Among DESs, natural deep eutectic solvents (NADES) have gained attention as bio-based alternatives, derived from plant compounds such as organic acids, sugars, alcohols, amines, and amino acids.3,8–10 The application of DESs as phase forming components in ABSs was pioneered by Xu and colleagues.4,5,11,12 Studies on these ABSs13 have provided compelling evidence that the interactions between HBA and HBD are disrupted in the presence of water, leading to the complete breakdown of DES complexes at high water concentrations. Consequently, in DES-based ABSs, the molar ratio between HBA and HBD is disrupted in the coexisting phases, indicating that HBA and HBD function as separate phase forming components in ABSs, resulting in a quaternary mixture.13 In the context of this research, Farias et al.6 investigated the capability of natural deep eutectic solvents to form ternary-like ABSs. Their ABS system consisted of polypropylene glycol with a molar mass of 400 g mol−1 (PPG400) and the NADES, with choline chloride (ChCl) serving as the HBA and glucose or urea as the HBD.
This study revealed that the combination of various factors, such as the composition of the ABS components and the hydrophobicity/hydrophilicity of the hydrogen bond donor (HBD), enables the creation of ABS systems in which the stoichiometry of the hydrogen bond acceptor (HBA) to HBD, as used in the preparation of natural deep eutectic solvents (NADES), is preserved in the equilibrium phases. As a result, these ABSs exhibit behavior similar to ternary systems.6 Similarly, investigations have been conducted on the phase behavior of ABSs consisting of PPG400 and NADES (choline chloride: fructose) with different molar ratios.14 In our previous research on the stability of natural deep eutectic solvents in aqueous solutions using vapor–liquid equilibria (VLE), we discovered that the hydrogen bonds between the initial components of the NADES were weakened when diluted with water. Ultimately, at approximately 75 wt% water content, the hydrogen bonds completely vanished.15,16
In this work, we investigated an aqueous biphasic system consisting of PPG400 and a natural deep eutectic solvent (NADES) composed of choline chloride as the hydrogen bond acceptor (HBA) and sucrose as the hydrogen bond donor (HBD) with molar ratios of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The experiments were conducted at a temperature of 298.15 K and atmospheric pressure (approximately 85 kPa). The binodal data and tie-lines were determined for these ABSs. Equations proposed by Merchuk17 and Zafarani-Moattar et al.18 were employed to fit binodal data. The binodal theory based on effective excluded volume (EEV)19 was utilized to describe the influence of the two different molar ratios of NADES on the position of the binodal curves.
1. The experiments were conducted at a temperature of 298.15 K and atmospheric pressure (approximately 85 kPa). The binodal data and tie-lines were determined for these ABSs. Equations proposed by Merchuk17 and Zafarani-Moattar et al.18 were employed to fit binodal data. The binodal theory based on effective excluded volume (EEV)19 was utilized to describe the influence of the two different molar ratios of NADES on the position of the binodal curves.
Tie-lines were also determined for the ABSs consisting of PPG400, ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose (in 2
sucrose (in 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratios), and water. The purpose was to investigate whether the stoichiometry of the initial components of NADES is maintained in the top and bottom phases. Based on the obtained data, it was observed that these studied ABSs behave as either ternary or quaternary systems. The experimental tie-lines were fitted using two local composition models, namely NRTL20 and UNIQUAC.21,22
1 molar ratios), and water. The purpose was to investigate whether the stoichiometry of the initial components of NADES is maintained in the top and bottom phases. Based on the obtained data, it was observed that these studied ABSs behave as either ternary or quaternary systems. The experimental tie-lines were fitted using two local composition models, namely NRTL20 and UNIQUAC.21,22
In addition, our research delved into the use of these aqueous biphasic systems to separate diclofenac potassium, acetaminophen, and salicylic acid. We calculated partition coefficients (K) and their corresponding extraction efficiencies (EE%) at various tie-lines to explore how the ratio of natural deep eutectic solvents (NADES) and the characteristics of the drugs influenced their separation. To further analyze the results, we applied the Diamond–Hsu model and its modified version to fit the partition coefficient values.
2. Chemicals and methods
2.1. Chemicals
The choline chloride (>99 wt%) was provided from Daejung. Merck provided sucrose with a purity greater than 99.5 wt%, as well as PPG with a molar mass of 400 g mol−1. Diclofenac potassium, acetaminophen, and salicylic acid, each with a purity exceeding 99.5 wt%, were sourced from Danna Pharmaceutical Company in Iran. These chemicals were used without further purification. For solution preparation, double-distilled deionized water with a conductivity of 0.055 μS cm−1 was used. The Karl-Fischer technique was employed to determine the water content of the compounds, and additional information about the chemicals is detailed in Table 1.
Table 1 Descriptions of the used chemicals
| Material |
Provenance |
CAS number |
Purity (mass fraction) |
Purification method |
Water contenta (mass fraction) |
| Determined by Karl-Fischer method. |
| Choline chloride |
Daejung |
67-48-1 |
>0.99 |
Dried in vacuum over P2O5 |
0.0008 |
| PPG400 |
Fluka |
25322-69-4 |
>0.99 |
None |
0.0020 |
| Sucrose |
Merck |
57-50-1 |
>0.995 |
Dried in vacuum over P2O5 |
0.0007 |
| Diclofenac potassium |
Danna. Iran |
— |
>0.995 |
None |
0.0001 |
| Salicylic acid |
Danna. Iran |
— |
>0.995 |
None |
0.0001 |
| Acetaminophen |
Danna. Iran |
— |
>0.995 |
None |
0.0001 |
2.2. Preparation of NADES
In this research, a particular type of natural deep eutectic solvent (NADES) was prepared using choline chloride as the hydrogen bond acceptor (HBA) and sucrose as the hydrogen bond donor (HBD) in different molar ratios of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The preparation of NADES followed the procedure outlined in previous studies.23,24 Initially, choline chloride and sucrose were combined in a 50 mL round-bottom flask. The flask was then placed in a paraffin oil-bath heated by a hot plate stirrer. The mixture was stirred for 2 hours at a temperature of 353.15 K until a colorless and homogeneous liquid was obtained. The temperature of the NADES was continuously monitored using a thermometer with an accuracy of ±0.01 K. Subsequently, all samples were carefully stored in tightly sealed vials within a controlled moisture environment.
1. The preparation of NADES followed the procedure outlined in previous studies.23,24 Initially, choline chloride and sucrose were combined in a 50 mL round-bottom flask. The flask was then placed in a paraffin oil-bath heated by a hot plate stirrer. The mixture was stirred for 2 hours at a temperature of 353.15 K until a colorless and homogeneous liquid was obtained. The temperature of the NADES was continuously monitored using a thermometer with an accuracy of ±0.01 K. Subsequently, all samples were carefully stored in tightly sealed vials within a controlled moisture environment.
To assess the water content in the prepared NADES, Karl-Fischer analysis was conducted, revealing a mass fraction of water content of 0.0008.
2.3. Methods
2.3.1. Determination of phase diagrams and tie-lines. To construct the phase diagrams, the cloud point titration method was employed, following established techniques described in previous studies.25–27 The experiments were conducted at a temperature of 298 K and atmospheric pressure (85 kPa). The method involved the gradual addition of NADES aqueous solution dropwise to a PPG400 solution until the appearance of a cloudy solution, indicating the presence of a biphasic region. Subsequently, water was added dropwise until a clear and monophasic region was observed. Aqueous solutions of PPG400 at a concentration of 60 wt% and NADES at a concentration of 60 wt% were utilized to determine the binodal curves. Throughout the experiment, continuous stirring was maintained. During the preparation of the solutions, the water contents of the chemicals were considered, and measurements were conducted using a Karl Fischer coulometer (Metrohm 751 GPD). A Shimadzu analytical balance (321-34553, Shimadzu Co., Japan) with a precision of ±1 × 10−7 kg was used to determine the mass fraction of the components. The maximum uncertainty associated with determining the mass fraction of the polymer and NADES was found to be 0.002.To determine the tie-lines, a total of five solutions with different compositions were prepared for each aqueous biphasic system (ABS) comprising of {PPG400 + NADES (ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose 2
sucrose 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratios) + water}. For each tie-line, a precise gravimetric preparation of the biphasic region was carried out with an accuracy of ±10−7 kg, involving the combination of NADES, polymer, and water. These solutions were vigorously stirred for 30 minutes, followed by centrifugation and placement in a water bath at 298 K until equilibrium was reached. The compositions of the coexisting phases were then determined through analytical methods.
1 molar ratios) + water}. For each tie-line, a precise gravimetric preparation of the biphasic region was carried out with an accuracy of ±10−7 kg, involving the combination of NADES, polymer, and water. These solutions were vigorously stirred for 30 minutes, followed by centrifugation and placement in a water bath at 298 K until equilibrium was reached. The compositions of the coexisting phases were then determined through analytical methods.
The quantification of sucrose compositions was accomplished using the phenol–sulfuric acid method.28,29 In this procedure, a 2 mL aliquot of the carbohydrate solution was mixed with 1 mL of a 5% aqueous solution of phenol in a test tube. Subsequently, 5 mL of concentrated sulfuric acid was rapidly added to the mixture. The test tubes were allowed to stand for 10 minutes, followed by vortexing for 30 seconds before being placed in a water bath at room temperature for 20 minutes to develop color. The light absorption at 490 nm was then recorded using a spectrophotometer (model: SPECORD 40-Series Analytik Jena AG-Germany).
For the preparation of reference solutions, the same procedure as described above was followed, with the exception that the 2 mL aliquot of carbohydrate solution was replaced with double distilled deionized water.
To ascertain the polymer concentration in both phases, the refractive index method introduced by Cheluget et al.30 was employed. The refractive index of the solutions was measured using a refractometer (ATAGO DR-A1, Japan) with a precision of 0.0001. The uncertainty associated with the refractive index measurement was estimated to be 0.0002.
According to the refractive index method,30 for dilute aqueous solutions of each phase of an ABS, there is a relation between the refractive index of solution, nD, and the corresponding components mass fractions. The relation between nD and mass fractions of polymer, wp, choline chloride, wc and sucrose, wsu, takes the following form:
| | |
nD = n0 + apwp + acwc + asuwsu
| (1) |
here,
n0 is the refractive index of pure water for which the value 1.3325 at
T = 298.15 K was obtained. The values of constants
ap,
ac and
af corresponding to polymer, choline chloride and sucrose respectively were obtained from the linear calibration plots of the corresponding refractive index of the solutions diluted in mass fraction range (
C range (w/w)) as showed in
Table 2. These constants together with the coefficient of determination values,
R2, are reported in
Table 2. By knowing these constants, we have four unknowns in
eqn (1). The
nD of diluted solutions of each phase in the mass fraction range of
Table 2, was measured by a refractometer. The sucrose mass fraction
wsu was determined by phenol–sulfuric acid procedure outlined above. Now by inserting the measured
nD and
wsu in
eqn (1), we obtain an equation with only two unknowns
wp, and
wc. On the other hand the sum of mass fractions in each phase is equal to unity (
ww +
wp +
wc +
wsu = 1, here
ww is water mass fraction); so that, by inserting the water contents
ww value of each phase, measured by the Karl Fischer method, we will reach the second equation again with two unknowns
wp, and
wc. By solving these mentioned two equations for
wp, and
wc the mass fractions of polymer and choline chloride were determined. The uncertainty by this method was about 0.008 for each mass fraction of the ABS components.
Table 2 The parameter values of eqn (1), am, for ABS containing {ChCl (c)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose (f) +PPG400 (p) + water (w)}
sucrose (f) +PPG400 (p) + water (w)}
| Material |
Constant |
Value |
C range (w/w) |
R2a |
| Where the coefficient of determination, R2, represents the respective correlation coefficient value of the linear calibration plot of the refractive index against the mass fraction of ChCl, polymer, and sucrose within the mass fraction range (C range) of each material. |
| PPG400 |
ap |
0.1323 |
0 to 0.10 |
0.9994 |
| ChCl |
ac |
0.1452 |
0 to 0.08 |
0.9987 |
| Sucrose |
af |
0.1486 |
0 to 1.80 |
0.9968 |
2.3.2. Drugs partition coefficient and the corresponding extraction efficiency. To evaluate the effectiveness of the investigated ABSs in terms of drug partitioning and extraction efficiency, five mixture compositions (as presented in Table 5) were selected based on the previously determined phase diagrams for {NADES (ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose) + PPG400 + H2O} systems. These mixtures were designed to have similar overall compositions to those used for obtaining the tie-lines. The prepared mixtures were subjected to vigorous stirring for a duration of 30 minutes. Subsequently, they were carefully transferred to a water bath, where they were maintained at the desired temperature. Upon the observation of phase separation, 1 mL of each phase was meticulously isolated. These separated phases were then combined and further supplemented with a 0.002 mass fraction of the drugs (diclofenac potassium, salicylic acid, and acetaminophen) under investigation.
sucrose) + PPG400 + H2O} systems. These mixtures were designed to have similar overall compositions to those used for obtaining the tie-lines. The prepared mixtures were subjected to vigorous stirring for a duration of 30 minutes. Subsequently, they were carefully transferred to a water bath, where they were maintained at the desired temperature. Upon the observation of phase separation, 1 mL of each phase was meticulously isolated. These separated phases were then combined and further supplemented with a 0.002 mass fraction of the drugs (diclofenac potassium, salicylic acid, and acetaminophen) under investigation.The samples were then subjected to centrifugation at 2000 rpm for 10 minutes and kept in a water bath for 24 hours to ensure complete phase separation and reach equilibrium. After the establishment of equilibrium, the concentrations of diclofenac potassium, salicylic acid, and acetaminophen in both phases were determined using UV spectroscopy with a spectrophotometer mentioned earlier at specific wavelengths: 284 nm for diclofenac potassium, 261 nm for salicylic acid, and 303 nm for acetaminophen. In order to mitigate interference from the components present in the phases, the samples were appropriately diluted and analyzed alongside blanks containing the same phase components but without the drugs.31
The partitioning coefficient, K, and extraction efficiency, EE%, were calculated respectively by eqn (2) and (3) as below:
| |
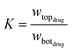 | (2) |
| |
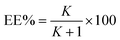 | (3) |
here,
wtopdrug and
wbotdrug are the mass fractions of drug in the top and bottom phases respectively.
3. Results and discussion
3.1. Phase diagram
The phase diagrams of studied ABS composed of PPG400, NADES (obtained at two molar ratios of ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose (2
sucrose (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1)), and water at 298.15 K are plotted in Fig. 1, and the experimental mass fraction data are also listed in Table 3.
1)), and water at 298.15 K are plotted in Fig. 1, and the experimental mass fraction data are also listed in Table 3.
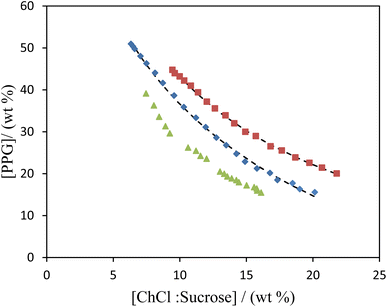 |
| | Fig. 1 Experimental binodal data of ABS composed of mixtures of ChlCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose at different molar ratio, PPG400, and water at 298.15 K: 2 sucrose at different molar ratio, PPG400, and water at 298.15 K: 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (♦); 1 1 (♦); 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (■); PPG400 + ChCl + water (▲);32 (---) line is calculated binodal data from eqn (4). 1 (■); PPG400 + ChCl + water (▲);32 (---) line is calculated binodal data from eqn (4). | |
Table 3 Experimental binodal data of mass fraction (wt%) for the systems containing {ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose (wNADES) + PPG400 (wp) + H2O} at 298.15 K and atmospheric pressure (≈85 kPa)a
sucrose (wNADES) + PPG400 (wp) + H2O} at 298.15 K and atmospheric pressure (≈85 kPa)a
wNADES molar ratio 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
wp |
wNADES molar ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
wp |
| The standard uncertainties σ for temperature, pressure, and mass fraction are: σ(T) = 0.05 K; σ(p) = 0.5 kPa; and σ(wi) = 0.005, respectively. |
| 6.33 |
50.97 |
9.44 |
44.77 |
| 6.48 |
50.36 |
9.62 |
43.98 |
| 6.61 |
49.75 |
9.99 |
43.21 |
| 7.04 |
48.04 |
10.33 |
42.21 |
| 7.49 |
46.30 |
10.83 |
40.99 |
| 8.14 |
44.04 |
11.37 |
39.40 |
| 8.72 |
41.63 |
12.03 |
37.18 |
| 9.57 |
38.63 |
12.64 |
35.57 |
| 10.30 |
35.88 |
13.43 |
33.91 |
| 11.21 |
33.33 |
14.09 |
32.01 |
| 11.94 |
31.10 |
14.92 |
29.98 |
| 12.74 |
28.61 |
15.71 |
28.98 |
| 13.48 |
26.79 |
16.82 |
26.53 |
| 14.25 |
24.74 |
17.66 |
25.53 |
| 14.90 |
22.86 |
18.68 |
23.88 |
| 15.79 |
21.23 |
19.74 |
22.59 |
| 16.77 |
20.17 |
20.68 |
21.44 |
| 17.33 |
18.49 |
21.79 |
20.05 |
| 18.47 |
17.73 |
|
|
| 19.01 |
16.32 |
|
|
| 20.14 |
15.58 |
|
|
The binodal data presented in Table 3 were fitted to the equations presented by Merchuk,17 eqn (4), and Zafarani-Moattar et al.,18 eqn (5) using a nonlinear least-square regression method.
| |
wp = a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(bwNADES0.5 − cwNADES3) exp(bwNADES0.5 − cwNADES3)
| (4) |
| |
wp = α + β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(wNADES) + γwNADES ln(wNADES) + γwNADES
| (5) |
In above equations wp and wNADES are mass fractions of polymer and NADES, respectively. The adjustable parameters of eqn (4) and (5) {(a, b, and c) and (α, β and γ)} together with the corresponding standard deviation, sd, are presented in Table 4. The obtained sd values indicate a good performance of both equations in regeneration of binodal data.
Table 4 The parameters values of eqn (4), (a, b, c), eqn (5), (α, β, γ), and eqn (6)  , for {PPG400 + ChCl (HBA) + sucrose (HBD) + H2O} systems at 298.15 K
, for {PPG400 + ChCl (HBA) + sucrose (HBD) + H2O} systems at 298.15 K
HBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD HBD |
Merchuk (eqn (4)) |
| a |
b |
c |
100 sda |
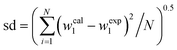 where N and w1 represented number of binodal data and mass fraction of PPG400, respectively. where N and w1 represented number of binodal data and mass fraction of PPG400, respectively. |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1.9800 |
−4.8015 |
5.3315 |
0.27 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1.7492 |
−4.8182 |
40.0377 |
0.53 |
HBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD HBD |
Zafarani-Moattar et al. (eqn (5)) |
| α |
β |
γ |
100 sd |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
−0.5674 |
−0.4034 |
0.6976 |
0.21 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
−0.4509 |
−0.3453 |
0.2146 |
0.49 |
3.1.1. The effect of molar ratio of NADES on the phase formation. The impact of the molar ratio of NADES on the biphasic region in the (PPG400 + NADES + water) system can be examined by referring to Fig. 1. The figure illustrates that the biphasic region for NADES expands as the molar ratio increases, suggesting that an elevated concentration of ChCl promotes phase separation. In order to assess the influence of ChCl on the phase separation, the binodal curve for the ternary (PPG400 + ChCl + water) system32 is also depicted in Fig. 1. It is evident that the biphasic region for the ABS comprising PPG400 and ChCl is larger when compared to the ABS involving the (PPG400 + NADES + water) system, indicating a more pronounced salting-out effect when pure ChCl is employed.A similar trend was observed in the comparison of ABSs containing NADES (ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose) and PPG400 with various molar ratios, as well as ABSs consisting of ChCl and PPG400, as reported by Farias et al.6 It has been postulated32,33 that in these types of ABSs, the formation of ABS is driven by a salting-out mechanism induced by ChCl, which exhibits salt-like behavior and possesses a higher capacity for forming hydration complexes. Consequently, ChCl acts as a potent salting-out agent.
glucose) and PPG400 with various molar ratios, as well as ABSs consisting of ChCl and PPG400, as reported by Farias et al.6 It has been postulated32,33 that in these types of ABSs, the formation of ABS is driven by a salting-out mechanism induced by ChCl, which exhibits salt-like behavior and possesses a higher capacity for forming hydration complexes. Consequently, ChCl acts as a potent salting-out agent.
In order to assess the impact of the molar ratio of NADES on the stability of the salting-out phenomenon, the binodal model developed by Guan and colleagues19 was employed. This model enabled the correlation of the experimental binodal data presented in Table 3 with eqn (6). By utilizing this correlation, the effective excluded volume (EEV), which serves as an indicator of salting-out strength, could be determined:34
| |
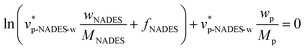 | (6) |
| |
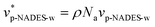 | (7) |
Here,

denotes the polymer's effective excluded volume (EEV) in an aqueous solution containing NADES. This parameter shows the spacing of the nearest polymer molecular centers.
fNADES is the volume fraction of the unfilled effective available volume after tight packing of NADES molecules into the network of the polymer molecules in the polymer aqueous solution.
νp-NADES-w is the volume of polymer species at constant solution density,
ρ, in presence of NADES.
Mp,
MNADES,
wp and
wNADES are molar masses and mass fractions of polymer and NADES, respectively.
The EEV values,  , presented in Table 4 and binodal curves depicted in Fig. 1 indicate that the larger EEV values are obtained for system with greater salting-out strength. These values are increased by increasing molar ratio of HBA
, presented in Table 4 and binodal curves depicted in Fig. 1 indicate that the larger EEV values are obtained for system with greater salting-out strength. These values are increased by increasing molar ratio of HBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD from (1
HBD from (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) to (2
1) to (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) indicating that choline chloride plays an important role as the salting-out effect.
1) indicating that choline chloride plays an important role as the salting-out effect.
3.2. Analysis of tie-lines
The tie-lines and binodal curves for the ABSs composed of PPG400 and NADES (ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose) with two molar ratios (2
sucrose) with two molar ratios (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) are presented in Fig. 2. The experimental tie-lines and their corresponding tie-line lengths (TLL) for the investigated systems are summarized in Table 5. The results demonstrate a consistent pattern, with the top phase consistently enriched in PPG400 (>79 wt%) across different molar ratios of NADES and tie-line lengths. The majority of the bottom phase composed of water (>50 wt%), as well as higher concentrations of ChCl and sucrose compared to the polymer, thus indicating a ChCl-rich phase. This behavior aligns with previous findings for ABSs containing NADES (ChCl
1) are presented in Fig. 2. The experimental tie-lines and their corresponding tie-line lengths (TLL) for the investigated systems are summarized in Table 5. The results demonstrate a consistent pattern, with the top phase consistently enriched in PPG400 (>79 wt%) across different molar ratios of NADES and tie-line lengths. The majority of the bottom phase composed of water (>50 wt%), as well as higher concentrations of ChCl and sucrose compared to the polymer, thus indicating a ChCl-rich phase. This behavior aligns with previous findings for ABSs containing NADES (ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose or urea) and PPG400 with varying molar ratios.6
glucose or urea) and PPG400 with varying molar ratios.6
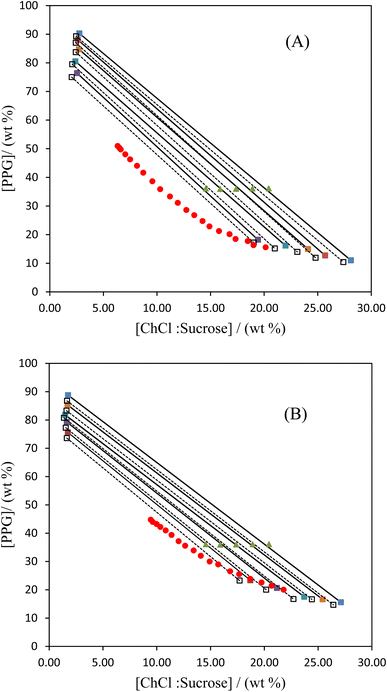 |
| | Fig. 2 Phases diagram for the ABS composed of {NADES [ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose] + PPG400 + H2O} at 298 K and different ChCl sucrose] + PPG400 + H2O} at 298 K and different ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose molar ratios: (A) 2 sucrose molar ratios: (A) 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1; (B) 1 1; (B) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1; tie-line overall composition (▲), binodal curve (●), tie-line phase composition (■).■—■, experimental tie-lines; □….□, calculated tie-lines using the NRTL model. 1; tie-line overall composition (▲), binodal curve (●), tie-line phase composition (■).■—■, experimental tie-lines; □….□, calculated tie-lines using the NRTL model. | |
Table 5 Experimental tie-line values of {ChCl (HBA) + sucrose (HBD) + PPG400 + H2O} systems at 298.15 K and atmospheric pressure (≈85 kPa)a
HBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD molar ratio HBD molar ratio |
Overall composition/wt% |
HBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD (mol HBD (mol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mol) mol) |
TLL |
[HBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD] HBD] |
[PPG] |
PPG-rich phase |
ChCl-rich phase |
| The standard uncertainty of mass percent for each component is 0.8. |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
14.56 |
36.07 |
2.491 ± 0.13 |
1.931 ± 0.09 |
63.10 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1.194 ± 017 |
0.982 ± 0.20 |
61.12 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
15.9 |
35.92 |
2.351 ± 0.10 |
2.119 ± 0.10 |
66.50 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1.231 ± 0.18 |
1.242 ± 0.19 |
65.10 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
17.38 |
35.98 |
2.799 ± 0.12 |
2.035 ± 0.08 |
66.81 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1.090 ± 0.21 |
1.157 ± 0.20 |
65.89 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
18.91 |
36.07 |
2.489 ± 0.12 |
2.091 ± 0.08 |
67.52 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1.225 ± 0.12 |
1.178 ± 0.20 |
68.51 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
20.43 |
36.1 |
2.598 ± 0.14 |
2.033 ± 0.09 |
68.21 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1.295 ± 0.12 |
1.173 ± 0.20 |
71.76 |
Fig. 2 further reveals that, among ABSs with different molar ratios, the ChCl-rich phase is more influenced by variations in the TLL compared to the PPG400-rich phase. Increasing the TLL leads to a significant reduction in the water content of the bottom phase, resulting in higher concentrations of ChCl and sucrose. However, the composition of the PPG-rich phase only undergoes slight changes in response to variations in the TLL or overall compositions. To investigate the final stoichiometry of the hydrogen bond acceptor to hydrogen bond donor (HBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD) in the coexisting phases, the ChCl
HBD) in the coexisting phases, the ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
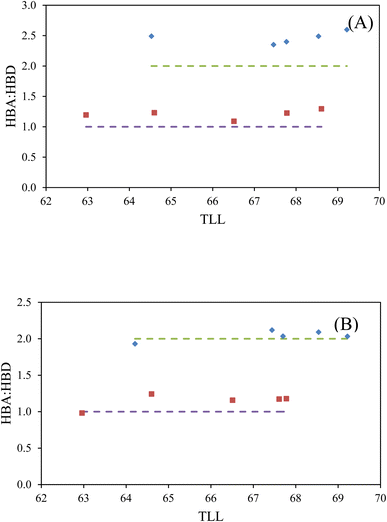
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose molar ratios were calculated for both phases of the studied tie-lines, and the results are presented in Table 6 and Fig. 3. This comparison allows us to assess the agreement between the initially selected molar ratios (2
sucrose molar ratios were calculated for both phases of the studied tie-lines, and the results are presented in Table 6 and Fig. 3. This comparison allows us to assess the agreement between the initially selected molar ratios (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and the calculated final molar ratios. The fairly good agreement observed suggests that the initial molar ratios are approximately maintained, supporting the characterization of the studied ABS as a ternary-like system. Similar behaviors have been reported for ternary-like ABSs comprising PPG400 and deep eutectic solvents (ChCl
1) and the calculated final molar ratios. The fairly good agreement observed suggests that the initial molar ratios are approximately maintained, supporting the characterization of the studied ABS as a ternary-like system. Similar behaviors have been reported for ternary-like ABSs comprising PPG400 and deep eutectic solvents (ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose or urea),6 demonstrating consistency with our findings. This behavior arises when both the HBA and HBD possess highly hydrophilic properties and exhibit poor solubility in the PPG-rich phase, which serves as a hydrophobic ABS former.6
glucose or urea),6 demonstrating consistency with our findings. This behavior arises when both the HBA and HBD possess highly hydrophilic properties and exhibit poor solubility in the PPG-rich phase, which serves as a hydrophobic ABS former.6
Table 6 The HBA (ChCl) and the HBD (sucrose) molar ratios in the ABS coexisting phases composed of mixtures of ChCl and sucrose, PPG400, and water
HBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD molar ratio HBD molar ratio |
Overall composition/wt% |
HBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD (mol HBD (mol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mol) mol) |
TLL |
[HBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD] HBD] |
[PPG] |
PPG-rich phase |
ChCl-rich phase |
| |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
14.56 |
36.07 |
2.491 ± 0.13 |
1.931 ± 0.09 |
63.10 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1.194 ± 017 |
0.982 ± 0.20 |
61.12 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
15.9 |
35.92 |
2.351 ± 0.10 |
2.119 ± 0.10 |
66.50 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1.231 ± 0.18 |
1.242 ± 0.19 |
65.10 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
17.38 |
35.98 |
2.799 ± 0.12 |
2.035 ± 0.08 |
66.81 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1.090 ± 0.21 |
1.157 ± 0.20 |
65.89 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
18.91 |
36.07 |
2.489 ± 0.12 |
2.091 ± 0.08 |
67.52 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1.225 ± 0.12 |
1.178 ± 0.20 |
68.51 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
20.43 |
36.1 |
2.598 ± 0.14 |
2.033 ± 0.09 |
68.21 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
1.295 ± 0.12 |
1.173 ± 0.20 |
71.76 |
 |
| | Fig. 3 Stoichiometry of the HBA (ChCl) and the HBD (sucrose) molar ratio in the coexisting phases of ABS composed of {NADES [ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose] + PPG400 + H2O}: 2 sucrose] + PPG400 + H2O}: 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (◆); 1 1 (◆); 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (■). (A) Molar ratio in the top phase; (B) molar ratio in the bottom phase. Dashed lines represent initial molar ratios. 1 (■). (A) Molar ratio in the top phase; (B) molar ratio in the bottom phase. Dashed lines represent initial molar ratios. | |
The findings presented in Table 6 demonstrate that the PPG-rich phase, regardless of the molar ratio (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), contains only trace amounts of NADES components. This behavior can be attributed to the highly hydrophilic nature of choline chloride and sucrose, as indicated by their log
1), contains only trace amounts of NADES components. This behavior can be attributed to the highly hydrophilic nature of choline chloride and sucrose, as indicated by their log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow values of −0.325 and −3.70, respectively.35 Due to their hydrophilicity, these components exhibit low solubility in the extremely hydrophobic polymer-rich phase, favoring their retention in the NADES-rich phase. Similar observations have been reported for ABSs consisting of PPG400 and NADES (ChCl
Kow values of −0.325 and −3.70, respectively.35 Due to their hydrophilicity, these components exhibit low solubility in the extremely hydrophobic polymer-rich phase, favoring their retention in the NADES-rich phase. Similar observations have been reported for ABSs consisting of PPG400 and NADES (ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose) with various molar ratios,6 supporting this rationale.
glucose) with various molar ratios,6 supporting this rationale.
From vapor liquid equilibrium studies on the aqueous NADESs (ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose, ChCl
sucrose, ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fructose and ChCl
fructose and ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) urea) solutions15,16 it was concluded that by diluting these NADESs the interaction between HBD and HBA is almost retained when the water content is less than 75 wt%. On the basis of data presented in Table 5, in the studied ABS the water contents of both phases are much lower than 75 wt% (i.e., about 6–19 wt% and 55–62 wt% in polymer-rich and NADES-rich phases, respectively), therefore NADESs are most likely stable in both phases and maintained their HBD
urea) solutions15,16 it was concluded that by diluting these NADESs the interaction between HBD and HBA is almost retained when the water content is less than 75 wt%. On the basis of data presented in Table 5, in the studied ABS the water contents of both phases are much lower than 75 wt% (i.e., about 6–19 wt% and 55–62 wt% in polymer-rich and NADES-rich phases, respectively), therefore NADESs are most likely stable in both phases and maintained their HBD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBA ratio making the ABS to behave as a ternary-like mixture.
HBA ratio making the ABS to behave as a ternary-like mixture.
3.2.1. Local composition models for estimating the tie-line compositions. For representing the tie-line compositions two commonly used local composition models, the Nonrandom Two-Liquid (NRTL)20 and Universal Quasi-Chemical theory (UNIQUAC)21 which usually give satisfactory results in fitting LLE data, were applied.
3.2.1.1 NRTL model. Renon and Prausnitz20 used the concept of local composition in the derivation of NRTL (Nonrandom Two-Liquid) equation. This equation is applicable to partially miscible as well as completely miscible systems. The activity coefficient in NRTL model is defined as follows:20| |
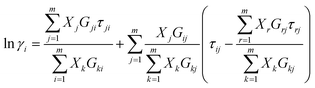 | (8) |
where Gij = exp(−αijτij), αij = αji and τii = τjj = 0.In this equation αij is a non-randomness parameter and usually set between 0.01–0.4 values. In this study, αij was fixed at 0.1. Also τij is the binary interaction parameter which is expressed by the following equation:20
| |
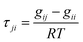 | (9) |
where
gij is an energy parameter characteristic of the
i–
j interaction. The adjustable interaction parameter, Δ
gij, for this model is defined with Δ
gij =
gij −
gii.
3.2.1.2 UNIQUAC model. UNIQUAC (the Universal Quasi-Chemical theory) for ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi consists of two parts: on the one hand, a combinatorial part, ln
γi consists of two parts: on the one hand, a combinatorial part, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γCi, which describes the entropic contribution, and on the other hand a residual part, ln
γCi, which describes the entropic contribution, and on the other hand a residual part, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γRi, which accounts for the intermolecular forces that are responsible for the enthalpy of mixing. The combinatorial part depends on the composition, the size and the shape of the molecules. The residual part depends on intermolecular forces. The UNIQUAC equation21 contains adjustable interaction parameters and is defined as:
γRi, which accounts for the intermolecular forces that are responsible for the enthalpy of mixing. The combinatorial part depends on the composition, the size and the shape of the molecules. The residual part depends on intermolecular forces. The UNIQUAC equation21 contains adjustable interaction parameters and is defined as:| |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi = ln γi = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γCi + ln γCi + ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γRi γRi
| (10) |
| |
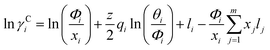 | (11) |
| |
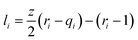 | (12) |
| |
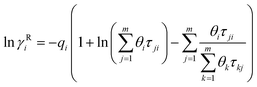 | (13) |
| |
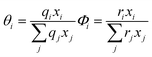 | (14) |
The variables θi, Φi, and τji are the volume fraction, area fraction, and interaction parameter between molecules i and j, respectively. The coordination number, denoted as Z, represents the count of molecules that surround the central molecule. In this context, Z is assigned a value of 10. Additionally, the parameters r and q serve as pure component molecular-structure constants, which are contingent upon the molecular size and the external surface areas. The mentioned parameters for NADES are calculated by:
Here the mole fractions of choline chloride and fructose are denoted by
x1 and
x2, respectively. The related adjustable interaction parameter to an energy parameter characteristic of the
i–
j interaction (Δ
uij) for this model is:
| |
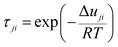 | (16) |
The interaction parameters of the NRTL and UNIQUAC models were determined by minimizing the objective function eqn (17).
| |
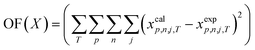 | (17) |
In eqn (17), xp,l,j,T is the mol fraction of the component j in the phase p for n tie-line at working temperature. The superscripts “cal” and “exp” refer to the calculated and experimental values, respectively. LLE data of Table 5 were correlated using eqn (17) and the equilibrium condition:
| | |
(xiγi)top = (xiγi)bot
| (18) |
The tabulated outcomes of tie-line data fitting for ABS comprising (PPG400 + NADES (with two different molar ratios of HBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD, namely 2
HBD, namely 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) + water) employing the NRTL and UNIQUAC models have been compiled in Table 7. The negligible standard deviations exhibited in Table 7 signify that both models adequately correlate the tie-line data. Furthermore, it is observed that the NRTL model demonstrates slightly superior performance in representing tie-lines compared to the UNIQUAC model.
1) + water) employing the NRTL and UNIQUAC models have been compiled in Table 7. The negligible standard deviations exhibited in Table 7 signify that both models adequately correlate the tie-line data. Furthermore, it is observed that the NRTL model demonstrates slightly superior performance in representing tie-lines compared to the UNIQUAC model.
Table 7 The parameters values of NRTL and UNIQUAC models for systems containing {NADES [ChCl (HBA)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose (HBD)] + PPG400 + H2O} at T = 298.15 K
sucrose (HBD)] + PPG400 + H2O} at T = 298.15 K
Molar ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
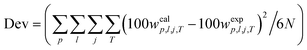 where wp,l,j,T is the mass fraction of the component j (i.e. DES, polymer or water) and N is the number of tie-line data. where wp,l,j,T is the mass fraction of the component j (i.e. DES, polymer or water) and N is the number of tie-line data. |
| NRTL |
| τNADESw |
τwNADES |
τpw |
τwp |
τNADESp |
τpNADES |
100 Deva |
| 814.8449 |
−136.9850 |
38.5273 |
−27.8779 |
−14.8109 |
−105.7515 |
0.04 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| UNIQUAC |
| ΔuNADESw |
ΔuwNADES |
Δupw |
Δuwp |
ΔuNADESp |
ΔupNADES |
100 Dev |
| −565.892 |
−801.410 |
−289.023 |
301.543 |
−1436.431 |
1632.871 |
0.41 |
Molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
| NRTL |
| τNADESw |
τwNADES |
τpw |
τwp |
τNADESp |
τpNADES |
100 Dev |
| 40.8927 |
−12.5615 |
6.3442 |
−2.5538 |
−3.0350 |
−10.2793 |
0.03 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| UNIQUAC |
| ΔuNADESw |
ΔuwNADES |
Δupw |
Δuwp |
ΔuNADESp |
ΔupNADES |
100 Dev |
| 413.301 |
−512.325 |
−211.765 |
143.572 |
−1736.245 |
−2005.231 |
0.39 |
3.3. The performance of NADES–PPG ABS in the partition behavior of drugs
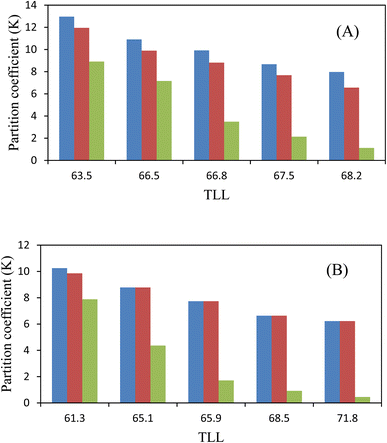
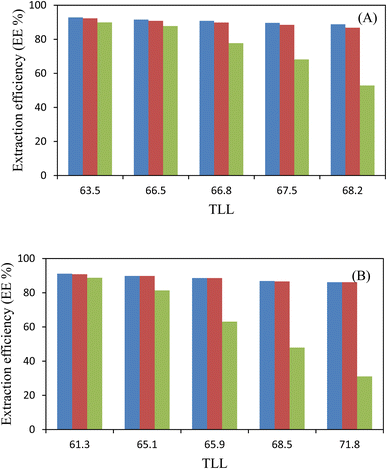
Table 8 displays the experimental partition coefficients, K, and the percentage extraction efficiencies, EE%, for the drugs under investigation, namely diclofenac potassium, salicylic acid, and acetaminophen. The variation of these coefficients concerning the Tie-Line Length (TLL) is illustrated in Fig. 4 and 5, respectively. For both molar ratios of Natural Deep Eutectic Solvents (NADES), the observed trend is consistently as follows: K (diclofenac potassium) > K (salicylic acid) > K (acetaminophen). The data in Table 8 evidently indicates that the drugs predominantly partition into the more hydrophobic phase, which is the PPG-rich phase.
Table 8 Partitioning coefficients, K, and extraction efficiency, EE%, values of studied drugs for the system composed of {NADES [ChCl (HBA)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose (HBD)] + PPG400 + H2O} at 298.15 K and atmospheric pressure (≈85 kPa)a
sucrose (HBD)] + PPG400 + H2O} at 298.15 K and atmospheric pressure (≈85 kPa)a
HBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HD molar ratio HD molar ratio |
Overall composition/wt% |
K |
EE% |
[HBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD] HBD] |
[PPG] |
| The standard uncertainties σ for partitioning coefficient, temperature and pressure are: σ(K) = 0.15, σ(T) = 0.05 K and σ(p) = 0.5 kPa respectively. |
| Diclofenac potassium |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
14.56 |
36.07 |
12.96 |
92.84 |
| 17.90 |
36.09 |
10.91 |
91.60 |
| 17.38 |
35.98 |
9.92 |
90.84 |
| 18.91 |
36.07 |
8.67 |
89.66 |
| 20.43 |
36.10 |
7.97 |
88.85 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
14.56 |
36.07 |
10.25 |
91.11 |
| 17.90 |
36.09 |
9.79 |
89.78 |
| 17.38 |
35.98 |
8.62 |
88.58 |
| 18.91 |
36.07 |
7.81 |
86.85 |
| 20.43 |
36.10 |
7.20 |
86.15 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Salicylic acid |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
14.56 |
36.07 |
11.95 |
92.28 |
| 17.90 |
36.09 |
9.89 |
90.82 |
| 17.38 |
35.98 |
8.81 |
89.81 |
| 18.91 |
36.07 |
7.68 |
88.48 |
| 20.43 |
36.10 |
6.56 |
86.77 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
14.56 |
36.07 |
9.85 |
90.78 |
| 17.90 |
36.09 |
8.78 |
89.78 |
| 17.38 |
35.98 |
7.73 |
88.55 |
| 18.91 |
36.07 |
6.63 |
86.59 |
| 20.43 |
36.10 |
6.22 |
86.15 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Acetaminophen |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
14.56 |
36.07 |
8.91 |
89.91 |
| 17.90 |
36.09 |
7.16 |
87.75 |
| 17.38 |
35.98 |
3.49 |
77.73 |
| 18.91 |
36.07 |
2.14 |
68.15 |
| 20.43 |
36.10 |
1.12 |
52.83 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
14.56 |
36.07 |
7.88 |
88.74 |
| 17.90 |
36.09 |
4.36 |
81.34 |
| 17.38 |
35.98 |
1.71 |
63.10 |
| 18.91 |
36.07 |
0.92 |
47.92 |
| 20.43 |
36.10 |
0.45 |
31.03 |
 |
| | Fig. 4 Values of partition coefficient, K, in function of the TLL for each drug in ABS composed of {NADES [ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose] + PPG400 + H2O} at two ChCl sucrose] + PPG400 + H2O} at two ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose molar ratios: (A) 2 sucrose molar ratios: (A) 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1; (B) 1 1; (B) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Diclofenac potassium 1. Diclofenac potassium  , salicylic acid , salicylic acid  , acetaminophen , acetaminophen  . . | |
 |
| | Fig. 5 Extraction efficiency, EE%, for each studied drug in ABS {NADES [ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose] + PPG400 + H2O} at different ChCl sucrose] + PPG400 + H2O} at different ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose molar ratios: (A) 2 sucrose molar ratios: (A) 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1; (B) 1 1; (B) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Diclofenac potassium 1. Diclofenac potassium  , salicylic acid , salicylic acid  , acetaminophen , acetaminophen  . . | |
3.3.1. The effect of NADES molar ratio on the drug partitioning behavior. The data presented in Table 8 at 298.15 K for each drug within the ABS system {NADES [choline chloride![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose] + PPG400 + H2O}, employing different molar ratios of hydrogen bond acceptor (HBA) to hydrogen bond donor (HBD) (2
sucrose] + PPG400 + H2O}, employing different molar ratios of hydrogen bond acceptor (HBA) to hydrogen bond donor (HBD) (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), reveals distinct values of partition coefficients (K) and extraction efficiencies (EE%). Notably, the K values exhibit the following order: choline chloride
1), reveals distinct values of partition coefficients (K) and extraction efficiencies (EE%). Notably, the K values exhibit the following order: choline chloride![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose (HBA
sucrose (HBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD molar ratio of 2
HBD molar ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) > choline chloride
1) > choline chloride![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose (HBA
sucrose (HBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD molar ratio of 1
HBD molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). This observation suggests that with an increase in choline chloride concentration, the studied drugs preferentially transfer to the PPG400 top phase. Similar results regarding drug partitioning into the top polymer-phase have been previously reported in the literature for other ABS systems, such as {NADES [choline chloride
1). This observation suggests that with an increase in choline chloride concentration, the studied drugs preferentially transfer to the PPG400 top phase. Similar results regarding drug partitioning into the top polymer-phase have been previously reported in the literature for other ABS systems, such as {NADES [choline chloride![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose] + PPG400 + H2O},6 and {NADES [choline chloride
glucose] + PPG400 + H2O},6 and {NADES [choline chloride![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose] + polyethylene glycol dimethyl ether + H2O}.36
sucrose] + polyethylene glycol dimethyl ether + H2O}.36
3.3.2. The effect of drug structure on the drug partitioning behavior. The observed trend of the partition coefficients (K) and extraction efficiencies (EE%) values for the drugs, as presented in Table 8, can be attributed to the chemical structures and polarities of the drugs. All of the drugs under investigation are characterized as non-polar, leading to favorable interactions with the hydrophobic constituents in the top phase. Consequently, drug partitioning to the choline chloride (ChCl)-rich phase occurs to a lesser extent. Notably, the presence of non-polar functional groups in the drug structures enhances their affinity for the PPG-rich top phase. The high values of EE% obtained, as compiled in Table 8, indicate that a significant portion of all studied drugs is predominantly partitioned into the polymer top phase. Furthermore, the trend observed for the K values aligns well with the hydrophobicity of the drugs, which is represented by the logarithm of the octanol/water partition coefficient (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow). A higher log
Kow). A higher log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow value indicates a higher degree of hydrophobicity for the solute, resulting in a lower tendency to associate with water molecules.25 For the drugs diclofenac potassium, salicylic acid, and acetaminophen, the log
Kow value indicates a higher degree of hydrophobicity for the solute, resulting in a lower tendency to associate with water molecules.25 For the drugs diclofenac potassium, salicylic acid, and acetaminophen, the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow values are reported as 4.50,36 2.34 (ref. 37) and 0.46,38 respectively. Thus, the order of drug extraction efficiency is as follows: diclofenac potassium > salicylic acid > acetaminophen. This study, along with a previous investigation,38 underscores the significance of drug hydrophobicity as a useful criterion in predicting drug partitioning between the two phases of an Aqueous Biphasic System (ABS).
Kow values are reported as 4.50,36 2.34 (ref. 37) and 0.46,38 respectively. Thus, the order of drug extraction efficiency is as follows: diclofenac potassium > salicylic acid > acetaminophen. This study, along with a previous investigation,38 underscores the significance of drug hydrophobicity as a useful criterion in predicting drug partitioning between the two phases of an Aqueous Biphasic System (ABS).
3.3.3. Correlations of the partition coefficients. In order to regenerate the partition coefficient data, a model is necessary. In this study, the equation suggested by Diamond–Hsu22 (eqn (19)) was used for correlation of experimental partition coefficients values of the studied drugs. We also attempted to improve the quality of the Diamond–Hsu model by adding one extra term to the right hand side of eqn (19) and refitting the K values to the modified polynomial equation (eqn (20)). Also, the relation between partition coefficient and NADES overall composition was established using a similar polynomial equation as eqn (21):| |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = AΔw(PPG400) + BΔw(PPG400)2 K = AΔw(PPG400) + BΔw(PPG400)2
| (19) |
| |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = A1 + B1Δw(PPG400) + C1Δw(PPG400)2 K = A1 + B1Δw(PPG400) + C1Δw(PPG400)2
| (20) |
| |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = A2 + B2w(NADES) + C2w(NADES)2 K = A2 + B2w(NADES) + C2w(NADES)2
| (21) |
In above relations, (A and B), (A1, B1, and C1) and (A2, B2, and C2) are respectively the adjustable parameters of eqn (19)–(21). The symbols Δw(PPG400) and w(NADES) are used for the mass fraction difference of PPG400 in the top and bottom phase and the overall composition of NADES, respectively.
For each drug the results of fitting experimental partition coefficients values to eqn (19)–(21) are reported in Table S1.† To evaluate the ability of eqn (19)–(21) in representing the partition coefficient values, the variation of experimental and calculated K values by these equations are plotted in Fig. S1 to S3,† respectively. According to the sd values in Table S1 and Fig. S1–S3,† it can be concluded that the correlation with all of the eqn (19)–(21) is satisfactory; and excellent performance is obtained with the eqn (21) in which variation of K with NADES overall concentrations is considered.
4. Conclusion
Phase diagrams of an Aqueous Biphasic System (ABS) were investigated at 298.15 K and under atmospheric pressure (approximately 85 kPa). The ABS was comprised of polypropylene glycol with a molar mass of 400 g mol−1, and Natural Deep Eutectic Solvents (NADES) derived from mixtures of choline chloride (ChCl) and sucrose at molar ratios of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, acting as the hydrogen bond acceptor (HBA) and hydrogen bond donor (HBD), respectively. Through a meticulous examination of tie-lines, it was determined that the original HBA
1, acting as the hydrogen bond acceptor (HBA) and hydrogen bond donor (HBD), respectively. Through a meticulous examination of tie-lines, it was determined that the original HBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD stoichiometry of the NADES was approximately maintained in the equilibrium phases, suggesting that the ABS exhibits ternary-like system behavior. This finding confirms the retention of hydrogen bonding interactions between the components of NADES in the ABS. Similar results were reported in previous studies, which investigated the stability of NADES in water via vapor–liquid equilibrium experiments, proposing that the hydrogen bonds between the initial components of NADES remain mostly preserved when the water content of the NADES solution is below 75 wt%. Both the NRTL and UNIQUAC local composition activity coefficient models yielded satisfactory outcomes in representing the experimental tie-lines. Additionally, the observed stronger salting-out effect of the natural deep eutectic solvent at higher molar ratios was confirmed by employing the effective excluded volume theory, which demonstrated an expansion of the biphasic region with an increase in the HBA
HBD stoichiometry of the NADES was approximately maintained in the equilibrium phases, suggesting that the ABS exhibits ternary-like system behavior. This finding confirms the retention of hydrogen bonding interactions between the components of NADES in the ABS. Similar results were reported in previous studies, which investigated the stability of NADES in water via vapor–liquid equilibrium experiments, proposing that the hydrogen bonds between the initial components of NADES remain mostly preserved when the water content of the NADES solution is below 75 wt%. Both the NRTL and UNIQUAC local composition activity coefficient models yielded satisfactory outcomes in representing the experimental tie-lines. Additionally, the observed stronger salting-out effect of the natural deep eutectic solvent at higher molar ratios was confirmed by employing the effective excluded volume theory, which demonstrated an expansion of the biphasic region with an increase in the HBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD molar ratio. Furthermore, partitioning studies of drugs within these ABSs revealed an extraction efficiency trend of diclofenac potassium > salicylic acid > acetaminophen, indicating that the drugs exhibited a preference for extraction into the polymer-rich top phase.
HBD molar ratio. Furthermore, partitioning studies of drugs within these ABSs revealed an extraction efficiency trend of diclofenac potassium > salicylic acid > acetaminophen, indicating that the drugs exhibited a preference for extraction into the polymer-rich top phase.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
We are grateful to history of Tabriz research council for the financial support of this research.
References
- P.-Å. Albertsson, Partition of proteins in liquid polymer–polymer two-phase systems, Nature, 1958, 182, 709–711 CrossRef CAS PubMed.
- R. D. Rogers and M. A. Eiteman, Aqueous Biphasic Separations, Springer, 1995 Search PubMed.
- Y. Song, R. P. Chandra, X. Zhang and J. N. Saddler, Non-productive celluase binding onto deep eutectic solvent (DES) extracted lignin from willow and corn stover with inhibitory effects on enzymatic hydrolysis of cellulose, Carbohydr. Polym., 2020, 250, 116956 CrossRef CAS PubMed.
- K. Xu, Y. Wang, Y. Huang, N. Li and Q. Wen, A green deep eutectic solvent-based aqueous two-phase system for protein extracting, Anal. Chim. Acta, 2015, 864, 9–20 CrossRef CAS PubMed.
- Q. Zeng, et al., Deep eutectic solvents as novel extraction media for protein partitioning, Analyst, 2014, 139, 2565–2573 RSC.
- F. O. Farias, H. Passos, A. l. S. Lima, M. R. Mafra and J. o. A. Coutinho, Is it possible to create ternary-like aqueous biphasic systems with deep eutectic solvents?, ACS Sustain. Chem. Eng., 2017, 5, 9402–9411 CrossRef CAS.
- A. P. Abbott, G. Capper, D. L. Davies, R. K. Rasheed and V. Tambyrajah, Novel solvent properties of choline chloride/urea mixtures, Chem. Commun., 2003, 70–71 RSC.
- Y. H. Choi, et al., Are natural deep eutectic solvents the missing link in understanding cellular metabolism and physiology?, Plant Physiol., 2011, 156, 1701–1705 CrossRef CAS PubMed.
- M. Marchel, J. Niewisiewicz, A. S. Coroadinha and I. M. Marrucho, Purification of virus-like particles using aqueous biphasic systems composed of natural deep eutectic solvents, Sep. Purif. Technol., 2020, 252, 117480 CrossRef CAS.
- V. Selvanathan, A. D. Azzahari, A. A. A. Halim and R. Yahya, Ternary natural deep eutectic solvent (NADES) infused phthaloyl starch as cost efficient quasi-solid gel polymer electrolyte, Carbohydr. Polym., 2017, 167, 210–218 CrossRef CAS PubMed.
- N. Li, et al., Development of green betaine-based deep eutectic solvent aqueous two-phase system for the extraction of protein, Talanta, 2016, 152, 23–32 CrossRef CAS PubMed.
- H. Zhang, et al., Ternary and binary deep eutectic solvents as a novel extraction medium for protein partitioning, Anal. Methods, 2016, 8, 8196–8207 RSC.
- Y. Dai, G.-J. Witkamp, R. Verpoorte and Y. H. Choi, Tailoring properties of natural deep eutectic solvents with water to facilitate their applications, Food Chem., 2015, 187, 14–19 CrossRef CAS PubMed.
- F. Ghaffari, M. T. Zafarani-Moattar and H. Shekaari, Aqueous biphasic systems created with choline chloride-fructose natural deep eutectic solvents and polypropylene glycol 400 and usage of these systems for extraction of some commonly used drugs, Fluid Phase Equilib., 2021, 113348 Search PubMed.
- M. T. Zafarani-Moattar, H. Shekaari and F. Ghaffari, Vapor–Liquid Equilibria Study of the Aqueous Systems Containing {Choline Chloride + Glucose or Urea} and Their Deep Eutectic Solvents at 298.15 K and 85 kPa, J. Chem. Eng. Data, 2019, 64, 4754–4762 CrossRef CAS.
- M. T. Zafarani-Moattar, H. Shekaari and F. Ghaffari, The study of extent of interactions between components of natural deep eutectic solvents in the presence of water through isopiestic investigations, J. Mol. Liq., 2020, 311, 113347 CrossRef CAS.
- J. C. Merchuk, B. A. Andrews and J. A. Asenjo, Aqueous two-phase systems for protein separation: studies on phase inversion, J. Chromatogr. B: Biomed. Sci. Appl., 1998, 711, 285–293 CrossRef CAS PubMed.
- M. T. Zafarani-Moattar and E. Nemati-Kande, Study of liquid–liquid and liquid–solid equilibria of the ternary aqueous system containing poly ethylene glycol dimethyl ether 2000 and tri-potassium phosphate at different temperatures: experiment and correlation, Calphad, 2010, 34, 478–486 CrossRef CAS.
- Y. Guan, T. H. Lilley and T. E. Treffry, A new excluded volume theory and its application to the coexistence curves of aqueous polymer two-phase systems, Macromolecules, 1993, 26, 3971–3979 CrossRef CAS.
- H. Renon and J. M. Prausnitz, Local compositions in thermodynamic excess functions for liquid mixtures, AIChE J., 1968, 14, 135–144 CrossRef CAS.
- D. S. Abrams and J. M. Prausnitz, Statistical thermodynamics of liquid
mixtures: a new expression for the excess Gibbs energy of partly or completely miscible systems, AIChE J., 1975, 21, 116–128 CrossRef CAS.
- A. D. Diamond and J. T. Hsu, Fundamental studies of biomolecule partitioning in aqueous two-phase systems, Biotechnol. Bioeng., 1989, 34, 1000–1014 CrossRef CAS PubMed.
- Y. Dai, J. van Spronsen, G.-J. Witkamp, R. Verpoorte and Y. H. Choi, Natural deep eutectic solvents as new potential media for green technology, Anal. Chim. Acta, 2013, 766, 61–68 CrossRef CAS PubMed.
- A. Hayyan, et al., Fruit sugar-based deep eutectic solvents and their physical properties, Thermochim. Acta, 2012, 541, 70–75 CrossRef CAS.
- H. Passos, D. J. Tavares, A. M. Ferreira, M. G. Freire and J. o. A. Coutinho, Are aqueous biphasic systems composed of deep eutectic solvents ternary or quaternary systems?, ACS Sustain. Chem. Eng., 2016, 4, 2881–2886 CrossRef CAS.
- M. T. Zafarani-Moattar, H. Shekaari and P. Jafari, Thermodynamics of acetaminophen and bovine serum albumin partitioning in ternary aqueous solutions comprising polyethylene glycol dimethyl ether 250 and choline bitartrate: Liquid-liquid equilibria, volumetric and acoustic investigations, J. Mol. Liq., 2021, 323, 115072 CrossRef CAS.
- M. T. Zafarani-Moattar, H. Shekaari and E. Pourbagherian, Study of the liquid-liquid equilibrium for aqueous ternary systems containing choline bitartrate and 1-propanol or 2-propanol at different temperatures and their performances in acetaminophen separation and alcohols recovery, Fluid Phase Equilib., 2020, 514, 112536 CrossRef CAS.
- A. A. Albalasmeh, A. A. Berhe and T. A. Ghezzehei, A new method for rapid determination of carbohydrate and total carbon concentrations using UV spectrophotometry, Carbohydr. Polym., 2013, 97, 253–261 CrossRef CAS PubMed.
- M. Dubois, K. A. Gilles, J. K. Hamilton, P. t. Rebers and F. Smith, Colorimetric method for determination of sugars and related substances, Anal. Chem., 1956, 28, 350–356 CrossRef CAS.
- E. Cheluget, S. Marx, M. Weber and J. Vera, Equilibrium in biphasic aqueous systems: a model for the excess gibbs energy and data for the system H2O− NaCl-1-propanol at 25 °C, J. Solution Chem., 1994, 23, 275–305 CrossRef CAS.
- G. M. Ferreira, G. M. Ferreira, A. O. Maldaner, L. H. M. da Silva and M. C. Hespanhol, Partitioning of cocaine and its adulterants in aqueous two-phase systems: An alternative drug identification method, Fluid Phase Equilib., 2020, 506, 112367 CrossRef CAS.
- M. V. Quental, et al., Enhanced extraction of proteins using cholinium-based ionic liquids as phase-forming components of aqueous biphasic systems, Biotechnol. J., 2015, 10, 1457–1466 CrossRef CAS PubMed.
- C. M. Neves, et al., Aqueous biphasic systems composed of ionic liquids and polypropylene glycol: insights into their liquid–liquid demixing mechanisms, Phys. Chem. Chem. Phys., 2016, 18, 20571–20582 RSC.
- J. G. Huddleston, H. D. Willauer and R. D. Rogers, Phase diagram data for several PEG+ salt aqueous biphasic systems at 25 C, J. Chem. Eng. Data, 2003, 48, 1230–1236 CrossRef CAS.
- S. Pradhan, P. Kumar and I. Mehrotra, Characterization of aqueous organics by specific ultraviolet absorbance and octanol water partition coefficient, J. Environ. Eng., 2014, 140, 06013001 CrossRef.
- P. Jafari and A. Jouyban, Partitioning behavior of caffeine, lamotrigine, clonazepam and oxcarbazepine in a biodegradable aqueous two-phase system comprising of polyethylene glycol dimethyl ether 250 and choline chloride/saccharose deep eutectic solvent, J. Mol. Liq., 2021, 323, 115055 CrossRef CAS.
- F. H. Clarke and N. M. Cahoon, Ionization constants by curve fitting: determination of partition and distribution coefficients of acids and bases and their ions, J. Pharm. Sci., 1987, 76, 611–620 CrossRef CAS PubMed.
- F. Ghaffari, M. Khorsandi, M. T. Zafarani-Moattar and H. Shekaari, Liquid–liquid equilibrium measurements and computational study of salt–polymer aqueous two phase system for extraction of analgesic drugs, Sci. Rep., 2022, 12, 13848 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article * and
Hemayat Shekaari
* and
Hemayat Shekaari
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). By analyzing the compositions of tie-lines, it was observed that these ABSs, which consist of four components, exhibit characteristics similar to ternary systems. To examine the influence of molar ratios on phase separation, the binodal model was applied to the obtained binodal data. The NRTL and UNIQUAC models were employed to establish correlations for the tie-lines. Moreover, we examined the extraction capabilities of the aforementioned ABSs for three commonly used drugs: diclofenac potassium, acetaminophen, and salicylic acid. To assess the efficiency of extraction, partition coefficients and extraction efficiencies were calculated for each drug. The results revealed that the extraction efficiency of these drugs into the polymer-rich top phase is dependent on their hydrophobicity. Furthermore, we employed the Diamond–Hsu equation, along with its modified version, to establish correlations between the experimental partition coefficients of the drugs and NADES overall concentrations.
1). By analyzing the compositions of tie-lines, it was observed that these ABSs, which consist of four components, exhibit characteristics similar to ternary systems. To examine the influence of molar ratios on phase separation, the binodal model was applied to the obtained binodal data. The NRTL and UNIQUAC models were employed to establish correlations for the tie-lines. Moreover, we examined the extraction capabilities of the aforementioned ABSs for three commonly used drugs: diclofenac potassium, acetaminophen, and salicylic acid. To assess the efficiency of extraction, partition coefficients and extraction efficiencies were calculated for each drug. The results revealed that the extraction efficiency of these drugs into the polymer-rich top phase is dependent on their hydrophobicity. Furthermore, we employed the Diamond–Hsu equation, along with its modified version, to establish correlations between the experimental partition coefficients of the drugs and NADES overall concentrations.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The experiments were conducted at a temperature of 298.15 K and atmospheric pressure (approximately 85 kPa). The binodal data and tie-lines were determined for these ABSs. Equations proposed by Merchuk17 and Zafarani-Moattar et al.18 were employed to fit binodal data. The binodal theory based on effective excluded volume (EEV)19 was utilized to describe the influence of the two different molar ratios of NADES on the position of the binodal curves.
1. The experiments were conducted at a temperature of 298.15 K and atmospheric pressure (approximately 85 kPa). The binodal data and tie-lines were determined for these ABSs. Equations proposed by Merchuk17 and Zafarani-Moattar et al.18 were employed to fit binodal data. The binodal theory based on effective excluded volume (EEV)19 was utilized to describe the influence of the two different molar ratios of NADES on the position of the binodal curves.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose (in 2
sucrose (in 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratios), and water. The purpose was to investigate whether the stoichiometry of the initial components of NADES is maintained in the top and bottom phases. Based on the obtained data, it was observed that these studied ABSs behave as either ternary or quaternary systems. The experimental tie-lines were fitted using two local composition models, namely NRTL20 and UNIQUAC.21,22
1 molar ratios), and water. The purpose was to investigate whether the stoichiometry of the initial components of NADES is maintained in the top and bottom phases. Based on the obtained data, it was observed that these studied ABSs behave as either ternary or quaternary systems. The experimental tie-lines were fitted using two local composition models, namely NRTL20 and UNIQUAC.21,22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The preparation of NADES followed the procedure outlined in previous studies.23,24 Initially, choline chloride and sucrose were combined in a 50 mL round-bottom flask. The flask was then placed in a paraffin oil-bath heated by a hot plate stirrer. The mixture was stirred for 2 hours at a temperature of 353.15 K until a colorless and homogeneous liquid was obtained. The temperature of the NADES was continuously monitored using a thermometer with an accuracy of ±0.01 K. Subsequently, all samples were carefully stored in tightly sealed vials within a controlled moisture environment.
1. The preparation of NADES followed the procedure outlined in previous studies.23,24 Initially, choline chloride and sucrose were combined in a 50 mL round-bottom flask. The flask was then placed in a paraffin oil-bath heated by a hot plate stirrer. The mixture was stirred for 2 hours at a temperature of 353.15 K until a colorless and homogeneous liquid was obtained. The temperature of the NADES was continuously monitored using a thermometer with an accuracy of ±0.01 K. Subsequently, all samples were carefully stored in tightly sealed vials within a controlled moisture environment.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose 2
sucrose 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratios) + water}. For each tie-line, a precise gravimetric preparation of the biphasic region was carried out with an accuracy of ±10−7 kg, involving the combination of NADES, polymer, and water. These solutions were vigorously stirred for 30 minutes, followed by centrifugation and placement in a water bath at 298 K until equilibrium was reached. The compositions of the coexisting phases were then determined through analytical methods.
1 molar ratios) + water}. For each tie-line, a precise gravimetric preparation of the biphasic region was carried out with an accuracy of ±10−7 kg, involving the combination of NADES, polymer, and water. These solutions were vigorously stirred for 30 minutes, followed by centrifugation and placement in a water bath at 298 K until equilibrium was reached. The compositions of the coexisting phases were then determined through analytical methods.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose (f) +PPG400 (p) + water (w)}
sucrose (f) +PPG400 (p) + water (w)}
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose) + PPG400 + H2O} systems. These mixtures were designed to have similar overall compositions to those used for obtaining the tie-lines. The prepared mixtures were subjected to vigorous stirring for a duration of 30 minutes. Subsequently, they were carefully transferred to a water bath, where they were maintained at the desired temperature. Upon the observation of phase separation, 1 mL of each phase was meticulously isolated. These separated phases were then combined and further supplemented with a 0.002 mass fraction of the drugs (diclofenac potassium, salicylic acid, and acetaminophen) under investigation.
sucrose) + PPG400 + H2O} systems. These mixtures were designed to have similar overall compositions to those used for obtaining the tie-lines. The prepared mixtures were subjected to vigorous stirring for a duration of 30 minutes. Subsequently, they were carefully transferred to a water bath, where they were maintained at the desired temperature. Upon the observation of phase separation, 1 mL of each phase was meticulously isolated. These separated phases were then combined and further supplemented with a 0.002 mass fraction of the drugs (diclofenac potassium, salicylic acid, and acetaminophen) under investigation.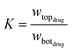
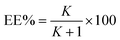
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose (2
sucrose (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1)), and water at 298.15 K are plotted in Fig. 1, and the experimental mass fraction data are also listed in Table 3.
1)), and water at 298.15 K are plotted in Fig. 1, and the experimental mass fraction data are also listed in Table 3.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose at different molar ratio, PPG400, and water at 298.15 K: 2
sucrose at different molar ratio, PPG400, and water at 298.15 K: 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (♦); 1
1 (♦); 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (■); PPG400 + ChCl + water (▲);32 (---) line is calculated binodal data from eqn (4).
1 (■); PPG400 + ChCl + water (▲);32 (---) line is calculated binodal data from eqn (4).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose (wNADES) + PPG400 (wp) + H2O} at 298.15 K and atmospheric pressure (≈85 kPa)a
sucrose (wNADES) + PPG400 (wp) + H2O} at 298.15 K and atmospheric pressure (≈85 kPa)a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(bwNADES0.5 − cwNADES3)
exp(bwNADES0.5 − cwNADES3)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(wNADES) + γwNADES
ln(wNADES) + γwNADES
 , for {PPG400 + ChCl (HBA) + sucrose (HBD) + H2O} systems at 298.15 K
, for {PPG400 + ChCl (HBA) + sucrose (HBD) + H2O} systems at 298.15 K
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD
HBD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose) and PPG400 with various molar ratios, as well as ABSs consisting of ChCl and PPG400, as reported by Farias et al.6 It has been postulated32,33 that in these types of ABSs, the formation of ABS is driven by a salting-out mechanism induced by ChCl, which exhibits salt-like behavior and possesses a higher capacity for forming hydration complexes. Consequently, ChCl acts as a potent salting-out agent.
glucose) and PPG400 with various molar ratios, as well as ABSs consisting of ChCl and PPG400, as reported by Farias et al.6 It has been postulated32,33 that in these types of ABSs, the formation of ABS is driven by a salting-out mechanism induced by ChCl, which exhibits salt-like behavior and possesses a higher capacity for forming hydration complexes. Consequently, ChCl acts as a potent salting-out agent.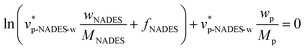
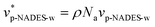
 denotes the polymer's effective excluded volume (EEV) in an aqueous solution containing NADES. This parameter shows the spacing of the nearest polymer molecular centers. fNADES is the volume fraction of the unfilled effective available volume after tight packing of NADES molecules into the network of the polymer molecules in the polymer aqueous solution. νp-NADES-w is the volume of polymer species at constant solution density, ρ, in presence of NADES. Mp, MNADES, wp and wNADES are molar masses and mass fractions of polymer and NADES, respectively.
denotes the polymer's effective excluded volume (EEV) in an aqueous solution containing NADES. This parameter shows the spacing of the nearest polymer molecular centers. fNADES is the volume fraction of the unfilled effective available volume after tight packing of NADES molecules into the network of the polymer molecules in the polymer aqueous solution. νp-NADES-w is the volume of polymer species at constant solution density, ρ, in presence of NADES. Mp, MNADES, wp and wNADES are molar masses and mass fractions of polymer and NADES, respectively.
 , presented in Table 4 and binodal curves depicted in Fig. 1 indicate that the larger EEV values are obtained for system with greater salting-out strength. These values are increased by increasing molar ratio of HBA
, presented in Table 4 and binodal curves depicted in Fig. 1 indicate that the larger EEV values are obtained for system with greater salting-out strength. These values are increased by increasing molar ratio of HBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD from (1
HBD from (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) to (2
1) to (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) indicating that choline chloride plays an important role as the salting-out effect.
1) indicating that choline chloride plays an important role as the salting-out effect.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose) with two molar ratios (2
sucrose) with two molar ratios (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) are presented in Fig. 2. The experimental tie-lines and their corresponding tie-line lengths (TLL) for the investigated systems are summarized in Table 5. The results demonstrate a consistent pattern, with the top phase consistently enriched in PPG400 (>79 wt%) across different molar ratios of NADES and tie-line lengths. The majority of the bottom phase composed of water (>50 wt%), as well as higher concentrations of ChCl and sucrose compared to the polymer, thus indicating a ChCl-rich phase. This behavior aligns with previous findings for ABSs containing NADES (ChCl
1) are presented in Fig. 2. The experimental tie-lines and their corresponding tie-line lengths (TLL) for the investigated systems are summarized in Table 5. The results demonstrate a consistent pattern, with the top phase consistently enriched in PPG400 (>79 wt%) across different molar ratios of NADES and tie-line lengths. The majority of the bottom phase composed of water (>50 wt%), as well as higher concentrations of ChCl and sucrose compared to the polymer, thus indicating a ChCl-rich phase. This behavior aligns with previous findings for ABSs containing NADES (ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose or urea) and PPG400 with varying molar ratios.6
glucose or urea) and PPG400 with varying molar ratios.6
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD molar ratio
HBD molar ratio![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD (mol
HBD (mol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mol)
mol)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD]
HBD]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD) in the coexisting phases, the ChCl
HBD) in the coexisting phases, the ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose molar ratios were calculated for both phases of the studied tie-lines, and the results are presented in Table 6 and Fig. 3. This comparison allows us to assess the agreement between the initially selected molar ratios (2
sucrose molar ratios were calculated for both phases of the studied tie-lines, and the results are presented in Table 6 and Fig. 3. This comparison allows us to assess the agreement between the initially selected molar ratios (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and the calculated final molar ratios. The fairly good agreement observed suggests that the initial molar ratios are approximately maintained, supporting the characterization of the studied ABS as a ternary-like system. Similar behaviors have been reported for ternary-like ABSs comprising PPG400 and deep eutectic solvents (ChCl
1) and the calculated final molar ratios. The fairly good agreement observed suggests that the initial molar ratios are approximately maintained, supporting the characterization of the studied ABS as a ternary-like system. Similar behaviors have been reported for ternary-like ABSs comprising PPG400 and deep eutectic solvents (ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose or urea),6 demonstrating consistency with our findings. This behavior arises when both the HBA and HBD possess highly hydrophilic properties and exhibit poor solubility in the PPG-rich phase, which serves as a hydrophobic ABS former.6
glucose or urea),6 demonstrating consistency with our findings. This behavior arises when both the HBA and HBD possess highly hydrophilic properties and exhibit poor solubility in the PPG-rich phase, which serves as a hydrophobic ABS former.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD molar ratio
HBD molar ratio![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD (mol
HBD (mol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mol)
mol)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD]
HBD]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), contains only trace amounts of NADES components. This behavior can be attributed to the highly hydrophilic nature of choline chloride and sucrose, as indicated by their log
1), contains only trace amounts of NADES components. This behavior can be attributed to the highly hydrophilic nature of choline chloride and sucrose, as indicated by their log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow values of −0.325 and −3.70, respectively.35 Due to their hydrophilicity, these components exhibit low solubility in the extremely hydrophobic polymer-rich phase, favoring their retention in the NADES-rich phase. Similar observations have been reported for ABSs consisting of PPG400 and NADES (ChCl
Kow values of −0.325 and −3.70, respectively.35 Due to their hydrophilicity, these components exhibit low solubility in the extremely hydrophobic polymer-rich phase, favoring their retention in the NADES-rich phase. Similar observations have been reported for ABSs consisting of PPG400 and NADES (ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose) with various molar ratios,6 supporting this rationale.
glucose) with various molar ratios,6 supporting this rationale.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose, ChCl
sucrose, ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) fructose and ChCl
fructose and ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) urea) solutions15,16 it was concluded that by diluting these NADESs the interaction between HBD and HBA is almost retained when the water content is less than 75 wt%. On the basis of data presented in Table 5, in the studied ABS the water contents of both phases are much lower than 75 wt% (i.e., about 6–19 wt% and 55–62 wt% in polymer-rich and NADES-rich phases, respectively), therefore NADESs are most likely stable in both phases and maintained their HBD
urea) solutions15,16 it was concluded that by diluting these NADESs the interaction between HBD and HBA is almost retained when the water content is less than 75 wt%. On the basis of data presented in Table 5, in the studied ABS the water contents of both phases are much lower than 75 wt% (i.e., about 6–19 wt% and 55–62 wt% in polymer-rich and NADES-rich phases, respectively), therefore NADESs are most likely stable in both phases and maintained their HBD![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBA ratio making the ABS to behave as a ternary-like mixture.
HBA ratio making the ABS to behave as a ternary-like mixture.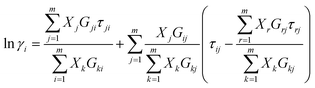
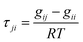
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi consists of two parts: on the one hand, a combinatorial part, ln
γi consists of two parts: on the one hand, a combinatorial part, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γCi, which describes the entropic contribution, and on the other hand a residual part, ln
γCi, which describes the entropic contribution, and on the other hand a residual part, ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γRi, which accounts for the intermolecular forces that are responsible for the enthalpy of mixing. The combinatorial part depends on the composition, the size and the shape of the molecules. The residual part depends on intermolecular forces. The UNIQUAC equation21 contains adjustable interaction parameters and is defined as:
γRi, which accounts for the intermolecular forces that are responsible for the enthalpy of mixing. The combinatorial part depends on the composition, the size and the shape of the molecules. The residual part depends on intermolecular forces. The UNIQUAC equation21 contains adjustable interaction parameters and is defined as:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γi = ln
γi = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γCi + ln
γCi + ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γRi
γRi
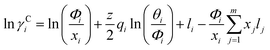
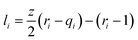
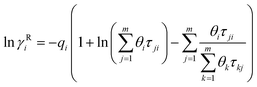
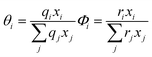
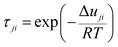
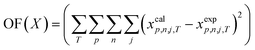
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD, namely 2
HBD, namely 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) + water) employing the NRTL and UNIQUAC models have been compiled in Table 7. The negligible standard deviations exhibited in Table 7 signify that both models adequately correlate the tie-line data. Furthermore, it is observed that the NRTL model demonstrates slightly superior performance in representing tie-lines compared to the UNIQUAC model.
1) + water) employing the NRTL and UNIQUAC models have been compiled in Table 7. The negligible standard deviations exhibited in Table 7 signify that both models adequately correlate the tie-line data. Furthermore, it is observed that the NRTL model demonstrates slightly superior performance in representing tie-lines compared to the UNIQUAC model.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose (HBD)] + PPG400 + H2O} at T = 298.15 K
sucrose (HBD)] + PPG400 + H2O} at T = 298.15 K
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1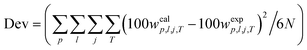 where wp,l,j,T is the mass fraction of the component j (i.e. DES, polymer or water) and N is the number of tie-line data.
where wp,l,j,T is the mass fraction of the component j (i.e. DES, polymer or water) and N is the number of tie-line data.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose (HBD)] + PPG400 + H2O} at 298.15 K and atmospheric pressure (≈85 kPa)a
sucrose (HBD)] + PPG400 + H2O} at 298.15 K and atmospheric pressure (≈85 kPa)a
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HD molar ratio
HD molar ratio![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD]
HBD]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose] + PPG400 + H2O}, employing different molar ratios of hydrogen bond acceptor (HBA) to hydrogen bond donor (HBD) (2
sucrose] + PPG400 + H2O}, employing different molar ratios of hydrogen bond acceptor (HBA) to hydrogen bond donor (HBD) (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), reveals distinct values of partition coefficients (K) and extraction efficiencies (EE%). Notably, the K values exhibit the following order: choline chloride
1), reveals distinct values of partition coefficients (K) and extraction efficiencies (EE%). Notably, the K values exhibit the following order: choline chloride![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose (HBA
sucrose (HBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD molar ratio of 2
HBD molar ratio of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) > choline chloride
1) > choline chloride![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose (HBA
sucrose (HBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD molar ratio of 1
HBD molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). This observation suggests that with an increase in choline chloride concentration, the studied drugs preferentially transfer to the PPG400 top phase. Similar results regarding drug partitioning into the top polymer-phase have been previously reported in the literature for other ABS systems, such as {NADES [choline chloride
1). This observation suggests that with an increase in choline chloride concentration, the studied drugs preferentially transfer to the PPG400 top phase. Similar results regarding drug partitioning into the top polymer-phase have been previously reported in the literature for other ABS systems, such as {NADES [choline chloride![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) glucose] + PPG400 + H2O},6 and {NADES [choline chloride
glucose] + PPG400 + H2O},6 and {NADES [choline chloride![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sucrose] + polyethylene glycol dimethyl ether + H2O}.36
sucrose] + polyethylene glycol dimethyl ether + H2O}.36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow). A higher log
Kow). A higher log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow value indicates a higher degree of hydrophobicity for the solute, resulting in a lower tendency to associate with water molecules.25 For the drugs diclofenac potassium, salicylic acid, and acetaminophen, the log
Kow value indicates a higher degree of hydrophobicity for the solute, resulting in a lower tendency to associate with water molecules.25 For the drugs diclofenac potassium, salicylic acid, and acetaminophen, the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kow values are reported as 4.50,36 2.34 (ref. 37) and 0.46,38 respectively. Thus, the order of drug extraction efficiency is as follows: diclofenac potassium > salicylic acid > acetaminophen. This study, along with a previous investigation,38 underscores the significance of drug hydrophobicity as a useful criterion in predicting drug partitioning between the two phases of an Aqueous Biphasic System (ABS).
Kow values are reported as 4.50,36 2.34 (ref. 37) and 0.46,38 respectively. Thus, the order of drug extraction efficiency is as follows: diclofenac potassium > salicylic acid > acetaminophen. This study, along with a previous investigation,38 underscores the significance of drug hydrophobicity as a useful criterion in predicting drug partitioning between the two phases of an Aqueous Biphasic System (ABS).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = AΔw(PPG400) + BΔw(PPG400)2
K = AΔw(PPG400) + BΔw(PPG400)2
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = A1 + B1Δw(PPG400) + C1Δw(PPG400)2
K = A1 + B1Δw(PPG400) + C1Δw(PPG400)2
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = A2 + B2w(NADES) + C2w(NADES)2
K = A2 + B2w(NADES) + C2w(NADES)2
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, acting as the hydrogen bond acceptor (HBA) and hydrogen bond donor (HBD), respectively. Through a meticulous examination of tie-lines, it was determined that the original HBA
1, acting as the hydrogen bond acceptor (HBA) and hydrogen bond donor (HBD), respectively. Through a meticulous examination of tie-lines, it was determined that the original HBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD stoichiometry of the NADES was approximately maintained in the equilibrium phases, suggesting that the ABS exhibits ternary-like system behavior. This finding confirms the retention of hydrogen bonding interactions between the components of NADES in the ABS. Similar results were reported in previous studies, which investigated the stability of NADES in water via vapor–liquid equilibrium experiments, proposing that the hydrogen bonds between the initial components of NADES remain mostly preserved when the water content of the NADES solution is below 75 wt%. Both the NRTL and UNIQUAC local composition activity coefficient models yielded satisfactory outcomes in representing the experimental tie-lines. Additionally, the observed stronger salting-out effect of the natural deep eutectic solvent at higher molar ratios was confirmed by employing the effective excluded volume theory, which demonstrated an expansion of the biphasic region with an increase in the HBA
HBD stoichiometry of the NADES was approximately maintained in the equilibrium phases, suggesting that the ABS exhibits ternary-like system behavior. This finding confirms the retention of hydrogen bonding interactions between the components of NADES in the ABS. Similar results were reported in previous studies, which investigated the stability of NADES in water via vapor–liquid equilibrium experiments, proposing that the hydrogen bonds between the initial components of NADES remain mostly preserved when the water content of the NADES solution is below 75 wt%. Both the NRTL and UNIQUAC local composition activity coefficient models yielded satisfactory outcomes in representing the experimental tie-lines. Additionally, the observed stronger salting-out effect of the natural deep eutectic solvent at higher molar ratios was confirmed by employing the effective excluded volume theory, which demonstrated an expansion of the biphasic region with an increase in the HBA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HBD molar ratio. Furthermore, partitioning studies of drugs within these ABSs revealed an extraction efficiency trend of diclofenac potassium > salicylic acid > acetaminophen, indicating that the drugs exhibited a preference for extraction into the polymer-rich top phase.
HBD molar ratio. Furthermore, partitioning studies of drugs within these ABSs revealed an extraction efficiency trend of diclofenac potassium > salicylic acid > acetaminophen, indicating that the drugs exhibited a preference for extraction into the polymer-rich top phase.