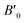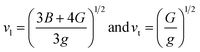Open Access Article
Open Access ArticleAb initio investigations of the structure-stability, mechanical, electronic, thermodynamic and optical properties of Ti2FeAs Heusler alloy
Anjali Kumaria,
Abhishek Kumar Mishra†
a,
Ramesh Sharma b,
Samah Al-Qaisic,
A. J. A. Moayad*d,
Ali S. Alshomranye,
N. Sfinaf,
Sajad Ahmed Darg and
Vipul Srivastava
b,
Samah Al-Qaisic,
A. J. A. Moayad*d,
Ali S. Alshomranye,
N. Sfinaf,
Sajad Ahmed Darg and
Vipul Srivastava *h
*h
aDepartment of Physics, Applied Science Cluster, University of Petroleum and Energy Studies, Bidholi via Premnagar, Dehradun, Uttrakhand 248007, India
bDepartment of Applied Science, Feroze Gandhi Institute of Engineering and Technology, Raebareli, 229001, Uttar Pradesh, India
cPalestinian Ministry of Education and Higher Education, Nablus, Palestine
dDepartment of Material Science, Malawi University of Science and Technology, Limbe, Malawi. E-mail: mailme_moya123@gmail.com
eDepartment of Physics, College of Sciences, Umm Al-Qura University, Al Taif HWY, Mecca 24381, Saudi Arabia
fCollege of Sciences and Arts in Mahayel Asir, Department of Physics, King Khalid University, Abha, Saudi Arabia
gDepartment of Physics, Govt. Motilal Vigyan Mahavidyalaya College, Bhopal, Madhya Pradesh, India
hDepartment of Physics, School of Chemical Engineering & Physical Sciences, Lovely Professional University, Delhi-Jalandhar Highway, Phagwara-144411, Punjab, India. E-mail: vipsri27@gmail.com
First published on 23rd February 2024
Abstract
In this study, we employed density functional theory coupled with the full-potential linearized augmented plane-wave method (FP-LAPW) to investigate the structural, electronic, and magnetic properties of the Ti2FeAs alloy adopting the Hg2CuTi-type structure. Our findings demonstrate that all the examined structures exhibit ferromagnetic (FM) behaviour. By conducting electronic band structure calculations, we observed an energy gap of 0.739 eV for Ti2FeAs in the spin-down state and metallic intersections at the Fermi level in the spin-up state. These results suggest the half-metallic (HM) nature of Ti2FeAs, where the Ti-d and Fe-d electronic states play a significant role near the Fermi level. Additionally, the obtained total magnetic moments are consistent with the Slater–Pauling rule (Mtot = Ztot − 18), indicating 100% spin polarization for these compounds. To explore their optical properties, we employed the dielectric function to compute various optical parameters, including absorption spectra, energy-loss spectra, refractive index, reflectivity, and conductivity. Furthermore, various thermodynamic parameters were evaluated at different temperatures and pressures. The results obtained from the elastic parameters reveal the anisotropic and ductile nature of the Ti2FeAs compound. These findings suggest that Ti2FeAs has potential applications in temperature-tolerant devices and optoelectronic devices as a UV absorber.
1. Introduction
Spintronics, a rapidly growing field in electronics, utilizes the intrinsic angular momentum or spin of electrons to process information. The discovery of giant magnetoresistance (GMR) in 1988 paved the way for significant advancements in nano-magnetism and spintronics.1–5 In this field, materials known as spintronic materials, such as ferromagnetic metals, magnetic semiconductors (with or without doping), and a special class called “half metals,” play a crucial role. Among them, half-metallic ferromagnets (HMFs) are desirable due to their unique characteristic of 100% spin polarization at the Fermi level. This means that they conduct electricity only with one spin orientation, while acting as insulators for the other, thereby exhibiting both metallic and semiconducting behaviours.6 HMFs serve as efficient spin filters, enabling high spin-polarized currents and playing a vital role in various spin-dependent phenomena such as tunnelling magnetoresistance (TMR) and spin injection into semiconductors.7–9 These materials are identified through spin-dependent band-structure computations and hold potential importance as sources and analysers of polarized electrons in spintronic devices. De Groot et al. reported the first prediction of half-metallic behaviour while studying NiMnSn using ab initio calculations.10 The other materials investigated in this field include double perovskites, Heusler alloys, rare-earth nitrides, zinc blende transition metal pnictides, and chalcogenides.11–17 Specifically, Heusler alloys show relatively high Curie temperatures, showing an advantage over other half-metallic systems.18–21 Thus, they have been explored for application as spin filters, tunnel junctions, and GMR devices.22,23 Half-Heusler alloys such as NiMnSb have attracted significant interest and full-Heusler alloys have also been extensively studied due to their diverse magnetic phenomena.24–28 The transition from a ferromagnetic phase to an antiferromagnetic phase by modifying the carrier concentration has become a prominent area of study in full-Heusler alloys.29 Full-Heusler alloys are the X2YZ type, where X and Y represent transition metals or lanthanides and Z represents an atom from the main group (III or IV) of the periodic table.30 These alloys crystallize in an L21 structure, consisting of four FCC sublattices. The full-Heusler alloys containing cobalt were first synthesized, and compounds such as Co2MnZ (Z = Si and Ge) were proposed to be half-ferromagnets.31–34 The complex nature of the full-Heusler alloys, which have two X atoms, adds to their intrigue for magneto-electronic applications due to their semiconductor-like structure and high Curie temperature.35–38For the development of high-performance spintronic devices, three crucial requirements need to be satisfied for HMFs, as follows: (1) a high Curie temperature for room-temperature applications, (2) a large bulk magneto-crystalline anisotropy energy to counteract unwanted spin switching caused by thermal fluctuations and (3) a wide half-metallic gap to effectively prevent spin-flip transitions due to thermal excitation.39 Therefore, understanding the stability and Curie temperature of HM materials is essential for their development and utilization in spintronic devices. Our present study on DFT calculations for Ti2FeAs was motivated by considering a literature review on the marvellous applications of similar Heusler alloys in the field of technology. The integration of spin-based electronics is expected to revolutionize the fields of information technology, memory technology, and telecommunications, offering numerous advantages.
This paper is organized as follows: Section 2 describes the methods and essentials of the code to calculate physical properties. Section 3 presents the potential results and discussion on the various physical properties of the Ti2FeAs compound. In Section 4, the results are concluded with the scope of this study.
2. Computational details
The calculations for determining the electronic structure were performed by the implementation of the FP-LAPW method40–42 based on density functional theory (DFT)43,44 via the WIEN2k code.45 To account for the exchange–correlation effects, the generalized gradient approximation (PBE-GGA) by Perdew, Burke, and Ernzerhof46 as well as the local spin-density approximation (LSDA) by Perdew and Wang47 was employed. Furthermore, for the accurate determination of electronic properties, the modified Becke–Johnson (mBJ) exchange potential developed by Trans and Blaha (TB)48 was utilized. The TB-mBJ(GGA) approach was employed to address the underestimation of the band gap using GGA and increase the accuracy of other related properties. The real space was partitioned into two areas using the FP-LAPW approach, as follows: (1) incorporating non-overlapping spheres escorted by a muffin-tin radius (RMT) around the atomic sites and (2) corresponding to the interstitial region. Inside the first domain, the wave functions, electron density, and potential were enlarged using spherical harmonic combinations up to lmax = 10, while in domain 2, a Fourier series or plane waves up to a cutoff radius of RMT × Kmax = 8 were employed. The chosen muffin-tin radii for Ti, Fe, and As were 2.20 a.u, 2.00 a.u, and 2.00 a.u, respectively, to ensure non-overlapping of the muffin-tin spheres. The specific values of RMT utilized in this study are provided in Table 1. The maximum vector responsible for Fourier expansion of the density (Gmax) was set to a magnitude of 14. For sampling the first Brillouin zone, a total of 1000 special k points was selected. The power-cut zone, which separated the valence and core region, was set to −6.0 Ry. Within 0.1 mRy, when the total energy stabilised, the self-consistent computations were regarded as having converged. In our calculations, the electronic configuration of Ti [Ar]: 3d2, 4s2; Fe [Ar]: 3d6, 4s2; and As [Ar]: 3d10, 4s2, 4p3 were treated as valence states.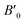 equilibrium total energy E0, cohesive energy (ECoh) and formation energy (ΔH)f for Ti2FeAs for phases in the NM and FM states using the GGA-PBE and LSDA approximation
equilibrium total energy E0, cohesive energy (ECoh) and formation energy (ΔH)f for Ti2FeAs for phases in the NM and FM states using the GGA-PBE and LSDA approximation
| Ti2FeAs | Phases | a0 (Å) | V0 (a.u3) | E0 (Ry) | ECoh (eV per atom) | (ΔH)f (eV per atom) | ΔE (Ry) = ENM − EFM | |
|---|---|---|---|---|---|---|---|---|
| PBE-GGA | FM | 6.07 | 379.04 | 6.36 | −10483.105 | 5.37 | −0.71 | 0.016049 |
| NM | 6.06 | 376.26 | 7.80 | −10483.089 | ||||
| LSDA | FM | 6.07 | 378.54 | 6.11 | −10483.103 | 66.99 | −0.64 | 17.71 |
| NM | 5.93 | 352.13 | 3.15 | −10465.391 | ||||
| Ref. 54 |
3. Results and discussion
3.1 Structure stability
As stated in the Introduction, Heusler alloys have the chemical formula of X2YZ, where X and Y represent transition elements and Z denotes a main group atom. The ordered cubic alloy X2YZ can adopt two distinct structures, i.e., the “regular” type, exemplified by Cu2MnAl with the L21 prototype structure (space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m no. 225) and the “inverse” Heusler type, such as Hg2CuTi (XA), which follows the Li2AgSb structure (space group F
m no. 225) and the “inverse” Heusler type, such as Hg2CuTi (XA), which follows the Li2AgSb structure (space group F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m no. 216). In, the present study, the structural, electronic, and magnetic properties of the Ti2FeAs (Hg2CuTi, prototype XA) structure, as shown in Fig. 1, with the space group F
3m no. 216). In, the present study, the structural, electronic, and magnetic properties of the Ti2FeAs (Hg2CuTi, prototype XA) structure, as shown in Fig. 1, with the space group F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m no. 216 were calculated. The LSDA and PBE-GGA methods were used to study the structural properties. To examine the magnetic stability of the Ti2FeAs compound, we initiated the calculation by determining the energy difference (ΔE = ENM − EFM) between the nonmagnetic (NM) and ferromagnetic (FM) configurations. In this case, we employed the Birch–Murnaghan equation of state,49 which characterizes the energy variation with respect to volume (as depicted in Fig. 2). The lattice parameter utilized in our calculations is the predicted value obtained from earlier works.50,51 The obtained equilibrium lattice constants (a0), bulk modulus (B0), pressure derivative
3m no. 216 were calculated. The LSDA and PBE-GGA methods were used to study the structural properties. To examine the magnetic stability of the Ti2FeAs compound, we initiated the calculation by determining the energy difference (ΔE = ENM − EFM) between the nonmagnetic (NM) and ferromagnetic (FM) configurations. In this case, we employed the Birch–Murnaghan equation of state,49 which characterizes the energy variation with respect to volume (as depicted in Fig. 2). The lattice parameter utilized in our calculations is the predicted value obtained from earlier works.50,51 The obtained equilibrium lattice constants (a0), bulk modulus (B0), pressure derivative 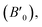 and minimum total energies (E) for both the FM and NM configurations, together with other relevant theoretical data51,52 are presented in Table 1. The results confirmed that the ferromagnetic configuration is stable for LSDA and PBE-GGA (Table 1) with the same energy. Our findings indicate an energy difference (ΔE) of 0.01604 eV between the FM and NM states, suggesting the increased stability of the FM configuration of Ti2FeAs. It is worth noting that available literature does not contain any confirmed theoretical or experimental information about the structural characteristics of Ti2FeAs, thus making our results a prediction for this compound.
and minimum total energies (E) for both the FM and NM configurations, together with other relevant theoretical data51,52 are presented in Table 1. The results confirmed that the ferromagnetic configuration is stable for LSDA and PBE-GGA (Table 1) with the same energy. Our findings indicate an energy difference (ΔE) of 0.01604 eV between the FM and NM states, suggesting the increased stability of the FM configuration of Ti2FeAs. It is worth noting that available literature does not contain any confirmed theoretical or experimental information about the structural characteristics of Ti2FeAs, thus making our results a prediction for this compound.
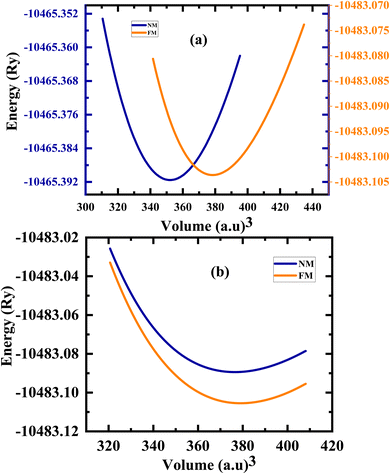 | ||
| Fig. 2 Curve between energy (Ry) and volume of (a) LDA and (b) PBE-GGA for non-magnetic and ferromagnetic properties. | ||
The assessment of stability can be approached from various perspectives, including physical, chemical, and mechanical aspects. One method to evaluate physical stability is through the calculation of cohesive energy, which quantifies the binding force between the atoms in a solid. The cohesive energy can be computed using the following relation:53
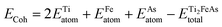 | (1) |
In addition, the formation energy, which determines the chemical stability of a compound, is calculated as follows:54
| (ΔH)f = ETi2FeAs − 2ETi − EFe − EAs | (2) |
3.2 Mechanical properties
The elastic properties were calculated using the IRelast55 method developed by J. Morteza as implemented in WIEN2k. Moreover, the mechanical stability was determined by calculating the elastic constants, which are only three for a cubic crystal, i.e., C11, C12, and C44, and the mechanical stability of the material cannot be ensured unless56
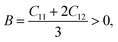 | (3) |
| C11 − C12 > 0, | (4) |
| C44 > 0, | (5) |
The elastic properties provide insightful information about the bonding nature between adjacent atomic planes. The elastic constants are utilized to evaluate the mechanical stability of the deformation of a crystal, given that they represent the coefficients that relate applied stress to strain. These constants describe the response, strength, and mechanical stability of a material under compression. In the case of a cubic crystal, mechanical stability is achieved when specific conditions are satisfied for the elastic constants (C11, C12 and C44). These conditions include C11 + 2C12 > 0, C11 > 0, C44 > 0, C11 − C12 > 0, and C12 < B < C11.56
Table 2 presents the computed elastic constants Cij (i,j = 1,2), different elastic moduli, Poisson ratio, Vickers hardness, Pugh ratio, Frantsevich ratio, anisotropy factor, Cauchy pressure, different velocities, Debye temperature and melting temperature of Ti2FeAs. It can be concluded from Table 2 that the studied compound is mechanically stable given that all the elastic constants are positive and fulfil the stability conditions for the crystal lattice. C11 and C12 describe the response of the crystal to unidirectional compression, while C44 is proportional to the shear modulus and indicates shear deformation. The value of C11 is 88% higher than that of C44, indicating greater resistance to compression compared to shear deformation. Table 2 demonstrates that the calculated bulk modulus at zero pressure, which was derived from the elastic constants, is 1.3% higher than that obtained through total energy optimization. Our findings highlight the significance of the C11 constant over the other constants, emphasizing its importance in resisting length changes in this compound.
| Material property | Calculated value |
|---|---|
| Elastic constant C11 (GPa) | 126.54 |
| Elastic constant C12 (GPa) | 69.04 |
| Elastic constant C44 (GPa) | 15.08 |
| Bulk modulus, B (GPa) | 88.21 (ref. 55) |
| Shear modulus, G (GPa) | 20.55 |
| Young's modulus, E (GPa) | 57.21 |
| Poisson ratio, σ (GPa) | 0.39 |
| Vickers hardness | 1.49 |
| Pugh ratio, B/G | 4.29 |
| Frantsevich ratio, G/B | 0.23 |
| Shear anisotropy factor, A (GPa) | 0.52 |
| Cauchy pressure CP (GPa) | 53.96 |
| Transverse sound velocity (m s−1) | 1738 |
| Longitudinal sound velocity (m s−1) | 4200 |
| Average sound velocity (m s−1) | 1967 |
| Temperature θD (K) | 192 |
| Melting temperature Tmelt (K) | 1762.3 |
The Hill approximation can be used to derive modulus B, shear modulus G, Young's modulus E, and Poisson ratio σ from the elastic constants. This approximation is based on the principles of the Reuss and Voigt approaches.57,58
With B = BH = BV = BR and 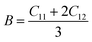 (Hill's bulk modulus) and
(Hill's bulk modulus) and
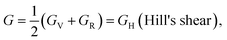 | (6) |
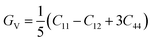 | (7) |
Reuss's shear modulus
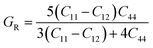 | (8) |
The calculated results are presented in Table 2. The value of E and σ are determined by the following relation:
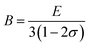 | (9) |
This relation determines the resistance of a material to volume changes upon the application of pressure with the help of the bulk modulus.59
In cubic materials, second-order elastic constants are used to estimate the shear modulus (G), which quantifies the resistance of a material to plastic deformation. Alternatively, E is an essential parameter that represents the ratio of tensile stress to tensile strain. It provides a measure of the stiffness of a solid, where a higher Young's modulus indicates greater stiffness. Based on the values presented in Table 2, it can be inferred that the Ti2FeAs compound exhibits high rigidity due to its elevated Young's modulus. According to Frantsevich et al.,61 metals having σ above 1.75 are considered ductile, while those with σ below 1.75 are deemed brittle. Therefore, the Ti2FeAs compound can be classified as ductile. However, due to the lack of available data for comparison, a direct assessment of our elastic constants, bulk modulus, and shear modulus results was not possible.
The computed elastic constants were also utilized to calculate the anisotropy parameter (A) using the following equation:
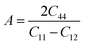 | (10) |
This parameter provides crucial information about the stability of a structure and is closely associated with the potential development of micro-cracks in materials. Our results indicate significant anisotropy in the elastic properties of the compound. A value of A of less than 1 suggests that the rigidity of the material is along the cube axis, while a value greater than 1 indicates greater rigidity along the diagonals of the body. According to our findings, the calculated value of A is 0.52, indicating that the material is most rigid along the cube axis of the considered structure.
According to Pugh's criterion,60 the B/G ratio (bulk modulus to shear modulus ratio) defines the brittleness and ductility of a material. The material is regarded as brittle if its B/G value is less than 1.75, whereas ductile if the B/G value is more than or equal to 1.75. In the case of the considered present material i.e., Ti2FeAs, its value was calculated to be 4.29. This value serves as an indicator of the ductility of the material, and considering that it is larger than 1.75, it confirms its ductile nature. Further, Poisson's ratio (σ) can also be defined as the ratio of transverse contraction to longitudinal extension in the direction of elastic stress. For most metals, the lower limit of σ is approximately 0.25.
The Debye temperature was determined from the average sound velocity, as indicated in eqn (11).
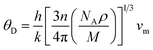 | (11) |
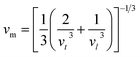 | (12) |
The Debye temperature (θD), along with the compressional and shear wave velocities, was calculated and presented in Table 2. The Debye temperature is a crucial parameter that is strongly correlated with the melting point and specific heats of solids. Notably, our study provides the first reported value of θD for Ti2FeAs. A high Debye temperature indicates a rigid crystal structure and is associated with an elevated melting point. Given that the Debye temperature represents the energy required to activate all phonon modes in a crystal, the θD value implies greater energy needed to excite phonons, making this material well-suited for thermoelectric power generation. Moreover, a Debye temperature of 300 K or higher indicates high thermal conductivity in the crystal.38 Given that the compound under investigation exhibits a Debye temperature of 192.8 K, we can conclude that it possesses high thermal conductivity.
The following empirical relation was used to compute the melting point of the compounds:31
| Tmelt = 607 + 9.3 × B ± 555 | (13) |
According to this equation, the higher melting temperature of Ti2FeAs can be attributed to its higher bulk modulus. These findings are consistent with the methodology employed in previous ref. 17 for calculating mechanical properties. The computed formation energies and mechanical properties for Ti2FeAs are in agreement with that of other theoretically predicted Heusler alloys, as reported in ref. 52.
3.3 Electronic properties
The electron spin polarisation (SP) of a substance at EF is defined as follows:
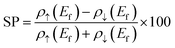 | (14) |
To explain the electronic structure of the considered alloy, we employed the optimized lattice constant within the lowest energy structures. Using three different approximations, i.e., LSDA, PBE-GGA, and TB-mBJ, the spin-polarized band structures along the high-symmetry direction (W–L–G–X–W–K) in the first Brillouin zone are plotted in Fig. 3(a)–(c), respectively. Fig. 3 displays the electronic band structures for both spins and confirms the half-metallic nature of the material. It can be observed from Fig. 3(a) that according to the LSDA and GGA-PBE approximations, the conduction and valence bands overlap at the Fermi level in both spins, indicating the metallic behaviour of Ti2FeAs. However, given that LSDA and PBE-GGA often underestimate the band structure, we employed the improved TB-mBJ functional to reveal the presence of a gap in the spin-down channels of the Ti2FeAs alloy. It was confirmed that LSDA and PBE-GGA do not show 100% spin polarization at EF; however, when treated with mBJ, it showed 100% spin polarization. According to Fig. 3, it is evident that Ti2FeAs retains its half-metallic (HM) character with an increased value of band gap in the minority spin state, which is approximately 1.005 eV, and a half-metallic band gap of 0.739 eV. A similar trend was observed for the TB-mBJ approximation, where the spin-up states exhibit conducting behaviour, while the spin-down states behave as a semiconductor. As a result of the majority spin states anchoring the Fermi level, the band structure of Ti2FeAs demonstrates metallic characteristics. Conversely, in the minority spin state, the Fermi level resides within a band gap. Based on our findings, we can conclude that Ti2FeAs is a highly robust half-metallic ferromagnetic alloy, featuring an HM gap of 0.739 eV. This value is notably larger than the HM gaps reported in the literature for other Ti-based half-Heusler alloys, such as Ti2FeSi, Ti2VAl, Ti2VGa, Ti2VIn, Ti2FeGe and Ti2FeSn, which exhibit HM gaps of 0.45 eV, 0.52 eV, 0.51 eV, 0.59 eV, and 0.60, respectively.50–52 Briefly, the band structures of Ti2FeAs exhibit semiconducting character, with 100% spin polarization at the Fermi level, indicating the full half-metallic nature of the Ti2FeAs alloy.
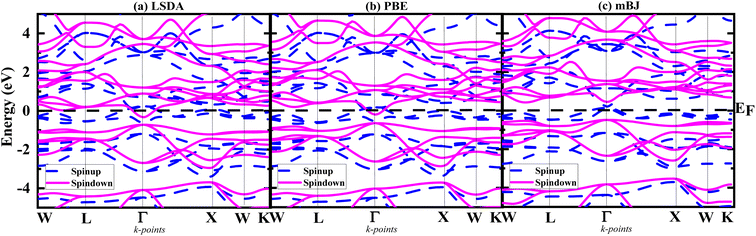 | ||
| Fig. 3 Band structures of majority spin up and minority spin down of Ti2FeAsfor (a) LSDA, (b) PBE and (c) mBJ approximation. | ||
3.4 Density of states
In general, the utilization of DOS spectral curves is valuable for providing a detailed description and explanation of the electronic structure of a material. Fig. 4(a) and (b) display the calculated spin-polarized total density of states (DOS) for the Ti2FeAs alloy at its equilibrium state by LDA, PBE-GGA and mBJ-GGA. It can be clearly observed in Fig. 4(a) and (b) that the system is not an HMF given that its EF is not located in the gap of the minority spin with both LSDA and PBE-GGA approximations but becomes an HMF system when treated with the mBJ-GGA method.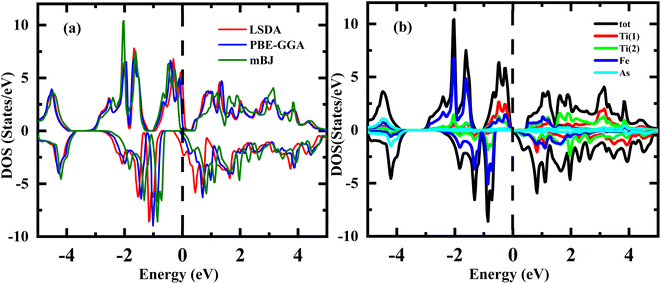 | ||
| Fig. 4 Spin-polarized (a and b) total densities of states of majority spin (up) and minority spin (dn) for Ti2FeAs alloy, respectively. | ||
Several findings can be concluded from the partial density of states (PDOS) analysis of the Ti2FeAs alloy, as shown in Fig. 5. The energy bands in the Ti2FeAs alloy, for both the majority and minority spin states, can be divided into three distinct regions. The energy bands in the vicinity of the Fermi level, spanning approximately −5 to 5 eV, are primarily associated with the d states (t2g) at the Ti(1), Ti(2), and Fe atoms. Additionally, the energy bands within the range of −4 to 4 eV predominantly originate from the s and p states of the As atoms. The half-metallic (HM) nature of the Ti2FeAs alloy is confirmed by the existence of a majority state at the Fermi level and a band gap in the minority state. It is worth noting that the band gap in the HM region is due to the strong hybridization between the Ti(1)/Ti(2) atoms and the Fe atom.
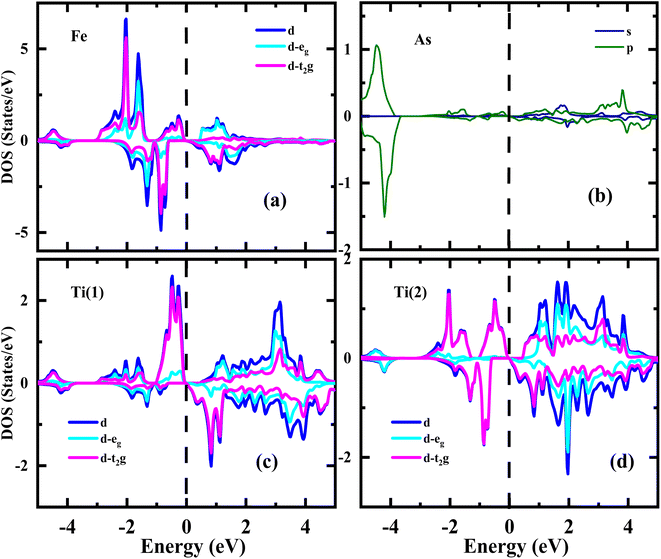 | ||
| Fig. 5 Spin-polarized partial densities of states of majority spin (up) and minority spin (dn) for Ti2FeAs alloy for Fe (a), As (b), Ti(1) (c) and Ti(2) (d). | ||
To examine the characteristics of chemical bonding in the Heusler alloys,62 we conducted an analysis of the charge density distribution and ELF along the (110) plane of the Ti2FeAs compound, as illustrated in Fig. 6. This plot reveals that there is a significant distribution of charge located between the TiAs atoms and between the FeAs atoms.
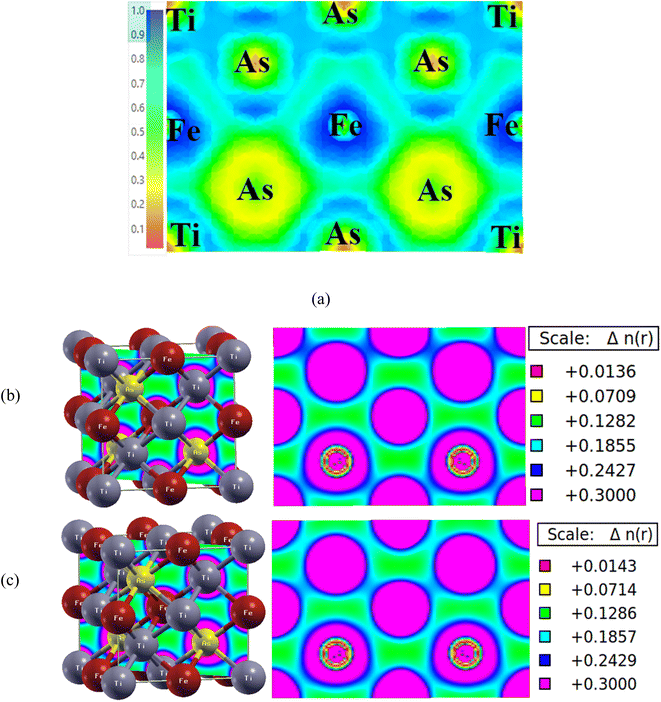 | ||
| Fig. 6 (a) Electron localization function (ELF) along the 110 plane and plot of charge density distribution along the (110) plane of Ti2FeAs compound for (b) spin up and (c) spin down, respectively. | ||
The calculated atomic magnetic moments for the LSDA, PBE-GGA and mBJ are presented in Table 3. The total magnetic moment (Mtot) of these alloys remains constant at 3.0 μB per formula unit in both the GGA and mBJ approximations. This consistency is in agreement with the Slater–Pauling equation63 (SP), where Mtot = Ztot − 18, indicating that Mtot represents the total magnetic moment and Ztot represents the total number of valence electrons. In the case of Ti2FeAs, N is equal to 21. The calculated magnetic moment for Ti2FeAs yields an integer value of 3 μB, corresponding to the Hg2CuTi-type structure. This result is consistent with the predictions from the Slater–Pauling rule, indicating the potential for half-metallicity in the present case.
| Ti2FeAs | Magnetic moments | ||
|---|---|---|---|
| XC | LSDA | PBE | mBJ |
| Mint (μB) | 0.42059 | 0.47275 | 0.38518 |
| MTi (μB) | 1.05515 | 1.27260 | 1.29355 |
| MTi (μB) | 0.32871 | 0.38989 | 0.30102 |
| MFe (μB) | 0.66295 | 0.79218 | 1.01465 |
| MAs (μB) | 0.02388 | 0.02199 | 0.00579 |
| Mtot (μB) | 2.49127 | 2.94942 | 3.00020 |
The magnetic moment of Ti2FeAs is zero due to the interplay between the 3d electrons of iron and the 3d electrons of titanium, which align in opposite directions and cancel the overall moment. The Mtot in the Ti2FeAs alloy is comprised of contributions from four entities: Ti(1), Ti(2), Fe, and As atoms. Analysis of the interstitial region reveals that in principle, the participation originates from the Mtot of the Ti(1) atoms. The Ti(1) and Ti(2) atoms exhibit positive magnetic moments, while the Fe atom shows a negative magnetic moment. The As atoms contribute minimally to the overall magnetic moment, with very small values.64
The Curie temperature will be discussed in the next section because it is crucial in real-world use. In comparison to the state with spin polarisation, the calculations for the paramagnetic state without spin polarisation demonstrate a superior total energy value. The Curie temperature can be described using the nearest neighbour Heisenberg model within the conventional statistical approach. In this context, the simplest mean-field approximation (MFA) is employed. According to the MFA, the Curie temperature is the temperature at which the average magnetic moment of a three-dimensional Heisenberg ferromagnet cancels out. Consequently, the energy difference between the ferromagnetic ground state and the nonmagnetic state directly provides an estimate of the TMFA C value. Subsequently, this relation was employed to determine the transition temperature of the standard three-dimensional Heisenberg ferromagnet within the mean-field approximation,65 as follows:
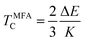 | (15) |
3.5 Thermodynamic properties
The thermodynamic properties of Ti2FeAs were determined using the quasi-harmonic Debye model, which utilizes the non-equilibrium Gibbs function G*(V;P,T).68| G*(V;P,T) = E(V) + PV + Avib[V,T] | (16) |
The thermal characteristics were computed in the temperature range of 0 to 1200 K. Also, the effect of pressure was calculated in the range of 0 to 180 GPa.
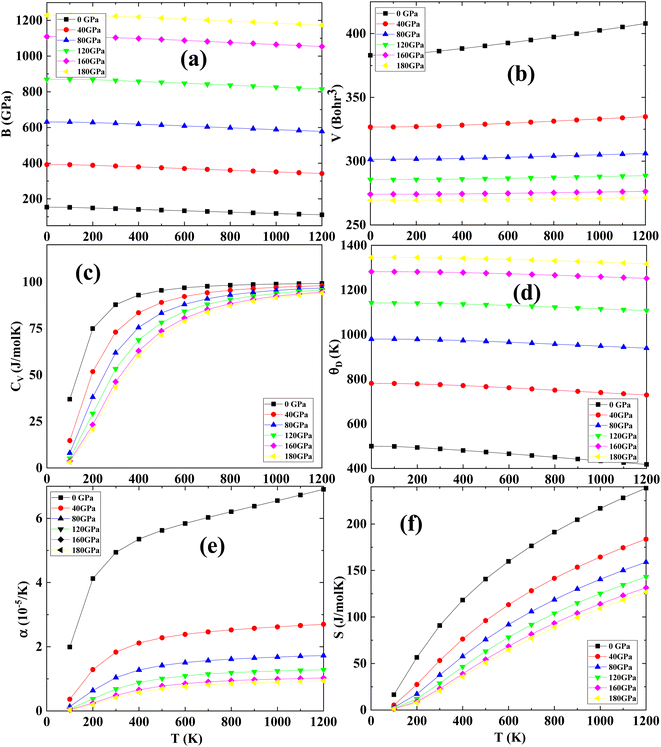
Fig. 7(a) depicts the correlation between the bulk modulus and pressure, showing linearity in the temperature range of 0 to 1200 K. At a given temperature, the bulk modulus of the Ti2FeAs alloy increases with pressure, whereas it decreases with temperature at a given pressure, exhibiting similar behaviour. The bulk modulus represents a measure of the resistance of the compound to volume change when subjected to compression.
In the temperature range of 0 to 100 K, the bulk modulus (B) remains nearly constant. However, for temperatures above 100 K, at a constant pressure, B declines linearly as the temperature increases. Additionally, at a specific temperature, the compressibility grows significantly with pressure, suggesting that the Ti2FeAs structure becomes more malleable as it enters a new bonding arrangement. At the earliest state of zero temperature and pressure, the estimated bulk modulus is 157.50 GPa, which is reasonably consistent with the value of 153.641 GPa obtained from structural characteristic. Furthermore, at 300 K and zero pressure, the measured bulk modulus is 88.21 GPa. These observations indicate that the studied material exhibits significant compressibility and strong hardness.
Fig. 7(b) illustrates the variation in the unit cell volume with temperature at a fixed pressure in the range of 0 to 180 GPa. It is evident that at a given temperature, the volume decreases as the pressure increases. Conversely, at a given pressure, the volume shows a very slow increase with temperature. Analysis of the data in Fig. 7(b) reveals that the determined volume for Ti2FeAs at zero pressure and zero temperature is 346.17 bohr3, which agrees well with the data obtained from the structural properties (344.795 bohr3).
The specific heat capacity (Cv) is a crucial parameter that provides valuable insights into the motion of molecules, lattice vibration, and phase transitions in crystals. Fig. 7(c) illustrates the relationship between Cv and temperature at various pressure values for the Ti2FeAs compound. It can be observed that Cv exhibits a rapid increase with temperature, following the Debye law (Cv ∝ T3).71 As the temperature reaches 600 K, the rate of increase in Cv is slow, eventually approaching a value of 75 J mol−1 K−1. This value corresponds to the Dulong–Petit classical limit, which is a common phenomenon observed in all solids.72
In the quasi-harmonic method, the Debye temperature (θD) serves as a fundamental parameter, which provides valuable insights into various physical characteristics of solids, including elastic constants, specific heat, and melting temperature. Within the quasi-harmonic Debye model, the highest parameter concerning crystal vibration is θD. Fig. 7(d) illustrates the relationship between pressure and θD at a constant temperature. It can be observed that increasing the pressure from 0 to 180 GPa leads to an augmentation in θD, while it decreases linearly with temperature. At room temperature and 0 GPa, θD was estimated to be approximately 201.65 K.73
Additionally, the thermal expansion coefficient (α), which characterizes the propensity of a material to change size with a variation in temperature, was calculated. Fig. 7(e) displays the variation in the thermal expansion coefficient (α) as a function of temperature at a pressure in the range of 0 to 180 GPa, where α exhibits a linear increase with temperature up to 400 K, particularly at 0 GPa. However, at high temperatures (T > 400 K), the rate of increase slows down, eventually converging to a constant value.74 Fig. 7(e) demonstrates that pressure has the opposite effect on the coefficient of thermal expansion; as pressure increases, the thermal expansion decreases. At a temperature of 400 K and pressure of 0 GPa, the coefficient of thermal expansion (α) was measured to be 2.56 × 10−5 K−1. On average, the values of the thermal expansion coefficient at 0 GPa range from about 22.6 × 10−5 K−1 at ambient temperature to approximately 54 × 10−5 K−1 at 1200 K.75 This behaviour can be attributed to the influence of the harmonic term in the cohesive energy, which governs the small displacements of the atom around its equilibrium position.
The entropy (S) is a significant thermodynamic property that is subjected to investigation. It provides crucial insights into the vibrational properties of a material and describes the precise physical state of a system. Entropy plays a vital role in the functioning of various devices, including refrigerators, heat pumps, and heat engines. Fig. 7(f) presents the variation in entropy (S) as a function of temperature at different pressures for Ti2FeAs. Observing the curves, it can be noted that they originate from an entropy value of zero at 0 K and 0 GPa. Subsequently, as the temperature increases, the entropy rises exponentially. Under the conditions of 300 K and 0 GPa, the entropy reaches a value of 80.38 J mol−1 K−1. Additionally, for temperatures exceeding 700 K, the entropy becomes significantly high. This indicates that elevated temperatures contribute to an increase in the vibrational entropy of the material, while simultaneously decreasing its cohesive energy.76
3.6 Optical properties
The development of optical technology and its applications depends on exact and reliable measurements of the optical characteristics of materials. These measurements include dielectric functions, index of refraction, optical conduction, absorbance, reflectance, transmittance, and emittance. The electronic band structure of a material mostly affects its optical characteristics. Consequently, optical investigations are frequently employed to determine the electronic band structure of solids in a quantitative manner. In this regard, the optical performance of Ti2FeAs was examined using the WIEN2k code.Firstly, the dielectric function ε(ω) provides valuable insights into the optical properties of a material, given that it quantifies the linear response of the system to an external electromagnetic field, as described by the following equation:77
| ε(ω) = ε1(ω) + iε2(ω). | (17) |
The formula for the imaginary part ε2(ω) is
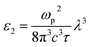 | (18) |
Moreover, the Kramers–Kronig transformation (KKT) gives the value of the real part of ε(ω) i.e. ε1(ω)
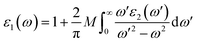 | (19) |
We also calculated the refractive index n(ω) acquired in connection with the complex dielectric function as follows:78
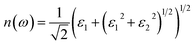 | (20) |
The reflectivity R(ω) of Ti2FeAs is obtained directly from ε1(ω) and ε2(ω).
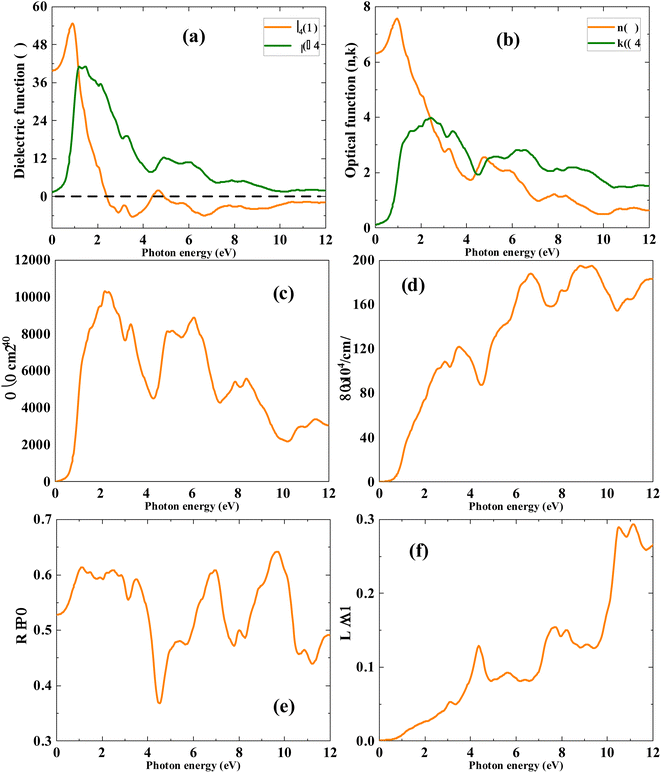
Fig. 8(a) illustrates the real and imaginary components of the total dielectric function for Ti2FeAs. The presence of peaks in these components can be attributed to the transitions occurring in the spin-down channel, as deduced from the analysis of the band structure and density of states (DOS). Notably, the calculated values of the real component ε1(ω) at (0 eV) exhibit striking similarity. Furthermore, the significant magnitude of the imaginary component of the dielectric function, ε2(ω), serves as evidence for the metallic nature of the compounds.
The refractive index of a material plays a crucial role in photoelectric applications. Fig. 8(b) depicts the refractive index of Ti2FeAs, showing peaks in the lower energy region, which gradually approach zero in the visible domain. These peaks originate from interband transitions between the valence and the conduction band. The presence of peaks in the infrared region indicates nonlinear behaviour in the refractive index. Additionally, a few smaller peaks are observed at higher energies due to this nonlinearity. The optical conductivity depicted in Fig. 8(c) characterizes the metallic behaviour of the material, emphasizing its ability to conduct light.
Fig. 8(d) displays the absorption coefficients, indicating the presence of peaks in the high energy region. Further, according to this figure, the absorption of photons occurs in the range of 3–4 eV and mostly in the higher energy side of 6–9 eV (UV-region).
Fig. 8(e) presents the reflectivity, showing the maximum reflectivity in the lower energy region. The reflectivity remains relatively constant in the intermediate energy range, but a peak is also observed at higher energies. Furthermore, the real part of the dielectric function (ε1(ω)) becomes negative for energetic photons, resulting in reflectivity peaks. This observation further confirms the metallic nature of the compound, given that it exhibits an energy range where it becomes highly reflective to incident photons.
4. Conclusion
The structural, mechanical, electronic, optical, thermodynamic and magnetic properties of the Ti2FeAs alloy of the Hg2CuTi-type structure were investigated using DFT calculations. We carried out our analysis within the modified Becke and Johnson potential (mBJ) exchange–correlation potential, the generalised gradient approximation (GGA), and LDA using the first-principles plane-wave (FP-LAPW) technique. Additionally, the mechanical stability of the Ti2FeAs alloy was determined by its high melting temperatures. Our calculations demonstrated that Ti2FeAs exhibits characteristics of a half-metallic (HMF) ferromagnet with a spin-gap value of 0.739 eV, as evidenced by the electronic band structure calculations. At the equilibrium volume for mBJ approximations, the compound possesses a magnetic moment of 3.0 μB per formula unit. The analysis of the real and imaginary parts of the dielectric function, reflectivity, and optical conductivity revealed that the compound displays optical metallic behavior, as reflected in the imaginary part of the dielectric function (ε2). The alloy exhibits optical activity at both lower and higher energies, indicating its highly nonlinear nature. The magnetic moments are reasonably consistent with the Slater–Pauling rule, confirming 100% spin polarization at the Fermi level, which is crucial for spintronic applications. The structural optimization further established the stability of the compound and satisfies the requirement of a relatively high Curie temperature. The heat capacity, thermal expansion, Debye temperature, and entropy factors were all calculated. Furthermore, neither experimental nor theoretical data are available for this compound; however, it is anticipated that these data will validate the present numerical data. Therefore, the full-Heusler metal Ti2FeAs would be significant in the applications of spintronics, design cues and UV-absorber.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University (Abha, Saudi Arabia) for funding this work through Research Groups Program under grant number (RGP.2/60/44).References
- M. N. Baibich, J. M. Broto, A. Fert, F. N. V. Dau, F. Petroff, P. Etienne, G. Creuzet, A. Friederich and J. Chazelas, Giant magnetoresistance of (001) Fe/(001) Cr magnetic superlattices, Phys. Rev. Lett., 1988, 61(21), 2472 CrossRef CAS PubMed.
- N. Kaur, V. Srivastava, S. A. Dar, R. Khenata and R. Sharma, A unified DFT exploration on transport and thermodynamic properties of L21 structure of Rh2XZn (X = Mn, Fe) ferromagnets, Mater. Sci. Eng., B, 2023, 287, 116099 CrossRef CAS.
- N. Kaur, V. Srivastava and S. A. Dar, GGA based study on electronic structure and thermoelectric properties of Mn2PtCo full-Heusler compound, Indian J. Phys., 2022, 96(1), 71–77 CrossRef CAS.
- S. Pawar, H. Duadi and D. Fixler, Recent Advances in the Spintronic Application of Carbon-Based Nanomaterials, Nanomaterials, 2023, 13(3), 598 CrossRef CAS PubMed.
- B. Dieny, I. L. Prejbeanu, K. Garello, P. Gambardella, P. Freitas, R. Lehndorff and W. Raberg, et al., Opportunities and challenges for spintronics in the microelectronics industry, Nat. Electron., 2020, 3(8), 446–459 CrossRef.
- S. A. Chambers and Y. K. Yoo., New materials for spintronics, MRS Bull., 2003, 28(10), 706–710 CrossRef CAS.
- G. Schmidt, D. Ferrand, L. W. Molenkamp, A. T. Filip and B. J. Van Wees, Fundamental obstacle for electrical spin injection from a ferromagnetic metal into a diffusive semiconductor, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62(8), R4790 CrossRef CAS.
- R. Fiederling, M. Keim, G. a. Reuscher, W. Ossau, G. Schmidt, A. Waag and L. Molenkamp, Nature, 1999, 402, 787 CrossRef.
- Y. Ohno, D. K. Young, B. Beschoten, F. Matsukura, H. Ohno and D. D. Awschalom, Electrical spin injection in a ferromagnetic semiconductor heterostructure, Nature, 1999, 402(6763), 790–792 CrossRef CAS.
- R. A. De Groot, F. M. Mueller, P. G. V. van Engen and K. H. J. Buschow, New class of materials: half-metallic ferromagnets, Phys. Rev. Lett., 1983, 50(25), 2024 CrossRef CAS.
- K.-I. Kobayashi, T. Kimura, H. Sawada, K. Terakura and Y. Tokura, Room-temperature magnetoresistance in an oxide material with an ordered double-perovskite structure, Nature, 1998, 395(6703), 677–680 CrossRef CAS.
- G. D. Liu, X. F. Dai, H. Y. Liu, J. L. Chen, Y. X. Li, G. Xiao and G. H. Wu, Mn2Coz (z = Al, Ga, In, Si, Ge, Sn, Sb) compounds: structural, electronic, and magnetic properties, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77(1), 014424 CrossRef.
- K. Özdoğan, E. Şaşıoğlu, B. Aktaş and I. Galanakis, Doping and disorder in the Co2MnAl and Co2MnGa half-metallic Heusler alloys, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74(17), 172412 CrossRef.
- H. Luo, G. Liu, F. Meng, J. Li, E. Liu and G. Wu, Half-metallicity in Fe-based Heusler alloys Fe2TiZ (Z = Ga, Ge, As, In, Sn and Sb), J. Magn. Magn. Mater., 2012, 324(20), 3295–3299 CrossRef CAS.
- C. M. Aerts, P. Strange, M. Horne, W. M. Temmerman, Z. Szotek and A. Svane, Half-metallic to insulating behavior of rare-earth nitrides, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69(4), 045115 CrossRef.
- V. Srivastava, N. Kaur, X. Wang, M. Mushtaq and S. Ahmad Dar, First-principles study on structural, electronic, magnetic, elastic, mechanical and thermodynamic properties of Mn2PtCo Heusler alloy, Int. J. Energy Res., 2021, 45(7), 11305–11319 CrossRef CAS.
- V. Srivastava, N. Kaur, R. Khenata and S. A. Dar, J. Magn. Magn. Mater., 2020, 513, 167107 CrossRef CAS.
- H. P. J. Wijn, Alloys and compounds of 3d elements with main group elements, in Magnetic Properties of Metals: D-Elements, Alloys and Compounds, Springer Berlin Heidelberg, Berlin, Heidelberg, 1988, pp. 95–158 Search PubMed.
- K. R. A. Ziebeck and K. U. Neumann, Magnetic properties of metals, Landolt-Bornstein III, 2001, vol. 32 Search PubMed.
- R. J. Soulen Jr, J. M. Byers, M. S. Osofsky, B. Nadgorny, T. Ambrose, S. F. Cheng and P. R. Broussard, et al., Measuring the spin polarization of a metal with a superconducting point contact, Science, 1998, 282(5386), 85–88 CrossRef PubMed.
- C. Ciccarelli, L. Anderson, V. Tshitoyan, A. J. Ferguson, F. Gerhard, C. Gould and L. W. Molenkamp, et al., Room-temperature spin–orbit torque in NiMnSb, Nat. Phys., 2016, 12(9), 855–860 Search PubMed.
- K. A. Kilian and R. H. Victora, Electronic structure of Ni2MnIn for use in spin injection, J. Appl. Phys., 2000, 87(9), 7064–7066 CrossRef CAS.
- Ch Hordequin, J. P. Nozieres and J. Pierre, Half metallic NiMnSb-based spin-valve structures, J. Magn. Magn. Mater., 1998, 183(1–2), 225–231 CrossRef CAS.
- S. Ishida, S. Fujii, S. Kashiwagi and S. Asano, Search for half-metallic compounds in Co2MnZ (Z = IIIb, IVb, Vb element), J. Phys. Soc. Jpn., 1995, 64(6), 2152–2157 CrossRef CAS.
- S. Fujii, S. Sugimura and S. Asano, Hyperfine fields and electronic structures of the heusler alloys Co2MnX (X = Al, Ga, Si, Ge, Sn), J. Phys.: Condens. Matter, 1990, 2(43), 8583 CrossRef CAS.
- S. Fujii, S. Ishida and S. Asano, A half-metallic band structure and Fe2MnZ (Z = Al, Si, P), J. Phys. Soc. Jpn., 1995, 64(1), 185–191 CrossRef CAS.
- H. P. J. Wijn, Alloys and compounds of 3d elements with main group elements, in Magnetic Properties of Metals: D-Elements, Alloys and Compounds, Springer Berlin Heidelberg, Berlin, Heidelberg, 1988, pp. 95–158 Search PubMed.
- H. C. Kandpal, G. H. Fecher, C. Felser and G. Schönhense, Correlation in the transition-metal-based Heusler compounds Co2MnSi and Co2FeSi, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(9), 094422 CrossRef.
- X.-P. Wei, J.-B. Deng, G.-Y. Mao, S.-B. Chu and X.-R. Hu, Half-metallic properties for the Ti2YZ (Y = Fe, Co, Ni, Z = Al, Ga, In) Heusler alloys: a first-principles study, Intermetallics, 2012, 29, 86–91 CrossRef CAS.
- N. Zheng and Y. Jin, Band-gap and Slater–Pauling rule in half-metallic Ti2-based Heusler alloys: a first-principles study, J. Magn. Magn. Mater., 2012, 324(19), 3099–3104 CrossRef CAS.
- H. M. Huang, S. J. Luo and K. L. Yao, First-principles study of half-metallic properties of the Heusler alloy Ti2CoGe, J. Magn. Magn. Mater., 2012, 324(16), 2560–2564 CrossRef CAS.
- I. Galanakis, P. H. Dederichs and N. Papanikolaou, Slater-Pauling behavior and origin of the half-metallicity of the full-Heusler alloys, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66(17), 174429 CrossRef.
- I. Galanakis, and P. H. Dederichs, Half-metallicity and Slater-Pauling behavior in the ferromagnetic Heusler alloys, Half-Metallic Alloys: Fundamentals and Applications, 2005, pp. 1–39 Search PubMed.
- K. R. A. Ziebeck and K. U. Neumann, Magnetic properties of metals, Landolt-Bornstein III, vol. 32, 2001 Search PubMed.
- I. Galanakis, K. Özdoğan, B. Aktaş and E. Şaşıoğlu, Effect of doping and disorder on the half metallicity of full Heusler alloys, Appl. Phys. Lett., 2006, 89(4), 042502 CrossRef.
- A. Kumar and P. C. Srivastava, Synthesis and characterization of Co2FeAl Heusler alloy nanoparticles, Mater. Sci.-Pol., 2013, 31, 501–505 CrossRef CAS.
- N. Rabie, G. R. Gordani and A. Ghasemi, Enhancement of magnetic properties of Co2MnSi Heusler alloy prepared by mechanical alloying method, J. Magn. Magn. Mater., 2017, 434, 135–142 CrossRef CAS.
- K. R. Sapkota, P. Gyawali, A. Forbes, I. L. Pegg and J. Philip, Synthesis and characterization of Co2FeAl nanowires, J. Appl. Phys., 2012, 111, 123906 CrossRef.
- J. H. Du, Y. L. Zuo, Z. Wang, J. H. Ma and L. Xi, Properties of Co2FeAl Heusler alloy nano-particles synthesized by coprecipitation and thermal deoxidization method, J. Mater. Sci. Technol., 2013, 29(3), 245–248 CrossRef CAS.
- K. Hotta, K. Nakamura, T. Akiyama, T. Ito, T. Oguchi and A. J. Freeman, Atomic-layer alignment tuning for giant perpendicular magnetocrystalline anisotropy of 3d transition-metal thin films, Phys. Rev. Lett., 2013, 110(26), 267206 CrossRef CAS PubMed.
- D. Behera, R. Sharma, H. Ullah, H. S. Waheed and S. K. Mukherjee, Electronic, optical, and thermoelectric investigations of Zintl phase AAg2Se2 (A = Sr, Ba) compounds: a first-principle approach, J. Solid State Chem., 2022, 312, 123259 CrossRef CAS.
- D. Behera, A.-R. Ahmed, A. Bouhenna, M. M. Salah, S. Ahmed and S. K. Mukherjee, First-Principles Studies on the Physical Properties of the Half Heusler RbNbCd and RbNbZn Compounds: A Promising Material for Thermoelectric Applications, Crystals, 2023, 13(4), 618 CrossRef CAS.
- P. Kurz, G. Bihlmayer and S. Blügel, Magnetism and electronic structure of hcp Gd and the Gd (0001) surface, J. Phys.: Condens. Matter, 2002, 14(25), 6353 CrossRef CAS.
- P. Hohenberg and W. Kohn, Inhomogeneous electron gas, Phys. Rev., 1964, 136(3B), B864 CrossRef.
- K. Schwarz, P. Blaha and G. K. H. Madsen, Electronic structure calculations of solids using the WIEN2k package for material sciences, Comput. Phys. Commun., 2002, 147(1–2), 71–76 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS PubMed.
- U. Von Barth and L. Hedin, A local exchange-correlation potential for the spin polarized case. i, J. Phys. C: Solid State Phys., 1972, 5(13), 1629 CrossRef CAS.
- F. Tran and P. Blaha, Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential, Phys. Rev. Lett., 2009, 102(22), 226401 CrossRef PubMed.
- F. D. Murnaghan, The compressibility of media under extreme pressures, Proc. Natl. Acad. Sci. U. S. A., 1944, 30(9), 244–247 CrossRef CAS PubMed.
- M. Drief, Y. Guermit, N. Benkhettou, D. Rached, H. Rached and T. Lantri, First-Principles Study of Half-Metallic Ferrimagnet Behavior in Titanium-Based Heusler Alloys Ti2FeZ (Z = Al, Ga, and In), J. Supercond. Novel Magn., 2018, 31, 1059–1065 CrossRef CAS.
- S. Galehgirian and F. Ahmadian, First principles study on half-metallic properties of Heusler compounds Ti2VZ (Z = Al, Ga, and In), Solid State Commun., 2015, 202, 52–57 CrossRef CAS.
- X.-P. Wei, Ge-Y. Mao, S.-B. Chu, H. Deng, J.-B. Deng and X.-R. Hu, First-principles investigations of stability, electronic and thermodynamic properties of Ti2FeGe and Ti2FeSn, J. Magn. Magn. Mater., 2013, 341, 122–128 CrossRef CAS.
- M. Pugaczowa-Michalska, Theoretical prediction of ferrimagnetism in Mn2FeB, Mn2CoB and Mn2NiB, Intermetallics, 2012, 24, 128–134 CrossRef CAS.
- J. M. K. Al-zyadi, G. Y. Gao and K.-L. Yao, First-principles investigation of the structural and electronic properties of bulk full-Heusler alloy Mn2CoSn and its (001) surface, J. Alloys Compd., 2013, 565, 17–21 CrossRef.
- M. Jamal, IRelast and 2DR-optimize packages are provided by M. Jamal as Part of the Commercial Code WIEN2K, 2014 Search PubMed.
- M. Born, K. Huang and M. Lax, Dynamical theory of crystal lattices, Am. J. Phys., 1955, 23(7), 474 CrossRef.
- W. Voigt, On the relationship between the two elasticity constants of isotropic bodies, Ann. Phys., 1889, 274(12), 573–587 CrossRef.
- A. Reuss, Calculation of the flow limits of mixed crystals on the basis of the plasticity of monocrystals, Z. Angew. Math. Mech., 1929, 9, 49–58 CrossRef CAS.
- R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349 CrossRef.
- S. F. Pugh, XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals, Lond. Edinb. Dubl. Phil. Mag., 1954, 45(367), 823–843 CAS.
- I. N. Frantsevich, Elastic constants and elastic moduli of metals and insulators, Reference Book, 1982 Search PubMed.
- X. Qin and X. Yang, Theoretical design of Ti2-based magnetic shape memory alloys from first-principles, J. Magn. Magn. Mater., 2023, 170876 CrossRef CAS.
- S. Skaftouros, E. Ş. Kemal Özdoğan and I. Galanakis, Generalized Slater-Pauling rule for the inverse Heusler compounds, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87(2), 024420 CrossRef.
- N. Kervan and S. Kervan, Half-metallic properties of Ti2FeSi full-Heusler compound, J. Phys. Chem. Solids, 2011, 72(11), 1358–1361 CrossRef CAS.
- L. Offernes, P. Ravindran and A. Kjekshus, Electronic structure and chemical bonding in half-Heusler phases, J. Alloys Compd., 2007, 439(1–2), 37–54 CrossRef CAS.
- I. Galanakis, P. H. Dederichs and N. Papanikolaou, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66(17), 174429 CrossRef.
- P. Kurz, G. Bihlmayer and S. Blügel, Magnetism and electronic structure of hcp Gd and the Gd (0001) surface, J. Phys.: Condens. Matter, 2002, 14(25), 6353 CrossRef CAS.
- M. A. Blanco, E. Francisco and V. Luana, GIBBS: isothermal-isobaric thermodynamics of solids from energy curves using a quasi-harmonic Debye model, Comput. Phys. Commun., 2004, 158(1), 57–72 CrossRef CAS.
- M. Flórez, J. M. Recio, E. Francisco, M. A. Blanco and A. Martín Pendás, First-principles study of the rocksalt–cesium chloride relative phase stability in alkali halides, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66(14), 144112 CrossRef.
- X.-Z. Wang, Extension of Debye's theory of specific heats of solids, J. Phys.: Condens. Matter, 2008, 20(29), 295207 CrossRef.
- M. M. Petit and I. Dulong, XLIV. Researches on some important points of the theory of heat, Philos. Mag., 1819, 54(258), 267–275 CrossRef.
- M. Chehrouri, B. Doumi, A. Mokaddem, Y. Mogulkoc, M. Berber and A. Boudali, Investigation of structural stability, elastic properties, electronic structure and ferrimagnetic behavior of Mn2RhGe full-Heusler alloy, J. Alloys Compd., 2017, 722, 564–568 CrossRef CAS.
- J. L. Moran-Lopez, R. Rodriguez-Alba and F. Aguilera-Granja, Modeling the magnetic properties of Heusler alloys, J. Magn. Magn. Mater., 1994, 131(3), 417–426 CrossRef CAS.
- L. Wollmann, S. Chadov, J. Kübler and C. Felser, Magnetism in cubic manganese-rich Heusler compounds, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90(21), 214420 CrossRef.
- J. M. K. Al-zyadi, G. Y. Gao and K.-L. Yao, First-principles investigation of the structural and electronic properties of bulk full-Heusler alloy Mn2CoSn and its (001) surface, J. Alloys Compd., 2013, 565, 17–21 CrossRef.
- J. Ma, J. He, D. Mazumdar, K. Munira, S. Keshavarz, T. Lovorn, C. Wolverton, A. W. Ghosh and W. H. Butler, Computational investigation of inverse Heusler compounds for spintronics applications, Phys. Rev. B, 2018, 98(9), 094410 CrossRef CAS.
- C. Ambrosch-Draxl and J. O. Sofo, Linear optical properties of solids within the full-potential linearized augmented planewave method, Comput. Phys. Commun., 2006, 175(1), 1–14 CrossRef CAS.
- N. Kaur, R. Sharma, Y. Al-Douri, V. Srivastava and A. F. A. El-Rehim, Thermodynamic, thermoelectric and optoelectronic performances of Co2MB (M = Nb, Ta) full-heusler compounds for solar cell and UV absorber applications, Mater. Sci. Semicond. Process., 2023, 165, 107676 CrossRef CAS.
Footnote |
| † Computational Materials and Photonics, FB 16, University of Kassel, Wilhelmshöher Allee 71, 34121, Germany. |
| This journal is © The Royal Society of Chemistry 2024 |