Open Access Article
Open Access ArticleA DFT approach to correlate the physical characteristics of novel chalcopyrites ASbN2(A = Li, Na) for green technology
Junaid Munir a,
Saif M. H. Qaidb,
Masood Yousafc,
Moeen ud dind,
Hamid M. Ghaithan
a,
Saif M. H. Qaidb,
Masood Yousafc,
Moeen ud dind,
Hamid M. Ghaithan b,
Abdullah Ahmed Ali Ahmede and
Quratul Ain
b,
Abdullah Ahmed Ali Ahmede and
Quratul Ain *f
*f
aDepartment of Physics, Riphah International University, Lahore, Pakistan
bDepartment of Physics & Astronomy, College of Sciences, King Saud University, P.O. Box 2455, Riyadh 11451, Saudi Arabia
cDepartment of Physics, University of Education, Lahore, Pakistan
dDepartment of Physics, National Taiwan University, Taipei City, 10617, Taiwan
eCenter for Hybrid Nanostructures (CHyN) and Fachbereich Physik, Universität Hamburg, Hamburg, 20146, Germany
fDepartment of Physics, University of Management and Technology, Lahore, Pakistan. E-mail: ainnie357@yahoo.com
First published on 13th February 2024
Abstract
Semiconductor chalcopyrite compounds have been a subject of research interest due to their diverse range of physical properties that have captured the attention of scientists. In this ongoing research, we have examined the physical characteristics of LiSbN2 and NaSbN2 chalcopyrites using DFT. The modified Becke–Johnson (mBJ) potential is utilized for the computation of electronic structures. The stability is attained with negative formation energies and optimization curves. A bandgap of 2.60 eV in LiSbN2 and 3.15 eV in NaSbN2 has been achieved, which is further endorsed by the density of states. An in-depth analysis of the optical properties unveils the potential utility of LiSbN2 and NaSbN2 in various photovoltaic devices, attributed to its pronounced absorption in the UV spectrum. The transport characteristics are also assessed through various transport characteristics. The large electrical conductivity and ZT values for both chalcopyrite compounds are attained. Due to their remarkable capability to convert heat into electricity, these materials display potential for use in thermoelectric devices.
Introduction
Thermoelectric materials have gathered significant attention recently due to their extraordinary capability to transform heat into electricity and vice versa.1 This property makes them essential components in various energy conversion and harvesting applications, ranging from powering spacecraft to improving the efficiency of industrial processes.2,3 The literature suggests different classes of materials that exhibit excellent thermoelectric and optical characteristics, such as perovskites,4–8 Zintl compounds,9–12 Heusler alloys,13–16 chalcogenides17,18 and many more. In past years, there has been a developing interest in chalcopyrite-type semiconductors owing to their expanding technological use.19 The chalcopyrite possesses two general structures, AIBIIICV2 and AIIBIVCV2, which are derived from II–VI and III–V semiconductors, where A and B represent cations and C denotes anion. Chalcopyrites are at the leading position of renewable energy technologies due to their capacity to become indispensable, enhance their functionality, and expand their applicability across various fields.20,21 The chalcopyrite structure CuInSe2 exhibits excellent optical properties and is used as an absorber in solar energy applications.22 The flexibility of Cu(In,Ga)Se2 makes them high efficiency solar cell materials with record efficiency of 20.8%.23 The AgInSe2 is observed to be high performance thermoelectric material with ZT of 1.2 at 900 K.24 The insulating state's three-dimensional topology is observed in the potential candidate AuInSe2 chalcopyrite structure.25 The magnetic characteristics are evaluated by exercising density functional theory in the CuFeS2 semiconductor with 3.64 μB magnetic moment.26 The AgGaX2 (X = Te, S, Se) chalcopyrite with bandgap (1.36 eV − 2.73 eV) have been studied to understand the nonlinear and linear optical effects by utilizing real space atom cutting analysis.27 The carbon-doped BeSi1−xCxP2 and BeGe1−xCxP2 show improved optoelectronic (α–105 cm−1) and related characteristics.28 The dispersion curves of refractive index have proven the BeSiN2 and BeCN2 ternary compounds to possess extraordinary optical response.29 High Seebeck coefficient is seen in n-type tin-substituted Cu1−xSnxFeS2 in comparison with p-type chalcopyrite.30 The computed data for CuPN2 with bandgap of 2.135 eV and HPN2 with 2.4 eV bandgap shows admirable performance in terms of optical and thermoelectric attributes.31. There are many other Chalcopyrites such as XPN2 (X = Na, Li)32 CdXP2 (X= Sn/Ge/Si),33 CuGaTe2,34 ACuS2(A = In, Al and Ga),35 LiGaX2 (X= S, Se, Te),36 Ag1−xInTe2,37 AgX (X = In,Ga)Te2 (ref. 38) whose exceptional properties have been investigated. The Cu1−xInTe2 shows high performance in terms of thermoelectric attributes at high temperatures.39 While existing literature has extensively investigated various chalcopyrite structures, the increasing demand for environmentally sustainable technologies necessitates the exploration of additional materials with a wider range of characteristics. Enhancing the current properties of chalcopyrites or exploring novel materials with exceptional characteristics is essential for uncovering and advancing new configurations that exhibit favorable thermoelectric and optical properties. Considering the real-world applications, we intend to thoroughly investigate the structural, elastic, thermal, and optical properties of novel LiSbN2 and NaSbN2 chalcopyrites in the current study.Methodology
DFT stands out as a highly effective approach within the array of computational methods employed for electronic structure calculations. DFT has acquired considerable significance in the assessment of aromaticity, the determination of electronic stability, and the analysis of molecular system dynamics.40 The DFT calculations were performed within the Wien2k41 package by using full-potential augmented plane wave42 approach. Generalized gradient approximation (GGA)43 is utilized for the computation of optimized parameters and mechanical characteristics. The inaccurate solution of exchange correlation potential with GGA leads to misleading bandgap values. The exchange correlation term is best solved with modified Becke–Johnson44 potential, which results in precise values of bandgap and comparable to experimental data. In the calculations, the volume of unit cells is partitioned into muffin-tin spheres characterized by atomic-like wave functions, along with the remaining interstitial space. The energy eigen values converged by expanding the wave function using cutoff RMTKmax = 7 in plane waves. Where RMT stands for the radius of muffin-tin sphere and Kmax represents prime K vector magnitude in the expansion of plane wave. The lmax = 10 is used inside the sphere which shows the expansion of wave function. The Gmax = 12 (a.u.)−1 was set to signify the Fourier expansion of the charge density. The total energy convergence criteria involve ensuring its stability within a margin of 0.0001 (Ryd) and achieving a charge convergence of less than 0.0001 (e a.u.−3). A condensed mesh of 1500 K points was chosen within the irreducible Brillouin zone using the Monkhorst–Pack method. The VESTA software was used to acquire the crystal structures and Wyckoff atomic positions. The Wien2k code was employed to assess the elastic constants (Cij) using the Charpin technique.45 The BoltzTraP code is utilized to apply semi-classical Boltzmann theory using relaxation time approximation for the interpretation of thermoelectric response. The relaxation time can be evaluated using the conductivity tensor.46| σαβ(i,k) = e2τi,kνα(i,k)νβ(i,k) | (1) |
Crystal system and optimization
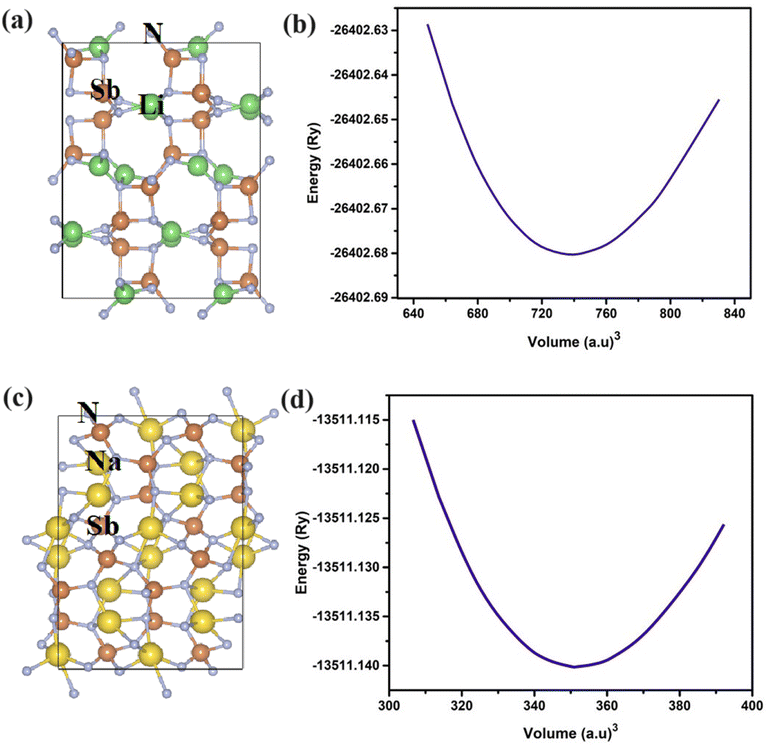
Chalcopyrite structures possess the general formula of ABC2, where A and B represent cations and C is the anion. Our under investigated structures LiSbN2 and NaSbN2 exhibit the orthorhombic symmetry in the space group of Pbca. The selected Wyckoff positions for LiSbN2 are Li (0.48, 0.05, 0.24), Sb (0.63, 0.94, 0.44) and N (0.78, 0.46, 0.31) and for NaSbN2, these are Na (0.27, 0.28, 0.31), Sb (0.76, 0.27, 0.43), N (0.56, 0.48, 0.20). The energetically stable configuration of a structure is crucial in predicting the fundamental properties accurately and it can be achieved through structure relaxation. For this purpose, we use the optimization process to attain the ground state energies of LiSbN2 and NaSbN2 structures. Birch–Murnaghan equation47 is utilized to derive the critical parameters.
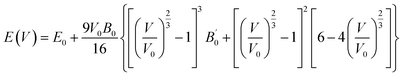 | (2) |
Formation energy is the energy change linked with the creation of a compound from its constituent elements, indicating the stability of the compound and is given as:
| EF = ETotal − (ELi/Na + ESb + 2 EN) | (3) |
The total energy is given with ETotal and the individual element energies are ELi/Na, ESb and EN. The negative EF values energetically favor the material's stability, while the positive values imply that the material's formation is not thermodynamically favored. Our calculated EF values, as presented in Table 1, endorsed that LiSbN2 and NaSbN2 are more stable and likely to form under standard conditions.
| Materials | Lattice constant (Å) | B (GPa) | B′ (GPa) | Vo (a.u3) | Eo (Ry) | EF (eV per atom) |
|---|---|---|---|---|---|---|
| LiSbN2 | a = 5.78, b = 11.77, c = 14.69 | 115.5 | 4.6 | 738.055 | −26402.689 | −1.417 |
| NaSbN2 | a = 5.50, b = 11.12, c = 15.29 | 110.3 | 3.6 | 351.45 | −13511.143 | −1.154 |
Electronic structure
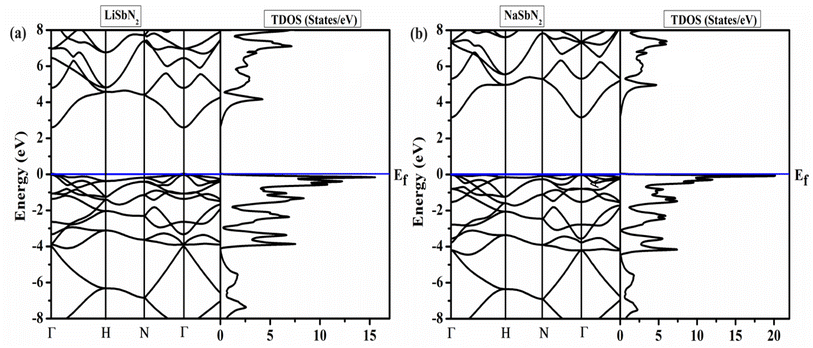
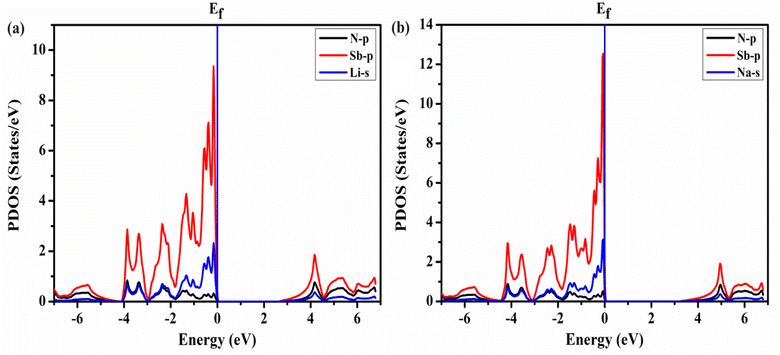
To analyze the energy gap and the role of electrons in various atomic orbitals, we examine the electronic band structure and the overall density of electronic states with the utilization of the mBJ potential. Additionally, it imparts valuable insights into the permissible electronic states and their associated energy levels within the material.48,49 The band structures of ASbN2(A = Li, Na) and are portrayed in Fig. 1. The LiSbN2 exhibits direct band gap characterized by the valence band maximum (VBM) and conduction band minimum (CBM) residing on similar symmetry lines (Γ–Γ), with an energy difference of 2.60 eV. Substituting Li with Na leads to a higher band gap value, resulting in a new value of 3.15 eV along the symmetry lines (Γ–Γ). In both LiSbN2 and NaSbN2, the VBM intersects with the Fermi level in the band structures, suggesting that both chalcopyrites demonstrate p-type semiconductor characteristics. The importance of the distribution of electronic states becomes evident when examining the total density of states (TDOS). It acts as a significant and essential element for forecasting the physical properties of materials. The computed TDOS, depicted in Fig. 2, provides a comprehensive representation of the band structure characteristics in both chalcopyrites materials.A precise and detailed insight into the localized electronic states can be obtained by examining the partial density of states (PTDOS). Our estimation of PTDOS allows for a comprehensive understanding of the electrical contributions, and the outcomes are illustrated in Fig. 3. For LiSbN2, Sb-p and Li-s states exhibit major effect in the valence band and small presence of N-p states. The conduction band includes the contribution of Li-s, Sb-p and N-p states. For NaSbN2, Sb-p and Li-s again display their major effect in the valence band with the small presence of N-p states and the conduction band includes the role of N-p, Sb-p and Li-s states.
Optical properties
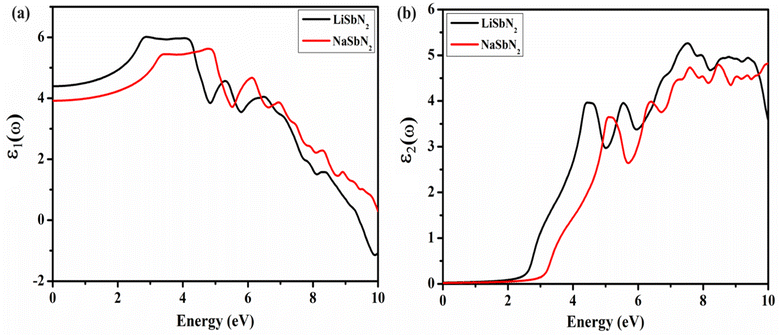
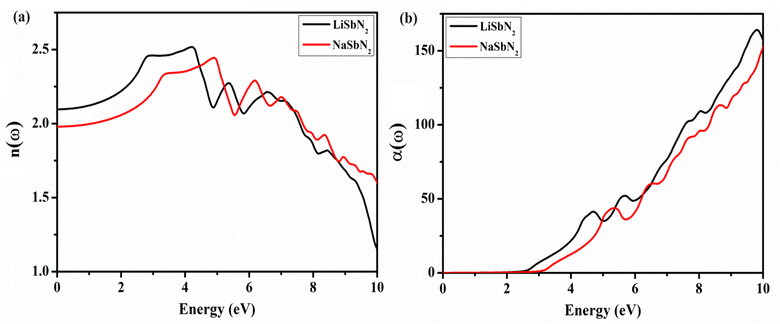
Optical characteristics are of great significance in the creation of optoelectronic devices because they enable the assessment of how a material responds to electromagnetic waves.50 The dielectric function ε(ω) is a crucial component in explaining the optical characteristics of substances. It elucidates the manner in which a material engages with light and can be employed to compute essential optical parameters. The optical characteristics of a material are associated with its frequency due to their dependence on frequency. The ε1(ω) governs a material's ability to store electrical energy and has a direct impact on the refractive index and plotted in Fig. 4a. The electrons within the material react to the electric field of the falling light, causing them to move away from their equilibrium positions. The charges' acceleration induces polarization, which in turn alters the speed of light as it travels through the material. The static dielectric ε1(0) function is crucial for understanding a material's response to a steady electric field. The ε1(0) value for LiSbN2 is 4.4 and the substitution of Na results in the decline of ε1(0) values and a new value of 3.9 is attained for NaSbN2. For LiSbN2, the initial and highest peak is detected at 2.88 eV, followed by a subsequent peak at 4.05 eV. In the case of NaSbN2, the initial peak is identified at 3.45 eV, leading to the highest peak at 4.78 eV. The ε2(ω) characterizes the absorption coefficient of the material and its capacity to interrelate with electromagnetic energy. It has a direct correlation with the electronic structure. The electronic alteration between energy states in distinct states results in the generation of the imaginary component. These electronic transitions cause the observable peaks in the ε2(ω) curves. Fig. 4b displays the ε2(ω) plots for LiSbN2 and NaSbN2. In both compounds, the initial peak arises from the transition of electrons from the valence band, mainly composed of p-states, to the conduction band, which includes both p and d-states. These peaks are photon energy dependent and also generate higher transitions. For LiSbN2, the top value at 4.4 eV is observed and the substitution of Li moves the peak to the higher energy at 5.1 eV. As the energy continues to rise, additional peaks emerge due to interband transitions.The refractive index n(ω) is a gauge of how the speed of light in a given medium compares to its speed in a vacuum. The medium's characteristics dictate the speed at which light travels through it. The n(ω) is a dimensionless ratio that illustrates how photons interact with an optical medium. It serves as a duplicate of the real part and exhibits similar behavior to ε1(ω). The n(ω) for LiSbN2 and NaSbN2 is displayed in Fig. 5a. At ω = 0, the n(ω) is 2.09 for LiSbN2 and 1.98 for NaSbN2. The first topmost value is noticed at 2.9 eV for LiSbN2 and 3.5 eV for NaSbN2. A small rise of energy generated the maximum values at 4.2 eV for LiSbN2 and 4.8 eV for NaSbN2. The absorption coefficient quantifies the extent to which a material absorbs and attenuates the intensity of incident electromagnetic radiation. A comprehensive knowledge of light absorption can be derived from the graphical representations of the absorption coefficient α(ω), presented in Fig. 5b. The graphs depict the highest absorption in the UV range, while visible region also shows some absorption. The first hump is witnessed at 3.0 eV for LiSbN2 and 3.5 eV for NaSbN2, which lead to higher absorption peaks in UV region.
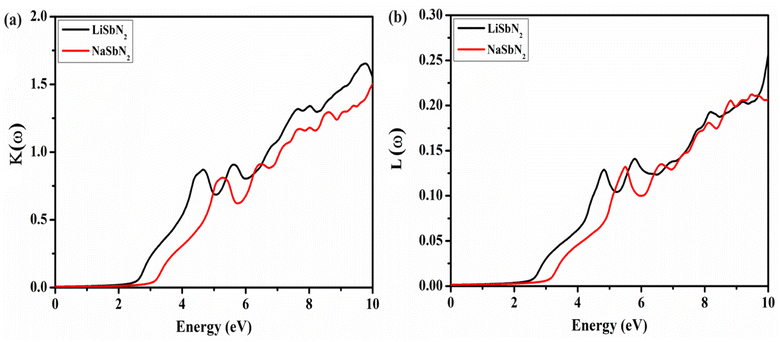
The extinction coefficient K(ω) displays a similar pattern to the imaginary component of the dielectric function and carries equivalent significance. The extinction coefficient offers valuable insights for computing the absorption of incoming photons. The plotted K(ω) values against energy are presented in Fig. 6a. The first hump is viewed at 2.9 eV for LiSbN2 and 3.4 eV for NaSbN2, which lead to first maxima at 4.6 eV for LiSbN2 and 5.2 eV for NaSbN2. The higher absorption peaks are observable in UV region. The optical loss function serves as a critical optical parameter for evaluating a material's ability to resist high-speed electrons. Minimal energy loss is observed for LiSbN2 and NaSbN2, as presented in Fig. 6b.
Transport characteristics
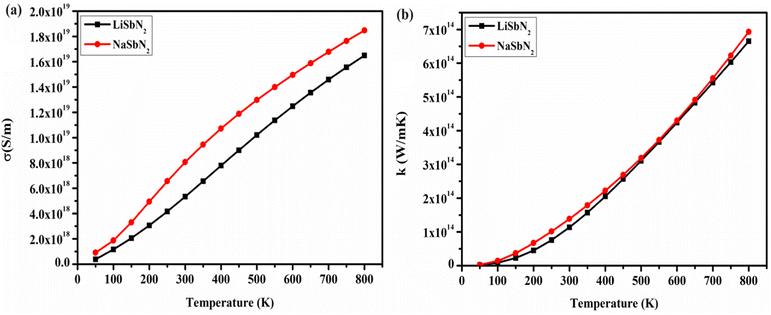
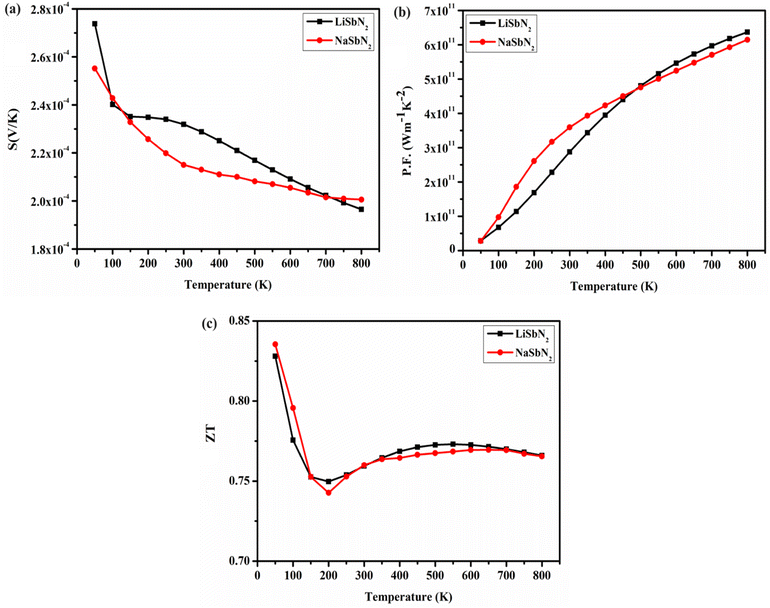
Modern power generation systems utilize thermoelectric applications to enhance the conversion of waste heat into electricity, thereby increasing overall efficiency. Thermoelectric cooling is versatile in its applications due to its ability to function without generating vibrations or noise resulting from vibrational movements. The BoltzTraP algorithm is employed to demonstrate how transport parameters are influenced at various temperature levels. The energy bands and transport characteristics are strongly interconnected with the energy level of the Fermi band. The replacement of Li with Na in the section on electronic structure leads to notable enhancements in the values of the bandgap. The bandgap primarily dictates the charge carriers involved in the transport system. Consequently, the bandgap value meaningfully influences transport parameters, for instance, conductivity and the Seebeck coefficient. To gain a deeper insight into how the bandgap influences transport characteristics, we analyzed the thermoelectric parameters using the mBJ potential. The essential parameter is the electrical conductivity (σ) that is contingent on the density of charge carriers, displayed in Fig. 7a. For LiSbN2, the obtained σ values are 5.33 × 1018 (S m−1) at 300 K and 1.64 × 1019 (S m−1) at 800 K. For NaSbN2, the obtained σ values are 8.08 × 1018 (S m−1) at 300 K and 1.84 × 1019 (S m−1) at 800 K. A gradual increase in σ is noted as the temperature rises for both materials. The capability of a substance to transfer heat through lattice vibrations is referred to as thermal conductivity (k). The calculated electrical component pertains to the holes and electrons responsible for heat conduction. In Fig. 7b, the electronic section of thermal conductivity is illustrated as temperature gradient. The figure shows that as the temperature increases, Kel experiences rapid growth. For LiSbN2, at 300 K, the k possesses the value of 1.14 × 1014 (Wm−1 K−1). A gradual growth in k values is noticed beyond 300 K, resulting in an updated value of 6.64 × 1014 (Wm−1 K−1) at 800 K. For NaSbN2, the thermal conductivity possesses the value of 1.38 ×1014 (Wm−1 K−1) at 300 K. A further growth in k values is noticed above 300 K, and at 800 K, a new value of 6.9 ×1014 (Wm−1 K−1) is attained.The Seebeck coefficient (S) quantifies a compound's capability to generate an electric voltage when exposed to a temperature gradient. Metals exhibit low Seebeck coefficient (S) values when compared to the high Seebeck coefficient of insulators. The Seebeck coefficient is significantly influenced by alterations in the bandgap. Seebeck coefficient is higher in band structures that are in close proximity to the Fermi level. Fig. 8a illustrates the temperature dependent Seebeck coefficient for both materials. For LiSbN2, the S values are 2.31 × 10− 4 (V K−1) at 300 K and 1.97 × 10− 4 (V K−1) at 800 K. For NaSbN2, the S values are 2.15 × 10− 4 (V K−1) at 300 K and 2.00 × 10− 4 (V K−1) at 800 K. The power factor (P.F.) plays a critical role in precisely assessing the potential of a thermoelectric material. The power factor is computed and plotted in the form of graphs for both materials in Fig. 8b. Growing the temperature (100–800 K) results in a gradual enhancement of the power factor (P.F.) values for both chalcopyrites. At 300 K, the P.F has the value of 2.87 × 1011 (Wm−1 K−2), which increases to 6.37 × 1011 (Wm−1 K−2) at 800 K for LiSbN2. For NaSbN2, the P.F is noted as 3.58 × 1011 (Wm−1 K−2) at 300 K that further rises to 6.14 × 1011 (Wm−1 K−2) at 800 K.
The figure of merit (ZT) is a vital parameter in thermoelectric materials, serving as a fundamental measure of the material's effectiveness in transforming heat into electrical energy. A higher ZT value signifies a more efficient thermoelectric material, as it combines aspects like the Seebeck coefficient, electrical conductivity, and thermal conductivity to evaluate performance in energy conversion applications. The ZT for LiSbN2 and NaSbN2 is plotted in Fig. 8c. For LiSbN2, ZT possesses a value of 0.83, at 50 K, which shows a drop to 200 K with a value of 0.75. After 200 K, a gradual rise is noticed in ZT and it has 0.76 values at 300 K. This increase in ZT continuous until 800 K, where it possesses the value of 0.77. For NaSbN2, the same trend is observed as in LiSbN2. At 50 K, the ZT is 0.84, which reduces to 0.74 at 200 K. At 300 K, it is 0.76 and at 800 K, it is 0.77. The significant electrical conductivity and Seebeck values observed in both chalcopyrites, coupled with their impressive ZT values, provide strong support for considering LiSbN2 and NaSbN2 as promising candidates for renewable energy applications.
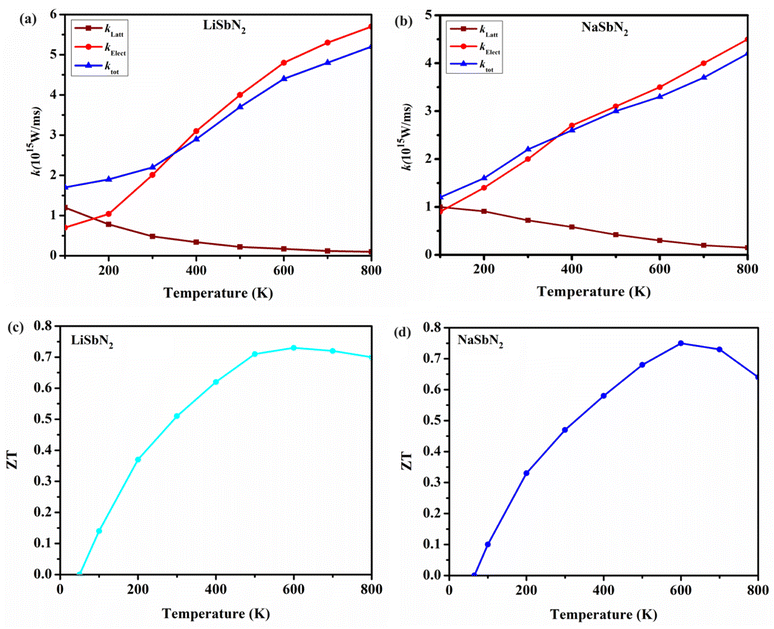
In addition, the combined effect of thermal conductivity containing electronic and lattice thermal conductivities are evaluated and presented in Fig. 9a and b. The lattice vibrations shows a decreasing trend with the temperature rise and simultaneously, the electronic part and total thermal conductivity shows an increasing trend for LiSbN2 and NaSbN2. It can be concluded from the graphs that electronic part plays a major role in thermal conductivity. Furthermore, the phonon dependent ZT values for LiSbN2 and NaSbN2 are also computed and presented in Fig. 9c and d. A sharp rise in the value of ZT is noticed after 50 K for both materials. The ZT highest value of 0.73 (600 K) for LiSbN2 and 0.75 (600 K) for NaSbN2 is achieved. After 600 K, a small decline is noticed in the ZT values of LiSbN2 and NaSbN2.
Conclusion
The physical characteristics of LiSbN2 and NaSbN2 are assessed using the FP-LAPW method incorporated within the Wein2K code. The stability of materials was convincingly established through an analysis of the volume optimization curve and formation energy. The confirmation of their semiconductor character is based on the computed electronic bandgap and the overall DOS. A comprehensive examination of the optical characteristics unveiled their suitability for use in photovoltaic technology. At 800 K, a ZT of 0.77 is attained for both materials, indicating their potential suitability for consumption in thermoelectric devices.Data availability
Data will be made available on request.Conflicts of interest
There is no conflicts to declare.Acknowledgements
The authors extend their appreciation to the Deputyship for Research and Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project no. (IFKSUOR3–073–16).References
- J. R. Sootsman, D. Y. Chung and M. G. Kanatzidis, New and old concepts in thermoelectric materials, Angew. Chem., Int. Ed., 2009, 48(46), 8616–8639 CrossRef CAS PubMed.
- L. Yang, et al., High performance thermoelectric materials: progress and their applications, Adv. Energy Mater., 2018, 8(6), 1701797 CrossRef.
- L. Zhang, et al., Flexible thermoelectric materials and devices: From materials to applications, Mater. Today, 2021, 46, 62–108 CrossRef CAS.
- J. Munir, et al., First-principles investigations of the mechanically and thermodynamically stable potassium-based double perovskites K2TlAsX6 (X= Cl, Br) for optoelectronic and renewable applications, J. Mater. Sci. Eng. B, 2023, 298, 116830 CrossRef CAS.
- S. M. Qaid, et al., A computational insight into Rb2ASbX6 (A= Tl, Cu & X= I, Cl) double perovskites for energy storage and optoelectronic applications, Phys. Scr., 2023, 98(10), 105910 CrossRef.
- M. U. Din, et al., Scrutinized the spin-orbit coupling effect on the elastically and thermodynamically stable Rb2BCl6 (B= Pb, Ti) double perovskites for photocatalytic, optoelectronic and renewable energy applications, Mater. Sci. Semicond. Process., 2023, 163, 107569 CrossRef CAS.
- J. Munir, et al., Electronic structure and optical and thermoelectric response of lead-free double perovskite BaMgLaBiO6: a first-principles study, J. Comput. Electron., 2023, 1–13 Search PubMed.
- J. Munir, et al., Physical properties of elastically and thermodynamically stable magnetic AcXO3 (X= Cr, Fe) perovskite oxides: a DFT investigation, Phys. Scr., 2023, 98(6), 065513 CrossRef.
- Q. Ain, H. Ullah and J. Munir, Structural, optoelectronic and thermal response of new stable MgBe2X2 (X= As, P) Zintl phases: First-principles calculation, J. Mater. Sci. Eng. B, 2023, 287, 116136 CrossRef CAS.
- K. Fatima, et al., Ground state electronic structure, optical and thermoelectric response of Zintl phase MgAl2X2 (X= C, Sb) for renewable energy applications, Phys. B, 2022, 631, 413688 CrossRef CAS.
- J. Munir, et al., An insight into the electronic, optical and transport properties of promising Zintl-phase BaMg2P2, Phys. B, 2021, 618, 413181 CrossRef CAS.
- J. Munir, et al., A computational insight into the Zintl SZr2N2 and BaAg2S2 phases for optoelectronic thermoelectric applications, Phys. B, 2023, 671, 415403 CrossRef CAS.
- Q. Ain, et al., A promising optoelectronic and thermoelectric response of full Heusler Na2TlX (X= Bi, Sb) alloys: A DFT approach, Phys. Scr., 2023, 98, 115920 CrossRef.
- F. Firdous, et al., Half-metallicity, magnetic and optical attributes of mechanically stable half-Heusler VSnX (X= Pt, Pd) alloys for spintronics: a DFT study, Eur. Phys. J. Plus, 2023, 138(8), 699 CrossRef CAS.
- Q. Ain, et al., Electromagnetic, optical and thermoelectric response of full-Heusler Co2VGe alloy for spintronic and thermoelectric applications: DFT+ SOC study, Phys. B, 2023, 657, 414820 CrossRef CAS.
- Q. Ain, et al., First-principles analysis of the physical properties of XAcTe2 (X= Li, Na) Heusler alloys for optoelectronic and thermoelectric devices, Comput. Mater. Sci., 2023, 224, 112156 CrossRef CAS.
- M. Nadeem, et al., Exploring the physical properties of Cu2WSe4 for optoelectronic and thermoelectric applications: a DFT study, ECS J. Solid State Sci. Technol., 2022, 11(3), 033009 CrossRef.
- Y. Shi, C. Sturm and H. Kleinke, Chalcogenides as thermoelectric materials, J. Solid State Chem., 2019, 270, 273–279 CrossRef CAS.
- S. Das, et al., Structure, electronic and optical properties of chalcopyrite-type semiconducting materials XGaY2 (X= Cu, Ag, Au; Y= S, Se, Te) for solar cell applications: a DFT study, Phys. B, 2022, 646, 414305 CrossRef CAS.
- K. Khan, et al., First principle study of optical and electronic response of Ca-based novel chalcopyrite compounds, Phys. Scr., 2023, 98(3), 035821 CrossRef.
- H. Xie, et al., High Thermoelectric Performance in Chalcopyrite Cu1−xAgx GaTe2–ZnTe: Nontrivial Band Structure and Dynamic Doping Effect, J. Am. Chem. Soc., 2022, 144(20), 9113–9125 CrossRef CAS PubMed.
- A. R. Uhl, et al., Liquid-selenium-enhanced grain growth of nanoparticle precursor layers for CuInSe2 solar cell absorbers, Prog. Photovoltaics, 2015, 23(9), 1110–1119 CAS.
- R. Carron, et al., Advanced alkali treatments for high-efficiency Cu (In, Ga) Se2 solar cells on flexible substrates, Adv. Energy Mater., 2019, 9(24), 1900408 CrossRef.
- S. Huang, et al., High Performance of N-type thermoelectric Material AgInSe2 Originated from Strong Acoustic Phonon Scattering, Mater. Lab., 2023, 2, 1–7 Search PubMed.
- W. Feng and Y. Yao, Three-dimensional topological insulators: A review on host materials, Sci. China: Phys., Mech. Astron., 2012, 55, 2199–2212 CrossRef.
- M. Zhou, et al., Structural, electronic, and elastic properties of CuFeS2: first-principles study, Appl. Phys. A, 2015, 118, 1145–1152 CrossRef CAS.
- L. Bai, et al., Mechanism of linear and nonlinear optical effects of chalcopyrite AgGaX2 (X= S, Se, and Te) crystals, J. Chem. Phys., 2004, 120(18), 8772–8778 CrossRef CAS PubMed.
- F. Mekkaoui, et al., Insight into physical properties of carbon-doped BeSiP2 and BeGeP2 chalcopyrite: An ab initio study, J. Solid State Chem., 2023, 323, 124054 CrossRef CAS.
- T. Dahame, et al., Electronic, elastic, linear and nonlinear optical properties of beryllium based chalcopyrite BeMN2 (M= C, Si): An ab initio study, Phys. B, 2019, 561, 37–42 CrossRef CAS.
- S. Tippireddy, et al., Tin-substituted chalcopyrite: an n-type sulfide with enhanced thermoelectric performance, Chem. Mater., 2022, 34(13), 5860–5873 CrossRef CAS PubMed.
- T. Ghellab, et al., Ab initio full-potential study of the fundamental properties of chalcopyrite semiconductors XPN2 (X= H, Cu), Mater. Res. Express, 2019, 6(7), 075906 CrossRef CAS.
- T. Ghellab, et al., Structural, elastic, electronic and thermoelectric properties of XPN2 (X= Li, Na): First-principles study, Int. J. Mod. Phys. B, 2019, 33(21), 1950234 CrossRef CAS.
- N. Megag, et al., Band parameters and thermoelectric properties of chalcopyrite ternary compounds CdXP2 (X= Si, Ge and Sn), Comput. Condens. Matter, 2021, 28, e00577 CrossRef.
- T. Plirdpring, et al., Chalcopyrite CuGaTe2: a high-efficiency bulk thermoelectric material, Adv. Mater., 2012, 24(27), 3622–3626 CrossRef CAS PubMed.
- I. Ghazal, et al., Investigation of the electronic, structural, optical and thermoelectric properties of ternary chalcopyrite ACuS2 (A= Al, Ga and In): Ab initio study, Optik, 2022, 260, 169077 CrossRef CAS.
- M. Yaseen, G. Murtaza and R. M. A. Khalil, Ab-initio study of Li based chalcopyrite compounds LiGaX2 (X= S, Se, Te) in tetragonal symmetry: A class of future materials for optoelectronic applications, Curr. Appl. Phys., 2018, 18(10), 1113–1121 CrossRef.
- Y. Aikebaier, et al., High-temperature thermoelectric properties of non-stoichiometric Ag1−xInTe2 with chalcopyrite structure, J. Mater. Sci. Eng. B, 2012, 177(12), 999–1002 CrossRef CAS.
- J. Yang, Q. Fan and X. Cheng, Prediction for electronic, vibrational and thermoelectric properties of chalcopyrite AgX (X= In, Ga) Te2: PBE+ U approach, R. Soc. Open Sci., 2017, 4(10), 170750 CrossRef PubMed.
- A. Kosuga, et al., High-temperature thermoelectric properties of Cu1−xInTe2 with a chalcopyrite structure, Appl. Phys. Lett., 2012, 100(4), 042108 CrossRef.
- M. Orio, D. A. Pantazis and F. Neese, Density functional theory, Photosynth. Res., 2009, 102, 443–453 CrossRef CAS PubMed.
- P. Blaha, et al., wien2k. An augmented plane wave+ local orbitals program for calculating crystal properties, 2001 Search PubMed.
- M. Petersen, et al., Improving the efficiency of FP-LAPW calculations, Comput. Phys. Commun., 2000, 126(3), 294–309 CrossRef CAS.
- Z. Wu and R. E. Cohen, More accurate generalized gradient approximation for solids, Phys. Rev. B, 2006, 73(23), 235116 CrossRef.
- D. Koller, F. Tran and P. Blaha, Improving the modified Becke–Johnson exchange potential, Phys. Rev. B, 2012, 85(15), 155109 CrossRef.
- A. Bouhemadou, et al., FP-APW+ lo calculations of the elastic properties in zinc-blende III-P compounds under pressure effects, Comput. Mater. Sci., 2009, 45(2), 474–479 CrossRef CAS.
- G. K. Madsen and D. J. Singh, BoltzTraP. A code for calculating band-structure dependent quantities, Comput. Phys. Commun., 2006, 175(1), 67–71 CrossRef CAS.
- T. Katsura and Y. Tange, A simple derivation of the Birch–Murnaghan equations of state (EOSs) and comparison with EOSs derived from other definitions of finite strain, Minerals, 2019, 9(12), 745 CrossRef CAS.
- H. Murtaza, et al., Exploring the optoelectronic attributes, thermoelectric and photocatalytic potential of double perovskites Cs2BB′H6 (B= Al, Na and B′= Tl, In): A DFT study, J. Mater. Sci. Eng. B, 2024, 301, 117171 CrossRef CAS.
- H. Murtaza, et al., Scrutinize the physical attributes of thermodynamically and elastically stable double perovskite oxides Ba2CdXO6 (X= Mo, U) for optoelectronics, photocatalytic and green technology, Comput. Mater. Sci., 2024, 232, 112674 CrossRef CAS.
- S. M. Qaid, et al., First-principles investigations on the structural, optoelectronic, mechanical and transport properties of new stable lead-free double perovskites Cs2BB′ I6 (B= Ag/Rb, B′= Bi/Ga) halides, J. Mater. Sci. Eng. B, 2024, 301, 117176 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |