Tunable ohmic van der Waals-type contacts in monolayer C₃N field-effect transistors

Abstract

Monolayer (ML) C₃N, a novel two-dimensional flat crystalline material with a suitable bandgap and excellent carrier mobility, is a prospective channel material candidate for next-generation field-effect transistors (FETs). The contact properties of ML C₃N–metal interfaces based on FETs have been comprehensively investigated with metal electrodes (graphene, Ti₂C(OH/F)₂, Zr₂C(OH/F)₂, Au, Ni, Pd, and Pt) by employing ab initio electronic structure calculations and quantum transport simulations. The contact properties of ML C₃N are isotropic along the armchair and zigzag directions except for the case of Au. ML C₃N establishes vertical van der Waals-type ohmic contacts with all the calculated metals except for Zr₂CF₂. The ML C₃N–graphene, –Zr₂CF₂, –Ti₂CF₂, –Pt, –Pd, and –Ni interfaces form p-type lateral ohmic contacts, while the ML C₃N–Ti₂C(OH)₂ and –Zr₂C(OH)₂ interfaces form n-type lateral ohmic contacts. The ohmic contact polarity can be regulated by changing the functional groups of the 2D MXene electrodes. These results provide theoretical insights into the characteristics of ML C₃N–metal interfaces, which are important for choosing suitable electrodes and the design of ML C₃N devices.

---

1. Introduction

With the scaling of silicon-based transistors down to the 10 nm threshold, their performance has reached the physical limit owing to the unavoidable high heat dissipation and short-channel effects.^1,2 Numerous semiconductors with excellent structural stability and electronic and optical properties have attracted extensive attention.^3–7 Graphene, as the first fabricated two-dimensional (2D) material, is a plausible candidate in electronics and has replaced the traditional bulk silicon owing to its good carrier transport properties and atomic thickness,^8,9 and thus motivating the extensive study of other 2D materials, such as silicene,^10,11 germanene,¹² transition metal dichalcogenides,^13–16 and black phosphorene.¹⁷ However, the zero bandgap of graphene leads to a small on/off ratio, thus restricting its application in field effect transistors (FETs).^9,18 Although lots of methods have been used to open the bandgap of graphene, such as applying an electric field, adsorbing atoms/molecules on graphene, and sandwiching graphene with a BN single layer, the bandgap still cannot fulfill the requirement application.^18–20 Another promising method for opening the bandgap of graphene is to replace carbon with nitrogen atoms, which creates a strong covalent organic framework.^21–27 Recently, crystalline carbon nitride C₃N, a new 2D hole-free graphene-like material with a honeycomb structure and identical distribution of carbon and nitrogen atoms, has been successfully synthesized on a massive scale.^20,28–31 Experiments have shown that the on/off ratio of 2D C₃N FET is 6.2 × 10¹⁰, and the electron and hole mobilities reach 992 and 6220 cm² V⁻¹ s⁻¹, respectively.³⁰ Additionally, the excellent electronic,¹⁸ optical,^18,26 magnetic,³⁰ and thermal properties^32,33 of monolayer (ML) C₃N make it a very novel candidate material for next-generation low-cost nanoelectronics and nano-optoelectronic devices.

During the application of 2D semiconductors, they inevitably come in contact with metals used as electrodes due to the lack of effective doping methods, so metal–semiconductor contacts have become an increasingly important aspect of electronic devices. Schottky barriers are always present in 2D metal–semiconductor systems, causing an increase in contact resistance and a reduction in carrier injection efficiency.^15,34–38 Generally, bulk metals are used as electrodes in 2D semiconductor FETs, and the Fermi level pinning (FLP) effect can be observed in these devices as they suffer from strong interface interactions between bulk metals with dangling bonds and 2D semiconductors.^39–42 Hence, changing the work function of the metal hinders the tailoring of the Schottky barrier height (SBH). In general, the Schottky barrier is tuned freely to suppress FLP using several methods, such as buffer layer insertion,^17,28–30 metal surface passivation with external atoms,⁴³ and using transferred metal films.⁴⁴ Fortunately, to effectively suppress FLP and establish ohmic contacts, the most straightforward method is to use 2D metal electrodes with naturally clean and saturated surfaces.^{15,35,45–48} Furthermore, the formation of a van der Waals (vdW) heterojunction and low-resistance ohmic contacts can effectively control the optoelectronic and electrical properties, which is essential for the application of 2D semiconductor devices.^30–32,35 However, a thorough investigation of the contact properties of ML C₃N FETs has not been reported; thus it is indeed necessary to explore this aspect with regard to the formation of desired ohmic contacts.

In this work, 2D metals (graphene, Ti₂C(OH/F)₂, and Zr₂C(OH/F)₂) and bulk metals (Au, Ni, Pd, and Pt) were tested as electrodes to systematically study their contact properties with ML C₃N in FETs based on first principles calculations. We discovered that vdW forces play a dominant role in binding at all examined interfaces, preventing chemical disorder. In addition, interface dipoles are severely suppressed, preventing the FLP effect. Further, the properties of ML C₃N FETs were investigated by employing ab initio quantum transport simulations. The vertical interface properties in FETs demonstrate that ohmic contacts can be formed in both 2D and bulk metal electrodes except for the Zr₂CF₂ electrode. As for lateral contact in ML C₃N FETs, all metals form ideal ohmic contacts in the armchair direction and the ML C₃N–2D metal interfaces form ohmic contacts in the zigzag direction. Furthermore, it is a useful method to form physical contact with 2D semiconductors as well as good ohmic contacts in devices by using OH and F functional groups to adjust the work function of MXenes.

2. Methodology

2.1. Interface and device models

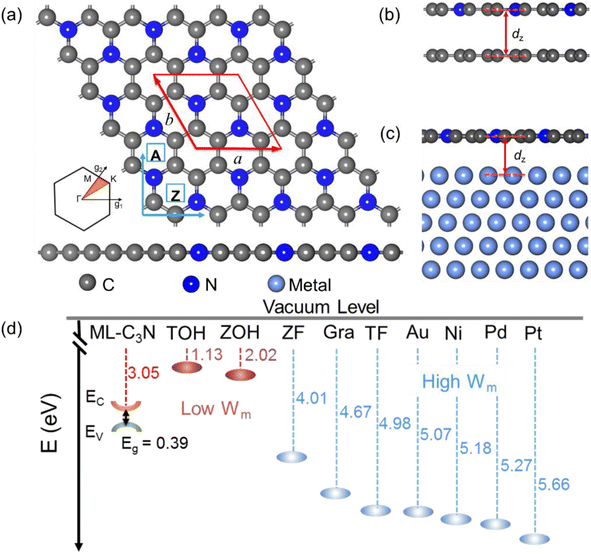
Considering the usability of the electrode in experiments and their lattice mismatch with ML C₃N, bulk metals, including Pt, Pd, Au, and Ni, were chosen.^49–52 In addition, we considered 2D MXenes, including Zr₂CF₂, Ti₂CF₂, Zr₂C(OH)₂, and Ti₂C(OH)₂, because 2D MXenes can form van der Waals contacts with 2D semiconductors, which suppress Fermi level pinning and aid in achieving desired ohmic contacts.^53–56 To simulate the metal surface, five layers of metal atoms were constructed for the bulk Au, Ni, Pd, and Pt electrodes, while the ML configuration was constructed for the layered 2D metals. ML C₃N was adsorbed on one side of these electrodes. Fig. 1(b) and (c) present the side and top views of ML C₃N stacking on the 2D metals and bulk metal surfaces, respectively. To adapt to the lattice constants of ML C₃N, the lattice constants of the metal surfaces were adjusted according to Table S1.† The 2 × 2 supercells of graphene and Ni (111) surface, as well as the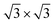 supercells of the Au (111), Pd (111), and Pt (111) surfaces, were all compatible with 1 × 1 ML C₃N. Besides, the 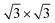supercell of ML C₃N matched the 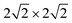supercells of the Ti₂C(F/OH)₂ and Zr₂C(F/OH)₂ surfaces. For graphene, Pd, Ni, Au, Ti₂C(OH)₂, Zr₂C(OH)₂, Zr₂CF₂, Ti₂CF₂, and Pt metal contact systems, the lattice constant mismatches with respect to ML C₃N were 0.81%, 1.33%, 1.65%, 1.80%, 2.08%, 2.08%, 2.64%, 2.64%, and 3.27%, respectively. During the calculation, we fixed the bottom two layers of metal atoms in the bulk metal electrodes because ML C₃N predominantly couples with the top three layers of metal atoms. The work function of a metal is defined as the energy barrier for an electron to escape from the surface of the metal. Both 2D and bulk metals, including graphene, Ti₂C(OH/F)₂, Zr₂C(OH/F)₂, Au, Ni, Pd, and Pt, were tested as electrodes in an extensive range of work functions from 1.13 eV to 5.66 eV, as shown in Fig. 1(d). The role of the work function of these metals is mainly to regulate the contact properties of the charge carriers at the interface.

Fig. 1 (a) Top and side views of the free-standing ML C₃N. The red rhombus indicates the unit cell of the ML C₃N (defined by a and b), and the arrows A and Z represent the armchair and zigzag directions of transport, respectively. The lower left panel plots the Brillouin zone associated with the two lattices. (b) Side view of the ML C₃N contact with 2D metals (the 2D graphene as an example) and (c) bulk metals. (d) Computed band alignments between the ML C₃N and work functions of metals (W_m). E_C, E_V, and E_g represent the conduction band edge, valence band edge, and band gap of the ML C₃N, respectively. The TOH, ZOH, ZF, Gra, and TF stand for Ti₂C(OH)₂, Zr₂C(OH)₂, Zr₂CF₂, graphene, and Ti₂CF₂, respectively.

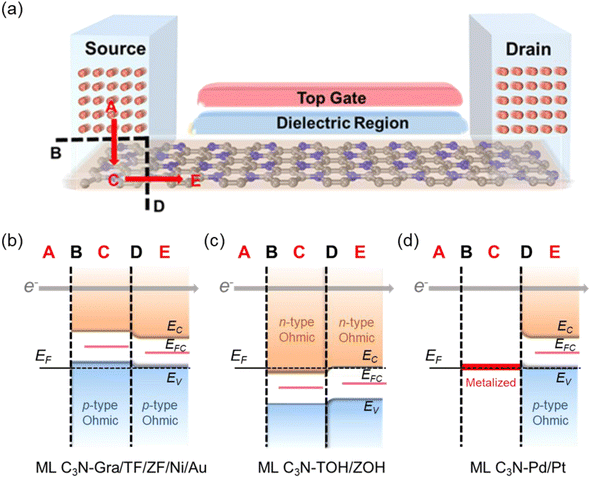
The two-probe ML C₃N-based FET model established to investigate the contact barriers of ML C₃N FETs is shown in Fig. 6(a). The optimized ML C₃N–metal contacts are distributed in the left and right semi-infinite-length electrode regions. Meanwhile, the pristine ML C₃N was used as the channel, and the channel length was 5–6 nm. Carrier injection in ML C₃N-based FETs involves two interfaces: the interface B between the metal electrode A and the bottom ML C₃N region C and the interface D between the source/drain region and channel region E. Because of the anisotropy of ML C₃N, we further assessed the transport properties of ML C₃N FETs along the zigzag direction and armchair direction.

2.2. Computational methods

The Vienna ab initio simulation package (VASP) code was applied to determine the geometrical optimizations and electronic properties of ML C₃N–metal contact systems based on the density functional theory (DFT).^57–59 The interaction between ions and electrons is described using projected augmented wave (PAW) approximation.⁶⁰ The exchange–correlation interactions are described by generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE).⁶¹ We set 500 eV as the cut-off energy when using the plane-wave basis set. By using Grimm's zero damping DFT-D3 approach, vdW correction was processed.⁶² During geometry optimization, the convergence threshold for the residual force was at least 0.001 eV Å⁻¹, and the energy difference was converged to less than 1 × 10⁻⁵ eV per atom. The Monkhorst–Pack k-point grid was sampled in the Brillouin zone with a separation of 0.02 Å⁻¹.⁶³ The vacuum region was set to no less than 15 Å to avoid interaction between adjacent slabs.

The ML C₃N FET simulations were performed by using DFT and the nonequilibrium Green's function (NEGF) method in the Quantum Atomistix Tool Kit (Quantum ATK) 2019 package.^64,65 The double-ζ polarization (DZP) form takes into account the linear combination of atomic orbits (LCAO) basis set. The cut-off energy for the real space was set to 125 eV. The transmission coefficient T(k_y, E) was calculated by using the following formula:

T(k_y, E) = Tr[Γ_L(k_y, E)G(k_y, E)Γ_R(k_y, E)G⁺(k_y, E)]

where k_y is the y portion of the reduced wave vector, and G(k_y, E) (G⁺(k_y, E)) represents the retarded (advanced) Green function in the central region. The self-energy correction term Γ_L/R = i(∑^r_L/R − ∑^a_L/R) represents the widening of the energy level due to the interaction between the central region and the left/right (L/R) electrode, and the self-energy (∑_L/R) of the electrode can be regarded as a useful Hamiltonian for describing the interplay between the lead and the device. The temperature was set to 300 K during the simulation computation process. The Monkhorst–Pack k-point meshes were sampled 8 in the x orientation and 80 in the z orientation in the device.⁶³ In the x, y, and z orientations of the ML C₃N FETs, Periodic, Neumann, and Dirichlet boundary conditions were implemented, respectively.⁶⁶ Previous studies have proven that the GGA-PBE calculation based on single-electron approximation works very well in FET simulation to evaluate the SBH at the interfaces because the doped carriers strongly hinder the electron–electron interaction between the channel region and the electrode region.^{37,40,42,67–69} For example, the bandgap of the degenerately doped ML MoSe₂ was calculated as 1.52 eV based on the DFT-PBE method,⁷⁰ which is in agreement with the values obtained (1.59 eV) from high-level GW calculation⁷¹ and angle-resolved photoemission spectroscopy (1.58 eV).⁷²

3. Results and discussions

3.1. Atomic structure and binding behavior of the ML C₃N–metal interfaces

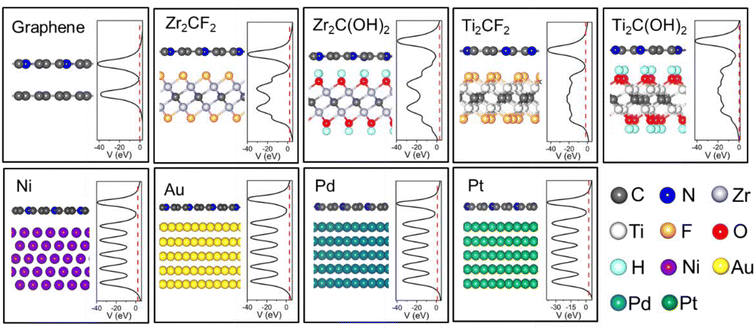
The atomic structure of ML C₃N is illustrated in Fig. 1(a). ML C₃N possesses P/6mmm symmetry with a planar hexagonal structure. The planar lattice constants of ML C₃N obtained by PBE-vdW functional optimization are a = 4.86 Å and b = 4.21 Å, which are in agreement with the previous theoretical results.^73,74 Fig. 2 displays the optimized atomic structure of the ML C₃N–metal interfaces. The relaxed structure of ML C₃N on each metal surface is well-maintained and similar to the initial structure. The equilibrium interface distance (d_z) and the binding energy (E_b) were combined to analyze the binding level between ML C₃N and the metals. As shown in Fig. 1(b), d_z is defined as the average distance from the interface between the topmost layer of metal atoms and the neighboring ML C₃N layer in the vertical direction. To further explore the binding characteristics at the metal–ML C₃N interfaces, the binding energy E_b was calculated by E_b = (E_C3N + E_M − E_sys)/n, where E_C3N, E_M, and E_sys represent the relaxed energies of isolated C₃N, the free-standing metal surfaces, and the combined system, respectively, and n is the total number of C and N atoms in a C₃N supercell. For Zr₂C(OH)₂, Ti₂C(OH)₂, Zr₂CF₂, Ti₂CF₂, Pt, Pd, Au, Ni, and graphene, the d_z values from ML C₃N were 2.17, 2.26, 2.94, 2.95, 3.18, 3.22, 3.39, 3.41, and 3.47 Å, respectively, which is consistent with the approximate distance values of their vdW interaction.³⁵ Because of the large distance between ML C₃N and metals at the interfaces, there was no direct wave function overlap. The sum of the covalent radii of the C atom and the metal atom in the weak bond was much larger than the vertical distance between the layers, indicating that ML C₃N and metals are connected by vdW stacking. The atomic structures of the monolayer C₃N/metal interfaces were well-retained after optimization, as shown in Fig. 2, indicating the good stability of the interfaces. According to previous reports, we used the binding energies of the interfaces to further study their stability.^21,34,42,45 The binding energies E_b of the ML C₃N/metal interfaces were in the range of 0.04–0.14 eV, thus suggesting that weak vdW interactions are established between ML C₃N and metals to prevent chemical disturbances and maintain structural stability, which further demonstrates the good stability of the interfaces (Table 1).

Fig. 2 Optimized side-views and the average electrostatic potential distribution in the planes normal to the interfaces of the ML C₃N on graphene, Zr₂CF₂, Zr₂C(OH)₂, Ti₂CF₂, Ti₂C(OH)₂, Ni, Au, Pd, and Pt surfaces. The Fermi level is represented by red dashed lines.

Table 1 Calculated interfacial properties of the ML C₃N–metal interfaces. [small epsilon, Greek, macron] is the average absolute ML C₃N surface lattice constant mismatch. The equilibrium distance d_z is the average distance between the ML C₃N–metal interfaces in the vertical direction. The binding energy E_b is the energy per ML C₃N being removed from the metal surface. W_M and W_C-M are the calculated work function for clean metals surface and adsorbed the ML C₃N–metal system, respectively. Φ^e,A/Z_L(Φ^h,A/Z_L) is the transport SBH of the electron (hole) along the armchair/zigzag direction in the lateral interface by LDDOS calculation. E^A/Z_g is the transport gap by the LDDOS calculation along zigzag armchair orientation, defined as E^A/Z_g = Φ^e,A/Z_L + Φ^h,A/Z_L. ΔQ is the charge transfer from the metal to the ML C₃N. L^A/Z_g is the channel length of the ML C₃N FET. The calculated work function of the ML C₃N is W = 3.05 eV

	Graphene	Zr2CF2	Ti2CF2	Ti2C(OH)2	Zr2C(OH)2	Ni	Au	Pd	Pt
[small epsilon, Greek, macron] (%)	0.81	2.64	2.64	2.08	2.08	1.65	1.80	1.33	3.27
dz (Å)	3.47	2.94	2.95	2.26	2.17	3.41	3.39	3.22	3.18
Eb (eV)	0.04	0.05	0.06	0.08	0.09	0.10	0.10	0.10	0.14
WC-M (eV)	3.56	3.37	4.40	1.96	2.22	4.43	3.92	4.04	4.24
WM (eV)	4.67	4.01	4.98	1.13	2.02	5.18	5.07	5.27	5.66
ΔQ (e Å^−1)	−0.02	−0.03	−0.06	0.07	0.095	−0.04	−0.05	−0.04	−0.07
Φ^e,ZL (eV)	0.38	0.39	0.43	−0.16	−0.19	0.23	0.34	0.43	0.36
Φ^h,ZL (eV)	0.00	−0.03	−0.11	0.43	0.52	0.00	0.07	0.00	0.00
E^Zg (eV)	0.38	0.36	0.32	0.27	0.33	0.23	0.41	0.43	0.36
Φ^e,AL (eV)	0.38	0.42	0.36	−0.17	−0.24	0.35	0.49	0.42	0.39
Φ^h,AL (eV)	0.00	−0.07	−0.02	0.38	0.41	−0.03	−0.10	0.00	0.00
E^Ag (eV)	0.38	0.35	0.34	0.21	0.17	0.32	0.39	0.42	0.39
L^Zg (Å)	53	58	58	58	58	53	53	53	53
L^Ag (Å)	50	50	50	50	50	50	50	50	50

---

According to previous reports, 2D metals (such as graphene and MXenes) are capable of forming weak bonds with 2D semiconductors, while bulk metals (such as Au, Ni, and Pd) prefer to form strong bonds with 2D semiconductors.^34,47,67,75 Compared with the other C-based 2D semiconductor ML C₂N, ML C₂N–Pd interface forms medium binding with E_b of 0.14 eV and d_z of 2.55 Å, and the ML C₂N–Al and Sc interfaces form strong binding with E_b of 0.22 eV and 0.78 eV, and d_z of 1.80 Å and 1.71 Å, respectively. This indicates that ML C₂N forms stronger interactions with metals than ML C₃N.⁴⁰

3.2. Electronic structure of the ML C₃N–metal interfaces

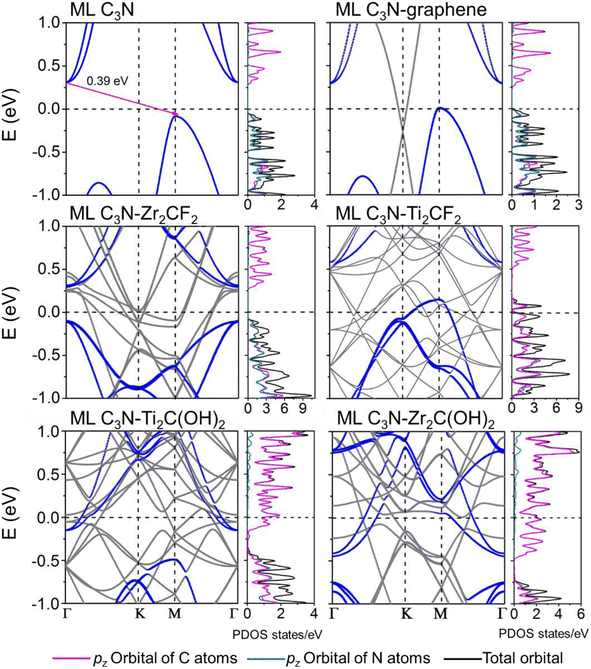
Fig. 3 shows that ML C₃N is a p-type semiconductor with an indirect bandgap of 0.39 eV, in which the valence band maximum (VBM) and the conduction band minimum (CBM) are located at the Γ point and the M point, respectively. This is exactly the same as the findings from previous theoretical calculations at the PBE level and experimental values.^28,30,73 By fitting the CBM and VBM of ML C₃N to parabolic functions, the effective masses of electrons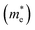 and holes 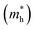were calculated as 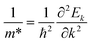, where k is the wave vector and E_k is the energy corresponding to the wave vector k. According to the above formula, the calculated effective masses of ML C₃N were 0.53 m_e for the electrons and 0.21 m_e for the holes in the armchair direction, 0.31 m_e for the electrons and 0.72 m_e for the holes in the zigzag direction, respectively (m_e is the effective mass of free electrons). The effective electron mass in the zigzag direction of ML C₃N is almost two times smaller than that in the armchair direction, while the effective hole mass in the zigzag direction of ML C₃N is around three times larger than that in the armchair direction. Therefore, the above results demonstrate that the effective masses of electrons and holes have obvious anisotropy. Meanwhile, these small effective masses promise large carrier mobility (the predicted hole mobility is 1.08 × 10⁴ cm² V⁻¹ s⁻¹ according to the literature),²⁸ which fully embodies the superior electron transmission capability of ML C₃N.

Fig. 3 Band structures and PDOS of the pristine ML C₃N and the ML C₃N–graphene, Zr₂CF₂, Ti₂CF₂, Ti₂C(OH)₂, and Zr₂C(OH)₂ systems. Gray and blue lines are the band structure of the interfacial systems and the band structures of the interfacial systems projected to the ML C₃N. The purple (green) and the black lines are the DOS of the p_z orbital of C (N) atoms and the total orbital for the interfacial systems projected to the ML C₃N, respectively. The Fermi level is set at zero energy and denoted by the lateral black dashed lines.

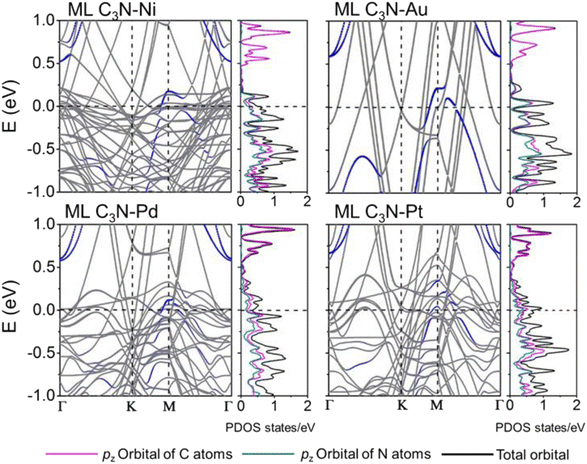
The band structures of the ML C₃N–metal systems are shown in the left part of Fig. 3 and 4. Except for the Pd and Pt electrodes, the inherent band structure of ML C₃N was retained in the selected electrodes compared to the pristine ML C₃N, even though in supercell computation band folding would be considered. The band gaps of ML C₃N were 0.30, 0.32, 0.32, 0.35, 0.36, 0.37, and 0.39 eV in the ML C₃N–graphene, –Zr₂C(OH)₂, –Ti₂C(OH)₂, –Ni, –Ti₂CF₂, –Au, and –Zr₂CF₂ systems, respectively, which are consistent with the 0.39 eV bandgap of isolated ML C₃N. On the other hand, the bandgap of ML C₃N disappeared and its band structure was significantly hybridized after contact with Pd and Pt metals. Due to electron transfer between ML C₃N and the metals, the energy transfer of ML C₃N was observed at the interfaces. The band energy of ML C₃N moved down, and the CBM of ML C₃N passed through the Fermi level after contact with Ti₂C(OH)₂ and Zr₂C(OH)₂, which indicates the formation of n-type contacts. Meanwhile, the band energy of ML C₃N moved upward, and the VBM of ML C₃N was closer to the Fermi level after contact with graphene, Ti₂CF₂, Zr₂CF_2, and all bulk metals, which indicates p-type contacts at these ML C₃N–metal interfaces.

Fig. 4 Band structures and PDOS of the pristine ML C₃N–Ni, Au, Pd, and Pt systems. Gray and blue lines are the band structure of the interfacial systems and the band structures of the interfacial systems projected to the ML C₃N. The purple (green) and the black lines are the DOS of the p_z orbital of C (N) atoms and the total orbital for the interfacial systems projected to the ML C₃N, respectively. The Fermi level is set at zero energy and denoted by the lateral black dashed lines.

The interaction at the ML C₃N–metal interfaces was further analyzed by evaluating their density of states (DOS) in the interfacial systems, as shown in the right part of Fig. 3 and 4. In Fig. S1,† the DOS of pristine ML C₃N near the CBM is primarily composed of the p_z orbitals of C atoms, while that near the VBM is primarily composed of the p_z orbitals of C atoms and N atoms. Similarly, the orbital contribution of ML C₃N in the composite systems was almost consistent with that in pristine ML C₃N. The band gap of ML C₃N was maintained well even after coming in contact with Zr₂C(OH)₂, Ti₂C(OH)₂, Ti₂CF₂, Zr₂CF₂, graphene, Ni, and Au metals due to weak vdW bonding. In addition, a small electronic state appeared in the DOS of ML C₃N after coming in contact with Pt and Pd metals, indicating the absence of bandgap and hybridization of the orbitals. Therefore, the contact types of ML C₃N with metals obtained from the PDOS are the same as those inferred from the band structure.

To further explore electronic transfer at the ML C₃N–metal interfaces, we calculated the plane-averaged charge density difference along the vertical z-direction to better see the gain and loss of interface charge, as shown in Fig. 5. The charge density difference Δρ is defined by the following equation.

Δρ = ρ_A − ρ_M − ρ_C3N

where ρ_A, ρ_M, and ρ_C3N are the charge densities of the complexes, pure metal, and ML C₃N, respectively. In the five layers of bulk metals, the distribution of charge accumulation (depletion) in the metal layer away from ML C₃N was negligible compared with those in the first and second layers near C₃N. This confirms that ML C₃N mainly reacts with the first and second layers of the bulk metals. A large charge depletion area appeared on the ML C₃N side for the ML C₃N–Au, –Ni, –Pd, –Pt, –Ti₂CF₂, and –Zr₂CF₂ interfaces, indicating the occurrence of charge transfer from ML C₃N to these metals with the corresponding values of 0.065, 0.045, 0.043, 0.071, 0.059, and 0.028 e Å⁻¹. On the contrary, a charge accumulation area appeared on the ML C₃N side for the ML C₃N–Zr₂C(OH)₂ and –Ti₂C(OH)₂ interfaces, which indicates charge transfer from these metals to ML C₃N with the corresponding values of 0.095 and 0.071 e Å⁻¹. These match with the electronic states obtained from the band structure and PDOS. The electron wave function is polarized, and interface dipoles would be formed at the ML C₃N–metal interfaces due to the presence of charge depletion and accumulation. The interface band alignment is altered specifically because of the interface dipole, which will affect the Schottky barriers at the interfaces.

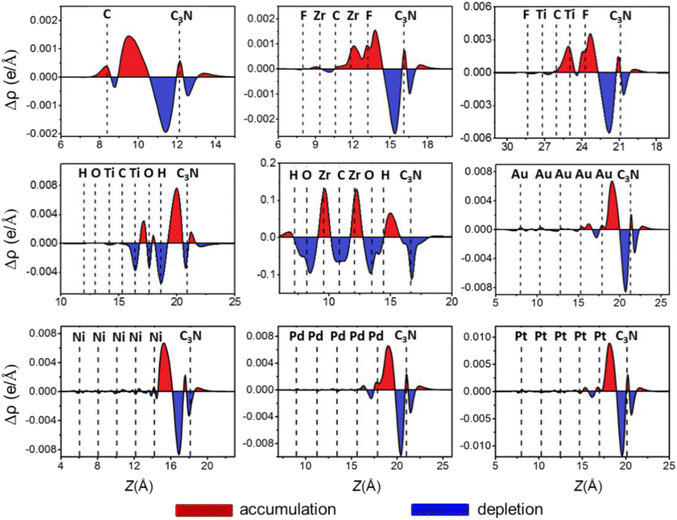Fig. 5 Plane-averaged charge difference along the vertical z-direction to the metals–ML C₃N interfaces. The red (blue) region represents charge accumulation (depletion) regions.

3.3. Barriers in the ML C₃N FETs

To further investigate the barriers in the contact systems, we constructed a two-probe FET model based on ML C₃N with a 5–6 nm channel length along the armchair and zigzag directions, as described in Fig. 6(a). Two different types of interfaces are encountered by carriers transferred from an electrode to a channel. The interface between ML C₃N and the metal on the electrode in the vertical direction is labelled as interface B, while the other interface between the ML C₃N–metal complexes and the ML C₃N channel in the lateral direction is labelled as interface D. Tunneling barriers may appear due to the existence of the vdW gap at interface B, and Schottky barriers may appear at interfaces B and D. In Fig. 2, the tunneling barrier is viewed as an effective potential above the Fermi level at the ML C₃N–metal contacts. In the systems under consideration, because the effective potentials at all interfaces are below the Fermi level, there is no tunneling barrier at the interfaces with a tunneling probability of 100%.

Fig. 6 (a) Schematic diagram of the ML C₃N FET. The carrier paths are marked by red arrows. A, C, and E represent three regions, and black dashed lines B and D represent two interfaces in the ML C₃N FET, i.e., vertical interface B and lateral interface D. (b–d) Three possible band diagrams in terms of the quantum transport calculations of ML C₃N FETs with graphene, Ti₂C(OH/F)₂, Zr₂C(OH/F)₂, Au, Ni, Pd, and Pt electrodes. E_C and E_V are the conduction and valence band edges of the ML C₃N, respectively. E_F and E_FC denote the Fermi level of the ML C₃N-electrode junctions and the band gap center of the channel ML C₃N, respectively. The TOH, ZOH, ZF, Gra, and TF stand for Ti₂C(OH)₂, Zr₂C(OH)₂, Zr₂CF₂, graphene, and Ti₂CF₂, respectively.

SBH is an essential parameter for evaluating the metal–semiconductor contact in the ML C₃N FETs, and it is also a vital factor for determining carrier injection efficiency and resistance. The vertical Schottky barriers of the 2D semiconductor FETs at interface B can be obtained from the commonly used method, namely band structure calculations, wherein the electron/hole SBH is obtained by the observable CBM/VBM of the 2D semiconductor and the energy differences between the Fermi levels of the systems. From the band structure in Fig. 3, it can be inferred that the ML C₃N–Zr₂CF₂ contact system forms a p-type Schottky contact, and the ML C₃N–Zr₂C(OH)₂ and –Ti₂C(OH)₂ contact systems form n-type ohmic contacts with the Fermi level above the CBM of ML C₃N, while the ML C₃N–graphene, –Ti₂CF₂, –Ni, and –Au contact systems form p-type ohmic contacts with the Fermi level below the VBM of ML C₃N. In particular, the band structure of ML C₃N hybridizes when it comes in contact with Pd and Pt electrodes, allowing carriers to pass directly through the electrode to the underside of ML C₃N without a vertical Schottky barrier.

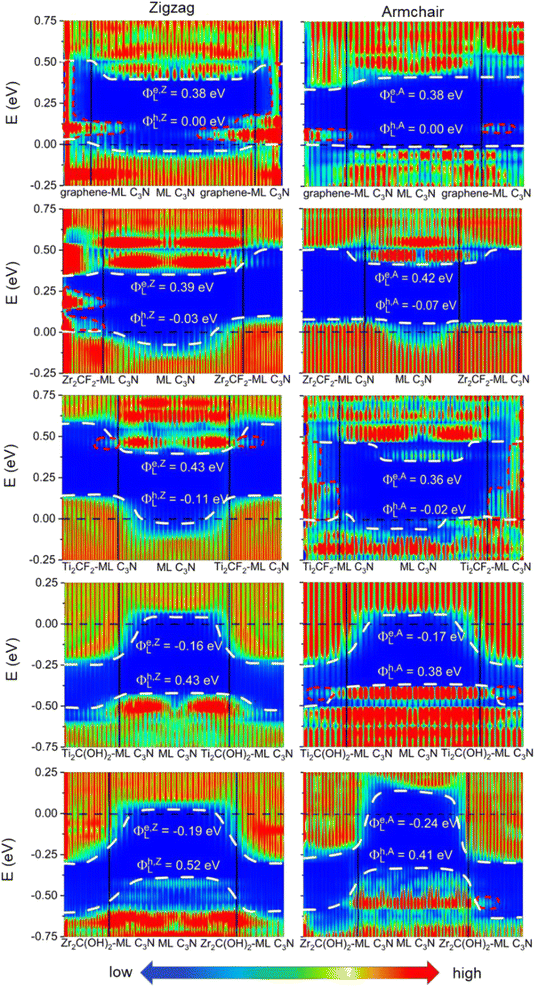
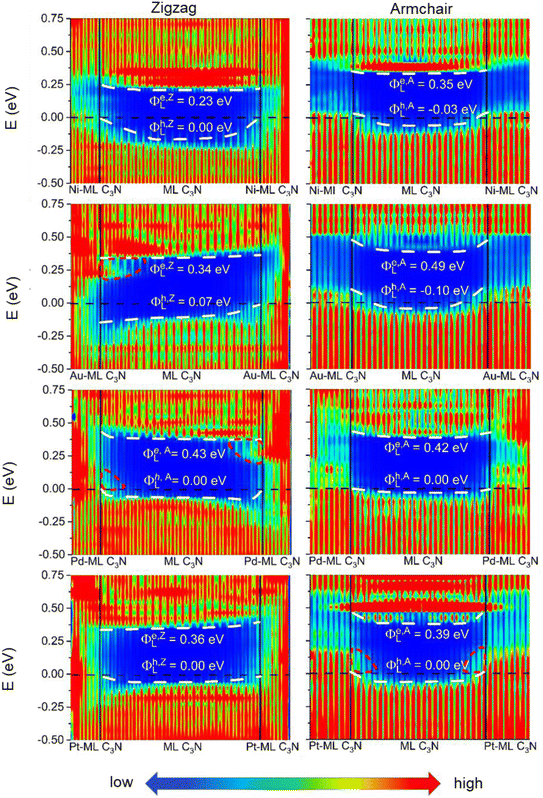
To evaluate the more reliable vertical SBH of the 2D semiconductor FETs, quantum transport simulations were adopted by constructing a two-probe FET model.³⁷ Using Pt, Pd, Ni, Au, Zr₂C(OH)₂, Ti₂C(OH)₂, Ti₂CF₂, Zr₂CF₂, and graphene electrodes, the local device density of states (LDDOS) of the ML C₃N–metal systems projected into ML C₃N under zero bias and zero gate voltage were estimated based on quantum transport simulations, as presented in Fig. 7 and 8. We further explored the transport properties at the ML C₃N–metal interfaces based on FETs in the zigzag direction and armchair direction due to the anisotropy of ML C₃N. The ML C₃N–metal interfaces formed ohmic contacts and the same type of vertical contact in both directions. The bandgap of the ML C₃N underneath the electrode was well-preserved in the ML C₃N–graphene, –Zr₂CF₂, –Ti₂CF₂, –Ti₂C(OH)₂, and –Zr₂C(OH)₂ contact systems, of which p-type ohmic contacts were obtained with graphene, Zr₂CF₂, and Ti₂CF₂ electrodes, while n-type ohmic contacts were obtained with Ti₂C(OH)₂ and Zr₂C(OH)₂ electrodes. The electrode region of the ML C₃N–graphene and –Zr₂CF₂ systems in the zigzag direction and the ML C₃N–graphene, –Ti₂CF₂, and –Ti₂C(OH)₂ systems in the armchair direction had gap states, which can be regarded as metal-induced gap states (MIGS). On the other hand, the p-type vertical ohmic contacts are obtained due to the strong interaction between ML C₃N and the bulk metals, and electronic states appeared in the bandgap of their electrode regions.

Fig. 7 Zero-bias and zero-gate voltage LDDOS of the ML C₃N FETs with graphene, Zr₂CF₂, Ti₂CF₂, Ti₂C(OH)₂, and Zr₂C(OH)₂ electrodes, and the channel lengths are L = 5–6 nm. The Fermi level is represented by the black dashed line. The white dashed lines represent the VBM and CBM of ML C₃N. The interface states are represented by the red short dash lines.

Fig. 8 Zero-bias and zero-gate voltage LDDOS of the ML C₃N FETs with Pt, Pd, Ni, and Au electrodes, and the channel lengths are L = 5–6 nm. The Fermi level is represented by the black dashed line. The white dashed lines represent the VBM and CBM of ML C₃N. The interface states are represented by the red short dash lines.

The vertical barriers estimated from the quantum transport simulation were not exactly the same as those from the band structure calculation. For the ML C₃N-based FET with the Zr₂CF₂ electrode, a p-type Schottky contact was obtained as per band structure calculations, while a p-type ohmic contact was obtained by the quantum transport simulations. Additionally, p-type ohmic contacts were obtained by both the above methods for the ML C₃N–Ni and –Au systems. However, the band structure of the systems was maintained well, and the Fermi level was lower than the VBM of ML C₃N in the band structure calculations, while in the quantum transport simulations, the appearance of gap states leads to the hybridization of ML C₃N and the metal electrodes. The main reason for the difference between these two methods is that the effect of the channels in ML C₃N is ignored in the band structure calculations, while the electrode region and ML C₃N channels are calculated as a whole in quantum transport simulations, and coupling between the two parts is also considered. Therefore, coupling between the electrode and the channel is crucial for evaluating the vertical SBHs of the ML C₃N-based FETs and may also result in MIGS at the ML C₃N–metal vertical interfaces.

Work function approximation is a typical method of assessing lateral Schottky barriers, in which the electrode and channel are regarded as separate parts.^34,42 Therefore, this method ignores the coupling between the two parts. However, coupling between the electrode and channel is considered in quantum transport simulations because they are taken as a whole, which may lead to MIGS at the lateral interfaces and is crucial to studying lateral SBH. Previous studies using quantum transport simulation show that the lateral hole SBHs of trilayer/bilayer/ML black phosphorene systems are 0.20/0.19/0.26 eV, which are well in line with the experimental values of 0.21/0.23/0.35 eV.^34,41,76,77 As a result, we employed quantum transport simulations to evaluate the lateral SBHs in the ML C₃N–metal contact systems.

In the quantum transport simulations, the lateral electron/hole SBH Φ^e,A/Z_L/Φ^h,A/Z_L was determined from the energy differences between the Fermi level of the ML C₃N–metal contacts and the CBM/VBM of the ML C₃N channel at the interface D of the FETs:

Φ^e,A/Z_L = E_C − E_F and Φ^h,A/Z_L = E_F − E_V

where E_F is the Fermi level of the ML C₃N FET, and E_C and E_V denote the CBM and VBM of the ML C₃N channel. In Fig. 7 and 8, the projected LDDOS of ML C₃N is depicted. Due to the possibility of asymmetry in the FET structure, the lateral SBH was estimated as the average of the left and right SBHs. The same contact type was observed along the zigzag and armchair directions, but the lateral SBHs were slightly different along the two directions. For the ML C₃N-based FETs with graphene, Zr₂CF₂, Ti₂CF₂, Ni, Pd, and Pt metals, ideal p-type ohmic contacts were formed with the Fermi level below the VBM of the ML C₃N channel in both directions, while the Fermi level above the CBM of the ML C₃N channel in the ML C₃N–Ti₂C(OH)₂ and –Zr₂C(OH)₂ contact systems caused the formation of ideal n-type ohmic contacts in both directions. Different from the above contacts, a p-type quasi-ohmic contact with a lateral hole SBH Φ^h,Z_L of 0.07 eV was obtained for the ML C₃N–Au system because its Fermi level was very close to the VBM of the ML C₃N channel in the zigzag direction, whereas a p-type ohmic contact was obtained in the armchair direction. In addition, the sum of the electron and hole SBHs was used to compute and define the transmission gap: E^A/Z_g = Φ^e,A/Z_L + Φ^h,A/Z_L. The transport gaps of the ML C₃N FETs with Ni, Ti₂C(OH)₂, Ti₂CF₂, Zr₂C(OH)₂, Pt, Zr₂CF₂, graphene, Au, and Pd as electrodes along the zigzag (armchair) direction were 0.23 (0.32), 0.27 (0.21), 0.32 (0.34), 0.33 (0.17), 0.36 (0.39), 0.36 (0.35), 0.38 (0.38), 0.41 (0.39), and 0.43 (0.42) eV, respectively. The results show that the transport gaps do not exactly correspond to free-standing ML C₃N with a bandgap of 0.39 eV. The reason for this difference is that the coexistence of the interface states and the interaction between the metal electrode and the ML C₃N channel are considered in the quantum transport simulation.

3.4. Discussion

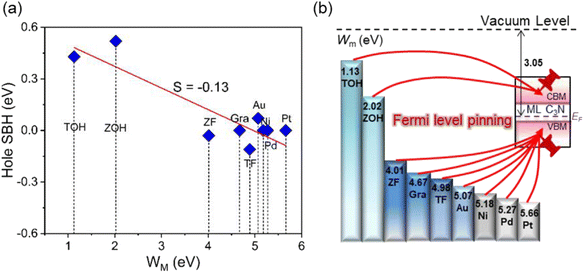
Based on quantum transport simulations, the tunnel barriers and Schottky barriers of the ML C₃N–metal contacts can be classified into three types along the armchair direction, as shown in Fig. 6(b)–(d). In ML C₃N FETs with graphene, Ti₂CF₂, Zr₂CF₂, Ni, and Au electrodes, the bandgap is preserved in both the electrode and channel regions, and the Fermi level lowers the VBM of ML C₃N, forming p-type ohmic contacts at both interfaces B and D, as depicted in Fig. 6(b). Moreover, in ML C₃N FETs with Ti₂C(OH)₂ and Zr₂C(OH)₂ electrodes, n-type ohmic contacts are formed at both interfaces as the Fermi level is above the CBM of ML C₃N, and the band gap is equally maintained in both electrode and channel regions, as depicted in Fig. 6(c). In ML C₃N FETs with Pd and Pt electrodes, the strong interaction between ML C₃N and the electrodes causes electronic states to arise in the bandgap of the electrode region, resulting in significant metallization of the interface B, and a p-type ohmic contact is also observed at the interface D for the same reason, as shown in Fig. 6(d). Due to the isotropic interfacial properties of the ML C₃N FETs, the ML C₃N–metal systems have the same contact type in both the zigzag and armchair directions, except for the ML C₃N–Au contact system, which forms a p-type quasi-ohmic contact because its Fermi level is remarkably close to the VBM of ML C₃N, as shown in Fig. S2.† All three types of ML C₃N–metal contact systems mentioned above can form ohmic contacts at interfaces B and D, which can facilitate electron injection and electron transport to the ML C₃N channel.

Remarkably, the presence of interface gap states and electronic transmission may cause the Fermi energy to be fixed at a special level, making it challenging to experimentally adjust the Schottky barriers to achieve ideal ohmic contacts. To quantitatively analyze the degree of FLP limitations, the Schottky barrier pinning factor S was obtained as S = |dΦ_L/dW_m|, where Φ_L represents the lateral Schottky barrier of the contact system, and W_m is the work function of the metal. If the slope of the linear dependence data is close to 1, there is no FLP according to the Schottky–Moore rule, whereas, a slope close to 0 indicates complete FLP. As illustrated in Fig. 9(a), since the Schottky barriers of the ML C₃N–metal interfaces do not exhibit significant anisotropy, the zigzag direction was chosen to study the FLP effect. The lateral hole SBH demonstrated linear dependence on the work function with a pinning factor of −0.13, which is close to 0, indicating strong FLP. The Fermi level of ML C₃N in the ML C₃N FETs is fixed above the CBM or under the VBM, as presented in Fig. 9(b), while the Fermi level of some other 2D semiconductors is pinned in the gap states.^78–81 Thus, strong FLP results in the formation of ohmic contacts in the C₃N FETs rather than Schottky contacts, unlike in other 2D semiconductors FETs. This is mainly due to the narrow band gap (0.39 eV) of ML C₃N and the inherent properties of the ML C₃N–metal contact systems.

Fig. 9 (a) Lateral hole SBH of the metal–ML C₃N systems versus the work function values of metals. The slope presents the FLP strength. (b) Schematic plot of the FLP for ML C₃N FETs. The TOH, ZOH, ZF, Gra, and TF stand for Ti₂C(OH)₂, Zr₂C(OH)₂, Zr₂CF₂, graphene, and Ti₂CF₂, respectively.

The ideal ohmic contacts are realized with the 2D MXenes of TiC and ZrC with F and OH functional groups, and the different functional groups can modulate the type of ohmic contacts, i.e., the carrier polarity of the transistors can shift from n-type with OH functional group to p-type with F functional group. This is mainly because 2D MXenes with the OH functional group have a small work function, while 2D MXenes with the F functional group have a large work function. Thus, 2D MXenes are ideal electrodes for forming ohmic contacts in ML C₃N FETs, and an appropriate functional group can be selected to change the contact type in these systems.

4. Conclusion

In this work, the contact properties of ML C₃N FETs with various 2D metal electrodes (graphene, Ti₂C(OH/F)₂, and Zr₂C(OH/F)₂) and bulk metals (Au, Ni, Pd, and Pt) are comprehensively explored by employing ab initio electronic structure calculations and quantum transport simulations. Vertical ohmic contacts are formed with both 2D and bulk metal electrodes in ML C₃N FETs except for Zr₂CF₂. Meanwhile, isotropic properties are observed in terms of the type and height of the lateral Schottky barriers along the zigzag and armchair directions. In ML C₃N-based FETs, n-type lateral ohmic contacts are formed with Ti₂C(OH)₂ and Zr₂C(OH)₂ metals, while p-type lateral ohmic or quasi-ohmic contacts are formed with graphene, Ti₂CF₂, Zr₂CF₂, Au, Ni, Pd, and Pt metals. Conspicuously, the type of ohmic contact with the 2D MXene electrodes can be tuned by modulating their functional groups. A strong FLP effect (pinning factor of −0.13) is present at the Fermi levels pinned above the CBM and under the VBM of ML C₃N, which is beneficial for the formation of ohmic contacts. This study not only offers a theoretical basis for the interfacial properties of ML C₃N FETs with different electrodes but also guides the design of ML C₃N FETs that form ohmic contacts.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (No. 11904409 and 51572296), Youth Innovation Technology Project of Higher School in Shandong Province (2022KJ139), Postdoctoral Research Foundation of China (No. 2018M642721), and Shandong Postdoctoral Funded Project (201901012).

References

1. Y. Liu, X. Duan, Y. Huang and X. Duan, Chem. Soc. Rev., 2018, 47, 6388–6409.
2. R. Quhe, L. Xu, S. Liu, C. Yang, Y. Wang, H. Li, J. Yang, Q. Li, B. Shi, Y. Li, Y. Pan, X. Sun, J. Li, M. Weng, H. Zhang, Y. Guo, L. Xu, H. Tang, J. Dong, J. Yang, Z. Zhang, M. Lei, F. Pan and J. Lu, Phys. Rep., 2021, 938, 1–72.
3. Y. Pan, J. Phys. Chem. Solids, 2023, 174, 111152.
4. Y. Pan, S. Chen, P. Wang, Y. Li and Q. Zheng, Ceram. Int., 2019, 45, 19534–19537.
5. Y. Pan and W. M. Guan, Int. J. Hydrogen Energy, 2019, 44, 10407–10414.
6. Y. Pan, Mater. Sci. Eng., C, 2022, 281, 115746.
7. Y. Pan, J. Electron. Mater., 2019, 48, 5154–5160.
8. F. Schwierz, Nat. Nanotechnol., 2010, 5, 487–496.
9. K. Kim, J. Y. Choi, T. Kim, S. H. Cho and H. J. Chung, Nature, 2011, 479, 338–344.
10. S. Cahangirov, M. Topsakal, E. Akturk, H. Sahin and S. Ciraci, Phys. Rev. Lett., 2009, 102, 236804.
11. P. Vogt, P. De Padova, C. Quaresima, J. Avila, E. Frantzeskakis, M. C. Asensio, A. Resta, B. Ealet and G. Le Lay, Phys. Rev. Lett., 2012, 108, 155501.
12. E. Bianco, S. Butler, S. Jiang, O. D. Restrepo, W. Wind and J. E. Goldberger, ACS Nano, 2013, 5, 4412–4421.
13. L. Xie, M. Liao, S. Wang, H. Yu, L. Du, J. Tang, J. Zhao, J. Zhang, P. Chen, X. Lu, G. Wang, G. Xie, R. Yang, D. Shi and G. Zhang, Adv. Mater., 2017, 29, 1702522.
14. S. B. M. Desai, S. R. Madhvapathy, A. B. Sachid, J. P. Llinas, Q. Wang, G. H. Ahn, G. Pitner, M. J. Kim, J. Bokor, C. Hu and H. S. P. Wong, Science, 2016, 354, 99.
15. J. Kang, W. Liu, D. Sarkar, D. Jena and K. Banerjee, Phys. Rev. X, 2014, 4, 031005.
16. T. D. Ngo, T. Huynh, H. Jung, F. Ali, J. Jeon, M. S. Choi and W. J. Yoo, Adv. Sci., 2023, 10, e2301400.
17. L. Li, Y. Yu, G. J. Ye, Q. Ge, X. Ou, H. Wu, D. Feng, X. H. Chen and Y. Zhang, Nat. Nanotechnol., 2014, 9, 372–377.
18. A. Bafekry, D. Gogova, M. M. Fadlallah, N. V. Chuong, M. Ghergherehchi, M. Faraji, S. A. H. Feghhi and M. Oskoeian, Phys. Chem. Chem. Phys., 2021, 23, 4865–4873.
19. M. Xu, T. Liang, M. Shi and H. Chen, Chem. Rev., 2013, 113, 3766–3798.
20. W. Wei, S. Yang, G. Wang, T. Zhang, W. Pan, Z. Cai, Y. Yang, L. Zheng, P. He, L. Wang, A. Baktash, Q. Zhang, L. Liu, Y. Wang, G. Ding, Z. Kang, B. I. Yakobson, D. J. Searles and Q. Yuan, Nat. Electron., 2021, 4, 486–494.
21. Z. Chen, X. Li and J. Yang, Adv. Theory Simul., 2019, 2, 1800161.
22. J. Mahmood, E. K. Lee, M. Jung, D. Shin, I. Y. Jeon, S. M. Jung, H. J. Choi, J. M. Seo, S. Y. Bae, S. D. Sohn, N. Park, J. H. Oh, H. J. Shin and J. B. Baek, Nat. Commun., 2015, 6, 6486.
23. W. Liu, J. Wang, X. Zheng, K. Zhang and X. Liu, Phys. Chem. Chem. Phys., 2022, 24, 29601–29608.
24. M. Amiri, F. Bagherpour and H. Hadipour, Phys. Rev. Mater., 2022, 6, 094004.
25. K. Ma, Y. Wang, Y. Zheng, J. Xiao, L. Xu, X. Dai and Z. Wang, Adv. Theory Simul., 2022, 6, 2200611.
26. Z. Tang, G. J. Cruz, Y. Wu, W. Xia, F. Jia, W. Zhang and P. Zhang, Phys. Rev. A, 2022, 17, 034068.
27. D. Wang, Y. Bao, T. Wu, S. Gan, D. Han and L. Niu, Carbon, 2018, 134, 22–28.
28. X. Wang, Q. Li, H. Wang, Y. Gao, J. Hou and J. Shao, Phys. B, 2018, 537, 314–319.
29. L. Zhou, S. Yang, G. Ding, J.-Q. Yang, Y. Ren, S.-R. Zhang, J.-Y. Mao, Y. Yang, Y. Zhou and S.-T. Han, Nano Energy, 2019, 58, 293–303.
30. S. Yang, W. Li, C. Ye, G. Wang, H. Tian, C. Zhu, P. He, G. Ding, X. Xie, Y. Liu, Y. Lifshitz, S. T. Lee, Z. Kang and M. Jiang, Adv. Mater., 2017, 29, 1605625.
31. J. Xu, J. Mahmood, Y. Dou, S. Dou, F. Li, L. Dai and J. B. Baek, Adv. Mater., 2017, 29, 1702007.
32. G. Qin, J. Lin, H. Wang, J. Hu, Z. Qin and M. Hu, J. Mater. Chem. C, 2022, 10, 12080–12090.
33. W. Y. Jiao, R. Hu, S. H. Han, Y. F. Luo, H. M. Yuan, M. K. Li and H. J. Liu, Nanotechnology, 2021, 33, 045401.
34. Y. Pan, Y. Wang, M. Ye, R. Quhe, H. Zhong, Z. Song, X. Peng, D. Yu, J. Yang, J. Shi and J. Lu, Chem. Mater., 2016, 28, 2100–2109.
35. A. Allain, J. Kang, K. Banerjee and A. Kis, Nat. Mater., 2015, 14, 1195–1205.
36. K. Zhong, J. Li, G. Xu, Y. Yang, J.-M. Zhang and Z. Huang, J. Appl. Phys., 2021, 130, 124305.
37. Y. Wang, S. Liu, Q. Li, R. Quhe, C. Yang, Y. Guo, X. Zhang, Y. Pan, J. Li, H. Zhang, L. Xu, B. Shi, H. Tang, Y. Li, J. Yang, Z. Zhang, L. Xiao, F. Pan and J. Lu, Rep. Prog. Phys., 2021, 84, 056501.
38. X. He, W. Z. Li, Z. Gao, Z. H. Zhang and Y. He, J. Mater. Chem. C, 2023, 11, 4728–4741.
39. M. M. Dong, G. P. Zhang, Z. L. Li, M. L. Wang, C. K. Wang and X. X. Fu, Phys. Chem. Chem. Phys., 2020, 22, 28074–28085.
40. Z. Chen, R. Zhang and J. Yang, Langmuir, 2018, 34, 2647–2653.
41. Y. Pan, Y. Dan, Y. Wang, M. Ye, H. Zhang, R. Quhe, X. Zhang, J. Li, W. Guo, L. Yang and J. Lu, ACS Appl. Mater. Interfaces, 2017, 9, 12694–12705.
42. Y. Shu, Y. Liu, Z. Cui, R. Xiong, Y. Zhang, C. Xu, J. Zheng, C. Wen, B. Wu and B. Sa, Adv. Electron. Mater., 2023, 9, 2201056.
43. Q. Peng, C. Si, J. Zhou and Z. Sun, Appl. Surf. Sci., 2019, 480, 199–204.
44. G. Iannaccone, F. Bonaccorso, L. Colombo and G. Fiori, Nat. Nanotechnol., 2018, 13, 183–191.
45. T. Shen, J. C. Ren, X. Liu, S. Li and W. Liu, J. Am. Chem. Soc., 2019, 141, 3110–3115.
46. D. Çakır and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 245403.
47. H. Zhong, R. Quhe, Y. Wang, Z. Ni, M. Ye, Z. Song, Y. Pan, J. Yang, L. Yang, M. Lei, J. Shi and J. Lu, Sci. Rep., 2016, 6, 21786.
48. C. Gong, L. Colombo, R. M. Wallace and K. Cho, Nano Lett., 2014, 14, 1714–1720.
49. X. Liu, M. S. Choi, E. Hwang, W. J. Yoo and J. Sun, Adv. Mater., 2022, 34, e2108425.
50. L. Kong, R. Wu, Y. Chen, Y. Huangfu, L. Liu, W. Li, D. Lu, Q. Tao, W. Song, W. Li, Z. Lu, X. Liu, Y. Li, Z. Li, W. Tong, S. Ding, S. Liu, L. Ma, L. Ren, Y. Wang, L. Liao, X. Duan and Y. Liu, Nat. Commun., 2023, 14, 1014.
51. J. Kim, D. Rhee, M. Jung, G. J. Cheon, K. Kim, J. H. Kim, J. Y. Park, J. Yoon, D. U. Lim, J. H. Cho, I. S. Kim, D. Son, D. Jariwala and J. Kang, ACS Nano, 2023, 1073–1083.
52. A. Grillo, A. Di Bartolomeo, F. Urban, M. Passacantando, J. M. Caridad, J. Sun and L. Camilli, ACS Appl. Mater. Interfaces, 2020, 12, 12998–13004.
53. Y. Liu, H. Xiao and W. A. Goddard 3rd, J. Am. Chem. Soc., 2016, 138, 15853–15856.
54. C. Wang, X. Xu, S. Tyagi, P. C. Rout, U. Schwingenschlogl, B. Sarkar, V. Khandelwal, X. Liu, L. Gao, M. N. Hedhili, H. N. Alshareef and X. Li, Adv. Mater., 2023, 35, e2211738.
55. B. Lyu, M. Kim, H. Jing, J. Kang, C. Qian, S. Lee and J. H. Cho, ACS Nano, 2019, 13, 11392–11400.
56. J. Yan, D. Cao, M. Li, Q. Luo, X. Chen, L. Su and H. Shu, Small, 2023, 19, e2303675.
57. G. F. Kresse and J. Furthmiiller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
58. G. F. Kresse and J. Furthmiiller, Comput. Mater. Sci., 1996, 6, 15–50.
59. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
60. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
61. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
62. J. Klimes, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2010, 22, 022201.
63. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
64. J. Taylor, H. Guo and J. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245407.
65. M. Brandbyge, J.-L. Mozos, P. Ordejón, J. Taylor and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165401.
66. A. H. D. Cheng and D. T. Cheng, Eng. Anal. Bound. Elem., 2005, 29, 268–302.
67. Y. Pan, J. Dai, Z. Liu, M. Wu, H. Hu and J. Lu, J. Mater. Sci., 2020, 55, 11439–11450.
68. Y. Guo, G. Zhao, F. Pan, R. Quhe and J. Lu, J. Electron. Mater., 2022, 51, 4824–4835.
69. H. Li, Y. Liu, Z. Bai, J. Xiong, F. Liu, G. Zhou, T. Qing, S. Zhang and J. Lu, Phys. Lett. A, 2022, 433, 128029.
70. S. Liu, J. Li, B. Shi, X. Zhang, Y. Pan, M. Ye, R. Quhe, Y. Wang, H. Zhang, J. Yan, L. Xu, Y. Guo, F. Pan and J. Lu, J. Mater. Chem. C, 2018, 6, 5651–5661.
71. Y. Liang and L. Yang, Phys. Rev. Lett., 2015, 114, 063001.
72. Y. Zhang, T. R. Chang, B. Zhou, Y. T. Cui, H. Yan, Z. Liu, F. Schmitt, J. Lee, R. Moore, Y. Chen, H. Lin, H. T. Jeng, S. K. Mo, Z. Hussain, A. Bansil and Z. X. Shen, Nat. Nanotechnol., 2014, 9, 111–115.
73. A. Bafekry, S. Farjami Shayesteh and F. M. Peeters, Phys. Chem. Chem. Phys., 2019, 21, 21070–21083.
74. J. Mahmood, E. K. Lee, M. Jung, D. Shin, H. J. Choi, J. M. Seo, S. M. Jung, D. Kim, F. Li, M. S. Lah, N. Park, H. J. Shin, J. H. Oh and J. B. Baek, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 7414–7419.
75. D. S. Gavali, Y. Kawazoe and R. Thapa, J. Colloid Interface Sci., 2022, 610, 80–88.
76. S. Das, W. Zhang, M. Demarteau, A. Hoffmann, M. Dubey and A. Roelofs, Nano Lett., 2014, 14, 5733–5739.
77. X. Zhang, Y. Pan, M. Ye, R. Quhe, Y. Wang, Y. Guo, H. Zhang, Y. Dan, Z. Song, J. Li, J. Yang, W. Guo and J. Lu, Nano Res., 2017, 11, 707–721.
78. C. Kim, I. Moon, D. Lee, M. S. Choi, F. Ahmed, S. Nam, Y. Cho, H.-J. Shin, S. Park and W. J. Yoo, ACS Nano, 2017, 11, 1588–1596.
79. J. Li, X. Sun, C. Xu, X. Zhang, Y. Pan, M. Ye, Z. Song, R. Quhe, Y. Wang, H. Zhang, Y. Guo, J. Yang, F. Pan and J. Lu, Nano Res., 2018, 11, 1834–1849.
80. H. Zhang, J. Xiong, M. Ye, J. Li, X. Zhang, R. Quhe, Z. Song, J. Yang, Q. Zhang, B. Shi, J. Yan, W. Guo, J. Robertson, Y. Wang, F. Pan and J. Lu, Phys. Rev. Appl., 2019, 11, 064001.
81. J. Yan, X. Zhang, Y. Pan, J. Li, B. Shi, S. Liu, J. Yang, Z. Song, H. Zhang, M. Ye, R. Quhe, Y. Wang, J. Yang, F. Pan and J. Lu, J. Mater. Chem. C, 2018, 6, 6153–6163.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra08338a

---