Open Access Article
Open Access ArticleAn investigation using DFT into the impact of hydrogen on oxygen migration processes during aluminum anodization
Zeyu An a,
Shiyang Sun
a,
Shiyang Sun b and
Binghai Dong*a
b and
Binghai Dong*a
aSchool of Materials Science and Engineering, Hubei University, Wuhan, Hubei 430000, P. R. China. E-mail: wwwdbh@163.com
bSchool of Mechanical Engineering, Inner Mongolia University of Science & Technology, Baotou, Inner Mongolia 014010, P. R. China
First published on 11th April 2024
Abstract
First-principles computations were utilized to examine the impact of H atoms on the surface behavior of O atoms on the (111) surface of Al and their infiltration behavior into the Al crystal, with the aim of elucidating the behavior of ions in the anodic process during aluminum oxidation. According to the findings, the “abstract” action of H atoms significantly lowers the energy barrier preventing O from entering the Al crystal. The addition of a H atom influences the diffusion of O atoms in the Al crystal as well, and this can lower the activation energy of O atom migration between the tetrahedral interstitial locations from 1.23 eV to 0.35 eV. We can benefit from knowing how ions are transported and anodic oxidation occurs.
1. Introduction
Since the beginning of the 20th century, anodic aluminium oxide (AAO) has been widely used in industry for several applications, such as corrosion protection, colouring, and production of capacitors, due to its highly ordered arrangement, stable physical and chemical properties, and low cost.1,2 The electrochemical method for producing aluminum oxide thin films was first proposed by Keller et al. in 1953. However, it is labor-intensive, time-consuming, and has a low repetition rate.3 AAO was prepared using a two-step anodic oxidation approach by Masuda et al. in 1995.4 Due to its excellent reproducibility and stable pore formation, this approach gained recognition in academia.In order to understand the growth mechanism of the porous layers during anodizing, several experimental studies5 have investigated the effect of the anodizing conditions, especially the chemical composition of the electrolyte, voltage or current density, on most structural parameters of AAO, such as nanopore diameter and wall thickness. Furthermore, several models, such as the field-assisted model,6,7 the stress-induced plastic flow model,8,9 the volume expansion stress model10,11 and the oxygen bubble mold model,12–14 were proposed to elaborate the growth mechanism of the porous layers during anodizing. Although these theories are different, they are all based on a common cognition: the formation of AAO is a competition between the two reactions of aluminium oxidation and alumina dissolution. AAO grows stably when the reaction rates of these two reactions are in equilibrium. Fig. 1 shows that the electrochemical reactions and ion paths occur during the anodizing of aluminium. For electrode reactions, the following reaction equation is generally accepted in academia:15
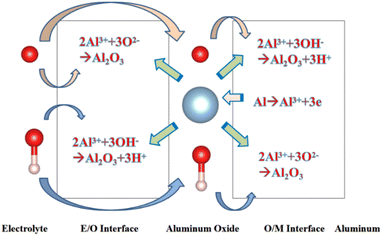 | ||
| Fig. 1 Schematic diagram showing the electrochemical reactions and ionic paths occurring during aluminium anodizing. | ||
Anode:
| Al → Al3+ + 3e− | (1) |
| 2Al + 3O2− → Al2O3 + 6e− | (2) |
| Al + 6OH− → Al2O3 + 3H2O + 6e− | (3) |
Cathode:
| 2H+ + 2e− → H2↑ | (4) |
Total:
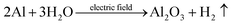 | (5) |
The rate of growth of anodic films during anodization under mild experimental conditions is limited by the solid-state transport of ions within the oxide layer formed on the anode.2 Several models, such as Cabrera and Mott's model,16,17 Verwey's model,18 Dewald's model,19,20 point defect model (PDM)21–25 and Lohrengel's model26 were proposed to explain the process of ionic functional group (OH−) transport. Those models all emphasize the important role of electric field strength E. Subsequent researchers obtained the following empirical equation from experience:27,28
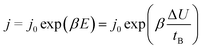 | (6) |
The eqn (6) empirically explains the relationship between field strength and ion migration rate. This equation is reliable when the process occurs in the alumina solid state, because of the migration of vacancies inside the alumina under the action of an electric field. Existing study had got the result of the migration and activation energy of O atoms on the surface of aluminum, which the energy is large and ion diffusion is difficult.29
Density functional theory (DFT) has been the most effective tool in condensed matter physics for computing electronic structure and its properties since its inception in the 1960s, when it was initially used to derive the well-known Kohn–Sham (KS) equation under the local density approximation (LDA). Numerous atomic and molecular physics puzzles, including those involving catalytic active sites,30,31 geometric structure,32,33 and material electronic structure properties,34,35 can be resolved with DFT. DFT is also commonly used to calculate the functions of the ions during chemical reactions,36,37 as it can accurately reveal reaction pathways clearly.
In this study, the first-principles calculations were used to compare the migration and diffusion behaviours of O atom and O–H group on the surface of aluminum and inside the crystal of aluminum. Thus, we also discuss the role of H, the smaller atom, in the process of aluminium anodizing.
2. Calculation method and details
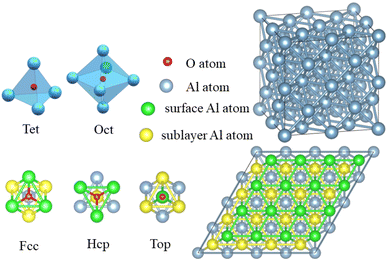
The Vienna ab initio simulation package (VASP),38 which is based on the pseudopotential plane wave approach and density functional theory, was used to conduct the simulations. The electron projector-augmented wave method39 was used to predict the interactions between ions and valence electrons. The Perdew–Burke–Ernzerhof generalized gradient approximation40 was used to determine the exchange-correlation function. The conjugate gradient method41 was used to optimize the geometric structure of the model. The electronic occupancy was determined using the Methfessel–Paxton method,42 in which the smearing width was 0.05 eV. Self-consistent iterative matrix diagonalization uses the residual minimization scheme-direct inversion in the iterative subspace (RMM–DIIS) algorithm.43 All self-consistent loops were iterated until the total energy difference among the systems, which was measured between the adjacent iterating steps reached less than 1 × 10−5 eV. The cutoff energy for the plane waves was 400 eV.To investigate the role of smaller atom H during the oxidation of aluminium, surface and crystal models were established. The surface model contained 96 atoms distributed over 6 layers, in which the upper four layers were relaxed and the lower two layers were fixed. To avoid the effect of the periodic boundary conditions, a vacuum layer was set at more than 18 Å. In the top view, the slab of (111) surface of Al was built as a rhombic consisting of 4 × 4 primitive unit cells. As shown in the Fig. 2, there were three adsorption sites: face-centered cubic (Fcc), hexagonal closest packing (Hcp), and Top, which were located in the three-fold hollow site on the surface, in the other three-fold hollow site on surface as well as on the top of the sublayer atoms, and on the top of the surface atoms, respectively. The crystal model contained 32 Al atoms and 2 × 2 × 2 cubic unit cells. In the crystal model, all atoms were relaxed. There were two occupied positions: the octahedral interstitial (Oct) and the tetrahedral interstitial (Tet) positions. All the mentioned adsorption or doping positions refer to the occupation of the O atom, and the distance between O–H was initially set to 0.98 Å, based on the single bond distance between O atom and H atom.44
When the O–H group is adsorbed on the surface of aluminum, due to the strong Al–O interaction, the distance between O–H will increase significantly, under the condition of the electric field does not play a leading role. After that, OH will dissociate on the surface of aluminum that is not completely ionized. Once the Al ionized completely, OH and the Al ions generate the ionic compound.45,46 Therefor the calculation in this paper adopts the O–H group and O atom. Even if charged ions were used, the adsorption structure and migration path of charged ions were the same, so the results and the conclusion were all the same.47 Therefore, the calculational results here are appropriate when things come down to the experiments. The Monkhorst–Pack method48 was used to divide the Brillouin zone using [5 × 5 × 1] and [7 × 7 × 7] k-points for the surface and crystal models, respectively.
Adsorption energy (Ead) and binding energy (Ebd) characterize the adsorption of the O atom and the connection model on the surface of aluminum and within the aluminum crystal, respectively, which are defined by eqn (7) and (8) as follows:
| Ead = Esurf + EOH − Etot | (7) |
| Ebd = EAl + EOH − Etot | (8) |
According to the transition-state theory, the migration activation energy (Esp) can be defined as the difference between the lowest energy and the saddle point (SP) energy on the migration path. The SP is the highest energy point on the migration path and the lowest energy point on the other directions. The migration path was investigated using the Nudged elastic band method49 to map the minimum energy path between the initial and final systems. Five initial images were created by linear interpolation.
As is known to all, much of oxygen's chemistry is driven by electron spin. The spin of oxygen had been considered. However, when spin is turned on, the required computation time will triple, even when using only the original cell. Considering the computational cost, preliminary calculations were conducted on the process to determine whether it was necessary to incorporate spin. The calculation involves using an oxygen atom and an O–H group to adsorb on the surface of aluminum and comparing the difference in adsorption energy between using spin and not using spin. The results showed that there was no change in the energies of two absorption models and two surface models, while the energy of the O atoms decreased by 1.49 eV. As a result, the absorption energy decreased by 1.49 eV. These results suggest that the spin of the oxygen does not influence the energy of the models, except for its own energy. The same results were obtained when it comes to the O–H group, showed an energy decrease of 0.44 eV. Furthermore, the literature suggests that the barriers arise from the energetic cost of initiating abrupt charge transfer from the metal surface to the membrane, and there is no need to consider non-destructive surface hopping or spin selection rules to explain the barrier.50 Therefore, all the calculations in this paper did not consider the spin of oxygen, except for the Ead and the Ebd.
3. Results and discussion
3.1 Adsorption and migration processes on the surface of aluminum
Adsorption distance and energy are both important and foundational reaction mechanism properties. The adsorption distance of O atom and O–H group on the (111) surface of aluminum had been tested in two different lengths on the Top position, 1.856 Å and 1.969 Å, which are two different bond lengths in α-alumina. As shown in Table 1, the energies and the distances after calculation between different distances were almost same. The different of energy (ΔE) was only 0.0004 eV of the adsorption of O atom on the (111) surface of aluminum, and 0.0017 eV of the adsorption of O–H group on the (111) surface of aluminum. On the other hand, the different of distance (ΔD) was only 0.001 and 0.0003 for the absorption of atom O and O–H group respectively. The ΔD of O–H in different lengths was also very small, which is 0.0006 Å. As a result, all the data above indicate that the absorption distance of Al and O in two conditions (atom O and O–H group) should be 1.68 Å and 1.69 Å. And the distance of atom O and atom H should be 0.96 Å in the case of O–H group adsorption on (111) surface of aluminium.| Case of length (Å) | Distance (Å) | Energy (eV) | ΔE (eV) (absolute value) | ΔD (Å) (absolute value) | ||
|---|---|---|---|---|---|---|
| Atom O | Al–O | 1.856 | 1.6809 | −235.0523 | 0.0004 | 0.0010 |
| 1.969 | 1.6798 | −235.0519 | ||||
| O–H group | Al–O | 1.856 | 1.6959 | −239.9108 | 0.0017 | 0.0003 |
| 1.969 | 1.6962 | −239.9125 | ||||
| O–H | 1.856 | 0.9574 | −239.9108 | 0.0006 | ||
| 1.969 | 0.9580 | −239.9125 | ||||
The O atom's adsorption energies on the (111) surface of Al is displayed in Table 2. In comparison to the adsorption energy at the Hcp and Fcc positions, the Top position had a significantly lower level of stability. Given that the adsorption energies of the Hcp and the Fcc were comparable, but the Fcc position had the highest energy, the O atom should be adsorbed at the Fcc site. That results are similar with the literature reported before.51 However, things change a little bit after the H atom enters the migratory process. The migratory activation energy is reduced by the H atom, but the adsorption location and migration course of the O atom remain same. When O atoms infiltrate and diffuse through crystals of Al, this phenomenon is more noticeable.
| Fcc | Hcp | Top | Oct | Tet | ||
|---|---|---|---|---|---|---|
| Atom O | Etot (eV) | −237.87 | −237.57 | −235.05 | −126.72 | −128.15 |
| Ead or Ebd (eV) | 6.82 | 6.56 | 3.97 | 5.51 | 6.91 | |
| O–H group | Etot (eV) | −241.01 | −240.73 | −239.91 | — | −130.92 |
| Ead or Ebd (eV) | 4.89 | 4.62 | 3.80 | — | 3.70 | |
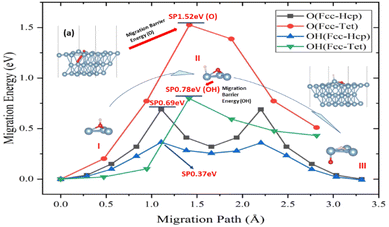
Aluminium oxidation includes O atom penetration and diffusion within the crystal of aluminum in addition to surface adsorption and migration processes. The tetrahedral interstitial position, created by aluminum atoms of the surface and subsurface layers, was discovered to be the point where the O atom infiltrates the crystal of aluminum from the surface. This position was also the occupancy position in the crystal of aluminum model. The location and migratory path remain the same when the H atoms engage in the infiltration process, just like they do on the surface. The addition of H atoms was shown to lower the infiltration activation energy of O atoms by 49%, despite the fact that the activation energy of the infiltration process is larger than the migration on the surface of aluminum (Fig. 3).
It was discovered that the O atom entered the crystal of aluminum at the tetrahedral interstitial location, which is just under the surface atom of aluminum (top view). When the O atom enters the crystal of aluminum from the surface, an energy barrier must be overcome in order to “lift” the surface aluminum atom (Fig. 3a). The surface of aluminum layer spacing will rise from 2.34 Å to 2.45 Å as a result of the invading process. The gradual deep oxidation of aluminum may possibly be connected to the process's high activation energy (1.52 eV).
However, atom H complicates the diffusion process, which may be divided into three stages (points I–III in Fig. 3). First, the H atom is adsorbed on top of the O atom at the Fcc location on the surface of aluminum, connecting it to the O atom. Because O–Al has a higher binding energy than O–H, the latter dissociates on the surface of aluminum. Following the dissociation, the O atoms and H adsorbed at the Fcc and the closest Top positions, respectively (Fig. 3b). The link between H and Al induces charge transfer, which causes the atom aluminum to leave the surface, known as the “abstract” effect.52,53 This impact lowers the activation energy of the migratory process. The O atom then goes down into the crystal of aluminum, while atoms H move from the top to the Fcc location. In this stage, the links between O atoms of and Al atoms between two surfaces must be disrupted in order for O atom to make new bonds with three atoms of Al in the sublayer. The presence and movement of H atoms dramatically minimize energy fluctuations during bond breaking, making it easier for O atom to be adsorbed on the surface of aluminum. Furthermore, the effect of H atoms causes O atom to penetrate the crystal of aluminum from the surface more easily.
In order to accurately understand the charge transfer between O atom and H atom on the (111) surface of aluminium and inside the crystal of aluminium, the Bader charge had been calculated, and the specific results are shown in Table 3. Where the Aln (n in 1, 2, 3, 4, 5, 6) means the Al atom around the O atom or H atom.
| Atom | Charge (q/e) | Changes in charge (q/e) | Atom | Charge (q/e) | Changes in charge (q/e) | |
|---|---|---|---|---|---|---|
| O-Fcc | Al1 | 2.45 | −0.55 | Al | 2.453 | −0.55 |
| Al2 | 2.45 | −0.55 | O | 7.60 | +1.60 | |
| O-Hcp | Al1 | 2.48 | −0.52 | Al3 | 2.47 | −0.53 |
| Al2 | 2.48 | −0.52 | O | 7.60 | +1.60 | |
| O-Top | Al | 1.90 | −1.10 | O | 7.22 | +1.22 |
| OH-Fcc | Al1 | 2.66 | −0.34 | O | 7.65 | +1.65 |
| Al2 | 2.66 | −0.34 | H | 0.34 | −0.66 | |
| Al3 | 2.66 | −0.34 | ||||
| OH-Hcp | Al1 | 2.65 | −0.35 | O | 7.61 | +1.61 |
| Al2 | 2.65 | −0.35 | H | 0.40 | −0.60 | |
| Al3 | 2.65 | −0.35 | ||||
| OH-Top | Al | 2.05 | −0.95 | O | 7.49 | +1.49 |
| H | 0.35 | −0.65 | ||||
| O-Tet | Al1 | 2.55 | −0.45 | Al4 | 2.55 | −0.45 |
| Al2 | 2.55 | −0.45 | O | 7.81 | +1.81 | |
| Al3 | 2.55 | −0.45 | ||||
| O-Oct | Al1 | 2.61 | −0.39 | Al5 | 2.61 | −0.39 |
| Al2 | 2.61 | −0.39 | Al6 | 2.61 | −0.39 | |
| Al3 | 2.61 | −0.39 | O | 8.13 | +2.13 | |
| Al4 | 2.61 | −0.39 | ||||
| OH-Tet | Al1 | 2.50 | −0.50 | Al4 | 2.68 | −0.32 |
| Al2 | 2.50 | −0.50 | O | 7.82 | +1.82 | |
| Al3 | 2.50 | −0.50 | ||||
| Al4 | 2.77 | −0.23 | Al | 2.76 | −0.24 | |
| Al5 | 2.77 | −0.23 | H | 2.13 | +0.13 | |
| Al6 | 2.77 | −0.23 |
Starting with the absorption of the O and the O–H group on the (111) surface of aluminium. At the Top position, the charge of the O atom increased by 1.22, while the charges at the Hcp and Fcc positions are both 1.60 (the charge at the Fcc position is slightly larger than that at the Hcp position). When the hydrogen atom enters, the charge transferred to the oxygen atom increases. However, the number of atoms at the Hcp and Fcc positions is still higher than that at the Top position. These results correspond exactly to the calculated adsorption energy.
3.2 Occupancy and migration processes within the crystal of aluminum
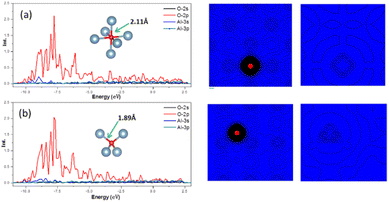
In crystal of aluminum, there were two solid solution positions: the octahedral (Oct) interstitial position and the tetrahedral (Tet) interstitial position. For O atom, the binding energy at the Oct interstitial position was much smaller than that at the Tet interstitial position, indicating that the Tet interstitial position is more stable. In general, the octahedral interstitial position has a larger space in face-cantered cubic crystal. The radius of O atom is 0.74 Å, whereas the radius of the octahedral and tetrahedral interstitial spheres of the lattice of aluminum were found to be 0.146a and 0.080a, respectively, where a is the lattice constant of the crystal of aluminum.29 Thus, O atoms should easily occupy and remain stable in the octahedral interstitial positions. This could be caused by the formation of solid solution which is related to the electronegativity difference and bonding type between the atoms. Fig. 4 shows that there is a significant charge transfer between the Al atoms and O atoms. The density of states results (Fig. 4) show that the 2p orbital of O atoms resonates with the 3s orbital of the Al atoms, indicating the formation of a chemical bond. The differential charge density shows that at the Oct interstitial position, the O atom obtains electrons to form ionic bonds. However, at the Tet interstitial position, the O atom forms an ionic bond and contributes part of the electrons to form covalent bonds. The O–Al bond length at the Tet interstitial position is closer to that in alumina (there are two bond lengths between O atoms and Al inside alumina: 1.89 Å and 1.93 Å).54,55 This indicates that chemical bonds which are similar to those in the compound can also be formed in a solid solution system. This system is formed between elements with a large difference in electronegativity when the solubility is insufficient to form a compound. This phenomenon was confirmed in other interstitial solid solution systems.56–59As shown in Table 3, in the case of the occupation of the O atom and O–H group within the crystal of aluminium, the charge transferred to the O atom at the Tet position is much lower than that at the Oct position. These results suggest the same outcome as the binding energy calculation, indicating that the occupation of the O atom at the Tet position is more stable. When it comes to the O–H group, the result shows that the charge transferred to the O atom is nearly the same as that of the O atom at the Tet position. Here, the Al atom has been divided into two parts. One part is a tetrahedron centered on oxygen atoms, and the other is a tetrahedron centered on hydrogen. And the charge transferred to the O atom is slightly larger when there is an H atom present compared to when there is no H atom. The presence of an H atom indicates that the occupation of the O atom becomes more unstable, making migration easier.
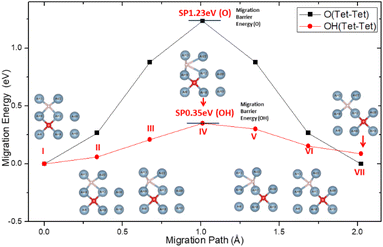
Inside Al crystals, the O atom occupies the tetrahedral interstitial positions and the migration of O between the interstitial positions of the stable tetrahedron becomes more difficult. For which the migration activation energy is as high as 1.23 eV, as shown in Fig. 5. This is consistent with the results reported in the literature.60
When H atoms are introduced into the solid solution system of O in the crystal of aluminum, H atoms will occupy the interstitial positions of the tetrahedron of the lattice and form a diagonal space relationship with the interstitial O atoms in the nearest neighbour space according to the formation energy result.
The presence of H atoms aggravates the distortion of the Al lattice around the O atoms, making it easier for the O atoms to migrate between the interstitial positions of the tetrahedron. The activation energy on the migration path was greatly reduced from the original 1.23 eV to 0.35 eV, which is the energy barrier for the migration of O atoms on the surface of aluminum. This indicates that the migration and diffusion processes of O atoms in the crystals of aluminum are easier than when there are H atoms in the crystal.
In addition, the easier migrating of atoms will not cause any accumulation to hinder further oxidation on the surface. This can be attributed to the coupling action of H atoms and O in the migration process, as shown in the inserts in Fig. 5. Until it reached the SP, the migration of O atom was found to drive the adjustment of the surrounding Al atoms. Although the H atoms also follow the same diffusion path, the O–H spacing gradually increases (points I–III on Fig. 5). At the SP, the system energy was the highest along the migration path, and the distance between the H atom and the Al atom (No. 12 and No. 22) was maximized (point IV on Fig. 5). After the SP, the system energy began to decrease, and the H–Al distance gradually recovered (points V–VII on Fig. 5). This may be attributed to the spatial occlusion, because the process of H–Al distance change is not a sudden change. The phenomenon of following of H atom and adjustment of the surrounding Al atoms can be attributed to the polarization of the local Al atoms under the influence of the H added O atoms. Furthermore, the competition between H, Al, and O slows the energy fluctuation during migration.
The O atom occupies the Tet interstitial position in Al crystals stably and it migrates with difficulty due to the higher activation energy required. When the H atom is nearby, the H atom will occupy the interstitial position of the tetrahedron of the crystal lattice and form a diagonal relationship with the O atom in the nearest neighbour space. As the diffusion of the H atom follows that of the O atom and due to the adjustment of surrounding Al atoms, the energy barrier is reduced. Thus, the internal migration of O becomes comparable to the surface migration.
Based on the adsorption and migration behaviour on the (111) surface of Al, pass through the surface to crystal (migration only) and inside the crystal, we can guess that it is still difficult for O atoms to enter the crystal of aluminum to achieve further oxidation when anions reach the M/O surface, which is due to the O atoms very easily bonding with Al atoms and migrating quickly on the surface of aluminum to form a dense and stable oxide layer, even if there are vacancies after Al cations diffuse.
Result of the O–H effect after the introduction of H atoms, the behaviour of O atoms on the surface of aluminum and inside the crystal of aluminum is affected. On the one hand, the “abstract” effect of H atoms significantly reduces the energy barrier for O atoms to penetrate into the crystal from the surface of aluminum; on the other hand, the following and coordinating role of H atoms significantly lower the energy barrier of void O atoms migration inside the crystal of aluminum. Thus, H atoms have an important influence on the oxidation of Al. According to the calculations in this paper, the growth rate of the oxide layer depends on the concentration of H atoms under the situation of without considering the effect of electric field and the migration of cations (Al3+). For the resource of H atoms, it can be considered that if H atoms are from the dissociation of OH ions at the M/O interface, then the growth rate of the oxide layer depends on the pH value of the electrolyte. It is not difficult to understand that in the electrolyte close to neutral, high OH concentration leads to the rapid growth of oxide layer and finally forms dense barrier oxide. However, in the anodic oxidation of acidic solution, the concentration of H atoms at the M/O interface is limited by a smaller number of hydroxide ions, which leads to the balance of oxidation and dissolution rates and finally realized a porous oxide.
4. Conclusions
To elucidate the behaviour of the ions in the anodic reaction during the anodizing of aluminium, the first-principles calculations were used to study the influence of H atoms on the surface behaviour of O atoms on the (111) surface of Al and its infiltration behaviour into the crystal phase. The main conclusions are as follows:(1) In the process of Al oxidation, the “abstract” effect of H atoms greatly reduces the energy barrier for O entering the crystal of aluminum, from 1.52 eV to 0.78 eV, which is from the dissociation of O–H atomic groups.
(2) The introduction of H atom also effects the diffusion of O atom in the crystal of aluminum, which can significantly reduce the activation energy for O atom to migrate between the tetrahedral interstitial positions, from 1.23 eV to 0.34 eV. This is due to the following and coordinating effect of H atom on O atom during the migration process.
It is helpful for us to understand the anodic oxidation process and ion transport process.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Key Projects in Hubei Province (Grant No. 2022BGE251 and 2022BAD005), the Key Projects in Wuhan City (2022012202015030), and Key Program for Intergovernmental S&T Innovation Cooperation Projects of National Key R&D Program of China (2022YFE0138100). The author would also like to thank Professor Li Zongbao from Wuhan Textile University for his assistance during the paper revision process.References
- K. S. Thamida and H. C. Chang, Chaos, 2002, 12(1), 240–251 CrossRef PubMed.
- D. S. Grzegorz, Introduction to Anodization of Metals, Elsevier, Amsterdam, Netherlands, 2020, pp. 1–34 Search PubMed.
- F. Keller, M. S. Hunter and D. L. Robinson, J. Electrochem. Soc., 1953, 100, 411 CrossRef CAS.
- H. Masuda and K. Fukuda, Science, 1995, 268, 1466–1468 CrossRef CAS PubMed.
- J. Oh and C. V. Thompson, Electrochim. Acta, 2011, 56(11), 4044–4051 CrossRef CAS.
- J. P. O'Sullivan and G. C. Wood, Proc. R. Soc. A, 1970, 317(1531), 511–543 Search PubMed.
- T. P. Hoar and N. F. Mott, J. Phys. Chem. Solids, 1959, 9(2), 97–99 CrossRef CAS.
- P. Skeldon, G. E. Thompson and S. J. Garcia-Vergara, et al, Electrochem. Solid-State Lett., 2006, 9(11), B47 CrossRef CAS.
- J. E. Houser and K. R. Hebert, Nat. Mater., 2009, 8(5), 415–420 CrossRef CAS PubMed.
- H. Ghaforyan and M. J. Ebrahimzadeh, J. Mater. Sci. Eng. B, 2011, 1(1), 82–85 CAS.
- O. Jessensky, F. Muller and U. Gosele, Appl. Phys. Lett., 1998, 72(10), 1 CrossRef.
- X. F. Zhu, D. D. Li and Y. Song, et al, Mater. Lett., 2005, 59(24/25), 3160–3163 CrossRef CAS.
- X. F. Zhu, L. Liu and Y. Song, et al, Chem. Mon., 2008, 139(9), 999–1003 CrossRef CAS.
- X. F. Zhu, L. Liu and Y. Song, et al, Mater. Lett., 2008, 62(24), 4038–4040 CrossRef CAS.
- D. Losic and A. Santos. Nanoporous Alumina, Springer, 2015, pp. 1–30 Search PubMed.
- N. F. Mott, Trans. Faraday Soc., 1947, 43, 472–483 RSC.
- N. Cabrera and N. F. Mott, Rep. Prog. Phys., 1949, 12, 163–184 CrossRef CAS.
- E. J. W. Verwey, Physica, 1935, 2(1), 1059–1063 CrossRef CAS.
- J. F. Dewald, Acta Metall., 1954, 2(2), 340–341 CrossRef.
- J. F. Dewald, J. Electrochem. Soc., 1955, 102, 1–6 CrossRef CAS.
- C. Y. Chao, L. F. Lin and D. D. Macdonald, J. Electrochem. Soc., 1981, 128, 1187–1194 CrossRef CAS.
- D. D. Macdonald, J. Electrochem. Soc., 1992, 139, 3434–3449 CrossRef CAS.
- D. D. Macdonald, S. R. Biaggio and H. Song, J. Electrochem. Soc., 1992, 139, 170–177 CrossRef CAS.
- D. D. Macdonald, J. Electrochem. Soc., 1993, 140, L27–L30 CrossRef CAS.
- L. Zhang, D. D. Macdonald and E. Sikora, et al, J. Electrochem. Soc., 1998, 145, 898–905 CrossRef CAS.
- M. M. Lohrengel, Mater. Sci. Eng., R, 1993, 11(6), 243–294 CrossRef.
- A. Güntherschulz and H. Betz, Z. Phys., 1931, 68, 145–161 CrossRef.
- A. Güntherschulz and H. Betz, Z. Phys., 1934, 92(5–6), 367–374 CrossRef.
- P. P. Xu, S. Y. Sun and S. Y. Sun, et al, Chem. Phys. Lett., 2020, 744, 137237 CrossRef CAS.
- K. Giewont, E. A. Kyriakidou and E. A. Walker, J. Phys. Chem. C, 2021, 125, 15262–15274 CrossRef CAS.
- Y. Zhang, J. Zhang, H. Wang, W. Yang, C. Wang, Y. Peng, J. Chen, J. Li and F. Gao, J. Phys. Chem. C, 2022, 126, 8720–8733 CrossRef CAS.
- S. Sun, S. Sun, Y. Ren, X. Tan and P. Xu, Surf. Interface Anal., 2019, 52, 167–173 CrossRef.
- J. Cao, Z. Liang, Z. Li, B. Jin, Y. Liu, Y. Zhu, S. Wang, B. Dong and C. Wu, Adv. Energy Sustainability Res., 2022, 3(9), 2200076 CrossRef CAS.
- B. Chatterjee and J. Kolorenč, Phys. Rev. B: Condens. Matter Mater. Phys., 2021, 103(20), 205146 CrossRef CAS.
- J. Cao, C. Duan, Z. Li, B. Jin, J. Li, L. Wan, L. Zhao, B. Dong and C. Wu, ACS Mater. Lett., 2023, 5, 970–978 CrossRef CAS.
- A. Luo and J. Chen, Appl. Surf. Sci., 2022, 595, 153553 CrossRef CAS.
- Z. Tayyab, S. Rauf, M. Bilal Hanif, H. I. Ahmad Qazi, N. Mushtaq, M. Motola, S. Yun, C. Xia, D. A. Medvedev, M. I. Asghar, A. N. Alodhayb, A. Hussain, M. K. Majeed, R. Iqbal, A. Saleem, W. Xu and Y. Yang, Chem. Eng. J., 2024, 482, 148750 CrossRef CAS.
- Z. Siwei, W. Lizhen and L. Chen, et al, Electrochem. Commun., 2018, 93, 25–30 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 50(24), 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS PubMed.
- M. C. Payne, M. P. Teter and D. C. Allan, et al, Rev. Mod. Phys., 1992, 64(4), 1045–1097 CrossRef CAS.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40(6), 3616–3621 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11185 CrossRef CAS PubMed.
- D. Eisenberg and W. Kauzmann, The Structure and Properties of Water, Claderon Press, Oxford, UK, 2006, pp. 11–270 Search PubMed.
- J. U. Xue-Hai, Environ. Chem., 2007, 3, 347–351 Search PubMed.
- S. Alvarez-Barcia and J. R. Flores, Chem. Phys., 2010, 374, 131–137 CrossRef CAS.
- X. Jin and Y. Yan, Environ. Chem., 2013, 32(07), 1123–11228 CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 16(4), 1746–1747 Search PubMed.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113(22), 9978–9985 CrossRef CAS.
- F. Libisch, C. Huang, P. Liao, M. Pavone and E. A. Carter, Phys. Rev. Lett., 2012, 109(19), 198303 CrossRef PubMed.
- Y. Yourdshahyan, B. Razaznejad and B. I. Lundqvist, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 075416 CrossRef.
- M. Schmid, G. Leonardelli and R. Tscheließnig, Surf. Sci., 2001, 478(3), L355–L362 CrossRef CAS.
- A. J. Komrowski, J. Z. Sexton and A. C. Kummel, et al, Phys. Rev. Lett., 2001, 87(24), 246103 CrossRef CAS PubMed.
- E. R. Dobrovinskaya, L. A. Lytvynov and V. Pishchik, Properties of Sapphire, Springer, New York, USA, 2009 Search PubMed.
- S. Y. Sun, P. P. Xu and B. Y. Ma, et al, Comput. Mater. Sci., 2019, 157, 37–42 CrossRef CAS.
- B. Y. Ma, A. Zhang and H. L. Shang, Acta Phys. Sin., 2014, 63(13), 136801 CrossRef.
- S. Y. Sun, H. L. Shang and B. Y. Ma, et al, Comput. Mater. Sci., 2018, 142, 325–331 CrossRef CAS.
- S. Y. Sun, C. Ding and Y. Ren, et al, Comput. Mater. Sci., 2019, 170, 109159 CrossRef CAS.
- I. Matsui, S. Ono and Y. Hanaoka, et al, Philos. Mag. Lett., 2014, 94(2), 63–71 CrossRef CAS.
- A. J. Ross, H. Z. Fang and S. L. Shang, Comput. Mater. Sci., 2017, 140, 47–54 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |

![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ).
).