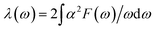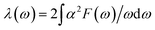Open Access Article
Open Access ArticleStructure searches and superconductor discovery in XB2 (X = Sc, Ti, V, Cr, and Tc)†
Jingjing Meng a,
Pengyu Zhenga,
Yiran Penga,
Rui Liua,
Ying Yanga and
Zhiping Yin
a,
Pengyu Zhenga,
Yiran Penga,
Rui Liua,
Ying Yanga and
Zhiping Yin *ab
*ab
aDepartment of Physics, Center for Advanced Quantum Studies, Beijing Normal University, Beijing 100875, China. E-mail: yinzhiping@bnu.edu.cn
bKey Laboratory of Multiscale Spin Physics, Ministry of Education, Beijing Normal University, Beijing 100875, China
First published on 2nd April 2024
Abstract
With extensive structure searches for XB2 (X = Sc, Ti, V, Cr, and Tc) under pressures up to 100 GPa, we uncovered that the crystal structures of these compounds with the lowest enthalpy have the same space group (P6/mmm) as MgB2 at ambient pressure. Among them, ScB2, TiB2 and VB2 are dynamically stable at ambient pressure, but they do not superconduct. CrB2 becomes dynamically stable at 108 GPa and shows superconductivity with a transition temperature (Tc) of 26.0 K. TcB2 is not dynamically stable until 9 GPa. At 20 GPa, it has a Tc of 23.5 K. Further calculations indicate that CrB2 and TcB2 are also thermodynamically stable, suggesting that it is highly likely that they can be synthesized successfully in the laboratory. We found that transition metal atoms (Cr/Tc) dominate soft phonon vibrations and make significant contributions to the electron–phonon coupling (EPC) and superconductivity in CrB2/TcB2, which is in strong contrast to the case of MgB2, where high-frequency B vibrations dominate the EPC and superconductivity. Our work enriches the understanding of superconductivity in transition metal borides.
1 Introduction
Searching for high transition temperature (high-Tc) superconductors has been an active research area in condensed matter physics and material sciences for a long time. Since the discovery of superconductivity in 2001, MgB2 has attracted the attention of researchers worldwide. Extensive work has been done on this compound,1–14 including some impressive theoretical investigations that have provided important insights.1–5,14 MgB2 is a conventional BCS superconductor with a Tc of 39 K.15 First-principles calculations have revealed its electronic structure, phonon spectra, and EPC.3,12,13 As a metallic layered compound10 with multiple bands crossing the Fermi level, MgB2 comprises fully ionized Mg atoms5 and exhibits strong covalent bonds among B atoms within its honeycomb layer. Moreover, this compound manifests metallic bonds between different B layers, contributing to its distinctive characteristics.3 Further research indicates that the E2g mode involving the in-plane vibration of two boron ions in opposite directions contributes significantly to its superconductivity.2 Given the remarkable performance of MgB2, researchers have turned to investigating other boride compounds,16–35 such as LiBC and Ca–B, Be–B, and Y–B binary compounds. Many materials, for example, B24, MgB6, GaB5, InB6, and CaB6, have been confirmed to be superconductors.16,19,20,29,36 However, the Tc of these superconductors is generally much lower than that of MgB2.Transition metal borides have usually appeared as superhard materials in previous studies. For example, TiB2, the compound with the lowest density and highest hardness among the metal borides, is an important modern ceramic material.37 In recent years, with an improvement in experimental equipment, researchers have been able to obtain new materials under very high pressures in the laboratory. For example, in 2015, SH3 was synthesized and compressed up to 250 GPa experimentally by A. Drozdov et al. using a diamond anvil cell (DAC),38 which has a Tc value between 191 K and 204 K at 200 GPa.38,39 With this technique, a transition-metal boride MoB2 was experimentally discovered at about 100 GPa, which sparked great excitement among researchers because it has a high Tc of 32 K.36 This breakthrough indicates it would be interesting to investigate other transition metal borides.
In this work, we search the crystal structures of five transition metal borides (ScB2, TiB2, VB2, CrB2, and TcB2) under pressures up to 100 GPa using an efficient structural prediction method called Crystal Structure Analysis by Particle Swarm Optimization (i.e., the CALYPSO code).40–42 We find that the crystal structures of XB2 (X = Sc, Ti, V, Cr, and Tc) with the lowest enthalpy have the same space group (P6/mmm) as MgB2 at ambient pressure. Among them, ScB2, TiB2 and VB2 are dynamically stable without superconductivity at ambient pressure. CrB2 and TcB2 become dynamically stable under 108 GPa and 9 GPa, respectively. CrB2 and TcB2 are conventional superconductors with high EPC strength and superconducting temperatures up to 26.0 K (at 108 GPa) and 23.5 K (at 20 GPa), respectively. The strong electron–phonon coupling comes mostly from low-frequency acoustic phonon modes involving mainly vibrations of the transition metal atoms, whose d electrons dominate electronic states around the Fermi level. This is in strong contrast to MgB2 whose moderate electron–phonon coupling is mainly contributed by B atoms. Interestingly, the electron–phonon coupling and superconducting temperature in TcB2 show very weak pressure dependence in the studied pressure range of 20–100 GPa.
2 Computational methods
We explore the crystal structures of XB2 (X = Sc, Ti, V, Cr, and Tc) from ambient pressure to 100 GPa using fixed composition calculations with cells containing 1–4 formula units implemented in the CALYPSO code.40–42 In this study, the number of generations is set to 50, and the population size is set to 30. Crystal structures are generated randomly in the first generation. In each subsequent generation, 60% of the structures are generated from the lowest-enthalpy structures provided by the previous generation; the remaining 40% are generated randomly.The CALYPSO software employs a set of special structural evolution techniques.40–42 However, it relies on third-party software to optimize and compute the enthalpies of the crystal structures generated by CALYPSO. In this study, we employ the VASP code43,44 to relax the structures with the generalized gradient approximation (GGA)45 employing the projected augmentation wave method.46 We employ a plane-wave cut-off energy of 420 eV and k-mesh with a grid spacing of 0.20 Å−1. The relaxation continues until the forces on all atoms become smaller than 10−3 eV Å−1 while maintaining an electronic self-consistency threshold of 10−6 eV per cell.
Finally, we select the crystal structure with the lowest enthalpy of each composition under various pressures produced by CALYPSO and calculate their electronic properties using VASP. To further investigate the lattice dynamics and electron–phonon coupling of these materials, we employ density functional perturbation theory (DFPT)47 implemented in the QUANTUM ESPRESSO48 package to compute these properties. The Perdew–Burke–Ernzerhof (PBE)49 exchange-correlation function is utilized, along with 18 × 18 × 18 Monkhorst–Pack k-point grids. Norm-conserving PBE pseudopotentials50 with a cutoff energy of 90 Ry are used for wave functions. Dynamical matrices are calculated on a 6 × 6 × 6 q-point mesh. Finally, we estimate the superconducting critical temperature (Tc) using the Allen–Dynes–McMillan equation51 with a typical value of the Coulomb pseudopotential μ* = 0.1.
3 Theoretical background
According to the Bardeen–Cooper–Schrieffer (BCS) theory of superconductivity, there is a relationship among the superconducting transition temperature Tc, the typical phonon energy 〈ω〉 and interaction strength N(0)V:52| Tc = 1.14〈ω〉exp[−1/N(0)V]. | (1) |
Since the BCS theory was proposed,53 significant advances have been made in comprehending the role of the electron–phonon interaction in normal and superconducting metals.52 Among them, the Eliashberg equations represent the state of the art in the theory of conventional superconductivity.52 Subsequently, the most extensive study of the relation between microscopic theory and observed superconducting transition temperature was made by McMillan. The McMillan equation is a significant accumulation of microscopic information on strong-coupling superconductors by solving the finite-temperature Eliashberg theory to find Tc.51 The total EPC constant λ is obtained via the isotropic Eliashberg function:51,52,54
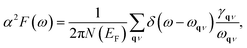 | (2) |
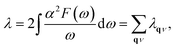 | (3) |
The parameter λ, which roughly corresponds to N(0)V in the BCS theory, serves as a dimensionless measure of the strength of α2F.
α2F(ω) is the Eliashberg function, F(ω) is the phonon density of states, α2 is an average of the electron–phonon interaction, N(EF) is the DOS at the Fermi level, ωqν is the phonon frequency of the νth phonon mode with wave vector q, and γqν is the phonon linewidth, which can be estimated by51
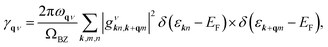 | (4) |
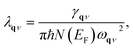 | (5) |
Tc is estimated using the McMillan–Allen–Dynes formula:51
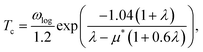 | (6) |
The hysteretic Coulomb pseudopotential μ* in eqn (6) is set to a typical value of 0.1, and the logarithmic average of the phonon frequencies ωlog is defined as51
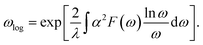 | (7) |
4 Results and discussions
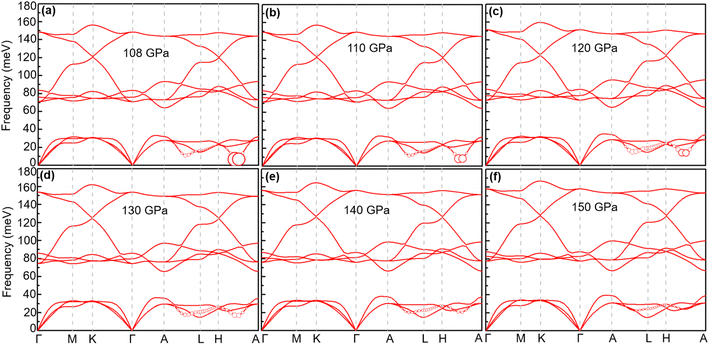
In our structural searches, ScB2, TiB2 and VB2 are dynamically stable at ambient pressure with no imaginary frequency in their phonon–dispersion curves (shown in Fig. S1†). Table SI† shows that their formation enthalpies are −0.85, −1.08, and −0.73 eV per atom, respectively. The EPC strength is 0.28 for ScB2, 0.1 for TiB2 and 0.3 for VB2, which are too weak to support conventional superconductivity in these materials. Information on their crystal structures is shown in Table SI.†The phonon–dispersion curve of CrB2 has imaginary frequencies under pressures until 108 GPa. For TcB2, it turns to be dynamically stable at 9 GPa. However, the phonon–dispersion curves of TcB2 exhibit a significant softening at 9 GPa and 10 GPa (shown in Fig. S2†), suggesting that the structures may be unstable in the laboratory. Therefore, we discuss the physical properties of TcB2 at 20 GPa as being typical. In the following, we will focus on investigating the crystal structures, electronic properties, lattice dynamics and superconductivity of CrB2 at 108 GPa and TcB2 at 20 GPa.
4.1 Physical properties of CrB2
| Compound | Lattice parameters (Å) | λ | ωlog (meV) | Tc (K) | Pressure (GPa) | Formation enthalpy (eV per atom) | Bond lengths (Å) | ||
|---|---|---|---|---|---|---|---|---|---|
| a | c | B–B | Cr–B | ||||||
| CrB2 | 2.8 | 2.62 | 1.4 | 21.2 | 26.0 | 108 | −1.30 | 1.61 | 2.08 |
| CrB2 | 2.75 | 2.56 | 0.75 | 38.9 | 18.3 | 150 | −1.36 | 1.59 | 2.04 |
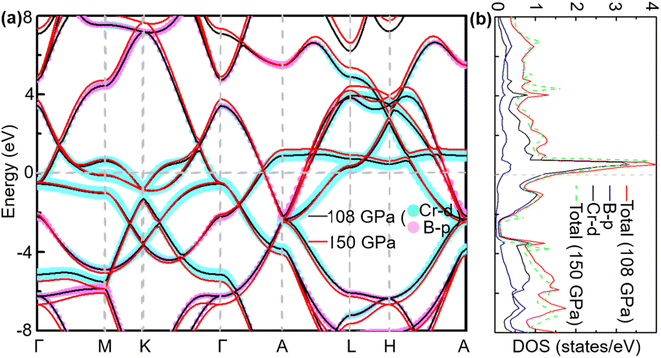
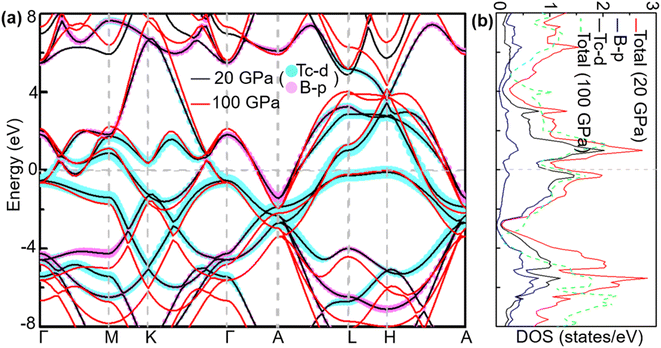
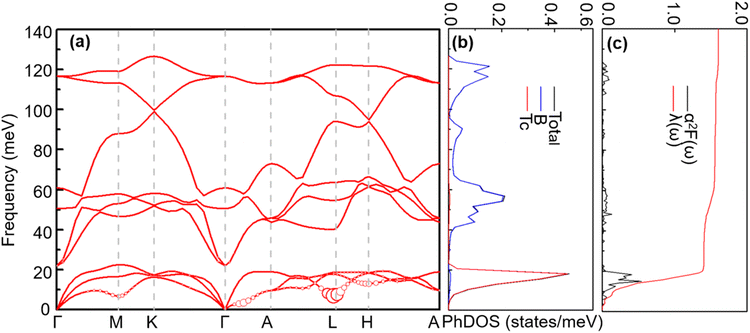
To analyse electronic properties, we plot the band structure and electronic density of states (DOS) in Fig. 1. Herein, we project Cr-d orbitals and B-p orbitals (relevant to our discussion) onto the band structure. The orbital-resolved band structure shows metallic characteristics with three bands crossing the Fermi level. The DOS reveals that overlaps between the two elements are moderate, and the total DOS at the Fermi level is 1.49 states per eV. As can be seen in Fig. 1, Cr-d orbitals play a dominant role around the Fermi level. Since the EPC parameter λ corresponds roughly to N(EF)V in the BCS theory, we can speculate that Cr-d orbitals near the Fermi level are closely related to EPC and superconductivity in CrB2. Comparison of band structures at 108 GPa and 150 GPa reveals that most bands around the Fermi level remain unchanged except those near the A point, resulting in nearly identical Fermi surfaces. Therefore, the pressure has little effect on its Fermi surfaces. However, a decrease of approximately 8.1% in the total DOS at the Fermi level is observed at 150 GPa from that at 108 GPa (Fig. 2).
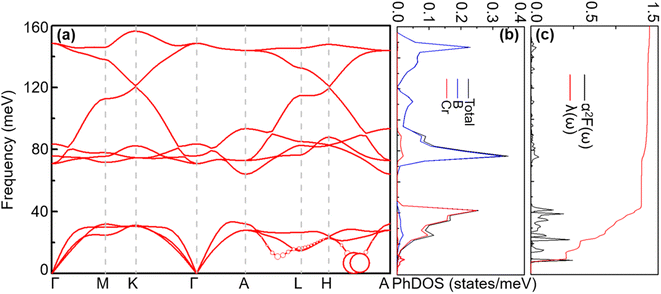
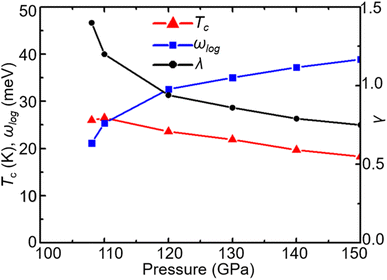
With increasing pressure, as shown in Fig. 4, Tc rises slightly at 110 GPa and later shows a decreasing tendency. According to the phonon dispersion curves with the strength of mode- and q-resolved λqν illustrated in Fig. 5, all phonon modes shift towards higher frequencies with increasing pressure, as expected. Meanwhile, there is an apparent decrease in the aforementioned strong electron–phonon coupling of the acoustic phonon mode around the q point (0.167, 0.167, and 0.5) with increasing pressure, accompanied by hardening of the corresponding phonon mode. Taking 108 GPa and 150 GPa for example, the logarithmic average phonon frequency (ωlog) increases from 21.2 meV to 38.9 meV, whereas the EPC parameter (λ) decreases from 1.40 to 0.75, as shown in Table 1. As a result, Tc decreases from 26 K to 18.3 K.
4.2 Physical properties of TcB2
| Compound | Lattice parameters (Å) | λ | ωlog (meV) | Tc (K) | Pressure (GPa) | Formation enthalpy (eV per atom) | Bond lengths (Å) | ||
|---|---|---|---|---|---|---|---|---|---|
| a | c | B–B | Tc–B | ||||||
| TcB2 | 2.9 | 3.31 | 1.61 | 16.7 | 23.5 | 20 | −0.31 | 1.68 | 2.36 |
| TcB2 | 2.76 | 3.15 | 0.97 | 26.8 | 20.6 | 100 | −0.87 | 1.59 | 2.24 |
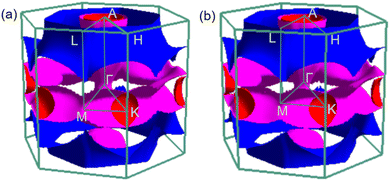
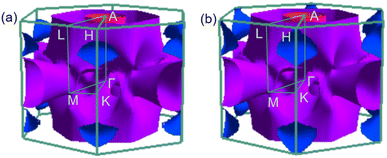
As shown in Fig. 6, the electronic structure of TcB2 is similar to that of CrB2. The DOS near the Fermi level is mostly contributed by Tc-d orbitals, whereas the B-p orbitals contribute only a rather small portion. The band structure with four bands crossing the Fermi level shows metallic characteristics. The total DOS at the Fermi level is 1.34 states per eV at 20 GPa. Compared with CrB2, the DOS of TcB2 is not so localized and is more evenly distributed around the Fermi level. With increasing pressure from 20 GPa to 100 GPa, the total DOS at the Fermi level decreases by 10.5%. The band shifting around the Fermi level is more pronounced than that in CrB2. The most significant distinction among the Fermi surfaces can be observed in the blue region shown in Fig. 7, where an enlargement occurs around these sheets under increasing pressure. Furthermore, there is an increase in size for the spherical Fermi surface centered at point A.
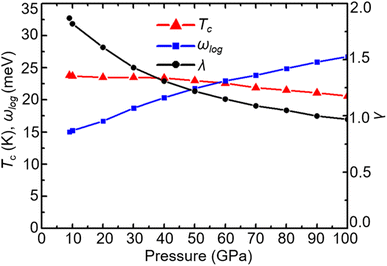
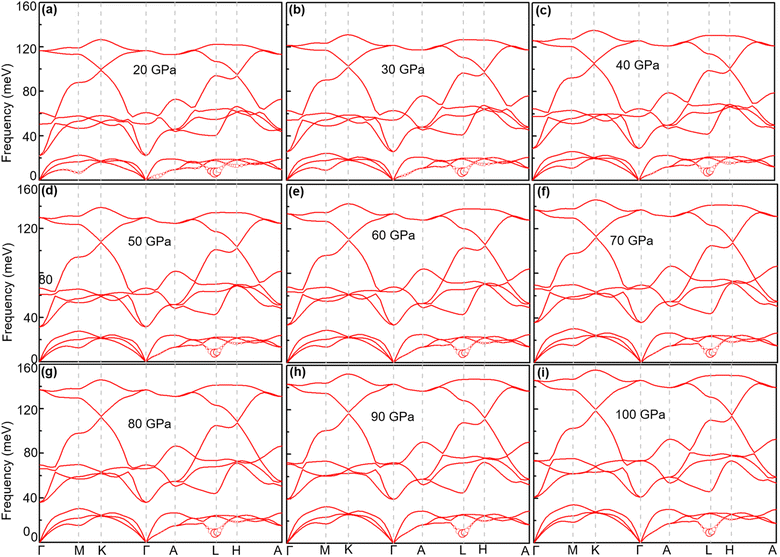
When the pressure increases from 20 GPa to 100 GPa, while the logarithmic average phonon frequency ωlog increases, the total EPC λ and superconducting temperature Tc decrease with pressure, as shown in Fig. 9. Fig. 10 shows the phonon spectra with mode- and momentum-dependent EPC λqν of TcB2 at different pressures from 20 GPa to 100 GPa. It is evident that all the phonon modes are shifted to higher frequencies with increasing pressure. As shown in Table 2, the logarithmic average phonon frequency increases from 16.7 meV at 20 GPa to 26.8 meV at 100 GPa, whereas the total EPC λ decreases from 1.61 to 0.97, and the superconducting temperature Tc decreases from 23.5 K to 20.6 K correspondingly. In contrast to CrB2, the aforementioned most important phonon mode, i.e., the acoustic phonon mode around point L dominated by in-plane vibrations of the Tc atoms, shows little change in the mode-dependent EPC λqν and almost no hardening of the phonons with increasing pressure. Instead, the EPC λqν of the lowest acoustic phonon along Γ–A and around point H decrease substantially with increasing pressure, which is responsible for the corresponding reduction of the total EPC and EPC λ and superconducting temperature Tc as the pressure increases. As a result, the decreasing rate of the total EPC λ with increasing pressure in TcB2 is only half the value in CrB2 (0.008/GPa vs. 0.015/GPa). More importantly, this leads to a much slower rate of decrease of the superconducting temperature Tc of 0.036 K GPa−1 in TcB2 compared to 0.18 K GPa−1 in CrB2 over the pressure range studied.
5 Conclusion
We carried out an extensive structure search and found that all five XB2 (X = Sc, Ti, V, Cr, and Tc) crystallize in the P6/mmm space group under pressures up to 100 GPa. Unlike MoB2, which has a structural phase transition at 70 GPa, none of the XB2 (X = Sc, Ti, V, Cr, and Tc) undergoes a phase transition below 100 GPa. Among them, ScB2, TiB2, and VB2 are dynamically stable at ambient pressure but are not conventional superconductors. On the other hand, CrB2 becomes dynamically stable when it transforms into a conventional superconductor at 108 GPa with a critical superconducting temperature Tc of 26.0 K. With increasing pressure, its Tc rises slightly at 110 GPa and gradually decreases to 18.3 K at 150 GPa. TcB2 is also a conventional superconductor within the pressure range 20–100 GPa, with less dependence of Tc on pressure. Its Tc is 23.5 K at 20 GPa and 20.6 K at 100 GPa. In addition, the negative formation enthalpy and absence of imaginary phonon frequency suggest that it is possible to synthesize both CrB2 and TcB2 successfully in experiments.In both CrB2 and TcB2, the electronic states around the Fermi level mainly come from the d electrons of the transition metal atoms Cr/Tc, suggesting the electron–phonon coupling is dominated by the transition metal atoms instead of boron atoms, in strong contrast to MgB2 where the EPC comes mainly from the B atoms. Most of the strong total EPC (λ > 1) in both CrB2 and TcB2 comes from the low-frequency acoustic phonon modes involving vibrations of the transition metal atoms, which is similar to the case of MoB2.36 In CrB2, the acoustic phonon mode around q = (0.167, 0.167, and 0.5) with Cr atoms moving along the c-axis has dominated the EPC mode, which decreases rapidly with increasing pressure. On the contrary, in TcB2, the acoustic phonon mode around the L point (0.5, 0, and 0.5) with Cr atoms moving in the ab-plane has dominated the EPC mode, which shows very weak pressure dependence. As a result, the superconducting temperature in TcB2 has very weak pressure dependence. Combined with the relatively low pressure of 20 GPa and high Tc of 23.5 K, TcB2 is perhaps the most interesting transition metal boride studied so far.
Author contributions
Z. P. Yin conceived and directed this project. J. J. Meng performed structure searches and DFT and DFPT calculations. All the authors participated in discussing the results and writing the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 12074041 and 11674030) and the National Key Research and Development Program of China through Contract No. 2016YFA0302300. The calculations were carried out using the high-performance computing cluster of Beijing Normal University in Zhuhai.Notes and references
- H. J. Choi, D. Roundy, H. Sun, M. L. Cohen and S. G. Louie, Nature, 2002, 418, 758–760 CrossRef CAS PubMed.
- J. A. Alarco, A. Chou, P. C. Talbot and I. D. Mackinnon, Phys. Chem. Chem. Phys., 2014, 16, 24443–24456 RSC.
- I. Mazin and V. Antropov, Phys. C, 2003, 385, 49–65 CrossRef CAS.
- J. Alarco, P. Talbot and I. Mackinnon, Model. Numer. Simul. Mater. Sci., 2018, 8, 8374921–8374946 Search PubMed.
- J. Kortus, I. I. Mazin, K. D. Belashchenko, V. P. Antropov and L. L. Boyer, Phys. Rev. Lett., 2001, 86, 4656–4659 CrossRef CAS PubMed.
- J. M. Rowell, Supercond. Sci. Technol., 2003, 16, R17 CrossRef CAS.
- M. Eisterer, Supercond. Sci. Technol., 2007, 20, R47 CrossRef CAS.
- W. Kang, H.-J. Kim, E.-M. Choi, C. U. Jung and S.-I. Lee, Science, 2001, 292, 1521–1523 CrossRef CAS PubMed.
- F. Bouquet, Y. Wang, R. Fisher, D. Hinks, J. Jorgensen, A. Junod and N. Phillips, Europhys. Lett., 2001, 56, 856 CrossRef CAS.
- X. Xi, Rep. Prog. Phys., 2008, 71, 116501 CrossRef.
- C. Buzea and T. Yamashita, Supercond. Sci. Technol., 2001, 14, R115 CrossRef CAS.
- H. J. Choi, M. L. Cohen and S. G. Louie, Phys. C, 2003, 385, 66–74 CrossRef CAS.
- J. Kortus, Phys. C, 2007, 456, 54–62 CrossRef CAS.
- J. An and W. Pickett, Phys. Rev. Lett., 2001, 86, 4366 CrossRef CAS PubMed.
- J. Nagamatsu, N. Nakagawa, T. Muranaka, Y. Zenitani and J. Akimitsu, Nature, 2001, 410, 63–64 CrossRef CAS PubMed.
- S. Shah and A. N. Kolmogorov, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 014107 CrossRef.
- S. Okatov, A. Ivanovskii, Y. E. Medvedeva and N. Medvedeva, Phys. Status Solidi B, 2001, 225, R3–R5 CrossRef CAS.
- D. V. Rybkovskiy, A. G. Kvashnin, Y. A. Kvashnina and A. R. Oganov, J. Phys. Chem. Lett., 2020, 11, 2393–2401 CrossRef CAS PubMed.
- L. Yan, T. Bo, P.-F. Liu, L. Zhou, J. Zhang, M.-H. Tang, Y.-G. Xiao and B.-T. Wang, J. Mater. Chem. C, 2020, 8, 1704–1714 RSC.
- T. Bo, P.-F. Liu, L. Yan and B.-T. Wang, Phys. Rev. Mater., 2020, 4, 114802 CrossRef CAS.
- H. Rosner, A. Kitaigorodsky and W. Pickett, Phys. Rev. Lett., 2002, 88, 127001 CrossRef CAS PubMed.
- E. Deligoz, K. Colakoglu and Y. Ciftci, Solid State Commun., 2009, 149, 1843–1848 CrossRef CAS.
- K. Togano, P. Badica, Y. Nakamori, S. Orimo, H. Takeya and K. Hirata, Phys. Rev. Lett., 2004, 93, 247004 CrossRef CAS PubMed.
- Y. Liang, M. Xu, Z. Qu, S. Lin, J. Hao and Y. Li, J. Mater. Chem. C, 2021, 9, 8258–8264 RSC.
- K. Flachbart, S. Gabáni, J. Kačmarčik, T. Mori, S. Otani and V. Pavlík, AIP Conf. Proc., 2006, 850(1), 635–636 CrossRef CAS.
- H. Ozisik, E. Deligoz, K. Colakoglu and Y. Ciftci, Comput. Mater. Sci., 2011, 50, 1057–1063 CrossRef CAS.
- J. Meléndez-Martınez, A. Domınguez-Rodrıguez, F. Monteverde, C. Melandri and G. De Portu, J. Eur. Ceram. Soc., 2002, 22, 2543–2549 CrossRef.
- D. Portehault, S. Devi, P. Beaunier, C. Gervais, C. Giordano, C. Sanchez and M. Antonietti, Angew. Chem., Int. Ed., 2011, 50, 3262–3265 CrossRef CAS PubMed.
- Q. Yang, J. Lv, Q. Tong, X. Du, Y. Wang, S. Zhang, G. Yang, A. Bergara and Y. Ma, Phys. Rev. B, 2021, 103, 024505 CrossRef CAS.
- I. Felner, Phys. C, 2001, 353, 11–13 CrossRef CAS.
- P. Vajeeston, P. Ravindran and H. Fjellvåg, RSC Adv., 2012, 2, 11687–11694 RSC.
- G. Profeta, A. Continenza, F. Bernardini and S. Massidda, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 054502 CrossRef.
- A. Wallash, J. Crow and Z. Fisk, J. Magn. Magn. Mater., 1986, 54, 547–548 CrossRef.
- C. Giannelli, B. Jüttler and H. Speleers, Computer Aided Geometric Design, 2012, 29, 485–498 CrossRef.
- E. Sanz-Luque, F. Ocana-Calahorro, A. Galván and E. Fernández, Plant Signaling Behav., 2015, 10, e1042638 CrossRef PubMed.
- C. Pei, J. Zhang, Q. Wang, Y. Zhao, L. Gao, C. Gong, S. Tian, R. Luo, M. Li and W. Yang, Natl. Sci. Rev., 2023, 10, nwad034 CrossRef CAS PubMed.
- X. Huang, G. Tu, S. Wang, J. Song, Y. Liu and Z. Wang, Rare Met. Mater. Eng., 2022, 51(3), 1087–1099 CAS.
- A. Drozdov, M. Eremets, I. Troyan, V. Ksenofontov and S. I. Shylin, Nature, 2015, 525, 73–76 CrossRef CAS PubMed.
- D. Duan, Y. Liu, F. Tian, D. Li, X. Huang, Z. Zhao, H. Yu, B. Liu, W. Tian and T. Cui, Sci. Rep., 2014, 4, 6968 CrossRef CAS PubMed.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Physics, 2010, 82, 7174–7182 Search PubMed.
- J. Lv, Y. Wang, L. Zhu and Y. Ma, J. Chem. Phys., 2012, 137, 084104 CrossRef PubMed.
- Y. Wang, L. Jian, Z. Li and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS.
- G. G. Kresse and J. J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys, 1996, 54, 11169 CrossRef CAS PubMed.
- A. Gk and B. Jf, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef.
- J. P. Perdew and Y. Wang, Phys. Rev. B, 2018, 45, 13244 CrossRef PubMed.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys, 1994, 50, 17953–17979 CrossRef PubMed.
- S. Baroni, S. D. Gironcoli, A. Corso, S. Scuola, I. Superiore, I. Istituto, F. Materia, I. Trieste and P. Giannozzi, Rev. Mod. Phys., 2001, 73(2), 515 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- D. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085117 CrossRef.
- P. B. Allen and R. C. Dynes, Phys. Rev. B: Solid State, 1975, 12, 905–922 CrossRef CAS.
- W. McMillan, Phys. Rev., 1968, 167, 331 CrossRef CAS.
- J. Bardeen, L. N. Cooper and J. R. Schrieffer, Phys. Rev., 1957, 108, 1175 CrossRef CAS.
- H.-D. Liu, Y.-P. Li, L. Yang, N. Jiao, M.-M. Zheng, H.-Y. Lu and P. Zhang, Phys. Rev. B, 2022, 105, 224501 CrossRef CAS.
- E. Deligoz, K. Colakoglu, H. Ozisik and Y. Ciftci, Solid State Sci., 2012, 14, 794–800 CrossRef CAS.
- S. Aydin and M. Simsek, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 134107 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra08746h |
| This journal is © The Royal Society of Chemistry 2024 |