Open Access Article
Open Access ArticleDesign of N–N ylide bond-based high energy density materials: a theoretical survey†
Jingfan Xin *a,
Xiaoxu Bob,
Wenmin Xiaoa,
Yihong Ding
*a,
Xiaoxu Bob,
Wenmin Xiaoa,
Yihong Ding *cd,
Ruifa Jin
*cd,
Ruifa Jin *a and
Suhua Yanga
*a and
Suhua Yanga
aInner Mongolia Key Laboratory of Photoelectric Functional Materials, College of Chemistry and Life Science, Chifeng University, Chifeng 024000, China. E-mail: xinjingfan25@163.com
bDepartment of Agriculture and Biotechnology, Wenzhou Vocational College of Science and Technology, No. 1000 Liuhongqiao Road, Wenzhou 325006, People's Republic of China
cKey Laboratory of Carbon Materials of Zhejiang Province, Wenzhou Key Lab of Advanced Energy Storage and Conversion, Zhejiang Province Key Lab of Leather Engineering, College of Chemistry and Materials Engineering, Wenzhou University, Wenzhou 325035, P. R. China
dLaboratory of Theoretical and Computational Chemistry, Institute of Theoretical Chemistry, Jilin University, Changchun, China
First published on 2nd February 2024
Abstract
The generally encountered contradiction between large energy content and stability poses great difficulty in designing nitrogen-rich high-energy-density materials. Although N–N ylide bonds have been classified as the fourth type of homonuclear N–N bonds (besides >N–N<, –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–, and N
N–, and N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N), accessible energetic molecules with N–N ylide bonds have rarely been explored. In this study, 225 molecules with six types of novel structures containing N–N ylide bonds were designed using density functional theory and CBS-QB3 methods. To guide future synthesis, the effects of substitution on the thermal stability, detonation velocity, and detonation pressure of the structures were evaluated under the premise that the N–N ylide skeleton remains stable. The calculations show that the bond dissociation energy values of the N–N ylide bonds of the designed 225 structures were in the range of 61.21–437.52 kJ mol−1, except for N-1NNH2. Many of the designed structures with N–N ylide bonds exhibit high detonation properties, which are superior to those of traditional energetic compounds. This study convincingly demonstrates the feasibility of the design strategy of introducing an N–N ylide bond to develop new types of energetic materials.
N), accessible energetic molecules with N–N ylide bonds have rarely been explored. In this study, 225 molecules with six types of novel structures containing N–N ylide bonds were designed using density functional theory and CBS-QB3 methods. To guide future synthesis, the effects of substitution on the thermal stability, detonation velocity, and detonation pressure of the structures were evaluated under the premise that the N–N ylide skeleton remains stable. The calculations show that the bond dissociation energy values of the N–N ylide bonds of the designed 225 structures were in the range of 61.21–437.52 kJ mol−1, except for N-1NNH2. Many of the designed structures with N–N ylide bonds exhibit high detonation properties, which are superior to those of traditional energetic compounds. This study convincingly demonstrates the feasibility of the design strategy of introducing an N–N ylide bond to develop new types of energetic materials.
1. Introduction
High energy density materials (HEDMs) play an important role in military and civil fields.1–6 Finding an ideal HEDM molecule is always an extraordinary challenge due to the great difficulty in achieving the intrinsic requirements, i.e., structural stability (to allow safe usage) and large energy release (to ensure excellent detonation properties). It is known that among the known N–N bond-containing non-salt-like high-energy materials, the N–N bonds in the skeleton structure mostly take the form of N–N single or double bonds. This is due to the large energy difference between the N–N single bond (∼160 kJ mol−1), double bond (∼420 kJ mol−1), and triple bond (close to 1 MJ mol−1), which means that there is a higher energy release, meeting the requirements of candidate energetic materials.7,8Among the known N–N bond-containing HEDM compounds (Scheme 1), the skeletal N–N bond mostly takes the normal N–N single or double bonding forms. The N–N ylide bond is the fourth homonuclear N–N bond, and the other three normal N–N key types are >N–N<, –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–, and N
N–, and N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N. Since the first report of synthesis in the 1950s,9 the N–N ylide family has grown into two known structural types, i.e., the pyridine type (sp2 type) and the aminimide type (sp3 type).10–12 Due to their zwitterionic properties, they exhibit unique physicochemical properties and are therefore widely used in a variety of applications, such as polymer additives in binders and surfactants.13,14 In recent years, the development of more concise and efficient methods for the generation and application of N–N ylide to synthesize highly functional compounds has been of great interest.15–17 The bond energy of the N–N ylide bond is similar to that of an N–N single bond, which is very advantageous as a high-energy structure. However, skeleton structures with N–N ylide bonds have barely been investigated in the high energy density material field. The successful synthesis of new types of energetic compounds with N–O ylide bonds in recent years18–21 has greatly increased our confidence in the introduction of N–N ylide bond-containing structures into the field of energetic materials.
N. Since the first report of synthesis in the 1950s,9 the N–N ylide family has grown into two known structural types, i.e., the pyridine type (sp2 type) and the aminimide type (sp3 type).10–12 Due to their zwitterionic properties, they exhibit unique physicochemical properties and are therefore widely used in a variety of applications, such as polymer additives in binders and surfactants.13,14 In recent years, the development of more concise and efficient methods for the generation and application of N–N ylide to synthesize highly functional compounds has been of great interest.15–17 The bond energy of the N–N ylide bond is similar to that of an N–N single bond, which is very advantageous as a high-energy structure. However, skeleton structures with N–N ylide bonds have barely been investigated in the high energy density material field. The successful synthesis of new types of energetic compounds with N–O ylide bonds in recent years18–21 has greatly increased our confidence in the introduction of N–N ylide bond-containing structures into the field of energetic materials.
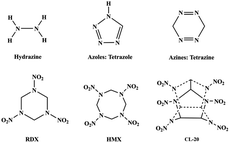 | ||
| Scheme 1 Some known HEDMs containing normal N–N single or double bonds. Hydrogen atoms attached to carbon are not shown. | ||
In this work, we report a novel class of skeleton energetic structures, i.e., N–N ylide bond-based structures. Six types of structures were designed with different substitution effects, leading to 225 molecules in total. A thorough study of their thermal stability and detonation properties showed that appropriate substitution effects can provide both structural thermal stability and energy enrichment, satisfying the ever-challenging and severe criteria of stability and detonation. Our work exemplifies for the first time that structures with the N–N ylide bond can act as promising HEDMs. This work opens up a new avenue for energetic compounds, namely HEDMs, with a fourth type of homonuclear N–N bond, i.e., the N–N ylide bond.
2. Computational methods
The density functional theory method (DFT) is a powerful tool for studying the structures and energetic properties of energetic materials.22–24 The electronic structures, heats of formation, thermal stabilities, and impact sensitivities were studied by DFT using the Gaussian 09 (ref. 25) program packages. For energy refinement, the composite CBS-QB3 method26 was applied; the B3LYP/6-311G(2d,d,p) geometries and frequencies were used, followed by a series of high-level single-point energy calculations.The bond dissociation energies (BDE) of the designed structures were calculated using the following equations.27
| BDE(A–B) = E(A·) + E(B·) − E(A–B) | (1) |
The heat of formation in the gas phase (ΔHf,gas) was determined using the atomization equation. The known enthalpies of formation of N(g), H(g), O(g), and C(g) were taken from the NIST Chemistry Webbook.28
To estimate the detonation performance of the title compounds, their solid-phase heats of formation (ΔHf,solid) were calculated. According to Hess's law,29,30 ΔHf,solid can be obtained by
| ΔHf,solid = ΔHf,gas − ΔHsub | (2) |
| ΔHsub = αA2 + β(vσtotal2)1/2 + γ | (3) |
The detonation velocity (D in km s−1) and detonation pressure (P in GPa) of the title compounds were estimated using eqn (4) and (5).34
D = 1.01(N![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) 0.5Q0.5)0.5(1 + 1.3ρ) 0.5Q0.5)0.5(1 + 1.3ρ)
| (4) |
P = 1.558ρ2N![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) 0.5Q0.5 0.5Q0.5
| (5) |
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) is the mean molecular weight of the gaseous detonation products. Q is the heat of detonation (cal g−1), and it equals the negative of the enthalpy change ΔH during the reaction. ρ is the density of the explosive (g cm−3). To obtain the theoretical density, we applied the improved equation proposed by Politzer et al.,35 according to which the interaction index vσtot2 is:
is the mean molecular weight of the gaseous detonation products. Q is the heat of detonation (cal g−1), and it equals the negative of the enthalpy change ΔH during the reaction. ρ is the density of the explosive (g cm−3). To obtain the theoretical density, we applied the improved equation proposed by Politzer et al.,35 according to which the interaction index vσtot2 is:
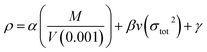 | (6) |
3. Results and discussion
3.1 Optimized structures
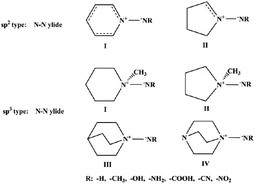
The simplest form of the N–N ylide bond structure is H3N–NH, which is an isomer of the energetic structure H2N–NH2. In order to prevent the transfer of H over H3N+–, the N–N ylide bond is broken. Six types of N–N ylide bond skeleton structures were designed to maintain the N–N ylide bond type by using rigid five- and six-membered ring structures. For ease of discussion, these six N–N ylide-type structures are categorized as pyridine type (sp2 type) and aminimide type (sp3 type) (Fig. 1).In the six optimized types of N–N ylide bond skeleton structures, the bond length of the N–N ylide bond was between 1.30 and 1.44 Å, which is slightly shorter than that of H3NNH (1.46 Å) and longer than that of the classical N–N double bond (1.24 Å). Further, Mayer bond order calculations showed that the N–N ylide bond can be considered a single bond. The highest occupied orbital (HOMO) and lowest unoccupied orbital (LUMO) of the six types of N–N ylide bond skeleton structures were calculated, and their electronic properties were analyzed. The HOMO–LUMO orbitals of the N–N ylide bond skeleton structures (R = H) are shown in Fig. 2. The HOMO–LUMO gap ranged from 4.17 to 4.80 eV, which is larger than that of H3NNH (3.81 eV), indicating that these structures can be considered thermodynamically stable (see Table 1 and Fig. 2).
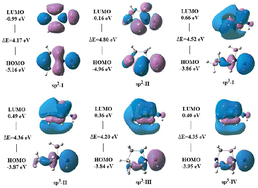 | ||
Fig. 2 HOMO–LUMO orbitals and HOMO–LUMO gaps of the six types of N–N ylide bond skeleton structures (R![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) H) at the B3LYP/6-311G(2d,d,p) level. H) at the B3LYP/6-311G(2d,d,p) level. | ||
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) H) designed at the B3LYP/6-311G(2d,d,p) level
H) designed at the B3LYP/6-311G(2d,d,p) level
| Bond length | Bond index | HOMO | LUMO | ΔE | |
|---|---|---|---|---|---|
| sp2-I | 1.31 | 1.28 | −5.16 | −0.99 | 4.17 |
| sp2-II | 1.30 | 1.32 | −4.96 | −0.16 | 4.80 |
| sp3-I | 1.44 | 0.95 | −3.86 | 0.66 | 4.52 |
| sp3-II | 1.43 | 0.97 | −3.87 | 0.49 | 4.36 |
| sp3-III | 1.43 | 0.97 | −3.84 | 0.36 | 4.20 |
| sp3-IV | 1.43 | 0.97 | −3.95 | 0.40 | 4.35 |
| H3NNH | 1.46 | 0.95 | −3.88 | −0.07 | 3.81 |
| N2H4 | 1.49 | 0.97 | −5.59 | 1.07 | 6.66 |
| N2H2 | 1.24 | 1.89 | −6.63 | −1.56 | 5.07 |
For future experimental synthesis, the substitution effects of different groups were calculated. Selected representative energetic substituted groups, i.e., –CH3, –OH, –NH2, –COOH, –CN, and –NO2, were used to replace H of –NH in the N–N ylide bonds. Meanwhile, CH with N in the five- and six-membered ring rigid skeletons was replaced by an isoelectronic body. The purpose of this study is to explore the influence of substituents on structural thermal stability and energetic properties. A total of 225 structures containing N–N ylide bonds with the functional group and isoelectronic substitutions were optimized at the B3LYP/6-31G(2d,d,p) level. The cartesian coordinates of the optimized structures, bond lengths, and bond dissociation energies of the N–N ylide bonds in all these structures are listed in the ESI (Tables S1–S3).†
3.2 Bond dissociation energies
Bond dissociation energies (BDE) provide useful information regarding the thermal stability of structures.27,28 The higher the BDE, the better the thermal stability. The calculated BDEs of the N–N ylide bonds of the 225 designed structures are listed in Table S3.† Their BDE values were found to be in the range from 61.21 to 437.52 kJ mol−1, except for N-1NNH2. In general, the structures substituted with electron-withdrawing groups have larger BDEs than those substituted with electron-donating groups, which might indicate higher thermal stability.3.3 Detonation performance
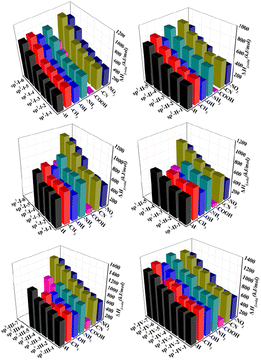
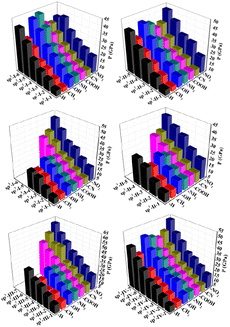
It is well known that ideal energetic materials not only require high thermal conductivity but also must exhibit excellent detonation performance (density ρ ≈ 1.9 g cm−3, detonation velocity D ≈ 9.0 km s−1, and P ≈ 40.0 GPa). For comparison, the properties of known species, such as 2,4,6-trinitrotoluene (TNT), 1,3,5-trinitro-1,3,5-triazinane (RDX), and 1,3,5,7-tetranitro-1,3,5,7-tetrazocane (HMX), are also provided. The heats of formation, crystal density (ρ), detonation velocity (D), and detonation pressure (P) of the 225 structures were calculated, and the results are listed in Table S4.†The solid-phase heats of formation (ΔHf,solid) of the 225 structures are shown in Fig. 3. All structures were found to have positive heat of formation values from 28.94 kJ mol−1 to 1276.21 kJ mol−1. In each type of structural skeleton, the heat of formation was higher as the number of isoelectronic bodies (N) increased (see Fig. 3).
The ρ values of all the designed structures are shown in Fig. 4. In each type of structural skeleton, the ρ value increased as the number of isoelectronic bodies (N) increased. In general, among molecules with the same skeleton structure but different substituents, the densities of the electron-withdrawing-group-substituted structures were greater than those of the electron-donating-group-substituted structures.
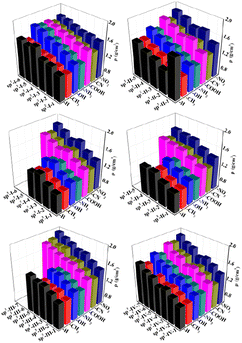
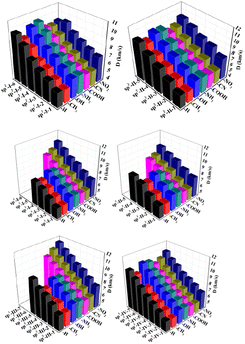
The detonation velocity and detonation pressure are extremely important for the detonation performance of energetic materials. The D values of all 225 designed structures were found to be between 5.25 and 11.43 km s−1, whereas the P values of all 225 designed structures were found to be from 9.19 to 60.64 GPa. Among them, sp3-III-7 (R = –NO2) has the highest detonation performance, while sp2-I-1(R = –CH3) has the lowest detonation performance. In each type of structural skeleton, the detonation velocity and detonation pressure increased with the number of isoelectronic bodies (N) (see Fig. 5 and 6). In general, among molecules of the same structural type but with different substituents, the electron-withdrawing-group-substituted structures (R = –NO2) has higher detonation velocity and detonation pressure, whereas the electron-donating substituted structure (R = –CH3) has lower detonation velocity and detonation pressure.
Thus, quite promisingly, with an increase in N content in the skeleton structure, the structures containing the N–N ylide bond exhibit much better ΔHf,solid, ρ, D, and P values while retaining appreciable thermal stability. On comparing with the calculated substitution effect, it is found that the structures substituted with electron-withdrawing groups have higher detonation performances than those with electron-donating substituents.
4. Conclusions
In this study, we designed six types of N–N ylide bond-based energetic structures. To ensure thermal stability and detonation properties, different types of substituents (substituent effect) and N content regulation (isoelectronic substitution) in the skeleton structure were employed to obtain 225 structures. In general, the results reveal that the electron-withdrawing-group substitution effect is more beneficial to thermal stability and detonation properties. In addition, the detonation properties of each type of N–N ylide bond-based skeleton structure improve with increasing N content, and some even exceed the values of classical energetic structures. The six types of N–N ylide bond-based structures designed in this work possess excellent thermal stability and detonation properties. Among them, sp3-III-7 (R = –NO2) has the highest detonation properties (D, P). The combination of the thermal stability and detonation properties suggests that the designed six types of N–N ylide bond-based structures are metastable HEDM candidates worthy of further investigation.Author contributions
X. J. investigated and wrote the original manuscript. D. Y. wrote programs for detonation properties, guided the entire research, and reviewed and edited the draft. B. X. and X. W. analysed or synthesized the study data. J. R. provided the servers and software for the calculations. Y. S. collected the data.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Natural Science Foundation of the Inner Mongolia Autonomous Region (No. 2023LHMS02009, 2021LHMS02001, 2023LHMS02013) and the Research Program of Sciences at the Universities of the Inner Mongolia Autonomous Region (No. NJZY21124, NJZY21133, NJZY22192). Y.H. Ding thanks the funding from the National Natural Science Foundation of China (No. 22073069, 21773082).References
- Q. Lang, Q. Sun, Q. Wang, Q. H. Lin and M. Lu, J. Mater. Chem. A, 2020, 8, 11752–11760 RSC.
- J. Singh, R. J. Staples and J. M. Shreeve, ACS Appl. Mater. Interfaces, 2021, 13, 61357–61364 CrossRef CAS PubMed.
- J. Singh, R. J. Staples and J. M. Shreeve, J. Mater. Chem. A, 2023, 11, 12896–12901 RSC.
- X. Y. Yang, R. Ahuja and W. Luo, Nano Energy, 2023, 113, 108557–108566 CrossRef CAS.
- E. Thimsen, J. Phys. Chem. C, 2023, 127, 6601–6609 CrossRef CAS.
- S. Banik, V. D. Ghule and S. Dharavath, Mater. Chem. Phys., 2023, 301, 127678–127686 CrossRef CAS.
- X. H. Jin, F. Yuan, Y. Shen, Y. F. Liu, S. N. Yao, S. C. Bai and B. C. Hu, J. Phys. Org. Chem., 2023, 36, e4469 CrossRef CAS.
- A. A. Larin, D. D. Degtyarev, I. V. Ananyev, A. N. Pivkina and L. L. Fershtat, Chem. Eng. J., 2023, 470, 144144–144154 CrossRef CAS.
- S. Wawzonek and D. Meyer, J. Am. Chem. Soc., 1954, 76, 2918–2920 CrossRef CAS.
- J. A. Pople, K. Raghavachari, M. J. Frisch, J. S. Binkley and P. v. R. Schleyer, J. Am. Chem. Soc., 1983, 105, 6389–6398 CrossRef CAS.
- S. L. Jain, V. B. Sharma and B. Sain, Tetrahedron Lett., 2003, 44, 4385–4387 CrossRef CAS.
- M. Ochiai, Y. Kawano, T. Kaneaki, N. Tada and K. Miyamoto, Org. Lett., 2009, 11, 281–284 CrossRef CAS PubMed.
- J. J. Mousseau, J. A. Bull and A. B. Charette, Angew. Chem., Int. Ed., 2010, 49, 1115–1118 CrossRef CAS PubMed.
- L. Maestre, R. Dorel, Ó. Pablo, I. Escofet, W. M. C. Sameera, E. Álvarez, F. Maseras, M. M. Díaz-Requejo, A. M. Echavarren and P. J. Pérez, J. Am. Chem. Soc., 2017, 139, 2216–2223 CrossRef CAS PubMed.
- H. G. Im, W. J. Choi and S. Hong, Angew. Chem., Int. Ed., 2020, 132, 17664–17669 CrossRef.
- M. M. Xu, W. B. Cao, X. P. Xu and S. J. Ji, Adv. Synth. Catal., 2022, 364, 2211–2220 CrossRef CAS.
- W. Lee, Y. Koo, H. Jung, S. Chang and S. Hong, Nat. Chem., 2023, 15, 1091–1099 CrossRef CAS PubMed.
- D. E. Chavez, D. A. Parrish, L. Mitchell and G. H. Imler, Angew. Chem., Int. Ed., 2017, 56, 1–5 CrossRef PubMed.
- C. M. Ma, Y. Pan, J. C. Jiang, Z. L. Liu and Q. Z. Yao, New J. Chem., 2018, 42, 11259–11263 RSC.
- J. Li, Y. B. Liu, W. Q. Ma, T. Fei, C. L. He and S. P. Pang, Nat. Chem., 2022, 13, 5697–5713 CAS.
- R. Z. Gilmanov, V. G. Nikitin, F. G. Khayrutdinov, K. V. Strizhenko, K. Yu. Suponitsky and A. B. Sheremetev, Mendeleev Commun., 2022, 32, 114–116 CrossRef CAS.
- Q. Lang, Q. H. Lin, P. C. Wang, Y. G. Xu and M. Lu, Front. Chem., 2022, 10, 993036–993045 CrossRef CAS PubMed.
- A. V. Makarenkov, S. S. Kiselev, E. G. Kononova, F. M. Dolgushin, A. S. Peregudov, Y. A. Borisov and V. A. Ol’shevskaya, Molecules, 2022, 27, 7484–7505 CrossRef CAS PubMed.
- J. Singh, S. Lal, R. J. Staples and J. M. Shreeve, Mater. Chem. Front., 2022, 6, 933–938 RSC.
- M. J. Frisch,G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09. Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- J. A. Montgomery Jr, M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 2000, 112, 6532–6542 CrossRef.
- (a) S. J. Blanksby and G. B. Ellison, Acc. Chem. Res., 2003, 36, 255–263 CrossRef CAS PubMed; (b) F. Bao, G. Z. Zhang, S. H. Jin, Y. P. Zhang, Q. H. Shu and L. J. Li, J. Mol. Model., 2018, 24, 85–91 CrossRef PubMed.
- http://webbook.nist.gov/chemistry/form-ser.html.
- P. W. Atkins, Physical Chemistry, Oxford University Press, Oxford, 1982 Search PubMed.
- Y. Liu, P. He, L. S. Gong, X. F. Mo and J. G. Zhang, RSC Adv., 2021, 11, 27420–27430 RSC.
- E. F. Byrd and B. M. Rice, J. Phys. Chem. A, 2006, 110, 1005–1013 CrossRef CAS PubMed.
- F. A. Bulat, A. Toro-Labbé, T. Brinck, J. S. Murray and P. Politzer, J. Mol. Model., 2010, 16, 1679–1691 CrossRef CAS PubMed.
- T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- M. J. Kamlet and S. Jacobs, J. Chem. Phys., 1968, 48, 23–35 CrossRef CAS.
- P. Politzer, J. Martinez, J. S. Murray, M. C. Concha and A. Toro- Labbé, Mol. Phys., 2009, 107, 2095–2101 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra08799a |
| This journal is © The Royal Society of Chemistry 2024 |