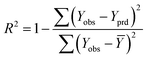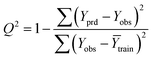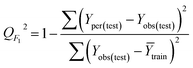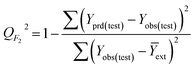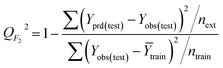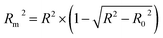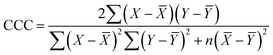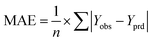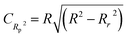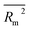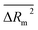Open Access Article
Open Access ArticleQSAR models for the ozonation of diverse volatile organic compounds at different temperatures†
Ali Azimia,
Shahin Ahmadi *b,
Marjan Jebeli Javanb,
Morteza Rouhani
*b,
Marjan Jebeli Javanb,
Morteza Rouhani a and
Zohreh Mirjafarya
a and
Zohreh Mirjafarya
aDepartment of Chemistry, Science and Research Branch, Islamic Azad University, Tehran, Iran
bDepartment of Pharmaceutical Chemistry, Faculty of Pharmaceutical Chemistry, Tehran Medical Sciences, Islamic Azad University, Tehran, Iran. E-mail: ahmadi.chemometrics@gmail.com
First published on 7th March 2024
Abstract
In order to assess the fate and persistence of volatile organic compounds (VOCs) in the atmosphere, it is necessary to determine their oxidation rate constants for their reaction with ozone (kO3). However, given that experimental values of kO3 are only available for a few hundred compounds and their determination is expensive and time-consuming, developing predictive models for kO3 is of great importance. Thus, this study aimed to develop reliable quantitative structure–activity relationship (QSAR) models for 302 values of 149 VOCs across a broad temperature range (178–409 K). The model was constructed based on the combination of a simplified molecular-input line-entry system (SMILES) and temperature as an experimental condition, namely quasi-SMILES. In this study, temperature was incorporated in the models as an independent feature. The hybrid optimal descriptor generated from the combination of quasi-SMILES and HFG (hydrogen-filled graph) was used to develop reliable, accurate, and predictive QSAR models employing the CORAL software. The balance between the correlation method and four different target functions (target function without considering IIC or CII, target function using each IIC or CII, and target function based on the combination of IIC and CII) was used to improve the predictability of the QSAR models. The performance of the developed models based on different target functions was compared. The correlation intensity index (CII) significantly enhanced the predictability of the model. The best model was selected based on the numerical value of Rm2 of the calibration set (split #1, Rtrain2 = 0.9834, Rcalibration2 = 0.9276, Rvalidation2 = 0.9136, and 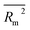 calibration = 0.8770). The promoters of increase/decrease for log
calibration = 0.8770). The promoters of increase/decrease for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 were also computed based on the best model. The presence of a double bond (BOND10000000 and $10
kO3 were also computed based on the best model. The presence of a double bond (BOND10000000 and $10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000), absence of halogen (HALO00000000), and the nearest neighbor codes for carbon equal to 321 (NNC-C⋯321) are some significant promoters of endpoint increase.
000), absence of halogen (HALO00000000), and the nearest neighbor codes for carbon equal to 321 (NNC-C⋯321) are some significant promoters of endpoint increase.
1. Introduction
Organic structures with high vapor pressure, low boiling point, and low water solubility at room temperature and pressure (293.15 K and 101.325 kPa, respectively) are known as volatile organic compounds (VOCs).1 VOCs come from two primary sources, namely, anthropogenic VOCs (AVOCs) released from humans and biogenic VOCs (BVOCs) from soil ecosystems. It should be noted that AVOCs are hydrocarbons released by human activities. These compounds are emitted from various daily activities such as industrial processes, traffic, energy production, and the use of solvents, paints, adhesives, lubricants, wear-reducing products, cosmetics, and personal care items.2 Alternatively, BVOCs are mostly derived from microorganisms, plants, and animals.3Typical VOCs are halogenated compounds, aromatic compounds, aldehydes, ketones, alcohols, and ethers. High concentrations of these VOCs can lead to headaches, nausea, dizziness, and irritation. Unfortunately, significant amounts of VOCs are being emitted into the environment, posing a potentially significant threat to both climate and life.4 Also, they secondarily act as ozone/smog precursors and directly as poisonous materials in the environment. Inferior indoor air quality can lead to various short-term and long-term harmful health effects.5 In this case, reaction with ozone is a meaningful way to remove most VOCs in the atmosphere.6 The kinetic rate constant for the degradation of VOCs is a crucial parameter that must be considered to assess their removal efficiency and the ecological risk of contaminants.7
Ozonolysis is a chemical reaction involving the breakdown of organic compounds in the presence of ozone (O3). This process plays a central role in atmospheric chemistry, contributing to the formation of secondary organic aerosols and the degradation of VOCs emitted by diverse sources. The chemical oxidation process in the atmosphere plays a primary role in the composition of the atmosphere, resulting in the elimination of initially released species and the production of secondary products. In many instances, emitted species or their oxidation products adversely affect the air and climate quality.8 Among the many ingredients of atmospheric aerosol fragments, organic aerosol particles are less well-known.9 Secondary organic aerosol (SOA) is a significant component of organic aerosols. Thus, identifying the chemical pathways of compressible products is essential for predicting the formation of SOA.10–13
Quantitative structure–property relationship (QSAR) is a computational tool for building models to predict various activities.14,15 In this case, different machine learning packages are available to build reliable models. Among them, CORAL is one of the user-friendly packages for building valid QSAR models based on the simplified molecular-input line-entry system (SMILES) notation.16,17 One of the excellent applications of CORAL software is entering the experimental condition into SMILES of a molecule, namely as quasi-SMILES.18–21
To date, researchers have developed various QSAR models for predicting the reaction rate constants of organic compounds in ozonation reactions. Zhu et al. (2014 and 2015) constructed two optimized QSAR models to estimate the reaction rate constants in ozonation reactions under acidic and neutral conditions at room temperature. These models successfully predicted the reaction rates of diverse organic compounds, yielding the determination coefficients of R2 = 0.802 and 0.723, respectively. In both models, the Fukui indices of a molecule had a notable impact on the reaction rate constants.22,23 Sudhakaran et al. (2013) developed a QSAR model for the ozone oxidation of organic micropollutants. This model incorporated parameters such as double bond equivalence, solvent accessible surface area, and ionization potential, achieving a notable determination coefficient of 0.832.24 In a separate study, McGillen et al. (2008) employed an SAR model to predict the rates of alkyl substituents. The results indicated a strong agreement between the experimental and predicted values.25
Due to the significant impact of temperature on degradation behavior, it is imperative to incorporate this variable as an independent factor in QSAR models for accurately predicting the reaction rate constants at various temperatures. Recently, several temperature-dependent QSAR models have been developed. For example, Li et al. (2014) devised a QSAR model for room temperature and a temperature-dependent model for the hydroxyl radical oxidation process, demonstrating high goodness-of-fit and robustness measures.26 Similarly, Gupta et al. (2016) established QSAR models for nitrate radical oxidation at room temperature and under temperature-dependent conditions. In a recent study, our group investigated the quantitative relationship between the rate of Fenton oxidation and various parameters, including temperature and quantum chemical and physical–chemical properties of molecules. The findings indicated that temperature exerted the most significant influence on the reaction rate constants.27
Li et al. (2013) constructed a QSAR model for predicting ozonation reaction rates at different temperatures, displaying robust predictive capability for 379 reaction rate values,28 despite the limitation that the molecular weights (MWs) of the studied organics were 200.03 (linalool) or smaller.
Liu et al. (2021) developed QSAR models to predict the rate constant of VOC degradation by O3. The models were developed based on factors such as bond order, Fukui indices, and other relevant descriptors, in addition to considerations related to temperature. The utilized dataset consisted of 302![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 values, ranging from 178 to 409 K. This dataset was partitioned into training and test sets for the development and evaluation of the model. The optimized QSAR model demonstrated a favorable determination coefficient for both the training and test sets, achieving R2 and Q2 values of 0.83 and 0.72, respectively. These temperature-dependent QSAR models have expanded the applicability domain of traditional QSAR models. However, it is crucial to acknowledge that measured data are subject to errors, impacting the reliability of the models. In this case, utilizing data obtained within the same laboratory can mitigate these errors and enhance the accuracy of the models.
kO3 values, ranging from 178 to 409 K. This dataset was partitioned into training and test sets for the development and evaluation of the model. The optimized QSAR model demonstrated a favorable determination coefficient for both the training and test sets, achieving R2 and Q2 values of 0.83 and 0.72, respectively. These temperature-dependent QSAR models have expanded the applicability domain of traditional QSAR models. However, it is crucial to acknowledge that measured data are subject to errors, impacting the reliability of the models. In this case, utilizing data obtained within the same laboratory can mitigate these errors and enhance the accuracy of the models.
This study aimed to develop a simple and reliable model to predict the rate constants of VOC reaction with ozone at different temperatures based on the Monte Carlo technique. To identify the optimal model, various target functions were assessed through the utilization of the correlation intensity index (CII) and the index of ideality correlation (IIC) employing the CORAL software.
2. Materials and methods
2.1. Dataset
The data set included diverse organic compounds such as alkanes, alkenes, alkynes, and aldehydes. It also included aromatic compounds containing nitrogen, oxygen, and fluorine. Here, 302![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 values in a broad temperature range (178–409 K) for 149 VOCs were obtained from the literature.29 Log
kO3 values in a broad temperature range (178–409 K) for 149 VOCs were obtained from the literature.29 Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 was selected as the dependent variable for QSAR modeling, which ranged from −25.3 to −13.92. All QSAR models were constructed using the latest version of the CORAL free software (https://www.insilico.eu/coral).
kO3 was selected as the dependent variable for QSAR modeling, which ranged from −25.3 to −13.92. All QSAR models were constructed using the latest version of the CORAL free software (https://www.insilico.eu/coral).
2.2. Optimal quasi-SMILES descriptors
In the CORAL software, three types of optimal descriptors are available, i.e., SMILES-based, graph-based, and hybrid descriptors (a combination of SMILES and graph) for the creation of QSAR models.30,31One of the excellent features of the CORAL software is entering the experimental condition with SMILES of the compounds.18 Here, the experimental temperature was entered as quasi-SMILES. The temperature with a 5° increment was divided, and each increment was defined as [T0], [T1], [T2], etc., as shown in Table 1.
| T (K) range | Code | T (K) range | Code | T (K) range | Code | T (K) range | Code |
|---|---|---|---|---|---|---|---|
| T ≤ 178 | [T0] | 233 < T ≤ 238 | [T12] | 293 < T ≤ 298 | [T24] | 353 < T ≤ 358 | [T36] |
| 178 < T ≤ 183 | [T1] | 238 < T ≤ 243 | [T13] | 298 < T ≤ 303 | [T25] | 358 < T ≤ 363 | [T37] |
| 183 < T ≤ 188 | [T2] | 243 < T ≤ 248 | [T14] | 303 < T ≤ 308 | [T26] | 363 < T ≤ 368 | [T38] |
| 188 < T ≤ 193 | [T3] | 248 < T ≤ 253 | [T15] | 308 < T ≤ 313 | [T27] | 368 < T ≤ 373 | [T39] |
| 193 < T ≤ 198 | [T4] | 253 < T ≤ 258 | [T16] | 313 < T ≤ 318 | [T28] | 373 < T ≤ 378 | [T40] |
| 198 < T ≤ 203 | [T5] | 258 < T ≤ 263 | [T17] | 318 < T ≤ 323 | [T29] | 378 < T ≤ 383 | [T41] |
| 203 < T ≤ 208 | [T6] | 263 < T ≤ 268 | [T18] | 323 < T ≤ 228 | [T30] | 383 < T ≤ 388 | [T42] |
| 208 < T ≤ 213 | [T7] | 268 < T ≤ 273 | [T19] | 328 < T ≤ 333 | [T31] | 3888 < T ≤ 393 | [T43] |
| 213 < T ≤ 218 | [T8] | 273 < T ≤ 278 | [T20] | 333 < T ≤ 338 | [T32] | 393 < T ≤ 398 | [T44] |
| 218 < T ≤ 223 | [T9] | 278 < T ≤ 283 | [T21] | 338 < T ≤ 343 | [T33] | 398 < T ≤ 403 | [T45] |
| 223 < T ≤ 228 | [T10] | 283 < T ≤ 288 | [T22] | 343 < T ≤ 348 | [T34] | 403 < T ≤ 408 | [T46] |
| 228 < T ≤ 233 | [T11] | 288 < T ≤ 293 | [T23] | 348 < T ≤ 353 | [T35] | >408 | [T47] |
Each quasi-SMILES for each data point was obtained by combining the SMILES with code for temperature [Tx]. Some examples of the created quasi-SMILES and the relevant experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 of the VOCs are presented in Table 2. The corresponding quasi-SMILES for the total dataset are presented in Table S1.†
kO3 of the VOCs are presented in Table 2. The corresponding quasi-SMILES for the total dataset are presented in Table S1.†
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 of VOCs
kO3 of VOCs
| No. | Name | T (K) | SMILES | Code for T (K) | Quasi-SMILES | Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 (exp.) kO3 (exp.) |
|---|---|---|---|---|---|---|
| 1 | Alpha-phellandrene | 295 | CC(C)C1CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(C)C C(C)C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1 C1 |
[T24] | CC(C)C1CC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(C)C C(C)C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1[T24] C1[T24] |
−13.92 |
| 10 | 2,3-Dimethyl-2-butene | 227 | CC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(C)C)C C(C)C)C |
[T10] | CC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(C)C)C[T10] C(C)C)C[T10] |
−15.05 |
| 61 | trans-4-Octene | 290 | CCC\C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C\CCC C\CCC |
[T22] | CCC\C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C\CCC[T22] C\CCC[T22] |
−16.00 |
| 128 | Trimethylamine | 296 | CN(C)C | [T24] | CN(C)C[T24] | −17.01 |
| 242 | 1,1,1-Trifluoroethane | 298 | CC(F)(F)F | [T24] | CC(F)(F)F[T24] | −25.30 |
| 183 | Tetrachloroethene | 409 | ClC(Cl)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(Cl)Cl C(Cl)Cl |
[T47] | ClC(Cl)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(Cl)Cl[T47] C(Cl)Cl[T47] |
−18.23 |
| 185 | trans-1,2-Dichloroethene | 380 | Cl\C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C\Cl C\Cl |
[T40] | Cl\C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C\Cl[T40] C\Cl[T40] |
−18.25 |
| 251 | cis-2-Butene | 336 | C\C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C/C C/C |
[T31] | C\C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C/C[T31] C/C[T31] |
−15.71 |
| 300 | Ethene | 193 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C |
[T3] | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C[T3] C[T3] |
−19.83 |
Following the generation of quasi-SMILES, the dataset was divided nine times. Subsequently, each VOC within each split was randomly allocated to the active training (ATRN, 25%), passive training (PTRN, 25%), calibration (CAL, 20%), and validation (VAL, 30%) sets. The quasi-SMILES symbol, split distribution, observed log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 and calculated log
kO3 and calculated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 are presented in Table S1.† The role of each set in the developing QSAR models was previously described in the literature.32,33
kO3 are presented in Table S1.† The role of each set in the developing QSAR models was previously described in the literature.32,33
The one variable model used in this study is based on the “descriptors of correlation weights” (DCWs). In the CORAL software, the DCWs for each feature are optimized by the Monte Carlo algorithm. The final QSAR equation is a univariate equation based on the summation of DCWs. Here, the hybrid descriptor was used to build the QSAR models.34,35 The following equations were used based on optimal descriptors for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 modeling:
kO3 modeling:
| DCW(T*, N*) = SMILESDCW(T*, N*) + GraphDCW(T*, N*) | (1) |
| SMILESDCW(T*, N*) = ∑CW(SSSk) + CW(BOND) + CW(NOSP) + CW(HALO) + CW(HARD) | (2) |
| GraphDCW(T*, N*) = ∑CW(EC2k) + ∑CW(pt2k) + ∑CW(pt3k) + ∑CW(VS2k) + ∑CW(nnk) + ∑CW(APPk) | (3) |
The notation details presented in eqn (2) are as follows: SSSk is fragments of SMILES containing one symbol; the presence/absence of double (‘![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ’), triple (‘#’), and stereochemical (‘@’ or ‘@@’) bonds are indicated by BOND; the presence/absence of nitrogen (N), oxygen (O), sulfur (S), and phosphorus (P) is displayed by NOSP; HALO is the presence of fluorine, chlorine, and bromine; and HARD implies the combination of BOND, NOSP, and HALO. CW(F) demonstrates the correlation weight for the SMILES features, e.g., SSSk, BOND, NOSP, HALO, and HARD.36
’), triple (‘#’), and stereochemical (‘@’ or ‘@@’) bonds are indicated by BOND; the presence/absence of nitrogen (N), oxygen (O), sulfur (S), and phosphorus (P) is displayed by NOSP; HALO is the presence of fluorine, chlorine, and bromine; and HARD implies the combination of BOND, NOSP, and HALO. CW(F) demonstrates the correlation weight for the SMILES features, e.g., SSSk, BOND, NOSP, HALO, and HARD.36
Moreover, in eqn (3), the attribute EC2 is the extended Morgan's connectivity of second order; pt2k and pt3k are the number of path lengths 2 and 3, which start from the kth vertex of the molecular graph, respectively; VS2 is the valence shells of radius 2 in the hydrogen field graph (HFG); and nnk is the nearest neighbor code for the kth vertex of the molecular graph. The correlation weights (CWs) were calculated using Monte Carlo optimization.37–41
Using the APPk features in the CORAL software is another new conceptual method to improve the predictability of models. APPk is the vector of the atom pair proportions35 related to fluorine (‘F’), chlorine (‘Cl’), bromine (‘Br’), nitrogen (‘N’), oxygen (‘O’), double bonds (‘![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ’), and triple bond (‘#’) proportions. APPk indicates that the compound contains atoms Atom1 and Atom2 and the ratio of Atom1 and Atom2 in the molecule, e.g., 2
’), and triple bond (‘#’) proportions. APPk indicates that the compound contains atoms Atom1 and Atom2 and the ratio of Atom1 and Atom2 in the molecule, e.g., 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 1
1, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 2
3, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, and 3
3, and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
The correlation weights for these events (positions in compounds) can be derived through the Monte Carlo approach. Finally, by calculating the numerical data of DCW (algebraic sum of weights for all features included in the model), the prediction of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 of VOCs by the least square method is obtained based on the following equation:
kO3 of VOCs by the least square method is obtained based on the following equation:
Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 = C0 + C1 × DCW(T*, N*) kO3 = C0 + C1 × DCW(T*, N*)
| (4) |
2.3. Monte Carlo optimization
In this study, four distinct types of target functions, namely TF0, TF1, TF2, and TF3, were employed for the development of robust QSAR models. Subsequently, the resultant statistical outcomes were compared for evaluation.42The following equations are the mathematical relationship for each target function:
| TF0 = RATRN + RPTRN − |RATRN − RPTRN| × drweight | (5) |
| TF1 = TF0 + IICCAL × weight for IIC (IICweight) | (6) |
| TF2 = TF0 + CIICAL × weight for CII (CIIweight) | (7) |
| TF3 = TF0 + IICCAL × IICweight + CIICAL × CIIweight | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 for the active and passive training sets were denoted by RATRN and RPTRN, respectively. The parameters drweight, IICweight, and CIIweight represent the weights assigned to IIC and CII, and they are constant throughout the analysis. Here, the numerical values assigned to the parameters drweight, IICweight, and CIIweight were 0.1, 0.5, and 0.3, respectively.
kO3 for the active and passive training sets were denoted by RATRN and RPTRN, respectively. The parameters drweight, IICweight, and CIIweight represent the weights assigned to IIC and CII, and they are constant throughout the analysis. Here, the numerical values assigned to the parameters drweight, IICweight, and CIIweight were 0.1, 0.5, and 0.3, respectively.
IICCAL and CIICAL were computed for the calibration set using eqn (9).
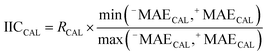 | (9) |
The correlation coefficient between the observed and predicted values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 for the calibration set is indicated by RCAL. −MAE and +MAE are the mean absolute of negative and positive errors, which were calculated using the following equations:
kO3 for the calibration set is indicated by RCAL. −MAE and +MAE are the mean absolute of negative and positive errors, which were calculated using the following equations:
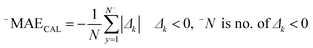 | (10) |
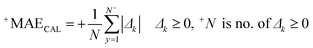 | (11) |
| Δk = Expk − Prdk | (12) |
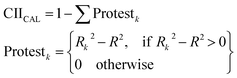 | (13) |
R2 is the correlation coefficient for a set with n samples. Rk2 is the correlation coefficient for n − 1 samples of a set after removing the kth sample. Therefore, if (Rk2 − R2) > 0, the kth substance is an “oppositionist” for the correlation between the observed and predicted values of the set. The more “intensive” correlation appears with the small sum of “protest”.
2.4. Domain of applicability
Applicability domain (AD) analysis indicates whether the developed QSAR model can be applied to any set of chemicals. AD is defined based on the theoretical region in the chemical space of molecular descriptors and the activity region modeled by the training dataset. In the CORAL software, AD assessment is done through the probability density distribution. The distribution of the quasi-SMILES features in the ATRN, PTRN, and CAL sets defines AD. Thus, the AD of the model built by Monte Carlo optimization varies depending on the distribution of the datasets in the training and calibration sets. In the CORAL software, the statistical defects of quasi-SMILES are used to define AD. The “statistical defect,” d(A) is obtained by the following equation:43
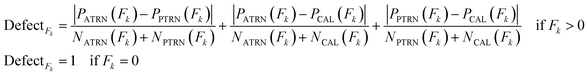 | (14) |
The statistical defect of quasi-SMILES was obtained from the sum of the statistical defects of all the features.
 | (15) |
A quasi-SMILES is considered an outlier if:
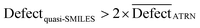 | (16) |
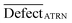 represents the average statistical defects for the active training set.
represents the average statistical defects for the active training set.
2.5. QSAR model validation
The goodness-of-fit of the generated QSAR models for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 of VOCs was assessed based on three methods, as follows: (i) internal validation by measuring R2, IIC, CCC, Q2, and F test in the training set; (ii) external validation by measuring Q2F1, Q2F2, Q2F3, CRp2, RMSD, MAE,
kO3 of VOCs was assessed based on three methods, as follows: (i) internal validation by measuring R2, IIC, CCC, Q2, and F test in the training set; (ii) external validation by measuring Q2F1, Q2F2, Q2F3, CRp2, RMSD, MAE, ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) m2, and ΔRm2 using the test set materials and (iii) data randomization or Y-scrambling (Table 3).
m2, and ΔRm2 using the test set materials and (iii) data randomization or Y-scrambling (Table 3).
In Table 3, Yobs is the experimental activity; Yprd is the calculated activity; R2 and R02 are the squared correlation coefficient values between the experimental and predicted property/activity with intercept and without intercept, respectively; and Rr2 is R2 for the randomized models.
3. Results and discussion
3.1. QSAR models
To obtain predictive and reliable models, nine different QSAR models were constructed for each type of objective function (TF0, TF1, TF2, and TF3) using hybrid optimal descriptors. Fig. 1 depicts a graphical representation of the attributes and various goodness-of-fit criteria for split #1, as determined by TF2 using the CORAL software. This figure shows the graphics of the software. The descriptors derived from SMILES and GRAPH are marked in green and pink, respectively. The different types of descriptors selected are marked with a tick mark. Also, the type of the target function and the corresponding coefficients can be seen. In addition, a plot of the predicted values according to the experimental values of log kO3 can be seen on the left side of the graph. | ||
Fig. 1 Graphical representation of the attributes used for modeling and the predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 for best model (split #1) based on TF2 by the CORAL software. kO3 for best model (split #1) based on TF2 by the CORAL software. | ||
The goodness-of-fit criteria for all the models obtained by TF2 are shown in Table 4. The goodness-of-fit criteria for all splits obtained by TF0, TF1, TF2, and TF3 are indicated in Table S2.†
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 of VOCs
kO3 of VOCs
| Split | Set | n | R2 | CCC | IIC | CII | Q2 | QF12 | QF22 | QF32 | RMSE | MAE | F | Y-test | CRp2 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ATRN | 79 | 0.9834 | 0.9916 | 0.7888 | 0.9882 | 0.9825 | 0.215 | 0.156 | 4551 | 0.9768 | ||||||
| PTRN | 68 | 0.9578 | 0.9710 | 0.8675 | 0.9682 | 0.9554 | 0.382 | 0.289 | 1498 | 0.9532 | |||||||
| CAL | 65 | 0.9276 | 0.9592 | 0.7878 | 0.9615 | 0.9230 | 0.9129 | 0.9129 | 0.9224 | 0.455 | 0.359 | 807 | 0.8770 | 0.0709 | 0.9218 | ||
| VAL | 90 | 0.9136 | 0.9464 | 0.5804 | 0.9410 | 0.9086 | 0.5730 | 0.4433 | 937 | 0.8698 | 0.0824 | 0.0141 | |||||
| 2 | ATRN | 79 | 0.9650 | 0.9822 | 0.9578 | 0.9749 | 0.9630 | 0.308 | 0.215 | 2125 | 0.9568 | ||||||
| PTRN | 79 | 0.9446 | 0.9662 | 0.8630 | 0.9617 | 0.9416 | 0.442 | 0.321 | 1313 | 0.9383 | |||||||
| CAL | 54 | 0.8982 | 0.9416 | 0.6120 | 0.9563 | 0.8893 | 0.8894 | 0.8894 | 0.9200 | 0.462 | 0.367 | 459 | 0.8364 | 0.0978 | 0.8932 | ||
| VAL | 90 | 0.9037 | 0.9501 | 0.8266 | 0.9324 | 0.8998 | 0.5670 | 0.4319 | 823 | 0.8589 | 0.0555 | 0.0093 | |||||
| 3 | ATRN | 88 | 0.9866 | 0.9932 | 0.8665 | 0.9901 | 0.9860 | 0.191 | 0.132 | 6325 | 0.9832 | ||||||
| PTRN | 87 | 0.9574 | 0.9777 | 0.8604 | 0.9695 | 0.9556 | 0.411 | 0.297 | 1912 | 0.9532 | |||||||
| CAL | 42 | 0.9361 | 0.9231 | 0.6887 | 0.9850 | 0.9268 | 0.8914 | 0.7953 | 0.9450 | 0.425 | 0.324 | 586 | 0.7224 | 0.1087 | 0.9236 | ||
| VAL | 85 | 0.8955 | 0.9368 | 0.7375 | 0.9386 | 0.8897 | 0.5178 | 0.4113 | 712 | 0.8149 | 0.1030 | 0.0148 | |||||
| 4 | ATRN | 84 | 0.9707 | 0.9851 | 0.8956 | 0.9815 | 0.9691 | 0.229 | 0.166 | 2713 | 0.9648 | ||||||
| PTRN | 70 | 0.9509 | 0.9736 | 0.9504 | 0.9630 | 0.9481 | 0.431 | 0.303 | 1318 | 0.9487 | |||||||
| CAL | 61 | 0.9495 | 0.9641 | 0.6687 | 0.9769 | 0.9412 | 0.9177 | 0.9159 | 0.8759 | 0.567 | 0.390 | 1109 | 0.8105 | 0.0684 | 0.9445 | ||
| VAL | 87 | 0.8952 | 0.9334 | 0.6880 | 0.9443 | 0.8872 | 0.5348 | 0.4116 | 747 | 0.8102 | 0.1041 | 0.0138 | |||||
| 5 | ATRN | 75 | 0.9739 | 0.9868 | 0.9110 | 0.9808 | 0.9725 | 0.239 | 0.163 | 2726 | 0.9689 | ||||||
| PTRN | 80 | 0.9460 | 0.9714 | 0.9139 | 0.9654 | 0.9421 | 0.327 | 0.223 | 1365 | 0.9386 | |||||||
| CAL | 61 | 0.9419 | 0.9686 | 0.8129 | 0.9688 | 0.9327 | 0.9415 | 0.9409 | 0.8781 | 0.504 | 0.361 | 956 | 0.8846 | 0.0587 | 0.9337 | ||
| VAL | 86 | 0.8910 | 0.9434 | 0.7194 | 0.9266 | 0.8852 | 0.5330 | 0.4071 | 687 | 0.8412 | 0.0156 | 0.0134 | |||||
| 6 | ATRN | 84 | 0.9810 | 0.9904 | 0.8584 | 0.9857 | 0.9801 | 0.228 | 0.155 | 4227 | 0.9783 | ||||||
| PTRN | 71 | 0.9569 | 0.9723 | 0.7565 | 0.9677 | 0.9543 | 0.391 | 0.282 | 1532 | 0.9483 | |||||||
| CAL | 56 | 0.9097 | 0.9422 | 0.8120 | 0.9543 | 0.9006 | 0.8668 | 0.8639 | 0.8902 | 0.546 | 0.432 | 544 | 0.7757 | 0.1033 | 0.8990 | ||
| VAL | 91 | 0.9126 | 0.9471 | 0.6621 | 0.9469 | 0.9073 | 0.5758 | 0.4389 | 929 | 0.8488 | 0.0856 | 0.0105 | |||||
| 7 | ATRN | 86 | 0.9786 | 0.9892 | 0.7470 | 0.9844 | 0.9776 | 0.238 | 0.156 | 3842 | 0.9730 | ||||||
| PTRN | 80 | 0.9546 | 0.9761 | 0.8704 | 0.9667 | 0.9526 | 0.370 | 0.256 | 1641 | 0.9529 | |||||||
| CAL | 43 | 0.9124 | 0.9289 | 0.5774 | 0.9727 | 0.9009 | 0.9098 | 0.8295 | 0.9362 | 0.421 | 0.317 | 427 | 0.7824 | 0.1000 | 0.8968 | ||
| VAL | 93 | 0.9085 | 0.9432 | 0.5673 | 0.9365 | 0.9046 | 0.5763 | 0.4287 | 902 | 0.8661 | 0.0266 | 0.0124 | |||||
| 8 | ATRN | 83 | 0.9817 | 0.9907 | 0.9672 | 0.9853 | 0.9808 | 0.231 | 0.156 | 4336 | 0.9762 | ||||||
| PTRN | 73 | 0.9509 | 0.9713 | 0.5904 | 0.9637 | 0.9485 | 0.450 | 0.319 | 1375 | 0.9433 | |||||||
| CAL | 59 | 0.9080 | 0.9509 | 0.8728 | 0.9655 | 0.8972 | 0.8983 | 0.8968 | 0.9198 | 0.498 | 0.408 | 562 | 0.8609 | 0.0876 | 0.9012 | ||
| VAL | 87 | 0.9031 | 0.9478 | 0.5651 | 0.9485 | 0.8953 | 0.4817 | 0.3752 | 812 | 0.8387 | 0.0940 | 0.0124 | |||||
| 9 | ATRN | 91 | 0.9828 | 0.9913 | 0.7435 | 0.9873 | 0.9821 | 0.236 | 0.163 | 5099 | 0.9711 | ||||||
| PTRN | 71 | 0.9830 | 0.9797 | 0.4955 | 0.9889 | 0.9812 | 0.313 | 0.264 | 3999 | 0.9778 | |||||||
| CAL | 52 | 0.8898 | 0.9395 | 0.9119 | 0.9602 | 0.8794 | 0.8696 | 0.8693 | 0.9237 | 0.467 | 0.392 | 404 | 0.8274 | 0.1050 | 0.8813 | ||
| VAL | 88 | 0.9173 | 0.9501 | 0.6652 | 0.9431 | 0.9142 | 0.5463 | 0.4355 | 954 | 0.8787 | 0.0202 | 0.0097 |
The comparison of the fit criteria of the models shows that for all models, the R2 of the validation set based on TF2 (eqn (7)) is higher than that of the other target functions. Fig. 2 compares the R2 for the validation set across all models obtained based on the four target functions. The R2 of the validation set for split 1 (0.9136) calculated based on TF2 is the highest, and thus this split was selected as the best model.
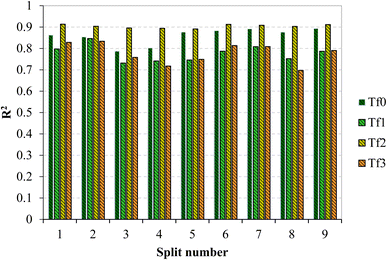 | ||
| Fig. 2 Comparison of determination coefficients of models constructed based on TF0, TF1, TF2, and TF3 of all nine splits. | ||
In the validation of models, apart from evaluating R2, it is essential to check the value of MAE. Based on the comparison of this parameter in all the models, it can be concluded that split 1 exhibits the lowest value of MAE (Fig. 3). Therefore, in this study, TF2 was chosen as the best target function and split #1 as the best split.
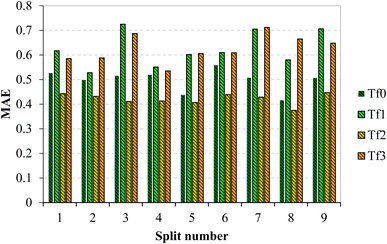 | ||
| Fig. 3 Comparison of mean absolute error of models constructed based on TF0, TF1, TF2, and TF3 of all nine splits. | ||
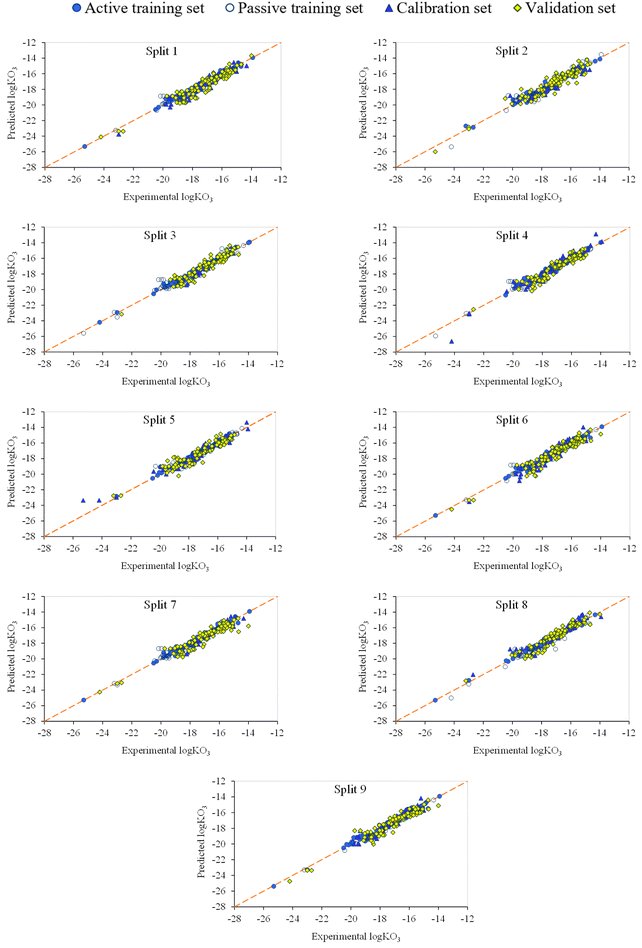
The observed versus predicted graph is a valuable tool in modeling to evaluate the performance of a forecasting model. Model evaluation, accuracy evaluation, pattern recognition, outlier detection, heterogeneity analysis, and model refinement are several methods in which this chart is helpful. Fig. 4 presents a direct comparison between the experimental values of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 and the corresponding predictions generated by the model. This visual inspection helps to understand how well the model captures the underlying patterns in the data. By evaluating the proximity of points to the diagonal line (y = x), one can gauge the accuracy of the model. The points near the diagonal line indicate accurate predictions, while deviations from the line suggest discrepancies between the predicted and observed values. Also, the plot helps identify systematic patterns or trends in the predictions by the model. Detecting any consistent overestimation or underestimation can provide insights into potential biases in the model. Outliers, or data points that deviate significantly from the general trend, are shown on the graph. Recognizing and understanding these outliers are crucial for improving the robustness of the model. Heteroscedasticity, which is the presence of non-constant variability in the errors across predicted values, can be observed in the plot. Uneven spreads of points around the diagonal line may indicate varying levels of uncertainty in the model predictions. The insights gained from the graph can guide model refinement. Adjustments, such as feature engineering or modifying the model structure, can be informed by the observed patterns to enhance the predictive accuracy. In essence, the observed vs. predicted plot serves as a diagnostic tool, offering a visual representation of how well the model aligns with actual data. It helps modelers understand the strengths and weaknesses of the model, facilitating informed decisions for model improvement.
kO3 and the corresponding predictions generated by the model. This visual inspection helps to understand how well the model captures the underlying patterns in the data. By evaluating the proximity of points to the diagonal line (y = x), one can gauge the accuracy of the model. The points near the diagonal line indicate accurate predictions, while deviations from the line suggest discrepancies between the predicted and observed values. Also, the plot helps identify systematic patterns or trends in the predictions by the model. Detecting any consistent overestimation or underestimation can provide insights into potential biases in the model. Outliers, or data points that deviate significantly from the general trend, are shown on the graph. Recognizing and understanding these outliers are crucial for improving the robustness of the model. Heteroscedasticity, which is the presence of non-constant variability in the errors across predicted values, can be observed in the plot. Uneven spreads of points around the diagonal line may indicate varying levels of uncertainty in the model predictions. The insights gained from the graph can guide model refinement. Adjustments, such as feature engineering or modifying the model structure, can be informed by the observed patterns to enhance the predictive accuracy. In essence, the observed vs. predicted plot serves as a diagnostic tool, offering a visual representation of how well the model aligns with actual data. It helps modelers understand the strengths and weaknesses of the model, facilitating informed decisions for model improvement.
As shown in Fig. 4, there are no outliers, and the points near the diagonal line indicate accurate prediction. Furthermore, there is no bias and non-linearity in the reported models.
The following equations represent the QSAR models for predicting the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 of VOCs from 9 splits by TF2:
kO3 of VOCs from 9 splits by TF2:
Split 1
Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 = −22.1732(±0.0087) + 0.3161(±0.0005) × DCW(1, 15) kO3 = −22.1732(±0.0087) + 0.3161(±0.0005) × DCW(1, 15)
| (17) |
Split 2
Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 = −22.0600(±0.0151) + 0.2551(±0.0007) × DCW(1, 15) kO3 = −22.0600(±0.0151) + 0.2551(±0.0007) × DCW(1, 15)
| (18) |
Split 3
Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 = −21.9851(±0.0063) + 0.1813(±0.0002) × DCW(1, 15) kO3 = −21.9851(±0.0063) + 0.1813(±0.0002) × DCW(1, 15)
| (19) |
Split 4
Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 = −21.9109(±0.0124) + 0.2606(±0.0006) × DCW(1, 15) kO3 = −21.9109(±0.0124) + 0.2606(±0.0006) × DCW(1, 15)
| (20) |
Split 5
Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 = −21.7750(±0.0115) + 0.2765(±0.0006) × DCW(1, 15) kO3 = −21.7750(±0.0115) + 0.2765(±0.0006) × DCW(1, 15)
| (21) |
Split 6
Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 = −23.1789(±0.0103) + 0.2412(±0.0003) × DCW(1, 15) kO3 = −23.1789(±0.0103) + 0.2412(±0.0003) × DCW(1, 15)
| (22) |
Split 7
Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 = −21.7489(±0.0076) + 0.2546(±0.0004) × DCW(1, 15) kO3 = −21.7489(±0.0076) + 0.2546(±0.0004) × DCW(1, 15)
| (23) |
Split 8
Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 = −22.3377(±0.0088) + 0.2845(±0.0004) × DCW(1, 15) kO3 = −22.3377(±0.0088) + 0.2845(±0.0004) × DCW(1, 15)
| (24) |
Split 9
Log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 = −22.5932(±0.0082) + 0.2430(±0.0004) × DCW(1, 15) kO3 = −22.5932(±0.0082) + 0.2430(±0.0004) × DCW(1, 15)
| (25) |
Ojha et al. (2010) proposed Rm2 as a reliable criterion for determining the optimal model.49 The best split is split #1, with the maximum average Rm2 for the CAL and VAL sets. According to the AD results for the models in Table S3,† 86%, 88%, 85%, 90%, 91%, 91%, 91, 90%, and 86% of the dataset are in the AD models for splits 1–9, respectively. This shows that nine reliable and robust QSAR models can predict more than 85% of the new data.
3.2. Model interpretation
Mechanistic interpretation is one of the basic steps in QSAR modeling. In the CORAL software, the procedure is carried out relying on the structural features extracted from SMILES or HFG, which are responsible for the enhancement or reduction of the targeted activity. If the correlation weight of these structural features is negative in at least three Monte Carlo optimization runs, then these structural attributes are considered activity reduction drivers. Otherwise, if the correlation weights of these structural attributes are positive in at least three runs, these structural attributes are considered triggers for increasing the activity. However, if the correlation weights of the structural features are positive in some optimization runs and negative in others, the structural features are not considered.The promoters responsible for an increase/decrease in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 were calculated from the best model (split 1) and are shown in Table 5. The presence of a double bond (BOND10000000 and $10
kO3 were calculated from the best model (split 1) and are shown in Table 5. The presence of a double bond (BOND10000000 and $10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000), absence of a halogen atom (HALO00000000), the number of paths of length two, which started from a carbon atom, is equal to 2, 3, or 5 (PT2-C⋯2…, PT2-C⋯3…, and PT2-C⋯5…), the number of paths of length three, which started from a carbon atom, is equal to 6 (PT3-C⋯6…), valence shell of second order for hydrogen atom equal to 5 (VS2-H⋯5…), valence shell of second order for carbon atom equal to 6 (VS2-C⋯6…), Morgan extended connectivity of second-order for hydrogen atom equal to 9 (EC2-H⋯9…), two successive aliphatic carbon with a double bond (C⋯C⋯=
000), absence of a halogen atom (HALO00000000), the number of paths of length two, which started from a carbon atom, is equal to 2, 3, or 5 (PT2-C⋯2…, PT2-C⋯3…, and PT2-C⋯5…), the number of paths of length three, which started from a carbon atom, is equal to 6 (PT3-C⋯6…), valence shell of second order for hydrogen atom equal to 5 (VS2-H⋯5…), valence shell of second order for carbon atom equal to 6 (VS2-C⋯6…), Morgan extended connectivity of second-order for hydrogen atom equal to 9 (EC2-H⋯9…), two successive aliphatic carbon with a double bond (C⋯C⋯=![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) …), carbon-bonded double bond with branching (
…), carbon-bonded double bond with branching (![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ⋯C⋯(⋯), the nearest neighbor codes for carbon equal to 312 (NNC-C⋯312), and temperature between 353 and 358 K ([T24]…) were some significant promoters of a log
⋯C⋯(⋯), the nearest neighbor codes for carbon equal to 312 (NNC-C⋯312), and temperature between 353 and 358 K ([T24]…) were some significant promoters of a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 increase. The nearest neighbor code for hydrogen is equal to 110 (NNC-H⋯110), Morgan extended connectivity of second-order for hydrogen atoms equal to 5 and 7 (EC2-H⋯5… and EC2-H⋯7…), Morgan extended connectivity of second-order for carbon atoms equal to 19, 22, and 26 (EC2-C⋯19…, EC2-C⋯22…, and EC2-C⋯26…), the number of paths of length three, which started from a hydrogen atom, is equal to three (PT3-H⋯3…), the number of paths of length three, which started from a carbon atom, is equal to three (PT3-C⋯3…), the number of paths of length two, which started from a carbon atom, is equal to four and six (PT2-C⋯4…, and PT2-C⋯6…), valence shell of second order for a carbon atom equal to 13 (VS2-C⋯13…), two aliphatic carbons joined by a double bond (C⋯
kO3 increase. The nearest neighbor code for hydrogen is equal to 110 (NNC-H⋯110), Morgan extended connectivity of second-order for hydrogen atoms equal to 5 and 7 (EC2-H⋯5… and EC2-H⋯7…), Morgan extended connectivity of second-order for carbon atoms equal to 19, 22, and 26 (EC2-C⋯19…, EC2-C⋯22…, and EC2-C⋯26…), the number of paths of length three, which started from a hydrogen atom, is equal to three (PT3-H⋯3…), the number of paths of length three, which started from a carbon atom, is equal to three (PT3-C⋯3…), the number of paths of length two, which started from a carbon atom, is equal to four and six (PT2-C⋯4…, and PT2-C⋯6…), valence shell of second order for a carbon atom equal to 13 (VS2-C⋯13…), two aliphatic carbons joined by a double bond (C⋯![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ⋯C…), two successive aliphatic carbons with branching (C⋯C⋯(⋯)), carbon-bonded double bond with branching (C…
⋯C…), two successive aliphatic carbons with branching (C⋯C⋯(⋯)), carbon-bonded double bond with branching (C…![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ⋯(⋯)), and presence of oxygen (NOSP01000000) were some significant promoters of a log
⋯(⋯)), and presence of oxygen (NOSP01000000) were some significant promoters of a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 decrease.
kO3 decrease.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 for the best model based on TF2
kO3 for the best model based on TF2
| No. | Structural attributes | CWs probe 1 | CWs probe 2 | CWs probe 3 | NATRNa | NPTRNb | NCALc | Defect | Description |
|---|---|---|---|---|---|---|---|---|---|
| a Frequencies of SMILES feature in the active training.b Frequencies of SMILES feature in the passive training.c Frequencies of SMILES feature in the calibration sets. | |||||||||
The promoters of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 increase kO3 increase |
|||||||||
| 1 | BOND10000000 | 2.67165 | 2.51987 | 3.83649 | 73 | 62 | 61 | 0.0001 | Presence of double bond |
| 2 | HALO00000000 | 1.07055 | 0.84955 | 1.74407 | 68 | 55 | 52 | 0.0005 | Absence of halogen |
| 3 | PT2-C⋯5… | 0.17027 | 0.12434 | 0.99446 | 68 | 61 | 60 | 0.0005 | The no. of paths of length 2, which started from a carbon atom, is equal to 5 |
| 4 | NNC-C⋯321 | 0.87169 | 0.98392 | 0.73303 | 61 | 49 | 47 | 0.0005 | The nearest neighbor codes for carbon equal to 321 |
| 5 | PT2-C⋯2… | 0.08082 | 0.02056 | 0.49237 | 60 | 52 | 46 | 0.0005 | The no. of paths of length 2, which started from a carbon atom, is equal to 2 |
| 6 | VS2-H⋯5… | 0.47711 | 1.07817 | 0.36872 | 58 | 53 | 49 | 0.0002 | Valence shell of second order for hydrogen atom equal to 5 |
| 7 | PT2-C⋯3… | 0.22796 | 0.97566 | 0.40759 | 49 | 35 | 30 | 0.002 | The no. of paths of length 2, which started from a carbon atom, is equal to 3 |
| 8 | $10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
1.56878 | 2.33819 | 2.97527 | 48 | 39 | 42 | 0.0004 | Presence of a double bond |
| 9 | PT3-C⋯6… | 0.83176 | 0.09089 | 0.24243 | 48 | 38 | 37 | 0.0005 | The no. of paths of length 3 which started from a carbon atom is equal to 6 |
| 10 | EC2-H⋯9… | 0.71934 | 0.08452 | 0.1885 | 44 | 39 | 34 | 0.0004 | Morgan extended connectivity of second-order for hydrogen atom equal to 9 |
| 11 | [T24]… | 1.62695 | 1.40185 | 1.67637 | 44 | 32 | 36 | 0 | Temperature between 124 and 298 K |
| 12 | NNC-C⋯312 | 0.55561 | 0.81517 | 0.50168 | 28 | 26 | 13 | 0.0038 | The nearest neighbor codes for carbon equal to 312 |
| 13 | VS2-C⋯6… | 0.44593 | 0.00567 | 0.79277 | 28 | 10 | 15 | 0.0029 | Valence shell of second order for carbon atom equal to 6 |
| 14 | C⋯C⋯![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) … … |
0.51624 | 0.59934 | 0.09671 | 27 | 15 | 21 | 0.0004 | Two successive aliphatic carbon with double bond |
| 15 | ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ⋯C⋯(⋯) ⋯C⋯(⋯) |
0.40825 | 0.1176 | 0.13709 | 24 | 13 | 14 | 0.0023 | Carbon-bonded double bond with branching |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||
The promoters of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 decrease kO3 decrease |
|||||||||
| 1 | NNC-H⋯110 | −0.08218 | −0.20453 | −0.02848 | 71 | 57 | 53 | 0.0007 | The nearest neighbors code for hydrogen equal to 110 |
| 2 | EC2-H⋯7… | −0.21406 | −0.25547 | −0.08738 | 63 | 46 | 45 | 0.001 | Morgan extended connectivity of second-order for hydrogen atom equal to 7 |
| 3 | C⋯![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ⋯C… ⋯C… |
−0.75092 | −0.15264 | −0.72575 | 58 | 46 | 48 | 0 | Two aliphatic carbons joined by double bond |
| 4 | PT3-H⋯3… | −0.03253 | −0.00237 | −0.24255 | 53 | 41 | 38 | 0.0009 | The no. of paths of length 3, which started from a hydrogen atom, is equal to 3 |
| 5 | PT3-C⋯3… | −0.28429 | −0.0233 | −0.53459 | 39 | 40 | 42 | 0.0019 | The no. of paths of length 3, which started from a carbon atom, is equal to 3 |
| 6 | EC2-C⋯26… | −0.14966 | −0.33885 | −0.48099 | 28 | 15 | 21 | 0.0006 | Morgan extended connectivity of second-order for carbon atom equal to 26 |
| 7 | EC2-H⋯5… | −0.43867 | −0.24929 | −0.21481 | 28 | 22 | 14 | 0.0033 | Morgan extended connectivity of second-order for hydrogen atom equal to 5 |
| 8 | PT2-C⋯4… | −0.52364 | −0.36281 | −0.64257 | 26 | 15 | 8 | 0.0061 | The no. of paths of length 2, which started from a carbon atom, is equal to 4 |
| 9 | PT2-C⋯6… | −0.08319 | −0.10097 | −0.35475 | 26 | 13 | 23 | 0.0005 | The no. of paths of length 2, which started from a carbon atom, is equal to 6 |
| 10 | C⋯C⋯(⋯) | −0.85339 | −1.02505 | −1.27507 | 24 | 13 | 19 | 0.0003 | Two successive aliphatic carbons with branching |
| 11 | EC2-C⋯22… | −0.4121 | −0.20762 | −0.92869 | 21 | 11 | 16 | 0.0005 | Morgan extended connectivity of second-order for carbon atom equal to 22 |
| 12 | C⋯![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) …(⋯) …(⋯) |
−0.78929 | −1.29912 | −1.39466 | 17 | 15 | 12 | 0.0011 | Carbon-bonded double bond with branching |
| 13 | NOSP01000000 | −0.7395 | −0.10479 | −0.05487 | 16 | 8 | 7 | 0.0041 | Presence of oxygen |
| 14 | VS2-C⋯13… | −0.79019 | −0.16384 | −1.07209 | 12 | 10 | 14 | 0.0024 | Valence shell of second order for carbon atom equal to 13 |
| 15 | EC2-C⋯19… | −0.00369 | −0.47041 | −0.23522 | 11 | 7 | 2 | 0.0083 | Morgan extended connectivity of second-order for carbon atom equal to 19 |
Table S4† presents the correlation weights assigned to each attribute incorporated in the model for split #1 based on TF2. Another noteworthy observation is that despite the evident impact of temperature on VOC degradation, as indicated in Table S4,† the correlation weights for temperature (CW(SAK)) are predominantly positive, with the exception of some lower temperatures, where they exhibit a negative trend. Furthermore, a positive coefficient of temperature is also found in increasing descriptors ([T24], temperature between 353 and 358 K), also explaining the positive effect of high temperature on the degradation of VOCs. This conclusion is consistent with the results of the latest QSAR model for this data set.29
3.3. Reliability of QSAR models compared to the best available predictive methods
The literature review shows that only one QSAR model has been reported to predict the rate constants of 302 VOCs with ozone reaction.50 Table 6 compares the goodness-of-fit criteria of the current QSAR model with previous QSAR models. Based on statistical criteria, all the proposed models show a good performance. The datasets for models no. 1, 2, 3, 4, 5, and 7 (Table 6) are relatively small, and the influence of temperature was not considered. Moreover, the previous model was performed with only one partition, but in the current QSAR models, nine partitions were produced to design 36 QSAR models using four objective functions (TF0, TF1, TF2, and TF3). In this study, two crucial criteria, namely the ideal correlation index (IIC) and the correlation intensity index (CII), were explored. These criteria have not been examined in previous studies. The numerical value of the coefficient of determination for the validation set (Rval2) of the QSAR model obtained by TF2 for split 1 is 0.914, which is better than the proposed model based on the same data.29 Thus, the current QSAR model is more accurate and robust.| No. | Set | n | T (K) | Descriptor generator package | Regression method | R2 | RMSD | Ref. |
|---|---|---|---|---|---|---|---|---|
| 1 | Total set | 117 | 298 | MOPAC and CODESSA | MLR | 0.83 | 0.99 | 51 |
| 2 | Training | 83 | 298 | DRAGON | MLR | 0.88 | 0.73 | 52 |
| Test | 42 | — | — | |||||
| 3 | Training | 103 | 298 | CODESSA | ANN | 0.99 | 0.36 | 53 |
| Test | 17 | 0.98 | 0.46 | |||||
| Validation | 17 | 0.98 | 0.48 | |||||
| 4 | Training | 93 | 298 | CODESSA | Projection pursuit regression | 0.92 | 0.66 | 54 |
| Test | 23 | 0.91 | 1.04 | |||||
| 5 | Training | 68 | 298 | Gaussian | Support vector machine | 0.86 | 0.68 | 55 |
| Validation | 36 | 0.77 | 0.77 | |||||
| Test | 35 | — | 0.71 | |||||
| 6 | Training | 306 | 178–409 | MOPAC and DRAGON | PLS | 0.840 | 0.551 | 28 |
| Test | 73 | 0.813 | 0.612 | |||||
| 7 | Training | 109 | 295 | DRAGON and Gaussian | MLR | 0.734 | 1.05 | 56 |
| Validation | 27 | 0.797 | 0.858 | |||||
| Training | 109 | SVM | 0.862 | 0.801 | ||||
| Validation | 27 | 0.782 | 0.970 | |||||
| 8 | Training | 242 | 178–409 | Gaussian, Material Studio | MLR | 0.83 | 0.48 | 29 |
| Test | 60 | 0.72 | — | |||||
| 9 | ATRN | 79 | 178–409 | CORAL package | LR | 0.983 | 0.215 | Present work (split 1) |
| PTRN | 68 | 0.958 | 0.382 | |||||
| CAL | 65 | 0.928 | 0.455 | |||||
| VAL | 90 | 0.914 | 0.573 |
4. Conclusion
In this study, 36 QSAR models were developed to predict 302![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 values from 149 VOCs across a broad temperature range (178–409 K). These models were derived from nine random splits of the dataset. The QSAR modeling was done using the CORAL software based on the Monte Carlo approach. The different temperature feature was incorporated in models by considering the quasi-SMILES of compounds instead of SMILES. To investigate the importance of different target functions for the optimization weights of descriptors, four different target functions were used based on IIC and CII or without using these objective functions. The QSAR models using CII (TF2) produce more predictive and reliable models. All the proposed models provided satisfactory fit criteria for predicting the log
kO3 values from 149 VOCs across a broad temperature range (178–409 K). These models were derived from nine random splits of the dataset. The QSAR modeling was done using the CORAL software based on the Monte Carlo approach. The different temperature feature was incorporated in models by considering the quasi-SMILES of compounds instead of SMILES. To investigate the importance of different target functions for the optimization weights of descriptors, four different target functions were used based on IIC and CII or without using these objective functions. The QSAR models using CII (TF2) produce more predictive and reliable models. All the proposed models provided satisfactory fit criteria for predicting the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3 of VOCs. However, TF2 for split #1 was identified as the best model. Various goodness-of-fit criteria such as R2, IIC, CII, CCC, Q2, QF12, QF22, QF32, s, MAE, F, RMSE,
kO3 of VOCs. However, TF2 for split #1 was identified as the best model. Various goodness-of-fit criteria such as R2, IIC, CII, CCC, Q2, QF12, QF22, QF32, s, MAE, F, RMSE, 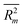 ,
, 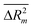 , CRp2 and Y-test were used to assess the reliability and predictive ability of all the proposed models. The applicability domain of the models is defined based on “statistical defect” d(A). Structural features based on both graphs and SMILES were generated from split #1 (considered the best model) and employed to identify the factors promoting either an increase or decrease in log
, CRp2 and Y-test were used to assess the reliability and predictive ability of all the proposed models. The applicability domain of the models is defined based on “statistical defect” d(A). Structural features based on both graphs and SMILES were generated from split #1 (considered the best model) and employed to identify the factors promoting either an increase or decrease in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kO3. The presence of a double bond (BOND10000000 and $10
kO3. The presence of a double bond (BOND10000000 and $10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000), absence of halogen (HALO00000000), and the nearest neighbor codes for carbon equal to 321 (NNC-C⋯321) are some of the significant promoters of endpoint increase. Alternatively, two successive aliphatic carbons with branching (C⋯C⋯(⋯)), valence shell of second order for carbon atom equal to 13 (VS2-C⋯13…), and two aliphatic carbons joined by a double bond (C⋯
000), absence of halogen (HALO00000000), and the nearest neighbor codes for carbon equal to 321 (NNC-C⋯321) are some of the significant promoters of endpoint increase. Alternatively, two successive aliphatic carbons with branching (C⋯C⋯(⋯)), valence shell of second order for carbon atom equal to 13 (VS2-C⋯13…), and two aliphatic carbons joined by a double bond (C⋯![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ⋯C…) are some significant promoters of endpoint decrease.
⋯C…) are some significant promoters of endpoint decrease.
Author contributions
S. Ahmadi designed the study. A. Azimi performed data processing and building the QSAR models. S. Ahmadi and M. Jebeli Javan and wrote the manuscript and performed the interpretation of models. M. Rouhani and Zohreh Mirjafary participated in editing the manuscript.Conflicts of interest
The authors declare no competing interests.Acknowledgements
The authors express their deepest gratitude to Dr Alla P. Toropova and Dr Andrey A. Toropov for providing the CORAL software.References
- D. M. Kialengila, K. Wolfs, J. Bugalama, A. Van Schepdael and E. Adams, J. Chromatogr. A, 2013, 1315, 167–175 CrossRef PubMed
.
- M. Rissanen, J. Phys. Chem. A, 2021, 125, 9027–9039 CrossRef CAS PubMed
.
- M. P. Vermeuel, G. A. Novak, D. B. Kilgour, M. S. Claflin, B. M. Lerner, A. M. Trowbridge, J. Thom, P. A. Cleary, A. R. Desai and T. H. Bertram, Atmos. Chem. Phys., 2023, 23, 4123–4148 CrossRef CAS
.
- J. Rovira, M. Nadal, M. Schuhmacher and J. L. Domingo, Sci. Total Environ., 2021, 787, 147550 CrossRef CAS PubMed
.
- P. Piscitelli, A. Miani, L. Setti, G. De Gennaro, X. Rodo, B. Artinano, E. Vara, L. Rancan, J. Arias and F. Passarini, Environ. Res., 2022, 211, 113038 CrossRef CAS PubMed
.
- B. Liu, J. Ji, B. Zhang, W. Huang, Y. Gan, D. Y. Leung and H. Huang, J. Hazard. Mater., 2022, 422, 126847 CrossRef CAS PubMed
.
- M. H. Abdurahman and A. Z. Abdullah, Chem. Eng. Process., 2020, 154, 108047 CrossRef CAS
.
- J. Hammes, A. Lutz, T. Mentel, C. Faxon and M. Hallquist, Atmos. Chem. Phys., 2019, 19, 13037–13052 CrossRef CAS
.
- M. Glasius and A. H. Goldstein, Environ. Sci. Technol., 2016, 50, 2754–2764 CrossRef CAS PubMed
.
- M. Hallquist, J. C. Wenger, U. Baltensperger, Y. Rudich, D. Simpson, M. Claeys, J. Dommen, N. Donahue, C. George and A. Goldstein, Atmos. Chem. Phys., 2009, 9, 5155–5236 CrossRef CAS
.
- P. J. Ziemann and R. Atkinson, Chem. Soc. Rev., 2012, 41, 6582–6605 RSC
.
- M. Ehn, J. A. Thornton, E. Kleist, M. Sipilä, H. Junninen, I. Pullinen, M. Springer, F. Rubach, R. Tillmann and B. Lee, Nature, 2014, 506, 476–479 CrossRef CAS PubMed
.
- G. McFiggans, T. F. Mentel, J. Wildt, I. Pullinen, S. Kang, E. Kleist, S. Schmitt, M. Springer, R. Tillmann and C. Wu, Nature, 2019, 565, 587–593 CrossRef CAS PubMed
.
- S. Ahmadi and A. Abdolmaleki, Vitam. Horm., 2022, 121, 1–43 Search PubMed
.
- R. Singh, P. Kumar, J. Sindhu, M. Devi, A. Kumar, S. Lal and D. Singh, Comput. Biol. Med., 2023, 157, 106776 CrossRef CAS PubMed
.
- A. A. Toropov, A. P. Toropova, D. Leszczynska and J. Leszczynski, Nanomaterials, 2023, 13, 1852 CrossRef CAS PubMed
.
- A. P. Toropova, A. A. Toropov, A. Roncaglioni and E. Benfenati, Toxicol. in Vitro, 2023, 105629 CrossRef CAS PubMed
.
- S. Ahmadi and N. Azimi, in QSPR/QSAR Analysis Using SMILES and Quasi-SMILES, Springer, 2023, pp. 191–210 Search PubMed
.
- S. Ahmadi, Chemosphere, 2020, 242, 125192 CrossRef CAS PubMed
.
- A. Kumar and P. Kumar, J. Hazard. Mater., 2021, 402, 123777 CrossRef CAS PubMed
.
- A. A. Toropov, M. Di Nicola, A. P. Toropova, A. Roncaglioni, J. Dorne and E. Benfenati, Chemosphere, 2023, 312, 137224 CrossRef CAS PubMed
.
- H. Zhu, Z. Shen, Q. Tang, W. Ji and L. Jia, Chem. Eng. J., 2014, 255, 431–436 CrossRef CAS
.
- H. Zhu, W. Guo, Z. Shen, Q. Tang, W. Ji and L. Jia, Chemosphere, 2015, 119, 65–71 CrossRef CAS PubMed
.
- S. Sudhakaran and G. L. Amy, Water Res., 2013, 47, 1111–1122 CrossRef CAS PubMed
.
- M. R. McGillen, T. J. Carey, A. T. Archibald, J. C. Wenger, D. E. Shallcross and C. J. Percival, Phys. Chem. Chem. Phys., 2008, 10, 1757–1768 RSC
.
- C. Li, X. Yang, X. Li, J. Chen and X. Qiao, Chemosphere, 2014, 95, 613–618 CrossRef CAS PubMed
.
- Z. Cheng, B. Yang, Q. Chen, Z. Shen and T. Yuan, Chem. Eng. J., 2018, 350, 534–540 CrossRef CAS
.
- X. Li, W. Zhao, J. Li, J. Jiang, J. Chen and J. Chen, Chemosphere, 2013, 92, 1029–1034 CrossRef CAS PubMed
.
- Y. Liu, S. Liu, Z. Cheng, Y. Tan, X. Gao, Z. Shen and T. Yuan, Environ. Pollut., 2021, 273, 116502 CrossRef CAS PubMed
.
- P. Achary, A. Toropova and A. Toropov, Food Res. Int., 2019, 122, 40–46 CrossRef CAS PubMed
.
- N. Rezaie-keikhaie, F. Shiri, S. Ahmadi and M. Salahinejad, J. Iran. Chem. Soc., 2023, 20, 2609–2620 CrossRef CAS
.
- A. Kumar and P. Kumar, Struct. Chem., 2021, 32, 149–165 CrossRef CAS
.
- S. Ahmadi, S. Ketabi and M. Qomi, New J. Chem., 2022, 46, 8827–8837 RSC
.
- P. Kumar, A. Kumar and D. Singh, Environ. Toxicol. Pharmacol., 2022, 93, 103893 CrossRef CAS PubMed
.
- A. P. Toropova, A. A. Toropov and E. Benfenati, Struct. Chem., 2021, 32, 967–971 CrossRef CAS
.
- S. Lotfi, S. Ahmadi, A. Azimi and P. Kumar, New J. Chem., 2023, 47, 19504–19515 RSC
.
- A. P. Toropova and A. A. Toropov, J. Mol. Struct., 2019, 1182, 141–149 CrossRef CAS
.
- A. P. Toropova, A. A. Toropov, E. Benfenati, D. Leszczynska and J. Leszczynski, BioSystems, 2018, 169, 5–12 CrossRef PubMed
.
- P. Kumar and A. Kumar, Chemom. Intell. Lab. Syst., 2020, 200, 103982 CrossRef CAS
.
- S. Lotfi, S. Ahmadi and P. Kumar, J. Mol. Liq., 2021, 338, 116465 CrossRef CAS
.
- S. Lotfi, S. Ahmadi and P. Kumar, RSC Adv., 2021, 11, 33849–33857 RSC
.
- S. Ahmadi, S. Lotfi, H. Hamzehali and P. Kumar, RSC Adv., 2024, 14, 3186–3201 RSC
.
- A. P. Toropova, A. A. Toropov, A. Roncaglioni, E. Benfenati, D. Leszczynska and J. Leszczynski, Arch. Environ. Contam. Toxicol., 2023, 84, 504–515 CrossRef CAS PubMed
.
- A. Shayanfar and S. Shayanfar, Eur. J. Pharm. Sci., 2014, 59, 31–35 CrossRef CAS PubMed
.
- V. Consonni, D. Ballabio and R. Todeschini, J. Chem. Inf. Model., 2009, 49, 1669–1678 CrossRef CAS PubMed
.
- K. Roy and S. Kar, Eur. J. Pharm. Sci., 2014, 62, 111–114 CrossRef CAS PubMed
.
- I. Lawrence and K. Lin, Biometrics, 1992, 599–604 Search PubMed
.
- C. Rücker, G. Rücker and M. Meringer, J. Chem. Inf. Model., 2007, 47, 2345–2357 CrossRef PubMed
.
- P. K. Ojha, I. Mitra, R. N. Das and K. Roy, Chemom. Intell. Lab. Syst., 2011, 107, 194–205 CrossRef CAS
.
- C. Rojas, P. R. Duchowicz and E. A. Castro, J. Food Sci., 2019, 84, 770–781 CrossRef CAS PubMed
.
- M. Pompe and M. Veber, Atmos. Environ., 2001, 35, 3781–3788 CrossRef CAS
.
- P. Gramatica, P. Pilutti and E. Papa, QSAR Comb. Sci., 2003, 22, 364–373 CrossRef CAS
.
- M. Fatemi, Anal. Chim. Acta, 2006, 556, 355–363 CrossRef CAS
.
- Y. Ren, H. Liu, X. Yao and M. Liu, Anal. Chim. Acta, 2007, 589, 150–158 CrossRef CAS PubMed
.
- X. Yu, B. Yi, X. Wang and J. Chen, Atmos. Environ., 2012, 51, 124–130 CrossRef CAS
.
- Y. Huang, T. Li, S. Zheng, L. Fan, L. Su, Y. Zhao, H.-B. Xie and C. Li, Sci. Total Environ., 2020, 715, 136816 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra08805g |
| This journal is © The Royal Society of Chemistry 2024 |