Open Access Article
Open Access ArticleMachine learning guided tuning charge distribution by composition in MOFs for oxygen evolution reaction†
Licheng Yu,
Wenwen Zhang,
Zhihao Nie,
Jingjing Duan and
Sheng Chen
and
Sheng Chen *
*
Key Laboratory for Soft Chemistry and Functional Materials (Ministry of Education), School of Chemistry and Chemical Engineering, School of Energy and Power Engineering, Nanjing University of Science and Technology, Nanjing, 210094, China. E-mail: sheng.chen@njust.edu.cn
First published on 18th March 2024
Abstract
Traditional design/optimization of metal–organic frameworks (MOFs) is time-consuming and labor-intensive. In this study, we utilize machine learning (ML) to accelerate the synthesis of MOFs. We have built a library of over 900 MOFs with different metal salts, solvent ratios, reaction durations and temperatures, and utilize zeta potentials as target variables for ML training. A total of four ML models have been used to train the collected dataset and assess their convergence performances, where Random Forest Regression (RFR) and Gradient Boosting Regression (GBR) models show strong correlation and accurate predictions. We then predicted two kinds of MOFs from RFR and GBR models. Remarkably, the experimentally data of the synthesized MOFs closely matched the predicted results, and these MOFs exhibited excellent electrocatalytic performances for oxygen evolution. This study would have general implications in the utilization of machine learning for accelerating the synthesis of MOFs for diverse applications.
Introduction
In recent years, metal–organic frameworks (MOFs) have gained significant attention in research due to their unique composition, combining organic ligands and inorganic metal nodes, which enables them to exhibit properties of both metals and organic compounds.1–3 This intriguing combination has made MOFs a hot topic of investigation. One of the key advantages of MOFs is their ability to possess predictable and well-defined atomic structures. The properties of MOFs are closely linked to the selection of the constituent metals and structured modules. This implies that by carefully choosing these components, it is possible to customize MOF materials with desired physical and chemical properties. The customization potential of MOFs has led to the synthesis and characterization of tens of thousands of different MOFs to date.4–6 The versatility of MOFs stems from the ability to manipulate the reaction conditions and combine various organic ligands and inorganic metal nodes.7–9 This flexibility allows for the proposal of an almost infinite number of MOFs with different compositions and structures. By adjusting these conditions, researchers can explore an extensive range of MOFs with diverse properties. However, due to the vast number of possible compositions, structures, and resulting properties, relying solely on chemical intuition10 and traditional trial-and-error experiments becomes impractical and inefficient. Conventional approaches not only consume significant resources and manpower but also hinder the discovery of the most optimal MOFs for specific applications. To overcome these challenges, machine learning and computational modelling techniques have been employed to accelerate the discovery and design of MOFs with desired properties. These methods utilize large datasets and algorithms to predict and identify promising MOF candidates based on established trends and patterns. By using machine learning, researchers can narrow down the search space and guide experimental efforts toward the most promising MOFs, saving time and resources. In summary, the field of MOFs has seen tremendous growth in recent years, driven by their unique composition and customizable properties. The finite resources available for experimentation, combined with the vast possibilities of MOF compositions, make machine learning and computational modelling essential tools for efficiently discovering the most suitable MOFs for specific applications.The application of ML in materials science, particularly in catalytic science, is rapidly advancing, because ML has successfully enabled predictions related to elemental composition, crystal structure, microstructure images, surface reaction networks, and surface phase diagrams of catalysts.11–13 One key aspect of applying ML in material development lies in the representation of input descriptors. Selecting appropriate descriptors plays a crucial role in enhancing the accuracy of ML model training. By harnessing data-driven technologies, not only can ML serve as a powerful tool for discovering new electrocatalysts, it also provides a deeper understanding of the relationship between inherent characteristics of MOF materials and their electrocatalytic performance. Recent advancements14,15 in this field have led to the development of Machine Learning (ML) models16 that can further enhance and expedite the design and discovery process of MOFs. ML-assisted screening research has proven successful in various applications, particularly in the areas of H2 storage,17–19 CO2 separation/capture,20–22 and other gas storage and separation fields. These ML models leverage high-throughput density functional theory (DFT) workflows23–25 to construct large-scale electronic structure26 performance databases encompassing materials ranging from inorganic solids to molecular systems. The combination of high-throughput DFT databases27–29 with ML has facilitated the discovery of materials with desirable properties across different domains.30–33 For example, this approach has led to the identification of materials for high-efficiency organic light-emitting diodes,34 super-hard inorganic materials,35 thermal conductive polymers,36 and more. To unlock the full potential of network chemistry37 and accelerate material discovery, it is crucial to develop a similar database that encompasses MOF material properties calculated using DFT. Establishing a comprehensive MOF property database, coupled with ML techniques, will contribute to advancing network chemistry and expediting material discovery processes.38–40 Overall, the integration of ML models in MOF research has revolutionized the screening and discovery process. By leveraging the power of ML algorithms and the wealth of computational data, researchers can efficiently explore the vast space of MOF structures, leading to the identification of promising candidates for various applications.
In this work, we employed a hydrothermal method to synthesize a significant number of MOF materials in batches. Although the dataset may be relatively small compared to most machine learning (ML) studies, it is considered substantial within the field of experimental ML integration. When the dataset is small, complex models are prone to overfitting, so it is necessary to simplify the model or use regularization techniques to improve generalization ability. And when the dataset is small, it is prone to underfitting, and feature selection becomes more important because too many features may also lead to overfitting. In big datasets, there may be a large number of features, which increases the complexity of feature selection and feature engineering; of course, when the dataset is large, more complex models can be trained because having more data helps reduce the risk of overfitting. The size of the dataset directly affects the generalization ability of the model. A larger dataset can provide more training samples, enabling the model to better understand the distribution and patterns of data, thereby improving generalization ability. Smaller datasets may not provide sufficient training samples, resulting in poor performance of the model on new, unseen data. Therefore, for large datasets, more complex algorithms and models can be used, such as deep learning models or ensemble learning algorithms. For small datasets, simpler algorithms or ensemble methods may be needed to improve the model's generalization ability. In summary, the size of the dataset has a significant impact on the generalized ability of machine learning models. In order to achieve good generalization ability, it is necessary to comprehensively consider factors such as feature selection, model complexity, regularization, and algorithm selection based on the size of the dataset.
The zeta potential of MOF material dispersion was selected as the output descriptor, which has a correlation with the material size. A higher absolute value of the zeta potential indicates better stability of the dispersion and often corresponds to smaller material sizes, which can influence the electrocatalytic performance of the MOFs. Using the zeta potential data collected from experimental synthesis as the dataset, you trained four ML models. Among them, the Random Forest Regressor (RFR) and Gradient Boosting Regressor (GBR) models showed good training effects. These two models were then used to predict the zeta potential of five-metal MOFs, and corresponding experimental synthesis parameters were obtained. Subsequently, these two types of MOFs were synthesized. The zeta potentials of their dispersions were measured, and it was found that the results were consistent with the ML predictions, validating the rationality of the ML model selection. Furthermore, electrocatalytic oxygen evolution reaction (OER) tests were conducted on the two predicted MOF materials. It was observed that the predicted MOFs exhibited smaller OER overpotentials at a current density of 10 mA cm−2. This suggests that the ML-guided approach holds promise for guiding material development for electrocatalytic OER. The work provides practical ideas for researchers to conduct large-scale material development and demonstrates the potential of ML-guided strategies in accelerating the discovery and optimization of materials for specific applications, such as electrocatalytic OER. By combining experimental synthesis, ML models, and validation through characterization and testing, this research contributes to the advancement of materials science and the application of ML in material development.
Results and discussions
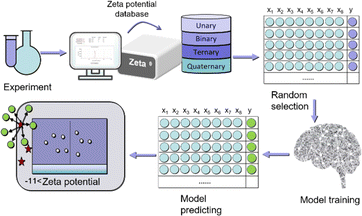
Our goal is to use advanced ML technology to predict 30 zeta potential values of a five-element metal MOF – CuFeZnMnCd MOF under different conditions. The predicted values are compared with experimental values, and the rationality of the model is verified through matching degree. The reaction conditions corresponding to materials with larger absolute zeta potential values are identified, and the OER performance of the materials is measured.We achieve this goal by adopting appropriate input feature selection, which depends on their importance and potential impact on the prediction results. For the input features, we selected 8 descriptors, which are the atomic radius (R), electronegativity (E), main group number (group), outermost electron number (n), atomic number (N) of the metal in the material, as well as the temperature (T), time (t), and solvent ratio (per) of the synthesis reaction. These properties can be obtained at any time from the periodic table and experimental conditions. From a practical perspective, it is important to choose easily obtainable feature values as descriptors in order to effectively bypass time-consuming DFT calculations and maintain good prediction accuracy. We use the Scikit Learn package to develop our ML model. Firstly, we normalize the data, which is an important step in mitigating potential biases caused by differences in feature scales.
The next step is to experimentally synthesize 1–4 metal MOF materials (900 types), test their dispersion to form a dataset of zeta potentials, randomly shuffle and divide 900 sets of data, with 25% as the training set and 75% as the testing set, select appropriate machine learning models, including k-near neighbor (KNN), support vector regression (SVR), random forest regression (RFR), and gradient boosting regression (GBR) to evaluate the zeta potential of the training set, To predict the zeta potential of the test set. The model was comprehensively evaluated using mean absolute error (MAE), root mean square error (RMSE), and coefficient of determination (R2) scores. At the same time, we conducted a single experiment of 100 random leave-n-out trials by repeating 100 random tests/training segmentation, and used the average of 100 RMSE estimates as the prediction accuracy of the ML model (Fig. 1).
In the experiment, five-metal salts (copper acetate, iron nitrate, zinc acetate, manganese acetate, and cadmium acetate) were chosen as organic ligands, along with pyromellitic acid. The reaction time and solvent ratio (water vs. ethanol) were varied, resulting in the synthesis of 900 different MOF materials under hydrothermal conditions at a temperature of 65 °C. To assess the dispersion stability of each material, the zeta potential measurements were conducted. Each material's dispersion was measured three times to reduce measurement errors. The collected data from these measurements formed a dataset that is represented in Fig. S1–S6,† which likely shows the zeta potential values for the different MOF materials synthesized under varying reaction conditions. This dataset serves as valuable information for further analysis and can be used as input for machine learning algorithms to predict and understand the relationship between synthesis parameters and the resulting properties of the MOF materials.
To evaluate the impact of individual input features on model output, we use features from sklearn_ Importances_ Attribute is used to obtain the importance value of each feature in the decision tree. In decision trees, the importance of features can be measured by observing the role of each feature in the decision-making process of the model. Specifically, if a feature plays an important distinguishing role at each node of the decision tree, then that feature is considered important. Therefore, the decision tree is of great significance for tasks such as feature selection and model optimization. As shown in Fig. S9,† which shows the feature importance scores of 7 descriptors, we found that R and per have a prominent effect.
In addition, we also use Pearson correlation coefficient to evaluate the correlation of input features. We found that the correlation of temperature (T) is 0, so it is not input as a feature. The highest Pearson correlation coefficient between other features is only 0.7, which is lower than 0.8. These features have no dependency in terms of quantity and will not bring information redundancy, so they will not reduce generalization ability and the model will not overfit.
In the next step of the study, preliminary fitting was carried out on the structures of the 900 synthesized MOFs. Following this, four ML models were selected for training and convergence using the dataset. The chosen ML models were k-near neighbor (KNN), gradient boosting regression (GBR), random forest regression (RFR), and support vector regression (SVR). Fig. 2 shows the convergence graphs of the dataset training for the four models. It can be observed that the training results of the RFR and GBR models are more consistent with the test results and demonstrate better convergence compared to the other models. This finding is further supported by Fig. S7,† which displays the training errors of the different models. Among the four selected models, GBR and RFR have high R2 values of 0.940 and 0.948, respectively. The GBR and RFR models exhibit relatively small mean absolute error (MAE) values of 1.32 and 1.34, respectively, as well as root mean squared error (RMSE) values of 1.1 and 1.11, respectively. On the other hand, the KNN and SVR models have slightly higher MAE values of 1.56 and 1.53, respectively, and RMSE values of 2.59 and 1.8, respectively. Based on these evaluation metrics, it can be concluded that the GBR and RFR models demonstrate superior performance in accurately predicting the zeta potential of the MOF materials, as they achieve lower errors and better convergence during training.
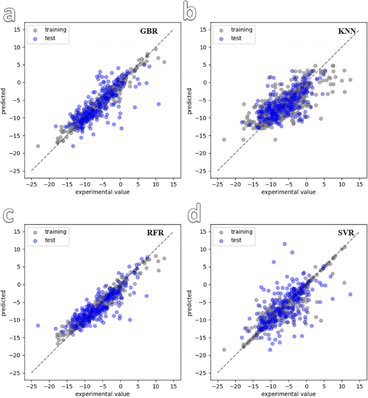 | ||
| Fig. 2 Convergence graph of four ML models used for dataset training. (a–d) are GBR, KNN, RFR and SVR. | ||
To verify the prediction of the ML model, GBR and RFR models were used to predict the zeta potential of five-metal MOFs. As shown in Fig. S10,† the predicted values of GBR and RFR models are in good agreement with the experimental values. Generally speaking, the higher the absolute zeta potential of the nanomaterial dispersion, the smaller the nanomaterial, and the better the catalytic effect. Therefore, we selected materials with higher absolute values from the predicted values of GBR and RFR models for synthesis, and tested their electrocatalytic OER performance. The reaction conditions predicted by the GBR model are a reaction time of 26 hours, a solvent ratio of DIW![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Et = 3
Et = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, a reaction temperature of 65 °C, and a predicted zeta potential of −11.11 mV for the MOF dispersion. The RFR model predicts a reaction time of 29 hours, a solvent ratio of DIW
2, a reaction temperature of 65 °C, and a predicted zeta potential of −11.11 mV for the MOF dispersion. The RFR model predicts a reaction time of 29 hours, a solvent ratio of DIW![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Et = 1
Et = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, a reaction temperature of 65 °C, and a predicted zeta potential of −11.86 mV for the MOF dispersion. Based on these predictions, two types of MOFs composed of five metals were synthesized using a simple solvothermal reaction. Fig. 3 shows the surface morphology of the synthesized MOFs, exhibiting linear microstrip structures with different boundaries. In addition, the energy dispersive X-ray spectroscopy (EDS) of both MOFs confirmed the presence of all five metals in the MOF structure. This validation experiment emphasizes the reliability of the ML model in predicting the zeta potential of MOF material dispersion and guiding the synthesis process. The synthesized MOFs demonstrate the expected characteristics based on ML prediction, further supporting the rationality and accuracy of ML model selection and its application in material development.
4, a reaction temperature of 65 °C, and a predicted zeta potential of −11.86 mV for the MOF dispersion. Based on these predictions, two types of MOFs composed of five metals were synthesized using a simple solvothermal reaction. Fig. 3 shows the surface morphology of the synthesized MOFs, exhibiting linear microstrip structures with different boundaries. In addition, the energy dispersive X-ray spectroscopy (EDS) of both MOFs confirmed the presence of all five metals in the MOF structure. This validation experiment emphasizes the reliability of the ML model in predicting the zeta potential of MOF material dispersion and guiding the synthesis process. The synthesized MOFs demonstrate the expected characteristics based on ML prediction, further supporting the rationality and accuracy of ML model selection and its application in material development.
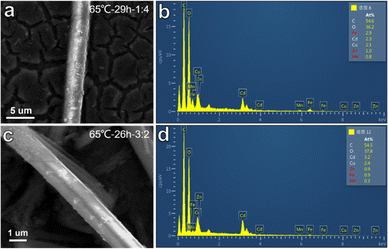 | ||
| Fig. 3 SEM and EDS images of two five-metal MOFs predicted by GBR and RFR models, where (a and b) are RFR and (c and d) are GBR. | ||
Fig. S10† shows the zeta potential of the dispersion of five-metal MOFs synthesized at different reaction times and solvent ratios. It is interesting that as the proportion of ethanol in the solvent increases, the zeta potential value does not show a consistent trend. On the contrary, they exhibit a fluctuating pattern. It is worth noting that the turning points in the predicted trends of GBR and RFR models are consistent. These findings demonstrate the complexity of the relationship between reaction conditions, solvent ratio, and zeta potential of the obtained dispersion. The ability of ML models to capture and predict these complex patterns supports their usefulness in guiding material synthesis and understanding the factors that affect the performance of MOF materials.
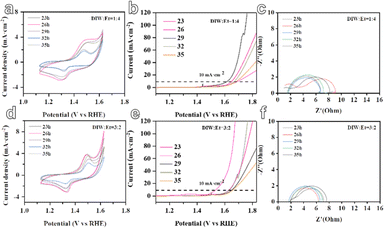
In the subsequent stage, the five-metal MOF materials were assembled into electrodes for the electrocatalytic oxygen evolution reaction (OER), as depicted in Fig. 4. It is observed that when the solvent ratio is DIW![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Et = 1
Et = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, the RFR model predicts that the MOF material synthesized with a reaction time of 29 hours demonstrates a smaller overpotential of only 388 mV. The overpotentials at different reaction times are reported as 420 mV at 23 hours, 464 mV at 26 hours, 440 mV at 32 hours, and 455 mV at 35 hours. Similarly, when the solvent ratio is DIW
4, the RFR model predicts that the MOF material synthesized with a reaction time of 29 hours demonstrates a smaller overpotential of only 388 mV. The overpotentials at different reaction times are reported as 420 mV at 23 hours, 464 mV at 26 hours, 440 mV at 32 hours, and 455 mV at 35 hours. Similarly, when the solvent ratio is DIW![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Et = 3
Et = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, the GBR model predicts that the MOF material synthesized with a reaction time of 26 hours exhibits a smaller overpotential of only 306 mV. The overpotentials at different reaction times are reported as 403 mV at 23 hours, 423 mV at 29 hours, 406 mV at 32 hours, and 430 mV at 35 hours. In addition, from the electrochemical impedance spectroscopy (EIS) curves generated by the two models, it can be observed that the selected materials with larger zeta potentials predicted by the GBR and RFR models exhibit smaller impedances. This suggests improved catalytic activity and more efficient electron transfer at the electrode–electrolyte interface (Fig. 4c and f). These results indicate the potential of the ML models in predicting and optimizing the electrocatalytic performance of MOF materials for the OER. By considering various reaction conditions and solvent ratios, the models can guide the synthesis process to achieve MOF materials with enhanced electrocatalytic activity.
2, the GBR model predicts that the MOF material synthesized with a reaction time of 26 hours exhibits a smaller overpotential of only 306 mV. The overpotentials at different reaction times are reported as 403 mV at 23 hours, 423 mV at 29 hours, 406 mV at 32 hours, and 430 mV at 35 hours. In addition, from the electrochemical impedance spectroscopy (EIS) curves generated by the two models, it can be observed that the selected materials with larger zeta potentials predicted by the GBR and RFR models exhibit smaller impedances. This suggests improved catalytic activity and more efficient electron transfer at the electrode–electrolyte interface (Fig. 4c and f). These results indicate the potential of the ML models in predicting and optimizing the electrocatalytic performance of MOF materials for the OER. By considering various reaction conditions and solvent ratios, the models can guide the synthesis process to achieve MOF materials with enhanced electrocatalytic activity.
Conclusions
In summary, the study involved the synthesis of 900 MOFs through a solvothermal reaction by adjusting various parameters such as temperature, metal species, solvent ratio, and reaction time. The zeta potential of the MOF dispersion was measured as an output parameter, representing dispersion stability and having some correlation with the micro size of the MOF material. This data formed a dataset that was used to train and converge machine learning models. The trained ML models were then utilized to predict the zeta potential of five specific metal MOFs. Experimental synthesis of these MOFs confirmed the validity of the predictions. Furthermore, the synthesized MOFs were applied in electrocatalytic OER reactions, exhibiting low overpotential, indicating their promising catalytic properties. The successful application of machine learning in this study demonstrates the feasibility of using ML-assisted approaches in materials research. It provides researchers with a potential avenue to reduce the need for repetitive and complex manual synthesis by utilizing predictive models. This can lead to more efficient and targeted development of new materials with desired properties in future research endeavours.Author contributions
Licheng Yu, Zhihao Nie, and Wenwen Zhang contributed equally. Sheng Chen provided guidance on the ideas of the paper and made modifications. Wenwen Zhang conducted machine learning calculations, Zhihao Nie, Licheng Yu and Jingjing Duan conducted material synthesis and analyses. All authors discussed and cowrite the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge the financial supports from Jiangsu Natural Science Foundation (Grant No. BK20230097), National Natural Science Foundation (Grant No. 92163124, 51888103 and 52376193), Jiangsu innovative/entre-perineurial talent program (2019) and Fundamental Research Funds for the Central Universities (Grant No. 30920041113 and 30921013103). The authors also thank Yue Chen from Shiyanjia Lab (https://www.Shiyanjia.com) for the TEM measurements.Notes and references
- T. Gadzikwa, Nat. Chem., 2023, 15, 1324–1326 CrossRef CAS PubMed.
- Y. Zou, C. Liu, C. Zhang, L. Yuan, J. X. Li, T. Bao, G. F. Wei, J. Zou and C. Z. Yu, Nat. Commun., 2023, 14, 5780 CrossRef CAS PubMed.
- S. Jeong, J. Seong, S. W. Moon, J. Lim, S. B. Baek, S. K. Min and M. S. Lah, Nat. Commun., 2022, 13, 1027 CrossRef CAS PubMed.
- M. J. Kalmutzki, N. Hanikel and O. M. Yaghi, Sci. Adv., 2018, 4, eaat9180 CrossRef CAS PubMed.
- P. Z. Moghadam, A. Li, S. B. Wiggin, A. Tao, A. G. P. Maloney, P. A. Wood, S. C. Ward and F. J. David, Chem. Mater., 2017, 29, 2618–2625 CrossRef CAS.
- Y. G. Chung, E. Haldoupis, B. J. Bucior, M. Haranczyk, S. Lee, H. Zhang, K. D. Vogiatzis, M. Milisavljevic, S. Ling, J. S. Camp, B. Slater, J. I. Siepmann, D. S. Sholl and R. Q. Snurr, J. Chem. Eng. Data, 2019, 64, 5985–5998 CrossRef CAS.
- C. E. Wilmer, M. Leaf, C. Y. Lee, O. K. Farha, B. G. Hauser, J. T. Hupp and R. Q. Snurr, Nat. Chem., 2012, 4, 83–89 CrossRef CAS PubMed.
- Y. J. Colón, D. A. Gómez-Gualdrón and R. Q. Snurr, Cryst. Growth Des., 2017, 17, 5801–5810 CrossRef.
- P. G. Boyd and T. K. Woo, CrystEngComm, 2016, 18, 3777–3792 RSC.
- A. Ejsmont, J. Andreo, A. Lanza, A. Galarda, L. Macreadie, S. Wuttke, S. Canossa, E. Ploetz and J. Goscianska, Coord. Chem. Rev., 2020, 430, 213655 CrossRef.
- Y. C. Xie, C. Zhang, X. Q. Hu, C. Zhang, P. K. Steven, L. A. Jerry and J. Lin, J. Am. Chem. Soc., 2020, 3, 1475–1481 CrossRef PubMed.
- P. Raccuglia, K. Elbert, P. Adler, F. Casey, M. B. Wenny, M. Aurelio, Z. Matthias, A. F. Sorelle, S. Joshua and J. N. Alexander, Nature, 2016, 533, 73–76 CrossRef CAS PubMed.
- J. L. Beckham, K. M. Wyss, Y. C. Xie, E. A. McHugh, J. T. Li, P. A. Advincula, W. Y. Chen, J. Lin and J. M. Tour, Adv. Mater., 2022, 34, 2106506 CrossRef CAS PubMed.
- Y. J. Colón and R. Q. Snurr, Chem. Soc. Rev., 2014, 43, 5735–5749 RSC.
- K. M. Jablonka, D. Ongari, S. M. Moosavi and B. Smit, Chem. Rev., 2020, 120, 8066–8129 CrossRef CAS PubMed.
- S. Chibani and F. X. Coudert, APL Mater., 2020, 8, 80701 CrossRef CAS.
- G. Anderson, B. Schweitzer, R. Anderson and D. A. Gomez-Gualdron, J. Phys. Chem. C, 2018, 123, 120–130 CrossRef.
- B. J. Bucior, N. S. Bobbitt, T. Islamoglu, S. Goswami, A. Gopalan, T. Yildirim, O. K. Farha, N. Bagheri and R. Q. Snurr, Mol. Syst. Des. Eng., 2019, 4, 162–174 RSC.
- A. W. Thornton, C. M. Simon, J. Kim, O. Kwon, K. S. Deeg, K. Konstas, S. J. Pas, M. R. Hill, D. A. Winkler, M. Haranczyk and B. Smit, Chem. Mater., 2017, 29, 2844–2854 CrossRef CAS PubMed.
- R. Anderson, J. Rodgers, E. Argueta, A. Biong and D. A. Gomez-Gualdron, Chem. Mater., 2018, 30, 6325–6337 CrossRef CAS.
- H. Dureckova, M. Krykunov, M. Z. Aghaji and T. K. Woo, J. Phys. Chem. C, 2019, 123, 4133–4139 CrossRef CAS.
- Z. Yao, B. Sanchez-Lengeling, N. S. Bobbitt, B. J. Bucior, S. G. H. Kumar, S. P. Collins, T. Burns, T. K. Woo, O. K. Farha, R. Q. Snurr and A. Aspuru-Guzik, Nat. Mach. Intell., 2021, 3, 76–86 CrossRef.
- O. A. von Lilienfeld, K. R. Müller and A. Tkatchenko, Nat. Rev. Chem., 2020, 4, 347–358 CrossRef PubMed.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Nature, 2018, 559, 547–555 CrossRef CAS PubMed.
- C. Chen, Y. Zuo, W. Ye, X. Li, Z. Deng and S. P. Ong, Annu. Rev. Mater. Res., 2020, 50, 71–103 CrossRef.
- A. Jain, G. Hautier, C. J. Moore, S. Ping Ong, C. C. Fischer, T. Mueller, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2011, 50, 2295–2310 CrossRef CAS.
- J. S. Smith, O. Isayev and A. E. Roitberg, Sci. Data, 2017, 4, 170193 CrossRef CAS PubMed.
- S. Blau, E. Spotte-Smith, B. Wood, S. Dwaraknath and K. Persson, ChemRxiv, 2020, preprint, DOI:10.26434/chemrxiv.13076030.
- D. Balcells and B. B. Skjelstad, J. Chem. Inf. Model., 2020, 60, 6135–6146 CrossRef CAS PubMed.
- K. T. Winther, M. J. Hoffmann, J. R. Boes, O. Mamun, M. Bajdich and T. Bligaard, Sci. Data, 2019, 6, 75 CrossRef PubMed.
- S. S. Borysov, R. M. Geilhufe and A. V. Balatsky, PLoS One, 2017, 12, e0171501 CrossRef PubMed.
- C. Draxl and M. Scheffler, MRS Bull., 2018, 43, 676–682 CrossRef.
- L. Chanussot, A. Das, S. Goyal, T. Lavril, M. Shuaibi, M. Riviere, K. Tran, J. Heras-Domingo, C. Ho, W. H. Hu, A. Palizhati, A. Sriram, B. Wood, J. Yoon, D. Parikh, C. L. Zitnick and Z. Ulissi, ACS Catal., 2021, 10, 6059–6072 CrossRef.
- A. Mansouri Tehrani, A. O. Oliynyk, M. Parry, Z. Rizvi, S. Couper, F. Lin, L. Miyagi, T. D. Sparks and J. Brgoch, J. Am. Chem. Soc., 2018, 140, 9844–9853 CrossRef CAS PubMed.
- S. Wu, Y. Kondo, M. Kakimoto, B. Yang, H. Yamada, I. Kuwajima, G. Lambard, K. Hongo, Y. B. Xu, J. Shiomi, C. Schick, J. Morikawa and R. Yoshida, npj Comput. Mater., 2019, 5, 66 CrossRef.
- H. Lyu, Z. Ji, S. Wuttke and O. M. Yaghi, Chem, 2020, 6, 2219–2241 CAS.
- M. M. Flores-Leonar, L. M. Mejía-Mendoza, A. Aguilar-Granda, B. Sanchez-Lengeling, H. Tribukait, C. Amador-Bedolla and A. Aspuru-Guzik, Sustainable Chem., 2020, 25, 100370 Search PubMed.
- D. P. Tabor, L. C. Roch, S. K. Saikin, C. Kreisbeck, D. Sheberla, J. H. Montoya, S. Dwaraknath, M. Aykol, C. Ortiz, H. Tribukait, C. Amador-Bedolla, C. J. Brabec, B. Maruyama, K. A. Persson and A. Aspuru-Guzik, Nat. Rev. Mater., 2018, 3, 5–20 CrossRef CAS.
- C. W. Coley, N. S. Eyke and K. F. Jensen, Angew. Chem., Int. Ed., 2020, 59, 22858–22893 CrossRef CAS PubMed.
- C. W. Coley, N. S. Eyke and K. F. Jensen, Angew. Chem., Int. Ed., 2020, 59, 23414–23436 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ra08873a |
| This journal is © The Royal Society of Chemistry 2024 |