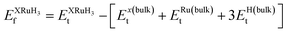A DFT investigation on structural, electronic, magnetic, optical, elastic and hydrogen storage properties of Ru-based hydride-perovskites XRuH₃ (X = Cr, V, Ni)

Abstract

The present investigation delves into various physical properties exhibited by CrRuH₃, VRuH₃ and NiRuH₃. Notably adopting a stable cubic configuration, both compounds manifest a distinct metallic demeanor characterized by an absolute absence of band gap. In-depth analysis through Total Density of States (TDOS) and Partial Density of States (PDOS) justify this metallic conduct by distinctly showcasing peak conductivity at the Fermi level. The materials' magnetic behavior reveals an antiferromagnetic disposition for CrRuH₃ and NiRuH₃, while their intrinsic attributes emerge as anisotropic and rigid. Applying Poisson's ratio (ν) and the B/G ratio, all investigated compounds show ductility, but the CrRuH₃ is superior among them. The heightened values of Young's modulus, Bulk modulus, and mean shear modulus observed in CrRuH₃ underscore its enhanced rigidity as compared to VRuH₃ and NiRuH₃. Within the optical realm, CrRuH₃ displays notable optical conductivity and absorption, particularly within the lower energy spectrum. Remarkably, at 0 eV, CrRuH₃ showcases elevated reflectivity and refractive index as compared to the other investigated materials. On the hydrogen storage front, XRuH₃ (X = Cr, V, Ni) exhibit promising potential, yet CrRuH₃ emerges as the more favorable candidate for hydrogen storage applications.

---

1. Introduction

Technological advancements in modern societies have generated an escalating demand for energy. This surge in energy requirements can be attributed to improved living standards and population growth. The global energy agency confirms that fossil fuels continue to serve as the primary source fulfilling these mounting energy demands.^1,2 It is imperative to acknowledge that while fossil fuels fulfill our energy needs, they concurrently release a significant volume of CO₂, posing a grave environmental threat. Environmental pollution stems from the release of CO₂ through the combustion of various fossil fuels. This emission plays a pivotal role in global warming and exerts detrimental effects on the natural environment.^3,4 Astonishingly, CO₂ emissions, which were approximately 20.7 billion tons in 1990, surged dramatically to an astounding 32.5 billion tons in 2006.^5,6 Furthermore, a study examining hydrogen storage revealed a substantial CO₂ emission rate of 35%.⁷ While a minor concentration of CO₂ in the air poses no harm to humans, heightened emissions could potentially lead to health issues such as headaches, dizziness, and confusion. This concern extends to animals and aquatic life as well. Escalating CO₂ emissions also exacerbate global warming, resulting in severe weather phenomena like floods, deforestation, and droughts. The continuous reliance on fossil fuels not only inflicts adverse impacts on the environment but also depletes finite natural resources, underscoring the critical need to explore renewable energy sources capable of meeting societal needs without inflicting environmental harm. Emerging as an auspicious alternative to fossil fuels due to its abundance and environmental compatibility, hydrogen deserves attention. Its combustion exclusively produces water, rendering it a clean choice.³ Crucially, hydrogen combustion avoids the release of carbon dioxide, positioning it as a genuinely green energy source. Despite hydrogen's threefold higher energy content by weight compared to gasoline, its volume energy content lags, a fact countered by the superior efficiency of hydrogen fuel cells when compared to gasoline engines.^4,8 The applicability of hydrogen extends beyond vehicles to industries, promoting ecological sustainability. Recently, perovskite hydrides have garnered attention for hydrogen storage applications.^9,10 Adhering to the ABX₃ formula,^10,11 with A and B representing cations and X denoting an anion, these materials prove adaptable. The anion X can be interchanged with oxygen as well as nitrogen and we can also change it with halogens and fluorine,^12,13 rendering perovskite hydrides a versatile solution for hydrogen storage.^7,14,15 A perovskite material assumes the designation “halide perovskite” upon the substitution of X with an element from the halide group. Correspondingly, it is commonly referred to as “nitride-perovskite”, “oxide-perovskite”, or “fluoro-perovskite” at the point when nitrogen, oxygen, or fluorine replaces X, respectively. These variants adhere to the general formulae^16–19 ABO₃, ABN₃, and ABF₃, with each fulfilling distinct roles: nitride-perovskites in electronic components, oxide-perovskites in photocatalytic applications, and fluoro perovskites in lens materials. Intriguingly, halide-perovskites have proven highly effective for modern solar cells.^20–25 The introduction of hydrogen into ABX₃ yields a hydride perovskite,^26,27 denoted as ABH₃. However, the challenge of employing hydrogen as a fuel lies in its intricate storage requirements.^28–30 Significantly, the prospects for employing perovskite hydrides, denoted by the chemical configuration ABH₃, as a resolution for hydrogen storage are quite promising.^31–39 These compounds display fundamental attributes, such as strong hydrogen bonding, spacious gaps facilitating considerable hydrogen storage, catalytic properties that augment hydrogen uptake, and suitable gravimetric hydrogen storage capabilities. Generally, hydride perovskites demonstrate gravimetric densities spanning from 1.2 to 6.0 weight percent.³³ The transition metal based hybrid perovskites XCuH₃ (X = Co, Ni, Zn) possess a high gravimetric hydrogen storage capacity and are considered as a promising choice for hydrogen storage application.⁴⁰ Compared to alternative methods, metal hydride perovskites offer a safer and more efficient option for hydrogen storage^41–43 This comprehensive study investigates the structural, optical, electronic, mechanical, magnetic, and hydrogen storage properties of novel ternary perovskite hydrides incorporating XRuH₃ (X = Cr, V, Ni). Through Density Functional Theory (DFT), we will analyze the properties of investigated compounds for hydrogen storage applications. The scrutiny spans an in-depth assessment of the structural, optical, electronic, mechanical, and magnetic attributes of XRuH₃ (X = Cr, V, Ni). This leads us to an in-depth assessment of the structural, optical, electronic, mechanical, and magnetic properties of XRuH₃ (X = Cr, V, Ni). We hope this research article significantly play a role as a bridge between theoretical and experimental literature and offers contribution to the scholarly corpus. We divide our research into different sections to make it reader friendly and more understandable: our first section which is actually an Introduction part where we discuss the scope, utility, hurdles and their solutions as well as the applications of perovskite hydride. Section 2 elaborates the computational work which we employed. In Section 3, we delve into outcomes and discussions concerning perovskite hydrides XRuH₃ (X = Cr, V, Ni). Ultimately, Section 4 discuss the conclusion and findings of our research.

2. Computational methodology

The CASTEP package⁴⁴ was utilized to finely tune the arrangement of the XRuH₃ (X = Cr, V, Ni) hydride perovskites. This code, CASTEP, was also put to use to thoroughly examine various aspects of these materials. We adopted a method called the GGA exchange–correlation functional from ultra-soft USP plane wave PBE to delve into the characteristics of XRuH₃ (X = Cr, V, Ni), including their shape, electrical properties, magnetic behavior, optical response, and mechanical strength. We employed the plane wave pseudopotential technique rooted in density functional theory (DFT) to address the Kohn–Sham equations. This technique creates a set of plane waves as a foundation, extending the concept through periodic boundary conditions.^45,46 Then we employed first principles pseudopotentials to effectively manage interactions between electrons and ions within the Vanderbilt-type ultrasoft formulations, mimicking how they interact in reality.⁴⁷ Prior research highlighted the superiority of the BFGS energy minimization approach in evaluating electron wave functions and charge distributions in crystalline materials. To facilitate this study, the Pulay density mixing approach was also applied.^48,49 The Monkhorst–Pack technique was harnessed to meticulously sample unique points within the first Brillouin zone. An energy cutoff value of 600 eV was selected, complemented by k-points mesh featuring 6 × 6 × 6 points, chosen for greater precision. The discrepancy in energy per atom was confined to 2 × 10⁻⁵ eV. Notably, the ionic Hellmann–Feynman force was restricted to a maximum of 0.05 eV Å⁻¹. Throughout the calculations, the stress was managed to stay within the confines of 0.1 GPa, while the most considerable atomic displacement was limited to 2 × 10⁻³ Å. For all calculations, a highly refined self-consistent field (SCF) convergence threshold and energy tolerance per atom were upheld. The PBE-GGA approach was additionally employed for the purpose of assessing elastic constants, a crucial aspect in the evaluation of structural integrity and correlated mechanical characteristics. In each instance of elongation or compression, a structured four-step methodology was implemented, employing a peak strain amplitude of 0.003 as the upper limit. The variance in energy per atom was maintained at a level of 4 × 10⁻⁶ eV, while the upper threshold for ionic Hellmann–Feynman force was confined to 0.01 eV Å⁻¹. When examining the effects of compression, a maximum atomic displacement of 4 × 10⁻⁴ Å was selected. The application of an ultra-fine convergence threshold ensured accuracy both in optimizing geometry and evaluating measures of elasticity. The inquiry into these characteristics was undertaken only after confirming the optimal configuration of the fundamental building block.

3. Results and discussions

3.1. Structural properties

In this section, we present an examination of the structural attributes exhibited by hydrides following the perovskite-type arrangement, denoted as XRuH₃ (X = Cr, V, Ni). These specific perovskite hydrides showcase a cubic crystal configuration, categorized within the pm3̄m space group with international number of 221. The depiction of the cubic crystal structure of XRuH₃ (X = Cr, V, Ni) can be observed in Fig. 1. During the process of optimizing the unit cell, a systematic approach was adopted, involving the strategic positioning of X cations at the corners, with the central point occupied by the less abundant metal, Ru, and the face-centered sites adorned by hydrogen atoms. Detailed information regarding the lattice constants, volume, and band gap energy specific to the XRuH₃ (X = Cr, V, Ni) perovskite hydrides is presented in Table 1. It's noteworthy that the lattice constant of VRuH₃ surpasses that of CrRuH₃ and NiRuH₃, similarly reflecting a greater volume for VRuH₃ in contrast to CrRuH₃ and NiRuH₃ perovskite hydrides. The formation enthalpy of all the compounds was calculated with the help of the following equation⁵⁰

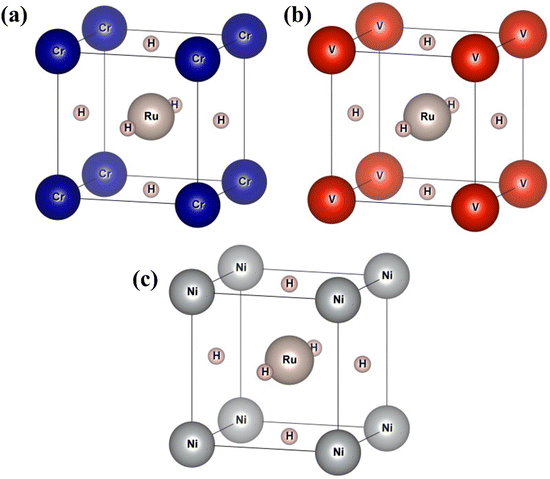Fig. 1 Unit cell of (a) CrRuH₃, (b) VRuH₃ and (c) NiRuH₃.

Table 1 The values of band gap energy, volume and lattice parameters

Compound	Lattice constant (Å) (a = b = c)	Volume (Å)^3	Band gap (eV)	Reference
CrRuH3	3.350	37.597	0	Present study
VRuH3	3.385	38.004	0	Present study
NiRuH3	3.348	37.516	0	Present study
CoCuH3	3.328	36.882	0	40
NiCuH3	3.324	36.742	0	40
ZnCuH3	3.612	47.160	0	40

---

The formation energy is found −1.72, −1.09 and −1.30 eV per atom for CrRuH₃, NiRuH₃, and VRuH₃ respectively. Further the stability of investigated compounds is also analyzed using the phonon spectra in Fig. 4 where the graph clearly depicts that the NiRuH₃.has no negative frequencies as compared to the other two compounds. The resulting cohesive energy values of −5.11, −4.63 and −4.00 eV per atom affirm the robustness of the crystal structures of CrRuH₃, VRuH₃ and NiRuH₃. However, in light of the more negative cohesive energy, the crystal structure of CrRuH₃ holds a stronger recommendation for stability compared to the other investigated compounds. Moving beyond, we delve into the mechanical aspect of stability, gauged through an assessment of elastic constants. The outcome of this evaluation, as expounded in Section 3.4, reveals the mechanical stability of compounds under investigation.

3.2. Electronic band structure and density of states

When analyzing the electronic attributes of a substance, careful consideration of the examination of its electronic band structure and DOS becomes of utmost significance. The compound's electronic band arrangement can be comprehended through the application of TDOS and PDOS, elucidating the atomic interactions and the relaxation of these atoms contribute to the electronic band configuration.

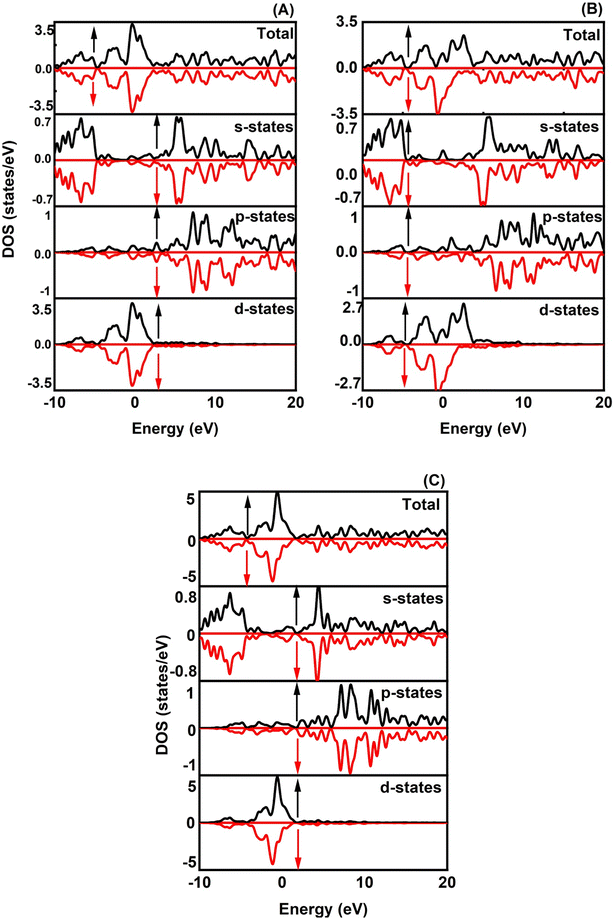
Fig. 2 shows how atoms in XRuH₃ (X = Cr, V, Ni) are arranged to create electronic bands. The point of zero energy, known as the Fermi level, is marked by a dashed black line at 0 eV in these bands. Think of the bands as different energy levels within the material. The upper part is like a busy highway for electrons, called the conduction band, while the lower part is like a resting area, called the valence band. The gap between them is called the band gap. But interestingly, for XRuH₃ (X = Cr, V, Ni), these bands overlap, which means there's no clear band gap. This suggests that the material behaves more like a metal in this case. In Fig. 3, we have graphs that show the overall amount of energy states (TDOS) and partial density of states (PDOS) in XRuH₃ (X = Cr, V, Ni). Think of these energy states as distinct positions within a framework. Some positions are more populated than others, indicating where energy levels gather. Specifically, in the valence region (analogous to the lower segment of this framework), energy levels reach their highest values at 0.60 eV, 0.99 eV, and 2.62 eV for CrRuH₃, VRuH₃, and NiRuH₃ respectively, precisely aligned with the Fermi level. We also see more peaks at 17.45 eV, 17.10 eV, and 8.35 eV for CrRuH₃, VRuH₃, and NiRuH₃ respectively. Looking deeper into how the electrons are arranged, the TDOS helps. In the valence area, the d-states contributes to energy levels from −10 to 0 eV, while the p-states affect energy levels from 10 to 20 eV in the upper region. Interestingly, the s-states do not play a big role in the lower part for any compound, but it's more active in the upper parts of all the materials we're studying. The coexistence of s-states and p-states at the Fermi level solidifies the metallic nature of these compounds, signifying their potential as novel materials for harnessing low-energy incident radiations. This unique property positions these compounds as capable hydrogen storage vessels owing to their intermetallic phase.⁵¹ Moving onward, CrRuH₃ exhibits bond lengths of 1.68 Å (H–Ru) and 2.37 Å (H–Cr), VRuH₃ exhibits bond lengths of 1.69 Å (H–Ru) and 2.39 Å (H–V), whereas NiRuH₃ displays bond lengths of 1.67 Å (H–Ru) and 2.37 Å (H–Ni). Notably, the bond lengths within VRuH₃ exceed those in CrRuH₃ and NiRuH₃ attributed to differences in ionic radii. This difference highlights the substantial bond strength present in these compounds, thereby enhancing their potential for hydrogen storage. The ionic radii of Cr, V, Ni, and Ru, measuring at 200, 179, 163, and 205 picometers respectively, could induce matrix distortion upon doping or substitution, resulting in matrix expansion. This expansion effectively increases interstitial sites, thus bolstering the capacity for hydrogen storage or absorption. Furthermore, these compounds are capable of experiencing the creation of intermetallic compounds through chemical reactions with hydrogen, contributing to the further enhancement of the storage process.

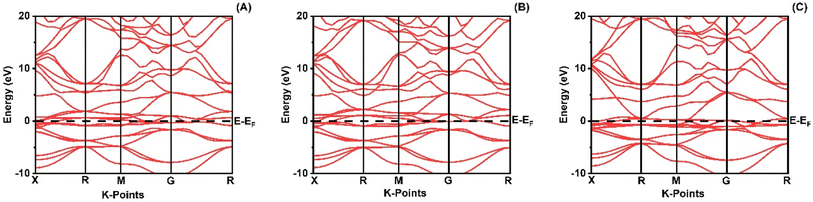Fig. 2 Band structure of (A) CrRuH₃, (B) VRuH₃ and (C) NiRuH₃.

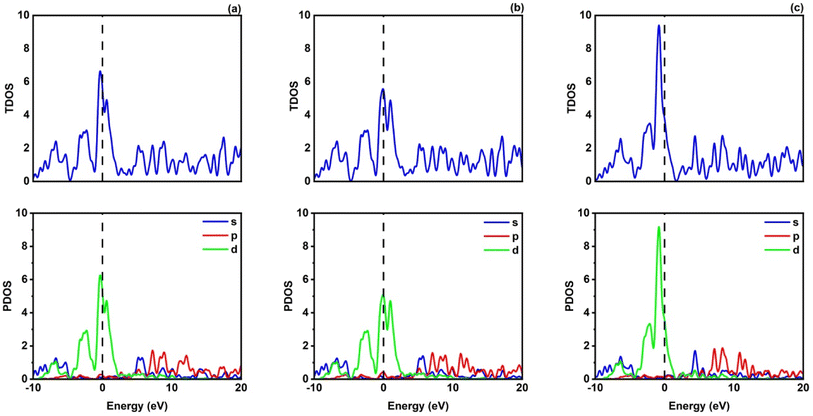Fig. 3 TDOS and PDOS of (a) CrRuH₃, (b) VRuH₃ and (c) NiRuH₃.

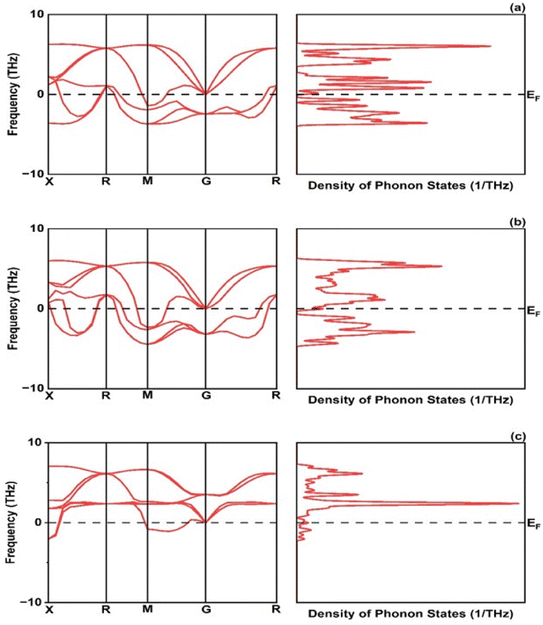Fig. 4 Phonon dispersion and density of phonon states: (a) CrRuH₃, (b) VRuH₃ and (c) NiRuH₃.

3.3. Magnetic properties

The magnetic properties of XRuH₃ (X = Cr, V, Ni) arise due to a combination of inherent material traits and the specific arrangement of atoms. To understand these magnetic behaviors better, we conducted a detailed examination of the spin-polarized band structures of XRuH₃ (X = Cr, V, Ni) using the PBE + GGA functional approach, which is a specific method for studying these materials. These band structures are like visual maps that show how electrons in the material's atoms behave. In these maps, the red lines represent electrons with one kind of spin (a property related to their movement), and blue lines represent electrons with a different spin. Similarly, when we looked at the density of different energy states, we used black lines for one type of spin and red lines for the other. The Fermi level is a special energy point in the material, and we indicated it with a red line on these maps, right at 0 eV. We looked at how different materials (XRuH₃ where X is Cr, V, or Ni) behave when it comes to magnets. To do this, we checked the way the spins of the particles are arranged and how they affect the energy levels of the materials. In the pictures labeled Fig. 5 and 6, we showed how these spins affect the energy levels. Among the materials we studied, CrRuH₃ and NiRuH₃ don't act like magnets because their spins are like mirror images of each other, both in the parts with more energy and in the parts with less energy. This means they don't create any overall magnetic force. Our findings about how the spins are arranged in CrRuH₃ and NiRuH₃ support the idea that these materials don't act like regular magnets. This is because their spins cancel each other out; making them what we call “antiferromagnetic compounds”. In simple terms, the way their tiny magnetic forces add up is zero.⁵² Nevertheless, the VRuH₃ demonstrates magnetic nature due to the imbalance noted in the spin up↑ and down↓ conditions. The magnetism attribute of VRuH₃, being of a metallic disposition, renders it a distinctive substance for the storing of hydrogen. There were some variations in the spin behavior in VRuH₃ compared to the others. This is linked to our earlier observation that there is no clear gap in energy levels (band gap) in both CrRuH₃ and NiRuH₃ compounds. Additionally, we noticed that the energy levels where electrons can be found were getting really close to each other, suggesting that these materials can easily conduct electricity. For a deeper understanding of how electrons are behaving and why the materials show magnetic properties, we also looked at the density of states with different spins. This gives us information about how many energy states are available for different types of electron spins. Fig. 6 illustrates these densities for the materials we studied. We marked the Fermi level with precision, and it's still at 0 eV. What's interesting is that the graphs representing densities for different spins look very similar to each other, except for VRuH₃, where they seem to be like mirror images, just opposite to each other. This suggests that the overall magnetic behavior in these materials is neutral; they don't have a dominant magnetic direction. As a result, both CrRuH₃ and NiRuH₃ show an antiferromagnetic behavior, meaning their magnetic behavior opposes the usual magnetic patterns. This antiferromagnetic property is also noticeable when looking at certain energy states within the spin-polarized density of states. The spin-separated partial density of states for the s- and p-electrons also shows mirrored patterns in CrRuH₃ and NiRuH₃. This confirms that these materials behave in an antiferromagnetic way. It exerts a notable influence on both the electronic and magnetic characteristics of our compounds. These materials lack conventional macroscopic magnetization, the presence of antiferromagnetic order is important for understanding their unique magnetic behavior, which has implications for their suitability in hydrogen storage and other potential applications.

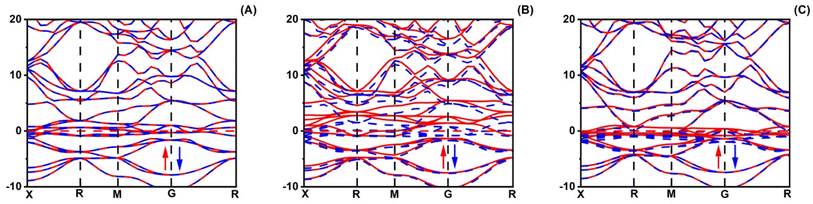Fig. 5 Spin polarized band structure of (A) CrRuH₃, (B) VRuH₃ and (C) NiRuH₃.

Fig. 6 Spin polarized TDOS and PDOS of (A) CrRuH₃, (B) VRuH₃ and (C) NiRuH₃.

3.4. Optical properties

Optical parameters offer valuable insights into how materials interact with incident electromagnetic radiation. The intricate dielectric functions and other optical parameters that vary with frequency offer a holistic understanding of the optical characteristics of the materials under investigation. By analyzing reflectivity, we can effectively measure a material's ability to reflect incoming light. Fig. 7 illustrates the reflectivity graph for CrRuH₃, VRuH₃ and NiRuH₃. Notably, the static values for CrRuH₃, VRuH₃ and NiRuH₃ are 0.73, 0.8 and 0.61, respectively. The peak values stand at 0.53 (at 24.53 eV) for CrRuH₃ and 0.50 (at 24.04 eV) for VRuH₃ and 0.44 (at 24.14 eV) for NiRuH₃. Beyond energies of 50 eV, 54 eV and 49 eV, respectively for CrRuH₃, VRuH₃ and NiRuH₃, the reflectivity diminishes, ultimately reaching zero. The results clearly shows that reflectivity of CrRuH₃ > VRuH₃ > NiRuH₃. The absorption coefficient, presented in Fig. 7, offers insights into how materials absorb photons. A high absorption coefficient signifies efficient photon absorption. CrRuH₃, VRuH₃ and NiRuH₃ show no absorption when not exposed to incident radiations. For all compounds, absorption rises between 0 and 23 eV and decreases between 23 and 34 eV and then again increasing trend seen in all compounds from 38 to 50 eV. In contrast, CrRuH₃ displays increasing absorption from 0.94 to 22.67 eV, followed by a continuous decrease beyond 22.67 eV. CrRuH₃'s maximum absorption occurs at 44.01 eV, VRuH₃ shows maximum peak at 39 eV and NiRuH₃'s maximum peak of absorption is at 43.12 eV. At higher energies, all compounds show reduced absorption, reaching zero beyond 55.79 eV. Absorption graph clearly depicts that the absorption of CrRuH₃, > VRuH₃ > NiRuH₃. The refractive index n(ω), depicted in Fig. 7, aids in predicting material transparency. The refractive index can be calculated using the equation⁵³

n = (1 − R)/(1 + R), (1)

where R is the Fresnel's reflectance. Other optical properties such as reflectivity (R), energy loss (L), refractive index (n), and absorption coefficient (I) are computed using specific equations.

ε(ω) = ε₁(ω) + iε₂(ω) (2)

n(ω) = [ε₁(ω)/2 + {ε₁²(ω) + ε₁²(ω)}^1/2/2]^1/2 (3)

L(ω) = −I′m(ε(ω)⁻¹) = ε₂(ω)/ε₁(ω)² + ε₂(ω)² (4)

I(ω) = 2^1/2ω[{ε₁²(ω) + ε₁²(ω)}^1/2 − ε₁(ω)]^1/2 (5)

R(ω) = (n + k −1)/(n + k + 1) (6)

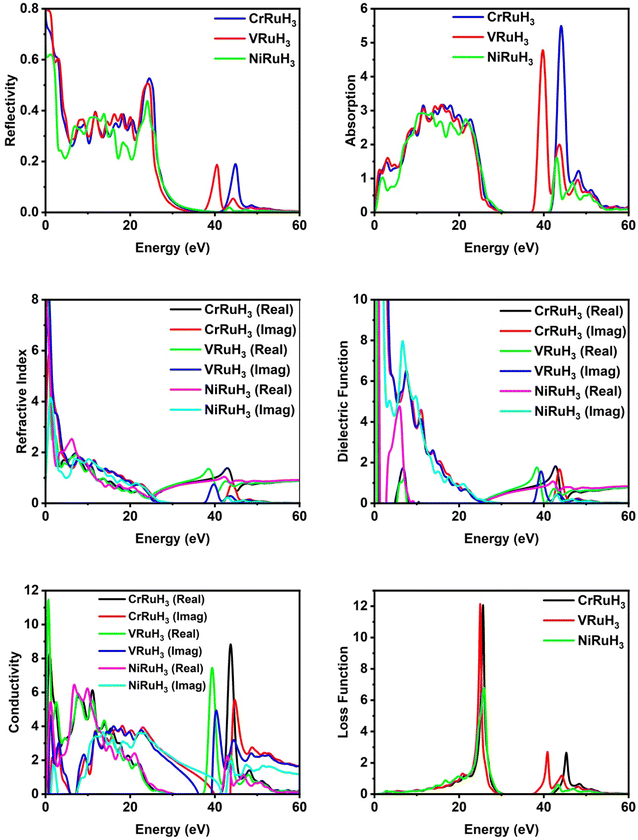Fig. 7 Comparative analysis of optical properties of CrRuH₃, VRuH₃ and NiRuH₃.

The static refractive index values for CrRuH₃, VRuH₃ and NiRuH₃ are 3.68, 2.82 and 4.79, respectively. Furthermore, their peak refractive indices are 1.37 (at 42.89 eV) for CrRuH₃, 1.35 (at 38.35 eV) for VRuH₃ and 1.74 (at 6.77 eV) for NiRuH₃. These values decrease as incident photon energy increases. The graph clearly depict that the refractive index of NiRuH₃ > CrRuH₃ > VRuH₃. The dielectric function ε(ω) plays a pivotal role in assessing optical properties. Comprising real ε₁(ω) and imaginary ε₂(ω) parts, ε(ω) predicts polarization and photon dispersion. The real part reveals polarization, while the imaginary part indicates absorptive nature. The real and imaginary parts are combined through Kramers–Kronig's relation.⁵⁴ The actual component of the dielectric function, ε₁(ω), across all the compounds examined, displayed in Fig. 7, demonstrates stationary values of 1.05 eV for CrRuH₃, 0.65 for VRuH₃ and 1.33 for NiRuH₃. Real peak values of ε₁(ω) for CrRuH₃, VRuH₃ and NiRuH₃ are 1.83 (at 42.72 eV), 1.76 (at 38.19 eV) and 4.73 (at 5.80 eV), respectively. Imaginary peak values occur at 7.27, 7.46 and 6.58 eV for CrRuH₃, VRuH₃ and NiRuH₃, resulting in optical losses and poor transmission. Optical conductivity informs about conduction mechanisms due to photoelectrons. Real and imaginary parts of conductivity, as seen in Fig. 7, indicate the breaking of bonds. NiRuH₃ exhibit zero conductivity in the absence of incident photons at 0 eV but CrRuH₃, VRuH₃ shows conductivity at 0 eV. CrRuH₃ has higher conductivity, with a peak real conductivity value of 8.79 (at 43.68 eV) and imaginary conductivity of 5.51 (at 44.67 eV). The graph clearly shows that the conductivity of CrRuH₃ > VRuH₃ > NiRuH_3. The energy loss function, shown in Fig. 7, indicates scattering probability of photoelectrons. The highest energy loss values are 12.12 (VRuH₃) at 24.95 eV, 12.10 (CrRuH₃) at 25.55 eV and 6.80 (NiRuH₃) at 25.83 eV. Energy loss drops to zero beyond 50.83 eV. The results clearly shows that the loss function is VRuH₃ > CrRuH₃ > NiRuH₃.

3.5. Mechanical properties

The evaluation of a material's response to applied forces necessitates the utilization of mechanical properties, particularly elastic constants. These elastic constants play a crucial role in exploring the mechanical behavior of the materials under investigation. In cubic crystals, such as the ones examined in this study, there are typically three elastic constants: C₁₁, C₁₂, and C₄₄. The calculated elastic constants for CrRuH₃, VRuH₃ and NiRuH₃ can be found in assessing the mechanical stability of crystal structures is of significant importance when investigating their mechanical properties. This stability in cubic crystals can be ascertained through the following criteria:⁵⁵

C₁₁ + 2C₁₂ > 0; C₁₁ − C₁₂ > 0; C₄₄ > 0 (7)

Here, C₁₁, C₁₂, and C₄₄ represent the elastic constants for cubic crystals. Both compounds fulfill these criteria, indicating their mechanical stability as given in the above equation. In Table 2, we showcase the anisotropic factor, Young's modulus, Poisson's ratio which are represented as A, E, ν respectively, and Pugh's index ratio for XRuH₃ (X = Cr, V, Ni). These values were determined using the equations detailed below, shedding light on the material's mechanical properties and how it responds to external forces:⁵⁶

A = (2C₄₄)/(C₁₁ − C₁₂) (8)

B = (C₁₁ + 2C₁₂)/3 (9)

G_v = (C₁₁ − C₁₂ + 3C₄₄)/5 (10)

G_R = 5C₄₄(C₁₁ − C₁₂)/4C₄₄ + 3(C₁₁ − C₁₂) (11)

G = (G_v + G_R)/2 (12)

Table 2 The computed values for elastic constants and other parameters

Parameters	CrRuH3	VRuH3	NiRuH3
C11	255.97	237.32	295.79
C12	141.22	140.60	89.67
C44	35.55	23.61	6.89
A	0.62	0.49	0.07
B	179.47	172.84	158.38
Gv	44.28	33.51	45.36
GR	41.93	29.69	10.99
G	43.11	31.60	28.18
E	119.73	89.35	79.80
ν	0.56	0.60	0.61
B/G	4.16	5.47	5.62

---

The equation stated above encompasses three distinct moduli: G_v, referred to as the Voigt modulus, which characterizes the upper bound; G_R, which stands for the Reuss modulus, indicating the lower bound; and G, representing the mean shear modulus, capturing the average mechanical response of the material.

E = (9BG)/(3B + G) (13)

In the above equation, encompasses three pivotal moduli: the Bulk modulus (B), the mean shear modulus (G), and the Young's modulus (E), the latter symbolized as (E). These moduli collectively contribute to our understanding of the material's mechanical behavior.

ν = (3B − 2G)/2(2B + G) (14)

In this context, B signifies the Bulk modulus, G represents the shear modulus, and ν provides insight into the Poisson's ratio. When considering cubic crystals, the elastic constants denoted as C₁₁, C₁₂, and C₄₄ are expressed through eqn (4)–(7). These constants pave the way for assessing diverse mechanical properties once they are integrated. The anisotropy factor A serves as a tool for distinguishing whether the materials exhibit an isotropic or anisotropic nature. A numeric value of 1 indicates isotropy, while deviation from 1 signifies anisotropy. In this case, both materials exhibit an anisotropic nature due to the departure of A from 1. Bulk modulus (B) relates to material hardness. Both compounds exhibit positive bulk modulus values, indicating inherent hardness. CrRuH₃, with a higher bulk modulus of 179.47, is comparatively harder than VRuH₃ which has 172.84 and NiRuH₃ which contains bulk modulus of 158.38. Mean shear modulus (G) and Young's modulus (E) corroborate the materials' inherent hardness, with CrRuH₃ displaying greater hardness due to higher values of G and E. Poisson's ratio ν signifies material ductility or brittleness. All compounds under investigation exhibits ductile nature as results clearly shows that their ν > 0.26. The B/G ratio aids in characterizing ductile or brittle materials. Ductile materials have B/G > 1.75, reinforcing ductility of all investigated materials. Analyzing these mechanical properties indicates that CrRuH₃ is a more favorable candidate for hydrogen storage devices as compared to other investigated compounds due to its desirable properties.

3.6. Hydrogen storage properties

Several challenges hinder the widespread adoption of hydrogen, as a potential fuel source, stands as one of the noteworthy contenders, which involves the lack of viable methods to efficiently contain hydrogen using sufficient gravimetric storage capacity. A key solution to this issue lies in the development of compounds capable of effectively reversing the accumulated hydrogen at higher densities. Diverse approaches to hydrogen storage exist, including solid-state, liquid, and gaseous methods. To address this goal, an extensive array of compounds has been explored, encompassing metal hydride perovskites. Assessing gravimetric hydrogen storage capacities proves instrumental in gauging a material's maximum ability to store hydrogen. For CrRuH₃, VRuH₃ and NiRuH₃, these capacities are calculated using the formula:⁴⁰

C_wt% = [pM_H/(M_com + pM_H)] × 100% (15)

In this equation, p denotes the ratio of hydrogen atoms to material atoms, M_com stands for the molar mass of the compound, and M_H represents the molar mass of hydrogen. The gravimetric hydrogen storage capacity is quantified at 3.66%, 3.68% and 3.52% for CrRuH₃, VRuH₃ and NiRuH₃, respectively. This establishes XRuH₃ (X = Cr, V, Ni) as viable candidates for hydrogen storage applications. Notably, the gravimetric hydrogen storage capacity of XRuH₃ lies within the range of 3.52 to 3.68% which makes a potential for hydrogen storage application.

4. Conclusion

The structural, electronic, optical, magnetic, hydrogen storage and mechanical characteristics of perovskites based on ruthenium hydrides XRuH₃ (where X = Cr, V, Ni) have been systematically investigated utilizing the CASTEP computational tool. The calculations are performed employing the PBE exchange–correlation functional within the framework of generalized gradient approximation (GGA). Both compounds exhibit a stable crystal lattice arrangement and demonstrate metallic behavior, characterized by a complete absence of a band gap. The obtained lattice parameters match well with a previous study of transition metal based hydride perovskites. Notably, the Fermi level analysis through Total Density of States (TDOS) and Partial Density of States (PDOS) confirms the presence of maximum conductivity. An examination of the anisotropy factor ‘A’ reveals the inherent anisotropic nature of both materials. Further insight into mechanical properties discloses that CrRuH₃ exhibits greater hardness than VRuH₃ and NiRuH₃, as evidenced by higher values of Young's modulus, bulk modulus and mean shear modulus. Additionally, the mechanical behavior is assessed through Poisson's ratio and B/G ratio, revealing that all compounds show ductile nature and results shows that CrRuH₃ is the superior among them. The optical conductivity and absorption behaviors of these materials display pronounced characteristics in the lower energy spectrum. In terms of reflectivity CrRuH₃ shows maximum peak and in terms of refractive index, NiRuH₃ shows maximum value. The ability of the materials we studied to store hydrogen has been figured out. We found that VRuH₃ can hold the most hydrogen by weight (about 3.68%), while NiRuH₃ can hold the least (about 3.52%). When it comes to magnets, NiCuH₃ and ZnCuH₃ behave in an antiferromagnetic way, whereas VRuH₃ is a strong magnetic material. All compounds under investigation demonstrate potential for hydrogen storage; however, CrRuH₃ emerges as the superior choice, offering enhanced hydrogen storage capabilities. These theoretical calculations are expected to inspire researchers to create real CrRuH₃, VRuH₃, and NiRuH₃ hydride perovskites in experiments. These materials are anticipated to have significant potential for use in hydrogen storage applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University, Saudi Arabia, for funding this work through research group program under grant number R.G.P. 2/570/44.

References

1. A. Gencer, G. Surucu and S. Al, MgTiO3Hx and CaTiO3Hx perovskite compounds for hydrogen storage applications, Int. J. Hydrogen Energy, 2019, 44(23), 11930–11938.
2. I. Sreedhar, et al., A bird's eye view on process and engineering aspects of hydrogen storage, Renewable Sustainable Energy Rev., 2018, 91, 838–860.
3. L. Zhou, Progress and problems in hydrogen storage methods, Renewable Sustainable Energy Rev., 2005, 9(4), 395–408.
4. M. Granovskii, I. Dincer and M. A. Rosen, Environmental and economic aspects of hydrogen production and utilization in fuel cell vehicles, J. Power Sources, 2006, 157(1), 411–421.
5. M. R. Raupach, et al., Global and regional drivers of accelerating CO2 emissions, Proc. Natl. Acad. Sci. U. S. A., 2007, 104(24), 10288–10293.
6. P. J. Pearson and T. J. Foxon, A low carbon industrial revolution? Insights and challenges from past technological and economic transformations, Energy Policy, 2012, 50, 117–127.
7. Z. Guo, C. Shang and K. Aguey-Zinsou, Materials challenges for hydrogen storage, J. Eur. Ceram. Soc., 2008, 28(7), 1467–1473.
8. R. K. Ahluwalia, et al., Fuel economy of hydrogen fuel cell vehicles, J. Power Sources, 2004, 130(1–2), 192–201.
9. H. H. Raza, et al., First-principle investigation of XSrH3 (X= K and Rb) perovskite-type hydrides for hydrogen storage, Int. J. Quantum Chem., 2020, 120(24), e26419.
10. G. Surucu, et al., CaXH3 (X= Mn, Fe, Co) perovskite-type hydrides for hydrogen storage applications, Int. J. Energy Res., 2020, 44(3), 2345–2354.
11. M. A. H. Shah, et al., Exploring pressure induced thermoelectric properties of LiAeH3 (Ae= Ca, Sr, Ba) perovskite hydrides along with optoelectronic features, Mater. Sci. Semicond. Process., 2022, 137, 106238.
12. M. R. Kabli, et al., Structural, electronics and optical properties of sodium based fluoroperovskites NaXF3 (X= Ca, Mg, Sr and Zn): first principles calculations, Phys. Lett. A, 2021, 412, 127574.
13. J. ur Rehman, et al., First-principles calculations to investigate structural, electronic and optical properties of Na based fluoroperovskites NaXF3 (X= Sr, Zn), Solid State Commun., 2021, 334, 114396.
14. M. Hirscher, et al., Materials for hydrogen-based energy storage–past, recent progress and future outlook, J. Alloys Compd., 2020, 827, 153548.
15. M. B. Ley, et al., Complex hydrides for hydrogen storage–new perspectives, Mater. Today, 2014, 17(3), 122–128.
16. A. Laref, et al., Impact of fluorine on organic cation for determining the electronic and optical properties of CH3− xFxNH3PbI3 (x= 0, 1, 2, 3) hybrid perovskites-based photovoltaic devices, Sol. Energy, 2019, 177, 517–530.
17. A. Abate, et al., Supramolecular halogen bond passivation of organic–inorganic halide perovskite solar cells, Nano Lett., 2014, 14(6), 3247–3254.
18. H.-S. Kim, S. H. Im and N.-G. Park, Organolead halide perovskite: new horizons in solar cell research, J. Phys. Chem. C, 2014, 118(11), 5615–5625.
19. B. M. Lefler, S. J. May and A. T. Fafarman, Role of fluoride and fluorocarbons in enhanced stability and performance of halide perovskites for photovoltaics, Phys. Rev. Mater., 2020, 4(12), 120301.
20. C. Ortiz-Cervantes, P. Carmona-Monroy and D. Solis-Ibarra, Two-dimensional halide perovskites in solar cells: 2D or not 2D?, ChemSusChem, 2019, 12(8), 1560–1575.
21. T. K. Ng, et al., Group-III-nitride and halide-perovskite semiconductor gain media for amplified spontaneous emission and lasing applications, J. Phys. D: Appl. Phys., 2021, 54(14), 143001.
22. X. Jiang and W.-J. Yin, High-throughput computational screening of oxide double perovskites for optoelectronic and photocatalysis applications, J. Energy Chem., 2021, 57, 351–358.
23. M. Sohail, et al., First-principal investigations of electronic, structural, elastic and optical properties of the fluoroperovskite TlLF 3 (L= Ca, Cd) compounds for optoelectronic applications, RSC Adv., 2022, 12(12), 7002–7008.
24. W.-J. Yin, et al., Oxide perovskites, double perovskites and derivatives for electrocatalysis, photocatalysis, and photovoltaics, Energy Environ. Sci., 2019, 12(2), 442–462.
25. Y.-W. Fang, et al., Lattice dynamics and ferroelectric properties of the nitride perovskite LaWN 3, Phys. Rev. B, 2017, 95(1), 014111.
26. Y. Li, J. S. Chung and S. G. Kang, First-principles computational screening of perovskite hydrides for hydrogen release, ACS Comb. Sci., 2019, 21(11), 736–742.
27. M. A. H. Shah, et al., Hydrostatic pressure on XLiH3 (X= Ba, Sr, Ca) perovskite hydrides: an insight into structural, thermo-elastic and ultrasonic properties through first-principles investigation, Solid State Commun., 2021, 328, 114222.
28. S. Sharma and S. K. Ghoshal, Hydrogen the future transportation fuel: from production to applications, Renewable Sustainable Energy Rev., 2015, 43, 1151–1158.
29. S. Dutta, A review on production, storage of hydrogen and its utilization as an energy resource, J. Ind. Eng. Chem., 2014, 20(4), 1148–1156.
30. B. L. Salvi and K. Subramanian, Sustainable development of road transportation sector using hydrogen energy system, Renewable Sustainable Energy Rev., 2015, 51, 1132–1155.
31. Z.-M. Wang, et al., The improvement of dehydriding the kinetics of NaMgH3 hydride via doping with carbon nanomaterials, Metals, 2016, 7(1), 9.
32. S. Benlamari, et al., Structural, electronic, elastic, and thermal properties of CaNiH3 perovskite obtained from first-principles calculations, Chin. Phys. B, 2018, 27(3), 037104.
33. K. Ikeda, T. Sato and S.-i. Orimo, Perovskite-type hydrides–synthesis, structures and properties, Int. J. Mater. Res., 2008, 99(5), 471–479.
34. R. Sato, et al., Formation process of perovskite-type hydride LiNiH3: in situ synchrotron radiation X-ray diffraction study, Appl. Phys. Lett., 2013, 102(9), 091901.
35. K. Ikeda, et al., Formation of perovskite-type hydrides and thermal desorption processes in Ca–T–H (T= 3d transition metals), Scr. Mater., 2006, 55(9), 827–830.
36. T. Sato, et al., Hydrides with the perovskite structure: general bonding and stability considerations and the new representative CaNiH3, J. Solid State Chem., 2005, 178(11), 3381–3388.
37. B. G. Yalcin, B. Salmankurt and S. Duman, Investigation of structural, mechanical, electronic, optical, and dynamical properties of cubic BaLiF3, BaLiH3, and SrLiH3, Mater. Res. Express, 2016, 3(3), 036301.
38. K. Komiya, et al., Synthesis and decomposition of perovskite-type hydrides, MMgH3 (M= Na, K, Rb), J. Alloys Compd., 2008, 453(1–2), 157–160.
39. H. H. Raza, G. Murtaza and R. M. A. Khalil, Optoelectronic and thermal properties of LiXH3 (X= Ba, Sr and Cs) for hydrogen storage materials: a first principle study, Solid State Commun., 2019, 299, 113659.
40. S. Hayat, et al., First-principles investigations of the structural, optoelectronic, magnetic and thermodynamic properties of hydride perovskites XCuH3 (X= Co, Ni, Zn) for hydrogen storage applications, Optik, 2021, 228, 166187.
41. R. Khalil, et al., DFT based first principles study of novel combinations of perovskite-type hydrides XGaH3 (X= Rb, Cs, Fr) for hydrogen storage applications, AIP Adv., 2021, 11(2), 025032.
42. F. Schüth, B. Bogdanović and M. Felderhoff, Light metal hydrides and complex hydrides for hydrogen storage, Chem. Commun., 2004,(20), 2249–2258.
43. S.-i. Orimo, et al., Complex hydrides for hydrogen storage, Chem. Rev., 2007, 107(10), 4111–4132.
44. S. J. Clark, et al., First principles methods using CASTEP, Z. Kristallogr. - Cryst. Mater., 2005, 220(5–6), 567–570.
45. F. Bloch, Quantum mechanics of electrons in crystal lattices, Z. Phys., 1928, 52, 555–600.
46. N. Marzari, D. Vanderbilt and M. C. Payne, Ensemble density-functional theory for ab initio molecular dynamics of metals and finite-temperature insulators, Phys. Rev. Lett., 1997, 79(7), 1337.
47. D. Vanderbilt, Soft self-consistent pseudopotentials in a generalized eigenvalue formalism, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41(11), 7892.
48. D. Alfe, Ab initio molecular dynamics, a simple algorithm for charge extrapolation, Comput. Phys. Commun., 1999, 118(1), 31–33.
49. G. Pilania, et al., Accelerating materials property predictions using machine learning, Sci. Rep., 2013, 3(1), 2810.
50. M. Usman, et al., First-principles calculations to investigate structural, electronics, optical, and mechanical properties of Bi-based novel fluoroperovskites TBiF3 (T= Hg, Xe) for optoelectronic applications, Mater. Sci. Semicond. Process., 2023, 160, 107399.
51. P. Dantzer, Properties of intermetallic compounds suitable for hydrogen storage applications, Mater. Sci. Eng. A, 2002, 329, 313–320.
52. S. Haid, et al., Thermoelectric, structural, optoelectronic and magnetic properties of double perovskite Sr2CrTaO6: first principle study, Mater. Sci. Eng. B, 2019, 245, 68–74.
53. J. U. Rehman, et al., First-principles calculations to investigate structural, electronics, optical and elastic properties of Sn-based inorganic halide-perovskites CsSnX3 (X= I, Br, Cl) for solar cell applications, Comput. Theor. Chem., 2022, 1209, 113624.
54. K. Xiong, J. Robertson and S. Clark, Defect states in the high-dielectric-constant gate oxide LaAlO3, Appl. Phys. Lett., 2006, 89(2), 022907.
55. R. Hill, The elastic behaviour of a crystalline aggregate, Proc. Phys. Soc., London, Sect. A, 1952, 65(5), 349.
56. S. Pugh, XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals, London, Edinburgh Dublin Philos. Mag. J. Sci., 1954, 45(367), 823–843.

---