Open Access Article
Open Access ArticleMultiscale mechanical characterization of biobased photopolymers towards sustainable vat polymerization 3D printing
Derek Lublinab,
Taige Haoc,
Raj Malyalab and
David Kisailus *c
*c
aMaterials and Manufacturing Technology Program, School of Engineering, University of California at Irvine, Irvine, CA 92697, USA
bGlidewell Dental, Irvine, CA 92612, USA
cDepartment of Materials Science and Engineering, University of California at Irvine, Irvine, CA 92697, USA. E-mail: david.k@uci.edu
First published on 2nd April 2024
Abstract
In vat polymerization (VP) 3D printing, there is an urgent need to expand characterization efforts for resins derived from natural resources to counter the increasing consumption of fossil fuels required to synthesize conventional monomers. Here, we apply multiscale mechanical characterization techniques to interrogate a 3D printed biobased copolymer along a controlled range of monomer ratios. We varied the concentration of two dissimilar monomers to derive structural information about the polymer networks. Current research primarily considers the macroscale, but recent understanding of the process-induced anisotropy in 3D printed layers suggests a multiscale approach is critical. By combining typical macroscopic techniques with micro- and nanoscale analogues, clear correlations in the processing–structure–property relationships appeared. We observed that measured moduli were always greater via surface-localized methods, but property differences between formulations were easier to identify. As researchers continue to develop novel sustainable biopolymers that match or exceed the performance of commercial resins, it is vital to understand the multiscale relationships between the VP process, the structure of the formed polymer networks, and the resultant properties.
Introduction
Additive manufacturing, or 3D printing, enables manufacturers to design complex geometries and quickly produce them with minimal material waste. Vat photopolymerization (VP) is a subset of 3D printing which uses UV light to selectively polymerize a bed of liquid thermosetting resin.1 VP has matured from a rapid prototyping tool into a valuable technology to manufacture end products in many industries2 (e.g., automotive,3 dental,4 and medical5). However, commercial resins are not environmentally friendly. A consequence of the expanding adoption of VP is the increased consumption of fossil fuels due to the inherent robustness of petroleum-based monomers.6 Improving the sustainability of VP requires extensive research to ensure there are viable green alternatives to the conventional materials. The mechanical properties of current biobased resins are generally “lower with respect to commercial standards”,7 and thus have not had their properties rigorously explored. Therefore, there is an urgent need to identify and fully characterize resins containing monomers with a high biobased content, defined as the ratio of renewable organic carbon to total organic carbon within a polymer.A primary focus of this work is to expand upon previous characterization of biopolymer resins. Formulations consisting of primarily biobased (i.e., >75% biobased content) monomers were selected as promising and established resins initially studied by Voet et al.7,8 Varying the ratio of monomers in these formulations provided good control over mechanical properties to study.
A second focus of this paper is the interconnection between process, structure, and properties critical to understanding 3D printed materials. Since its development in the 1980s by Kodama and Hull,9,10 VP has come to encompass multiple processes including stereolithography (SLA), digital light processing (DLP), and masked stereolithography (mSLA).1,11 Each VP process utilizes a different UV light source: laser for SLA, projector for DLP, and an LED matrix for mSLA. However, each process operates by exposing a layer of liquid resin to UV light which is then solidified, primarily via free radical polymerization. A new layer of liquid resin is subsequently exposed over the previous solidified layer until all layers are completed. The typical thickness of a printed layer is between 50 and 100 μm. While VP is a relatively isotropic process compared with other 3D printing techniques due to its generation of crosslinks within and between exposed layers, researchers have begun to uncover complexities that add anisotropy. For example, light may attenuate as it travels across a single layer, creating a gradient in conversion that could affect material properties and surface homogeneity.12 Conversely, deeply penetrating light may transmit through a single layer to provide extra exposure to underlying layers, creating another gradient between the initial and final layers.12 The interface between layers may also be weaker due to oxygen diffusing through a permeable membrane at the bottom of the printing vat and dissolving in the resin. Oxygen commonly inhibits free radical polymerization, leading to lower conversion and properties.13 Recently, Caplins et al. characterized spatial variation in irradiance within a commercial mSLA printer,14 which led to heterogeneity of the surface texture of printed parts.
Because of the anisotropy inherent in 3D printed objects, it is important to characterize properties at multiple length scales. Researchers often rely on macroscopic methods, such as a tensile test or dynamic mechanical analysis (DMA), to measure the physical and viscoelastic behavior of a 3D printed polymer. However, these techniques may not always be sufficient to understand the level of surface inhomogeneity within their printed part15,16 and how it may affect macroscopic properties.
In this manuscript we utilize DLP to print varied ratios of biobased photopolymers and characterize their physical, mechanical, and viscoelastic properties. We combine common macroscopic characterization techniques, tensile and DMA, with nano- and micro-scale techniques, nanoindentation and dynamic nanoindentation, to correlate multiscale properties. We perform tests at multiple strain rates to observe property trends as they relate to physical properties of the polymer networks, which we characterize regarding crosslink density (DMA), glass transition temperature (DMA), and degree of conversion (ATR-FTIR).
Materials and methods
Materials
Epoxidized soybean oil acrylate (ESOA, contains 4000 ppm monomethyl ether hydroquinone as inhibitor) and 2,5-bis(5-tert-butyl-benzoxazol-2-yl) thiophene (BBOT, 99%) were purchased from Sigma Aldrich. Phenylbis(2,4,6-trimethylbenzoyl) phosphine oxide (BAPO, OMNIRAD 819) was supplied by IGM Resins. Isobornyl methacrylate (IBOMA, GENOMER 1121M) was supplied by RAHN AG (Fig. 1). ESOA and IBOMA properties are detailed in Table 1.| Monomer | Molecular weight (g mol−1) | (Meth)acrylate groups | Tg (°C) |
|---|---|---|---|
| ESOA | 1200 | 3–4 | 13 °C |
| IBOMA | 222.32 | 1 | 110 °C |
Preparation of 3D printing resins
ESOA, IBOMA, BBOT, and BAPO were mixed using an overhead stirrer (RW 20, IKA, USA) at 400 rpm for 60 min. Four formulations were prepared by first mixing varied ratios of oligomer![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) reactive diluent (ESOA
reactive diluent (ESOA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IBOMA), then adding 1 wt% of photoinitiator (BAPO) and 0.05% of photoabsorber (BBOT). The four compositions are summarized in Table 2.
IBOMA), then adding 1 wt% of photoinitiator (BAPO) and 0.05% of photoabsorber (BBOT). The four compositions are summarized in Table 2.
| Formulation | ESOA (wt%) | IBOMA (wt%) | BAPO (wt%) | BBOT (wt%) |
|---|---|---|---|---|
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 60 |
39.58 | 59.38 | 1.00 | 0.05 |
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 50 |
49.48 | 49.48 | 1.00 | 0.05 |
60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 40 |
59.38 | 39.58 | 1.00 | 0.05 |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 30 |
69.27 | 29.69 | 1.00 | 0.05 |
Preparation of samples
Testing specimens were designed and converted into standard tessellation language (STL) models using SolidWorks 2020 (Dassault Systèmes SolidWorks Corp, USA). Models were imported into a slicing software, Asiga Composer (Version 1.3, Asiga, Alexandria, Australia), which positions the models and sends printing instructions to the printer. Specimens were printed with a DLP 3D printer (Asiga Pico 2, Asiga, Alexandria, Australia) equipped with a UV LED projector utilizing a 405 nm wavelength. Each model layer was printed at a thickness of 100 μm at room temperature and exposed for seven seconds at an irradiance of 6.13 mW cm−2. We found these printing parameters to produce accurate dimensions across all formulations by measuring calibration prints with a caliper. Tensile and DMA bars were printed flat with their largest faces against the build plate of the printer.After printing, samples were submerged in an agitating bath (Form Wash, Formlabs, Somerville, MA, USA) filled with isopropanol (99%) for three minutes, followed by two minutes in a second identical bath as a “clean” wash. Parts were immediately dried with compressed air and placed into a post-cure box (Form Cure, Formlabs) containing UV LEDs (405 nm wavelength, 39 W) for 60 minutes with no heating.
For nanoindentation samples, resins were cast into stainless steel washers (1 mm thickness, 10 mm diameter) and covered on both sides by microscope slides to ensure sufficient flatness. These samples were placed over the DLP projector and exposed for 10 seconds at the printing irradiance. Partially polymerized discs were removed from the washers and placed into the Form Cure for 60 minutes with no heating.
Quasi-static nanoindentation and imaging
Quasi-static nanoindentation was performed with a Hysitron TI 950 TriboIndenter (Bruker, USA) to determine the micro- and nanoscale stiffness of each polymer. Testing followed the Oliver–Pharr method17 using a pyramidal Berkovich diamond tip. All samples were tested under a force-controlled trapezoidal load function. Indentation parameters will be discussed in the Results and discussions section. A range of loading and unloading times were tested and compared.Tensile testing
Tensile tests were performed according to ASTM D638-14 using a universal testing machine (AGS-X 10 kN, Shimadzu, Kyoto, Japan) with an axial extensometer (Model 3442, Epsilon Technology Corp, Jackson, WY, USA). The geometry of the samples was ASTM D638 Type V. Each formulation was tested at three crosshead speeds: 1, 10, and 100 mm min−1 with five samples per speed to determine sensitivity to high strain rates.Dynamic nanoindentation
The Hysitron TI 950 TriboIndenter is capable of performing dynamic nanoindentation, utilizing a high bandwidth transducer and software to characterize viscoelastic properties.18 The nanoDMA II technique involves loading the indenter probe into the surface of a sample up to a certain load (quasi-static load), and then the transducer oscillates the probe at specified frequencies and forces (dynamic load). This technique was performed to measure the storage and loss moduli of the polymers over a range of frequencies. Testing parameters included a four second loading time up to the same quasi-static loads utilized in the quasi-static nanoindentation tests. Dynamic loads were selected for each sample to create an oscillation amplitude between 1–2 nm.Dynamic mechanical analysis
Bulk viscoelastic properties were characterized with DMA (Q800, TA Instruments, New Castle, DE, USA). Rectangular samples (5 mm × 15 mm × 1 mm) were used in tension clamps. Temperature sweeps were performed from 30–200 °C at a 5 °C min−1 ramp rate, a 1 Hz frequency, a 0.1% strain amplitude.Fourier transform infrared spectroscopy
Changes in chemical structures during polymerization were characterized with a Fourier transform infrared spectrometer (FTIR) (Alpha, Bruker, Billerica, MA, USA) in attenuated total reflectance (ATR) mode. Samples were measured over a wavenumber range of 4000–400 cm−1 at 4 cm−1 resolution through a diamond crystal window. Resins were placed into 1 mm thick stainless steel washers over the window and exposed to 405 nm light via a single UV LED (Cure Beam, Phrozen Technology, Hsinchu, Taiwan) for 30 seconds each. Throughout the exposure, spectral scans were repeated every 2–5 seconds to capture changes.Results and discussions
Quasi-static nanoindentation
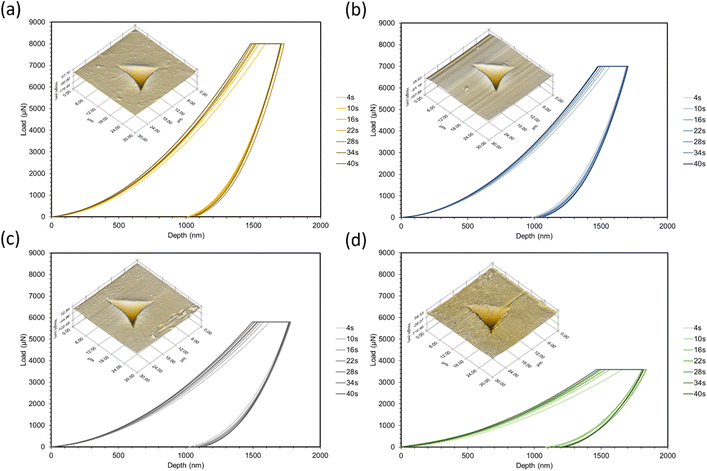
Nanoindentation curves are provided in Fig. 2. Each graph displays multiple loading/unloading times, ranging from 4–40 seconds. Maximum loads varied at the selected indentation depth of 1.5 μm. SPM micrographs have been superimposed onto the indentation graphs, showing the surface of each material and a representative indent for the 4 seconds curves. Reduced moduli were extrapolated by eqn (1) using the contact area of the indenter probe (A(hc)) and stiffness (S) from the initial unloading regions of the load-depth curves in Fig. 2. Five indents were tested per point of data. The reduced modulus differs from Young's modulus by accounting for the simultaneous deformation of the sample and indenter tip.17 Due to the large differences in stiffness between the polymers and diamond, we assumed that the reduced modulus is approximately equal to Young's modulus.
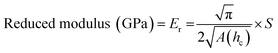 | (1) |
To choose the maximum load for each formulation, strain-controlled tests were performed to determine the load at a 1.5 μm depth. This large indentation depth was selected in order to minimize inaccuracies caused by surface effects.19,20 Due to the viscoelastic nature of the polymers, creep and adhesion between the surface and probe were also considered. Creep can cause significant deviations in modulus measurements and is often a result of a short holding time at the maximum load before unloading.21,22 To overcome this phenomenon, tests were performed at increasing holding times until a sufficient time for all formulations (30 seconds) was found. Past this point, modulus values were consistent and the bulging “nose”21 at the onset of unloading disappeared. Adhesion can also be problematic for soft polymers as it may increase contact area and stiffness,23–25 as well as make it difficult to find the initial contact point of the indenter.26 To check for adhesion between the probe and surface, the indenter was lifted 100 nm above the surface after unloading; there were no forces found above the surface plane. After testing, indents were imaged with the TriboIndenter's in situ scanning probe microscopy (SPM) mode to produce 3D topographical maps.
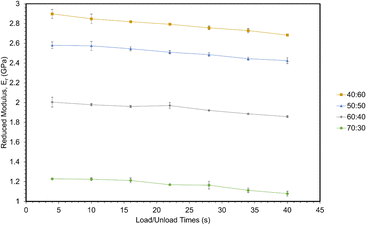
In all cases, increasing the concentration of ESOA decreased reduced modulus, shown in Fig. 3. The decrease is not linear, dropping by a greater amount for each subsequent formulation from 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 to 70
60 to 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30. ESOA is a flexible monomer with a low homopolymer glass transition temperature (Tg) despite its ability to crosslink. IBOMA, on the other hand, has a bulky structure due to its bicyclic camphene group, evidenced by a high homopolymer Tg. At increasing concentrations of IBOMA, there is an increase in reduced moduli suggesting the more significant influence of steric hindrance than the crosslink density for these polymer networks. The SPM micrographs attached to each set of curves in Fig. 2 may also indicate this behavior qualitatively, as Fig. 2c and d show more prominent striations induced from the indenter probe during scans across each surface, with Fig. 2d exhibiting the most notable features. In addition, all polymers showed linear decreases in modulus with respect to increasing loading and unloading times. This is due to the polymers' viscoelastic behavior wherein molecular mobility is limited at higher strain rates, resulting in increased resistance to deformation. There does not appear to be a significant difference in rate-induced stiffening among the polymers. It could be that the range of strain rates was not large enough to distinguish between the polymers. Another possibility is that the relatively small volume of material affected during nanoindentation was insufficient to capture any difference.
30. ESOA is a flexible monomer with a low homopolymer glass transition temperature (Tg) despite its ability to crosslink. IBOMA, on the other hand, has a bulky structure due to its bicyclic camphene group, evidenced by a high homopolymer Tg. At increasing concentrations of IBOMA, there is an increase in reduced moduli suggesting the more significant influence of steric hindrance than the crosslink density for these polymer networks. The SPM micrographs attached to each set of curves in Fig. 2 may also indicate this behavior qualitatively, as Fig. 2c and d show more prominent striations induced from the indenter probe during scans across each surface, with Fig. 2d exhibiting the most notable features. In addition, all polymers showed linear decreases in modulus with respect to increasing loading and unloading times. This is due to the polymers' viscoelastic behavior wherein molecular mobility is limited at higher strain rates, resulting in increased resistance to deformation. There does not appear to be a significant difference in rate-induced stiffening among the polymers. It could be that the range of strain rates was not large enough to distinguish between the polymers. Another possibility is that the relatively small volume of material affected during nanoindentation was insufficient to capture any difference.
Tensile testing
Tensile stress–strain plots in Fig. 4 show average curves at three crosshead speeds (1, 10, 100 mm min−1) for each resin. From these curves, tensile strength, Young's modulus, elongation at break, and toughness were computed and are represented in Fig. 5. Strength and modulus values primarily decreased with increasing ESOA concentration. Modulus data, however, had large standard deviations due to extensometer slippage and alignment issues. This is visible at the onset of each curve in Fig. 4. A noncontact extensometer could produce better consistency by eliminating the possibility of poor contact or alignment.27 Tensile strength and modulus typically correlate with each other, so strength, which is dependent on the sensitivity of the load cell and not the extensometer, will be discussed in more detail. Strengths correlate similarly to the reduced moduli from Fig. 3. Increasing the ESOA concentration decreased the tensile strength by a greater amount in each step as it largely depended on the steric hindrance by IBOMA. Another similarity between the tensile strengths and reduced moduli is the linear increase as strain rate increases due to the limitation of mobility in the polymer networks. The range of rates in this test was 10× higher than that of the nanoindentation despite the similar trend. In all cases, reduced moduli produced from nanoindentation were greater than Young's moduli. Comparing values directly, nanoindentation is known to overestimate modulus due to size scale effects at the surface that do not occur at the bulk for macroscopic techniques.28 A major example is when surface material is displaced and piles up beneath the probe during indentation, “which increases the contact area with respect to the one calibrated on the standard material due to the viscoelastic behavior of polymer materials”.28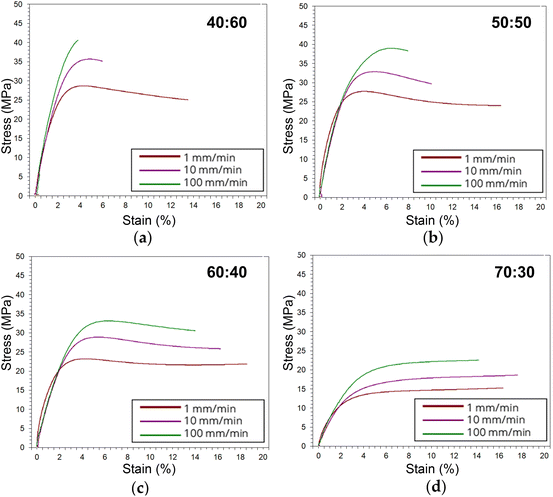 | ||
Fig. 4 Average stress–strain curves for multiple strain rate tensile tests corresponding to (a) 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60, (b) 50 60, (b) 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50, (c) 60 50, (c) 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40, (d) 70 40, (d) 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30. 30. | ||
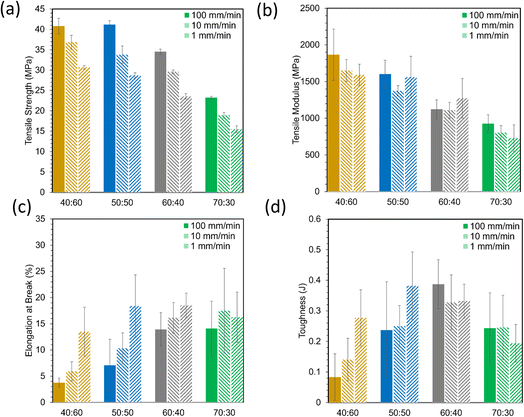 | ||
| Fig. 5 Material properties derived from tensile stress strain curves, (a) tensile strength, (b) tensile modulus, (c) elongation at break, (d) toughness. | ||
Elongation at break data in Fig. 5c were more variable than strength and modulus data, but they appear to show opposite behavior, primarily increasing with ESOA concentration. This is expected as a loss in ductility often follows a gain in strength and rigidity. Elongation values for ductile materials such as polymers are often difficult to predict due to unstable necking following ultimate strength.29 During this instability, the polymer is susceptible to early fracture in the presence of defects or unintended multiaxial stresses. Elongation values also seemed to decrease with strain rate. Interestingly, the polymers with the greater fractions of ESOA (i.e., 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40, 70
40, 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30) experienced less variation in elongation with increased strain rate than those with greater amounts of IBOMA. A loss in ductility at high strain rates could indicate brittleness as the polymer networks may be too immobile to deform and adequately distribute stress. Tensile toughness values in Fig. 5d, corresponding to the amount of energy absorbed before fracture, were calculated by the area under the stress–strain curves. They were the most inconsistent data as they compounded the deviations in stress and elongation. Nonetheless, they suggest that the polymers with intermediate compositions, 50
30) experienced less variation in elongation with increased strain rate than those with greater amounts of IBOMA. A loss in ductility at high strain rates could indicate brittleness as the polymer networks may be too immobile to deform and adequately distribute stress. Tensile toughness values in Fig. 5d, corresponding to the amount of energy absorbed before fracture, were calculated by the area under the stress–strain curves. They were the most inconsistent data as they compounded the deviations in stress and elongation. Nonetheless, they suggest that the polymers with intermediate compositions, 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 and 60
50 and 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40, had an optimal combination of strength and ductility, with 60
40, had an optimal combination of strength and ductility, with 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 demonstrating the toughest.
40 demonstrating the toughest.
Dynamic nanoindentation
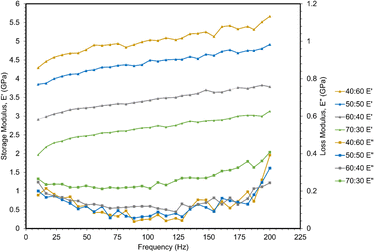
A frequency sweep from 10–200 Hz was applied to measure storage and loss moduli via dynamic nanoindentation (Fig. 6). Storage modulus is related to Young's modulus, providing structural information about a material by measuring its elastic response to deformation. However, polymers are not purely elastic materials, but rather viscoelastic, exhibiting both elastic and viscous behavior. This accounts for their dependency on strain rate displayed in the quasi-static nanoindentation and tensile testing in previous sections.30 However, those tests do not capture viscous behavior, which is measured as the loss modulus. All storage moduli were larger than loss moduli for these polymers, and thus, are primarily elastic in nature.Storage moduli decreased with increasing ESOA concentration, which correlates with the quasi-static nanoindentation and tensile results. Storage moduli also increased linearly with frequency. This result is analogous to the increase in strength and modulus at higher strain rates observed in the previous mechanical tests as higher frequency of indents inhibits the polymer chains from responding to applied load.31
A less significant correlation was observed between loss moduli and ESOA concentrations below 70 wt%. 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 had the largest values, indicating potential dissipation of energy during indentation.32 The remaining formulations' loss moduli demonstrated no significant trend. The loss moduli of each polymer formulation demonstrated a nonlinear relationship with increasing frequency, decreasing slightly from ∼10 to 125 Hz, and then increasing until 200 Hz.
30 had the largest values, indicating potential dissipation of energy during indentation.32 The remaining formulations' loss moduli demonstrated no significant trend. The loss moduli of each polymer formulation demonstrated a nonlinear relationship with increasing frequency, decreasing slightly from ∼10 to 125 Hz, and then increasing until 200 Hz.
Dynamic mechanical analysis
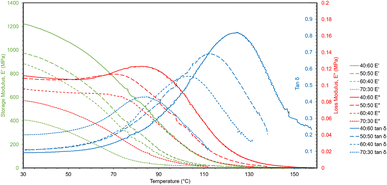
A temperature sweep was performed with DMA to measure the change in storage and loss moduli as the polymers were heated (Fig. 7). The temperature sweep data were plotted to show storage modulus, loss modulus, and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, which is the ratio of loss to storage modulus and indicates the relative degree of energy dissipation or damping by the polymer. At the initial temperature (30 °C), storage moduli for the polymers were much closer to the Young's moduli found by tensile testing than the reduced moduli from nanoindentation as DMA is also a bulk characterization technique. The storage moduli likewise decreased with increasing ESOA concentrations. Tan
δ, which is the ratio of loss to storage modulus and indicates the relative degree of energy dissipation or damping by the polymer. At the initial temperature (30 °C), storage moduli for the polymers were much closer to the Young's moduli found by tensile testing than the reduced moduli from nanoindentation as DMA is also a bulk characterization technique. The storage moduli likewise decreased with increasing ESOA concentrations. Tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ curves also provide structural information about the polymers. As can be seen in Fig. 7, as ESOA increased, the magnitude of tan
δ curves also provide structural information about the polymers. As can be seen in Fig. 7, as ESOA increased, the magnitude of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ decreased and the maximum shifted to a lower temperature. Greater tan
δ decreased and the maximum shifted to a lower temperature. Greater tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ values correspond to larger energy damping capacities, and the temperature of the peak is commonly used to represent the glass transition temperature, or the point at which a glassy polymer becomes exponentially more ductile. A higher Tg is often correlated with more rigid materials,33,34 which is the case for our polymer formulations.
δ values correspond to larger energy damping capacities, and the temperature of the peak is commonly used to represent the glass transition temperature, or the point at which a glassy polymer becomes exponentially more ductile. A higher Tg is often correlated with more rigid materials,33,34 which is the case for our polymer formulations.
A useful application of DMA is deriving the crosslink density using Hill's criterion,35,36 or the concentration of crosslinks per unit volume of polymer, using eqn (2). The technique assumes that at high temperatures (above Tg), but below the decomposition temperature of the polymer, its storage modulus reaches a “rubbery plateau”. In this region, a non-crosslinked polymer (thermoplastic) would melt as the van der Waals interactions between chains are disrupted by heat. At those same temperatures, crosslinked polymers, which have strong covalent bonds (crosslinks) between chains, will not melt. The modulus in this region can thus be attributed directly to the crosslinks.37,38 In eqn (3), this relationship is adjusted to calculate the average molecular weight between crosslinks, a useful parameter for characterizing the structure of a polymer network. The calculations from eqn (2) and (3) are included in Table 3.
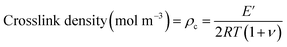 | (2) |
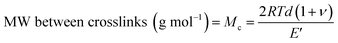 | (3) |
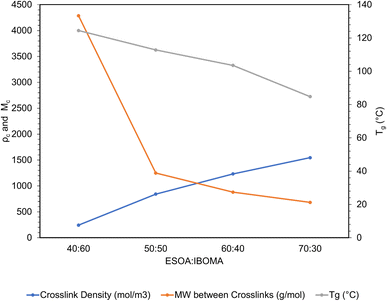
Formulation (ESOA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IBOMA) IBOMA) |
E′ rubbery (MPa) | Solid density (g cm−3) | Tg (°C) | Crosslink density (mol m−3) | MW between crosslinks (g mol−1) |
|---|---|---|---|---|---|
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 60 |
5.84 | 1.04 | 124.4 | 242.8 | 4283.8 |
50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 50 |
7.65 | 1.05 | 112.8 | 841.8 | 1248.3 |
60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 40 |
10.01 | 1.08 | 103.5 | 1231.5 | 879.2 |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 30 |
12.62 | 1.06 | 84.8 | 1545.4 | 682.7 |
These polymers exhibited atypical behavior with respect to crosslink density and Tg. Higher Tg and stiffness are usually associated with thermosets that have high crosslink density,39 as crosslinks limit the mobility of a polymer network. However, in this case, Tg was inversely proportional to crosslink density, as shown in Fig. 8. We have observed that higher concentrations of ESOA lead to lower modulus, yet each molecule contains 3–4 acrylate groups that serve as crosslinking sites. IBOMA, conversely, has only one acrylate group and cannot crosslink, which requires the ability to create branches by connecting several molecules to itself. Thus, increasing IBOMA concentration reduces the number of crosslinks in a network. The inherent bulkiness of IBOMA creates a polymer where steric hindrance dominates crosslink density in limiting molecular mobility.
Fourier transform infrared spectroscopy
FTIR spectra before and after photopolymerization are shown in Fig. 9a with corrected baselines, and the extent of this reaction, as well as the time to reach its saturation point are shown in Fig. 9b. After polymerization, peak wavenumbers were observed to shift slightly. This shift could represent the decrease in mobility of measured bonds as the polymer network forms, hindering their ability to bend or stretch. Degree of conversion (DC) is a common parameter to characterize the extent to which monomers convert to polymers during polymerization.40 A typical method to assess DC for (meth)acrylate-based photopolymers is to quantify the decrease in intensity of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds, which can be primarily attributed to crosslinking between (meth)acrylate groups.41,42 FTIR provides a method to measure this directly by acquiring spectra throughout a reaction and comparing the intensity values to those at the initiation of polymerization. As the free radical polymerization in our formulations proceeded, the C
C bonds, which can be primarily attributed to crosslinking between (meth)acrylate groups.41,42 FTIR provides a method to measure this directly by acquiring spectra throughout a reaction and comparing the intensity values to those at the initiation of polymerization. As the free radical polymerization in our formulations proceeded, the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds converted into C–C bonds, thus lowering the C
C bonds converted into C–C bonds, thus lowering the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C peak. The degree of change can be calculated and normalized to the absorbance or transmittance magnitude of a bond that is known to not react during the reaction. It should be noted, however, that during polymerization, a portion of converted C
C peak. The degree of change can be calculated and normalized to the absorbance or transmittance magnitude of a bond that is known to not react during the reaction. It should be noted, however, that during polymerization, a portion of converted C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds may include monomers that do not crosslink into the primary polymer network. Instead, short chain cyclic structures may form that have been terminated early and do not contribute to the overall crosslink density of the polymer. DC cannot differentiate between these cases. This calculation is performed via eqn (4), and using the wavenumber ∼1630 cm−1, which corresponds to the C
C bonds may include monomers that do not crosslink into the primary polymer network. Instead, short chain cyclic structures may form that have been terminated early and do not contribute to the overall crosslink density of the polymer. DC cannot differentiate between these cases. This calculation is performed via eqn (4), and using the wavenumber ∼1630 cm−1, which corresponds to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond, and ∼1710 cm−1 corresponding to a C
C double bond, and ∼1710 cm−1 corresponding to a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O ref. 41 The results from these calculations are shown in Fig. 9b.
O ref. 41 The results from these calculations are shown in Fig. 9b.
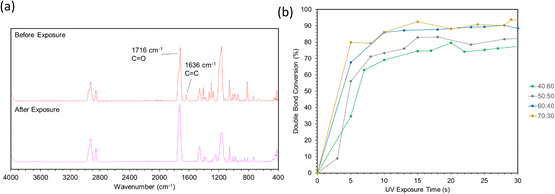 | ||
| Fig. 9 (a) Spectra before and after curing via ATR-FTIR. (b) Double bond conversion calculations over 30 seconds of light exposure. | ||
Double bond conversion occurred rapidly for all samples, reaching near their maximum after approximately 15 seconds. The final conversion values increased with ESOA concentrations of 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60, 50
60, 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50, and 60
50, and 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40; however, 60
40; however, 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 and 70
40 and 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 were not possible to distinguish. This increase in conversion can be attributed to the increased number of crosslink sites available in formulations with larger amounts of ESOA, which has 3–4 acrylate groups per molecule whereas IBOMA cannot crosslink. A higher concentration of crosslink sites often corresponds with faster reaction kinetics, allowing a greater number of molecules to polymerize.43 This trend follows the crosslink density calculations in Fig. 8, and it is logical for a greater number of crosslink sites to result in a more complete reaction and lower molecular weight between crosslinks.
30 were not possible to distinguish. This increase in conversion can be attributed to the increased number of crosslink sites available in formulations with larger amounts of ESOA, which has 3–4 acrylate groups per molecule whereas IBOMA cannot crosslink. A higher concentration of crosslink sites often corresponds with faster reaction kinetics, allowing a greater number of molecules to polymerize.43 This trend follows the crosslink density calculations in Fig. 8, and it is logical for a greater number of crosslink sites to result in a more complete reaction and lower molecular weight between crosslinks.
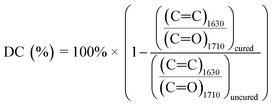 | (4) |
Conclusion
Here, several multiscale mechanical characterization techniques were applied to interrogate an established biobased copolymer along a controlled range of monomer ratios. There is an urgent need to expand characterization efforts for green resins derived from natural resources to counter the increasing consumption of fossil fuels to synthesize conventional monomers. Current research primarily considers the macroscale, but recent understanding of the process-induced anisotropy in 3D printed layers suggests a multiscale approach is critical. By combining typical macroscopic techniques such as tensile testing and DMA with micro- and nanoscale analogues, clear correlations in the processing–structure–property relationships appeared. While measured moduli were always greater via surface-localized methods, property differences between formulations were easier to identify. Structural information was also derived by measuring crosslink density by DMA, polymerization kinetics and degree of conversion by FTIR. As researchers continue to develop novel sustainable biopolymers that match or exceed the performance of commercial resins, it will be vital to understand the multiscale relationships between the VP process, the structure of the polymer networks, and the resultant properties.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors wish to acknowledge funding from the Air Force Office of Scientific Research, Natural Materials and Systems Program, grant numbers FA9550-15-1-0009 and FA9550-23-1-0209, and the Mechanics of Multifunctional Materials and Microsystems Program, grant number FA9550-20-1-0292 and the Army Research Office, Biochemistry Program, grant number W911NF-20-1-0201.References
- P. F. Jacobs, Rapid Prototyping & Manufacturing: Fundamentals of Stereolithography, Society of Manufacturing Engineers, 1992 Search PubMed.
- N. Guo and M. C. Leu, Front. Mech. Eng., 2013, 8, 215–243 CrossRef.
- F. Zareanshahraki, A. Davenport, N. Cramer, C. Seubert, E. Lee, M. Cassoli and X. Wang, 3D Print. Addit. Manuf., 2021, 8, 302–314 CrossRef PubMed.
- O. N. Tosun, C. Bilmenoglu and A. K. Özdemir, J. Prosthodontics, 2022, 32, 64–70 Search PubMed.
- L. A. Van Der Elst, M. Gokce Kurtoglu, T. Leffel, M. Zheng and A. Gumennik, Adv. Eng. Mater., 2020, 22, 2000759 CrossRef CAS PubMed.
- E. M. Maines, M. K. Porwal, C. J. Ellison and T. M. Reineke, Green Chem., 2021, 23, 6863–6897 RSC.
- J. Guit, M. B. L. Tavares, J. Hul, C. Ye, K. Loos, J. Jager, R. Folkersma and V. S. D. Voet, ACS Appl. Polym. Mater., 2020, 2, 949–957 CrossRef CAS.
- V. S. D. Voet, T. Strating, G. H. M. Schnelting, P. Dijkstra, M. Tietema, J. Xu, A. J. J. Woortman, K. Loos, J. Jager and R. Folkersma, ACS Omega, 2018, 3, 1403–1408 CrossRef CAS PubMed.
- H. Kodama, Rev. Sci. Instrum., 1981, 52, 1770–1773 CrossRef.
- C. Hull, US Pat., 4575330, 1984 Search PubMed.
- F. Zhang, L. Zhu, Z. Li, S. Wang, J. Shi, W. Tang, N. Li and J. Yang, Addit. Manuf., 2021, 48, 102423 CAS.
- A. C. Uzcategui, C. I. Higgins, J. E. Hergert, A. E. Tomaschke, V. Crespo-Cuevas, V. L. Ferguson, S. J. Bryant, R. R. McLeod and J. P. Killgore, Small Sci., 2021, 1, 2000017 CrossRef CAS PubMed.
- H. Gojzewski, Z. Guo, W. Grzelachowska, M. G. Ridwan, M. A. Hempenius, D. W. Grijpma and G. J. Vancso, ACS Appl. Mater. Interfaces, 2020, 12, 8908–8914 CrossRef CAS PubMed.
- B. W. Caplins, C. I. Higgins, T. J. Kolibaba, U. Arp, C. C. Miller, D. L. Poster, C. J. Zarobila, Y. Zong and J. P. Killgore, Addit. Manuf., 2023, 62, 103381 CAS.
- L. Zorzetto, L. Andena, F. Briatico-Vangosa, L. De Noni, J.-M. Thomassin, C. Jérôme, Q. Grossman, A. Mertens, R. Weinkamer, M. Rink and D. Ruffoni, Sci. Rep., 2020, 10, 22285 CrossRef CAS PubMed.
- M. Robakowska, I. Gibson, R. Akkerman, F. R. Wurm and H. Gojzewski, Polym. Test., 2023, 129, 108243 CrossRef CAS.
- W. C. Oliver and G. M. Pharr, J. Mater. Res., 1992, 7, 1564–1583 CrossRef CAS.
- nanoDMA III - Dynamic Nanoindentation, https://www.bruker.com/en/products-and-solutions/test-and-measurement/nanomechanical-test-systems/nanomechanical-test-system-upgrade-options/nanodma-iii.html, accessed 22 December 2023.
- T.-Y. Zhang and W.-H. Xu, J. Mater. Res., 2002, 17, 1715–1720 CrossRef CAS.
- F. Alisafaei and C.-S. Han, Adv. Condens. Matter Phys., 2015, 2015, e391579 Search PubMed.
- B. J. Briscoe, L. Fiori and E. Pelillo, J. Phys. D: Appl. Phys., 1998, 31, 2395–2405 CrossRef CAS.
- A. Flores, Pure Appl. Chem., 2023 DOI:10.1515/pac-2023-1004.
- K. L. Johnson, Contact Mechanics, Cambridge University Press, 1st edn, 1985 Search PubMed.
- C. Klapperich, K. Komvopoulos and L. Pruitt, J. Tribol., 2001, 123, 624–631 CrossRef CAS.
- C. Jin and D. M. Ebenstein, J. Mater. Res., 2017, 32, 435–450 CrossRef CAS.
- J. C. Kohn and D. M. Ebenstein, J. Mech. Behav. Biomed. Mater., 2013, 20, 316–326 CrossRef CAS PubMed.
- B. Becker and M. Dripke, Adv. Mater. Proc., 2011, 169, 17–21 Search PubMed.
- A. Mokhtari, N. Tala-Ighil and Y. A. Masmoudi, J. Mater. Eng. Perform., 2022, 31, 2715–2722 CrossRef CAS.
- Standard Test Method for Tensile Properties of Plastics, https://www.astm.org/d0638-14.html, accessed 8 December 2024.
- C. Y. Zhang, Y. W. Zhang, K. Y. Zeng and L. Shen, Philos. Mag., 2006, 86, 4487–4506 CrossRef CAS.
- A. Chafidz, I. Ali, M. E. A. Mohsin, R. Elleithy and S. Al-Zahrani, J. Polym. Res., 2012, 19, 9906 CrossRef.
- E. G. Herbert, W. C. Oliver and G. M. Pharr, J. Phys. D: Appl. Phys., 2008, 41, 074021 CrossRef.
- S. Pankaj, E. Hempel and M. Beiner, Macromolecules, 2009, 42, 716–724 CrossRef CAS.
- R. Xie, A. R. Weisen, Y. Lee, M. A. Aplan, A. M. Fenton, A. E. Masucci, F. Kempe, M. Sommer, C. W. Pester, R. H. Colby and E. D. Gomez, Nat. Commun., 2020, 11, 893 CrossRef CAS PubMed.
- L. W. Hill, Prog. Org. Coat., 1997, 31, 235–243 CrossRef CAS.
- F. S. Sorce, S. Ngo, C. Lowe and A. C. Taylor, Prog. Org. Coat., 2019, 137, 105338 CrossRef CAS.
- P. J. Flory, Principles of Polymer Chemistry, Cornell Univ. Press, Ithaca, NY, 2006 Search PubMed.
- L. Li, X. Chen and J. M. Torkelson, ACS Appl. Polym. Mater., 2020, 2, 4658–4665 CrossRef CAS.
- R. F. Landel and L. E. Nielsen, Mechanical Properties of Polymers and Composites, CRC Press, 1993 Search PubMed.
- L. G. P. Moraes, R. S. F. Rocha, L. M. Menegazzo, E. B. de AraÚjo, K. Yukimitu and J. C. S. Moraes, J. Appl. Oral Sci., 2008, 16, 145–149 CrossRef CAS PubMed.
- A. Badev, Y. Abouliatim, T. Chartier, L. Lecamp, P. Lebaudy, C. Chaput and C. Delage, J. Photochem. Photobiol., A, 2011, 222, 117–122 CrossRef CAS.
- R. Anastasio, W. Peerbooms, R. Cardinaels and L. C. A. Van Breemen, Macromolecules, 2019, 52, 9220–9231 CrossRef CAS PubMed.
- G. A. Altun-Ciftçioğlu, A. Ersoy-Meriçboyu and C. L. Henderson, Polym. Eng. Sci., 2014, 54, 1737–1746 CrossRef.
| This journal is © The Royal Society of Chemistry 2024 |