Open Access Article
Open Access ArticleMicrowave engineered NiZrO3@GNP as efficient electrode material for energy storage applications
J. John Benittoa,
J. Judith Vijaya *a,
B. Saravanakumar
*a,
B. Saravanakumar b,
Hamad Al-Lohedanc and
Stefano Belluccid
b,
Hamad Al-Lohedanc and
Stefano Belluccid
aCatalysis and Nanomaterials Research Laboratory, Department of Chemistry, Loyola College, Chennai-600034, Tamil Nadu, India
bDepartment of Physics, Dr. Mahalingam College of Engineering and Technology, Pollachi, Tamil Nadu-642 003, India
cDepartment of Chemistry, College of Science, King Saud University, P. O. Box 2455, Riyadh, 11451, Saudi Arabia
dINFN-Laboratori Nazionali di Frascati, Frascati, Italy
First published on 11th March 2024
Abstract
Supercapacitors (SCs) have emerged as attractive energy storage devices due to their rapid charge/discharge rates, long cycle life, and high-power density. However, the development of innovative electrode materials to achieve high-performance remains crucial to meet future requirements in supercapacitor technology. In this work, we have explored the potential of a microwave-engineered NiZrO3@GNP composite as a promising electrode material for SCs. A microwave assisted hydrothermal approach was adopted for the fabrication of the NiZrO3@GNP nanocomposite. Structural and morphological investigations showed its structural richness and its chemical compositions. When applied as a SC electrode, this innovative combination exhibits battery-like behaviour with higher specific capacity (577.63 C g−1) with good cyclic stability, and good performance. We have assembled an asymmetric-type two-electrode SC device and analysed its electrochemical features. This NiZrO3@GNP device exhibits the specific capacity of 47 C g−1 with capacitance retention of 70% after 2000 charge–discharge cycles. Further research on optimizing the synthesis process and exploring different device configurations could pave the way for even higher-performance supercapacitors in the future.
1. Introduction
Supercapacitors (SCs) have emerged as a promising energy storage technology with the potential to revolutionize the energy industry. Unlike traditional batteries, which store energy through chemical reactions, SCs store energy through the separation of charges at the interface between two electrodes, resulting in a much faster charge–discharge process.1 This unique characteristic makes them highly suitable for applications that require high power density, fast charge, and discharge rates, and a long cycle life, such as electric vehicles, grid-level energy storage, and portable electronics.2 In recent years, there has been a growing interest in developing supercapacitor technology for various applications, including renewable energy integration, regenerative braking systems, and portable electronic devices.3 The advantages of SCs over traditional batteries, such as high-power density, rapid charging and discharging, and long cycle life, make them a highly attractive option for energy storage. Additionally, SCs have the potential to overcome some of the major challenges associated with battery technology, such as safety concerns, limited cycle life, and environmental impact.2 As a result, research in the field of supercapacitors has gained significant momentum, with many studies focusing on developing novel materials and designs that can further enhance their performance and efficiency.Presently, with researchers focusing on the utilization of renewable energy sources and energy conservation for a sustainable and eco-conscious environment, SCs are garnering significant attention owing to their substantial advantages. A huge range of energy storage devices have been developed, from batteries to multi-modal energy storage systems (Pumped Hydro Storage, Compressed Air Energy Storage, Thermal Energy Storage, Hydrogen Storage, Supercritical CO2 Energy Storage, Molten Salt Energy Storage, Hydraulic Accumulators, and Capacitive Deionization). However, these come with several drawbacks like cost ineffectiveness, low energy density, reduced power density, less efficiency, poor shelf life, etc. SCs are energy storage devices that store energy as charges.4 They are more advantageous due to high power and energy density, longevity with respect to shelf life, and cyclic stability. SCs are being used in various industrial equipment, electronic gadgets, electric vehicles and several other major applications. Since the proposal of the Helmholtz concept of capacitive performance of the electrical double layer formed at the electrode–electrolyte interface, followed by Becker's first application of it to electrolytic capacitors, supercapacitors, also called electrical double layer capacitors or ultracapacitors, have undergone various advances to increase the efficiency by increasing their energy storage capacity.5
Supercapacitors are of different types: electrochemical double-layer capacitor (EDLC), pseudocapacitor, and hybrid capacitor. Electrochemical double-layer capacitors involve the accumulation of charges at the electrode surface.6 They exhibit rapid charge–discharge cycles along with high power density but suffer from aging, especially when subjected to high voltage and temperatures over a period of time.7,8 Hybrid capacitors combine the characteristics of SCs and batteries with one electrode being a faradaic electrode and the other a capacitive electrode.9 However, the high energy and power performances are decoupled and do not compete with the conventional lithium-ion batteries.10
SCs store energy by faradaic electron transfer of metal ions and EDLC capacitance through surface reactions at the electrode.11 SCs have exceptional power density and cycle stability and are anticipated to a good competitors against batteries. However, lesser energy density and capacity fading hamper its commercial application.12 The effectiveness of SCs relies on the innovative features of the electrode and electrolyte materials, as well as the mechanism for storing electric charge.4 A 2 M KOH solution served as the electrolyte, where the highly mobile OH− ions facilitated efficient charge transport within the supercapacitor, enhancing its power density.13 The superior ionic conductivity of 2 M KOH, coupled with the exceptional charge storage and robust composite structure of NiZrO3/NiZrO3@GNP electrodes, paves the way for efficient energy storage and rapid delivery. This synergy is further bolstered by NiZrO3's inherent stability, ensuring long-lasting performance.
Recent research has focused on the use of carbon materials,14 molecular organic frameworks,15 different structured metal oxides (spinel, perovskite, corundum, ilmenite, wurtzite, rutile, etc.),16 chalcogenides,17 conducting polymers18 and different kinds of composites. Considering all the above concerns, we have prepared an attractive electrode combination of NiZrO3 on GNP using a fast and cost-effective microwave approach. Microwave (MW) heating presents a compelling alternative to traditional thermal heating methodologies, offering distinct advantages such as rapid and uniform heating, cost-effectiveness, and reduced energy consumption. Unlike conventional methods that rely on conductive heat transfer from the exterior, MW heating leverages its volumetric nature to achieve uniform heating throughout the material's volume. This is accomplished through direct radiation that penetrates the material's molecules, ensuring consistent thermal distribution.19 Also the MW method facilitates fast synthesis of samples. This unique heating mechanism presents a promising avenue for potentially enhancing the mechanical strength and morphology of materials compared to conventional techniques. The structural and morphological properties of the samples were analysed using different analytical tools. Further, the synthesized samples were explored towards supercapacitor electrode applications. As an SC electrode, this new combination exhibits higher capacitance, better rate performance, and good cyclic stability.
2. Experimental details
2.1 Materials
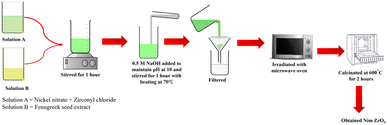
Zirconyl chloride(IV) octahydrate (ZrOCl2·8H2O) (98% purity), nickel(II) nitrate hexahydrate (Ni(NO3)2·6H2O) (98% purity), graphite expandable (EG) and sodium hydroxide (NaOH) were used as the starting materials. All the metal salts were obtained from Merck, India (analytical grade) and were used without further purification. Trigonella foenum-graecum seeds were collected from the local fields in Chennai, Tamil Nadu, India.2.2 Synthesis of NiZrO3 (NZ)
Firstly, 6.04 g of nickel nitrate (Ni (NO3)2·6H2O) and 8.10 g of zirconyl chloride (ZrOCl2) were dissolved separately in double distilled water (DDW). 20 mL of each solution was taken and stirred for about 1 h.20 Both the solutions were mixed and kept for stirring to obtain a homogenous clear solution and kept as solution A. 10 mL of Trigonella foenum-graecum seed extract was used as a gelling agent and it was mixed with the obtained homogenous solution with constant stirring at room temperature and kept as solution B. The molar ratio of Ni/Zr was kept constant at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The pH was maintained at 10 by the addition of NaOH. In the temperature range of 60–70 °C, the reaction mixture was heated under constant stirring to obtain a gel. The gel was kept under microwave irradiation (800 W) for 15 minutes for a combustion reaction. The obtained powder was calcinated at 600 °C for about 2 h to get NiZrO3 powder. Fig. 1 depicts schematic illustration of synthesis of NiZrO3 (NZ).
1. The pH was maintained at 10 by the addition of NaOH. In the temperature range of 60–70 °C, the reaction mixture was heated under constant stirring to obtain a gel. The gel was kept under microwave irradiation (800 W) for 15 minutes for a combustion reaction. The obtained powder was calcinated at 600 °C for about 2 h to get NiZrO3 powder. Fig. 1 depicts schematic illustration of synthesis of NiZrO3 (NZ).
2.3 Preparation of Trigonella foenum-graecum seed extracts
Around 25 g of Trigonella foenum-graecum seeds were finely ground. About 2–3 g of the obtained powder was dissolved in 50 mL of double distilled water. The combination was stirred thoroughly using a magnetic stirrer at room temperature to get a homogenous solution. The obtained solution was filtered and used as a gelling agent.2.4 Synthesis of graphene nanoplatelets (GNP)
Commercial expandable graphite (EG) was obtained, characterized by intercalations with chemicals such as sulfates and nitrates. The EG sample was placed inside a microwave oven. The microwave power setting was optimized at 800 W. The EG was heated rapidly using the microwave until it reached an activation temperature of 130 °C within seconds. The swift heating caused the intercalated molecules between the graphite layers to vaporize and move away, resulting in thermal expansion.2.5 Synthesis of NiZrO3@GNP (NG) composite
NiZrO3 and GNP were taken at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio and dissolved in a beaker using dimethylsulfoxide (DMSO) as solvent. The mixture was sonicated for 30 minutes at room temperature. Then the mixture was heated at 70 °C then it undergoes auto combustion. Then dried powder was obtained as NiZrO3@GNP (NG) composite.
1 ratio and dissolved in a beaker using dimethylsulfoxide (DMSO) as solvent. The mixture was sonicated for 30 minutes at room temperature. Then the mixture was heated at 70 °C then it undergoes auto combustion. Then dried powder was obtained as NiZrO3@GNP (NG) composite.
2.6 Material characterization
The synthesised NiZrO3 and NiZrO3@GNP powder samples were analysed by X-Ray Diffractometer (XRD) using BRUKER USA D8 Advance, Davinci. Surface morphology was analysed by Scanning Electron Microscopy (SEM) using EVO 15-CARL ZEISS, Germany which is connected with smart EDX (Energy Dispersive X-ray Analysis) for EDX analysis. In addition, the band gap was analysed by UV-Visible Diffuse Reflectance Spectrophotometer (DRS) using Thermo Fisher Scientific (DRA-EV-300).2.7 Electrochemical investigations
The working electrode was prepared by mixing 85 wt% of active material, polytetrafluoroethylene, and 10 wt% of activated carbon along with ethanol as solvent (a few drops). All the chemicals were purchased from Sigma-Aldrich. Paste like blended material was formed with these materials and was pasted on a nickel foam (1 × 1 cm2) with a mass loading of 1.0 mg cm−2. Then the coated electrode was dried overnight in a hot air oven at 80 °C which was used as the working electrode. To measure the electrochemical properties of NiZrO3 and NiZrO3@GNP an electrochemical workstation (CHI 660C, USA) was deployed. All the electrochemical measurements were conducted at room temperature. This electrochemical workstation is having three electrode setup having KOH (2 M) aqueous as electrolyte solution in which active material coated on nickel foam was taken as the working electrode and platinum wire was utilized as counter the electrode and Ag/AgCl as a reference electrode. The CV measurements obtained between −0.1 to 1.0 V potential and at various scan rates which are deployed to evaluate the capacitance values of the active material which is based on the equation given below| C = (∫Idv)/2mv (C g−1) | (1) |
From GCD evaluations, the capacitance values were calculated using the following equation given below:
| C = (2I∫vdt)/(m × v) | (2) |
2.8 Asymmetric supercapacitor device
The practicability of the NG material as device was assessed by fabrication of an asymmetric type supercapacitor cell in an electrode configuration.21 The activated carbon and NG nanocomposite were constructed as anode and cathode correspondingly.22 The slurry of active material (NG), PVDF, and carbon black in the ratio of 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 was prepared and coated on the electrode which is used as anode. Activated carbon and PVDF were mixed in the ratio of 95
15 was prepared and coated on the electrode which is used as anode. Activated carbon and PVDF were mixed in the ratio of 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 which is used as cathode.
5 which is used as cathode.
3. Results and discussion
3.1 Morphological analysis
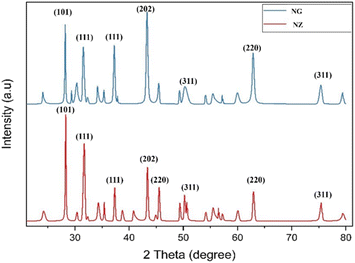
The structural modifications and phase variations of the NiZrO3 and NiZrO3@GNP were scrutinized by XRD analysis which is shown in Fig. 2. It was observed that all the reflection peaks of the synthesized NiZrO3 samples at 2θ = 30.1615, 31.6918, 36.8464, 45.2385, 50.4659, 59.436, 60.236, 64.654 and 67.021 and can be indexed with (101), (111), (111), (202), (220), (311), (220) and (311) planes of the NiZrO3 respectively. All the detectable peaks in the XRD patterns could be matched with the standard JCPDS data of (81-1314) and (89-7131). The addition of GNP onto NZ broadens the peak at 30°, 51° and 63° and this may be due to the presence of GNP can induce strain in the NZ lattice. The presence of a new peak around 2θ = 26°, indicates its presence in the composite material.23 The observed peak broadening and the presence of a new peak indicate that GNP is incorporated into the NiZrO3 lattice and potentially interacts with it. The lower intensities of the NiZrO3 peaks suggest a decrease in NZ content or X-ray scattering effects from GNP. The evaluation of the average crystallite size of nickel zirconate is calculated by using the Debye–Scherrer formula as given below
D = 0.9λ/(β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) θ)
| (3) |
SEM analysis was employed to conduct morphological observations, including the examination of shape, size, and agglomeration, for the prepared nanomaterial powders. The obtained results are presented in Fig. 3(a) and (b). The SEM image of NZ display nanoparticles are well dispersed, spherically shaped particles with an average size of 45 nm and a reasonably narrow size distribution in the range of 40 to 69 nm, SEM images of NG nanocomposite reveal that spherical shaped NZ material dispersed onto GNP surface.24,25 GNPs exhibited crumpled and wrinkled morphology.26 Additionally, the particles appear to be well-dispersed, as evident from their distribution and absence of significant agglomeration. The improved dispersion of NZ on NG nanocomposite is particularly noteworthy. The rougher surface texture and potential graphene presence in the NG image suggest a higher effective surface area compared to pure NZ. This increased surface area can provide more active sites for electrolyte interaction, potentially leading to higher capacitance in a supercapacitor.
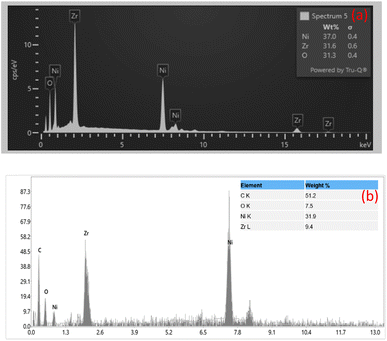
The chemical composition of NZ and NG nano composite has been determined by EDX analysis which is displayed in Fig. 4(a) and (b). From the results of NZ material, the spectrum distinctly reveals prominent peaks corresponding to three elements: nickel (Ni), zirconium (Zr), and oxygen (O). This alignment is consistent with the anticipated composition of NiZrO3. Notably, there are no discernible peaks for any other elements, suggesting a lack of significant impurities or contamination in the sample. This attests to the purity and reliability of the analysed material, bolstering confidence in its compositional integrity. NG spectrum additionally shows a clear peak for carbon (C), indicating the presence of the successful incorporation of graphene.
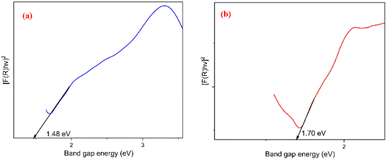
Optical properties of the NZ and NG nanocomposites were studied through UV-DRS analysis which is shown in Fig. 5(a) and (b) respectively. The optical band gap energy value has been determined by means of the Kubelka–Munk function (Tauc plot).27 The graph represents [F(R)hν]2 vs. hν plots, where F(R) is denoted as Kubelka function F(R) = (1 − R)2/2R and R is denoted as reflectance in UV-visible spectra. From the Tauc plot, the estimated band gap values are 1.48 and 1.70 eV for NZ and NG respectively. The bandgap of NG (1.70 eV) is slightly higher than that of pure NZ (1.48 eV), suggesting a modification in the electronic structure due to GNP incorporation.
3.2 Electrochemical analysis
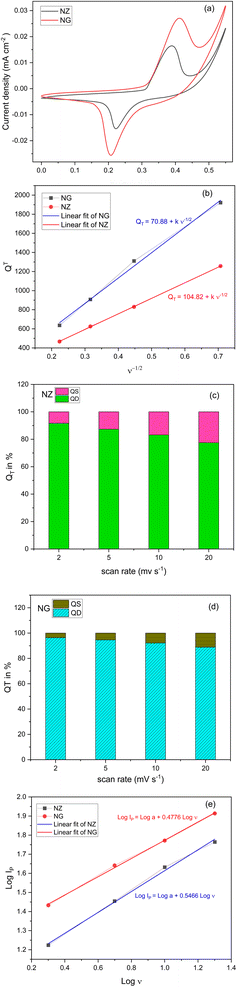
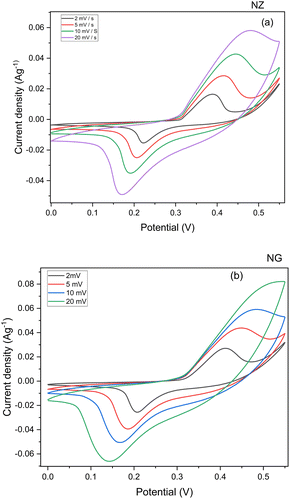
The Cyclic Voltammogram (CV) of pristine NZ and NG composite electrodes are depicted in Fig. 6(a). The CV measurements were exhibited to ascertain the charge storage mechanism, applicable potential window, and electrochemical reversibility of the NZ and NG. The CV curves were measured with a potential window of −0.1 to 0.1 V with different scan rates from 2 mV s−1 to 100 mV s−1. The CV curves of NZ reveal distinctive redox peaks that represent reversible redox reactions that arise on the surface of the electrode. The present magnitude expands correspondingly with the scan rate in response to the applied potential difference. Evidently, from the CV curves of NZ, a high-rate faradaic charge storage mechanism dominates in NZ, and its capacitance hinges on the pseudocapacitance originating from the reversible electrochemical reactions involving Ni–O–ZrO2. In redox reactions, typically electron transfer process relies on the surface characteristics of the electrode material and the density of the electronic states.28 Owing to the synergistic effect of GNP on the surface NZ demonstrates enhanced electron transport between the electrode and surface of the NZ. Merely a little inclusion of graphene nanoplatelets substantially boosted the supercapacitor's performance and consequently, the area of NZ increased as depicted in Fig. 6(a), which implies enhanced electron conduction. The observed increase in peak separation suggests the presence of mass transport limitations within the electrode material. During electrochemical reactions, the reaction rate is often governed by the rate of ion diffusion.29 The introduction of NGPs may have occluded some of the pre-existing pores in the NZ material, potentially leading to a decrease in overall porosity within the NG. This decrease in porosity could hinder ion diffusion, resulting in the observed increase in peak separation for NG compared to NZ.The management of charges between the electrodes is greatly influenced by 2 M KOH solution and a combination of its low viscosity and elevated conductivity in KOH, results in a more pronounced current response from the electrode. The area under the CV was used to evaluate the specific capacity of the active material NZ and NG. Those capacitance values are 1254, 830, 625, and 466 C g−1 for NZ and 1921.60, 1310.66, 907.49, and 636.59 C g−1 for NG which were recorded at the scan rate of 2, 5, 10, 20 mV s−1. According to the aforementioned findings, following a scan rate of 20 mV s−1, NZ and NG, respectively, preserved 37.21% and 33.13% capacitance. This could be due to the limited interaction of the electrolyte solution with the surface of the active material. Also, it is valid to indicate the presence of GNP in NZ nanocomposite effectively enhances conductivity leading the higher capacitance.
Then Dunn's method was used to evaluate the electrochemical kinetics of NZ and NG.30 Understanding the charge storage mechanisms of SCs is aided by the distinction made by Dunn's method between surface-controlled (capacitive) and diffusion-controlled processes.31 Hence total charge quantity (QT) stored in an electrode during electrochemical performance is the sum of surface capacitive charges (QS) and diffusion-controlled charges (QD).
| QT = QS + QD32 | (4) |
While diffusion-controlled charges (QD) were slowly stored using a semi-indefinite diffusion controlled redox process which is influenced by the reciprocal of the square root of the scan rate (ν−1/2) whereas surface capacitive charges (QS) accumulated rapidly through an electric double layer process which is independent of scan rate (ν).33,34 This can be depicted as follows
| QT = QS + constant 1/(√ν) | (5) |
Diffusion-controlled charges (QD) are determined by subtracting surface-controlled charges (QS) which is the intercept value obtained from an extrapolated line from a linear plot of QT versus the inverse square root of scan rates which is shown in Fig. 6(b) (plot of square root of scan rate vs. total charge (QT)).
The obtained QS values for are 70.88 C g−1 and 104.82 C g−1 for the NG and NZ respectively. Therefore, the diffusion-controlled charge contribution is calculated by deducting the surface contribution from the total charges (QT). Fig. 6(c) and (d) depicts the percentage of surface and diffusion charges that to the overall charge (QT) in the electrode materials NZ and NG respectively. From this analysis, it is apparent that the diffusion-controlled process contributes more in lower scan rates and surface contributes less so it may undergo intercalative process during charge storage mechanism. Fig. 6(e) depicts the energy storage device for characterization by determining the slope value using linear fit. As the slope values lies on 0.5466 and 0.4776 for NZ and NG respectively, which indicates that NZ behave like supercapacitor and NG behave like capacitor type.35 This may be due to the agglomeration found in SEM images that may clogged the pores in the NZ pores.
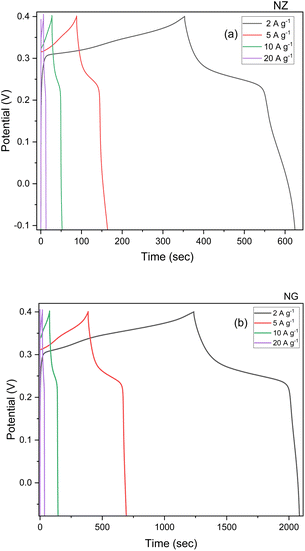
The sample was analysed with GCD to evaluate capacitive behaviour and real time application of the sample after the CV. Fig. 7 depicts the performance of GCD with varying current densities ranging from 2 to 20 A g−1 with the operating potential window of −0.15 to 0.5 mV. This study was evaluated by the discharge time of the electrode material and from this study, longer discharge time will contribute to the greater specific capacity of the material which proves that energy storage will directly be influenced by the electrochemical redox process. The specific capacity was calculated using the eqn (6). The evaluated specific capacity was 577, 355, 274, and 136 C g−1 at a specific current of 2, 5, 10, and 20 A g−1 respectively for NZ. The specific capacity of NG was calculated by the same above-mentioned method and evaluated specific capacitance (coulombic efficiency) were 1996, 1777, 796, and 398 C g−1 which were recorded at the specific current of 2, 5, 10, and 20 A g−1 respectively. Due to the synergistic effect of the GNP, obtained better results for NG when compared to NZ. At higher specific current, ions present in the electrolyte solution have reduced time to diffuse into ions in the electrode material. So less pushing of charges results in decreased specific capacity at the higher specific current.36,37
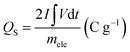 | (6) |
An AC impedance analysis was utilized to elucidate the reaction kinetics and impedance in our electrochemical system of NZ of NG which is associated with the diffusion of ions at the boundary between electrode and electrolyte interface. The analysis was conducted employing an AC signal with an amplitude of 5 mV across the frequency range of 10 mHz to 100 kHz. Nyquist plot depicted in Fig. 8(a) shows the impedance which is fitted on the modified Randle's circuit. Randle's circuit encompassing solution resistance (RS), charge transfer resistance (RCT), double layer capacitance (Cdl), and Warburg impedance (ZW).38,39
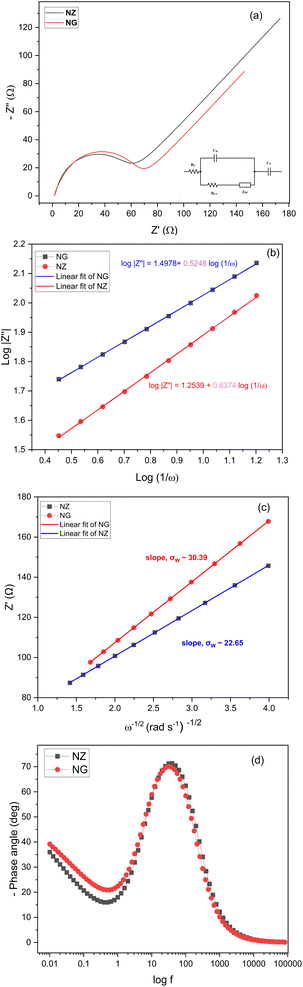 | ||
Fig. 8 (a) Nyquist plot. (b) Plot of log(1/ω) vs. log|Z′′|. (c) Plot of ω−1/2 (rad s−1)−1/2 vs. Z′. (d) Plot of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f vs. −phase angle (°). f vs. −phase angle (°). | ||
The high-frequency region of the plot displays a semicircular shape, implying that the rate of charge transfer is the dominant factor governing the electrochemical process. At lower frequencies, the plot transitions to an inclined line, suggesting that the diffusion of electrolyte ions becomes the primary factor influencing the storage of electrical energy. The slight leftward shift of the semicircle's center suggests that the electrode resistance plays a more significant role compared to the electrolyte resistance.40 This could be due to factors like the contact resistance between the electrode material and the nickel foam current collector, or possibly due to the intrinsic resistance of NZ itself.
The electrolyte solution resistance yielded from the interception of X in the semicircle is 1.44 Ω which is obtained from high frequency region, while its diameter indicates charge transfer resistance of 44.62 Ω and 59.18 Ω for NZ and NG respectively. In a similar vein, the inclined linear portion of the low-frequency region indicates that the electrochemical process is primarily driven by the diffusion of electrolyte ions. The electrochemical kinetics of the NZ electrode in KOH electrolyte can be further investigated under ac perturbation and the system behaves as follows: the CV analysis and GCD profiles exposed faradaic reaction of the NZ electrode, OH− ions transported through diffusion process onto the surface of the electrode is dominant. Faradaic impedance can be attributed mathematically by the sum of charge transfer resistance and diffusion controlled process (ZF(ω) = RCT + ZW(ω)). In the limit of ω → 0, the electrochemical behavior transitions to diffusion-controlled, characterized by a linear response with a slope of 45° in the low-frequency region of the impedance spectrum.
Mathematically, the impedance (ZW) at an angular frequency (ω) can be expressed using the Warburg coefficient (σ), the imaginary unit (j), and the transfer coefficient (α) and which can be written as 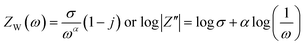 .41 This equation can also be written in logarithmic form. A value of 0.5 for a signifies diffusion-controlled behavior. This relationship can be expressed in both complex and logarithmic forms. Fig. 8(b) depicts log(1/ω) vs. log|Z′′|. The slope of a logarithmic plot of absolute impedance versus inverse frequency provides the transfer coefficient, with a value of 0.5248 for NG and 0.6374 for NGZ indicating diffusion-dominant behavior enhanced by the addition of GNP. The hydroxyl ion diffusion (σ) coefficient is estimated using the following equation,42
.41 This equation can also be written in logarithmic form. A value of 0.5 for a signifies diffusion-controlled behavior. This relationship can be expressed in both complex and logarithmic forms. Fig. 8(b) depicts log(1/ω) vs. log|Z′′|. The slope of a logarithmic plot of absolute impedance versus inverse frequency provides the transfer coefficient, with a value of 0.5248 for NG and 0.6374 for NGZ indicating diffusion-dominant behavior enhanced by the addition of GNP. The hydroxyl ion diffusion (σ) coefficient is estimated using the following equation,42
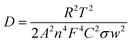 | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1), the molar concentration of OH− ions (2 × 10−3 mol cm−3 for three electrode setup) and σW, Warburg coefficient (∼22.65 for NZ and ∼30.39 for NG) respectively and these values are obtained from the slope of
485 C mol−1), the molar concentration of OH− ions (2 × 10−3 mol cm−3 for three electrode setup) and σW, Warburg coefficient (∼22.65 for NZ and ∼30.39 for NG) respectively and these values are obtained from the slope of 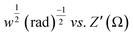 plot as shown in Fig. 8(c).43 Based on the above equation, the calculated diffusion coefficient is 2.45 × 10−13 s−1 for NZ and 9.39 × 10−12 s−1 for NG material. These results indicate that NG material exhibits a significantly higher diffusion coefficient than NZ, so the addition of GNP enhances NG allows OH− ions for faster diffusion. The Bode phase angle plot of NZ and NG are depicted in Fig. 8(d). Purely capacitive systems usually have a low-frequency phase angle in a Bode diagram that approaches −90°.44 On the other hand, the Bode phase angle plots of NZ and NG show outstanding redox performance, with the latter showing an intercept at low frequency around a phase angle of −40 and −45° respectively. Better charge storage efficiency and faster ion diffusion are associated with smaller phase angles.45 The centre frequency region of the Bode phase angle plot shows a single time constant, indicating the double layer capacitance mechanism.44
plot as shown in Fig. 8(c).43 Based on the above equation, the calculated diffusion coefficient is 2.45 × 10−13 s−1 for NZ and 9.39 × 10−12 s−1 for NG material. These results indicate that NG material exhibits a significantly higher diffusion coefficient than NZ, so the addition of GNP enhances NG allows OH− ions for faster diffusion. The Bode phase angle plot of NZ and NG are depicted in Fig. 8(d). Purely capacitive systems usually have a low-frequency phase angle in a Bode diagram that approaches −90°.44 On the other hand, the Bode phase angle plots of NZ and NG show outstanding redox performance, with the latter showing an intercept at low frequency around a phase angle of −40 and −45° respectively. Better charge storage efficiency and faster ion diffusion are associated with smaller phase angles.45 The centre frequency region of the Bode phase angle plot shows a single time constant, indicating the double layer capacitance mechanism.44
3.3 Two electrode system: asymmetric supercapacitor
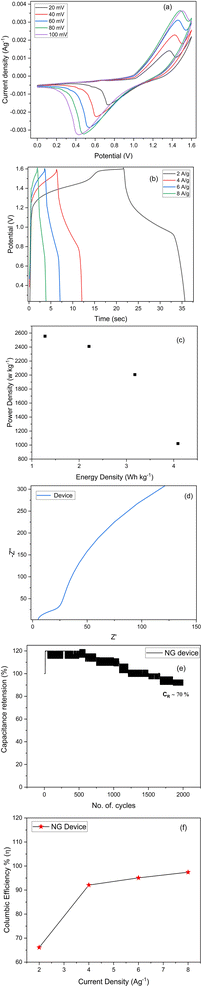
An asymmetric supercapacitor device was assembled and used to examine the NG electrode's application in practice.46 As prepared NG sample and activated carbon was utilized as electrodes for assembling two electrode system. The CV curves of this NG based device was presented in Fig. 9(a) with a potential window of 0 to 1.6 V in a 2 M KOH solution. The device's behaviour was demonstrated by the quasi-rectangular nature of the curve with visible peaks showing the influence of redox reactions.As demonstrated in Fig. 9(b), the device's estimated specific capacity based on the GCD profiles is found to start decreasing with an increase in current density, i.e., 47.10, 36.6, 25.44, and 19.2 C g−1 at 2, 4, 6, and 8 A g−1, respectively. At higher currents, the electrolyte ions struggle to reach deeper pores or active regions, resulting in incomplete utilization of the electrode's full capacity. This translates to a lower apparent specific capacity. We estimate the specific energy and power of the system using eqn (8) and (9) (ref. 37) and display the results in a Ragone plot as depicted in Fig. 9(c).
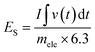 | (8) |
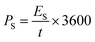 | (9) |
The coulombic efficiency (η%) is evaluated from η = Td/Tc × 100 (Td and Tc represent the discharging and charging time respectively) from the GCD curves.49 The calculated coulombic efficiency (%) is 66.12, 92.06, 95.08 and 97.42 respectively for 2, 4, 6 and 8 A g−1 as plotted in Fig. 9(f). The low coulombic efficiency at low current density is due to the morphology of the electrode material and the shorter charging/discharging times and lower charge loss at high current densities. The spherical-shaped surface is evenly dispersed with metal oxide on the graphene nanoplatelets that facilitate the electron/ions intercalation at high current densities. They provide adequate opportunities for OH− ions to make contact with electrode active sites, thus enabling the transfer of electrons and ions at higher current densities.
4. Conclusion
NiZrO3@GNP (NG) composite was designed using microwave assisted synthesis procedure and exploited its usefulness for SC electrode material. The presence of GNP with NiZrO3 showing a synergistic effect in terms of enhancement of electrochemical features. GNP blended NiZrO3 showing a higher capacitance of 577.63 C g−1 with better cyclic stability. The supercapacitor features of NiZrO3@GNP composite are higher than the bare NiZrO3 due to the presence of highly conductive GNP. The asymmetric supercapacitor fabricated with NG as the positive electrode demonstrates an impressive maximum energy density of 4.08 W h kg−1 and remarkable cyclability, retaining 70% of its initial capacity after 2000 cycles. This study paves the way for further advancements in supercapacitor technology, potentially accelerating the development of efficient and sustainable energy storage solutions for future applications (Fig. 10).Author contributions
J. John Benitto: conceptualization, methodology, data curation, and formal analysis, writing the original draft. J. Judith Vijaya: supervision, formal analysis, paper reviewing, and editing. B. Saravanakumar: data curation, formal analysis, paper reviewing. Hamad Al-Lohedan: formal analysis, paper reviewing, and editing. Stefano Bellucci: review and editing.Conflicts of interest
All authors declare that they have no conflicts to declare.Acknowledgements
The authors would like thank Loyola College for their infrastructural facilities and support offered in completing the present work. The author Hamad Al-Lohedan extend his appreciation to Researchers Supporting Project number (RSP2024R54) for financial support, King Saud University, Riyadh, Saudi Arabia.Notes and references
- M. Şahin, F. Blaabjerg and A. Sangwongwanich, Energies, 2022, 15, 674 CrossRef.
- S. Huang, X. Zhu, S. Sarkar and Y. Zhao, APL Mater., 2019, 7, 100901 CrossRef.
- W. Raza, F. Ali, N. Raza, Y. Luo, K.-H. Kim, J. Yang, S. Kumar, A. Mehmood and E. E. Kwon, Nano Energy, 2018, 52, 441–473 CrossRef CAS.
- P. Sharma and V. Kumar, J. Electron. Mater., 2020, 49, 3520–3532 CrossRef CAS.
- A. K. Samantara and S. Ratha, in Materials Development for Active/Passive Components of a Supercapacitor, Springer Singapore, Singapore, 2018, pp. 9–10 Search PubMed.
- J. Sung and C. Shin, Micromachines, 2020, 11, 1125 CrossRef PubMed.
- A. M. Bittner, M. Zhu, Y. Yang, H. F. Waibel, M. Konuma, U. Starke and C. J. Weber, J. Power Sources, 2012, 203, 262–273 CrossRef CAS.
- A. Lewandowski and M. Galinski, J. Power Sources, 2007, 173, 822–828 CrossRef CAS.
- L. Dong, W. Yang, W. Yang, Y. Li, W. Wu and G. Wang, J. Mater. Chem. A, 2019, 7, 13810–13832 RSC.
- A. Vlad, N. Singh, J. Rolland, S. Melinte, P. M. Ajayan and J.-F. Gohy, Sci. Rep., 2014, 4, 4315 CrossRef CAS PubMed.
- M. Dai, D. Zhao and X. Wu, Chin. Chem. Lett., 2020, 31, 2177–2188 CrossRef CAS.
- S. Mahala, K. Khosravinia and A. Kiani, J. Energy Storage, 2023, 67, 107558 CrossRef.
- J. Zhang, F. Liu, J. P. Cheng and X. B. Zhang, ACS Appl. Mater. Interfaces, 2015, 7, 17630–17640 CrossRef CAS PubMed.
- S. Najib and E. Erdem, Nanoscale Adv., 2019, 1, 2817–2827 RSC.
- W. Zhao, Y. Zeng, Y. Zhao and X. Wu, J. Energy Storage, 2023, 62, 106934 CrossRef.
- A. Pramitha and Y. Raviprakash, J. Energy Storage, 2022, 49, 104120 CrossRef.
- X. Zhu, J. Energy Storage, 2022, 49, 104148 CrossRef.
- R. B. Choudhary, S. Ansari and M. Majumder, Renewable Sustainable Energy Rev., 2021, 145, 110854 CrossRef CAS.
- M. Oghbaei and O. Mirzaee, J. Alloys Compd., 2010, 494, 175–189 CrossRef CAS.
- Y. Lu, X. Liang, J. Xu, Z. Zhao and G. Tian, Sens. Actuators, B, 2018, 273, 1146–1155 CrossRef CAS.
- R. Vinodh, R. S. Babu, R. Atchudan, H.-J. Kim, M. Yi, L. M. Samyn and A. L. F. De Barros, Catalysts, 2022, 12, 375 CrossRef CAS.
- H. Pourfarzad, R. Badrnezhad, M. Ghaemmaghami and M. Saremi, Ionics, 2021, 27, 4057–4067 CrossRef CAS.
- T. Batakliev, I. Petrova-Doycheva, V. Angelov, V. Georgiev, E. Ivanov, R. Kotsilkova, M. Casa, C. Cirillo, R. Adami, M. Sarno and P. Ciambelli, Appl. Sci., 2019, 9, 469 CrossRef CAS.
- A. M. El-Khatib, M. S. Badawi, G. D. Roston, R. M. Moussa and M. M. Mohamed, J. Cluster Sci., 2018, 29, 1321–1327 CrossRef CAS.
- M. Eshed, S. Pol, A. Gedanken and M. Balasubramanian, Beilstein J. Nanotechnol., 2011, 2, 198–203 CrossRef CAS PubMed.
- D. D. La, J. M. Patwari, L. A. Jones, F. Antolasic and S. V. Bhosale, ACS Omega, 2017, 2, 218–226 CrossRef CAS PubMed.
- M. Patel, A. Chavda, I. Mukhopadhyay, J. Kim and A. Ray, Nanoscale, 2016, 8, 2293–2303 RSC.
- I. Cho, P. Wagner, P. C. Innis, S. Mori and A. J. Mozer, J. Am. Chem. Soc., 2021, 143, 488–495 CrossRef CAS PubMed.
- N. F. Sylla, N. M. Ndiaye, B. D. Ngom, D. Momodu, M. J. Madito, B. K. Mutuma and N. Manyala, Sci. Rep., 2019, 9, 13673 CrossRef CAS PubMed.
- I. M. Babu, J. J. William and G. Muralidharan, Appl. Surf. Sci., 2019, 480, 371–383 CrossRef CAS.
- S. Fleischmann, J. B. Mitchell, R. Wang, C. Zhan, D.-e. Jiang, V. Presser and V. Augustyn, Chem. Rev., 2020, 120, 6738–6782 CrossRef CAS PubMed.
- Q. Yao, H. Wang, C. Wang, C. Jin and Q. Sun, ACS Sustain. Chem. Eng., 2018, 6, 4695–4704 CrossRef CAS.
- A. M. Patil, A. C. Lokhande, P. A. Shinde and C. D. Lokhande, ACS Appl. Mater. Interfaces, 2018, 10, 16636–16649 CrossRef CAS PubMed.
- S. D. Perera, X. Ding, A. Bhargava, R. Hovden, A. Nelson, L. F. Kourkoutis and R. D. Robinson, Chem. Mater., 2015, 27, 7861–7873 CrossRef CAS.
- V. Vivier and M. E. Orazem, Chem. Rev., 2022, 122, 11131–11168 CrossRef CAS PubMed.
- J. Johnson William, I. Manohara Babu and G. Muralidharan, Chem. Eng. J., 2021, 422, 130058 CrossRef CAS.
- A. Laheäär, P. Przygocki, Q. Abbas and F. Béguin, Electrochem. Commun., 2015, 60, 21–25 CrossRef.
- K. K. Purushothaman, I. M. Babu and B. Saravanakumar, Int. J. Hydrogen Energy, 2017, 42, 28445–28452 CrossRef CAS.
- M. S. Park, Y. M. Kang, G. X. Wang, S. X. Dou and H. K. Liu, Adv. Funct. Mater., 2008, 18, 455–461 CrossRef CAS.
- I. Manohara Babu, J. J. William and G. Muralidharan, ChemElectroChem, 2020, 7, 535–545 CrossRef CAS.
- S. Sarker, A. J. S. Ahammad, H. W. Seo and D. M. Kim, Int. J. Photoenergy, 2014, 2014, 1–17 CrossRef.
- I. Shakir, Z. Almutairi and S. Saad Shar, Ceram. Int., 2021, 47, 1191–1198 CrossRef CAS.
- K. A. Yasakau, M. Starykevich, M. G. S. Ferreira and M. L. Zheludkevich, Electrochim. Acta, 2021, 378, 138091 CrossRef CAS.
- F. Lyu, Y. Bai, Q. Wang, L. Wang, X. Zhang and Y. Yin, Dalton Trans., 2017, 46, 10545–10548 RSC.
- A. Asokan, S. Abu Khalla and M. E. Suss, ECS Meeting Abstracts, 2022, MA2022-02, 1605 CrossRef.
- B. Carmel Jeeva Mary, J. J. Vijaya, B. Saravanakumar, M. Bououdina and L. J. Kennedy, Synth. Met., 2022, 291, 117201 CrossRef CAS.
- J. J. William, I. M. Babu and G. Muralidharan, New J. Chem., 2019, 43, 15375–15388 RSC.
- X. Zhang, W. Shi, J. Zhu, W. Zhao, J. Ma, S. Mhaisalkar, T. L. Maria, Y. Yang, H. Zhang, H. H. Hng and Q. Yan, Nano Res., 2010, 3, 643–652 CrossRef CAS.
- S. Sarkar, R. Akshaya and S. Ghosh, Electrochim. Acta, 2020, 332, 135368 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |