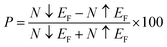Open Access Article
Open Access ArticlePhysical properties of ferromagnetic Mn-doped double perovskites (DPs) Cs2AgInCl/Br6 for spintronics and solar cell devices: DFT calculations
N. A. Noor *a,
Wasim Tahir
*a,
Wasim Tahir b,
Sohail Mumtaz
b,
Sohail Mumtaz c and
Hosam O. Elansaryd
c and
Hosam O. Elansaryd
aDepartment of Physics, RIPHAH International University, Campus Lahore, Pakistan. E-mail: naveedcssp@gmail.com
bInstitute of Physics, The Islamia University of Bahawalpur, Bahawalpur 63100, Pakistan
cElectrical and Biological Physics, Krangwoon University, Seoul, 01897, South Korea
dPlant Production Department, College of Food and Agriculture Sciences, King Saud University, P. O. Box 2460, Riyadh 11451, Saudi Arabia
First published on 20th March 2024
Abstract
A computational framework based on density functional theory (DFT) has been effectively employed to investigate the wide-ranging physical characteristics of ferromagnetic manganese (Mn)-substituted double perovskites (DPs) with composition Cs2AgIn1−xMnxCl/Br6 (x = 0.0, 0.25). This research covers a systematic exploration of the mentioned DPs for potential applications in the domains of spintronics and energy conversion devices. The physics concerning ferromagnetic (FM) Cs2AgIn0.75Mn0.25Cl/Br6 DPs was studied computationally using the modified Becke–Johnson (mBJ-LDA) potential and the generalized gradient approximation (PBEsol GGA) method introduced by Perdew, Burke, and Ernzerhof. The structural, electronic, magnetic, and transport behavior of materials were investigated using these computations. Structural parameters for both perovskite materials were computed subsequent to their optimization in FM phase. According to evaluations of the electronic band structure and density of states (DOS), the incorporation of Mn ions into the host lattice causes exchange splitting induced by p–d hybridization, consequently stabilizing the FM state. Probing the sharing of magnetic moment, charge, and spin between the substituent cations and the host anions led to the comprehensive elaboration of this exchange splitting of bands. Important parameters such as exchange constants (N0α, N0β), and direct spin-exchange splitting Δx(d), support the stability of the FM state. Finally, we briefly explored the spin effect on other aspects of electronic transport, the Seebeck coefficient, and the power factor, using the conventional Boltzmann transport theory.
1. Introduction
During the recent past, perovskite nano-crystals with chemical composition (APbX3, where A = Cs1+, CH(NH2)21+, CH3NH31+; X = Br1−, Cl1−, I1−) have attracted significant interest from the materials science community because of their outstanding optical characteristics. Owing to their appealing optoelectronic features, these materials are frequently used in numerous devices, including solar cells, photo-detectors, and light emitting diodes (LEDs).1,2 However, the main issue impeding the usage of lead halide perovskites is their lower stability over prolonged light exposure, high temperature, or humidity. In addition, lead's toxicity and bioaccumulation in the environment present another problem. These challenges are currently provoking materials scientists to search for new stable, ecologically friendly metal halide perovskite NCs having analogous optoelectronic characteristics.3–9 In this context, the replacement of toxic lead (Pb2+) ions with other not much toxic divalent cations of IV-group of the periodic table (i.e. Sn2+, Ge2+) can be the best possible approach to develop lead-free halides.10–14 But the observed conversion of the oxidation state from divalent (Sn2+, Ge2+) configuration to tetravalent (Sn4+, Ge4+) configuration, puts a question mark on the stability of these halides. Fortunately, this dilemma is finely addressed by material researchers through the substitution of two divalent lead (Pb2+) cations by one monovalent (M+) and one trivalent (M3+) cation, consequently maintaining the overall neutrality of the crystal. Thus a new class of materials with composition A2M+M3+X6, named doubled perovskites (DPs), was developed that exhibits 3D perovskite structure and also maintains crystal neutrality.15,16 Historically, such kind of materials have been previously investigated as ferroelectric in the 1960s under the name “elpasolites” with numerous compositions A2M+M3+X6 (here A and M+ = Na+, K+, Li+, Rb+, Cs+, Tl+, Ag+ etc.; M3+ = Fe3+, Al3+, Bi3+, Ln3+, Ga3+, etc.; X = Cl1−, Br1−, F1−, I1−).17–19Currently, two potential members of the DP family, Cs2AgBiBr6 and Cs2AgBiCl6, have been suggested owing to their promising air-exposed stability and photovoltaic (PV) uses.20–27 These materials, on the other hand, exhibit weak photoluminescence (PL) output as well as low efficiency of power conversion (2.2%) for photovoltaic device applications that are attributed to their indirect band-gap.28 Therefore, current investigations are focused on direct band-gap DP systems as an alternate potential choice.29–33 Computational studies regarding various A–M+–M3+–X compositions have anticipated diverse stable DPs, such as Cs2AgInX6, Rb2AgInX6, and Rb2CuInX6 (X = Cl1−, Br1−), that essentially show a direct band-gap across the entire spectral range essential regarding conversion of solar energy (i.e. 1.5–2.5 eV).34,35 After Volonakis et al.'s groundbreaking breakthrough in 2016,8 the synthesis of bulk Cs2AgInCl6 perovskite material was reported by various investigators which exhibits a DP structure at room temperature and belongs to the space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m. Moreover, the said material also shows a fundamental direct band-gap of about 2 eV (described range 2.1–2.6 eV), extended carrier lifetime (6 s), and excellent stability (regarding heat, light, and moisture), making it a possible substitute for Pb-based halide perovskites.36–39 Through the use of DFT calculations, it has been found that the material Cs2AgInCl6 exhibits a flat valence band maximum (VBM) that is primarily determined by Ag-4d orbitals and Cl-3p orbitals, and a dispersive conduction band minimum (CBM) originated from the delocalized 5s states.36
m. Moreover, the said material also shows a fundamental direct band-gap of about 2 eV (described range 2.1–2.6 eV), extended carrier lifetime (6 s), and excellent stability (regarding heat, light, and moisture), making it a possible substitute for Pb-based halide perovskites.36–39 Through the use of DFT calculations, it has been found that the material Cs2AgInCl6 exhibits a flat valence band maximum (VBM) that is primarily determined by Ag-4d orbitals and Cl-3p orbitals, and a dispersive conduction band minimum (CBM) originated from the delocalized 5s states.36
Moreover, the energy needed for the transition of photo-generated carriers is decreased by the direct transport pathway in Cs2InAgCl6, which improves the polycarboxylate superplasticizer (PCE). Nevertheless, even though films with a stable double perovskite structure were successfully synthesized in the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group, the PBE method's estimated gap values of 2.9–3.3 eV became challenging for the photovoltaic application of Cs2InAgCl6 compound. While the broad band-gap problem may be resolved by using a BrCl solution, it should be noted that the synthesis of Cs2InAgBr6 became a difficult task partly because bromine speeds up the compound's instability.39 From this angle, it can be perceived that the field of double perovskites for solar applications is noticeably lacking in practical solutions thus prompting us to investigate other constituents.40–43 The material's remarkable stability and comparatively large bandgap energy (Egopt) were the driving force for Nandha et al.'s work comprising the addition of Mn2+ cations to Cs2AgInCl6 powders in order to improve the optical properties of substituted compound.38 The most extensively studied tactic for doping II–VI semiconductors and halide perovskite nano-crystals (NCs)44,45 has been the incorporation of Mn into a wide band-gap semiconductor host lattice.45 These systems produce d–d orbital emission (yellow–orange) because the photo-excited host lattice efficiently transfers its energy to manganese (Mn) ions, which in turn facilitates electronic transitions within d-orbitals. Such color-centered impurities, namely Mn2+ ions, give rise to photoluminescence (PL) with striking characteristics including prolonged lifetimes, substantial PL quantum yield (QY) as well as a significant Stokes shift that consequently reduces the possibility of self-absorption in the system.46–49 Orange emission was detected at approximately 630 nm in Mn-substituted Cs2AgInCl6 powders (at Mn2+ concentration = 0.9%) having PLQY of almost 3–5%, consequently making it an attractive lead-free DP.38
m space group, the PBE method's estimated gap values of 2.9–3.3 eV became challenging for the photovoltaic application of Cs2InAgCl6 compound. While the broad band-gap problem may be resolved by using a BrCl solution, it should be noted that the synthesis of Cs2InAgBr6 became a difficult task partly because bromine speeds up the compound's instability.39 From this angle, it can be perceived that the field of double perovskites for solar applications is noticeably lacking in practical solutions thus prompting us to investigate other constituents.40–43 The material's remarkable stability and comparatively large bandgap energy (Egopt) were the driving force for Nandha et al.'s work comprising the addition of Mn2+ cations to Cs2AgInCl6 powders in order to improve the optical properties of substituted compound.38 The most extensively studied tactic for doping II–VI semiconductors and halide perovskite nano-crystals (NCs)44,45 has been the incorporation of Mn into a wide band-gap semiconductor host lattice.45 These systems produce d–d orbital emission (yellow–orange) because the photo-excited host lattice efficiently transfers its energy to manganese (Mn) ions, which in turn facilitates electronic transitions within d-orbitals. Such color-centered impurities, namely Mn2+ ions, give rise to photoluminescence (PL) with striking characteristics including prolonged lifetimes, substantial PL quantum yield (QY) as well as a significant Stokes shift that consequently reduces the possibility of self-absorption in the system.46–49 Orange emission was detected at approximately 630 nm in Mn-substituted Cs2AgInCl6 powders (at Mn2+ concentration = 0.9%) having PLQY of almost 3–5%, consequently making it an attractive lead-free DP.38
Consistent with our extensive literature exploration, a comprehensive analysis regarding structural, electrical, and magnetic investigations of Mn-substituted Cs2AgInCl/Br6 FM double perovskites is still unreported. Furthermore, DFT computations related to the thermoelectric characteristics of Mn-substituted Cs2AgInCl/Br6 DPs are also unreported in the published literature. This research article designates the outcomes regarding DFT simulations to investigate the structural, electronic, elastic, magnetic, and thermoelectric characteristics of Mn-substituted Cs2AgInCl/Br6 dual perovskites with a particular emphasis on the 25% Mn content.
2. Computational scheme
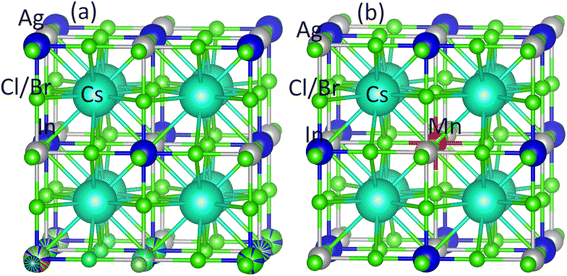
Ab initio modeling is a widely employed approach for investigating materials titled for cutting-edge device applications. To investigate the existence of a stable FM semiconducting ground state within Mn-substituted Cs2AgInCl/Br6 dual perovskites, we have worked with FP-LAPW+lo approach, incorporated within the Wein2k software,50 and originated from spin-polarized DFT. Using the PBEsol generalized gradient approximation, the structural and electronic properties are computed, and the Kohn–Sham orbitals are evaluated in a self-consistent mode.51 Precise electrical and optical features are determined, using the newly presented modified Becke–Johnson (mBJ) functional,52 revealing remarkable consistency with experimental findings.53 The band gap computed using the modified Becke–Johnson (mBJ) functional was found closely consistent with experimental outcomes that in turn outclass the already used functionals. Already published article52 offers a complete comparative analysis of band gap calculations performed by employing different methods, revealing the dominance of mBJ functional with respect to accuracy.Using a 1 × 1 × 1 supercell, the pure Cs2AgInCl/Br6 and substituted Cs2AgIn1−xMnxCl/Br6 (x = 0.25) binary perovskites having space group Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (cubic) are probed at room temperature (see Fig. 1(a) and (b)). Fig. 1(b) depicts that the substituted DPs exhibited the existence of Fm
m (cubic) are probed at room temperature (see Fig. 1(a) and (b)). Fig. 1(b) depicts that the substituted DPs exhibited the existence of Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group at substitution level x = 0.25. To facilitate subsequent computations, PBEsol-GGA functional is employed to optimize the experimentally measured lattice parameters.
m space group at substitution level x = 0.25. To facilitate subsequent computations, PBEsol-GGA functional is employed to optimize the experimentally measured lattice parameters.
The cut-off parameter was determined by multiplying the maximum plane wave vector (Kmax) and the muffin-tin sphere's radius was set at 8. Additionally, utilizing Gmax = 18 a.u.−1, the potential inside the interstitial void is computed. The values of Muffin-tin radii regarding Cs, Ag, Mn, Cl, and Br atoms were used as 2.45 (a.u.), 2.40 (a.u.), 2.35 (a.u.), 2.21 (a.u.) and 2.25 (a.u.), respectively. A 10 × 10 × 10 k-mesh is used for the integration of the Brillouin zone. The charge and total energy were allowed for preferable convergence to values 10−3 e and 10−4 Ry, respectively. We employed the BoltzTraP software54 which is customized for the electronic structure of Mn-substituted Cs2AgInCl/Br6 DPs, to study the transport properties effectively. It is important to remember that a higher-level selection of k points was carried out for all BoltzTrap computations. Finally, the parameters such as electrical conductivity (σ), thermal conductivity (κ), Seebeck coefficient (S), and power factor were studied within the temperature range (200–800 K).
3. Results and discussions
3.1 Structural and elastic properties
For all the four investigated materials [Cs2AgIn1−xMnxCl6 (x = 0.00, 0.25), Cs2AgIn1−xMnxBr6 (x = 0.00, 0.25)], the optimized lattice parameters (a) and bulk moduli (B), presented in Table 1, are obtained by optimization and fitting of the computed volume and energy with well-known Birch–Murnghan equation.55Physically, bulk modulus indicates the crystal's hardness by elucidating the crystal's capacity to withstand deformations induced by uniform pressure. The validity of our computed results regarding lattice parameters and bulk moduli (Table 1) can be assessed by their complete agreement with previously published theoretical and experimental research articles.56,57 An increase in lattice parameter (a) with enhancement in Mn content has been observed which is ascribed to a smaller ionic radius of Mn2+ (0.80 Å) compared with In2+ (0.81 Å). Moreover, a decrease in bulk modulus (B) with an increase of parameter (a) was observed which revealed the inverse relation of a with B.58,59 Understanding the stability comparison between the nonmagnetic (NM) and ferromagnetic (FM) states was achieved by comparing the total energy of these states as estimated using the relation ΔE1 = ENM − EFM. The stability of the FM phase was validated through a positive value of ΔE1 (see Fig. 2(a) and (b)) and their calculated FM Cs2AgIn0.75Mn0.25Cl/Br6 DPs are given in Table 1.
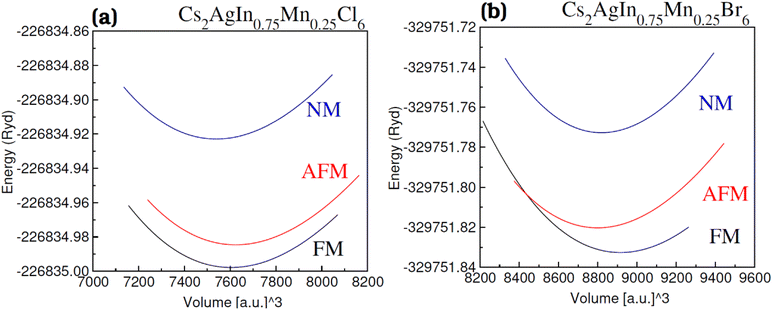 | ||
| Fig. 2 Volume optimization plot of DPs (a) Cs2AgIn0.75Mn0.25Cl6 and (b) Cs2AgIn0.75Mn0.25Br6 in nonmagnetic (NM), antiferromagnetic (AFM) and ferromagnetic (FM) phase. | ||
The orientation of magnetic moments is detailed for both ferromagnetic (FM) and anti-ferromagnetic (AFM) configurations within Mn-substituted Cs2AgInCl/Br6 DPs, with a consistent arrangement of spins in antiparallel and parallel directions between Mn atoms. The magnetic interconnection among the two Mn atoms is expressed as energy difference among the AFM and FM structures ΔE = EFM − EAFM. The energy values for Mn-substituted Cs2AgInCl/Br6 DPs compounds are recorded 2.24 eV and 1.85 eV respectively. It can be seen that the FM structure exhibits superior characteristics compared to the AFM states for all aspects. The Curie temperature (TC) has been determined by employing smearing in mean-field approximations, expressed as 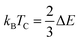 and the Heisenberg model.60 Table 1 shows the anticipated TC values, aligning with the recently disclosed range of 600 to 1000 K.61 The investigated Mn-substituted exhibit a notably high Curie temperature (TC), which is ascribed to the substantial energy difference (ΔE) among the ferromagnetic (FM) and antiferromagnetic (AFM) states.
and the Heisenberg model.60 Table 1 shows the anticipated TC values, aligning with the recently disclosed range of 600 to 1000 K.61 The investigated Mn-substituted exhibit a notably high Curie temperature (TC), which is ascribed to the substantial energy difference (ΔE) among the ferromagnetic (FM) and antiferromagnetic (AFM) states.
The computed elastic constants Cij for undoped and Mn-doped Cs2AgInCl/Br6 are presented in Table 2. These computed elastic constants satisfy the mechanical stability criteria, specifically (C11–C12) > 0, C11 > 0, C44 > 0 and C12 > 0 which are typically for a cube crystal structure.62 This adherence to the stability criteria is crucial when considering these materials for fabrication of devices. Additionally, the bulk modulus (B) has been determined using the formula B = (C11 + 2C12)/3 based on the calculated elastic constants63 and the resulting values align well with the bulk modulus (B0) estimates through volume optimization plot. The Poisson ratio (ν) with a value exceeding 0.26 and the Pugh ratio (B0/G) surpassing 1.75 serve as matrices to distinguishing between brittle and ductile behavior of materials, as detailed in ref. 64. Table 1 shows that our materials exhibit brittle behavior as determined by the computed values of ν and B0/G. Furthermore, anisotropy factor denoted as A and calculated by using the formula A = 2C44/(C11 − C12) represents another parameter characterizing the directional properties of the materials under examination. The unit value of A indicates isotropic materials whereas values greater or smaller than unity suggest anisotropic behavior. Clearly our material exhibits anisotropic properties.
| C11 | C12 | C44 | B0 | G | Y | B0/G | ν | A | |
|---|---|---|---|---|---|---|---|---|---|
| Cs2AgInCl6 | 89.44 | 11.18 | 14.08 | 37.26 | 21.51 | 54.12 | 1.73 | 0.26 | 0.36 |
| Cs2AgIn0.75Mn0.25Cl6 | 55.28 | 24.01 | 28.55 | 34.43 | 22.42 | 55.26 | 1.54 | 0.23 | 0.31 |
| Cs2AgInBr6 | 81.28 | 5.50 | 10.57 | 30.76 | 18.18 | 45.57 | 1.69 | 0.25 | 0.28 |
| Cs2AgIn0.75Mn0.25Br6 | 57.52 | 11.48 | 16.23 | 26.82 | 18.67 | 45.47 | 1.44 | 0.22 | 0.24 |
3.2 Electronic studies
Fig. 3 depicts the computed band structures including spin polarization for Cs2AgIn1−xMnxCl/Br6 (x = 0.25) using the optimized lattice constant. The precise investigations regarding the electronic characteristics of Cs2AgIn1−xMnxCl/Br6 compounds were accomplished through well-known mBJ functional. Zero energy Fermi level was adopted as a reference point. It is obvious that the conduction band (CB) minima represent the direction of X-symmetry, while the valence band (VB) minima represent the direction of Γ-symmetry that traverses Fermi level in spin-up (↑) mode. Conversely, the symmetric position of CB minima and VB minima is noticed at Γ-symmetry direction in the spin-down (↓) channel as well as inside the Fermi level. The presence of the mentioned exchange mechanism in these materials led to an insulating bandgap. Therefore, one can say that Half Metallic Ferromagnets (HFM) comprise spin-down channel, insulating bandgap, and spin-up channel with a metallic character.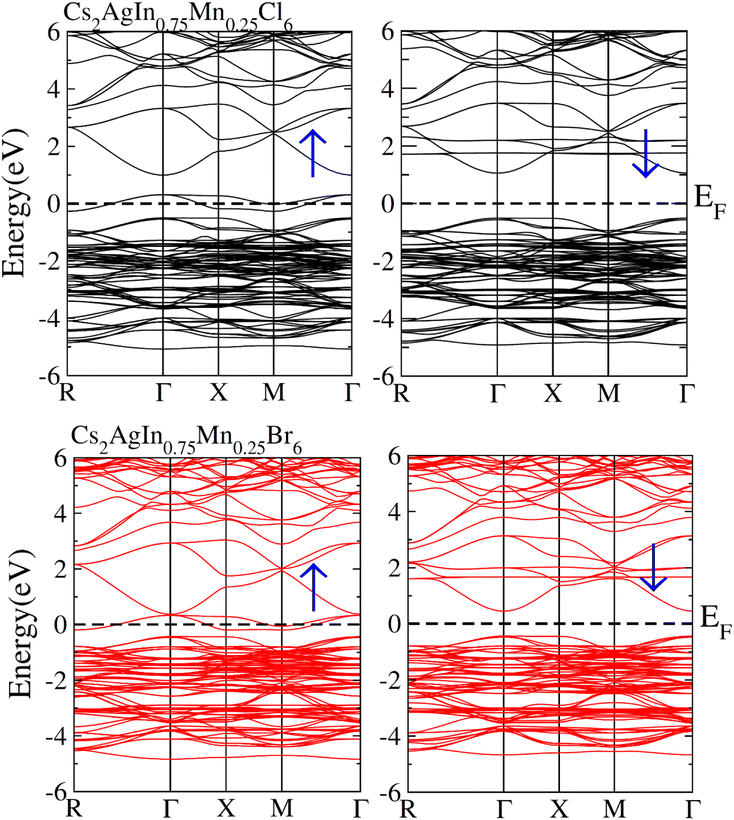 | ||
| Fig. 3 Calculated spin polarized band structures plot for FM Cs2AgIn0.75Mn0.25Cl6 and (FM) Cs2AgIn0.75Mn0.25Br6. | ||
Table 3 presents our calculated results regarding spin down bandgap revealing that investigated spinels show emissions in the visible portion of the electromagnetic spectrum, thus suitable for solar cell applications. A similar trend has been observed for computed total density of states (TDOS) as depicted in Fig. 4–6. The calculations regarding TDOS and PDOS were executed to study exchange energies behavior and the HMF nature of materials. Spin polarizability (P) was calculated using DOS employing the following relation:65
| Doped DPs | ↓Eg (eV) | gh (eV) | μB (total) | μB (Mn) | μB (Cs) | μB (Ag) | μB (In) | μB (Cl/Br) |
|---|---|---|---|---|---|---|---|---|
| Cs2AgIn0.75Mn0.25Cl6 | 1.7 | 0.5 | 4.000 | 4.009 | 0.0003 | −0.042 | −0.002 | 0.0005 |
| Cs2AgIn0.75Mn0.25Br6 | 1.0 | 0.4 | 4.000 | 4.015 | 0.0001 | −0.027 | −0.001 | 0.0006 |
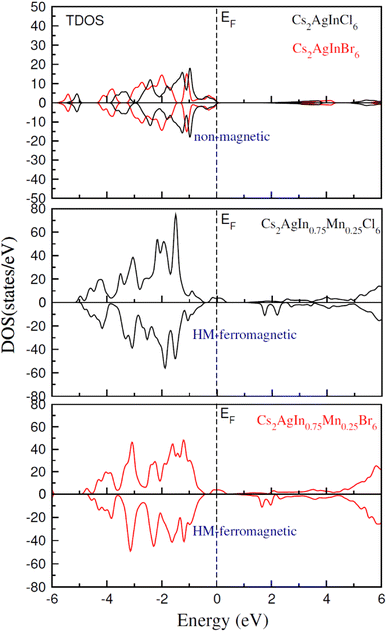
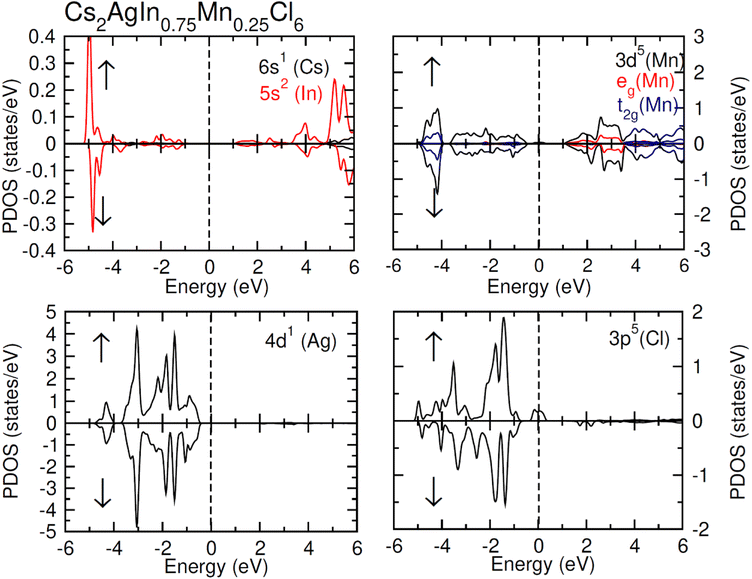
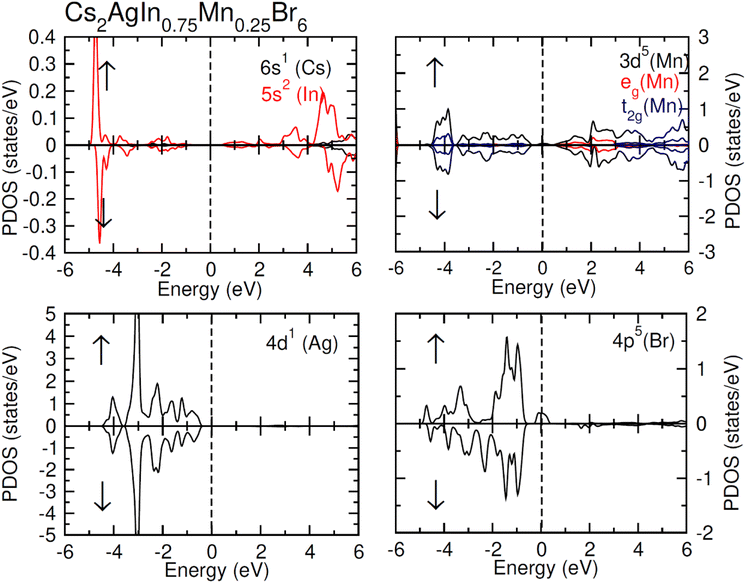
TDOS and PDOS illustrated in Fig. 4–6 were computed using modified Becke–Johnson (mBJ) potential and correspondingly describe the atomic plus orbital level configuration of different band states. For un-substituted materials (Cs2AgInCl/Br6) complete absence of spin-splitting between spin (↑) and spin (↓) states has been observed as depicted in Fig. 4(a). However, the substitution of Mn2+ ions triggered the spin-splitting process by simultaneous shifting of VBM towards Ef and CBM away from Ef towards the high energy terminal. But, for spin-down channel, a converse trend is observed as obvious in Fig. 4(b) and (c). Furthermore, the probability of exhibiting half-metallic nature can be disregarded, and it can be assumed that compounds display semiconducting properties as in both spin channels, no states are possible at Ef, and Ef lies inside the band gap. It is quite clear from PDOS plots, as demonstrated in Fig. 5 and 6, that the lower portion of VB, located at about −5 eV, is narrow and mostly contains Ag-d states having minor contributions from Cl/Br-s states. Hybridization of Mn-3d states with Ag-d and Cl/Br-p states constitute the upper portion of VB.
The replacement of In2+ ions with Mn2+ ions creates Mn-3d states that undergo a splitting process through the crystal field to yield doubly degenerated (eg) and triply degenerated (t2g) states. The semiconducting nature of compounds is also verified through the spin-flip approach describing the inevitable provision of band gap energy for an electron to jump from the majority band to the minority band. The origin of ferromagnetism can be elucidated through different methods including the Stoner model, Zener model (p–d hybridization), and double exchange. Our results do not support a half-metallic nature as the majority of d-band above VB remains below EF. So, free carrier-mediated ferromagnetic interactions cannot be the probable cause of ferromagnetism. Therefore, the direct exchange interactions involving the hybridization of impurity d-states with Cl/Br p-states in spin-up and spin-down band (exchange split) are considered as sources of ferromagnetism in investigated compounds as illustrated in Fig. 4. The partial DOS for Cs2AgIn0.75Mn0.25Cl6 exhibits distinct d-states in both spin channels and comparably sharp degenerated t2g and eg states (see Fig. 5), but in the case of Cs2AgIn0.75Mn0.25Br6 an increase in broadness and decrease in sharpness of both degenerated states has been identified (see Fig. 6).
3.3 Absorption spectra
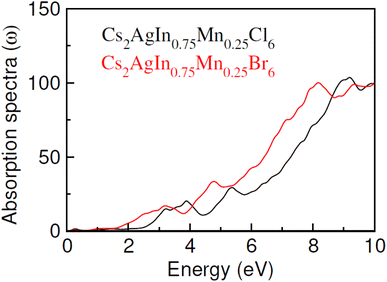
Optical characteristics of Mn-doped Cs2AgInCl/Br6 have been investigated to explore potential applications in optoelectronics. The calculated absorption spectra against incident photon energy (0 to 10 eV) denoted as α(ω) and depicted in Fig. 7, serves as a useful indicator of the materials absorbent properties. The energy range within which α(ω) become negligible is indicative of the transparency of the materials to incident energy. The absorption edge is the critical threshold at which the absorption of intruding energy begins. The absorption edge of Cs2AgIn0.75Mn0.25Cl/Br6 is observed at 2.0 eV and 1.4 eV, respectively in the current study. Moreover, the difference between absorption edge and the calculated band gap can be clarified by the fact that we define the energy at which substantial absorption becomes clearly evident as the absorption edge, this not accounting for the minor absorptions linked to fundamental band gaps. The absorption exhibits a linear increase with energy after this edge point, culminating at a maximum point. Additionally, when the X-ions shift from Cl to Br and in Cs2AgIn0.75Mn0.25Cl/Br6, a red shift in the absorption edge is observed, accompanied by predominant absorption, which is a result of the widened energy band gap.3.4 Magnetic studies
The ferromagnetic character of studied Mn substituted DPs (Cs2AgInCl/Br6) originated because the presence of magnetic substituted ions initiates strong exchange interactions between p-states of anions and d-states of substituted cations by way of p–d hybridization causing edge splitting of VB and CB. The Hamiltonian (H) in mean field theory (MFT) can be expressed in terms of cations content (N0), p–d exchange factor (β), free hole spins (s), and Mn spins (S), as:66,67| H = −N0βsS | (1) |
The above relation was employed to compute exchange constants N0α and N0β that respectively account for the strength of s–d and p–d interactions that can be expressed as:
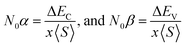 | (2) |
The terms x and 〈S〉 symbolize the concentration and mean magnetic moment of Mn2+ ions. While ΔEC and ΔEV denote band edge splitting associated with CB and VB, respectively. The negative signs of computed exchange constants (N0α and N0β) reveal the ferromagnetic nature of s–d and p–d interactions. Moreover, ferromagnetism is favored by Mn-doped Cs2AgInCl/Br6 compounds owing to a greater magnitude of N0β compared to N0α. Further investigations regarding the ferromagnetic behavior of probed DPs were done through direct exchange constant Δx(d) deduced by the equation Δx(d) = d↓ − d↑ with the help of Fig. 5, and then compared with crystal field energy (Ecrys = dt2g − deg). One can deduce from Fig. 5 and Table 4 that Δx(d) ≫ Ecrys that in turn authenticate the vital role of Ecrys in the band splitting procedure and hence stabilize the ferromagnetic state.
| Parameters | Cs2AgIn0.75Mn0.25Cl6 | Cs2AgIn0.75Mn0.25Br6 |
|---|---|---|
| Ecrys | 2.4 | 2.0 |
| Δx(d) | 6.4 | 5.8 |
| Δx(pd) | −0.6 | −0.5 |
| N0α | 0.7 | 0.5 |
| N0β | −0.30 | −0.25 |
The measured value of the total magnetic moment was found to be 3 μB. The local magnetic moments of various ions present in the structure of studied compounds (i.e. Mn2+, In3+, Ag1+, Cs+ and Cl1−/Br1−) are presented in Table 3. It can be seen that Mn2+ ions provide the main contribution to mtotal, whereas a small contribution is furnished by In3+ and Cl/Br ions. The variations in the magnetic moment of (In, Cl/Br) sites at the expense of the magnetic moment of Mn sites were attributed to exchange interactions between Mn-3d and Cl/Br-p states. However, the presence of various exchange coupling among various lattice sites leads to the transfer of magnetic moments towards nonmagnetic sites.
3.5 Thermoelectric properties
The transport (electronic and thermoelectric) features of spin-polarized materials play a key role in designing spintronic and thermoelectric appliances.68,69 Thermoelectric devices can convert heat into electrical energy using temperature divergence, and their efficiency can be determined through thermoelectric parameters including Seebeck coefficient (S), power factor (σS2/τ), thermal (κ/τ) and electrical conductivity (σ/τ). The thermoelectric performance of Cs2AgIn1−xMnxCl/Br6 (x = 0.00, 0.25) double perovskites have been studied for their promising use in thermoelectric devices. The calculated results regarding the mentioned thermoelectric parameters (S, σS2/τ, κ/τ, σ/τ), within the temperature extent 200–800 K, are presented in Fig. 8a–d and 9a–d.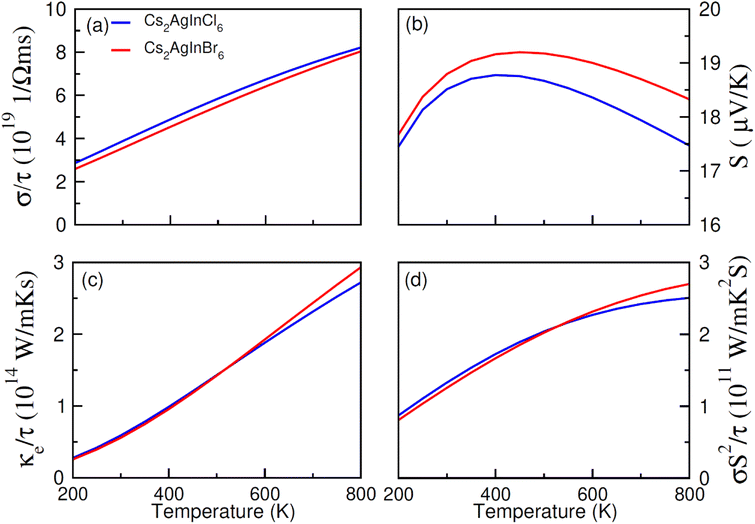 | ||
| Fig. 8 The calculated (a) electrical (σ/τ), (b) Seebeck coefficient (S), (c) thermal (ke/τ) conductivities, (d) and power factor for NM Cs2AgInCl/Br6 against temperatures (200 K–800 K). | ||
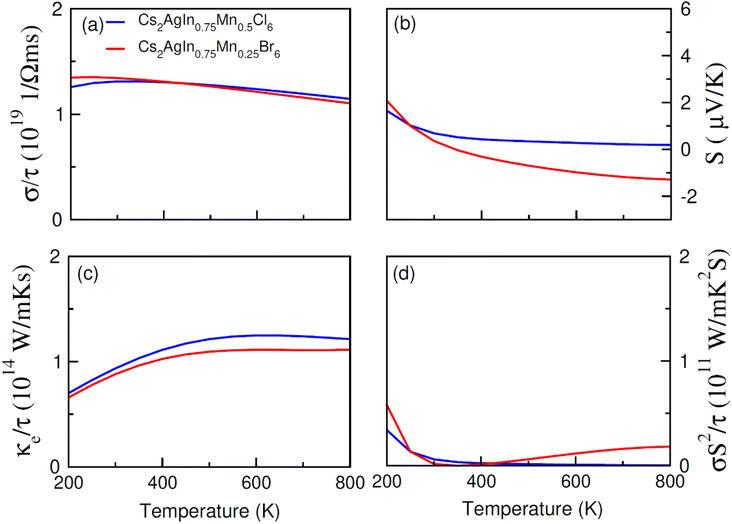 | ||
| Fig. 9 The calculated (a) electrical (σ/τ), (b) Seebeck coefficient (S), (c) thermal (ke/τ) conductivities, (d) and power factor for FM Cs2AgIn0.75Mn0.25Cl6 against temperatures (200–800 K). | ||
An increase in electrical conductivity takes place due to the charges' flow and it leads to a forward current. For Cs2AgIn1−xMnxCl/Br6 (x = 0.25) ferromagnetic compounds, a decrease in σ/τ with a rise of temperature up to 800 K has been observed. However, the rate of increment of σ/τ for Cs2AgIn1−xMnxCl6 (x = 0.00, 0.25) compounds remained comparatively smaller than Cs2AgIn1−xMnxBr6 (x = 0.00, 0.25), that can be observed in Fig. 8a and 9a. The interactions of charge carriers with lattice vibrations in the form of phonon waves give rise to thermal conductivity (κ/τ). We have studied only the electronic part of thermal conductivity (κe/τ) due to deficiency associated with the BoltzTrap code as it is based on the classical transport model.
Thermal conductivity can be calculated by using the relation between the rate of heat flow and temperature gradient as described by Fourier law given by the relation: q = −κdT/dx, here, q stands for heat transfer rate, dT/dx denotes temperature gradient, and κ is coefficient of κe/τ. It is found that for DPs Cs2AgIn1−xMnxCl/Br6 (x = 0.00, 0.25) thermal conductivity increased gradually up to 800 K indicating the active and dynamic contribution of charge carriers for energy transportation during the whole temperature range. It is obvious from Fig. 8c and 9c that at 800 K Cs2AgIn1−xMnxCl6 (x = 0.0, 0.25) compounds showed the lowest value of thermal conductivity but the highest value was observed for Cs2AgIn1−xMnxBr6 (x = 0.0, 0.25) compounds. It is deduced from Weidman–Franz law (LT = κ/σ) that compounds exhibiting smaller κ/τ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ/τ ratio are considered as good for thermoelectric applications. The computed ratio (κ/τ
σ/τ ratio are considered as good for thermoelectric applications. The computed ratio (κ/τ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) σ/τ) for Cs2AgIn1−xMnxCl/Br6 (x = 0.00, 0.25) compounds is about 10−6 revealing the capability of study materials to be utilized in thermoelectric devices.
σ/τ) for Cs2AgIn1−xMnxCl/Br6 (x = 0.00, 0.25) compounds is about 10−6 revealing the capability of study materials to be utilized in thermoelectric devices.
To measure the temperature gradient, the Seebeck coefficient (S) between two incompatible metals was computed. The analysis of calculated S values (at 200 K) revealed that for Cs2AgIn1−xMnxBr6 (x = 0.00, 0.25) compounds, the Seebeck coefficient is relatively small as compared to Cs2AgIn1−xMnxCl6 (x = 0.00, 0.25) as depicted in Fig. 8b and 9b. For both series of DPs (Cs2AgIn1−xMnxCl6 and Cs2AgIn1−xMnxBr6) investigations also showed the convergence of S at 250 K and then divergence was observed up to 800 K. Furthermore, the maximum S value was found for Cs2AgIn1−xMnxBr6 (x = 0.00, 0.25), while the minimum was realized for Cs2AgIn1−xMnxCl6 (x = 0.00, 0.25). Additionally, the observation regarding the negative Seebeck coefficient for both DP series exhibits their n-type behavior.
Power factor (S2σ/τ) may be used to deduce thermoelectric efficiency; however, because thermal conductivity is not taken into account, the calculated values may be overestimated. However, our discussed results showed accurate trends in this regard. For both compounds, Cs2AgIn1−xMnxCl/Br6 (x = 0.25), the value of power factor showed an increasing tendency up to 400 K and decreased afterward as depicted in Fig. 9d. The observed decrease in power factor at higher temperatures can be attributed to negative Seebeck coefficient (S).
4. Conclusion
This study was mainly focused on clarifying the physical properties of Cs2AgIn1−xMnxCl/Br6 double perovskite materials with specific Mn contents (i.e. x = 0.00, 0.25). We used the Wien2k and BoltzTraP software to investigate the electrical transport and ferromagnetic behavior of these DPs. Optimization process revealed that the FM state exhibits maximum free energy compared to NM and AFM states. Calculated values of Curie temperature of Mn contents exhibit a notably high Curie temperature (TC). It was observed that Mn substitution led to a decrease in B0 and an increase of a0 in the FM phase. Interestingly, our calculated values of a0 for un-substituted DPs (Cs2AgInCl/Br6) agree quite well with experimental values. These computed elastic constants satisfy the mechanical stability criteria and materials exhibit brittle behavior as determined by the computed values of ν and B0/G. Additionally, DOS studies and spin-polarized band structure analysis designated the half-metallic ferromagnetic character of the studied DPs. Analysis of the density of states (PDOS and TDOS) for Cs2AgIn1−xMnxCl/Br6 (x = 0.25) yielded exchange interactions, and strong hybridization validated the ferromagnetic nature caused by electronic spin. Moreover, the difference between absorption edge and the calculated band gap can be justified. Furthermore, our computed exchange energy values revealed a higher direct energy (Δx(d)) value compared to the indirect energy (Δx(pd)) value, which consequently support the ferromagnetism. Moreover, it was noticed that the decrease in energy associated with the spin-down channel was attributed to N0β as well as to the observed red shift in Δx(pd). Notably, the DPs Cs2AgInCl/Br6 revealed higher thermoelectric conductivity values compared to Cs2AgIn1−xMnxCl/Br6 (x = 0.25), as inferred from measurements of the κ/σ ratio and the power factor.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Researchers Supporting Project number (RSP2024R118), King Saud University, Riyadh, Saudi Arabia.References
- Q. A. Akkerman, G. Rainò, M. V. Kovalenko and L. Manna, Nat. Mater., 2018, 17, 394–405 CrossRef CAS PubMed.
- M. Saliba, T. Matsui, J.-Y. Seo, K. Domanski, J.-P. Correa-Baena, M. K. Nazeeruddin, S. M. Zakeeruddin, W. Tress, A. Abate, A. Hagfeldt and M. Gratzel, Energy Environ. Sci., 2016, 9, 1989–1997 RSC.
- C. N. Savory, A. Walsh and D. O. Scanlon, ACS Energy Lett., 2016, 1, 949–955 CrossRef CAS PubMed.
- Z. Huang, P. Luo, S. Jia, H. Zheng and Z. Lyu, J. Phys. Chem. Solids, 2022, 167, 110746 CrossRef CAS.
- S. Mu, Q. Liu, P. Kidkhunthod, X. Zhou, W. Wang and Y. Tang, Nat. Sci. Rev., 2020, 8, 178 CrossRef PubMed.
- Z. Deng, F. Wei, S. Sun, G. Kieslich, A. K. Cheetham and P. D. Bristowe, J. Mater. Chem. A, 2016, 4, 12025–12029 RSC.
- Z. Huang, P. Luo, Q. Wu and H. Zheng, J. Phys. Chem. Solids, 2022, 161, 110479 CrossRef CAS.
- G. Volonakis, M. R. Filip, A. A. Haghighirad, N. Sakai, B. Wenger, H. J. Snaith and F. Giustino, J. Phys. Chem. Lett., 2016, 7, 1254–1259 CrossRef CAS PubMed.
- X. Li, S. Aftab, S. Hussain, F. Kabir, A. M. A. Henaish, A. G. Al-Sehemi and G. Koyyada, Dimensional diversity (0D, 1D, 2D, and 3D) in perovskite solar cells: exploring the potential of mixed-dimensional integrations, J. Mater. Chem. A, 2024, 12, 4421–4440 RSC.
- L. K. Ono, E. J. Juarez-Perez and Y. Qi, ACS Appl. Mater. Interfaces, 2017, 9, 30197–30246 CrossRef CAS PubMed.
- A. Wang, X. Yan, M. Zhang, S. Sun, M. Yang, W. Shen, X. Pan, P. Wang and Z. Deng, Chem. Mater., 2016, 28, 8132–8140 CrossRef CAS.
- J. Guo, B. He, Y. Han, H. Liu, J. Han, X. Ma, J. Wang, W. Gao and W. Lü, Nano Lett., 2024, 24, 1114–1121 CrossRef CAS PubMed.
- J. Zhang, Y. Yang, H. Deng, U. Farooq, X. Yang, J. Khan, J. Tang and H. Song, ACS Nano, 2017, 11, 9294–9302 CrossRef CAS PubMed.
- S. Fu, H. Wu, W. He, Q. Li, C. Shan, J. Wang and C. Hu, Conversion of Dielectric Surface Effect into Volume Effect for High Output Energy, Adv. Mater., 2023, 35, 2302954 CrossRef CAS PubMed.
- T. C. Jellicoe, J. M. Richter, H. F. J. Glass, M. Tabachnyk, R. Brady, S. E. Dutton, A. Rao, R. H. Friend, D. Credgington, N. C. Greenham and M. L. Böhm, J. Am. Chem. Soc., 2016, 138, 2941−–2944 CrossRef CAS PubMed.
- X.-G. Zhao, J.-H. Yang, Y. Fu, D. Yang, Q. Xu, L. Yu, S.-H. Wei and L. Zhang, J. Am. Chem. Soc., 2017, 139, 2630–2638 CrossRef CAS PubMed.
- L. R. Morss, M. Siegal, L. Stenger and N. Edelstein, Inorg. Chem., 1970, 9, 1771–1775 CrossRef CAS.
- F. Wei, Z. Deng, S. Sun, F. Xie, G. Kieslich, D. M. Evans, M. A. Carpenter, P. D. Bristowe and A. K. Cheetham, Mater. Horiz., 2016, 3, 328–332 RSC.
- Z. Deng, F. Wei, F. Brivio, Y. Wu, S. Sun, P. D. Bristowe and A. K. Cheetham, J. Phys. Chem. Lett., 2017, 8, 5015–5020 CrossRef CAS PubMed.
- A. H. Slavney, T. Hu, A. M. Lindenberg and H. I. Karunadasa, J. Am. Chem. Soc., 2016, 138, 2138–2141 CrossRef CAS PubMed.
- E. T. McClure, M. R. Ball, W. Windl and P. M. Woodward, Chem. Mater., 2016, 28, 1348–1354 CrossRef CAS.
- M. R. Filip, S. Hillman, A. A. Haghighirad, H. J. Snaith and F. Giustino, J. Phys. Chem. Lett., 2016, 7, 2579–2585 CrossRef CAS PubMed.
- Z. Huang, Y. Zhang, H. Wang and J. Li, Appl. Phys. Lett., 2023, 123, 103501 CrossRef CAS.
- Y. Bekenstein, J. C. Dahl, J. Huang, W. T. Osowiecki, J. K. Swabeck, E. M. Chan, P. Yang and A. P. Alivisatos, Nano Lett., 2018, 18, 3502–3508 CrossRef CAS PubMed.
- X. Zhang, Y. Tang, F. Zhang and C. Lee, Adv. Energy Mater., 2016, 6, 1502588 CrossRef.
- B. Yang, et al., Angew. Chem., Int. Ed., 2018, 57, 5359–5363 CrossRef CAS PubMed.
- M. Wang, C. Jiang, S. Zhang, X. Song, Y. Tang and H. Cheng, Reversible calcium alloying enables a practical room-temperature rechargeable calcium-ion battery with a high discharge voltage, Nat. Chem., 2018, 10, 667–672 CrossRef CAS PubMed.
- W. Gao, et al., ChemPhysChem, 2018, 19, 1696–1700 CrossRef CAS PubMed.
- H.-J. Feng, W. Deng, K. Yang, J. Huang and X. C. Zeng, J. Phys. Chem. C, 2017, 121, 4471–4480 CrossRef CAS.
- W. Meng, X. Wang, Z. Xiao, J. Wang, D. B. Mitzi and Y. J. Yan, Phys. Chem. Lett., 2017, 8, 2999–3007 CrossRef CAS PubMed.
- S. Ye, J. Zhu, S. Zhu, Y. Zhao, M. Li, Z. Huang and J. He, Design Strategies for Perovskite-Type High-Entropy Oxides with Applications in Optics, ACS Appl. Mater. Interfaces, 2023, 15, 47475–47486 CrossRef CAS PubMed.
- L.-Z. Lei, Z.-F. Shi, Y. Li, Z.-Z. Ma, F. Zhang, T.-T. Xu, Y.-T. Tian, D. Wu, X.-J. Li and G.-T. Du, J. Mater. Chem. C, 2018, 6, 7982–7988 RSC.
- Y. Zhao, J. Jing, L. Chen, F. Xu and H. Hou, Current Research Status of Interface of Ceramic-Metal Laminated Composite Material for Armor Protection, Acta Metall. Sin., 2021, 57, 1107–1125 CAS.
- A. Jain, O. Voznyy and E. H. Sargent, J. Phys. Chem. C, 2017, 121, 7183–7187 CrossRef CAS.
- X.-G. Zhao, D. Yang, Y. Sun, T. Li, L. Zhang, L. Yu and A. Zunger, J. Am. Chem. Soc., 2017, 139, 6718–6725 CrossRef CAS PubMed.
- R. Yang, W. Yao, L. Zhou, F. Zhang, Y. Zheng, C. Lee and Y. Tang, Secondary Amines Functionalized Organocatalytic Iodine Redox for High-Performance Aqueous Dual-Ion Batteries, Adv. Mater., 2024, 2314247 CrossRef PubMed.
- J. Luo, S. Li, H. Wu, Y. Zhou, Y. Li, J. Liu, J. Li, K. Li, F. Yi, G. Niu and J. Tang, ACS Photonics, 2018, 5, 398–405 CrossRef CAS.
- S. Guan, J. Zhou, S. Sun, Q. Peng, X. Guo, B. Liu and Y. Tang, Adv. Funct. Mater., 2024, 2314890 CrossRef.
- T. Wei, Y. Zhou, C. Sun, X. Guo, S. Xu, D. Chen and Y. Tang, Nano Res., 2023, 1–7 Search PubMed.
- A. De, N. Mondal and A. Samanta, Nanoscale, 2017, 9, 16722–16727 RSC.
- R. Buonsanti and D. Milliron, J. Chem. Mater., 2013, 25, 1305–1317 CrossRef CAS.
- A. K. Guria, S. K. Dutta, S. D. Adhikari and N. Pradhan, ACS Energy Lett., 2017, 2, 1014–1021 CrossRef CAS.
- H. Yang, S. Santra and P. H. Holloway, J. Nanosci. Nanotechnol., 2005, 5, 1364–1375 CrossRef CAS PubMed.
- K. Xu and A. Meijerink, Chem. Mater., 2018, 30, 5346–5352 CrossRef CAS PubMed.
- C. Jiang, Z. Deng, B. Liu, J. Li, Z. Han, Y. Ma and Y. Ma, ACS Photonics, 2022, 9, 3089–3093 CrossRef CAS.
- R. N. Bhargava, D. Gallagher, X. Hong and A. Nurmikko, Phys. Rev. Lett., 1994, 72, 416–419 CrossRef CAS PubMed.
- T. Xin, S. Tang, F. Ji, L. Cui, B. He, X. Lin and M. Ferry, Acta Mater., 2022, 239, 118248 CrossRef CAS.
- A. Nag, S. Chakraborty and D. D. Sarma, J. Am. Chem. Soc., 2008, 130, 10605–10611 CrossRef CAS PubMed.
- X. Chen and T. Yu, Molecules, 2023, 28, 8087 CrossRef CAS PubMed.
- P. Blaha, K. Schwarz, G. Madsen, D. Kvasnicka and J. Luitz, An Augmented Plane Wave Plus Local Orbital Program for Calculating Crystal Properties, Vienna University of Technology, Vienna, Austria, 2001 Search PubMed.
- Z. Wu and E. R. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235116 CrossRef.
- F. Tran and P. Blaha, Phys. Rev. Lett., 2009, 102, 226401 CrossRef PubMed.
- X. Chen, Inorganics, 2023, 11, 215 CrossRef CAS.
- G. K. Madsen and D. J. Singh, Comput. Phys. Commun., 2006, 175, 67 CrossRef CAS.
- F. Murnaghan, Proc. Natl. Acad. Sci., 1944, 30, 244–247 CrossRef CAS PubMed.
- G. Xing, N. Mathews, S. Sun, S. S. Lim, Y. M. Lam, M. Grätzel, S. Mhaisalkar and T. C. Sum, Science, 2013, 342, 344 CrossRef CAS PubMed.
- Y. Liu, I. J. Cleveland, M. N. Tran and E. S. Aydil, J. Phys. Chem. Lett., 2023, 14(12), 3000–3006 CrossRef CAS PubMed.
- P. K. Lam, M. L. Cohen and G. Martinez, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 9190 CrossRef PubMed.
- S. D. Reddy, M. Reddy, N. Raok, K. Gunasekhar and S. P. Reddy, J. Optoelectron. Adv. Mater., 2007, 9, 3743–3746 Search PubMed.
- G. S. Rushbrooke and P. J. Wood, On the Curie points and high temperature susceptibilities of Heisenberg model ferromagnetics, Mol. Phys., 1958, 1, 257–283 CrossRef CAS.
- B. Cai, X. Chen, M. Xie, S. Zhang, X. Liu, J. Yang, W. Zhou, S. Guo and H. Zeng, A class of Pb-free double perovskite halide semiconductors with intrinsic ferromagnetism, large spin splitting and high Curie temperature, Mater. Horiz., 2018, 5, 961–968 RSC.
- M. Mattesini, R. Ahuja and B. Johansson, Cubic Hf3N4 and Zr3N4: a class of hard materials, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68(18), 184108 CrossRef.
- N. Wang, W.-Y. Yu, B.-Y. Tang, L.-M. Peng and W.-J. Ding, Structural and mechanical properties of Mg17Al12 and Mg24Y5 from first-principles calculations, J. Phys. D Appl. Phys., 2008, 41(19), 195408 CrossRef.
- W. Voigt, Reprinted (1928) with an additional appendix, Leipzig, Teubner, New York, Johnson Reprint, 1966.
- T. T. Q. Hoa, N. D. The, S. McVitie, N. H. Nam, L. V. Vu, T. D. Canh and N. N. Long, Opt. Mater., 2011, 33, 308–314 CrossRef CAS.
- B. Yang, H. Wang, M. Zhang, F. Jia, Y. Liu and Z. Lu, Chem. Eng. J., 2023, 476, 146834 CrossRef CAS.
- Z.-Z. Luo, S. Cai, S. Hao, T. P. Bailey, Y. Luo, W. Luo and Y. Yu, Extraordinary role of Zn in enhancing thermoelectric performance of Ga-doped n-type PbTe, Energy Environ. Sci., 2022, 15, 368–375 RSC.
- M. Sajjad, Q. Mahmood, N. Singh and J. A. Larsson, Ultralow lattice thermal conductivity in double perovskite Cs2PtI6: a promising thermoelectric material, Appl. Energy Mater., 2020, 3(11), 11293–11299 CrossRef CAS.
- Y. Wang, J. Zhu, M. Li, G. Shao, H. Wang and R. Zhang, Thermal properties of high-entropy RE-disilicates controlled by high throughput composition design and optimization, Mater. Des., 2023, 236, 112485 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |