Open Access Article
Open Access ArticleFirst-principles study for quasi-static growth model in FeAl intermetallic based on Wulff cluster model
Lin Songa,
Anchen Shaoa,
Dong Lid,
Xuelei Tianb,
Zhuhui Qiao *ac,
Huaguo Tang*ac and
Xiaohang Lin
*ac,
Huaguo Tang*ac and
Xiaohang Lin *b
*b
aShandong Laboratory of Advanced Materials and Green Manufacturing at Yantai, Yantai, 264006, People's Republic of China
bKey Laboratory for Liquid-Solid Structural Evolution and Processing of Materials, Ministry of Education, Shandong University, Jinan 250061, People's Republic of China. E-mail: lxh12345@sdu.edu.cn
cState Key Laboratory of Solid Lubrication, Lanzhou Institute of Chemical Physics, Chinese Academy of Sciences, Lanzhou, 730000, People's Republic of China. E-mail: laotang@licp.cas.cn; zhqiao@licp.cas.cn
dShandong Ludian Line Equipment Co. Ltd, China
First published on 8th March 2024
Abstract
In order to investigate the structure of FeAl mesoscopic crystals segregating in liquid state alloys, we have determined their equilibrium structures (Wulff shape) based on the Wulff cluster model. For non-stoichiometric surface terminations, the chemical environment is taken into account through the chemical potential of the constituents. In this case, different cluster shapes change as a function of the chemical environment. In order to model the growth process in more detail, we propose a quasi-static growth model based on the sequential addition of (sub-)monolayers in the most favorable surface directions. Thus, a sequence of different Wulff shapes results in the growth process, as illustrated for the FeAl intermetallic compound. This model is proved preliminarily by calculating the concentration trend of Al/Fe atoms on both Al-terminated and Fe-terminated surfaces, and by simulating the most stable layer adsorbed on these two surfaces. This model might be helpful in analyzing the growth processes including nucleation barriers during nucleation processes theoretically.
1. Introduction
Solidification processes are necessary and important for most alloy manufacturing. The solidification processes, especially the nucleation stage, have a significant influence on the properties of the alloys including mechanical properties, electrochemical properties, catalytic properties, etc.1–3 In short, nucleation is the process in which the nanoparticles grow gradually and reach the critical nucleation radius under certain supercooling conditions in alloy melts. Obviously, the structure and growth process of nanoparticles in melts, as an origin, will directly affect the nucleation process.The ways to research the melts' properties could mainly be divided into experimental and theoretical methods. For experimental ones, high temperature X-ray diffraction (HTXRD)4,5 and neutron diffraction6 were adopted to explore the structures of metallic melts.4–18 The theoretical methods, including molecular dynamics (MD),14–18 phase fields, cellular automata (CA) and first principle simulation are used to study the crystallization and growth process after nucleation.19–22 Unfortunately, due to the limitation of high temperature, the behavior of nanoparticles in melts at the atomic level, especially the growth process, is still unclear.
In previous research, we proposed a model (Wulff cluster model) to investigate the ordering structures in metallic melts. It uses the most probable structure as the equivalent structure to describe the short-range ordering distribution of metallic melts under the thermal equilibrium state. In this model, the equivalent structure is determined by the Wulff construction with the crystal structures inside. The simulated XRD results of the model show good agreement with the high-temperature X-ray diffraction (HTXRD) experiments, which indicates that it is a reasonable equivalent model to describe pure metals, binary homogeneous alloys, eutectic alloys, and intermetallic compound melt systems.23–26 This model gives us a chance to further investigate the growth processes, especially the processes before nucleation.
The FeAl intermetallic shows many attractive properties like high strength, excellent corrosion, low density at high temperature and economical price.27–30 Exactly these fantastic characteristics make the FeAl intermetallic a potential candidate for high temperature alloys. Moreover, FeAl which has a wide range of phase diagram components is one of the simplest intermetallic compounds. Therefore, it was selected to explore the structure of nanoparticles in the melt before nucleation and the effect of external environment on the structure growth mechanism. In addition, this paper attempted to explain the mechanism/processes for the growth order of the FeAl compound before nucleation.
Recently, first principle calculations based on density functional theory was widely used to investigate the structures and other properties of nano-particles at the atomic level.31,32 In this work, DFT calculations were applied to study the equilibrium shape as a function of the chemical environment. A quasi-static model based on the chemical potential correction was proposed to determine the evolution of the growth morphology of nanoparticles. The non-equilibrium growth process is approximated to a series of equilibrium nodes to better understand the growth process. Finally, the mechanism/processes for the FeAl intermetallic growth order is given by calculation.
2. Theoretical calculations
2.1 Numerical simulation details
All DFT33,34 total energy calculations in this paper have been performed using the Vienna Ab initio Simulation Package (VASP) within the generalized gradient approximation (GGA) to describe the exchange–correlation effects, employing the Perdew, Burke and Ernzerhof (PBE) exchange–correlation functional.35–38 The ionic cores are represented by projector augmented wave (PAW) potentials39 as constructed by Kresse and Joubert.40 It has already been proved to give reasonable results of Fe–Al system with enough accuracy. The structures were optimized until atomic forces were converged to 0.01 eV Å−1. A 7 × 7 × 1 k-point sampling is chosen for all calculations based on careful convergence tests.41 The plane wave cut-off energy was set to 400 eV. Moreover, due to magnetic of iron atoms, the spin polarization has been taken into considered.2.2 Surface models
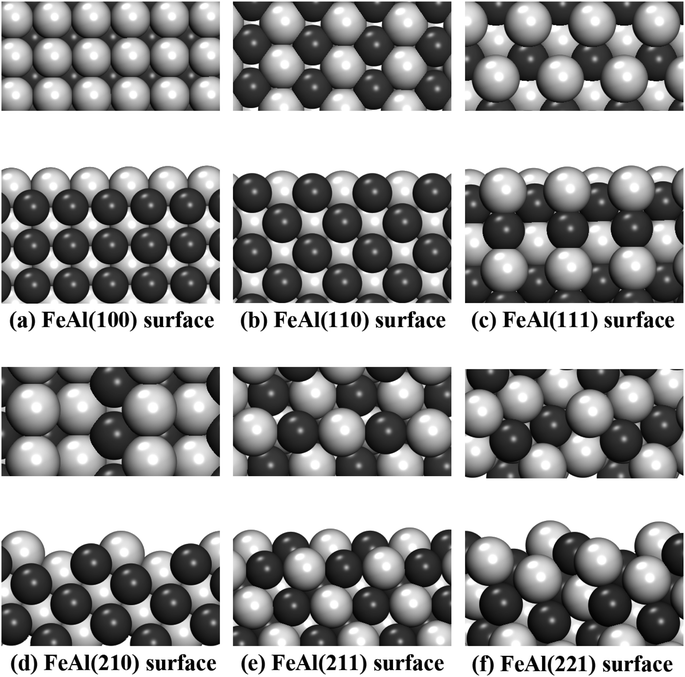
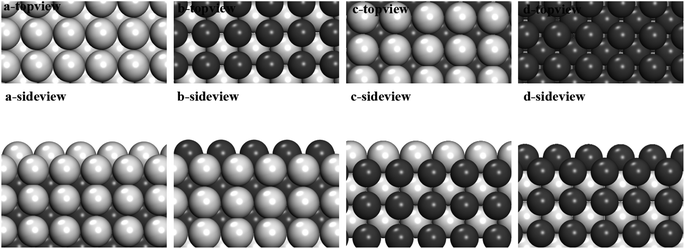
In this work, different types of low-index surfaces have been built, including FeAl(100), FeAl(110), FeAl(111), FeAl(210), FeAl(211) and FeAl(221) surfaces (Fig. 1). The calculation method of surface energy is a typical slab model. The thickness of vacuum layer is more than 20 Å to ensure the accuracy of surface calculation results. Both Fe-terminated and Al-terminated of FeAl are considered.For elemental materials, surface energies (ESurf) are defined according to
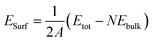 | (1) |
It can be seen from Fig. 1, the Fe and Al atoms in some stable slab structures are located on different layers, which results in different stoichiometric ratios in calculation. These surfaces with such characteristics appear on FeAl(100), FeAl(111), FeAl(210), FeAl(221) surfaces. In other faces, like FeAl(110) and FeAl(211) surfaces, each face has the same amount of Al and Fe atoms and the same layer structure. As a consequence, the values of chemical potential of these surfaces are invariant constants, which also correspond to the calculation results below.
Compared with elemental materials, surfaces of compounds are more complex as the stoichiometry at the surfaces might be different from the one in the bulk. Therefore, generally speaking, then the bulk energy can no longer be used as the only reference for the surface energy, in addition the chemical potential of the constituents has to be considered. Consequently, the most stable structure of a FeAl compound surface is given by the minimum of surface energy
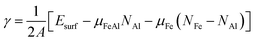 | (2) |
In addition, the chemical potential is related to the elemental bulk chemical potentials through the heat of formation ΔHFeAl, which is given by
| ΔHFeAl = Etot(FeAl) − Ebulk(Fe) − Ebulk(Al) | (3) |
Therefore, we obtain the possible range of Fe chemical potentials that is determined by the energy of bulk Fe and the heat of formation.
| μbulkFe − ΔHFeAl < μFe < μbulkFe | (4) |
3. Results and discussion
3.1 FeAl bulk calculation
FeAl bulk is a simple cubic structure which contains one Fe and Al atom in the unit cell. The calculated formation energy and lattice parameters of FeAl are shown in Table 1. From our calculation, the lattice constant is a = b = c = 2.872 Å, which only 0.59% differs from the experimental data.43 Furthermore, due to the presence of Fe element in the FeAl compounds, the results of magnetism have been considered. The ferromagnetism is the most stable state, which shows a good agreement with other results.44,45 Therefore, the subsequent calculations are all based on ferromagnetism.3.2 Surface energy
Based on Wulff cluster model mentioned above, the equivalent structure is determined by the Wulff construction with the crystal structures inside. According to Wulff theory,46 the shape with the lowest surface energy can be determined by the following methods: draw the radius vector from the origin of the polar diagram of surface energy. At the intersection, a plane perpendicular to the corresponding radius vector is constructed, and then the plane with the lowest surface energy is connected to form a closed convex shape.As the first step to derive the Wulff shape, we consider the surface energy of low-index surfaces. Recall that for non-stoichiometric surfaces the gas-phase environment contributes to the stability of the surfaces through the corresponding chemical potentials (shown in eqn (2)). In fact, most of the FeAl surfaces that we consider are not stochiometric. As we are using slab models to calculate surface energies, there are always two surfaces present in our surface model, which are furthermore not necessarily equal. However, typically the different surface energies for asymmetric slabs can not be separated so that only an average surface energy can be derived. In the case of the FeAl surfaces, we have been able to always construct slabs with the same first layer of atoms, but the second layer can differ. Still, we take the average value which is reasonable considering that the first layer on both sides is the same.
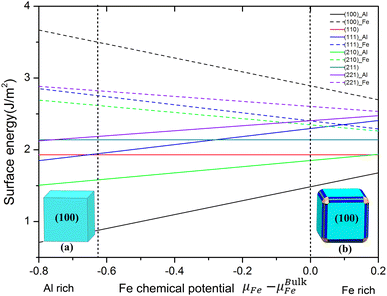
To deal with the non-stoichiometric surfaces, it is more common to plot the surface energy as a function of the chemical potential μFe of the constituents according to eqn (2), as we have done in Fig. 2. There, the dashed lines indicate the range of possible Fe chemical potentials given by eqn (3) and (4) with ΔHFeAl = 0.63 eV obtained from our calculation. Low Fe chemical potential is corresponding to the environment of Al-rich while the Fe bulk chemical potentials give the Fe-rich limit. It is obvious from Fig. 2 that the FeAl(100) surface of Al terminated has the lowest surface energy in the whole range of chemical potential. In particular, Fig. 2 shows that the surface energies of Al-terminated surface structures are totally lower (about 0.5–1 J m−2) than those surface energies of Fe-terminated surface structures. In other words, the surface structure of Al-terminated is more stable than that Fe-terminated ones from the thermodynamic equilibrium, which agrees with other results.47,48 These provide an important data foundation for the establishment of the subsequent nanoparticles Wulff shape.
The Wulff shape can be easily obtained from the surface energy corresponding to a certain chemical potential. Panels (a) and (b) in Fig. 2 illustrate the Wulff shape in the limit of Al rich and Fe rich condition. Upon increasing the chemical potential from the lower bound of the stability (shown in Fig. 2), the shape changes continuously. For Al rich conditions, we obtained the cubic Wulff shapes which are the FeAl(100) surface occupying the whole area. With the increase of Fe content in the chemical potential, the (210) and (110) surface exist on the edge; a (211) surface is formed on the vertex of the cubic shape. Note that although the (110) surface is the third stable surface, it only formed on the edge with the smallest area (area in blue in Fig. 2b). The results determine that FeAl(100) surface is the most stable surface of Wulff shape in FeAl intermetallics (the chemical potential changes from Al rich to Fe rich condition). Note that we have performed preliminary experiments of nucleation processes in Al/Cu melts at different temperatures. The results of first measurements using liquid X-ray diffraction (XRD) are in fact consistent with the predictions of our Wulff cluster model, giving credibility to the model presented here.23–26
3.3 The quasi-static growth model
In principle, the Wulff shape of FeAl mesoscopic crystals shows the equilibrium structure with the highest thermodynamic stability, which means that the mesoscopic FeAl crystals form such a shape in equilibrium. However, during the mesoscopic crystal growth to larger sizes in the ideal bulk structure, along one specific normal sub-monolayers of the involved species have to follow each other in the same order as in the bulk. This is the basis for our simple quasi-static growth model that will be explained in more detail below. We assume that always one type of facet grows completely by one (sub-)monolayer until the next surface will start to grow in another direction. Therefore, the growth process can be treated as a sequence of several quasi-static states, which can be described by a series of Wulff shapes.To grow an ideal bulk crystal, in one particular direction different types of surface terminations corresponding to a sequence of sub-monolayers should follow in a specific order, according to the surface structures illustrated in Fig. 1. When such a new surface termination is completed, the Wulff shape is determined by this new surface structure and the unchanged surfaces in the other directions, whereas the old surface termination is not relevant anymore. The starting structure of the growth process should be the Wulff shape with the highest thermodynamic stability, which is formed by the most stable surfaces in every direction. Generally speaking, the growth processes prefer to follow the path with a relatively low Gibbs free energy. We propose a quasi-static growth model in which growth occurs sequentially by adding (sub-)monolayers along one surface normal that have the highest probability, i.e., the Gibbs free energy per volume. Thus, we obtain a series of Wulff shapes corresponding to intermediate states which together describe the growth process from one most stable shape to the next larger one. In this model, we ignore the single deposition processes leading to the growth of a new (sub-)monolayer. Therefore, we call our approach a quasi-static model. Details of the growth of one particular facet are not considered, but still this model might give us a general idea about growth processes of mesoscopic crystals. This might be helpful in analyzing cluster shapes observed in cluster growth experiments.
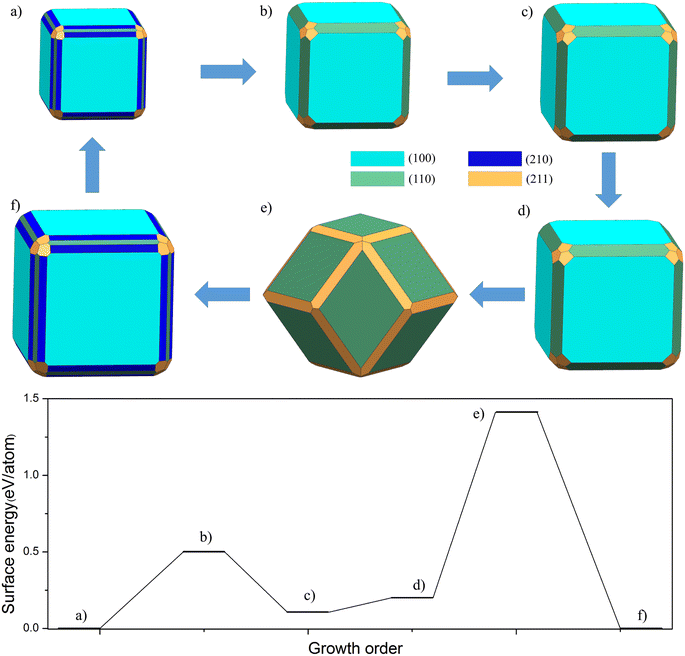
To illustrate our model, in Fig. 3 we show the sequence of Wulff shapes of FeAl that result from our quasi-static approach. The chosen Fe chemical potential corresponds to the one of bulk Fe. The process starts with the most stable shape, a cubic-like structure with FeAl(210) and FeAl(211) surfaces at the edge. After every growth event, the volume of the cluster increases according to the addition of a (sub-)monolayer along the chosen directions given by the termination with the lowest surface energy. The structure of cluster almost no change until the third step occurs, only FeAl(100), FeAl(110) and FeAl(211) surfaces. Then, the structure changes from a simple cubic to a dodecahedron. After that, the cycle of growth finishes, the structure that corresponds to the starting configuration is formed.
Moreover, the barrier of every growth model corresponding to the above structure in Fig. 3. We can clearly find that there is a small platform from (a) to (b). A key quantitative finding of this study is that a huge barrier (1.41 eV per atom) is crossed during the transition from cubic to dodecahedron. Although this growth barrier is not directly equivalent to the nucleation barrier, in our opinion, the barrier of this microstructure is closely related to the nucleation barrier under the undercooling condition. By comparing the nucleation and growth barriers of Fe containing intermetallics such as FeSi and FeAl, we believe that they are positively correlated. Thus, this model would be able to explain how clusters nucleated in a melt could keep their Wulff shape upon further growth.
Note that we have performed some preliminary experiments addressing the nucleation rate of undercooled Al/Cu melts, as mentioned above. The results of these experiments with respect to the structure of the nucleated clusters are consistent with our quasi-static growth model which will be the subject of a forthcoming publication.
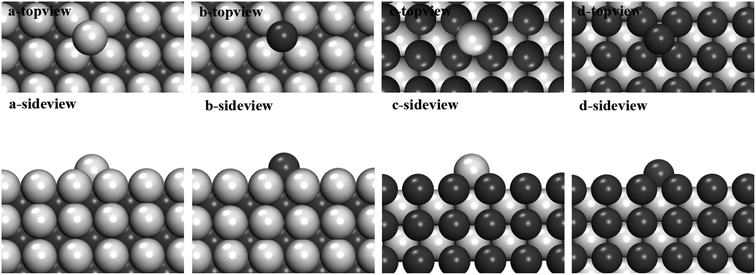
Here, we'd like to do some preliminary proof by simulation. Generally speaking, there are two completely different models of cluster growth including layer by layer growth and free atom adsorption in the melt. The layer–layer growth and free atom adsorption growth has been considered separately in the proof part. For the layer–layer growth, we use an approximation that a layer-by-layer growth happens following the order of compounds crystal structures to describe the growth of intermetallic compounds. This assumption is based on the fact that the intermetallic compounds' crystal structures do exist after the solidification of metallic melts. Could this model describe the growth processes of nanoparticle before nucleation correctly? In other words, we are wondering if it is really the favorable path to follow the order of crystal structure. We calculated the cohesive energy of Al layer (Fig. 4a)/Fe layer (Fig. 4b) adsorbed on Al-terminated FeAl(100) surface, which is defined by the following formula:
| Ecoh = Etot − Esurf − Nμadd | (5) |
Obviously, on the Al-terminated FeAl (100) surface, the cohesive energy of a Fe layer is much smaller than of a Al layer (1.6 eV Å−1 smaller). It is more favorable to grow a Fe layer on this surface, which is exactly the order of FeAl crystal. For the Al layer (Fig. 4c)/Fe layer (Fig. 4d) adsorbed on Fe-terminated FeAl (100) surface, Al layer is more stable (about 0.5 eV Å−1 smaller), which also follows the FeAl crystal structure.
For free atom adsorption growth, we calculate one single Al/Fe atom adsorbed on different FeAl (100) surfaces, in order to get the adsorption tendency of atomic type (Fig. 5). It is obvious that Fe atom (−3.32 eV) prefer to adsorb on Al-terminated surface compared with Al atom (−2.84 eV). This means that Fe free atom concentrated around Al-terminated surface in melts, which give the same results with the calculation above. For Fe-terminated surface, Al atom is more favorable.
All the results show that the intermetallic compounds formed when the nanoparticle grown in melts. The growth process following the order of crystal has the lowest Gibbs free energy, in other words, is the most favorable path. The quasi-static growth model is reasonable to describe the growth processes of intermetallic compounds, and make it possible to further investigate the nucleation barriers theoretically.
4. Conclusion
In this paper, we proposed a quasi-static growth model of compound clusters based on a sequence of stable surface terminations created by the addition of (sub-)monolayers. Based on Wulff cluster model, the corresponding stable cluster shapes are derived within the Wulff construction scheme. We illustrated this scheme using FeAl intermetallic compound cluster. The surface energies have been derived from first-principles electronic structure calculations. For non-stoichiometric surface termination, the surfaces energies depend on the chemical environment as reflected in the chemical potentials of the elements. In this case, the shape of the mesoscopic crystals' changes with respect to the chemical potential. Using quasi-static growth model to describe the growth processes, we visualize the resulting sequence of FeAl cluster shapes which can be used to analyze the cluster shapes observed in experiments addressing cluster growth processes. In addition, the growing barriers in different surfaces have also been determined. The barrier is applied to describe the growth cycle of microstructure, and it is likely to be closely related to the nucleation ratio under a supercooling condition. The model is proved preliminarily by calculating the adsorption trend of Al/Fe atom on both Al-terminated and Fe-terminated surfaces, and by simulating the most stable layer adsorbed on these two surfaces. The quasi-static growth model is reasonable to describe the growth processes of intermetallic compounds, and make it possible to further investigate the nucleation barriers theoretically.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The research is supported by the Strategic Priority Research Program of the Chinese Academy of Sciences (No. XDB0470103), Shandong Provincial Laboratory Project (SYS202204), the Basic research priorities program of Shandong Provincial Natural Science Foundation, China (Project No. ZR2021ZD22) and Youth Innovation Promotion Association CAS (grant numbers 2021423). Furthermore, we would like to thank Prof. Dr Axel Groβ from Institute of Theoretical Chemistry of Ulm University for fruitful discussions.References
- Y. Zhang, H. Zheng, Y. Liu, L. Shi and X. Tian, Cluster-assisted nucleation of Silicon phase in hypoeutectic Al-Si alloy with further inoculation, Acta Mater., 2014, 70, 162–173 CrossRef CAS.
- Y. Liu, Y. Zhang, W. Yu, X. Wang, H. Zheng and X. Tian, Pre-nucleation clusters mediated crystallization in Al-Si melts, Scr. Mater., 2016, 110, 87–91 CrossRef CAS.
- W. Yu, Y. Zhang, T. Yan, Y. Liu, A. Jiang, H. Zheng and X. Tian, Enhanced nucleation of primary silicon in Al-20 wt% Si alloy with Ni-Si inoculation, J. Alloys Compd., 2017, 693, 303–307 CrossRef CAS.
- X. Bian, J. Qin, W. Wang and X. Qi, Medium range order and microstructure of Al-1% Fe alloy, Mater. Sci. Forum, 2000, 331, 343–348 Search PubMed.
- J. Qin, X. Bian, S. Sliusarenko and W. Wang, Pre-peak in the structure factor of liquid Al-Fe alloy, J. Phys.: Condens.Matter, 1999, 10(6), 1211 Search PubMed.
- C. Ryu, W. Dmowski and T. Egami, Ideality of liquid structure: A case study for metallic alloy liquids, Phys. Rev. E, 2020, 101, 030601 CrossRef CAS PubMed.
- A. Il'inskii, S. Slyusarenko, O. Slukhovskii, I. Kaban and W. Hoyer, Structure of liquid Fe-Al alloys, Mater. Sci. Eng., A, 2002, 325(1), 98–102 CrossRef.
- L. Hui, Shoulder-peak formation in the process of quenching, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68(2), 024210 CrossRef.
- K. Kelton, G. Lee, A. Gangopadhyay, R. Hyers, T. Rathz, J. Rogers, M. Robinson and D. Robinson, First x-ray scattering studies on electrostatically levitated metallic liquids: Demonstrated influence of local icosahedral order on the nucleation barrier, Phys. Rev. Lett., 2003, 90(19), 195504 CrossRef CAS PubMed.
- T. Itami, S. Munejiri, T. Masaki, H. Aoki, Y. Ishii, T. Kamiyama, Y. Senda, F. Shimojo and K. Hoshino, Structure of liquid Sn over a wide temperature range from neutron scattering experiments and first-principles molecular dynamics simulation: A comparison to liquid Pb, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67(6), 064201 CrossRef.
- G. Lee, A. Gangopadhyay, K. Kelton, R. Hyers, T. Rathz, J. Rogers and D. Robinson, Difference in icosahedral short-range order in early and late transition metal liquids, Phys. Rev. Lett., 2004, 93(3), 037802 CrossRef CAS PubMed.
- T. Kim, G. Lee, B. Sieve, A. Gangopadhyay, R. Hyers, T. Rathz, J. Rogers, D. Robinson, K. Kelton and A. Goldman, In situ high-energy x-ray diffraction study of the local structure of supercooled liquid Si, Phys. Rev. Lett., 2005, 95(8), 085501 CrossRef CAS PubMed.
- P. Ganesh and M. Widom, Signature of nearly icosahedral structures in liquid and supercooled liquid copper, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74(13), 134205 CrossRef.
- N. Jakse and A. Pasturel, Local order of liquid and supercooled zirconium by ab initio molecular dynamics, Phys. Rev. Lett., 2003, 91(19), 195501 CrossRef PubMed.
- N. Jakse and A. Pasturel, Ab initio molecular dynamics simulations of local structure of supercooled Ni, J. Chem. Phys., 2004, 120(13), 6124–6127 CrossRef CAS PubMed.
- P. Ganesh and M. Widom, Ab initio simulations of geometrical frustration in supercooled liquid Fe and Fe-based metallic glass, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77(1), 134205 CrossRef.
- L. Huang, C. Wang and K. Ho, Structure and dynamics of liquid Ni36Zr64 by ab initio molecular dynamics, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83(18), 184103 CrossRef.
- S. Wu, M. Kramer, X. Fang, S. Wang, C. Wang, K. Ho, Z. Ding and L. Chen, Structural and dynamical properties of liquid Cu80Si20 alloy studied experimentally and by ab initio molecular dynamics simulations, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84(13), 134208 CrossRef.
- G. Boussinot and M. Apel, Phase field and analytical study of mushy zone solidification in a static thermal gradient: From dendrites to planar front, Acta Mater., 2017, 122, 310–321 CrossRef CAS.
- J. Li, Z. Wang, Y. Wang and J. Wang, Phase-field study of competitive dendritic growth of converging grains during directional solidification, Acta Mater., 2012, 60(4), 1478–1493 CrossRef CAS.
- F. Han, B. Tang, H. Kou, J. Li and Y. Feng, Cellular automata modeling of static recrystallization based on the curvature driven subgrain growth mechanism, J. Mater. Sci., 2013, 48(20), 7142–7152 CrossRef CAS.
- D. Li, H. Zhou and I. Honma, Design and synthesis of self-ordered mesoporous nanocomposite through controlled in-situ crystallization, Nat. Mater., 2003, 3(1), 65–72 CrossRef.
- L. Song, X. Tian, A. Shao, L. Li, Y. Zhang, H. Li and X. Lin, The structure of metallic melts in binary homogenous alloys: A thermodynamical understanding from the Wulff cluster mode, Phys. Chem. Chem. Phys., 2020, 22(40), 23237–23245 RSC.
- L. Song, X. Tian, Y. Yang, J. Qin, H. Li and X. Lin, Probing the microstructure in pure Al & Cu melts: Theory meets experiment, Front. Chem., 2020, 8, 607 CrossRef CAS.
- L. Song, X. Tian, A. Shao, M. Hua, L. Li, H. Li and X. Lin, The structure of metallic melts in eutectic alloys based on the Wulff cluster model: Theory meets experiment, Phys. Chem. Chem. Phys., 2021, 23(5), 3606–3614 RSC.
- A. Shao, L. Hu, L. Song, M. Hua, J. Xue, S. Wu, X. Tian and X. Lin, Revealing mechanism of non-Arrhenius viscosity change in metal melts based on Wulff cluster model, Scr. Mater., 2023, 234, 115571 CrossRef CAS.
- B. Silva, A. Garcia and J. Spinelli, The effects of microstructure and intermetallic phases of directionally solidified Al-Fe alloys on microhardness, Mater. Lett., 2012, 89, 291–295 CrossRef CAS.
- Y. Zheng, F. Wang, T. Ai and C. Li, Structural, elastic and electronic properties of B2-type modified by ternary additions FeAl-based intermetallics: First-principles study, J. Alloys Compd., 2017, 710, 581–588 CrossRef CAS.
- A. Hotar, M. Palm, P. Kratochvil, V. Vodickova and S. Danis, High-temperature oxidation behaviour of Zr alloyed Fe3Al-type iron aluminide, Corros. Sci., 2012, 63, 71–81 CrossRef CAS.
- S. Deevi and V. Sikka, Nickel and iron aluminides: an overview on properties, processing, and applications, Intermetallics, 1996, 4, 357 CrossRef CAS.
- G. Painter, C. Fu and F. Averill, First-principles atomic cluster study of boron interactions in Ni3Al, J. Appl. Phys., 1997, 81(5), 2135–2142 CrossRef CAS.
- M. Ruizpreciado, A. Kassiba, A. Morales-Acevedo and M. Makowska-Janusik, Vibrational and electronic peculiarities of nitio3 nanostructures inferred from first principle calculations, RSC Adv., 2015, 5(23), 17396–17404 RSC.
- P. Hohenberg and W. Kohn, Inhomogeneous electron gas, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. Sham, Self-consistent equations including exchange and correlation effects, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- G. Kresse and J. Furthmuller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and J. Furthmuller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- J. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation madesimple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. Perdew, A. Ruzsinszky and G. Csonka, Generalized gradient approximation for solids and their surfaces, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 159, 1758 CrossRef.
- H. Monkhorst and J. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- Y. Guo, J. Liang, X. Zhang, W. Tang, Y. Zhao and G. Rao, Effects of Mn and Cu doping in La (T, Al) 13 (T= Fe, Co) on crystal structure and magnetic properties, J. Alloys Compd., 1997, 257, 69–74 CrossRef.
- Y. Liu, X. Chong, Y. Jiang and J. Feng, Mechanical properties and electronic structures of Fe-Al intermetallic, Phys. B, 2017, 506, 1–11 CrossRef CAS.
- L. Song, X. Tian, H. Jiang, W. Yu, Z. Zhao, H. Zheng, J. Qin and X. Lin, Vacancies effect on the mechanical properties in B2 FeAl intermetallic by the first-principles study, Philos. Mag., 2019, 99(21), 2703–2717 CrossRef CAS.
- J. Bogner, W. Steiner, M. Reissner, P. Mohn, P. Blaha, K. Schwarz, R. Krachler, H. Ipser and B. Sepiol, Magnetic order and defect structure of FexAl 1 − x, alloys around x = 0.5: An experimental and theoretical study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 14922 CrossRef CAS.
- R. Tran, Z. Xu, B. Radhakrishnan, D. Winston, W. Sun, K. Persson and S. Ping, Surface energies of elemental crystals, Sci. Data, 2016, 3, 160080 CrossRef CAS PubMed.
- I. Berrached, M. Gallouze, L. Rouaiguia, L. Rabahi, T. Grosdidier, M. Drirl and A. Kellou, Physical properties investigation of Fe1-xAlx (x ≤ 50%-at) alloys using DFT and Wagner-Schottky model, Phys. Scr., 2020, 95, 115702 CrossRef CAS.
- M. Gallouze, A. Kellou, D. Hamoutene, T. Grosdidier and M. Drir, Absorption and adsorption of hydrogen in B2-FeAl: Ab initio study, Phys. B, 2013, 416, 1–7 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |