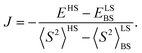Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Synthesis and photoinduced behavior of DPP-anchored nitronyl nitroxides: a multifaceted approach†
Evgeny
Tretyakov
 *a,
Dmitry
Gorbunov
*a,
Dmitry
Gorbunov
 b,
Nina
Gritsan
b,
Nina
Gritsan
 *b,
Ashok
Keerthi
*b,
Ashok
Keerthi
 c,
Martin
Baumgarten
c,
Martin
Baumgarten
 d,
Dieter
Schollmeyer
e,
Mikhail
Ivanov
f,
Anna
Sergeeva
a and
Matvey
Fedin
d,
Dieter
Schollmeyer
e,
Mikhail
Ivanov
f,
Anna
Sergeeva
a and
Matvey
Fedin
 f
f
aN.D. Zelinsky Institute of Organic Chemistry, Russian Academy of Sciences, Leninsky Ave. 47, Moscow 119991, Russian Federation. E-mail: tretyakov@ioc.ac.ru
bV.V. Voevodsky Institute of Chemical Kinetics and Combustion, 3 Institutskaya Str., Novosibirsk 630090, Russian Federation. E-mail: nina.gritsan@gmail.com
cDepartment of Chemistry, School of Natural Sciences, The University of Manchester, Oxford Road, M13 9PL, UK
dMax Planck Institute for Polymer Research, Ackermannweg 10, Mainz D-55128, Germany
eJohannes Gutenberg-University Mainz, Duesbergweg 10-14, 55128 Mainz, Germany
fInternational Tomography Center, 3a Institutskaya Str., Novosibirsk 630090, Russian Federation
First published on 19th February 2024
Abstract
Understanding and controlling spin dynamics in organic dyes is of significant scientific and technological interest. The investigation of 2,5-dihydropyrrolo[4,3-c]pyrrolo-1,4-dione derivatives (DPPs), one of the most widely used dyes in many fields, has so far been limited to closed-shell molecules. We present a comprehensive joint experimental and computational study of DPP derivatives covalently linked to two nitronyl nitroxide radicals (DPPTh-NN2). Synthesis, single crystal X-ray diffraction study, photophysical properties, magnetic properties established using steady-state and pulse EPR, fast spin dynamics, and computational modelling using density functional theory and ab initio methods of electronic structure and spectroscopic properties of DPPTh-NN2 are presented. The single-crystal X-ray diffraction analysis of DPPTh-NN2 and computational modeling of its electronic structure suggest that effective conjugation along the backbone leads to noticeable spin-polarization transfer. Calculations using ab initio methods predict a weak exchange interaction of radical centers through a singlet ground state of DPPTh with a small singlet–triplet splitting (ΔEST) of about 25 cm−1 (∼0.07 kcal mol−1). In turn, a strong ferromagnetic exchange interaction between the triplet state of DPPTh chromophore and nitronyl nitroxides (with J ∼ 250 cm−1) was predicted.
Introduction
Discovered in the early 1970s,1 diketopyrrolopyrroles (2,5-dihydropyrrolo[4,3-c]pyrrolo-1,4-diones, DPPs) remain one of the most widely used dyes, finding application in many areas of high technology. Numerous studies have been devoted to the development of DPP derivatives as high-performance materials for use in various applications such as high-performance pigments, organic field-effect transistors, bulk-heterojunction solar cells, dye-sensitized solar cells, organic light-emitting diodes, fluorescence imaging, and many other fields.2 Despite the significant progress achieved by researchers in the exploration of DPP-based compounds, only recently have their conjugated derivatives substituted with stable radical groups been obtained. Single crystal X-ray data on a DPP derivative bearing radical groups, namely, bis(thiophen-2-yl)-2,5-dihydropyrrolo[3,4-c]pyrrole-1,4-dione with terminal nitronyl nitroxide groups (DPPTh-NN2) were first reported in 2020.3Later, nitronyl-nitroxide diradicals with extended DPP-containing linkers (DPPTh-Ph-NN2, DPPFu-Ph-NN2, and DPPPh-Ph-NN2, Fig. 1) were obtained and partially characterized.4 In addition to the listed diradicals (Fig. 1), perylene bisimide (PBI) and iso-indigo (IIn) conjugated diradicals were also synthesized.4 Although all diradicals retain the intrinsic optical properties of the dyes or, more specifically, pi-conjugated chromophore, at the same time they exhibit an indirect spin coupling between two distant paramagnetic centres. Room temperature EPR data4 provided only nearly identical 9-line spectra, demonstrating that the exchange coupling parameter J is much larger than twice the hyperfine coupling constant. The distances between the radical units were very large (C2–C2′ distance in the range 2.2–2.4 nm for DPP-based diradicals) due to the additional phenyl rings connecting the NN moieties to the DPP core.4 To date, comprehensive temperature-dependent studies of liquid and frozen solutions via EPR spectroscopy, as well as magnetization measurements of polycrystalline powder, have not been conducted. These analyses are crucial for a deeper understanding and clear differentiation of the magnetic properties of such diradicals. Earlier, Matsuda et al. demonstrated the exponential distance dependence of the exchange interaction parameter over extended phenylacetylene bridged NN biradicals.5 Their findings indicate that the EPR spectra of the examined diradicals in liquid phase will display a consistent nine-line pattern (indicative of strong exchange) when the distance between the C2 atoms of the NN moieties ranges from 0.7 to 2.7 nm. This observation is coupled with significant variations (spanning orders of magnitude) in the exchange coupling parameters, highlighting the sensitivity of magnetic interactions to molecular spacing within these systems.
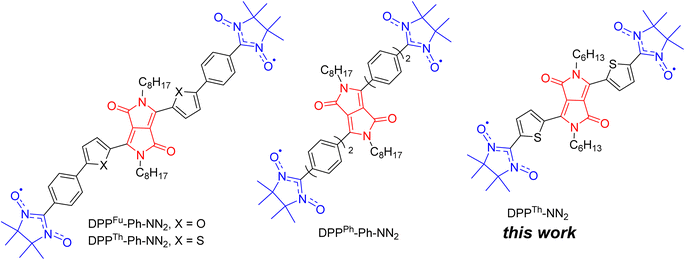 | ||
| Fig. 1 Chemical structures of DPP-linked nitronyl-nitroxide diradicals: DPPTh-NN2, DPPTh-Ph-NN2, DPPFu-Ph-NN2, and DPPPh-Ph-NN2. | ||
Thus, the magnetic properties of DPP-based diradicals require much more in-depth studies. Since DPP derivatives have found applications in the solar cells, OLEDs, fluorescence imaging, etc.,2d–g information available about their electronic absorption spectra is insufficient to understand their excitation relaxation dynamics which is very important to broaden the scope of these molecules in respective fields. Our study was undertaken with the aim of quantitatively elucidating the magnetic properties of the DPPTh-NN2 diradical. Continuous-wave and time-resolved EPR spectra were recorded, and exchange and dipole–dipole interactions were theoretically assessed not only in the ground state of DPP linker, but also in the case of its triplet excitation. Furthermore, we tried to resolve the issue of possible relaxation pathways for the excitation of the DPP chromophore. To do this, we performed both DFT and high-level calculations of the electronic structure of the DPPTh-NN2 diradical. In this paper, we described in detail the synthesis of DPPTh-NN2, single crystal analysis, insights into electronic structure, and the results on the continuous wave, echo-detected and time-resolved EPR study.
Results and discussion
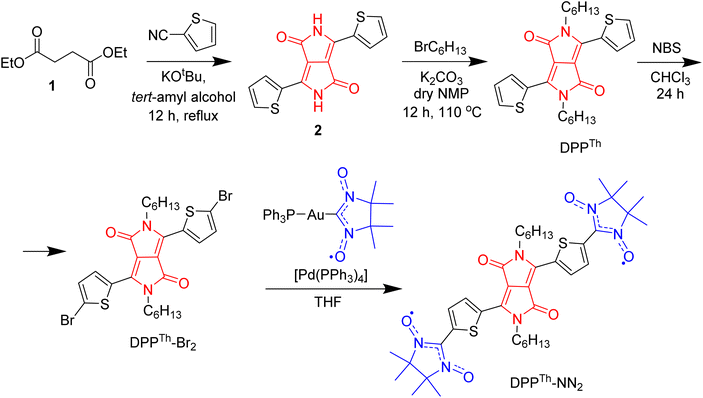
Synthesis and structure of the DPPTh-NN2 diradical
The synthetic route to the DPPTh-NN2 diradical is shown in Scheme 1. The diradical precursor, the corresponding dibromo-substituted DPPTh-Br2, was synthesized according to the literature-reported procedure6 with necessary modifications. To introduce two nitronyl nitroxide (NN) groups into the DPPTh core, we chose a palladium catalysed cross-coupling of bromo-derivative of DDP with the (nitronyl nitroxide-2-ide)(triphenylphosphine)gold complex. This method, originally proposed by Keiji Okada,7 with the recent significant improvements8,9 has become an efficient protocol for the directed synthesis of nitronyl nitroxides.10–12 Thus, a new path has been opened to various in-demand nitronyl nitroxides for a variety of research fields, including radical chemistry, the creation of high-spin systems and rechargeable batteries, the design of molecule-based magnets and molecular units for spintronics.13,14 Naturally, using the described approach, the DPPTh-NN2 diradical was successfully obtained in a moderate yield of ∼72% when using Pd(PPh3)4 catalyst (Scheme 1).In chemistry of diradicals, X-ray diffraction analysis is of paramount importance because it unveils valuable information about molecular organization and interactions in the solid state. We succeeded in growing single crystals of DPPTh-NN2 by slow diffusion of methanol into its solution in CH2Cl2 at 5 °C. The crystalline product appeared to be stable at ambient conditions and no phase transitions were observed in the DSC analysis in the temperature range from 20 °C to the melting point of 216 °C (see ESI†).
At room temperature, attempts to perform an X-ray diffraction analysis of DPPTh-NN2 single-crystal samples failed. Cooling the single-crystal sample at 193 K led to the freezing of the alkyl-chain movement, which made it possible to solve the molecular and crystal structure of the DPPTh-NN2 diradical. According to XRD, the crystal structure of DPPTh-NN2 is centrosymmetric (space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) and contains two crystallographically independent molecules in an asymmetric unit (hereafter called as A and B). The molecular structures of A and B DPPTh-NN2 molecules are depicted in Fig. 2. Bond lengths and angles in both forms of the molecule are similar (Table S1†) and comparable to typical values for similar molecular fragments, as indicated by a search in the Cambridge Structural Database using the Mogul program.15
) and contains two crystallographically independent molecules in an asymmetric unit (hereafter called as A and B). The molecular structures of A and B DPPTh-NN2 molecules are depicted in Fig. 2. Bond lengths and angles in both forms of the molecule are similar (Table S1†) and comparable to typical values for similar molecular fragments, as indicated by a search in the Cambridge Structural Database using the Mogul program.15
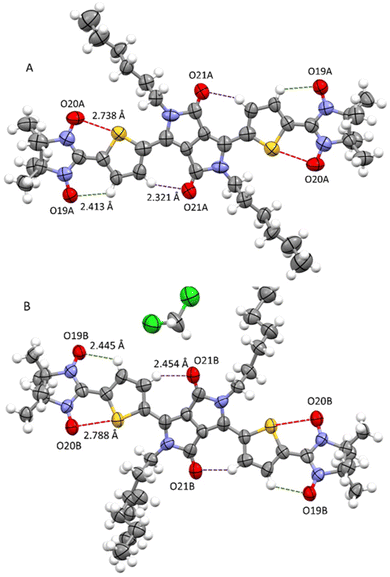 | ||
| Fig. 2 Structures of crystallographically independent molecules A and B (with solvate CH2Cl2) in crystals of the DPPTh-NN2 diradical. | ||
In the DPPTh-NN2 diradical, the π-conjugated system, consisting of the DPP core, thiophene rings, and nitronyl nitroxide moieties, presents high planarity with small interplanar twist angles. In molecules A and B, dihedral torsion angles between planes of the nitronyl nitroxide groups and planes of the nearest side thiophene rings are 2.90 and 13.24° respectively. In turn, the two thiophene rings are imposed in anti-orientation with respect to each other and twisted by 9.16° (in molecule A) and 20.69° (in molecule B) relative to the mean plane of DPPTh. The observed planarity of the thiophene–nitronyl nitroxide system leads to short intramolecular H-bonds O⋯H–C (2.41 and 2.45 Å, dotted lines in Fig. 2), as well as extremely short contacts between ONO and S atoms (2.74 and 2.79 Å) compared to the sum of the van der Waals radii of the S and O atoms (3.32 Å, dashed purple lines in Fig. 2). Small torsion angles provide efficient conjugation along the backbone, thereby facilitating the noticeable transfer of spin-polarization from the NN radical units to the DPPTh chromophore, as observed in the EPR spectra and demonstrated by DFT calculations (Fig. S6, ESI†).
The crystal packing shows that the molecules adopt weak intermolecular π–π stacking separated by distance of 3.74 Å between centroids of the DPPTh moieties (Fig. 3). Inside such stacks, short intermolecular contacts C–H⋯ONO (2.36, 2.45, 2.56, and 2.64 Å) are realized between the oxygen atoms of the nitroxide fragments and the hydrogen atoms of the methyl groups (Fig. 4a). Similar contacts are often observed in crystals of nitronyl nitroxides, and they are characterized by a rather high binding energy.16 Because of this, interactions of this type have a significant effect on the motif of the crystal packing of nitroxide radicals. The most important consequence of C–H⋯ONO interactions is the geometry of the mutual arrangement of nitroxide groups and, above all, the distances between the oxygen atoms of paramagnetic centers, since the latter predetermine the magnetic properties of paramagnetic samples. Moreover, C–H⋯ONO interactions predetermine the relative rotation angle of molecules in the stacks, as well as the shortest intermolecular distances between nitroxide oxygen atoms (3.617 and 3.887 Å). In addition, one can see multiple short intermolecular C–H⋯ONO contacts (2.40, 2.55, and 2.64 Å) between the DPPTh-NN2 diradicals belonging to neighbouring stacks (Fig. 4b). These interactions lead to the shortest intermolecular distances between the nitroxide oxygen atoms, equal to 3.653 Å. On the whole, in the solid phase of DPPTh-NN2, the shortest O⋯O distances between O atoms of nitroxide groups exceed 3.617 Å, which is much greater than the sum of the van der Waals radii of O atoms (3.04 Å). Therefore, in the crystalline phase of DPPTh-NN2 diradicals, both intra- and intermolecular exchange interactions should be weak.
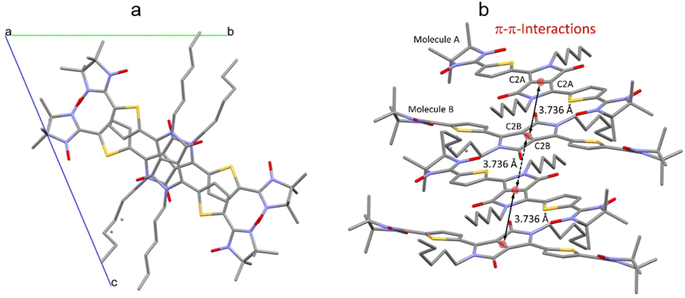 | ||
| Fig. 3 (a) Solid state molecular packing of DPPTh-NN2 with π–π-interactions; (b) side view of DPPTh-NN2 with π–π-distances between centroids of the DPPTh moieties. | ||
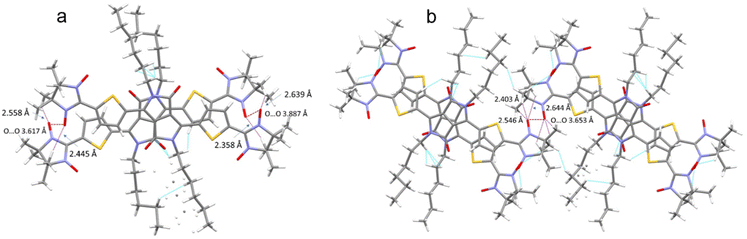 | ||
| Fig. 4 (a) Short C–H⋯ONO contacts and the shortest O⋯O distances between neighbouring DPPTh-NN2 molecules in a stack and (b) between DPPTh-NN2 molecules belonging to different stacks. | ||
DFT and ab initio calculations of the electronic structure and magnetic properties of the DPPTh-NN2 diradical
To better understand the magnetic and spectroscopic properties of the DPPTh-NN2 diradical, we performed a series of DFT and ab initio calculations. All calculations were performed for model geometries that differ from the geometry of the DPPTh-NN2 by replacing the long n-hexyl substituents with methyl groups. In addition, two types of model geometry were used in the calculations: one was based on the XRD analysis, and the other was optimized in a toluene solution.We also calculated the parameters of intermolecular exchange interactions of neighboring radical fragments in the stack. Interestingly, for a pair of diradicals, J parameters of different sign (−5.6 and 6.4 cm−1) were predicted for two pairs of adjacent radical fragments (Fig. S9, ESI†). An antiferromagnetic exchange interaction was predicted in the case when ONCNO fragments of neighboring radical fragments are almost parallel, and a ferromagnetic one, in the case of a significant deviation from parallel arrangement of the corresponding fragments.
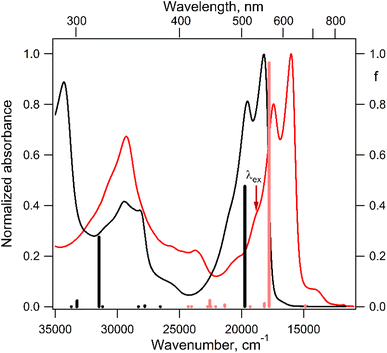
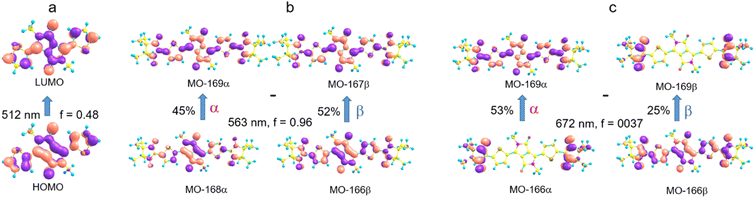
The electronic absorption spectrum of the DPPTh-NN2 diradical contains a very similar intense absorption band with the same structure as in the DPPTh spectrum, but noticeably red-shifted. Note that the DPPTh-NN2 spectrum was calculated for the high-spin triplet state of the diradical. The wavefunction of the ground open-shell singlet cannot be correctly described in the one-determinant approximation, and thus its UV-Vis spectrum cannot be calculated at the TD-DFT level. Fig. S7 (ESI†) represents the MO diagram with a series of α- and β-type MOs involved in electronic excitations of the DPPTh-NN2 diradical. It can be seen that highest occupied and lowest unoccupied MOs of both α- and β-types are similar to the HOMO and LUMO of the DPPTh (Fig. 6a) and differ from them only in some delocalization to NN fragments. According to the TD-UB3LYP calculation, the intense structured band in the spectrum of diradical also corresponds to a single intense transition (563 nm, f = 0.96, Fig. 5), which in turn corresponds to the HOMO → LUMO promotions for α- and β-electrons (Fig. 6b). Since these HOMO and LUMO are similar to those of the parent DPPTh (except for a slight delocalization), the intense long wavelength bands of the precursor and diradical have very similar shape and intensity, but the diradical band is red-shifted.
In addition, the diradical spectrum shows a weak feature (around 680 nm) at the tail of the absorption band discussed above. According to the calculations, the DPPTh-NN2 has two electronic transitions in this region: at 672 nm (f = 0.0037) and 673 nm (f = ∼10−8). In turn, the MO diagram (Fig. S7, ESI†) shows that two SOMOs (MO-166α and MO-167α) localized on the NN fragments are practically degenerate and lie below the HOMO by about 0.2 eV. The corresponding unoccupied MO-168β and MO-169β localized on the NN fragments (partners of the α-SOMOs) are also practically degenerate and lie above LUMO by about 0.2 eV. It is these MOs, along with HOMO and LUMO, that are involved in long wavelength low intensity transitions. Both transitions consist mainly of two contributions: the promotion of an α-electron from the SOMO to the LUMO and the promotion of a β-electron from the HOMO to the SOMO partner (Fig. 6c). These transitions are more complex than those previously calculated for a number of nitronyl nitroxide radicals.14
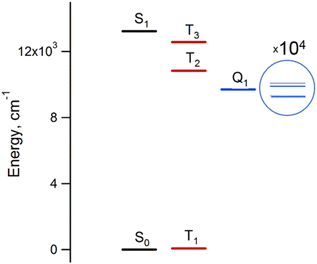
The results of the high-level calculations for the six low-energy DPPTh-NN2 multiplets are presented in Fig. 7 and S10 (ESI†), as well as in Table 1. Calculations were carried out both for the optimized and XRD-based geometries. An analysis of the CASSCF wave functions demonstrates that the Q1 state, as well as T2, T3, and S1 states, actually arose as a result of the exchange interaction of the local triplet state corresponding to the HOMO → LUMO excitation (Fig. 6a) with NN radical fragments (for details, see ESI, Section 3†). The energy splitting between these multiplets corresponds to the exchange interaction of the local triplet state with doublets of radical fragments (with parameter J1) and between radical fragments (with J2), respectively (Table 1). Results of Table 1 show that the exchange interaction of the radical fragments is weak and antiferromagnetic for both the ground and triplet excited states. In turn, the exchange interaction between the local triplet state and NN fragment is strong and ferromagnetic. The latter can be explained by the McConnell I mechanism,17 as carbon atom of ON-C-NO fragment has high negative spin population and is bound with carbon atom of thiophen ring with high positive spin population (Fig. S11†).
| Electronic state | E, cm−1 and J, cm−1 (mT) | Optimized geometry | ||
|---|---|---|---|---|
| XRD geometry | Opt. geometry | D, cm−1 (in mT) | E/D | |
a Parameters J1 and J2 of the exchange interaction correspond to the spin Hamiltonian of the form 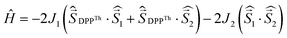 , where , where  is the spin of the DPPTh core triplet state, and is the spin of the DPPTh core triplet state, and 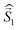 and and 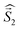 correspond to the NN radical fragments.
b ZFS parameters estimated at the CASSCF(10,10)/QDPT level.
c ZFS parameters estimated at the RO-B3LYP level. correspond to the NN radical fragments.
b ZFS parameters estimated at the CASSCF(10,10)/QDPT level.
c ZFS parameters estimated at the RO-B3LYP level.
|
||||
| S0 | 0 | 0 | No | No |
| T1 | 22.6 | 68.2 | −6.5 × 10−4 (−0.70)b | 0.077b |
| −6.8 × 10−4 (−0.73)c | 0.014c | |||
| J, cm−1 | −11.3 (−1.21 × 103) | −34.1 (−3.7 × 103) | — | — |
| Q1 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 603 603 |
9698 | −0.019 (−20.3)b | 0.05b |
| T2 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 052 052 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 832 832 |
−0.108 (−116)b | 0.01b |
| T3 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 570 570 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 011 011 |
0.052 (55.6)b | 0.02b |
| S1 | 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 067 067 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 234 234 |
No | No |
| J 1, cm−1 | 244 | 588 | — | — |
| J 2, cm−1 | −10.2 | −15.5 | — | — |
| T1 of DPPTh | — | — | −0.042 (−44.9)c | 0.20c |
For the parent DPPTh, previous femtosecond transient absorption spectroscopy and time-correlated single-photon counting studies18 have demonstrated that the singlet excited S1 state of this compound relaxes directly to the ground state via internal conversion and fluorescence, bypassing the triplet state. For the DPPTh-NN2 the energy diagram is much more complicated. Excitation of the diradical by the 532 nm laser pulse leads to both singlet and triplet states arising from the exchange interactions of NN fragments through the excited singlet state localized mainly on the DPPTh core. However, as was discussed previously, slightly below this pair of states, there are also states responsible for a weak feature in the UV-Vis spectrum (Fig. 5) (4 states in total - two triplets and two singlets). Finally, as shown by calculations, this sequence of excited states is closed by singlet, triplet, and quintet states presented in Fig. 7.
Thus, in the case of the DPPTh-NN2 diradical, between the state populated upon excitation and the ground state there are a large number of states, the energy gaps between which are small. In addition, among these states there are pairs of very close singlet and triplet levels that arise due to the exchange interaction of NN fragments. Therefore, one might expect a very fast conversion of the excited state (singlet or triplet), which occurs immediately after the excitation, into the Q1 state. At room temperature, the Q1 state is expected to be short-lived due to thermally activated relaxation through the T2 state. However, such a process is absent at cryogenic temperatures, and one can expect a sufficiently long-lived Q1 state at these temperatures.
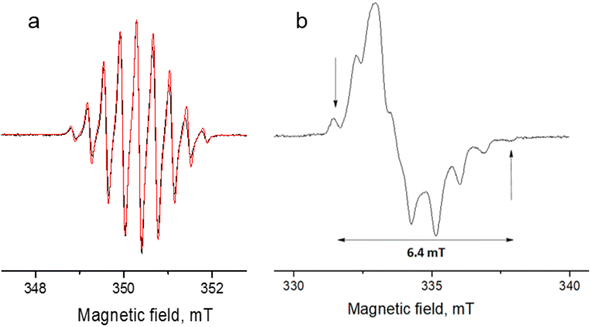 | ||
| Fig. 8 Experimental (black) and simulated (red) continuous-wave (CW) X-band EPR spectra of DPPTh-NN2 in toluene at room temperature (a) and in frozen toluene at 135 K (b) (C ≈ 0.1 mM). | ||
The EPR spectrum of the DPPTh-NN2 diradical in a frozen toluene solution at 135 K (Fig. 8b) is difficult to interpret, since the symmetry is partly lost and some anisotropic components may overlap in |ΔmS| = 1 region. This results in a different number of shoulders in the outermost regions of the spectrum. Therefore, the zero-field splitting parameters can be estimated roughly from the low temperature EPR experiment. However, clear evidence of a diradical character comes from the observed |ΔmS| = 2 transition. This signal has a low signal-to-noise ratio (S/N), because the average value of the N⋯N, O⋯O and N⋯O distances is large and estimated at 15.3 Å (for both the XRD and optimized structures), which implies a small |D| and, accordingly, a low probability of this transition. In the point dipole approximation, a distance of 15.3 Å leads to |D| = 0.81 mT (7.6 × 10−4 cm−1). Note that this value cannot explain the rather large width of the EPR spectrum (Fig. 8b). However, the calculation of the spin–spin contribution at the DFT level gave an even smaller but close value: D = −0.73 mT (−6.8 × 10−4 cm−1) and E/D = 0.014.
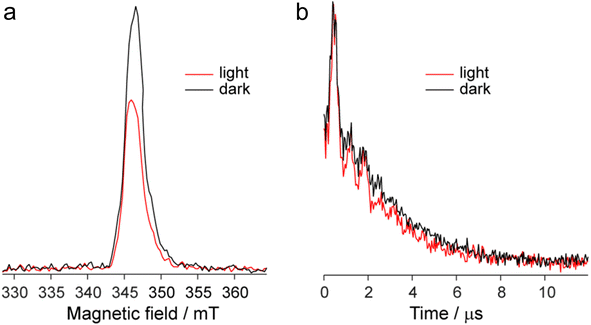
Fig. 9a shows the echo-detected (ED) EPR spectra of the DPPTh-NN2 diradical recorded at 10 K under the same conditions in the presence and absence of pulse laser excitation. The spectrum recorded in the absence of irradiation features one slightly asymmetric EPR line, the maximum of which corresponds to g = 2.008. This signal apparently corresponds to the lowest triplet state of the DPPTh-NN2 diradical (T1), and, according to calculations, its population at 10 K is low, although it cannot be ruled out that E(T1) may be substantially overestimated.
In the presence of laser radiation, the observed EPR signal retains its shape, but becomes less intense. Based on the quantum chemical calculations and discussion presented above, one should expect that the lowest excited quintet state (Q1) may be populated upon excitation, thus being paramagnetic. However, still we do not observe any reliable spectral manifestations of such state. In addition, the transverse relaxation curves in the presence and absence of photoexcitation are remarkably similar (Fig. 9b), indicating that they refer to the same paramagnetic species.
We also applied time-resolved (TR) EPR technique to probe the intermediate species formed upon photoexcitation of DPPTh-NN2 in toluene glass at 80 K. TR EPR is based on continuous wave detection and typically is more sensitive to photoexcited paramagnetic species compared to pulse EPR. However, no TR EPR signals were observed. In addition, the sample with pure DPPTh moiety (without radicals attached) has been investigated with the same zero TR EPR signal. The failure to detect the TR EPR signal in the case of DPPTh is consistent with the relaxation of the S1 state directly to the ground state, as discussed above. The failure in the case of the diradical may be due to the short lifetimes of T2, T3 and Q1 states, if they are actually formed.
The observed decrease of the echo signal under light can be assigned to a slight heating of the sample. Indeed, an insignificant heating by a few degrees (3–5 K) can noticeably modify EPR signal at 10 K, which is proportional to 1/T (see, e.g. ref. 19 and 20). At the same time, the opposite effect of heating should be present due to the higher population of T1 state at higher temperatures. Apparently, the former mechanism dominates, causing spectral changes shown in Fig. 9a. Additional perturbation of resonator under laser radiation can also contribute to the observed signal decrease.
Conclusions
In summary, we have synthesized a DPP-derivative bearing two radical groups, i.e. bis(thiophen-2-yl)-2,5-dihydropyrrolo[3,4-c]pyrrole-1,4-dione terminally capped with nitronyl nitroxide groups (DPPTh-NN2). Notably, we used palladium-catalyzed cross-coupling reaction of the corresponding dibromo-derivative with the (nitronyl nitroxide-2-ide)(triphenylphosphine)gold complex as a convergent step to synthesize DPPTh-NN2 diradical. The incorporation of two radicals resulted in interesting spectroscopic, photophysical, and magnetic properties, and the expected unusual excited-state dynamics. A computational study predicted that the DPPTh-NN2 diradical has singlet ground state with a small singlet–triplet energy gap ΔEST of about 0.2 kcal mol−1 in solution. This value is consistent with strong on the EPR scale exchange interactions observed in the EPR. The inclusion of two NN radicals leads to an increase in the number of excited states both due to excitations involving orbitals localized on NN fragments and due to the exchange interaction of these fragments. Consequently, the density of states increases and, in turn, the energy gaps between them decrease. This effect, combined with the removal of spin prohibition for certain transitions, is expected to significantly speed up the relaxation process of the excitation initially localized on the DPPTh core. Although we were unable to experimentally detect the low-energy quintet state, likely due to its brief lifetime or low yield, future studies using ultrafast techniques, such as femtosecond spectroscopy, could potentially reveal its properties.Experimental and computational details
Materials and instrumentation
All chemicals and reagents were purchased from commercial suppliers and used without further purification. Solvents used for spectroscopic measurements were spectral grade quality. 2,5-Dihydro-1,4-dioxo-3,6-dithienylpyrrolo[3,4-c]-pyrrole (2) was synthesized by adapting reported procedure.21 All reactions were monitored by thin-layer chromatography (TLC) carried out on silica gel plates. Preparative separations were performed by column chromatography on silica gel grade 60 (0.040–0.063 mm) from Merck.1H and 13C NMR spectra were recorded on Bruker Avance 300 (300 MHz) spectrometer. The chemical shifts were reported in ppm and referenced to the residual solvent peak. s = singlet, d = doublet, t = triplet, m = multiplet, b = broad. Infrared spectroscopy measurements were conceded on Nicolet 730 FTIR spectrometer equipped with an attenuated total reflection (ATR) setup. The UV/Vis spectra were recorded at 298 K with a PerkinElmer Lambda 900 spectrophotometer. Matrix-assisted laser desorption ionization time-of-flight (MALDI-TOF) mass spectra were acquired with a Bruker Reflex II MALDI-TOF mass spectrometer, calibrated against a mixture of C60/C70. The X-ray crystallographic data for the molecules were collected on a STOE IPDS 2T diffractometer using Cu-Kα IμS source. Crystal structure contains two independent molecules of NN2-DPP (A and B) both of them are located on an centre of inversion which result in a Ci symmetry. The alkyl chains are disordered. One solvent molecule (CH2Cl2) complete the unit cell.
Computational details
All quantum chemical calculations were performed for model structures that differ from the structures of the compounds under study by replacing the long n-butyl substituents with methyl groups. This substitution should only slightly affect the electronic and spectral properties of the parent DPPTh and the DPPTh-NN2 diradical.To analyze magnetic properties of polycrystalline samples, all quantum chemical calculations were performed for the model geometry of DPPTh-NN2 diradicals and their pairs obtained from XRD analysis. The parameters of the intramolecular exchange interaction 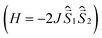 were computed using the accurate ab initio CASSCF22 and CASSCF/NEVPT2 (ref. 23 and 24) procedures. To calculate the J parameters for intermolecular exchange interactions, the spin-unrestricted broken-symmetry (BS) approach25 at the BS-B3LYP/def2-TZVP level of theory26–28 using the Yamaguchi formula29 was utilized
were computed using the accurate ab initio CASSCF22 and CASSCF/NEVPT2 (ref. 23 and 24) procedures. To calculate the J parameters for intermolecular exchange interactions, the spin-unrestricted broken-symmetry (BS) approach25 at the BS-B3LYP/def2-TZVP level of theory26–28 using the Yamaguchi formula29 was utilized
To rationalize the results of experiments performed in solutions, calculations were carried out using the model geometry optimized in toluene solution at the UB3LYP/def2-TZVP and UM06-2X/def2-TZVP levels of theory;30 the solvent was taken into account according to the CPCM model.31
The energies of electronic transitions and their oscillator strengths in the electronic absorption spectra of DPPTh and DPPTh-NN2 were calculated using the time-dependent DFT32 at the TD-B3LYP/def2-TZVP level. In the case of DPPTh-NN2, the calculations were performed for the high-spin triplet state of diradical. The zero-field splitting parameters (ZFS, D and E/D) for the lowest-energy triplet state of the DPPTh-NN2 diradical was calculated at the RO-BP86/def2-TZVP level,33,34 while the g-tensor and hyperfine splitting tensors at the B1LYP/def2-TZVP level.35
The energies of low-lying states (2 singlets, 3 triplets and 1 quintet) were also calculated at the CASSCF(14,13)/NEVPT2/def2-TZVP level. Moreover, the splittings of the triplet and quintet multiplets (ZFS) due to the dipolar spin–spin interaction and spin–orbit coupling (SOC) were evaluated using CASSCF(10,10) wavefunctions and quasi-degenerate perturbation theory (QDPT),36 as realized in the CASSCF and MRCI modules of the ORCA 5.0.5 software package.37 The contribution of SOC was calculated using the mean-field formalism (SOMF(1X))38 and found to be negligible. To the best of our knowledge, this work is the first to provide high-level calculations of the low-energy spectrum of a dye substituted with two radical fragments.
The same software package was used for all other calculations. The molecular orbitals were visualized using the Chemcraft software.39
Synthetic methods and characterization
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 50 mL) and filtered to get pigment cake, which was washed with water–methanol mixture until no color found in washings. The crude compound was dried at 100 °C in vacuo, and obtained 4.0 g of compound 2. The product was used in the next step without further purification.
1, 50 mL) and filtered to get pigment cake, which was washed with water–methanol mixture until no color found in washings. The crude compound was dried at 100 °C in vacuo, and obtained 4.0 g of compound 2. The product was used in the next step without further purification.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 55 ratio based on 1H NMR spectra. The crude mixture was purified on chromatography using 3% ethyl acetate in hexane as an eluent, and the solvent was removed under vacuum to obtain a pure product DPPTh in 40% yield. 1H NMR (300 MHz, CDCl3, ppm) δ = 8.92 (d, 2H Th–H), 7.64 (d, 2H, Th–H), 7.27 (m, 2H, Th–H), 4.07 (d, 4H, N–CH2), 1.74 (m, 4H, CH2–CH2), 1.41–1.28 (m, 12H), 0.87 (t, 12H). 13C NMR (125 MHz, CDCl3, ppm) δ = 161.37, 140.02, 135.21, 130.63, 129.77, 128.58, 107.70, 42.21, 31.39, 29.89, 26.53, 22.53, 13.98. MALDI-TOF, Mw 468.9518. Anal. calcd for C26H32N2O2S2: C, 66.63; H, 6.88; N, 5.98; S, 13.68. Found: C, 66.83; H, 7.01; N, 6.16; S, 13.42.
55 ratio based on 1H NMR spectra. The crude mixture was purified on chromatography using 3% ethyl acetate in hexane as an eluent, and the solvent was removed under vacuum to obtain a pure product DPPTh in 40% yield. 1H NMR (300 MHz, CDCl3, ppm) δ = 8.92 (d, 2H Th–H), 7.64 (d, 2H, Th–H), 7.27 (m, 2H, Th–H), 4.07 (d, 4H, N–CH2), 1.74 (m, 4H, CH2–CH2), 1.41–1.28 (m, 12H), 0.87 (t, 12H). 13C NMR (125 MHz, CDCl3, ppm) δ = 161.37, 140.02, 135.21, 130.63, 129.77, 128.58, 107.70, 42.21, 31.39, 29.89, 26.53, 22.53, 13.98. MALDI-TOF, Mw 468.9518. Anal. calcd for C26H32N2O2S2: C, 66.63; H, 6.88; N, 5.98; S, 13.68. Found: C, 66.83; H, 7.01; N, 6.16; S, 13.42.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DCM (1
DCM (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) as an eluent. Compound DPPTh-Br was obtained as a dark purple solid (0.58 g, yield 83%). 1H NMR (300 MHz, CD2Cl2, ppm) δ = 8.67 (d, 2H Th–H), 7.27 (d, 2H, Th–H), 3.98 (d, 4H, N–CH2), 1.64–1.74 (m, 4H), 1.30-8-1.40 (m, 12H), 0.89 (t, 6H). 13C NMR (75 MHz, CDCl3, ppm) δ = 160.95, 139.01, 135.32, 131.62, 131.12, 119.10, 107.90, 42.30, 31.90, 29.95, 26.80, 22.63, 14.07. UV/Vis (toluene): λmax: 550 nm. MALDI-TOF, Mw 626.47 (626.55). Anal. calcd for C26H30Br2N2O2S2: C, 49.85; H, 4.83; Br, 25.51; N, 4.47; O, 5.11; S, 10.24. Found: C, 49.76; H, 4.75; Br, 26.05; N, 4.55; S, 9.89.
1) as an eluent. Compound DPPTh-Br was obtained as a dark purple solid (0.58 g, yield 83%). 1H NMR (300 MHz, CD2Cl2, ppm) δ = 8.67 (d, 2H Th–H), 7.27 (d, 2H, Th–H), 3.98 (d, 4H, N–CH2), 1.64–1.74 (m, 4H), 1.30-8-1.40 (m, 12H), 0.89 (t, 6H). 13C NMR (75 MHz, CDCl3, ppm) δ = 160.95, 139.01, 135.32, 131.62, 131.12, 119.10, 107.90, 42.30, 31.90, 29.95, 26.80, 22.63, 14.07. UV/Vis (toluene): λmax: 550 nm. MALDI-TOF, Mw 626.47 (626.55). Anal. calcd for C26H30Br2N2O2S2: C, 49.85; H, 4.83; Br, 25.51; N, 4.47; O, 5.11; S, 10.24. Found: C, 49.76; H, 4.75; Br, 26.05; N, 4.55; S, 9.89.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) solvent mixture as an eluent. The resulted product was recrystallized two times from a mixture of CH2Cl2 with MeOH to obtain diradical NN2-DPP (90 mg, 72 %). Compound DPPTh-NN2 was eluted with Rf = 0.7 (10
1) solvent mixture as an eluent. The resulted product was recrystallized two times from a mixture of CH2Cl2 with MeOH to obtain diradical NN2-DPP (90 mg, 72 %). Compound DPPTh-NN2 was eluted with Rf = 0.7 (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of CH2Cl2/ethyl acetate); IR: ν = 2956, 2927, 2856, 1662, 1552, 1436, 1400, 1367, 1367, 1211, 1176, 1134, 1095, 870, 827, 729, 620, 540 cm−1; UV/Vis (toluene): λmax: two maxima at 573 and 624 nm and a shoulder at ∼680 nm; MALDI-TOF MS: m/z calcd. (%) for C52H76N4O4S4: 778.35 (100) [M]+, 779.36 (43) [M + 1]+; found: 778 (average MW); elemental analysis calcd: C 61.67, H 6.99, N 10.79, S 8.23; found: C 61.80, H 7.1, N 10.3, S 8.05. Melting point, 216 °C.
1 mixture of CH2Cl2/ethyl acetate); IR: ν = 2956, 2927, 2856, 1662, 1552, 1436, 1400, 1367, 1367, 1211, 1176, 1134, 1095, 870, 827, 729, 620, 540 cm−1; UV/Vis (toluene): λmax: two maxima at 573 and 624 nm and a shoulder at ∼680 nm; MALDI-TOF MS: m/z calcd. (%) for C52H76N4O4S4: 778.35 (100) [M]+, 779.36 (43) [M + 1]+; found: 778 (average MW); elemental analysis calcd: C 61.67, H 6.99, N 10.79, S 8.23; found: C 61.80, H 7.1, N 10.3, S 8.05. Melting point, 216 °C.
Single-crystal XRD analysis
Single crystal X–ray diffraction data for DPPTh-NN2 were collected at 193 K on a STOE IPDS 2T diffractometer with Cu-Kα IμS mirror system (Table 2). The structure was solved using direct methods, expanded with Fourier techniques and refined with the SHELXT software package. All non-hydrogen atoms were refined anisotropically. Hydrogen atoms were included in the structure factor calculation on geometrically idealized positions. Crystallographic data have been deposited with the Cambridge Crystallographic Data Centre as supplementary publication no. CCDC 1908216.†| Formula | C40H54N6O6S2, CH2Cl2 |
| Molecular weight | 863.93 g mol−1 |
| Absorption | μ = 2.66 mm−1 correction with six crystal faces |
| Transmission | T min = 0.7125, Tmax = 0.9602 |
| Crystal size | 0.020 × 0.020 × 0.180 mm3, black needle |
| Space group |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (triclinic) (triclinic) |
Lattice parameters (calculate from 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 587 reflections with 3.0° < θ < 62.2°) 587 reflections with 3.0° < θ < 62.2°) |
a = 7.4729(10) Å, α = 67.095(10)° |
| b = 16.121(2) Å, β = 88.242(11)° | |
| c = 19.743(3) Å, γ = 84.135(11)° | |
| V = 2179.4(5) Å3, z = 2, F(000) = 916.0 | |
| Temperature | 193 K |
| Density | d X-ray = 1.317 g cm−3 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Data collection | |
| Diffractometer | STOE IPDS 2T |
| Radiation | Cu-Kα IμS mirror system |
| Scan – type | ω scans |
| Scan – width | 1° |
| Scan range | 2° ≤ θ < 68° |
| −8 ≤ h ≤ 8, −19 ≤ k ≤ 18, −20 ≤ l ≤ 22 | |
| Number of reflections | |
| Measured | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 811 811 |
| Unique | 7446 (Rint = 0.183) |
| Observed | 1621 (|F|/σ(F) > 4.0) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|
| Data correction, structure solution and refinement | |
| Corrections | Lorentz and polarisation correction |
| Structure solution | Program: SHELXT-2014 |
| Refinement | Program: SHELXL-2014 (full matrix). 550 refined parameters, weighting scheme |
| w = 1/[σ2(Fo2) + (0.2 × P)2] with (max(Fo2,0) + 2 × Fc2)/3. H-atoms at calculated positions and refined with isotropic displacement parameters, non H-atoms refined anisotropically | |
| R-values | wR2 = 0.4395 (R1 = 0.1407 for observed reflections, 0.3430 for all reflections) |
| Goodness of fit | S = 0.881 |
| Maximum deviation of parameters | 0.001 × e.s.d |
| Maximum peak height in diff. Fourier synthesis | 0.52, −0.92 e Å−3 |
Photoinduced EPR experiments
Pulse EPR experiments were conducted at Bruker Elexsys E580 spectrometer at the Center of Collective Use ‘‘Mass spectrometric investigations’’ SB RAS at X-band (9 GHz). Spectrometer is equipped with flow helium cryostat (Oxford Instruments) and thermocontroller Lakeshore and allows measurements at T = 4–300 K. In order to measure echo-detected (ED) EPR spectra and transverse (phase) relaxation times (T2) we used standard two-pulse sequence with the pulse lengths being 10 and 20 ns for π/2 and π pulses, respectively. In case of T2 measurements, interpulse delay was incremented. Time-Resolved (TR) EPR experiments were performed using homemade spectrometer based on commercial Bruker EMX microwave bridge.In all cases the studied compounds were dissolved in toluene in concentrations ca. 0.5 mM and placed into quartz sample tubes with outer diameter of 2.8 mm. The samples were degassed by a few freeze–pump–thaw cycles and then sealed off in vacuo. EPR studies were performed for two samples: DPPTh-NN2 biradical and its photosensitive moiety DPPTh free of radical fragments.
Laser irradiation was provided by Nd:YaG LOTIS-TII system at 532 nm, power ∼ 20 mJ per pulse, 10 Hz repetition rate. In case of pulse EPR detection laser was synchronized with EPR spectrometer; laser pulse proceeded the first microwave pulse by 700 ns. In TR EPR experiments the detection was also synchronous with laser pulsing; microwave absorption was detected starting from 100 ns till 9 μs after the laser pulse.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. I. and M. F. thank the Ministry of Science and Higher Education of Russia for access to the EPR equipment. N. G. and D. G also acknowledge the Russian Science Foundation (Grant No. 22-13-00077) for financial support of the computational part of this work and the Supercomputer Centre of Novosibirsk State University for the computational resources. AK acknowledges Ramsay memorial fellowships trust, Royal Society research grant (RGS\R2\202036), EPSRC new horizons grant (EP/V048112/1).References
- D. G. Farnum, G. Mehta, G. G. I. Moore and F. P. Siegal, Tetrahedron Lett., 1974, 29, 2549 CrossRef.
- (a) B. Tieke, A. R. Rabindranath, K. Zhang and Y. Zhu, Beilstein J. Org. Chem., 2010, 6, 830 CrossRef; (b) S. Qu and H. Tian, Chem. Commun., 2012, 48, 3039 RSC; (c) C. B. Nielsen, M. Turbiez and I. McCulloch, Adv. Funct. Mater., 2013, 25, 1859 CrossRef CAS; (d) D. Chandran and K.-S. Lee, Macromol. Res., 2013, 21, 272 CrossRef CAS; (e) Y. Li, P. Sonar, L. Murphy and W. Hong, Energy Environ. Sci., 2013, 6, 1684 RSC; (f) M. Kaur and D. H. Choi, Chem. Soc. Rev., 2015, 44, 58 RSC; (g) M. Grzybowski and D. Gryko, Adv. Opt. Mater., 2015, 3, 280 CrossRef CAS.
- E. Tretyakov, A. Keerthi, M. Fedin, N. Troshkova, E. Zaytseva, I. Shundrina and M. Baumgarten, CCDC 1908216: Experimental Crystal Structure Determination, 2020 Search PubMed.
- R. Rausch, A.-M. Krause, I. Krummenacher, H. Braunschweig and F. Würthner, J. Org. Chem., 2021, 86, 2447 CrossRef CAS.
- M. Shinomiya, K. Higashiguchi and K. Matsuda, J. Org. Chem., 2013, 78, 9282 CrossRef CAS PubMed.
- B. W. H. Saes, M. Lutz, M. M. Wienk, S. C. J. Meskers and R. A. J. Janssen, J. Phys. Chem. C, 2020, 124, 25229 CrossRef CAS.
- R. Tanimoto, S. Suzuki, M. Kozaki and K. Okada, Chem. Lett., 2014, 43, 678 CrossRef CAS.
- E. Tretyakov, K. Okada, S. Suzuki, M. Baumgarten, G. Romanenko, A. Bogomyakov and V. Ovcharenko, J. Phys. Org. Chem., 2016, 29, 725 CrossRef CAS.
- I. Zayakin, E. Tretyakov, A. Akyeva, M. Syroeshkin, J. Burykina, A. Dmitrenok, A. Korlyukov, D. Nasyrova, I. Bagryanskaya, D. Stass and V. P. Ananikov, Chem.–Eur. J., 2022, e202203118 Search PubMed.
- E. Tretyakov, A. Keerthi, M. Baumgarten, S. Veber, M. Fedin, D. Gorbunov, I. Shundrina and N. Gritsan, ChemistryOpen, 2017, 6, 642 CrossRef CAS.
- M. Haraguchi, E. Tretyakov, N. Gritsan, G. Romanenko, D. Gorbunov, A. Bogomyakov, K. Maryunina, S. Suzuki, M. Kozaki, D. Shiomi, K. Sato, T. Takui, S. Nishihara, K. Inoue and K. Okada, Chem.–Asian J., 2017, 12, 2929 CrossRef CAS PubMed.
- E. V. Tretyakov, T. V. Makhneva, L. V. Politanskaya, I. Yu. Bagryanskaya and D. V. Stass, J. Struct. Chem., 2018, 59, 689 CrossRef CAS.
- M. Slota, A. Keerthi, W. K. Myers, E. Tretyakov, M. Baumgarten, A. Ardavan, H. Sadeghi, C. J. Lambert, A. Narita, K. Müllen and L. Bogani, Nature, 2018, 557, 691 CrossRef CAS PubMed.
- E. V. Tretyakov, V. I. Ovcharenko, A. O. Terent'ev, I. B. Krylov, T. V. Magdesieva, D. G. Mazhukin and N. P. Gritsan, Russ. Chem. Rev., 2022, 91, RCR5025 CrossRef CAS.
- I. J. Bruno, J. C. Cole, M. Kessler, J. Luo, W. D. S. Motherwell, L. H. Purkis, B. R. Smith, R. Taylor, R. I. Cooper, S. E. Harris and A. G. Orpen, J. Chem. Inf. Comput. Sci., 2004, 44, 2133 CrossRef CAS PubMed.
- A. Serykh, E. Tretyakov, P. Fedyushin, B. Ugrak, T. Dutova, A. Lalov, A. Korlyukov, A. Akyeva, M. Syroeshkin, A. Bogomyakov, G. Romanenko, N. Artiukhova, M. Egorov and V. Ovcharenko, J. Mol. Struct., 2022, 1269, 133739 CrossRef CAS.
- H. M. McConnell, J. Chem. Phys., 1963, 39, 1910 CrossRef CAS.
- Q. A. Alsulami, S. M. Aly, S. Goswami, E. Alarousu, A. Usman, K. S. Schanze and O. F. Mohammed, J. Phys. Chem. C, 2015, 119, 15919 CrossRef CAS.
- S. L. Veber, S. V. Tumanov, E. Yu. Fursova, O. A. Shevchenko, Ya. V. Getmanov, M. A. Scheglov, V. V. Kubarev, D. A. Shevchenko, I. I. Gorbachev, T. V. Salikova, G. N. Kulipanov, V. I. Ovcharenko and M. V. Fedin, J. Magn. Reson., 2018, 288, 11 CrossRef CAS PubMed.
- M. V. Fedin, E. G. Bagryanskaya, H. Matsuoka, S. Yamauchi, S. L. Veber, K. Yu. Maryunina, E. V. Tretyakov, V. I. Ovcharenko and R. Z. Sagdeev, J. Am. Chem. Soc., 2012, 134, 16319 CrossRef CAS PubMed.
- M. Fukuda, K. Kodama, H. Yamamoto and K. Mito, Dyes Pigm., 2004, 63, 115 CrossRef CAS.
- M. Frisch, I. N. Ragazos, M. A. Robb and H. B. Schlegel, Chem. Phys. Lett., 1992, 189, 524 CrossRef CAS.
- K. Andersson, P.-Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218 CrossRef CAS.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J. P. Malrieu, J. Chem. Phys., 2001, 114, 10252 CrossRef CAS.
- H. Nagao, M. Nishino, Y. Shigeta, T. Soda, Y. Kitagawa, T. Onishi, Y. Yoshika and K. Yamaguchi, Coord. Chem. Rev., 2000, 198, 265 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- T. Soda, Y. Kitagawa, T. Onishi, H. Nagao, Y. Yoshioka and K. Yamaguchi, Chem. Phys. Lett., 2000, 319, 223 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215 Search PubMed.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995 CrossRef CAS.
- A. Dreuw and M. Head-Gordon, Chem. Rev., 2005, 105, 4009 CrossRef CAS PubMed.
- A. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822 CrossRef.
- C. Adamo and V. Barone, Chem. Phys. Lett., 1997, 274, 242 CrossRef CAS.
- D. Ganyushin and F. Neese, J. Chem. Phys., 2006, 125, 024103 CrossRef.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- F. Neese, J. Chem. Phys., 2005, 122, 034107 CrossRef.
- ChemCraft – Graphical Software for Visualization of Quantum Chemistry Computations, Version 1.8, build 654, https://www.chemcraftprog.com Search PubMed.
- A. B. Tamayo, M. Tantiwiwat, B. Walker and T.-Q. Nguyen, J. Phys. Chem. C, 2008, 112, 15543 CrossRef CAS.
- A. B. Tamayo, B. Walker and T.-Q. Nguyen, J. Phys. Chem. C, 2008, 112, 11545 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Electronic absorption and FTIR spectra, CV profiles versus the Fc+/Fc redox couple, TGA and DSC curves of DPPTh-NN2, details of DFT and ab initio calculations were presented. CCDC 1908216 for DPPTh-NN2. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4ra00916a |
| This journal is © The Royal Society of Chemistry 2024 |