Open Access Article
Open Access ArticleModeling and optimization of transesterification of Jatropha oil to fatty acid methyl ester: application of response surface methodology (CCD) and Taguchi orthogonal method
Cyrus Aseibichin a,
Wisdom Chukwuemeke Ulakpa
a,
Wisdom Chukwuemeke Ulakpa *b,
Ikoko Omenogorc,
Emmanuel Doyah
*b,
Ikoko Omenogorc,
Emmanuel Doyah d,
Ayodeji Arnold Olaseinde
d,
Ayodeji Arnold Olaseinde e,
Oghenekome Cyril Anakpoha
e,
Oghenekome Cyril Anakpoha b,
Mabel Keke
b,
Mabel Keke b and
Shankar Karuppannan
b and
Shankar Karuppannan *fg
*fg
aDepartment of Chemical/Petrochemical Engineering, Rivers State University, Nkpolu-Oroworukwo, Port Harcourt, 500101, Nigeria
bDepartment of Chemical Engineering, Delta State University of Science and Technology, Ozoro, 334111, Nigeria. E-mail: ulakpa.wisdom@yahoo.com
cDepartment of Agriculture and Bioresource Engineering, Delta State Polytechnic, Ogwashi-Uku, 320107, Nigeria
dDepartment of Petroleum and Gas Engineering, Delta State University of Science and Technology, Ozoro, 334111, Nigeria
eDepartment of Materials Science and Engineering, College of Engineering, Computing and Applied Sciences, Clemson University, Clemson, South Carolina 26934, USA
fDepartment of Applied Geology, School of Applied Natural Science, Adama Science and Technology University, Adama, Ethiopia. E-mail: geoshankar1984@gmail.com
gDepartment of Research Analytics, Saveetha Dental College and Hospitals, Saveetha Institute of Medical and Technical Sciences (SIMATS), Saveetha University, Chennai 600077, Tamilnadu, India
First published on 12th April 2024
Abstract
The study effectively optimized the transesterification process of Jatropha oil to fatty acid methyl ester using response surface methodology (CCD) and Taguchi orthogonal method, leading to enhanced efficiency and product quality. The optimization of five process parameters was conducted to predict the biodiesel yield (%) from the transesterification of Jatropha oil. The procedure was made easier with the use of a nanocatalyst made from calcium oxide obtained from snail shells using the hydrothermal technique. The RSM approach yielded an optimal FAME of 94.10% under specific conditions: a methanol to oil ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, catalyst weight of 1.5 w/w, reaction temperature of 50 °C, reaction duration of 45 minutes, and an agitation speed of 250 rpm across 32 experimental trials. On the other hand, the Taguchi method predicted a higher FAME yield of 86.36% using specific operational parameters. These parameters included a methanol to oil ratio of 4
1, catalyst weight of 1.5 w/w, reaction temperature of 50 °C, reaction duration of 45 minutes, and an agitation speed of 250 rpm across 32 experimental trials. On the other hand, the Taguchi method predicted a higher FAME yield of 86.36% using specific operational parameters. These parameters included a methanol to oil ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, catalyst weight of 0.5 w/w, reaction temperature of 60 °C, reaction duration of 25 minutes, and an agitation speed of 200 rpm. These parameters were determined through 16 experimental trials. The RSM technique yielded impressive results with a determined coefficient of determination (R2) of 0.9943, adjusted R2 of 0.9838, predicted R2 of 0.8470, and a coefficient of variance (CV) of 0.65. On the other hand, the Taguchi method had coefficients of 0.8994, 0.7483, and 1.95. The FAME yield of RSM was slightly higher, but the Taguchi method was much more cost-efficient. The analysis of variance (ANOVA) results showed that the methanol to oil ratio had the highest influence on the yield, accounting for 49.61% of the variation. This highlights the significant impact of this factor on the overall process. The study highlights the significance of utilizing advanced techniques such as TOA and RSM, which are known for their effectiveness. The study aims to enhance the yield and efficiency of the transesterification process, thereby increasing the overall production of fatty acid methyl ester from Jatropha oil. This innovative approach efficiently generates biodiesel from renewable resources, like Jatropha oil, in a manner that is both environmentally friendly and maximizes the effectiveness of the process parameters.
1, catalyst weight of 0.5 w/w, reaction temperature of 60 °C, reaction duration of 25 minutes, and an agitation speed of 200 rpm. These parameters were determined through 16 experimental trials. The RSM technique yielded impressive results with a determined coefficient of determination (R2) of 0.9943, adjusted R2 of 0.9838, predicted R2 of 0.8470, and a coefficient of variance (CV) of 0.65. On the other hand, the Taguchi method had coefficients of 0.8994, 0.7483, and 1.95. The FAME yield of RSM was slightly higher, but the Taguchi method was much more cost-efficient. The analysis of variance (ANOVA) results showed that the methanol to oil ratio had the highest influence on the yield, accounting for 49.61% of the variation. This highlights the significant impact of this factor on the overall process. The study highlights the significance of utilizing advanced techniques such as TOA and RSM, which are known for their effectiveness. The study aims to enhance the yield and efficiency of the transesterification process, thereby increasing the overall production of fatty acid methyl ester from Jatropha oil. This innovative approach efficiently generates biodiesel from renewable resources, like Jatropha oil, in a manner that is both environmentally friendly and maximizes the effectiveness of the process parameters.
1. Introduction
Energy serves as a critical catalyst in facilitating socioeconomic progress and enhancing human welfare. The current global energy landscape is dominated by fossil fuels. The escalating global energy needs have in turn amplified the exploration of these energy sources. The finite nature of fossil fuel reserves, coupled with the environmental degradation they cause and their fluctuating prices, underscore the necessity for energy security and environmental preservation.1The exploitation of fossil fuels often results in detrimental ecological impacts, including the greenhouse effect, global warming, and acid deposition.2 These adverse effects have catalyzed the quest for alternative energy sources. Researchers are zeroing in on viable substitutes for fossil fuels, with an emphasis on renewable energy sources such as solar, wind, and hydropower. Biodiesel, in particular, is being viewed as a promising alternative to reduce humankind's excessive reliance on fossil fuels.3 Because of its unique qualities; biodiesel has recently gained popularity as a possible substitute for petroleum diesel. When compared to diesel fuel, biodiesel boasts several advantages including renewability, biodegradability, a high flash point, high combustion efficiency, a high cetane number, low sulfur content, and less environmental harm.3 Greater use of biodiesel could effectively minimize pollutants and mobile carcinogens. Biodiesel is obtained from sustainable resources, including oil-producing plants and microscopic algae.
The right feedstock has the potential to cut the total biodiesel production cost by a third.4 Oil-producing plants can be classified into two types: those that produce edible oils and those that yield non-edible oils. The category of edible oils includes oils derived from soybeans, peanuts, coconuts, corn, palm, and sunflowers. The use of edible plant oil poses a significant drawback – it competes with food production, thereby potentially limiting food availability and escalating food prices.
Research is underway to identify alternative feedstock options for producing biodiesel.2 Non-edible oils, on the other hand, include Jatropha curcas, oil from the neem tree, Jojoba extract, apricot kernel oil, cottonseed oil, and tobacco seed oil. Other substances encompass animal-derived fats, recycled vegetable oil, and pork fat also serve as sources for biodiesel production. WVO, in particular, can help lower production costs as its procurement doesn't incur additional expenses. Non-edible oils also help mitigate the problem of food competition. They are not without their shortcomings, such as low yields and high-cost reactions that demand increased volumes of alcohol.5 To overcome these obstacles associated with non-edible plant oils, researchers are innovating processing techniques that enhance biodiesel production efficiency and pave the way for large-scale commercial production. Moreover, biodiesel can be generated using a variety of methods, including pyrolysis, micro-emulsification, dilution, and transesterification/esterification.4,6
The transesterification process involves the continuous and reversible transformation of triglycerides into a mixture of esters (biodiesel) and glycerol with the help of a catalyst. This process consists of three distinct phases where triglycerides are converted into diglycerides, monoglycerides, and glycerol, while simultaneously producing one mole of ester at each stage in both laboratory and industrial settings.7,8 A key aspect of this reaction is the substantial use of alcohol, as this promotes a shift in the reaction equilibrium favoring the generation of more biodiesel. Literature reported that catalyst is the crucial factor in converting triglycerides (oil) to FAMEs (biodiesel) under a transesterification reaction.11 Among the different types of catalyst materials are commonly used in industrial applications, including homogeneous alkaline or acidic catalysts like NaOH, KOH, and H2SO4. Despite their widespread use, these catalysts have limitations such as soap formation, reactor corrosion, and difficulties in catalyst recovery. To address these challenges, the development and utilization of heterogeneous catalysts offer advantages over homogeneous catalysts and help overcome their drawbacks.9,10 Basic and acidic catalysts are essential to expedite the transesterification process and enhance its yield. The three distinct categories of catalysts include homogeneous, heterogeneous, and biocatalysts.13 The transesterification process offers the advantage of versatility, permitting the use of diverse feedstock types to create fuels with characteristics akin to traditional diesel.
Both heterogeneous and homogeneous catalysts have been utilized in biodiesel production. Various types of animal and plant waste have been employed in the synthesis of heterogeneous catalysts, which could consist of acids, bases, or enzymes.11
To separate the product, neutralisation and separation steps must be included when using homogeneous catalysts for esterification processes. It becomes necessary to employ heterogeneous acidic catalysts that do not necessitate these additional stages. The process of biodiesel production achieves its highest potential with the use of a heterogeneous catalyst. Calcium oxide (CaO) derived from waste shells is an exceptionally effective base heterogeneous catalyst for biodiesel production. CaO catalysts exhibit high catalytic activity, are cost-effective, and exhibit minimal solubility in methanol and biodiesel.12
Several optimization studies have demonstrated that operational parameters significantly impact the production process. Factors influencing biodiesel production include reaction temperature, reaction duration, methanol to oil ratio, catalyst quantity, and mixing strength. The impact of these factors on yield is typically assessed individually.13
Numerous methodologies including response surface methodology (RSM), Taguchi orthogonal array, artificial neural networks (ANN), matrix laboratory (MATLAB), simulink, adaptive neuro-fuzzy inference systems (ANFIS), Box–Behnken design, and genetic algorithm (GA) have been employed to enhance the transesterification of vegetable oil into Fatty Acid Methyl Esters (FAME). These methodologies can be applied individually, blended, or juxtaposed with other techniques utilizing soft computing methods to maximize FAME yield.14 Experimental procedures, often referred to as one-variable-at-a-time (OVAT), are undertaken by altering a single variable while maintaining others constant. This process must be repeated for all influential parameters, leading to an unpredictable number of experiments. Yet, to effectively optimize these influential factors and decrease the number of experiments, the implementation of experimental design techniques can be advantageous. Thus, software-guided methodologies can be efficiently used that require a limited number of experimental runs and scrutinize the derived results for their precision through statistical ANOVA (analysis of variance). Among these, RSM-based methodologies like CCD (central composite design) and BBD (Box–Behnken design) still employ repeated runs around the central points for optimizing the conversion process. Fractional factorial design (FFD), one of the methods for CCD, is a thorough and multipurpose method for creating models, planning experiments, analysing the effects of various parameters and their interactions, and identifying the best response variables.15 A superior and alternative approach is factorial methods such as Taguchi OA (orthogonal array) and PBD (Plackett Burmann design) which require a significantly fewer number of runs with no repetitions and display the results as effects of individual parameters on the process response, unlike RSM methods which indicate interactive effects on the process response. The response surface approach encapsulates a variety of mathematical and statistical techniques used to scrutinize data, formulate models, identify optimal conditions, and rank the significance of factors influencing a process. Within the biodiesel industry, efficiency and cost-effectiveness are of utmost importance, thus optimizing the production process is a primary concern for researchers.16 TDA ensures superior performance in the design phase of products or processes. Taguchi design method is an optimization tool that offers a straightforward, effective, and systematic approach to enhance the design for performance, quality, and cost.17 Incorporating the Taguchi design method in the production process can result in reduced process variability, coupled with the need for less time, reagents, and experimental runs.17
The optimization process utilizes the CCD approach with a total of 32 runs along with an L16 Taguchi matrix. This combination denotes the amalgamation of necessary parametric factors for process fine-tuning, while also minimizing the number of required experiments. The research analyzes the parameter influence on the process and their individual effects, using Analysis of Variance (ANOVA). This technique also effectively contrasts the gathered data with mathematically forecasted values, and demonstrates experimental precision through statistically significant factors.
The transesterification of Jatropha oil to fatty acid methyl ester is the main subject of this study, with a particular emphasis on the creative application of response surface methodology (CCD) and Taguchi orthogonal approach. In order to improve the productivity and efficiency of the transesterification process and ultimately increase the amount of fatty acid methyl ester that is produced from Jatropha oil, these cutting-edge procedures are essential. The goal of the research is to optimize process parameters and support the sustainable manufacture of biodiesel from renewable sources, such as Jatropha oil, by adopting these approaches.
Modeling and optimizing the transesterification of Jatropha oil to fatty acid methyl ester is highly beneficial for enhancing productivity, sustainability, and expertise in renewable energy production.
The justification behind using the Taguchi orthogonal method and response surface methodology (CCD) for the optimisation process is that both are well-known and often applied methods in the field of experimental design and optimisation. Response surface methodology (CCD) enables the investigation of the relationship between input variables and output responses, making it especially helpful for modelling and optimising processes with multiple variables. However, the Taguchi orthogonal approach is well-known for being an efficient way to run tests because it minimises the number of repetitions required to obtain the best findings. The study sought to increase efficiency and product quality by methodically optimising the transesterification process of Jatropha oil to fatty acid methyl ester.
Process optimisation can be approached methodically and effectively with the use of RSM (CCD) and TOA methods. These methods offer benefits including robustness to noise, efficient experimental design, thorough design space exploration, and statistical analysis capabilities.
2 Materials and methods
2.1 Materials
The primary material chosen for this study was snail shell, owing to its plentiful availability in Nigeria. The feedstock selected for the experiment was Jatropha oil (JCO). For this research, specific analytical grade reagents like methanol with a purity level of 99.9% were obtained from Palmlac Chemicals, Minna, Niger State, in Nigeria. Deionized distilled water with a purity level of 99% was consistently used in all experimental procedures. The feedstock chosen was Jatropha oil from National Research Institute for Chemical Technology, Zaria, Kaduna State, Nigeria in order to produce biodiesel.2.2 Transesterification process
The process of transesterification was executed within a batch reactor, utilizing CaO nanocatalyst as a significant component. The methodology of the experiment was constructed on the principles of a central composite design (CCD) featuring 32 runs, along with the Taguchi orthogonal array L16 (45). The independent variables accounted for in the process included reaction temperature (measured in °C), catalyst weight (w/w), reaction duration (in minutes), the molar ratio of methanol to oil (M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O), and the speed of agitation (rpm). The chemical reaction involving Jatropha oil (JO) and methanol was conducted under a range of varying conditions. The temperature of the reaction was maintained at different degrees, specifically 50, 60, and 70 °C, primarily around the methanol's boiling point (65 °C) to reduce evaporation losses. This was facilitated by a reflux condenser which recycled the methanol vapor back into the reaction vessel. An initial study was conducted to ascertain the possibility of biodiesel formation under the least values of the varied conditions. To eliminate errors, all experimental runs were duplicated, and only the consistent outcomes were taken into account. Factors such as the value of methanol, catalyst concentration, reaction temperature, reaction duration, and agitation speed were dependent on the specific run being executed.
O), and the speed of agitation (rpm). The chemical reaction involving Jatropha oil (JO) and methanol was conducted under a range of varying conditions. The temperature of the reaction was maintained at different degrees, specifically 50, 60, and 70 °C, primarily around the methanol's boiling point (65 °C) to reduce evaporation losses. This was facilitated by a reflux condenser which recycled the methanol vapor back into the reaction vessel. An initial study was conducted to ascertain the possibility of biodiesel formation under the least values of the varied conditions. To eliminate errors, all experimental runs were duplicated, and only the consistent outcomes were taken into account. Factors such as the value of methanol, catalyst concentration, reaction temperature, reaction duration, and agitation speed were dependent on the specific run being executed.
The ultimate resolution was subsequently subjected to vacuum filtration to retrieve the catalyst. The sieved mixture was then shifted into a spotless separating funnel, leaving it untroubled overnight. Glycerol was detected to clot at the base of the separating funnel. After this, the clotting glycerol was discharged, and the residual crude was decanted. The raw biodiesel was later moved into a glass receptacle for further refinement and assessment. The output of biodiesel creation was appraised through a designated mathematical formula (1).
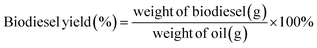 | (1) |
The primary difficulties in transesterification of Jatropha oil to fatty acid methyl ester include unpredictability in reaction conditions, contaminants in the raw materials, and the formation of unwanted byproducts. The difficulties were overcome in the design and optimisation of the experiment by adjusting the temperature, catalyst concentration, and reaction time, choosing premium raw materials, implementing purification techniques, and closely monitoring the progress of the reaction. By carefully planning experiments and optimising process parameters, it is possible to increase the efficiency and yield of the manufacture of fatty acid methyl ester from Jatropha oil.
2.3 Modeling and optimization by response surface methodology-RSM (CCD)
The process of enhancing biodiesel production from the transesterification of Jatropha oil into methyl ester was carried out by utilizing the central composite design (CCD) from the response surface methodology variant of the design of experiment (DOE) accessible through the Design-Expert software. Response surface methodology (RSM) serves as a statistical tool for modeling and optimization of intricate processes. In this research, RSM grounded on CCD was used to assess the impact of process variables on FAME yield. A quadratic model was established using ANOVA to anticipate the FAME yield as a function of independent variables. The exploration of parametric elements in the transesterification process of Jatropha oil was aimed at enhancing the process. These elements included the ratio of methanol to oil, catalyst concentration, reaction temperature, reaction time, and the speed of agitation, as shown in Table 1. The study involved a total of 32 runs, including 24 non-central points, 6 central points, and an alpha of 2. User inputs of low (−α) and high (+α) levels are incorporated into the software, which generates additional levels. (RSM CCD) with the aid of Design Expert Software version 13.0.1.0. The experimental factors and their levels were determined based on preliminary study and literature. The choice of this methodology was dictated by the quantity of variables and levels. Data from the 32 experimental runs was evaluated using the Response Surface Methodology Central Composite Design.| Factor | Name | Units | −α | −1 | 0 | +1 | +α |
|---|---|---|---|---|---|---|---|
| A | Methanol to oil ratio | mol/mol | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
| B | Catalyst weight | w/w | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
| C | Reaction temperature | OC | 30 | 40 | 50 | 60 | 70 |
| D | Reaction time | min | 25.00 | 35 | 45 | 55 | 65 |
| E | Agitation speed | rpm | 150.00 | 200 | 250. | 300 | 350 |
2.4 Modeling and optimization by Taguchi orthogonal method
The Taguchi orthogonal technique is a reliable design strategy aiming to curtail the impact of noise factors on the outcome. This procedure entails selecting a suitable orthogonal array and carrying out a signal-to-noise ratio (S/N) analysis to pinpoint the best levels of process variables. The primary benefit of the Taguchi approach is its capability to ensure robustness and stability during the optimization process, enabling it to identify minor variables swiftly. The factors examined encompass the ratio of methanol to oil, catalyst concentration, reaction temperature, reaction duration, and the speed of agitation. By utilizing the Taguchi technique, a mere 16 experiments are necessary to ascertain the optimal levels of the variables (Table 6). As such, the Taguchi approach can decrease the number of tests, save time, cut costs, and identify key factors swiftly, all without adversely impacting the operating parameters, while preserving all necessary details.18 In this research, the L16 (415) design was selected, featuring 16 rows that accommodate four levels and five parameters in the Taguchi method. The number of runs, N, was calculated using eqn (2).| N = (L − 1)P + 1 | (2) |
In this context, ‘P’ represents the quantity of selected design and control parameters, while ‘L’ stands for the number of levels. According to eqn (2), the total number of runs using Taguchi Orthogonal Array (OA) is 16. The results of the experiment were scrutinized using the signal-to-noise (S/N) ratio to determine the influence of the variables on the Fatty Acid Methyl Ester (FAME) yield. The signal-to-noise ratio (SNR) is essentially the logarithmic function of the calculated outcome. The S/N ratio falls into three distinct categories – smaller-the-better, larger-the-better, and nominal-the-better.14 However, in this research, the larger-the-better S/N was chosen due to the primary goal of the optimization being to attain the highest possible yield. The effect of the variables on FAME yield was evaluated by analyzing the experimental results using the S/N ratio. The S/N ratio was used to compute the discrepancy between the response and the expected outcome.
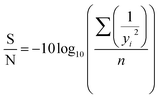 | (3) |
The equation, where yi represents the response value and n signifies the number of experimental runs, is used for S/N ratio analysis. This analysis enables the identification of the optimal level for each parameter, as well as the optimized parameter set that results in the highest FAME yield. Consequently, the most beneficial mix of parameters governing the process can be projected. However, this method falls short in explicating the individual parameters' influence on the FFA conversion. This gap can be filled by employing an analysis of variance to estimate the statistical parameters.19 In the ANOVA study, the Fisher test (F-value) is used to ascertain the importance of the selected model and the individual parameter's impact on the response. The p-value, on the other hand, offers insight into the likelihood of attaining an F-value of this magnitude. The sum of squares derived from the model and individual parameter was employed to ascertain each parameter's contribution factor and assess its effect on biodiesel yield. An ultimate experiment was carried out three times over to validate the predictions at the optimal process parameters and to look for any variances between the actual and predicted response.19 The contribution factor for each parameter gives an understanding of its effect on the process and can be computed using eqn (4).
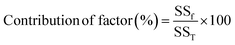 | (4) |
In this context, SSf denotes the sum of squares of a specific variable, while SST represents the sum of squares of all variables. The objective of this analysis is to enhance the conversion rate of FFA. As a result, the optimal condition was selected with the aim of maximizing the target. A linear regression model formula can establish a relationship between the anticipated response and the actual response, ascertained through experimental runs, for all process variables. This can be instrumental in verifying the accuracy of the model.20
3. Results and discussion
3.1 Response surface method (CCD) statistical results
Table 2 illustrates the outcomes from the transesterification process of Jatropha into FAME, utilizing the RSM through CCD experimental methodology. The FAME yield, derived from actual experiments, fluctuated within the range of 75.73% to 94.20%. The genuine yields were evaluated to create a feasible and functional regression model. The model was chosen from an array of types such as mean, linear, quadratic, cubic, quartic, and so forth. A quadratic regression model was devised and applied to ascertain the ideal parameters for the transesterification of JCO into biodiesel utilizing the software. The digital model was articulated as a second-order polynomial equation in an encoded form, as illustrated in eqn (5).| Yield = +81.21 − 1.37A − 0.9942B − 0.2700C − 1.17D + 1.07E + 2.38AB − 0.7050AC − 0.5350AD − 1.68AE + 0.9075BC + 0.3375BD − 1.16BE − 0.4225CD + 0.2700CE − 1.64DE + 0.9102A2 + 0.2465B2 − 0.5123C2 − 0.8898D2 + 2.10E2 | (5) |
| Run | A: methanol to oil ratio (mol/mol) | B: catalyst weight (w/w) | C: reaction temperature (°C) | D: reaction time (min) | E: agitation speed (rpm) | Actual yield (%) | Predicted yield (%) |
|---|---|---|---|---|---|---|---|
| 1 | 4 | 2 | 60 | 35 | 300 | 86.39 | 86.63 |
| 2 | 4 | 2 | 60 | 55 | 200 | 81.43 | 81.45 |
| 3 | 4 | 2 | 40 | 55 | 300 | 79.29 | 79.53 |
| 4 | 4 | 1 | 40 | 55 | 200 | 86.03 | 85.72 |
| 5 | 5 | 1.5 | 50 | 45 | 250 | 81.18 | 81.21 |
| 6 | 5 | 1.5 | 50 | 45 | 250 | 81.18 | 81.21 |
| 7 | 5 | 1.5 | 50 | 25 | 250 | 79.75 | 79.99 |
| 8 | 5 | 1.5 | 50 | 45 | 150 | 86.78 | 87.46 |
| 9 | 5 | 1.5 | 50 | 45 | 250 | 81.18 | 81.21 |
| 10 | 6 | 1 | 40 | 55 | 300 | 78.97 | 79.21 |
| 11 | 6 | 2 | 40 | 55 | 200 | 85.86 | 85.88 |
| 12 | 5 | 1.5 | 70 | 45 | 250 | 79.04 | 78.62 |
| 13 | 5 | 1.5 | 30 | 45 | 250 | 79.46 | 79.70 |
| 14 | 7 | 1.5 | 50 | 45 | 250 | 82.54 | 82.12 |
| 15 | 5 | 1.5 | 50 | 65 | 250 | 75.73 | 75.31 |
| 16 | 5 | 1.5 | 50 | 45 | 250 | 81.18 | 81.21 |
| 17 | 5 | 1.5 | 50 | 45 | 250 | 81.18 | 81.21 |
| 18 | 5 | 0.5 | 50 | 45 | 250 | 83.94 | 84.18 |
| 19 | 4 | 1 | 60 | 55 | 300 | 88.24 | 88.48 |
| 20 | 4 | 1 | 40 | 35 | 300 | 94.2 | 94.10 |
| 21 | 6 | 2 | 40 | 35 | 300 | 83.45 | 83.69 |
| 22 | 4 | 1 | 60 | 35 | 200 | 83.22 | 82.90 |
| 23 | 3 | 1.5 | 50 | 45 | 250 | 87.34 | 87.58 |
| 24 | 6 | 2 | 60 | 35 | 200 | 84.65 | 84.67 |
| 25 | 4 | 2 | 40 | 35 | 200 | 76.94 | 76.63 |
| 26 | 6 | 1 | 60 | 35 | 300 | 83.11 | 83.35 |
| 27 | 6 | 1 | 60 | 55 | 200 | 76.77 | 76.79 |
| 28 | 6 | 1 | 40 | 35 | 200 | 82.22 | 81.91 |
| 29 | 5 | 1.5 | 50 | 45 | 250 | 81.18 | 81.21 |
| 30 | 5 | 1.5 | 50 | 45 | 350 | 92.6 | 91.74 |
| 31 | 6 | 2 | 60 | 55 | 300 | 77.51 | 78.08 |
| 32 | 5 | 2.5 | 50 | 45 | 250 | 80.63 | 80.21 |
The yield of Fatty Acid Methyl Esters (FAME) is symbolized as ‘y’ in percentage. The variables A, B, C, D, and E represent the ratio of methanol to oil, the weight of the catalyst, the temperature and the duration of the reaction, as well as the speed of agitation, respectively. Positive coefficients (linear, interactive, or quadratic) positively impact the FAME yield, while negative coefficients have an adverse effect. Table 2 reveals that the highest FAME yield, predicted at 91.74% by the Response Surface Methodology (RSM) regression model, was achieved with specific conditions: a methanol to oil ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5, a catalyst weight of 1.5, a reaction temperature of 50 °C, a reaction time of 45 minutes, and an agitation speed of 350 rpm. These factors, particularly the methanol to oil ratio, catalyst, reaction time, and agitation speed, significantly influence the FAME yield.
5, a catalyst weight of 1.5, a reaction temperature of 50 °C, a reaction time of 45 minutes, and an agitation speed of 350 rpm. These factors, particularly the methanol to oil ratio, catalyst, reaction time, and agitation speed, significantly influence the FAME yield.
As indicated in Table 3, both the F-value and the P-value signify that the model, the terms, the term squares, and their interactions have substantial importance. A p-value of less than 0.05 implies statistical significance when exploring the relation between these factors and FAME content.13 The model equation was evaluated for its statistical significance using the ANOVA test, R2, and Radj2 (Table 4). The model's F-value and p-value were calculated at 95.35 and less than 0.0001, respectively. This suggests that the model has a statistical significance at the 95% confidence interval level (p less than 0.05). In this model, the variable ‘A’ with the highest F-test value of 153.02 and a p-value less than 0.0001, was the most statistically significant parameter. This implies that the methanol to oil ratio was the most crucial factor influencing FAME yield, as shown in Table 3.
| Source | Sum of squares | df | Mean square | F-value | p-value | |
|---|---|---|---|---|---|---|
| Model | 558.62 | 20 | 27.93 | 95.35 | <0.0001 | Significant |
| A – methanol to oil ratio | 44.83 | 1 | 44.83 | 153.02 | <0.0001 | |
| B – catalyst weight | 23.72 | 1 | 23.72 | 80.97 | <0.0001 | |
| C – reaction temperature | 1.75 | 1 | 1.75 | 5.97 | 0.0326 | |
| D – reaction time | 32.95 | 1 | 32.95 | 112.47 | <0.0001 | |
| E – agitation speed | 27.48 | 1 | 27.48 | 93.80 | <0.0001 | |
| AB | 90.44 | 1 | 90.44 | 308.73 | <0.0001 | |
| AC | 7.95 | 1 | 7.95 | 27.15 | 0.0003 | |
| AD | 4.58 | 1 | 4.58 | 15.63 | 0.0023 | |
| AE | 45.43 | 1 | 45.43 | 155.07 | <0.0001 | |
| BC | 13.18 | 1 | 13.18 | 44.98 | <0.0001 | |
| BD | 1.82 | 1 | 1.82 | 6.22 | 0.0298 | |
| BE | 21.44 | 1 | 21.44 | 73.18 | <0.0001 | |
| CD | 2.86 | 1 | 2.86 | 9.75 | 0.0097 | |
| CE | 1.17 | 1 | 1.17 | 3.98 | 0.0714 | |
| DE | 42.90 | 1 | 42.90 | 146.45 | <0.0001 | |
| A2 | 24.30 | 1 | 24.30 | 82.96 | <0.0001 | |
| B2 | 1.78 | 1 | 1.78 | 6.08 | 0.0313 | |
| C2 | 7.70 | 1 | 7.70 | 26.28 | 0.0003 | |
| D2 | 23.22 | 1 | 23.22 | 79.27 | <0.0001 | |
| E2 | 129.08 | 1 | 129.08 | 440.63 | <0.0001 | |
| Residual | 3.22 | 11 | 0.2929 | |||
| Lack of fit | 3.22 | 6 | 0.5371 | |||
| Pure error | 0.0000 | 5 | 0.0000 | |||
| Cor total | 561.85 | 31 |
| Std. dev. | 0.5412 | R2 | 0.9943 |
| Mean | 82.60 | Adjusted R2 | 0.9838 |
| CV (%) | 0.6553 | Predicted R2 | 0.8470 |
| Adeq precision | 42.8714 |
Table 5 displays the results of the significance test for the model. The model's accuracy and precision were confirmed through the R2 and Radj2 values. An R2 value of 0.9943 signifies that 99.43% of the total data harmonized with the forecasted data and its variability. An Radj2 value of 0.9838 signifies a satisfactory fitness level for the model. A signal-to-noise (S/N) ratio greater than 4 is considered to be favorable and beneficial. The S/N ratio of 42.87 indicates the model's adaptability to navigate the design space and further validates the statistical significance of the created model (Table 4). A standard deviation of 0.5412 was observed, and a minimal coefficient of variation (CV) of 0.655% indicates the model's high accuracy and reliability.
| Factor | Coefficient estimate | df | Standard error | 95% CI low | 95% CI high | VIF |
|---|---|---|---|---|---|---|
| Intercept | 81.21 | 1 | 0.2159 | 80.73 | 81.68 | |
| A – methanol to oil ratio | −1.37 | 1 | 0.1105 | −1.61 | −1.12 | 1.0000 |
| B – catalyst weight | −0.9942 | 1 | 0.1105 | −1.24 | −0.7510 | 1.0000 |
| C – reaction temperature | −0.2700 | 1 | 0.1105 | −0.5132 | −0.0268 | 1.0000 |
| D – reaction time | −1.17 | 1 | 0.1105 | −1.41 | −0.9285 | 1.0000 |
| E – agitation speed | 1.07 | 1 | 0.1105 | 0.8268 | 1.31 | 1.0000 |
| AB | 2.38 | 1 | 0.1353 | 2.08 | 2.68 | 1.0000 |
| AC | −0.7050 | 1 | 0.1353 | −1.00 | −0.4072 | 1.0000 |
| AD | −0.5350 | 1 | 0.1353 | −0.8328 | −0.2372 | 1.0000 |
| AE | −1.68 | 1 | 0.1353 | −1.98 | −1.39 | 1.0000 |
| BC | 0.9075 | 1 | 0.1353 | 0.6097 | 1.21 | 1.0000 |
| BD | 0.3375 | 1 | 0.1353 | 0.0397 | 0.6353 | 1.0000 |
| BE | −1.16 | 1 | 0.1353 | −1.46 | −0.8597 | 1.0000 |
| CD | −0.4225 | 1 | 0.1353 | −0.7203 | −0.1247 | 1.0000 |
| CE | 0.2700 | 1 | 0.1353 | −0.0278 | 0.5678 | 1.0000 |
| DE | −1.64 | 1 | 0.1353 | −1.94 | −1.34 | 1.0000 |
| A2 | 0.9102 | 1 | 0.0999 | 0.6903 | 1.13 | 1.02 |
| B2 | 0.2465 | 1 | 0.0999 | 0.0265 | 0.4664 | 1.02 |
| C2 | −0.5123 | 1 | 0.0999 | −0.7322 | −0.2923 | 1.02 |
| D2 | −0.8898 | 1 | 0.0999 | −1.11 | −0.6698 | 1.02 |
| E2 | 2.10 | 1 | 0.0999 | 1.88 | 2.32 | 1.02 |
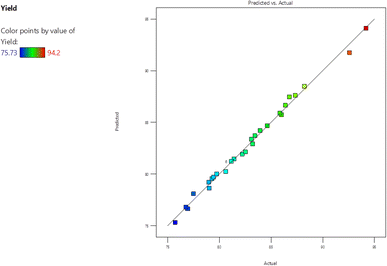
Fig. 1 illustrates the definitive outcomes gleaned from the conducted trials in comparison to the forecasted data derived from the empirical model. The graph displays a line with a unit slope, a perfect fit line, which corresponds to zero discrepancy between the hypothesized and factual values. As depicted in Fig. 1, the model provides a fairly comprehensive representation of the experimental data concerning the yield of FAME. The proximity of all the points to the line of perfect fit, as evident from the graph, indicates a considerable correlation between the predicted and experimental values of the independent variable. This further expounds on the adequacy of the mode.
3.2 Process parameters interactions
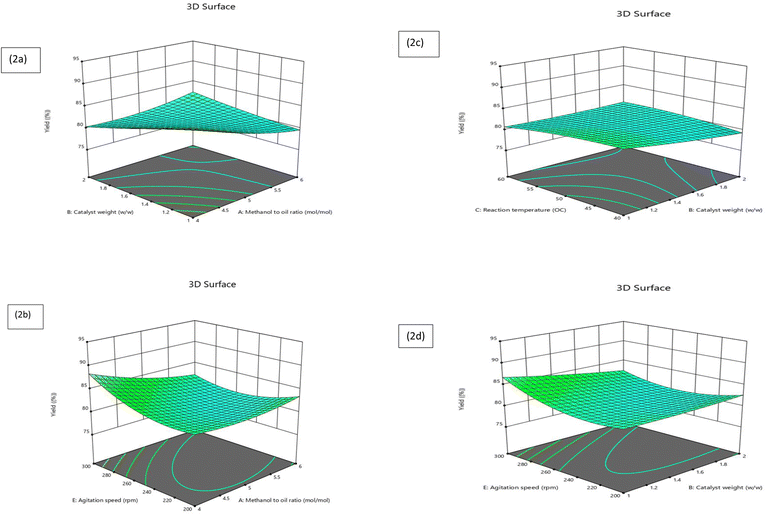
In this research, a three-dimensional plot was employed to explore the impact of various elements on the outcome, specifically, biodiesel output derived from the transesterification procedure of Jatropha oil using a calcium oxide nanocatalyst. The results from the three-dimensional (3D) surface plots generated from the Response Surface Methodology (RSM) can provide valuable insights into the correlations among process parameters and optimizing FAME yield. By visualizing the interactions between different variables on the surface plots, researchers can identify optimal operating conditions that lead to maximum FAME yield. These plots help in understanding the complex relationships between process parameters and their impact on the outcome, allowing for more informed decision-making in optimizing the transesterification process. Additionally, the 3D surface plots can aid in identifying potential areas for further experimentation or refinement to enhance FAME yield. A 3D plot offers a visual depiction of the regression formula that illustrates two elements, while keeping the remaining factors constant, as stated by eqn (5). Displayed in Fig. 2 is the 3D plot where the y-axis is displaced from the x-axis. It was discovered that the process variables exhibited substantial interactive effects.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 results in a downturn in the FAME yield. This aligns with prior conclusions, affirming that an optimal methanol to oil ratio positively influences the FAME yield during biodiesel production via the transesterification process. Additionally, a larger methanol to oil ratio fosters a surge in FAME formation. Similarly, an increase in the catalyst content catalyzes the ester yield. However, the ester yield commences to decline when the catalyst content approximates 1.5 wt%. A higher methanol-to-oil molar ratio also positively affects the ester yield up to a certain limit. Notably, a methanol-to-oil molar ratio exceeding approximately 5
1 results in a downturn in the FAME yield. This aligns with prior conclusions, affirming that an optimal methanol to oil ratio positively influences the FAME yield during biodiesel production via the transesterification process. Additionally, a larger methanol to oil ratio fosters a surge in FAME formation. Similarly, an increase in the catalyst content catalyzes the ester yield. However, the ester yield commences to decline when the catalyst content approximates 1.5 wt%. A higher methanol-to-oil molar ratio also positively affects the ester yield up to a certain limit. Notably, a methanol-to-oil molar ratio exceeding approximately 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is considered unfavorable for attaining a higher ester yield in the current study. The methanol to oil ratio exhibits a more pronounced effect.
1 is considered unfavorable for attaining a higher ester yield in the current study. The methanol to oil ratio exhibits a more pronounced effect.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 5
1 to 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, coupled with a surge in agitation speed up to 250 rpm, leads to a notable augmentation in yield. However, surpassing a methanol to oil ratio of 5
1, coupled with a surge in agitation speed up to 250 rpm, leads to a notable augmentation in yield. However, surpassing a methanol to oil ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and an agitation speed of 250 rpm results in a yield decrease.
1 and an agitation speed of 250 rpm results in a yield decrease.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The yield of FAME shows a gradual increase with the enhancement of the catalyst quantity. Furthermore, a rise in the reaction temperature boosts the FAME yield linearly, indicating that temperature plays a more pivotal role in influencing FAME yield than the quantity of catalyst.
1. The yield of FAME shows a gradual increase with the enhancement of the catalyst quantity. Furthermore, a rise in the reaction temperature boosts the FAME yield linearly, indicating that temperature plays a more pivotal role in influencing FAME yield than the quantity of catalyst.3.3 Taguchi orthogonal method results
| Run | A: methanol to oil ratio (mol/mol) | B: catalyst weight (w/w) | C: reaction temperature (OC) | D: reaction time (min) | E: agitation speed (rpm) | Actual yield (%) | Predicted yield |
|---|---|---|---|---|---|---|---|
| 1 | 4 | 1 | 30 | 65 | 300 | 86.39 | 85.87 |
| 2 | 6 | 2.5 | 40 | 25 | 300 | 81.43 | 81.73 |
| 3 | 7 | 2 | 40 | 65 | 150 | 79.29 | 79.17 |
| 4 | 7 | 2.5 | 30 | 55 | 200 | 86.03 | 86.36 |
| 5 | 6 | 2 | 30 | 35 | 350 | 81.18 | 82.59 |
| 6 | 7 | 1 | 60 | 25 | 350 | 81.18 | 80.27 |
| 7 | 4 | 2.5 | 60 | 35 | 150 | 79.75 | 81.98 |
| 8 | 4 | 2 | 70 | 25 | 200 | 86.78 | 86.26 |
| 9 | 7 | 0.5 | 70 | 35 | 300 | 81.18 | 81.88 |
| 10 | 3 | 2 | 60 | 55 | 300 | 78.97 | 78.48 |
| 11 | 6 | 0.5 | 60 | 65 | 200 | 85.86 | 85.03 |
| 12 | 3 | 1 | 40 | 35 | 200 | 79.04 | 80.05 |
| 13 | 3 | 0.5 | 30 | 25 | 150 | 79.46 | 78.24 |
| 14 | 4 | 0.5 | 40 | 55 | 350 | 82.54 | 81.35 |
| 15 | 3 | 2.5 | 70 | 65 | 350 | 75.73 | 76.43 |
| 16 | 6 | 1 | 70 | 55 | 150 | 81.18 | 80.30 |
| Source | Sum of squares | df | Mean square | F-value | p-value | Contribution factors (%) | Optimum value | |
|---|---|---|---|---|---|---|---|---|
| Model | 135.29 | 9 | 15.03 | 5.96 | 0.0208 | Significant | ||
| A – methanol to oil ratio | 67.12 | 3 | 22.37 | 8.87 | 0.0126 | 49.61 | 4 | |
| C – reaction temperature | 15.97 | 3 | 5.32 | 2.11 | 0.2003 | 11.80 | 60 | |
| E – agitation speed | 52.20 | 3 | 17.40 | 6.90 | 0.0226 | 38.58 | 200 | |
| Residual | 15.13 | 6 | 2.52 | |||||
| Cor total | 150.42 | 15 |
The coefficient of determination (R2), adjusted R2, and predicted R2 are illustrated in Table 8, also derived from the ANOVA study. The F-value of 5.96 affirms the model's adequate fit. Any model term with a p-value less than 0.05 was deemed significant. In this context, the methanol to oil ratio, reaction temperature, and agitation speed were significant model terms, while catalyst weight and reaction time were not. Furthermore, the R2 value of 0.8994 suggests that the operating variables studied accounted for 89.94% of the total variation, leaving only 10.06% of the variation unexplained by the model. The proximity of the R2 value to unity indicates the model's linearity and suitability. The adjusted R2 value was found to be 0.7485, while the predicted R2 was 0.2846 for the selected model.
| Std. dev. | 1.59 | R2 | 0.8994 |
| Mean | 81.62 | Adjusted R2 | 0.7485 |
| CV (%) | 1.95 | Predicted R2 | 0.2846 |
| Adeq precision | 7.9149 |
Adequate precision, which assesses the signal-to-noise ratio, is desirable when greater than 4. However, in this study, a value of 7.914 suggested a satisfactory signal, as shown in Table 8. This adequate precision of 7.914 demonstrates that the model is capable of predicting the dependent variable and optimizing FAME yield effectively. Moreover, the standard deviation was deduced to be 1.59, while the variance coefficient was 1.95%, affirming the model's competence to precisely predict the optimal parameters. The proportionate contribution (CP) of each vital process parameter was evaluated using eqn (4) (Table 7). The contribution factors of the methanol to oil ratio, reaction temperature, and agitation speed were determined to be 44.62%, 10.61% and 34.70%, respectively. The methanol to oil ratio had the paramount CP, indicating its significant influence on the transesterification process. The contribution factor outcome aligns with the ANOVA result, demonstrating that the methanol to oil ratio exercises the most substantial impact on FAME yield. A multiple regression model analysis was conducted to ascertain the impact of each parameter on biodiesel yield. The numerical values obtained for each significant parameter coefficient at a 95% confidence level are articulated in mathematical terms for predicting FAME yield and are illustrated in eqn (5). The mathematical model equation from the Taguchi method (eqn (5) correlates the three significant parameters in predicting the response.
| Y = +81.62 − 3.32A[1] + 2.24A[2] + 0.7881A[3] + 1.64C[1] − 1.05C[2] − 0.1844C[3] −1.70E[1] + 2.80E[2] + 0.3681E[3] | (6) |
In this context, Y denotes the percentage yield of Fatty Acid Methyl Esters (FAME), while A[1], A[2], and A[3] represent the methanol to oil ratio. C[1], C[2], and C[3] indicate the reaction temperature, whereas E[1], E[2], and E[3] signify the agitation speed, as detailed in Table 9. This equation is instrumental in distinguishing the comparative effects of these factors by contrasting their coefficients. The model equation incorporates only crucial parameters, namely the methanol to oil ratio, reaction temperature, and agitation speed.
| Term | Coefficient estimate | df | Standard error | 95% CI low | 95% CI high |
|---|---|---|---|---|---|
| Intercept | 81.62 | 1 | 0.3970 | 80.65 | 82.60 |
| A[1] | −3.32 | 1 | 0.6877 | −5.01 | −1.64 |
| A[2] | 2.24 | 1 | 0.6877 | 0.5579 | 3.92 |
| A[3] | 0.7881 | 1 | 0.6877 | −0.8946 | 2.47 |
| C[1] | 1.64 | 1 | 0.6877 | −0.0421 | 3.32 |
| C[2] | −1.05 | 1 | 0.6877 | −2.73 | 0.6333 |
| C[3] | −0.1844 | 1 | 0.6877 | −1.87 | 1.50 |
| E[1] | −1.70 | 1 | 0.6877 | −3.39 | −0.0217 |
| E[2] | 2.80 | 1 | 0.6877 | 1.12 | 4.49 |
| E[3] | 0.3681 | 1 | 0.6877 | −1.31 | 2.05 |
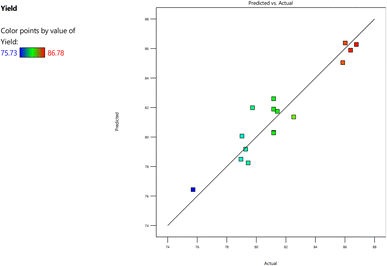
The negligible parameters, such as reaction time and catalyst weight, were excluded from the model equation. The graph delineating the experimental and projected values is illustrated in Fig. 3. This graph demonstrates that the values closely align with the favored model, thereby underscoring the model's importance and reliability in assessing the yields. The model's degree of freedom equates to one, with a confidence interval of 95% and the standard error of the parameters being 0.68 (Table 9). The linear regression model equation possesses the ability to prognosticate the FAME yield using the parameters and data provided in Table 6. The impact of the three significant parameters on biodiesel yield is exhibited in Fig. 3a–c.
3.3.2.1 Effect of methanol to oil ratio. The study demonstrates that the ratio of methanol to oil significantly influences the yield of Jatropha biodiesel (Table 7). The optimal Fatty Acid Methyl Ester (FAME) yield was achieved under specific reaction conditions: a catalyst weight of 0.5, a reaction temperature of 30 °C, a reaction duration of 25 minutes, and an agitation speed of 150 rpm. The most effective methanol to oil ratio was determined to be 4
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, as corroborated by Fig. 4a. This is because, stoichiometrically, maintaining a molar ratio of 3
1, as corroborated by Fig. 4a. This is because, stoichiometrically, maintaining a molar ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 throughout the entire reaction is necessary, making a ratio of 4
1 throughout the entire reaction is necessary, making a ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ample. Conversely, an excess of alcohol can dilute the reaction system to such an extent that the reactant molecules and catalyst are unable to interact sufficiently, thereby slowing the reaction rate. It is crucial to exercise caution to prevent the catalyst from being diluted with surplus methanol, as this could deactivate the catalyst's functionality within the reaction process. Consequently, an excessive increase in the methanol to oil ratio can impede the separation of glycerol, which in turn results in a reduced biodiesel yield.14,21
1 ample. Conversely, an excess of alcohol can dilute the reaction system to such an extent that the reactant molecules and catalyst are unable to interact sufficiently, thereby slowing the reaction rate. It is crucial to exercise caution to prevent the catalyst from being diluted with surplus methanol, as this could deactivate the catalyst's functionality within the reaction process. Consequently, an excessive increase in the methanol to oil ratio can impede the separation of glycerol, which in turn results in a reduced biodiesel yield.14,21
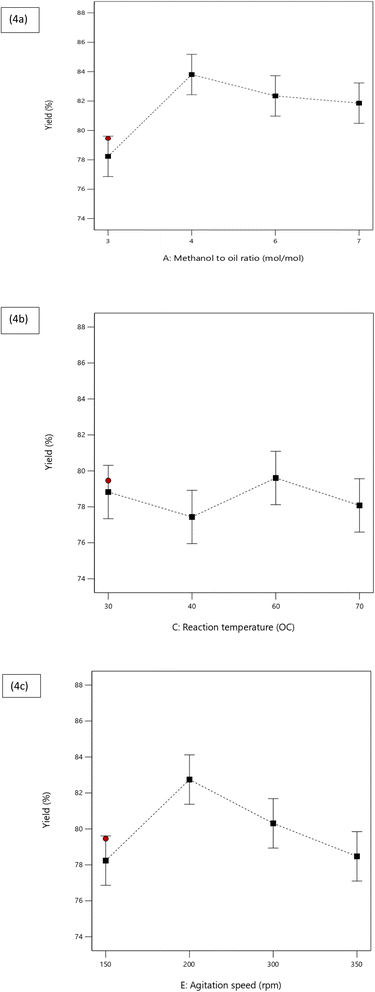 | ||
| Fig. 4 (a) Effect of methanol to oil ratio ratio (mol/mol), (b) reaction temperature (°C), and (c) agitation speed (rpm) of FAME yield (%). | ||
3.3.2.2 Effect of reaction temperature. Fig. 4b illustrates the significant impact of the reaction temperature on the reaction rate and product yield. The temperature range examined, from 30 °C to 70 °C, encompassed four distinct levels, with 60 °C identified as the optimal temperature for the highest reaction rate. As indicated in Fig. 4b, the yield surges from 30 °C and peaks at 60 °C, only to plummet dramatically with any further temperature increase. While a temperature elevation accelerates the reaction rate, an excessive increase surpassing the boiling point of methanol during production is counterproductive. This can disturb the molar ratio of methanol in the reaction mixture due to evaporation. The corresponding effect can potentially cause a shift in the reversible equilibrium towards the retrograde reaction, thereby promoting the formation of triglycerides, or soap. However, from data presented in Table 7, it can be inferred that this parameter only contributes 11.80% to the overall process, which suggests that even at the bare minimum optimization level, the reaction temperature remains a crucial factor in product formation. 20–22
3.3.2.3 Effect of agitation speed. Fig. 4c clearly demonstrates that the ideal output was attained at a stirring velocity of 200 rotations per minute (rpm). Stirring speed plays a critical role in the transesterification process of biodiesel, as evidenced by Fig. 4c. The yield of biodiesel escalates as the stirring speed intensifies, suggesting that the turbidity induced by swift stirring contributes to the elevated recurrence of reactant interactions at a molecular level. Intense stirring also curtails the opposition faced during mass transitioning, thereby augmenting the reaction rate and yield. However, a slight reduction in yield is noticed beyond 200 rpm, likely due to inadequate interaction time amongst the reactants when agitation is excessive.23
3.4 Comparison of RSM and Taguchi method
The current research compared the efficacy of the Fatty Acid Methyl Ester (FAME) yield prediction using the Response Surface Methodology (RSM) optimization modality against the Taguchi Orthogonal Array (OA) method. The parallel findings from both optimization methods were consistent and harmonious, identifying critical parameters for the FAME yield prediction based on the predetermined factors and levels. Both methodologies constructed model equations derived from the significant factors identified.The RSM and Taguchi method concurred on the significant parameters relevant to the model. However, the Taguchi method demanded less experimental data, reduced operational costs, and optimized results for maximum yield, while RSM was also capable of utilizing quadratic or cubic regression. The congruency in the predicted and actual FAME yield suggested a consensus between the two optimization techniques.
The RSM models highlighted five key parameters influencing the FAME yield, while the Taguchi model outlined only three. The RSM's prediction of the optimal FAME yield surpassed that of the Taguchi method. According to RSM and Taguchi, the parameters most significantly impacting FAME yield were reaction time and the methanol to oil ratio, respectively.
The RSM utilized a methanol to oil ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mol/mol, a catalyst weight of 1.5% wt, a reaction temperature of 50 degrees Celsius, a reaction time of 45 minutes, and a speed of 250 rpm for optimal yield. In contrast, the Taguchi orthogonal method applied a methanol to oil ratio of 4
1 mol/mol, a catalyst weight of 1.5% wt, a reaction temperature of 50 degrees Celsius, a reaction time of 45 minutes, and a speed of 250 rpm for optimal yield. In contrast, the Taguchi orthogonal method applied a methanol to oil ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mol/mol, a catalyst weight of 0.5% wt, a reaction temperature of 60 degrees Celsius, a reaction time of 25 minutes, and an agitation speed of 200 rpm for optimal yield. In the RSM, the methanol to oil molar ratio, catalyst weight, reaction time, and agitation speed emerged as significant parameters, with the methanol to oil ratio being the most significant. Conversely, the Taguchi method identified the methanol to oil ratio, reaction temperature, and agitation speed as significant parameters, with the methanol to oil ratio being the most influential.The RSM, with 32 experimental runs, resulted in an R2 value of 0.9943, an adjusted R2 value of 0.9838, and a coefficient of variation (CV) of 0.6553. Meanwhile, the Taguchi method with 16 experimental runs had an R2 value of 0.8994, an adjusted R2 value of 0.7485, and a CV of 1.95.
1 mol/mol, a catalyst weight of 0.5% wt, a reaction temperature of 60 degrees Celsius, a reaction time of 25 minutes, and an agitation speed of 200 rpm for optimal yield. In the RSM, the methanol to oil molar ratio, catalyst weight, reaction time, and agitation speed emerged as significant parameters, with the methanol to oil ratio being the most significant. Conversely, the Taguchi method identified the methanol to oil ratio, reaction temperature, and agitation speed as significant parameters, with the methanol to oil ratio being the most influential.The RSM, with 32 experimental runs, resulted in an R2 value of 0.9943, an adjusted R2 value of 0.9838, and a coefficient of variation (CV) of 0.6553. Meanwhile, the Taguchi method with 16 experimental runs had an R2 value of 0.8994, an adjusted R2 value of 0.7485, and a CV of 1.95.
4. Conclusion
This research examined the transesterification of Jatropha oil into FAME, employing a CaO nanocatalyst. The study applied response surface methodology (RSM) and Taguchi's orthogonal approach (TOA) to optimize the process parameters. Both methodologies offered valuable understanding of how these variables influence FAME yield, leading to the identification of ideal conditions. The outcomes indicated that both the RSM and Taguchi techniques are efficacious in optimizing the transesterification process. The models generated from both methods were significant, with their derived equations predicting FAME yield with an acceptable margin of error. RSM predicted a higher optimum FAME yield than Taguchi, demonstrating RSM's superior optimization capability. In the RSM model, four out of the five parameters tested were deemed significant, with the methanol to oil ratio (mole/mole) identified as the most statistically significant parameter due to its highest F-value of 153.02. In the Taguchi method, the methanol to oil ratio was also the most significant among the three significant parameters, having an F-value of 8.87 and a contribution factor of 49.61. The variance analysis for FAME yield revealed that both the R2 and Radj2 confirmed the validation and consistency of the models with the predicted value, thus certifying their acceptability and adequacy. Although RSM was more precise, the Taguchi method, requiring only 16 runs, proved to be more cost-effective and less time-demanding than RSM with 32 runs.One notable advancement in the subject has been the modeling and optimization of the transesterification of Jatropha oil to fatty acid methyl ester by the use of Taguchi orthogonal technique and response surface methodology (CCD). These cutting-edge methods have been essential in increasing the transesterification process's output and efficiency, which has improved the amount of biodiesel that can be produced from Jatropha oil. The study has emphasized the significance of sustainable production practices and the possibility for future developments in the field of renewable energy sources by improving process parameters through these approaches. The incorporation of these techniques has opened up avenues for additional study and advancement within the biodiesel manufacturing sector.
Expanding the optimised transesterification process for converting Jatropha oil to fatty acid methyl ester can yield substantial environmental and economic benefits. Looking at it from an environmental perspective, utilising Jatropha oil for biodiesel production has the potential to lower greenhouse gas emissions in comparison to conventional fossil fuels. Biodiesel is a sustainable and eco-friendly fuel that plays a crucial role in reducing air pollution and promoting environmental sustainability. Companies can enhance efficiency, decrease waste generation, and lessen environmental impact by refining the transesterification process using methods such as response surface methodology (CCD) and Taguchi orthogonal method.
From an economic perspective, expanding the optimised transesterification process can result in cost savings by improving production efficiency and increasing yields. Through careful adjustment of process parameters and streamlining the production workflow, businesses can reduce production expenses and enhance overall financial performance. Moreover, the increasing interest in biodiesel as a sustainable substitute for traditional diesel fuels offers chances for market growth and potential income. On the whole, scaling up the optimised transesterification process can bring about favourable outcomes for the environment and the economy, fostering sustainable practices and enhancing the efficiency of the energy sector.
In order to further advance the field of biodiesel production from Jatropha oil via process parameter optimization, the following future research directions can be suggested based on the findings of the study on transesterification of Jatropha oil to fatty acid methyl ester using response surface methodology and Taguchi orthogonal method: optimizing the process parameters found in the study to increase fatty acid methyl ester yield and quality could be the subject of future research. This could entail experimenting with various catalysts, mixing ratios, and reaction temperatures in order to maximize transesterification process efficiency. Pilot-scale trials may potentially be used in future studies to evaluate the economic and practicality of extending the optimized process to a greater scale.
In conclusion, the novelty of modeling and optimizing the transesterification of Jatropha oil to fatty acid methyl ester using response surface methodology (CCD) and Taguchi orthogonal method lies in its innovative approach to enhancing the efficiency, quality, and practical applicability of biodiesel production processes. By leveraging these advanced optimization techniques, researchers are able to push the boundaries of traditional methods and pave the way for more sustainable and effective biodiesel production practices.
Abbreviations
| ANOVA | Analysis of variance |
| CCD | Central composite design |
| CV | Coefficient of variance |
| DOE | Design of experiment |
| FAME | Fatty acid methyl ester |
| FFD | Fractional factorial design |
| R2 | Coefficient of determination |
| RSM | Response surface methodology |
| TOA | Taguchi orthogonal approach |
Author contributions
Wisdom Chukwuemeke Ulakpa: conceptualization, investigation, methodology, writing – original draft; Aseibichin Cyrus: writing – reviewing and editing; Ikoko Omenogor: supervision, writing – reviewing and editing; Emmanuel Doyah: conceptualization, methodology and supervision; Ayodeji Arnold Olaseinde: writing – reviewing and editing; Oghenekome Cyril Anapoha,: conceptualization, methodology and supervision; Mabel Keke: reviewing and editing; Shankar Karuppannan: reviewing and editing.Conflicts of interest
The authors confirm no conflict of interest.Acknowledgements
The authors acknowledged the Department of Agricultural and Bio resource Engineering, Federal University of Technology, Minna, Niger State and the Department of Chemical Engineering, Delta State University of Science and Technology, Ozoro for the analysis.References
- C. M. Agu, K. A. Ani, O. N. Ani, P. C. Nnaji a, C. H. Kadurumba and C. E. Esonye, Application of efficient soft computing approaches for modeling methyl ester yield from Azadirachta Indical (Neem) seed oil: A comparative study of RSM, ANN and ANFIS, Green Technologies and Sustainability, 2024, 2, 100057, DOI:10.1016/j.grets.2023.100057.
- W. Lu, H. Wang, J. Fan and Z. Han, Synthesis, catalysts and enhancement technologies of biodiesel from oil feedstock – A review, Sci. Total Environ., 2023, 904, 166982, DOI:10.1016/j.scitotenv.2023.166982.
- J. Q. M. Almarashi, S. E. El-Zohary, M. A. Ellabban and A. E.-F. Abomohra, Enhancement of lipid production and energy recovery from the green microalga Chlorella vulgaris by inoculum pretreatment with low-dose cold atmospheric pressure plasma (CAPP), Energy Convers. Manage., 2020, 204, 112314, DOI:10.1016/j.enconman.2019.112314.
- E. O. Babatunde, B. Karmakar, M. A. Olutoye, U. G. Akpan, M. Auta and G. Halder, Parametric optimization by Taguchi L9 approach towards biodiesel production from restaurant waste oil using Fe-supported anthill catalyst, J. Environ. Chem. Eng., 2020, 8(5), 104288, DOI:10.1016/j.jece.2020.104288.
- M. A. Bashir, S. Wu, J. Zhu, A. Krosuri, M. U. Khan and R. J. Ndeddy, Recent development of advanced processing technologies for biodiesel production: a critical review, Fuel Process. Technol., 2022, 227, 107120, DOI:10.1016/j.fuproc.2021.107120.
- W. C. Ulakpa, R. O. E. Ulakpa, M. C. Egwunyenga and T. C. Egbosiuba, Transesterification of non-edible oil and effects of process parameters on biodiesel yield, Cleaner Waste Systems, 2022, 3, 100047, DOI:10.1016/j.clwas.2022.100047.
- M. Athar and S. Zaidi, S, A review of the feedstocks, catalysts, and intensification techniques for sustainable biodiesel production, J. Environ. Chem. Eng., 2020, 8, 104523, DOI:10.1016/j.jece.2020.104523.
- L. Peng, A. Bahadoran, S. Sheidaei, P. J. Ahranjani, H. Kamyab, B. Oryani, S. S. Arain and S. Rezani, Magnetic graphene oxide supported tin oxide (SnO) nanocomposite as a heterogeneous catalyst for biodiesel production from soybean oil, Renewable Energy, 2024, 120050, DOI:10.1016/j.renene.2024.120050.
- J. A. Okolie, J. I. Escobar, G. Umenweke, W. Khanday and P. U. Okoye, Continuous biodiesel production: a review of advances in catalysis, microfluidic and cavitation reactors, Fuel, 2022, 307, 121821, DOI:10.1016/j.fuel.2021.121821.
- B. H. Jume, E. Parandi, M. Nouri, B. Aghel, A. Gouran, H. R. Nodeh, H. kamyab, J. Cho and S. Rezania, Chem. Eng. Process., 2023, 191, 109479, DOI:10.1016/j.cep.2023.109479.
- O. Awogbemi, D. V. VonKallon and V. S. Aigbodion, Trends in the development and utilization of agricultural wastes as heterogeneous catalyst for biodiesel production, J. Energy Inst., 2021, 98, 244–258 CrossRef CAS.
- F. A. Aisien, K. O. Uwadiae and E. T. Aisien, Process optimization for blended waste frying oil in biodiesel production using CaO derived from African periwinkle shell catalyst through response surface methodology, Sustainable Chemistry for the Environment, 2023, 4, 100042, DOI:10.1016/j.scenv.2023.100042.
- W. C. Ulakpa, C. N. Ude and R. O. Ulakpa, Optimization, Kinetics and Thermodynamics Study of Transesterification of Neem Oil Using Heterogeneous Catalyst Derived from Waste of Goat Bones, Int. J. Eng. Res. Technol., 2019, 7(9), 7–18 Search PubMed.
- A. Omojola, F. L. Inambao and E. I. Onuh, Modelling and Optimization of Transesterification of Waste Sunflower Oil to Fatty Acid Methyl Ester: A case of Response Surface Methodology vs Taguchi Orthogonal Approach, Int. J. Eng. Res. Technol., 2019, 12, 2346–2361 Search PubMed.
- R. Parichehreh, R. Gheshlaghi, M. A. Mahdavi and H. Kamyab, Investigating the effects of eleven key physicochemical factors on growth and lipid accumulation of Chlorella sp. as a feedstock for biodiesel production, J. Biotechnol., 2021, 340(10), 64–74, DOI:10.1016/j.jbiotec.2021.08.010.
- W. C. Ulakpa, R. O. E. Ulakpa, E. O. Eyankware and M. C. Egwunyenga, Statistical optimization of biodiesel synthesis from waste cooking oil using NaOH/bentonite impregnated catalyst, Cleaner Waste Systems, 2022, 3, 100049, DOI:10.1016/j.clwas.2022.100049.
- A. S. Yusuff, O. A. Ajayi and L. T. Popoola, Application of Taguchi design approach to parametric optimization of adsorption of crystal violet dye by activated carbon from poultry litter, Sci. Afr., 2021, 13, e00850, DOI:10.1016/j.sciaf.2021.e00850.
- S. Shojaei, S. Shojaei, S. S. Band, A. A. K. Farizhandi, M. Ghoroqi and A. Mosavi, Application of Taguchi method and response surface methodology into the removal of malachite green and auramine-O by NaX nanozeolites, Sci. Rep., 2021, 11, 16054, DOI:10.1038/s41598-021-95649-5.
- B. Karmakar, S. H. Dhawane and G. Halder, Optimization of biodiesel production from castor oil by Taguchi design, J. Environ. Chem. Eng., 2018, 6, 2684–2695, DOI:10.1016/j.jece.2018.04.019.
- S. H. Dhawane, T. Kumar and G. Halder, Biodiesel synthesis from Hevea brasiliensis oil employing carbon supported heterogeneous catalyst: optimization by Taguchi method, Renewable Energy, 2016, 89, 506–514 CrossRef CAS.
- A. Etim, P. Musonge, C. Andrew and E. Eboka, A Novel Green Bio-composite Heterogeneous Catalyst Synthesis for the Optimized Transesterification of Linseed-Marula bi-oil Methyl Ester Production, 33rd JOHANNESBURG Int'l Conference on “Chemical, Biological & Environmental Engineering” (JCBEE-22), Johannesburg (South Africa), 2022, pp. 113–121, DOI:10.17758/IICBE3.C0322225.
- B. Karmakar, S. H. Dhawane and G. Halder, Optimization of biodiesel production from castor oil by Taguchi design, J. Environ. Chem. Eng., 2018, 6, 2684–2695, DOI:10.1016/j.jece.2018.04.019.
- G. Halder, B. Karmakar and S. H. Dhawane, Optimization of biodiesel production from castor oil by Taguchi design, J. Environ. Chem. Eng., 2018, 6, 2684–2695 CrossRef.
| This journal is © The Royal Society of Chemistry 2024 |