Open Access Article
Open Access ArticleMechanism of cationic ring-opening polymerisation of ε-caprolactone using metallocene/borate catalytic systems: a DFT and NCI study on chain initiation, propagation and termination†
Wijitra Meeluaab,
Mikko Linnolahti c and
Jitrayut Jitonnom
c and
Jitrayut Jitonnom *b
*b
aDemonstration School, University of Phayao, Phayao 56000, Thailand
bUnit of Excellence in Computational Molecular Science and Catalysis, and Division of Chemistry, School of Science, University of Phayao, Phayao 56000, Thailand. E-mail: jitrayut.018@gmail.com; jitrayut.ji@up.ac.th
cDepartment of Chemistry, University of Eastern Finland Joensuu Campus, Yliopistokatu 7, FI-80100 Joensuu, Finland
First published on 11th April 2024
Abstract
We present a comprehensive DFT investigation on the cationic ring-opening polymerisation (CROP) of ε-caprolactone (CL) using zirconocene/borate catalyst systems. All possible pathways of the interaction between cationic species [Cp2ZrMe+] and counteranions, [A−] = [MeB(C6F5)3]− and [B(C6F5)4]−, were examined during chain initiation, propagation, and termination steps. The calculations reveal an active chain-end mechanism with O-alkyl bond cleavage of the polymerisation. The catalytic performance of the two counteranions is found to be identical, and they influence the initial process through stabilisation of the cationic species via non-covalent interactions (NCI), with the [MeB(C6F5)3]− anion stabilising the catalyst–monomer complex more effectively than the [B(C6F5)4]− anion by 24.3 kJ mol−1. The first two propagations are likely the rate-determining step, with calculated free-energy barriers of 61.4–71.2 and 73.9–80.6 kJ mol−1 with and without the anions (A−), respectively. The presence of the counteranion significantly affects the third propagation rate, lowering the barriers up to 20 kJ mol−1. Comparison of the first termination and the third propagation shows that they are not competitive, with the termination being less facile. We also studied the initiation and propagation steps for the hafnocene catalyst and found that the Hf catalyst slightly favours the CL CROP in comparison to the Zr catalyst. Analysis of solvent and dispersion interaction demonstrates that both factors play an important role in the process. NCI analysis reveals weak (van der Waals) interactions at the contacts between the cationic species and the counteranions during the reaction course. Overall, our results offer insights into the structures and interactions involved in the polymerisation.
1 Introduction
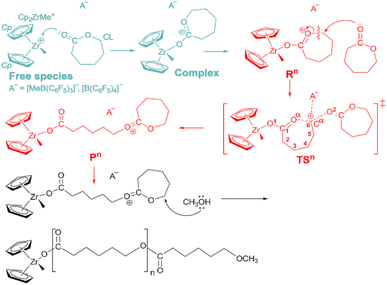
Polycaprolactone (PCL) is a popular biodegradable and biocompatible material that attracts industrial needs and has potential in biomedical and pharmaceutical applications.1–3 Recently, PCLs have been a promising target towards functionalized polymers;4,5 for example, they can be used as engineering plastics with high thermal stability and impact resistance. Synthesis of PCLs can be obtained from ring-opening polymerisation of cyclic esters, which is achieved by radical, anionic or cationic mechanisms,6 through the ring opening of the cyclic monomer (Scheme 1).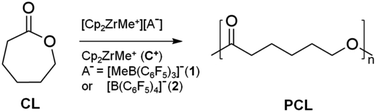 | ||
| Scheme 1 Cationic ring-opening polymerisation (CROP) of ε-caprolactone (CL) using zirconocene/borate systems. | ||
A wide variety of catalysts/initiators have extensively been developed for the ring-opening polymerisation of cyclic esters.7–11 Among them, Group 4 metallocene complexes are of particular interest in the synthesis of functionalized polymers, besides their well-known function as catalysts for olefin polymerisation.12–14 In comparison with the metallocene-catalysed olefin polymerisation, there have been relatively few reports for the cationic ring-opening polymerisation (CROP) by these catalysts,15 which makes them worthy of investigation.
Group 4 metallocene/borate catalytic systems15 have been efficiently used in the cationic polymerisation of oxazolines,16,17 vinyl ethers,18 lactones,19,20 cyclic carbonates,21 and methyl methacrylate.20 Current applications of these catalytic systems in polymer synthesis are, however, limited by their practical use, as they show less controlled molecular weight distribution (Mw/Mn), depending on many factors such as side reactions (unwanted species e.g., aniline disrupts the catalyst performance, chain termination/chain transfer), concentration, and temperature. Besides, selecting appropriate catalyst/cocatalyst systems that match the polymerisation performance must be tested. Because of these practical limitations, understanding these catalytic processes would be the key for the design and improvement of the catalytic systems.
Two types of borate anions, methyltris(pentafluorophenyl)borate [MeB(C6F5)3]− and tetrakis-(pentafluorophenyl)borate [B(C6F5)4]−, play a key role in the metallocene-mediated CROP reaction of cyclic esters and related monomers. These important species can be obtained via a catalyst activation using three different borate cocatalysts (B(C6F5)3, [B(C6F5)4]−[Ph3C]+ and [B(C6F5)4]−[Me2NHPh]+): a cocatalyst abstracts a methide group from Cp2ZrMe2 to yield the ion-pair [Cp2ZrMe]+[AMe]− via ion-pair formation and separation steps. The final step separates the ion-pair species to produce a cationic species Cp2ZrMe+. The Cp2ZrMe+ is the active species in the polymerisation process and that the propagation occurs through the active chain-end (ACE) mechanism (Scheme 2),22,23 where each propagating chain end featuring tertiary oxonium ions is initiated by a molecule of monomer, e.g. ε-caprolactone (CL).
Although the structural difference between the two anions is small, it is experimentally reported that polymerisation reaction by zirconocene catalyst with [B(C6F5)4]− tends to provide different outcomes compared to that with [MeB(C6F5)3]−. For examples, Hayakawa et al. first utilized the well-known [Cp2ZrMe]+[B(C6F5)4]− to initiate the living CROP of CL (affording PCL with narrow polydispersities, Mw/Mn = 1.06–1.3)24 or cyclic carbonates such as 1,3-dioxepan-2-one.21 Zirconium cations containing different methyl substituents on Cp ligand were used to polymerise the CL in toluene at room temperature or 60 °C.19 The best catalytic system [CpCp*ZrMe]+[B(C6F5)4]− was shown to polymerise CL with good control (Mw/Mn < 1.13, Mn,calcd ≈ Mn,GPC), and the molecular weight of the resulting PCLs increased with monomer conversion. In 2007, Kostakis and co-workers20 performed the CROP of CL and δ-valerolactone using three zirconocene complexes and three borate cocatalysts as initiation systems. Polymerisation of CL with [Cp2ZrMe]+[MeB(C6F5)3]− reached a quantitative yield (>95% within 3–24 h at 25 °C) with very narrow polydispersity (Mw/Mn < 1.10), although experimental molecular weight higher than its theoretical value. Similar polymerisation results were also reported for the CROP of 1,5,7,11-tetraoxaspiro-[5,5]undecane, which was complete within 2 h at 55 °C with low polydispersity (Mw/Mn ≤ 1.2).25 On the contrary, the bulkier cocatalyst system [Cp2ZrMe]+[B(C6F5)4]− polymerised CL in a controlled manner with agreement between calculated and observed molecular weight (yield >90% after 24 h at 25 °C). However, the molecular weights of the produced PCL can be varied (Mn = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–38 000 g mol−1) depending on the choice of zirconocene complex and cocatalyst. The same catalytic system was also used in the block copolymerisation with methyl methacrylate.
000–38 000 g mol−1) depending on the choice of zirconocene complex and cocatalyst. The same catalytic system was also used in the block copolymerisation with methyl methacrylate.
Similar distinct differences based on the two counteranions were also observed in CROP of poly(oxazoline)s:17 the [Cp2ZrMe]+[MeB(C6F5)3]− system gave a maximum yield of only 65% after 12.5 h while a quantitative polymerisation can be obtained in 5 h for the [Cp2ZrMe]+[B(C6F5)4]− systems using B(C6F5)3 or [B(C6F5)4]−[Me2NHPh]+ as cocatalysts. The same catalytic systems were also used in the synthesis of diblock copolymers and triblock terpolymers.16,26 Overall, these experimental studies highlight the role of the counteranion in the CROP process and the polymerisation activity strongly depends on the bulkiness of the catalytic systems. In this study, we focus on the microscopic elucidation of the CROP reaction with CL in the presence of borate cocatalysts.
Theoretical studies have provided valuable insights into the reaction mechanism as well as elucidated factors (e.g., counterion, solvent or metal) that are crucial for the metallocene-catalysed olefin and lactone polymerisations.27 Most of the works have been carried out in the absence of cocatalyst and this simplified “naked cation” model28,29 may not result in full understanding of the catalytic process. This is probably due to the size and conformational complexity of the ion-pair system,30 so that theory and modelling could play an important role in this regard. Whereas numerous studies have focused on the effects of the catalyst structure using the naked model and the results have been interpreted in terms of a combination of steric and electronic effects, the molecular level details of the function of the cocatalyst are not fully understood for the zirconocene catalysts. It is expected for metallocene/borate-mediated CROP that the effect of counteranions will be small, due to the weakly coordinating nature of F–H interaction of the cocatalyst as well as the diluted concentration of the dissociative counteranion caused by solvent and/or monomer during the reaction. Nevertheless, this hypothesis has never been verified in any previous studies.
Here, we first begin by modelling the reaction pathway of the chain initiation and propagation mechanism (Scheme 2) and identify the rate-determining step of the CL CROP reaction. Then, we examine the competitive reactions between the termination and the propagation. We analyse the effectiveness of both boron cocatalysts anions, [MeB(C6F5)3]− and [B(C6F5)4]−, in the polymerisation with respect to the naked cation model lacking the anion. The influence of non-covalent interactions (NCIs) on the reaction kinetics of the process is further investigated by NCI analysis. The effects of metal, solvent, and dispersion interactions are also examined, and are found to be critical for the studied process.
2 Computational details
Geometries were fully optimised both in gas-phase and in solution using density functional theory (DFT)31,32 at the B3LYP level with the Gaussian 09 program.33 We used the effective core potential double-ζ basis set (LANL2DZ)34 for Zr and Hf atoms and a double-ζ basis set, 6-31G(d), for all non-metal atoms (C, H, O, B, and F). This DFT/mixed basis set method has been widely used for transition metal complexes.35–38 Vibrational frequency calculations were carried out to confirm the transition states and local minima obtained and to determine the zero-point vibrational energies (ZPE) and thermal corrections to the enthalpic (H) and Gibbs free energies (G) at standard temperature and pressure (298.15 K and 101.325 kPa). Geometry optimizations were also performed in toluene at the same level as the gas-phase optimised geometries, using the SMD/SCRF method39 (toluene, ε = 2.374). Dispersion interactions were calculated using DFT-D3 method40 with Becke–Johnson (BJ) damping scheme.41 Thus, all reported energies account for zero-point, thermal, solvent and dispersion effects, unless noted otherwise. Population analysis (NBO, Mulliken and Hirshfeld charges) as implemented in Gaussian 09 was performed in gas-phase using the same functional and basis set as geometry optimizations. Here we have compared Gibbs free energies of species with differing numbers of molecules (i.e., complex → R1, P1 → R2, and P2 → R3) using two energy correction schemes: the one where the reactants were completely isolated (named as “energy correction I”) and the other one where the reactants were treated in the vicinity of each other (named as “energy correction II”), thus adopting the approach described by Gupta et al. for the metallocene/olefin systems.42 The results of these two schemes are provided in Table S1 and Fig. S1 of ESI.† The energy correction II was used to produce the whole Gibbs free energy profiles for the studied CROP reaction.The employed SMD(toluene)-B3LYP-D3(BJ)/LANL2DZ+6-31G(d) method was validated by comparison to a closely related reaction (Table 1), for which experimentally measured thermodynamic functions were available in toluene solution, together with X-ray geometry of the reactant.43,44 The reaction enthalpy was reproduced by computations within a few kJ mol−1, while reaction entropy was overestimated, because the SMD/SCRF method does not consider the reduced translational entropy in solution. Using a Goodvibes script45 modified to include molarity (9.4 mol dm−3) and molecular volume (138.4 Å3) of toluene,46 we evaluated a correction to translational entropy (S-tr), as proposed by Whitesides et al.,47 which brings the reaction entropy close to the experiment. However, the correction does not improve the prediction of reaction Gibbs energy because of the slight overestimation of reaction enthalpy. Benchmarking tests on computed reaction barriers with different DFT functionals and calculations of relative propagation energies (R1, TS1 and P1) were also carried out, which further confirm that B3LYP-D3(BJ) is a suitable method for the current investigation as it provides the lowest barrier with a reasonable agreement in the calculated energetics between the employed method and the higher-level calculations (Fig. S2 and S3 of ESI†). Thus, the results of SMD(toluene)-B3LYP-D3(BJ)/LANL2DZ+6-31G(d) calculations are used for discussion throughout the study.
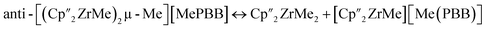 a
a
| Thermodynamic functionb | B3LYP-D3(BJ)/LANL2DZ+6-31G(d) | Experimental |
|---|---|---|
| a Toluene solution, 298 K, Cp′′ = η5-1,2-Me2C5H3, Me(PBB)− = [MeB(ArF)3]− with ArF = o-(C6F5–C6F4).b ΔE, ΔH, and ΔG in kJ mol−1, ΔS in J K−1 mol−1 with estimated standard deviation in parentheses.c Corrected for reduced translational entropy in solution. | ||
| ΔE | 56.9 | |
| ΔH | 47.6 | 42.9(8) |
| ΔS | 148.2 | 110.7(17) |
| ΔG | 3.5 | 10.1(2) |
| ΔS-trc | 101.9 | 110.7(17) |
| ΔG-trc | 17.3 | 10.1(2) |
A conformational analysis was conducted to obtain the most stable configurations for the ion-pair model systems. In particular, different arrangements of CL monomer around the Zr centre at the complex were searched for the most stable geometry using a relaxed potential energy surface (PES) scan with the same level as geometry optimizations. During the scan, all the geometrical parameters were fully relaxed while the dihedral angle Me–Zr–C1–Oα is varied in steps of 10° ranging from −180° to 180° (Fig. S4†). Points on the potential surface were then optimized, followed by frequency calculations to obtain various thermodynamic values. Once the stable complex structures (both front and side attacks) are located, the effect of the conformation of the counteranions ([MeB(C6F5)3]− and [B(C6F5)4]−) around the Zr centre were evaluated for the catalytic species (complex → P1) (see Fig. S5 and S6 of ESI† for details).
To analyse the nature of interactions present between the cationic zirconocene species and the counteranions during the CL CROP, non-covalent interaction (NCI) analysis48,49 is performed on important reaction intermediates and transition states using the NCIweb server (https://nciweb.dsi.upmc.fr/).50 Contreras-Garcia et al. have recently introduced this user-friendly platform to study NCIs, based on the analysis of electron density, ρ, and reduced density gradient, s (also referred to as RDG), according to the eqn (1).
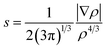 | (1) |
3 Results and discussions
3.1 General consideration
The cationic polymerisation of cyclic esters with boron cocatalyst15,19,20 generally consists of four complex steps: precatalyst activation, initiation, propagation, and termination. In the current study, we focus mainly on the initiation, propagation, and termination of CL CROP. Our goal is to explore mechanistic aspects of the CL CROP and try to understand the impact of the borate cocatalyst on the CROP activity of CL. We have previously shown that, by using a naked cation approach,28,29 the first propagation is likely the rate-determining step of the CROP reaction.37,52,53 However, to our best of knowledge, there is no systematic study in clarifying the influence of cocatalyst on the process. Here, three catalytic systems for CROP of CL have been modelled (Scheme 1): the first takes into account only the cationic zirconocene catalyst, Cp2ZrMe+, and CL monomer(s) (hereafter called the naked cation system, C+), while the second and third considered the C+ system in the presence of the cocatalyst anions (A− = [MeB(C6F5)3]− (1) and [B(C6F5)4]− (2), respectively), which are the results of abstraction of one methyl group of the dimethylzirconocene, Cp2ZrMe2, yielding three different routes of catalyst activation (see eqn (2)–(4)).| Cp2ZrMe2 + B(C6F5)3 → Cp2ZrMe+ + [MeB(C6F5)3]− (1) | (2) |
| Cp2ZrMe2 + [B(C6F5)4]−[Me2NHPh]+ → Cp2ZrMe+ + [B(C6F5)4]− (2) + Me2NPh + CH4 | (3) |
| Cp2ZrMe2 + [B(C6F5)4]−[Ph3C]+ → Cp2ZrMe+ + [B(C6F5)4]− (2) + Ph3CMe | (4) |
All model systems in the present work contain a 1 to 1 ratio of Zr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) B, as experimentally reported by Hayakawa et al.19 and Kostakis et al.20 for lactone polymerisations using zirconocene/borate catalytic systems. The initiation, chain propagation, and termination mechanism is depicted in Scheme 2. All configurations of catalytic species found along the mechanism are provided in the ESI.† From the isolated reactants (Cp2ZrMe+ + CL + A−; free species), the reaction starts with the insertion of the first CL monomer into the cationic site of Cp2ZrMe+, followed by the formation of a monomer-activated complex (Cp2ZrMe-CL+, complex); hence this step is known as the “initiation” step. In the next step, the second CL monomer inserts into the Cα–Oα bond of the CL ring of the activated complex (R1) and generates a six-carbon polymer chain product (P1), through a transition state (TS1). This step is the first propagation step of the overall chain propagation. The next insertion of the third monomer and so on also follows the same process and continues until the quantitative polymer is obtained, once the growing chain end is terminated by a terminating agent (e.g., methanol).20
B, as experimentally reported by Hayakawa et al.19 and Kostakis et al.20 for lactone polymerisations using zirconocene/borate catalytic systems. The initiation, chain propagation, and termination mechanism is depicted in Scheme 2. All configurations of catalytic species found along the mechanism are provided in the ESI.† From the isolated reactants (Cp2ZrMe+ + CL + A−; free species), the reaction starts with the insertion of the first CL monomer into the cationic site of Cp2ZrMe+, followed by the formation of a monomer-activated complex (Cp2ZrMe-CL+, complex); hence this step is known as the “initiation” step. In the next step, the second CL monomer inserts into the Cα–Oα bond of the CL ring of the activated complex (R1) and generates a six-carbon polymer chain product (P1), through a transition state (TS1). This step is the first propagation step of the overall chain propagation. The next insertion of the third monomer and so on also follows the same process and continues until the quantitative polymer is obtained, once the growing chain end is terminated by a terminating agent (e.g., methanol).20
We have organised our results into the following sections: we first examined the most favourable CROP pathway by considering possible configurations for the metallocene/borate model system. Second, we focus on the mechanism of chain initiation, propagation, and termination steps of the CL CROP reaction (Scheme 2), as promoted by three different catalytic systems (C+, [C+][MeB(C6F5)3−] (1), and [C+][B(C6F5)4−] (2)). Then, the effects of metal, solvent, and dispersion on the process were discussed. Finally, we identify and characterise weak interactions during the reaction course by means of NCI analysis.
3.2 Metallocene/borate models and possible CROP pathways
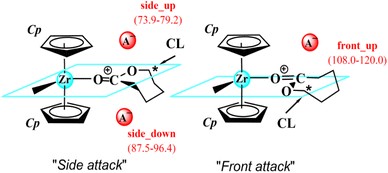
Presently, there are limited experimental data to support the initial configurations for the metallocene/borate catalytic systems [Cp2XMe+][A−] (X = Zr, Hf; A− = MeB(C6F5)3− and B(C6F5)4−) due to the probable dynamics of several species in solution.46,54 Moreover, an experimental determination of toluene separated ion-pair for indenyl-based zirconocenes has recently been reported.55 Therefore, current DFT calculations could allow us to gain insights into the structure and nature of active sites in metallocene/borate catalysts for cationic polymerisation of heterocyclic monomer.15,56 To model the [Cp2XMe+][A−] system, in this study, we consider possible modes of CL coordination in combination with two different structures of the counteranions, [MeB(C6F5)3]− and [B(C6F5)4]−. In the previous studies,37,53 two different possible modes were considered for CL insertion into the cationic site of metallocene (namely front and side attack of CL; Scheme 3). Such insertion modes lead to the growing polymer chain in the front and side direction of the catalyst, respectively. A relaxed PES scan (Fig. S4†) was also performed in gas-phase for the complex between the side and front conformers, which are separated by a free-energy barrier height of 22 kJ mol−1 (Fig. S4(c), ESI†). This data indicates that both modes can be selective at least in the absence of counteranion at room temperature. For the [Cp2ZrMe+][A−] models, we first placed the counteranion in various positions around the metal centre of the catalyst (both complex and P1) and found that, after the conformational analysis (Fig. S5 and S6†), only three distinct configurations (side_up, side_down, and front_up) of the anion (see Scheme 3) were stably located, with respect to the plane of growing polymer chain in an extended conformation. Any configurations that lead to the coil polymer chain were excluded, since this would make the CL insertion inaccessible. Thus, eight different configurations were randomly selected (see Fig. 1 and Scheme 3): two for the naked cation system (front and side) and three (side_up, side_down, front_up) for the [Cp2ZrMe+][A−] systems.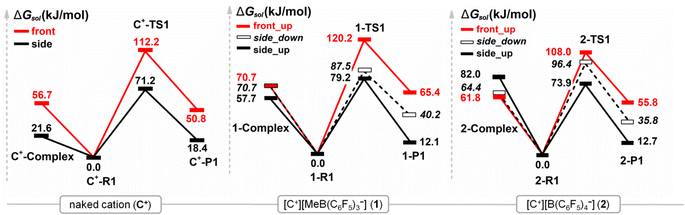 | ||
| Fig. 1 Gibbs free energy profiles in toluene for the initiation and first propagation for various reaction pathways for the naked cation (C+), [C+][MeB(C6F5)3−] (1) and [C+][B(C6F5)4−] (2) systems. The Gibbs energy of each structure is given relative to the reactant of the first propagation (R1). All of the stationary structures shown in this figure are provided in the ESI.† | ||
As shown in Fig. 1, the side pathway is kinetically and thermodynamically favoured over the front pathway for all configurations. The free energies of complex relative to R1 are in the ranges of 21.6–82.0 (side) and 56.7–70.7 (front) kJ mol−1, whereas the reaction barriers and reaction free energies for the first propagation are in the ranges of 71.2–96.4 and 18.4–40.2 kJ mol−1 for the side pathway and 108.0–120.2 and 50.8–65.4 kJ mol−1 for the front pathway, respectively. For the naked cation (C+) system, the side attack is kinetically favoured over the front attack by 41 kJ mol−1 and the relative stability of complex is 35.1 kJ mol−1 lower. For the [Cp2ZrMe+][A−] systems (1 and 2), the side_up configuration is favoured over the other two configurations (side_down and front_up) with the barrier differences of ∼8–40 kJ mol−1 at 1-TS1 and ∼22–34 kJ mol−1 at 2-TS1 in comparison with the front_up one, respectively. There is a significant difference in relative complexation energies and activation free energies between both side_up and side_down configurations of the anion systems. We thus selected the side_up instead of the side_down to represent the [MeB(C6F5)3]− containing system 1 not only because of an energetic preference but also its equivalence in position and composition to the side_up of the [B(C6F5)4]− containing system 2, thus enabling direct comparisons. The optimised transition-state structures of the eight configurations are shown in Fig. 2. Apparently, the hydrogen bond (F–H) interactions between the cationic species and the counteranion lower free-energy barriers in the R1 → P1 step (see the side pathway in Fig. 1). Among them, the side_up configurations yield the lowest barriers of ∼74–79 kJ mol−1 for both cocatalysts. Details of charge distribution of the ligand, monomer, functional groups on the free species, complex, R1 and TS1 structures for the side_up configurations are summarised in Tables S2 and S3 (ESI).†
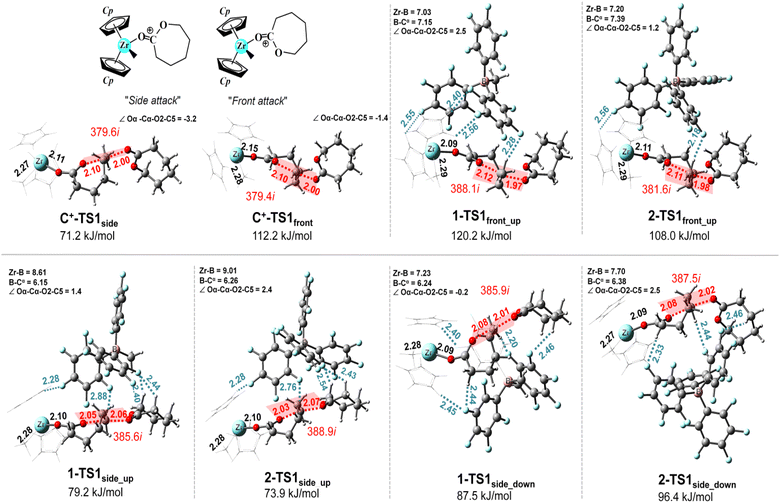 | ||
| Fig. 2 Optimised transition-state structures (TS1, distances in Å) and their corresponding activation energies (free energies in kJ mol−1) relative to R1 for the eight configurations in Fig. 1. Imaginary frequencies (in cm−1) are also indicated. A small torsional angle (in deg.) of Oα–Cα–O2–C5 ≈ 0–3 deg. represents a planar alignment of the four-centred transition states. Other planes were also seen for further chain propagations (see ESI†). Hydrogen bond (F–H) interactions between the cationic species C+ and the counteranion are indicated by the dotted line. | ||
Overall, the results clearly indicate that, for all catalytic systems, the side pathway is favoured for the CL polymerisation, which is in accordance with our previous studies for trimethylene carbonate (TMC) polymerisation catalysed by the naked cation species.53 Thus, we focus on the initiation and propagation steps via the side_up pathway for the remaining study.
3.3 Exploring the mechanism of CL CROP
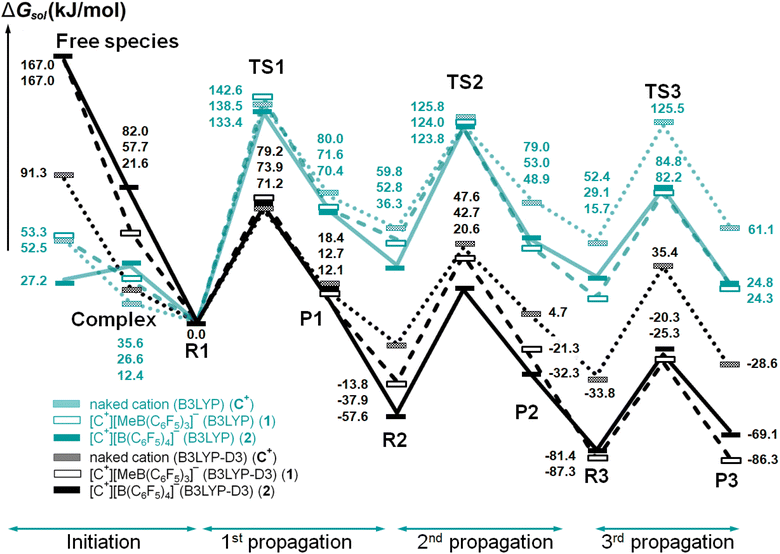 | ||
| Fig. 3 Gibbs free energy profiles in toluene (shown in black) for the initiation and propagation mechanism of the three catalytic systems (C+, 1, and 2). The uncorrected free energy profiles for the dispersion interaction were also included for comparison (shown in cyan). Relative barrier heights for each of propagation steps were also included in Table 2. | ||
| Reaction steps | C+ | 1 | 2 |
|---|---|---|---|
| a Toluene solution, 298 K. | |||
| Initiation (free species → complex) | −69.7 | −109.3 | −85.0 |
| First propagation (R1 → TS1) | 71.2 | 79.2 | 73.9 |
| Second propagation (R2 → TS2) | 61.4 | 80.6 | 78.2 |
| Third propagation (R3 → TS3) | 69.2 | 62.0 | 61.1 |
| First termination (R3ter → TS3ter) | 85.1 | 55.9 | 74.5 |
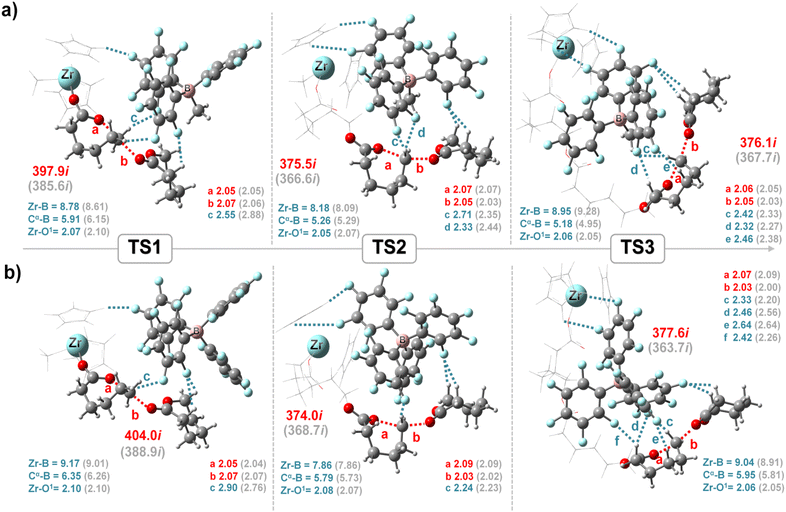
The optimised transition-state structures in toluene for the first three propagations (TS1, TS2, TS3) are shown in Fig. 4. All configurations of the stationary points (free species, complex, Rn, TSn, Pn; n = 1–3) are given in the ESI.† Using its fluorides, the cocatalyst forms hydrogen-bond (H-bond) interactions with the methylene atoms at the Cα position, facilitating the chain propagation. At TS1, due to the spatial separation, only Cα atom can directly interact with the –C6F5 ring of the cocatalyst (see distance c, Fig. 4a and b), with 1 being shorter than 2 (2.55 vs. 2.90 Å, respectively). This F–H interaction limits the formation of the first transition state and hence a relatively higher barrier at TS1 is observed for 1 compared to that for 2 (79.2 vs. 73.9 kJ mol−1). However, in the second and third propagations (TS2 and TS3), the –C6F5 ring of the cocatalyst ring can effectively stabilise the growing reactive species, as can be seen from the more numerous H-bond interactions (distances c–e). At TS3 of both systems, the incoming monomer interacts with two H-bonds, but the –C6F5 rings of the [B(C6F5)4]− cocatalyst form more numerous F–H interactions with the ancillary Cp ligand of the metallocene, as well as with the growing chain, in comparison to the case of the [MeB(C6F5)3]− anion (see TS3 in Fig. 4). These interactions are consistent with more van der Waals contacts between the cationic zirconocene species and the counteranion revealed by the NCI analysis below.
Comparing the activation energies of the first propagation obtained using the naked model in this work (71.2 kJ mol−1) with the data reported in the literature, it was found that the CROP reaction with CL has a faster propagation step compared to zirconocene-initiated TMC propagation (115.9 kJ mol−1)53 and methyl tosylate-initiated propagation with 2-R-2-propyl-oxazoline (R = cyclopropyl, n-propyl, isopropyl) (95–110 kJ mol−1).57
The solvent effect is addressed by a comparison between the Gibbs energy profiles in toluene solution with the gas-phase Gibbs energy profiles (Fig. S9†). Generally, the toluene Gibbs energy profiles show a similar trend as in the gas-phase. Interestingly, the solvent clearly destabilises the catalytic species, thus increasing the reaction barriers and relative energies of the propagating intermediates (cyan lines, Fig. 3). The reaction barriers of the first propagation for systems C+, 1, and 2 are 138.5, 142.6, and 133.4 kJ mol−1 in toluene, in comparison to the corresponding values, 85.8, 73.0, and 74.8 kJ mol−1 in gas-phase, respectively (Fig. S9†). The notable decrease in the complex stability, and the higher energy profile for chain propagation, indicate that the solvent largely disfavours both initiation and propagation steps. The initiation is even kinetically disfavoured for the case of [B(C6F5)4]−, with a small barrier of 8.4 kJ mol−1 for the free species → R1 step (Fig. 3). Electronically, the LUMO energies, HOMO–LUMO gaps, and Mulliken charges on the Zr atom along the reaction pathway are relatively higher in toluene solution compared to the gas-phase (Fig. S10 and Table S5, ESI†). Overall, the solvent favours the separation of the ion species, rather than stabilising the ion pair.
Besides showing the importance of the solvent effect, we demonstrate in the following that the dispersion interactions are important, as well. The dispersion corrected Gibbs energy profiles in toluene solution for the three catalytic systems (C+, 1, and 2) are compared to the corresponding uncorrected results in Fig. 3. The barriers for the first propagation step (R1 → TS1) range between 133.4–142.6 and 71.2–79.2 kJ mol−1 for the uncorrected and corrected free energy profiles, respectively. The results clearly indicate that the catalytic species are greatly stabilised by the multitude of noncovalent interactions involved in the system, which clearly cannot be omitted in the calculations. With dispersion interactions included, the overall Gibbs energy reaction profile ends up exergonic, as it needs to be for a spontaneous reaction.
These results altogether indicate that both solvent and dispersion effects are important for the CROP mechanism: solvent destabilises the reaction intermediates, whereas dispersive interactions strongly stabilise them. Thus, the overall propagation rate of the three catalytic systems is likely dictated in the initial stage of the chain propagation, in accordance with a similar study on the ROP of 1,5,7,11-tetraoxaspiro[5,5]undecane using [Cp2ZrMe+][MeB(C6F5)3−].25
3.4 NCI analysis
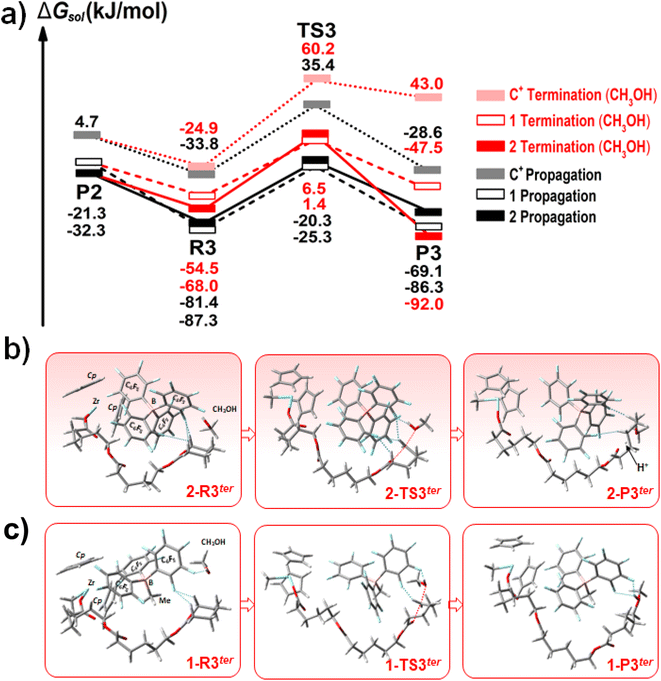
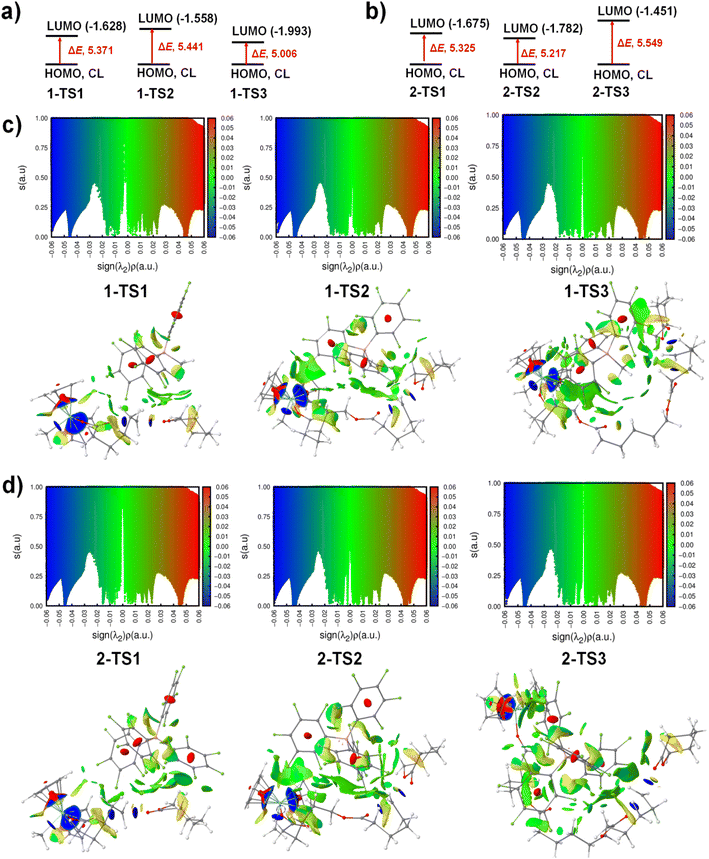
Non-covalent interactions play a crucial role in the stability and reactivity of organometallic systems.58 To gain a deeper insight into the non-covalent interactions (NCIs) that influence the dispersion effect and F–H interactions during the reaction course, the intramolecular NCIweb calculations of intermediates and transition-state structures were performed. A pictorial representation of NCI isosurfaces in 2D and 3D for the transition states (TS1, TS2, and TS3) in chain propagation is shown in Fig. 6, with the HOMO–LUMO gaps included for comparison. The NCI results for other intermediates and integrals of electron density can be found in the ESI.† The 2D NCI plots are almost identical for all catalytic species and highlight three distinct NCI regions of attractive (blue), van der Waals (green), and repulsive (red) non-covalent interactions (Fig. 6c, d and S12†). Two blue peaks of localized and attractive (electrostatic) interactions appear at higher negative values of sign(λ2)ρ on the 2D-RDG: the sharp and low-density peak (at sign(λ2)ρ = −0.06 a.u.) corresponds to the transient Cα–Oα/Cα–O2 bonds and the Zr–Me/Zr–O1 bonds, with blue and donut-shaped isosurfaces, and the wider one at greater densities appears between sign(λ2)ρ = −0.04 and −0.05 a.u., which corresponds to the strong attractive interactions between the Zr atom and the Cp ligands (the large blue 3D isosurfaces on catalyst, see lower panels in Fig. 6c and d). At higher positive values of sign(λ2)ρ, in red, we recognise the repulsive interaction regions inside the –C6F5 rings of counteranions, shown in red compact isosurfaces. A green wider NCI region on 2D-RDG, at both negative and positive scales of sign(λ2)ρ, indicates the existence of delocalized and van der Waals (vdW) interactions, which corresponds to green isosurfaces at the contacts between the cationic zirconocene species and the counteranion. The similarity of the 2D-RDG spectra in all TSs (upper panel, Fig. 6c and d) also explain the same kinetic behaviours observed in Table 2 for the chain propagation between the two cocatalyst systems. Notably, two attractive and vdW interactions are primarily observed at the reactive chain end, facilitating the stabilization of the developing positive charge (Cα) in the transition states. This provides an evidence for the roles of multiple NCIs in transition-state charge stabilization in CROP.59Despite the fact that both cocatalyst systems show the same interaction types, their HOMO–LUMO properties and interaction strengths differ significantly as the reaction progresses. The HOMO–LUMO gaps (ΔE) decrease in the [MeB(C6F5)3]− anion (ΔE = 5.371 eV at 1-TS1 to 5.006 eV at 1-TS3), while [B(C6F5)4]− shows opposite trends (see Fig. 6a and b). Interestingly, the LUMO energies at TSs are strongly influenced by the NCIs: [MeB(C6F5)3]− effectively stabilises the TS3 with a lower E(LUMO) value (−1.993 eV) compared to that in [B(C6F5)4]− (E(LUMO) = −1.451 eV). These energy gaps also correlate well with the transition-state barriers (R2 = 0.99) (Fig. S17†). Since the interaction strengths can be quantitatively estimated from the integration of electron density (see ∫ρ(r)dr in Fig. S18†), we recognised that, from TS1 to TS3, the strength of attractive vdW interactions becomes stronger (with higher ∫ρ(r)dr values) and, due to the larger size, [B(C6F5)4]− creates more contacts with the cationic species and hence stronger dispersion forces between them, as compared to the [MeB(C6F5)3]− anion (see Fig. 6c, d and S13†). The relatively higher ∫ρ(r)dr values found in the [B(C6F5)4]− system are consistent with more numbers of F–H interactions at 2-TS3 (Fig. 4b). Overall, this NCI index, together with HOMO–LUMO gaps, further confirms the influence of weak (vdW) interactions in stabilising the propagating transition states via LUMO orbitals, with the third propagation showing the strongest one, and this may explain the reduced barriers observed in the third propagation of the cocatalyst systems.
4 Conclusions
A computational study of three model catalytic species, namely, methylzirconocene cation, Cp2ZrMe+, and two ion pairs of composition [Cp2ZrMe+][A−] (A− = [MeB(C6F5)3]− and [B(C6F5)4]−) and their CROP reaction with CL was carried out for the chain initiation, propagation, and termination mechanism. DFT calculations clearly show that the initiation is thermodynamically favoured for the CL insertion at the catalytic metal centre, whereas the propagation is kinetically controlled for successive insertion via CL ring-opening. The first two propagation steps, with relatively high and comparable barriers in the presence of the cocatalysts (79.2–80.6 and 73.9–78.2 kJ mol−1 for 1 and 2), are likely the rate-determining steps of the CL CROP mechanism, and these data further verify the naked cation model applied in the literature,60–62 including our previous studies.53,63 The calculations support the cationic ACE mechanism with O-alkyl bond cleavage. Comparison of the first termination and the third propagation steps was also studied, and, with the exception of [MeB(C6F5)3]−, they are not competitive with the termination being less facile compared to the propagation step: the catalytic system 2 exhibits the more feasible termination over the system 1 when using methanol as a terminating agent. For most cases, the third propagation is found to be kinetically and thermodynamically favoured over the termination.Despite the similar effect of the two counteranions on the reaction kinetics of CL CROP, the counteranion (A−) stabilises the cationic species immediately after the first monomer insertion, and the [MeB(C6F5)3]− anion effectively stabilises the catalyst–monomer complex more than the [B(C6F5)4]− anion by ∼24 kJ mol−1. The anions greatly stabilises the terminating species after the first methanol insertion at the chain end. The NCI analysis reveals that the counteranions mainly participate in the reaction through weak interactions, with a distinct impact on the HOMO–LUMO gaps and transition-state stabilisation.
We also studied the initiation and propagation steps of the hafnocene catalyst, revealing that the Hf catalyst slightly favours the CL CROP mechanism compared to the Zr catalyst. The effects of solvent and dispersion on the reaction energetics were analysed, demonstrating that both factors are crucial for the polymerisation. Overall, this study provides a comprehensive understanding of the CL CROP mechanism, revealing the influence of weak interactions at the contacts between the cationic species and the counteranions during chain initiation, propagation and termination.
Author contributions
Conceptualization: W. M., J. J.; investigation: W. M., J. J.; analysis and visualisation: J. J.; funding acquisition: J. J.; software: M. L., J. J.; supervision: M. L., J. J.; validation: M. L., J. J.; writing initial draft: W. M., J. J.; writing – review and editing: W. M., M. L., J. J.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial supports of the Thailand Science Research and Innovation Fund and the University of Phayao (UP) under Fundamental Fund 2024 (Project No. 224/2567) and the School of Science, UP (Grant No. PBTSC66002 and PBTSC66023) are gratefully acknowledged. M. L. acknowledges the support of the Research Council of Finland, decision 357509.References
- P. R. Schmitt, K. D. Dwyer and K. L. K. Coulombe, ACS Appl. Bio Mater., 2022, 5, 2461–2480 CrossRef CAS PubMed.
- S. Espinoza, I. Patil, E. San Martín-Martínez, M. Martinez, R. Casañas Pimentel, P. Pradum, P. Ige, R. Pimentel and P. Ige, Int. J. Polym. Mater. Polym. Biomater., 2020, 69, 85–126 CrossRef CAS.
- T. Abudula, K. Gauthaman, A. Mostafavi, A. Alshahrie, N. Salah, P. Morganti, A. Chianese, A. Tamayol and A. Memic, Sci. Rep., 2020, 10, 20428 CrossRef CAS PubMed.
- K. Kaluzynski, J. Pretula, P. Lewinski, S. Kaźmierski and S. Penczek, Macromolecules, 2022, 55, 2210–2221 CrossRef CAS.
- C. Jérôme and P. Lecomte, Adv. Drug Delivery Rev., 2008, 60, 1056–1076 CrossRef PubMed.
- O. Nuyken and S. D. Pask, Polymers, 2013, 5, 361–403 CrossRef.
- O. Santoro, X. Zhang and C. Redshaw, Catalysts, 2020, 10, 800 CrossRef CAS.
- M. Hong, J. Chen and E. Y. X. Chen, Chem. Rev., 2018, 118, 10551–10616 CrossRef CAS PubMed.
- D. M. Lyubov, A. O. Tolpygin and A. A. Trifonov, Coord. Chem. Rev., 2019, 392, 83–145 CrossRef CAS.
- L.-J. Wu, W. Lee, P. Kumar Ganta, Y.-L. Chang, Y.-C. Chang and H.-Y. Chen, Coord. Chem. Rev., 2023, 475, 214847 CrossRef CAS.
- S. Kaler and M. D. Jones, Dalton Trans., 2022, 51, 1241–1256 RSC.
- R. A. Collins, A. F. Russell and P. Mountford, Appl. Petrochem. Res., 2015, 5, 153–171 CrossRef CAS.
- L. Resconi, L. Cavallo, A. Fait and F. Piemontesi, Chem. Rev., 2000, 100, 1253–1346 CrossRef CAS PubMed.
- Y. Nakayama and T. Shiono, Molecules, 2005, 10, 620–633 CrossRef CAS PubMed.
- Y. Sarazin and J.-F. Carpentier, Chem. Rev., 2015, 115, 3564–3614 CrossRef CAS PubMed.
- M.-E. Kourti, E. Fega and M. Pitsikalis, Polym. Chem., 2016, 7, 2821–2835 RSC.
- M.-E. Kourti, G. C. Vougioukalakis, N. Hadjichristidis and M. Pitsikalis, J. Polym. Sci., Part A: Polym. Chem., 2011, 49, 2520–2527 CrossRef CAS.
- E. Batagianni, A. Marathianos, A. Koraki, A.-P. Maroudas and M. Pitsikalis, J. Macromol. Sci., Part A: Pure Appl. Chem., 2016, 53, 140–151 CrossRef CAS.
- M. Hayakawa, M. Mitani, T. Yamada and T. Mukaiyama, Macromol. Chem. Phys., 1997, 198, 1305–1317 CrossRef CAS.
- K. Kostakis, S. Mourmouris, G. Karanikolopoulos, M. Pitsikalis and N. Hadjichristidis, J. Polym. Sci., Part A: Polym. Chem., 2007, 45, 3524–3537 CrossRef CAS.
- M. Hayakawa, M. Mitani, T. Yamada and T. Mukaiyama, Macromol. Rapid Commun., 1996, 17, 865–870 CrossRef CAS.
- S. Penczek, M. Cypryk, A. Duda, P. Kubisa and S. Słomkowski, Prog. Polym. Sci., 2007, 32, 247–282 CrossRef CAS.
- S. Penczek and J. Pretula, ACS Macro Lett., 2021, 10, 1377–1397 CrossRef CAS PubMed.
- T. Mukaiyama, M. Hayakawa, K. Oouchi, M. Mitani and T. Yamada, Chem. Lett., 1995, 24, 737–738 CrossRef.
- Z. Ariffin, D. Wang and Z. Wu, Macromol. Rapid Commun., 1998, 19, 601–604 CrossRef CAS.
- M.-E. Kourti, G. Fotinogiannopoulou, E. Fega and M. Pitsikalis, J. Macromol. Sci., Part A: Pure Appl.Chem., 2015, 52, 630–641 CrossRef CAS.
- I. Nifant'ev and P. Ivchenko, Molecules, 2019, 24, 4117 CrossRef PubMed.
- J. Sassmannshausen, Dalton Trans., 2009, 8993–8999 RSC.
- G. Lanza and I. L. Fragalà, Top. Catal., 1999, 7, 45–60 CrossRef CAS.
- R. Parveen, T. R. Cundari, J. M. Younker and G. Rodriguez, Organometallics, 2020, 39, 2068–2079 CrossRef CAS.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- R. G. Parr and W. Yang, Density-functional Theory of Atoms and Molecules, Oxford University Press, 1994 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 09, Revision A.02, 2009 Search PubMed.
- Y. Yang, M. N. Weaver and K. M. Merz Jr, J. Phys. Chem. A, 2009, 113, 9843–9851 CrossRef CAS PubMed.
- J. Jitonnom and W. Meelua, Chem. Phys. Lett., 2020, 750, 137482 CrossRef CAS.
- J. Jitonnom, R. Molloy, W. Punyodom and W. Meelua, Comput. Theor. Chem., 2016, 1097, 25–32 CrossRef CAS.
- J. Jitonnom and W. Meelua, J. Theor. Comput. Chem., 2017, 16, 1750003 CrossRef.
- J. Jitonnom and W. Meelua, Chiang Mai J. Sci., 2014, 41(5.2), 1220–1229 CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem., 2009, 113, 6378–6396 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- J. Kumawat and V. K. Gupta, ACS Catal., 2020, 10, 1704–1715 CrossRef CAS.
- Y.-X. Chen, M. V. Metz, L. Li, C. L. Stern and T. J. Marks, J. Am. Chem. Soc., 1998, 120, 6287–6305 CrossRef CAS.
- S. Beck, M.-H. Prosenc, H.-H. Brintzinger, R. Goretzki, N. Herfert and G. Fink, J. Mol. Catal. A: Chem., 1996, 111, 67–79 CrossRef CAS.
- G. Luchini, J. Alegre-Requena, I. Funes-Ardoiz and R. Paton, F1000Research, 2020, 9, 291 Search PubMed.
- M. Linnolahti and S. Collins, Dalton Trans., 2022, 51, 11152–11162 RSC.
- M. Mammen, E. I. Shakhnovich, J. M. Deutch and G. M. Whitesides, J. Org. Chem., 1998, 63, 3821–3830 CrossRef CAS.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- R. Laplaza, F. Peccati, R. A. Boto, C. Quan, A. Carbone, J.-P. Piquemal, Y. Maday and J. Contreras-García, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1497 CAS.
- T. Novoa, R. Laplaza, F. Peccati, F. Fuster and J. Contreras-García, J. Chem. Inf. Model., 2023, 63, 4483–4489 CrossRef CAS PubMed.
- J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef PubMed.
- W. Meelua, N. Keawkla, J. Oláh and J. Jitonnom, J. Organomet. Chem., 2020, 905, 121024 CrossRef CAS.
- J. Jitonnom and W. Meelua, J. Organomet. Chem., 2017, 841, 48–56 CrossRef CAS.
- A. Correa and L. Cavallo, J. Am. Chem. Soc., 2006, 128, 10952–10959 CrossRef CAS PubMed.
- L. Sian, A. Dall'Anese, A. Macchioni, L. Tensi, V. Busico, R. Cipullo, G. P. Goryunov, D. Uborsky, A. Z. Voskoboynikov, C. Ehm, L. Rocchigiani and C. Zuccaccia, Organometallics, 2022, 41, 547–560 CrossRef CAS.
- F. Ruipérez, Int. Rev. Phys. Chem., 2019, 38, 343–403 Search PubMed.
- H. Goossens, S. Catak, M. Glassner, V. R. de la Rosa, B. D. Monnery, F. De Proft, V. Van Speybroeck and R. Hoogenboom, ACS Macro Lett., 2013, 2, 651–654 Search PubMed.
- Y. Cornaton and J.-P. Djukic, Acc. Chem. Res., 2021, 54, 3828–3840 CrossRef CAS PubMed.
- C. Uyeda and E. N. Jacobsen, J. Am. Chem. Soc., 2011, 133, 5062–5075 CrossRef CAS PubMed.
- A. Laine, B. B. Coussens, J. T. Hirvi, A. Berthoud, N. Friederichs, J. R. Severn and M. Linnolahti, Organometallics, 2015, 34, 2415–2421 CrossRef CAS.
- S. Collins and M. Linnolahti, ChemCatChem, 2022, 14, e202101918 CrossRef CAS.
- F. Zaccaria, C. Ehm, P. H. M. Budzelaar and V. Busico, ACS Catal., 2017, 7, 1512–1519 CrossRef CAS.
- W. Meelua, T. Wanjai and J. Jitonnom, Sci. Rep., 2024, 14, 3952 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Gibbs free energy profiles resulting from two energetic correction Schemes I and II; validation of the chosen method; conformational analysis of CL and counteranions; charge analysis of ligands, monomer (CL), functional groups; data supporting the effects of metal and solvent; NCI results; cartesian coordinates (XYZ) of all optimised structures. See DOI: https://doi.org/10.1039/d4ra01178c |
| This journal is © The Royal Society of Chemistry 2024 |