Open Access Article
Open Access ArticleHalf-decomposition of salt-bearing dolomite
Ju Huang ,
Zanqun Liu
,
Zanqun Liu *,
Yu Cui,
Qiang Yuan and
Dehua Deng
*,
Yu Cui,
Qiang Yuan and
Dehua Deng
School of Civil Engineering, Central South University, Changsha, Hunan 410075, China. E-mail: zanqun.liu@csu.edu.cn
First published on 9th April 2024
Abstract
Half-calcined dolomites (HCDs) have been widely used in environmental remediation, medicine, and construction. However, advanced calcination technologies are required to modify their microstructure and thus improve their working performance. Herein, we investigated the effects of a variety of inorganic salts on the decomposition of dolomite based on thermogravimetric, compositional, and morphological analysis. The thermogravimetric data showed that certain salts significantly lowered the half-decomposition temperature of dolomite, which included LiCl, CaCl2, MgCl2, AlCl3, LiNO3, KNO3, K2CO3, Li2CO3, Li2SO4, Na3PO4, and K3PO4. Compositional analysis demonstrated that only half-decomposition occurred when salt-bearing dolomite was calcined at a temperature of 723–923 K, leading to the formation of CaO-free HCDs composed of periclase and Mg-calcite having a Mg level of 2.0–10.5 mol%. Morphological analysis showed that porous HCDs were feasibly obtained by calcining salt-bearing dolomite at 723–923 K. MgO coarsening occurred at a temperature above 873 K, but it could be avoided by controlling the calcination time. The mechanism of salts may be related to the heterovalent doping effect, which may lead to an increase in the concentration of vacancies in the dolomite lattice.
Introduction
Half-calcined dolomites (HCDs) are of industrial importance as a source of MgO for construction,1,2 catalysis,3,4 and biomaterials;5 as an absorbent for pollutant gases (H2S, SOx, and CO2);6–10 and as a scrubber for several metal elements (Ag, As, B, Ba, Co, Cr, Hg, Mn, Ni, Pb, Sn, Sr, Ti, and V) and anions (F−, PO43−, and AsO43−) in wastewater.11–14 Studies have demonstrated that the performance of HCDs is closely related to their microstructures.12,13,15,16 The ion uptake mechanism of HCDs involves surface complexation, ion exchange, and chemical precipitation of metals as oxides, hydroxides, and carbonates.11,12,16,17 Therefore, the removal efficiency of HCDs is largely dependent on their effective pore size for the diffusion of ions, specific surface area, concentration of low-coordinated sites, and crystal defects.12,17 Concerning the capture of pollutant gases, gas diffusion through the pores of HCD particles is an important factor affecting the overall reaction rate.7 A stable pore structure is also essential for the rapid absorption and desorption kinetics of HCDs after multiple carbonation–calcination cycles.9 When used as a construction material, the activity of MgO is one of the most important parameters since it impacts both the reaction rate and composition in cement.18,19 The factors influencing the activity of MgO include the crystallite size and lattice defects of MgO crystals and specific surface and pore structures of HCDs.13,20,21The microstructure of HCDs is determined by their calcination history.13,19,22 As a double carbonate consisting of alternating calcium and magnesium cation layers interspersed with CO32− groups,23 dolomite has the most complex decomposition kinetics among all the carbonates. Typically, dolomite decomposes into a mixture of oxides via one step in an atmosphere with low CO2 partial pressure (PCO2):24,25
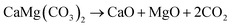 | (1) |
The presence of CaO adversely affects the usage of MgO owing to its distinct chemical activities.22 In this case, the half-decomposition instead of the full-decomposition of dolomite should be controlled to obtain high-quality products. The half-decomposition of dolomite is commonly performed in an atmosphere with sufficiently high CO2 partial pressure at 973–1073 K, where dolomite undergoes direct breakdown into MgO and CaO, while the CaO crystals are rapidly carbonated to CaCO3.26,27
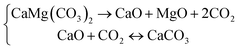 | (2) |
The introduction of chlorides or fluorides in dolomite is another effective method to control its half-decomposition.29–31 These halides can lower the half-decomposition temperature of dolomite, while having an insignificant effect on the subsequent decomposition of CaCO3. Dolomite containing NaCl or MgCl2 decomposed via two steps, with its half-decomposition occurring at 893–993 K.31 Fluorides (LiF and NaF) were also reported to increase the decomposition rate at a calcination temperature of 900–983 K,29 therefore shortening the calcination time required for the half-decomposition. In general, crystal structure refinement and particle coarsening together with pore structure evolution take place with an increase in the calcination temperature and extension of the calcination time. Therefore, the addition of these salts to dolomite may be conducive to the improvement of the microstructure of HCDs. However, neither a compositional analysis nor morphological analysis have been carried out on calcined dolomite containing halides.
Given that the coarsening of MgO occurs at 873 K, better candidates than halides are required to further shift the half-decomposition temperature of dolomite downward to avoid the co-formation of CaO and the coarsening of MgO. Besides, studies are also required to understand to what extent these candidates will affect the microstructure of HCDs. Thus, to fill these knowledge gaps, herein, the effects of sulfates, chlorides, phosphates, nitrates, and carbonates on the decomposition of dolomite were first investigated based on thermogravimetric (TG) analysis. A compositional analysis was performed to determine the phases in the HCDs. A morphological analysis was also carried out to understand the effect of salts on the microstructure of HCDs. Finally, the possible mechanism of inorganic salts was discussed for the discovery of more potential candidates.
Results
Thermogravimetric analysis
Salt-bearing dolomites were prepared by mixing 1.0 wt% salt in natural dolomite particles. The TG/DTG tests of natural dolomite and salt-bearing dolomites were investigated in the temperature range of 308–1223 K, at a heating rate of 20 K min−1. The nitrogen flow (20 mL min−1) was used as the purge gas to eliminate the effect of CO2 on the decomposition of dolomite. The results are shown in Fig. 1. Hereinafter, the dolomite containing certain salt is named “M-dolomite”, where M denotes the salt added to the dolomite.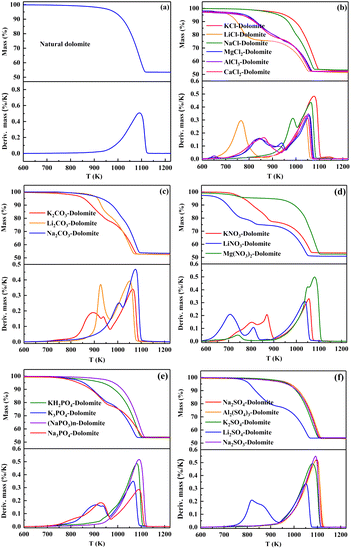 | ||
| Fig. 1 TG/DTG curves of (a) natural dolomite and dolomite containing 1.0 wt% of (b) chlorides, (c) carbonates, (d) nitrates, (e) phosphates, and (f) sulphates. | ||
Natural dolomite decomposes in the temperature range of 900–1115 K, with a single DTG peak at 1091 K (Fig. 1(a)). This demonstrates that natural dolomite decomposes into calcium oxide, magnesium oxide, and carbon dioxide in one step, as shown in eqn (1). In the case of the salt-bearing dolomite, two types of TG/DTG curves can be observed, as follows: (I) TG curves having one S-shaped segment and showing one DTG peak and (II) TG curves consisting of two S-shaped segments, showing two DTG peaks. The type I curves are very similar to that of the natural dolomite, both of which show only one DTG peak at ca. 1080–1090 K. This demonstrates that these salts substantially have no effect on the decomposition of dolomite, including KCl, Na2SO4, Al2(SO4)3, K2SO4, Na2SO3, KH2PO4, (NaPO3)n, and Mg(NO3)2.
The TG curves of dolomite containing other salts are type II curves, indicating that these salts can alter the decomposition path of natural dolomite from a “one-step” into a “two-step” mechanism. When dolomite decomposes via two steps, it is commonly believed that the first step is associated with half-decomposition to form MgO and CaCO3, while the second step corresponds to the subsequent decomposition of CaCO3 to CaO.32 According to the temperature regions of the two decomposition steps, it can be deduced that these salts play their role by pushing the half-decomposition temperatures of dolomite downward, while imposing a very limited effect on the subsequent decomposition of CaCO3.
However, these salts have very different capabilities to lower the temperature for the half-decomposition of dolomite. Specifically, LiCl and LiNO3 are the most effective candidates that can shift the onset half-decomposition temperature of dolomite to 678 K and 635 K, respectively. The maximum half-decomposition rates of LiCl-dolomite and LiNO3-dolomite were achieved at a temperature (767 K and 707 K, respectively) which is much lower than the onset decomposition temperature of CaCO3 in the second step (879.7 K and 889.1 K, respectively). Therefore, HCDs can be feasibly obtained through the calcination of LiCl-dolomite and LiNO3-dolomite at a temperature in the range of 750–800 K. In contrast, the incorporation of 1.0 wt% of NaCl and Na2CO3 only caused a slight decrease in thermal requirement for the half-decomposition of dolomite. The rapid half-decomposition of NaCl-dolomite and Na2CO3-dolomite was only achieved at a temperature above 950 K, at which the decomposition of CaCO3 already occurred (indicated by the overlapping S-shaped segments), making it challenging to obtain CaO-free half-calcined products. The other salts, including CaCl2, MgCl2, AlCl3, K2CO3, Li2CO3, Li2SO4, Na3PO4, and K3PO4, presented an effect weaker than LiCl but stronger than Na2CO3. These salts caused two distinguishable decomposition steps, with the DTG peak temperature of half-decomposition at ca. 850–923 K. Thus, these salts can be used to produce the HCDs without CaO, but the proper calcination conditions should be further confirmed by compositional and morphological analysis.
The effect of the content of salt added to dolomite on its decomposition was further investigated. LiCl (strong), Na3PO4 (medium), Na2CO3 (weak), and KCl (none) were selected due to their different effects on the decomposition of dolomite and the results are presented in Fig. 2.
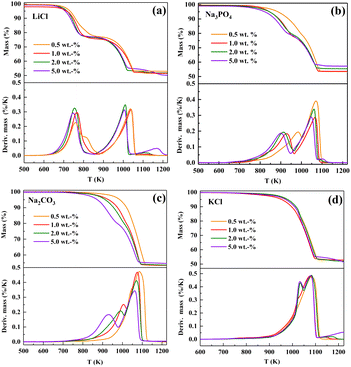 | ||
| Fig. 2 TG/DTG curves of dolomite containing different amounts of (a) LiCl, (b) Na3PO4, (c) Na2CO3, and (d) KCl. | ||
As seen from the TG/DTG curves in Fig. 2(a), the addition of 0.5 wt% of LiCl led to two well-separated decomposition steps. The first step (half-decomposition) occurred in the temperature range of 650–900 K, showing a DTG peak temperature at 757 K. Increasing the content of LiCl to 1.0 wt% did not further shift the half-decomposition temperature downward, but it led to an increase in the decomposition rate (e.g., from 4.56% per min to 5.98% per min at 750 K). However, the addition of a higher content (2.0 wt% and 5.0 wt%) did not further contribute to the significant increase in the decomposition rate.
The addition of 0.5 wt% of Na3PO4 (Fig. 2(b)) only resulted in a slight abnormality in the TG curve. Thus, to cause two well-separated decomposition steps, the amount of Na3PO4 added should be at least 1.0 wt%. An increase in the content added to 1.0 wt% and 5.0 wt% led to not only a shift in the first DTG peak at 983 K downward to 928 K and 900 K, respectively, but an increase in the half-decomposition rate at 873 K.
The effect of Na2CO3 was more dependent on its content (Fig. 2(c)). The addition of 0.5 wt% of Na2CO3 to dolomite caused an insignificant effect on its decomposition. Increasing the content of Na2CO3 to above 1.0 wt% led to a split in the DTG peak. The TG curve of dolomite containing 5.0 wt% of Na2CO3 consisted of two well-separated S-shaped segments. The first decomposition step occurred at 800–977 K and the second decomposition step occurred at 977–1100 K. Therefore, HCDs can be produced from Na2CO3-dolomite by increasing the content of Na2CO3 to 5.0 wt%.
The effect of the content of KCl added on the decomposition of dolomite is displayed in (Fig. 2(d)). When the content of KCl in dolomite was less than 2.0 wt%, it only caused a slight abnormality in the TG curve, with only one DTG peak at 1084 K. Increasing the content of KCl added to above 2.0 wt% resulted in the splitting of this DTG. However, the half-decomposition rate of KCl-dolomite did not become rapid unless the temperature increased to above 950 K even at an addition of 5.0 wt%. Therefore, it is impossible to obtain CaO-free HCDs while avoiding the coarsening of MgO through the calcination of KCl-dolomite.
Compositional analysis
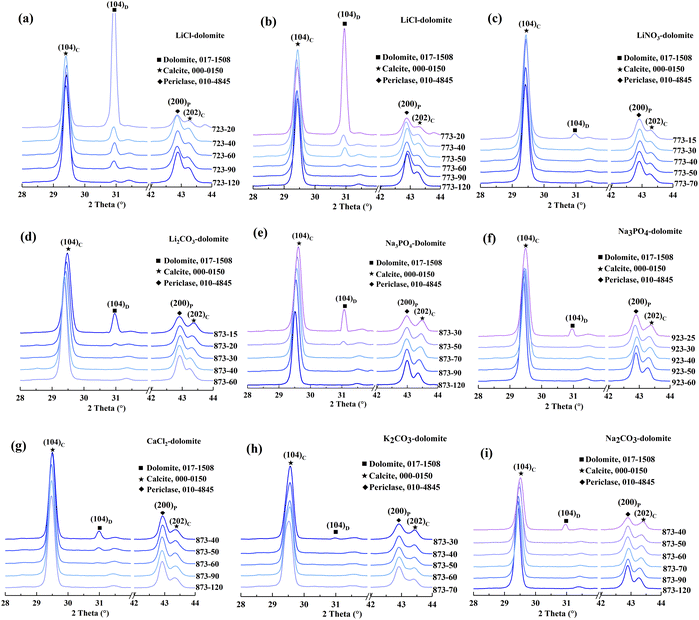
A compositional analysis was performed to verify the compositions in HCDs. The XRD patterns of the calcined salt-bearing dolomites are presented in Fig. 3. The calcination temperatures of the salt-bearing dolomite were determined based on the first DTG peak temperatures in the TGA analysis.As shown in Fig. 3, the (104)C and (202)C peaks are ascribed to calcite (ICSD – #000-0150), while the (104)D and (200)P peaks correspond to dolomite (ICSD – #017-1508) and periclase (ICSD – #010-0845), respectively. The samples were named “T–t”, where T is the calcination temperature and t is the calcination time. The main phases found in the calcined products at the initial time are dolomite, calcite, and periclase. With the extension of calcination time, the intensity of the (104)D diffraction peak decreased, while the intensity of the (104)C, (202)C, and (200)P diffraction peaks became sharper. However, diffraction peaks for CaO crystals were not found. This suggests that only half-decomposition rather than full-decomposition of the salt-bearing dolomite occurred under the experimental conditions independent of the added salts.
The (104)C and (202)C peaks of pure calcite were located at 2θ = 29.390° and 2θ = 43.179°, respectively.33 However, the (104)C and (202)C peaks of calcite in the half-calcined dolomite shifted to higher angles. The peak shift suggests that the calcite in the half-calcined dolomite has smaller d-spacing values than the pure calcite. This indicates the incorporation of smaller Mg ions into the calcite lattice (0.72 Å for Mg2+ compared to 1.00 Å for Ca2+ in sixfold coordination).34 In other words, the magnesian calcite (Mg-calcite, Ca1−xMgxCO3) rather than pure calcite was formed during the half-decomposition of the salt-bearing dolomite. The XRD results suggest that the half-decomposition of the salt-bearing dolomite involves a more complex process than that described by eqn (2). Our data favors the “solid-solution” model proposed by Hashimoto H.35 who described the half-decomposition of dolomite as the topotactic transformation of dolomite–calcite, leading to the formation of interstitial Mg ions, which then diffuse outward to the CaCO3/MgO interface. In this model, the Mg-calcite would be likely to be formed in the half-decomposition of dolomite if some Mg ions are trapped in the calcite crystal lattice.
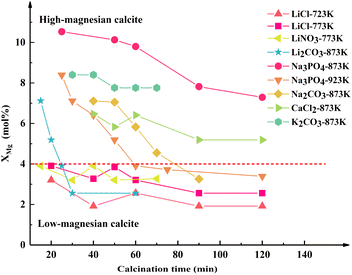
The shift in the (202)C peak with an extension of the calcination time varied depending on the salt added to the dolomite. Specifically, the (202)C peak of the Mg-calcite in the dolomite containing LiCl, LiNO3, and K2CO3 did not shift, while that of the Mg-calcite containing other salts shifted toward a lower 2θ angle with an extension of the calcination time. Given that the reduction in the d-spacing values can be described as a linear relationship with Mg substitution between 2 and 16 mol% in calcite,34 the Mg content in Mg-calcite (XMg) can be quantified by the shift in the d202 values.36 The variation in XMg versus calcination time and calcination temperature is shown in Fig. 4.
As shown in Fig. 4, the Mg-calcite in the half-calcined dolomite is defined as “M–T”, where “M” denotes the added salts in dolomite and “T” denotes the calcination temperature. Notably the Mg content in the Mg-calcite greatly depended on the calcination conditions and the added salt in dolomite. The highest Mg content (10.5 mol%), at an Mg level of the biogenic calcite in some marine organisms,36 was found in Na3PO4-873-30. The Mg content decreased slightly to 7.3 mol% with the prolongation of calcination time to 120 min. The Mg content in Na3PO4-923-t decreased rapidly from 8.4 mol% to 3.9 mol% within 35 min, but then declined slowly to 3.3 mol% within the following 60 min. The XMg values in Na2CO3-873-t and Li2CO3-873-t presented a similar trend. Alternatively, the Mg-calcite crystals in the half-calcined dolomite containing CaCl2, LiCl, and LiNO3 possessed a relatively stable Mg content even after a long calcination time. Particularly, the Mg-calcite crystals in the half-calcined dolomite containing lithium salts had an Mg level below 4 mol%, while that having other salts had an Mg level above 4 mol% when the calcination time was controlled. This indicates that lithium may have a stronger ability to facilitate the outward diffusion of Mg ions from the dolomite lattice during the half-decomposition.
The Mg-calcite crystals containing more than about 4 mol% Mg in their crystal lattice are metastable phases.23 Therefore, it is customary to divide Mg-calcite into low-magnesian calcite and high-magnesian calcite based on a boundary of 4 mol% in geology.23 In the skeletal components in some marine organisms, the Mg level in the calcite can frequently be above 10 mol%.36 Previous studies have demonstrated that the incorporation of Mg significantly strengthens calcite via the solid solution hardening mechanism.37,38 Thus, the hardness and elastic modulus of Mg-calcite increase linearly with the amount of Mg in the solid solution.37 Besides, the Mg ions are strongly hydrated, endowing the high-magnesian calcite with higher solubility than the aragonite.39 These features make high-magnesian calcite an ideal material for biogenic applications such as bone regeneration. High-magnesian calcite crystals are commonly prepared from complex solution systems, but our XRD results demonstrated that high-magnesian calcite with an Mg level above 10 mol% can be obtained through solid-reactions during the half-decomposition of Na3PO4-dolomite at 873 K.
Morphological analysis
The performance of HCDs greatly depends on their microstructure, and thus a morphological analysis of natural dolomite and HCDs was performed, as shown in Fig. 5.Natural dolomite (Fig. 5(a)) had very smooth and dense surface, while the HCDs presented a porous structure. LiCl-773-60 (Fig. 5(b)) presented a laminated structure that resembles the layered structure of nacre.40 The formed magnesian calcite layers with a thickness of ca. 100 nm were parallel with each other and the nano-sized MgO crystals filled in the gap, giving rise to the slit-shaped pores. This is the first time that the CaCO3/MgO interface in the half-decomposed dolomite has been demonstrated. The layered structure demonstrates that the long-distance diffusion of ions does not occur during the half-decomposition of dolomite, but instead, the local arrangement of ions in the sites of new products takes place, accompanied by local shrinkage to form pores.27 This may be related to the shear-transformation mechanism driven by the tension at the reactant–product interface due to their molar volume difference.24 This parallel structure was slightly disturbed with the extension of calcination time to 120 min (Fig. 5(c)), and the resultant local disorders led to the formation of irregular pores. In contrast, there is no significant growth in the size of the MgO nanospheres, indicating that MgO coarsening does not occur at 773 K.
However, the layered structure was not observed in the half-calcined dolomite containing other inorganic salts. In Li2CO3-873-30 (Fig. 5(d)), the MgO nanospheres were attached to the surface of the particles, which have a uniform size of ca. 40–50 nm. When a longer calcination time was applied (Fig. 5(e)), the diameter of the MgO nanoparticles increased slightly to ca. 100 nm and local collapse occurred, resulting in the formation of pores with a diameter of >100 nm. This suggests that considerable coarsening of MgO already occurred at 873 K.
The MgO crystals in CaCl2-873-60 (Fig. 5(f)) presented a worm-like shape rather than a spherical shape. Prolonging the calcination time to 120 min (Fig. 5(g)) led to the development of long and winding crystals, creating slit-shaped pores. Although the formation of crystals with this unique shape remains a puzzle, the microstructure evolution at 873 K suggests that the HCD experienced shear deformation under the build-up of mechanical tension.27
In Na3PO4-923-25 (Fig. 5(h)), the MgO nanospheres were found on the particle surface, showing a similar morphology as Li2CO3-873-30. In contrast, the occurrence of local collapse indicates a higher level of mechanical tension under this condition. At higher calcination temperatures, the tension inside the particles may exceed a critical cohesion value among the decomposed grains, leading to their collapse and or rearrangement inside the particles.27 Besides, the coarsening of MgO nanospheres at this temperature became very significant. In Na3PO4-923-75 (Fig. 5(i)), the diameter of the MgO nanospheres increased significantly at the cost of a reduction in their quantity. Spherical MgO nanoparticles with a size of up to 120–150 nm could be observed in Na3PO4-923-130 (Fig. 5(j)), and grain boundaries started to form between the MgO nanoparticles, which is known as “necking”. The considerable sintering under this condition caused pore shrinkage, and thus a reduction in the BET surface area. Therefore, the calcination time of Na3PO4-923-t should be controlled strictly to obtain half-calcined products with high porosity and activity.
Discussions
To understand the underlying mechanism of the effect of salts on the decomposition of dolomite, the TG data for the salt-bearing dolomite and the melting and Tammann temperature of the salts are summarized in Table 1.| Salt | Temperature range (K) | DTG peak temperature (K) | Melting temperature46 (K) | Tammann temperaturea (K) | ||
|---|---|---|---|---|---|---|
| First step | Second step | First step | Second step | |||
| a Tammann temperature is estimated as 2/3 of the melting point of the salt based on the Tammann rule.47 | ||||||
| Nat. | 900–1115 | 1091 | — | — | ||
| KCl | 877–1107 | 1077 | 1044 | 699 | ||
| Na2SO4 | 882–1124 | 1098 | — | — | ||
| K2SO4 | 882–1117 | 1078 | 1342 | 899 | ||
| Na2SO3 | 882–1117 | 1091 | — | — | ||
| Al2SO4·18H2O | 881–1128 | 1097 | — | — | ||
| KNO3 | 710–904 | 904–1078 | 870 | 1049 | 606 | 406 |
| K2CO3 | 745–956 | 956–1078 | 927 | 1060 | 1174 | 786 |
| NaCl | 807–1006 | 1006–1089 | 988 | 1061 | 1074 | 719 |
| Na2CO3 | 727–935 | 935–1079 | 892 | 1059 | 1131 | 758 |
| MgCl2 | 717–955 | 955–1081 | 844 | 1055 | 987 | 661 |
| LiCl | 678–866 | 880–1062 | 767 | 1036 | 886 | 594 |
| Li2CO3 | 844–968 | 968–1070 | 928 | 1049 | 993 | 665 |
| Li2SO4 | 761–936 | 936–1078 | 821 | 1049 | 1132 | 758 |
| LiNO3 | 635–838 | 889–1063 | 707 | 1036 | 528 | 354 |
| AlCl3·6H2O | 717–948 | 948–1076 | 844 | 1055 | — | — |
| CaCl2 | 731–933 | 933–1071 | 864 | 1043 | 1048 | 702 |
Some authors argued that the effect of salts may be associated with their low melting temperatures.41,42 The salts would melt during the decomposition of dolomite, and therefore enhance the heat transfer or act as ions channel.43 This hypothesis is based on the fact that the porous product at the outer layers has lower thermal conductivity, and thereby hinders heat transfer to the core.42 This hypothesis seems plausible for dolomite containing nitrates, which have very low melting points.44 However, it fails to explain why the carbonates can also lead to the half-decomposition of dolomite at ca. 750 K, which is a temperature much lower than their melting points. The melting points of salts are much higher than the onset decomposition of salt-bearing dolomite, which indicates that the salts are not necessarily in a molten state to trigger the half-decomposition of dolomite. Besides, the enhanced heat transfer cannot explain why the onset half-decomposition temperatures are reduced, a phenomenon that may be linked to the lower reaction energy barrier.45
Therefore, not merely a physical reason but a chemical interaction is involved in the half-decomposition of salt-bearing dolomite. W. R. Bandi32 proposed that salt catalyzes the disintegration of carbonate ions at the magnesium sites to form CO2 and O2−, and then the salt also catalyzes the rearrangement of Ca2+, Mg2+, CO32−, and O2− to complete the half-decomposition of dolomite, leading to the formation of MgO and CaCO3. This mechanism demonstrates that salts can lower the thermal requirement of half-decomposition, enabling the half-decomposition of dolomite to occur at a lower temperature. However, it remains unclear how this catalytic process occurs.
The XRD analysis showed that the half-decomposition of dolomite follows a solid-solution model, which can be expressed with Kröger's notation, as follows:48
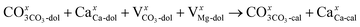 | (3) |
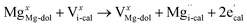 | (4) |
It corresponds to the change in calcium and carbonate ions of dolomite into calcium and carbonate ions of calcite through vacancies, creating interstitial Mg ions that then diffuse outward to the CaCO3/MgO interface, respectively. The equations demonstrate that the diffusion of ions in crystalline dolomite takes place by the movement of vacancies. The outward growth of MgO toward the interface and the local arrangement of ions at the sites of new phases, as demonstrated by the SEM image of the half-calcined LiCl-dolomite, is solid evidence for the solid-solution model.
In previous studies, halides are the only reported effective additives that can control the half-decomposition of dolomite.29–31 However, our data shows that the effective salts to cause the two-step decomposition of dolomite are not limited to chlorides, but include nitrates, sulfates, carbonates, and orthophosphates. These effective salts can be classified into three categories, as follows: (1) salts containing heterovalent cations, including Na2CO3, K2CO3, and Li2CO3; salts containing heterovalent anions, including MgCl2 and CaCl2; and the salts containing both heterovalent cations and anions, including NaCl, LiCl, LiNO3, and KNO3. In ionic crystals, additional defects are created by introducing aliovalent impurities (dopants), which differ in charge from the host ions.49 Therefore, it can be inferred that heterovalent doping may be the possible mechanism of these salts.
In the case of carbonates containing only heterovalent cations, the replacement of two Ca ions or Mg ions (depending on the size of cations) with two monovalent ions leads to the formation of anion vacancy to maintain charge neutrality, as follows:
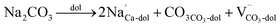 | (5) |
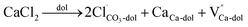 | (6) |
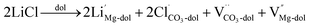 | (7) |
To cause these reactions, the temperature should be higher than the Tammann temperature (Tt) above which the constitutive ions become mobile.47 However, precise Tammann temperature is difficult to obtain given that scarce literature data are available. However, the Tammann-rule has been proposed, where the defect concentration in solids becomes substantial at about 2/3 of the melting point (Tm).47 Therefore, it is assumed that Tt = 2/3 Tm. This explains why the salts can play a role at a temperature lower than their melting temperatures. The salts having a lower Tammann temperature can lead to a lower onset half-decomposition. In contrast, the salts having a high Tammann temperature, for example, K2SO4, may fail to cause substantial point defects in dolomite, and thus show no contribution to its decomposition. The interaction of the two oppositely charged defects is primarily an attractive Coulomb interaction, which reduces the effective formation enthalpy of point defects.47 Hence, it becomes easier for the next defects to be formed. In other words, more defects lead to even more defects. This explains why the addition of only a small amount of salt can lead to a significant shift in the half-decomposition temperature of dolomite downward, and why the salts containing both heterovalent anions and cations (e.g., LiCl) show a more significant effect than other salts. Given that the defect concentration is dependent on the doping concentration, the addition of a higher content of salt can intensify their effect.
Conclusions
Based on the TGA data, compositional analysis, and morphological analysis, herein, we investigated the effects of inorganic salts on the decomposition of dolomite. Several conclusions can be drawn from this study as follows:(1) Natural dolomite decomposes via a one-step decomposition mechanism in a nitrogen atmosphere, while dolomite containing certain salts decomposes via a two-step mechanism, with the first step to form MgO and CaCO3 and the subsequent decomposition of CaCO3 in the next step. The salts significantly lower the onset half-decomposition temperature of dolomite, while imposing a very limited effect on the subsequent decomposition of CaCO3. The effective salts causing the two-step decomposition of dolomite include but are not limited to chlorides (LiCl, CaCl2, MgCl2, and AlCl3), nitrates (LiNO3 and KNO3), and carbonates (Li2CO3, Na2CO3, and K2CO3), which contain non-divalent cations or anions. An appropriate increase in the content of salts added can promote the effect of salts.
(2) The compositional analysis showed that only half-decomposition takes place when the salt-bearing dolomite is calcined at 723–923 K. Magnesian calcite rather than pure calcite is formed during the half-decomposition of salt-bearing dolomite. The low-magnesian calcite crystals (having an Mg level below 4 mol%) form in the half-calcined dolomite containing lithium salts, while adding other effective salts leads to the formation of high-magnesian calcite.
(3) The morphological analysis showed that the microstructure of HCDs is dependent on the salt added and the calcination conditions. LiCl-dolomite-723 and LiCl-dolomite-773 presented a laminated structure, which was not observed in the other HCDs calcined at higher temperatures. Local collapse occurs at a temperature of 873 K, leading to the formation of large pores in HCDs. MgO coarsening occurs at a temperature of 923 K but it can be avoided by controlling the calcination time.
(4) The mechanism of salts to cause the two-step decomposition of dolomite may be associated with their role as heterovalent dopants, which can create more point defects in the dolomite crystal lattice. The heterovalent doping effect of a salt is related to the Tammann temperature of the salt and the ion species contained in the salt.
Experimental
Materials
Natural dolomite was sourced from Hebei, China, with a purity of 98.45%. The dolomite has a nearly ideal stoichiometric formula of CaMg(CO3)2. The crushed dolomite particles were wet-ground in alcohol for 5 h in a planetary ball mill. The salt-bearing dolomites were prepared by adding 1.0 wt% of salts to dolomite and the powders were softly ground in a pestle to form homogenous mixtures. The used salts included chlorides (NaCl, LiCl, MgCl2, CaCl2, AlCl3·6H2O, and KCl), sulphates (Na2SO4, K2SO4, and Al2(SO4)3·18H2O), nitrates (KNO3, LiNO3 and Mg(NO3)2·2H2O), and carbonates (Na2CO3, Li2CO3, K2CO3, and Mg2(OH)2CO3). The salts were of analytical purity and used without further treatment.Thermogravimetric analysis
Thermal tests were performed using a Mettler TOLEDO TGA 2(SF) equipped with a high sensitivity balance (0.1 mg) with a minimum baseline dynamic drift (<10 mg). Samples of fixed mass (20 ± 2 mg) were tested in all the TGA runs. The temperature was recorded using a thermocouple positioned underneath and close to the sample. A low nitrogen gas flow rate (20 cm3 min−1) was used as the purge gas to facilitate CO2 removal. The temperature was increased from 308 K to 1223 K at a heating rate of 20 K min−1.Compositional analysis
Salt-bearing dolomite particles were calcined in a tubular furnace to obtain products for further analysis. The powders of fixed mass (20 ± 0.05 g) were placed in an alumina crucible and inserted in the tubular furnace that was pre-heated to target temperatures. A thermocouple was inserted into the tubular furnace and contacted with the crucible to monitor the temperature variations. After a certain time, the samples were taken out, and then cooled and sealed for further analysis. XRD tests of half-calcined dolomite were performed with a Rigaku Smartlab 9kW using Cu-Kα as the radiation source. The XRD patterns were collected in the 2θ range of 20° to 70° at a step of 0.01° and 0.6 s per step. The phase identification was performed using the MID Jade 6 software with the Inorganic Crystal Structure Database (ICSD). The inclusion of Mg in the calcite lattice (XMg) was calculated based on the shift in the (202) diffraction peak:
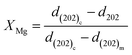 | (8) |
Morphological analysis
The morphology of natural dolomite particles and HCDs was observed using a JSM-5900 scanning electron microscope (JEOL, Ltd, Japan).Author contributions
Ju Huang: methodology, data curation, investigation, conceptualization, formal analysis, writing – original draft, writing – review & editing. Yu Cui: validation, investigation, methodology, writing – review & editing. Zanqun Liu: methodology, conceptualization, funding acquisition, project administration, supervision, validation, writing – review & editing. Dehua Deng: conceptualization, validation, supervision, writing – review & editing. Qiang Yuan: validation, supervision, writing – review & editing.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.References
- Z. Liu, S. Wang, J. Huang, Z. Wei, B. Guan and J. Fang, Constr. Build. Mater., 2015, 85, 247–255 CrossRef.
- Y. Chen, C. Wu, H. Yu, W. Chen, C. Chen, S. Zheng and F. Chen, Adv. Cem. Res., 2018, 30, 437–450 CrossRef.
- Z. A. Shajaratun Nur, Y. H. Taufiq-Yap, M. F. Rabiah Nizah, S. H. Teo, O. N. Syazwani and A. Islam, Energy Convers. Manage., 2014, 78, 738–744 CrossRef CAS.
- M. W. Islam, Fuel, 2020, 267, 1–17 CrossRef.
- O. Yamamoto, T. Ohira, K. Alvarez and M. Fukuda, Mater. Sci. Eng., B, 2010, 173, 208–212 CrossRef CAS.
- T. Kaljuvee, A. Trikkel and R. Kuusik, J. Therm. Anal. Calorim., 2001, 64, 1229–1240 CrossRef CAS.
- T. N. L. Thao Ngo and K.-Y. Chiang, J. Environ. Chem. Eng., 2023, 11, 109592 CrossRef CAS.
- B. Dou, K. Wu, H. Zhang, B. Chen, H. Chen and Y. Xu, Chem. Eng. J., 2023, 452, 139703 CrossRef CAS.
- M. Mohammadi, P. Lahijani, Z. A. Zainal and A. R. Mohamed, Chem. Eng. J., 2014, 240, 169–178 CrossRef CAS.
- J. E. Readman and R. Blom, Phys. Chem. Chem. Phys., 2005, 7, 1214–1219 RSC.
- I. L. Calugaru, T. Genty and C. M. Neculita, Miner. Eng., 2021, 160, 106666 CrossRef CAS.
- I. L. Calugaru, C. M. Neculita, T. Genty and G. J. Zagury, J. Environ. Manage., 2018, 212, 142–159 CrossRef CAS PubMed.
- K. Sasaki, M. Yoshida, B. Ahmmad, N. Fukumoto and T. Hirajima, Colloids Surf., A, 2013, 435, 56–62 CrossRef CAS.
- S. Karaca, A. Gurses, M. Ejder and M. Acikyildiz, J. Hazard. Mater., 2006, 128, 273–279 CrossRef CAS PubMed.
- Z.-f. Cao, P. Chen, F. Yang, S. Wang and H. Zhong, Colloids Surf., A, 2018, 539, 201–208 CrossRef CAS.
- J. Pesonen, P. Myllymäki, S. Tuomikoski, G. Vervecken, T. Hu, H. Prokkola, P. Tynjälä and U. Lassi, ChemEngineering, 2019, 3, 40 CrossRef CAS.
- Y. Xu, H. Hong, F. Yang, L. Zhang, J. Xu, L. Dou, Y. Hao, G. Qian and J. Zhou, Chemosphere, 2019, 235, 1015–1021 CrossRef CAS PubMed.
- K. Li, Y. Wang, N. Yao and A. Zhang, Constr. Build. Mater., 2020, 255, 119381 CrossRef CAS.
- S. Ruan, J. Liu, E.-H. Yang and C. Unluer, J. Mater. Civ. Eng., 2017, 29, 04017236 CrossRef.
- L. Huang, Z. Yang and S. Wang, Constr. Build. Mater., 2020, 262, 120776 CrossRef CAS.
- L. Mo, J. Fang, W. Hou, X. Ji, J. Yang, T. Fan and H. Wang, Constr. Build. Mater., 2019, 207, 206–217 CrossRef CAS.
- G. Bole and J. Shaw, J. Am. Ceram. Soc., 1922, 5, 817–822 CrossRef CAS.
- J. M. Gregg, D. L. Bish, S. E. Kaczmarek, H. G. Machel and C. Hollis, Sedimentology, 2015, 62, 1749–1769 CrossRef CAS.
- C. Rodriguez-Navarro, K. Kudlacz and E. Ruiz-Agudo, Am. Mineral., 2012, 97, 38–51 CrossRef CAS.
- M. Samtani, D. Dollimore and K. Alexander, Thermochim. Acta, 2002, 392, 135–145 CrossRef.
- J. M. Valverde, A. Perejon, S. Medina and L. A. Perez-Maqueda, Phys. Chem. Chem. Phys., 2015, 17, 30162–30176 RSC.
- D. T. Beruto, R. Vecchiattini and M. Giordani, Thermochim. Acta, 2003, 405, 183–194 CrossRef CAS.
- S. Kleiman and R. Chaim, Mater. Lett., 2007, 61, 4489–4491 CrossRef CAS.
- M. Q. Li and G. L. Messing, Thermochim. Acta, 1984, 78, 9–16 CrossRef CAS.
- M. Q. Li and G. L. Messing, Thermochim. Acta, 1983, 68, 1–8 CrossRef CAS.
- T. Chernykh, A. Nosov and L. Y. Kramar, IOP Conf. Ser.: Mater. Sci. Eng., 2015, 71, 012045 Search PubMed.
- W. R. Bandi and G. Krapf, Thermochim. Acta, 1976, 14, 221–243 CrossRef CAS.
- J. Huang, Y. Cui, Z. Liu and D. Deng, Thermochim. Acta, 2023, 726, 179541 CrossRef CAS.
- J. Titschack, F. Goetz-Neunhoeffer and J. Neubauer, Am. Mineral., 2011, 96, 1028–1038 CrossRef CAS.
- E. K. H. Hashimoto, F. Hayashi and T. Uematsu, Faculty of Engineering, J. Solid State Chem., 1980, 32, 251 Search PubMed.
- J. J. Lenders, A. Dey, P. H. Bomans, J. Spielmann, M. M. Hendrix, G. de With, F. C. Meldrum, S. Harder and N. A. Sommerdijk, J. Am. Chem. Soc., 2012, 134, 1367–1373 CrossRef CAS PubMed.
- M. E. Kunitake, S. P. Baker and L. A. Estroff, MRS Commun., 2012, 2, 113–116 CrossRef CAS.
- N. Bianco-Stein, I. Polishchuk, A. Lang, L. Portal, C. Dejoie, A. Katsman and B. Pokroy, Proc. Natl. Acad. Sci. U.S.A., 2022, 119, e2120177119 CrossRef CAS PubMed.
- K. E. Chave, K. S. Deffeyes, P. K. Weyl, R. M. Garrels and M. E. Thompson, Science, 1962, 137, 33–34 CrossRef CAS PubMed.
- H. B. Yao, J. Ge, L. B. Mao, Y. X. Yan and S. H. Yu, Adv. Mater., 2014, 26, 163–187 CrossRef CAS PubMed.
- J.-M. Huang and K. E. Daugherty, Thermochim. Acta, 1987, 115, 57–62 CrossRef CAS.
- J.-M. Huang and K. E. Daugherty, Thermochim. Acta, 1987, 118, 135–141 CrossRef CAS.
- X. Yang, L. Zhao and Y. Xiao, Energy Fuels, 2013, 27, 7645–7653 CrossRef CAS.
- C. Villada, A. Bonk, T. Bauer and F. Bolívar, Appl. Energy, 2018, 226, 107–115 CrossRef CAS.
- A. Remhof, O. Friedrichs, F. Buchter, P. Mauron, A. Zuttel and D. Wallacher, Phys. Chem. Chem. Phys., 2008, 10, 5859–5862 RSC.
- J. Speight, Lange's Handbook of Chemistry, 2005 Search PubMed.
- R. Merkle and J. Maier, Z. Anorg. Allg. Chem., 2005, 631, 1163–1166 CrossRef CAS.
- H. Galai, M. Pijolat, K. Nahdi and M. Trabelsiayadi, Solid State Ionics, 2007, 178, 1039–1047 CrossRef CAS.
- H. Mehrer, Diffusion in Solids : Fundamentals, Methods, Materials, Diffusion-Controlled Processes, Springer Science & Business Media, 2007 Search PubMed.
| This journal is © The Royal Society of Chemistry 2024 |