Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Retracted Article: Structural, morphological, electrical, and dielectric properties of Na2Cu5(Si2O7)2 for ASSIBs
Mohamed Ben Bechir *a and
Mehdi Akermibc
*a and
Mehdi Akermibc
aLaboratory of Spectroscopic and Optical Characterization of Materials (LaSCOM), Faculty of Sciences, University of Sfax, BP1171, 3000 Sfax, Tunisia. E-mail: mohamedbenbechir@hotmail.com
bDepartment Physics, College of Sciences, Jazan University, P. O. Box. 114, Jazan, 45142, Kingdom of Saudi Arabia. E-mail: makermi@jazanu.edu.sa
cLaboratory of Interfaces and Advanced Materials, Faculty of Science, Boulevard of the Environment, University of Monastir, 5019, Monastir, Tunisia
First published on 19th March 2024
Abstract
Solid inorganic electrolyte materials are fundamental components for constructing all-solid-state sodium-ion batteries. These solid electrolytes offer considerable benefits related to safety, electrochemical performance, and mechanical stability in comparison to liquid organic electrolyte systems. This study investigates the sodium ion conduction mechanism and relaxation kinetics in the sorosilicate material Na2Cu5(Si2O7)2, a potential solid electrolyte, using impedance spectroscopy. Analysis of the DC conductivity data demonstrates that sodium ion mobility follows Arrhenius behavior with a thermal activation energy barrier of 1.21 eV. This work highlights the importance of carefully choosing an appropriate equivalent circuit model to extract DC conductivity parameters from impedance data, given the contributions from both grain and grain boundary effects. Analysis of the AC conductivity and dielectric constant as a function of frequency and temperature demonstrates that ionic conduction takes place in this material through a process in which charge carriers overcome correlated energy barriers, known as correlated barrier hopping. The neutron diffraction patterns were analyzed using soft bond valence sum (BVS) techniques to map the possible ionic conduction pathways within the unit cell. Examination of the data points to obstructions in the sodium ion diffusion routes along the a-axis and diagonal of the bc plane within the triclinic unit cell. These bottlenecks likely contribute to the high activation energy and correspondingly low ionic conductivity observed. Analysis of dielectric properties by modulus verified that the ionic conduction relaxation phenomena exhibit thermal activation and a distribution of relaxation times. In summary, this work elucidates the microscopic ionic conduction mechanism in Na2Cu5(Si2O7)2 through extensive analysis encompassing DC/AC conductivity, electric modulus, and dielectric constant measurements. The insights gained into the ionic conduction mechanism will aid in engineering optimized ionic conductor materials for battery technologies.
1. Introduction
Sodium ion batteries (SIBs) are gaining significant attention as a promising and economically viable battery technology. This growing interest is primarily attributed to the ample and widely distributed reserves of sodium, which surpass the availability of lithium used in lithium-ion batteries (LIBs).1–3 Furthermore, SIBs can utilize aluminum, a readily accessible and lighter alternative to copper, as the current collector, and they can employ hard carbon derived from sustainable sources as the anode material. These features collectively contribute to a reduction in the overall cost of SIBs.4–6 Over the last decade, substantial endeavors have been dedicated to the advancement of electrode materials designed for the storage of sodium ions. This includes the innovation of novel anode materials like hard carbon, phosphides, and intermetallic compounds, as well as cathode materials such as sodium layered oxides, and sodium layered sulfates.7–9 Nevertheless, just like LIBs, the domain of electrolyte engineering in sodium-ion batteries (SIBs) has been somewhat marginalized in terms of the focus it has received when juxtaposed with the extensive attention given to electrode materials.1 The limited investigation of electrolytes in SIBs can be attributed to the complexities associated with establishing links between the kinetic aspects of electrolytes at the molecular level and the overall performance of batteries on a macroscopic scale. For example, several additives introduced to the electrolyte, such as FEC (fluoroethylene carbonate) and TMP (trimethyl phosphate), have demonstrated significant improvements in battery performance.10,11 However, the underlying reasons for these enhancements remain uncertain. Similarly, the mechanisms by which interactions among cations, anions, and solvent molecules enhance both the rate and cycle performance of batteries remain a topic of incomplete comprehension. Thankfully, the advent of the solid electrolyte interphase (SEI) theory has provided a viable approach to scrutinize the micro-level dynamics of electrolyte constituents.12 In recent times, all-solid-state batteries have garnered global interest due to various advantages, including their leak-proof nature, wide electrochemical operational limits, and impressive thermal resilience.13 Hence, the advantages of ASSIBs make them particularly well-suited for applications requiring high-capacity, large-scale energy storage and stringent safety considerations, such as public transportation.13 A significant hurdle encountered in the advancement of ASSIBs is the absence of a solid electrolyte composed of sodium that exhibits noteworthy ionic conductivity under standard ambient temperature conditions. It is imperative to engineer a new solid electrolyte with superior ionic conductivity through meticulous development of its chemical composition and internal structure.14,15In the not-so-distant past, within the framework of a broader assessment initiative for effective solid electrolyte materials in sodim-ion batteries, several silicate compounds with a sodium-ion foundation have been explored as Na2Si2O5 (∼10−2 S m−1) at 773 K.16 In this current investigation, we focus on the sorosilicate material Na2Cu5(Si2O7)2, notable for its captivating magnetic characteristics attributable to the presence of copper ion dimers and trimers. Our current research is inspired by the unique crystal arrangement (in the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (no. 2) space group) characterized by the placement of sodium ions within the channels formed by a framework consisting of copper and silicon polyhedra. This particular crystal structure potentially offers a straightforward route for sodium ion migration via the channels, which, in turn, promotes efficient sodium-ion conduction. Consequently, Na2Cu5(Si2O7)2 holds promise as a viable option for solid-state electrolytes in sodium-ion batteries. In pursuit of this goal, our research has encompassed the exploration of Na+ ionic conduction and an in-depth analysis of the crystal structure, as well as the possible pathways for conduction and the electrical characteristics of Na2Cu5(Si2O7)2.
(no. 2) space group) characterized by the placement of sodium ions within the channels formed by a framework consisting of copper and silicon polyhedra. This particular crystal structure potentially offers a straightforward route for sodium ion migration via the channels, which, in turn, promotes efficient sodium-ion conduction. Consequently, Na2Cu5(Si2O7)2 holds promise as a viable option for solid-state electrolytes in sodium-ion batteries. In pursuit of this goal, our research has encompassed the exploration of Na+ ionic conduction and an in-depth analysis of the crystal structure, as well as the possible pathways for conduction and the electrical characteristics of Na2Cu5(Si2O7)2.
This work implements extensive impedance spectroscopy measurements and data analysis to comprehensively characterize the ionic conduction properties of Na2Cu5(Si2O7)2. The conduction and relaxation mechanisms were elucidated through integrated analysis of DC/AC conductivity, modulus, and dielectric constant data. The crystal structure was probed through a joint examination utilizing X-ray and neutron powder diffraction techniques. The pathways for ionic conduction within the unit cell of the crystal structure were ascertained via a soft BVS analysis of the neutron powder diffraction pattern. Moreover, this study explores the significance of selecting the appropriate equivalent circuit model for impedance data analysis, enabling the accurate extraction of conduction characteristics. Additionally, our research discloses that ion conduction occurs through the CBH model. Furthermore, we have identified a thermally induced relaxation process for ionic conduction that deviates from the typical Debye-type behavior. The comprehension of the mechanism underlying Na-ion conduction, as unveiled in this study, is vital for the design of efficient electrolyte materials.
2. Methods
2.1 Materials
Sodium carbonate (Sigma-Aldrich, 99.9% trace metals basis), copper oxide (Sigma-Aldrich, >99.99%), and Silicon dioxide (Sigma-Aldrich, ∼99%) weren't further purified; they were used as received.2.2 Synthesis
The Na2Cu5(Si2O7)2 material was prepared using a standard solid-state reaction approach as follows:| Na2CO3 + 5CuO + 4SiO2 → Na2Cu5(Si2O7)2 + CO2↑ | (1) |
The starting materials of Na2CO3, CuO, and SiO2 were combined in stoichiometric ratios. These materials were thoroughly mixed together in an agate mortar to obtain a homogeneous mixture.
The prepared mixture underwent calcination by gradually heating to 800 K over 24 hours. The calcined powder was then mechanically ground for 1 hour duration. Next, the ground powder was fired at 1150 K for 48 hours to synthesize the final Na2Cu5(Si2O7)2 powder.
2.3 Characterizations
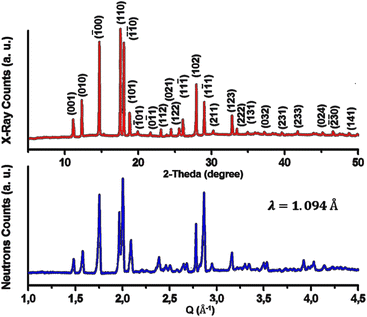
To obtain finely powdered samples suitable for powder X-ray diffraction (PXRD), a small quantity of Na2Cu5(Si2O7)2 powder was subjected to mechanical grinding using a pestle and an agate mortar. The PXRD analysis was conducted at room temperature over the range of 2θ = 5°–50° using Cu Kα line radiation (λ = 1.54 Å) and a step size of 0.04°, employing a Rigaku MiniFlex 600 benchtop diffractometer. The lower angle limit of 5° allows for the detection of diffraction peaks corresponding to larger interplanar spacings, providing insights into the long-range ordering and structural features of the material. On the other hand, the upper limit of 50° includes higher-angle diffraction peaks, which are valuable for resolving fine details in the crystal structure and identifying potential secondary phases or subtle structural variations. Neutron powder diffraction (NPD) measurements at room temperature were conducted utilizing the neutron powder diffractometer (PD-1). The NPD patterns were collected within the 2θ angular range of 5 to 50°, using three linear positions sensitive He3 neutron detectors. This span covered the Q range of 0.5 to 5 Å−1 (where Q = 4π![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ).
θ/λ).
The examination of the Na2Cu5(Si2O7)2 morphology was carried out by employing scanning electron microscopy (SEM) with a Philips XL30 microscope operating at 20 kV.
The complex impedance spectroscopy assessments were performed on a disk-shaped pellet with dimensions of 8 mm in diameter, approximately 1 mm in thickness, and a relative density of 95.17%, composed of Na2Cu5(Si2O7)2. The pellet was subjected to sintering in an air environment at 1100 K, followed by the application of a silver coating. The flat surfaces of the pellet were silver-painted, left to dry at room temperature for approximately 2 hours, and subsequently exposed to a temperature of 600 K for 2 hours to eliminate volatile compounds from the silver paste. The pellet was placed between two matching circular Ni electrodes, and impedance assessments were executed utilizing a TH2828A impedance analyzer operating within a frequency range of 100–105 Hz. This setup was connected to a temperature controller (TP94, Linkam, Surrey, UK) with a heating rate of 5 K per minute. The applied ac voltage for measurements was maintained at 0.5 V.
3. Results and discussion
Fig. 1 shows the PXRD pattern of Na2Cu5(Si2O7)2 at ambient temperature. All observed reflection peaks were indexed to the triclinic phase with the space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (no. 2) at approximately 297 K. The lattice parameters of the selected unit cell, a = 5.709(3) Å, b = 7.677(2) Å, c = 7.691(4) Å, α = 64.234(3)°, β = 88.417(5)°, and γ = 70.588(4)° were refined using Celeref3 software,17,18 consistent with values reported in the literature.19 The table, denoted as Table 1, contains the atomic positions and site occupation numbers.19
(no. 2) at approximately 297 K. The lattice parameters of the selected unit cell, a = 5.709(3) Å, b = 7.677(2) Å, c = 7.691(4) Å, α = 64.234(3)°, β = 88.417(5)°, and γ = 70.588(4)° were refined using Celeref3 software,17,18 consistent with values reported in the literature.19 The table, denoted as Table 1, contains the atomic positions and site occupation numbers.19
| Atom | Wyckoff site | x | y | z | Uiso |
|---|---|---|---|---|---|
| Cu1 | 1a | 0.5 | 0.5 | 0.5 | 0.0057(6) |
| Cu2 | 2i | 0.1747(2) | 0.9277(2) | 0.2209(2) | 0.0069(4) |
| Cu3 | 2i | 0.5832(2) | 0.1020(2) | 0.3195(2) | 0.0063(4) |
| Si1 | 2i | 0.2345(6) | 0.6295(5) | 0.0518(5) | 0.0068(1) |
| Si2 | 2i | 0.9921(5) | 0.2617(4) | 0.3683(3) | 0.0068(1) |
| Na1 | 2i | 0.6954(5) | 0.7165(4) | 0.0956(4) | 0.002(8) |
| O1 | 2i | 0.9477(9) | 0.4979(7) | 0.2082(6) | 0.01(2) |
| O2 | 2i | 0.4897(9) | 0.7066(7) | 0.2449(7) | 0.01(2) |
| O3 | 2i | 0.5786(9) | 0.7029(7) | −0.0733(7) | 0.01(2) |
| O4 | 2i | 1.2849(9) | 0.1478(7) | 0.4492(7) | 0.01(2) |
| O5 | 2i | 0.9058(9) | 0.1371(8) | 0.2673(7) | 0.01(2) |
| O6 | 2i | 0.8097(9) | 0.2789(7) | 0.5226(7) | 0.01(2) |
| O7 | 2i | 0.8121(1) | 0.8960(8) | 0.0360(7) | 0.01(2) |
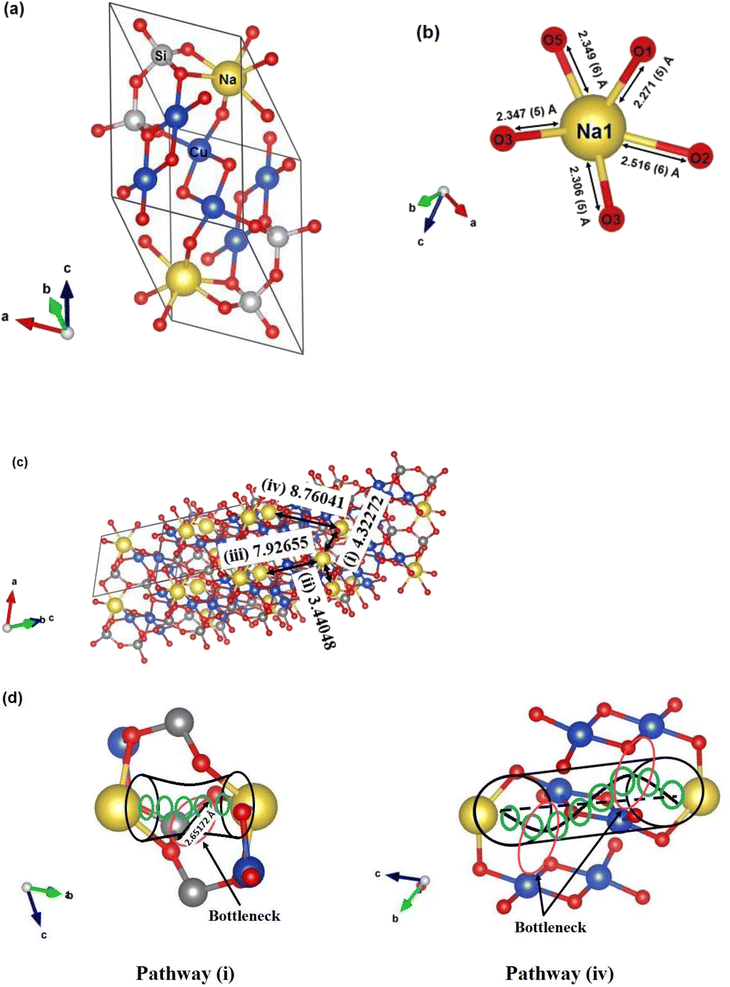
The crystallographic structure of Na2Cu5(Si2O7)2 comprises Si2O7 double tetrahedra, three distinct copper polyhedra, and one sodium polyhedron (as illustrated in Fig. 2(a)).20 The sodium ions are situated at the 2i crystallographic site, with complete occupancy, and they are surrounded by a coordination of five oxygen atoms, as shown in Fig. 2(b). To provide a more detailed depiction of the Na ion's location, Fig. 2(c) presents an extended perspective of the crystal structure. The linkage between the Cu and Si polyhedra is established by sharing oxygen atoms at their corners, creating a sturdy framework. This framework, in turn, establishes pathways within the unit cell that enable the diffusion of Na ions. The Na–O bond distances fall within the range of 2.271–2.516 Å (as detailed in Table 2). To clarify the pathways for ionic conduction, we employ the soft BVS method.21–23 This approach has been effectively utilized to discern conduction routes in various ionic conductors using neutron diffraction analysis. In computing the BVS, we applied the soft bond valence parameters established by Adams. The bond valence landscape (BVL) map, which illustrates the isosurface map for a designated BVS mismatch above the defined bond valence mismatch threshold, is presented in Fig. 2(c). This visualization was created with the aid of VESTA software.24 BVL mappings of Na2Cu5(Si2O7)2 demonstrate that sodium conduction occurs in all three crystallographic orientations. Within these mappings, we can identify four distinct effective pathways for sodium-ion conduction, marked as i, ii, iii, and iv (as illustrated in Fig. 2(c)). The conduction pathways, denoted as (i), are primarily oriented along the a-axis, featuring a Na–Na distance of approximately 4.32272 Å. Meanwhile, pathways (ii) align closely with the b-axis, with a Na–Na separation of about 3.44048 Å. In contrast, pathways (iii) predominantly follow the c-axis, exhibiting a Na–Na spacing of around 7.92655 Å, while pathways (iv) traverse the diagonal direction within the bc plane, with a Na–Na distance of roughly 8.76041 Å. Moreover, the identified pathways indicate the presence of constriction points within certain conduction routes, significantly impacting ionic conduction. These constriction points can be quantified by measuring the shortest distance between mobile sodium ions and the adjacent oxygen/silicon ions at the narrowest segments of these pathways, and these specific measurements are referred to as bottleneck radii. As Fig. 2(c) illustrates, it is clear that pathways (ii) and (iii) lack any constriction points, providing an unobstructed route for the movement of sodium ions. However, along pathways (i), a constriction point occurs as a result of the proximity of neighboring oxygen ions (with an O–O distance of 2.65172 Å), as depicted in Fig. 2(d). Moreover, as we examine pathways (iv), the inclusion of oxygen ions within the sodium-ion conduction routes (as depicted in Fig. 2(c)) creates constriction points, which, in turn, hinder the ionic conduction within Na2Cu5(Si2O7)2. In Fig. 3, the SEM image of the Na2Cu5(Si2O7)2 polycrystalline sample is presented. We analyzed to determine the average grain size, which was estimated to be approximately 3 μm.
| Na–O1 | 2.271(5) | Na–O3 | 2.347(5) |
| Na–O2 | 2.516(6) | Na–O5 | 2.349(6) |
| Na–O3 | 2.306(5) | Na–Na | 3.44048 |
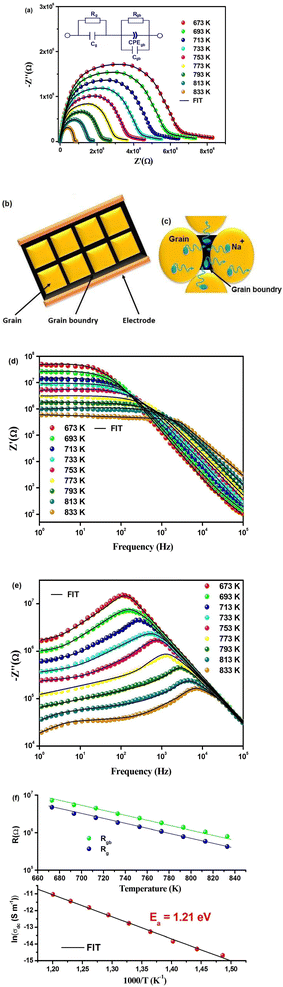
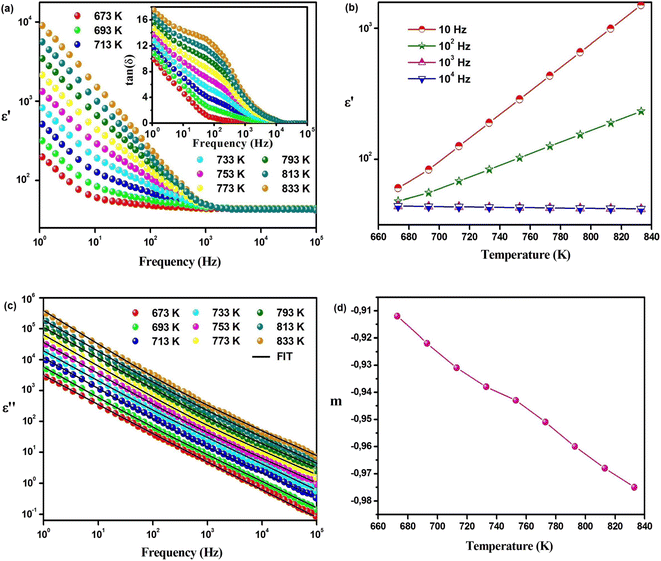
Impedance spectroscopy stands as a firmly established method for investigating a material's conductivity across varying temperatures and frequencies. It serves the purpose of discerning both the real and imaginary components of a range of electrical parameters, including impedance, dielectric constant, AC conductivity, and polarizability.25–27 These findings are instrumental in comprehending the electrical attributes of the material. By offering distinct data on the roles of both grains and grain boundaries in ionic conduction, this method adds a valuable layer of understanding.28 Displayed in Fig. 4(a) are the Cole–Cole plots illustrating the impedance (−Z′′ vs. Z′) at different temperatures spanning from 673 to 833 K. The Cole–Cole plot inherently incorporates frequency, with a range spanning from 100 to 105 Hz. In the −Z′′ vs. Z′ curves, two semicircles become distinctly apparent at elevated temperatures, as depicted in Fig. 4(a). These semicircles exhibit non-Debye characteristics, as evidenced by their altered shapes and center positions situated below the Z′ axis (horizontal).
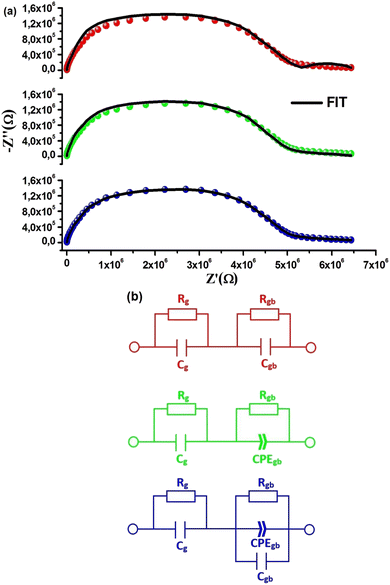
The decreasing nature of the semi-circle radii with increasing temperature in the Cole–Cole plot again confirms the Negative Temperature Coefficient Resistance (NTCR) behavior of the material. This also indicates that the conduction process is thermally activated.27 These findings are instrumental in comprehending the electrical attributes of the material. By offering distinct data on the roles of both grains and grain boundaries in ionic conduction, this method adds a valuable layer of understanding.27 The Cole–Cole plots find their elucidation in an equivalent circuit model. This model primarily comprises arrangements of resistors, capacitors, inductors, constant phase elements, and other components organized in serial and/or parallel configurations.27 Every electrical element within the equivalent circuit possesses distinctive traits and reacts to an externally applied electric field in its unique manner. Considering the microstructural aspect, it's common for polycrystalline compounds to comprise multiple electrical components, each with its distinct resistive and capacitive behavior.29 These components arise due to the presence of various electroactive zones (grains, grain boundaries, and electrode interfaces).29 Each electroactive region's influence is discernible within distinct frequency bands evident in the Cole–Cole plots, as each region operates on its specific time scale. In the examination and interpretation of these plots, a brick-layer model is typically employed and has been extensively explored in prior literature, especially in the context of powder samples.30–33 Following this model, a material is conceptualized as a three-dimensional, uniform arrangement of cubic grains, alongside identical grain boundaries, as depicted in Fig. 4(b). The motion of mobile ions involves traversing these grain boundaries as they transfer from one grain to another, illustrated in Fig. 4(c). In the case of Na2Cu5(Si2O7)2, the presence of dual semicircles within the Cole–Cole plots indicates the involvement of two electroactive areas, specifically the grain and the grain boundary. With this in mind, the equivalent circuit necessitates a model with two time constants, comprising a series arrangement of two subcircuits. One of these subcircuits signifies the contribution from the grains, while the other encapsulates the contribution from the grain boundaries. The most optimal fit for the Cole–Cole plots is achieved through the utilization of ZView software,27 employing an equivalent circuit model, as shown in the inset of Fig. 4(a). This particular equivalent circuit model employs a series arrangement of two subcircuits. The first subcircuit encompasses a parallel combination of resistance (Rg) and capacitance (Cg), signifying the characteristics of the grain interior. Meanwhile, the second subcircuit features a parallel combination of resistance (Rgb), capacitance (Cgb), and a constant phase element (CPEgb) designed to represent contributions from the grain boundaries. The CPE is formally characterized as a capacitance exhibiting fractal behavior with a constant phase within a complex plane, and this can be expressed through the eqn (2).
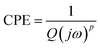 | (2) |
An equivalent circuit akin to this has been employed in prior instances to suitably model Cole–Cole plots for numerous compounds.30–33 We will delve into the specifics of the equivalent circuit selection in subsequent discussion. Fig. 4(d) illustrates the frequency-dependent behavior of the real component of impedance (Z′) at specific temperatures. It is observed that Z′ decreases with an increase in both frequency and temperature, confirming the NTCR behavior of Na2Cu5(Si2O7)2. Notably, a plateau emerges in the low-frequency range, particularly evident at elevated temperatures. The Z′ value experiences a significant and rapid reduction at the plateau as the temperature rises, indicating a robust reliance on temperature. At a specific temperature, Z′ diminishes as the frequency increases beyond the critical frequency, implying that an increase in AC conductivity may arise due to a decrease in the concentration of trapped charges and an enhancement in charge carrier mobility.26 Moreover, as seen in Fig. 4(e), the frequency-dependent behavior of −Z′′ reveals a distinctive peak at a specific frequency. At low temperatures, immobile species/electrons, and at high temperatures, defects/vacancies may be a valid reason behind the relaxation process. A well-defined characteristic peak, conventionally termed as the “relaxation frequency,” has been observed for each spectrum. The width of the peak indicates a significant deviation from an ideal Debye-type nature.27
The movement of long-range charge carriers is primarily responsible for transport below the peak loss frequency, and it is contributed to by the motion of localized carriers above the relaxation frequency. The peak height decreases with temperature, suggesting that grain/grain boundary resistance decreases with temperature.26 This peak undergoes a transition towards higher frequencies and experiences broadening as the temperature is elevated. The presence of this peak can be attributed to the conduction relaxation phenomenon in the system. As the temperature increases, the peak's migration toward higher frequencies indicates a decrease in the relaxation time of mobile Na-ions with rising temperature.25 Nevertheless, the substantial widening of the peak as the temperature rises implies the existence of a time-distributed relaxation process.25 At higher frequencies, the Z′′ values for all temperatures converge onto a unified curve, potentially signifying the influence of space charges. Regarding the equivalent circuit model provided in the inset of Fig. 4(a), the characteristic equations for the real and imaginary components of electrical impedance are expressed as eqn (3) and (4).
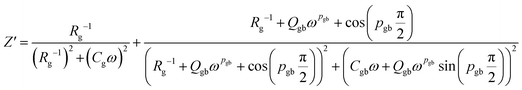 | (3) |
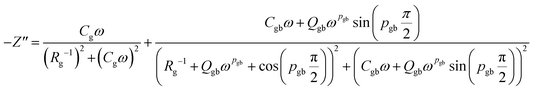 | (4) |
The symbols in these equations retain their standard meanings and interpretations.
Here, it's worth noting that the computed values of Z′ and Z′′ (utilizing the parameters acquired through Cole–Cole fitting) using eqn (2) and (3) accurately replicate the experimental Z′ and Z′′ curves, as depicted in Fig. 4(d) and (e). The resistance values associated with the grain (Rg) and grain boundary (Rgb), determined from the data in Fig. 4(a), showcase an exponential decrease with rising temperature. This trend signifies the semiconducting nature of the compound, as evidenced in Fig. 4(f).
Illustrated in Fig. 4(a) and (f), it is evident that, irrespective of temperature variations, Rgb consistently surpasses the magnitude of Rg. This observation underscores that, given the equation R = Rg + Rgb, the total resistance is predominantly influenced by the contributions from grain boundaries. Certainly, within ceramic materials, the resistivity of grain boundaries exceeds that of the grains. This disparity in resistive characteristics leads to a notable elevation in the quantity of space charges at the grain boundaries, a phenomenon attributed to polarization known as the Maxwell–Wagner effect.27 The aggregate resistance, denoted as Rdc, is derived by adding the individual grain and grain boundary resistances (Rg + Rgb). The direct current conductivity, denoted as σdc, is computed using the eqn (5).
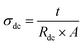 | (5) |
In this equation, Rdc represents the total resistance of the material, ‘t’ signifies the thickness of the pellet, and ‘A’ corresponds to the cross-sectional area of the pellet.
The temperature-dependent behavior of σdc adheres to the Arrhenius pattern (eqn (6)), as depicted in Fig. 4(f).
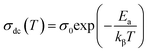 | (6) |
The symbols in these equations retain their standard meanings and interpretations.
The computed activation energy is Ea = 1.21 eV. Notably, this Ea value falls within the moderate range when compared to others sodium-ion-based silicate compound.
In order to grasp the ionic conduction mechanism, an examination of the ac conductivity was conducted. The connection between the real component of ac conductivity (σ′) and impedance can be expressed as shows in eqn (7).
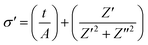 | (7) |
As the temperature rises, there is a noticeable increase in the overall value of σ′, a trait commonly associated with semiconducting materials. Fig. 5(a) displays the frequency-dependent behavior of σ′ at specific temperatures. The curves of σ′(f) exhibit a constant portion that remains independent of frequency at lower frequencies, alongside a frequency-dependent component at higher frequencies. The frequency-dependent pattern of σ′ at a particular temperature aligns well with Jonscher's power law, elucidating the behavior (eqn (8)).34,35
| σ′(T,ω) = σdc(T) + A(T)ωs(T) | (8) |
 | ||
| Fig. 5 (a) Variation of σ′(f) at different temperatures. (b) Variation of s with temperature. (c) The temperature dependency of the ln(σ′) at various frequencies. (d) Frequency dependence of Ea (eV). | ||
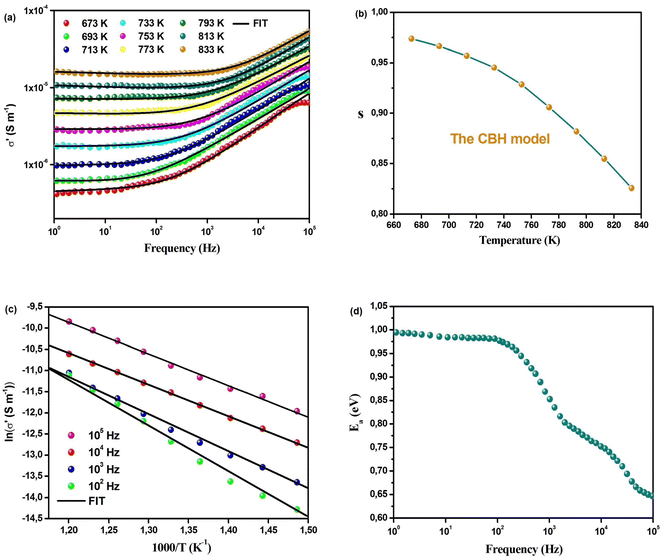
The expression introduces σdc as the direct current conductivity, attainable by extrapolating the curves to zero frequency. A(T) and s(T) are parameters subject to variation with temperature. The parameter s(T) serves as the power exponent and offers valuable information concerning the extent of interactions between mobile ions and their adjacent environment. It is worth noting that the value of s(T) falls within the range of 0 to 1.
In accordance with a model based on jump relaxation,36,37 the parameter denoted as s(T) is representable as the ratio of the rate at which particles backtrack (referred to as br) to the rate at which sites undergo relaxation (referred to as sr), this ratio is expressed as br/sr. The reverse movement of the mobile ion to its original position occurs due to the repulsive Coulomb interaction between mobile ions. Site relaxation, on the other hand, is triggered by the reorganization of neighboring ions around the hopping location. The curves fitted using Jonscher's power law (Fig. 5(a)) align well with the data points for all temperatures. This observation suggests that the current compound adheres to the universal power law. As illustrated in Fig. 5(b), the parameter s(T) diminishes as the temperature rises. Across all the recorded temperatures, the fitted s(T) values consistently fall far below unity, signifying that the rate of backward hopping is slower than the rate of site relaxation. Consequently, this leads to a coordinated movement of Na ions, characterized by translational motion, signifying long-range ionic conduction. The decelerated reverse movement can be attributed to the weakened coulombic interactions among the mobile ions. Moreover, the dependence of s(T) on temperature suggests that the conduction mechanism aligns with the correlated barrier hopping (CBH) approach, a phenomenon previously observed in various other substances.38–40 In the following section, we will engage in a more comprehensive exploration of the conduction mechanism and its interplay with dc conductivity. As depicted in Fig. 5(a), it's apparent that σ′ rises with increasing temperature across all frequencies. To ascertain the activation energies at various frequencies, we have employed the Arrhenius model (eqn (9)).
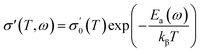 | (9) |
The symbols in these equations retain their standard meanings and interpretations.
Fig. 5(c) presents the Arrhenius curves corresponding to various frequencies. In Fig. 5(d), we depict the relationship between activation energy and frequency, which discloses a consistent value up to approximately 10 Hz, followed by a decline as the frequency further increases. This pattern illustrates a frequency-enhanced conduction mechanism, indicating an improved mobility of sodium ions. This aligns with the behavior of the real part of impedance. The lower activation energy observed at higher frequencies suggests that sodium ions have increased access to neighboring sites for hopping during ac conduction.15
To delve into the study of conductivity and the related relaxation phenomenon, we have conducted an analysis of the electric modulus. The electric modulus is a vital tool for investigating both relaxation processes and electric responses within a material, particularly in cases where long-range migration of charge carriers plays a predominant role. The primary benefit of utilizing the electric modulus lies in its capacity to exclude the influence of electrode polarizations. This exclusion, in turn, offers a unique opportunity to focus exclusively on the investigation of the relaxation process associated with ionic conduction.24–27 The real (M′) and imaginary (M′′) components of the electrical modulus (M) are determined through eqn (10) and (11), which are derived from the values of Z′ and Z′′.
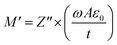 | (10) |
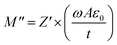 | (11) |
The symbols in these equations retain their standard meanings and interpretations.
Fig. 6(a) illustrates the electric modulus spectra's real component concerning frequency across various temperature values. The fluctuation in the real part of the electric modulus (M′) with frequency indicates that M′ attains a highly negligible value, approaching zero, in the low-frequency range across all temperature conditions. The observed pattern, coupled with the sigmoidal character of M′, arises from the extended mobility of charge carriers in the conduction mechanism and the disregard of electrode polarization. A slight modification occurs in the peak of the real part of the electric modulus (M′) as the temperature rises within the high-frequency range.26,27 The near-zero M′ value observed at lower frequencies suggests that the conduction process might lack the restorative force that typically influences the movement of charge carriers when subjected to an induced electric field. Such behavior strongly indicates that the conduction phenomenon arises from the unimpeded long-range mobility of charge carriers, and it remains unaffected by electrode polarization or electrode capacitances.41,42 The conductive relaxation time effect is represented by the dispersion zone of M′(f) plots. Furthermore, the attainment of a saturation point in M′ at elevated frequencies reinforces the hypothesis that the conduction process arises from the short-range mobility of charge carriers influenced by frequency. In these high-frequency domains, ions demonstrate swifter motion across limited distances, aligning with the noted dispersion and the heightened ac conductivity observed at such frequencies.41,42 Fig. 6(b) shows the M′′(f) plots, which display a loss peak at a particular frequency. We note that this particular frequency is connceted with the depression zone of M′(f) plots. In the region above this peak, we observe short-range mobility of charge carriers. Furthermore, there is a noticeable shift of the M′′ loss peak towards higher frequencies as the temperature increases, indicating a reduction in relaxation time with rising temperature. Furthermore, the peak exhibits an increased width and asymmetry as the temperature rises.25 In materials undergoing an ionic conduction process, the frequency-dependent behavior of M′′ can be elucidated using the Kohlraush–Williams–Watts (KWW) model eqn (12).24
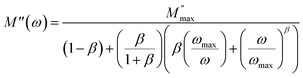 | (12) |
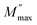 and ωmax retain their conventional definitions, while β serves as the Kohlrausch–Williams–Watts (KWW) shape parameter, offering a quantitative measure for assessing the extent of asymmetry and broadening observed in the loss peak. The parameter β falls within the interval of 0 < β < 1, and it offers insights into the character of the relaxation process. A β value of 1 signifies the presence of a Debye relaxation process, while any deviation from this value indicates a relaxation process that deviates from the Debye type.
and ωmax retain their conventional definitions, while β serves as the Kohlrausch–Williams–Watts (KWW) shape parameter, offering a quantitative measure for assessing the extent of asymmetry and broadening observed in the loss peak. The parameter β falls within the interval of 0 < β < 1, and it offers insights into the character of the relaxation process. A β value of 1 signifies the presence of a Debye relaxation process, while any deviation from this value indicates a relaxation process that deviates from the Debye type.
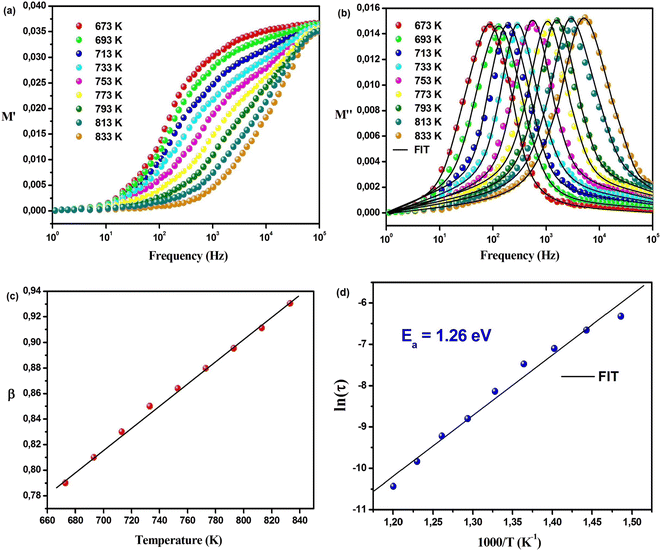 | ||
Fig. 6 Temperature-dependent changes in (a) M′(f) and (b) M′′(f) for Na2Cu5(Si2O7)2. (c) Variation of β with temperature. (d) Arrhenius plot of 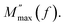 | ||
In the case of Na2Cu5(Si2O7)2, the β parameter is consistently below 1 across all tested temperatures. Notably, as the temperature rises, the β value demonstrates an ascending trend, indicating a non-Debye type of conduction procedure (as depicted in Fig. 6(c)).43 It is worth noting that our findings align with a similar conclusion derived from the study of dc conductivity, as we discussed previously. It's essential to note that the conductivity relaxation time (τm) can be computed by utilizing the peak frequency of the M′′(f) plots, which can be related through the equation ωmax × τm = 1. The τm value represents the time most likely for the conduction relaxation process in the material, as illustrated in Fig. 6(d). In our specific case, it is observed that τm conforms to the Arrhenius model eqn (13).
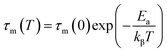 | (13) |
The symbols in these equations retain their standard meanings and interpretations.
We note that Ea = 1.26 eV, this value close to that found in the analysis of the dc conductivity shows that the relaxation comportment procedure and the conduction mechanism verified to be similar (eqn (14)).
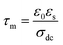 | (14) |
This connection also suggests that the mobile Na-ions encounter a consistent energy barrier for both conduction and relaxation procedure.
The dielectric constant also imparts crucial insights into the hopping mechanism of charge carriers within an ionic conductor.25 Both the real (ε′) and imaginary (ε′′) components of the dielectric constant can be determined as eqn (15) and (16).
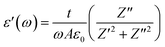 | (15) |
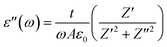 | (16) |
The symbols in these equations retain their standard meanings and interpretations.
Investigations into the dielectric constants concerning frequency within the temperature range of 673–833 K reveal notable variations. Fig. 7(a)–(c) confirm that, as the frequency increases, the dielectric constant gradually decreases for Na2Cu5(Si2O7)2. Simultaneously, it maintains a considerable magnitude at a specific temperature within the low-frequency spectrum. The management of ionic conduction involves various polarization types, namely interfacial, orientational, electronic, and ionic. Both ε′(ω) and ε′′(ω) play pivotal roles in this process. Interfacial and orientational polarizations are attributed to the relaxation component of polarizability, while electronic and ionic polarizations represent the deformational component of polarizability.25,26
 | ||
| Fig. 7 Temperature-dependent of (a) ε′(f) and (c) ε′′(f) for Na2Cu5(Si2O7)2. (b) Frequency-dependent of ε′(T). (d) Variation of m with temperature. | ||
The Maxwell–Wagner interfacial polarization, in alignment with Koop's phenomenological theory, enables an explanation of the variations observed in the real part of permittivity as a function of frequency.26 Within this model, inadequately conductive grain boundaries act as dividers between conductive grains constituting the compound. Consequently, charge carriers become entrapped at the interface of these grain boundaries, impeding their free movement.27 In the process of interfacial polarization, electrons are exchanged among ions originating from the same molecules. The reconfiguration of negative and positive space charges is a consequence of the compound's imperfections and deformities. Positive charges are directed towards the negative poles of the applied field, while negative charges move towards the positive poles, responding to the influence of the applied electric field.27 In the low-frequency domain, it is observed that electron movement through hopping facilitates their arrival at the grain boundary for Na2Cu5(Si2O7)2 (refer to Fig. 7(a) and (b)). However, owing to the elevated resistance at the grain boundary, electrons amass in that region, instigating the polarization phenomenon. Nevertheless, when the frequency is high, electrons are unable to track the oscillation of the applied field, hindering their continued accumulation even though they move in the opposite direction. Consequently, as the frequency increases, the likelihood of electrons reaching the grain boundary diminishes, resulting in reduced polarization.27 Due to the relaxation process, the presence of a hump can characterize the fluctuation in ε′(ω) within the mid-frequency range. The temperature-induced dielectric response occurs as the hump position shifts towards the low-frequency region with changes in temperature. However, there is no notable alteration in the ε′(ω) value at high frequency. This “unrelaxed” permittivity value signifies the presence of both atomic and electronic polarization. Consequently, the decrease in temperature is associated with a decline in the real part of the dielectric constant, ε′(ω). This phenomenon is likely a result of the reduced reactivity of conducting electrons and involved ions at lower temperatures.38 The energy absorption per unit volume when exposed to an alternating electric field is described by the imaginary part of the dielectric constant, ε′′. Fig. 7(c) illustrates the frequency dependency of ε′′. At a constant temperature, ε′′ decreases consistently with increasing frequency, whereas at a fixed frequency, ε′′ shows an increase with rising temperature. Based on the analysis of ac conductivity, it's evident that as temperature rises, conductivity increases, resulting in a higher ε′′.38 Consequently, the primary factor contributing to ε′′ is ionic conduction attributed to the charge carriers' hopping mechanism. This observation aligns well with the eqn (17).
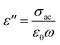 | (17) |
In this context, the symbols maintain their standard interpretations. Additionally, the universal power law provides a suitable fit for the imaginary component of the dielectric constant.
Fitting the ε′′(ω) plots using the eqn (18) (Fig. 7(c)) demonstrates that the synthesized material conforms to the universal power law.
| ε′′(T,ω) = a(T)ωm(T) | (18) |
In this equation, a(T) represents a constant of proportionality, while m(T) signifies the exponent that varies with temperature.
The plot of m(T), presented in Fig. 7(d), demonstrates a consistent downward trend as temperature increases, ultimately converging toward −1 at elevated temperatures. This decline in the m(T) value with rising temperature unmistakably indicates the dominance of a correlated barrier hopping (CBH) mechanism in the ionic conduction of Na2Cu5(Si2O7)2. Consequently, investigations into both ac conduction and dielectric constant unveil that the charge carriers' conduction process is facilitated through a hopping mechanism. The dielectric loss factor is a measure of the inherent dissipation of electrical energy within a dielectric medium when subjected to an alternating current field. It can be expressed for a specific medium through the eqn (19).
| tan(δ) = ε′(ω)/ε′′(ω) | (19) |
The symbols in these equations retain their standard meanings and interpretations.
In the inset of Fig. 7(a), we can observe the frequency-dependent behavior of the loss factor at specific temperatures. In the case of Na2Cu5(Si2O7)2, the loss factor falls within the range of 0 to 18. This range is notably lower when compared to the reported values for other electrolytes.38 The loss factor value experiences a decrease as the frequency increases, ultimately reaching near-zero levels beyond 104 Hz. This phenomenon indicates that the frequency-enhanced hopping of charge carriers is taking place. The presence of low-energy-loss characteristics in materials like this is particularly advantageous, especially in the context of energy storage systems. In brief, the various analytical approaches employed in this study collectively elucidate a long-range sodium-ion conduction mechanism characterized by minimal dielectric losses within Na2Cu5(Si2O7)2. Our investigation demonstrates that the ac conductivity is ensured by the correlated barrier hopping mechanism. Furthermore, our research identifies a distribution of relaxation times within the conduction relaxation process.
Let's now explore the influence of the microstructure on ionic conduction within Na2Cu5(Si2O7)2. Ionic conduction plays a pivotal role in determining a material's suitability for energy storage systems. It governs the movement of ions within the material, thereby influencing other critical factors. Establishing ionic conductivity relies significantly on interpreting Cole–Cole curves through the application of an equivalent circuit model. Nevertheless, the selection of an appropriate equivalent circuit holds paramount importance in accurately deriving the transport properties. We employed modeling techniques to analyze the Cole–Cole curve at 713 K (Fig. 8(a) and (b)) by implementing various equivalent circuits. These circuits feature a series connection between two parallel RC(CPE) components, and the corresponding simulated plots are depicted as continuous lines. The simulated plot generated by the equivalent circuit model, depicted in Fig. 8(a) and (b) (red model), appears to anticipate the presence of two pristine semicircles. However, it falls short of accurately matching the observed curve. The deviations in the semicircular patterns may arise due to variations in the dielectric properties with frequency and the existence of spatial irregularities.44 These effects are not taken into account by a basic equivalent circuit model composed of resistance (R) and capacitance (C) components (red model). As reported in existing literature, spatial irregularities and localized phenomena, like diffusion, contribute to the distribution of relaxation times for charge carriers. This, in turn, leads to the observed attenuation of the semicircular pattern in the Cole–Cole curve. Examination of our electrical modulus results reveals a spread of relaxation times. To address this situation for the current compound, we substituted one of the capacitors with a Constant Phase Element (CPE) as illustrated in Fig. 8(a) and (b) (green model). The fitted plot generated by the second model continues to demonstrate a poor fit with the measured data, indicating that the chosen equivalent circuit in this context lacks completeness in capturing the impedance data. Given that the CPE affects electrical data across an extensive frequency spectrum, enhancing the fit can be achieved by restricting its contributions both at larger and smaller frequency extremes. In recent literature, it has been noted that the unbounded influence of CPE can be constrained by introducing a parallel combination of a capacitor and a resistor alongside it.45 The existence of a parallel capacitor, denoted as C, can effectively counteract the impact of the CPE at elevated frequencies. Conversely, the parallel resistor, represented by R, counteracts the CPE's influence at smaller frequencies. With this notion in consideration, we have opted for a third model, featuring a series pairing of two subsidiary circuits. The fitted plot by the third model exhibits a considerably improved agreement with the experimental data, effectively recapitulating all the observed characteristics (blue model). Therefore, it can be concluded that the third equivalent circuit is well-suited for the material under the current research, Na2Cu5(Si2O7)2. Table 3 lists the determined values for all elements of the equivalent circuit. Typically, in the case of powdered oxide compounds, the resistance Rgb exceeds that Rg. The third model agrees with this proposal contrary to the first and second models. These divergent findings emphasize that an inappropriate selection of an equivalent circuit approach can result in inaccurate forecasts of Rg/Rgb values and, consequently, conductivity. The distinction between Rg/Rgb values signifies the accumulation of space charge at grain boundaries, resulting in the development of polarization. This polarization is observable through Z′′(f) variation.46
 | ||
| Fig. 8 Utilizing various equivalent circuit models for fitting experimental impedance Cole–Cole plot at 713 K. | ||
| Model 1 | Model 2 | Model 3 | |
|---|---|---|---|
| Rg (Ω) | 5.208 × 106 | 4.543 × 106 | 2.475 × 106 |
| Rgb (Ω) | 1.155 × 106 | 2.296 × 106 | 4.821 × 106 |
| Rg/Rgb | 4.50 | 1.97 | 0.51 |
We will now explore the intricacies of charge transport and relaxation mechanisms, both pivotal aspects for elucidating the behavior of mobile ions within a material. In the realm of ionic conductors, the motion of mobile ions at a microscopic level manifests through two distinct mechanisms: hopping and quantum mechanical tunneling. Derived from these principles, we present two novel approaches to elucidate the behavior of mobile ions within a compound. These approaches encompass correlated barrier hopping (CBH) and quantum mechanical tunneling (QMT). The thermal evolution of the exponent ‘s’ can help us determine the appropriate conduction mechanism in Na2Cu5(Si2O7)2. Fig. 5(b) shows that ‘s’ decreases with increasing temperature to a minimum value then increases slightly with temperature. As a result, the (OLPT) model stands as the appropriate choice.25 In accordance with this model, the frequency exponent is intricately linked to the binding energy (Wm) of the charge carrier at its respective hopping location (eqn (20)).47
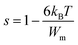 | (20) |
The symbols in these equations retain their standard meanings and interpretations.
Utilizing the previous equation, we determine Wm to be approximately 1.22 eV, a value in close agreement with the activation energy calculated from dc conductivity. This observation indicates that ion conduction predominantly occurs via charge carriers traversing localized crystallographic sites through their hopping mechanism. Moreover, the frequency exponent m(T), as determined from the imaginary component of the dielectric constant, provides additional evidence supporting the applicability of the CBH approach to the conduction mechanism within Na2Cu5(Si2O7)2. Additionally, a material's ionic relaxation mechanism can manifest in two distinct categories: the Debye and non-Debye processes. In the Debye process, uniform dipoles must be uniformly aligned and exhibit consistent responses to the applied field. Nonetheless, in the case of the non-Debye type, a variation in relaxation times emerges as a result of contributions stemming from diverse polarization mechanisms within the compound. In the case of Na2Cu5(Si2O7)2, the discerned variation in relaxation times, coupled with the distinctive asymmetric nature of the loss peaks, as evidenced by the electric modulus data, points to the presence of a relaxation process consistent with the non-Debye type. Additionally, a scrutiny of the electric modulus discloses a transition from the extended-range migration to a restricted-range movement as the frequency increases.
Let's now explore the influence of the crystal structure on the ionic conduction process. The spatial arrangement of mobile ions (Na+) within the crystal lattice, as well as the local environment enveloping these ions, delineates the feasible routes for ion migration within the unit cell. Within Na2Cu5(Si2O7)2, the existence of constriction points within pathways A (aligned with the a axis) and D (spanning the diagonal direction of the bc plane in the triclinic unit cell) imposes constraints on the mobility of sodium ions.
Among all the sodium silicate compounds reported, including the compound we've investigated, Na4SiO4 boasts the highest ionic conductivity. Its structure is notably characterized by an isolated silicon polyhedron free from any impediments. Conversely, the Na2Cu5(Si2O7)2 crystal structure is distinguished by a dual silicon polyhedral network alongside three distinct copper polyhedral configurations. Furthermore, the partially filled Na-ion sites within Na4SiO4 promote ionic conduction, a characteristic that differs from Na2Cu5(Si2O7)2, in which the Na sites are entirely occupied. Therefore, this comprehensive analysis highlights a crucial insight: the unimpeded conduction pathways within a lattice structure, combined with the fractional occupancy of alkali-metal ions, constitute essential factors in the design of an efficient ionic conductor tailored for ASSIBs.
4. Conclusions
This study employed impedance spectroscopy and neutron diffraction techniques to analyze the crystal structure, ionic conduction, and prospective lithium ion diffusion routes within Na2Cu5(Si2O7)2. An assessment of the conductivity data demonstrated that ion mobility through the material is activated by thermal energy input, with an energy barrier of 1.21 eV needing to be overcome to allow conduction. The conduction process aligns with the correlated barrier hopping (CBH) model, based on the analysis. The data also showed that the mobility of the charge carriers varied based on the frequency. Examining the neutron diffraction patterns using a soft BVS technique indicated potential partial obstructions along some of the possible sodium ion diffusion routes. Our analysis highlighted that these obstructions likely contribute to the high activation energy and resulting low ionic conductivity measured in Na2Cu5(Si2O7)2. Examining the impedance and electric modulus data together demonstrated that the conduction relaxation in Na2Cu5(Si2O7)2 does not follow Debye behavior, but rather shows a distribution of relaxation times. The analysis showed the timescales for conductivity relaxation are approximately 10−4 seconds. The data indicated minimal dissipation of energy takes place in Na2Cu5(Si2O7)2, as evidenced by the low loss tangent value, which is promising for potential uses. In summary, this extensive study significantly enhances our comprehension of the process enabling ionic conduction, the behavior of ion movements, and how the crystal structure impacts ion transport through this material. The insights gained from this comprehensive study will assist in developing and optimizing suitable ion-conducting materials to potentially serve as solid electrolytes in advanced battery designs.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number ISP23-164.References
- Z. Tian, Y. Zou, G. Liu, Y. Wang, J. Yin, J. Ming and H. N. Alshareef, Electrolyte Solvation Structure Design for Sodium Ion Batteries, Advanced Science, 2022, 9(22), 2201207, DOI:10.1002/advs.202201207.
- K. M. Abraham, How Comparable Are Sodium-Ion Batteries to Lithium-Ion Counterparts?, ACS Energy Lett., 2020, 5(11), 3544–3547, DOI:10.1021/acsenergylett.0c02181.
- U. Fegade, G. Jethave, F. Khan, A. Al-Ahmed, R. Karmouch, M. Shariq, Inamuddin and M. F. Ahmer, Recent Development of Aqueous Zinc-ion Battery Cathodes and Future Challenges: Review, Int. J. Energy Res., 2022, 46(10), 13152–13177, DOI:10.1002/er.8018.
- A. Ponrouch and M. R. Palacín, Post-Li Batteries: Promises and Challenges, Philos. Trans. R. Soc., A, 2019, 377(2152), 20180297, DOI:10.1098/rsta.2018.0297.
- A. A. Alzharani, M. K. Shehab, D. Rodene, J. U. Ahmed, A. M. Bakry, M. M. Kaid and H. M. El-Kaderi, Surface Modification of Partially Reduced Graphene Oxide for Advanced Electrode Material in Rechargeable Sodium Batteries, Energy Fuels, 2022, 36(9), 4967–4977, DOI:10.1021/acs.energyfuels.2c00193.
- Y. Zhao, Y. Kang, J. Wozny, J. Lü, H. Du, C. Li, T. Li, F. Kang, N. Tavajohi and B. Li, Recycling of Sodium-Ion Batteries, Nat. Rev. Mater., 2023, 8(9), 623–634, DOI:10.1038/s41578-023-00574-w.
- D. A. Stevens and J. R. Dahn, High Capacity Anode Materials for Rechargeable Sodium-Ion Batteries, J. Electrochem. Soc., 2000, 147(4), 1271, DOI:10.1149/1.1393348.
- F. H. Gandoman, A. El-Shahat, Z. Alaas, Z. M. Ali, M. Berecibar and S. H. E. A. Aleem, Understanding Voltage Behavior of Lithium-Ion Batteries in Electric Vehicles Applications, Batteries, 2022, 8(10), 130, DOI:10.3390/batteries8100130.
- M. Han, E. Gonzalo, G. Singh and T. Rojo, A Comprehensive Review of Sodium Layered Oxides: Powerful Cathodes for Na-Ion Batteries, Energy Environ. Sci., 2015, 8(1), 81–102, 10.1039/c4ee03192j.
- Z. Zeng, X. Jiang, R. Li, D. Yuan, X. Ai, H. Yang and Y. Cao, A Safer Sodium-Ion Battery Based on Nonflammable Organic Phosphate Electrolyte, Adv. Sci., 2016, 3(9), 1600066, DOI:10.1002/advs.201600066.
- S. Komaba, T. Ishikawa, N. Yabuuchi, W. Murata, A. Ito and Y. Ohsawa, Fluorinated Ethylene Carbonate as Electrolyte Additive for Rechargeable NA Batteries, ACS Appl. Mater. Interfaces, 2011, 3(11), 4165–4168, DOI:10.1021/am200973k.
- M. Hou, Y. Zhou, L. Feng, H. Zhao, D. Ji, D. Zhang, L. Li and Y. Lei, Research Progress of Solid Electrolyte Interphase for Sodium Metal Anodes, Chem. Eng. J., 2023, 475, 146227, DOI:10.1016/j.cej.2023.146227.
- X. Zhan, M. Li, S. Li, X. Pang, F. Mao, H. Wang, Z. Sun, X. Han, B. Jiang, Y. He, M. Li, Q. Zhang and L. Zhang, Challenges and Opportunities towards Silicon-Based All-Solid-State Batteries, Energy Storage Mater., 2023, 61, 102875, DOI:10.1016/j.ensm.2023.102875.
- X. Gao, Z. Xing, M. Wang, C. Nie, Z. Shang, Z. Bai, S. X. Dou and N. Wang, Comprehensive Insights into Solid-State Electrolytes and Electrode-Electrolyte Interfaces in All-Solid-State Sodium-Ion Batteries, Energy Storage Mater., 2023, 60, 102821, DOI:10.1016/j.ensm.2023.102821.
- M. B. Bechir and A. B. Rhaiem, The Sodium-Ion Battery: Study of Alternative Current Conduction Mechanisms on the Na3PO4 - Based Solid Electrolyte, Phys. E, 2020, 120, 114032, DOI:10.1016/j.physe.2020.114032.
- Y. Jee, P. Chien, E. Villarreal, Y. Hu and K. Huang, Crystallization of Amorphous Na2Si2O5 as a Na-Ion Conductor, Solid State Ionics, 2016, 296, 63–70, DOI:10.1016/j.ssi.2016.09.005.
- M. B. Bechir and A. B. Rhaiem, Structural Phase Transition, Vibrational Analysis, Ionic Conductivity and Conduction Mechanism Studies in an Organic-Inorganic Hybrid Crystal: [N(CH3)3H]2CdCl4, J. Solid State Chem., 2021, 296, 122021, DOI:10.1016/j.jssc.2021.122021.
- M. B. Bechir, K. Karoui, M. Tabellout, K. Guidara and A. B. Rhaiem, Dielectric Relaxation, Modulus Behavior and Thermodynamic Properties in [N(CH3)3H]2ZnCl4, Phase Transitions, 2015, 91(8), 901–917, DOI:10.1080/01411594.2014.987673.
- A. M. D. Santos, P. Brandão, A. N. Fitch, M. S. Reis, V. S. Amaral and J. Rocha, Synthesis, Crystal Structure and Magnetic Characterization of Na2Cu5(Si2O7)2: An Inorganic Ferrimagnetic Chain, J. Solid State Chem., 2007, 180(1), 16–21, DOI:10.1016/j.jssc.2006.09.012.
- The Materials Project, Materials Data on Na2Cu5(Si2O7)2 by Materials Project, United States, 2019, DOI:10.17188/1276456.
- A. K. Bera and S. M. Yusuf, Temperature-Dependent Na-Ion Conduction and Its Pathways in the Crystal Structure of the Layered Battery Material Na2Ni2TeO6, J. Phys. Chem. C, 2020, 124(8), 4421–4429, DOI:10.1021/acs.jpcc.9b11191.
- D. R. Bhosale, S. M. Yusuf, A. Kumar, M. D. Mukadam and S. I. Patil, High Oxide Ion Conductivity below 500∘C in the Garnets LaxY, Phys. Rev. Mater., 2017, 1(1), 015001, DOI:10.1103/physrevmaterials.1.015001.
- R. Xiao, H. Li and L. Chen, High-Throughput Design and Optimization of Fast Lithium Ion Conductors by the Combination of Bond-Valence Method and Density Functional Theory, Sci. Rep., 2015, 5(1), 14227, DOI:10.1038/srep14227.
- M. B. Bechir, A. Almeshal and M. H. Dhaou, Structural Evolution, Dielectric Relaxation, and Charge Transport Characteristics of Formamidinium Lead Iodide (FAPbI3) Perovskite, Mater. Res. Bull., 2023, 157, 112012, DOI:10.1016/j.materresbull.2022.112012.
- M. B. Bechir and M. H. Dhaou, Study of Charge Transfer Mechanism and Dielectric Relaxation of CSCUCL3 Perovskite Nanoparticles, Mater. Res. Bull., 2021, 144, 111473, DOI:10.1016/j.materresbull.2021.111473.
- I. Romdhane, M. B. Bechir and M. H. Dhaou, Impedance Spectroscopic Study of Charge Transport and Relaxation Mechanism in the Lead-Free Hybrid Perovskite CH3NH3CuCl3, Phys. E, 2022, 136, 115008, DOI:10.1016/j.physe.2021.115008.
- M. B. Bechir, A. Almeshal and M. H. Dhaou, Dielectric Properties and Charge Transfer Mechanism of Li1+xAlxTi2−x(PO4)3 Ceramic Electrolyte Used in Lithium Batteries, Ionics, 2022, 28(12), 5361–5376, DOI:10.1007/s11581-022-04779-x.
- M. B. Bechir, K. Karoui, A. Bulou, M. Tabellout, K. Guidara and A. B. Rhaiem, [N(CH3)3H]2ZnCl4: Ferroelectric Properties and Characterization of Phase Transitions by Raman Spectroscopy, J. Appl. Phys., 2014, 116(21), 214104, DOI:10.1063/1.4903303.
- I. M. Hodge, M. D. Ingram and A. R. West, Impedance and Modulus Spectroscopy of Polycrystalline Solid Electrolytes, J. Electroanal. Chem. Interfacial Electrochem., 1976, 74(2), 125–143, DOI:10.1016/s0022-0728(76)80229-x.
- R. Chakroun, B. Jamoussi, B. A. Al-Mur, A. Timoumi and K. Essalah, Impedance Spectroscopy and Dielectric Relaxation of Imidazole-Substituted Palladium(II) Phthalocyanine (IMPDPC) for Organic Solar Cells, ACS Omega, 2021, 6(16), 10655–10667, DOI:10.1021/acsomega.1c00034.
- P. Gupta, R. Padhee, P. K. Mahapatra and R. N. P. Choudhary, Structural and Electrical Characteristics of Bi2YTiVO9Ceramic, Mater. Res. Express, 2018, 5(4), 045905, DOI:10.1088/2053-1591/aabe06.
- L. T. H. Phong, N. T. Dang, N. Van Dang, N. Van Quynh, D. H. Manh, P. H. Nam, L. H. Nguyên and P. T. Phong, Structural, Optical and Conductivity Properties in Tetragonal BaTi1−xCoxO3 (0≤ x ≤0.1), RSC Adv., 2022, 12(25), 16119–16130, 10.1039/d2ra01411d.
- K. S. Chikara, A. K. Bera, A. Kumar and S. M. Yusuf, Role of Crystal Structure on the Ionic Conduction and Electrical Properties of Germanate Compounds A2Cu3Ge4O12 (A = Na, K), ACS Appl. Electron. Mater., 2023, 5(5), 2704–2717, DOI:10.1021/acsaelm.3c00176.
- K. Funke, Jump Relaxation in Solid Electrolytes, Prog. Solid State Chem., 1993, 22(2), 111–195, DOI:10.1016/0079-6786(93)90002-9.
- K. Funke, Ion Transport in Fast Ion Conductors — Spectra and Models, Solid State Ionics, 1997, 94(1–4), 27–33, DOI:10.1016/s0167-2738(96)00500-0.
- M. Ravi, Y. Pavani, S. Bhavani, A. Sharma and V. Rao, Investigations on Structural and Electrical Properties of KClO4Complexed PVP Polymer Electrolyte Films, Int. J. Polym. Mater. Polym. Biomater., 2012, 61(5), 309–322, DOI:10.1080/00914037.2011.584225.
- M. Ghanathe, A. K. Bera, A. Kumar and S. M. Yusuf, Mixed Ionic–Electronic Conduction and Magnetoelectric Coupling in Li0.5Fe2.5–xCrxO4 (x = 1.0, 1.1, 1.3, 1.5, and 1.6) Involving Magnetization Compensation Phenomenon, ACS Appl. Electron. Mater., 2022, 4(1), 394–405, DOI:10.1021/acsaelm.1c01058.
- B. Saha, A. K. Bera and S. M. Yusuf, Mechanism of Na-Ion Conduction in the Highly Efficient Layered Battery Material Na2Mn3O7, ACS Appl. Energy Mater., 2021, 4(6), 6040–6054, DOI:10.1021/acsaem.1c00825.
- R. Mguedla, A. B. J. Kharrat, N. Moutia, K. Khirouni, N. Chniba-Boudjada and W. Boujelben, Gd Doping Effect on Structural, Electrical and Dielectric Properties in HoCrO3 Orthochromites for Electric Applications, J. Alloys Compd., 2020, 836, 155186, DOI:10.1016/j.jallcom.2020.155186.
- H. M. Gomaa, A. M. Moneep, A. S. Abdel-Moety, A. A. Bendary, I. S. Yahia and S. H. Zyoud, Influence of Incorporation of Fe2O3 Content on the Structural and the Dielectric Relaxation Properties of Lithium Boro-Vanadate Oxide Glass: Toward Ideal Cathode Glasses, Appl. Phys. A: Mater. Sci. Process., 2022, 129(1), 70, DOI:10.1007/s00339-022-06350-x.
- R. T. Abdulwahid, S. B. Aziz, M. F. Z. Kadir, N. M. Sadiq, N. A. Halim, M. H. Hamsan, S. R. Saeed and H. Woo, Biodegradable Polymer Membrane K+ Ion Conductor for Electrochemical Device Application, J. Mater. Sci., 2022, 57(42), 19902–19923, DOI:10.1007/s10853-022-07825-1.
- K. P. Padmasree, D. K. Kanchan and A. R. Kulkarni, Impedance and Modulus Studies of the Solid Electrolyte System 20CdI2–80[xAg2O–y(0.7V2O5–0.3B2O3)], Where 1≤x/Y≤3, Solid State Ionics, 2006, 177(5–6), 475–482, DOI:10.1016/j.ssi.2005.12.019.
- M. Ram and S. Chakrabarti, Dielectric and Modulus Studies on LiFe1/2Co1/2VO4, J. Alloys Compd., 2008, 462(1–2), 214–219, DOI:10.1016/j.jallcom.2007.08.001.
- J. R. Macdonald and W. B. Johnson, Fundamentals of Impedance Spectroscopy, Impedance Spectroscopy: Theory, Experiment, and Applications, 2nd edn, 2005, pp. 1–26. DOI:10.1002/0471716243.ch1.
- M. Hernández, N. Masó and A. R. West, On the Correct Choice of Equivalent Circuit for Fitting Bulk Impedance Data of Ionic/Electronic Conductors, Appl. Phys. Lett., 2016, 108(15), 152901, DOI:10.1063/1.4946008.
- J. Wu and X. Guo, Origin of the Low Grain Boundary Conductivity in Lithium Ion Conducting Perovskites: Li3xLa0.67−xTiO3, Phys. Chem. Chem. Phys., 2017, 19(8), 5880–5887, 10.1039/c6cp07757a.
- M. B. Bechir, K. Karoui, M. Tabellout, K. Guidara and A. B. Rhaiem, Alternative Current Conduction Mechanisms of Organic-Inorganic Compound [N(CH3)3H]2ZnCl4, J. Appl. Phys., 2014, 115(15), 153708, DOI:10.1063/1.4871662.
| This journal is © The Royal Society of Chemistry 2024 |