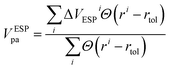Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Physics of band-filling correction in defect calculations of solid-state materials†
Harshan Reddy Gopidi a,
Lovelesh Vashista and
Oleksandr I. Malyi
a,
Lovelesh Vashista and
Oleksandr I. Malyi *ba
*ba
aCentre of Excellence ENSEMBLE3 Sp. z o. o., Wolczynska Str. 133, 01-919, Warsaw, Poland
bQingyuan Innovation Laboratory, Quanzhou, 362801, P. R. China. E-mail: oleksandrmalyi@gmail.com
First published on 4th June 2024
Abstract
In solid-state physics/chemistry, a precise understanding of defect formation and its impact on the electronic properties of wide-bandgap insulators is a cornerstone of modern semiconductor technology. However, complexities arise in the electronic structure theory of defect formation when the latter triggers partial occupation of the conduction/valence band, necessitating accurate post-process correction to the energy calculations. Herein, we dissect these complexities, focusing specifically on the post-process band-filling corrections, a crucial element that often demands thorough treatment in defect formation studies. We recognize the importance of these corrections in maintaining the accuracy of electronic properties predictions in wide-bandgap insulators and their role in reinforcing the importance of a reliable common reference state for defect formation energy calculations. We explored solutions such as aligning deep states and electrostatic potentials, both of which have been used in previous works, showing the effect of band alignment on defect formation energy. Our findings demonstrate that the impact of defect formation on electronic structure (even deep states) can be significantly dependent on the supercell size. We also show that within band-filling calculations, one needs to account for the possible change of electronic structure induced by defect formation, which requires sufficient convergence of electronic structure with supercell size. Thus, this work emphasizes the critical steps to accurately predict defect formation energy and paves the way for future research to overcome these challenges and advance the field with more efficient and reliable predictive models.
Introduction
Point defects are present in all materials as their formation arises from a balance between the energy cost needed for their formation and the configuration entropy gain due to increased defect concentration.1–3 Despite being present only in low concentrations under normal conditions in most materials, defects often significantly influence the properties of materials, such as color, equilibrium Fermi level, and doping response.4–8 With recent advancements in electronic structure theory, defect physics and hence materials properties can be accurately predicted using first-principles calculations. However, it is important to note that density functional theory (DFT) is still usually limited to supercell calculations of only a few hundred atoms. Hence, when computing defect properties for typical supercells, the first-principles results should be extrapolated to the dilute limit. This can be achieved by either (i) scaling corresponding properties (e.g., vacancy formation energy) for different defects as a function of supercell size9–12 or (ii) applying post-process corrections.13–17 While the former approach is theoretically exact and only requires sufficient supercomputer resources, it can be challenging to apply for many defects due to the need to scale each defect individually. In contrast, the latter approach typically involves applying post-process corrections to extrapolate the limit of defect formation energy and is becoming increasingly popular in modern research.Previous works13–19 have shed some light on post-process corrections, and several post-process correction codes have been developed to automate defect calculations. Thus, it becomes clear that the formation energy of a point defect in an insulator is directly affected by the formation energies of other charged defects, which are a function of the parametric Fermi level. Hence, the calculation of equilibrium defect concentration or equilibrium Fermi level corresponding to given environmental conditions requires a self-consistent solution that follows the charge neutrality4,5,20,21 rule and accounts for the effect of the defect on the average electrostatic potential as well as the accounting for energy correction due to periodic interaction between point defects. Moreover, dielectric screening, which can vary anisotropically along different directions, must be considered when dealing with charged point defects.
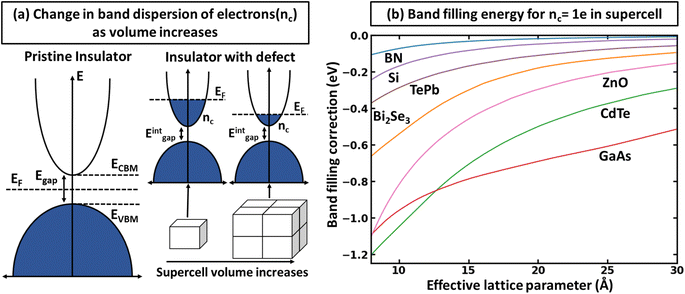
There is a common misconception that post-process corrections are only necessary when dealing with charged defects and that uncharged defects do not require such corrections. This is only partially accurate. For instance, both charged and uncharged point defects can cause partial occupation of the conduction or valence band. Within electronic structure theory for a finite supercell size, such electrons or holes are spread in energy range. In contrast, in the dilute limit (one which we often aim to represent within electronic structure theory), they are expected to only contribute to the tip of band edges (see Fig. 1a). This thus implies that formation energy of point defect adding free carriers to the system requires post-process energy corrections that accounts for additional energy cost corresponding to band-filling. This additional correction for the doped insulator can be calculated by summing over the eigenvalues14,16,18 as:
For n-type dopants:
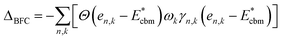 | (1) |
For p-type dopants:
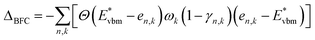 | (2) |
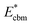 is the aligned conduction band minimum (CBM) of supercell without defects,
is the aligned conduction band minimum (CBM) of supercell without defects, 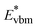 is the aligned valence band maximum (VBM) of the supercell without defects. While some papers in the literature touch upon band-filling correction, most are anchored in exploring defect physics specific to particular compounds or simply providing eqn (1) and (2). Moreover, while thousands of papers reported defect calculations for different systems, only very small fractions of those works accounted for band-filling correction correctly. Because of this, our objective is to bridge this knowledge gap by presenting a thorough discussion and analysis of the topic. In this way, we revisit the fundamentals of band-filling correction and establish a foundational understanding of it. We elucidate the alignment of band edges relevant to band-filling correction, emphasize situations where it is crucial, offer extended methodological advice, and outline its principal limitations. This endeavor is accomplished through detailed first-principles calculations across a spectrum of different insulators, unveiling the intricacy of band-filling calculations, elucidating why eqn (1) and (2) cannot be directly employed in defect calculations, and steering how the band-filling correction ought to be accurately executed within the DFT calculations. Through this approach, we furnish not only methodological guidance but also delineate factors that may influence outcomes, thereby elucidating the physics underlying band-filling correction.
is the aligned valence band maximum (VBM) of the supercell without defects. While some papers in the literature touch upon band-filling correction, most are anchored in exploring defect physics specific to particular compounds or simply providing eqn (1) and (2). Moreover, while thousands of papers reported defect calculations for different systems, only very small fractions of those works accounted for band-filling correction correctly. Because of this, our objective is to bridge this knowledge gap by presenting a thorough discussion and analysis of the topic. In this way, we revisit the fundamentals of band-filling correction and establish a foundational understanding of it. We elucidate the alignment of band edges relevant to band-filling correction, emphasize situations where it is crucial, offer extended methodological advice, and outline its principal limitations. This endeavor is accomplished through detailed first-principles calculations across a spectrum of different insulators, unveiling the intricacy of band-filling calculations, elucidating why eqn (1) and (2) cannot be directly employed in defect calculations, and steering how the band-filling correction ought to be accurately executed within the DFT calculations. Through this approach, we furnish not only methodological guidance but also delineate factors that may influence outcomes, thereby elucidating the physics underlying band-filling correction.
Results and discussion
Band-filling correction within the rigid shift model
To illustrate the need for accurate accounting of band-filling correction, in Fig. 1b, we show the expected band-filling correction due to the rigid shift of the Fermi level in the conduction band for some well-known insulators. In such an approximation, we directly use eqn (1) and calculate the band-filling correction using dense k-point sampling and estimating the carrier concentration corresponding to the addition of a single electron to the supercell of a given size. Here, the number of electrons (ne) at a given parametric![[E with combining low line]](https://www.rsc.org/images/entities/i_char_0045_0332.gif) F is calculated as
F is calculated as 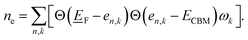 The results demonstrate that band-filling correction is highly sensitive to the free carrier concentration and differs for different materials. One of the key points here is that an increase in band dispersion (often simply characterized by low effective mass) increases the expected band-filling correction. As an illustration, for an effective lattice parameter (defined as the cubic root of the system volume) of around 10 Å, the magnitude of band-filling correction for the system containing 1e in the conduction band is around 1 eV for CdTe, ZnO, and GaAs. At the same time, the corresponding value for BN is less than 0.1 eV. Another important conclusion is that even for very large supercells (over 20 Å), the band-filling correction is larger than 0.3 eV for a range of systems. For instance, for GaAs, the expected band-filling correction is about 0.5 eV for an effective (lattice) parameter of 30 Å. These results demonstrate that ignoring band-filling correction can completely change the defect picture of the entire compound, resulting in unphysical predictions, especially taking into account that many defects can add more than a single electron/hole to the compound. Unfortunately, since the electronic structure of real material is usually not characterized by a simplified parabolic form in the wide energy range, it is not possible to define a simplified expression correlating band-filling correction directly to the effective mass. It should also be noted that results herein are presented for Perdew–Burke–Ernzerhof (PBE)22 exchange-correlation (XC) functional, which tends to underestimate the band gap energy compared to experimental data.23,24 This underestimation can directly affect defect properties.25,26 However, the focus of this work is not to attain precise calculations of defect formation energies but to develop a deeper understanding of the band-filling correction and practical insight on accounting for such correction in defect calculations. Even with the band gap underestimation issue inherent to the PBE functional, it provides a reasonable qualitative picture of the electronic structure sufficient for studying band-filling corrections. In this context, the absolute value of the band gap is less important than the relative positions of the energy levels and the behavior of the electrons within them. However, in general, for a specific compound, the effective mass is sensitive to the choice of XC functional.27–30 Therefore, the absolute value of the band-filling correction (but not the main physics presented in this work) may also be affected as a result.
The results demonstrate that band-filling correction is highly sensitive to the free carrier concentration and differs for different materials. One of the key points here is that an increase in band dispersion (often simply characterized by low effective mass) increases the expected band-filling correction. As an illustration, for an effective lattice parameter (defined as the cubic root of the system volume) of around 10 Å, the magnitude of band-filling correction for the system containing 1e in the conduction band is around 1 eV for CdTe, ZnO, and GaAs. At the same time, the corresponding value for BN is less than 0.1 eV. Another important conclusion is that even for very large supercells (over 20 Å), the band-filling correction is larger than 0.3 eV for a range of systems. For instance, for GaAs, the expected band-filling correction is about 0.5 eV for an effective (lattice) parameter of 30 Å. These results demonstrate that ignoring band-filling correction can completely change the defect picture of the entire compound, resulting in unphysical predictions, especially taking into account that many defects can add more than a single electron/hole to the compound. Unfortunately, since the electronic structure of real material is usually not characterized by a simplified parabolic form in the wide energy range, it is not possible to define a simplified expression correlating band-filling correction directly to the effective mass. It should also be noted that results herein are presented for Perdew–Burke–Ernzerhof (PBE)22 exchange-correlation (XC) functional, which tends to underestimate the band gap energy compared to experimental data.23,24 This underestimation can directly affect defect properties.25,26 However, the focus of this work is not to attain precise calculations of defect formation energies but to develop a deeper understanding of the band-filling correction and practical insight on accounting for such correction in defect calculations. Even with the band gap underestimation issue inherent to the PBE functional, it provides a reasonable qualitative picture of the electronic structure sufficient for studying band-filling corrections. In this context, the absolute value of the band gap is less important than the relative positions of the energy levels and the behavior of the electrons within them. However, in general, for a specific compound, the effective mass is sensitive to the choice of XC functional.27–30 Therefore, the absolute value of the band-filling correction (but not the main physics presented in this work) may also be affected as a result.
Band-filling correction beyond the rigid shift model
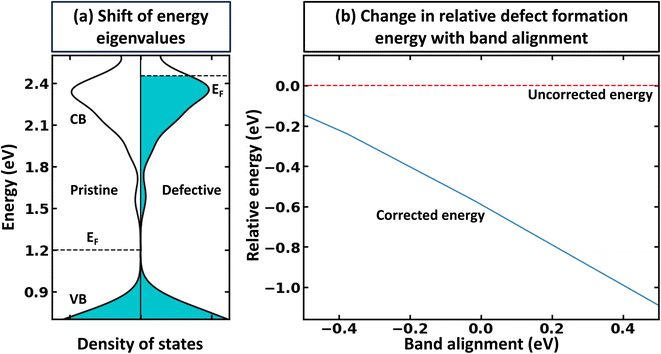
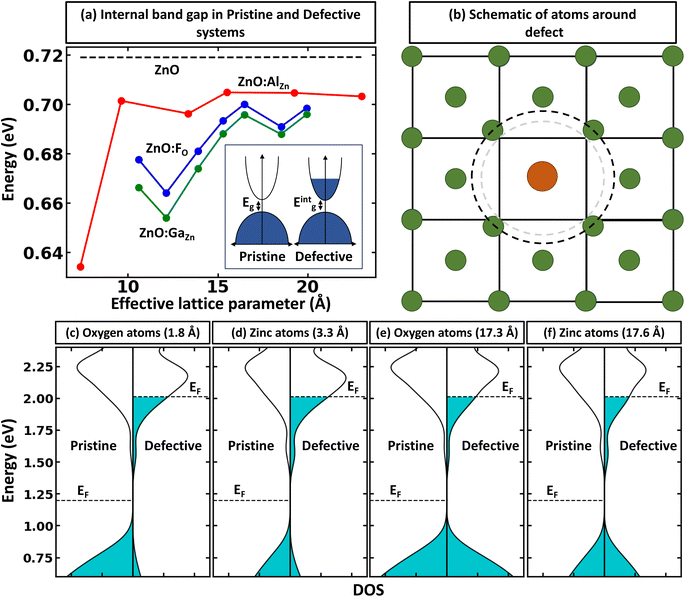
The rigid band approximation represents an ideal scenario, typically unattainable in common materials. Indeed, in many cases, doping can result in a reactive response or a noticeable change in electronic structure.31,32 Hence, in practice, one must deal with materials response to doping in the self-consistent energy minimization picture. Unfortunately, eqn (1) and (2) cannot be directly used because modern first principles codes (e.g., VASP33–36 and Quantum Espresso37–39) do not use common reference energy but provide direct Kohn–Sham-eigenvalues for a set of k-points. To illustrate this point, we examine the case of defect formation in ZnO – a conventional example of a wide band gap insulator (Fig. 2). Our findings suggest that defect formation results in the shift of the absolute energies of eigenvalues. Consequently, comparing eigenvalues for pristine and defective systems becomes meaningless. Moreover, the shift of absolute eigenvalues differs for different compounds, defects, and supercells, suggesting that eqn (1) and (2) mentioned above necessitates the use of a common reference state. Such a common reference state, however, should distinguish, for instance, the shift of Kohn–Sham-eigenvalues due to a non-common reference state as well as change in electronic properties caused by the formation of the defect (e.g., due to localized structural displacements or change local bonding environments). Hence, one cannot directly align the valence/conduction bands for defective and pristine systems. For example, Fig. 2a demonstrates the electronic density of states for pristine and defective ZnO systems, revealing a clear shift in eigenvalue energies between the two systems. Thus, it can be inferred that comparing the electronic structures of different systems is only meaningful when a common reference state is defined, thus making band alignment very challenging and an essential step of calculations for band-filling correction. The sensitivity of defect formation energy to band alignment (where it is treated as a parametric value) is shown in Fig. 2b. The question then arises as to how we define the common reference state. The answer is not straightforward and is contingent upon the specifics of the system under examination, which we will discuss further.Alignment of deep states (average) as the reference state for band-filling correction
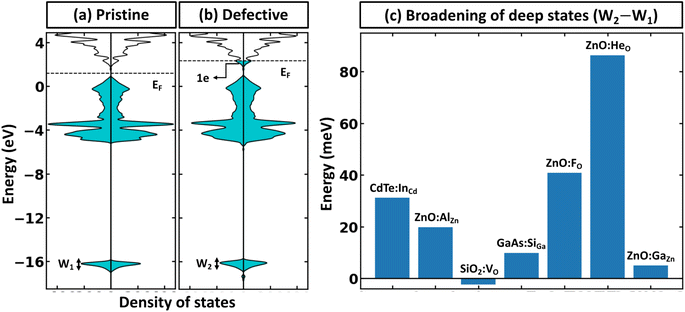
Within the global scientific community, there is recognition of the significant role that the reorganization of valence states plays in the formation and nature of chemical bonds. The foundation of this principle is based on the idea that transitions in the electron states of an atom's outermost shell do not simply dictate the variety of bonds that the atom is capable of forming. In addition, these shifts also wield a considerable influence on key factors such as the strength, stability, and overall reactivity of the bonds themselves. Because of this, core electrons or, more generally, deep states, which occupy lower energy levels and are somewhat insulated by the outer electron shell from direct influences of other atoms (they still indirectly influence bonding) can be used as potential consistent reference points across various systems to compare the electronic structure of different systems.40 In the case of full electron codes (e.g., Wien2k41), one can explicitly calculate the position of the deepest orbitals and align them to define the common reference state. We note, however, that the most widely used first-principles codes use the pseudopotentials42–44 to simplify the computational process and reduce the computational cost associated with solving the Kohn–Sham equation.45 As a result, the position of the deep state is only 10–25 eV below the Fermi level, depending on the considered valence configuration. Because of this, such states can often be affected by local structural/bonding changes. In Fig. 3a and b, we summarize the effect of defect formation on the deep states for a few representative compounds and supercells without any relaxation for the defective systems. These results show that even deep states can have substantial broadening. For instance, for CdTe:InCd described within a 54-atom supercell, the broadening is 31 meV (Fig. 3c). It should also be noted that defect formation can, in principle, cause interference of defect-deep states with the states of the host atoms as seen in Fig. 3b. One might initially think that a small change or broadening of the deep states would not significantly affect the defect formation energy. However, as shown in Fig. 2b, the band alignment does directly affect the results, and the effect is expected to increase with higher free carrier concentration introduced by the defects. This means that accurate defect calculations will require not only accounting of band-filling correction but also an accurate alignment of energy states of pristine and defective systems. It is also probable that for many such systems, one cannot solely rely on utilizing modern pseudopotential-based DFT codes to align deep states (at least without including spatial dependence of energy for such states).Alignment of electrostatic potentials as reference state for band-filling correction
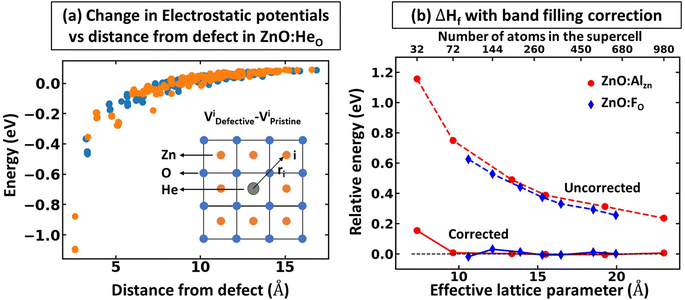
While defects can significantly influence the electronic properties of materials – given that these properties are highly sensitive to specific atomic arrangements, bonding situations, and shifts in the local environment28,46–48 – the average electrostatic potentials at cores, as calculated by VASP, within the system, remain comparatively undisturbed. This stability stems from the fact that electrostatic potential is a long-range attribute derived from charge interactions spanning vast distances. Consequently, the effects of large-scale environmental shifts are averaged out, while the impact of the local environment remains crucial. As one moves sufficiently far from the defect, the local environments mirror that of the pristine system. In such regions, comparing the electrostatic potentials offers insight into energy alignment. Consequently, it is viable to use the mean electrostatic potentials – particularly, potentials that are spherically averaged around atoms within a specified distance – for two systems as a common method for energy alignment. This strategy is particularly applicable when calculating defect formation energy. However, we note that introducing the defect inside the supercell results in symmetry breaking, making different atoms inequivalent to each other and resulting in the space and atomic identity-dependent electrostatic potentials. This is shown in Fig. 4a, where one can see that the change in relative electrostatic potential slowly converges with moving away from the defect, reaching the constant value (within 0.01 eV) at about 15 Å away from the defect, as shown by an example of ZnO:HeO system (herein, modeled as 640-atom supercell)- a type of functional defect resulting in putting Fermi level to the conduction band with 2e spread over a wide energy range in the conduction band.49,50 We also note that the tolerance value for band alignment needed for accurate calculation of defect formation energy differs for different systems as the band filling correction is affected by the band alignment and free carrier concentration. In other words, the large free carrier concentration (intrinsic or doping induced) requires more accurate band alignment calculations. While the results are demonstrated on example ZnO, as noted in Fig. 1, the effect is expected to be present for all compounds. To show the power of band-filling correction, we consider ZnO:AlZn, a system where the formation of the point defect (Al on Zn site) puts 1e in the conduction band. Indeed, Al is one of the standard n-type dopants in ZnO to realize n-type transparent conductive oxides.51–53 The uncorrected PBE defect formation energy has a strong supercell size dependence of defect formation energy (Fig. 4b), with relative defect formation energy changing by 0.5 eV as supercell size increases from 72 to 980 atoms. Importantly, when band-filling correction is accounted for (accounting for energy alignment using an electrostatic potential for atoms most remote from the defect), the defect formation energy becomes almost supercell independent. These results thus demonstrate the power of band-filling correction to eliminate a significant part of supercell size dependence of defect formation energy. Moreover, similar to the rigid shift model, we show that even for 980-atom supercell, there is sufficient large band filling correction (over 0.2 eV).Other factors that should be accounted for in the post-process correction
We must recognize that the lack of dependence of defect formation energy on the supercell size, even after considering the post-process band-filling correction, does not necessarily stand as a complete representation of accurately depicted primary physics. Eqn (1) and (2) take into account the effect of band-filling on the kinetic energy of a system composed of non-interacting particles within the context of Kohn–Sham DFT. However, this method does not account for the relaxation or displacement convergence relative to the supercell size. For certain systems, this particular aspect may be profoundly significant. This is well illustrated in the scenario of noble gas functional defects that exhibit atypical relaxation patterns in solids. For instance, achieving convergence of atomic displacements in noble gas-doped ZnO often necessitates the use of a supercell comprised of more than 500 atoms.50 Moreover, it is crucial to acknowledge that the correction detailed in Eqn (1) and (2) only extends to the band edge of the pristine system. Therefore, if the defect formation results in alterations of the internal band gap, the band-filling correction will not account for these changes. Let us understand the latter case in detail. When a defect is introduced, it breaks the internal symmetry. This symmetry breaking may modify the local density of states for the nearest atoms significantly, resulting in a change in the overall internal band gap energy. For instance, Fig. 5a demonstrates the convergence of the PBE internal band gap between principal band edges of ZnO:AlZn as a function of supercell size with atom projected density of states. Here, one can see two main points: (i) there is supercell size dependence of internal band gap; (ii) the defected system has an internal gap between principal band edges smaller than the undoped system in the dilute limit (infinite supercell). It is critical to note that the reduction of band gap energy in the dilute limit can be a fully physical phenomenon originating from the formation of different motifs contributing differently to electronic properties. This, indeed, is a common phenomenon in the case of symmetry breaking in quantum materials.28,46 From Fig. 5b–f, it is evident that the principal valence band sensitivity is significantly influenced by the proximity to the defect. As one moves further from the defect, the local environment increasingly resembles the electronic structure of pristine ZnO. Such behavior underscores the profound impact of the Al defect on the system and the origin for the change of internal band gap energy. However, the change in electronic properties can also be an example of artificial interaction between the defect-induced local environment and its periodic images. Thus, as shown in Fig. 5a, at the small size of supercells, the internal band gap energy can be substantially smaller than the asymptotic band gap energy. These results thus demonstrate that while band-filling correction can account for artificial filling of the conduction band, additional correction may need to be used when the electronic structure or atomic displacements are not converged with supercell size.Conclusions
This study highlights the necessity of applying post-process band-filling corrections in defect energy calculation when defects trigger partial occupation of the conduction or valence band. We underline the need for a robust, common reference state (energy alignment) in defect formation energy calculations, which becomes challenging given the local perturbation of structure and potential changes to the internal band gap upon defect formation. We have explored possible solutions, including aligning deep states and electrostatic potentials (which are used in some of the previous works), but have also highlighted the inherent difficulties in each approach. We have also pointed out that the impact of defect formation on electronic properties can be notably supercell size-dependent in some cases. This study thus serves as an important stepping stone towards a more comprehensive understanding of defect formation and electronic structure theory. It underscores the urgency of developing more accurate, encompassing methodologies to better predict and account for these dynamics in the context of varying supercell sizes and defect-induced alterations. Future research should tackle these challenges to advance the field and realize more efficient and reliable predictive models.Methods
First-principles calculations
All calculations at the first-principle level were performed using the Vienna Ab initio Simulation Package (VASP),33–36 employing the PBE22 XC functional. For plane wave basis, the cutoff energy levels were set to 520 eV and 500 eV for volume relaxation (carried out only for primitive undoped cells) and structural relaxation, respectively (except for ZnO:FO, ZnO:HeO and, ZnO:GaZn calculations of volume and structural relaxations, if performed, are done with 550 and 450 eV respectively). The atomic relaxations were carried out (unless otherwise specified) until the intrinsic forces were below 0.01 eV Å−1. The Γ-centered Monkhorst–Pack k-grid54 with the density of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 per reciprocal atom was used for all main calculations (which is sufficient to capture the main physics of the band-filling correction). The results were analyzed using Pymatgen55 and Vesta.56
000 per reciprocal atom was used for all main calculations (which is sufficient to capture the main physics of the band-filling correction). The results were analyzed using Pymatgen55 and Vesta.56
Defect calculations
To study the defect formation energy in the dilute limit, only one defect is created per supercell and the lattice parameters of supercells were fixed for defect relaxations. The defect formation energy was calculated aswhere EDFTD and EDFTB are the energy of defective and pristine systems, respectively; ni is the number of atoms of type i added/removed (if removed, ni > 0; if added, ni < 0) to the system. μi is the chemical potential of atom type i. ΔBFC is the band filling correction (this term is excluded when we present uncorrected defect formation energy). The primary focus of our study is to elucidate the impact of band-filling correction rather than to determine the exact value of defect formation energy. Because of this and since for a given type of defect
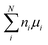 is a constant, we present results for relative defect formation energy, which is independent on the chemical potential term.
is a constant, we present results for relative defect formation energy, which is independent on the chemical potential term.
Alignment using the electrostatic potentials (ESP) is performed by aligning the averages of electrostatic potentials of most remote atoms in the system. The calculation is based on the average fluctuation in electrostatic potentials for atoms positioned within spherical shells defined by two radii, rmax and rmax − rtol, here, rmax represents the maximum radial distance of any atom within the supercell from the defect, while rtol is a tolerance radius set to be 2 Å. The formula for the potential alignment using ESP (VESPpa) is be given by:
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
The authors have no conflicts to disclose.Acknowledgements
The authors thank the “ENSEMBLE3 – Centre of Excellence for nanophotonics, advanced materials and novel crystal growth-based technologies” project (GA No. MAB/2020/14) carried out within the International Research Agendas programme of the Foundation for Polish Science co-financed by the European Union under the European Regional Development Fund and the European Union's Horizon 2020 research and innovation programme Teaming for Excellence (GA No. 857543) for support of this work. We gratefully acknowledge Poland's high-performance computing infrastructure PLGrid (HPC Centers: ACK Cyfronet AGH) for providing computer facilities and support within computational grant no. PLG/2023/016228 and for awarding project access to the LUMI supercomputer, owned by the EuroHPC Joint Undertaking, hosted by CSC (Finland) and the LUMI consortium through grant no. PLL/2023/04/016500.References
- J. H. Crawford and L. M. Slifkin, Point Defects in Solids: General and Ionic Crystals, Springer Science & Business Media, 2013 Search PubMed.
- C. Kittel, Introduction to Solid State Physics, John Wiley & sons, inc, 2005 Search PubMed.
- I. Mosquera-Lois, S. R. Kavanagh, J. Klarbring, K. Tolborg and A. Walsh, Chem. Soc. Rev., 2023, 52, 5812–5826 RSC.
- A. Zunger and O. I. Malyi, Chem. Rev., 2021, 121, 3031–3060 CrossRef CAS PubMed.
- C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van de Walle, Rev. Mod. Phys., 2014, 86, 253–305 CrossRef.
- G. Wolfowicz, F. J. Heremans, C. P. Anderson, S. Kanai, H. Seo, A. Gali, G. Galli and D. D. Awschalom, Nat. Rev. Mater., 2021, 6, 906–925 CrossRef CAS.
- O. I. Malyi and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2020, 101, 235202 CrossRef CAS.
- O. I. Malyi, M. T. Yeung, K. R. Poeppelmeier, C. Persson and A. Zunger, Matter, 2019, 1, 280–294 CrossRef.
- K. V. Sopiha, O. I. Malyi, C. Persson and P. Wu, ACS Appl. Mater. Interfaces, 2021, 13, 33664–33676 CrossRef CAS PubMed.
- H.-P. Komsa and A. Pasquarello, Phys. Rev. Lett., 2013, 110, 095505 CrossRef PubMed.
- C. Freysoldt, J. Neugebauer and C. G. Van De Walle, Phys. Rev. Lett., 2009, 102, 016402 CrossRef PubMed.
- N. D. M. Hine, K. Frensch, W. M. C. Foulkes and M. W. Finnis, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 024112 CrossRef.
- S. Muy, C. Johnston and N. Marzari, Electron. Struct., 2023, 5, 024009 CrossRef.
- A. Goyal, P. Gorai, H. Peng, S. Lany and V. Stevanović, Comput. Mater. Sci., 2017, 130, 1–9 CrossRef.
- D. Broberg, B. Medasani, N. E. R. Zimmermann, G. Yu, A. Canning, M. Haranczyk, M. Asta and G. Hautier, Comput. Phys. Commun., 2018, 226, 165–179 CrossRef CAS.
- S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 235104 CrossRef.
- H.-P. Komsa, T. T. Rantala and A. Pasquarello, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 045112 CrossRef.
- C. Persson, Y.-J. Zhao, S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 035211 CrossRef.
- Y. Kumagai and F. Oba, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 195205 CrossRef.
- J. Neugebauer and C. G. Van de Walle, Appl. Phys. Lett., 1996, 68, 1829–1831 CrossRef CAS.
- A. Walsh and A. Zunger, Nat. Mater., 2017, 16, 964–967 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. Borlido, J. Schmidt, A. W. Huran, F. Tran, M. A. L. Marques and S. Botti, npj Comput. Mater., 2020, 6, 96 CrossRef CAS.
- Z. Wan, Q.-D. Wang, D. Liu and J. Liang, Comput. Mater. Sci., 2021, 198, 110699 CrossRef CAS.
- A. Alkauskas, P. Broqvist and A. Pasquarello, Phys. Status Solidi B, 2011, 248, 775–789 CrossRef CAS.
- A. Alkauskas, P. Broqvist and A. Pasquarello, Phys. Rev. Lett., 2008, 101, 046405 CrossRef PubMed.
- M. Laurien and O. Rubel, Phys. Rev. B: Condens. Matter Mater. Phys., 2022, 106, 045204 CrossRef CAS.
- Z. Wang, O. I. Malyi, X. Zhao and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2021, 103, 165110 CrossRef CAS.
- K. Berland and C. Persson, J. Appl. Phys., 2018, 123, 205703 CrossRef.
- Y.-S. Kim, K. Hummer and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 035203 CrossRef.
- O. I. Malyi, G. M. Dalpian, X.-G. Zhao, Z. Wang and A. Zunger, Mater. Today, 2020, 32, 35–45 CrossRef CAS.
- Q. Liu, G. M. Dalpian and A. Zunger, Phys. Rev. Lett., 2019, 122, 106403 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli and M. Cococcioni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- P. Giannozzi, O. Baseggio, P. Bonfà, D. Brunato, R. Car, I. Carnimeo, C. Cavazzoni, S. de Gironcoli, P. Delugas, F. Ferrari Ruffino, A. Ferretti, N. Marzari, I. Timrov, A. Urru and S. Baroni, J. Chem. Phys., 2020, 152, 154105 CrossRef CAS PubMed.
- P. Dahinden, P. Broqvist and A. Pasquarello, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085331 CrossRef.
- P. Blaha, K. Schwarz, F. Tran, R. Laskowski, G. K. H. Madsen and L. D. Marks, J. Chem. Phys., 2020, 152, 074101 CrossRef CAS PubMed.
- J. C. Phillips, Phys. Rev., 1958, 112, 685–695 CrossRef CAS.
- J. Harris and R. O. Jones, Phys. Rev. Lett., 1978, 41, 191–194 CrossRef CAS.
- A. Zunger, S. Topiol and M. A. Ratner, Chem. Phys., 1979, 39, 75–90 CrossRef CAS.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- O. I. Malyi and A. Zunger, Applied Physics Reviews, 2020, 7, 041310 CrossRef CAS.
- O. I. Malyi, X.-G. Zhao and A. Zunger, Phys. Rev. Mater., 2023, 7, 074406 CrossRef CAS.
- I. Mosquera-Lois, S. R. Kavanagh, A. Walsh and D. O. Scanlon, npj Comput. Mater., 2023, 9, 25 CrossRef CAS.
- O. I. Malyi, K. V. Sopiha and C. Persson, npj Comput. Mater., 2019, 5, 38 CrossRef.
- L. Vashist, H. R. Gopidi, M. R. Khan and O. I. Malyi, J. Phys. Chem. Lett., 2023, 14, 9090–9095 CrossRef CAS PubMed.
- S. Lany and A. Zunger, Phys. Rev. Lett., 2007, 98, 045501 CrossRef PubMed.
- M.-C. Jun, S.-U. Park and J.-H. Koh, Nanoscale Res. Lett., 2012, 7, 639 CrossRef PubMed.
- S. Vunnam, K. Ankireddy, J. Kellar and W. Cross, Nanotechnology, 2014, 25, 195301 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra01528b |
| This journal is © The Royal Society of Chemistry 2024 |