Experimental and theoretical studies of the LiBH₄–LiI phase diagram

Abstract

The hexagonal structure of LiBH₄ at room temperature can be stabilised by substituting the BH₄⁻ anion with I⁻, leading to high Li-ion conductive materials. A thermodynamic description of the pseudo-binary LiBH₄–LiI system is presented. The system has been explored investigating several compositions, synthetized by ball milling and subsequently annealed. X-ray diffraction and Differential Scanning Calorimetry have been exploited to determine structural and thermodynamic features of various samples. The monophasic zone of the hexagonal Li(BH₄)_1−x(I)_x solid solution has been experimentally defined equal to 0.18 ≤ x ≤ 0.60 at 25 °C. In order to establish the formation of the hexagonal solid solution, the enthalpy of mixing was experimentally determined, converging to a value of 1800 ± 410 J mol⁻¹. Additionally, the enthalpy of melting was acquired for samples that differ in molar fraction. By merging experimental results, literature data and ab initio theoretical calculations, the pseudo-binary LiBH₄–LiI phase diagram has been assessed and evaluated across all compositions and temperature ranges by applying the CALPHAD method.

---

Introduction

The sector of renewable energy nowadays is constantly evolving to reduce emissions of harmful gases, and, at the same time, to supply the constant increase of energy demand globally,¹ especially linked to developing countries. One of the main problems of renewable energies is related to their storage. In recent years, the focus of research for energy storage has shifted to electrochemical systems, i.e., batteries. Starting from 2010, the global demand for energy storage in batteries increased by 30% annually and reached a ceiling of 180 GW h in 2018. Furthermore, a continuous growth is expected for the battery market, equal to an increase of 25% annually up to an estimated energy storage capacity of 3600 GW h by 2030.²

One of the well-established type of batteries is based on lithium-ion (LIB). Currently, the main goals of the research on LIB are to increase their safety and energy density. Nowadays, the electrolyte of LIB consists in lithium salts, that are dissolved in flammable organic solvents, such as diethyl carbonate or tetrahydrofuran.³ From a safety point of view, the presence of these organic solvents is an open issue since they are highly flammable and volatile. When a LIB is fast charged, it often develops an important generation of heat, that cannot easily be dissipated, resulting in possible thermal runways and explosions.⁴

With the introduction of a solid-state electrolytes, these problems can be overcome, and the research towards new solid-state electrolytes (SSEs) can lead to the development of new technologies, such as all solid-state batteries (SSBs).⁵ In SSBs it's possible to use a lithium metal anode that is one of the most desirable materials in the field of high-energy applications, due to its low reduction potential and theoretical capacity. In fact, this type of anode cannot be implemented in a classical LIB, because of the occurrence of an uneven Li deposition, that can lead to short-circuits. Furthermore, by using SSEs, it is possible to limit or avoid the formation of dendrites, that could also lead to a short-circuit in the battery, so improving the safety of the device.⁶ Several materials have been studied as possible SSE candidates,⁷ such as LISICON-type,⁸ oxide-like lithium lanthanum titanate,⁹ Li₂NH¹⁰ and NASICON-type materials.¹¹ In the last years, complex hydrides have been also considered as good candidates as SSE for all solid-state batteries.^12,13

In this field, LiBH₄ has been proved to be an interesting compound. In fact, despite being a strong reducing agent, LiBH₄ has several good qualities for SSE, such as being a lightweight material, with a density of 0.666 g cm⁻³, having a large electrochemical window and, therefore, being electrochemically stable up to 2.2 V versus Li⁺/Li.^14,15 This material shows a polymorphic transition, with a crystallographic structure change from an orthorhombic unit cell at room temperature (RT), with a space group (s. g.) Pnma, to a hexagonal unit cell, s. g. P6₃mc,¹⁶ above 110 °C. Even though the hexagonal polymorph has a remarkable ionic conductivity (σ ∼ 10⁻³ S cm⁻¹ at 120 °C), the orthorhombic phase is much less conductive, with σ amounting to 10⁻⁸ S cm⁻¹ at 30 °C, resulting in making a RT battery target unviable.¹⁷ To increase the lithium-ion conductivity of LiBH₄, several approaches have been investigated, such us the anionic substitution, the formation of a composite with oxides and the nanoconfinement in suitable scaffolds.^14,18–21 Several studies have demonstrated that it is possible to stabilize the high ionic conductive hexagonal phase of LiBH₄ at RT via anionic substitution, by replacing the BH₄⁻ anion with halides.^14,22 For example, fast Li-ion conductivity, at RT, have been observed in h-Li(BH₄)_1−α(Br)_α hexagonal solid solutions (e.g., ∼10⁻⁵ S cm⁻¹ for h-Li(BH₄)_0.7(Br)_0.3).¹⁴ In this case it has been reported that the solid solution is stable at RT in the range of 0.30 ≤ α ≤ 0.55.²³ The hexagonal h-Li(BH₄)_1−α(I)_α solid solutions is reported to be stable at RT in the range of 0.20 ≤ α ≤ 0.50.²⁴ By adding 25 mol% of LiI, the LiBH₄–LiI hexagonal solid solution showed a Li-ion conductivity of about 10⁻⁴ S cm⁻¹ at 30 °C. This system has an excellent thermal stability, that makes it a good SSE candidate. This aspect has been investigated with calorimetric techniques.^12,25 In fact, the Differential Scanning Calorimetry (DSC) trace of the LiBH₄–LiI solid solution containing a molar fraction of LiI equal to 0.25 does not show any variations after 20 cooling–heating cycles. The LiI-rich solid solutions have been investigated by Miyazaki et al.,²⁶ which highlighted that an excess of lithium iodide makes difficult to obtain a single hexagonal phase. In fact, it has been shown that a 1 : 1 and a 1 : 2 LiBH₄–LiI ratios lead to the formation of a hexagonal monophasic solution, synthesized through the ball milling technique at room temperature. A further increase of LiI in the mixture leads to the segregation of cubic LiI. In fact, the preparation of the mixture with 1 : 3 LiBH₄–LiI ratio at room temperature leads to the formation of a biphasic mixture, containing LiI in its cubic structure, together with the hexagonal solid solution. However, when using cryo-ball-milling, the amount of unreacted LiI decreased significantly. After an annealing process at 120 °C, the 1 : 3 LiBH₄–LiI solution leads to the segregation of LiI, thus suggesting the formation of a metastable solid solution.

A comprehensive assessment of the thermodynamic properties of borohydrides and their mixtures is crucial for the evaluation of their function as SSEs. This objective can be achieved through the CALPHAD method, which relies on a parametric representation of the Gibbs free energy as a function of temperature and composition. This approach is based on a combination of ab initio calculations with experimental results.²⁷ By employing experimental data as input, the CALPHAD method allows the assessment of numerous parameters describing the Gibbs free energy of all phases, refining the phase diagram of the studied system. Ab initio calculations play a crucial role in determining the Gibbs free energy of compounds with a crystalline structure that is unstable within the investigated temperature and pressure ranges.

The implementation of the CALPHAD method has already proven successful in determining various thermodynamic properties of borohydrides, including isobaric heat capacity, (C_p) and the assessment of multiple phase diagrams as functions of temperature and composition.^23,28,29 Regarding the LiBH₄–LiI phase diagram, it is not reported in the literature yet, and only few experimental data are available concerning the thermodynamic aspect of this system. In this study, the thermodynamics of the LiBH₄–LiI system has been investigated, combining both an experimental and a theoretical approach, to determine the phase diagram. Starting from an analysis of existing literature, new experiments and ab initio calculations have been performed. Obtained data have been used as input for the assessment of the thermodynamics of the system, using the CALPHAD approach. The assessment enables the establishment of phase stabilities and limits of solubility in the full composition range and in a wide temperature range.

Experimental

Synthesis

The manipulation of the prepared samples was performed in an Argon-filled glovebox (MBraun Lab Star glove box supplied with pure 5.5 grade Argon, 95% from SigmaAldrich). LiBH₄ and LiI (purity > 99% from Sigma-Aldrich) were mixed in different ratios, as reported in Table 1.

Table 1 Composition and synthesis conditions of the prepared samples (BM: ball milling; ANN: annealing)

Name	Composition (molar fraction)		Synthesis
	LiBH4	LiI
S1	0.33	0.67	BM + ANN
S2	0.40	0.60	BM + ANN
S3	0.50	0.50	BM + ANN
S4	0.67	0.33	BM + ANN
S5	0.80	0.20	BM + ANN
S6	0.85	0.15	BM + ANN
S7	0.90	0.10	BM + ANN
S8	0.95	0.05	BM + ANN
S9	0.50	0.50	Hand mixed

---

All samples were prepared by ball milling (BM) technique by using a Fritsch Pulverisette 6 planetary mill, using an 80 mL tungsten carbide vials with tungsten carbide balls (5 mm outside diameter). The ball-to-sample mass ratio was 30 : 1 and approximately 1 g of mixture was prepared for each sample. The mechanochemical treatment was performed for a total time of 1.5 h under Argon atmosphere at 350 rpm for periods of 10 min of milling, separated by 2 min breaks to avoid overheating. To reach the equilibrium conditions, samples were annealed (ANN) at 250 °C for 4 h in a quartz tube under vacuum, with a heating/cooling rate of 5 °C min⁻¹ to reach the annealing temperature or cooling down to RT. To obtain information on the enthalpy of mixing, sample S9 has been simply hand mixed in a mortar of agata at RT for few minutes.

X-ray powder diffraction and Rietveld analysis

Samples in powder form were characterized by X-ray powder diffraction (XRD) at RT (ex situ) using a Panalytical X-pert Pro MPD (Cu K_α1 = 1.54059 Å, K_α2 = 1.54446 Å) in Debye–Scherer configuration. Patterns were collected in the 2θ range from 10° to 80°, with a time step of 160 s. Glass capillaries (0.8 mm) were used as sample holders and they were filled and sealed under Ar atmosphere inside the glove box, to ensure the controlled atmosphere during the measurement.

The Rietveld refinement of XRD patterns has been performed using the Materials Analysis Using Diffraction (MAUD) software.³⁰ The instrumental function was determined using pure Si. The background was described through a polynomial function with 4 parameters. The peak broadening was described using the Caglioti formula³⁰ and the peak shape was fitted with a pseudo-Voigt function. The parameters were also refined to consider possible instrument misalignments. Reliability parameters R_wp, R_exp, and χ² were used to evaluate the quality of the fitted patterns with selected structural and microstructural (i.e., crystallite size and microstrain) parameters. The following sequence was applied for the refinement of parameters: (1) scale factor, (2) background parameters, (3) lattice parameters, (4) crystallite size, and (5) microstrain. In some cases, the occupancy and position of the 2b site in the hexagonal crystal structure were also refined.

Differential scanning calorimetry

To analyse the thermal behaviour of the samples, a high-pressure 204 Netzsch Differential Scanning Calorimetry (DSC) was used. The instrument is placed inside an Ar-filled glovebox to ensure sample handling under inert atmosphere. About 5–8 mg of the sample was loaded into closed aluminium crucibles with a pierced lid. The samples were heated and cooled in the desired temperature range at 5 °C min⁻¹ (20 °C min⁻¹ for the hand mixed sample) under 2 bars of H₂. The instrument was calibrated for temperature and heat flow using the melting temperature and the latent heat of fusion of high-purity standards (Bi, In, Sn, Zn). The same crucible, heating rate, and H₂ pressure have been used for measurements and calibrations.

Attenuated total reflection infrared spectroscopy

The infrared spectra were collected by Attenuated Total Reflection Infrared Spectroscopy (IR-ATR) using a Bruker Alpha-P spectrometer, equipped with a diamond crystal. The instrument is located inside a nitrogen-filled glovebox. All spectra were recorded with a resolution of 2 cm⁻¹ in a 5000–500 cm⁻¹ range, with an average number of scans of 50.

Modelling

Ab initio

The adopted level of theory for the computational study is in the framework of density functional theory (DFT) with the generalized gradient approximation (GGA) PBE functional.³¹ The calculations were performed using the periodic quantum-mechanical software CRYSTAL23,^32,33 which utilizes localized Gaussian functions to describe electrons.³⁴ The basis sets on the atoms have been modified with respect to the original ones in the following way:

• Li: cc-pvqz, where the 3 most diffuse functions of contracted s shells and the most diffuse non-contracted s function were removed, as well as the most diffuse functions from f, d, and g shells (1 each), and all valence shell exponents were optimized;

• I: def2-QZVPP, where all valence shell exponents were optimized;

• B: def2-TZVPP, where the most diffuse s and p non-contracted functions were removed, and all valence shell exponents were optimized;

• H: def2-TZVPP, unmodified.

For the numerical integration-correlation term of all calculations of exchange, 99 radial points and 1454 angular points (XXLGRID) in a Lebedev scheme in the region of chemical interest were adopted; moreover, the DFT grid weight and density tolerances were increased to 10⁻²⁰ and 10⁻¹⁰, respectively. The Pack–Monkhorst/Gilat shrinking factors for the reciprocal space were set to 6. Tolerances of the integral calculations were set to 10–11 a.u. for Coulomb overlap and Coulomb penetration in the direct space. The self-consistent field (SCF) iterative procedure was converged to a tolerance in total energy of ΔE = 1 × 10⁻¹¹ a.u. As regards geometry optimization, both atomic positions and cell parameters were set free to relax, setting the tolerances for the convergence of the maximum allowed gradient and the maximum atomic displacement to 3 × 10⁻⁵ Hartree Bohr⁻¹ and 1.2 × 10⁻⁴ Bohr, respectively.

Phonons at Γ point in the harmonic approximation on the optimized geometry were computed by numerical differentiation of the analytical first derivatives using the central difference formula (i.e. two displacements for each atom in each cartesian direction) to derive the thermodynamic functions by diagonalizing the associated mass-weighted Hessian matrix (for details on the computational procedure see ref. 35 and 36). Enthalpy data were obtained by computing the electronic energy, inclusive of the zero-point energy correction (ZPE), and the thermal factor at T = 25 °C.

CALPHAD

The Gibbs free energy of single phases was described according to the CALPHAD approach:³⁷

^φG = ^φG^ref − TS^id + ^φG^exc (1)

^φG^ref = x^φG(LiBH₄) + (1 − x)^φG(LiI) (2)

S^id = –R[x ln(x) + (1 − x)ln(1 − x)] (3)

where φ is the considered phase (i.e., CUB: cubic, ORT: orthorhombic, HEX: hexagonal, LIQ: liquid), x is the molar fraction of LiBH₄, T is the temperature and R os the gas constant. G^ref, −TS^id and G^exc are the reference, ideal and the excess contributions to the Gibbs energy, respectively. Excess Gibbs energy was modelled according to the Redlich–Kister expansion series³⁸ truncated to the first contribution, since the agreement with thermodynamic data was satisfactory:

^φG^exc = x(1 − x)(a + bT) (4)

where a and b are optimized parameters.

Starting from the enthalpy difference between the stable and the metastable structures, as obtained from ab initio calculations, thermodynamic functions for missing end-members (i.e., ORT-LiI, HEX-LiI and CUB-LiBH₄) were evaluated adding the assessed values to the Gibbs energy of the stable phases, and then assessed to coherently model experimental data.

Results and discussion

Solubility

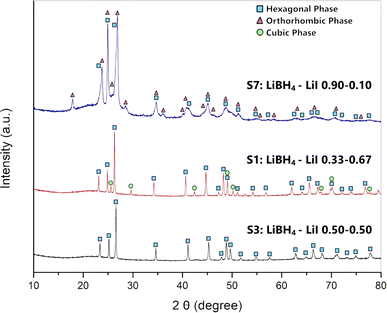
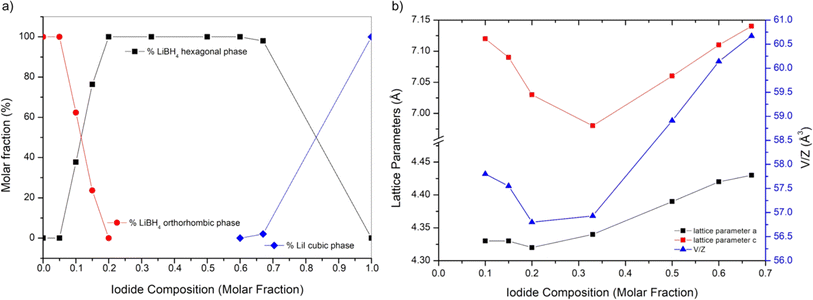
XRD analysis at room temperature, coupled with Rietveld refinement, was conducted on all the prepared samples in order to evaluate the solubility limits of the system. Results are shown in Fig. 1 for selected samples (S1, S3 and S7). Results for other samples are reported in ESI (Fig. S1 and S2).† Sample S1 (Fig. 1) is biphasic, showing both the hexagonal and the cubic phases. Samples S3 (Fig. 1) S2, S4 and S5 are monophasic, showing only diffraction peaks of the hexagonal phase, indicating that the stabilization of the hexagonal phase at RT has been obtained. Samples S6, S7 (Fig. 1) are biphasic, showing both a hexagonal and an orthorhombic phase, even if diffraction peaks of the orthorhombic phase are barely observable in samples S6. Finally, sample S8 is monophasic, showing only the orthorhombic phase.

Fig. 1 XRD pattern of samples S1 (middle), S3 (bottom) and S7 (top). The turquoise squares are referred to peaks related to the hexagonal phase, green circles are referred to the cubic phase, and violet triangles refer to the orthorhombic phase.

By carrying out the Rietveld refinement, the hexagonal solid solution was treated as isostructural to the hexagonal polymorph of LiBH4 (space group P6₃mc), employed as the initial structural model. It was assumed that both I⁻ and BH₄⁻ retained their initial positions (2b site x = 0.3333, y = 0.6667, z = 0.553).¹⁶ It is fundamental to acknowledge that the intense X-ray scattering of I⁻ provides a clear and unequivocal confirmation regarding the occupancy of the I⁻ anion. The molar fraction of hexagonal solid solution and the occupancy of the 2b site in the hexagonal structure obtained by the Rietveld refinement for various samples are reported in ESI (Tables S1 and S2).† The phase fractions obtained for each sample are reported in Fig. 2a as a function of iodide composition. Based on the obtained results for samples S1 and S2, an extension of the hexagonal solid solution up to a molar fraction of LiI equal to 0.60 can be inferred. On the other end, results on occupancy obtained for samples S6 and S7, a limit of the hexagonal solid solution down to a molar fraction of LiI equal to 0.18 has been obtained.

Fig. 2 (a) Phase fraction and (b) lattice parameters and unit volume of the cell (V/Z) of the hexagonal phase as a function of the nominal LiI molar fraction for all the synthetized samples. Connecting lines are a guide for the eyes.

The cell parameters of various crystal structures were obtained for all samples, and corresponding values are reported in ESI (Table S3).† Results of lattice constants and cell volume for the hexagonal phase in samples S1–S7 are reported in Fig. 2b as a function of iodide composition. The parameters obtained in this study are compared in ESI (Fig. S3–S5)† to available literature data,^25,39,40 showing a good agreement. Observed small changes are likely due to different applied annealing conditions. As expected, compared to those of the pure LiBH₄, the hexagonal phase of synthetized samples has larger cell parameters and cell volume, since the atomic radius of the iodine ions is larger than that of BH₄⁻. The lattice parameter a and c linearly increase with the molar fraction of LiI between 0.33 and 0.67, while a shrinking is observed for lower iodide concentrations. Considering the difference of the dimension between I⁻ and BH₄⁻ anions, this non-monotonic trend is unexpected, even if it was already reported in literature for the lattice parameter c by Sveinbjörnsson.⁴⁰ This behaviour has been explained considering the formation of intermediate phases⁴¹ or the presence of different solid solutions containing various amounts of iodine, therefore having different lattice parameters, which merge into one upon heating.²⁵ As already reported by Sveinbjörnsson et al.⁴⁰ these effects could be the origin of the rather asymmetric diffraction peak shape and of the large peak broadening observed in the XRD pattern for sample S7, as reported in Fig. 1.

The cell parameters of the orthorhombic phase observed in samples S6, S7 and S8 are reported in ESI (Fig. S6).† It is possible to notice a slight change in all the lattice parameters, leading to a different cell volume, if compared to that of the pure LiBH₄. These results suggest a small solubility of LiI inside LiBH₄ orthorhombic phase, up to a molar fraction of 5%. On the other hand, by comparing the cell parameter of the cubic phase in samples S1 (a = 6.030 Å) to the cell parameter of pure LiI (a = 6.026 Å) any solubilization of BH₄⁻ inside the cubic structure of LiI can be excluded.

In order to validate the solubility limits of the hexagonal solid solution acquired from the Rietveld refinement of XRD pattern of sample S2, the molar balance reported in eqn (5) has been applied:

fLi[(1 − α)H₄α] + (1 − f)LiI = 1 (5)

where f and (1 − f) are, respectively, the molar fraction of the hexagonal phase of the solid solution h-Li(BH₄)_1−α(I)_α and LiI molar fraction. α and (1 − α) are the molar fractions in the hexagonal structure, and therefore the occupancy of the I⁻ and BH₄⁻ ions in the 2b site. By solving the balance, the extension of the hexagonal monophasic range up to 0.60 of LiI has been confirmed.

By performing the Rietveld refinement on sample S6 and S7, the molar fraction of the hexagonal phase turned out equal to 38% for sample S7 and 76% for sample S6. In this case, to confirm results obtained from the Rietveld refinement, the lever rule has been applied, considering a solubility of 5% of LiI into the orthorhombic phase and of 18% into the hexagonal phase. Results confirmed obtained limits of solubility, as reported in ESI (Table S1).†

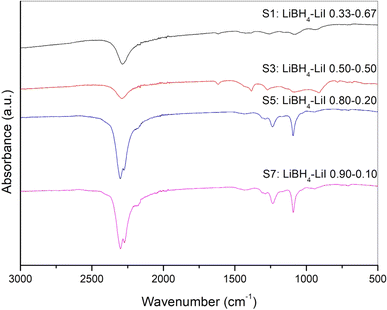
IR-ATR analysis was conducted for all samples in order to explore variations in the vibrational properties of LiBH₄ resulting from anionic substitution that led to the stabilization of the hexagonal phase. Results were compared to those obtained for the pure orthorhombic LiBH₄.

The IR-ATR spectra of sample S1, S3, S5 and S7 are shown in Fig. 3, while results obtained for other samples are reported in the ESI (Fig. S7).† It has already been reported^25,42–44 that the orthorhombic LiBH₄ spectra shows main absorption bands in two different regions, i.e. the 2400–2000 cm⁻¹ and 1600–800 cm⁻¹ ranges, which correspond, respectively, to the B–H stretching and bending vibrational modes. Differences in the spectra due to the presence of the hexagonal solid solutions, in both absorption bands of B–H, have been already reported⁴⁴ in the literature caused by the change of BH₄⁻ site symmetry. This peculiar behaviour has been reported for different anionic substitution in order to stabilize for the hexagonal phase stabilized at room temperature by adding I⁻,²⁵ by Cl⁻⁴³ and Br⁻.⁴⁴ It is worth noting that for sample S5, that from XRD analysis appears to be monophasic, i.e. only composed by the hexagonal phase, some traces of the orthorhombic phase seem to be present from the IR-ATR spectrum (Fig. 3), suggesting a possible extension of the orthorhombic–hexagonal biphasic region up to a LiI molar fraction equal to 0.2.

Fig. 3 IR-ATR spectra of samples S1, S3, S5 and S7.

Phase transitions

By using the DSC technique, the thermal stability of all samples was established, and the temperature of solidus, liquidus and of solid-state phase transition has been determined. The DSC traces obtained for various samples are reported in ESI (Fig. from S8 to S14).† From the DSC traces, also the enthalpy of phase transitions has been determined, and obtained data are reported in ESI (Tables from S4 to S10).† Results of DSC analysis well reproduce the different zones of the phase diagram, which will be described for a continuous increasing of the LiI content.

For sample S8, which is composed by a single orthorhombic solid solution with 5% molar fraction of LiI into LiBH₄, a main DSC endothermic peak is observed at about 82 °C, followed by a smaller one at about 95 °C. These signals correspond to the orthorhombic-to-hexagonal phase transition, which is characterized by a small temperature range with the co-existence of the two phases. As expected, the observed temperatures are lower than that of the phase transition in pure LiBH₄ and the measured enthalpy of transition (4.1 ± 0.1 ±kJ mol⁻¹) is comparable to that of pure LiBH₄ (5.3 ± 0.9 kJ mol⁻¹)⁴⁵ (Table S10†). At about 288 °C, a single DSC peak related to the melting of the sample is observed, suggesting that solidus and liquidus temperatures are quite similar. On cooling, all phase transitions are well reproduced, confirming that equilibrium conditions are explored during the experiment. In addition, DSC traces related to following cycles are well overlapping, confirming that no degradation of the sample is occurring during the measurement.

Samples S6 and S7 are located in the biphasic zone, where orthorhombic and hexagonal phases coexist. The details of the DSC traces on heating in three subsequent thermal cycles are reported in the ESI (Fig. S12 and S14).† Considering the trace for sample S7, the signal due to the solid-state phase transition should show a single endothermic peak, related to the change from the orthorhombic–hexagonal biphasic zone to the single hexagonal phase area in the phase diagram. Actually, in the first run, two different endothermic peaks are observed, as it would be observed if a single orthorhombic phase is present in the sample. From the XRD analysis, the presence of the hexagonal phase in the S7 sample has been difficult to be observed, so the composition corresponding to this sample is likely rather close the phase boundary of the orthorhombic solid solution. By comparing the DSC traces of sample S7 obtained in different runs, it can be noticed that the observed temperatures of endothermic peaks shifted towards lower temperatures after the first cycle, but they remined quite similar between the second and the third cycle. This behaviour is related to the thermal process followed during the DSC measurements where, even by applying a cooling ramp of 5 °C min⁻¹, not a perfect equilibrium is obtained after cooling from the first heating. In fact, observing the cooling DSC curves in ESI (Fig. S13),† a significant undercooling of the solid-state phase transition is occurring, leading to the observed shift of transition temperatures. For this reason, only data related to the first heating ramp have been considered for the assessment of the phase diagram. To confirm the presence of a thermodynamic equilibrium in the as-prepared conditions, the DSC measurement was repeated on sample S7 after 1 year, as reported in ESI (Fig. S15).† As expected, data turned out quite reproducible, confirming the suitability of experimental data for the assessment of the phase diagram. A similar behaviour has been observed for sample S6, as shown in ESI (Fig. S12).† In this case, considering the higher molar fraction of LiI with respect to sample S7, a single endothermic signal is observed. On the other hand, the undercooling effect seems more evident, as shown by the absence of an exothermic peak in the DSC traces on cooling. On heating in the DSC measurements, after reaching the monophasic zone of the hexagonal solid solution, the samples showed the endothermic signal related to the melting. In this case, a single peak is observed, with a slight shoulder in the high temperature side. This trend suggests again that the solidus and liquidus temperatures are quite similar. In case of melting, a rather well reproducibility of the DSC trace is observed on cycling, suggesting that the observed behaviour refers to equilibrium conditions. This observation is confirmed by the evident exothermic DSC peak due to the solidification observed on cooling, as shown in ESI (Fig. S12).†

Samples S3 and S4 are located in the monophasic zone of the hexagonal solid solution. In this case, no solid-state transformations are expected. In fact, for all samples, basically no DSC signals have been observed before melting (Fig. S10 and S11†), either on heating or on cooling. In some cases, tiny thermal effects are observed for the first heating, which might be related to small inhomogeneities in the sample, but they disappear in following thermal cycles. In this case, DSC signals related to the solidification show a different trend for different runs, suggesting that possible undercooling effects in the liquid phase might be occurred.

Finally, sample S1 allows to explore the biphasic zone with the hexagonal and cubic phases. By performing the DSC measurement, this samples showed a very different behaviour compared to all the others. In fact, during the first heating ramp, it showed an exothermic peak at about 75 °C, as evidenced in ESI (Fig. S8).† This peak suggests that a reaction is acting, may be due to a further dissolution of cubic LiI into the hexagonal solid solution. This behaviour seems to be related to the high fraction of LiI, since also sample S2 (Fig. S9†) showed a similar behaviour. At higher temperatures, a composed melting process can be outlined, with a preliminary small endothermic peak, followed by the main one. After the first run, a change in shape of DSC peaks can be spotted, indicating that the material might have changed its composition, maybe due to a degradation in the liquid phase.

Based on the results obtained from DSC measurements, only the first heating ramp has been taken in consideration for the definition of temperatures and enthalpies of phase transformations for the CALPHAD assessment.

Enthalpy of mixing

To assess the LiBH₄–LiI phase diagram, the evaluation of the enthalpy of mixing for the hexagonal solid solution is necessary. Therefore, the S9 sample was prepared by hand mixing LiBH₄ and LiI (with 0.5 : 0.5 molar ratio) in an agate mortar for only 5 minutes, to avoid the formation of the hexagonal phase. This sample was used for a DSC measurement aimed to determine the enthalpy of mixing, as already performed for the LiBH₄–LiBr system.²³ The annealing program used for the analysis was as follows: isothermal step at 60 °C for 2.5 hours to equilibrate the DSC signal, heating ramp (20 °C min⁻¹) to reduce the temperature range in which the thermally unwanted activated process could happen, isotherm of 4 hours at the maximum temperature reached during the temperature ramp to ensure that the thermally activated process is completed. The cycle was repeated twice, to obtain a DSC signal that could be used as a baseline for the integration of the DSC peak. Three different maximum temperatures (i.e. 250 °C, 270 °C and 285 °C) have been selected. As an example of the acquired DSC traces, the result obtained for the maximum temperature of 270 °C is shown in Fig. 4.

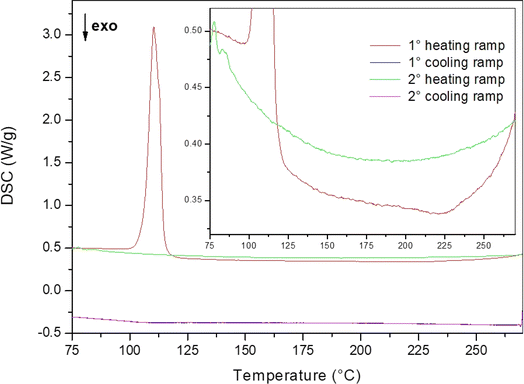Fig. 4 DSC trace of sample S9 used to determine the enthalpy of mixing of the hexagonal solid solution. An enlarged view is shown in the inset.

In the first DSC heating run, and endothermic peak due to the orthorhombic-to-hexagonal phase transformation of LiBH₄ is observed at about 110 °C, followed by a broad exothermic peak related to the formation of the hexagonal solid solution. By comparing the first and second heating ramps, it can be noticed a slight change in the baseline level. This behaviour finds an explanation by taking in account that the molar heat capacity (C_p) of the orthorhombic phase of LiBH₄ is higher than that of the hexagonal phase.⁴⁵ Indeed, during of the first heating ramp, LiBH₄ is still in the orthorhombic phase before the phase transition temperature, while during the second heating ramp, LiBH₄ is solubilized in the hexagonal solid solution. The first cooling DSC trace does not show any signal, confirm the occurrence of a full solubilization of parent LiBH₄ and LiI into the hexagonal solid solution during the first heating. The second cooling DSC trace is well overlapping the first one, confirming that the second DSC heating ramp can be used as a baseline for the determination of the enthalpy of mixing.

After the DSC analysis up to 250 °C and 285 °C, PXRD measurements were performed, and the pattern are reported in ESI (Fig. S20).† From the Rietveld analysis, less than 5 wt% of residual cubic LiI was found inside the sample. This result can be due to the hand mixing process, leaving a small fraction of LiI being strongly compacted, so not able to react with LiBH₄ for kinetic reasons. The obtained cell parameters of the hexagonal solid solution are documented in ESI (Table S11)† and turned out comparable to those of sample S3, that was synthetized with a LiI molar fraction of 50% via ball milling followed by an annealing process, confirming the occurrence of the desired solution reaction.

To determine the enthalpy of mixing for the hexagonal solid solution from the observed DSC traces, it is to be considered that, by preparing the sample via hand mixing, the reproducibility of the sample cannot be fully guaranteed and even slight differences in pressure and rotational speed can change the outcome of the sample preparation. Therefore, the real composition of the sample analysed via DSC was taken in account by comparing the enthalpy of transition of pure LiBH₄ and the enthalpy of transition obtained for hand mixed samples, as described in ESI.† In fact, the large endothermic peak around 110 °C has been observed in all held experiments. This peak, which is due to the orthorhombic-to-hexagonal phase transformation of parent LiBH_4, has been used as an internal standard to determine the right molar fraction composition of each sample, which is necessary to accurately determine the enthalpy of mixing of the hexagonal solid solution. The obtained enthalpy of transition for pure LiBH₄ was equal to 5.3 kJ mol⁻¹ (Fig. S16 in the ESI†), in good agreement with the literature value of 5.3 ± 0.9 kJ mol⁻¹.⁴⁵ Following the observed endothermic DSC peak on heating, it can be assumed that the LiBH₄ present in the sample is in the hexagonal phase. So, the broad exothermic peak observed in all the DSC traces after the phase transition in the first heating cycle can be associated to the enthalpy of reaction (ΔH_rea) leading to the h-Li(BH₄)_1−α(I)_α solid solution. In fact, it is not present in the second heating ramp.

It is worth noting that the observed mixing reaction actually starts from hexagonal LiBH₄ and cubic LiI, giving the h-Li(BH₄)_1−α(I)_α solid solution. So, the average value of enthalpy of mixing (ΔH_mix) of h-Li(BH₄)_1−α(I)_α solid solution was calculated by the following formula:

ΔH_mix = ΔH_rea − ΔH_trsC–H(LiI) (6)

where ΔH_rea is the enthalpy of reaction obtained by the integration of the broad DSC exothermic peak, and ΔH_trsC–H(LiI) is the enthalpy of cubic-to-hexagonal phase transition for LiI. The last value cannot be experimentally measured, and it has been calculated by DFT. As described in detail in next section, a value of 2.6 kJ mol⁻¹ has been considered. The details on the integration procedure performed for the three DSC traces are reported in ESI (Fig. from S17 to S19)† and obtained results are reported in Table 2. The obtained enthalpy of mixing for the hexagonal solid solution is provided together with the actual composition of the sample, as determined from the calibration based on the enthalpy of the orthorhombic-to-hexagonal phase transformation of LiBH4. Considering an average composition of 50% molar fraction of LiI, an average value of −1.81 ± 0.4 kJ mol⁻¹ has been obtained for the enthalpy of mixing of the hexagonal solid solution. It is worth noting that the maximum temperature reported in Table 2 refers to the selected temperature for the final isotherm in the DSC experiments, but the reaction to form the solid solution is spread in a wide temperature range. So, a constant value for ΔH_mix has been considered.

Table 2 ΔH collected via DSC analysis and related determination of the enthalpy of mixing of the hexagonal solid solution, considering the cubic-to-hexagonal enthalpy of transition for LiI determined by DFT

Max T (°C)	Composition% mol of LiI	ΔHrea (J g^−1)	ΔHtrsC–H(LiI) (J g^−1)	ΔHmix (kJ mol^−1)
250	46	−2.76	16.28	−1.39
270	43	−10.53	15.93	−1.84
285	61	−6.83	17.60	−2.20
Average	50			−1.81 ± 0.4

---

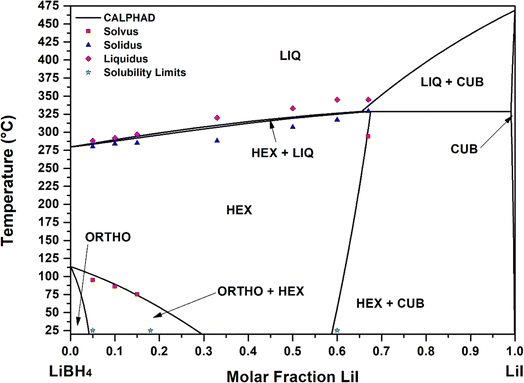
Assessment of the phase diagram

In order to describe the LiBH₄–LiI phase diagrams, the determination of the parameters of thermodynamic functions for different solution phases (hexagonal, cubic, orthorhombic and liquid) is necessary. In addition, pure components end-members, starting from values calculated by DFT, need also to be validated to reach a good agreement with experimental data. The procedure for the assessment takes in consideration both results from experiments (Table 3) and ab initio calculations used as initial starting point. Assessed thermodynamic parameters are reported in Table 4, and corresponding calculated data are reported in Table 3.

Table 3 Experimental and calculated thermodynamic data for LiBH₄–LiI system. ΔH_m is the enthalpy of melting, SOLV: solvus, SOL: solidus, LIQ: liquidus

Phase	Experimental	Calculated
Ortho	0 ≤ XLiI ≤ 0.05 molar fraction at 25 °C	0 ≤ XLiI ≤ 0.04 molar fraction at 25 °C
Hexa	0.18 ≤ XLiI ≤ 0.60 at 25 °C	0.28 ≤ XLiI ≤ 0.59 at 25 °C
S1, XLiI = 0.67	TSOLV = 294 °C	TSOLV = 309 °C
S6, XLiI = 0.15	TSOLV = 75 °C	TSOLV = 72 °C
S7, XLiI = 0.10	TSOLV = 86 °C	TSOLV = 87 °C
S8, XLiI = 0.05	TSOLV = 95 °C	TSOLV = 100 °C
Cubic	XLiI = 1 at 25 °C	XLiI = 1 at 25 °C
Liquid
S1, XLiI = 0.67	TSOL–LIQ = 329–345 °C	TSOL–LIQ = 329–337 °C
S2, XLiI = 0.60	TSOL–LIQ = 317–345 °C	TSOL–LIQ = 325–326 °C
S3, XLiI = 0.50	TSOL–LIQ = 307–333 °C	TSOL–LIQ = 319–321 °C
S4, XLiI = 0.33	TSOL–LIQ = 288–320 °C	TSOL–LIQ = 307–310 °C
S6, XLiI = 0.15	TSOL–LIQ = 285–297 °C, ΔHm = 8.3 kJ mol^−1	TSOL–LIQ = 292–294 °C, ΔHm = 8.7 kJ mol^−1
S7, XLiI = 0.10	TSOL–LIQ = 284–292 °C, ΔHm = 7.7 kJ mol^−1	TSOL–LIQ = 288–290 °C, ΔHm = 8.5 kJ mol^−1
S8, XLiI = 0.05	TSOL–LIQ = 290–288 °C, ΔHm = 5.9 kJ mol^−1	TSOL–LIQ = 283–285 °C, ΔHm = 8.4 kJ mol^−1

---

Table 4 Determined Gibbs free energy in the LiBH₄–LiI system

Gibbs free energy (J mol^−1)	Model
^CUBG(LiBH4) = ^ORTHG(LiBH4) + 3600	Ab initio from ref. 29
^ORTG(LiI) = ^CUBG(LiI) + 31 100	Ab initio
^HEXG(LiI) = ^CUBG(LiI) + 2600	Ab initio
^CUBG^exc = x(1 − x)(+10 000)	Regular
^ORTG^exc = x(1 − x)(−30 000)	Regular
^HEXG^exc = x(1 − x)(−8840 + 4 × T)	Redlich–Kister
^LIQG^exc = x(1 − x)(−13 000 + 12 × T)	Redlich–Kister

---

Data regarding LiBH₄ lattice stabilities were acquired from the literature.²⁹ For the determination of the relative stability of metastable LiI structures and the support of the assessment of CALPHAD end-members, energies have been evaluated with the CRYSTAL code. Starting from the crystal structures of LiBH₄, metastable structures for LiI were obtained by the full substitution of BH₄⁻ with I⁻. The end-members enthalpies have been calculated with respect to the stable cubic structure, and obtained values are +31 100 J mol⁻¹ and +2600 J mol⁻¹ for the orthorhombic and hexagonal phases, respectively (Table 4).

The obtained values are rather different, indicating that the hexagonal structure of LiI is much more stable than the orthorhombic one, being only slightly unstable with respect to the cubic phase observed in equilibrium conditions.

The obtained experimental data elucidated that solubility of LiI into orthorhombic LiBH₄ is limited, but can go up to 0.05 molar fraction at 25 °C. To fully model this solubility range, a regular solution model was assumed, and, to match experimental data, it was necessary to introduce a negative parameter ^ORTa = −30000 J mol⁻¹ (Table 4). This value is strongly negative, suggesting a tendency of LiI to be solubilized in LiBH₄, but the observed solubility is limited by the strong instability of orthorhombic LiI with respect to the stable cubic structure. In fact, the assessment indicated a solubility of 0.04 molar fraction of LiI into o-LiBH₄ (Table 3).

In all the conducted experiments, it has never been observed a solubility of LiBH₄ into cubic LiI. Consequently, a positive parameter in the excess Gibbs free energy function for the cubic phases have been set within the regular solution model, i.e., ^CUBa = +10 000 J mol⁻¹.

By considering the lowest values including experimental errors, the interaction parameter for the hexagonal solid solution has been fixed by taking in consideration the experimental value of enthalpy of mixing (i.e. −1800 ± 410 J mol⁻¹) for the sample S9 (0.5LiI–0.5LiBH₄ molar fraction, hand mixed). So, based on a Redlich–Kister solution model, ^HEXa turned out to be equal to −8840 J mol⁻¹ (Table 4). By also fixing a Redlich–Kister parameter ^HEXb to +4 J mol⁻¹ K⁻¹ (Table 4), the description of solubility limits of the hexagonal solid solution is in good agreement with experimental values in the whole temperature range. A notable difference is recorded for the lower solubility limit, being 0.18 molar fraction of LiI the experimental value, to be compared with a 0.28 assessed value (Table 3). On the other hand, as previously mentioned, the presence of a small fraction of orthorhombic phase in sample S5 cannot be excluded, suggesting a solubility limit higher than 0.20. Experimental solvus temperatures reported in Table 3 refer to DSC peak temperatures determined in the first heating ramp, and they are in good agreement with the calculated values.

The liquid phase has been treated as a regular solution and assessed on the base of liquidus (melting peak temperature) and solidus temperatures (melting onset temperature) obtained by DSC analysis during the first heating and cooling ramps. The optimised Redlich–Kister parameters regarding the liquid phase converged to a value equal to ^LIQa = −13000 J mol⁻¹ and ^LIQb = +12 J mol⁻¹ K⁻¹ (Table 4), that led to a reasonable match of solidus and liquid temperatures, as well as a good agreement for values of the enthalpy of melting (Table 3).

Fig. 5 the calculated curves and experimental points are reported, showing a good agreement. The occurrence of a peritectic reaction at 329 °C in correspondence of 0.68 LiI molar fraction was demonstrated via CALPHAD calculations. A similar result was obtained for the LiBH₄–LiBr phase diagram.²³

Fig. 5 Lines: assessed phase diagram for the LiBH₄–LiI system. Experimental temperature data determined in this work from DSC are reported as: red squares (solvus), blue triangles (solidus), pink diamonds (liquidus). Light blue stars indicate solubility limits determined in this work by XRD and Rietveld analysis at room temperature.

Conclusions

The LiBH₄–LiI phase diagram has been systematically explored by using both an experimental approach, combining different techniques such as of XRD, ATR-IR and DSC, and a theoretical approach by using the CALPHAD method in combination with ab initio calculations. Thermodynamic properties have been fully assessed. The composition range of monophasic zone of the hexagonal LiBH₄–LiI solid solution has been experimentally identified to be equal to 0.18 ≤ x ≤ 0.60 at room temperature. Various points of the phase diagram, like liquidus, solidus, and solvus temperatures, have been experimentally determined by employing the DSC technique. In order to obtain the assessment of LiBH4–LiI phase diagram, the enthalpy of mixing of the hexagonal solid-state solution has been acquired experimentally. By considering a hand-mixed sample, exothermic peaks have been obtained through the DSC technique, providing a value of −1.81 ± 0.4 kJ mol⁻¹ for the enthalpy of mixing of the hexagonal solid solution with a composition of 50% molar fraction of LiI.

By using experimental values and results from ab initio calculations, thermodynamic properties of the LiBH₄–LiI pseudo-binary system have been assessed by the CALPHAD. From these values, the corresponding phase diagram has been calculated.

Author contributions

Conceptualization: Baricco, Palumbo; methodology: Palumbo, Sgroi, Corno; formal analysis and investigation: Mazzucco, Dematteis, Gulino; writing – original draft preparation: Mazzucco; writing – review and editing: Mazzucco, Dematteis, Corno, Baricco; funding acquisition: Baricco; resources: Baricco; supervision: Baricco, Palumbo.

Conflicts of interest

All authors declare that they have no conflicts of interest.

Acknowledgements

Authors acknowledge support from the Project CH4.0 under the MUR program “Dipartimenti di Eccellenza 2023–2027” (CUP: D13C22003520001).

References

1. A. Züttel, A. Remhof, A. Borgschulte and O. Friedrichs, Hydrogen: the future energy carrier, Philos. Trans. R. Soc., A, 2010, 368, 3329–3342.
2. World Economic Forum, and Global Battery Alliance, A Vision for a Sustainable Battery Value Chain in 2030: Unlocking the Full Potential to Power Sustainable Development and Climate Change Mitigation, 2019.
3. K. Xu, Nonaqueous liquid electrolytes for lithium-based rechargeable batteries, Chem. Rev., 2004, 104(10), 4303–4418.
4. A. Ulvestad, A Brief Review of Current Lithium Ion Battery Technology and Potential Solid State Battery Technologies, arXiv, 2018, preprint, arXiv:1803.04317,  DOI:10.48550/arXiv.1803.04317.
5. J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Inorganic Solid-State Electrolytes for Lithium Batteries: Mechanisms and Properties Governing Ion Conduction, Chem. Rev., 2016, 116(1), 140–162.
6. J. M. Tarascon and M. Armand, Issues and challenges facing rechargeable lithium batteries, Nature, 2001, 414, 6861.
7. A. Ahniyaz, I. de Meatza, A. Kvasha, O. Garcia-Calvo, I. Ahmed, M. F. Sgroi, M. Giuliano, M. Dotoli, M. A. Dumitrescu, M. Jahn and N. Zhang, Progress in solid-state high voltage lithium-ion battery electrolytes, Adv. Appl. Energy, 2021, 4, 100070.
8. M. Murayama, R. Kanno, M. Irie, S. Ito, T. Hata, N. Sonoyama and Y. Kawamoto, Synthesis of New Lithium Ionic Conductor Thio-LISICON—Lithium Silicon Sulfides System, J. Solid State Chem., 2002, 168(1), 140–148.
9. S. Stramare, V. Thangadurai and W. Weppner, Lithium Lanthanum Titanates: A Review, Chem. Mater., 2003, 15(21), 3974–3990.
10. B. A. Boukamp and R. A. Huggins, Ionic conductivity in lithium imide, Phys. Lett. A, 1979, 72(6), 464–466.
11. G. F. Ortiz, M. C. López, P. Lavela, C. Vidal-Abarca and J. L. Tirado, Improved lithium-ion transport in NASICON-type lithium titanium phosphate by calcium and iron doping, Solid State Ionics, 2014, 262, 573–577.
12. M. Matsuo and S. I. Orimo, Lithium Fast-Ionic Conduction in Complex Hydrides: Review and Prospects, Adv. Energy Mater., 2011, 1(2), 161–172.
13. A. Unemoto, K. Yoshida, T. Ikeshoji and S. I. Orimo, Bulk-Type All-Solid-State Lithium Batteries Using Complex Hydrides Containing Cluster-Anions, Mater. Trans., 2016, 57(9), 1639–1644.
14. V. Gulino, M. Brighi, E. M. Dematteis, F. Murgia, C. Nervi, R. Černý and M. Baricco, Phase Stability and Fast Ion Conductivity in the Hexagonal LiBH4–LiBr–LiCl Solid Solution, Chem. Mater., 2019, 31(14), 5133–5144.
15. R. Asakura, L. Duchêne, R. S. Kühnel, A. Remhof, H. Hagemann and C. Battaglia, Electrochemical Oxidative Stability of Hydroborate-Based Solid-State Electrolytes, ACS Appl. Energy Mater., 2019, 2(9), 6924–6930.
16. J. Soulié, G. Renaudin, R. Černý and K. Yvon, Lithium boro-hydride LiBH4, J. Alloys Compd., 2002, 346(1–2), 200–205.
17. M. Matsuo, Y. Nakamori, S. I. Orimo, H. Maekawa and H. Takamura, Lithium superionic conduction in lithium borohydride accompanied by structural transition, Appl. Phys. Lett., 2007, 91(22), 224103.
18. V. Gulino, M. Brighi, F. Murgia, P. Ngene, P. de Jongh, R. Černý and M. Baricco, Room-Temperature Solid-State Lithium-Ion Battery Using a LiBH 4-MgO Composite Electrolyte, ACS Appl. Energy Mater., 2021, 4(2), 1228–1236.
19. V. Gulino, L. Barberis, P. Ngene, M. Baricco and P. E. De Jongh, Enhancing Li-Ion Conductivity in LiBH4-Based Solid Electrolytes by Adding Various Nanosized Oxides, ACS Appl. Energy Mater., 2020, 3(5), 4941–4948.
20. D. Blanchard, A. Nale, D. Sveinbjörnsson, T. M. Eggenhuisen, M. H. W. Verkuijlen, V. T. Suwarno, A. P. M. Kentgens and P. E. de Jongh, Nanoconfined LiBH4 as a Fast Lithium Ion Conductor, Adv. Funct. Mater., 2015, 25(2), 184–192.
21. Y. S. Choi, Y. S. Lee, K. H. Oh and Y. W. Cho, Interface-enhanced Li ion conduction in a LiBH4–SiO2 solid electrolyte, Phys. Chem. Chem. Phys., 2016, 18(32), 22540–22547.
22. H. Maekawa, M. Matsuo, H. Takamura, M. Ando, Y. Noda, T. Karahashi and S. I. Orimo, Halide-stabilized LiBH4, a room-temperature lithium fast-ion conductor, J. Am. Chem. Soc., 2009, 131(3), 894–895.
23. V. Gulino, E. M. Dematteis, M. Corno, M. Palumbo and M. Baricco, Theoretical and Experimental Studies of LiBH 4 −LiBr Phase Diagram, ACS Appl. Energy Mater., 2021, 4(7), 7327–7337.
24. H. Oguchi, M. Matsuo, J. S. Hummelshøj, T. Vegge, J. K. Nørskov, T. Sato, Y. Miura, H. Takamura, H. Maekawa and S. Orimo, Experimental and computational studies on structural transitions in the LiBH4–LiI pseudobinary system, Appl. Phys. Lett., 2009, 94(14), 141912.
25. L. H. Rude, E. Groppo, L. M. Arnbjerg, D. B. Ravnsbæk, R. A. Malmkjær, Y. Filinchuk, M. Baricco, F. Besenbacher and T. R. Jensen, Iodide substitution in lithium borohydride, LiBH4-LiI, J. Alloys Compd., 2011, 509(33), 8299–8305.
26. R. Miyazaki and T. Hihara, Fabrication of LiI-LiBH 4 solid solutions by cryomilling, Mater. Lett., 2020, 271, 127775.
27. H. L. Lukas, S. G. Fries and B. Sundman, Computational Thermodynamics: The Calphad Method, 2007.
28. E. M. Dematteis, E. R. Pinatel, M. Corno, T. R. Jensen and M. Baricco, Phase diagrams of the LiBH4–NaBH4–KBH4 system, Phys. Chem. Chem. Phys., 2017, 19(36), 25071–25079.
29. E. M. Dematteis, E. Roedern, E. R. Pinatel, M. Corno, T. R. Jensen and M. Baricco, A thermodynamic investigation of the LiBH 4-NaBH 4 system, RSC Adv., 2016, 6(65), 60101.
30. L. Lutterotti, S. Matthies and H. R. Wenk, MAUD: A Friendly Java Program for Material Analysis Using Diffraction, CPD newsletter, 1999, 21, 14–15.
31. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865.
32. R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rérat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Quantum-mechanical condensed matter simulations with CRYSTAL, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(4), e1360.
33. R. Dovesi, V. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. Harrison, I. Bush, M. Llunell, M. Causà, Y. Noël, L. Maschio, A. Erba, M. Rérat, S. Casassa, B. Searle and J. Desmarais, CRYSTAL23 User's Manual, 2023.
34. K. Doll and H. Stoll, Ground-state properties of heavy alkali halides, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57(8), 4327.
35. F. Pascale, C. M. Zicovich-Wilson, F. López Gejo, B. Civalleri, R. Orlando and R. Dovesi, The calculation of the vibrational frequencies of crystalline compounds and its implementation in the CRYSTAL code, J. Comput. Chem., 2004, 25(6), 888–897.
36. C. M. Zicovich-Wilson, F. J. Torres, F. Pascale, L. Valenzano, R. Orlando and R. Dovesi, Ab initio simulation of the IR spectra of pyrope, grossular, and andradite, J. Comput. Chem., 2008, 29(13), 2268–2278.
37. H. Lukas, S. G. Fries and B. Sundman, Computational Thermodynamics, Cambridge University Press, Cambridge, 2007.
38. A. T. Kister and O. Redlich, Algebraic representation of thermodynamic properties and the classification, Ind. Eng. Chem., 1948, 40(2), 345–348.
39. G. Valerio, LiBH4 as Solid-State Electrolyte for Li-Ion Batteries: Modeling, Synthesis, Characterization and Application, Università degli Studi di Torino, 2020.
40. D. Sveinbjörnsson, J. S. G. Myrdal, D. Blanchard, J. J. Bentzen, T. Hirata, M. B. Mogensen, P. Norby, S. I. Orimo and T. Vegge, Effect of heat treatment on the lithium ion conduction of the LiBH 4-Lii solid solution, J. Phys. Chem. C, 2013, 117(7), 3249–3257.
41. H. Oguchi, M. Matsuo, J. S. Hummelshøj, T. Vegge, J. K. Nørskov, T. Sato, Y. Miura, H. Takamura, H. Maekawa and S. Orimo, Experimental and computational studies on structural transitions in the LiBH4-LiI pseudobinary system, Appl. Phys. Lett., 2009, 94(14), 141912.
42. H. Hagemann, Y. Filinchuk, D. Chernyshov and W. van Beek, Lattice anharmonicity and structural evolution of LiBH4: an insight from Raman and X-ray diffraction experiments, Phase Transitions, 2009, 82(4), 344–355.
43. O. Zavorotynska, M. Corno, E. Pinatel, L. H. Rude, P. Ugliengo, T. R. Jensen and M. Baricco, Theoretical and Experimental Study of LiBH4-LiCl Solid Solution, Crystals, 2012, 2, 144–158.
44. L. H. Rude, O. Zavorotynska, L. M. Arnbjerg, D. B. Ravnsbæk, R. A. Malmkjær, H. Grove, B. C. Hauback, M. Baricco, Y. Filinchuk, F. Besenbacher and T. R. Jensen, Bromide substitution in lithium borohydride, LiBH4–LiBr, Int. J. Hydrogen Energy, 2011, 36(24), 15664–15672.
45. A. El Kharbachi, E. Pinatel, I. Nuta and M. Baricco, A thermodynamic assessment of LiBH4, Calphad, 2012, 39, 80–90.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra01642d

‡ Present address: LeydenJar, Luchthavenweg 10, 5657 EB Eindhoven, The Netherlands.

---