Electronic, magnetic and optical properties of the charge-disproportionated YNiO₃ compound calculated using the GGA+U method

Abstract

The electronic, magnetic and optical properties of YNiO₃ were studied using the GGA+U method. This compound presents charge disproportionation with two nonequivalent Ni ion sites, namely, Ni1 with Ni^(3−δ)+ and Ni2 with Ni^(3+δ)+. A band-structure calculation was performed for the observed P2₁/n monoclinic phase; a 2 × 1 × 2 supercell with 80 atoms was used to reproduce the observed magnetic ordering. The density of states (DOS) calculation clearly showed the bonding differences between the Ni1 and the Ni2 sites; the Ni1 site has a more ionic character, whereas the Ni2 site presents a more covalent character. The band-structure results correspond to an insulator phase with a band gap of about 0.5 eV. The magnetic ordering is antiferromagnetic and the magnetic moments are about 1.24 μ_B for Ni1 and around 0.00 μ_B for Ni2. The calculated magnetic ordering results are in good agreement with neutron diffraction results. The calculated optical conductivity is similar to previous experimental data.

---

1 Introduction

The rare-earth nickelates present a broad range of very interesting physical properties. These include, for instance, a metal–insulator transition, diverse structural and magnetic transitions, as well as charge disproportionation.^1–3 This variety is partly related to the interplay between the electronic, magnetic and structural degrees of freedom in these compounds. In addition, the highly correlated electronic structures of the rare-earth nickelates adds to the complexity of their physical properties. To this end, the study of the relationship between their electronic structures and their physical properties is highly desirable. The aim of this work is to study the electronic structure of the YNiO₃ compound using the GGA+U method. The theoretical results are compared to the experimental electronic, magnetic and optical properties of this compound.

The YNiO₃ oxide presents a metal–insulator phase transition around 582 K, which also involves structural and magnetic ordering changes.^4–6 In the low-temperature phase, the YNiO₃ compound is an antiferromagnetic insulator (AFM-I); the electrical conductivity and the magnetic susceptibility results reflect electron-correlation effects.⁷ The crystal structure in this phase is monoclinic with space group P2₁/n;⁵ the schematic representation of the crystalline structure of YNiO₃ is shown in Fig. 1. The AFM-I phase is characterized by a distortion of the NiO₆ octahedra, which gives rise to two nonequivalent Ni sites: Ni1 sites with larger Ni–O bonds and Ni2 sites with shorter Ni–O bonds. This difference was attributed to charge disproportionation with charge ordering leading to Ni^(3−δ)+ and Ni^(3+δ)+ ionic states.^5,8,9 Hereafter, all the calculations and comparisons will be only concerned with the low-temperature AFM-I phase.

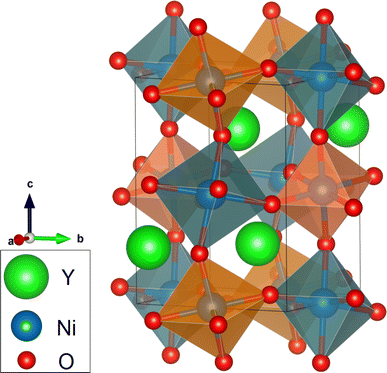Fig. 1 Schematic VESTA representation of the crystalline structure of YNiO₃ with shorter and larger Ni–O bonds indicated by orange and dark green octahedra, respectively.¹⁰

The electronic structure of YNiO₃ was studied using soft X-ray resonant magnetic powder diffraction,¹¹ X-ray absorption spectroscopy (XAS)¹² and optical absorption.⁷ The magnetic and structural properties of this oxide were investigated using synchrotron radiation diffraction,¹³ neutron and synchrotron radiation diffraction,^5,14 and electron spin resonance (ESR) and susceptibility.^15,16 The electronic structure of YNiO₃ was calculated using several band-structure methods, including: LDA,¹⁷ LDA+U,¹⁸ LSDA+U,¹⁹ GGA+U,²⁰ and the Hartree–Fock approach.²¹ Recent results include studies of the optical spectra,²² and additional band-structure calculations.²³

Considerable insight on the properties of YNiO₃ was obtained from the above band structure and by modeling Hamiltonian models. But a comprehensive comparison of the calculations and the experimental results is still lacking and would be desirable. This work presents the electronic structure of YNiO₃ calculated by the GGA+U method. The results are in reasonable agreement with the available experimental data, and help to explain the electronic, magnetic and optical properties of this compound. The results are also interpreted in terms of the configuration interaction (CI) scheme of highly correlated pd models. Finally, the interplay between the structural, charge and spin degrees of freedom is discussed using the CI language.

2 Calculation details

Calculations for the AFM-I phase at room temperature were performed using the WIEN2k package,²⁴ mainly because most of the available experimental results were obtained under this condition. This program is based in the full-potential linearized augmented plane wave (LAPW) method. The GGA exchange–correlation potential was obtained using the PBEsol scheme,²⁵ and the on-site Hubbard parameter U was set to 1.5 eV. This value was chosen because it yields the best overall agreement with the experimental results. We also note that this value is in line with those previously used for this compound.^19,20,26

The spin–orbit splitting of the Ni 3d orbitals was included to determine the magnetic ordering. The spin–orbit coupling determines the orientation of the spin, so it is crucial for the calculation of the magnetic ordering. But the value of the coupling constant (about 0.04 eV for Ni) is relatively small, and does not affect much the electronic structure or the physical properties. The calculation of the magnetic ordering was unconstrained, and all the magnetic moments were allowed to rotate, until the criterion of total energy convergence was achieved.

The crystal structure was monoclinic and the space group was P2₁/n. The lattice parameters are listed in Table 1; the experimental values were retrieved from Alonso et al.,⁵ and the theoretical parameters were obtained by a total energy calculation. The cell volume was reduced about 2.8% from 211.85 ų (experimental) to 205.98 ų (calculated).

Table 1 Comparison between the experimental (taken from Alonso et al.⁵) and calculated lattice parameters in YNiO₃ (all values in Å)

	Experimental	Calculated
a	5.17932	5.13105
b	5.51529	5.46389
c	7.41656	7.34744

---

The nonequivalent atomic positions are given in Table 2; the experimental results were retrieved from Alonso et al.⁵ and the theoretical positions were obtained by an atomic force calculation (the convergence criteria for the force was 1 mRy Bohr⁻¹). The experimental and calculated average Ni–O bond lengths are in excellent agreement: 1.994 Å (exper.) vs. 1.993 Å (theor.) at the Ni1 site, and 1.923 Å (exper.) vs. 1.922 Å (theor.) at the Ni2 site.

Table 2 Comparison between the experimental (taken from Alonso et al.⁵) and calculated relative atomic positions of the different nonequivalent atoms in YNiO₃ referred to the monoclinic axes

Atom	Experimental			Calculated
	x	y	z	x	y	z
Y	0.9816	0.0729	0.2502	0.9796	0.0735	0.2505
Ni1	0.5000	0.5000	0.0000	0.5000	0.5000	0.0000
Ni2	0.5000	0.0000	0.5000	0.5000	0.0000	0.5000
O1	0.0998	0.4705	0.2457	0.0977	0.4729	0.2504
O2	0.6973	0.3080	0.0467	0.6942	0.3011	0.0472
O3	0.1882	0.2038	0.9465	0.1952	0.2002	0.9501

---

The maximum wavevector of the plane-wave basis set was given by R_MTK_MAX = 7.0, the integration was performed using 500 k-points in the irreducible part of the Brillouin zone, the energy convergence criteria was set to 10⁻⁵ Ry, and the 2 × 1 × 2 super-cell was formed by 80 atoms (please note that the monoclinic cell contains four chemical formulas with 20 atoms).

3 Results and discussion

3.1 Band structure and band gap

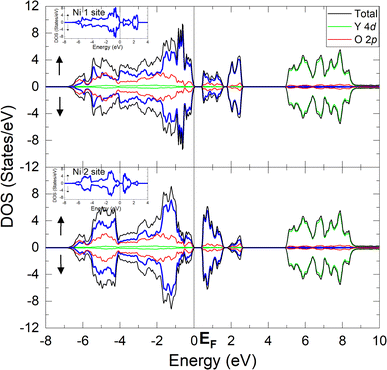
Fig. 2 shows the projected density of states (DOS) of the YNiO₃ compound, separated into the Ni1 (upper panel) and the Ni2 (lower panel) nonequivalent sites.^5,13,14 These results correspond to a stable and fully converged antiferromagnetic insulating (AFM-I) phase. The DOS for each nonequivalent site are split into the majority (above) and minority (below) spin bands. The Fermi level (E_F = 0 eV) separates the occupied states in the valence band and the unoccupied states in the conduction band. The Ni 3d and the O 2p bands present a strong covalent mixing from −7 to +3 eV, whereas the Y 4d bands exhibit a more ionic character from +5 to +9 eV.

Fig. 2 Projected density of states (DOS) of the YNiO₃ compound separated into the Ni1 (upper panel) and the Ni2 (lower panel) nonequivalent sites. The DOS in each panel are split in the majority (above) and minority (below) spin bands. The Fermi level separates the occupied states in the valence band from the unoccupied states in the conduction band.

The Ni 3d bands of the Ni1 and Ni2 nonequivalent sites show clear differences; see the inset in Fig. 2. In particular, the Ni 3d states contribute more to the bonding part of the Ni 3d–O 2p bands, from −7 to −4 eV, in the Ni2 site (lower panel). This means that, as expected, the Ni1 site is slightly more ionic, whereas the Ni2 site is more covalent; see below.

The calculated DOS presented here are in good agreement with previous results in the literature.^8,18,19,27 The calculated band gap between the valence and the conduction band, about 0.5 eV, agrees with the optical band gap measured by Arima and Tokura,²⁸ around 0.3 eV, although the present calculation slightly overestimated the value of the experimental band gap. We note that the value of the band gap found here is similar to those reported in recent studies.^19,20,26

3.2 Magnetic moments and magnetic ordering

The calculated magnetic moments for the Ni ions at the Ni1 sites are about 1.24 μ_B and for those at the Ni2 sites they are around 0.00 μ_B. A comparison with the experimental values obtained by Alonso et al.⁵ using neutron diffraction is shown in Table 3. The results at the Ni1 site, 1.4 (exper.) vs. 1.24 μ_B (theor.), are in reasonable agreement, but the values at the Ni2 site, 0.7 (exper.) vs. 0.00 μ_B (theor.), are in clear disagreement. It is worth noting that recent calculations by other groups also yield a negligible magnetic moment at the Ni2 site.^29,30 Additional work, both theoretical and experimental, would be desirable to reconcile this discrepancy.

Table 3 Comparison between the calculated and experimental values of the magnetic moments in the YNiO₃ compound

Magnetic moments (μB)
Ni sites	Experimental^5	This work
Ni1	1.4	1.24
Ni2	0.7	0.00

---

Fig. 3 compares the antiferromagnetic ordering of the YNiO₃ oxide at room temperature obtained by Alonso et al.⁵ (top) with the result of the present calculation produced with the VESTA program¹⁰ (bottom). The small arrows at the Ni2 sites represent the orientation of the residual 0.0083 μ_B magnetic moments given by the calculation. Despite the discrepancy in the value of the magnetic moment at the Ni2 site, there is an overall good agreement in the relative orientation of these moments. Please note that the use of the 2 × 1 × 2 supercell structure with 80 atoms and the inclusion of the spin–orbit coupling of the Ni 3d orbitals were crucial to reproduce the experimental magnetic ordering.

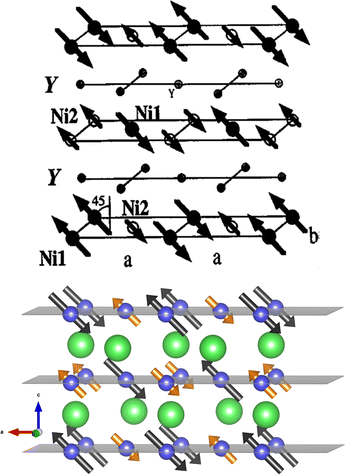Fig. 3 Antiferromagnetic ordering of the YNiO₃ perovskite at room temperature obtained by Alonso et al.⁵ (top) compared to the present calculated result produced with the VESTA program¹⁰ (bottom).

3.3 Optical conductivity

Fig. 4 compares the optical conductivity obtained by Arima and Tokura²⁸ at room temperature and the calculated value of σ(ω) for the YNiO₃ compound. The experimental optical conductivity of the YNiO₃ compound presents a narrow band gap of about 0.3 eV,²⁸ whereas the calculated result yields a slightly larger band gap of around 0.5 eV. Both the experimental and calculated optical conductivity values reflect the insulating character of the YNiO₃ compound at room temperature. Please note the absence of the Drude peak in the spectra, which is a characteristic of a metallic phase. The increase of σ(ω) at higher energies, above 5 eV, is attributed to the onset of interband O 2p to Ni 3d transitions.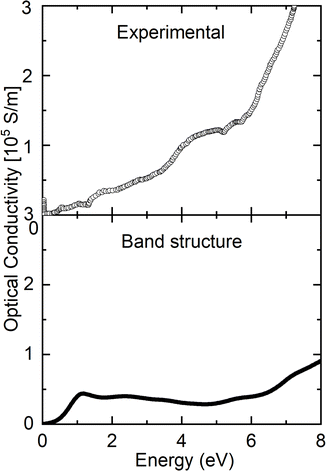

Fig. 4 Experimental optical conductivity extracted from Arima and Tokura (ref. 28) compared to the calculation of the YNiO₃ compound.

3.4 Configuration interaction description

The electronic state of the divalent Ni²⁺ ions in NiO oxide is mainly represented by an ionic 3d⁸ configuration.^31,32 However, the trivalent Ni³⁺ ions in the LaNiO₃ compound are not dominated by the ionic 3d⁷ configuration, but rather by the covalent 3d⁸L̲ configuration, where L̲ corresponds to a ligand (O 2p) hole.^33,34 This means that the third hole does not go to the Ni 3d states, as expected in an ionic approximation, but rather to the O 2p orbitals, which reflects the larger covalent contribution to the bonding in this material. In terms of the highly correlated pd models used to study these materials, this corresponds to the so-called negative charge-transfer regime.³⁵

In the LaNiO₃ compound, the oxygen octahedra are similar and the 3d⁸L̲ configuration is uniformly spread throughout the crystal. In the YNiO₃ oxide, there is a structural distortion in the octahedra, which produces two nonequivalent Ni sites. The ensuing charge disproportionation is the result of a charge redistribution between the Ni^(3−δ)+ site and the Ni^(3+δ)+ site. The charge redistribution does not involve the strongly bound Ni 3d states, but rather the loosely bound hole in the O 2p orbitals. In particular, the Ni1 site (with a larger octahedron and weaker Ni 3d–O 2p interactions) is better described by a 3d⁸ configuration, whereas the Ni2 sites (with a smaller octahedron and stronger Ni 3d–O 2p interactions) is mainly given by a 3d⁸L̲² configuration.^26,36

The DFT band-structure method is an independent particle approach, but it is a first-principles method and takes into account translational invariance. On the other hand, the highly correlated pd models consider many-body effects, but they are based on adjustable parameters and are often applied to small systems. This discussion illustrates that they have complementary advantages and limitations. In the present work, the first method is mostly used because it provides straightforward results that can be compared with the experimental results.

3.5 Structural, charge and spin interactions

The YNiO₃ material presents a clear interaction between the structural, charge and spin degrees of freedom. The structural distortion produces a Ni1 site at the larger octahedra with larger Ni–O bonds, and a Ni2 site at the smaller octahedra with smaller Ni–O bonds. This results in charge disproportionation with a more ionic Ni1 site with a 3d⁸ configuration, and a more covalent Ni2 site with a 3d⁸L̲² configuration. The spin at the Ni1 site, with the 3d⁸ configuration, corresponds to a S = 1 high-spin state, whereas the spin at the Ni2 site, with the 3d⁸L̲² configuration, is given by a S=O low-spin state.^26,36 In turn, this helps to explain the calculated 1.24 μ_B magnetic moment at the Ni1 site, and the 0.00 μ_B magnetic moment at the Ni2 site. For an easier reference, the relationships between the Ni–O bonds, the electronic configuration and the spin state for each nonequivalent site are listed in Table 4.

Table 4 Relationships between the structural (Ni–O bonds), charge (Configuration) and spin (Spin) degrees of freedom for the Ni1 and the Ni2 nonequivalent sites of the YNiO₃ compound

Degrees of freedom
Ni sites	Ni–O bonds	Configuration	Spin
Ni1	Larger	3d^8	S = 1
Ni2	Shorter	3d^8L̲^2	S = 0

---

3.6 Charge disproportionation

Alonso et al.⁵ used the phenomenological Brown bond-valence model to estimate the Ni valence; they obtained two different values of the delta parameter: around δ = 0.38 at the Ni1 site and about δ′ = 0.17 at the Ni2 site. Later on, in the analysis of the different models used to interpret the neutron diffraction results, they concluded that δ = δ′ = 0.35.⁵ The present band-structure calculation gives a smaller estimate of around δ = 0.05. But, as discussed above, a double-cluster method predicts small changes at the Ni sites and larger changes at the ligand (O 2p) band³⁶ (this is reasonable because O 2p–O 2p charge fluctuations cost less energy than Ni 3d–Ni 3d charge variations). Using this method, we estimate that the ligand contribution is about δ = 0.3.³⁶ The combination of δ = 0.05 from the band structure and δ = 0.3 from the double-cluster calculations is similar to the value δ = 0.35 obtained from neutron diffraction data by Alonso et al.⁵

4 Summary and conclusions

In summary, we studied the electronic structure of the YNiO₃ compound using the GGA+U method with U = 1.5 eV. In particular, we investigated the charge disproportionation between the nonequivalent Ni1 and Ni2 sites. The stable phase at room temperature is an antiferromagnetic insulating (AFM-I) state. The density of states (DOS) at the nonequivalent Ni1 and the Ni2 sites present clear differences; in particular, the Ni 3d–O 2p bonds are more ionic at the Ni1 site and more covalent at the Ni2 site. The calculated band-gap energy is in reasonable agreement with the experimental value. The calculated magnetic moment at the Ni1 site is in agreement with the experimental value, but there is a discrepancy in the calculated moment at the Ni2 site. Despite this disagreement, the calculated magnetic ordering agrees with the neutron diffraction results. We note that the use of a 2 × 1 × 2 supercell structure with 80 atoms and the inclusion of the Ni 3d spin–orbit coupling were crucial to obtain the orientation of the magnetic moments. The calculated optical conductivity is in reasonable agreement with the experimental result. The results are also interpreted in terms of the configuration interaction (CI) scheme of highly correlated pd models. Finally, the interactions between the structural, charge and spin degrees of freedom in YNiO₃ are also discussed.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was partially supported by the Brazilian funding agencies Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) and Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES).

References

1. J. B. Torrance, P. Lacorre, A. I. Nazzal, E. J. Ansaldo and C. Niedermayer, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 8209–8212.
2. G. Catalan, Phase Transitions, 2008, 81, 729–749.
3. M. L. Medarde, J. Phys.: Condens. Matter, 1997, 9, 1679–1707.
4. J. L. García-Muñoz, J. Rodriguez-Carvajal, P. Lacorre and J. B. Torrance, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 4414.
5. J. A. Alonso, J. L. García-Muñoz, M. T. Fernández-Díaz, M. A. G. Aranda, M. J. Martínez-Lope and M. T. Casais, Phys. Rev. Lett., 1999, 82, 3871–3874.
6. J.-S. Zhou and J. B. Goodenough, Phys. Rev. Lett., 2005, 94, 065501.
7. T. Arima, Y. Tokura and J. B. Torrance, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 17006–17009.
8. I. I. Mazin, D. I. Khomskii, R. Lengsdorf, J. A. Alonso, W. G. Marshall, R. M. Ibberson, A. Podlesnyak, M. J. Martínez-Lope and M. M. Abd-Elmeguid, Phys. Rev. Lett., 2007, 98, 176406.
9. U. Staub, G. I. Meijer, F. Fauth, R. Allenspach, J. G. Bednorz, J. Karpinski, S. M. Kazakov, L. Paolasini and F. d'Acapito, Phys. Rev. Lett., 2002, 88, 126402.
10. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
11. Y. Bodenthin, U. Staub, C. Piamonteze, M. García-Fernández, M. Martínez-Lope and J. Alonso, J. Phys.: Condens. Matter, 2011, 23, 036002.
12. A. Y. Ramos, C. Piamonteze, H. C. Tolentino, N. M. Souza-Neto, O. Bunau, Y. Joly, S. Grenier, J.-P. Itié, N. E. Massa and J. A. Alonso, et al., Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 045102.
13. J. A. Alonso, M. J. Martinez-Lope, M. T. Casais, M. A. G. Aranda and M. T. Fernandez-Diaz, J. Am. Chem. Soc., 1999, 121, 4754–4762.
14. J. A. Alonso, M. J. Martínez-Lope, M. T. Casais, J. L. García-Muñoz and M. T. Fernández-Díaz, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 1756.
15. M. Causa, R. Sánchez, M. Tovar, J. Alonso and M. Martinez-Lope, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 024429.
16. R. Sánchez, M. Causa, M. Tovar, J. Alonso and M. Martinez-Lope, J. Magn. Magn. Mater., 2004, 272–276, 390–391.
17. X. Xu, X. Meng, C. Wang, F. Wu and G. Chen, J. Phys. Chem. B, 2004, 108, 1165–1167.
18. Y. Quan, V. Pardo and W. E. Pickett, Phys. Rev. Lett., 2012, 109, 216401.
19. S. Yamamoto and T. Fujiwara, J. Phys. Chem. Solids, 2002, 63, 1347–1351.
20. A. Mercy, J. Bieder, J. Íñiguez and P. Ghosez, Nat. Commun., 2017, 8, 1677.
21. T. Mizokawa, D. I. Khomskii and G. A. Sawatzky, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 11263–11266.
22. J. Bieder, A. Mercy, W.-Y. Tong and P. Ghosez, Phys. Rev. B, 2020, 102, 081111.
23. L. Binci, M. Kotiuga, I. Timrov and N. Marzari, Phys. Rev. Res., 2023, 5, 033146.
24. P. Blaha, K. Schwarz, G. Madsen, D. Kvasnicka and J. Luitz, WIEN2k: An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties, Technische Universität Wien, Wien, 2001, vol. 28.
25. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
26. J. Varignon, M. N. Grisolia, J. Íñiguez, A. Barthélémy and M. Bibes, npj Quantum Mater., 2017, 2, 21.
27. A. Hampel and C. Ederer, Phys. Rev. B, 2017, 96, 165130.
28. T. h. Arima and Y. Tokura, J. Phys. Soc. Jpn., 1995, 64, 2488–2501.
29. J. Du, S.-L. Shang, Y. Wang, A. Zhang, S. Xiong, F. Liu and Z.-K. Liu, AIP Adv., 2021, 11, 015028.
30. J. Du, O. Malyi, S.-L. Shang, Y. Wang, X.-G. Zhao, F. Liu, A. Zunger and Z.-K. Liu, Mater. Today Phys., 2022, 27, 100805.
31. G. A. Sawatzky and J. W. Allen, Phys. Rev. Lett., 1984, 53, 2339–2342.
32. A. Fujimori and F. Minami, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 957–971.
33. M. Abbate, G. Zampieri, F. Prado, A. Caneiro, J. M. Gonzalez-Calbet and M. Vallet-Regi, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 155101.
34. E. Alves, H. Martins, S. Domenech and M. Abbate, Phys. Lett. A, 2019, 383, 2952–2956.
35. P. Kuiper, G. Kruizinga, J. Ghijsen, G. A. Sawatzky and H. Verweij, Phys. Rev. Lett., 1989, 62, 221–224.
36. R. J. Green, M. W. Haverkort and G. A. Sawatzky, Phys. Rev. B, 2016, 94, 195127.

---