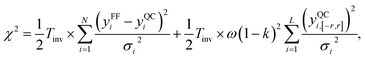Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Getting the intermolecular forces correct: introducing the ASTA strategy for a water model†
Jiří Mareš * and
Pau Mayorga Delgado
* and
Pau Mayorga Delgado
Department of Physics, University of Oulu, Finland. E-mail: jiri.mares@iki.fi
First published on 15th August 2024
Abstract
Having a force field for water providing good bulk properties is paramount for modern studies of most biological systems. Some of the most common three-site force fields are TIP3, SPC/ε or OPC3, providing a decent range of bulk properties. That does not mean though, that they have realistic inter-atomic forces. These force fields have been parameterized with a top-down approach, meaning, by fitting the force field parameters to the experimental bulk properties. This approach has been the governing strategy also for many variants of four- and more-site models. We test a bottom-up approach, in which the force field is parameterized by optimizing the non-bonded inter-atomic forces. Our philosophy is that correct inter-atomic forces lead to correct geometrical and dynamical properties. The first system we try to optimize with the accurately system tailored atomic (ASTA) approach is water, but we aim to eventually probe other systems in the future as well. We applied our ASTA strategy to find a good set of parameters providing accurate bulk properties for the simple three-site force field forms, and also for AMOEBA, a more detailed and polarizable force field. Even though our bottom-up approach did not provide satisfactory results for the simple three-site force fields (with fixed charges), for the case of the AMOEBA force field it led to a modification of the original strategy, giving very good intra- and inter-molecular forces, as compared to accurate quantum chemically calculated reference forces. At the same time, important bulk properties, in this study restricted to the density and diffusion, were accurately reproduced with respect to the experimental values.
1 Introduction
There are different background ideas and strategies behind the current biomolecular force fields. These can be illustrated on several examples. For instance, OPLSA aims at optimized parameters for liquid state simulations.1–3 GROMOS is famous in its importance for thermodynamics.4–10 Amber, with its several flavors, is known for its importance in the partial charges.11–15 CHARMM is widely used for biological systems such as proteins or bilayers.16–19Besides these simple force fields, there are more physically detailed ones. For example, the fix-charges approximation has been extended with the drude-polarization force fields.20–22 On the other hand, the AMOEBA force field includes not only the polarizability, but also an important fine-graining of the charge interactions, expanding the charge density into atom-centered multipoles, up to quadrupole.23
In many applications, an exclusive attention has been given to water, forming possibly the most common solvent. At the same time, when developing a new form of force field, establishing the water model is usually the first step, as without that, its applicability would be very limited. On the other hand, when developing force fields with a known form but focused specifically on certain application or approach for parameterization, it is often decided which water model would be the most compatible. For example, GROMOS8 uses SPC,24 the MADRID 2019 force field uses the TIP42005,25 the CHARMM 2019 polarizable force field22 used mainly the SWM4NDP as a water model,26,27 and AMOEBA force field28 has developed its own AMOEBA water model.23
As compared to parameters of other atoms and molecules, water molecules are evaluated from many perspectives. These are both bulk, such as density including its temperature maximum or diffusion constant, as well as microscopic properties, such as rotational diffusion, correlation time, radial distribution functions or electric dipole. Many of these properties are determined not only by the molecular model, but also by the simulation protocol and its approximations in commonly used periodic boundary conditions with Ewald summation for long-range charge interactions, and dielectric constant of unity. In order to approximately fulfill at least some of these properties, many different models are commonly introduced. Some of the common ones include artificial (dummy) interaction centers, starting from the various flavors of the TIP4 (ref. 25 and 29–31) model. This many-perspective evaluation makes the water model development special and more demanding, as compared to solute molecules.
In the accurately system tailored atomic (ASTA) approach, we concentrate on obtaining the inter-atomic forces, which belong to the standard ingredients in any force field development.31 In our approach, the system to calculate and optimize forces is closely related to the one for which the force field would be used. In the case of water, we do not start with isolated molecules or gas phase, but rather, with a bigger system containing many water molecules, approximating the condensed phase.
We will see how accurately can variations of the water models probed in this study reproduce the inter-atomic forces, and how the inaccuracies, together with other approximations of the overall simulation protocol, determine the water bulk properties.
This manuscript starts with a detailed explanation of the strategy used for parameterization of the non-bonded forces. Then, we show its performance for the case of simple force fields, by optimizing them against the forces on atomic resolution, followed by coarse-graining through intermediate to a molecular resolution. After that, the finer-grained AMOEBA force field water model is revisited. The modification of the ASTA approach is introduced and assessed both for the simple force field and for the more detailed AMOEBA force field.
2 Methods
2.1 Parameterization strategy of the force field
Subsequently, in order to avoid high-energy contacts, every selected configuration was preoptimized using extended tight binding XTB33 on a “Geometry, Frequency, Noncovalent, eXtended TB” (GFN2-xTB) level, with a maximum of 60 optimization steps. This yielded four reference configurations, i.e., four snapshots, which all together contained enough good sampled parameters. Thus, this corresponded to (60 waters) × (4 reference configurations) × (3 atoms per molecule) × (3 coordinates) = 2160 Cartesian force components. In order to calculate the force differences corresponding only to the non-bonded interactions, a second set of configurations was created by randomly moving the water molecules, as rigid bodies, by 0.025 Å, as shown in the Fig. 1.
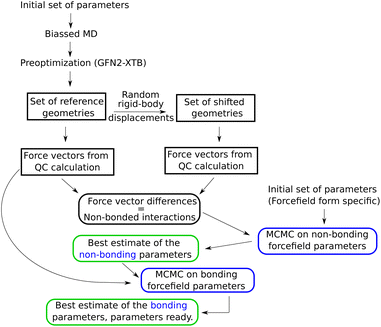 | ||
| Fig. 1 Optimization flow chart for a simple, non-polarizable force field. For description of the steps in this chart, see text of Section 2.1. | ||
The atomic-force components were computed as negative energy gradients in ORCA 5.0.4, using the ωB97X34 density functional theory (DFT) functional with D4 dispersion correction35,36 and the def2-QZVPP37 with Coulomb fitting basis.38 The “VeryTightSCF” and “DEFGRID3” options were set for the ORCA calculations. The largest force component difference was 3.09 kcal mol−1 Å−1.
For comparison, the same set of configurations was also calculated using the double hybrid DSD-PBEP86 functional,39 with D3-BJ40,41 dispersion correction. A correlation between both QC methods is shown in the ESI (Fig. 1).†
Two independent strategies were used to optimize the parameters of the AMOEBA force field. On one hand we followed the ASTA algorithm showed in Fig. 1. On the other hand we used a more practical approach by modifying the ASTA strategy. The AMOEBA parameters obtained from this last method were further assessed by using a cubic box with 216 water molecules, supplied with the Tinker package42 as watersmall.xyz. This coordinate file in Tinker format has a cubic box for periodic boundary simulations, with a size of 18.643 Å, corresponding to experimental water density, and water molecules from a snapshot of a MD simulation using the AMOEBA force field with the original water parameters. Here the forces were also computed on the ωB97X/def2-QZVPP level.
For the case of simple force fields, the algorithm shown in Fig. 1 was used to obtain the best parameters, where all the forces for the Monte Carlo simulations were calculated using a Python code written by the author. On the other hand, the forces required to optimize the AMOEBA water parameters were obtained using OpenMM46 version 8.0, and verified by the testgrad utility from the Tinker distribution.42
From now on and unless explicitly pointed out, when referring to the optimized or the best parameters, we refer to the best estimates obtained from the MCMC simulation.
2.2 Forms for van der Waals interactions
This study is focused on non-bonding, inter-molecular forces. The bonding interactions were fitted in order to complete the models, but without any modifications of the original form of the bond and angle harmonic potentials.For the non-bonding interactions, we tested several widely-implemented forms of the van der Waals potential energy functions, as seen in eqn (1) for the classical 12-6 LJ potential, and in eqn (2) and (3) for softer repulsion forms of the LJ. In addition, alternative potentials were probed, such as the Buckingham (eqn (4)) and the Morse (eqn (5)) potentials. For the case of the AMOEBA water potential,23 there were no modifications for neither non-bonding nor bonding forms.
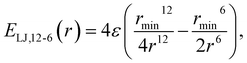 | (1) |
On the other hand, we set up the explicit atom-type pairs (vdWpr in the Tinker42 nomenclature). This gave us three pairs of LJ parameters (εHH, εHO, εOO, rHHmin, rHOmin, rOOmin), summing up to seven fitting parameters with the oxygen charge.
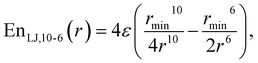 | (2) |
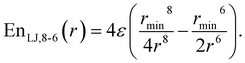 | (3) |
Additionally, we tested Buckingham potential52
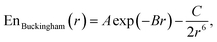 | (4) |
| EnMorse(r) = D(1 − exp(−A(r − Re)))2. | (5) |
2.3 Atomic, molecular and intermediate resolution of forces
Initially, the whole set of 2160 Cartesian force component differences for the non-bonded interactions, mentioned in Section 2.1.1, were used to fit the van der Waals potentials (eqn (1)–(5)) for each water atom separately together with the partial charge of the oxygen atom. This is illustrated in Fig. 2a. This approach is, perhaps, the most natural, and we have called it “atomic resolution”.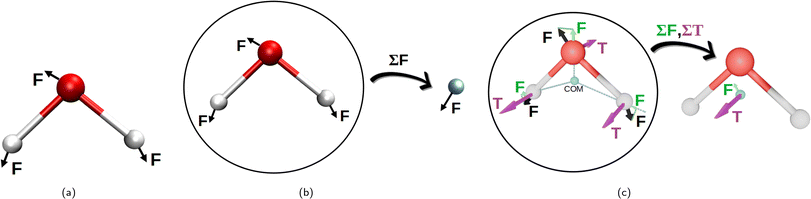 | ||
| Fig. 2 Visualization of the three resolutions used to compute the forces for the non-bonding interaction fits to the eqn (1)–(5). Panel (a) depicts the “atomic resolution”, where force vectors are separate for each atom, panel (b) the molecular resolution where the force vectors are summed over the whole water molecule and panel (c) shows the intermediate resolution, where the forces are decomposed into their projections through center of mass and torques acting on the center of mass, summing up to two resulting vectors per water molecule. This decomposition is depicted in green for the force projections, and in purple are the torques (T). (a) Atomic resolution. (b) Molecular resolution. (c) Intermediate resolution. | ||
After that, we summed up the vector forces from each atom over each molecule, and fitted the resulting vectors as done previously. This is inspired by the fact that many water models have only one vdW center at the oxygen site and thus, the forces on the hydrogen sites are only electrostatic, which somewhat underrates their importance. We end up with 2160/3 = 740 force component differences to fit, for a loss in the atomic details. This is depicted in Fig. 2b and called “molecular resolution”.
Alternatively, we also approached the fitting forces by computing a translational vector acting on the center of mass (COM) of the water molecule on one hand, and a rotational vector in a form of torque around an axis going through the COM on the other. The first was obtained by projecting the force vector along the vector going from the center of the atoms through the COM and summing them all up at the COM. For the latter, we summed up the torque affecting each atom, to the COM. This is illustrated in Fig. 2c and called “intermediate resolution”. This approach should preserve the forces responsible for translational and rotational diffusion, while hiding possibly less relevant details of the individual atomic components. Here we have a total of 1440 force component differences to fit.
2.4 Bonding parameters
This manuscript is focused mainly on the non-bonded parameters for the van der Waals and electrostatic interactions. Despite of that, in order to obtain complete model for the MD simulation, we also fit the bonded parameters. For that, instead of using the force difference vectors, as for the case of non-bonded interactions, here the atomic force vectors were compared against the full-force ones, which were computed using QC, as described in the Subsection 2.1.1. Thus, the forces from the original set of reference geometries (see Fig. 1) were used. The fits for the bonded parameters were done by keeping the fitted non-bonding parameters as constants, with only the bonding parameters as fitting variables.2.5 Calculation of errors
The MCMC algorithm results in a posterior distribution, force field parameters in our case, based in a prior reference data, i.e., force differences in this study, and their error estimates in a given (inverse) temperature. The error is computed using the common expression for χ2,
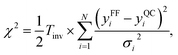 | (6) |
2.6 Molecular dynamics and water properties
The fitted water models were tested to simulate the water dynamics, in order to obtain some bulk parameters to compare with both, experiments and other known models. Initially, 2000 water molecules were assembled in a 4 nm side cubic box with Packmol56 version 20.3.5. After that, in order to avoid molecular overlapping and other nonphysical geometrical distributions, a minimization with the steepest descend algorithm was performed with GROMACS57 2022.4. The energy tolerance for minimization was 1000 kJ mol−1 nm−1 with a maximum step-size of 0.01 nm. The long range electrostatics were handled with PME58 with a Coulomb and van der Waals cutoff radius of 1.3 nm, and the Verlet cutoff-scheme.59Once the water system reached a minimum energy, the system was equilibrated for 10 ns with a 0.5 fs step as a NPT ensemble at 298.15 K and 1 bar with the Berendsen thermostat and barostat.60 The long equilibration is to ensure a proper resizing of the simulation box, which will depend on the water model tested.
The production stage was set up for a NPT ensemble with the v-rescale61 and c-rescale62 algorithms for the thermostat and barostat respectively. The MD was performed obtaining a 20 ns trajectory, with 0.5 fs time step. For both, equilibration and production, the LINCS constrain algorithm63 for bonds, including the H-atom, was used. Also, the leap-frog algorithm64 implemented in GROMACS was used to update the atomic positions and velocities. Periodic boundary conditions for a cubic box were used throughout the simulations.
The MD simulations performed about 100 ns per day with 128 CPUs. The CPUs are based on AMD Zen 2 architecture, supporting the AVX2 vector instruction set, and running at 2.6 GHz base frequency. On the other hand, the AMOEBA23 forms of the water model were simulated with OpenMM.46
The water bulk density was obtained for a given box volume with the GROMACS command gmx energy. The water translational diffusion was computed by fitting a straight line starting at 10% until 90% of the mean square displacement, taking into account the Stokes–Einstein relation.65 This is implemented in GROMACS and available through the command gmx msd.
The simulation with AMOEBA force field, we used a preequilibrated box from the Tinker distribution (watersmall.xyz with 216 molecules) which we assembled into a 3 × 3 × 3 cube with 5832 water molecules and with a size of ≈5.6 nm. We used the OpenCL platform of OpenMM with double precision, NPT ensemble with the Nose Hoover thermostat at 300 K, Monte Carlo barostat at 1 Bar, integration time step of 1.0 fs, periodic conditions, non-bonded cutoff at 1.2 nm, and PME for the long-range electrostatics. The diffusion coefficient was calculated using MDanalysis.66,67 Trajectories of 1.25 ns have been simulated, out of which last 0.25 ns has been used to obtain the density, and diffusion coefficient.
3 Results and discussion
Most of this work is aimed at the non-polarizable water models, in which different forms of van der Waals are tested, i.e., eqn (1)–(5). Here we use all the parameters for the three considered cases, as mentioned in Subsection 2.3, with the goal of finding a water model, with improved non-bonding inter-molecular forces with respect to the available three-center models, and at the same time, achieving good bulk properties.In addition, we also attempt to optimize the AMOEBA water model with the same level of theory and basis set as described in Section 2.1.1, succeeding in improving the inter- and intra-molecular forces while keeping the experimental density and diffusion coefficients.
3.1 Atomic resolution
In a search for a most suitable three-site model, we allowed for the vdW to be nonzero on both atom types, i.e., H and O, such as in the case of TIP3 CHARMM17 model. In addition, we also probed models where explicit pair-wise vdW parameters (vdWpr) were set between each atom types, instead of relying on standard combination rules, as mentioned in Subsection 2.2.1.
The modified Lennard-Jones with softer repulsive part, i.e., the LJvdW,10-6 and LJvdW,8-6 (eqn (2) and (3) respectively) were also probed, as well as the corresponding ones with vdWpr, i.e., LJvdWpr,10-6 and LJvdWpr,8-6. Moreover, less-commonly used potentials, such as the Buckingham and Morse (eqn (4) and (5) respectively) were tested with the vdWpr parameters.
In Table 1 we have summarized the statistical measures for all these potentials with the obtained best parameter estimates. The optimized parameters are found ESI, Table 1.† Fig. 3a shows a correlation plot for the fitted LJvdW,12-6 forces compared with the forces computed with a DFT method. In order to emphasize the deviation of the small-force components of this model from the QC, a slope has been explicitly drawn in the central region (see the corresponding k in Table 1). This deviation is interpreted as having oversensitive forces to the change of interatomic distances. There is a slight but clear improvement of this deviation when using explicit pairwise parameters LJvdWpr,12-6 with further improvements when using softer repulsion forms of LJvdWpr,10-6 and LJvdWpr,8-6. On the other hand, the Buckingham and Morse potentials have a worse performance, as seen in the slope and the statistical measures from Table 1.
| vdW form | MSDa | MADb | SDc | AMAXd | ke | pf |
|---|---|---|---|---|---|---|
| a Mean signed deviation.b Mean absolute deviation.c Standard deviation.d Absolute maximum deviation.e Slope of the correlation for the range of −0.8 to 0.8 kcal mol−1 Å−1.f Pearson correlation coefficient. | ||||||
| LJvdW,12-6 | 0.0 | 0.11 | 0.16 | 0.75 | 0.688 | 0.922 |
| LJvdWpr,12-6 | 0.0 | 0.11 | 0.15 | 0.72 | 0.718 | 0.927 |
| LJvdWpr,10-6 | 0.0 | 0.10 | 0.15 | 0.73 | 0.743 | 0.932 |
| LJvdWpr,8-6 | 0.0 | 0.10 | 0.14 | 0.73 | 0.762 | 0.935 |
| BuckinghamvdWpr | 0.0 | 0.12 | 0.17 | 0.76 | 0.622 | 0.905 |
| MorsevdWpr | 0.0 | 0.14 | 0.20 | 1.69 | 0.575 | 0.863 |
Based on the deviation of the small forces, i.e., slope (k) from Table 1, none of the probed potential forms is able to provide satisfactory results for the atom-wise force model (Fig. 2a). This is somewhat surprising, since these cover some commonly used three-point water models. On the other hand, models with an interaction (charged) center out of the physical atomic centers are also very widely used. This suggests that for the force field variants present in this study, it may be appropriate to compare only the sum of atomic forces, instead of including each force per atom individually. Thus, we would be effectively lowering the resolution from “atomic” to “molecular” (see Fig. 2b). We try this approach in Subsection 3.2.
| vdW form | MSD | MAD | SD | AMAX | p |
|---|---|---|---|---|---|
| LJvdW,12-6 | 0.0 | 2.018 | 2.6 | 15.3 | 0.908 |
| LJvdWpr,12-6 | 0.0 | 2.018 | 2.6 | 14.7 | 0.908 |
3.2 The molecular resolution
Being aware of this simplification, i.e., the molecular resolution, in Table 3 we show the statistical information for each of the considered potentials for the non-bonded interactions. The parameters for all the potentials are found in the ESI, Table 3.† The correlation plot for the common LJvdW,12-6 case is shown in Fig. 3b.
| vdW form | MSD | MAD | SD | AMAX | k | p |
|---|---|---|---|---|---|---|
| LJvdW,12-6 | 0.00 | 0.12 | 0.16 | 0.64 | 0.897 | 0.974 |
| LJvdW,10-6 | 0.00 | 0.11 | 0.14 | 0.59 | 0.918 | 0.978 |
| LJvdW,8-6 | 0.00 | 0.097 | 0.13 | 0.53 | 0.930 | 0.982 |
| LJvdWpr,12-6 | 0.00 | 0.11 | 0.15 | 0.56 | 0.885 | 0.976 |
| LJvdWpr,10-6 | 0.00 | 0.10 | 0.14 | 0.52 | 0.926 | 0.979 |
| LJvdWpr,8-6 | 0.00 | 0.096 | 0.13 | 0.56 | 0.938 | 0.982 |
| MorsevdWpr | 0.00 | 0.18 | 0.24 | 0.93 | 0.737 | 0.936 |
We see an overall improvement of the statistics in Table 3 compared with the atomic resolution in Table 1. The trend for the slope of the softer repulsion in 10-6 and 8-6 potentials is similar to the observed for the atomic resolution. Also, it seems that the differences between the explicit pairwise vdWpr interactions and their vdW counterpart are rather negligible. On the other hand, the Morse potential seems to have an inferior performance as compared to the variants of the LJ potential, similarly as observed for the atomic resolution in Table 1.
It is worth mentioning that the vdWpr variants of the LJ potentials seem to have about three orders of magnitude higher energy minimum of the O–H group (εOH) than the εO for the case of the vdW (Table 3 in ESI†). This means that in the case of vdWpr, the LJ potential has also a significant contribution to the attraction interaction, whereas commonly, its contribution is negligible compared with the electrostatic forces.
| vdW form | MSD | MAD | SD | AMAX | p |
|---|---|---|---|---|---|
| LJvdW,12-6 | 0.0 | 2.320 | 3.03 | 17.2 | 0.878 |
| LJvdWpr,12-6 | 0.0 | 2.26 | 2.94 | 16.6 | 0.888 |
As a note for consideration, even though the non-bonded parameters were obtained on the “molecular resolution”, the atom-specific parameters were used to fit the bonding ones. As a result of that, the coarse graining, i.e., the loss of detail, of the non-bonded parameters is transferred into hard-to-predict inaccuracies of the bonded parameters.
3.3 Intermediate resolution: linear and tangential forces on the COM
This is an additional alternative to probe the non-bonding parameters for the three-site water models, i.e., it provides more detail than the molecular resolution but it is more coarse-grained than the atomic resolution. The forces responsible for molecular translation and rotation are separated as explained in Section 2.3 and visualized in Fig. 2c.The parameterization for this resolution is done only for the non-bonding parameters and just for the LJvdW,12-6 and LJvdWpr,12-6 potentials. In Table 5 are shown the statistics while the best adjustable parameters are found in Table 5 in the ESI.† Fig. 3c shows the correlation plot for this level of resolution for the LJvdW,12-6 potential.
| vdW form | MSD | MAD | SD | AMAX | k | p |
|---|---|---|---|---|---|---|
| LJvdW,12-6 | 0.0 | 0.11 | 0.15 | 0.76 | 0.722 | 0.909 |
| LJvdWpr,12-6 | 0.0 | 0.11 | 0.15 | 0.77 | 0.744 | 0.916 |
Comparing Tables 1, 3 and 5 it can be concluded that the inappropriateness of the three-site force field models gets again more pronounced as we get to the finer-grained model.
3.4 Beyond the well-justified solutions
The same can be achieved more intuitively by requiring the slope of the small-force-difference correlation closer to one. This allows us to get values closer to the QC for that region, while sacrificing the accuracy in the regions of larger force differences. Therefore, we modified the eqn (6) by adding an extra term to the χ2 expression, as
Here we would expect a monotonic convergence of the force field parameters with respect to the weight ω. The same idea is applicable for any chosen resolution. We probed both potentials, LJvdW,12-6 and LJvdWpr,12-6, for the atomic resolution and the intermediate resolution, with their respective statistics in Tables 6 and 7 correspondingly. The resulting non-bonded parameters for different weights is shown in the ESI, Table 6.†
| vdW form | MSD | MAD | SD | AMAX | k | p |
|---|---|---|---|---|---|---|
| LJvdW,12-6,ω=1 | 0.0 | 0.11 | 0.15 | 0.73 | 0.748 | 0.921 |
| LJvdW,12-6,ω=10 | 0.0 | 0.13 | 0.18 | 1.08 | 0.903 | 0.909 |
| LJvdW,12-6,ω=100 | 0.0 | 0.14 | 0.21 | 1.34 | 0.984 | 0.899 |
| LJvdWpr,12-6,ω=1 | 0.0 | 0.11 | 0.15 | 1.78 | 0.772 | 0.926 |
| LJvdWp,12-6,ω=10 | 0.0 | 0.12 | 0.17 | 1.12 | 0.922 | 0.916 |
| LJvdWpr,12-6,ω=100 | 0.0 | 0.13 | 0.19 | 1.31 | 0.991 | 0.909 |
| vdW form | MSD | MAD | SD | AMAX | k | p |
|---|---|---|---|---|---|---|
| LJvdW,12-6,ω=1 | 0.0015 | 0.11 | 0.16 | 0.79 | 0.775 | 0.909 |
| LJvdW,12-6,ω=10 | 0.0022 | 0.12 | 0.18 | 0.94 | 0.921 | 0.902 |
| LJvdW,12-6,ω=100 | 0.0026 | 0.13 | 0.20 | 1.08 | 0.997 | 0.898 |
| LJvdWpr,12-6,ω=1 | 0.0008 | 0.10 | 0.15 | 0.81 | 0.798 | 0.916 |
| LJvdWpr,12-6,ω=10 | 0.0012 | 0.11 | 0.17 | 1.07 | 0.930 | 0.910 |
| LJvdWpr,12-6,ω=100 | 0.0014 | 0.12 | 0.19 | 1.23 | 0.998 | 0.906 |
The parameterization is largely affected by this procedure. For example, for the atomic resolution of the LJvdW,12-6 potential, the partial charges of the oxygen atom are −0.80, −0.95 and −1.01 for ω = 1, 10 and 100 respectively. For the intermediate resolution, they are −0.80, −0.92 and −0.98 for the same respective weights. Thus, the absolute value of the oxygen partial charges grows steadily as the weight increases, and it is more pronounced for the forces at higher resolution. As the partial charges spans a region of values common for the three-site water models, there should be an optimal weight leading to good water parameters. As such a weight is unknown, we would require additional data or prior knowledge, none of which would be compatible with the aim of this study, since we want to obtain good bulk properties from the correct forces. In other words, the combination of unjustified weight on the central region with experimental bulk properties was not pursued here.
In this subsection we modified, on one hand, the Coulomb force, by introducing a global adjustable factor cf, such that (leaving out the constants) the force changes from 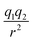 to
to 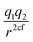 . On the other hand, we also included the LJ repulsion power as an adjustable parameter N. First, we fitted the coefficient cf of the attractive potential with the basic LJvdW,12-6, obtaining the best fit with cf = 0.58. Then, we fitted cf together with the power N from the LJ, i.e., having the form LJvdW,N-6. This last procedure gave us an optimal fit with cf = 0.7 and N = 9.65. The statistics for such a fit for the atomic resolution are shown in Table 8 and their corresponding non-bonded parameters in the ESI, Table 10.†
. On the other hand, we also included the LJ repulsion power as an adjustable parameter N. First, we fitted the coefficient cf of the attractive potential with the basic LJvdW,12-6, obtaining the best fit with cf = 0.58. Then, we fitted cf together with the power N from the LJ, i.e., having the form LJvdW,N-6. This last procedure gave us an optimal fit with cf = 0.7 and N = 9.65. The statistics for such a fit for the atomic resolution are shown in Table 8 and their corresponding non-bonded parameters in the ESI, Table 10.†
| vdW form | MSD | MAD | SD | AMAX | k | p |
|---|---|---|---|---|---|---|
| LJvdWpr,cf | 0.0 | 0.10 | 0.14 | 0.73 | 0.748 | 0.933 |
| LJvdWpr,N-6,cf | 0.0 | 0.10 | 0.14 | 0.71 | 0.773 | 0.935 |
Comparing the results presented in Table 8 with the results of the unmodified potential in Table 1, we concluded that the improvement is not significant for such a dramatic change of the force field form. Therefore, we did not follow this path further.
3.5 Monte Carlo insight: distribution of parameters
Within the error estimate that we assigned to the primary data, i.e., the force-component differences, it is instructive to see distributions of the force field parameters of the model in question. The range and possible asymmetry of the distribution of each parameter is interesting, along with the pooling behavior that they seem to have, as seen in Fig. 4 for the LJvdW,12-6 potential in the atomic resolution.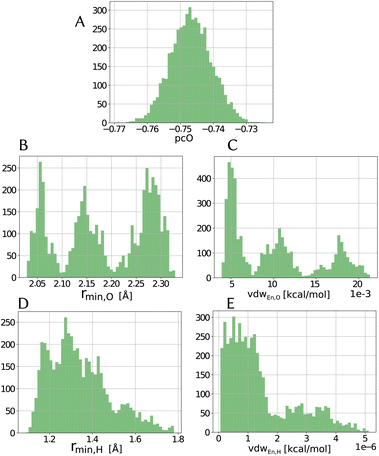 | ||
| Fig. 4 Distribution of parameters for the LJvdW,12-6 potential for the atomic resolution from the MCMC simulation. | ||
Especially for the case of pooling parameters, it is even more interesting to see how do they look in the multidimensional parameters space, i.e., how are the parameters correlated, as illustrated in Fig. 5.
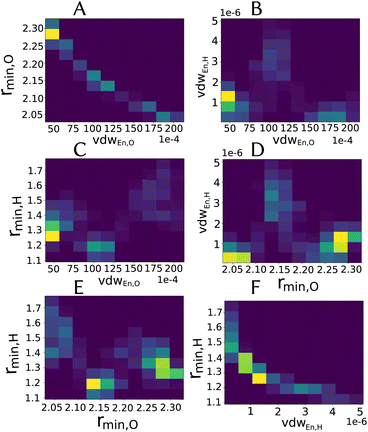 | ||
| Fig. 5 Two-dimensional histograms for the combination between different parameters (excluding partial charge) for the LJvdW,12-6 potential for the atomic resolution model from the MCMC simulation. | ||
As we see in Fig. 4A, the distribution of the oxygen partial charge can be well approximated by a normal distribution. On the other hand, its van der Waals parameters seem to form three distinct pools (panels B amd C). By plotting together the oxygen van der Waals parameters in a 2D histogram, we can see in panel A of Fig. 5 that they anti-correlate, which is not surprising, since both parameters compensate each other in the LJ potential (see eqn (1)). Despite of that, further investigation would be required to explain the formation of these three pools.
In a similar manner, the distribution of the vdW parameters of the hydrogen (Fig. 4D and E) is more uniform compared with the oxygen parameters, i.e., less defined pools. Still, the same expected anti-correlation behavior is seen in Fig. 5F.
It is known71 that in order to achieve a correct density and diffusion water properties, the parameter ranges of the water models needs to fulfill rmin,O < 2.0 Å and |pcO| > 0.8 respectively. Using the unbiased prior distribution of force differences, we obtained that except for the molecular resolution, for the other two cases all the potentials gave |pcO| < 0.8, and for all the cases rmin,O > 2.0 Å (Tables shown in the ESI†). It is then clear, that the right parameter space is never sampled in order to obtain good parameters of the water model and thus, we do not investigate it further.
3.6 Bulk properties
The water density and self-diffusion parameters belong to the basic bulk properties, which the commonly used models usually fulfill rather well. For a comprehensive report, we refer the reader to ref. 72. Briefly, the experimental density at 300 K is 997 kg m−3, whereas for different models it ranges from 972 kg m−3 for the SPC model, up to 1027 kg m−3 for TIP3P/Fw. The experimental self-diffusion coefficient is 2.3 × 10−5 cm2 s−1, whereas it ranges from 1.21 × 10−5 cm2 s−1 for TIP4P/Ice to 7.7 × 10−5 cm2 s−1 for the PCFF. The TIP3P is a widely used model with D = 5.72 × 10−5 cm2 s−1, i.e., roughly 2.5 times the experimental values.From the Table 9, we conclude that these basic properties of our parameterized models are very unsatisfactory. There is not a single set of parameters giving at the same time better results than the worse of the currently used models. For comparison, we present also a GAFF water model, obtained by standard Antechamber parameterization,31 which is far from perfect with respect to the experimental density and diffusion coefficient, but still remarkably good taking into account its simplicity as compared to the procedure of this study.
| ρ [kg m−3] | Da [cm2 s−1] × 105 | |
|---|---|---|
| a Uncorrected values from periodic cubic box simulation of 2000 water molecules. | ||
| LJARvdW,12-6 | 627.8 | 20.04 |
| LJMRvdW,12-6 | 777.3 | 5.41 |
| LJMRvdWpr,12-6 | 880.71 | 5.72 |
| LJARvdW,12-6,w=10 | 913.86 | 0.47 |
| LJARvdW,12-6,w=100 | 965.31 | 0.02 |
| LJARvdWpr,12-6,w=10 | 812.4 | 2.76 |
| LJARvdWpr,12-6,w=100 | 865.73 | 0.64 |
| LJIRvdW,12-6,w=10 | 837.8 | 1.60 |
| LJIRvdW,12-6,w=100 | 880.57 | 0.26 |
| LJIRvdWpr,12-6,w=10 | 709.5 | 6.58 |
| LJIRvdWpr,12-6,w=100 | 773.4 | 2.75 |
| GAFF | 1045.6 | 6.17 |
| Experimental | 997 | 2.3 |
3.7 Comparison of nonbonding forces for common water models
In Table 10 it is shown a comparison between the non-bonding forces for common three-site water models with the QC references used throughout this study. From this table, it is concluded that all the models are reasonably good, similar in many statistical measures. Mostly the MAD and SD from Table 10 are similar to the worst model (in terms of forces) we tried in Table 1, i.e., the Morse vdWpr potential. At the same time, the correlation slope for the models in Table 10 are closer to 1.0 compared with the results in Table 1. In ESI, Fig. 3† are shown the correlation plots of these common water models with respect to our QC.| Water model | MSD | MAD | SD | AMAX | k | p |
|---|---|---|---|---|---|---|
| TIP3 orig | 0.000 | 0.14 | 0.20 | 1.3 | 0.837 | 0.888 |
| TIP3 EW | 0.000 | 0.14 | 0.21 | 1.3 | 0.737 | 0.856 |
| TIP3 CHARMM | 0.000 | 0.13 | 0.19 | 1.2 | 0.853 | 0.913 |
| SPC | 0.000 | 0.14 | 0.21 | 1.56 | 0.865 | 0.897 |
| SPC/ε | 0.000 | 0.14 | 0.22 | 1.55 | 0.889 | 0.892 |
| OPC3 | 0.000 | 0.16 | 0.25 | 1.95 | 0.979 | 0.890 |
| AMOEBA | 0.000 | 0.13 | 0.24 | 2.9 | 0.805 | 0.825 |
The OPC3 water model stands out among the other ones, since its slope for small-force differences is very close to one. Besides that, all the other statistical measures are worst compared with the other models. This is a rather interesting combination, since the density of the OPC3 model is 991 kg m−3 and its diffusion is D = 2.28 × 10−5 cm2 s−1, i.e. the closest to the experimental values from the known three-site models. Based on that, we could assume that for a simple water model, it is important to catch the correct trend at the small-force differences, rather than having the best statistics over the slightly larger range of force differences.
From the three-center water models, the OPC3 has also the largest partial charges (−0.89517 on oxygen atom), which is however, only negligibly larger than SPC/ε,73 with −0.89000. The sensitivity of bulk properties on the parameters can be sensed from the fact that the SPC/ε has D = 1.55 × 10−5 cm2 s−1.
Another surprising model is the AMOEBA water, which overall does not provide more accurate forces than the simple water models. We return to it in Subsection 3.9.
3.8 Intermediate evaluation
With the first results in Section 3.1, we have seen that none of the probed force field parameter sets could capture the dependence of the forces, as a function of atomic coordinates of the reference data with a satisfactory accuracy (see eqn (1) and Fig. 3). This is somewhat surprising, since the form of the probed force field covers the commonly (three-site) used ones. Also, the reference data should be rather realistic, since a sample of sixty water molecules should be already giving inter-atomic forces near to the bulk conditions. In addition, the force differences are small, posing no high demands on the models.Therefore, it is alarming that the probed models have difficulty to fit the data and, consequently, it would be rather fortuitous to obtain good bulk properties using the parameterization of these models against the atomic forces. In fact, we have already seen in Subsection 3.5 that the posterior distribution of force field parameters does seem to be compatible with good basic bulk water properties. Actually, after checking all the MCMC simulations for the simple (fixed charges) vdW water models probed, there was not a good set of parameters to be found, i.e., fitting the forces from our starting geometries does not result in a model possessing good bulk properties. Knowing that, we do not continue the search for a good possible simple water model. Thus, a parameterized model, like OPC3, from the atomic forces and with as good resulting bulk properties, is not reached in this study. In particular, for the prior force differences obtained from four 60-water molecules snapshots, the smallest χ2 obtained from MCMC simulations for the LJvdW,12-6 model (with 5 parameters to optimize) is 2600, and for the OPC3 (with only 3), it is 6500. The OPC3 parameters would be sampled only in Tinv ∼ 10−3. Brief explanation is given in ESI, Fig. 5.†
Instead, we briefly move our attention towards polarizable water models, which should offer more transferable accuracy for the non-bonded interactions, specially when dealing with charges. It would be natural to start with simpler polarizable force fields, such as the Drude-oscillator forms,26,27,70,74,75 which contain also parameterization for the ions.76 As tempting as these models would be, their non-atomic interaction centers prevents them from a one-to-one correspondence at the level of atomic forces. Therefore, we proceeded by probing the AMOEBA water model.23 This model has already excellent bulk properties,77 despite its mediocre performance for the inter-atomic forces compared with the simple water models (Table 10). Thus, we proceeded by testing what would be the possibilities when optimizing the AMOEBA water model against the atomic forces.
3.9 Optimizing the AMOEBA water model
The AMOEBA non-bonding interactions included less common buffered 14-7 potential for the van der Waals interactions, and charge–multipole interaction, up to quadrupole and an isotropic polarizability on every atom. This gives a force field with a physically relevant and flexible form.We have followed two independent approaches for the optimization of this polarizable force field (using the same set of reference geometries and forces as for the simple models). In our first approach, we used the same ASTA strategy as the one used for the simple water models, i.e., we aimed at reproducing the force-component differences with the same conditions and without restricting the fitting parameters with any prior knowledge. Based on the difficulties encountered with this strategy for the simple force field forms, we called the optimized force field resulting from this first approach as AMOEBA-ASTA-TEST. In this case, the number of parameters to optimize is far larger, as well as its computational demands. Therefore, the results of this model come from a far less exhaustive sampling of the parameters, as compared to the simple force field models. Thus, a possible consequence of this is that the sampled parameters could be further away from a possible global minimum.
The AMOEBA-ASTA-TEST force field overestimates the density and underestimates by more than four times the experimental diffusion, as seen in Table 12. Thus, the first approach with unrestricted fitting parameters seems unsuccessful. On the other hand, the statistical measures for the correlation of the force components with the reference DFT set (see Table 11) is far superior as compared to simple water models (Table 1), including the slope k of the low-force difference region. At this moment we left the original strategy, depending solely on the reference forces, and attempted to modify the optimized parameters, such that also the bulk properties would be satisfied, effectively, including them into the parameter optimization. To include the density and diffusion parameters would require demanding molecular dynamic simulations and thus, every trial change of the force field parameters would demand hours of computational time. This can be implemented as an outer optimization cycle. However, in this trial, we decided to do this outer cycle only manually, giving us understanding of the dependence of the bulk properties on the parameters and forcing us to select hopefully the most sensitive parameters in order to converge in as few steps as possible. At the same time, this step of the optimization is surely not as systematic as it could be. The knowledge obtained here will, however, benefit later studies.
| WRT reference set | MSD | MAD | SD | AMAX | k | p |
|---|---|---|---|---|---|---|
| a Compare with Table 2. | ||||||
| AMOEBA-orig | 0.000 | 0.13 | 0.24 | 2.9 | 0.805 | 0.825 |
| AMOEBA-ASTA-TEST | 0.000 | 0.069 | 0.098 | 0.51 | 0.887 | 0.967 |
| AMOEBA-ASTA-0 | 0.000 | 0.074 | 0.107 | 0.70 | 0.950 | 0.969 |
| Full forces | ||||||
| AMOEBA-orig | 0.000 | 6.41 | 7.94 | 30.64 | — | −0.280 |
| AMOEBA-ASTA-0a | 0.000 | 1.39 | 1.81 | 11.85 | — | 0.956 |
| WRT 216 AMOEBA box | ||||||
| Non-bonding | ||||||
| AMOEBA-orig | 0.000 | 0.22 | 0.38 | 3.9 | 0.780 | 0.847 |
| AMOEBA-ASTA-0 | 0.000 | 0.13 | 0.21 | 2.38 | 0.896 | 0.961 |
| Full forces | ||||||
| AMOEBA-orig | 0.000 | 6.38 | 8.24 | 35.87 | — | 0.914 |
| AMOEBA-ASTA-0 | 0.000 | 2.89 | 3.78 | 16.68 | — | 0.986 |
The semi-manual optimization procedure was further divided into two stages. In the first stage, we used the intuitive fact that the density is mostly dependent on the rmin of the vdW parameters. Therefore, we reset rmin of both O and H to the values of the original AMOEBA water parameterization, and re-optimized the other nonbonding parameters. As the density obtained by these parameters was still too large (data not shown), we continued by increasing the rmin parameters step-wise. After each increase, the other parameters were re-optimized in order to ensure the best possible agreement with the reference QC forces. After the rmin increased by 2.0%, the density was already very close to the experimental one, so we proceeded with a second, fine-tuning stage. Here we continued modifying the rmin for the density, but to achieve also the experimental diffusion coefficient, we chose the polarizability as the parameter to modify. This choice was somewhat arbitrary, since it is likely that the Thole damping parameter would be similarly effective, and many other parameters can be effective as well. Therefore, in this stage we changed these two parameters in several steps, but unlike with the first stage, the other non-bonding parameters were not re-optimized any more, as these little adjustments have only minute effect on the forces. Within several trials, we obtained parameters where the van der Waals radii are 2.91% larger that the original AMOEBA water radii. At the same time, the polarizabilities are increased by 4% with respect to those optimized in the first stage of this procedure, which is only about 20 and 76% (for O and H respectively) with respect to the original AMOEBA water parameters. At the same time, however, the Thole parameter is also very different from the original value of 0.39, namely 0.48 and 0.82 for O and H respectively. So whereas the polarizabilities are far smaller, the increased Thole parameters cause smaller damping of the polarization and therefore, these changes partly compensate each other.
This model, called AMOEBA-ASTA-0, is the final one of this study, but as the “zero” suggests, it is not expected that this would be the very best model due to the limited systematicity of its development and testing. As with the other models, we checked its performance against the QC forces, and compared them with the AMOEBA-ASTA-TEST and the original AMOEBA water parameters (AMOEBA-orig). The statistical measures for non-bonded and full forces on the 60 water molecule boxes are shown in the first half of Table 11. There are several important points to notice. Comparing the AMOEBA-ASTA-TEST and AMOEBA-ASTA-0, we can see that there is only slight increase in MAD and SD for the latter one. This means that even though the rmin was adjusted to obtain agreement with the experimental density, and the polarizability was increased to get the experimental diffusion coefficient, the error with respect to the reference QC forces has increased only very little. Actually, the Pearson coefficient p got even improved as well as the correlation coefficient k. Importantly, the similar values MAD and SD imply, that the parameters of AMOEBA-ASTA-0 should be present near the parameter space obtained from the MCMC simulation. More relevant is to use directly the χ2 value determining the distributions. The smallest χ2 obtained from MCMC simulations for the AMOEBA-ASTA-TEST model was 1045, and for the case of AMOEBA-ASTA-0, 1234. With 17 non-bonding parameters to optimize for the AMOEBA water model, the AMOEBA-ASTA-0 parameters are reachable already in slightly increased temperature, around Tinv ∼ 10−1. A brief explanation is provided in ESI, Fig. 5.†
We therefore postulate, that adding the experimental values in our optimization, i.e., density and diffusion coefficients, can be seen as selecting a subspace of parameters from the MCMC Bayesian distribution obtained in common (Tinv = 1) or slightly increased temperature, and therefore, that the selected (discrete) point in the space of simulated parameters (here corresponding to the AMOEBA-ASTA-0 parameters) is within (or nearby) such a distribution obtained without the experimental restrictions. Even though it can be computationally tested whether these points are in the convex hull of the simulated distribution, in the present study we did not attempt to prove it, as sampling the space sufficiently well in all its dimensions is limited by a rather high computational demand, and therefore, the time needed for each force evaluation when using the AMOEBA force field would be substantial. For the same reason, we do not present any slices of the posterior distribution of parameters in a similar way that we did for the simple force fields in Section 3.5.
We can also notice, that the full forces of the AMOEBA-orig in Table 11 have large error, and unusually bad p correlation with respect to the QC forces. Even though this may seem quite dramatic, the original AMOEBA water has simply different equilibrium geometry than the one used in our QC and thus, this comparison is not quite fair.
Therefore, we decided to supply a different reference, where the results were not biased in favor of our results. We used a box of AMOEBA water supplied with the Tinker package as watersmall.xyz with 216 water molecules, for which the AMOEBA-ASTA-0 was not optimized. For the non-bonding force differences, the molecules were displaced in random directions by 0.025 and 0.035 Å. The performance of the AMOEBA-orig and AMOEBA-ASTA-0 on this reference geometries is shown in the second half of Table 11. The statistical measures cannot be compared to the QC box, i.e., the 60 water molecule box (the first half of the Table 11), but the two water models can be compared between each other. It would be expected that the original AMOEBA water model would perform far better on its own geometry, especially for the full forces. We note, that the AMOEBA-orig gives this time a good p correlation coefficient for the full forces. Surprisingly, however, also in this case, the AMOEBA-ASTA-0 gave significantly better results not only for the non-bonding forces, but also for the bonding ones. In Fig. 6 are shown the non-bonded Cartesian force correlations for the original water AMOEBA force field and both approaches. In the ESI† are shown the original AMOEBA and AMOEBA-ASTA-0 parameters in Tinker format. Parameters in the OpenMM format are given in a separate XML file.
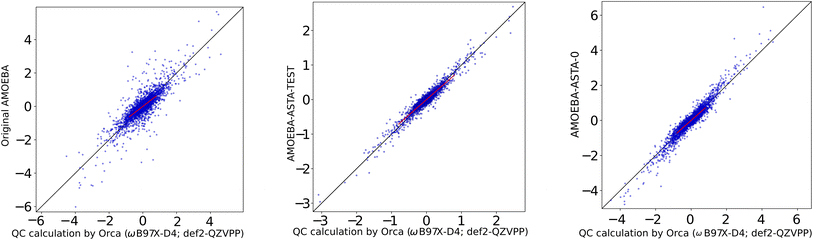 | ||
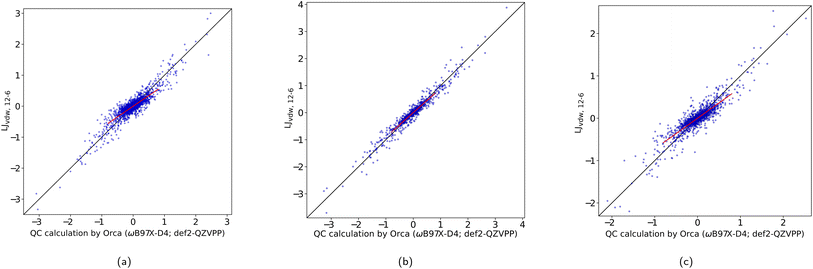
| Fig. 6 Original AMOEBA (left), AMOEBA-ASTA-TEST (center) and AMOEBA-ASTA-0 (right), correlation of (non-bonding) force differences [kcal mol−1 Å−1]. | ||
Table 12 shows the density and diffusion for the original AMOEBA and both approaches, after re-optimizing their bonded parameters. These bulk parameters were computed in a box of 5832 water molecules.
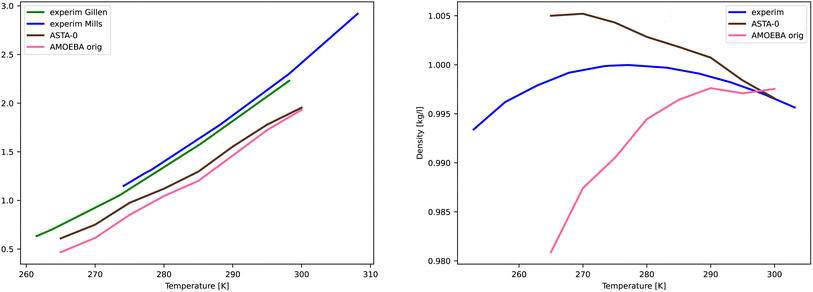
For AMOEBA-ASTA-0, no other than the temperature of 300 K was used to fine tune the parameters. As we see from Fig. 7, for the diffusion coefficient, the values are in good agreement with experimental ones, with AMOEBA-ASTA-0 being slightly better than the original AMOEBA. In the case of density, the situation is more complicated. The original AMOEBA has clearly inferior behavior near the 4 °C, where the density should reach its maximum. Based on the sparse values obtained in this study, the AMOEBA-ASTA-0 shows maximum density at around −4 °C. Even though the agreement with experimental dependence is far from perfect, it can be seen as an encouraging improvement over the original AMOEBA model, especially since no data from other than 300 K was used in optimization. Clearly the agreement can be improved by including those in an outer optimization cycle as mentioned in Section 3.9.
3.10 Further discussion
We hypothesize that having the correct bulk properties does not imply having all the inter-atomic forces correct. That could cause an unpredictable behavior of properties that are not included in the parameterization. A discrepancy of the dynamics by a common force field and NMR relaxation data has been reported e.g. in ref. 83, and a subsequent procedure to optimize the force field with respect to the experimental data in ref. 84. Another example is the application of quadrupolar NMR relaxation using the Madrid-2019 force field, where the force field-derived electric field gradient (EFG) tensors have to be supplemented by QC calculations.85,86
On the other hand, there is a huge amount of successful application of the current bio-molecular force fields, even for events requiring accurate thermodynamic measures determining the peptide folding,87 with optimization protocol, recently detailed in ref. 9. Our choice of examples is biased by our own scientific interests, but undoubtedly, equivalent examples can be found, where the importance of accurate forces is seen from other perspectives.
In the case of the AMOEBA force field, we have seen sufficient flexibility for our current procedure.
Another source of bias to be expected is from the QC method itself. Unfortunately, many DFT methods give basic bulk properties of water with an unacceptable inaccuracy,88 with only a recent study89 providing a specific example of a method reproducing the density and diffusion coefficient of water accurately.
In the case of AMOEBA, we have seen a lot of similarities between its original water parameters, and the parameters derived in this study (ESI†). Especially, the bonding parameters and the partial charges are very similar. Although there are big differences in higher multipoles and polarizability parameters, it would be particularly interesting to compare how these difference translate, e.g., into EFG tensors, and subsequent NMR quadrupole relaxation observables. Currently, also in the case of the AMOEBA force field, we do not stress the physical interpretation of the optimized parameters, as the main purpose is to obtain the forces accurately.
By comparing two very similar water models, i.e., SPC/ε and OPC3, their parameters mostly differ only on third decimal place (Table 13) and yet, their self-diffusion coefficient differs by one third (1.55 vs. 2.28 × 10−5 cm2 s−1).
| Model | Bond | Angle | pcO | rmin [Å] | εk [kcal mol−1] |
|---|---|---|---|---|---|
| SPC/ε | 1.0000 | 109.45 | −0.89000 | 1.7838728 | 0.168704 |
| OPC3 | 0.97888 | 109.47 | −0.89517 | 1.7814988 | 0.163406 |
These little differences in parameters, such as partial charges differing by about 0.5%, are in contrast with practical and clearly successful force fields, like the cases of prosECCo75 (ref. 92) and Madrid-2019,93,94 where the formal charges are scaled by a factor of 25% and 15% respectively. This further shows the exclusive, and maybe not fully justified, demands on the neat water properties.
Stating this, we can hypothesize, that our approach, even if not directly leading to parameters compatible with good bulk water properties, is likely to be still very useful for parameterization other moieties in the role of solute, especially for more detailed and flexible force fields like AMOEBA. We expect that similarly to the approach for obtaining the AMOEBA-ASTA-0 water parameters, every additional experimental property narrows down the parameters towards an optimal set. It is left for the future studies to clarify, how quickly will such selection converge, how many and what kind of experimental quantities would be the most suitable to include for different systems.
4 Conclusions
In this study, we aimed at obtaining accurate force field parameters, with the main focus on the non-bonding interactions. The forces were computed by a QC method with proven accuracy. The reference geometries used were chosen, with the goal of representing a system, close to the one we would ultimately use in a MD simulation. At the same time, we aim for a general procedure without the need of introducing extra information besides the starting geometries. With this, we would not be limited, when using this algorithm for any complex mixture of molecules, for which experimental data is not necessarily available. We also avoid using periodic conditions for the reference calculations, as this would narrow down the choice of QC methods available. We eventually reconsidered the strategy, allowing for a (small) number of experimental inputs.4.1 For the case of simple force fields
We tested fine-grained parameters sets and also sets with the pair-wise van der Waals parameters. We also probed to lower the resolution of forces such that only translational force and torque around the axis through COM would be compared, or even the vector sum of all forces of water atoms. Furthermore, besides the most common Lennard-Jones potential, we attempted other forms of the van der Waals interactions. We also tried less justifiable approaches, such as effectively adding extra statistical weight on the low-force difference region for the reference data, or modifying the Coulomb interaction together with adjustable Lennard-Jones repulsion exponent, which improved the ability of the force field to fit the reference non-bonding force differences.Using all these unbiased approaches, with a choice of the reference geometries and corresponding forces, the obtained posterior Bayesian distributions do not contain parameters compatible with good bulk water properties. We conclude thus, that for the simple force field models, this bottom-up approach is not applicable for the neat water properties. Instead, the top-down approach, starting from the know dynamics, and thermodynamic properties, should be a more practical approach, keeping in mind that the underlying inter-atomic forces may have limited accuracy.
4.2 For the case of AMOEBA force field
For the more detailed and physically meaningful force field, the situation is entirely different. It is seen that the dependence of the non-bonding forces on the underlying geometries is fulfilled much better than in the case of simple force fields. Thus, it is not necessary to try less justifiable or practical approaches to bias the fitting towards the desired results. Even though the unrestricted parameterization of all the atomic forces does not immediately provide parameters for good bulk water properties, the Bayesian distribution of such parameters is within the correct range and thus, there exist a subspace of these parameters providing good bulk properties. For their selection, we currently use a rather practical approach, instead of the “ab initio” attempts used so far. Thus, we provide one such parameter set for AMOEBA water with greatly improved accuracy in both non-bonding as well as full (and therefore also bonding) inter-atomic forces, for which, at the same time, the density and self-diffusion coefficients are at the very top of accuracy.Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Jiří Mareš: responsible of conceptualization, formal analysis, investigation, methodology (implementation of all the ASTA algorithm), software (in-house python codes, simulation of AMOEBA in OpenMM for bulk properties, QC in ORCA) and writing the original draft. Pau Mayorga Delgado: conceptualization, analysis, simulated the system to test the bulk properties of the simple water force fields, visualization, thorough revision, restructuring and editing the original manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from the European Research Council (project number 772110) is gratefully acknowledged. Computational resources of CSC (Espoo, Finland), project 2006675 and the Finnish Grid and Cloud Infrastructure project (persistent identifier urn:nbn:fi:research-infras-2016072533) are also acknowledged.Notes and references
- W. L. Jorgensen and J. Tirado-Rives, J. Am. Chem. Soc., 1988, 110, 1657–1666 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- M. J. Robertson, J. Tirado-Rives and W. L. Jorgensen, J. Chem. Theory Comput., 2015, 11, 3499–3509 CrossRef CAS PubMed.
- X. Daura, A. E. Mark and W. F. V. Gunsteren, J. Comput. Chem., 1998, 19, 535–547 CrossRef CAS.
- W. R. P. Scott, P. H. Hünenberger, I. G. Tironi, A. E. Mark, S. R. Billeter, J. Fennen, A. E. Torda, T. Huber, P. Krüger and W. F. van Gunsteren, J. Phys. Chem. A, 1999, 103, 3596–3607 CrossRef CAS.
- C. Oostenbrink, A. Villa, A. E. Mark and W. F. V. Gunsteren, J. Comput. Chem., 2004, 25, 1656–1676 CrossRef CAS PubMed.
- C. Oostenbrink, T. A. Soares, N. F. A. van der Vegt and W. F. van Gunsteren, Eur. Biophys. J., 2005, 34, 273–284 CrossRef CAS PubMed.
- M. M. Reif, M. Winger and C. Oostenbrink, J. Chem. Theory Comput., 2013, 9, 1247–1264 CrossRef CAS PubMed.
- M. P. Oliveira, M. Andrey, S. R. Rieder, L. Kern, D. F. Hahn, S. Riniker, B. A. C. Horta and P. H. Hünenberger, J. Chem. Theory Comput., 2020, 16, 7525–7555 CrossRef CAS PubMed.
- M. P. Oliveira and P. H. Hünenberger, J. Chem. Theory Comput., 2023, 19, 2048–2063 CrossRef CAS PubMed.
- W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179–5197 CrossRef CAS.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713 CrossRef CAS PubMed.
- K. T. Debiec, D. S. Cerutti, L. R. Baker, A. M. Gronenborn, D. A. Case and L. T. Chong, J. Chem. Theory Comput., 2016, 12, 3926–3947 CrossRef CAS PubMed.
- C. Tian, K. Kasavajhala, K. A. A. Belfon, L. Raguette, H. Huang, A. N. Migues, J. Bickel, Y. Wang, J. Pincay, Q. Wu and C. Simmerling, J. Chem. Theory Comput., 2020, 16, 528–552 CrossRef PubMed.
- B. R. Brooks, R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan and M. Karplus, J. Comput. Chem., 1983, 4, 187–217 CrossRef CAS.
- A. D. J. MacKerell, D. Bashford, M. Bellott, R. L. J. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef CAS PubMed.
- B. R. Brooks, C. L. Brooks III, A. D. Mackerell Jr, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614 CrossRef CAS PubMed.
- A. D. Mackerell Jr, M. Feig and C. L. Brooks III, J. Comput. Chem., 2004, 25, 1400–1415 CrossRef PubMed.
- P. Lopes, B. Roux and A. MacKerell, Theor. Chem. Acc., 2009, 124, 11–28 Search PubMed.
- P. E. M. Lopes, J. Huang, J. Shim, Y. Luo, H. Li, B. Roux and A. D. J. MacKerell, J. Chem. Theory Comput., 2013, 9, 5430–5449 CrossRef CAS PubMed.
- F.-Y. Lin, P. E. M. Lopes, E. Harder, B. Roux and A. D. J. MacKerell, J. Chem. Inf. Model., 2018, 58, 993–1004 CrossRef CAS PubMed.
- P. Ren and J. W. Ponder, J. Phys. Chem. B, 2003, 107, 5933–5947 CrossRef CAS.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- J. L. F. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505 CrossRef CAS PubMed.
- G. Lamoureux, A. D. MacKerell and B. Roux, J. Chem. Phys., 2003, 119, 5185 CrossRef CAS.
- G. Lamoureux, E. Harder, I. V. Vorobyov, B. Roux and A. D. MacKerell, Chem. Phys. Lett., 2006, 418, 245–249 CrossRef CAS.
- J. W. Ponder, C. Wu, P. Ren, V. S. Pande, J. D. Chodera, M. J. Schnieders, I. Haque, D. L. Mobley, D. S. Lambrecht, R. A. DiStasio, M. Head-Gordon, G. N. I. Clark, M. E. Johnson and T. Head-Gordon, J. Phys. Chem. B, 2010, 114, 2549–2564 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- H. W. Horn, W. C. Swope, J. W. Pitera, J. D. Madura, T. J. Dick, G. L. Hura and T. Head-Gordon, J. Chem. Phys., 2004, 120, 9665–9678 CrossRef CAS PubMed.
- L.-P. Wang, T. J. Martinez and V. S. Pande, J. Phys. Chem. Lett., 2014, 5, 1885–1891 CrossRef CAS PubMed.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- N. Mardirossian and M. Head-Gordon, Phys. Chem. Chem. Phys., 2014, 16, 9904–9924 RSC.
- E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112 CrossRef PubMed.
- E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- S. Kozuch and J. M. L. Martin, Phys. Chem. Chem. Phys., 2011, 13, 20104–20107 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- J. A. Rackers, Z. Wang, C. Lu, M. L. Laury, L. Lagardère, M. J. Schnieders, J.-P. Piquemal, P. Ren and J. W. Ponder, J. Chem. Theory Comput., 2018, 14, 5273–5289 CrossRef CAS PubMed.
- W. Von Der Linden, R. Preuss and V. Dose, Maximum Entropy and Bayesian Methods Garching, Germany, 1998, vol. 1999, pp. 319–326 Search PubMed.
- P. Håkansson, Phys. Chem. Chem. Phys., 2021, 23, 2637–2648 RSC.
- J. Mareš, J. Karjalainen, P. Håkansson, S. Michaeli and T. Liimatainen, Phys. Chem. Chem. Phys., 2023, 25, 22965–22978 RSC.
- P. Eastman, J. Swails, J. D. Chodera, R. T. McGibbon, Y. Zhao, K. A. Beauchamp, L.-P. Wang, A. C. Simmonett, M. P. Harrigan, C. D. Stern, R. P. Wiewiora, B. R. Brooks and V. S. Pande, PLoS Comput. Biol., 2017, 13, e1005659 CrossRef PubMed.
- J. E. Jones and S. Chapman, Proc. R. Soc. London, Ser. A, 1997, 106, 463–477 Search PubMed.
- H. A. Lorentz, Ann. Phys., 1881, 248, 127–136 CrossRef.
- D. Berthelot, C. R. Hebd. Seances Acad. Sci., 1898, 126, 1703–1855 Search PubMed.
- J. Wang, P. Cieplak and P. A. Kollman, J. Comput. Chem., 2000, 21, 1049–1074 CrossRef CAS.
- W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179–5197 CrossRef CAS.
- R. A. Buckingham and J. E. Lennard-Jones, Proc. R. Soc. London, Ser. A, 1997, 168, 264–283 Search PubMed.
- P. M. Morse, Phys. Rev., 1929, 34, 57–64 CrossRef CAS.
- S. Spicher, E. Caldeweyher, A. Hansen and S. Grimme, Phys. Chem. Chem. Phys., 2021, 23, 11635–11648 RSC.
- M. Müller, A. Hansen and S. Grimme, J. Chem. Phys., 2023, 158, 014103 CrossRef PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef.
- T. Darden, D. York and L. Pedersen, Particle mesh Ewald: An Nlog(N) method for Ewald sums in large systems, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- S. Páll and B. Hess, Comput. Phys. Commun., 2013, 184, 2641–2650 CrossRef.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- M. Bernetti and G. Bussi, J. Chem. Phys., 2020, 153, 114107 CrossRef CAS PubMed.
- B. Hess, H. Bekker, H. J. Berendsen and J. G. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- W. F. Van Gunsteren and H. J. Berendsen, Mol. Simul., 1988, 1, 173–185 CrossRef.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, USA, 1989 Search PubMed.
- N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, J. Comput. Chem., 2011, 32, 2319–2327 CrossRef CAS PubMed.
- R. J. Gowers, M. Linke, J. Barnoud, T. J. E. Reddy, M. N. Melo, S. L. Seyler, J. Domański, D. L. Dotson, S. Buchoux, I. M. Kenney and O. Beckstein, Proceedings of the 15th Python in Science Conference, 2016, pp. 98–105 Search PubMed.
- D. J. Price and C. L. Brooks III, J. Chem. Phys., 2004, 121, 10096–10103 CrossRef CAS PubMed.
- S. Izadi and A. V. Onufriev, J. Chem. Phys., 2016, 145, 074501 CrossRef PubMed.
- F. H. Stillinger and A. Rahman, J. Chem. Phys., 1974, 60, 1545–1557 CrossRef CAS.
- D. van der Spoel, P. J. van Maaren and H. J. C. Berendsen, J. Chem. Phys., 1998, 108, 10220–10230 CrossRef CAS.
- S. P. Kadaoluwa Pathirannahalage, N. Meftahi, A. Elbourne, A. C. G. Weiss, C. F. McConville, A. Padua, D. A. Winkler, M. Costa Gomes, T. L. Greaves, T. C. Le, Q. A. Besford and A. J. Christofferson, J. Chem. Inf. Model., 2021, 61, 4521–4536 CrossRef CAS PubMed.
- R. Fuentes-Azcatl, N. Mendoza and J. Alejandre, Phys. A, 2015, 420, 116–123 CrossRef CAS.
- P. J. van Maaren and D. van der Spoel, J. Phys. Chem. B, 2001, 105, 2618–2626 CrossRef CAS.
- W. Yu, P. E. M. Lopes, B. Roux and A. D. MacKerell Jr, J. Chem. Phys., 2013, 138, 034508 CrossRef PubMed.
- H. Yu, T. W. Whitfield, E. Harder, G. Lamoureux, I. Vorobyov, V. M. Anisimov, A. D. MacKerell and B. Roux, J. Chem. Theory Comput., 2010, 6, 774–786 CrossRef CAS PubMed.
- P. Ren and J. W. Ponder, J. Phys. Chem. B, 2004, 108, 13427–13437 CrossRef CAS.
- C. Vega and J. L. F. Abascal, J. Chem. Phys., 2005, 123, 144504 CrossRef CAS PubMed.
- A. M. Nikitin, ChemistrySelect, 2018, 3, 2017–2020 CrossRef CAS.
- R. Mills, J. Phys. Chem., 1973, 77, 685–688 CrossRef CAS.
- K. T. Gillen, D. C. Douglass and M. J. R. Hoch, J. Chem. Phys., 1972, 57, 5117–5119 CrossRef CAS.
- D. E. Hare and C. M. Sorensen, J. Chem. Phys., 1987, 87, 4840–4845 CrossRef CAS.
- J. S. Anderson, G. Hernández and D. M. LeMaster, J. Chem. Theory Comput., 2020, 16, 2896–2913 CrossRef CAS PubMed.
- J. S. Anderson, G. Hernández and D. M. LeMaster, J. Chem. Theory Comput., 2022, 18, 2091–2104 CrossRef CAS PubMed.
- I. Chubak, L. Scalfi, A. Carof and B. Rotenberg, J. Chem. Theory Comput., 2021, 17, 6006–6017 CrossRef CAS PubMed.
- I. Chubak, L. Alon, E. V. Silletta, G. Madelin, A. Jerschow and B. Rotenberg, Nat. Commun., 2023, 14, 84 CrossRef CAS PubMed.
- W. Huang, Z. Lin and W. F. van Gunsteren, J. Chem. Theory Comput., 2011, 7, 1237–1243 CrossRef CAS PubMed.
- M. J. Gillan, D. Alfè and A. Michaelides, J. Chem. Phys., 2016, 144, 130901 CrossRef PubMed.
- S. Dasgupta, E. Lambros, J. P. Perdew and F. Paesani, Nat. Commun., 2021, 12, 6359 CrossRef CAS PubMed.
- A. Stone, Chem. Phys. Lett., 1981, 83, 233–239 CrossRef CAS.
- A. J. Stone, J. Chem. Theory Comput., 2005, 1, 1128–1132 CrossRef CAS PubMed.
- E. Duboué-Dijon, M. Javanainen, P. Delcroix, P. Jungwirth and H. Martinez-Seara, J. Chem. Phys., 2020, 153, 050901 CrossRef PubMed.
- S. Blazquez, M. M. Conde, J. L. F. Abascal and C. Vega, J. Chem. Phys., 2022, 156, 044505 CrossRef CAS PubMed.
- I. M. Zeron, J. L. F. Abascal and C. Vega, J. Chem. Phys., 2019, 151, 134504 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra02685c |
| This journal is © The Royal Society of Chemistry 2024 |