Open Access Article
Open Access ArticleIntrinsic and environmental modulation of stereoselective aldol organocatalyzed reactions by proline-containing lipopeptides†‡
Pedro Tendrih Sodré a,
Andrea Maria Aguilarb,
Wendel Andrade Alves
a,
Andrea Maria Aguilarb,
Wendel Andrade Alves a and
Maurício Domingues Coutinho-Neto
a and
Maurício Domingues Coutinho-Neto *a
*a
aCentro de Ciências Naturais e Humanas, Universidade Federal do ABC, 09210-580 Santo André, Brazil. E-mail: mauricio.neto@ufabc.edu.br
bInstituto de Ciências Ambientais, Químicas e Farmacêuticas, Universidade Federal de São Paulo, 09972-270, Diadema, Brazil
First published on 3rd July 2024
Abstract
Proline, along with its derivatives, has been employed as an efficient organocatalyst for aldol reactions, with the ability to promote the creation of stereoselective C–C bonds. Even though the Houk–List transition state model is able to explain the stereoselectivity observed when proline is used as a catalyst, few studies investigate the role of microheterogeneous media in modulating the reaction outcome. In this work, molecular dynamics and electronic structure calculations were used to investigate the aldol reaction in the condensed phase. Our research focused on a lipopeptide compound incorporating the proline residue within the sequence PRWG-(C18H37), where P represents L-proline, R stands for L-arginine, W for L-tryptophan, and G for L-glycine. This sequence is covalently bonded to a hydrophobic segment formed by a long aliphatic chain, acting as an organocatalyst in an aqueous solution. This catalytic phase utilizes the complex chemical environment of the solution to achieve high selectivity. Our findings indicate a Houk–List-like mechanism, in which the amide acts as an H-bond donor, complemented by a mechanism in which the counter ion, trifluoracetic acid (TFA), acts as a proton shuttle. Both mechanisms demonstrated low energy barriers—12.23 and 1.42 kcal mol−1 for the (S,R) stereoisomer formation, computed using DLPNO-CCSD with def2-TZVPP basis set. Further, to explore the catalytic effect of the PRWG-(C18H37) lipopeptide in water, molecular dynamics simulations were conducted. It was observed that the micellar phase significantly enhances stereospecific encounters, favouring the experimentally observed ratio of (SR/SS) isomers, in contrast to reactions in a pure cyclohexanone medium. By quantifying the effects enabled by the supramolecular assembly, we were able to shed light on the factors that modify and enhance the stereoslectivity of the reaction.
Introduction
Organocatalytic aldol reactions have great synthetic significance, generating β-hydroxy carbonyl compounds in a stereoselective approach. Since the seminal work of List and Barbas in 2000,1,2 the amino acid proline and proline derivatives have been used as catalysts in aldol reactions, showcasing their ability to promote stereoselective C–C bond formation. This phenomenon has been explored experimentally and theoretically, with Bahmanyar and Houk using density functional theory (DFT) calculations to elucidate kinetic barriers and proposed mechanisms.3,4 Their work highlighted the critical role of intermolecular interactions at the transition state geometry in determining the experimental outcome, particularly the hydrogen bond between the carbonyl moiety and the acidic group from the amino acid during C–C bond formation. These studies suggest a stereoselective reaction through enamine formed in the reaction medium from a carbonyl compound and L-proline nitrobenzaldehyde.Further investigations, such as those by Clemente and colleagues, involved calculating a series of different transition states (TS) and intermediates, including enaminium, a reaction mechanism with two proline molecules, a mechanism with the formation of a L-proline derived enamine intermediate and, the TS for the uncatalyzed reaction.5 The lower energy associated with the enamine intermediary supported its intermediary role in C–C bond formation, distinguishing it from other pathways. DFT results underlined the enamine intermediate's significantly lower energy than the uncatalyzed reaction, whereas enaminium displayed higher energy. The experimental detection of the L-proline derived enamine intermediates in DMSO in 2010 provided concrete evidence supporting these theoretical findings.6 The Houk–List mechanism (HL), introduced by Houk and List in 2003, integrates these insights, offering a comprehensive explanation for the fundamental intramolecular interactions that govern C–C bond formation in proline-organocatalyzed aldol reactions.
Barbas and Mase's demonstration that proline derivatives containing alkyl long-chain could act as organocatalysts in water, with acidic additives like trifluoracetic acid (TFA) enhancing the enantiomeric excess,7 further highlighted the versatility of proline-based catalysis.
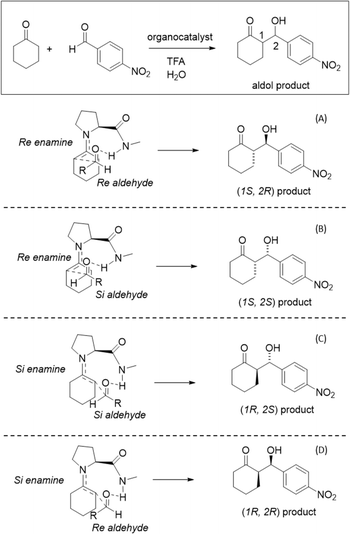
In 2014, Armstrong and collaborators revisited the Houk–List mechanism with updated computational methods, reflecting new techniques and increased computational power available.8 Their investigation focused on the effects of dispersion corrections, more extensive basis sets, and implicit solvent optimization on the reaction mechanism. Armstrong's group findings emphasized the role of aromatic ring stacking and intramolecular hydrogen bond interactions at the transition state.8 In conjunction with an enamine mechanism, these interactions favoured the nucleophilic enamine approach to Re over the Si carbonyl face of the electrophilic carbonyl reagent. This led to a preference for Re-enamines that yield (S,R) and (S,S) products over Si enamines that lead to (R,R) and (R,S) products. The Re enamine features a more stable chair-like conformation, whereas the Si conformation adopts a twisted boat. These interactions highlight the importance of the cyclohexene ring's intermolecular interactions and conformation for selectivity, with non-covalent interaction (NCI) plots suggesting that dispersion and electrostatic intermolecular interactions also contribute to these TS conformations. Bahmanyar studies show the relevance of the hydrogen bond and the prochiral carbonyl faces, with the TS energies being sensitive to the formed hydrogen bond configuration.3,4
Gong, Wu, and collaborators described the use of amides prepared from proline as catalysts to extend the application of proline derivatives.9,10 By modifying the strength of the intramolecular hydrogen bond through strategic substitution on proline amides, researchers aimed to refine a presumed mechanism related to the original Houk–List proposal that involves a hydrogen bond stabilized transition state. They observed improvements in catalysis when electron-withdrawing groups were added to the catalyst. The stereoselective C–C bond formation between the enamine and an electrophile carbonyl compounds, such as acetone, benzaldehyde, or p-nitrobenzaldehyde, was central to these studies.
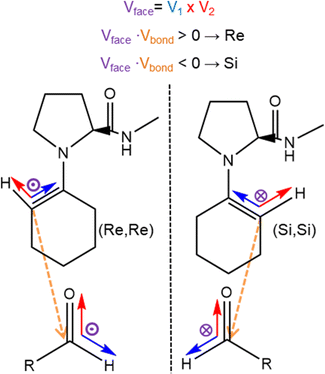
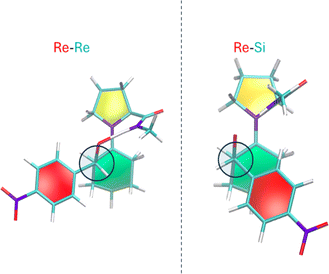
The proposed enamine intermediate formation mechanism9 encompasses several steps similar to the original Houk–List proposed mechanism, starting from an initial nucleophilic attack, followed by forming an iminium ion that rearranges to an enamine intermediate. Fig. 1 depicts the enamine formation starting from cyclohexanone and N-methyl-L-prolinamide. This key intermediate is a potent nucleophile whose attack results in novel C–C bonds with specific stereochemistry. In Fig. 1, we specify a given pro-chiral encounter Re–Re that results in a product with (S,R) stereochemistry.
In a further DFT investigation of aldol reaction between p-nitrobenzaldehyde and cyclohexanone described by Rzepa and collaborators,8 the transition states are discussed in terms of distinct prochiral faces of electrophilic carbonyl reagent. This analysis showed how the cyclohexanone ring conformation is related to the developed positive charge on the nitrogen atom. As the carbon–carbon bond is formed, an intramolecular hydrogen bond stabilizes the alkoxide negative charge.
Introducing proline-containing peptides and modified proline derivatives with long alkyl tails represents a novel approach11,12 to aldol catalysis.11,12 Replacing the carboxylic acid for an amide group allows the amide to act as an H bond donor, putatively following a Houk List-like mechanism similar to the one proposed by Wu et al.6 However, unlike previous catalysts, lipopeptides self-assemble to form aggregates in water, creating a complex array of chemical environments ranging from typically organic at the aggregate centre, through an interfacial charged and hydrophilic region to the bulk.12 This diversity can stabilize distinct transition states, with more hydrophilic environments favouring zwitterionic intermediates.
Experimental evidence shows that proline-containing supramolecular aggregates in water enhance yield and selectivity compared to a pure cyclohexanone medium, where the aggregate is absent.11,12 Theoretical investigations of aggregate lipopeptide structures are essential to help characterize their influence on the catalytical process. Previous investigations in our group have shown that proline lies at the micelle interface, where the water content is about half of its bulk value.11,12 Our results suggest that the environmental effect provided by the aggregate may influence the protonation equilibrium of both L-proline and TFA and can be fundamental for catalysis.12 The L-proline derived enamine and p-nitrobenzaldehyde molecules constitute the reactants for the aldol C–C bond formation step. The stereoselective step in the conventional Houk–List mechanism is facilitated by an intramolecular proton transfer from the carboxylic acid group of proline to the aldehyde.
This work employs a multiscale approach using molecular dynamics simulations and electronic structure calculations to investigate the factors governing the stereoselectivity of aldol organocatalyzed reaction by L-proline-containing lipopeptides. We focus on environmental and intrinsic factors affecting the reaction's stereoselective determining step (SDS). Especially, we investigate in detail the reaction of p-nitrobenzaldehyde with cyclohexanone catalysed by a lipopeptide composed of the Proline-Arginine-Tryptophan-Glycine-C18H37 [PRWG-(C18H37)] sequence originally investigated by W. Alves and colleagues.11 We used molecular dynamics simulations of PRWG-C18H37 aggregates to assess the molecular interactions promoted by the aggregate that may affect the reaction's SDS. In addition, electronic structure calculations have been employed to investigate the SDS explicitly.
To improve computational efficiency, we employ a methyl-capped N-methyl-prolinamide enamine, as depicted in Fig. 1, instead of the entire PRWG-C18H37 enamine for all electronic structure calculations. Fig. 2 shows all four possible pro-chiral encounters and subsequent products for the reaction.
Molecular dynamics simulation
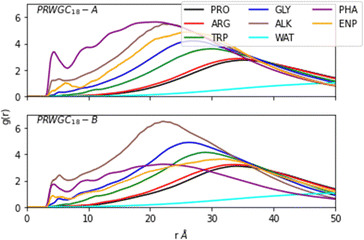
To investigate the dynamics of the reactant pair formation at the SDS in the condensed media, we modelled a PRWG-C18H37 micelle using 160 lipopeptide chains with 20 modified prolines to act as enamines. In addition, 432 p-nitrobenzaldehyde molecules were added to the simulation box. This concentration saturates the micelle in water and should enhance the statistics of encounters. We paid particular attention to the micellar aggregate's enamine-p-nitrobenzaldehyde reactant pair formation. The L-prolinamide-derived enamine (L-prolinamide-enamine) and p-nitrobenzaldehyde structures have been obtained using density functional theory (DFT). The protocols employed for micelle construction and simulations were similar to the ones employed in previous publications.11,12 Details are given in the Methods section.Fig. 3 illustrates the micellar structure described by radial distribution functions (RDFs) g(r). This function quantifies the distribution of residues and molecules as a function of the radial distance from the hydrophobic core, defined as the position of the group formed by the first carbon (C1) of the alkyl chains. The figure shows the micellar aggregate's layered structure, highlighting a pre-concentration effect of the p-nitrobenzaldehyde molecules shown as PHA in Fig. 3. This effect results from the micelle's ability to accumulate reactant molecules within its hydrophobic core, facilitating their interaction with the enamine intermediate. Two distinct initial conditions were used for p-nitrobenzaldehyde placement. For initial condition A (simulation A), the aldehydes were placed in the micelle's hydrophobic core. In contrast, for B (simulation B) they were evenly distributed outside the micellar assembly. Fig. 3 shows that even after 600 ns of simulation, the distribution of aldehyde molecules varies between scenarios A and B due to slow diffusion. Correlating to their respective initial condition, the aldehyde molecules predominantly accumulate inside the aggregate for A. In contrast, these molecules are more broadly distributed in B. Nonetheless, even when starting with molecules evenly distributed on the outside, most of the p-nitrobenzaldehyde molecules migrate to the interior of the micelle during simulation B. A third simulation (simulation C) was carried out using a pure cyclohexanone medium with identical concentration of lipopeptides and reactant pairs ENP and PHA for comparison.
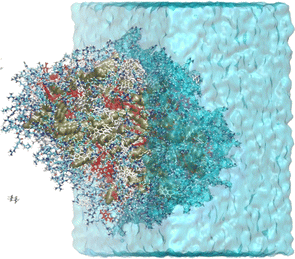
The light blue curve (WAT in Fig. 3) shows the g(r) of water, which increases from zero at the organic core to one at the bulk. This water content gradient underscores how the chemical environment changes within the aggregate as a function of the radial position, r. From the RDFs, one can see that most encounters between p-nitrobenzaldehyde and the L-prolinamide-enamine intermediate (PHA and ENP in Fig. 3) happen in the intermediate region, known as the micelle palisade region, where water content is about half its bulk value according to our simulations. Fig. 4 depicts an illustration derived from the final frame of simulation A. It displays water, represented in blue, together with the organic core in ochre. Additionally, the illustration includes amino acids and p-nitrobenzaldehyde molecules in the palisade region. p-Nitrobenzaldehyde molecules less than 4 Angstroms from L-prolinamine-enamine are shown in white.
We propose using a dimensionless empirical function—hereafter referred to as the proximity function or pij(x) —that counts putative reactive encounters between L-prolinamine-enamine (ENP) and p-nitrobenzaldehyde molecules (PHA). This function counts and classifies encounters that happen within a given distance threshold. Put differently, this function aims to estimate the probability of a reactive encounter to occur between enamine-modified prolines and p-nitrobenzaldehyde molecules in the dynamic environment of the micelle.
Fig. 5 illustrates the orientation vectors used for the pair formation analysis in computing pij(x). A reference vector Vref represents the forming C–C bond going from the enamine to the aldehyde, while the cross product V1 × V2 = Vface results in an orientation that distinguishes the prochiral face, indicated by the purple vectors entering or leaving the plane in Fig. 5. To effectively distinguish between faces, we employed the dot product Vface × Vbond to evaluate its relative orientation concerning the nascent C–C bond. For positive values Vface is aligned to Vbond, indicating a Re face. Conversely, negative values indicate that Vface is anti-aligned to Vbond and corresponds to a Si face. The full expression for the function including the distance dependence term is given by:
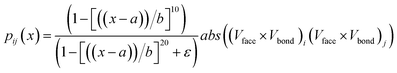 | (1) |
Proximity functions pij(x) were computed for simulations using two different initial conditions (simulations A and B, as previously described) and an additional simulation carried out in a pure cyclohexanone medium (simulation C). Cyclohexanone serves as a neat organic medium, which, according to experimental results,11,12 yields lower reaction efficiency and stereoselectivity. We note that no micellar aggregate is formed in the cyclohexanone medium.
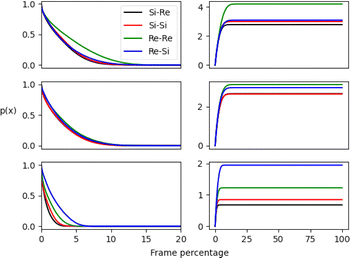
The pij(x) results are displayed in Fig. 6 along its integral and are presented as a percentage of the total number of frames from MD simulations. The outcomes for the micellar and non-micellar phases show a substantial difference, with a larger number of interactions occurring for the micellar systems. This enhancement results from a pre-concentration effect promoted by the aggregate and is apparent in the RDF results. Results show that the aldehyde Re face encounters occur more frequently than Si configurations for all systems, as shown by the blue and green curves. However, the final preferred stereoselectivity varies for the aggregate simulations. The isotropic neat cyclohexanone medium favors (Re,Si) encounters, as shown by the blue curve in Fig. 6. Meanwhile, the aggregate simulations promote (Re,Re) pro-chiral encounters, as shown by the green curves (see Fig. 2 for the prochiral face to final product stereochemistry mapping). In short, unlike neat cyclohexanone simulations that favour (Re,Si) encounters leading to (S,S) stereoisomer, micelle simulations show a preference for (Re,Re) face encounters, possibly enhancing the formation of the (S,R) stereoisomer.
To better gauge the enhancement or suppression induced by the aggregate phase, we compute the ratio between integral values of pij(x) for each stereoisomer, having the largest value at the denominator for each simulation. We also calculated an enhancement factor by computing the ratio of the integrals for simulations A and B, having simulation C in pure cyclohexanone as a reference.
The results shown in Table 1 undoubtedly demonstrate that the micellar environment facilitates reactive encounters compared to neat cyclohexanone. Our results agree with experiments that observed an enhancement for the major observed stereoisomer (S,R) over the second (S,S) and better total yield promoted by PRWG-C18H37 aggregates compared to the neat medium.11,12 Furthermore, simulation A exhibits the largest enhancements due to the higher concentration of p-nitrobenzaldehyde molecules within the micellar system than B, with a 3.45 enhancement factor for encounters with Re–Re pro-chiral faces. The proximity function analysis highlights a significant catalytic role for micellar or supramolecular catalysis, enhancing reactant encounters and favoring a particular pro-chiral configuration.
| Encounter stereochemistry | Simulation A | Simulation B | Simulation C |
|---|---|---|---|
| (Si,Re) | 0.66 (4.08) | 0.85 (3.92) | 0.35 |
| (Si,Si) | 0.71 (3.35) | 0.85 (3.13) | 0.44 |
| (Re,Re) | 1.0 (3.45) | 1.0 (2.57) | 0.63 |
| (Re,Si) | 0.74 (1.59) | 0.95 (1.53) | 1.0 |
In the following section, we examine two mechanisms for the stereochemical determining step: one bimolecular mechanism with reacting L-prolinamide-enamine and p-nitrobenzaldehyde molecules and a tri-molecular mechanism with trifluoroacetic acid acting as a proton donor to the L-proleneamide-enamine – p-nitrobenzaldehyde pair. Molecular dynamics simulations can be used to examine the probability of bimolecular and tri-molecular encounters as a function of the distance from the micelle centre. Fig. S3† shows the probability of reactant encounters computed as the product of normalized radial distribution functions. For the bimolecular mechanism, the product between g(r) for L-prolinamide-enamine and p-nitrobenzaldehyde (ENP-PHA pair) shows a clear maximum at circa 25 Å from the micelle centre, close to the maximum of the L-proline derived enamine g(r) distribution shown on Fig. 3. The tri-molecular encounter probability estimated as a product between g(r) for L-prolinamide-enamine, p-nitrobenzaldehyde and TFA (ENP-PHA-TFA) displays a maximum further away at circa 30 Å from the micelle centre. Both product distributions exhibit maximum at the palisade region, supporting the argument that the reaction should take place in an environment with reduced water content.
Reaction mechanisms from electronic structure calculations
The micellar environment, characterized by reduced water content and numerous positively charged groups, can significantly influence the protonation equilibrium and reaction barriers. Molecular dynamics results identify at least three distinct environments within our mostly spherical micellar lipopeptide system: the water-free organic core, an intermediate partially hydrophilic interface region, and the micelle surface. These regions are typically known as the micelle core, palisade region, and outer surface, exhibiting markedly distinct chemical environments. Previously,12 we have computed the proton transfer equilibrium between trifluoroacetic acid (TFA), present in all lipopeptide salts, and a L-prolinamide model molecule across three distinct environments: water, cyclohexanone, and n-heptane. These environments serve as a proxy to model the bulk and interface region, the intermediate palisade region, and the micelle core, respectively.As stated earlier, we utilize an enamine produced from a methyl-capped N-methyl-prolinamide instead of the enamine derived from PRWG-C18H37 in our studies. We performed all investigations in a cyclohexanone medium. Cyclohexanone has been used as a neat reaction medium with PRWG-C18H37 lipopeptides as catalysts. We reason that the cyclohexanone medium is a good proxy for the palisade region and that the reaction mechanism for the SDS in cyclohexanone is similar to the one occurring in the PRWG-C18H37 micelle with some key differences. Results from molecular dynamics indicate that the palisade region is the most probable region for ENP and PHA encounters. As previously discussed, most reactive encounters should happen in the intermedia palisade region between 25 and 30 Å from the micelle core as shown in Fig. S3.† Additionally, we conducted investigations in DMSO, a solvent commonly used for studying proline organocatalysis.
Nudge elastic band calculations in its climbing image version (NEB-CI) can probe both the reaction mechanism and kinetic barriers. The geometries generated through NEB calculations approximate the MEP and are stabilized on the energy surface by virtual springs.13,14 When reactant and product conformations are appropriately chosen, the TS can be identified by optimizing the highest energy image (HEI), providing insights into the reaction's energetic landscape and mechanistic pathway. While NEB has been successfully utilized to study diffusion and reactions on solid surfaces, its application to molecular systems has recently been facilitated with implementations such as in the ORCA software package.13–15 We explored the proposed mechanisms using nudge elastic band (NEB) calculations with the B3LYP functional and 6-31G(d,p) basis set augmented with Grimme's D3 corrections (named B3LYP-D3/6-31G(d,p)). All calculations were performed using the ORCA package v4.12 and v5.03. We also performed transition state calculations from NEB climbing images for the bimolecular HLWT mechanism.
Two reaction mechanisms were investigated for the C–C bond formation step. The first is a bimolecular mechanism related to the Houk–List mechanism,1,3,4 which was further explored by Wo and collaborators using prolinamides as catalysts.9 We named this mechanism herein the Houk–List–Tang–Wo (HLTW) or bimolecular mechanism. In this scenario, the hydrogen of the amide forms a hydrogen bond with the oxygen of the aldehyde during the C–C bond formation. Only conformations where the amide hydrogen can form a hydrogen bond with the aldehyde group were considered for these investigations.
A second trimolecular mechanism was also investigated. This mechanism is hypothesized to be facilitated by the micelle's environment and its potential to aggregate reactants. In the trimolecular mechanism, we propose that TFA acts as a proton shuttle within the micellar environment for the reaction. It is important to note that TFA is not the only entity capable of acting as a proton reservoir for the reaction, especially considering the shifts in pKa values expected for charged species at the interface. Nonetheless, previously computed values indicate a shift in TFA's pKa from −0.56 (with the experimental value being 0.3) to 3.7 and 16.6 when transitioning from water to cyclohexanone and n-heptane, respectively.12 Furthermore, the proton equilibrium between L-proline and TFA is highly dependent on the medium, with ΔG changing from a significantly positive 14.4 kcal mol−1 to 4.35 kcal mol−1 when moving from an aqueous environment (bulk) to an organic cyclohexanone medium. Thus, the closer to the micelle centre, the easier for a direct proton transfer reaction to occur between TFA and a protonated L-proline residue. Additionally, TFA has been demonstrated to facilitate aldol catalysis in the presence of long-chained amines.7 Fig. S3† demonstrates that the likelihood of interaction between TFA and L-proline, calculated as the product of their g(r), peaks at approximately 35 Å from the micelle centre, at the edge of the palisade region where the water content is still half of its bulk value.
It is important to acknowledge that both proposed mechanisms are a simplification of the true range of possibilities provided by the aggregate environment. There may be several alternate routes to the suggested Houk–List–Tang–Wo that employ hydrogen bond donors other than the nearby amide group. The examination of hydrogen bonds in the MD trajectory for simulation A revealed that when p-nitrobenzaldehyde is close to enamine, with reacting carbons within a distance of 4.5 Å from each other, the amide N–H hydrogens are the most likely hydrogen bond donors to aldehyde oxygen. The interaction occurs in 2.5% of the total number of frames. Both intramolecular (1.2% of frames) and inter-molecular (1.3% of frames) amide groups can form H-bonds to p-nitrobenzaldehyde. Detailed results for hydrogen bond analysis are shown in Table S2.† Hydrogen bond stabilization by the arginine side chain occurs in only 0.8% of frames, of those, only 0.1% being of intramolecular nature. Hence, we believe that the proposed Houk–List–Tang–Wo is a representative mechanism involving H-bond stabilization of the nascent alkoxide present in the C–C bond formation in the micelle.
Table 2 presents the data for the bimolecular Houk–Listi–Tang–Wu mechanism. Computed transition state free energies (ΔG#) are computed as the energy difference between the transition state and the pre-reaction complex. Transition states were calculates starting from NEB highest energy images. Values for ΔG# in cyclohexanone are all within a 6.1 kcal mol−1 window, with transition state energies shown in Table S1† being about 3 kcal mol−1 lower. DMSO results are all within half a kcal mol−1 from cyclohexanone values with the exception of the (S,S) product. The experimentally observed (S,R) product has the lowest barrier at 10.41 (10.12) in cyclohexanone (DMSO) followed by the (R,S), (S,S) and finally (R,R) stereoisomers. Pre-reaction complexes stabilization energies, computed as the energy of the reaction complex minus the energy of the isolated species, are larger in modulus than the activation barriers with values for the Re enamine face being slightly lower in energy than their Si counterpart. With product energies very close to TS values, the transition state geometry resembles the product, with transition state C–C and O–H bond distances being remarkably similar for all stereochemistries. All transition states exhibit short hydrogen bonds, pointing to alkoxide stabilization by the amide hydrogen. Still, the amide present in our N-methyl-L-prolinamide is much less capable of stabilizing the emerging alkoxide when compared to the carboxylic acid group present in the standard Houk–List mechanism.
| Stereoisomer | Encounter | ΔGCMPX | ΔG# | ΔGR | rc–c | rO–H |
|---|---|---|---|---|---|---|
| (S,R) | Re–Re (A)-anti | −12.87 (−13.00) | 10.41 (10.12) | 10.36 (9.98) | 1.90 (1.89) | 1.70 (1.70) |
| (S,S) | Re–Si (B)-syn | −13.33 (−13.66) | 13.29 (15.79) | 13.57 (12.56) | 1.81 (1.80) | 1.73 (1.73) |
| (R,S) | Si–Si-HL (C)-anti | −11.79 (−12.27) | 13.03 (12.92) | 11.75 (9.30) | 1.93 (1.92) | 1.68 (1.68) |
| (R,R) | Si–Re-HL (D)-syn | −11.04 (−11.34) | 16.52 (16.37) | 14.33 (13.61) | 1.96 (1.96) | 1.75 (1.75) |
The stacking between rings in the Houk–List mechanism depends on the specific stereoisomer encounter. Fig. 7 represents the Re–Re and Re–Si encounters, with the former lacking a ring-stacking conformation. Rzepa8 showed that non-covalent interactions (NCI) are most relevant when the enamine moiety is planar. However, Re–Re exhibits a lower barrier and a more deformed conformation for the cyclohexene ring. Other transition states are shown in Fig. S1.†
Gong Wu reported an enantiomeric excess of roughly 30%,9 with DFT calculations showing barrier heights ranging from 10 to 15 kcal mol−1 in acetone, in line with our observations. They found that substituted proline amides with a secondary hydrogen bond and phenyl groups further stabilize the transition state and increase the experimental enantiomeric excess to 44%. Their findings confirm that the stabilization of alkoxide by hydrogen bonding significantly impacts the stereochemical consequence of the reaction. In our proposed HLWT mechanism, this role is played by the proline's amide, a comparatively weak H bond donor. This is also consistent with the shallow product basin found in our electronic structure calculations.
Despite the extensive usage of the B3LYP functional for predictions following the influential research by Houk and List, it may not be reliable for achieving chemical accuracy in estimating reaction barriers. To confirm our findings, we calculated single-point energies using the B2-BLYP and CCSD methods and the def2-TZVP basis set using B3LYP-D3/6-31G(d,p) geometries computed in cyclohexanone. The DLPNO approximation, standing for domain-based local pair natural orbital, is employed in all B2-PLYP and CCSD calculations. Its use in double hybrids has been recently benchmarked, producing excellent results for relatively large systems.16 Given that the energies and geometries computed in DMSO were nearly identical to the ones computed in cyclohexanone, we opted to continue our investigation in cyclohexanone medium only.
Results for the B2PLYP and CCSD calculations are shown in Table 3. The calculated barriers obtained from using the double-hybrid functional B2-PLYP (named DNPNO-B2-PLYP/def2-TZVP//B3LYP-D3/6-31g(d,p)) are slightly higher than the ones obtained from B3LYP-D3/6-31g(d,p). However, no change in barrier heigh ordering is observed when compared to B3LYP results. Results for DLPNO-CCSD/def2-TZVP//B3LYP-D3/6-31g(d,p) confirm the formation of very stable pre-reaction complexes and that the (S,R) stereoisomer has the lowest barrier. Additionally, the energy gap between the favoured (S,R) stereoisomer and the other pro-chiral configurations increase, showing a clear preference for the product found in experiments. DLPNO-CCSD results also show (S,S) as the second preferred stereoisomer, in agreement with experimental observations and in contrast to B3LYP and DLPNO-B2-PLYP results. In addition, the DLPNO-CCSD/def2-TZVP//B3LYP-D3/6-31g(d,p) results show more favourable ΔGR than DFT-based estimates. Despite their differences, all methods agree upon the preferred (S,R) stereoisomer and that the alkoxide intermediate product resides in a shallow basin. A proton donor is needed for the reaction to move forward. In the original Houk–List mechanism, the required stabilization comes from L-proline acidic proton, and for L-prolinamides, it comes from both amide hydrogen and terminal hydroxyl groups bound to aromatic rings or electron-withdrawing groups. Both features are lacking in our lipopeptide catalytic system.
| Product[b] | ΔECMPX | ΔE# | ΔER | ΔGCMPX | ΔG# | ΔGR |
|---|---|---|---|---|---|---|
| DNLPO-B2-PLYP | ||||||
| (S,R) | −13.32 | 9.11 | 9.15 | −10.66 | 11.14 | 11.54 |
| (S,S) | −14.50 | 12.05 | 12.43 | −10.93 | 14.53 | 15.27 |
| (R,S) | −12.69 | 12.03 | 7.74 | −10.83 | 15.23 | 12.56 |
| (R,R) | −11.78 | 15.19 | 11.66 | −8.97 | 19.10 | 17.99 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| DLPNO-CCSD | ||||||
| (S,R) | −11.22 | 12.23 | 9.70 | −8.56 | 14.26 | 12.09 |
| (S,S) | −12.32 | 14.12 | 12.91 | −8.75 | 16.60 | 15.75 |
| (R,S) | −12.59 | 17.18 | 6.70 | −10.74 | 20.38 | 11.52 |
| (R,R) | −10.56 | 20.53 | 10.04 | −7.75 | 24.43 | 16.38 |
Our proposed tri-molecular mechanism involves TFA acting as the proton donor to stabilize the nascent alkoxide, mimicking the role of proline's acid group in the original Houk–List mechanism. As previously discussed, TFA can undergo protonation in a mixed water-cyclohexanone media at the micelle palisade region, requiring an energy cost of 4.35 kcal mol−1.
As in the bimolecular HLTW mechanism, all geometry optimization and NEB-CI calculations have been performed using the B3LYP-D3/6-31G(d,p) method using nine energy images. However, unlike the HLTW bimolecular studies, no explicit transition state search and no zero-point energy or thermodynamic correction have been computed. Results for the bimolecular mechanism support using NEB highest energy image (HEI) as an approximation to the TS, as those were at most 1.5 kcal mol−1 off (about 15%) from true transition state energy values. Moreover, we would have reached similar conclusions if ΔE values were used instead of ΔG ones.
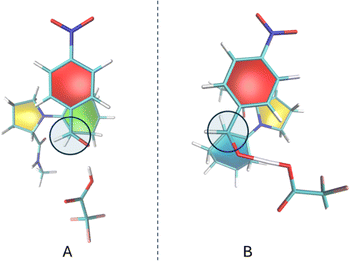
An explicit proton donor allows for more flexibility at the transition state. Two categories of transition state arrangements were investigated: one where the stacking of p-nitrobenzaldehyde occurs over proline's pyrrolidine five-member ring, and another involving the stacking over the six-member ring created by the enamine. The results for these two categories of TSs are labeled with a (5) or a (6) in Tables 4 and 5. Fig. 8 shows the two types of transition states for stereoisomer (S,R) as approximated by NEB-CI HEI. Transition states for all other cases are shown in Fig. S2.†
| Product | Encounter | ΔECMPX | ΔE# | ΔER | rC–C [Å] | rO–H [Å] |
|---|---|---|---|---|---|---|
| (S,R) | (Re,Re)-5 | −18.17 (−23.25) | 1.77 (1.40) | −20.97 (−22.55) | 2.48 | 1.15 |
| (S,R) | (Re,Re)-6 | −26.50 (−30.81) | 4.49 (4.54) | −15.55 (−17.02) | 2.68 | 1.53 |
| (S,S) | (Re,Si)-5 | −21.88 (−27,42) | 2.51 (3.29) | −17.45 (−19.45) | 2.74 | 1.59 |
| (S,S) | (Re,Si)-6 | −18.81 (−21.70) | 2.29 (2.04) | −20.90 (−22.84) | 2.45 | 1.50 |
| (R,S) | (Si,Si)-5 | −23.68 (−27.94) | 8.52 (7.90) | −19.11 (−20.23) | 1.85 | 1.44 |
| (R,S) | (Si,Si)-6 | −22.50 (−24.63) | 19.30 (17.21) | −20.72 (−21.83) | 4.08 | 1.88 |
| (R,R) | (Si,Re)-5 | −20.87 (−24.63) | 3.07 (2.44) | −19.44 (−22.96) | 1.88 | 1.10 |
| (R,R) | (Si,Re)-6 | −22.89 (−26.08) | 6.28 (6.04) | −15.96 (−18.58) | 2.30 | 1.39 |
| Isomer[b] | ΔECMPX | ΔE# | ΔER |
|---|---|---|---|
| (Re,Re)-5 | −11.39 | 1.42 | −26.99 |
| (Re,Si)-5 | −18.00 | 2.79 | −18.27 |
| (Re,Re)-6 | −19.22 | 3.46 | −20.62 |
| (Re,Si)-6 | −18.01 | 11.31 | −21.84 |
A clear difference between the bimolecular HLWT and the tri-molecular mechanisms is that the latter involves smaller barriers and exergonic reactions. All pre-reaction complexes have large stabilization energies, with the Re–Re pro chiral encounter having the lowest energy when p-nitrobenzaldehyde stacks over the enamine six-member ring. The pre-reaction complex stabilization energies are larger than the reaction activation barriers, indicating that an equilibrium between different conformations may not be achieved before the reaction occurs. This favours the path with the lowest barrier, regardless of the stabilization encountered.
The findings in Table 4 indicate that the (S,R) stereoisomer is the preferred species. It is generated by a pathway involving a stacked configuration between p-nitrobenzaldehyde and proline's pyrrolidine five-member ring with a very low 1.77 kcal mol−1 barrier. Results also indicate that (S,S) stereoisomer is the second favoured species, occurring through a pathway involving stacking over enamine's six member ring, albeit with a very small difference from the path that forms the product via a stacking interaction over pyrrolidine five-member ring. These results agree with experiments and with our previous findings for the HLWT bimolecular mechanisms. In addition, the lowest energy transition states found for the (S,R) and (S,S) products show shorter rO–H and longer rC–C bonds when compared to the bimolecular mechanism, indicating that the proton transfer and alkoxide stabilization occur before the formation of the C–C bond.
We assess our findings by employing DLPNO-CCSD/def2-TZVP//B3LYP-D3/6-31g(d,p) calculations to analyse the energetics of the (S,R) and (S,S) stereoisomers along their respective minimum energy paths, similar to what was done for the bimolecular mechanism. Results are show in Table 5. Compared to B3LYP-D3/6-31g(d,p) results, DLPNO-CCSD results exhibit smaller values for ΔECMPX but similar reaction barriers. Nonetheless, DLPNO-CCSD results confirm the (Re,Re)-5 configuration that leads to the (R,S) stereoisomer as having the lowest barrier, followed by the (Re,Si)-5 configuration that leads to the (S,S) stereoisomer. DLPNO-CCSD calculations reveal greater energy differences for the TS between the configurations in which p-nitrobenzaldehyde stacks above the pyrrolidine five-member ring than the one where it stacks over the enamine six-member ring, in comparison to B3LYP-D3 findings.
The tri-molecular mechanism has lower barriers compared to the bi-molecular HLWT mechanism due to the synchronous proton transfer for alkoxide stabilization occurring simultaneously with C–C bond formation. As such, it should be favoured in the aggregate's environment if the proton transfer equilibrium between TFA and proton-donating species is energetically allowed.
Methods
We employed the AMBER17,18 suite of programs in all molecular dynamics simulations using the pmemd.cuda module of AMBER19,20 with the ff14SB21 force field to model the peptide moiety and enamine. For the lipid part, we used the lipid21 (ref. 22) forcefield parameters. p-Nitrobenzaldehyde, cyclohexanone, and the enamine-modified L-proline used the general amber forcefield (GAFF)23 parameters. We employed the restrained electrostatic potential (RESP)23 procedure for non-standard residues to determine atomic charges from Hartree–Fock/6-31G* calculations using the AmberTools suite of codes. GAUSSIAN09 (ref. 24) program was used solely for the RESP calculations.The initial configuration of the micellar assemblies was built using the PACKMOL software25 using a procedure similar to the one used in our previous publications. Molecule geometries were visualized using Avogadro26 and the visual molecular dynamics (VMD) program,27 with the ring puckering being observed with the paperchain28,29 representation. Reaction mechanisms were plotted using Marvin Sketch.30
For the proximity function analysis, a Python script using NumPy,31 SciPy,32 and Matplotlib33 libraries were employed for array operations, integration of curves, and figure plotting, respectively. The stereochemical function inputs two datasets obtained from molecular dynamics runs using CPPTRAJ.34 For the first, we count geometries if the C–C distance is less than 4.5 A; for each enamine, only the closest aldehyde is considered. The second data is the vector data, for which we need to consider two vectors for each pro-chiral face (enamine and aldehyde) and a reference vector representing the C–C bond. The values assigned for a, b, and ε were 4.5, 1.5, and 10−5 respectively, to account for distances slightly larger than the van der Waals radius and closer to those in the pre-reactant complex.
The ORCA13–15 software versions 4.12 and 5.03 were used for all electronic structure calculations. B3LYP35,36 calculations augmented with dispersion corrections37–39 were performed using the 6-31G(d,p)40–42 basis set and the RIJCOSX approximation. The solvent environment was included using the SMD43 method. Single-point calculations using B2-BLYP and CCSD methods and the def2-TZVP basis set employed B3LYP-D3/6-31G(d,p) geometries. B2-BLYP calculations employed dispersions corrections. We named these approaches DLPNO-CCSD/def2-TZVP//B3LYP-D3/6-31g(d,p) and DLPNO-B2-PLYP/def2-TZVP//B3LYP-D3/6-31g(d,p). They employed the domain-based local pair natural orbital approximation (DLPNO)44–47 and used the auto default mode for auxiliar correlation and coulomb basis set in the RI (resolution of the identity) approach. Rection paths were investigated using NEB method48 in its climbing image (CI) variation as implemented in the ORCA49 program. Each NEB interpolates a pre-reaction complex conformation to a product complex to estimate a reaction path and TS. A total of nine images were used in all NEB calculations.
All ΔG values include zero-point energy and thermodynamic corrections according to the rigid rotor harmonic oscillator approximation. Thermodynamic and zero-point energy corrections from B3LYP-D3 calculations were incorporated into DLPNO-B2-BLYP and DLPNO-CCSD results when calculating ΔG for these approaches.
Conclusions
This study focused on investigating how the arrangement of molecules into supramolecular structures affects the ability of proline-containing lipopeptides to catalyze reactions. Using a combination of molecular dynamics and electronic structure methods, we explored the intricate catalytic landscapes orchestrated by macrostructured aggregates. A mechanism akin the Houk–List mechanism, herein named Houk–List–Tang–Wo (HLTW) mechanism, alongside a trimolecular mechanism facilitated by trifluoroacetic acid (TFA), revealed remarkable selectivity driven by specific hydrogen-bonded conformations and intermolecular interactions. We propose that TFA can act as a proton donor in a proton shuttle mechanism due to the ability of the aggregate environment in influencing the TFA's protonation equilibrium owing to the reduced water content present in the palisade region.Our results demonstrate that both the Houk–List–Tang–Wo and the proposed tri-molecular mechanisms, with TFA acting as a proton donor, effectively lead to the formation of the experimentally observed (S,R) stereoisomer product. The computed barriers using DLNPO-CCSD are 12.23 and 1.42 kcal mol−1 respectively, confirming the energetic feasibility of these mechanisms. Furthermore, as observed experimentally, both mechanism predict the (S,S) stereoisomer as the second preferred product.
The Houk–List mechanism utilizes the L-proline amino acid, which can donate a proton without external sources. While this hydrogen bond formation is also possible with L-prolinamides, the amide group's pKa is higher than that of the L-proline acid group, making it a weaker acid. On the other hand, given that TFA has a much lower pKa, it is a potent proton source in the tri-molecular mechanism investigated. Notably, the two stacking conformations (aldehyde-pyrrolidine ring and aldehyde-cyclohexene ring) are associated with the same stereoisomer, offering two different conformational paths to the same reaction mechanism. Fig. 8A and 7B depict these conformations, with TFA donating a proton to the oxygen atom and consequently stabilizing the alkoxide ion, illustrating the dynamic interplay of molecular interactions in facilitating the reaction.
Our results showed that the micellar environment significantly increased the interaction between aldehydes and Re enamines, in contrast to the restricted access in a pure cyclohexanone medium. This difference underscores the micelles' ability to enhance reaction efficiency and stereoselectivity and act as dynamic nanoreactors that intricately navigate the chemistry of aldol reactions. We noted that the micellar phase distinctly favours the formation of (S,R) over (S,S) stereoisomers compared to reactions in a cyclohexanone medium, highlighting the substantial influence of the micelle's supramolecular structure on reaction dynamics. This observation is further supported by the proximity function analysis, which indicates enhanced interactions between aldehydes and Re enamines within the micelle, crucial for the observed stereoselectivity.
Data availability
Data for this article, including output coordinates and molecular dynamics topology and coordinates are available at https://doi.org/10.5281/zenodo.11402726. The data supporting this article have also been included as part of the ESI.†Author contributions
Conceptualization, W. A. A. and M. D. C. N.; molecular dynamics simulations and quantum mechanical calculations, P. T. S. and M. D. C.·N.; writing original draft preparation W. A. A., A. M. A., P. T. S. and M. D. C. N.; writing review and editing, W. A. A., A. M. A., P. T. S. and M. D. C. N.; supervision M. D. C. N.; funding acquisition, W. A. A. and M. D. C. N. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – Brasil (CAPES) – Finance Code 001. This study was supported by FAPESP (2017/02317-2 and 2022/14753-0), CNPq (305574/2023-0), and the National Institute of Science and Technology in Bioanalytics (FAPESP 2014/50867-3 and CNPq 465389/2014-7) grants. The authors thank Central Computacional Multiusuario (CCM) from UFABC for the computational infrastructure provided.Notes and references
- B. List, et al., Proline-catalyzed direct asymmetric aldol reactions, J. Am. Chem. Soc., 2000, 122, 2395–2396 CrossRef CAS.
- B. List, Proline-catalyzed asymmetric reactions, Tetrahedron, 2002, 58, 5573–5590 CrossRef CAS.
- S. Bahmanyar and K. N. Houk, The origin of stereoselectivity in proline-catalyzed intramolecular aldol reactions, J. Am. Chem. Soc., 2001, 123, 12911–12912 CrossRef CAS PubMed.
- S. Bahmanyar, K. N. Houk, H. J. Martin and B. List, Quantum mechanical predictions of the stereoselectivities of proline-catalyzed asymmetric intermolecular aldol reactions, J. Am. Chem. Soc., 2003, 125, 2475–2479 CrossRef CAS PubMed.
- F. R. Clemente and K. N. Houk, Computational evidence for the enamine mechanism of intramolecular aldol reactions catalyzed by proline, Angew. Chem., Int. Ed., 2004, 43, 5766–5768 CrossRef CAS PubMed.
- M. B. Schmid, K. Zeitler and R. M. Gschwind, The elusive enamine intermediate in proline-catalyzed aldol reactions: NMR detection, formation pathway, and stabilization trends, Angew. Chem., Int. Ed., 2010, 49, 4997–5003 CrossRef CAS PubMed.
- N. Mase, et al., Organocatalytic direct asymmetric aldol reactions in water, J. Am. Chem. Soc., 2006, 128, 734–735 CrossRef CAS PubMed.
- A. Armstrong, et al., The Houk–List transition states for organocatalytic mechanisms revisited, Chem. Sci., 2014, 5, 2057–2071 RSC.
- Z. Tang, et al., Enantioselective direct aldol reactions catalyzed by L-prolinamide derivatives, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 5755–5760 CrossRef CAS PubMed.
- Z. Tang, et al., A highly efficient organocatalyst for direct aldol reactions of ketones with aldedydes, J. Am. Chem. Soc., 2005, 127, 9285–9289 CrossRef CAS PubMed.
- B. M. Soares, et al., Chiral organocatalysts based on lipopeptide micelles for aldol reactions in water, Phys. Chem. Chem. Phys., 2017, 19, 1181–1189 RSC.
- B. M. Soares, et al., Structure optimization of lipopeptide assemblies for aldol reactions in an aqueous medium, Phys. Chem. Chem. Phys., 2021, 23, 10953–10963 RSC.
- F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Software update: the ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, 4–9 Search PubMed.
- F. Neese, Software update: The ORCA program system—version 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606, DOI:10.1002/wcms.1606.
- H. Neugebauer, P. Pinski, S. Grimme, F. Neese and M. Bursch, Assessment of DLPNO-MP2 approximations in double-hybrid DFT, J. Chem. Theory Comput., 2023, 19, 7695–7703 CrossRef CAS PubMed.
- D. A. Case, et al., The Amber biomolecular simulation programs, J. Comput. Chem., 2005, 26, 1668–1688 CrossRef CAS PubMed.
- R. Salomon-Ferrer, D. A. Case and R. C. Walker, An overview of the Amber biomolecular simulation package, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 198–210 CAS.
- A. W. Götz, et al., Routine microsecond molecular dynamics simulations with AMBER on GPUs. 1. generalized born, J. Chem. Theory Comput., 2012, 8, 1542–1555 CrossRef PubMed.
- R. Salomon-Ferrer, A. W. Götz, D. Poole, S. Le Grand and R. C. Walker, Routine microsecond molecular dynamics simulations with AMBER on GPUs. 2. Explicit solvent particle mesh ewald, J. Chem. Theory Comput., 2013, 9, 3878–3888 CrossRef CAS PubMed.
- J. A. Maier, et al., ff14SB: improving the accuracy of protein side chain and backbone parameters from ff99SB, J. Chem. Theory Comput., 2015, 11, 3696–3713 CrossRef CAS PubMed.
- C. J. Dickson, R. C. Walker and I. R. Gould, Lipid21: complex lipid membrane simulations with AMBER, J. Chem. Theory Comput., 2022, 18, 1726–1736 CrossRef CAS PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general Amber force field, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- M. J. Frisch, et al., Gaussian 09, 2009 Search PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, PACKMOL: a package for building initial configurations for molecular dynamics simulations, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- D. E. Curtis, et al., Avogadro: an advanced semantic chemical editor, visualization, and analysis platform, J. Cheminform., 2012, 4, 17 CrossRef PubMed.
- W. Humphrey, A. Dalke and K. Schulten, VMD – visual molecular dynamics, J. Mol. Graph., 1996, 7855, 33–38 CrossRef PubMed.
- D. Cremer and J. A. Pople, A general definition of ring puckering coordinates, J. Am. Chem. Soc., 1975, 97, 1354–1358 CrossRef CAS.
- S. Cross, M. M. Kuttel, J. E. Stone and J. E. Gain, Visualisation of cyclic and multi-branched molecules with VMD, J. Mol. Graph. Model., 2009, 28, 131–139 CrossRef CAS PubMed.
- Marvin Was Used for Drawing, Displaying and Characterizing Chemical Structures, Substructures and Reactions, Marvin n.n.n, 201n, ChemAxon, 2019, https://www.chemaxon.com/ Search PubMed.
- C. R. Harris, et al., Array programming with {NumPy}, Nature, 2020, 585, 357–362 CrossRef CAS PubMed.
- P. Virtanen, et al., {SciPy} 1.0: fundamental algorithms for scientific computing in python, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- J. D. Hunter, Matplotlib: a 2D graphics environment, Comput. Sci. Eng., 2007, 9, 90–95 Search PubMed.
- D. R. Roe and T. E. Cheatham, PTRAJ and CPPTRAJ: software for processing and analysis of molecular dynamics trajectory data, J. Chem. Theory Comput., 2013, 9, 3084–3095 CrossRef CAS PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the colic-salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B Condens. Matter., 1998, 37, 785–789 CrossRef PubMed.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- A. D. Becke and E. R. Johnson, Exchange-hole dipole moment and the dispersion interaction, J. Chem. Phys., 2005, 122, 154104 CrossRef PubMed.
- A. D. McLean and G. S. Chandler, Contracted gaussian basis sets for molecular calculations. I. Second row atoms, Z = 11-18, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS.
- M. J. Frisch, J. A. Pople and J. S. Binkley, Self-consistent molecular orbital methods 25. Supplementary functions for Gaussian basis sets, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS.
- T. Clark, J. Chandrasekhar and G. W. Spitznagel, Efficient diffuse function-augmented basis sets for anion calculations, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- F. Neese, A. Hansen and D. G. Liakos, Efficient and accurate approximations to the local coupled cluster singles doubles method using a truncated pair natural orbital basis, J. Chem. Phys., 2009, 131, 064103 CrossRef PubMed.
- F. Neese, F. Wennmohs and A. Hansen, Efficient and accurate local approximations to coupled-electron pair approaches: an attempt to revive the pair natural orbital method, J. Chem. Phys., 2009, 130, 114108 CrossRef PubMed.
- A. Hansen, D. G. Liakos and F. Neese, Efficient and accurate local single reference correlation methods for high-spin open-shell molecules using pair natural orbitals, J. Chem. Phys., 2011, 135, 214102 CrossRef PubMed.
- C. Riplinger and F. Neese, An efficient and near linear scaling pair natural orbital based local coupled cluster method, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed.
- H. Jónsson, G. Mills and K. W. Jacobsen, Nudged elastic band method for finding minimum energy paths of transitions, in Classical and Quantum Dynamics in Condensed Phase Simulations, 1998, pp. 385–404, DOI:10.1142/9789812839664_0016.
- V. Ásgeirsson, et al., Nudged elastic band method for molecular reactions using energy-weighted springs combined with eigenvector following, J. Chem. Theory Comput., 2021, 17, 4929–4945 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Supplementary information contains figures for all transition states (Fig. S1 and S2) and additional radial distribution functions (Fig. S3). We also provide a table with energy only values for the HLTW mechanism (Table S1) and results for a detailed hydrogen bond analysis involved in the reaction complex in the aggregate. See DOI: https://doi.org/10.1039/d4ra03222e. |
| ‡ All geometries reported in this study along representative molecular dynamics frames have been deposited in https://doi.org/10.5281/zenodo.11402726 |
| This journal is © The Royal Society of Chemistry 2024 |

![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Phe-NO2. An enamine derived from
Phe-NO2. An enamine derived from