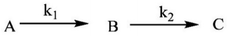Open Access Article
Open Access ArticleSynthesis, kinetics, mechanisms, and bioactivity evaluations of a novel Zn(II) complex
Anwesha Dey†
a,
Ramesh Kumar† b,
Bhramar Dutta
b,
Bhramar Dutta c,
Rajib Bandopadhyayc,
Sankha Chakrabortty
c,
Rajib Bandopadhyayc,
Sankha Chakrabortty d,
Moonis Ali Khan
d,
Moonis Ali Khan e,
Rijuta Ganesh Saratalef,
Ganesh Dattatraya Sarataleg,
Byong Hun Jeon
e,
Rijuta Ganesh Saratalef,
Ganesh Dattatraya Sarataleg,
Byong Hun Jeon *b and
Alak K. Ghosh
*b and
Alak K. Ghosh *a
*a
aDepartment of Chemistry, The University of Burdwan, Burdwan (E) 713104, West Bengal, India. E-mail: akghosh@chem.buruniv.ac.in
bDepartment of Earth Resources & Environmental, Engineering, Hanyang University, 222-Wangsimni-ro, Seongdong-gu, Seoul 04763, Republic of Korea. E-mail: bhjeon@hanyang.ac.kr
cDepartment of Botany, The University of Burdwan, Burdwan (E) 713104, West Bengal, India
dSchool of Chemical Engineering, Kalinga Institute of Industrial Technology, Bhubaneswar 751024, Odisha, India
eChemistry Department, College of Science, King Saud University, Riyadh 11451, Saudi Arabia
fResearch Institute of Integrative Life Sciences, Dongguk University-Seoul, Ilsandong-gu, Goyang-si, Gyeonggido 10326, Republic of Korea
gDepartment of Food Science and Biotechnology, Dongguk University-Seoul, 32 Dongguk-ro, Ilsandong-gu, Goyang-si, 10326, Gyeonggi-do, Republic of Korea
First published on 10th September 2024
Abstract
Zn(II)-based anticancer drugs can be suitable alternatives to conventional Pt(II)-based drugs because of the unique chemical properties of Zn(II) and low toxicity. In this study, a new hexadentate and heteroleptic Zn(II) complex ([Zn(bpy)2(OAc)2], 1) was prepared with a conventional N,N-donor ligand (2,2′-bipyridine) and a leaving group (OAc) and characterized via ESI-MS, UV-Vis, and FT-IR spectroscopy. Kinetic and mechanistic investigations of 1 were performed using two biologically relevant ligands (DL-penicillamine and L-cysteine) to understand its selectivity and reactivity. Substitution reactions were determined to be two-step processes in the associative activation mode. Bioactivity studies of 1 revealed moderate to strong DNA-binding, cleaving ability, and antimicrobial properties.
Introduction
Transition metal complexes are being explored as alternative antitumor agents to Pt(II) complexes, owing to their lower toxicity and higher efficacy compared to that of the latter.1 In particular, Ru(III), Ga, and As complexes have emerged as promising anticancer drugs.2 Some Zn(II) coordination complexes also showed promising DNA binding ability and antitumor activity.3,4 This is attributed to their unique chemical properties, diverse biological functionality, and lower toxicity at even higher doses compared to other metals,5,6 negligible side effects compared to the available anticancer drugs,7 and affordability.Zn has three unique chemical properties: (i) it has a 3d10 electronic configuration in the +2 state; thus, the Zn(II) coordination complexes have no ligand-field stabilization energy.8 Hence, they do not have preferential geometry and can form readily exchangeable, flexible, but strong complexes with organic ligands;9 (ii) Zn(II) has a filled 3d orbital and is thus redox inactive. Hence, they are highly stable in biological reactions and can easily enter biological systems without causing oxidative stress-mediated damage; and (iii) Zn(II) is classified as a borderline metal ion by Pearson in 1963.10 Therefore, it does not have preference among N, O, or S for coordination. In addition, Zn is an essential trace element and the second-most abundant element in the body.11 It is crucial for all forms of life on the planet. Zn is present in all body fluids and tissues, with maximum fractions in the muscle tissue, skeleton, and liver.12 It has diverse biological functions owing to its redox-inactive nature. Zn(II) complexes strengthen the immune system;13 regulate RNA transcription and DNA synthesis;14 heal wounds;15,16 maintain cell growth, cell division, differentiation, proliferation,17 and prostaglandin function;14 regulate body fluid pH; enhance collagen formation in hair, nails, and skin;18 and improve memory and mental health.
The physicochemical properties of Zn(II), such as its diamagnetism, strong Lewis acidity, and d10 configuration, enable the formation of different coordination geometries with chelating ligands of diverse donor atoms and hapticity.3 Moreover, Zn(II) complexes have exhibited antiproliferative activity, fast ligand exchange, Lewis acid activation, and catalytic activities in hydrolysis and DNA cleavage.19,20 In addition, they are non-toxic, even at high dosages. They have a preventative effect on infectious diseases and are less harmful anticancer drugs.21 In particular, zinc phthalocyanines serve as photosensitizers or light-sensitive compounds during the photodynamic treatment of tumor cells by producing reactive oxygen species (ROS).22 Moreover, Zn(II) forms dimeric and polymeric complexes with various donor atoms, such as N, O, and S, in ligands of different capacities, resulting in complexes of different geometries and coordination. In particular, Zn(II) complexes with N-donor ligands have been extensively explored as anticancer agents.3
To further explore the anticancer activity of Zn(II) complexes with N-donor ligands, in this study, we synthesized a six-coordinated Zn(II) complex bearing two N-donor ligands (2,2′-bipyridine; bpy) and two acetate groups and explored its kinetics and anticancer mechanistic aspects. The DNA binding ability, cleaving capacity, and germicidal activity of the Zn(II) complex were evaluated via several bioassays. The aromatic ligand bpy serves as a spectator ligand and facilitates a similar donor environment to that of cis-diamminedichloroplatinum(II).23
Materials and methods
Chemicals
All chemicals were reagent-grade and used without further purification. Chemicals, such as Zn(OAc)2, DL-penicillamine, L-cysteine, Tris buffer, pBR322, EtBr, and bpy were purchased from Sisco Research Laboratories Pvt. Ltd (India). Calf thymus DNA (ctDNA) and AgClO4 were purchased from Sigma-Aldrich (USA). Ampicillin and potato-dextrose agar were purchased from Hi-Media (USA). A constant ionic strength was maintained using a NaClO4 (0.1 M) solution, and the pH of all the solutions used for the kinetics experiments was adjusted using 1 M NaOH/HClO4 prior to the experiments.Analytical determination
A Shimadzu UV-vis spectrophotometer (Model UV-3600, Japan) was used for spectroscopic scanning. A Hi-Tech stopped-flow spectrophotometer (Model-TB 85) was used to obtain kinetic data at a controlled temperature. A Shimadzu IR Prestige-21 spectrophotometer (Japan) was used to collect FT-IR data. Mass spectra were obtained using ESI-MS equipment (Waters, Model-Xevo G2-XS QTof, USA) in a positive ion mode. A fluorometer (PerkinElmer, Model-L555 USA) was used to monitor fluorescence quenching. Plasmid DNA (pBR322) treated with [Zn(bpy)2(OAc)2] (1) was analyzed by agarose gel electrophoresis (Bio-Rad, USA).Synthesis of 1
Complex 1 was prepared by mixing the aqueous solutions of Zn(OAc)2 and bpy in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio. Aqueous solutions were prepared using double-distilled water. The solution of bpy was added to the solution of Zn(OAc)2 dropwise with continuous stirring using a magnetic stirrer for 8 h at 27 °C. The precipitated white solid was filtered and washed three times with distilled water.
2 molar ratio. Aqueous solutions were prepared using double-distilled water. The solution of bpy was added to the solution of Zn(OAc)2 dropwise with continuous stirring using a magnetic stirrer for 8 h at 27 °C. The precipitated white solid was filtered and washed three times with distilled water.
Kinetics evaluation
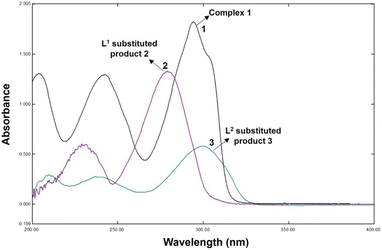
The reactions of 1 with DL-penicillamine (L1) and L-cysteine (L2) followed pseudo-first-order kinetics at three different concentrations of ligands and four different temperatures at a physiological pH of 7.4. As the reaction progressed, the maximum difference in the absorbances of 1 and the substituted products 2 (product of L1 and 1) and 3 (product of L2 and 1) were observed at 300 nm (Fig. 1).Hence, we monitored the reaction kinetics at 300 nm using five different concentrations (2.0–4.0 × 103 mol L−1) of L1 and L2 and four different temperatures (20–35 °C).
Job's method
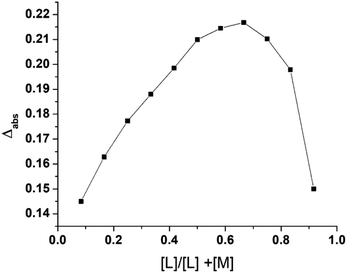
To determine the effect of continuous variation in the metal: ligand ratio in 2 and 3 and to obtain a bell-shaped curve, we used Job's method.24,25 Complex 1 and the ligands (L1 and L2) were mixed in an equimolar ratio of 2.0 × 10−4 mol L−1, and the pH of the solution was maintained at 7.4 at room temperature. The vessel was fitted with a reflux condenser to prevent solvent loss due to evaporation while heating the reaction mixture in a 60 °C water bath.Bioassays
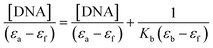 | (1) |
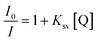 | (2) |
| KEtBr[EtBr] = Kapp[Q] | (3) |
log(F0 − F)/F = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KF + n KF + n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log[Q] log[Q]
| (4) |
Results and discussion
Characterization of 2 and 3
Products 2 and 3 were characterized via Job's method, FT-IR spectroscopy, and ESI-MS. Job's method revealed the metal![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ligand ratio (1
ligand ratio (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L1 and 1
L1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L2) in 2 and 3 to be 1
L2) in 2 and 3 to be 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
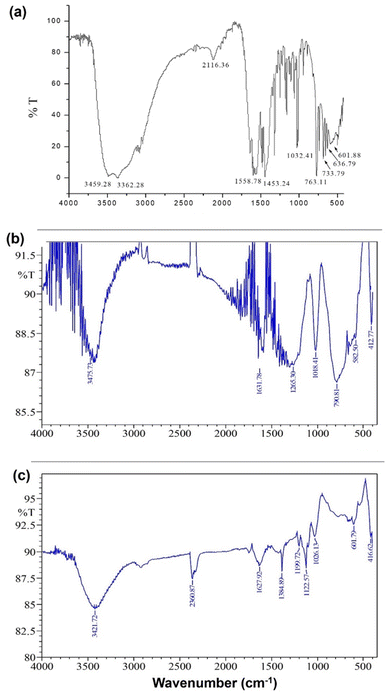
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (Fig. 2). Fig. 3(a)–(c) show the FT-IR spectra of 1, 2, and 3. The spectrum of 1 exhibited bands at 636.79 and 601.88 cm−1 corresponding to Zn–N stretching vibrations and 733.79 and 763.11 cm−1 corresponding to Zn–O stretching vibrations.35 The IR spectrum of 2 showed bands at 612.25 and 582.50 cm−1 corresponding to Zn–N bonds and 412.77 cm−1 corresponding to the newly formed Zn–S bonds in 2. The IR spectrum of 3 exhibited a band at ∼416.77 cm−1 corresponding to the newly formed Zn–S bond and 601.79 cm−1 corresponding to the Zn–N bonds.35,36
2 (Fig. 2). Fig. 3(a)–(c) show the FT-IR spectra of 1, 2, and 3. The spectrum of 1 exhibited bands at 636.79 and 601.88 cm−1 corresponding to Zn–N stretching vibrations and 733.79 and 763.11 cm−1 corresponding to Zn–O stretching vibrations.35 The IR spectrum of 2 showed bands at 612.25 and 582.50 cm−1 corresponding to Zn–N bonds and 412.77 cm−1 corresponding to the newly formed Zn–S bonds in 2. The IR spectrum of 3 exhibited a band at ∼416.77 cm−1 corresponding to the newly formed Zn–S bond and 601.79 cm−1 corresponding to the Zn–N bonds.35,36
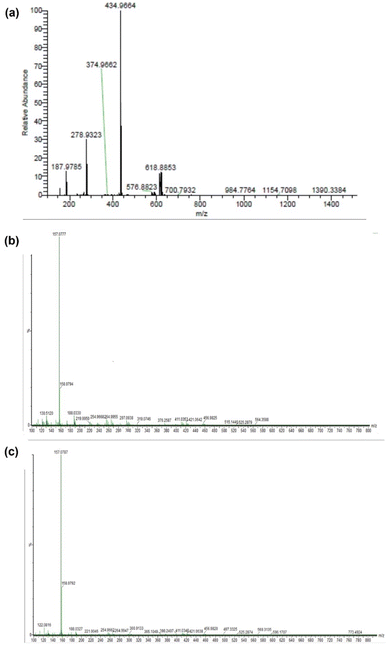
Fig. 4(a)–(c) show the ESI-MS spectra of 1, 2, and 3. The signals at 187.97, 279.93, 434.99, and 618.88 (Fig. 4(a)) correspond to [Zn2+ + 2bpy], [Zn2+ + 2bpy + OAc− + HClO4 + Na+], [Zn2+ + 2bpy + OAc−], and [Zn2+ + 2bpy + 2OAc− + HClO4 + Na+], respectively. The signals at 264.995 and 188.05 (Fig. 4(b)) are attributed to [Zn2+ + 2bpy + 2DL-penicillamine + H2O + ClO4− + 2H+] and [Zn2+ + 2bpy], respectively. The signals at 254.95 and 188.03 (Fig. 4(c)) correspond to [Zn2+ + 2bpy + 2L-cysteine + H2O + ClO4− + Na+] and [Zn2+ + 2bpy], respectively.
Kinetic studies
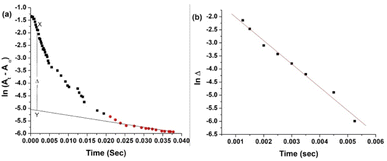
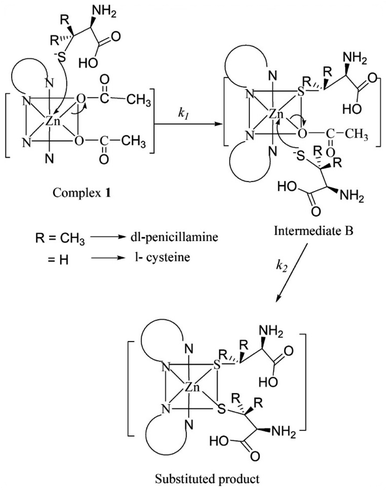
The pKa values for L1 are 1.90 (COOH), 7.88 (SH), and 10.58 (NH2) (Scheme 1),37 and those for L2 are 1.71 (COOH), 8.53 (SH), and 10.36 (NH2) (Scheme 2).38,39 These pKa values suggest that the S-containing ligands participate in the reactions in their anionic form (thiolate) at pH 7.4.The plot of ln(At − A∞) vs. t was non-linear; At and A∞ are absorbances at time t and after completion of the reaction, respectively (Fig. 5(a)). The plot curved initially before appearing linear with a constant slope. This indicates that the interactions of L1 and L2 with 1 proceed through two distinct steps (curved and linear). Scheme 3 was used to calculate the rate constants for both steps.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δ vs. t without using Origin software, as the slope of the best-fitted line of the first part of the ln(A∞ − At) vs. t plot did not work for calculations shown in Fig. 5(a).
Δ vs. t without using Origin software, as the slope of the best-fitted line of the first part of the ln(A∞ − At) vs. t plot did not work for calculations shown in Fig. 5(a).
(At − A∞) – a2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−k2t) = a1 exp(−k2t) = a1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−k1(obs)t) exp(−k1(obs)t)
| (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−k2t)] were calculated from X–Y values at different time intervals (Fig. 6(a)) and denoted as the ‘Δ’ values.
exp(−k2t)] were calculated from X–Y values at different time intervals (Fig. 6(a)) and denoted as the ‘Δ’ values.
Then, eqn (5) becomes
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δ = constant − k1(obs)t Δ = constant − k1(obs)t
| (6) |
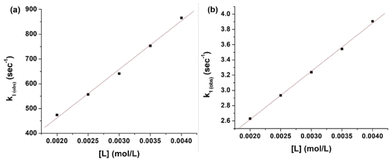
The k1(obs) was calculated from the slopes of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Δ vs. t plots (Fig. 5(b)) at ligand concentrations of 2.0, 3.0, and 4.0 × 10−3 mol L−1 at fixed [1], pH 7.4, ionic strength of 0.1 mol L−1 NaClO4, and different temperatures (20, 25, 30, and 35 °C). Tables 1 and 2 present the k1(obs) data.
Δ vs. t plots (Fig. 5(b)) at ligand concentrations of 2.0, 3.0, and 4.0 × 10−3 mol L−1 at fixed [1], pH 7.4, ionic strength of 0.1 mol L−1 NaClO4, and different temperatures (20, 25, 30, and 35 °C). Tables 1 and 2 present the k1(obs) data.
| System temperature (°C) | 103 [ligand] mol L−1 | |||||
|---|---|---|---|---|---|---|
| 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | ||
| L1 | 20 | 4.54 | 5.27 | 5.95 | 6.72 | 7.50 |
| 25 | 4.73 | 5.57 | 6.40 | 7.53 | 8.65 | |
| 30 | 4.78 | 5.72 | 6.66 | 7.83 | 9.01 | |
| 35 | 5.00 | 6.05 | 7.12 | 8.37 | 9.63 | |
| System temperature (°C) | 103 [ligand] mol L−1 | |||||
|---|---|---|---|---|---|---|
| 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | ||
| L2 | 20 | 1.51 | 2.13 | 2.75 | 3.39 | 3.83 |
| 25 | 2.63 | 2.94 | 3.24 | 3.65 | 4.05 | |
| 30 | 2.71 | 3.71 | 4.72 | 6.32 | 7.91 | |
| 35 | 5.06 | 7.03 | 9.00 | 10.4 | 11.8 | |
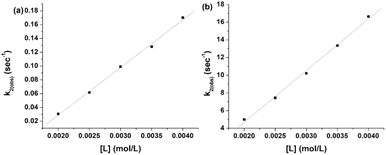
The plots of k1(obs) vs. [L] (Fig. 6(a) and (b)) are straight lines. The k1 values (slopes of the plots) at different [L] and temperatures (Tables 3 and 4) demonstrate that the rate increased as the [L] increased. The first step was ligand-dependent, which indicates that L1 or L2 attacks Zn(II) to form intermediate B in this step (Scheme 3).
| Ligand | Temperature (°C) | 10−5 k1 (L mol−1 s−1) |
|---|---|---|
| L1 | 20 | 1.48 ± 0.02 |
| 25 | 1.96 ± 0.08 | |
| 30 | 2.15 ± 0.07 | |
| 35 | 2.31 ± 0.06 |
| Ligand | Temperature (°C) | 10−1 k1 (L mol−1 s−1) |
|---|---|---|
| L2 | 20 | 1.27 ± 0.017 |
| 25 | 1.67 ± 0.05 | |
| 30 | 2.56 ± 0.31 | |
| 35 | 3.36 ± 0.32 |
| System temperature (°C) | 103 [ligand] mol L−1 | |||||
|---|---|---|---|---|---|---|
| 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | ||
| L1 | 20 | 2.51 | 5.15 | 6.62 | 10.25 | 12.73 |
| 25 | 3.07 | 6.17 | 8.57 | 12.79 | 17.01 | |
| 30 | 3.75 | 8.13 | 12.50 | 15.95 | 21.11 | |
| 35 | 5.01 | 9.80 | 14.50 | 18.75 | 23.01 | |
| L2 | 20 | 4.35 | 6.55 | 8.85 | 11.71 | 14.55 |
| 25 | 5.00 | 7.45 | 10.10 | 13.35 | 16.64 | |
| 30 | 6.67 | 9.88 | 13.10 | 16.66 | 20.22 | |
| 35 | 7.40 | 10.90 | 14.50 | 18.05 | 22.50 | |
| Ligand | Temperature (°C) | 10−1 k2 (L mol−1 s−1) |
|---|---|---|
| L1 | 20 | 5.10 ± 0.11 |
| 25 | 6.96 ± 0.70 | |
| 30 | 8.67 ± 0.04 | |
| 35 | 9.00 ± 0.007 | |
| L2 | 20 | 5.07 ± 0.33 |
| 25 | 5.85 ± 0.43 | |
| 30 | 6.66 ± 0.13 | |
| 35 | 7.55 ± 0.25 |
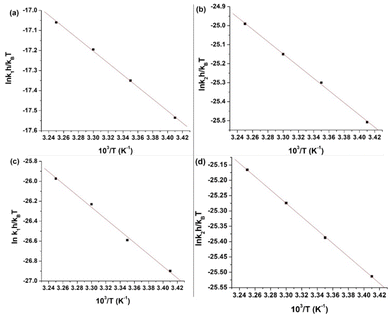
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) krh/kBT vs. 1/T) for the first and second steps of the reaction of L1 and 1 are shown in Fig. 8(a) and (b), whereas those of L2 are shown in Fig. 8(c) and (d). The enthalpy of activation values (ΔH≠1 and ΔH≠2) and the entropy of activation values (ΔS≠1 and ΔS≠2) are obtained from the slopes and the intercepts of the Eyring plots, respectively. The activation and thermodynamic parameters are listed in Table 7. The positive enthalpy and negative entropy values (Table 7) confirm the ligand dependency of 1 and the ligand interactions at each step.
krh/kBT vs. 1/T) for the first and second steps of the reaction of L1 and 1 are shown in Fig. 8(a) and (b), whereas those of L2 are shown in Fig. 8(c) and (d). The enthalpy of activation values (ΔH≠1 and ΔH≠2) and the entropy of activation values (ΔS≠1 and ΔS≠2) are obtained from the slopes and the intercepts of the Eyring plots, respectively. The activation and thermodynamic parameters are listed in Table 7. The positive enthalpy and negative entropy values (Table 7) confirm the ligand dependency of 1 and the ligand interactions at each step.
| Ligand | ΔH≠1 (kJ mol−1) | ΔS≠1 (J K−1 mol−1) | ΔH≠2 (kJ mol−1) | ΔS≠2 (J K−1 mol−1) |
|---|---|---|---|---|
| L1 | 24.81 ± 0.54 | −61 ± 1 | 26.76 ± 0.55 | −120 ± 1 |
| L2 | 49.51 ± 2.33 | −56 ± 2 | 18.09 ± 0.16 | −150 ± 0.5 |
The highly negative S≠1 and ΔS≠2 and the less positive ΔH≠1 and ΔH≠2, determined from ln(At − A∞) vs. t plots (Fig. 5(a)), indicate an associative mode of activation with two distinct steps (Scheme 3). Moreover, the rate constants (k1 and k2) depended on the ligand concentration. This suggests that, in the first step, one molecule of L attacks the Zn(II) to form intermediate B, which is further attacked by a second molecule of L to form the product.
The energy required for Zn–OAc bond cleavage is compensated by the energy released during Zn–L bond formation. The low ΔH≠1 and ΔH≠2 values support this inference. Our proposed mechanism is shown in Fig. 9.
Bioassays
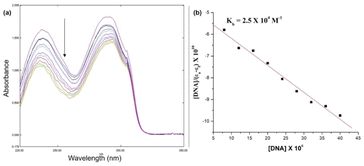
Fig. 10 shows the electronic absorption titration spectra of different ctDNA concentrations at a constant [1]. The absorption intensity decreased with increasing ctDNA concentrations without a red or blue shift (Fig. 10(a)). This hypochromism indicates an intercalative binding mode between 1 and ctDNA.44,45 The plot of [DNA]/(εb − εf) vs. [DNA] is linear (Fig. 10(b)). The Kb value (binding constant, 2.5 × 104 M−1) obtained from the slope of the plot indicates moderate to strong binding between 1 and ctDNA.
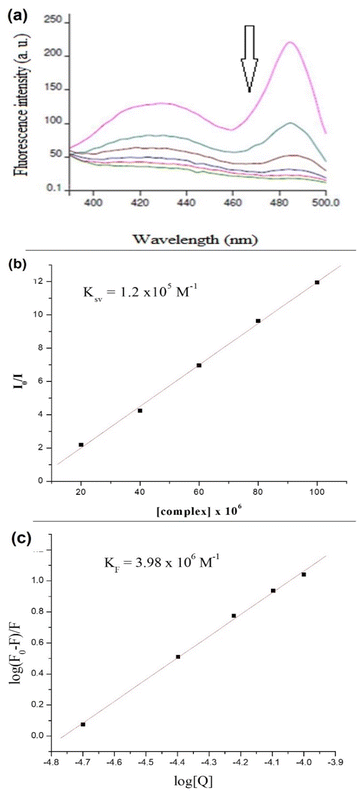
Increasing the concentration of 1 decreased the emission intensity of the EtBr–DNA solution owing to successive quenching. This indicates competition between 1 and EtBr for ctDNA binding (Fig. 11(a)). The Ksv value of 1.5 × 103 M−1 was obtained using the Stern–Volmer plot, whereas KF (4.57 × 106 M−1) and n (1.4) values were obtained using Scatchard plots of 1 and ctDNA (Fig. 11(b) and (c)).
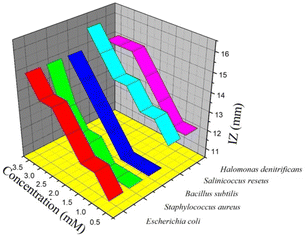
| Microorganisms | Zone of inhibition (mm) | |||||||
|---|---|---|---|---|---|---|---|---|
| bpy | L | M1 | M2 | H | H1 | H2 | H3 | |
| a [L] = 0.5 × 10−3 M; [M1] = 1.0 × 10−3 M; [M2] = 1.5 × 10−3 M; [H] = 2.0 × 10−3 M; [H1] = 2.5 × 10−3 M; [H2] = 3.0 × 10−3 M; and [H3] = 3.5 × 10−3 M. | ||||||||
| Gram-negative bacteria | ||||||||
| Enterobacter asburiae | — | — | — | — | — | — | — | — |
| Escherichia coli | 10 | 11 | 12 | 12 | 13 | 14 | 14 | 15 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Gram-positive bacteria | ||||||||
| Staphylococcus aureus | — | 11 | 11 | 11 | 12 | 12 | 13 | 15 |
| Bacillus subtilis | <10 | 11 | 11 | 11 | 12 | 13 | 14 | 15 |
| Salinicoccus roseus | 11 | 12 | 13 | 13 | 14 | 14 | 15 | 16 |
| Halomonas denitrificans | 11 | 12 | 12 | 13 | 14 | 15 | 15 | 15 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Fungus | ||||||||
| Aspergillus niger | — | — | — | — | — | — | — | — |
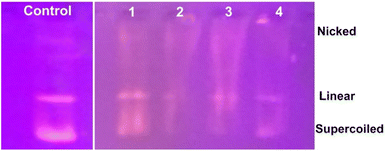
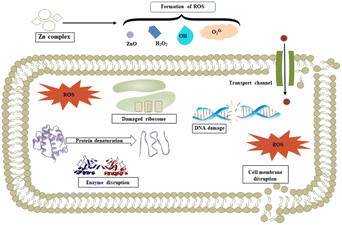
We propose a mechanism for the antimicrobial activity of 1 based on the literature and our findings (Fig. 14).50 The charge density of Zn2+ is reduced to chelation in 1, which reduces its hydrophilicity and enhances lipophilicity. This enables its quick entry through the cell membrane (due to its lipidic nature).51,52 Then, 1 participates in bactericidal (killing) or bacteriostatic (blocking of active sites) mechanisms. An increase in Zn2+ concentration above the optimal limit disrupts ion homeostasis. This allows the efflux of Zn2+ inside the cell, causing a cytotoxic effect. Moreover, Zn2+ has been attributed to the upregulation of ROS, which leads to oxidative stress in bacterial cells. This is consistent with previous reports, which demonstrated that the antimicrobial properties of Zn-based complexes are correlated to ROS overproduction, which may be the underlying mechanism for cell death caused by DNA damage.50,53 The increased membrane permeability of bacterial cells, mediated by Zn2+, facilitates ion channel dysfunction. This disrupts respiratory processes and reduces energy-producing adenosine triphosphate synthesis.
Conclusions
A novel six-coordinate Zn(II) complex was synthesized and characterized using electronic, FT-IR, and ESI-MS spectroscopy. Kinetic and mechanistic investigations were performed in an aqueous medium and under pseudo-first-order reaction conditions at physiological pH with two bio-relevant ligands bearing N, O, and S donor atoms. These substitution reactions involved two distinct ligand-dependent steps. Highly negative entropy of activation values and less positive enthalpy of activation values suggested an associative activation mode. The rate constants (k1) were in the following order: L1 (DL-penicillamine) ≫ L2 (L-cysteine). This was attributed to the lower pK2 value (SH) and +I effect of two methyl groups at the Cβ of L1. Even though both ligands have S and N donor sets, the ligands were bonded to Zn(II) via their S end. In vitro, DNA-binding studies indicated a positive interaction between 1 ([Zn(bpy)2(OAc)2]) and ctDNA. We also demonstrated the bactericidal and fungicidal effects of 1 against selected microbial strains. This study can be summarized as follows: (i) selection of a non-toxic metal center (Zn(II)); (ii) kinetic investigation to elucidate the selectivity and reactivity of different ligands; (iii) elucidation of DNA binding and cleavage capacity; and (iv) exploration of the antimicrobial activity of 1.Data availability
Data supporting this study are openly available from Prof. Alak K. Ghosh.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean Government (MSIT) (No. RS-2023-00219983). Moonis Ali Khan acknowledges financial support through the Researchers Supporting Project (RSP2024R345), King Saud University, Riyadh, Saudi Arabia. Another author (Dr R. Kumar) acknowledges support from the Creative and Challenging Research Program [grant number 2021R1I1A1A01060846] of the National Research Foundation (NRF) of the Republic of Korea.References
- S. Abdolmaleki, A. Aliabadi and S. Khaksar, Coord. Chem. Rev., 2024, 501, 215579 CrossRef CAS.
- S. Adhikari, P. Nath, A. Das, A. Datta, N. Baildya, A. K. Duttaroy and S. Pathak, Biomed. Pharmacother., 2024, 171, 116211 CrossRef CAS PubMed.
- M. Porchia, M. Pellei, F. Del Bello and C. Santini, Molecules, 2020, 25, 5814 CrossRef CAS.
- R. Ye, C. Tan, B. Chen, R. Li and Z. Mao, Front. Chem., 2020, 8, 402 CrossRef CAS PubMed.
- T. V. Soldatović, B. Šmit, E. M. Mrkalić, S. L. Matić, R. M. Jelić, M. Ć. Serafinović, N. Gligorijević, M. Čavić, S. Aranđelović and S. Grgurić-Šipka, J. Inorg. Biochem., 2023, 240, 112100 CrossRef PubMed.
- S. Singh and K. Pal, Int. J. Biol. Macromol., 2023, 234, 123602 CrossRef CAS.
- S. Bhattacharyya, A. Sarkar, S. K. Dey and A. Mukherjee, J. Inorg. Biochem., 2014, 140, 131–142 CrossRef CAS.
- Z. Wang, S. Gai, C. Wang, G. Yang, C. Zhong, Y. Dai, F. He, D. Yang and P. Yang, Chem. Eng. J., 2019, 361, 117–128 CrossRef CAS.
- M. Fakhar-e-Alam, I. Amjad, M. Saadullah, M. Tahir, M. Jawad, M. Asif, M. Atif, S. Zara and M. Rashad, J. Saudi Chem. Soc., 2024, 28, 101814 CrossRef CAS.
- R. G. Pearson, J. Am. Chem. Soc., 1963, 85, 3533–3539 CrossRef CAS.
- P. Gać, K. Czerwińska, P. Macek, A. Jaremków, G. Mazur, K. Pawlas and R. Poręba, Environ. Toxicol. Pharmacol., 2021, 82, 103553 CrossRef.
- C. B. Devi, T. Nandakishore, N. Sangeeta, G. Basar, N. O. Devi, S. Jamir and M. A. Singh, IOSR J. Dent. Med. Sci., 2014, 13, 18–23 CrossRef.
- P. J. Fraker, L. E. King, T. Laakko and T. L. Vollmer, J. Nutr., 2000, 130, 1399S–1406S CrossRef CAS PubMed.
- C. T. Chasapis, A. C. Loutsidou, C. A. Spiliopoulou and M. E. Stefanidou, Arch. Toxicol., 2012, 86, 521–534 CrossRef CAS.
- A. B. Lansdown, U. Mirastschijski, N. Stubbs, E. Scanlon and M. S. Ågren, Wound Repair Regen., 2007, 15, 2–16 CrossRef PubMed.
- S. S. Singh, B. Jena, S. Roy, S. Nayak, S. K. Behera, S. Chakrabortty, S. K. Tripathy, M. Ali Khan, R. Kumar, B.-H. Jeon, C. Stålsby Lundborg and A. Mishra, Chem. Eng. J., 2024, 490, 151788 CrossRef.
- R. S. MacDonald, J. Nutr., 2000, 130, 1500S–1508S CrossRef CAS PubMed.
- K. Sardana and V. K. Garg, Dermatol. Ther., 2010, 23, 411–418 CrossRef.
- J. Qian, L. Wang, W. Gu, X. Liu, J. Tian and S. Yan, Dalton Trans., 2011, 40, 5617–5624 RSC.
- S. Q. Zhang, X. F. Yu, H. B. Zhang, N. Peng, Z. X. Chen, Q. Cheng, X. L. Zhang, S. H. Cheng and Y. Zhang, Mol. Nutr. Food Res., 2018, 62, e1700981 CrossRef PubMed.
- M. Pellei, F. Del Bello, M. Porchia and C. Santini, Coord. Chem. Rev., 2021, 445, 214088 CrossRef CAS.
- L. P. Roguin, N. Chiarante, M. C. García Vior and J. Marino, Int. J. Biochem. Cell Biol., 2019, 114, 105575 CrossRef CAS.
- A. A. Franich, M. D. Živković, J. Milovanović, D. Arsenijević, A. Arsenijević, M. Milovanović, M. I. Djuran and S. Rajković, J. Inorg. Biochem., 2020, 210, 111158 CrossRef CAS PubMed.
- C. Y. Huang, in Methods in Enzymology, ed. D. L. Purich, Academic Press, 1982, vol. 87, pp. 509–525 Search PubMed.
- J. P. M. João, Ann. Chim. Appl., 1928, 113–203 Search PubMed.
- E. Gao, L. Liu, M. Zhu, Y. Huang, F. Guan, X. Gao, M. Zhang, L. Wang, W. Zhang and Y. Sun, Inorg. Chem., 2011, 50, 4732–4741 CrossRef CAS PubMed.
- A. Pal, B. Biswas, S. K. Mondal, C.-H. Lin and R. Ghosh, Polyhedron, 2012, 31, 671–675 CrossRef CAS.
- C. D. Kanakis, P. A. Tarantilis, M. Polissiou, S. Diamantoglou and H. Tajmir-Riahi, Cell Biochem. Biophys., 2007, 49, 29–36 CrossRef CAS.
- A. A. El-Bindary, N. Hassan and M. A. El-Afify, J. Mol. Liq., 2017, 242, 213–228 CrossRef CAS.
- I. Mitra, S. Mukherjee, V. P. Reddy B, S. Dasgupta, J. C. Bose K, S. Mukherjee, W. Linert and S. C. Moi, RSC Adv., 2016, 6, 76600–76613 RSC.
- P. Borst, IUBMB Life, 2005, 57, 745–747 CrossRef CAS.
- M. Balouiri, M. Sadiki and S. K. Ibnsouda, J. Pharm. Anal., 2016, 6, 71–79 CrossRef.
- R. Geetha, C. Sathian, V. Prasad and V. Gleeja, Asian J. Dairy Food Res., 2015, 34, 259–264 CrossRef.
- P. Ristivojević, I. Dimkić, J. Trifković, T. Berić, I. Vovk, D. Milojković-Opsenica and S. Stanković, PLoS One, 2016, 11, e0157097 CrossRef.
- D. Huang, Q. Xin, Y. Ni, Y. Shuai, S. Wang, Y. Li, H. Ye, L. Lin, X. Ding and Y. Zhang, RSC Adv., 2018, 8, 6099–6109 RSC.
- L.-N. Liu, J.-G. Dai, T.-J. Zhao, S.-Y. Guo, D.-S. Hou, P. Zhang, J. Shang, S. Wang and S. Han, RSC Adv., 2017, 7, 35075–35085 RSC.
- A. E. Martell and R. M. Smith, Critical Stability Constants, Springer, 1974 Search PubMed.
- G. Hager and A. G. Brolo, J. Electroanal. Chem., 2009, 625, 109–116 CrossRef CAS.
- A. H. Dourado, A. P. de Lima Batista, A. G. Oliveira-Filho, P. T. Sumodjo and S. I. C. de Torresi, RSC Adv., 2017, 7, 7492–7501 RSC.
- J. A. Weyh and R. E. Hamm, Inorg. Chem., 1969, 8, 2298–2302 CrossRef CAS.
- F. A. Cotton, G. Wilkinson, C. A. Murillo and M. Bochmann, Advances in Inorganic Chemistry, John Wiley & Sons, 1999 Search PubMed.
- B. M. Zeglis, V. C. Pierre and J. K. Barton, Chem. Commun., 2007, 4565–4579, 10.1039/B710949K.
- F. Arjmand, M. Aziz and M. Chauhan, J. Inclusion Phenom. Macrocyclic Chem., 2008, 61, 265–278 CrossRef CAS.
- M. J. Brabha and M. A. Malbi, Chem. Phys. Impact, 2023, 7, 100248 CrossRef.
- F. Arjmand and M. B. Chauhan, Helv. Chim. Acta, 2005, 88, 2413–2423 CrossRef CAS.
- C.-L. Zhang, D.-H. Cai, S. Chen, W. Liu, Y.-H. Xiong and X.-Y. Le, Transition Met. Chem., 2019, 44, 603–613 CrossRef CAS.
- Q. Zhang, Y. Xiang, D. Liang, Y. Peng and H. Guo, Bioorg. Med. Chem. Lett., 2012, 22, 1814–1817 CrossRef CAS.
- S. P. Santoso, S. Ismadji, A. E. Angkawijaya, F. E. Soetaredjo, A. W. Go and Y. H. Ju, J. Mol. Liq., 2016, 221, 617–623 CrossRef CAS.
- R. Sinha, R. Karan, A. Sinha and S. K. Khare, Bioresour. Technol., 2011, 102, 1516–1520 CrossRef CAS PubMed.
- I. Matai, A. Sachdev, P. Dubey, S. Uday Kumar, B. Bhushan and P. Gopinath, Colloids Surf., B, 2014, 115, 359–367 CrossRef CAS.
- Pranjal, G. Chandra Mahapatra, S. Chakrabortty, S. Banerjee, S. Chowdhury, M. Ali Khan, R. Kumar, B.-H. Jeon, A. Mishra, C. Stålsby Lundborg and S. K. Tripathy, Chem. Eng. J., 2024, 497, 154670 CrossRef CAS.
- B. Jena, S. S. Singh, S. Chakrabortty, S. K. Behera, S. K. Tripathy, C. S. Lundborg, R. Kumar, M. Ali Khan, B. H. Jeon and A. Mishra, J. Ind. Eng. Chem., 2024 DOI:10.1016/j.jiec.2024.04.049.
- F.-Y. Wang, Q.-Y. Xi, K.-B. Huang, X.-M. Tang, Z.-F. Chen, Y.-C. Liu and H. Liang, J. Inorg. Biochem., 2017, 169, 23–31 CrossRef CAS PubMed.
Footnote |
| † These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2024 |