Open Access Article
Open Access Article5-step algorithm to accelerate the prediction of [Au25(SR)19]z clusters (z = 1−, 0, 1+)†
A. Tlahuice-Flores *
*
Universidad Autónoma de Nuevo León, CICFIM,-Facultad de Ciencias Físico-Matemáticas, San Nicolás de los Garza, Nuevo León 66455, Mexico. E-mail: tlahuicef@gmail.com
First published on 18th June 2024
Abstract
Prediction of the structure of thiolated gold clusters is time demanding, and new strategies are needed to expedite this process. In this study, using one five-step algorithm and dispersion corrected density functional theory (DFT-D) calculations, new models are proposed for neutral and charged Au25(SR)19 clusters that contain one extra ligand with respect to the ubiquitous Au25(SR)18 cluster. The algorithm counts for constituting tetrahedra/octahedra units of related isomers, and it provides their energy order. In general, one structure comprising one Au11 inner core is found as energy minima of neutral and charged Au25(SR)19 clusters. Therefore, our new neutral structure is 0.20 eV (–CH3 and TPSS) more stable than the previously reported one. With respect to neutral and anionic structures containing inner cores with C2v symmetry, ultraviolet-visible/circular dichroism profiles are similar.
1 Introduction
The structural prediction of thiolated gold clusters continues due to the recent synthesis and characterization of stable clusters displaying new gold![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sulphur ratios. For example, the well-known Au25(SR)18[1−] cluster comprises one Au13 inner core (in fact, it can be observed to contain 20 distorted tetrahedra) and 12 gold adatoms forming part of 6 staple motifs (6 dimer motifs).1–5 Recently, Xie et al. reported a new size with a 25
sulphur ratios. For example, the well-known Au25(SR)18[1−] cluster comprises one Au13 inner core (in fact, it can be observed to contain 20 distorted tetrahedra) and 12 gold adatoms forming part of 6 staple motifs (6 dimer motifs).1–5 Recently, Xie et al. reported a new size with a 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 gold
19 gold![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sulphur ratio found during reactions with MHA ligands (6-mercaptohexanoic acid). These ligands conferred Au25(SR)18[1−] cluster and its counterpart Au25(SR)19[0] cluster with water solubility.6 The importance of structural isomerism and kernel atom packing is related to the selection of ligands during experiments, and some interesting properties such as photoluminescence, catalysis and optics are related to the mentioned core composition.7–11
sulphur ratio found during reactions with MHA ligands (6-mercaptohexanoic acid). These ligands conferred Au25(SR)18[1−] cluster and its counterpart Au25(SR)19[0] cluster with water solubility.6 The importance of structural isomerism and kernel atom packing is related to the selection of ligands during experiments, and some interesting properties such as photoluminescence, catalysis and optics are related to the mentioned core composition.7–11
Experimentally, the transformation to obtain Au25(SR)19[0] from Au25(SR)18[1−] cluster implies the introduction of one extra ligand during an oxidative etching reaction while the number of gold atoms is maintained. From a theoretical perspective, it is interesting to inquire about the induced structural change in the organic shell or inner core after introducing one extra ligand. In such a manner, the reversibility of the transformation from Au25(SR)19[0] to Au25(SR)18[1−] cluster (carbon monoxide reduction) must depend on the strength of structural distortion and energetic differences among implied species. It is important to mention that further fragmentation studies (tandem mass spectroscopy) on the produced Au25(SR)19[0] cluster revealed the presence of a lengthened motif (Au5SR5 unit) after ligand addition.6 It can be interpreted as one pentameric cycle comprising the inner core of the Au25(SR)19[0] cluster.
In 2023, C. Yan et al. proposed a simplified structural model for a neutral Au25(SR)19 cluster (considering –CH3 as a ligand) using a grand unified model (GUM).12,13 Reported isomer comprises one low symmetry (C1) Au11 core14 and is described in terms of fused Au3 and Au4 blocks, while parent Au25(SR)18[1−] cluster has one high symmetry Au13 inner core constituting of 20 distorted tetrahedra (Au4 units). The organic shell is also different, while the parent Au25(SR)18[1−] cluster is protected by six dimer motifs, and the Au25(SR)19[0] isomer is explained as protected by 1 pentamer, 2 trimers, 1 dimer and 1 monomer motif. However, the scarce resemblance between structural models of Au25(SR)18[1−] and Au25(SR)19[0] clusters must necessarily affect their reported reversibility of conversion.6 The availability of Au25(SR)19[0] cluster is expected soon, but before thinking about its possible applications, it is important to study its stability under various chemical reactions. Therefore, it is important to find one proper model of the Au25(SR)19[0] cluster. Some related questions emerge: Is the Au13 inner core of the Au25(SR)18[1−] cluster maintained after the addition of one extra ligand? Does the Au25(SR)19[0] cluster remain stable under various charge states? For example, Au25(SR)18 cluster is very stable independent of 1−, 0, or 1+ charge-states,15 and its stability can be explained in terms of superatom theory with an electronic counting of 8.16 Conversely, the electronic counting of Au25(SR)19[0] cluster is 6, and to reach high stability, it may reduce (holding anionic charge-states). This manuscript addresses a major study of (neutral/charged) structures related to the Au25(SR)19[0] cluster, and it reports a new 5-step algorithm that can speed up their structure prediction.
2 Methodology
The DFT-D3 methodology is used during calculation as implemented in the ORCA package,17–19 with consideration of longer-ranged van der Waals interactions using the method proposed by Grimme et al.20 The generalized gradient approximation (GGA),21 the Perdew–Burke–Ernzerhof (PBE),22 and exchange-correlation functional were used during the full optimization stage of geometries in the gas phase. Moreover, a meta-GGA exchange-correlation functional was used during the relaxation of clusters because the Tao–Perdew–Staroverov–Scuseria (TPSS)23 functional showed accuracy in describing aurophilic interactions in gold and related complexes, in such a manner that a better energy order among isomers is expected using it.24,25 The def2-TZVPP Ahlrichs basis set was employed for H, S, Cl, and C atoms, and the Coulomb-fitting auxiliary basis def2/J was used. Calculations were based on the RI-J approximation. Effective core potentials were defined for Au atoms (19 valence electrons). The energy and gradient convergence criteria were selected as 1.00 × 10−6 Hartree and 3.00 × 10−5 Hartree per Bohr, respectively. This election of parameters reduced the computation time without a lack of quality in the obtained results. The obtained new structures sustaining neutral/cationic/anionic charge were fully optimized (PBE/TPSS), and their spin multiplicity corresponded with singlet or doublet. All isomers were fully structural (angles and distances graphs) and vibrationally (IR spectra) characterized.26 Ultraviolet-Visible (UV-Vis) and circular dichroism (CD) spectra of PBE/TPSS relaxed geometries were calculated using single-point PBE calculations; TD-DFT calculations were performed by considering 300 singlet states. All depicted UV-Vis/CD spectra show a Gaussian curve with a full width at half-maximum (FWHM) of 0.1 eV.The optimization stage of a set of candidates was performed by the initial consideration of a simple ligand, such as chloride (–Cl) and two different charge states (0, 1−). The next optimization stages were carried out by substituting chloride with –H and –CH3 as ligands. The decomposition of isomers into tetrahedra/octahedra26 is performed throughout the process to find a tendency in the energy order. This step allows us to propose new models and reduce the used time. In the final part, cationic structures were included. In this study, the discussion is dedicated exclusively to the –CH3 ligand results. However, the results obtained with the –Cl and –SH ligands are provided in the ESI.†
2.1 Initial candidates
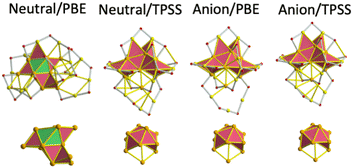
To determine the energy minimum of Au25(SR)19[z] [z = 1−, 0, 1+] clusters, it was considered one previously reported isomer comprising one Au11 inner core (C1 point group) and protected by long staple motifs (Fig. 1a).14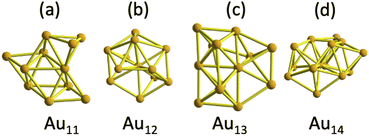 | ||
| Fig. 1 The anatomy of inner cores constituting the three lowest energy isomers of Au25(SR)19[0,1−,1+] clusters under the protection of three different ligands. (a) Au11 core comprised 3 Au4 building blocks, displaying a C1 symmetry, and it corresponds with a previously published isomer,9 (b) Au12 core with a loose C2v symmetry, resembling a centered defective icosahedron, and it represents the new one found in this work, (c) Au13 core comprised by Au4 and Au6 units (obtained from an initial FCC cluster) and displaying C1 symmetry. (d) Au14 core displaying a C1 symmetry. | ||
A second isomer, including one symmetric isomer, was obtained by a slight modification of the organic shell of the parent Au25(SR)18[1−] cluster. The addition of one extra ligand turned a dimer of the Au25(SR)18[1−] cluster into one trimer motif. The insertion was done by pulling out one gold atom from the inner core toward one staple motif, leaving one Au12 core that preserves a central gold atom. In terms of symmetry, the parent Au25(SR)18[1−] cluster comprised one Au13 inner core displaying a Ci symmetry,1 and accommodation of one gold atom from the inner core produced a pseudo-C2v core (Fig. 1b). Observing a C2v symmetry in the initial isomer is only possible when the trimer motif is not present and achiral ligands (such as –H or –Cl) are considered. Therefore, the symmetry of the core and gold–sulphur frameworks is reduced to the C1 point group by the insertion of the trimer motif. The third candidate holding one Au13 inner core was obtained from considering a compact face centred cubic (FCC) cluster, which maintained its Au6 and Au4 building blocks after various optimization steps (Fig. 1c).
3 Results
3.1 Anatomy of calculated isomers
Further examination of all the considered cases allows us to summarize our results as follows:
(a) Neutral isomer is constituted by one Au11 inner core, and it coincides with that reported previously14 only when the PBE XC-functional was used. This isomer was found to be a minimum when –H or –CH3 were considered ligands. However, the neutral charge-state and TPSS functional gave a preference for isomers holding one Au11 core with C2v symmetry.
(b) The charge-state effect on isomers can be observed as large energy differences between them. For example, anionic structures calculated with PBE displayed a major preference for isomers comprising C2v cores (by around 0.42 eV RE value); anionic charge and TPSS increased this energy preference to approximately 0.69 eV RE value. Finally, the cationic/PBE combination displayed a preference of 0.53 eV for isomers containing one Au11 (C2v) core.
(c) When chloride was used as a ligand, energy minima corresponded with isomers comprising Au13/Au14 cores, independent of charge state or used XC-functional (PBE or TPSS).
3.2 Polyhedra analysis of energy minima (bond length dispersion graphics)
Other structures obtained by considering –Cl and –H ligands with 0, −1, and +1 charge states are provided in the ESI.† Combinations of charge-state/–CH3 gave various isomers with Au11 inner cores displaying close RE values. In such a manner, a natural question emerged: what variable can be used to distinguish among isomers? A response was found after a polyhedra analysis of the optimized structures with our improved FORTRAN code (available upon request).26 This code determines the numbers of octahedra and tetrahedra that constitute protected-gold clusters and allows us to classify them in terms of their bond lengths as distorted tetrahedra or compact tetrahedra. Herein, the compact tetrahedra term refers to Au4 units with edges included in the range of 2.6–3.2 Å (to account for distances comparable to Au (core)–Au (core) distances), while consideration of distorted tetrahedra requires bond lengths of around 3.4 Å (experimental aurophilic bonding is determined in the range of 3.02–3.27 Å from the crystal).1The justification for considering tetrahedra and octahedra as part of thiolated gold clusters is that they are reduced to small pieces from bulk gold (having an FCC structure) and perturbed by sulphur atoms. In such a manner that, for thiolated gold, clusters seem viable to account for the number of tetrahedra and octahedra and the study of their edge lengths and face angles.
Their decomposition into polyhedra can be done for the full structure (inner core + gold–sulphur framework) by considering only their inner core. This analysis can reveal the number of polyhedra and the distribution of compact tetrahedra along the cluster anatomy.
Further polyhedral analysis reveals that the energy minimum of the neutral cluster (calculated with PBE XC-functional) is constituted by one octahedron and 4 compact tetrahedra (Fig. 2). However, using the TPSS XC-functional, the more stable isomer (C2v symmetry) features 12 compact tetrahedra instead of an isomer containing one octahedron.
In general, clusters holding a 1-charge state were found as energy minima when more tetrahedra formed part of the structure, independent of the XC-functional.
Based on the obtained results, it was determined that the stability of the isomers of Au25(SR)19[z] clusters [z = 1−, 0, 1+] can be related to the number/type of constituting polyhedra. Therefore, to gain insight into this correlation, the following formula was proposed:
A better agreement between the given formula and the energy order of the studied isomers is found in the following five steps:
(1) Find all constituting polyhedra (tetrahedra/octahedra) of the full structure (Au–S framework + inner core) and its inner core (compact tetrahedra or cT) for each isomer separately. Be aware that in full structure, Au–Au bond lengths are included in the range from 2.6 to 3.4 Å, while compact tetrahedra display bond lengths included in the range from 2.6 to 3.2 Å.
(2) Sort all isomers for each combination of the charge-state/XC-functional in descending order of constituting tetrahedra.
(3) Form sets with isomers displaying the same type of polyhedra. This means that isomers holding only tetrahedra must be included in one set, and those comprising a combination of octahedra and tetrahedra must form another set. In Fig. 3, text boxes allow us to distinguish each set of structures.
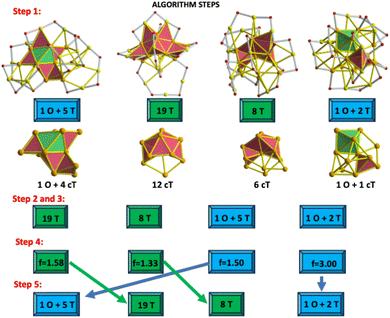 | ||
| Fig. 3 Implementation of a 5-step algorithm to determine the energy order between isomers of the Au25(SCH3)19[0] cluster. Colour code is the same as that shown in Fig. 2. Upper panel features the number and type of polyhedra found in each total structure (Au–S framework + inner core). The lower panel depicts compact tetrahedra (cT) constituting each inner core. Each step of the algorithm is given in the lower part. Highlighted boxes are used to distinguish between two sets of structures. The last row (step number 5) contains the ordered structures in terms of the corresponding T-factor values. | ||
(4) Calculate the T-factor value (T-f) using the given formula. When the number of compact tetrahedra is zero, to avoid zero division, the counting of tetrahedra is repeated by increasing the Au–Au bond lengths.
(5) Look for T-factor value in each set, and make sure that if this value is small, the full set (with all its isomers) needs to shift toward the left position to maintain the ascendent order in terms of factor value.
Remarkably, after applying step number (5), it is possible that the more stable isomers do not have a large number of tetrahedra, but the major stability can be related to a large T-factor value (proportion among constituting polyhedra).
In this study, a 5-step algorithm was helpful to distinguish among isomers of the neutral Au25(SCH3)19 cluster and to predict their expected energy order (Fig. 3). Proper schemes showing the implementation of the 5-step algorithm for each combination of the charge-state/ligand/XC functional are illustrated in Fig. S2.†
The obtained results can be summarized as follows.
(1) Chloride-protected clusters show an energy order consistent with a decrement in their calculated T-factor values. This means that the energy minimum corresponds to a large T-factor value. This result is independent of charge-state or XC-functional.
(2) Conversely, for H-protected clusters, more stable isomers correspond with small T-factor values. This rule applies to all studied charge-states/XC-functional combinations.
(3) CH3-protected clusters display an energy order with increment in T-factor values. The energy minimum holds a smaller T-factor value. A reversed order was found only for the combination of cationic/PBE cases.
3.3 Optical and chiroptical properties of Au25(SCH3)19[1−, 0, 1+] clusters)
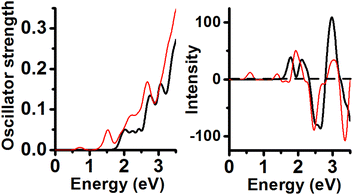
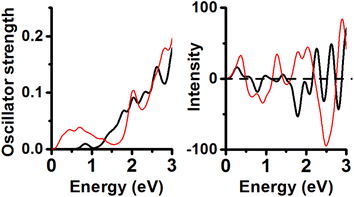
Neutral and PBE XC-functional yielded an energy minimum containing Au11 inner core with Cs symmetry. Its calculated UV-Vis lineshape shows 4 peaks (Fig. 4) included in the range from 1.5 to 3.0 eV (2.02, 2.25, 2.44 and 2.76 eV). These peaks can be compared with experimental peaks reported at 2.12, 2.28 and 2.82 eV.6The second isomer in energy (Au11 and C2v symmetry; 0.14 eV RE value) displayed peaks located at 0.72 eV (weak), 1.53, 1.91, 2.19 and 2.68 eV. The energy minimum shows CD peaks located at 1.77 (+), 2.11 (+), 2.65 (−), and one intense peak at 2.96 eV (+). The CD lineshape of the second energy isomer features signals located at 0.61 (+), 1.39 (+), 1.92 (+), 2.46 (−), 3.03 (+), and one intense peak located at 3.36 eV (−).
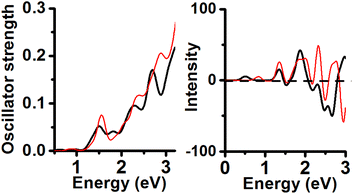
Consideration of the anionic structures yielded an increment in the energy separation among the isomers. The structure calculated with the Anionic/PBE combination has one Au11 core with C2v symmetry, and its profile has 4 peaks included in the range from 1.5 to 3.0 eV (1.51, 1.82, 2.29 and 2.69 eV). The second isomer in energy (0.42 eV RE value) corresponding to an isomer is constituted by one Au11 core and C1 symmetry. Its UV-Vis spectrum features one peak located at 0.87 eV (weak), an intense peak located at 1.55 eV and 3 more peaks under 3.0 eV (2.07, 2.36, and 2.88 eV). These 2 peaks under 2.0 eV were unexpected and not shown in the neutral/PBE case for CH3-protected clusters (Fig. 5). This result implies that a [1−] charge state produced a large change in the calculated UV-Vis spectrum with respect to the neutral Au11 (Cs) cluster (Charge-state effect). Comparison of the CD spectra of both lower energy isomers of Au25(SCH3)19[1−] clusters allows us to observe a coincidence in the position of 3 peaks included in the range from 1.0 to 2.0 eV (1.36, 1.54, and 1.88 eV). The energy minimum has one peak located at 0.50 eV (+) and a negative intense peak located at 2.65 eV. The second order in the energy isomer has one distinct negative peak located at 2.95 eV. It is noteworthy that both isomers feature weak CD profiles with respect to the neutral cases.
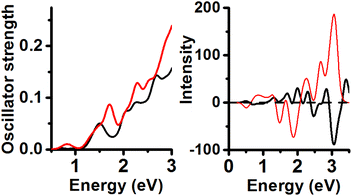
Anionic/TPSS combination yielded one Au11 isomer (C2v symmetry) displaying 4 peaks in the range from 1.0 to 3.0 eV (1.5, 2.05, 2.26 and 2.69 eV). Noticeable is that 3 last peaks are close to experimental values (Fig. 6). Only the first peak located at 1.5 eV is not shown in the experimental spectrum of the neutral Au25(SR)19 cluster. The second isomer in energy comprises one Au14 inner core (C1 symmetry) displaying UV-Vis peaks located at 0.82, 1.71, 2.28, and 2.54 eV. Further analysis of both CD spectra reveals that the energy minimum spectrum is less intense than the CD profile of the second isomer in energy. The energy minimum shows one negative CD peak located at 3.06 eV. The second isomer in energy (C1) shows two intense peaks located at 1.88 eV (−) and 3.06 eV (+).
Cationic Au25(SCH3)19 clusters were optimized using the PBE functional (Fig. 7). The energy minimum features UV-Vis peaks located at 0.84, 1.80, 2.04, 2.33, and 2.61 eV and CD peaks at 0.27 (+), 0.77 (−), 1.78 (−), 2.27 (+), and 2.63 eV (+). The second order in energy isomer has UV-Vis peaks under 1.0 eV (0.44, 0.70 eV) and 2 more peaks located at 2.03 and 2.83 eV; CD peaks at 0.36 (+), 0.91 (−), 1.27 (+), 2.04 (+), 2.50 (−) and 2.90 eV (+). It can be concluded that the effect of charge on the UV-Vis/CD spectra of isomer with inner core sustaining C1 point group is strong.
The effect of PBE or TPSS XC-functionals (during the optimization stage) on the calculated UV-Vis or CD spectra can be summarized as follows:
(1) Neutral isomer constituted by one Au11 core displaying a C2v symmetry optimized by either PBE or TPSS XC-functionals features similar UV-Vis and CD spectra (TDDFT calculations were carried out using the PBE XC-functional in both cases). The UV-Vis spectra depict more coincidences in peak position and in their intensity values from 0.5 to 3.0 eV (see Fig. S3†). In contrast, an isomer with one Au11 core (Cs symmetry) optimized with both XC-functionals features a pair of CD spectra with major coincidences (see Fig. S4†) rather than UV-Vis spectra.
(2) Anionic clusters with one Au11 core (C2v symmetry) show similar UV-Vis spectra, and a further polyhedra analysis reveals 12 constituted tetrahedra (see Fig. S5†).
(3) The charge-state effect is strong in the case of isomers with inner cores of Cs symmetry, and the respective UV-Vis/CD spectra appear different (see Fig. S6†). This means that anionic structures are more distorted, resulting in fewer tetrahedra. A similar behaviour is revealed in the case of cationic structures, where structural distortion is stronger than in neutral ones, and UV-Vis/CD spectra appear more perturbed (see Fig. S7†).
(4) In the case of isomers comprising Au11 inner cores and sustaining a C2v symmetry, neutral and anionic structures (see Fig. S8†) feature a superior match on their UV-Vis and CD profiles. Indeed, the number of constituted tetrahedra of the inner cores is preserved (12 compact tetrahedra), indicating less structural distortion with the shift of the charge state.
4 Conclusions
The provided 5-step algorithm was useful during the prediction of structures of neutral and charged Au25(SR)19[z] clusters because of its ability to predict the energy order of candidates. This algorithm was effective in determining the energetic order between the isomers of Au25(SR)19[z] clusters independently of the XC-functional/charge-state/ligand type combinations.The new isomer constituted by one Au11 inner core featuring one C2v symmetry is found as an energy minimum under various charge states and a combination of ligands and XC-functionals. The energy minimum of the neutral Au25(SR)19 cluster contains a pentamer motif, which is consistent with reported experimental results.6
The closeness in energy between our new isomer and that previously reported by Yan et al.14 is remarkable. For example, in the Neutral/PBE case and by considering –CH3 as ligands, a 0.14 eV RE value was obtained with respect to the isomer with one Au11 core (Cs symmetry).
In the case of Au25(SR)19[1−, 1+] clusters (R = H, CH3), new energy minima are consistent with isomers with one Au11 (C2v) inner core, and this result is consistent with that of the experimental data of Tandem mass spectroscopy carried out on the produced Au25(SR)19[0] cluster, revealing the presence of a lengthened motif (Au5SR5 unit) after ligand addition.6
Further analysis of isomers, including one Au11 inner core, allows us to know that neutral and anionic isomers feature similar UV-Vis/CD spectra for isomers with one inner core sustaining C2v symmetry (Fig. S8†). This means that the charge-state effect27,28 is minor for isomers based on a C2v core.
The applicability of our 5-step algorithm is tested to find the lowest energy isomers of crystallized thiolated gold clusters, and the partial results agree with the general conclusions of this study.
Finally, it is important to mention that the search for building blocks of novel functional materials is ongoing, and several structural search methods have been proposed. This development started from naked metal clusters to ligand-protected clusters. A recent review summarizes the timeline up to artificial intelligence.29
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
Author acknowledges the computer resources, technical expertise and support provided by the Laboratorio Nacional de Supercómputo del Sureste de México, CONAHCyT network of National laboratories.Notes and references
- M. W. Heaven, A. Dass, P. S. White, K. M. Holt and R. W. Murray, J. Am. Chem. Soc., 2008, 130, 3754–3755 CrossRef CAS PubMed.
- A. Tlahuice-Flores, Mol. Simul., 2012, 39, 428–431 CrossRef.
- F. P. Parker, C. A. Fields-Zinna and R. W. Murray, Acc. Chem. Res., 2010, 43, 1289–1296 CrossRef PubMed.
- M. Zhu, C. M. Aikens, F. J. Hollander, G. C. Schatz and R. Jin, J. Am. Chem. Soc., 2008, 130, 5883–5885 CrossRef CAS PubMed.
- J. Akola, M. Walter, R. L. Whetten, H. Häkkinen and H. Grönbeck, J. Am. Chem. Soc., 2008, 130, 3756–3757 CrossRef CAS PubMed.
- Y. Cao, V. Fung, Q. Yao, T. Chen, S. Zang, D.-e. Jiang and J. Xie, Nat. Commun., 2020, 11, 5498–5504 CrossRef CAS PubMed.
- S. Zhuang, L. Liao, J. Yaun, N. Xiz, Y. Zhao, C. Wang and Z. Wu, Angew. Chem., Int. Ed., 2019, 58, 4510–4514 CrossRef CAS PubMed.
- M. Zhu, H. Qian, B. A. Drake and R. Jin, Angew. Chem., Int. Ed., 2010, 49, 1295–1298 CrossRef PubMed.
- N. K. Chaki, H. Tsunoyama, Y. Negishi and T. Tsukuda, J. Phys. Chem. C, 2007, 111, 4885–4888 CrossRef CAS.
- M. A. Muhammed, P. K. Verma, S. K. Pal, R. C. Kumar, S. Paul, R. V. Omkumar and T. Pradeep, Chem.–A Eur. J., 2009, 15, 10110–10120 CrossRef CAS PubMed.
- I. Chakraborty and T. Pradeep, Chem. Rev., 2017, 12, 8208–8271 CrossRef PubMed.
- W. Xu, X. C. Zeng and Y. Gao, Acc. Chem. Res., 2018, 51, 2739–2747 CrossRef CAS PubMed.
- W. W. Xu, X. C. Zeng and Y. Gao, Nat. Commun., 2016, 7, 13574 CrossRef CAS PubMed.
- C. Yan, Y. Li, E. Wang and W. W. Xu, J. Phys. Chem. Lett., 2023, 14, 7632–7637 CrossRef CAS PubMed.
- C. B. Collins, M. A. Tofanelli, M. F. Crook, B. D. Phillips and C. J. Ackerson, RSC Adv., 2017, 7, 45061–45065 RSC.
- M. Walter, J. Akola, O. Lopez-Acevedo, P. D. Jadzinsky, G. Calero, C. J. Ackerson, R. W. Whetten, H. Grönbeck and H. Häkkinen, Proc. Natl. Acad. Sci. U.S.A., 2008, 105, 9157–9162 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 2, 73–78 Search PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- S. Grimme, Phys. Chem. Chem. Phys., 2006, 8, 5287–5293 RSC.
- J. P. Perdew, et al., Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671 CrossRef CAS PubMed.
- (a) A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS PubMed; (b) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401–146405 CrossRef PubMed.
- M. P. Johanson, A. Lechtken, D. Schooss, M. M. Kappes and F. Furche, Phys. Rev. A, 2008, 77, 053202–053209 CrossRef.
- F. Mendizabal and S. Miranda-Rojas, RSC Adv., 2020, 10, 33549–33557 RSC.
- A. Tlahuice-Flores, J. Phys. Chem. C, 2019, 123, 10831–10841 CrossRef CAS.
- H. Qian, M. Y. Sfeir and R. Jin, J. Phys. Chem. C, 2010, 114, 19935–19940 CrossRef CAS.
- A. Wing-Bocanegra, Phys. Chem. Chem. Phys., 2019, 21, 23855–23864 RSC.
- J. Gao, L. Zhao, Y. Chang, Y. Zhang, S. Qiu, Y. Zhao, H. Liu and J. Zhao, Adv. Intell. Syst., 2024, 2300716, DOI:10.1002/aisy.202300716.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed structures and calculated isomers by using three different ligands are provided. See DOI: https://doi.org/10.1039/d4ra03458a |
| This journal is © The Royal Society of Chemistry 2024 |