Open Access Article
Open Access ArticleStructural, morphological, magnetic and electrical properties of La0.8Na0.2−x□xMnO3 (0.00 ≤ x ≤ 0.15) manganites†
M. Walia,
W. Hizi *b,
R. Dhahria,
H. Rahmouni
*b,
R. Dhahria,
H. Rahmouni b,
K. Khirounic and
E. Dhahria
b,
K. Khirounic and
E. Dhahria
aLaboratoire de Physique Appliquée, Faculté des Sciences de Sfax, Université de Sfax, B.P. 1171, 3000, Sfax, Tunisia
bLaboratoire de Recherche Matériaux Avancés et Nanotechnologies, Institut Supérieur des Sciences Appliquées et de Technologie de Kasserine, Université de Kairouan, BP 471, Kasserine 1200, Tunisia. E-mail: widedph@live.com
cLaboratoire de Physique des Matériaux et des Nanomatériaux appliquée à l’Environnement, Faculté des Sciences de Gabès cité Erriadh, Université de Gabès, 6079 Gabès, Tunisia
First published on 28th August 2024
Abstract
La0.8Na0.2−x□xMnO3 (0.00 ≤ x ≤ 0.15) manganites were successfully synthesized using the solid-state route. X-ray diffraction was performed to check the samples' purity and phase structure. Scanning electron microscopy analysis reveals a decrease in the average grain size with an increase in the deficiency amount. Analysis of the temperature dependence of magnetization proved the presence of ferromagnetic–paramagnetic transition in all the studied samples. The magnetization derivative (d2M/dT2) curves demonstrated a decrease in the transition temperature with an increase in the deficiency amount. Such experimental observations can be correlated with bandwidth evolution, which affected double-exchange interactions. It can be equally accounted for by the average grain size decrease. In this regard, the experimental measurements of effective paramagnetic moments revealed the existence of ferromagnetic correlations within the paramagnetic phase. Notably, different electrical findings were addressed. Indeed, the frequency dependence of electrical conductivity displayed the coexistence of two frequency slopes reflecting the presence of Jonscher's double power law for all the studied samples. A significant decrease in conductivity values was observed when the deficiency amount increased. This experimental observation could be assigned to the decrease in the grain size (conductor region). Such assumption was confirmed by the evolution of the grain boundary resistance with deficiency level. Indeed, a significant mounting in the grain boundary resistance values was obtained presenting the increase of the resistive region for x = 0.15. It is worth noting that the Curie temperature for the x = 0.10 sample was found to be close to room temperature (TC = 297 K). These findings make the La0.8Na0.1□0.1MnO3 compound a powerful candidate for many technological applications.
1. Introduction
The discovery of the colossal magnetoresistance phenomenon1–3 and magnetocaloric effect4–6 has fueled much research on the outstanding physical properties of manganite compounds. Owing to such physical properties, manganites can be used for numerous applications, including magnetic refrigerants, magnetic sensors, magneto-resistive transducers, computer memory systems, spintronic devices, catalysts, and infrared detectors.7–11 Different interesting behaviors such as charge-ordering (CO),12 metamagnetic transition,13 colossal magnetoresistance14,15 and large magnetocaloric effects6,16 have been observed. In fact, several studies have widely reported many investigations on the structural, morphological, optical, magnetic, electronic and electrical properties of manganites.17–32 The parent compound (LaMnO3) of lanthanum manganite (La1−xAxMnO3) systems is an anti-ferromagnetic material.33 Substitution by a monovalent (Na+, Ag+, K+…) or divalent ion (Ca2+, Sr2+, Ba2+…) generates mixed-valence properties. Indeed, the partial substitution of La element by Na element provokes the hopping of an eg electron from the Mn3+ cation to the adjacent Mn4+ cation by the intermediary oxygen anion O2−. Such hops manifest into double-exchange (DE) interactions between these manganese cations.34 Accordingly, the Mn3+/Mn4+ ratio can be controlled by doping (site of doping, doping element, doping amount), leading to an improvement in physical properties. In this context, the effect of sodium doping on lanthanum manganite systems has been frequently studied.35–41 Arunachalam et al.36 reported that the particle size decreases with increasing sodium concentration. Such structural change has an effect on the electrical and magnetic properties. In addition, the ferromagnetic–paramagnetic phase transition temperature is increased with the increasing Na concentration.40 Furthermore, it was observed that the system resistivity values showed a significant decrease with the increase in the Na amount.40 Besides, the literature42–49 has presented that the creation of deficiencies can affect the physical properties of these kinds of systems. Indeed, A-site deficiency can modify the Mn3+/Mn4+ amount, which in turn can alter their magnetic and electrical properties. A magnetocaloric effect (MCE) was also reported in several deficient manganites. Indeed, Smari et al.50 argued that the La0.5Ca0.5−xAgxMnO3 deficient manganite had a large ΔSmaxM of 2.9 J K−1 kg−1 under a magnetic field of 0.9 T with a TC of 272 K. This indicates that La0.5Ca0.5−xAgxMnO3 could be used as an active magnetic refrigerant within the sub-room-temperature range. In addition, M'nassri et al.51 examined the effect of barium-deficiency on the structural, magnetic, and magnetocaloric properties of La0.6Sr0.2Ba0.2−x□xMnO3, where ΔSmaxM did not exceed 4 J K−1 kg−1 under a magnetic field of 4.5 T for all the studied samples.In the present investigation, interesting properties of La0.8Na0.2−x□xMnO3 (0.00 ≤ x ≤ 0.15) manganites were observed and discussed. The deficiency effect was obviously manifested in the structural, morphological, magnetic, and electrical properties. For instance, a decrease in the grain size was observed in the SEM study. The increasing deficiency level also provoked a decrease in the Curie temperature TC. The experimental measurements of the effective paramagnetic moments exceeded the corresponding theoretical values. Such a result proved the existence of ferromagnetic correlations within the paramagnetic phase. On the electrical side, the presence of double slopes in the dispersive region of the conductivity spectra was revealed for all the studied samples, which equally displayed a significant decrease in the conductivity values when the deficiency amount rose. For x = 0.10, the Curie temperature was found to be close to room temperature (TC = 297 K). Such an experimental observation makes the 10% deficiency sample a promising candidate for several technological applications.
2. Experimental details
The La0.8Na0.2−x□xMnO3 (0.00 ≤ x ≤ 0.15) materials were synthesized via the solid-state ceramic technique. The used precursors were lanthanum La2O3 and manganese MnO2 oxides as well as sodium carbonate Na2CO3 with purities greater than 99.9%. Lanthanum oxide and sodium carbonate were dehydrated at 400 °C for 1 h so as not to distort the weighing. The first synthesis step consisted of weighing the precursors in the desired stoichiometric proportions. These precursors were then finitely ground for 20 min to obtain a homogeneous mixture. The obtained powders were subsequently placed in alumina nacelles and brought to increasingly high temperatures, going from 700 °C to 1100 °C at an increase of 100 °C per day, interspersed with grinding. This step, called calcination, allowed, on the one hand the decomposition and release of gases (O2 and CO2) and, on the other hand, the partial formation of the intended phase in line with the following reaction:
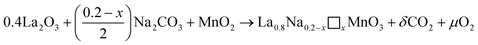 | (1) |
The obtained powders were ground again for 30 min in a dry environment. This grinding reduced the grain size, homogenized the product, and minimized the intergranular porosity. The next step consisted of pelletizing the samples to promote diffusion and vaporization–condensation mechanisms during the solid-state reaction. During this phase, the powders were molded into pellets under an axial pressure of 4 tons per cm2. The final step was sintering, which consisted of placing the pellets, in alumina or platinum crucibles to guarantee that a foreign phase was not formed by interaction with the crucible, in an oven under air at 1200 °C for an annealing time sufficient for the formation and growth of and grains. Rapid quenching in air was necessary to help maintain the structure at ambient temperature in equilibrium with the annealing temperature. These reactions are slow and result in a long-distance diffusion of the different ions. These methods have the advantage of being very easy to implement; however, they require several grinding and annealing cycles at high temperatures.
Alternatively, the samples underwent X-ray diffraction analysis using a Bruker D8 diffractometer, which featured a copper anticathode (λCuα1 = 1.5406 Å) and a rear graphite monochromator. The recording of the X-ray powder patterns was carried out at room temperature in an angular range varying from 10° to 100° in the 2θ mode at steps of 0.02° and an acquisition time of 1 s for each step.
The microstructure was examined by scanning electron microscopy (SEM). A vibrating sample magnetometry (VSM) instrument by Quantum Design was employed for the measurements of the magnetic fields. The magnetization versus magnetic field curves were recorded by varying the magnetic field between 0 and 5 T at temperatures both below and above the Curie temperature.
Electrical measurements were performed using an Agilent 4294A impedance analyzer for each prepared sample over a wide frequency range (40 Hz to 1 MHz) at room temperature.
3. Results and discussion
3.1. Scanning electron microscopy
The secondary electron SEM images for La0.8Na0.2−x□xMnO3 (0.00 ≤ x ≤ 0.15) are shown in Fig. 1(a)–(d). The micrographs obtained showed grains with various polygonal shapes with a non-uniform distribution. We could also observe in these images some black contrast voids associated with the porosity of the samples. The particle-size distribution was analyzed statistically using ImageJ software. Fig. 2(a)–(d) depicts histograms illustrating the grain sizes of the samples under investigation. As observed, the histograms were well modeled by the Lorentzian function. The average grain size was affected by the sodium vacancy rate, resulting in different values for the four samples: 2.358 μm for x = 0.00, 2.292 μm for x = 0.05, 2.087 μm for x = 0.10, and 1.994 μm for x = 0.15.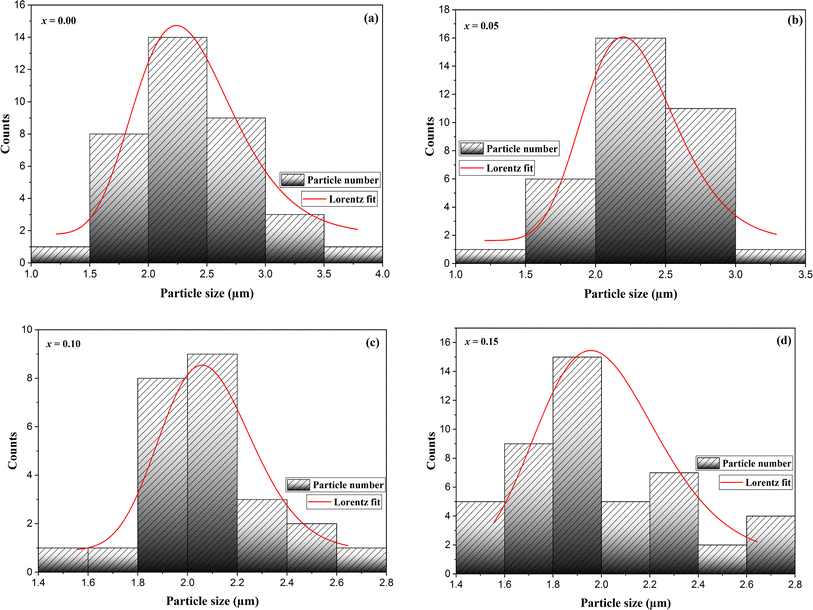 | ||
| Fig. 2 Size-distribution histograms of La0.8Na0.2−x□xMnO3: (a) x = 0.00, (b) x = 0.05, (c) x = 0.10 and (d) x = 0.15. | ||
3.2. Chemical analysis
The percentages of Mn3+ and Mn4+ ions in our La0.83+Na0.2−x+□x0(Mn0.6−x3+Mn0.4+x4+)O32− samples were determined using a conventional chemical technique. Initially, we dissolved the sample powder in oxalic acid dihydrate (H2C2O4·2H2O) and concentrated sulfuric acid (H2SO4). The resulting solutions were subsequently titrated with potassium permanganate (KMnO4). Table 1 depicts a comparison of the theoretical and experimental results of the Mn3+ and Mn4+ contents. The obtained data indicate that the experimental concentrations of manganese ions were very close to the theoretical values. Ultimately, it is noteworthy that our samples were prepared in air, ensuring they were stoichiometric in oxygen.| x | Theoretical content | Experimental content | ||
|---|---|---|---|---|
| Mn3+ (%) | Mn4+ (%) | Mn3+ (%) | Mn4+ (%) | |
| 0.00 | 60 | 40 | 62.14 | 37.86 |
| 0.05 | 55 | 45 | 56.02 | 43.98 |
| 0.10 | 50 | 50 | 51.17 | 48.83 |
| 0.15 | 45 | 55 | 45.84 | 54.16 |
3.3. Structural properties
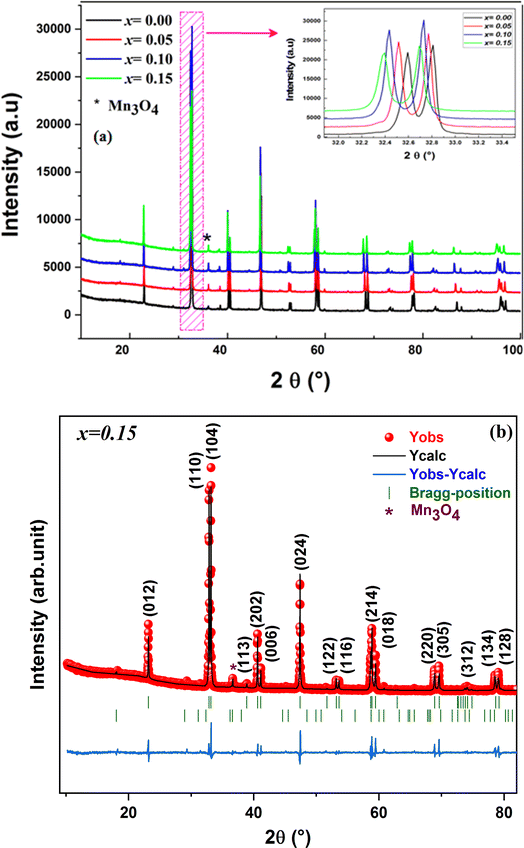
The X-ray diffraction pattern analysis confirmed the structural integrity and phase purity of our compounds. The X-ray diffraction patterns at room temperature for the La0.8Na0.2−x□xMnO3 (0.00 ≤ x ≤ 0.15) compounds are depicted in Fig. 3(a), which indicate that all the samples exhibited a consistent perovskite structure with identical peaks. These peaks were associated with the diffraction lines of the rhombohedral phase with the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group. All the peaks accurately correlated with the 2θ values of 23.3°, 32.4°, 33.2°, 40.1°,40.8° 47°, 59°, 69.4°, and 77.9° indicating the 012, 110, 104, 113, 202, 024, 214, 220, and 134 crystalline planes, respectively.
c space group. All the peaks accurately correlated with the 2θ values of 23.3°, 32.4°, 33.2°, 40.1°,40.8° 47°, 59°, 69.4°, and 77.9° indicating the 012, 110, 104, 113, 202, 024, 214, 220, and 134 crystalline planes, respectively.
Also, with the increase in vacancy content, the patterns showed a slight shift of the most intense peak toward smaller 2θ values (inset of Fig. 3(a)), suggesting that the vacancy had a larger ionic radius than Na. The displacement of the diffraction peaks toward smaller angles indicated that the cell parameters of the samples increased as the vacancy rate increased. The Rietveld technique produced satisfactory agreement factors and lattice parameters when refining the data using FULLPROF software.52 An example of the XRD pattern refinement for the x = 0.15 sample is shown in Fig. 3 (b). The refinement results (see the ESI†), as summarized in Table 2, indicated there was a slight increase in both the cell parameter and unit cell volume with the rising vacancy content.
| Vacancy content | x | 0.00 | 0.05 | 0.10 | 0.15 | |
|---|---|---|---|---|---|---|
La0.8Na0.2−x□xMnO3 (rhombohedral), R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
Lattice parameters | a = b (Å) | 5.412(6) | 5.427(5) | 5.440(1) | 5.448(7) |
| c (Å) | 13.132(4) | 13.145(3) | 13.153(2) | 13.16(5) | ||
| Unit cell volume (Å3) | 55.531 | 55.892 | 56.185 | 56.415 | ||
| dMn–O (Å) | 1.9250 | 1.9336 | 1.9374 | 1.9404 | ||
| θMn–O–Mn (°) | 164.5877 | 162.7587 | 162.5934 | 162.4338 | ||
| Rwp (%) | 5.20 | 5.36 | 6.14 | 4.68 | ||
| Rp (%) | 5.04 | 4.68 | 5.02 | 4.49 | ||
| Rf (%) | 2.18 | 2.24 | 1.18 | 1.81 | ||
| χ2 (%) | 3.41 | 4.13 | 2.74 | 2.11 | ||
| Mn3O4 (tetragonal), I41/amd | Lattice parameters | a = b (Å) | 5.734(6) | 5.731(8) | 5.731(5) | 5.739(4) |
| c (Å) | 9.467(9) | 9.458(7) | 9.453(5) | 9.455(2) | ||
| % | 0.08 | 0.11 | 0.08 | 0.16 | ||
In fact, we noted the existence of very low intensity peaks in the XRD patterns, which were associated with Mn3O4, as is frequently encountered in mixed-valence manganites. This Mn3O4 secondary phase had no significant effect on the stoichiometry of the materials, given its low concentration.53 Furthermore, it is important to highlight that the introduction of sodium vacancies did not lead to any changes in the space group of the parent compound La0.8Na0.2MnO3. The average crystallite size has been estimated using a variety of techniques, such as Scherrer's formula.54,55 The following formula was utilized here to calculate the average crystallite size DSC:
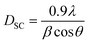 | (2) |
This formula makes it possible to extract the microstructural parameters of the diffraction peaks, but it only gives partial information. In this relationship, the broadening of the line characterized by the width at half maximum is linked to an effect of the size of the coherent diffraction domains (crystallite size). Applying Scherrer's formula, we calculated the size of the crystallites within our compounds, observing an increase as the vacancy rate (x) increased. The respective values for the four samples (x = 0.00, x = 0.05, x = 0.10, and x = 0.15) were 95, 108.2, 108.5, and 109.5 nm. The elemental volume increased as the vacancy rate rose, shifting from 55.5 Å to 56.5 Å when the vacancy rate increased from 0.00 to 0.15. To elucidate this variation, we took into account the following three factors:
• Variation in the average radius of B sites,
• Variation in the average radius of A sites,
• Variation of the Mn–O distance.
According to electrical neutrality, the La0.83+Na0.2−x+□x0(Mn0.6−x3+Mn0.4+x4+)O32− compounds contain (0.6 − x) Mn3+ ions and (0.4 + x) Mn4+ ions per formula unit. By increasing the rate of vacancies x, there is a conversion of a fraction x of the manganese Mn3+ ions into Mn4+ ions, whose radius is smaller (rMn3+ = 0.65 Å and rMn4+ = 0.53 Å56). Thus, the average ionic radius 〈rB〉 of the cations occupying the B site was determined from the following relation:
| 〈rB〉= (0.6 − x)rMn3+ + (0.4 + x)rMn4+ | (3) |
We observed that the variation in the average radius 〈rB〉 of the cations at the B site decreased, unlike the volume V, which increased with the vacancy rate x. This reduction in 〈rB〉 did not significantly affect the volume variation, as it did not exceed ∼2% in the best cases. To explain this evolution in volume, we studied the effect of a second parameter, namely the average ionic radius 〈rA〉 of the cations occupying the A site. Thus, the creation of vacancies at the sodium site in the La0.8Na0.2−x□xMnO3 series could increase the average ionic radius of the A site (with rLa3+ = 1.216 Å and rNa+ = 1.24 Å); therefore rV > rNa+. The creation of a vacancy in a monovalent or divalent site tends to increase the volume in relation to the vacancy rate x.57 Khlifi et al.57 showed, in the La0.8Ca0.2−x□xMnO3 series, that the vacancy would admit an rV radius greater than that of calcium (rCa2+ = 1.18 Å), consequently resulting in an expansion of the unit cell volume. Whereas the formation of a vacancy in a trivalent site typically results in a reduction in volume.58 Likewise, Skini et al.58 showed that, in La0.8−x□xCa0.2MnO3 compounds, the radius of the vacancy rV was smaller than rLa3+ = 1.216 Å. Then, rCa2+ ≤ rV ≤ rLa3+, causing a decrease in volume.
According to the structural refinement, we noticed that the Mn–O distance increased from 1.9250 Å to 1.9404 Å when the rate of vacancies in the A sites passed from 0.00 to 0.15. This variation in the Mn–O distance directly affected the cell parameters, which increased, and consequently the volume of the cell increased with the rate of vacancies in A sites increasing. In Fig. 4, we plotted the changes in both the Mn–O distance and the volume against the vacancy rate x. This graph vividly demonstrates there was an upward trend in the Mn–O distance, providing a clear explanation for the concurrent increase in volume as the vacancy rate x rose.
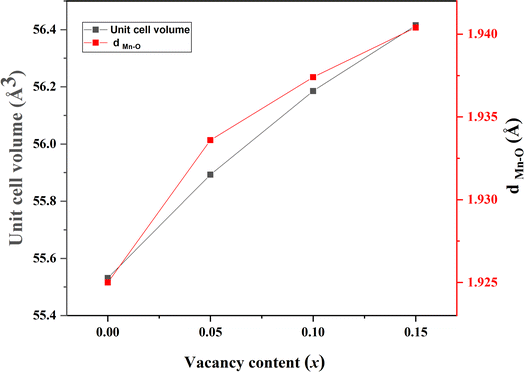 | ||
| Fig. 4 Variation in the volume V and the distance dMn–O as a function of the x rate vacancy of La0.8Na0.2−x□xMnO3 compounds (x = 0.00, 0.05, 0.10 and 0.15). | ||
3.4. Magnetic properties
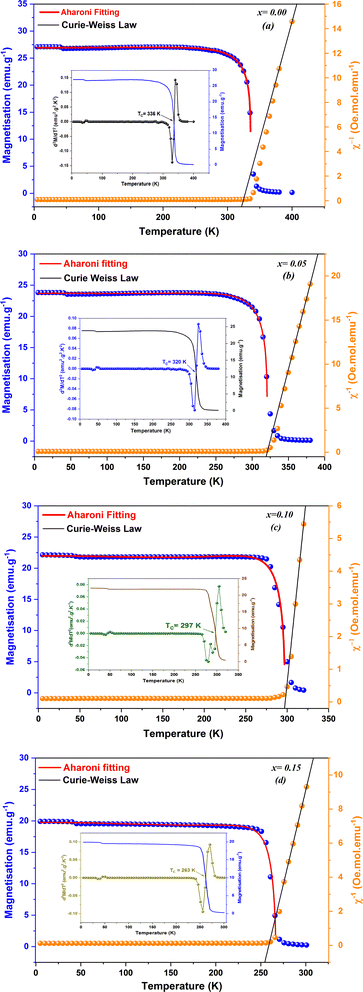
The magnetic properties were investigated by measuring the temperature-dependent magnetization (M(T)) under an applied field of 0.05 T for the compounds La0.8Na0.2−x□xMnO3 with vacancy rates ranging from 0.00 to 0.15, as illustrated in Fig. 5(a)–(d). The findings revealed a transition from ferromagnetic to paramagnetic states for all the samples as the temperature increased.59 Accordingly, it was evident that the magnetization declined as the sodium deficiency rate increased, attributable to the diminished presence of Mn3+ ions, distinguished by their elevated spin (S = 2), and the concomitant augmentation of Mn4+ ions (S = 3/2), as delineated by the equation La0.83+Na0.2−x+□x0(Mn0.6−x3+Mn0.4+x4+)O32−. Furthermore, there are two techniques available to identify the transition temperature (TC) from the ferromagnetic to the paramagnetic state.
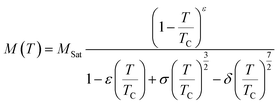 | (4) |
| x | MSat (emu g−1) | TtheoC (K) | TexpC (K) |
|---|---|---|---|
| 0.00 | 26.91 | 335.65 | 336 |
| 0.05 | 23.67 | 320.68 | 320 |
| 0.10 | 21.97 | 296.98 | 297 |
| 0.15 | 19.76 | 266.61 | 263 |
Moreover, to understand the magnetic behavior within the paramagnetic range, we investigated the temperature dependence of the inverse magnetic susceptibility (χ) for all the samples, as depicted in Fig. 5(a)–(d). It is evident that the 1/χ dependence of the temperature follows the Curie–Weiss law: 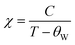 , where the Curie constant and Weiss temperature are represented by C and θW, respectively. The data's linear paramagnetic region can be used to obtain the Curie–Weiss parameters C and θW. Moreover, we calculated the experimental effective moment (μexpeff), which is defined as:
, where the Curie constant and Weiss temperature are represented by C and θW, respectively. The data's linear paramagnetic region can be used to obtain the Curie–Weiss parameters C and θW. Moreover, we calculated the experimental effective moment (μexpeff), which is defined as: 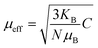 ,60 where N is the Avogadro number, μB is the Bohr magneton, and kB is the Boltzmann constant. We found the μexpeff values were 5.634, 4.775, 5.203, and 5.830 respectively. Assuming the orbital contribution to be quenched in both Mn3+ and Mn4+, the theoretical paramagnetic effective moment (μtheff) can be expressed as
,60 where N is the Avogadro number, μB is the Bohr magneton, and kB is the Boltzmann constant. We found the μexpeff values were 5.634, 4.775, 5.203, and 5.830 respectively. Assuming the orbital contribution to be quenched in both Mn3+ and Mn4+, the theoretical paramagnetic effective moment (μtheff) can be expressed as 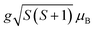 , where g = 2 represents the gyromagnetic factor and S is the spin of the cation. Therefore, the theoretical values were μtheff = 4.90 μB for Mn3+ and μtheff = 3.87 μB for Mn4+. Taking into account the rigid coupling of Mn3+ and Mn4+, the calculated effective paramagnetic moment per formula unit can be written as:
, where g = 2 represents the gyromagnetic factor and S is the spin of the cation. Therefore, the theoretical values were μtheff = 4.90 μB for Mn3+ and μtheff = 3.87 μB for Mn4+. Taking into account the rigid coupling of Mn3+ and Mn4+, the calculated effective paramagnetic moment per formula unit can be written as:
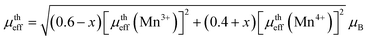 | (5) |
The theoretical values of the effective paramagnetic moments μtheff were calculated for all samples as 4.516, 4.465, 4.415, and 4.363 μB for x = 0.00, 0.05, 0.10, and 0.15, respectively. However, the experimental measurements of the effective paramagnetic moments surpassed the corresponding theoretical values. This discrepancy indicated the presence of Mn4+ and Mn3+ clusters,61 suggesting that in the paramagnetic state, the individual magnetic spins were not isolated; instead, they formed small groups, revealing the existence of ferromagnetic correlations within the paramagnetic phase. In Table 4, we report the Curie constant (C), the Weiss temperature (θW), as well as the theoretical (μtheff) and experimental (μexpeff) moments. In the table, positive values of θW could be observed, confirming the ferromagnetic characteristics of all the samples. Additionally, these values exhibited a decreasing trend with increasing x, mirroring the behavior of the Curie temperature (TC).
| x | TC (K) | C (K uem mol−1) | θW (K) | μtheff (μB) | μexpeff (μB) |
|---|---|---|---|---|---|
| 0.00 | 336 | 3.968 | 338.024 | 4.516 | 5.634 |
| 0.05 | 320 | 2.850 | 323.888 | 4.465 | 4.775 |
| 0.10 | 297 | 3.384 | 300.159 | 4.415 | 5.203 |
| 0.15 | 263 | 4.248 | 260.064 | 4.363 | 5.830 |
3.5. Electrical properties
Fig. 6 shows the electrical AC-conductivity spectrum for the parent compound La0.8Na0.2MnO3. A frequency-independent region could be clearly observed at low frequencies. Such a frequency range is associated with the DC-conductivity, as depicted in Fig. 6. Funke62 explained the electrical transport in such a regime by the long-range translational motion. Here, σAC remained constant as the frequency increased until reaching the hopping frequency. Such a characteristic frequency is defined by the frequency at which the conductivity changes the slope. Beyond this frequency, the electrical conductivity increased with the frequency increasing. Such an observation suggests the possibility of the presence of different electrical transport mechanisms, which has been widely studied using the Pike model63 and detected in several amorphous and perovskite materials.17–20,26,27,29,64–70 As indicated in Fig. 6, σAC showed a significant increase with two linear slopes. Thus, such a result leads to the fact that this spectrum presented two frequency exponents. Accordingly, the frequency dependence of AC-conductivity was governed by Jonscher's double power law:71–73| σAC = σDC + A1ωs1 + A2ωs2 | (6) |
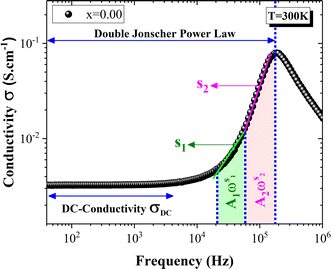 | ||
| Fig. 6 Frequency dependence of electrical conductivity at room temperature for the parent compound La0.8Na0.2MnO3. | ||
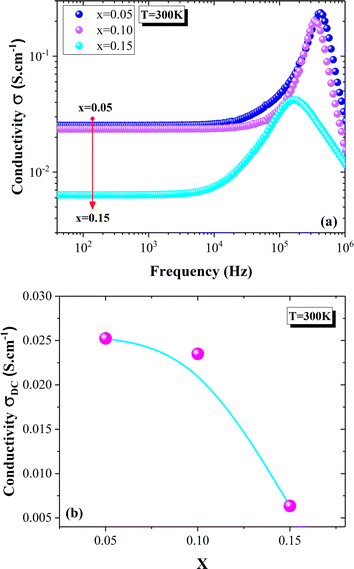 | ||
| Fig. 7 Conductivity spectra of La0.8Na0.2−x□xMnO3 (x = 0.05, 0.10 and 0.15) compounds (a). Evolution of DC-conductivity with the deficiency amount (b). | ||
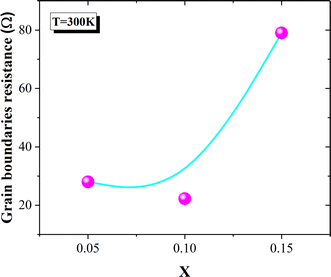
The conductivity spectra of the La0.8Na0.2−x□xMnO3 (x = 0.05, 0.10, 0.15) compounds are displayed in Fig. 7(a). At low frequencies, the conductivity showed a slight decrease with the deficiency ratio increasing from x = 0.05 to x = 0.10 (Fig. 7(a) and (b)). Then, a significant decrease in the conductivity values was observed when the deficiency ratio increased for x = 0.15. Various studies have reported that the transport properties in manganites are mainly controlled by the Mn3+–O2−–Mn4+ network and thus the Mn3+/Mn4+ concentration.17–19 Such a concentration can be modified by the bond length Mn–O, the bond angle Mn–O–Mn, the unit cell volume, the average grain size, and the oxygen vacancies.17–20,26,74 In our case, the decrease in the conductivity values could be explained by the decrease in the grain size (Fig. 1(a)–(d)), which prevented the double-exchange interactions. Indeed, the SEM micrographs showed a decrease in the average grain size with increasing the deficiency rate (2.358, 2.292, 2.087, and 1.994 μm respectively for x = 0.00, 0.05, 0.10, and 0.15) (Fig. 1(a)–(d)). In the literature,17,29,75–79 it has been frequently proved in manganites that the grain boundaries are more resistive than the grains. This could be due to the non-stoichiometric distribution of oxygen and the existence of dangling bonds in the grain boundaries region.80 These factors can lead to charge trapping and an increase in the barrier width, which would hamper the DE interactions in the Mn3+–O2−–Mn4+ chain. Therefore, the decrease in the conductor region (grains) leads then to an increase in the resistive region (grain boundaries) and the reduction of the grains connectivity when the deficiency ratio increases. Fig. 8 confirmed the significant increase in the grain boundary resistance for x = 0.15; whereas, such resistance values were very close for x = 0.05 and x = 0.10. Thus, the electrical conductivity decrease was an expected result (Fig. 7(a) and (b)).
4. Conclusion
Deficient La0.8Na0.2−x□xMnO3 (x = 0.00, 0.05, 0.10, and 0.15) manganites were successfully prepared via a solid-state reaction. The phase formation of the synthesized samples was confirmed using X-ray diffraction diagrams. The scanning electron microscopy analysis revealed there was a decrease in the average grain size. The evolution of magnetization (measured under an applied field of 0.05 T) with temperature indicated the presence of a ferromagnetic–paramagnetic transition for all the compounds. The transition temperature TC was found to decrease when the deficiency ratio increased. Measurements of the effective paramagnetic moments revealed the existence of ferromagnetic correlations within the paramagnetic phase. However, the electrical conductivity spectra showed the coexistence of two frequency slopes mirroring the presence of Jonscher's double power law. As the deficiency amount increased, a significant decrease in the conductivity values was obviously detected. Such an experimental result could be related to the decrease in the grain size. The significant increase in the grain boundary resistance for x = 0.15 confirmed the grain size effect on the transport properties. Eventually, it was observed that the Curie temperature for x = 0.10 was close to room temperature (TC = 297 K). Such a result indicates that the 10% deficiency sample may be a promising candidate for several technological applications.Ethical approval
This article does not contain any studies involving animal or human participants performed by any of the authors.Data availability
The data included in this manuscript are available and can be discussed (or shared), on request from the corresponding author.Author contributions
All the authors have accepted full responsibility for the content of this manuscript and have given their approval to its submission.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study is supported by the Tunisian Ministry of Higher Education and Scientific Research.References
- R. von Helmolt, J. Wecker, B. Holzapfel, L. Schultz and K. Samwer, Giant negative magnetoresistance in perovskite like La2/3Ba1/3MnOx ferromagnetic films, Phys. Rev. Lett., 1993, 71, 2331 CrossRef CAS PubMed.
- S. Jin, T. H. Tiefel, M. McCormack, R. A. Fastnacht, R. Ramesh and L. H. Chen, Thousandfold change in resistivity in magnetoresistive La-Ca-Mn-O films, Science, 1994, 264, 413 CrossRef CAS PubMed.
- M. McCormack, S. Jin, T. H. Tiefel, R. M. Fleming, J. M. Phillips and R. Ramesh, Very large magnetoresistance in perovskite-like La-Ca-Mn-O thin films, Appl. Phys. Lett., 1994, 64, 3045 CrossRef CAS.
- R. D. McMichael, R. D. Shull, L. J. Swartzendruber, L. H. Bennett and R. E. Watson, Magnetocaloric effect in superparamagnets, J. Magn. Magn. Mater., 1992, 111, 33 CrossRef.
- V. K. Pecharsky and K. A. Gschneidner Jr, Magnetocaloric effect and magnetic refrigeration, J. Magn. Magn. Mater., 1999, 200, 44 CrossRef CAS.
- V. Franco, J. S. Blázquez, J. J. Ipus, J. Y. Law, L. M. Moreno-Ramírez and A. Conde, Magnetocaloric effect: From materials research to refrigeration devices, Prog. Mater. Sci., 2018, 93, 112 CrossRef.
- S. Saha, K. Das, S. Bandyopadhyay and I. Das, A-site cationic disorder induced significantly large magnetoresistance in polycrystalline La0.2Gd0.5Ba0.3MnO3 compound, J. Magn. Magn. Mater., 2017, 442, 196 CrossRef CAS.
- Z. C. Xia, S. L. Yuan, W. Feng, L. J. Zhang, G. H. Zang, J. Tang, L. Liu, D. W. Liu, Q. H. Zheng, L. Chen, Z. H. Fang, S. Liu and C. Q. Tang, Magnetoresistance and transport properties of different impurity doped La0.67Ca0.33MnO3 composite, Solid State Commun., 2003, 127, 567 CrossRef CAS.
- Q. Zhang, L. Yin, W. Mi and X. Wang, Large Spatial Spin Polarization at Benzene/La2/3Sr1/3MnO3 Spinterface: Toward Organic Spintronic Devices, J. Phys. Chem. C, 2016, 120, 6156 CrossRef CAS.
- D. Robinson, C. Sepúlveda, E. J. Delgado, O. Peña, J. L. G. Fierro and G. Pecchi, Electronic properties and catalytic performance for DME combustion of lanthanum manganites with partial B-site substitution, J. Catal., 2016, 338, 47 CrossRef.
- N. Khare, D. P. Singh, H. K. Gupta, P. K. Siwach and O. N. Srivastava, Preparation and study of silver added La0.67Ca0.33MnO3 film, J. Phys. Chem. Solids, 2004, 65, 867 CrossRef CAS.
- Y. Tokura, Colossal Magnetoresistive Oxides, Gordon and Breach Science, New York, 2000 Search PubMed.
- T. Elovaara, H. Huhtinen, S. Majumdar and P. Paturi, Irreversible metamagnetic transition and magnetic memory in small-bandwidth manganite Pr1-xCaxMnO3 (x = 0.0–0.5), J. Phys.: Condens. Matter, 2012, 24, 216002 CrossRef CAS PubMed.
- Y. Tokura, Critical features of colossal magnetoresistive manganites, Rep. Prog. Phys., 2006, 69, 797 CrossRef CAS.
- A.-M. Haghiri-Gosnet and J.-P. Renard, CMR manganites: physics, thin films and devices, J. Phys. D: Appl. Phys., 2003, 36, R127 CrossRef CAS.
- V. S. Kolat, T. Izgi, A. O. Kaya, N. Bayri, H. Gencer and S. Atalay, Metamagnetic transition and magnetocaloric effect in charge-ordered Pr0.68Ca0.32−xSrxMnO3 (x = 0, 0.1, 0.18, 0.26 and 0.32) compounds, J. Magn. Magn. Mater., 2010, 322, 427 CrossRef CAS.
- H. Rahmouni, M. Smari, B. Cherif, E. Dhahri and K. Khirouni, Conduction mechanism, impedance spectroscopic investigation and dielectric behavior of La0.5Ca0.5−xAgxMnO3 manganites with compositions below the concentration limit of silver solubility in perovskites (0 ≤ x ≤ 0.2), Dalton Trans., 2015, 44, 10457 RSC.
- B. Cherif, H. Rahmouni, M. Smari, E. Dhahri, N. Moutia and K. Khirouni, Transport properties of silver–calcium doped lanthanum manganite, Phys. B, 2015, 457, 240 CrossRef CAS.
- W. Hizi, H. Rahmouni, K. Khirouni and E. Dhahri, Investigation of charge-carriers dynamics and sub/super-linear response for La0.8Na0.2−x□xMnO3 (x = 0 and 0.1) perovskite ceramics, Phys. B, 2024, 673, 415423 CrossRef CAS.
- W. Hizi, H. Rahmouni, K. Khirouni and E. Dhahri, Nanoparticles size effect on transport properties of doped manganite elaborated by sol–gel route, J. Mater. Sci.: Mater. Electron., 2023, 34, 1173 CrossRef CAS.
- H.-Y. Hou, S. Tian, H.-R. Ge, J.-D. Chen, Y.-Q. Li and J.-X. Tang, Recent progress of polarization-sensitive perovskite photodetectors, Adv. Funct. Mater., 2022, 32, 2209324 CrossRef CAS.
- S. Othmani, R. Blel, M. Bejar, M. Sajieddine, E. Dhahri and E. K. Hlil, New complex magnetic materials for an application in Ericsson refrigerator, Solid State Commun., 2009, 149, 969 CrossRef CAS.
- A. Žužić, L. Pavić, A. Bafti, S. Marijan, J. Macan and A. Gajović, The role of the A-site cation and crystal structure on the electrical conductivity of strontium-doped calcium and barium manganites, J. Alloys Compd., 2023, 935, 167949 CrossRef.
- D. I. Pchelina, V. D. Sedykh, N. I. Chistyakova, V. S. Rusakov, Y. A. Alekhina, A. N. Tselebrovskiy, B. Fraisse, L. Stievano and M. T. Sougrati, The structural and magnetic features of perovskite oxides La1−xSrxMnO3+δ (x = 0.05, 0.10, 0.20) depending on the strontium doping content and heat treatment, Ceram. Int., 2023, 49, 10774 CrossRef CAS.
- Y. Xin, L. Shi, J. Zhao, X. Yuan, L. Hou and R. Tong, Electrical transport properties driven by magnetic competition in hole-doped perovskite Pr1−xBaxMnO3 (0.25 ≤ x ≤ 0.36), Ceram. Int., 2021, 47, 19464 CrossRef CAS.
- H. Rahmouni, A. Selmi, K. Khirouni and N. Kallel, Chromium effects on the transport properties in La0.7Sr0.3Mn1−xCrxO3, J. Alloys Compd., 2012, 533, 93 CrossRef CAS.
- R. Hanen, A. Mleiki, H. Rahmouni, N. Guermazi, K. Khirouni, E. K. Hlil and A. Cheikhrouhou, Effect of the nature of the dopant element on the physical properties of X-PrCaMnO system (X = Cd, Sr, and Pb), J. Magn. Magn. Mater., 2020, 508, 166810 CrossRef CAS.
- H. Baaziz, A. Tozri, E. Dhahri and E. K. Hlil, Effect of particle size reduction on the structural, magnetic properties and the spin excitations in ferromagnetic insulator La0.9Sr0.1MnO3 nanoparticles, Ceram. Int., 2015, 41, 2955 CrossRef CAS.
- W. Hizi, M. Wali, H. Rahmouni, K. Khirouni and E. Dhahri, Examination of charge-carriers hopping and identification of relaxation phenomenon and blocking effect in perovskite system, Eur. Phys. J. Plus, 2024, 139, 156 CrossRef CAS.
- R. Mendoza, J. Oliva, K. P. Padmasree, A. I. Mtz-Enriquez, A. Hayat and V. Rodriguez- Gonzalez, A sustainable avocado-peel based electrode for efficient graphene supercapacitors: enhancement of capacitance by using Sr doped LaMnO3 perovskites, Ceram. Int., 2022, 48, 30967 CrossRef CAS.
- A. V. Pashchenko, N. A. Liedienov, I. V. Fesych, Q. Li, V. G. Pitsyuga, V. A. Turchenko, V. G. Pogrebnyak, B. Liu and G. G. Levchenko, Smart magnetic nanopowder based on the manganite perovskite for local hyperthermia, RSC Adv., 2020, 10, 30907 RSC.
- W. Hizi, H. Rahmouni, K. Khirouni and E. Dhahri, Consistency between theoretical conduction models and experimental conductivity measurements of strontium-doped lanthanum manganite, J. Alloys Compd., 2023, 957, 170418 CrossRef CAS.
- Y. Regaieg, G. Delaizir, F. Herbst, L. Sicard, J. Monnier, D. Montero, B. Villeroy, S. Ammar-Merah, A. Cheikhrouhou, C. Godart and M. Koubaa, Rapid solid-state synthesis by spark plasma sintering and magnetic properties of LaMnO3 perovskite manganite, Mater. Lett., 2012, 80, 195 CrossRef CAS.
- C. Zener, Interaction between the d-Shells in the Transition Metals. II. Ferromagnetic Compounds of Manganese with Perovskite Structure, Phys. Rev., 1951, 82, 403 CrossRef CAS.
- M. C. Dimri, H. Khanduri and R. Stern, Effects of aliovalent dopants in LaMnO3: Magnetic, structural and transport properties, J. Magn. Magn. Mater., 2021, 536, 168111 CrossRef CAS.
- M. Arunachalam, P. Thamilmaran, S. Sankarrajan and K. Sakthipandi, Ultrasonic studies on sodium-doped LaMnO3 perovskite material, Cogent Phys., 2015, 2, 1067344 CrossRef.
- A. Tozri, E. Dhahri and E. K. Hlil, Impact of vacancy and Na substitutions on the critical magnetic behavior in polycrystalline La0.8Pb0.2MnO3, Phys. Lett. A, 2011, 375, 1528 CrossRef CAS.
- H. Liu, Y. Li, H. Zhang, Y. Chen, L. Chen, X. Dong and K. Chen, The role of disorder in sodium-doped LaMnO3, Phys. Status Solidi A, 2011, 208, 2373 CrossRef CAS.
- L. Malavasi, M. C. Mozzati, I. Alessandri, L. E. Depero, C. B. Azzoni and G. Flor, Sodium-doped LaMnO3 thin films: Influence of substrate and thickness on physical properties, J. Phys. Chem. B, 2004, 108, 13643 CrossRef CAS.
- S. Roy, Y. Q. Guo, S. Venkatesh and N. Ali, Interplay of structure and transport properties of sodium-doped lanthanum manganite, J. Phys.: Condens. Matter, 2001, 13, 9547 CrossRef CAS.
- D. Varshney, D. Choudhary, M. W. Shaikh and E. Khan, Electrical resistivity behaviour of sodium substituted manganites: electron-phonon, electron-electron and electron-magnon interactions, Eur. Phys. J. Plus B, 2010, 76, 327 CrossRef CAS.
- J. Vergara, R. J. Ortega-Hertogs and V. Madurga, Effect of disorder produced by cationic vacancies at the B sites on the electronic properties of mixed valence manganites, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 1127 CrossRef CAS.
- M. Oumezzine, S. Kallel, O. Peña, N. Kallel, T. Guizouarn, F. Gouttefangeas and O. Mohamed, Correlation between structural, magnetic and electrical transport properties of barium vacancies in the La0.67Ba0.33−x□xMnO3 (x = 0, 0.05, and 0.1) manganite, J. Alloys Compd., 2014, 582, 640 CrossRef CAS.
- B. Arun, V. R. Akshay, K. Devi Chandrasekhar, G. R. Mutta and M. Vasundhara, Comparison of structural, magnetic and electrical transport behavior in bulk and nanocrystalline Nd-lacunar Nd0.67Sr0.33MnO3 manganites, J. Magn. Magn. Mater., 2019, 472, 74 CrossRef CAS.
- B. Sudakshina, K. K. Supin and M. Vasundhara, Effects of Nd-deficiency in Nd0.67Ba0.33MnO3 manganites on structural, magnetic and electrical transport properties, J. Magn. Magn. Mater., 2022, 542, 168595 CrossRef CAS.
- B. Arun, V. R. Akshay and M. Vasundhara, Observation of enhanced magnetocaloric properties with A-site deficiency in La0.67Sr0.33MnO3 manganite, Dalton Trans., 2018, 47, 15512 RSC.
- J. Makni-Chakroun, R. M’nassri, W. Cheikhrouhou-Koubaa, M. Koubaa, N. Chniba-Boudjada and A. Cheikhrouhou, Effect of A-site deficiency on investigation of structural, magnetic and magnetocaloric behaviors for (LaSr)-lacunar manganites, Chem. Phys. Lett., 2018, 707, 61 CrossRef CAS.
- F. Elleuch, M. Triki, M. Bekri, E. Dhahri and E. K. Hlil, A-site-deficiency-dependent structural, magnetic and magnetoresistance properties in the Pr0.6Sr0.4MnO3 manganites, J. Alloys Compd., 2015, 620, 249 CrossRef CAS.
- A. Bosak, C. Dubourdieu, M. Audier, J. P. Senateur and J. Pierre, Compositional effects on the structure and magnetotransport properties of lacunar La1−xMnO3−δ films (x > 0) grown by MOCVD, Appl. Phys. A, 2004, 79, 1979 CrossRef CAS.
- M. Smari, I. Walha, E. Dhahri and E. K. Hlil, Structural, magnetic and magnetocaloric properties of Ag-doped La0.5Ca0.5−xAgxMnO3 compounds with 0 ≤ x ≤ 0.4, J. Alloys Compd., 2013, 579, 564 CrossRef CAS.
- R. M’nassri, W. Cheikhrouhou-Koubaa, N. Chniba Boudjada and A. Cheikhrouhou, Effect of barium-deficiency on the structural, magnetic, and magnetocaloric properties of La0.6Sr0.2Ba0.2−x□xMnO3 (0 ≤ x ≤ 0.15), J. Appl. Phys., 2013, 113, 073905 CrossRef.
- R. A. Young, The Rietveld Method, Oxford University Press, New York, 1993 Search PubMed.
- B. Vertruyen, J.-F. Fagnard, Ph. Vanderbemden, M. Ausloos, A. Rulmont and R. Cloots, Electrical transport and magnetic properties of Mn3O4–La0.7Ca0.3MnO3 ceramic composites prepared by a one-step spray-drying technique, J. Eur. Ceram. Soc., 2007, 27, 3923 CrossRef CAS.
- N. Mtiraoui, A. Dhahri, M. Oumezine, J. Dhahri and E. Dhahri, Effects of nonmagnetic silver Ag doping on the structural, magnetic and electric properties in La0.67Pb0.33MnO3 manganese oxides, J. Magn. Magn. Mater., 2011, 323, 2831 CrossRef CAS.
- N. Dhahri, A. Dhahri, K. Cherif, J. Dhahri, H. Belmabrouk and E. Dhahri, Effect of Co substitution on magnetocaloric effect in La0.67Pb0.33Mn1−xCoxO3 (0.15 ≤ x ≤ 0.3), J. Alloys Compd., 2010, 507, 405 CrossRef CAS.
- D. Shannon, Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751 CrossRef.
- M. Khlifi, M. Bejar, O. EL Sadek, E. Dhahri, M. A. Ahmed and E. K. Hlil, Structural, magnetic and magnetocaloric properties of the lanthanum deficient in La0.8Ca0.2−x□xMnO3 (x = 0–0.20) manganites oxides, J. Alloys Compd., 2011, 509, 7410 CrossRef CAS.
- R. Skini, M. Khlifi, E. Dhahri and E. K. Hlil, Lanthanum Deficiency Effect on the Structural, Magnetic and Transport Properties of the La0.8−x□xCa0.2MnO3 Manganites Oxides, J. Supercond. Novel Magn., 2014, 27, 247 CrossRef CAS.
- M. Wali, R. Skini, M. Khlifi, E. Dhahri and E. K. Hlil, A giant magnetocaloric effect with a tunable temperature transition close to room temperature in Na-deficient La0.8Na0.2−x□xMnO3 manganites, Dalton Trans., 2015, 44, 12796 RSC.
- A. Hadded, J. Massoudi, S. Gharbi, E. Dhahri, A. Tozri and M. R. Berber, Study of physical properties of a ferromagnetic spinel Cu1.5Mn1.5O4: spin dynamics, magnetocaloric effect and critical behavior, RSC Adv., 2021, 11, 25664 RSC.
- S. Brion, F. Ciorcas, G. Chouteau, P. Lejay, P. Radaelli and C. Chaillout, Magnetic and electric properties of La1−δMnO3, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1304 CrossRef.
- K. Funke, Jump relaxation in solid electrolytes, Prog. Solid State Chem., 1993, 22, 111 CrossRef CAS.
- G. E. Pike, AC Conductivity of scandium oxide and a new hopping model for conductivity, Phys. Rev. B: Solid State, 1972, 6, 1572 CrossRef CAS.
- K. Maan Sangwan, N. Ahlawat, S. Rani, S. Rani and R. S. Kundu, Influence of Mn doping on electrical conductivity of lead free BaZrTiO3 perovskite ceramic, Ceram. Int., 2018, 44, 10315 CrossRef.
- A. S. Nowick and B. S. Lim, Analysis of ac conductivity data for Na2O3SiO2 glass by stretched exponential and Jonscher power-law methods, J. Non-Cryst. Solids, 1994, 172, 1389 CrossRef.
- W. Hizi, M. Gassoumi, H. Rahmouni, A. Guesmi, N. B. Hamadi and E. Dhahri, Effect of Sintering Temperature and Polarization on the Dielectric and Electrical Properties of La0.9Sr0.1MnO3 Manganite in Alternating Current, Materials, 2022, 15, 3683 CrossRef CAS PubMed.
- S. R. Elliott, A theory of ac conduction in chalcogenide glasses, Philos. Mag., 1977, 36, 1291 CrossRef CAS.
- M. Coşkun, Ö. Polat, F. M. Coşkun, Z. Durmuş, M. Çağlar and A. Türüt, Frequency and temperature dependent electrical and dielectric properties of LaCrO3 and Ir doped LaCrO3 perovskite compounds, J. Alloys Compd., 2018, 740, 1012 CrossRef.
- G. Nag Bhargavi, A. Khare, T. Badapanda, M. Shahid Anwar and N. Brahme, Electrical characterizations of BaZr0.05Ti0.95O3 perovskite ceramic by impedance spectroscopy, electric modulus and conductivity, J. Mater. Sci.: Mater. Electron., 2017, 28, 16956 CrossRef.
- Ch. Rayssi, S. El Kossi, J. Dhahri and K. Khirouni, Colossal dielectric constant and non-debye type relaxor in Ca0.85Er0.1Ti1−xCo4x/3O3 (x = 0.15 and 0.2) ceramic, J. Alloys Compd., 2018, 759, 93 CrossRef CAS.
- P. Bruce, High and low frequency Jonscher behavior of an ionically conducting glass, Solid State Ionics, 1985, 15, 247 CrossRef CAS.
- A. K. Jonscher, The universal dielectric response, Nature, 1977, 267, 673 CrossRef CAS.
- A. K. Jonscher and M. S. Frost, Weakly frequency-dependent electrical conductivity in a chalcogenide glass, Thin Solid Films, 1976, 37, 267 CrossRef CAS.
- L. Malavasi, M. C. Mozzati, C. B. Azzoni, G. Chiodelli and G. Flor, Role of oxygen content on the transport and magnetic properties of La1−xCaxMnO3+δ manganites, Solid State Commun., 2002, 123, 321 CrossRef CAS.
- W. Hizi, H. Rahmouni, N. E. Gorji, A. Guesmi, N. B. Hamadi, L. Khezami, E. Dhahri, K. Khirouni and M. Gassoumi, Impact of sintering temperature on the electrical properties of La0.9Sr0.1MnO3 manganite, Catalysts, 2022, 12, 340 CrossRef CAS.
- R. Charguia, S. Hcini, M. Boudard and A. Dhahri, Microstructural properties, conduction mechanism, dielectric behavior, impedance and electrical modulus of La0.6Sr0.2Na0.2MnO3 manganite, J. Mater. Sci.: Mater. Electron., 2019, 30, 2975 CrossRef CAS.
- H. Rahmouni, M. Nouiri, R. Jemai, N. Kallel, F. Rzigua, A. Selmi, K. Khirouni and S. Alaya, Electrical conductivity and complex impedance analysis of 20% Ti-doped La0.7Sr0.3MnO3 perovskite, J. Magn. Magn. Mater., 2007, 316, 23 CrossRef CAS.
- H. Rahmouni, R. Jemai, M. Nouiri, N. Kallel, F. Rzigua, A. Selmi, K. Khirouni and S. Alaya, Admittance spectroscopy and complex impedance analysis of Ti-modified La0.7Sr0.3MnO3, J. Cryst. Growth, 2008, 310, 556 CrossRef CAS.
- K. Hayat, M. A. Rafiq, S. K. Durrani and M. M. Hasan, Impedance spectroscopy and investigation of conduction mechanism in BaMnO3 nanorods, Phys. B, 2011, 406, 309 CrossRef CAS.
- A. I. Tovstolytkin, A. N. Pogorily, V. V. Kotov, A. G. Belous and O. I. V'yunov, Effect of the crystal structure defectiveness on magnetic state of sodium-doped lanthanum manganites, Funct. Mater., 2004, 11, 721 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra03519d |
| This journal is © The Royal Society of Chemistry 2024 |