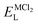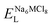Open Access Article
Open Access ArticleNa6MCl8 rock-salt compounds with M = Mg, Ca, Ba, Zn, Sr as components for solid-state sodium ion batteries†
Yohandys A. Zulueta a,
My Phuong Pham-Ho
a,
My Phuong Pham-Ho bc and
Minh Tho Nguyen
bc and
Minh Tho Nguyen *de
*de
aDepartamento de Física, Facultad de Ciencias Naturales y Exactas, Universidad de Oriente, CP 90500, Santiago de Cuba, Cuba
bFaculty of Chemical Engineering, Ho Chi Minh City University of Technology (HCMUT), 268 Ly Thuong Kiet Street, Dist. 10, Ho Chi Minh City, Vietnam
cVietnam National University Ho Chi Minh City, Linh Trung, Thu Duc City, Ho Chi Minh City, Vietnam
dLaboratory for Chemical Computation and Modeling, Institute for Computational Science and Artificial Intelligence, Van Lang University, Ho Chi Minh City, Vietnam. E-mail: minhtho.nguyen@vlu.edu.vn
eFaculty of Applied Technology, School of Technology, Van Lang University, Ho Chi Minh City, Vietnam
First published on 8th July 2024
Abstract
We investigate a new series of rock-salt type structures, Na6MCl8 with M = Mg, Ca, Ba, Zn and Sr using advanced atomistic simulations. Calculated results show a direct relationship between the size of the M2+ cation and lattice parameters as well as the defect formation energy variation. The NaCl Schottky defect type is highly favourable, and the Na6BaCl8 structure possesses the lowest values of defect formation energies. These structures are predicted to be mechanically stable and ductile, implying their compatibility with possible use as electrodes/electrolytes. The Na6MCl8 structures exhibit semiconductor characteristics with an energy gap ranging between 4.1–4.6 eV, which differs from the previous value of Na6MgCl8. A 3D migration pathway is identified in each rock-salt structure. Despite the small variation of the Na diffusivity and conductivity at 250 K within the structures considered, the Na6BaCl8 is characterized by the highest conductivity at 250 K, while the Na6MgCl8 structure has the highest conductivity and diffusivity values. The outstanding properties predicted for a Na ion battery suggest future development of synthetic strategies for their actual preparation.
1. Introduction
The search for new and improved compounds for use as electrolytes and electrodes in solid-state batteries is crucial for further advancing their performance and thereby their industrial applications. Na-ion batteries are considered an effective alternative technology to the popular Li-ion batteries due to their abundance, lower cost, and eco-friendliness.1–9 However, their lower energy density, as compared to that of Li-ion counterparts, remains an important issue to be solved, and therefore Na batteries are not widely commercialized yet. In this context, the discovery of new compounds can help improve the energy density, safety, sustainability, and power delivery of Na-ion batteries. This will not only increase their usage in various applications such as electric vehicles, grid storage, and backup power supplies, but also contribute to the development of sustainable energy solutions. In this context, the search for new compounds is essential for the advancement of Na-ion batteries, in particular the solid-state electrolytes (SSEs).1–14 The demand of conductivity for an SSE at 25 °C is <10−2 S cm−1.9–14 In the state-of-the-art of Na-ion battery technologies, there are not many compounds complying with this requirement, thus motivating intensive research on new materials.9–14 On the other hand, in order to prevent a premature device failure, an SSE must exhibit a negligible electronic and anionic conductivity, thus allowing for any undesirable reactions with the electrodes during the charge/discharge process to be avoided. Additionally, an SSE should be ductile and mechanically stable to ensure a good contact with the electrodes and prevent dendrite formation.Solid polymers, oxide and sulphide derivatives are the most common commercial compounds used for SSEs.5 While oxide based SSEs tend to lead to dendrite formation and high interfacial resistance, sulphide based compounds possess a poor air stability and also high interfacial resistance.1–9 To overcome these problems, halide-based sodium ion conductors emerge as better candidates for solid state electrolytes having excellent electrochemical stability and high conductivity.8,9,15–18
A high Na density is also required for a SSE compound, because the Na ions constitute the charge transfer source, ensuring the Na reactivity, cycling and durability. Na-rich antiperovskite Na3OX (X = Cl, Br) and other metal halide compounds have been studied, including the exploration of defect engineering with the aim to improve the conducting properties of defective A3OX (A = Li+, Na+, X = Cl−, Br−) structures.15–18 The effects on Na ion conductivity upon doping with divalent and trivalent dopants have been explored employing atomistic simulation computations.15 Favourable incorporation mechanisms have been found to increase the Na vacancy concentration with effective effect on the Na conductivity.18 The Na+ conductivity in the chloride Na3OCl amounts to 10−7 S cm−1 at 300 K.18 On the other hand, a theoretical study demonstrated that Na3YCl6 and Na3Y2Cl9 compounds are electrochemically stable with outstanding transport properties.7 Other promising halides such as NaAlCl4, Na3−xEr1−xZrxCl6, Na2+xZr1−xInxCl6, Na2ZrCl6 and Na3−xY1−xZrxCl6 have been synthesized, with the higher Na ionic conductivities of ∼10−5 S cm−1.6,19–22
Atomistic simulations provide us with a detailed understanding of the mechanisms that govern the properties of battery materials.23–25 Such a understanding is necessary for selection on the composition, crystal structure, and defect properties of the material. Simulations can also predict stability and reactivity with different electrolytes, particularly their electrochemical behaviour leading to better performance. Overall, atomistic simulations have been proved to be a powerful approach for materials design and discovery, essential for developing new and improved battery materials.15,23–27
In our previous work, advanced atomistic simulations have been used to evaluate the main properties of the Na6MgCl8 rock-salt material.27 The Na6MgCl8 has an insulating characteristic with an energy gap of 5.1 eV and is mechanically stable and ductile. Our simulations also predicted that the Zn2+ ion is the best divalent dopant, improving the defect characteristics and transport properties of Na6MgCl8. Na transport properties are significantly improved following doping of the Na6MgCl8 with the divalent Ba2+ and Zn2+ ions.27 Considering that the Zn2+, Ca2+, Sr2+ and Ba2+ ions are doubly charged as the Mg2+ cation, we set out to further explore the main properties of a new series of rock-salt structures, namely the Na6MgCl8 with divalent M2+ cations being Mg2+, Ca2+, Ba2+, Zn2+ and Sr2+, using advanced atomistic simulations. Structural, electronic and mechanical properties, including intrinsic defects formation and transport properties are investigated. Our simulation results suggest some novel compounds for subsequent experimental preparations and verifications to evaluate their potential application as electrolytes.
2. Computational methodology
Density functional theory (DFT) calculations are carried out using the CASTEP code,28 to explore the structural, electronic spectroscopy and mechanical properties of Na6MCl8 structure. We adopt the setup described in our previous work on Na6MgCl8.27 DFT calculations are performed using the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof exchange–correlation functional optimized for solid (PBESOL).29 The pseudoatomic functions for Na-2s22p63s1, M-2p63s2 and Cl-3s23p5 in the reciprocal representations are used to represent the electronic configuration of the constituent atoms in these structures. The convergence thresholds for self-consistent computation, and geometry optimization calculations are taken with a total energy change of 5 × 10−6 eV per atom, and maximum force, stress and atomic displacements of 10−2 eV Å−1, 2 × 10−2 GPa and 5 × 10−4 Å, respectively. Ultrasoft pseudopotentials with a plane-wave energy cut-off of 830 eV are adopted. A 4 × 4 × 4 k-point set along the Monkhorst–Pack scheme which is used to sample the Brillouin zone during the geometry optimization.30The General Utility Lattice Program (GULP) is used to perform force field-based computations.31 The potential (force field) parameters are taken from previous studies.15,27,32 The Buckingham approximation is used for the short-range interactions, while long-range interactions are treated as coulombic interactions where only the charge and the interatomic distance describe the long-range potential energy. The Dick–Overhauser model is included for consideration of the ionic polarization where each ion is approximated as a positively charged core and a negatively charged shell linked by a spring (with spring constant k), and the sum of the core–shell charge results in the formal charge (Z) of the polarizable species.33
The Mott–Littleton method is used for the defect calculations in which the crystal structure is divided into two concentrically spherical regions with the radius of R1 and R2 with R1 < R2.34 At the inner sphere, the isolated defect, or defect cluster, is positioned where the interaction between the defect(s) with the local structure is strong, while the region R2 is treated by a quasi-continuum approximation.34 Values of R1 = 13 Å and R2 = 27 Å are adopted, ensuring a smooth convergence of the simulations. The Broyden–Fletcher–Goldfarb–Shanno algorithm is used for geometry optimizations and defect energetics computations.31,35 This technique has extensively been used to explore the defect formation in different types of solid-state materials.17,23–27
The bond valence method is a simple and effective approach for determining the diffusion paths and activation energies for diffusion and conduction.21,36–38 This method identifies the mobile cation with regions of low bond valence site energy. The bond length between a cation A and an anion, denoted as X (LA–X), is evaluated with the help of tabulated empirical parameters L0,A–X and bA–X, and it is related to an individual bond valence (eqn (1)):
| SA–X = exp[(L0,A–X − LA–X)/bA–X] | (1) |
By adding the coulombic repulsive term (Erepulsion) of the mobile A ion respect to other immobile ions, the bond valence site energy of a cation A [EBVSE(A)] is evaluated in a similar way to the Morse empirical potentials:36–40
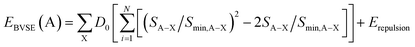 | (2) |
The bond valence pathway analyser (softBV-GUI) code is used for the computation EBVSE and the required parameters in eqn (2) are included in the code.40 For the analysis of the EBVSE(Na), while coulombic repulsions are considered between mobile Na and immobile M2+ cations, coulombic attraction interactions are included into the Morse type attraction terms. Furthers details on the bond valence approach can be found in ref. 36–40.
3. Results and discussion
3.1. Structural characterization and defect energetics of Na6MCl8 (M2+ = Mg2+, Zn2+, Ca2+, Sr2+, Ba2+)
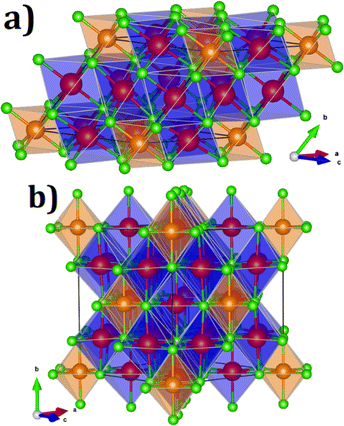
Fig. 1 displays the unit cell of these compounds in their primitive and conventional representations. On the basis of the Na6MgCl8 structure, the proposed Na6MCl8 (M2+ = Zn2+, Ca2+, Sr2+, Ba2+) compounds consist in a rock-salt structure with four Z formula units in the cubic Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group; the M2+ ion is bonded to six equivalent Cl− atoms forming [MCl6] octahedron, while the Na+ cations is 6-coordinated with Cl− anions sharing corned and edges with [MCl6] and [NaCl6] octahedra.
m space group; the M2+ ion is bonded to six equivalent Cl− atoms forming [MCl6] octahedron, while the Na+ cations is 6-coordinated with Cl− anions sharing corned and edges with [MCl6] and [NaCl6] octahedra.
To explore the lattice properties of Na6MCl8 (M2+ = Mg2+, Zn2+, Ca2+, Sr2+, Ba2+), the lattice energies of NaCl and MCl2 compounds are computed. In what follows, the Na2MgCl8 results previously reported in ref. 27 are included for a direct comparison of the structures considered. Following the computational protocol implemented in our previous work,24,27 the Na-, M- and Cl-vacancy energies (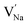 ,
,  and
and 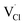 respectively) are computed. Table 1 collects the results for lattice parameters and basic defect formation of Na6MCl8. Inclusion of the ionic radius of M2+ in Table 1 serves to clarify the tendency of the lattice energy and cell parameters in response to changes in ionic size.
respectively) are computed. Table 1 collects the results for lattice parameters and basic defect formation of Na6MCl8. Inclusion of the ionic radius of M2+ in Table 1 serves to clarify the tendency of the lattice energy and cell parameters in response to changes in ionic size.
| (a) Na6MCl8 | M2+ | IR (CN VI) | a (Å) | ENavac | EMvac | EClvac | ||
|---|---|---|---|---|---|---|---|---|
| Na6MgCl8 | Mg | 0.72 | −26.52 | 11.085 | 5.181 | 21.765 | 5.435 | −75.255 |
| Na6ZnCl8 | Zn | 0.74 | −26.93 | 11.049 | 5.183 | 22.515 | 5.472 | −76.112 |
| Na6CaCl8 | Ca | 0.99 | −21.15 | 11.420 | 5.007 | 16.264 | 5.081 | −69.094 |
| Na6SrCl8 | Sr | 1.18 | −21.14 | 11.440 | 4.984 | 15.911 | 5.058 | −68.735 |
| Na6BaCl8 | Ba | 1.35 | −20.16 | 11.564 | 4.815 | 14.130 | 4.917 | −66.983 |
| (b) Interatomic distance (in Å) | Na6MCl8 | ||||
|---|---|---|---|---|---|
| Na6MgCl8 | Na6ZnCl8 | Na6CaCl8 | Na6SrCl8 | Na6BaCl8 | |
| dCl–Cl | 3.456 | 3.392 | 4.017 | 4.043 | 3.957 |
| dNa–Na | 3.919 | 3.906 | 4.038 | 4.045 | 4.088 |
| dM–M | 7.838 | 7.813 | 8.075 | 8.090 | 8.177 |
| dCl–Na | 2.785 | 2.762 | 2.855 | 2.860 | 2.892 |
| dCl–M | 2.443 | 2.399 | 2.840 | 2.862 | 2.984 |
| dM–Na | 3.919 | 3.906 | 4.038 | 4.045 | 4.088 |
| (c) Schottky formation energy (eV per defect) | |||||
|---|---|---|---|---|---|
| Na6MCl8 | M2+ | IR (CN VI) | NaCl Schottky | MCl2 Schottky | Na6MCl8 Schottky |
| Na6MgCl8 | Mg | 0.72 | 1.26 | 3.06 | 7.03 |
| Na6ZnCl8 | Zn | 0.74 | 1.28 | 3.27 | 7.09 |
| Na6CaCl8 | Ca | 0.99 | 0.99 | 2.64 | 5.96 |
| Na6SrCl8 | Sr | 1.18 | 0.97 | 2.44 | 5.85 |
| Na6BaCl8 | Ba | 1.35 | 0.82 | 1.90 | 5.12 |
As it is shown, the lattice energy of constituent chlorides and Na6MCl8 (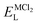 , ENaClL and
, ENaClL and 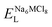 ), cell parameters and vacancy formation energies tend to decrease with increasing ionic radius. Another point of interest is that Na vacancy formation is associated with the lowest energy followed by the Cl vacancy energy. Various reports of such energetic behaviour subtend that both Na and Cl vacancies are the most abundant defect type in other Na–Cl containing materials.15,18,27 A clear influence of M2+ ionic radius on the lattice properties and vacancy formation is thus demonstrated. As the ionic radius increases, the lattice parameters of MCl2 and Na6MCl8 structures increase whereas the rest of the magnitude decrease.
), cell parameters and vacancy formation energies tend to decrease with increasing ionic radius. Another point of interest is that Na vacancy formation is associated with the lowest energy followed by the Cl vacancy energy. Various reports of such energetic behaviour subtend that both Na and Cl vacancies are the most abundant defect type in other Na–Cl containing materials.15,18,27 A clear influence of M2+ ionic radius on the lattice properties and vacancy formation is thus demonstrated. As the ionic radius increases, the lattice parameters of MCl2 and Na6MCl8 structures increase whereas the rest of the magnitude decrease.
Results of the interatomic distances (d) of each Na6MCl8 structure emphasize that the central cation size affects the Na–Na (dNa–Na) distance, which in turn determines the diffusion properties of these materials.27 The dNa–Na value decreases in going from Na6MgCl8 to Na6ZnCl8 and increase to 4.09 Å in Na6BaCl8. Several Na-containing structures currently considered in battery technologies exhibit similar Na–Na interatomic distances to those observed in the present Na6MCl8 compounds.15,19,20
Along with the results of basic defects formation, the intrinsic defects play an important role determining the transport properties of materials. In particular, the Schottky defect type is the most common defect scheme present in conducting materials. The Schottky formation mechanism is usually described in terms of three different schemes; the first scheme can be written in the Kröger–Vink notation,41 as expressed by eqn (3):
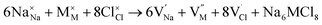 | (3) |
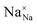 ,
, 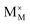 and
and 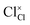 represent the host ions occupying its respective atomic position at the Na6MCl8 lattice structure, while
represent the host ions occupying its respective atomic position at the Na6MCl8 lattice structure, while 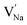 ,
, 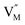 and
and 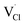 symbolize a Na, M and Cl-vacancy, respectively. In the present context, eqn (3) describes the full Schottky defect formation mechanism, in which formation of NaCl Schottky defect can be described by eqn (4):
symbolize a Na, M and Cl-vacancy, respectively. In the present context, eqn (3) describes the full Schottky defect formation mechanism, in which formation of NaCl Schottky defect can be described by eqn (4):
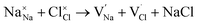 | (4) |
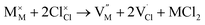 | (5) |
According to the defect-energetics computation protocols used in a previous work, the solution energy (Es) is computed as follows (eqn (6)–(8)):
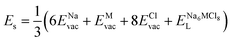 | (6) |
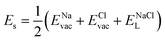 | (7) |
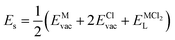 | (8) |
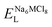 , ENaClL and
, ENaClL and 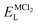 represent the lattice energy of Na6MCl8, NaCl and MCl2 compounds, respectively.
represent the lattice energy of Na6MCl8, NaCl and MCl2 compounds, respectively.
The results of basic defect formation energies are also included in Table 1. For the three Schottky defects type considered, the solution energies decrease with respect to the increment of the M2+ ionic radius. The most favorable Schottky defect formation corresponds to the NaCl in all structures, followed by the MCl2, and the unfavorable Na6MCl8 Schottky. In addition, within the Schottky defect type, the Na6BaCl8 structure has the lowest values of defect formation energy. Taking now a closer look into the M2+ ionic radius and the defect energetics behaviour, we note that the lattice parameters from Na6MgCl8 to Na6ZnCl8 decrease and gradually increases for the rest of structures considered. As was discussed before,27 a similar behavior upon the M2+ ionic radius is found for the interatomic distances. The behavior of the defect energetics is similar to those disclosed for the lattice parameters and interatomic distances. These results can be attributed to the increase in the average bond length and volume of the [MCl6] octahedron, which in turn affects the corresponding bond length and volume of the [NaCl] octahedron. This effect occurs with the increment of the M2+ ionic radius. These results point out a direct relationship between the M2+ ionic radius with the defect chemistry within the Na6MCl8 framework, including the aforementioned relation to the lattice parameters and interatomic distances.
Fig. 2 shows the band structure of Na6MgCl8 in which the Fermi level is taken as the 0 eV reference. The valence bands are located in the range of −3 eV and the Fermi level, and the conduction bands lies between 4.5 and 17 eV. The energy gap values are included in figures; these values are remarkably lower than that of 5.1 eV reported for Na6MgCl8 structure.27 In this sense, the new compound inherits the electronic characteristics of the Na6MgCl8 partner structure, in which many electrons are present at the top valence bands at the Γ-point. This aligns well with the criteria for consideration of SSEs, as these compounds possess a minimal electronic conduction. However, it is crucial to exercise caution while interpreting the computed energy gap due to the characteristic tendency of DFT computations to underestimate the band gaps and the absence of experimental results for calibration.42
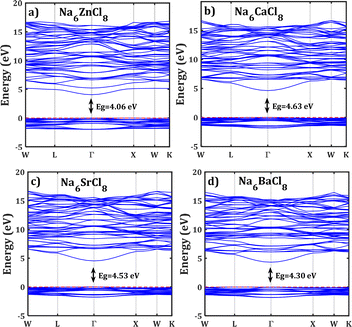 | ||
| Fig. 2 Band structure of the Na6MCl8 (M = Zn, Ca, Sr, Ba). The computed energy gap (Eg) are shown in each case. Horizontal red line represents the Fermi level. | ||
3.2. Mechanical stability
Exploration of mechanical properties is of great importance when choosing materials to be used as electrode or electrolyte in batteries.43–45 The key requirements for mechanical stability include moderate Young modulus in order to ensure optimal contact between a solid electrolyte and the electrodes, thus avoiding the presence of undesirable voids and cracks affecting the long range transport properties.43–45The mechanical response of a crystalline structure is described by the Hooke law, and expressed by the elastic constant matrix (Cij), defined as in eqn (9):
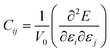 | (9) |
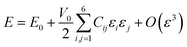 | (10) |
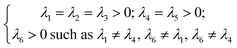 | (11) |
The Cij matrix elements of each compound are collected in the ESI file.† All the Cij values are positive. Moreover, the values of C44, C55 and C66 are significantly lower than the diagonal Cij (i, j = 1, 2, 3); elements for all Na6MCl8 structures, which implies that a shear deformation is more probable to occur as a consequence of the strong resistance to uniaxial stress.46–54 Shear deformations had been observed in other battery materials with consequences in their performances.46–54 Table 2 collects the computed eigenvalues of each Na6MCl8 structure considered, including those obtained in our previous work for Na6MgCl8 structure.27 All the eigenvalues are positive revealing that these structures are mechanically stable. Besides, in all cases λ1 < λ4 < λ6 and the same trend of λi values is observed upon the increment of M2+ ionic size (from Mg2+ to Zn2+ the λi increases and decreases from Zn2+ to Ba2+). This means that the central ionic size (i.e. the ionic radius of M2+ in the Na6MCl8 lattice structures) induces direct implications elucidating the mechanical stability.
| (a) Compound | λ1 | λ4 | λ6 |
|---|---|---|---|
| Na6MgCl8 | 13.74 | 34.81 | 79.72 |
| Na6ZnCl8 | 13.92 | 35.75 | 82.28 |
| Na6CaCl8 | 12.43 | 25.16 | 59.72 |
| Na6SrCl8 | 12.36 | 24.47 | 58.66 |
| Na6BaCl8 | 11.91 | 20.50 | 53.01 |
| (b) | Mechanical properties | Reuss | Voigt | Hill |
|---|---|---|---|---|
| Na6MgCl8 | B | 26.574 | 26.574 | 26.574 |
| G | 15.004 | 15.206 | 15.105 | |
| E(x,y,z) | 42.860 | 42.860 | 42.860 | |
| B/G | 1.771 | 1.748 | 1.759 | |
| Compressibility | 0.038 | |||
| Na6ZnCl8 | B | 27.426 | 27.426 | 27.426 |
| G | 15.270 | 15.500 | 15.385 | |
| E(x,y,z) | 44.053 | 44.053 | 44.053 | |
| B/G | 1.796 | 1.769 | 1.783 | |
| Compressibility | 0.036 | |||
| Na6CaCl8 | B | 19.906 | 19.906 | 19.906 |
| G | 12.490 | 12.490 | 12.490 | |
| E(x,y,z) | 31.175 | 31.175 | 31.175 | |
| B/G | 1.594 | 1.594 | 1.594 | |
| Compressibility | 0.050 | |||
| Na6SrCl8 | B | 19.555 | 19.555 | 19.555 |
| G | 12.311 | 12.311 | 12.311 | |
| E(x,y,z) | 30.367 | 30.367 | 30.367 | |
| B/G | 1.588 | 1.588 | 1.588 | |
| Compressibility | 0.051 | |||
| Na6BaCl8 | B | 17.670 | 17.670 | 17.670 |
| G | 11.186 | 11.246 | 11.216 | |
| E(x,y,z) | 25.771 | 25.771 | 25.771 | |
| B/G | 1.580 | 1.571 | 1.575 | |
| Compressibility | 0.057 | |||
To our knowledge, no report is actually available concerning the relation of λi absolute value with mechanical stability. In addition, as the λi depends on the Cij, and in considering eqn (11), we note the ordering relation λ1 < λ4 < λ6 which is an expression of high probability of shear deformation because of strong resistance to a uniaxial deformation. This criterion (i.e., λ1 < λ4 < λ6) can be used in other compounds with similar space group to elucidate shear deformation characteristics.
With the computed Cij elements, the bulk, shear, and Young modulus values are obtained by using the individual and polycrystalline Voigt–Reuss–Hill approximations. The formulations describing the relevant magnitudes can be found elsewhere.50–54 Table 2 includes the bulk (B), shear (S), Young modulus (E), B/G and compressibility of each compound. These parameters provide us with a support for the mechanical stability in relation with an external force inducing volume change and ductility of compounds. As it is shown, these magnitudes follow the same behaviour encountered before upon the variation of the ionic radius. The highest value of Young modulus of 44 GPa and the lowest value of 26 GPa correspond to those of Na6MgCl8 and Na6BaCl8, respectively. The values of Young modulus are comparable to those of available battery materials.
The Pugh's formula (B/G) establishes the limit of a material to be considered as ductile or brittle.54 The Na6ZnCl8 appears to be the most ductile material followed by Na6MgCl8 (B/G > 1.75). The B/G values of other compounds remain at ∼1.6, indicating that they can be classified as partially ductile compounds. In summary, the Na6MCl8 compounds are mechanically stable having appropriate mechanical properties, thus promoting them as applicable battery materials.
3.3. Transport properties of Na6MCl8 (M = Ca2+, Ba2+, Zn2+ and Sr2+)
Transport properties such as diffusion and conduction mechanisms are explored by using the BV method. The Na+ diffusion coefficient and conductivity within the electrode/electrolyte material determines the sodiation/desodiation rate during the charge/discharge cycles.1–5 In this sense, exploration of transport properties of emerging materials is essential for achieving high energy density, high power output, and long cycle life in Na-ion batteries, particularly for emerging applications such as electric vehicles and grid-scale energy storage.Following the approaches described in ref. 40, the first step deals with an exploration of the migration path derived from the bond valence site energy. Migration paths for Na+ ions contemplate regions of low bond valence site energy in mesh grids covering the Na6MCl8 structure models with a resolution of ±0.1 Å3.
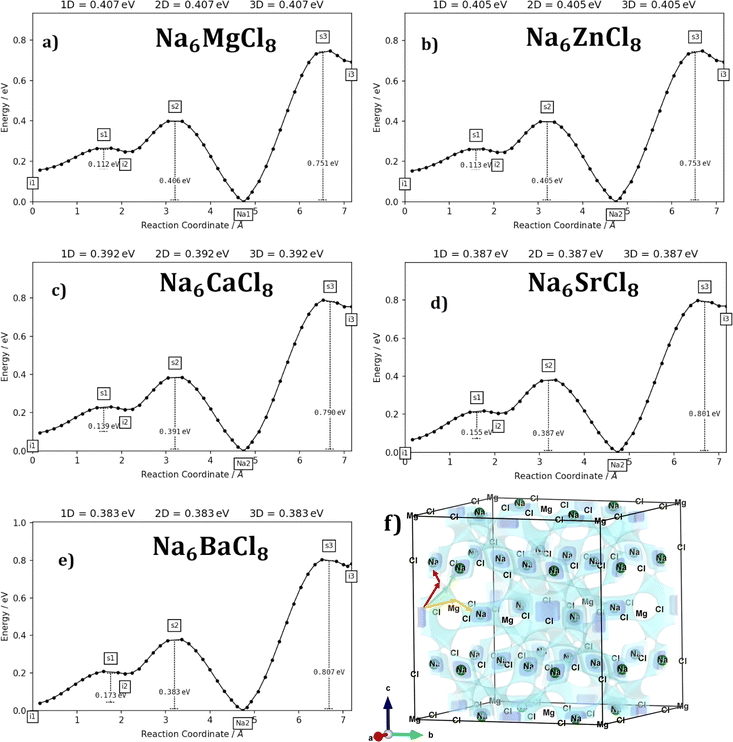
Fig. 3a–e displays the energy variation against the reaction coordinate of each Na6MCl8 (M = Ca2+, Ba2+, Zn2+ and Sr2+) structure. Fig. 3f depicts the energy surface describing the Na+ migration pathways into the Na6MgCl8. The isosurfaces of remaining Na6MCl8 structures are quite analogous to each other. Three 3D migration paths are found within each Na6MCl8 structure. Three saddle points (transition structures) are identified in all structures (denoted as s1, s2 and s3). Interstitial mechanism described by a Na Frenkel defect type 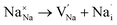 appears as the scheme describing the migration mechanism. In addition, three favourable interstitial sites are also identified, namely i1, i2 and i3, in these structures.
appears as the scheme describing the migration mechanism. In addition, three favourable interstitial sites are also identified, namely i1, i2 and i3, in these structures.
In Na6MCl8 compounds, variations in bond length and the Na–Na distance (diffusion length) occur due to changes in the M2+ ionic radius. As the M2+ ion size increases, more space becomes available between the [NaCl] and [MCl2] octahedra. This increased spacing allows additional Na ions to be accommodated, resulting in a favourable interstitial mechanism. Consequently, the diffusion length is reduced, leading to improved overall Na transport properties.
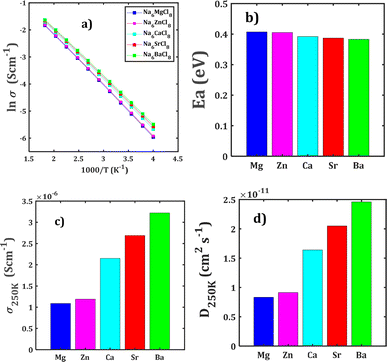
Fig. 4 collects the transport properties namely the conducing behaviour and relevant information concerning the diffusivity and conductivity at 250 K of all structures studied. The Arrhenius dependence of Na conductivity is observed in all samples. The calculated activation energy lies in the range of 0.38–0.41 eV in going from Na6BaCl8 to Na6MgCl8 structures. While the lowest Ea value corresponds to Na6BaCl8, the Na6MgCl8 structure has the highest one. Bearing in mind the ionic size of M cations, we can note the same behaviour of inverted proportionality of Ea against ionic radius.
The conductivity data are derived following the Nernst–Einstein equation in which the diffusion coefficient at each temperature is directly proportional with the conductivity of the mobile ion.15,23–25 In this case, the same Ea value obtained by BVSE method is used to derive the conductivity using the softBV-GUI computer code.40
From Fig. 4c and d, it can be observed that the highest value of Na+ conductivity and diffusivity at 250 K (σ250 K and D250 K, respectively) are found in the Na6BaCl8 structure, with values of 3.22 × 10−6 S cm−1 and 2.46 × 10−11 cm2 s−1 respectively. In contrast, the Na6MgCl8 structure has values of σ250 K = 1.19 × 10−6 S cm−1 and D250 K = 9.12 × 10−12 cm2 s−1. The Ea values of these structures comply with the requirement for battery materials. For instance, in our previous work, an activation energy of 0.45 eV and a conductivity of 7.12 × 10−7 S cm−1 of Na3OCl solid-state electrolyte were determined.27 In addition, a combined deep potential MD, ab initio MD and static simulations study of the Na+ migration in Na3OBr solid state electrolyte, reported a diffusion activation energy of 0.41–0.43 eV and a conductivity at 273 K of 2 × 10−7 S cm−1.15,18 In the particular case of Na6MgCl8 structure, we found that the Ba2+ doped Na6MgCl8 leading the stoichiometric Na6−xBaxMgCl8 promotes the Na vacancy concentration and improves the conductivity at 300 K as compared to the defective Na6−xMgCl8−x.27 Surprisingly, the Na6BaCl8 structure exhibits the most promising transport properties, making this new compound a novel candidate for Na ion battery technology.
In summary, the Na6MCl8 compounds with (M = Ca, Ba, Zn and Sr) structures comply with the requirements to be considered as cathode materials having favourable structural and electronic properties, mechanically stable and ductile and interesting transport properties. Besides, transport property of <10−5 S cm−1 is required to be considered as a solid-state electrolyte. Introduction of foreigner cations or designing polyanionic Na6MCl8−xAx compounds are recommendable approaches to improve their transport properties at 25 °C.
4. Concluding remarks
In this theoretical study, we explore a novel series of rock-salt type structures, Na6MCl8 (where M = Mg2+, Ca2+, Ba2+, Zn2+, and Sr2+), using advanced atomistic simulations. Our investigation focuses on their structural, electronic, and mechanical properties, including defect energetics and transport behaviour, with the goal of understanding their potential application in solid-state sodium-ion battery technology.The key findings include a direct correlation between the ionic size of the divalent M2+ cation and lattice parameters, as well as defect formation energy variations. As the M2+ cation size increases, lattice parameters, interatomic distances, and defect energies tend to decrease. The NaCl Schottky defect type is particularly favourable, and the Na6BaCl8 structure exhibits the lowest defect formation energy. The low defect formation energies determined in this work indicate that these materials can accommodate defects without compromising their stability, which is of crucial importance for any long-term battery operation.
Mechanical stability and ductility characterize these structures, suggesting a possible compatibility for both electrodes and electrolytes for Na-ion batteries. The Na6MCl8 compounds exhibit insulating properties, with an energy gap ranging from 4.1 to 4.6 eV, different from the reported value for Na6MgCl8 (5.1 eV). The energy gap within the Na6MCl8 compounds suggests their potential as solid-state electrolytes, allowing an efficient Na+ transport while preventing an electronic conduction.
The transport properties of Na6MCl8 compounds are disclosed by the bond valence site energy approach for rapid predictions. A 3D migration pathway is identified in each rock-salt structure. The corresponding activation energy lies in the range of 0.38–0.41 eV in going from Na6BaCl8 to Na6MgCl8 structures. Despite the small variation of the Na conductivity and diffusivity at 250 K within the structures considered, the Na6BaCl8 is characterized by the highest conductivity and diffusivity at 250 K of 3.22 × 10−6 S cm−1 and 2.46 × 10−11 cm2 s−1, respectively, while the Na6MgCl8 structure has respective values of 1.19 × 10−6 S cm−1 and 9.12 × 10−12 cm2 s−1. The Na6MCl8 structures, especially Na6BaCl8, show promising ionic conductivity. Their ability to facilitate the Na+ migration can greatly enhance the battery performance.
We hope that these outstanding predicted properties motivate following experimental syntheses and investigations of Na6MCl8 compounds, leading to practical applications in the current and future solid-state Na-ion batteries.
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
YAZ: conception, data acquisition and interpretation, original draft preparation, editing, review. MPPH: data analysis, editing, review. MTN: conception, project supervision, manuscript editing and review. All authors reviewed the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
MPPH acknowledges Ho Chi Minh City University of Technology (HCMUT) and Viet Nam National University VNU-HCM for supporting this study.Notes and references
- Y. Deng, C. Eames, L. H. B. Nguyen, O. Pecher, K. J. Griffith, M. Courty, B. Fleutot, J. N. Chotard, C. P. Grey, M. S. Islam and C. Masquelier, Chem. Mater., 2018, 30, 2618–2630 CrossRef CAS.
- H. Tian, S. Liu, L. Deng, L. Wang and L. Dai, Energy Storage Mater., 2021, 39, 232–238 CrossRef.
- K. Chayambuka, G. Mulder, D. L. Danilov and P. H. L. Notten, Adv. Energy Mater., 2018, 8, 1–49 Search PubMed.
- Y. Wang, S. Song, C. Xu, N. Hu, J. Molenda and L. Lu, Nano Mater. Sci., 2019, 1, 91–100 CrossRef.
- J. A. S. Oh, L. He, B. Chua, K. Zeng and L. Lu, Energy Storage Mater., 2021, 34, 28–44 CrossRef.
- E. A. Wu, S. Banerjee, H. Tang, P. M. Richardson, J. M. Doux, J. Qi, Z. Zhu, A. Grenier, Y. Li, E. Zhao, G. Deysher, E. Sebti, H. Nguyen, R. Stephens, G. Verbist, K. W. Chapman, R. J. Clément, A. Banerjee, Y. S. Meng and S. P. Ong, Nat. Commun., 2021, 12, 1256 CrossRef CAS PubMed.
- J. Xu, Y. Wang, S. Wu, Q. Yang, X. Fu, R. Xiao and H. Li, ACS Appl. Mater. Interfaces, 2023, 15, 21086–21096 CrossRef CAS.
- B. Tao, D. Zhong, H. Li, G. Wang and H. Chang, Chem. Sci., 2023, 14, 8693–8722 RSC.
- S. Bandyopadhyay and B. Nandan, Mater. Today Energy, 2023, 31, 101201 CrossRef CAS.
- Q. Zhao, S. Stalin, C. Z. Zhao and L. A. Archer, Nat. Rev. Mater., 2020, 5, 229–252 CrossRef CAS.
- M. Armand and J. M. Tarascon, Nature, 2008, 451, 652–657 CrossRef CAS PubMed.
- Q. Ma and F. Tietz, ChemElectroChem, 2020, 7, 2693–2713 CrossRef CAS.
- H. Ahmad, K. T. Kubra, A. Butt, U. Nisar, F. J. Iftikhar and G. Ali, J. Power Sources, 2023, 581, 233518 CrossRef CAS.
- N. Aslfattahi, L. Samylingam, M. S. Kiai, K. Kadirgama, V. Kulish, M. Schmirler and Z. Said, J. Energy Storage, 2023, 72, 108781 CrossRef.
- B. A. Goldmann, M. J. Clarke, J. A. Dawson and M. S. Islam, J. Mater. Chem. A, 2022, 10, 2249–2255 RSC.
- J. Zhu, Y. Wang, S. Li, J. W. Howard, J. Neuefeind, Y. Ren, H. Wang, C. Liang, W. Yang, R. Zou, C. Jin and Y. Zhao, Inorg. Chem., 2016, 55, 5993–5998 CrossRef CAS PubMed.
- J. Liang, X. Li, S. Wang, K. R. Adair, W. Li, Y. Zhao, C. Wang, Y. Hu, L. Zhang, S. Zhao, S. Lu, H. Huang, R. Li, Y. Mo and X. Sun, J. Am. Chem. Soc., 2020, 142, 7012–7022 CrossRef CAS PubMed.
- L. Van Duong, M. T. Nguyen and Y. A. Zulueta, RSC Adv., 2022, 12, 20029–20036 RSC.
- K.-H. Park, K. Kaup, A. Assoud, Q. Zhang, X. Wu and L. F. Nazar, ACS Energy Lett., 2020, 5, 533–539 CrossRef CAS.
- E. Sebti, J. Qi, P. M. Richardson, P. Ridley, E. A. Wu, S. Banerjee, R. Giovine, A. Cronk, S.-Y. Ham, Y. S. Meng, S. P. Ong and R. J. Clément, J. Mater. Chem. A, 2022, 10, 21565–21578 RSC.
- W. G. Zeier, R. Schlem, A. Banik, M. Eckardt and M. Zobel, ACS Appl. Energy Mater., 2020, 3, 10164–10173 CrossRef.
- L. Wang, Z. Song, X. Lou, Y. Chen, T. Wang, Z. Wang, H. Chen, W. Yin, M. Avdeev, W. H. Kan, B. Hu and W. Luo, Small, 2024, 2400195 CrossRef PubMed.
- Y. A. Zulueta and M. T. Nguyen, in Annual Reports in Computational Chemistry, Elsevier, 2023, vol. 19, pp. 1–43 Search PubMed.
- Y. A. Zulueta and M. T. Nguyen, Phys. Chem. Chem. Phys., 2023, 25, 27926–27935 RSC.
- A. A. Franco, A. Rucci, D. Brandell, C. Frayret, M. Gaberscek, P. Jankowski and P. Johansson, Chem. Rev., 2019, 119, 4569–4627 CrossRef CAS PubMed.
- H. J. Lee, B. Darminto, S. Narayanan, M. Diaz-Lopez, A. W. Xiao, Y. Chart, J. H. Lee, J. A. Dawson and M. Pasta, J. Mater. Chem. A, 2022, 10, 11574–11586 RSC.
- Y. A. Zulueta, M. P. Pham-Ho and M. T. Nguyen, J. Phys. Chem. Solids, 2024, 188, 111916 CrossRef CAS.
- M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045–1097 CrossRef CAS.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291–341 CrossRef CAS.
- Computational Modelling of Zinc Oxide and Related Oxide Ceramics, University of Surrey, https://openresearch.surrey.ac.uk/esploro/outputs/doctoral/Computational-Modelling-of-Zinc-Oxide-and/99512944702346, accessed 30 December 2023 Search PubMed.
- B. G. Dick and A. W. Overhauser, Phys. Rev., 1958, 112, 90–103 CrossRef.
- N. F. Mott and M. J. Littleton, Trans. Faraday Soc., 1938, 34, 485–499 RSC.
- J. D. Gale, J. Chem. Soc., Faraday Trans., 1997, 93, 629–637 RSC.
- L. L. Wong, K. C. Phuah, R. Dai, H. Chen, W. S. Chew and S. Adams, Chem. Mater., 2021, 33, 625–641 CrossRef CAS.
- S. Adams, Solid State Ionics, 2006, 177, 1625–1630 CrossRef CAS.
- S. Adams and R. P. Rao, Phys. Chem. Chem. Phys., 2009, 11, 3210–3216 RSC.
- I. D. Brown, Chem. Rev., 2009, 109, 6858–6919 CrossRef CAS PubMed.
- H. Chen, L. L. Wong and S. Adams, Acta Crystallogr., 2019, 75, 18–33 CAS.
- F. A. Kröger, The Chemistry of Imperfect Crystals, North-Holland Pub. Co., 1964 Search PubMed.
- M. G. Medvedev, I. S. Bushmarinov, J. Sun, J. P. Perdew and K. A. Lyssenko, Science, 2017, 355, 49–52 CrossRef CAS PubMed.
- Z. Ding, J. Li, J. Li and C. An, J. Electrochem. Soc., 2020, 167, 070541 CrossRef.
- X. Ke, Y. Wang, G. Ren and C. Yuan, Energy Storage Mater., 2020, 26, 313–324 CrossRef.
- M. Hou, F. Liang, K. Chen, Y. Dai and D. Xue, Nanotechnology, 2020, 31, 132003 CrossRef CAS PubMed.
- M. Born, K. Huang and M. Lax, Am. J. Phys., 1955, 23, 474 CrossRef.
- F. Mouhat and F. X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104 CrossRef.
- I. N. Frantsevich, F. F. Voronov and S. A. Bokuta, Elastic Constants and Elastic Moduli of Metals and Insulators Handbook, Naukova Dumka, Kiev, 1983, pp. 60–180 Search PubMed.
- F. I. Fedorov, Theory of Elastic Waves in Crystals, Springer US, Boston, MA, 1968 Search PubMed.
- W. Voigt, Lehrbuch der Kristallphysik, BG Teubner, Leipzig und 791 Berlin, 980 S, Reproduced 1966 Spring Fachmedien Wiesbaden GmbH, 1928 Search PubMed.
- A. Reuss, Z. Angew. Math. Mech., 1929, 9, 49–58 CrossRef CAS.
- R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349–354 CrossRef.
- R. Hill, J. Mech. Phys. Solids, 1963, 11, 357–372 CrossRef.
- S. F. Pugh, London, Edinburgh Dublin Philos. Mag. J. Sci., 1954, 45, 823–843 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra03533j |
| This journal is © The Royal Society of Chemistry 2024 |