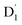DOI:
10.1039/D4RA03566F
(Paper)
RSC Adv., 2024,
14, 23987-23999
Deciphering the doublet luminescence mechanism in neutral organic radicals: spin-exchange coupling, reversed-quartet mechanism, excited-state dynamics†
Received
15th May 2024
, Accepted 17th July 2024
First published on 31st July 2024
Abstract
Neutral organic radical molecules have recently attracted considerable attention as promising luminescent and quantum-information materials. However, the presence of a radical often shortens their excited-state lifetime and results in fluorescence quenching due to enhanced intersystem crossing (EISC). Recently, an experimental report introduced an efficient luminescent radical molecule, tris(2,4,6-trichlorophenyl)methyl-carbazole-anthracene (TTM-1Cz-An). In this study, we systematically performed quantum theoretical calculations combined with the path integral approach to quantitatively calculate the excited-state dynamics processes and spectral characteristics. Our theoretical findings suggest that the sing-doublet D1 state, originating from the anthracene excited singlet state, is quickly converted to the doublet 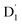 (trip-doublet) state via EISC, facilitated by a significant nonequivalence exchange interaction, with ΔJST = 0.174 cm−1. The formation of the quartet state (Q1, trip-quartet) was predominantly dependent on the exchange coupling 3/2JTR = 0.086 cm−1 between the triplet spin electrons of anthracene and the TTM-1Cz radical. Direct spin–orbit coupling ISC to the Q1 state was minimal due to the nearly identical spatial wavefunctions of the
(trip-doublet) state via EISC, facilitated by a significant nonequivalence exchange interaction, with ΔJST = 0.174 cm−1. The formation of the quartet state (Q1, trip-quartet) was predominantly dependent on the exchange coupling 3/2JTR = 0.086 cm−1 between the triplet spin electrons of anthracene and the TTM-1Cz radical. Direct spin–orbit coupling ISC to the Q1 state was minimal due to the nearly identical spatial wavefunctions of the 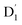 and Q1 levels. The effective occurrence of reverse intersystem crossing (RISC) from the Q1 to D1 state is a critical step in controlling the luminescence of TTM-1Cz-An. The calculated RISC rate kRISC, including the Herzberg–Teller effect, was 3.64 × 105 s−1 at 298 K, significantly exceeding the phosphorescence and nonradiative rates of the Q1 state, thus enabling the D1 repopulation. Subsequently, a strong electronic coupling of 37.4 meV was observed between the D1 and D2 states, along with a dense manifold of doublet states near the D1 state energy, resulting in a larger reverse internal conversion rate kRIC of 9.26 × 1010 s−1. Distributed to the D2 state, the obtained emission rate of kf = 2.98–3.18 × 107 s−1 was in quite good agreement with the experimental value of 1.28 × 107 s−1, and its temperature effect was not remarkable. Our study not only provides strong support for the experimental findings but also offers valuable insights for the molecular design of high-efficiency radical emitters.
and Q1 levels. The effective occurrence of reverse intersystem crossing (RISC) from the Q1 to D1 state is a critical step in controlling the luminescence of TTM-1Cz-An. The calculated RISC rate kRISC, including the Herzberg–Teller effect, was 3.64 × 105 s−1 at 298 K, significantly exceeding the phosphorescence and nonradiative rates of the Q1 state, thus enabling the D1 repopulation. Subsequently, a strong electronic coupling of 37.4 meV was observed between the D1 and D2 states, along with a dense manifold of doublet states near the D1 state energy, resulting in a larger reverse internal conversion rate kRIC of 9.26 × 1010 s−1. Distributed to the D2 state, the obtained emission rate of kf = 2.98–3.18 × 107 s−1 was in quite good agreement with the experimental value of 1.28 × 107 s−1, and its temperature effect was not remarkable. Our study not only provides strong support for the experimental findings but also offers valuable insights for the molecular design of high-efficiency radical emitters.
1. Introduction
Thermally activated delayed fluorescence (TADF) is widely recognized as a third-generation display and lighting technology and has attracted much attention both as an area of theoretical interest and for its potential applications in recent years.1–4 For TADF materials, the closed-shell molecules are usually chosen as emitters, in which the electrons are paired and filled to the highest occupied molecular orbital (HOMO) in the ground state according to the Aufbau principle.5 An electron in the ground state is excited from the HOMO and injected into the LUMO (lowest unoccupied molecular orbital), which leads to the formation of both emissive 25% singlet (S1) and nonemissive 75% triplet (T1) excitons.4 To overcome this statistical limitation, with the help of T1 to S1 upconversion called reverse intersystem crossing (RISC), TADF can achieve an internal quantum efficiency of nearly 100% in singlet emission.6,7 However, RISC requires a small energy gap (ΔEST) between the T1 and S1 excited states. This gap is approximately proportional to the electronic exchange interaction (J) between electrons in the HOMO and LUMO, expressed as ΔEST ≈ 2J. Furthermore, the J value is related to the spatial overlap between the HOMO and LUMO.8 Currently, most TADF emitters often adopt the covalently linked electron donor (D)–acceptor (A) structures for the spatial separation of the HOMO and LUMO to reduce the J interaction. However, this approach presents some unavoidable challenges due to the small spatial overlap between the HOMO and LUMO, including a slow fluorescence rate and low fluorescence oscillator strength.6,7 In addition, D–A type structures are usually flexible and result in significant structural relaxation and a low color purity in their excited states.
Therefore, organic radical emitters are attracting increasing interest as a new type of luminescent materials possessing multiple-spin states and potentially showing spin-luminescence-correlated properties.5,9–12 Generally speaking, there is now a type of luminescent radical that provides complete spin-allowed emission within a double manifold, such as the tris(2,4,6-trichlorophenyl) methyl-carbazole (TTM-Cz) and 9-(naphthalene-2-yl)-9H-carbazole (TTM-3NCz) emitters.13–16 These radical emitters provide a simple way to prevent 75% energy loss from the first-generation organic light-emitting diodes (OLEDs) based on traditional organic emitters. Unfortunately, currently most stable radicals are non-emissive, because their high-spin structures have high (approximately 1 eV) energy gaps between the photogenerated donor singlet state and the triplet manifold. Essentially, this prevents the RISC process from a dark state to a luminescent state.17,18
Additionally, in quantum-information science and technology, recent studies have also shown that strongly coupled photogenerated triplet-radical systems can be used as multi-level spin qubits, i.e., qubits, such as the perylene-diimide-2,2,6,6-tetramethylpi-perdiny-1-oxyl (PDI-TEMPO) stable radical.17–20 It is well known that electron spins are good qubits because the two spin states can exist in a superposition, and coupling two or more spins via spin–exchange coupling and/or zero-field interactions leads to versatile spin physics.21 However, as with all such systems, the primary challenge is that the high-spin structure also has a large energy difference between the quartet (‘trip-quartet’, S = 3/2) and doublet (‘trip-doublet’, S = 1/2) states, resulting in the RISC to a luminescent state becoming impossible, which prevents optical readout via emission.17,18
In order to overcome the limitations of the optical readout or luminescence above, Evans and co-workers put forward a novel design strategy,17 which involved introducing an energy resonance between the emissive doublet and donor triplet levels. To put it another way, the vital idea of this design strategy was to bring the donor triplet T1 level into energy resonance with a luminescent radical doublet D1 level based on a class of luminescent radicals that provide absolutely spin-allowed emission within the doublet manifold. Employing this strategy, they designed and synthesized an excited-state complex with a near-unity generation yield, specifically tris(2,4,6-trichlorophenyl)methyl-carbazole-anthracene (TTM-1Cz-An), as depicted in Fig. 1. Here, reducing the large energy gap between the emission state and the high-spin state enabled interconversion via RISC to emissive states, thereby making it possible to achieve luminescence from high-spin states with S > 1 in organic radical molecules.
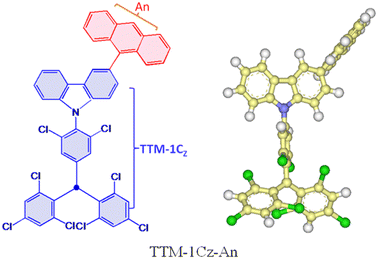 |
| | Fig. 1 Molecules featured in the covalent coupling of the tris(2,4,6-trichlorophenyl)methyl-carbazole radical (TTM-1Cz) and anthracene (An) studied in this work. | |
Compared to the experimental study of Evans and co-workers,17 up to now, there seems to have been relatively scarce theoretical exploration to provide a comprehensive and in-depth understanding of this original design strategy, especially, the influence of high-spin state RISC on the overall luminescence mechanism. To design a new generation of efficient radical emitters for OLEDs, we require a detailed understanding of the factors that govern the fluorescence characteristics of organic radicals at the molecular level. Consequently, in this investigation we systematically and quantitatively studied the excited-state dynamics of the TTM-1Cz-An system by applying time-dependent density functional theory combined with the path integral approach, to provide a quantitative understanding of the radical luminescence mechanism. Our motivation was to provide theoretical support for designing novel radical luminescent materials.
2. Computational details
2.1 Geometric structures and electronic properties
All calculations were performed using the ORCA 5.0.4 program.22 Geometry optimizations were performed with the range-separated hybrid ωB97X-D3 and CAM-B3LYP functionals and the Ahlrichs polarized def2-SVP basis sets, combined with the corresponding def2/J auxiliary basis sets for the RIJ approximation to the Coulomb integrals, while the exchange terms were efficiently accelerated using the “chain-of-spheres” (COSX) algorithm.23–28 The integration grids employed the default set (DEFGRID2) in the ORCA nomenclature, with tight energy convergence settings applied throughout the calculations.22 The surroundings were described with the conductor-like polarizable continuum model (C-PCM) with toluene solvent.29 Numerical frequency analysis was performed for all the optimized structures, and there were no imaginary vibration modes to ensure that the obtained structure was a local minimum on the potential energy surface (PES). In addition, the corresponding Hessian data were subsequently used for the excited-state dynamics calculations. In order to further improve the calculation of the doublet–doublet excitation energies, single point energies were recalculated using the range separation, and spin-component/opposite scaling (SCS/SOS), time-dependent double-hybrid density functionals, including SCS-ωB2GP-PLYP and SCS/SOS-ωB2PLYP, in conjunction with the larger def2-TZVP basis set, where applicable, and the corresponding auxiliary def2-TZVP/C and def2/J basis sets.30–32 Under the same conditions, the domain-based local pair natural orbital approach, and coupled cluster calculations (e.g., DLPNO-CCSD(T)) were also be applied to the single point energy calculations.33,34
2.2 Exchange coupling and zero-field splitting
The excited-state exchange–coupling interaction (JTR, where the subscript T denotes the anthracene triplet state, and R is the TTM-1Cz radical) was calculated using QD-NEVPT2/def2-TZVP on optimized CASSCF wavefunctions, where the selection of the active space is important to first understand the nature of the low-lying excited states by carefully assessing their orbital contributions. The starting orbitals of the CASSCF calculation,35 were obtained using TD-DFT at the ωB97X-D3/def2-TZVP level of theory with the RIJCOSX approximation for the Coulomb- and exchange integrals.23,25–28 TD-DFT provides rapid and comprehensive insights into the orbitals that play a crucial role in the excited-state mechanism, subsequently allowing defining the active space in the CASSCF calculation. The excited states of interest primarily originate from electronic transitions occurring within both the HOMO and LUMO orbitals of the anthracene, as well as the SOMO (single occupied molecular orbital) of the TTM-1Cz radical. Consistent with expectations, the active space in the CASSCF calculation, denoted as (3, 3), encompassed three electrons distributed in three orbitals, specifically, anthracene's HOMO and LUMO, along with the radical's SOMO. The minimal active space is instrumental in providing a qualitatively accurate portrayal of these states, ensuring that the fundamental characteristics of the excited states are captured effectively. The optimized active orbitals were localized by the Foster–Boys method for an easier interpretation of the excited states.36
The excited-state exchange coupling JTR between the anthracene triplet state and the TTM-1Cz radical doublet state can be calculated using the following formula:37
or approximated as:
| |
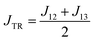 | (2) |
where the subscripts 1, 2, and 3 for
J refer to the electrons in the radical SOMO of the TTM-1Cz, and the HOMO and LUMO of the anthracene, respectively. Also, the individual exchange interactions (
J12,
J13, and
J23) were extracted by a numerical effective Heisenberg–Dirac–van Vleck Hamiltonian,
38 see
eqn (3), and the corresponding extraction details were shown recently in ref.
37.
| | |
ĤHDVV = −J12Ŝ1Ŝ2 − J13Ŝ1Ŝ3 − J23Ŝ2Ŝ3
| (3) |
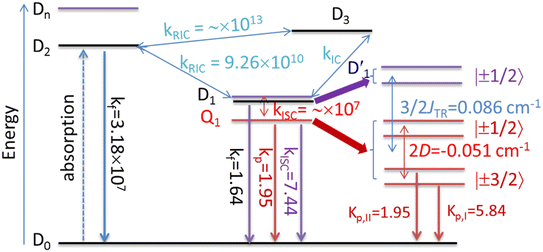
To characterize the mixed information of the excited quartet (Q1) and doublet (Dn) states by electron dipolar induction, the zero-field splitting (ZFS) interaction, which can be characterized by the aid of the two ZFS parameters D and E,39,40 was calculated using the ORCA 5.0.4 program at the ωB97X-D3 and CAM-B3LYP/def2-TZVP levels. The spin–orbit coupling (SOC) was calculated using the quasi-degenerate perturbation theory at the CASSCF (7,5)/def2-TZVP level. The selection of the active orbitals was guided by the same principles previously discussed for the CASSCF(3,3) method. Specifically, the TD-ωB97X-D3 calculation identified several orbitals that are pivotal to the mechanism of the excited state. These orbitals were then incorporated into the active space, which consisted of 7 electrons in 5 orbitals: the HOMO and LUMO of anthracene, along with the SOMO of the radical, and the two orbitals immediately below the HOMO, known as HOMO-1 and HOMO-2. The corresponding active orbitals are presented in Table S1 of the ESI.†41 In this approach, the SOC operator was handled with the efficient mean-field (SOMF) approximation to the Breit–Pauli operator (SOCType 3 in ORCA 5.0.4),41,42 called RI-SOMF, which makes use of the RI scheme to accelerate Coulomb integrals. Additionally, the gradient of the SOC matrix elements (∂〈SOC〉〉/∂Qk, where Qk is a mass-weighted normal coordinate) with respect to the normal modes was estimated using a finite-difference method.43 Here, the optimized structure at Qk = 0 was used to construct the molecular configuration, which was displaced along the vital normal mode by increments of 0.1 dimensionless normal coordinates.
2.3 Nonradiative decay rate
The nonradiative decay rate constants (kIC) were estimated by means of the Marcus–Levich–Jortner approach, with its one-effective mode equation expressed as:10,44| |
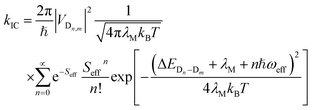 | (4) |
where ℏ, kB, and T, are the reduced Planck constant, the Boltzmann constant, and temperature, respectively; VDn,mis the electronic coupling interaction between the excited states (Dn and Dm), which was computed by the two-state generalized Mulliken–Hush approximation;45 ωeff and Seff are the effective vibrational frequency and corresponding Huang–Rhys factor, and they describe the quantum effect of the high-frequency normal modes by a single effective mode; and n is the vibrational quantum number of this effective mode.46,47 ωeff and Seff were calculated using the following equations:| |
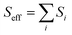 | (5) |
| |
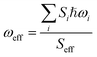 | (6) |
where λM is the classical reorganization energy that comes from the low-frequency vibrations (ℏωM < 1000 cm−1), and ΔEDn−Dm denotes the adiabatic energy between the doublet excited Dn and Dm states.
For the ISC and RISC rates, kISC and kRISC were computed using the ORCA_ESD module with default settings within the ORCA 5.0.4 package.22,48,49 The harmonic approximation to the PESs was based on the adiabatic Hessian model. It was assumed that the geometries and Hessians of the quartet Q1 and doublet D1 spin sublevels were the same.
2.4 Radiative rate and fluorescence spectrum
Within the framework of the Born–Oppenheimer approximation, the spin-allowed radiative rates (kf) between an initial state i and a final state f were determined using Fermi's golden rule, which encompasses integrates across the entire radiative spectrum. The corresponding equation, expressed in atomic units, is as follows:48,49| |
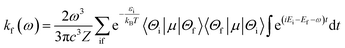 | (7) |
where ω represents the photon energy; μ is the electronic transition dipole; |Θ〉 denotes the vibrational wavefunction of either the initial or final state; 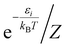 describes the initial state Boltzmann population at temperature T; εi is the total vibrational energy of initial state; and Z represents the vibrational partition function. After further manipulations, eqn (7) was ultimately transformed into a Discrete Fourier Transform (DFT) of a correlation function χ(t) with a time step Δt.49 The transformed formula is given by:
describes the initial state Boltzmann population at temperature T; εi is the total vibrational energy of initial state; and Z represents the vibrational partition function. After further manipulations, eqn (7) was ultimately transformed into a Discrete Fourier Transform (DFT) of a correlation function χ(t) with a time step Δt.49 The transformed formula is given by:| |
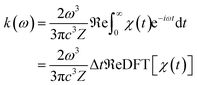 | (8) |
The χ(t) function was subsequently computed analytically at each time point t using “path integral methods”.
In our calculations, vibronic coupling, the so-called Herzberg–Teller (HT) effects, was considered by expanding the matrix elements of the μ(Qk) with respect to the normal coordinate Qk,50 as shown below:
| |
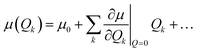 | (9) |
In this expression, the
μ0 term corresponds to the traditional Frank–Condon (FC) approximation, which keeps only the coordinate-independent term, whereas the second term represents the HT contribution.
3. Results and discussion
3.1 Resolved absorption spectra
To comprehensively understand the nature of the excited states of the TTM-1Cz-An compound, the vibrationally resolved absorption spectra for the transition from the doublet ground D0 to the different excited states with D1, D2, D3, and D4 were simulated in the gas and liquid phases, as shown in Fig. 2, which is helpful to elucidate the underlying nature of the experimental phenomenon. Specifically, in the case of the toluene solution, for the absorption profiles for the D0 → D1 transition (Fig. 2a), two prominent features were observed: a mountainous extension from 500 to 725 nm, and the main peak centered at 639 nm, both of which were in quite good agreement with experimental data of about 685 nm.17 At the level of the ωB97X-D3 theory, almost identical spectral data were obtained, as shown in Fig. 2c. Interestingly, the sharp peak at 354 nm (or 340 nm), corresponding to the high energy vibrational range, was primarily due to the excitation of two nearly degenerate electronic states, D2 and D3, which was in qualitative agreement with experimental value of 374 nm.17 We also noticed that these vibrational spectral bands significantly overlapped, which allows for the possibility for these states to undergo fast internal conversion (IC) through interactions such as SOC, configuration interaction, or possibly vibronic coupling. Moving to the gas phase, as could be noted by comparing Fig. 2b and d, the spectral band was relatively discrete, and the D0 → D1 transition significantly deviated from the experimental data of 685 nm.17 Also, the D2 and D3 excitations showed an overall redshift of the energies relative to the experimental data.
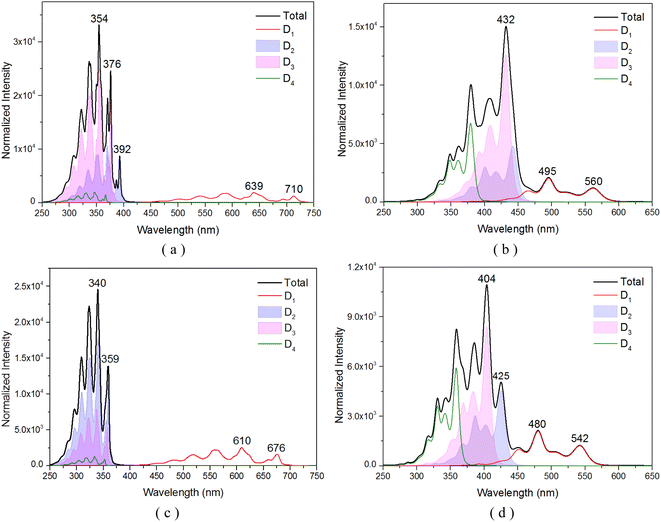 |
| | Fig. 2 Vibrationally resolved absorption spectra of several key doublet excited states for TTM-1Cz-An: (a) obtained at the CAM-B3LYP/def2-TZVP level in the toluene solvent, and (b) in the gas phase; (c) and (d) were obtained using the ωB97X-D3 method under liquid and gas environments, respectively. | |
3.2 Characterization of the excited states
Fig. 3 indicates electronic spin configurations of TTM-1Cz-An with the occupancies of the high-lying occupied and low-lying unoccupied orbitals, which were composed of three orbitals (HOMO−4, HOMO−1, and SOMO) in the located TTM-1Cz radical, of which two π-type orbitals (HOMO and LUMO) of the An unit, the corresponding natural transition orbitals, are displayed in Tables S1–S3 of the ESI.† The doublet ground state D0 has an unpaired electron primarily located on the SOMO, following the conventional Aufbau principle.5,10 In other words, the energy of the SOMO is generally located above the doubly occupied HOMO and below the LUMO. A critical electronic excitation can be described as a HOMO → LUMO transition (Fig. 3), resulting in the D1 excited state (i.e., sing-doublet state), which corresponds to the first excited singlet state S1 of anthracene upon light absorption. It exhibited a very small transition dipole moment of 0.0003 a.u. due to the parity-forbidden nature based on group theory considerations. In the presence of the radical, the triplet sublevel state T1, 0 (where 0 is the spin magnetic quantum number) of anthracene may then be generated by radical-enhanced intersystem crossing (EISC),37,51 and then the anthracene triplet state and radical doublet state will interact, with the details discussed below. As for the D2 and D3 excitations, they can be characterized as either a HOMO-1 → SOMO or HOMO-4 → SOMO transition, respectively. These excitations were localized in the TTM-1Cz radical fragment and exhibited strong transition dipole moments of 0.915 and 0.547 a.u. at the ωB97X-D3 level, respectively. To further characterize the rationality of the excitation configuration, the excited-state spin density and transition density difference are separately displayed in the upper part of the configuration, see Fig. 3 and Table S4 in the ESI,† which more reliably support the nature of the electron excitation.
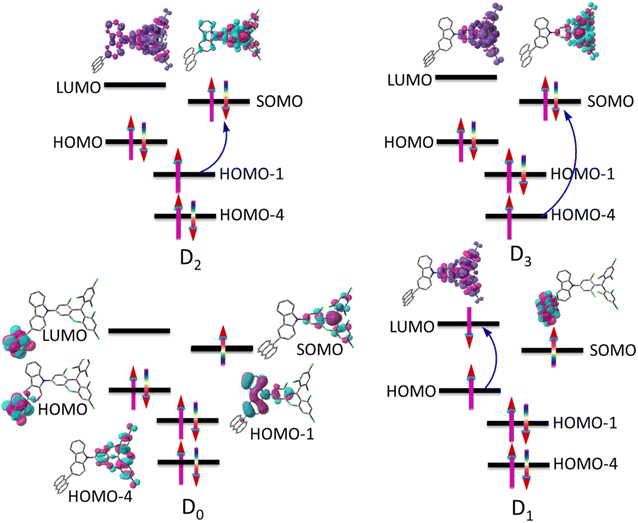 |
| | Fig. 3 Electronic spin configurations of the TTM-1Cz-An compound consisting of the doublet TTM-1Cz radical and the singlet An (anthracene). For the ground state D0, the vital natural active orbitals are inserted into the figure; the formation of excited states (D1, D2, and D3) in the electronic transitions is marked with blue arrows, and the spin density and transition density difference are separately displayed in the upper part of the configuration. | |
3.3 EISC and quartet state (Q1) formation
It is known that the EISC is a spin-allowed process due to the overall spin multiplicity conservation within the photoexcited TTM-1Cz-An radical system. The singlet excited state of anthracene, which involved a transition from the HOMO to LUMO (HOMO → LUMO), known as a sing-doublet state D1, was converted to a trip-doublet state  This conversion occurs by nonequivalent spin–exchange coupling of the singlet excited electrons of anthracene and the third radical electron mediated. This mechanism is referred to as the ΔJST mechanism,52 where ΔJST is defined as (J13 − J12)/2, and was calculated to be 0.174 cm−1 at the CASSCF/QD-NEVPT2 level, as detailed in Table 1. This process is schematically depicted in Fig. 4, with the corresponding visualization of the localized spin centers illustrated in Fig. 5.
This conversion occurs by nonequivalent spin–exchange coupling of the singlet excited electrons of anthracene and the third radical electron mediated. This mechanism is referred to as the ΔJST mechanism,52 where ΔJST is defined as (J13 − J12)/2, and was calculated to be 0.174 cm−1 at the CASSCF/QD-NEVPT2 level, as detailed in Table 1. This process is schematically depicted in Fig. 4, with the corresponding visualization of the localized spin centers illustrated in Fig. 5.
Table 1 Calculated exchange coupling constants (J cm−1) of the investigated TTM-1Cz-An molecular system at the CASSCF (3, 3)/def2-TZVP level. The subscripts 1, 2, and 3 refer to the electrons in the radical SOMO of the TTM-1Cz, and the HOMO and LUMO of anthracene, respectivelya
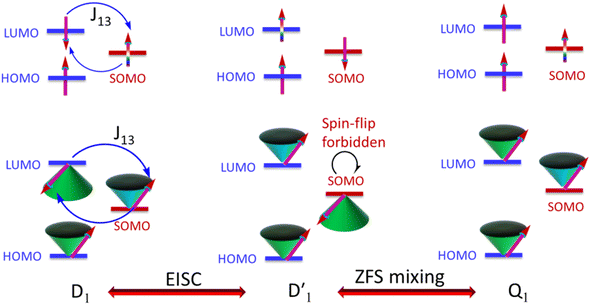 |
| | Fig. 4 Simplified vector picture of the EISC process generating a local triplet state on anthracene by dipolar-mediated interactions. | |
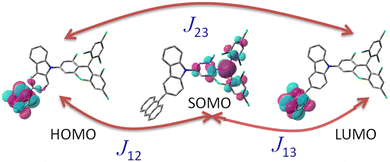 |
| | Fig. 5 Exchange interactions (J cm−1) illustration of the three-electron-three-center problem, including assignment of the orbitals for the investigated TTM-1Cz-An system. The subscripts 1, 2, and 3 refer to the electrons in the radical SOMO of TTM-1Cz, and the HOMO and LUMO of anthracene, respectively. | |
As can be seen from Fig. 4, the electrons in the LUMO of anthracene and the SOMO of the radical simultaneously flip their orientation through exchange coupling. This change conserves the overall doublet spin multiplicity while generating a local triplet state on the anthracene fragment, resulting in the 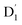 state. The formation of the quartet state (Q1, trip-quartet) predominantly relies on the exchange–coupling interaction JTR between the triplet spin electrons of anthracene and the TTM-1Cz radical.37,50 If the JTR interaction surpasses all other magnetic interactions within the TTM-1Cz-An radical system, the Q1 state can be formed through spin mixing. The data in Table 1 indicate that the exchange interaction, with a value of JTR = 0.057 cm−1 at the CASSCF/QD-NEVPT2 level (see out file of the JTR calculation in the ESI†), was sufficiently large to enable the formation of the Q1 state via spin exchange. It could also be noted that the JTR was positive, suggesting that the TTM-1Cz-An radical exhibits ferromagnetically coupling,50,51 which implies that the Q1 state was energetically favored over the
state. The formation of the quartet state (Q1, trip-quartet) predominantly relies on the exchange–coupling interaction JTR between the triplet spin electrons of anthracene and the TTM-1Cz radical.37,50 If the JTR interaction surpasses all other magnetic interactions within the TTM-1Cz-An radical system, the Q1 state can be formed through spin mixing. The data in Table 1 indicate that the exchange interaction, with a value of JTR = 0.057 cm−1 at the CASSCF/QD-NEVPT2 level (see out file of the JTR calculation in the ESI†), was sufficiently large to enable the formation of the Q1 state via spin exchange. It could also be noted that the JTR was positive, suggesting that the TTM-1Cz-An radical exhibits ferromagnetically coupling,50,51 which implies that the Q1 state was energetically favored over the 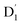 state. Regarding the individual contributions to JTR, it could be seen that both absolute magnitudes (J12 and J13) were bigger for the TTM-1Cz-An radical, and this can be explained by visualizing the spin center in a relatively direct manner, see Fig. 5. The interpretation of the reverse sign of the J12 and J13 interactions is more sophisticated, and the sign was likely decided by the symmetry of the individual spin centers.
state. Regarding the individual contributions to JTR, it could be seen that both absolute magnitudes (J12 and J13) were bigger for the TTM-1Cz-An radical, and this can be explained by visualizing the spin center in a relatively direct manner, see Fig. 5. The interpretation of the reverse sign of the J12 and J13 interactions is more sophisticated, and the sign was likely decided by the symmetry of the individual spin centers.
3.4 ISC and RISC processes
3.4.1 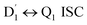 . Even though
. Even though 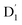 and Q1 were well separated by an energy gap of 3/2JTR = 0.086 cm−1, as shown in Fig. 6, the ZFS interaction, denoted as HZFS, of the two unpaired electrons localized on anthracene leads to a mixing of the
and Q1 were well separated by an energy gap of 3/2JTR = 0.086 cm−1, as shown in Fig. 6, the ZFS interaction, denoted as HZFS, of the two unpaired electrons localized on anthracene leads to a mixing of the 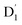 and Q1 states:39,40
and Q1 states:39,40| | |
HZFS = D(Sz2 − S2/3) + E(Sx2 − Sy2)
| (10) |
where D and E are the ZFS tensors. The rate of ISC from the spin sublevels of 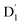 to those of Q1 is dependent on the prohibition factor, which is associated with the change in spin, denoted as fS (m2, m4), with m2 = ±1/2, and m4 = ±1/2, ±3/2, respectively:53
to those of Q1 is dependent on the prohibition factor, which is associated with the change in spin, denoted as fS (m2, m4), with m2 = ±1/2, and m4 = ±1/2, ±3/2, respectively:53| |
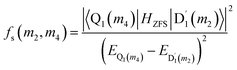 | (11) |
where the fS(m2, m4) term characterizes the spin-dependent transition strength due to the HZFS perturbation that mixes 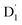 and Q1. This HZFS perturbation is often quantified by the ZFS tensors of D and E. The calculated D and E values at the ωB97X-D3/CAM-B3LYP levels are detailed in Table S5 of the ESI,† and the D tensor orientation and spin density of the quartet Q1 state are depicted in Fig. 7.
and Q1. This HZFS perturbation is often quantified by the ZFS tensors of D and E. The calculated D and E values at the ωB97X-D3/CAM-B3LYP levels are detailed in Table S5 of the ESI,† and the D tensor orientation and spin density of the quartet Q1 state are depicted in Fig. 7.
 |
| | Fig. 6 (a) Visualization of the dynamic electron polarization generation via the 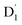 and Q1 quantum mixing states, which was constructed by a strong exchange coupling (J > D) between the doublet and triplet moieties; (b) projections of the eigenfunctions on the model space at the vibration coupling modes, here, C2|S, Ms〉, where C2 denotes the configuration weight coefficients, S is the spin quantum number, and MS denotes the spin sublevels. and Q1 quantum mixing states, which was constructed by a strong exchange coupling (J > D) between the doublet and triplet moieties; (b) projections of the eigenfunctions on the model space at the vibration coupling modes, here, C2|S, Ms〉, where C2 denotes the configuration weight coefficients, S is the spin quantum number, and MS denotes the spin sublevels. | |
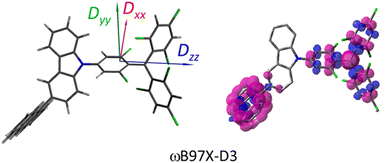 |
| | Fig. 7 Drawing of the ZFS tensor (D) orientations and spin density (right) of TTM-1Cz-An for the quartet Q1 state. | |
The ZFS tensors for TTM-1Cz-An were calculated to be D = −0.026 cm−1 and E = −0.005 cm−1 (Table S5†). The E value was extremely small, implying a negligible spin density distribution difference between the Dxx and Dyy directions, as can be seen in Fig. 7. Meanwhile, the substantial D value stemmed from the SOC contribution of −0.0296 cm−1 at the ωB97X-D3 level, which accounted for approximately 88% of the total D value, as shown in Table S5.† Upon decomposing the SOC contribution into different excitations, it was found that the maximum SOC contribution to the D tensor mainly came from the excitations of the spin-pairing transitions (approximately 0.455 cm−1 at the ωB97X-D3 level, Table S5†), accompanied by an α → β spin-flipping process, namely, quartet → doublet. This indicates a significant mixing of the excited 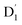 state into the Q1 state. Additionally, the D value was also expected to be negative (i.e., D < 0), implying a more “rod-like” spin density distribution that is “prolate” in shape, with the Dzz component of the ZFS tensor aligned parallel to the spin distribution within the carbazole plane,54 see Fig. 7.
state into the Q1 state. Additionally, the D value was also expected to be negative (i.e., D < 0), implying a more “rod-like” spin density distribution that is “prolate” in shape, with the Dzz component of the ZFS tensor aligned parallel to the spin distribution within the carbazole plane,54 see Fig. 7.
As a result, the ISC rate for TTM-1Cz-An was extremely fast due to the larger fs(m2, m4) value and the fact that the energy gaps between the 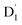 and Q1 states were sufficiently smaller than the vibrational quanta for any of the six allowed (Δm2,4 = ±1, ±2) transitions (Fig. 6a). Consequently, the vibrational relaxation within the
and Q1 states were sufficiently smaller than the vibrational quanta for any of the six allowed (Δm2,4 = ±1, ±2) transitions (Fig. 6a). Consequently, the vibrational relaxation within the 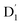 state was also very rapid, with the transition occurring between the zeroth vibrational levels of the
state was also very rapid, with the transition occurring between the zeroth vibrational levels of the 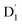 and Q1 states. In this case, the thermal energy of approximately 200 cm−1 at 298 K was most likely to significantly exceed |3/2JTR|, making the RISC from Q1 to
and Q1 states. In this case, the thermal energy of approximately 200 cm−1 at 298 K was most likely to significantly exceed |3/2JTR|, making the RISC from Q1 to 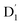 fully possible. This contrasts with scenarios involving a large energy gap, which are termed as the ‘reversed-quartet mechanism’. Furthermore, the vibrational mixing between Q1 and
fully possible. This contrasts with scenarios involving a large energy gap, which are termed as the ‘reversed-quartet mechanism’. Furthermore, the vibrational mixing between Q1 and 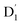 was investigated, with the projections of the eigenfunctions onto the model space at key vibrational coupling modes, as reported in Fig. 6b and Table S6.† It became evident that the Q1 and states were no longer “pure” excited quartet and doublet states (represented by |Φn〉),53 but rather, the Q1 substate was mixed with
was investigated, with the projections of the eigenfunctions onto the model space at key vibrational coupling modes, as reported in Fig. 6b and Table S6.† It became evident that the Q1 and states were no longer “pure” excited quartet and doublet states (represented by |Φn〉),53 but rather, the Q1 substate was mixed with 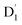 by 11%, and similarly, the
by 11%, and similarly, the 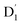 states were mixed with Q1 by 12%.
states were mixed with Q1 by 12%.
3.4.2 D1 ↔ Q1 RISC. The swift interconversion between the 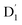 and D1 states was elucidated through EISC, ascribed to the inequality of the exchange interactions J13 and J12, denoted as ΔJST = 0.174 cm−1,52 as detailed in Table 1. Nevertheless, the efficacious occurrence of RISC from Q1 to D1 states is pivotal in the luminescence control of the TTM-1Cz-An radical complex, with possible deactivation pathways of the excited states, as shown in Fig. 8. It is a well-established notion that the RISC rates kRISC are predominantly dictated by three foundational factors: a strong SOC effect between the Q1 and D1 states, a diminutive energy gap ΔE(Q1 − D1), and a significant overlap of the vibrational wavefunctions between Q1 and D1. As anticipated, the computed adiabatic energy difference ΔE(Q1 − D1) for TTM-1Cz-An was notably small, approximately 745 cm−1 at the ωB97X-D3 level, which will be undoubtedly beneficial to augmenting the kRISC. The SOC constants, which are highly dependent on the electronic configuration of the Q1 and D1 states, are summarized in Tables 2 and S7.† According to EI-Sayed's rule,55 the direct SOC interaction between Q1 and D1 is forbidden due to the violation of the total angular momentum conservation principle, resulting in an exceedingly minute SOC constant of 〈Q1|ĤSOC|D1〉 = 0.002 cm−1 (see Table 2). Conversely, for those states with distinct transition characters, the SOC constants are comparatively larger, exemplified by 〈Q1|ĤSOC|D0 〉 = 0.025 cm−1, and 〈Q1|ĤSOC|D3 〉 = 0.093 cm−1. The inhibition SOC effect between Q1 and D1 would result in a relatively slow RISC rate of 2.41 × 101 s−1 at 298 K, as reported in Table 3. For meaningful RISC to occur, it is imperative that the kRISC rate of 2.41 × 101 s−1 at room temperature has to be larger than the radiative (kp = 1.95 s−1) and nonradiative (kRISC = 7.44 s−1, as listed in Fig. 8) rates of the Q1 state to the ground D0 state, which is patently insufficient.
and D1 states was elucidated through EISC, ascribed to the inequality of the exchange interactions J13 and J12, denoted as ΔJST = 0.174 cm−1,52 as detailed in Table 1. Nevertheless, the efficacious occurrence of RISC from Q1 to D1 states is pivotal in the luminescence control of the TTM-1Cz-An radical complex, with possible deactivation pathways of the excited states, as shown in Fig. 8. It is a well-established notion that the RISC rates kRISC are predominantly dictated by three foundational factors: a strong SOC effect between the Q1 and D1 states, a diminutive energy gap ΔE(Q1 − D1), and a significant overlap of the vibrational wavefunctions between Q1 and D1. As anticipated, the computed adiabatic energy difference ΔE(Q1 − D1) for TTM-1Cz-An was notably small, approximately 745 cm−1 at the ωB97X-D3 level, which will be undoubtedly beneficial to augmenting the kRISC. The SOC constants, which are highly dependent on the electronic configuration of the Q1 and D1 states, are summarized in Tables 2 and S7.† According to EI-Sayed's rule,55 the direct SOC interaction between Q1 and D1 is forbidden due to the violation of the total angular momentum conservation principle, resulting in an exceedingly minute SOC constant of 〈Q1|ĤSOC|D1〉 = 0.002 cm−1 (see Table 2). Conversely, for those states with distinct transition characters, the SOC constants are comparatively larger, exemplified by 〈Q1|ĤSOC|D0 〉 = 0.025 cm−1, and 〈Q1|ĤSOC|D3 〉 = 0.093 cm−1. The inhibition SOC effect between Q1 and D1 would result in a relatively slow RISC rate of 2.41 × 101 s−1 at 298 K, as reported in Table 3. For meaningful RISC to occur, it is imperative that the kRISC rate of 2.41 × 101 s−1 at room temperature has to be larger than the radiative (kp = 1.95 s−1) and nonradiative (kRISC = 7.44 s−1, as listed in Fig. 8) rates of the Q1 state to the ground D0 state, which is patently insufficient.
 |
| | Fig. 8 Possible deactivation mechanisms of the excited states for the TTM-1Cz-An complex. Here, kf denotes the fluorescence rate; kp is phosphorescence rate; kISC represents the intersystem crossing rate; kIC refers to the internal conversion rate; JTR is the exchange coupling, and the zero-field splitting tensor is D. All the rate units are in s−1. | |
Table 2 Spin–orbit coupling (SOC) matrix elements (cm−1) between excited states of TTM-1Cz-An calculated at the CASSCF level. S is the spin quantum number; MS denotes the spin sublevels
| State 1 |
State 2 |
〈S1 = 3/2, Ms1|ĤSOC|S2 = 1/2, Ms2〉a |
Total SOCb |
〈3/2|ĤSOC|1/2〉 = 〈−3/2|ĤSOC|−1/2〉, 〈1/2|ĤSOC|1/2〉 = 〈−1/2|ĤSOC|−1/2〉, and 〈−1/2|ĤSOC|1/2〉 = 〈1/2|ĤSOC|−1/2〉. 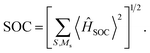 |
| Q1 |
D0 |
〈S1 = 3/2, 3/2|ĤSOC|S2 = 1/2, 1/2〉 = 0.013 + 0.006i |
0.025 |
| |
|
〈S1 = 3/2, 1/2|ĤSOC|S2 = 1/2, 1/2〉 = −0.000 + 0.005i |
|
| |
|
〈S1 = 3/2, −1/2|ĤSOC|S2 = 1/2, 1/2〉 = 0.008 − 0.003i |
|
| Q1 |
D1 |
〈S1 = 3/2, 3/2|ĤSOC|S2 = 1/2, 1/2〉 = −0.001 + 0.001i |
0.002 |
| |
|
〈S1 = 3/2, 1/2|ĤSOC|S2 = 1/2, 1/2〉 = −0.000 − 0.000i |
|
| |
|
〈S1 = 3/2, −1/2|ĤSOC|S2 = 1/2, 1/2〉 = −0.000 − 0.000i |
|
| Q1 |
D2 |
〈S1 = 3/2, 3/2|ĤSOC|S2 = 1/2, 1/2〉 = −0.003 + 0.003i |
0.008 |
| |
|
〈S1 = 3/2, 1/2|ĤSOC|S2 = 1/2, 1/2〉 = −0.000 − 0.002i |
|
| |
|
〈S1 = 3/2, −1/2|ĤSOC|S2 = 1/2, 1/2〉 = −0.002 − 0.002i |
|
| Q1 |
D3 |
〈S1 = 3/2, 3/2|ĤSOC|S2 = 1/2, 1/2〉 = 0.027 − 0.044i |
0.093 |
| |
|
〈S1 = 3/2, 1/2|ĤSOC|S2 = 1/2, 1/2〉 = −0.000 + 0.028i |
|
| |
|
〈S1 = 3/2, −1/2|ĤSOC|S2 = 1/2, 1/2〉 = 0.015 + 0.026i |
|
Table 3 Obtained intersystem crossing (ISC, D1 → Q1) and reverse intersystem crossing (RISC, Q1 → D1) rates with and without the HT effect between the D1 and Q1 states from 80 to 298 K for TTM-1Cz-An; all units are in s−1
| Temp. |
kISC(D1 → Q1) |
kRISC(Q1 → D1) |
| FC (×102) |
FCHT (×106) |
FC (×101) |
FCHT (×105) |
| Average |
1/2 → +3/2 |
1/2 → +1/2 |
1/2 → −1/2 |
Average |
+3/2 → 1/2 |
+1/2 → 1/2 |
−1/2 → 1/2 |
| 298 |
5.85 |
7.89 |
2.28 |
2.45 |
2.41 |
6.64 |
2.07 |
2.22 |
| 150 |
6.65 |
8.98 |
2.59 |
2.78 |
4.58 |
8.76 |
2.53 |
2.72 |
| 80 |
6.78 |
9.16 |
2.65 |
2.84 |
7.31 |
9.12 |
2.64 |
2.83 |
To gain further insights, it becomes imperative to consider the vibronic SOC effects, often referred to as the Herzberg–Teller (HT) term. The first derivatives of the SOC constants with respect to the mass-weighted normal coordinates, ∂〈Q1|ĤSOC|D1〉/∂Qk, at equilibrium geometry Qk = 0 of the Q1 state, were numerically computed using finite-difference methods, as illustrated in Fig. 9c, with the corresponding kRISC rate constants enumerated in Table 3. It was observed that the RISC rate kRISC, inclusive of the HT term, was 3.64 × 105 s−1 at 298 K, which was approximately four orders of magnitude greater than the FC rate of 2.41× 101 s−1, and significantly exceeded the phosphorescence and nonradiative rates of the Q1 state. This provides a condition for the repopulation of the D1 state. With respect to the vibration modes, only a select few are instrumental in altering the vibrational structure and inducing a more pronounced SOC interaction. The representative modes of ω170 = 1423 cm−1 and ω198 = 1684 cm−1, corresponding to the skeletal vibrations of the TTM-1Cz-An radical, were characterized by Huang–Rhys factors of S170 = 0.019 and S198 = 0.008, along with reorganization energies of λ170 = 27.19 cm−1 and λ198 = 5.51 cm−1, respectively, as shown in Fig. 9 and Table S8.† These vibrations significantly enhance ∂〈Q1|ĤSOC|D1〉/∂Qk due to the alterations in 〈Q1|ĤSOC|D1〉 (for instance, 0.228 cm−1 for ω198) as a result of the complete overlap of the molecular orbitals density pertinent to the Q1 ↔ D1 transition and the populations of the vibrational modes. Consequently, it is plausible to deduce that the vibronic SOC is the predominant coupling interaction facilitating RISC, and can remarkably enhance the RISC rates from Q1 to D1 by approximately four orders of magnitude.
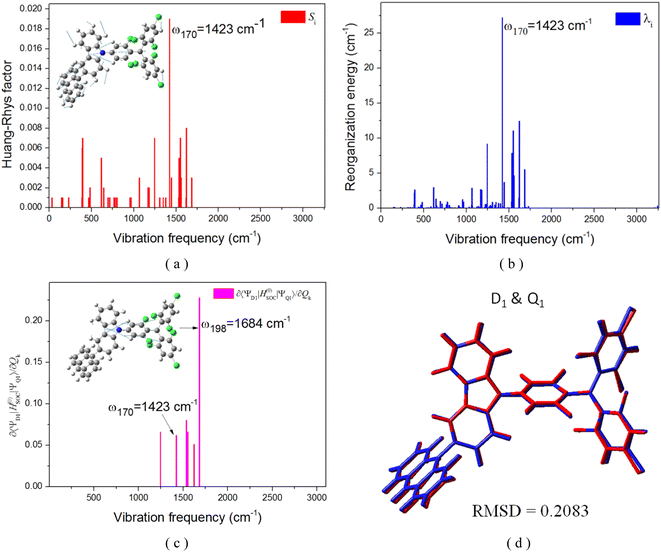 |
| | Fig. 9 Calculated Huang–Rhys factors (a) and reorganization energy (b) versus the normal vibration frequency between D1 and Q1 on the Q1 potential energy surface, respectively; size of the SOC matrix element depends on the motion along the representative promotion vibration mode (c); (d) root-mean-squared deviations (RMSD) in Å between the D1 and Q1 geometries. | |
3.5 Luminescence mechanism and internal conversion
In this section, we focus on the luminescence mechanism of the TTM-1Cz-An radical. The calculated fluorescence spectra and radiative rate constants (kf, unit in s−1) for the excited D2 and D1 states at different temperatures are presented Fig. 10 and S1.† It could be clearly seen that the D1 state exhibited a weak visible emission at 670 nm, close to the experimental value of 685 nm, even when driven by the HT effect. This suggests a small oscillator strength for the D1 → D0 emission, consistent with the inhibited D0 → D1 absorption transition discussed in Section 3.1. These characteristics indicate a relatively slow radiative rate from the D1 emission, kr = 1.64 s−1 at 298 K, resulting in ineffective luminescence. To enhance the luminescence efficiency of the TTM-1Cz-An radical compound, the D1 state must undergo reverse internal conversion and be effectively distributed to the D2 and D3 states, which possess a high oscillator strength, or alternatively, “borrow intensity” from the luminescent D2 state.10,11 Based on the perturbation theory of intensity borrowing, the small energy gaps between excited states (as seen Table S9†) involved in the internal conversion mechanism are likely to result in a significant mixing between states with doublet multiplicity, as indicated by the calculated electronic coupling interactions (VDn,m) using the two-state generalized Mulliken–Hush approximation, and the VDn,m values are listed in Table 4.45 The corresponding internal conversion rate constants, k(R)IC were also estimated and are listed in Table 5.
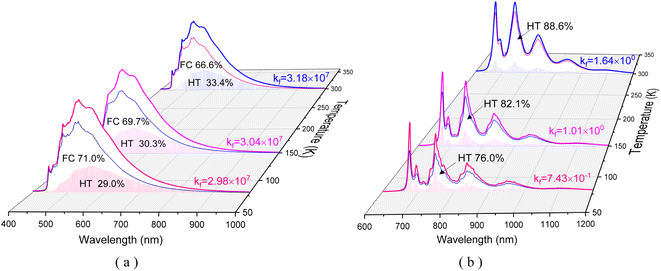 |
| | Fig. 10 Comparison diagrams of the contributions of the calculated HT and FC to the fluorescence spectra and radiation rates (kf, unit in s−1) for the excited D2 state (a) and D1 (b) states of TTM-1Cz-An at different temperatures. | |
Table 4 Parameters of the calculated electronic coupling interactions (VDn,m) between the excited states using the two-state generalized Mulliken–Hush approximation
| Method |
Transition state |
μ(Dn,m)/a.u. |
Δμ(Dn,m)/a.u. |
ΔE(Dn,m)/eV |
VDn,m/meV |
| ωb97X-D3 |
D1 → D2 |
0.09899 |
2.29722 |
0.871 |
〈D1|ĤV |D2〉 = 37.39 |
| |
D1 → D3 |
0.00134 |
0.64148 |
0.951 |
〈D1|ĤV |D3〉 = 1.99 |
| |
D2 → D3 |
0.68266 |
1.65574 |
0.080 |
〈D2|ĤV |D3〉 = 24.33 |
| CAM-B3LYP |
D1 → D2 |
0.12389 |
4.65726 |
0.735 |
〈D1|ĤV |D2〉 = 19.52 |
| |
D1 → D3 |
0.00247 |
0.54122 |
0.953 |
〈D1|ĤV |D3〉 = 4.35 |
| |
D2 → D3 |
0.61762 |
4.11604 |
0.218 |
〈D2|ĤV |D3〉 = 31.33 |
Table 5 Calculated internal conversion nonradiative rates (kIC, unit in s−1) between the D1 and D2 (or D3) states from 80 to 298 K for TTM-1Cz-An
| Temp. |
kRIC(D1 → D2) |
kIC(D2 → D1) |
kRIC (D2 → D3 |
kIC(D3 → D2) |
kIC(D3 → D1)a |
| kRIC(D1 → D3) was estimated but obtained an unreasonable value due to the significant activation energy gap and so is not listed. |
| ωB97X-D3/def2-TZVP |
| 298 |
9.26 × 1010 |
1.95 × 1012 |
1.13 × 1013 |
6.12× 1013 |
3.45 × 1010 |
| 150 |
6.55 × 109 |
1.67 × 1012 |
3.38 × 1013 |
8.79 × 1013 |
3.46 × 1010 |
| 80 |
1.30 × 109 |
1.59 × 1012 |
6.93 × 1013 |
1.14 × 1014 |
3.49 × 1010 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| CAM-B3LYP/def2-TZVP |
| 298 |
5.90 × 1010 |
5.35 × 1011 |
8.43 × 1013 |
9.48 × 1013 |
8.28 × 1010 |
| 150 |
3.04 × 1010 |
4.58 × 1011 |
6.20 × 1013 |
2.43 × 1014 |
7.78 × 1010 |
| 80 |
2.28 × 1010 |
4.39 × 1011 |
4.65 × 1013 |
3.43 × 1014 |
7.50 × 1010 |
The electronic coupling VD1,2 of the D1 and D2 states was notably strong, with an interaction of 37.4 meV at the ωB97X-D3 level, see Table 4. This leads to larger internal conversion rates k(R)IC from D1 ↔ D2. It could be observed from Table 5 that the kRIC(D1 → D2) rate was approximately 9.26 × 1010 s−1 at 298 K, which was roughly four orders of magnitude larger than the ISC rate from D1 to Q1, 7.89 × 106 s−1. This indicates that the D2 state is effectively populated at room temperature. Furthermore, it could be noted that the large kRIC(D1 → D2) rate of 9.26 × 1010 s−1 was predominantly influenced by a single vibrational mode “ω197” at 1673 cm−1, corresponding to the in-plane stretching vibration of the carbazole skeleton, as depicted in Fig. S2.† This frequency also matched the energy gap ΔE(D1 → D2) (Table S9†), which is crucial for significantly enhancing the RIC rate. Interestingly, the D2 and D3 states were closely matched in energy and both originated from local excitation on the TTM-1Cz moiety, as shown in Fig. 2, allowing for rapid interconversion into resonant states. Regarding the fluorescence emission of the D2 state, as illustrated in Fig. 10, TTM-1Cz-An was capable of generating effective radiative fluorescence. Here, the calculated emission rate kf = 2.98 to 3.18 × 107 s−1 was in good agreement with the experimental value of 1.28 × 107 s−1,56 and its temperature dependence was negligible. The aforementioned discussions provide the possible mechanisms for the optical readout of the stable TTM-1Cz-An radical in applications such as OLEDs and quantum-information technologies.
4. Conclusions
A thorough understanding of the molecular factors that control the fluorescence emission of organic radicals is essential for the design of a new generation of efficient radical emitters. To this end and to gain a comprehensive and systematic understanding of the luminescence mechanism of the TTM-1Cz-An radical, we employed quantum theoretical calculations to quantitatively predict the photophysical properties of TTM-1Cz-An radical, including the fluorescence emission rates, optical spectrum, and excited-state dynamics.
Our calculated results showed that the photoexcited sing-doublet D1 state from the anthracene singlet excited state was quickly converted to the doublet 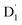 state by EISC with the help of the exchange-induced spin conversion, facilitated by the significant exchange interactions of J13 = 0.232 and J12 = −0.116 cm−1. In this process, the total spin multiplicity is conserved during the
state by EISC with the help of the exchange-induced spin conversion, facilitated by the significant exchange interactions of J13 = 0.232 and J12 = −0.116 cm−1. In this process, the total spin multiplicity is conserved during the 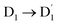 transition. Subsequently, the
transition. Subsequently, the 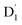 state can evolve into a quartet state by the exchange coupling 3/2JTR = 0.086 cm−1 between the triplet spin electrons of anthracene and the TTM-1Cz radical, which exceeds the zero-field splitting tensor of D = 0.026 cm−1. The direct SOC-induced ISC to the Q1 state was minimal due to the nearly identical spatial wavefunctions of the
state can evolve into a quartet state by the exchange coupling 3/2JTR = 0.086 cm−1 between the triplet spin electrons of anthracene and the TTM-1Cz radical, which exceeds the zero-field splitting tensor of D = 0.026 cm−1. The direct SOC-induced ISC to the Q1 state was minimal due to the nearly identical spatial wavefunctions of the 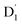 and Q1 levels. It is well known that the effective occurrence of RISC from Q1 to D1 states is a critical rate-determining step in controlling the luminescence of the TTM-1Cz-An radical complex. The calculated RISC rate, including the HT effect, was kRISC = 3.64 × 105 s−1 at 298 K, which was approximately four orders of magnitude greater than the FC rate of 2.41× 101 s−1, and far greater than the phosphorescence and nonradiative rates of the Q1 state, thus enabling the repopulation of the D1 state. However, the D1 emission exhibited a relatively slow radiative rate of kr = 1.64 s−1 at 298 K, resulting in ineffective luminescence. For the TTM-1Cz-An radical to exhibit effective luminescence, the D1 state must undergo reverse internal conversion and be effectively populated into the D2 or D3 states. In the case of the D2 state redistribution, there was a strong electronic coupling of 37.4 meV between the D1 and D2 states with a dense manifold of doublet states energetically close to the D1 state, leading to a larger reverse internal conversion rate of kRIC = 9.26 × 1010 s−1 into the D2 state. The calculated D2 emission rate of kf = 2.98 to 3.18 × 107 s−1 was in good agreement with the experimental value of 1.28 × 107 s−1. Our study provides valuable information on the radical luminescence mechanism, which will be helpful for the development of novel radical luminescent materials.
and Q1 levels. It is well known that the effective occurrence of RISC from Q1 to D1 states is a critical rate-determining step in controlling the luminescence of the TTM-1Cz-An radical complex. The calculated RISC rate, including the HT effect, was kRISC = 3.64 × 105 s−1 at 298 K, which was approximately four orders of magnitude greater than the FC rate of 2.41× 101 s−1, and far greater than the phosphorescence and nonradiative rates of the Q1 state, thus enabling the repopulation of the D1 state. However, the D1 emission exhibited a relatively slow radiative rate of kr = 1.64 s−1 at 298 K, resulting in ineffective luminescence. For the TTM-1Cz-An radical to exhibit effective luminescence, the D1 state must undergo reverse internal conversion and be effectively populated into the D2 or D3 states. In the case of the D2 state redistribution, there was a strong electronic coupling of 37.4 meV between the D1 and D2 states with a dense manifold of doublet states energetically close to the D1 state, leading to a larger reverse internal conversion rate of kRIC = 9.26 × 1010 s−1 into the D2 state. The calculated D2 emission rate of kf = 2.98 to 3.18 × 107 s−1 was in good agreement with the experimental value of 1.28 × 107 s−1. Our study provides valuable information on the radical luminescence mechanism, which will be helpful for the development of novel radical luminescent materials.
Data availability
The data supporting the findings of this study are available within the article and in the ESI.†
Conflicts of interest
All authors declare that they have no conflicts of interest.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (grant no. 22163008, and 21663025), Postgraduate Innovation Program of Tianshui Normal University (grant no. 0309-2024010304050), and “Fuxi” Innovation Team Project of Theoretical and Computational Chemistry (grant no. 0309-202101012 04).
References
- Z. Y. Yang, Z. Mao, Z. L. Xie, Y. Zhang, S. W. Liu, J. Zhao, J. R. Xu, Z. G. Chi and M. P. Aldred, Recent advances in organic thermally activated delayed fluorescence materials, Chem. Soc. Rev., 2017, 46, 915–1016 RSC.
- J. H. Kim, J. H. Yun and J. Y. Lee, Recent Progress of Highly Efficient Red and Near-Infrared Thermally Activated Delayed Fluorescent Emitters, Adv. Opt. Mater., 2018, 6, 1800255 CrossRef.
- J. M. Teng, Y. F. Wang and C. F. Chen, Recent progress of narrowband TADF emitters and their applications in OLEDs, J. Mater. Chem. C, 2020, 8, 11340–11353 RSC.
- Y. Xu, P. Xu, D. Hu and Y. Ma, Recent progress in hot exciton materials for organic light-emitting diodes, Chem. Soc. Rev., 2021, 50, 1030–1069 RSC.
- H. Guo, Q. Peng, X. K. Chen, Q. Gu, S. Dong, E. W. Evans, A. J. Gillett, X. Ai, M. Zhang, D. Credgington, V. Coropceanu, R. H. Friend, J.-L. Brédas and F. Li, High Stability and Luminescence Efficiency in Donor–Acceptor Neutral Radicals not Following the Aufbau Principle, Nat. Mater., 2019, 18, 977–984 CrossRef CAS PubMed.
- H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Highly efficient organic light-emitting diodes from delayed fluorescence, Nature, 2012, 492, 234–238 CrossRef CAS PubMed.
- Y. Tao, K. Yuan, T. Chen, P. Xu, H. H. Li, R. F. Chen, C. Zheng, L. Zhang and W. Huang, Thermally Activated Delayed Fluorescence Materials Towards the Breakthrough of Organo electronics, Adv. Mater., 2014, 26, 7931–7958 CrossRef CAS PubMed.
- R. Czerwieniec, M. J. Leitl, H. H. H. Homeier and H. Yersin, Cu(I) complexex-Thermally activated delayed fluorescence. Photophysical approach and material design, Coord. Chem. Rev., 2016, 325, 2–28 CrossRef CAS.
- L. Ji, J. Q. Shi, J. Wei, T. Yu and W. Huang, Air-Stable Organic Radicals: New-Generation Materials for Flexible Electronics?, Adv. Mater., 2020, 32, 1908015 CrossRef CAS PubMed.
- E. Cho, V. Coropceanu and J.-L. Brédas, Organic Neutral Radical Emitters: Impact of Chemical Substitution and Electronic-State Hybridization on the Luminescence Properties, J. Am. Chem. Soc., 2020, 142, 17782–17786 CrossRef CAS PubMed.
- A. Abdurahman, T. J. H. Hele, Q. Gu, J. Zhang, Q. Peng, M. Zhang, R. H. Friend, F. Li and E. W. Evans, Understanding the Luminescent Nature of Organic Radicals for Efficient Doublet Emitters and Pure-Red Light-Emitting Diodes, Nat. Mater., 2020, 19, 1224–1229 CrossRef CAS PubMed.
- H. Abroshan, V. Coropceanu and J.-L. Brédas, Radiative and Nonradiative Recombinations in Organic Radical Emitters: The Effect of Guest–Host Interactions, Adv. Funct. Mater., 2020, 30, 2002916 CrossRef CAS.
- V. Gamero, D. Velasco, S. Latorre, F. López-Calahorra, E. Brillas and L. Juliá, [4-(N-Carbazolyl)-2,6- dichlorophenyl]bis(2,4,6-tri-chlorophenyl)methyl Radical an Efficient Red Light-Emitting Paramagnetic Molecule, Tetrahedron Lett., 2006, 47, 2305–2309 CrossRef CAS.
- Q. Peng, A. Obolda and M. Z. F. Li, Organic Light-Emitting Diodes Using a Neutral p Radical as Emitter: The Emission from a Doublet, Angew. Chem., Int. Ed., 2015, 54, 7091–7095 CrossRef CAS PubMed.
- X. Ai, E. W. Evans, S. Dong, A. J. Gillett, H. Guo, Y. Chen, T. J. H. Hele, R. H. Friend and F. Li, Efficient Radical-based Light-Emitting Diodes with Doublet Emission, Nature, 2018, 563, 536–540 CrossRef CAS PubMed.
- E. Cho and V. Coropceanu, Jean-Luc Brédas, Impact of chemical modifications on the luminescence properties of organic neutral radical emitters, J. Mater. Chem. C, 2021, 9, 10794–10801 RSC.
- S. Gorgon, K. Lv, J. Grüne, B. H. Drummond, W. K. Myers, G. Londi, G. Ricci, D. Valverde, C. Tonnelé, P. Murto, A. S. Romanov, D. Casanova, V. Dyakonov, A. Sperlich, D. Beljonne, Y. Olivier, L. Feng, R. H. Friend and E. W. Evans, Reversible spin-optical interface in luminescent organic radicals, Nature, 2023, 62, 538–544 CrossRef PubMed.
- Y. Teki, Excited-state dynamics of non-luminescent and luminescent π-radicals, Chemistry, 2020, 26, 980–996 CrossRef CAS PubMed.
- M. Atzori and R. Sessoli, The second quantum revolution: role and challenges of molecular chemistry, J. Am. Chem. Soc., 2019, 141, 11339–11352 CrossRef CAS PubMed.
- A. Gaita-Ariño, F. Luis, S. Hill and E. Coronado, Molecular spins for quantum computation, Nat. Chem., 2019, 11, 301–309 CrossRef PubMed.
- T. Quintes, M. Mayländer and S. Richert, Properties and applications of photoexcited chromophore–radical systems, Nat. Rev. Chem, 2023, 7, 75–90 CrossRef PubMed.
- F. Neese, Software update: the ORCA 5.0 program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 Search PubMed.
- Y.-S. Lin, G.-D. Li, S.-P. Mao and J.-D. Chai, Long-Range Corrected Hybrid Density Functionals with Improved Dispersion Corrections, J. Chem. Theory Comput., 2013, 9, 263–272 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed.
- O. Vahtras, J. Almlöf and M. W. Feyereisen, Integral approximations for LCAO-SCF calculations, Chem. Phys. Lett., 1993, 213, 514–518 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Efficient, approximate and parallel Hartree−Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree−Fock exchange, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- D. M. York and M. Karplus, A Smooth Solvation Potential Based on the Conductor-Like Screening Model, J. Phys. Chem. A, 1999, 103, 11060–11079 CrossRef CAS.
- T. Schwabe and L. Goerigk, Time-dependent double-hybrid density functionals with spin-component and spin-opposite scaling, J. Chem. Theory Comput., 2017, 13, 4307–4323 CrossRef CAS PubMed.
- M. Casanova-Páez, M. B. Dardis and L. Goerigk, ωB2PLYP and ωB2GPPLYP: The first two double-hybrid density functionals with long-range correction optimized for excitation energies, J. Chem. Theory Comput., 2019, 15, 4735–4744 CrossRef PubMed.
- M. Casanova-Páez and L. Goerigk, Time-dependent long-range-corrected double-hybrid density functionals with spin-component and spin-opposite scaling: a comprehensive analysis of singlet-singlet and singlet-triplet excitation energies, J. Chem. Theory Comput., 2021, 17, 5165–5186 CrossRef PubMed.
- Y. Guo, C. Riplinger, U. Becker, D. G. Liakos, Y. Minenkov, L. Cavallo and F. Neese, Communication: An improved linear scaling perturbative triples correction for the domain based local pair-natural orbital based singles and doubles coupled cluster method [DLPNO-CCSD(T)], J. Chem. Phys., 2018, 148, 011101 CrossRef PubMed.
- Y. Guo, C. Riplinger, D. G. Liakos, U. Becker, M. Saitow and F. Neese, Linear scaling perturbative triples correction approximations for open-shell domain-based local pair natural orbital coupled cluster singles and doubles theory [DLPNO-CCSD(T0/T)], J. Chem.
Phys., 2020, 152, 024116 CrossRef CAS PubMed.
- C. Angeli, S. Borini, M. Cestari and R. Cimiraglia, A quasidegenerate formulation of the second order n-electron valence state perturbation theory approach, J. Chem. Phys., 2004, 121, 4043–4049 CrossRef CAS PubMed.
- S. F. Boys, Construction of some molecular orbitals to be approximately invariant for changes from one molecule to another, Rev. Mod. Phys., 1960, 32, 296 CrossRef CAS.
- M. Franz, F. Neese and S. Richert, Calculation of exchange couplings in the electronically excited state of molecular three-spin systems, Chem. Sci., 2022, 13, 12358–12366 RSC.
- D. Reta, I. P. R. de Moreira and F. Illas, Magnetic Coupling Constants in Three Electrons Three Centers Problems from Effective Hamiltonian Theory and Validation of Broken Symmetry-Based Approaches, J. Chem. Theory Comput., 2016, 12, 3228–3235 CrossRef CAS PubMed.
- F. Neese, Importance of Direct Spin−Spin Coupling and Spin-Flip Excitations for the Zero-Field Splittings of Transition Metal Complexes: A Case Study, J. Am. Chem. Soc., 2006, 128, 10213–10222 CrossRef CAS PubMed.
- B. Minaev, G. Baryshnikov and H. Ågren, Principles of phosphorescent organic light emitting devices, Phys. Chem. Chem. Phys., 2014, 16, 1719–1758 RSC.
- M. Roemelt, D. Maganas, S. DeBeer and F. Neese, A combined DFT and restricted open-shell configuration interaction method including spin-orbit coupling: Application to transition metal L-edge X-ray absorption spectroscopy, J. Chem. Phys., 2013, 138, 204101 CrossRef PubMed.
- F. Neese, Efficient and accurate approximations to the molecular spin-orbit coupling operator and their use in molecular g-tensor calculations, J. Chem. Phys., 2005, 122, 034107 CrossRef PubMed.
- M. C. Daza, M. Doerr, S. Salzmann, C. M. Marian and W. Thiel, Photophysics of phenalenone: quantum mechanical investigation of singlet–triplet intersystem crossing, Phys. Chem. Chem. Phys., 2009, 11, 1688–1696 RSC.
- V. Coropceanu, X. K. Chen, T. Wang, Z. Zheng and J. L. Brédas, Charge-Transfer Electronic States in Organic Solar Cells, Nat. Rev. Mater., 2019, 4, 689–707 CrossRef.
- R. J. Cave and M. D. Newton, Generalization of the Mulliken-Hush Treatment for the Calculation of Electron Transfer Matrix Elements, Chem. Phys. Lett., 1996, 249, 15–19 CrossRef CAS.
- Y. L. Niu, Q. Peng, C. Deng, X. Gao and Z. G. Shuai, Theory of Excited State Decays and Optical Spectra: Application to Polyatomic Molecules, J. Phys. Chem. A, 2010, 114, 7817–7831 CrossRef CAS PubMed.
- L. L. Lv, K. Yuan, T. Y. Zhao and Y. C. Wang, A new mechanistic study of a second generation TADF material based on the path integral approach incorporating Herzberg–Teller and Duschinsky rotation effects, J. Mater. Chem. C, 2020, 8, 10369–10381 RSC.
- B. de Souza, F. Neese and R. Izsák, On the theoretical prediction of fluorescence rates from first principles using the path integral approach, J. Chem. Phys., 2018, 148, 034104 CrossRef PubMed.
- B. de Souza, G. Farias, F. Neese and R. Izsák, Predicting Phosphorescence Rates of Light Organic Molecules Using Time-Dependent Density Functional Theory and the Path Integral Approach to Dynamics, J. Chem. Theory Comput., 2019, 15, 1896–1904 CrossRef CAS PubMed.
- A. Baiardi, J. Bloino and V. Barone, General Time Dependent Approach to Vibronic Spectroscopy Including Franck–Condon, Herzberg–Teller, and Duschinsky Effects, J. Chem. Theory Comput., 2013, 9, 4097–4115 CrossRef CAS PubMed.
- M. Mayländer, T. Quintes, M. Franz, X. Allonas, A. V. Jentzsch and S. Richert, Distance dependence of enhanced intersystem crossing in BODIPY–nitroxide dyads, Chem. Sci., 2023, 14, 5361–5536 RSC.
- Y. E. Kandrashkin and A. van der Est, Enhanced Intersystem Crossing due to Resonant Energy Transfer to a Remote Spin, J. Phys. Chem. Lett., 2021, 12, 7312–7318 CrossRef CAS PubMed.
- V. Rozenshtein, A. Berg, E. Stavitski, H. Levanon, L. Franco and C. Corvaja, Electron Spin Polarization of Functionalized Fullerenes. Reversed Quartet Mechanism, J. Phys. Chem. A, 2005, 109(49), 11144–11154 CrossRef CAS PubMed.
- S. Richert, C. E. Tait and C. R. Timmel, Delocalisation of photoexcited triplet states probed by transient EPR and hyperfine spectroscopy, J. Magn. Reson., 2017, 280, 103–116 CrossRef CAS PubMed.
- M. A. El-Sayed, Spin-orbit coupling and the radiationless processes in nitrogen heterocyclics, J. Chem. Phys., 1963, 38, 2834–2838 CrossRef CAS.
- A. Abdurahman, T. J. H. Hele, Q. Gu, J. Zhang, Q. Peng, M. Zhang, R. H. Friend, F. Li and E. W. Evans, Understanding the Luminescent Nature of Organic Radicals for Efficient Doublet Emitters and Pure-Red Light-Emitting Diodes, Nat. Mater., 2020, 19, 1224–1229 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab,
YanYing Zhanga and
ZiYe Ninga
*ab,
YanYing Zhanga and
ZiYe Ninga
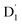 (trip-doublet) state via EISC, facilitated by a significant nonequivalence exchange interaction, with ΔJST = 0.174 cm−1. The formation of the quartet state (Q1, trip-quartet) was predominantly dependent on the exchange coupling 3/2JTR = 0.086 cm−1 between the triplet spin electrons of anthracene and the TTM-1Cz radical. Direct spin–orbit coupling ISC to the Q1 state was minimal due to the nearly identical spatial wavefunctions of the
(trip-doublet) state via EISC, facilitated by a significant nonequivalence exchange interaction, with ΔJST = 0.174 cm−1. The formation of the quartet state (Q1, trip-quartet) was predominantly dependent on the exchange coupling 3/2JTR = 0.086 cm−1 between the triplet spin electrons of anthracene and the TTM-1Cz radical. Direct spin–orbit coupling ISC to the Q1 state was minimal due to the nearly identical spatial wavefunctions of the 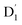 and Q1 levels. The effective occurrence of reverse intersystem crossing (RISC) from the Q1 to D1 state is a critical step in controlling the luminescence of TTM-1Cz-An. The calculated RISC rate kRISC, including the Herzberg–Teller effect, was 3.64 × 105 s−1 at 298 K, significantly exceeding the phosphorescence and nonradiative rates of the Q1 state, thus enabling the D1 repopulation. Subsequently, a strong electronic coupling of 37.4 meV was observed between the D1 and D2 states, along with a dense manifold of doublet states near the D1 state energy, resulting in a larger reverse internal conversion rate kRIC of 9.26 × 1010 s−1. Distributed to the D2 state, the obtained emission rate of kf = 2.98–3.18 × 107 s−1 was in quite good agreement with the experimental value of 1.28 × 107 s−1, and its temperature effect was not remarkable. Our study not only provides strong support for the experimental findings but also offers valuable insights for the molecular design of high-efficiency radical emitters.
and Q1 levels. The effective occurrence of reverse intersystem crossing (RISC) from the Q1 to D1 state is a critical step in controlling the luminescence of TTM-1Cz-An. The calculated RISC rate kRISC, including the Herzberg–Teller effect, was 3.64 × 105 s−1 at 298 K, significantly exceeding the phosphorescence and nonradiative rates of the Q1 state, thus enabling the D1 repopulation. Subsequently, a strong electronic coupling of 37.4 meV was observed between the D1 and D2 states, along with a dense manifold of doublet states near the D1 state energy, resulting in a larger reverse internal conversion rate kRIC of 9.26 × 1010 s−1. Distributed to the D2 state, the obtained emission rate of kf = 2.98–3.18 × 107 s−1 was in quite good agreement with the experimental value of 1.28 × 107 s−1, and its temperature effect was not remarkable. Our study not only provides strong support for the experimental findings but also offers valuable insights for the molecular design of high-efficiency radical emitters.
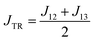
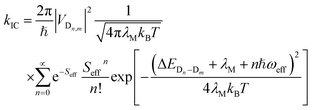
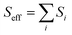
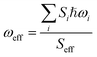
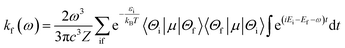
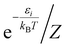 describes the initial state Boltzmann population at temperature T; εi is the total vibrational energy of initial state; and Z represents the vibrational partition function. After further manipulations, eqn (7) was ultimately transformed into a Discrete Fourier Transform (DFT) of a correlation function χ(t) with a time step Δt.49 The transformed formula is given by:
describes the initial state Boltzmann population at temperature T; εi is the total vibrational energy of initial state; and Z represents the vibrational partition function. After further manipulations, eqn (7) was ultimately transformed into a Discrete Fourier Transform (DFT) of a correlation function χ(t) with a time step Δt.49 The transformed formula is given by: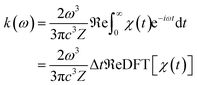
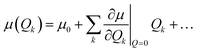
 This conversion occurs by nonequivalent spin–exchange coupling of the singlet excited electrons of anthracene and the third radical electron mediated. This mechanism is referred to as the ΔJST mechanism,52 where ΔJST is defined as (J13 − J12)/2, and was calculated to be 0.174 cm−1 at the CASSCF/QD-NEVPT2 level, as detailed in Table 1. This process is schematically depicted in Fig. 4, with the corresponding visualization of the localized spin centers illustrated in Fig. 5.
This conversion occurs by nonequivalent spin–exchange coupling of the singlet excited electrons of anthracene and the third radical electron mediated. This mechanism is referred to as the ΔJST mechanism,52 where ΔJST is defined as (J13 − J12)/2, and was calculated to be 0.174 cm−1 at the CASSCF/QD-NEVPT2 level, as detailed in Table 1. This process is schematically depicted in Fig. 4, with the corresponding visualization of the localized spin centers illustrated in Fig. 5.
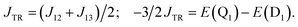
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300.1
300.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 215.4
215.4
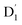 state. The formation of the quartet state (Q1, trip-quartet) predominantly relies on the exchange–coupling interaction JTR between the triplet spin electrons of anthracene and the TTM-1Cz radical.37,50 If the JTR interaction surpasses all other magnetic interactions within the TTM-1Cz-An radical system, the Q1 state can be formed through spin mixing. The data in Table 1 indicate that the exchange interaction, with a value of JTR = 0.057 cm−1 at the CASSCF/QD-NEVPT2 level (see out file of the JTR calculation in the ESI†), was sufficiently large to enable the formation of the Q1 state via spin exchange. It could also be noted that the JTR was positive, suggesting that the TTM-1Cz-An radical exhibits ferromagnetically coupling,50,51 which implies that the Q1 state was energetically favored over the
state. The formation of the quartet state (Q1, trip-quartet) predominantly relies on the exchange–coupling interaction JTR between the triplet spin electrons of anthracene and the TTM-1Cz radical.37,50 If the JTR interaction surpasses all other magnetic interactions within the TTM-1Cz-An radical system, the Q1 state can be formed through spin mixing. The data in Table 1 indicate that the exchange interaction, with a value of JTR = 0.057 cm−1 at the CASSCF/QD-NEVPT2 level (see out file of the JTR calculation in the ESI†), was sufficiently large to enable the formation of the Q1 state via spin exchange. It could also be noted that the JTR was positive, suggesting that the TTM-1Cz-An radical exhibits ferromagnetically coupling,50,51 which implies that the Q1 state was energetically favored over the 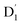 state. Regarding the individual contributions to JTR, it could be seen that both absolute magnitudes (J12 and J13) were bigger for the TTM-1Cz-An radical, and this can be explained by visualizing the spin center in a relatively direct manner, see Fig. 5. The interpretation of the reverse sign of the J12 and J13 interactions is more sophisticated, and the sign was likely decided by the symmetry of the individual spin centers.
state. Regarding the individual contributions to JTR, it could be seen that both absolute magnitudes (J12 and J13) were bigger for the TTM-1Cz-An radical, and this can be explained by visualizing the spin center in a relatively direct manner, see Fig. 5. The interpretation of the reverse sign of the J12 and J13 interactions is more sophisticated, and the sign was likely decided by the symmetry of the individual spin centers.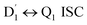 . Even though
. Even though 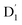 and Q1 were well separated by an energy gap of 3/2JTR = 0.086 cm−1, as shown in Fig. 6, the ZFS interaction, denoted as HZFS, of the two unpaired electrons localized on anthracene leads to a mixing of the
and Q1 were well separated by an energy gap of 3/2JTR = 0.086 cm−1, as shown in Fig. 6, the ZFS interaction, denoted as HZFS, of the two unpaired electrons localized on anthracene leads to a mixing of the 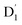 and Q1 states:39,40
and Q1 states:39,40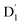 to those of Q1 is dependent on the prohibition factor, which is associated with the change in spin, denoted as fS (m2, m4), with m2 = ±1/2, and m4 = ±1/2, ±3/2, respectively:53
to those of Q1 is dependent on the prohibition factor, which is associated with the change in spin, denoted as fS (m2, m4), with m2 = ±1/2, and m4 = ±1/2, ±3/2, respectively:53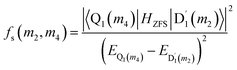
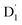 and Q1. This HZFS perturbation is often quantified by the ZFS tensors of D and E. The calculated D and E values at the ωB97X-D3/CAM-B3LYP levels are detailed in Table S5 of the ESI,† and the D tensor orientation and spin density of the quartet Q1 state are depicted in Fig. 7.
and Q1. This HZFS perturbation is often quantified by the ZFS tensors of D and E. The calculated D and E values at the ωB97X-D3/CAM-B3LYP levels are detailed in Table S5 of the ESI,† and the D tensor orientation and spin density of the quartet Q1 state are depicted in Fig. 7.

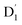 state into the Q1 state. Additionally, the D value was also expected to be negative (i.e., D < 0), implying a more “rod-like” spin density distribution that is “prolate” in shape, with the Dzz component of the ZFS tensor aligned parallel to the spin distribution within the carbazole plane,54 see Fig. 7.
state into the Q1 state. Additionally, the D value was also expected to be negative (i.e., D < 0), implying a more “rod-like” spin density distribution that is “prolate” in shape, with the Dzz component of the ZFS tensor aligned parallel to the spin distribution within the carbazole plane,54 see Fig. 7.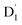 and Q1 states were sufficiently smaller than the vibrational quanta for any of the six allowed (Δm2,4 = ±1, ±2) transitions (Fig. 6a). Consequently, the vibrational relaxation within the
and Q1 states were sufficiently smaller than the vibrational quanta for any of the six allowed (Δm2,4 = ±1, ±2) transitions (Fig. 6a). Consequently, the vibrational relaxation within the 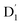 state was also very rapid, with the transition occurring between the zeroth vibrational levels of the
state was also very rapid, with the transition occurring between the zeroth vibrational levels of the 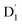 and Q1 states. In this case, the thermal energy of approximately 200 cm−1 at 298 K was most likely to significantly exceed |3/2JTR|, making the RISC from Q1 to
and Q1 states. In this case, the thermal energy of approximately 200 cm−1 at 298 K was most likely to significantly exceed |3/2JTR|, making the RISC from Q1 to 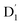 fully possible. This contrasts with scenarios involving a large energy gap, which are termed as the ‘reversed-quartet mechanism’. Furthermore, the vibrational mixing between Q1 and
fully possible. This contrasts with scenarios involving a large energy gap, which are termed as the ‘reversed-quartet mechanism’. Furthermore, the vibrational mixing between Q1 and 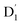 was investigated, with the projections of the eigenfunctions onto the model space at key vibrational coupling modes, as reported in Fig. 6b and Table S6.† It became evident that the Q1 and states were no longer “pure” excited quartet and doublet states (represented by |Φn〉),53 but rather, the Q1 substate was mixed with
was investigated, with the projections of the eigenfunctions onto the model space at key vibrational coupling modes, as reported in Fig. 6b and Table S6.† It became evident that the Q1 and states were no longer “pure” excited quartet and doublet states (represented by |Φn〉),53 but rather, the Q1 substate was mixed with 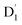 by 11%, and similarly, the
by 11%, and similarly, the 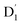 states were mixed with Q1 by 12%.
states were mixed with Q1 by 12%.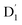 and D1 states was elucidated through EISC, ascribed to the inequality of the exchange interactions J13 and J12, denoted as ΔJST = 0.174 cm−1,52 as detailed in Table 1. Nevertheless, the efficacious occurrence of RISC from Q1 to D1 states is pivotal in the luminescence control of the TTM-1Cz-An radical complex, with possible deactivation pathways of the excited states, as shown in Fig. 8. It is a well-established notion that the RISC rates kRISC are predominantly dictated by three foundational factors: a strong SOC effect between the Q1 and D1 states, a diminutive energy gap ΔE(Q1 − D1), and a significant overlap of the vibrational wavefunctions between Q1 and D1. As anticipated, the computed adiabatic energy difference ΔE(Q1 − D1) for TTM-1Cz-An was notably small, approximately 745 cm−1 at the ωB97X-D3 level, which will be undoubtedly beneficial to augmenting the kRISC. The SOC constants, which are highly dependent on the electronic configuration of the Q1 and D1 states, are summarized in Tables 2 and S7.† According to EI-Sayed's rule,55 the direct SOC interaction between Q1 and D1 is forbidden due to the violation of the total angular momentum conservation principle, resulting in an exceedingly minute SOC constant of 〈Q1|ĤSOC|D1〉 = 0.002 cm−1 (see Table 2). Conversely, for those states with distinct transition characters, the SOC constants are comparatively larger, exemplified by 〈Q1|ĤSOC|D0 〉 = 0.025 cm−1, and 〈Q1|ĤSOC|D3 〉 = 0.093 cm−1. The inhibition SOC effect between Q1 and D1 would result in a relatively slow RISC rate of 2.41 × 101 s−1 at 298 K, as reported in Table 3. For meaningful RISC to occur, it is imperative that the kRISC rate of 2.41 × 101 s−1 at room temperature has to be larger than the radiative (kp = 1.95 s−1) and nonradiative (kRISC = 7.44 s−1, as listed in Fig. 8) rates of the Q1 state to the ground D0 state, which is patently insufficient.
and D1 states was elucidated through EISC, ascribed to the inequality of the exchange interactions J13 and J12, denoted as ΔJST = 0.174 cm−1,52 as detailed in Table 1. Nevertheless, the efficacious occurrence of RISC from Q1 to D1 states is pivotal in the luminescence control of the TTM-1Cz-An radical complex, with possible deactivation pathways of the excited states, as shown in Fig. 8. It is a well-established notion that the RISC rates kRISC are predominantly dictated by three foundational factors: a strong SOC effect between the Q1 and D1 states, a diminutive energy gap ΔE(Q1 − D1), and a significant overlap of the vibrational wavefunctions between Q1 and D1. As anticipated, the computed adiabatic energy difference ΔE(Q1 − D1) for TTM-1Cz-An was notably small, approximately 745 cm−1 at the ωB97X-D3 level, which will be undoubtedly beneficial to augmenting the kRISC. The SOC constants, which are highly dependent on the electronic configuration of the Q1 and D1 states, are summarized in Tables 2 and S7.† According to EI-Sayed's rule,55 the direct SOC interaction between Q1 and D1 is forbidden due to the violation of the total angular momentum conservation principle, resulting in an exceedingly minute SOC constant of 〈Q1|ĤSOC|D1〉 = 0.002 cm−1 (see Table 2). Conversely, for those states with distinct transition characters, the SOC constants are comparatively larger, exemplified by 〈Q1|ĤSOC|D0 〉 = 0.025 cm−1, and 〈Q1|ĤSOC|D3 〉 = 0.093 cm−1. The inhibition SOC effect between Q1 and D1 would result in a relatively slow RISC rate of 2.41 × 101 s−1 at 298 K, as reported in Table 3. For meaningful RISC to occur, it is imperative that the kRISC rate of 2.41 × 101 s−1 at room temperature has to be larger than the radiative (kp = 1.95 s−1) and nonradiative (kRISC = 7.44 s−1, as listed in Fig. 8) rates of the Q1 state to the ground D0 state, which is patently insufficient.
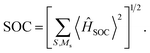
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
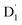 state by EISC with the help of the exchange-induced spin conversion, facilitated by the significant exchange interactions of J13 = 0.232 and J12 = −0.116 cm−1. In this process, the total spin multiplicity is conserved during the
state by EISC with the help of the exchange-induced spin conversion, facilitated by the significant exchange interactions of J13 = 0.232 and J12 = −0.116 cm−1. In this process, the total spin multiplicity is conserved during the 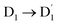 transition. Subsequently, the
transition. Subsequently, the 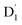 state can evolve into a quartet state by the exchange coupling 3/2JTR = 0.086 cm−1 between the triplet spin electrons of anthracene and the TTM-1Cz radical, which exceeds the zero-field splitting tensor of D = 0.026 cm−1. The direct SOC-induced ISC to the Q1 state was minimal due to the nearly identical spatial wavefunctions of the
state can evolve into a quartet state by the exchange coupling 3/2JTR = 0.086 cm−1 between the triplet spin electrons of anthracene and the TTM-1Cz radical, which exceeds the zero-field splitting tensor of D = 0.026 cm−1. The direct SOC-induced ISC to the Q1 state was minimal due to the nearly identical spatial wavefunctions of the 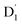 and Q1 levels. It is well known that the effective occurrence of RISC from Q1 to D1 states is a critical rate-determining step in controlling the luminescence of the TTM-1Cz-An radical complex. The calculated RISC rate, including the HT effect, was kRISC = 3.64 × 105 s−1 at 298 K, which was approximately four orders of magnitude greater than the FC rate of 2.41× 101 s−1, and far greater than the phosphorescence and nonradiative rates of the Q1 state, thus enabling the repopulation of the D1 state. However, the D1 emission exhibited a relatively slow radiative rate of kr = 1.64 s−1 at 298 K, resulting in ineffective luminescence. For the TTM-1Cz-An radical to exhibit effective luminescence, the D1 state must undergo reverse internal conversion and be effectively populated into the D2 or D3 states. In the case of the D2 state redistribution, there was a strong electronic coupling of 37.4 meV between the D1 and D2 states with a dense manifold of doublet states energetically close to the D1 state, leading to a larger reverse internal conversion rate of kRIC = 9.26 × 1010 s−1 into the D2 state. The calculated D2 emission rate of kf = 2.98 to 3.18 × 107 s−1 was in good agreement with the experimental value of 1.28 × 107 s−1. Our study provides valuable information on the radical luminescence mechanism, which will be helpful for the development of novel radical luminescent materials.
and Q1 levels. It is well known that the effective occurrence of RISC from Q1 to D1 states is a critical rate-determining step in controlling the luminescence of the TTM-1Cz-An radical complex. The calculated RISC rate, including the HT effect, was kRISC = 3.64 × 105 s−1 at 298 K, which was approximately four orders of magnitude greater than the FC rate of 2.41× 101 s−1, and far greater than the phosphorescence and nonradiative rates of the Q1 state, thus enabling the repopulation of the D1 state. However, the D1 emission exhibited a relatively slow radiative rate of kr = 1.64 s−1 at 298 K, resulting in ineffective luminescence. For the TTM-1Cz-An radical to exhibit effective luminescence, the D1 state must undergo reverse internal conversion and be effectively populated into the D2 or D3 states. In the case of the D2 state redistribution, there was a strong electronic coupling of 37.4 meV between the D1 and D2 states with a dense manifold of doublet states energetically close to the D1 state, leading to a larger reverse internal conversion rate of kRIC = 9.26 × 1010 s−1 into the D2 state. The calculated D2 emission rate of kf = 2.98 to 3.18 × 107 s−1 was in good agreement with the experimental value of 1.28 × 107 s−1. Our study provides valuable information on the radical luminescence mechanism, which will be helpful for the development of novel radical luminescent materials.