Open Access Article
Open Access ArticleComputational design of the novel Fe-doped single-layer SrS: structural, electro-magnetic, and optical properties
Warda Elaggoune *a,
Fatih Ersan
*a,
Fatih Ersan b and
Athmane Meddoura
b and
Athmane Meddoura
aLaboratoire de Physique des Matériaux, Université 8 Mai 1945, BP 401, Guelma, 24000, Guelma, Algeria. E-mail: elaggoune.warda@univ-guelma.dz
bDepartment of Physics, Faculty of Science, Aydin Adnan Menderes University, Aydin, 09010, Turkiye
First published on 1st July 2024
Abstract
The search for novel intrinsic two-dimensional (2D) magnetic materials is crucial to understand the fundamentals of 2D magnetism and realize next-generation magneto-electric and magneto-optical systems. Using the rigorous framework of spin-polarized density functional theory (SPDFT)-based ab initio calculations, this investigation systematically investigates the effects of a stepwise change in the Fe composition (x) on the structural, electro-magnetic and optical properties of the ordered SrS based single-layer alloys, with x encompassing values from 0 to 1. Our comprehensive analysis revealed that the calculated formation energies, cohesive energies, phonon dispersions, molecular dynamics, and elastic constants of both bare SrS and FeS monolayers indicate their thermodynamic, dynamic, thermal, and mechanical stability in hexagonal and square structures, respectively. Significantly, the introduction of magnetic Fe dopants into the non-magnetic SrS semiconductor enabled the creation of an intrinsic magnetic (FM) state characterized by spin-polarized charge carriers at the Fermi level (EF). As doping increases, the electronic structure shows a noticeable dependence on the chemical composition. It is noteworthy that the systems doped with 0.750 and 1 Fe exhibit metallic-magnetic and metallic non-magnetic properties, respectively, and the rest are half-semiconductors (HSC) according to the GGA approximation. Conversely, the HSE approach shows a transition to HSC for a doping level of 0.750, while others maintain the same behavior. The study of the optical properties shows improvements compared to the bare SrS monolayer through the incorporation of Fe dopants. The bare SrS has light absorption in the ultraviolet region, while the absorption band edges for HSC compounds change from the infrared to visible regions. This study proposes a practical method to tune the properties of the SrS single-layer by selectively adjusting the dopant concentration. Such control is promising for applications in spintronics and optical based nanodevices.
1 Introduction
Although generally viewed as an emerging research area, the field of elementary two-dimensional (2D) materials is currently experiencing remarkable growth. The resurgence has its roots in the advance of nanotechnology and molecular manufacturing, with a historical connection to Richard Feynman's influential 1960 research topic “There is plenty of room at the bottom”.1 Feynman's groundbreaking research lays the foundation for the systematic study of elementary monolayers and the broader category of 2D materials. After the breakthrough in 2004 that led to the isolation and exploration of the fascinating electronic and thermal properties of monolayer graphene,2 there has been interest in studying other two-dimensional (2D) layered materials such as chalcogenides, transition metal oxides and MXenes.3,4 This increased curiosity is driven by the anticipation of discovering new physical properties, including but not limited to valleytronics,5 non-trivial topology,6 high-temperature ballistic transport,7 and various optoelectronic functions.8 The intrinsic 2D structure of these materials has recently been elucidated in several comprehensive reviews,4,8,9 encouraging renewed and expanded interest in this diverse and dynamic research area. As a result, there is a concerted effort to identify atomically ultrathin materials with potential applications in various next-generation technologies, such as spintronics, engineered nanoelectronics, optoelectronics, nanosensing, and beyond. The growing interest in this search is illustrated by the growing list of elements that are consciously designed and are expected to exist in two-dimensional (2D) form. A successful synthesis has been achieved for fundamental 2D counterparts beyond graphene, including silicene, germanene, and phosphorene.10 Currently, a total of fifteen major elementary groups have been either theoretically predicted or experimentally generated in 2D form, marking the continually expanding landscape of this transformative field. In the post-graphene era, the importance of single-layer strontium sulfide (SrS) has increased significantly, positioning itself as a notable II–VI semiconductor. In particular, theoretical calculations suggest that SrS monolayers could be dynamically stable, unlike other 2D II–VI semiconductors.11 Furthermore, it is shown that its large bandgap, close to visible light, and a remarkably flat band in the upper valence band make it particularly attractive for applications in lasers, light-emitting diodes, and for increasing luminescence intensity through robust spin polarization hole doping.11 The flatness of the valence band could lead to superior charge carrier mobility compared to other II–VI materials, which is crucial for efficient electronic devices. Furthermore, the SrS monolayer was found to exhibit magnetism when doped with holes,12 a property that cannot be easily predicted for other common II–VI semiconductors. Since SrS monolayers are relatively easy to model theoretically, they could serve as a good benchmark for integration with other 2D materials to create van der Waals heterostructures that lead to more exciting functionalities. Similar to the experimental preparation methods for silicene, germanene and h-BN, SrS monolayers on substrates can be synthesized by various techniques.11,12 The existence of 2D SrS has been conclusively demonstrated through a combination of theoretical calculations and experimental validation.13–19 As computing technology advances, the need to extend and customize the physicochemical properties of two-dimensional (2D) materials becomes increasingly apparent. Various strategies such as doping, voltage and electric field application, heterostructure formation, chemical functionality, surface adsorption and planar buckling tuning have been used to modulate these properties.20 In particular, doping proves to be a particularly simple and controllable approach to changing the bandgap size, shifting the position of the Fermi level and influencing the type of charge carriers and thus regulating electronic, optical and magnetic properties.21,22 Modern semiconductor technology is based on theoretical research and technical advances in semiconductor doping. In the field of 2D materials, they are extremely sensitive to external factors due to their unique structure, where almost all atoms are exposed on the surface. Consequently, the band structures of 2D materials can be precisely controlled by substitute doping.23–26 The existing literature shows a notable lack of comprehensive theoretical studies on the effects of substitutional doping in monolayer SrS. A recent study by Yari et al.27 investigated the influence of Cr doping on the electronic, magneto-optical and thermoelectric properties of graphene-like SrS. The study predicted a transition from semiconductor behavior of bare SrS to half-metallic with 100% spin-polarization at a doping concentration of 12.5%. Remarkably, the light reflected from the surface of the Cr-doped monolayer SrS showed counterclockwise polarization at high energies and in the UV region. Another interesting study14 investigated hole doping at anionic and cationic sites of bare SrS and revealed the induction of spin-polarization. The systems showed a phase transition between a non-magnetic semiconductor, a half-metal, a magnetic semiconductor, and a non-magnetic metal when the hole density varied. Remarkably, a local magnetic moment was observed around the substitution sites, which was stabilized by ferromagnetic ordering at significant Curie temperatures. Both studies reported maximum magnetic moments greater than 1 μB and bandgaps no less than 2 eV. Although these studies provide insights into the optical properties and magnetism induced by doping in monolayer SrS,14,27 a notable gap exists in the literature regarding systematic theoretical studies on transition metal doping in monolayer SrS – a crucial aspect for the potential applications. This article addresses the study of structural, electro-magnetic, and optical properties in SrS-to-FeS monolayers, where we systematically vary the strontium ratio concentration using robust first-principles calculations. It is noteworthy that previous studies on Sr1−xFexS alloys mainly focused on the bulk phase,28 with conspicuously no reports on the monolayer forms of Sr1−xFexS alloys. Our results show significant changes in the electronic band structures upon the introduction of Fe atoms. In particular, the bandgaps exhibit non-monotonic changes with increasing concentration. Interestingly, the material undergoes a transformation from a semiconductor to half-semiconductor to metallic state as the dopant concentration varies. Furthermore, we observe a significant modulation of the optical properties by substitutional doping. Fine-tuning the electro-magnetic and optical properties in the doped single-layer SrS structure through doping engineering is of utmost importance for understanding the potential applications of this class of two-dimensional materials in nano-based spintronics and optoelectronics.2 Computational details
The computational simulations were performed using the Vienna Ab initio Simulation Package (VASP) program,29,30 within the framework of Spin-Polarized Density Functional Theory (SPDFT) and employing the Projector Augmented Wave (PAW) potential.31,32 The electron exchange–correlation functional was described using the Perdew–Burke–Ernzerhof (PBE) form of the generalized gradient approximation (GGA).33 To address potential underestimations inherent in the GGA framework, calculations were cross-checked using a non-local Heyd–Scuseria–Ernzerhof hybrid functional (HSE06),34 where the electron–electron interaction was modeled with an enhanced proportion of Hartree–Fock exchange, characterized by a parameter α = 0.25 and a default screening parameter of 0.2 Å−1. The investigation focused on the substitution of the strontium (Sr) atom with an iron (Fe) atom within the SrS host matrix. This substitution was carried out at various ratios (x), denoted as Sr1−xFexS; x = 0, 0.125, 0.166, 0.25, 0.333, 0.375, 0.50, 0.75, and 1. Using a supercell approach, all feasible configurations of the Fe atoms within the SrS monolayer were explored, with redundant configurations omitted from consideration. To prevent interlayer interactions between successive unit cells, a vacuum distance of 20 Å was assumed. The Brillouin zone (BZ) was sampled using a gamma scheme with a (12 × 12 × 1) k-point mesh automatically generated within the unit cells and scaled to (6 × 3 × 1) for x = 0.125 and 0.375, (6 × 4 × 1) for x = 0.166 and 0.333, and to (6 × 6 × 1) for x = 0.250, 0.500, and 0.750 within the supercells simulation. The ground state was optimized with an energy convergence criterion of 10−5 eV between two consecutive iteration steps and a maximum Hellmann–Feynman force on each atom of less than 10−3 eVÅ−1 during ionization relaxation. The plane wave kinetic energy limit was set at 500 eV and the maximum pressure on the cells was reduced to less than 0.1 kbar. Using Bader analysis, the charge distribution on the atoms was determined for different concentrations.35 The dynamic stabilities of bare SrS and FeS monolayers were evaluated by studying phonon band dispersion using the PHONOPY code.36 For this analysis, (7 × 7 × 1) and (6 × 6 × 1) supercells were used for each SrS and FeS monolayers, respectively, with a (3 × 3 × 1) k-point network. Additionally, ab initio molecular dynamics simulations (AIMD) were performed to investigate the thermal stabilities of the monolayers. Supercells of (6 × 6 × 1) and (5 × 5 × 1) were employed for SrS and FeS, respectively, at a temperature of 300 K with total simulation time of 3 ps in 1 fs time steps, which is controlled by a Nosé–Hoover thermostat.37 For the optical properties, a doubling of the Gamma grid for the k-point mesh was implemented, and the Lorentz broadening was set with gamma equal to 0.1 eV.3 Results and discussion
3.1 Atomic structure and energetic stability
The aim of this section is to study the geometric properties of Sr1−xFexS monolayers, with emphasis on the analysis of their crystalline structures. To provide a comparison, we will first present the optimized structures of the pristine SrS and FeS monolayers using the PBE functional. Bulk SrS is known to be characterized as an ionic compound with a cubic crystal structure that possesses a space group of Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (No. 225) and belongs to O6h point group symmetry. Unlike well-known materials such as tungsten disulfide (WS2) or molybdenum disulfide (MoS2), which have a layered structure with weak van der Waals bonds between the slabs, SrS does not naturally form different layers. Instead, it consists of a three-dimensional arrangement of strontium cations (Sr2+) and sulfide anions (S2−), held together by strong ionic bonds.28 Although the process of obtaining monolayers from SrS may be more complicated compared to exfoliating layered materials such as WS2 and MoS2, it is noteworthy that SrS has the potential to form monolayers. The SrS monolayer is characterized by a pronounced planar hexagonal honeycomb lattice configuration, which leads to a reduction in symmetry to P
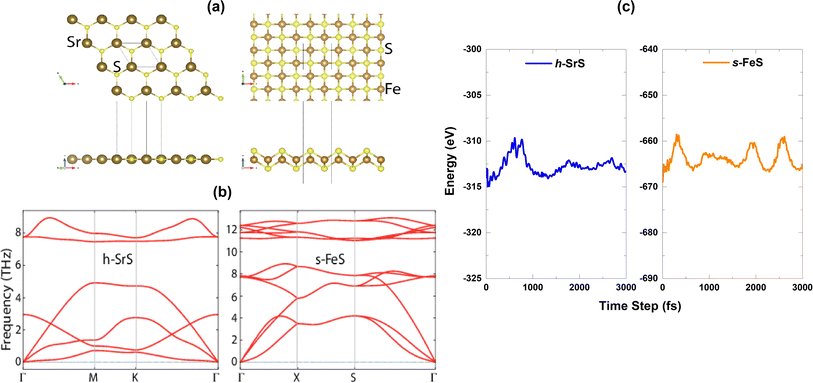
m (No. 225) and belongs to O6h point group symmetry. Unlike well-known materials such as tungsten disulfide (WS2) or molybdenum disulfide (MoS2), which have a layered structure with weak van der Waals bonds between the slabs, SrS does not naturally form different layers. Instead, it consists of a three-dimensional arrangement of strontium cations (Sr2+) and sulfide anions (S2−), held together by strong ionic bonds.28 Although the process of obtaining monolayers from SrS may be more complicated compared to exfoliating layered materials such as WS2 and MoS2, it is noteworthy that SrS has the potential to form monolayers. The SrS monolayer is characterized by a pronounced planar hexagonal honeycomb lattice configuration, which leads to a reduction in symmetry to P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2 (No. 187, belongs to the point group D3h) due to the loss of inversion symmetry. The ion positions and cell volume are then completely relaxed to ensure the stability of the resulting structure. The unit cell of the SrS monolayer consists of one Sr atom and one S atom. On the other hand, the FeS monolayer is known for its stabilized nonmagnetic square crystal structure with a space group of P4/nmm (No. 129). The FeS unit cell consists of a total of four atoms, including two Fe atoms and two S atoms. It is noteworthy that the FeS monolayer with a square lattice has a massive, naturally analogous, layered FeS mackinawite crystal,38 in which the layers of FeS lie within a weak van der Waals interaction along the z-direction.39 Fig. 1(a) shows a visual representation of both the top and side views of the h-SrS and s-FeS structures. The optimized lattice constants a (=b) (Å) and the bond lengths (Å) between cations (Sr and Fe) and anion (S) host elements (dSr–S/dFe–S) are listed in Table 1. The optimized lattice constant for the h-SrS system is 4.837 Å, with a dSr–S bond length of 2.793 Å. In contrast, the optimized lattice constant and bond length for the s-FeS system are 3.557 Å and dFe–S = 2.150 Å, respectively. These values are significantly underestimated compared to those of the pure monolayer h-SrS, which is mainly due to the smaller ionic radii of the Fe atom (0.55 Å) compared to that of the Sr atom (1.26 Å). These results are consistent with previous theoretical studies.13,14,40,41
m2 (No. 187, belongs to the point group D3h) due to the loss of inversion symmetry. The ion positions and cell volume are then completely relaxed to ensure the stability of the resulting structure. The unit cell of the SrS monolayer consists of one Sr atom and one S atom. On the other hand, the FeS monolayer is known for its stabilized nonmagnetic square crystal structure with a space group of P4/nmm (No. 129). The FeS unit cell consists of a total of four atoms, including two Fe atoms and two S atoms. It is noteworthy that the FeS monolayer with a square lattice has a massive, naturally analogous, layered FeS mackinawite crystal,38 in which the layers of FeS lie within a weak van der Waals interaction along the z-direction.39 Fig. 1(a) shows a visual representation of both the top and side views of the h-SrS and s-FeS structures. The optimized lattice constants a (=b) (Å) and the bond lengths (Å) between cations (Sr and Fe) and anion (S) host elements (dSr–S/dFe–S) are listed in Table 1. The optimized lattice constant for the h-SrS system is 4.837 Å, with a dSr–S bond length of 2.793 Å. In contrast, the optimized lattice constant and bond length for the s-FeS system are 3.557 Å and dFe–S = 2.150 Å, respectively. These values are significantly underestimated compared to those of the pure monolayer h-SrS, which is mainly due to the smaller ionic radii of the Fe atom (0.55 Å) compared to that of the Sr atom (1.26 Å). These results are consistent with previous theoretical studies.13,14,40,41
| Ratio (x) | a = b (Å) | d (Å) | Ef (eV) | Ecoh (eV) |
|---|---|---|---|---|
| h-SrS | 4.837 | dSr–S = 2.793 | −1.402 | 3.952 |
| 4.76 (ref. 13) | dSr–S = 2.75 (ref. 13) | −8.55 (ref. 13) | 4.85 (ref. 14) | |
| dSr–S = 2.80 (ref. 14) | — | — | ||
| 0.125 | 4.756 | dFe–S = 2.254 | −1.176 | 3.947 |
| 0.166 | 4.601 | dFe–S = 2.314 | −1.157 | 3.893 |
| 0.250 | 4.581 | dFe–S = 2.283 | −1.049 | 3.927 |
| 0.333 | 4.342 | dFe–S = 2.210 | −0.937 | 4.077 |
| 0.375 | 4.304 | dFe–S = 2.220 | −0.930 | 4.150 |
| 0.500 | 4.168 | dFe–S = 2.217 | −0.454 | 3.889 |
| 0.750 | 4.085 | dFe–S = 2.232 | −0.021 | 3.899 |
| s-FeS | 3.557 | dFe–S = 2.150 | −0.427 | 4.748 |
| 3.52 (ref. 40) | dFe–S = 2.18 (ref. 40) | — | — | |
| 3.59 (ref. 41) | — | — | — |
The transition from the 3D bulk to the 2D monolayer is expected to result in noticeable structural relaxation since there are no van der Waals interactions between the layers in the monolayer configuration. Upon complete relaxation, the h-SrS monolayer adopts a planar structure, with the in-plane lattice parameter about 20.7% smaller than that of the bulk phases (6.059 Å).28 This discrepancy can be attributed to the change in the structural arrangement and packing of the atoms. To probe systematically the relative stability of the pure monolayers h-SrS and s-FeS, we calculated the formation (Ef) and cohesive (Ecoh) energies. The formation energy (Ef) is determined via the following formula:
| Ef = (ET − nμESr − mμES)/(n + m) | (1) |
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) 3m space group; Sr adopts a magnesium structure and crystallizes in the hexagonal P63/mmc space group; and S adopts an alpha structure and crystallizes in the orthorhombic Fddd space group. The number of specific atoms in the unit cell is represented as n and m letters.
3m space group; Sr adopts a magnesium structure and crystallizes in the hexagonal P63/mmc space group; and S adopts an alpha structure and crystallizes in the orthorhombic Fddd space group. The number of specific atoms in the unit cell is represented as n and m letters.
The cohesive energy (Ecoh) is estimated by:
| Ecoh = (ET − nESr − mES)/(n + m) | (2) |
A more stable monolayer is indicated by a more negative formation energy. Table 1 shows the calculated formation energies of bare h-SrS and s-FeS, in which both are negative. This means that these compounds are exothermic and do not decompose easily once formed. In addition, the formation energy of h-SrS (−1.402 eV) was found to be lower than that of s-FeS (−0.427 eV), suggesting that the h-SrS environment is relatively more favorable for doping than s-FeS. Therefore, for efficient and effective doping, creating a Fe-based SrS environment is preferable and simpler and more stable than Sr-based FeS. A positive cohesive energy value indicates that the monolayers are energetically stable. The calculated Ecoh values for h-SrS (3.951 eV per atom) and s-FeS (4.748 eV per atom), as shown in Table 1, suggest that the formation of bare monolayers is energetically favorable and confirms the strong atomic bonding in these structures. The s-FeS has the largest Ecoh, which corresponds well to the lowest lattice constant value compared to the remaining h-SrS monolayer. The obtained values for Efor and Ecoh are slightly lower than the values reported in the literature.13 This underestimation can be attributed to the different calculation details used.
The dynamical stability of the h-SrS and s-FeS monolayers is verified using the Density Functional Perturbation Theory (DFPT) approach42 by calculating their phonon dispersion curves along the high symmetry lines in the first Brillouin zone, which are shown in the lower part of Fig. 1(b). It is evident that the phonon branches are free of any imaginary frequencies, suggesting that the structures are dynamically stable under ambient conditions. Based on the phonon diagrams, it is clear that the h-SrS monolayer has six phonon branches, consisting of three acoustic and three optical branches. On the other hand, the primitive cell of s-FeS, which consists of four atoms, gives rise to twelve phonon branches, including three acoustic and nine optical branches. The maximum frequency of these monolayers ranges up to 9 THz for h-SrS and 12 THz for s-FeS, which is in line with the findings from previous studies.14,40 Our observations have also revealed that the phonon spectra of both systems show non-degeneracy along the directions of the Brillouin zone. Additionally, we have noted an interesting phonon gap in the optical band, measuring approximately 3 THz and 2 THz for h-SrS and s-FeS, respectively. Notably, the phonon gap is most pronounced in h-SrS and smallest in s-FeS, which is mainly due to mass differences within their primitive cells. This phonon bandgap is capable of increasing thermal conductivity via specific phonon–phonon scattering processes, suggesting that s-FeS may have higher thermal conductivity than h-SrS. We should also noted that, we performed phonon calculations for optimized h-FeS monolayer. However, h-FeS monolayer has large imaginary frequencies in the phonon dispersion band structure.
To further evaluate the thermal stability of the materials, ab initio molecular dynamics (AIMD) simulations are performed. Fig. 1(c) shows the energy fluctuation of both monolayers at 300 K. Impressively, the AIMD simulations showed consistent energy values for the bare monolayers even after a simulation time of 3 ps. The small energy fluctuations observed are attributed to the ripple effect caused by temperature, which leads to minimal changes in energy levels. This observation highlights the commendable thermal stability of the materials at room temperature.
After determining the energetic, dynamic and thermal stability of the bare monolayers, we establish the final method to verify their stability, namely mechanical stability. We use the strain energy approach,43,44 which is a widely used method for analysing the mechanical properties of 2D materials. By varying the strain ratio in the range of −3% ≤ ∈ ≤ 3% with an incremental step size of 0.01, we obtained the corresponding energy (E) values. The obtained E vs. ∈ data are fitted to a quadratic polynomial equation, from which we are able to derive the in-plane stiffness using eqn (3):
| C = (1/A0)(∂2E/∂2∈) | (3) |
| C11 > 0, C11 > |C12| | (4) |
| C11 > 0, C66 > 0, C11 > |C12| | (5) |
The elastic constants are found to be C11 = 28.993 N m−1 and C12 = 23.801 N m−1 for h-SrS and C11 = 77.575 N m−1, C12 = 46.595 N m−1 and C66 = 60.542 N m−1 for s-FeS. Examining the single crystal elastic constants, it is clear that all values meet the stability criteria by being positive, meaning that both the h-SrS and s-FeS structures are mechanically stable. In particular, the elastic constant C11 quantifies the resistance of a material to linear compression along the x-direction.46 Our calculations show clearly high C11 values for the pristine monolayers, with s-FeS having the highest value of 77.575 N m−1, followed by h-SrS. This suggests that both systems exhibit significant resistance to uniaxial strain along the x-direction, with s-FeS exhibiting exceptional incompressibility in this orientation due to its remarkably large C11 value. However, it is important to note that experimental validation and further theoretical investigations are required to confirm these results.
To explore the different properties and feasibility of the new Fe-doped h-SrS 2D systems with the formula Sr1−xFexS, we have modeled different supercells of (2 × 4 × 1), (2 × 3 × 1), and (2 × 2 × 1) containing, respectively, 16 formula units for x = 0.125 and x = 0.375, 12 formula units for x = 0.166, 0.333, and 8 formula units for x = 0.250, 0.500, and 0.750 concentrations. To ensure the stability of the resulting alloys and to identify the most preferable positions for Fe, we tested different arrangements for each alloy type and evaluated the total energy per atom. The most energetically stable configuration for each compound is shown in Fig. 2. During geometric optimization, it was observed that all alloyed ground-state structures retained their original hexagonal structure, albeit with slight distortions in the shape of their unit cells. Despite these distortions, the compounds retain their unique molecular properties, suggesting that the structural changes do not have a significant impact on their overall behavior. This phenomenon highlights the remarkable resilience and adaptability of these compounds, which hold promising implications for their potential applications in various fields. Table 1 provides detailed information on the lattice constants, formation energy, cohesive energy, and bond lengths for the eight monolayers. Notably, the lattice parameters along the x-direction show a consistent decrease compared to the original h-SrS as the Fe concentration increases in h-SrS. This reduction can also be attributed to the inequality of ionic radii between Fe and Sr atoms. Furthermore, the 12.5%, 25%, 50%, and 75% Fe based-SrS show the same trend as their bulk counterparts,29 with a significant decrease in values from the bulk structure to the monolayer structure. This is also explained by the interatomic interactions resulting from the dimensional reduction and packing of the atoms. Regarding the bond lengths, the average distance between Fe and the nearest S atoms (dFe–S) in the doped monolayers is 2.210 to 2.314 Å depending on the specific doping concentration. Compared to the pristine h-SrS, the length of the metal–sulfur bond decreased and there is a slight shrinkage in the doped compounds. The different ionic radius contributes to the shortened metal–sulfur bond length. However, it is noteworthy that dFe–S exhibits minimal fluctuations with changes in doping concentration, indicating the structural stability of the monolayers. To assess the relative stability of Fe-doped SrS monolayer systems, we performed additional calculations to determine their Ef and Ecoh using the formulas described in eqn (1) and (2), respectively, as for the pristine compounds. From Table 1 we find that the Ef are negative, which reveal that Fe atoms can be successfully doped into the monolayer h-SrS within an exothermic process and these compounds do not decompose easily once they are formed. Furthermore, we observe a successive increase in Ef as the Fe-doping percentage increases from 12.5% to 75% Fe. This trend indicates that the h-SrS with 12.5% Fe doping exhibits the highest thermodynamic stability among the studied cases, suggesting that is the most favorable in terms of energy considerations. Comparing the Ef of 12.5%, 25%, 50% and 75% Fe-based SrS monolayers with their bulk counterparts,29 it is clear that the Ef in 2D configurations are higher than those in 3D configurations and therefore less stable. This suggests that atoms in a bulk structure build more connections and form a higher number of bonds, ultimately leading to increased binding energy and consequently lower formation energy. Also in terms of comparison, the stability demonstrated by co-doping SrS: Fe with alkali metals47 exceeds the stability achieved by reducing its dimensionality. This highlights the pronounced effectiveness of the co-doped method in improving stability in our particular case. The Ecoh of the Fe-doped SrS monolayers are all positive, indicating that their structures are energetically stable. Notably, 37.5% Fe exhibits the highest Ecoh among the different doping concentrations, further supporting its energetically favorable nature.
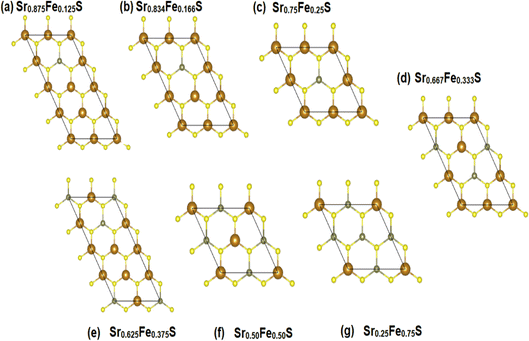 | ||
| Fig. 2 (a–g) The ground-state configurations of the predicted energetically stable Sr1−xFexS alloys. | ||
3.2 Electro-magnetic properties and Bader charge analysis
Investigating the interplay between electronic structure and magnetic properties represents a fundamental task in materials science, especially in the development of functional materials endowed with tailored magnetic properties. The use of an orbital-resolved methodology proves to be an indispensable tool for elucidating the complex role played by d-orbitals derived from substituted atoms in controlling magnetic behavior. Here we explain the apparent contributions of d-Fe orbitals to the band structure (BS), density of states (DOS), and charge redistribution (Δq) within the h-SrS monolayer resulting from their integration. In Fig. 3, we present the band structures of both pristines and the Sr1−xFexS ternary monolayers generated using the HSE06 method.34 Furthermore, we tabulated the calculated bandgaps (Eg) of these compounds in Table 2 and compared them with those obtained using the PBE method.33 It is important to note that the PBE method used in our computational analysis tends to underestimate the bandgaps of the studied compounds. This inherent limitation may affect the precision of our results, particularly in describing the electronic and optical properties of the materials. To mitigate this inherent challenge, the HSE06 has emerged as a promising alternative. Deviating from PBE, the HSE06 functional includes a fraction of the exact exchange, improving the treatment of electronic exchange and correlation effects. As a result, HSE06 has received widespread recognition for its ability to provide more reliable and accurate estimates of bandgap values. The analysis revealed that the pure h-SrS monolayer system has the characteristic features of a non-magnetic semiconductor with indirect bandgap of 2.825 eV for the PBE method and 3.861 eV for HSE06, as documented in Table 1, in alignment with previous research.13,14 Notably, the conduction band minimum (CBM) is located at the center of the Brillouin zone (BZ) point; while the valence band maximum (VBM) is at the M point, highlighting the anisotropic nature of the electronic structure. When moving from a two-dimensional (2D) configuration to a three-dimensional (3D), it is clear that the bandgap remains indirect, but shifts along the [Γ–X] direction with the value decreases from 3.861 eV calculated with the HSE06 functional to 3.435 eV when mBJ functional is used.29 This trend is consistent with the opposite behavior observed in the lattice parameters when transitioning from 2D to 3D. The increase in the bulk-to-monolayer gap value is usually attributed to the quantum confinement effect, which becomes more pronounced with increasing dimensionality reduction.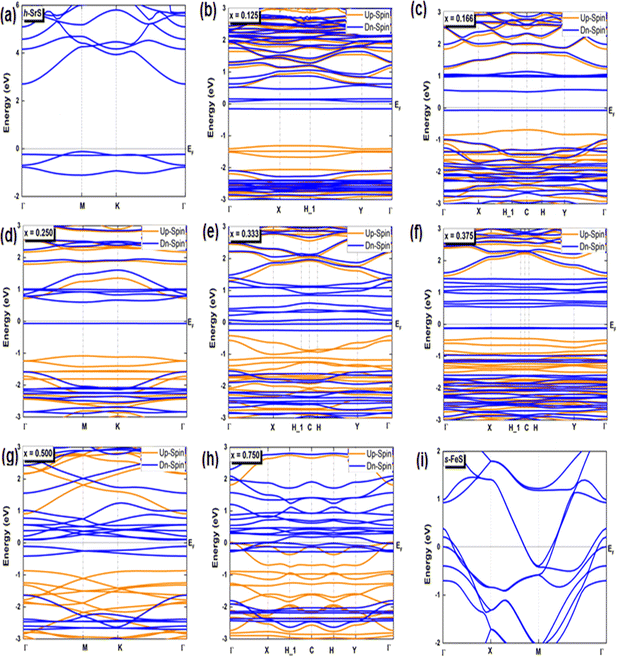 | ||
| Fig. 3 (a–i) Spin-polarized electronic band structures of the bare h-SrS, s-FeS and Sr1−xFexS doped monolayers for the HSE06 method. The Fermi level is set to zero. | ||
| Ratio (x) | Up-spin channel Eg (eV) | Dn-spin channel Eg (eV) | Δq (e) | |||
|---|---|---|---|---|---|---|
| h-SrS | PBE | [M–Γ] | 2.825 | — | 1.236 | |
| [M–Γ]13 | 2.77 (ref. 13) | — | — | |||
| [M–Γ]14 | 2.54 (ref. 14) | — | — | |||
| HSE | [M–Γ] | 3.860 | — | — | ||
| [M–Γ]14 | 3.74 (ref. 14) | — | — | |||
| 0.125 | PBE | [X–Γ] | 1.822 | [H–Γ] | 0.229 | 0.399 |
| HSE | [X–Γ] | 3.154 | [H–Γ] | 2.451 | — | |
| 0.166 | PBE | [C–Γ] | 1.912 | [Γ–Γ] | 0.580 | 0.512 |
| HSE | [C–Γ] | 3.079 | [Γ–Γ] | 3.097 | — | |
| 0.250 | PBE | [M–Γ] | 1.803 | [K–Γ] | 0.664 | 0.575 |
| HSE | [M–Γ] | 3.105 | [K–Γ] | 2.935 | — | |
| 0.333 | PBE | [Γ–Γ] | 1.731 | [C–X] | 0.085 | 0.050 |
| HSE | [Γ–Γ] | 3.003 | [C–X] | 2.709 | — | |
| 0.375 | PBE | [X–Γ] | 1.954 | [C–X] | 0.647 | 0.674 |
| HSE | [X–Γ] | 3.133 | [C–X] | 3.171 | — | |
| 0.500 | PBE | [Γ–Γ] | 1.780 | [Γ–K] | 0.198 | 0.609 |
| HSE | [Γ–Γ] | 3.049 | [Γ–K] | 2.564 | — | |
| 0.750 | PBE | Metal | Metal | 0.268 | ||
| HSE | [Γ–Γ] | 3.225 | [Γ–Γ] | 2.297 | — | |
| s-FeS | PBE | Metal | — | 0.771 | ||
| Metal40 | — | — | ||||
| HSE | Metal | — | — | |||
Interestingly, the BS of the s-FeS monolayer reveals metallic behavior where the EF intersects both the VB and CB regions, which is consistent with both the PBE and HSE06 leading to a non-magnetic metallic state. These results agree with and support the results of a previous study,40 thereby demonstrating the reliability and accuracy of the determined electronic properties. The introduction of Fe atoms through doping into the pure h-SrS monolayer leads to significant changes in its band structure (BS). This doping process introduces additional impurity levels within the native bandgap, thereby triggering a remarkable transformation of the electronic character to a spin-polarized half-semiconducting (HSC)/metallic nature. Importantly, this doping-induced change causes a noticeable downward shift in the conduction band minimum (CBM) position, which consequently results in a reduced spin-polarized bandgap for the system, as visually represented in Fig. 3. The bandgap of the pure h-SrS monolayer undergoes a significant reduction upon doping with Fe atoms, as shown in Table 2. According to the PBE method, the bandgap decreases from 2.825 eV in the pure state to values ranging from 1.964 eV to 0.000 eV, depending on the spin direction and the doping concentration of the monolayers (see Table 2). Similarly, the HSE06 method predicts a reduction in the bandgap from 3.861 eV in its pure form to values ranging from 3.225 eV to 2.297 eV. It is noteworthy that the influence of doping on the BS, as observed with both the PBE and HSE06 methods, shows a nonlinear correlation with the doping concentration. A more comprehensive visualization can be found in Fig. 4, which illustrates the fluctuation of the total gap within concentration when using both methods. The significant reduction in the bandgap of h-SrS can be attributed to the complicated interplay between the doped Fe atoms and their surrounding counterparts, as further explained in the following section using DOS analysis. The PBE results indicate a predominant HSC property with an indirect bandgap for most compositions, including Sr0.875Fe0.125S, Sr0.834Fe0.166S, Sr0.667Fe0.333S, Sr0.625Fe0.375S and Sr0.500Fe0.500S. However, certain compositions show deviations from this trend, i.e. Sr0.25Fe0.75S behaves like a metal. When using the HSE06 method, the electronic structure shows increased sensitivity to Fe concentration. Notably, the Sr0.667Fe0.333S and Sr0.25Fe0.75S transition into HSCs with total indirect/direct bandgaps of 2.593 and 2.263 eV, respectively. In contrast, the electronic properties of the other alloys remain largely unaffected and retain their semiconducting behavior without changes in the bandgap direction.
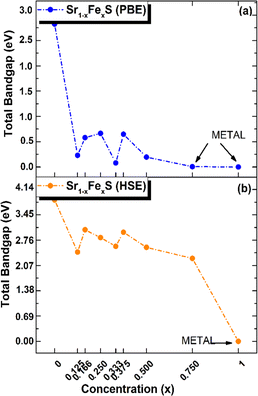 | ||
| Fig. 4 Total electronic bandgaps in all ordered alloy Sr1−xFexS monolayers, with both (a) PBE and (b) HSE values presented as a function of concentration x. | ||
Both the PBE and HSE methods show an almost uniform pattern in the variation of the bandgap values. In particular, the overall bandgap shows a decreasing trend from 0% to 12.5% Fe concentration, followed by an increasing trend for the following three concentrations (12.5%, 16.6%, and 25% Fe). This is followed by a decrease in the 33.3% Fe concentration, followed by an increase in the 37.5% Fe concentration and a subsequent decrease in the remaining concentrations (37.5%, 50%, 75% and 100% Fe), as presented in Table 2. Interestingly, the trend for the HSE method follows a similar pattern, except for the 25% Fe concentration where a decrease is observed, which is in contrast to the trend observed for the PBE method. When comparing the BS results of the doped monolayers, including the Sr0.875Fe0.125S, Sr0.750Fe0.250S, Sr0.500Fe0.500S and Sr0.250Fe0.750S with their bulk counterparts, as documented in a previous study,28 dimensionality reduction is found to induce a transition from half-metallic magnetic (HMM) to half-semiconductor magnetic (HSCM) behavior by introducing a gap in the spin-down channel. Furthermore, the doped monolayers exhibit a particularly flat valence band, a characteristic feature of their 2D configurations, confirming p-type semiconductor behavior. This flattened valence band represents an important and advantageous property to consider in the context of thermoelectric applications. Also in the same context of comparison, our determined bandgap values for doped-SrS monolayers are of the same order of magnitude with those reported for Cr-doped SrS (Eg = 2.95 eV obtained with the GGA method and Eg = 1.93 eV obtained with the mBJ method).28 This agreement underlines the robustness and validity of our bandgap assessments when studying doped SrS monolayers and further increases the credibility of our results in the broader context of materials research.
Bader charge analysis was performed to study the valence states of the TM atom and electron redistribution within the doped h-SrS monolayers. The results obtained are given in Table 2. It can be seen that the charge transfer from the Fe atom to the h-SrS lattice results in positive charges, indicating a robust interaction between the Fe and h-SrS. A net Bader charge transfer of 1.236e is observed in the pure h-SrS monolayer, which is due to electron redistribution between the cation and anion atoms due to their different electronegativities (0.95 for Sr and 2.58 for S). In contrast, in the pristine s-FeS monolayer, the electronegativity of Fe is increased to 1.83 compared to Sr, leading to a decrease in charge transfer to 0.771e. For doped monolayers, the magnitude of the charge transfer from Fe to S is between 0.268e and 0.674e depending on the doping concentration. The observed decrease in charge transfer from pure to doped monolayers is attributed to changes in electronegativity. Notably, the non-monotonic pattern observed in the charge transfer values within the doped monolayers is consistent with the corresponding bandgap fluctuations calculated using the PBE method. This trend may be due to changes in electronic structure or bonding interactions caused by the presence of dopant atoms.
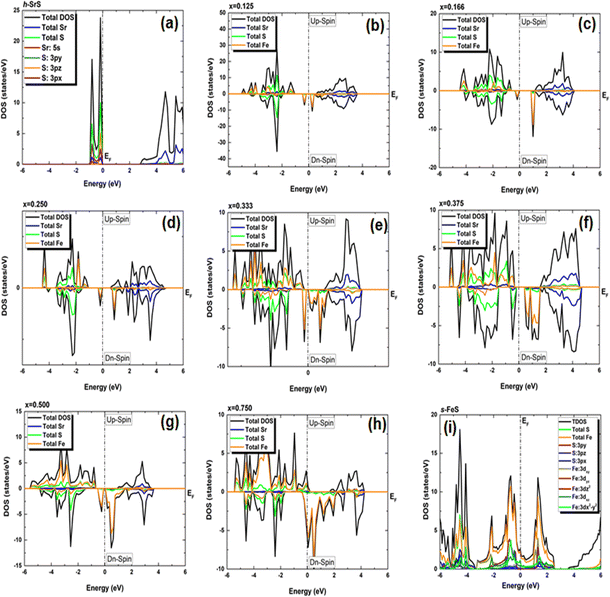
In our pursuit of a thorough understanding of the intricate interactions between the doped atoms and their surrounding counterparts, as well as the possible changes in the VBM and CBM within the Sr1−xFexS monolayers, we began a careful study of their total (TDOS) and partial (PDOS) densities of states. The insightful results of this analysis are clearly shown in Fig. 5 and 6, respectively. Studying the TDOS of the pristine h-SrS monolayer provides compelling evidence for its semiconducting behavior. This claim is supported by the striking absence of energy states at the EF, indicating a clear bandgap between the CB and the VB. Furthermore, careful analysis reveals two distinct peaks positioned exactly at the VB edge at energies of −0.164 eV and −0.815 eV, respectively, representing the highest occupied energy levels within the material. A deeper investigation using PDOS explains the underlying origins of these peaks.
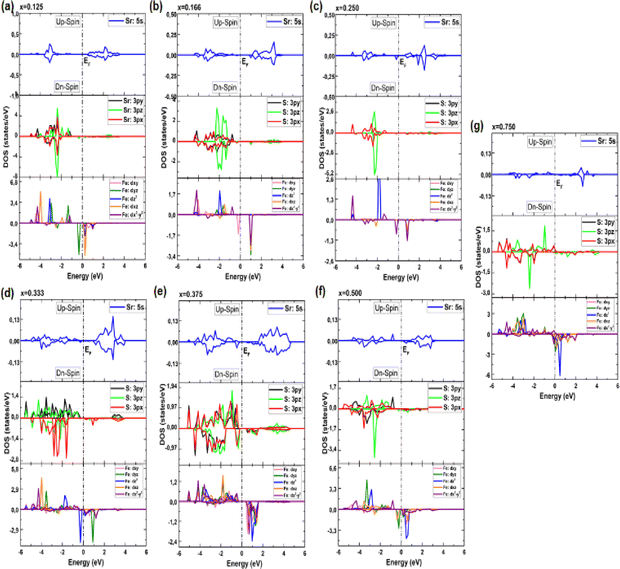 | ||
| Fig. 6 (a–g) Electronic partial density of states (PDOS) of Sr1−xFexS monolayer alloys in terms of concentration. | ||
In particular, the prominent peak in the VB, characterized by the highest DOS, comes predominantly from the 3pz orbitals of the S atom, complemented by a minor contribution from the S: 3px orbitals. Subsequently, the following peak is predominantly determined by the S: 3px orbitals, with a slight contribution of the Sr: 5s orbitals. In contrast, the manifestation of the CB in the energy range of 2.825 to 6 eV is mainly attributed to the 5s orbitals of the Sr atoms, accompanied by a minor contribution from the S: 3pz orbitals. These insightful observations are consistent with a previous study.14 The TDOS of the pure s-FeS monolayer has a distinct characteristic compared to that of h-SrS and shows a prominent peak extending toward the CB edge, indicating a metallic nature. Further investigation of the PDOS of s-FeS reveals insightful details about its electronic structure. In the energy range from −6 eV to 4 eV, the VB is predominantly influenced by the S: p orbitals and the Fe: d orbitals, with the highest contribution coming from S: 3pz and Fe: 3dx2−y2 states. As the energy range narrows to −3.5 eV to 2.5 eV, the influence of S: p states decreases and Fe: d states become more prominent. In particular, the Fe: 3dxy orbitals dominate from −3.5 eV to −2 eV, followed by the Fe: 3dz2 and Fe: 3dx2−y2 orbitals, which dominate from −2 eV to 1 eV and reach the EF. This characteristic feature confirms the metallic property of the bare s-FeS monolayer. In the energy interval from 1 eV to 2.5 eV, both Fe: 3dxy and Fe: 3dz2 orbitals remain dominant, with a small contribution from the S: 3pz orbitals. These results are consistent with the results presented in ref. 41 The introduction of Fe dopants into the h-SrS lattice resolves a remarkable observation regarding the asymmetry between the spin-up and spin-down TDOS within the Sr1−xFexS monolayers. This observed asymmetry is consistent with the magnetic ground states of all systems, strengthening their inherent magnetic nature and confirming their magnetic properties. Furthermore, a remarkable feature is revealed where impurity states are found in close proximity to the VB, suggesting the onset of p-type doping in the presence of Fe atoms. The incorporation of Fe atoms into the h-SrS monolayers leads to the precipitation of spin-polarized bandgap formation, thereby inducing intriguing modifications of the electronic structure. In particular, in the majority-spin channel, hybridization between Fe: 3d states and S: 3p states across all HSC compounds facilitates both the preservation and reduction of the bandgap compared to that of the pristine h-SrS. At the same time, p–d hybridization in the minority-spin channel leads to a shift of the Fe: 3d and S: 3p states toward the EF, while the bandgap is preserved. These results agree with the results derived from the band structure analysis. It is noteworthy that for the 75% Fe compound, both the majority and minority spin channels exhibit a metallic property, which is due to the formation of precursor states at the EF. An interesting observation is the increasing importance and prevalence of p–d hybridization with increasing dopant concentration. It is clear that the degree of spin asymmetry in the Fe: 3d orbitals exceeds that of the original 3p and 5s orbitals of S, and Sr, respectively. This discovery is consistent with the assumption that the magnetic moments are predominantly located on the Fe atoms adjacent to Sr and S, as shown in Fig. 5. Furthermore, our PDOS analysis yielded remarkable insights. In particular, we observed a shift in dominance toward the 3pz orbitals of the S atoms in the VB, displacing the previous dominance of the S: 3px orbitals in all compounds. As for the Fe: 3d orbitals, the Fe: 3dx2−y2 states predominantly occupy the lowest part of the majority spin VB, which ranges from about −5 eV to −4 eV. In the energy interval from about −4 eV to −2 eV, the states Fe: dyz, Fe: 3dz2 and Fe: dxz, are predominant. The positions of the VBM and CBM are primarily determined by the Fe: 3d states, with variations observed at different concentration ratios. For example, the Fe: dyz, and Fe: dxz, orbitals dominate on the VBM and CBM, respectively, for alloy ratios of x = 0.125, 0.500 and 0.750, while the Fe: dxy, and Fe: 3dx2−y2 orbitals dominate for alloy ratio of x = 0.166. Conversely, at concentration ratios of x = 0.250 and 0.375, the Fe: 3dx2−y2 orbitals prove to be dominant on both the VBM and the CBM. It is noteworthy that for x = 0.333, the in-plane orbitals of Fe: 3dz2 orbitals dominate on both edges. Furthermore, the CB in the energy range from about 1 eV to 4 eV is mainly determined by the Sr: 5s states. It is important to mention that the absence of PDOS projected onto the s orbitals of the doped Fe atom as well as its nearest neighbor S atom and d orbitals of the Sr atom from the recorded data are attributed to their complete electron filling, thereby making them be limited to low energy ranges. The noticeable differences observed in these states across different concentrations may be the reason behind the nonlinear fluctuations in the bandgap values. Referring to relevant literature,28 our investigation reveals notable differences in the behavior of the four concentrations, namely x = 0.125, 0.250, 0.500 and 0.750, compared to their bulk counterparts, in which the phenomena of p–d hybridization and the emergence of 3d states in the minority-states at the EF led to a HMM character characterized by 100% spin-polarization.
To elucidate the underlying mechanisms behind the induced magnetism in the original h-SrS structure, we performed a comprehensive analysis of the total magnetic moment (Mtot) per supercell for each concentration x through Sr1−xFexS systems, in addition to the local magnetic moments of the constituent atoms Sr, S and Fe, denoted as MSr, MS or MFe. These results are summarized in Table 3.
| Ratio (x) | Mtot (μB) | MFe (μB) | MSr (μB) | MS (μB) |
|---|---|---|---|---|
| h-SrS | — | — | — | — |
| 0.125 | 4.000 | 3.303 | 0.006 | 0.048 |
| 0.166 | 4.000 | 3.360 | 0.004 | 0.092 |
| 0.250 | 4.000 | 3.306 | 0.015 | 0.065 |
| 0.333 | 4.000 | 3.122 | 0.019 | 0.026 |
| 0.375 | 4.000 | 3.175 | 0.011 | 0.103 |
| 0.500 | 4.000 | 3.264 | 0.045 | 0.088 |
| 0.750 | 3.898 | 3.299 | 0.041 | 0.170 |
| s-FeS | — | — | — | — |
The Mtot for the compositions with 12.5%, 16.6%, 25%, 33.3%, 37.5%, and 50% Fe have an integer value corresponding to 4 μB per Fe atom, highlighting their HSC magnetic nature. Notably, the total magnetic moment Mtot of the iron-rich compound (75% Fe) deviates slightly from the expected integer value and is 3.898 μB, a property, which is often observed in metallic systems. The integer value observed for Mtot in the HSC compounds appears to be related to the number and position of Fe atoms in the cells considered. We can conclude that if the single Fe atom is surrounded by S atoms as the next nearest neighbor and then surrounded by Sr atoms as the second nearest neighbor, as in compositions with 12.5%, 16.6%, and 25%, alloy cell has an integer total magnetic moment. In the second case, when two Fe atoms in the cell form a pair, as is the case with compositions of 33.3%, 37.5% and 50%, the alloy cell has an integer total magnetic moment. However, when there are five Fe atoms in the cell, such as at a composition of 75%, the alloyed cell does not have an integer total magnetic moment due to the decoupled Fe atom.
When comparing the Mtot with the local magnetic moments per atom (see Table 3), it is clear that the main contribution to the Mtot comes from the Fe atom, a finding that is consistent with the results explained in the PDOS analysis (see Fig. 5). Smaller magnetic moments are attributed to the nearest neighboring atoms, which, due to their positive sign, exhibit magnetic coupling with their neighboring Fe atoms, which is due to the p–d hybridization mechanism.
Furthermore, an interesting observation revealed a nonlinear variation of Fe magnetic moment with increasing doping concentration, indicating a complex interplay between the Fe dopants and the surrounding lattice. It is noteworthy that this trend is in contrast to that observed in bulk structures for the previously studied concentrations, with MFe showing a decrease with increasing concentration. This disparity may also be due to differences in atom arrangement and interaction within the 2D monolayer structure, where there are fewer neighbouring atoms compared to bulk structures. However, the Mtot of the monolayers closely matches that of their bulk counterparts, as reported in ref. 28.
3.3 Optical properties
The Sr1−xFexS monolayer alloys offer immense potential and suitability for a wide range of optoelectronic and photonic device applications. Specifically, they hold great promise as absorber materials in solar cells, as their bandgap values fall within the visible to near-infrared spectrum. This advantageous characteristic enables efficient absorption of photons for enhanced photovoltaic performance. Therefore, it becomes imperative to investigate the response of electrons in crystalline Sr1−xFexS monolayers upon photon absorption. To gain comprehensive insights into this phenomenon, an in-depth analysis of the real part ε1(ω) and imaginary part ε2(ω) of the complex dielectric function, absorption coefficient α(ω), and reflectance R(ω) is conducted for all monolayer structures. Given that the s-FeS bare monolayer and iron-rich compound (75% Fe) structures are metallic, the calculation of their optical properties is not the focus of our study. Therefore, we have included only an analysis of the optical properties of the HSC compounds. In our study, we use the complex dielectric constant ε(ω) to characterize the macroscopic linear response of semiconductor systems to electromagnetic radiation. This dielectric constant is defined as ε(ω) = ε1(ω) + iε2(ω), where ε1 and ε2 are the real and imaginary parts of the complex dielectric function, respectively. The ε2(ω) results from the expression derived from the momentum matrix elements between the occupied and unoccupied wave functions in the long wavelength with q → 0 as follows:48
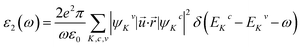 | (6) |
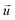 and
and 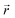 indicate the polarization and position vectors of electromagnetic field, respectively. The ε1(ω) can be derived from the ε2(ω) using a Kramers–Kronig transformation:48
indicate the polarization and position vectors of electromagnetic field, respectively. The ε1(ω) can be derived from the ε2(ω) using a Kramers–Kronig transformation:48
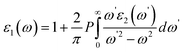 | (7) |
The Vasp code gives us the ε1(ω) and ε2(ω) after a self-consistent field ground-state calculation for the structure; one can then calculate the physical properties such as the absorption coefficient α(ω) and the reflectivity R(ω) via:48
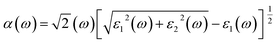 | (8) |
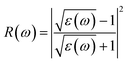 | (9) |
These parameters provide valuable insights into the interaction between photons and electrons within the materials.
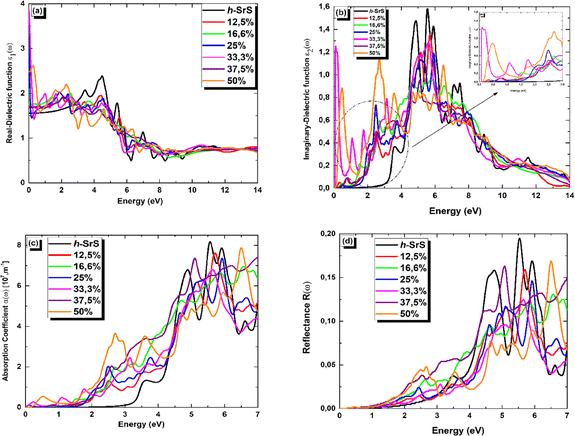
In Fig. 7 (a–d), we present the obtained optical parameters for the Sr1−xFexS structures, which were obtained using the PBE approach, covering the photon energy assortment of 0 to 14 eV. Due to the inequivalent lattice constants of the unit cells in Sr1−xFexS monolayers, which exhibit a hexagonal structure, the polarization vector is not parallel to the applied electric field. This leads to the optical parameters having two distinct values (xx and zz) for the same photon energy, indicating anisotropy. Notably, the optical parameters along the xx direction are larger in the desired visible range compared to those along the zz direction for both pure and Fe-doped h-SrS. Considering these characteristics, we have specifically plotted h-SrS based materials solely along the xx direction to maximize their efficiency in utilizing solar energy.
Fig. 7(a) shows the real part of the complex dielectric function ε1(ω). Within the complex dielectric function, ε1(ω) characterizes the extent of polarization in the 2D lattice resulting from the induced electric dipole moment caused by an external electric field. The influence of Fe doping on the main peak value of ε1(ω) is clearly visible in Fig. 7(a). In the low energy range below 2.5 eV, Fe doping significantly increases the real part of the dielectric constant. Specifically, the calculated static dielectric constants ε1(0), which correspond to the values of ε1(ω) at the energy limit towards zero, are as follows: 1.702, 1.751, 3.517, 3.855, 1.667 and 2.481 for Fe-doped h-SrS monolayers at doping concentrations of x = 0.125, 0.166, 0.250, 0.333, 0.375, and 0.500, respectively. These values confirm the semiconducting nature of the monolayers and are all higher than those of the pure structure (1.553 eV). Furthermore, it can be observed that the ε1(0) values of the doped h-SrS systems exhibit a nonmonotonic variation with increasing doping concentration. Among the six-doped systems, the 33.3% Fe-doped h-SrS system has the highest ε1(0) value, indicating its greater polarizability compared to the other alloys. Furthermore, the figure also shows that a clear difference between the profiles of the Fe-doped systems can be observed at low energies. In the case of x = 0.125, 0.166 and 0.375, ε1(ω) follows the same trend of pure h-SrS, which increases with increasing photon energy. While for x = 0.250, 0.333 and 0.500, ε1(ω) first decreases and then increases with energy, indicating a sharp peak. The trend of x = 0.125 in 2D is different from that of its 3D counterpart, which shows a negative response in the specific region attributed to the HMM character.28 As the photon energy increases in the range of 2.5–7 eV, which covers the near-visible to UV range, the ε1(ω) values of the doped systems first increase, reach their maximum and then decrease, alongside the pure h-SrS system. In this region, the pure h-SrS shows almost the highest response compared to the doped monolayers, which agree well with its bulk counterparts.28 Beyond this range, the ε1(ω) values stabilize with increasing photon energy for all monolayers, meaning that the doped systems have minimal interaction with high-energy incident photons. From these observations, we can deduce that the influence of Fe doping in the monolayers is pronounced in the infrared to visible range.
The imaginary part ε2(ω) of the complex dielectric constant characterizes the ability of the material to absorb photon energy. Fig. 7(b) clearly shows the influence of the doping concentration on the ε2(ω) and reflects the behavior observed in the real part. The doping induces a significant shift of the first peak of ε2(ω) towards lower energy ranges, and the change in the absorption edge energy of ε2(ω) follows the same trend as the bandgap. Notably, the doped systems exhibit a significant red shift of the absorption edge compared to the pure h-SrS monolayer, indicating the introduction of impurity levels within the intrinsic bandgap as a result of doping with Fe atoms. This observation is consistent with similar phenomena observed in bulk SrS:Fe structures doped with alkali metals.48 Notably, small sharp peaks appear in ε2(ω) at energy values of 0.229, 0.580, 0.664, 0.085, 0.647, and 0.198 eV for the doped monolayers at x = 0.125, 0.166, 0.250, 0.333, 0.375, and 0.500, respectively. These peaks can be attributed to transitions in the optical bandgap from Fe: 3d states to S: 3p states, confirming the semiconductor nature of the monolayers. Furthermore, a sharp and intense peak is observed in the visible energy range at 2.705 eV for the 50% Fe-doped monolayer, which represents the highest intensity peak among all concentrations. This peak corresponds to higher transitions within the band structure. As the photon energy increases, the ε2(ω) increases steadily until it reaches its maximum values at around 6 eV for all monolayers, except for 50%, which reach their maximum in the visible region. These elevated values are in the UV region and are attributed also to interband transitions between Fe: 3d states and S: 3p states, highlighting the pronounced activity of the monolayers in this spectral region. Subsequently, the ε2(ω) values of all monolayers progressively decrease with increasing photon energy until they reach their respective minimum values. This decrease indicates minimal interaction between photons and the material surface.
The absorption coefficient α(ω) serves as a valuable optical parameter and quantifies the extent to which light of a given wavelength can penetrate a material before it is absorbed. Fig. 7(c) shows the simulated plot of the absorption coefficients. In this figure, the α(ω) edges are shown at 2.825, 0.229, 0.580, 0.664, 0.085, 0.647 and 0.198 eV for the respective concentrations, x = 0, 0.125, 0.166, 0.250, 0.333, 0.375 and 0.500. Remarkably, the doped systems exhibit a redshift phenomenon consistent with α(ω) behavior, suggesting their superior photovoltaic optical properties. Furthermore, the maximum absorption peaks are observed at 8.134, 7.602, 6.948, 7.338, 6.806, 7.398, and 7.848 (× 107 m−1) for the photon energies of 5.563, 5.726, 6.581, 5.930, 5.630, 7.000, and 6.500 eV in the bare and doped h-SrS monolayer systems. Notably, the absorption of the doped systems exceeds that of the pure h-SrS monolayer in the visible and infrared regions, indicating that the pure h-SrS monolayer has high transmittance in the low energy region. Conversely, the pure h-SrS monolayer exhibits a higher absorption in the energy range of 5 to 6 eV, indicating its suitability for near-ultraviolet photodetectors compared to the doped SrS monolayer systems. Looking at the enlarged areas in the diagram, it is clear that the doped h-SrS monolayer systems are more suitable for solar cell applications, with the system having the highest absorption intensity over the entire visible region at a doping concentration of 50%.
Fig. 7(d) shows the reflectance (R(ω)) for both the pristine and the six doped monolayers. As shown, the R(ω) values are negligible for the doped monolayers and almost zero for the pristine system in the infrared region. This observation, coupled with the low absorption in this region, suggests that these monolayers exhibit polarizationally-transparent properties along the x-direction. However, R(ω) increases in the visible to UV range and peaks in the UV at 19.4%, 15.7%, 13%, 14.5%, 12.4%, 16.2% and 16.7% for the respective concentrations of x = 0, 0.125, 0.166, 0.250, 0.333, 0.375 and 0.500, at energies of 5.522, 5.712, 6.544, 5.930, 5.672, 5.075 and 6.513 eV. The average reflectance value is less than 16%, suggesting that the monolayers absorb light relatively well rather than reflecting it. This property is highly desirable for solar energy applications.
4 Conclusion
Briefly, we have performed comprehensive spin-resolved calculations on the crystal structure, electro-magnetic properties and optical properties of ordered single-layer Sr1−xFexS alloys with values in the range of x = 0–1 using a DFT approach based on the plane wave pseudopotential. We determined through calculations of formation energies, cohesive energies, molecular dynamics simulations, and elastic stiffness constants that each of the bare materials studied, SrS (FeS), is energetically favorable and thermally and mechanically stable under ambient conditions. Calculations of phonon spectra show that both materials are lattice dynamically stable. The ground state results show that SrS stabilizes in a hexagonal structure similar to graphene, while FeS prefers a square structure, which is consistent with previous theoretical studies. By doping the Sr sites with Fe impurities, all seven monolayers retain their hexagonal structural stability as well as their thermodynamic and energetic stability. Comparing the formation energies, we find that the 12.5% Fe-doped h-SrS monolayer system has the lowest energy, suggesting that it has the most stable composition. Furthermore, the 37.5% Fe-doped SrS monolayer exhibits the highest cohesive energy, indicating its superior stability with respect to the crystal lattice structure. To obtain a more accurate band structure, we also use the PBE + HSE06 method. Both PBE and HSE06 calculations confirm that the bare monolayer system h-SrS is a non-magnetic semiconductor with an indirect bandgap, while the s-FeS system is a non-magnetic metal. In terms of composition, the PBE results suggest that all doped systems exhibit half-semiconductor character (HSC), while the 0.750 and 1 Fe doped systems exhibit metallic-magnetic and metallic non-magnetic properties, respectively. On the other hand, using the HSE approach shows a transition to HSC for doping level of 0.750, while others maintain the same behavior. Furthermore, we observed that the low dimensionality of Sr1−xFexS (x = 0.125, 0.25, 0.50 and 0.75) affects the behavior of their bandgap, which is in contrast stands by what was observed in their bulk counterparts.29 This property proves to be advantageous for their optoelectronic applications. Our magnetic studies show that the introduction of Fe into monolayer compounds induces a total magnetization of 4 μB. Furthermore, the study of crystal field splitting shows that p–d hybridization is responsible for the observed HSC behavior. Finally, the optical properties show that doping with Fe atoms leads to a red shift of the absorption edge, extending the optical absorption range of the base material to the visible and near-infrared range, making these monolayers useable as solar cells. These results highlight the effectiveness of Fe doping as a means to tailor the properties of SrS monolayers to specific application requirements.Data availability
The data of this study are available from the corresponding author upon reasonable request.Author contributions
Warda Elaggoune: conceptualization, formal analysis, investigation, visualization, validation, writing – original draft. Fatih Ersan: conceptualization, methodology, software, validation, writing – review & editing, supervision. Athmane Meddour: conceptualization, validation, writing – review & editing, supervision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The calculations in this work were performed at the National Center for High-Performance Computing of Turkey (UHEM) under Grant No. 5011222021, and at the Aydin Adnan Menderes University high-performance computing center under Project No. FEF-21021.References
- R. P. Feynman, Feynman and computation, 2018, vol. 63, p. 76 Search PubMed.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D.-e. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, science, 2004, 306, 666–669 CrossRef CAS PubMed.
- A. J. Mannix, B. Kiraly, M. C. Hersam and N. P. Guisinger, Nat. Rev. Chem, 2017, 1, 0014 CrossRef CAS.
- S. Z. Butler, S. M. Hollen, L. Cao, Y. Cui, J. A. Gupta, H. R. Guti’errez, T. F. Heinz, S. S. Hong, J. Huang and A. F. Ismach, ACS Nano, 2013, 7, 2898–2926 CrossRef CAS PubMed.
- J. R. Schaibley, H. Yu, G. Clark, P. Rivera, J. S. Ross, K. L. Seyler, W. Yao and X. Xu, Nat. Rev. Mater., 2016, 1, 1–15 Search PubMed.
- C. L. Kane and E. J. Mele, Phys. Rev. Lett., 2005, 95, 226801 CrossRef CAS PubMed.
- A. S. Mayorov, R. V. Gorbachev, S. V. Morozov, L. Britnell, R. Jalil, L. A. Ponomarenko, P. Blake, K. S. Novoselov, K. Watanabe and T. Taniguchi, Nano Lett., 2011, 11, 2396–2399 CrossRef CAS PubMed.
- Q. H. Wang, K. Kalantar-Zadeh, A. Kis, J. N. Coleman and M. S. Strano, Nat. Nanotechnol., 2012, 7, 699–712 CrossRef CAS PubMed.
- T. Mueller and E. Malic, npj 2D Mater. Appl., 2018, 2, 29 CrossRef.
- A. Castellanos-Gomez, Nat. Photonics, 2016, 10, 202–204 CrossRef CAS.
- B. Feng, Z. Ding, S. Meng, Y. Yao, X. He, P. Cheng, L. Chen and K. Wu, Nano Lett., 2012, 12, 3507–3511 CrossRef CAS PubMed.
- M. Davila, L. Xian, S. Cahangirov, A. Rubio and G. Le Lay, New J. Phys., 2014, 16, 095002 CrossRef CAS.
- H. Zheng, X.-B. Li, N.-K. Chen, S.-Y. Xie, W. Q. Tian, Y. Chen, H. Xia, S. Zhang and H.-B. Sun, Phys. Rev. B, 2015, 92, 115307 CrossRef.
- H.-F. Lin, W.-M. Lau and J. Zhao, Sci. Rep., 2017, 7(1), 45869 CrossRef CAS PubMed.
- M. Sedighi, B. A. Nia, A. H. Hamad and M. S. Othman, Comput. Condens. Matter, 2020, 22, e00445 CrossRef.
- Y. Zhao, F. T. Rabouw, T. v. Puffelen, C. A. v. Walree, D. R. Gamelin, C. de Mello Donega and A. Meijerink, J. Am. Chem. Soc., 2014, 136, 16533–16543 CrossRef CAS PubMed.
- A. Khare, S. Mishra, D. Kshatri and S. Tiwari, J. Electron. Mater., 2017, 46, 687–708 CrossRef CAS.
- S. Mishra, D. Kshatri, A. Khare, S. Tiwari and P. K. Dwivedi, Mater. Lett., 2016, 83, 191–196 CrossRef.
- M. Yazdanmehr, H. Sadeghi, M. K. Tehrani, S. J. Hashemifar and M. Mahdavi, Opt. Mater., 2018, 75, 304–313 CrossRef CAS.
- A. Bao, X. Li, X. Guo, H. Yao and M. Chen, Vacuum, 2022, 203, 111226 CrossRef CAS.
- X. Zhou, C. Liu, L. Song, H. Zhang, Z. Huang, C. He, B. Li, X. Lin, Z. Zhang and S. Shi, Sci. China: Phys., 2022, 65, 276811 CAS.
- H. Zhu, X. Gan, A. McCreary, R. Lv, Z. Lin and M. Terrones, Nano Today, 2020, 30, 100829 CrossRef.
- L. Loh, Z. Zhang, M. Bosman and G. Eda, Nano Res., 2021, 14, 1668–1681 CrossRef CAS.
- F. Rana, O. Koksal, M. Jung, G. Shvets, A. N. Vamivakas and C. Manolatou, Phys. Rev. Lett., 2021, 126, 127402 CrossRef CAS PubMed.
- D. Shen, B. Zhao, Z. Zhang, H. Zhang, X. Yang, Z. Huang, B. Li, R. Song, Y. Jin and R. Wu, ACS Nano, 2022, 16, 10623–10631 CrossRef CAS PubMed.
- J.-h. Luo, B. Li, J.-m. Zhang, M.-z. Zhong, Q.-l. Xia, Y.-z. Nie and G. h. Guo, J. Magn. Magn. Mater., 2019, 486, 165269 CrossRef CAS.
- A. Yari, A. Boochani and S. Rezaee, Chem. Phys., 2021, 551, 111355 CrossRef CAS.
- W. Elaggoune, A. Meddour, C. Bourouis, M. H. Gous and Z. Bordjiba, Solid State Commun., 2023, 361, 115060 CrossRef CAS.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 Search PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 Search PubMed.
- R. F. W. Bader, P. L. A. Popelier and T. A. Keith, Angew Chem. Int. Ed. Engl., 1994, 33, 620–631 CrossRef.
- H. Y. Jeong, J. H. Lee and K. F. Hayes, Geochem. Cosmochim. Acta, 2008, 72, 493–505 CrossRef CAS PubMed.
- S. Nose, J. Chem. Phys., 1984, 81, 511–519 CrossRef CAS.
- O. Kouvo, Y. Vuorelainen and J. V. P. Long, Am. Mineral., 1963, 48(5–6), 511–524 CAS.
- H. T. Evans Jr, C. Milton, E. Chao, I. Adler, C. Mead, B. Ingram and R. A. Berner, US Geological Survey Professional Paper, 1964, vol. 475, pp. 64–69 Search PubMed.
- F. Chen, C. Gao, H. Li, J. Hou and D. Jiang, Surf. Sci., 2021, 707, 21818 Search PubMed.
- E. V. Sukhanova, V. S. Baidyshev, A. M. Manakhov, A. S. Al-Qasim and Z. I. Popov, Appl. Surf. Sci., 2023, 609, 155322 CrossRef CAS.
- X. Gonze and C. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 10355 CrossRef CAS.
- M. Topsakal, S. Cahangirov and S. Ciraci, Appl. Phys. Lett., 2010, 96, 6 CrossRef.
- H. ahin, S. Cahangirov, M. Topsakal, E. Bekaroglu, E. Akturk, R. T. Senger and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 155453 CrossRef.
- M. Born and K. Huang, Dynamical theory ofcrystal lattices, Oxford University Press, Clarendon, 1954, p. 420 Search PubMed.
- X. Gao, Y. Jiang, R. Zhou and J. Feng, J. Alloys Compd., 2014, 587, 819–826 CrossRef CAS.
- W. Elaggoune, A. Meddour and C. Bourouis, Mater. Sci. Semicond. Process., 2023, 165, 107684 Search PubMed.
- L.-Y. Xie and J.-M. Zhang, J. Alloys Compd., 2017, 702, 138–145 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |