Open Access Article
Open Access ArticleOptimizing methylene blue adsorption conditions on hydrothermally synthesized NaX zeolite through a full two-level factorial design†
Hammoudi Hadda Aya a,
Nibou Djamela,
Amokrane Samiraa,
Marta Otero
a,
Nibou Djamela,
Amokrane Samiraa,
Marta Otero b and
Moonis Ali Khan
b and
Moonis Ali Khan *c
*c
aLaboratory of Materials Technology, University of Science and Technology Houari Boumediene, B. P. 32, El-Alia, Bab-Ezzouar, Algiers, Algeria
bDepartmento de Química y Física Aplicadas, Universidad de León, Campus de Vegazana s/n, 24071 León, Spain
cChemistry Department, College of Science, King Saud University, Riyadh 11451, Saudi Arabia. E-mail: mokhan@ksu.edu.sa
First published on 29th July 2024
Abstract
Besides being hazardous to humans and aquatic organisms, dyes present in water reservoirs limit sunlight's availability to aquatic plants and animals, making significant impact on their growth and development. Herein, the adsorptive removal of methylene blue (MB) dye from aqueous solution using type X (NaX) zeolite by full experimental design 2n was studied. The physical and chemical properties of NaX zeolite were identified using various characterization techniques such as X-ray diffraction (XRD), scanning electron microscopy with energy dispersive X-ray (SEM-EDS), Fourier transform infra-red (FT-IR), and Brunauer–Emmett–Teller (BET) surface area analyses. Results confirmed that NaX zeolite had a cubic shaped crystalline structure with 2–4 μm size and high (375 m2 g−1) specific surface area, having 90% optimal adsorption efficiency. Langmuir and Elovich isotherm models were best fitted to adsorption experimental data and a pseudo-second-order kinetic model describes well the adsorption kinetic data. Akaike information criteria (AIC) was used to assess the best fitted models on the experimental data. A thermodynamic study reveals that the MB adsorption onto NaX was exothermic, spontaneous, and feasible.
1. Introduction
Different industrial establishments generate specific types of waste. These wastes, when discharged into watercourses, have damaging repercussions on humans and environmental health.1,2 One example of such discharges manifests in the form of toxic dyes that contaminate aquatic environments.3 Water, being the fundamental element of life, constitutes an invaluable resource. However, in recent decades, demographic growth and industrial development have had a detrimental environmental impact,4 particularly through a massive discharge of dyes into water bodies.5 Among these dyes, methylene blue (MB), classified as carcinogenic and hazardous to humans, is of concern because of its uncontrolled discharge from many industries.6Researchers have used various treatment technologies, such as ion-exchange,7 chemical precipitation,8 membrane processes,9 filtration,10 photocatalysis,11 solvent extraction,12 and adsorption5 to remove pollutants from water.13,14 Among them, adsorption stands out for its simplicity, affordability, ease of handling, and recyclability.15 Therefore, several authors in their current research have focused on developing methods to protect aquatic environments using adsorbents with a high adsorption capacity.15–19 Among adsorbents, synthetic and natural zeolites, due to their ability to adsorb drugs, pesticides, pharmaceuticals, metal ions, and dyes have been widely explored.20–22 Andrunik et al.20 tested the potential of fly ash-based zeolites and zeolite-carbon composites to remove pesticides from water. Amokrane et al.21 revealed that zeolites X and Y have better nitrogen adsorption capacity, unlike zeolite A. Senila et al.22 reviewed and summarized previous research into the modification of zeolites to improve their adsorption capacity, showing that natural zeolites can reduce costs and pollution compared with synthetic adsorbents. Synthetic zeolites are produced from mixtures of silicon and aluminum in basic or acidic media at temperatures ranging from 100 to 200 °C and under autogenous reactions.23 They have undeniable advantages,24 including reasonable processing costs, great versatility, and unique properties, such as their specific surface area and porosity, which give them an excellent capacity for adsorbing different types of pollutants.25,26 Zouaoui et al.25 showed that high-pressure CO2 adsorption on NaX, LiX, KX, ZnX and MgX zeolites varies as a function of exchange ions and temperatures. They found that the Na+ exchange with Li+ improves adsorption capacity by increasing pore volume and specific surface area, while exchange with Zn2+, Mg2+ and K+ decreases these parameters.
Zeolites are known to have the following composition: [M]x/zn+[(SiO2)x(AlO2−)y]mH2O (M: compensating ions, n: valency, x and y: molar fractions and m: number of water molecules).27 They have a cubic framework supported by silica and alumina tetrahedral units resulting in a net negative charge that is compensated by alkali ions. This three-dimensional network consisting a channel/void system which offers large possibilities for dyes and heavy metal ions to diffuse and exchange onto zeolite surfaces.23 Among zeolites, NaX is known by a super cage (13 Å) and external pores (8 Å), which are capable to contain and adsorb many organic or inorganic elements.28 Lin et al.29 synthesized a first aluminosilicate zeolite (ZEO-1) with multidimensional pores (up to 10 × 10 Å) and an interconnected supercages. Furthermore, Li et al.30 studied ZEO-3 and found that it exhibited exceptional performance in the reduction and recovery of volatile organic compounds, outperforming that of other zeolites and MOFs. Gao et al.31 reported that aluminosilicate zeolites with extra-large pores, could process bulky molecules and a new silicate chain expansion strategy, creates three-dimensional zeolites and efficient catalysts for alkene oxidation.
Although, previous studies have examined the effectiveness of zeolites in the adsorption of various pollutants, including heavy metals and dyes,19,32 very few have looked at the use of NaX zeolite for MB adsorption.33,34 Moreover, to the best of authors' knowledge, the optimization of the experimental conditions for MB adsorption onto NaX zeolite by an experimental design has never been reported. In this context, the current work demonstrated the ability of NaX zeolite synthesized by a hydrothermal process to remove the basic dye MB from an aqueous solution. The zeolite sample was subjected to various characterizations including X-ray diffraction (XRD), scanning electron microscopy (SEM), energy dispersive spectroscopy (EDS), Fourier transform infrared spectroscopy (FTIR) and Brunauer–Emmett–Teller (BET) surface area analyses. In addition, the MB adsorption onto the zeolite was described through isotherm, kinetic, and thermodynamic parameters. To reduce the number of trials and associated costs, parametric optimization using a full factorial design 24 was performed. This rigorous and efficient methodological approach enabled us to determine the optimum conditions for MB adsorption onto NaX zeolite, highlighting the importance of full factorial designs for such a purpose.
2. Experimental
2.1. Chemical and reagents
All the chemicals used during the study were analytical reagent (AR) grade or as reported. Methylene blue (MB) was procured from Sigma-Aldrich, Hydrochloric acid (HCl, 37%) and sodium hydroxide (NaOH, >99%) were purchased form Fluka. Silica (100% purity) was purchased from Prolabo. Aluminum isopropoxide (98% purity) was procured from Merck. To prepare solutions and to wash glassware, deionized (DI) water was used.2.2. Synthesis procedure of NaX zeolite
The NaX zeolite with molar composition 4.8Na2O, 1Al2O3, 3.8 SiO2, 224H2O was synthesized using a previously reported protocol.35 Briefly, a solution of sodium hydroxide (2.1 g) in DI water (21.6 g) was added to fumed silica (4.18 g), and the mixture was mechanically stirred for 2 h. Thereafter, aluminum isopropoxide (2.2 g) was gradually added under continuous stirring for 2 h, and the obtained gel was kept for incubation over 24 h to promote crystallization and complete the reaction for zeolite formation. The hydrothermal reaction was carried out in Teflon-lined stainless-steel autoclave at 100 °C for 24 h. The powder product was recovered by filtration, washed with DI water and overnight dried at 100 °C. Finally, the sample was calcined by heating at 300 °C in an air atmosphere for 6 h to get the NaX zeolite.2.3. MB adsorption procedure
Batch adsorption experiments were conducted in 500 mL Erlenmeyer flasks by stirring 200 mL of MB solution with varied initial concentration (from 5 to 120 mg L−1) together with NaX zeolite (0.04 to 0.7 g). The pH was monitored using a Hanna pH meter and adjusted using HCl and NaOH solutions. Aliquots (1 mL) were collected at regular time intervals and the solid/solution phases were separated through centrifugation. The absorbance of the supernatant solution was measured at λmax (665 nm) by UV-visible spectrophotometer (Optizen 2120 UV).The MB uptake percentage (%), adsorbed mass at the equilibrium (qe) and adsorbed mass any time t (qt) on NaX zeolite were respectively evaluated as:
 | (1) |
 | (2) |
 | (3) |
2.4. Characterization of NaX zeolite
The XRD (Philips PW 1710 diffractometer) analysis was carried out to identify the NaX zeolite structure. The surface morphology and elemental content of synthesized NaX zeolite was analysed by SEM coupled with EDX (XL-20 equipment) analysis. The chemical functionalities present on NaX zeolite surface were studied through FTIR (Nicolet iS10 spectrometer) analysis, and the specific surface area and pore volume of NaX zeolite were calculated through BET analysis of N2 adsorption–desorption results (Micromeritics ASAP 2010).2.5. Optimization of adsorption experiments
A full two-level factorial design with 4 factors and therefore involving 16 experiments was employed to optimize the experimental conditions for MB adsorption onto NaX zeolite. The considered experimental factors were pH, solid/liquid ratio (S/L), initial concentration and temperature, while the MB adsorption percentage was the response variable. A mathematical model that accurately describes the experimental process and optimizes the operating parameters was developed using the method of least squares to fit the data.36 An analysis of variance (ANOVA) was also performed to determine the significance of the factors and their interactions. The experimental conditions are listed in Table S1.† An empirical regression equation with four parameters and their interactions as shown in the eqn (4) was derived.| Adsorption uptake (%) = b0 + b1x1 + b2x2 + b3x3 + b4x4 + b12x1x2 + b13x1x3 + b14x1x4 + b23x2x3 + b24x2x4 + b34x3x4 + b123x1x2x3 + b124x1x2x4 + b134x1x3x4 + b234x2x3x4 + b1234x1x2x3x4 | (4) |
3. Results and discussion
3.1. Characterization of NaX zeolite
The XRD patterns of the here synthesized NaX zeolite is illustrated in Fig. 1a. The patterns correspond to the faujasite NaX structure, with a strong peak in the 2θ ranges of 5–30°, indicating successful synthesis of the microporous NaX zeolite structure. The main phase observed was consistent with previous literature35 and all planes were compared with those in crystallographic databases28,38 and identified as NaX structure. As shown in Fig. 1a, all the peaks were Miller-indexed (hkl), showing the important (111) plane with high intensity and belonging to the structure of NaX zeolite.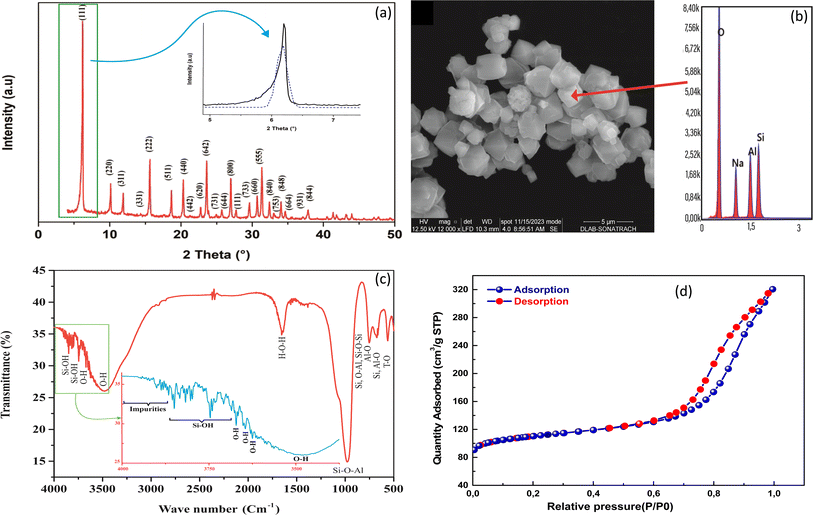 | ||
| Fig. 1 XRD pattern (a), SEM micrograph and EDX spectrum (b), FTIR spectrum (c) and N2 adsorption/desorption isotherms of NaX zeolite. | ||
Morphologically, NaX zeolite have cubic shaped crystals with an average dimension of about 2–4 μm, illustrated in Fig. 1b. The elemental composition of NaX zeolite showed that the main atoms Si and Al, together with the compensating Na, constitute the framework structure (Table S2†). The mass ratio of Si/Al was found to 1.198%, which corresponds to the synthesized NaX zeolite and was near to reported range (1.1–1.5).39 These results were in agreement with previous reports on NaX zeolites synthesized by other authors.35,40
FTIR spectrum of NaX zeolite highlights all absorption bands of different bonds attributed to its framework structure (Fig. 1c) in the frequency range from 4000 to 500 cm−1. Two important zones were defined in this spectrum, which revealed the functionalized groups (3880–3500 cm−1) and topological structure (1200–500 cm−1) as reported in the literature.27,41 The bands of the first zone of frequencies between 3880 and 3750 cm−1 were attributed to silanol (Si–OH) groups and to probable impurities. The bands at 3650 and 3500 cm−1 were assigned to the high and low frequencies of hydroxyl groups (O–H), respectively.41 The high frequency (HF) bands were found in the super cages of NaX zeolite (13 Å), in accordance to previous works of Breck27 and Nibou et al.41 that reported the localization of these HF bands and consequently facilitate the adsorption of MB molecules. In the second zone, the band at 989 cm−1 was due to the asymmetric elongation of Si–O–Al bond; the band at 755 cm−1 was associated with the symmetrical vibrations of Si–O–Al and Si–O–Si bonds; that at 679 cm−1 was assigned to the symmetrical vibration of Al–O bond; the absorption band at 565 cm−1 was characteristic to the double rings (DR) of NaX zeolite; and that at 510 cm−1 was assigned to the vibration deformation of the T–O (T; Si or Al) bond. Another absorption band was also observed at 1633 cm−1, corresponding to the vibration of the H–O–H bond of water molecules.
The specific surface area (SSA) and micropore volume of the synthesized NaX zeolite were determined by BET surface area analysis through N2 adsorption/desorption (Fig. 1d). The results revealed a high SSA of 375 m2 g−1 with respective microporous and external surfaces of about 255.3 and 119.7 m2 g−1. The obtained micropore volume of synthesized NaX was 0.120 cm3 g−1. The N2 adsorption/desorption curves (Fig. 1d) showed the presence of hysteresis,27 indicating a mesoporous volume of 0.20 cm3 g−1. The N2 maximum quantity adsorbed onto NaX using BET method was 0.320 cm3 g−1 (at P/P0 = 0.99). These results indicate that the textural properties of the synthesized NaX zeolite are favorable for the uptake of MB, with a large number of sites available for its adsorption.
3.2. Adsorption performance of NaX zeolite
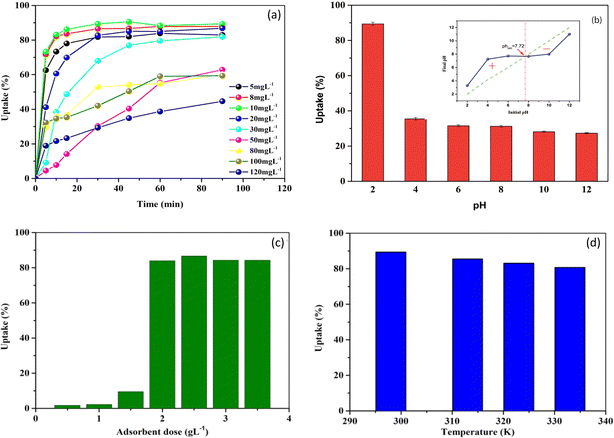 | ||
| Fig. 2 Effect of contact time at varied initial concentrations (a), pH (b), solid/liquid ratio (c), and temperature (d) on MB adsorption onto NaX zeolite. | ||
On the other hand, as it may be seen in Fig. 2a, the MB uptake percentage mostly decreased with the increase of the initial MB concentration from 5 to 120 mg L−1. Exceptionally, at the lowest concentrations (5–10 mg L−1), an increase of MB uptake percentage was observed with increasing initial concentration. This could be explained by the limited availability of MB molecules at very low initial concentrations, which may have limited their interaction with NaX sites. However, at concentrations higher than 20 mg L−1, a decrease in MB uptake with increasing initial concentration was observed in all cases.
Similar results on MB adsorption onto different adsorbents were observed by other authors. For example, Kuang et al.42 studied the adsorption of MB onto surfactant modified activated carbon and noticed that the uptake percentage decreased from 96.6 to 58.7% with an increase in the initial dye concentration from 10 to 50 mg L−1, while the adsorption capacity of the dye increased under the same conditions. Yagub et al.43 studied the adsorption of MB onto pine leaves with an equilibrium time of 240 min and found that, when the MB concentration was increased from 10 to 90 mg L−1, the dye removal percentage decreased from 96.5 to 40.9%.
The point of zero charge (pHpzc) corresponds to a neutral surface charge. Below the pHpzc, the surface becomes positively charged, attracting anions and repelling cations.5,40 During the current study, it was difficult to provide a definitive explication for the effect of pH on MB adsorption based solely on the pH values considered in relation to this pHpzc, which was determined to be 7.72 (Fig. 2b, inset). The increase in adsorption under acidic conditions may be due to the preference of dye cations for active sites and/or increased accessibility to interlayer regions of protonated (MB H2+) and monomeric species resulting from the removal of certain oxides from the NaX zeolite surface.
The MB adsorption capacity was highest at pH 2, where the surface charge of the particles was positively charged. This suggests that a negatively charged surface appears after the removal of certain species as [Al(OH)4]− and Al(OH)3 from NaX zeolite, leading to efficient adsorption of protonated and monomeric MB species. In contrast, to the decreasing tendency of oxide removal with increasing pH, alkali cations and other exchangeable metals on the surface and in the interlayer region of NaX zeolite undergo hydration creating a hydrophilic environment.49,50 This can also lead to a decrease in MB adsorption provided that the surface charge of the zeolite tends towards zero.
3.3. Adsorption modeling
| Parameters | Langmuir | Freundlich | Temkin | Elovich |
|---|---|---|---|---|
| Linear isotherm models | ||||
| qmL: 24.39 mg g−1 | KF: 3.01 mg g−1 | B: 571.16 J mol−1 | qmE: 9.10 mg g−1 | |
| KL: 0.12 L mg−1 | n: 1.97 | KT: 1.82 L mg−1 | KE: 0.43 L mg−1 | |
| Error functions | ||||
| R2 | 0.9949 | 0.9602 | 0.9870 | 0.9416 |
| Adj.R2 | 0.9881 | 0.9109 | 0.9706 | 0.8704 |
| SSE | 0.0897 | 0.5504 | 12.7122 | 56.0079 |
| χ2 | 0.0149 | 0.0786 | 1.8160 | 8.00113 |
| MSE | 0.0149 | 0.0786 | 1.8160 | 8.00113 |
| RMSE | 0.1223 | 0.2804 | 1.3476 | 2.8286 |
| AIC | −37.4795 | −21.1498 | 7.1080 | 20.4544 |
| AICc | −35.4795 | −19.1498 | 9.1081 | 22.4544 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Non-linear isotherm models | ||||
| Parameters | qm: 23.10 mg g−1 | KF: 3.89 mg g−1 | B: 571.19 J mol−1 | qmE: 5.45 mg g−1 |
| KL: 0.12 L mg−1 | n: 2.38 | KT: 1.83 L mg−1 | KE: 0.75 L mg−1 | |
| Error functions | ||||
| R2 | 0.9581 | 0.9716 | 0.9742 | 0.9776 |
| Adj.R2 | 0.9521 | 0.9676 | 0.9705 | 0.9745 |
| SSE | 20.6660 | 13.9783 | 12.7122 | 11.0190 |
| χ2 | 2.95233 | 1.9969 | 1.8160 | 1.5741 |
| MSE | 2.9523 | 1.9969 | 1.8160 | 1.5741 |
| RMSE | 1.7182 | 1.4131 | 1.3476 | 1.2546 |
| AIC | 11.4815 | 7.9625 | 7.1080 | 5.8215 |
| AICc | 13.4815 | 9.9625 | 9.1080 | 7.8215 |
As in may be seen in Table 1, the error functions, indicate that the Elovich isotherm model provided the best fittings to MB adsorption equilibrium data on NaX zeolite, followed by Temkin, Freundlich, and Langmuir isotherm models. A comparison between the error functions obtained by the linear and non-linear regression methods revealed a difference in errors for the non-linear method, apart from the Temkin isotherm model, where the error functions remain unchanged. This observation could be explained by a marked similarity between the linear and non-linear formulations of this model.
From Table 1, Langmuir and Elovich isotherm models appear the best suited to represent the experimental data with relatively high R2, Adj.R2 values and the lowest errors. Previous studies23,57 have pointed out that the application of linear regression often leads to values of qe that diverge considerably from the experimentally determined values. Comparing the experimental and predicted isotherms of MB adsorption on the two models it was clear that Langmuir was the best fitted model. The values of qmL were 24.39 and 23.10 mg g−1 for linear and non-linear isotherm models, respectively. These values were considerably near to the experimentally determined value (21.61 mg g−1). However, the values of qmE for linear and non-linear isotherm models were 9.10 and 5.45 mg g−1, respectively. There values were lower compared to Langmuir model. In addition, the lower values of (AIC) (−37.4795) and (AIC)c (−35.4795) (Table 1) affirmed the selection of the Langmuir isotherm model as the best fitted model. A non-dimensional (RL) known by Langmuir separation factor (RL) was calculated to approve the MB adsorption process onto NaX. The results in Table S5† revealed that the values of RL were <1, indicating that the adsorption process was effectively favorable.
3.4. Adsorption kinetic modelling
Pseudo-first-order (PFO) and pseudo-second-order (PSO) kinetic models57,58 for MB adsorption onto NaX zeolite were carried out by varying the initial MB concentrations from 5 to 120 mg L−1 and the temperature from 298 to 333 K. Fig. S2† presents the linearized experimental kinetic results for the adsorption of MB onto NaX zeolite. Tables 2 and 3 display the fitted parameters and the corresponding error functions, AIC, and AICc criteria. The best-fit kinetic model was selected based on higher R2, lower AIC and AICc criteria values and the error functions that produced minimum error distribution between the experimental and predicted values. The slopes and intercepts of plots of the linear representations (Fig. S2†) were obtained to determine the rate constants and equilibrium adsorption amount qe of kinetic models.| Initial concentration (C0, mg L−1) | qe,exp. (mg g−1) | qe, cal. (mg g−1) | K1 × 102 (1/min) | R2 | Adj.R2 | SSE | χ2 | MSE | RMSE | AIC | AICc | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 1.658 | 0.703 | 9.5 | 0.937 | 0.848 | 1.831 | 0.458 | 0.458 | 0.677 | −10.332 | −8.332 | ||
| 8 | 2.812 | 1.191 | 11.1 | 0.940 | 0.86 | 4.918 | 0.984 | 0.984 | 0.992 | −1.439 | 0.561 | ||
| 10 | 3.574 | 2.922 | 9.44 | 0.825 | 0.575 | 3.741 | 1.247 | 1.247 | 1.117 | −3.901 | −1.901 | ||
| 20 | 6.949 | 5.038 | 8.3 | 0.951 | 0.885 | 1.341 | 0.268 | 0.268 | 0.518 | −13.138 | −11.138 | ||
| 30 | 9.829 | 10.740 | 6.1 | 0.997 | 0.993 | 0.067 | 0.013 | 0.013 | 0.116 | −40.080 | −38.080 | ||
| 50 | 12.56 | 15.768 | 3.4 | 0.966 | 0.920 | 0.249 | 0.050 | 0.050 | 0.223 | −28.283 | −26.283 | ||
| 80 | 17.559 | 25.053 | 1.2 | 0.854 | 0.675 | 0.186 | 0.037 | 0.037 | 0.193 | −30.916 | −28.916 | ||
| 100 | 21.618 | 32.298 | 1.1 | 0.858 | 0.684 | 0.021 | 0.004 | 0.004 | 0.065 | −50.459 | −48.459 | ||
| 120 | 21.412 | 16.710 | 2.9 | 0.979 | 0.951 | 0.109 | 0.022 | 0.022 | 0.148 | −35.700 | −33.705 | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||||
| T (K) | |||||||||||||
| 298 | 3.574 | 2.54 | 6.2 | 0.825 | 0.575 | 3.74 | 1.247 | 1.247 | 1.117 | −3.901 | −1.901 | ||
| 313 | 3.420 | 0.42 | 5.4 | 0.912 | 0.798 | 3.029 | 0.606 | 0.606 | 0.778 | −5.800 | −3.800 | ||
| 323 | 3.323 | 2.02 | 7.6 | 0.926 | 0.829 | 2.677 | 0.535 | 0.535 | 0.732 | −6.913 | −4.913 | ||
| 333 | 3.227 | 0.12 | 5.4 | 0.824 | 0.614 | 6.371 | 1.274 | 1.274 | 1.129 | 0.890 | 2.890 | ||
| Initial concentration (C0, mg L−1) | qe,exp. (mg g−1) | qe, cal. (mg g−1) | K2 × 102 (g mg min−1) | R2 | Adj.R2 | SSE | χ2 | MSE | RMSE | AIC | AICc |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 1.658 | 1.678 | 663.955 | 0.999 | 0.999 | 1.021 | 0.170 | 0.170 | 0.412 | −15.589 | −13.589 |
| 8 | 2.812 | 2.833 | 525.776 | 0.999 | 0.999 | 0.109 | 0.018 | 0.018 | 0.135 | −35.694 | −33.694 |
| 10 | 3.574 | 3.597 | 585.485 | 0.999 | 0.999 | 0.146 | 0.024 | 0.024 | 0.156 | −33.069 | −31.069 |
| 20 | 6.949 | 7.143 | 47.689 | 0.999 | 0.997 | 0.383 | 0.064 | 0.064 | 0.253 | −24.402 | −22.402 |
| 30 | 9.829 | 11.765 | 4.643 | 0.944 | 0.874 | 9.826 | 1.638 | 1.638 | 1.280 | 4.790 | 6.790 |
| 50 | 12.559 | 14.493 | 2.542 | 0.717 | 0.432 | 50.24 | 8.374 | 8.374 | 2.894 | 19.477 | 21.477 |
| 80 | 17.559 | 20 | 9.579 | 0.977 | 0.947 | 0.343 | 0.069 | 0.069 | 0.262 | −25.400 | −23.400 |
| 100 | 21.618 | 23.810 | 6.945 | 0.978 | 0.947 | 0.241 | 0.048 | 0.048 | 0.219 | −28.591 | −26.591 |
| 120 | 21.412 | 22.728 | 4.059 | 0.989 | 0.947 | 0.492 | 0.082 | 0.082 | 0.286 | −22.159 | −20.159 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||
| T (K) | |||||||||||
| 298 | 3.574 | 3.597 | 3.597 | 0.999 | 0.999 | 0.146 | 0.024 | 0.024 | 0.156 | −33.069 | −31.069 |
| 313 | 3.420 | 3.436 | 3.436 | 0.999 | 0.999 | 0.064 | 0.011 | 0.011 | 0.103 | −40.537 | −38.537 |
| 323 | 3.324 | 3.344 | 3.344 | 0.999 | 0.999 | 0.143 | 0.024 | 0.024 | 0.154 | −33.294 | −31.294 |
| 333 | 3.228 | 3.236 | 3.237 | 0.999 | 0.999 | 0.013 | 0.002 | 0.002 | 0.047 | −54.867 | −52.867 |
Tables 2 and 3 showed that PSO model had higher R2 values than PFO model. Additionally, the error function, AIC, and AICc criteria of the PSO model had lower values than those of the PFO model for the entire range of experimental data. Based on these results, the PSO model was the most suitable among the considered models to describe MB adsorption data onto NaX zeolite. This was further confirmed by nearer qe,exp and qe,cal. values, suggesting that the rate-limiting step could correspond to a chemisorption process.
To verify the nature of adsorption process, activation energy (Ea) was determined by using the Arrhenius' equation by a plot between ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k2 and 1/T (figure not given).58
k2 and 1/T (figure not given).58
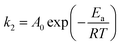 | (5) |
The determined Ea magnitude for MB adsorption on NaX zeolite was 0.0084 kJ mol−1, suggesting physical nature of adsorption process.
3.5. Adsorption thermodynamic modelling
The thermodynamic modelling parameters such as standard free energy change (ΔG°), standard enthalpy change (ΔH°), and standard entropy change (ΔS°)59 were obtained from the following equations:
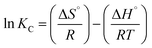 | (6) |
| ΔG° = ΔH° − TΔS° | (7) |
Eqn (6)60 relates the equilibrium constant Kc to the values of ΔS° and ΔH° and the universal gas constant (R), while eqn (7) expressed the relation between ΔG°, ΔH°, and ΔS° in terms of temperature (K).
Analyzing the ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kc plot using eqn (6) as a function of (1/T) (Fig. S3†) allowed the determination of ΔH° and ΔS° by using the slope and intercept of the curve; the results are summarized in Table 4. Thermodynamic parameters analysis revealed that the MB dye adsorption onto NaX was spontaneous reaction (ΔG° < 0), indicating a natural process occurrence. As temperature increases, the values of ΔG° become less negative, suggesting a decrease in the adsorption capacity, making adsorption thermodynamically favorable. The negative value of ΔH° confirms that MB adsorption onto NaX was an exothermic process. Furthermore, the negative value of ΔS° implies a reduction in disorder at the solid–liquid interface during dye adsorption, attesting to the dye's stability on the NaX surface.
Kc plot using eqn (6) as a function of (1/T) (Fig. S3†) allowed the determination of ΔH° and ΔS° by using the slope and intercept of the curve; the results are summarized in Table 4. Thermodynamic parameters analysis revealed that the MB dye adsorption onto NaX was spontaneous reaction (ΔG° < 0), indicating a natural process occurrence. As temperature increases, the values of ΔG° become less negative, suggesting a decrease in the adsorption capacity, making adsorption thermodynamically favorable. The negative value of ΔH° confirms that MB adsorption onto NaX was an exothermic process. Furthermore, the negative value of ΔS° implies a reduction in disorder at the solid–liquid interface during dye adsorption, attesting to the dye's stability on the NaX surface.
| ΔH° (kJ mol−1) | ΔS° (kJ mol−1 K−1) | ΔG° (kJ mol−1) | |||
|---|---|---|---|---|---|
| 298 K | 313 K | 323 K | 333 K | ||
| −16.478 | −0.0453 | −2.964 | −2.737 | −2.284 | −1.831 |
4. Determination of factors and modelling
4.1. Modelling uptake based on experimental parameters
Table 5 summarizes the experimental matrix containing the experimental conditions for each trial and the corresponding experimental results of MB adsorption uptake (uptakeexp. (%)). These results were obtained by various combinations of the factors: pH, S/L, initial concentration, and temperature. Analysis of the results revealed that the minimum adsorption uptake was found under the conditions of trial no. 14, i.e., for the following conditions: pH = 12, S/L ratio = 0.5, initial concentration = 120 and temperature = 60 °C. Meanwhile, the maximum uptake was observed in trial no. 3 with pH = 2, S/L ratio = 3.5, initial concentration = 5 and temperature = 25 °C.| No. | Configuration | x1(pH) | x2(S/L ratio) | x3(C0) | x4(T) | Uptakeexp. (%) |
|---|---|---|---|---|---|---|
| 1 | − − − − | −1 | −1 | −1 | −1 | 1.19 |
| 2 | + − − − | 1 | −1 | −1 | −1 | 14.05 |
| 3 | − + − − | −1 | 1 | −1 | −1 | 80.86 |
| 4 | + + − − | 1 | 1 | −1 | −1 | 25.49 |
| 5 | − − + − | −1 | −1 | 1 | −1 | 19.36 |
| 6 | + − + − | 1 | −1 | 1 | −1 | 0.11 |
| 7 | − + + − | −1 | 1 | 1 | −1 | 61.97 |
| 8 | + + + − | 1 | 1 | 1 | −1 | 3.1210 |
| 9 | − − − + | −1 | −1 | −1 | 1 | 0.07 |
| 10 | + − − + | 1 | −1 | −1 | 1 | 12.13 |
| 11 | − + − + | −1 | 1 | −1 | 1 | 68.73 |
| 12 | + + − + | 1 | 1 | −1 | 1 | 20.28 |
| 13 | − − + + | −1 | −1 | 1 | 1 | 17.02 |
| 14 | + − + + | 1 | −1 | 1 | 1 | 0.001 |
| 15 | − + + + | −1 | 1 | 1 | 1 | 55.83 |
| 16 | + + + + | 1 | 1 | 1 | 1 | 2.12 |
4.2. Calculation of effects
To calculate the main effects and interactions among the factors x1, x2, x3, and x4, an effects matrix has been included. This matrix, along with the coefficient values of the regression equation for the calculation of the modelled uptake (uptakemod. (%)) is given as:| Uptake (%) = 23.896 − 14.233pH + 15.904r (s/l) − 3.955C0 − 1.873T − 12.814pH × r (s/l) − 4.370pH × C0 + 0.844pH × T − 5.086r (s/l) × C0 − 1.187r(s/l) × T + 0.674C0 × T + 3.278pH × r (s/l) × C0 + 0.664pH × r (s/l) × T + 0.078pH × C0 × T + 0.600r (s/l) × C0 × T − 0.3005pH × r (s/l) × C0 × T | (8) |
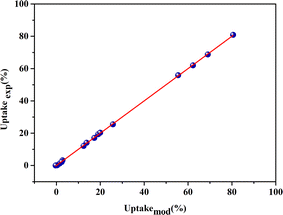
To compare the measured responses (uptakeexp. (%)) with the estimated responses (uptakemod. (%)), the adequacy graph has been plotted. Fig. 3 showed that the estimated responses were placed on the x-axis, and the measured responses were on the y-axis. The coefficient of determination (R2) equals 99.99%, indicating that the chosen models were appropriate.
4.3. The influence of individual factors and their combinations on yield
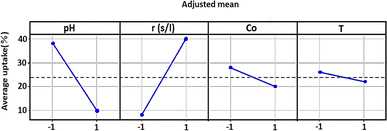
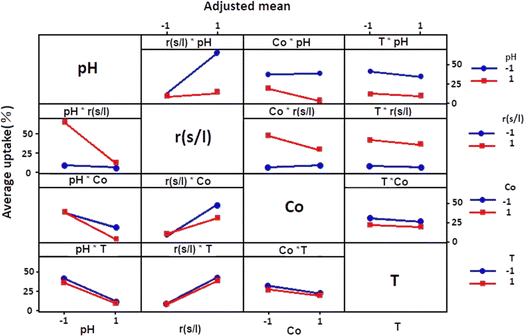
Fig. 4 showed how each independent variable (x1, x2, x3, and x4) affects the dependent response using the experiment matrix and the regression equation. A positive impact on uptake (%) was manifested for S/L. This observation suggests that the efficiency of the adsorption process was intensified by increasing this ratio.Conversely, negative effects on uptake (%) were exhibited by factors such as pH, concentration, and temperature, implying that high levels of these parameters were associated with a decrease in performance. In order to analyse if there is interaction between the considered experimental variables, the responses generated at the two levels (low and high) of each factor were measured. If the responses of two factors show an inverse variation, this indicates an interaction between them. More precisely, this interaction was observed when the two lines representing the respective variations in responses were not parallel. Fig. 5 graphically illustrates the obtained plots for each factor on the adsorption uptake. The interactions examined relate to the combination of the four variables and their influence on the response. Some of these interactions produced positive effects, while others had a negative impact on the course of the adsorption process.
As it may be seen in Fig. 5, there are marked interaction effects between pH and S/L, as well as between the initial dye concentration and the pH and S/L. However, the interaction between temperature and the other three variables was not significant.
4.4. Analysis of variance (ANOVA)
Significance verification is crucial to assessing the relevance of variables effects and of their interactions. Obtaining an adequate number of degrees of freedom for residues is essential as this allows precise estimation of residual variance (Table 6) and enhancing the reliability of hypothesis tests.| No. | Uptakeexp. (%) | Uptakemod. (%) | ei | ei2 |
|---|---|---|---|---|
| 1 | 1.19 | 1.49 | −0.30054375 | 0.090326546 |
| 2 | 14.05 | 13.75 | −ei | ei2 |
| 3 | 80.86 | 80.56 | −ei | ei2 |
| 4 | 25.49 | 25.79 | ei | ei2 |
| 5 | 19.36 | 19.06 | −ei | ei2 |
| 6 | 0.11 | −0.41 | ei | ei2 |
| 7 | 61.97 | 62.29 | ei | ei2 |
| 8 | 3.12 | 2.82 | −ei | ei2 |
| 9 | 0.07 | 0.23 | −ei | ei2 |
| 10 | 12.13 | 12.43 | ei | ei2 |
| 11 | 68.73 | 69.03 | ei | ei2 |
| 12 | 20.28 | 19.98 | −ei | ei2 |
| 13 | 17.02 | 17.32 | ei | ei2 |
| 14 | 0.001 | −0.30 | −ei | ei2 |
| 15 | 55.83 | 55.53 | −ei | ei2 |
| 16 | 2.12 | 2.42 | ei | ei2 |
In the case where the degrees of freedom for residues are zero (in cases where n = p, i.e., the number of parameters is equal to the number of observations), it becomes impossible to conduct hypothesis tests on residual effects as there is no freedom available to estimate residual variance. To solve this problem, an interaction was eliminated, leading to a simplification of the model equation as follows:
| Uptake (%) = 23.896 − 14.233pH + 15.904r (s/l) − 3.955C0 − 1.873T − 12.814pH × r (s/l) − 4.370pH × C0 + 0.844pH × T − 5.086r (s/l) × C0 − 1.187r (s/l) × T + 0.674C0 × T + 3.278 pH × r (s/l) × C0 + 0.664pH × r (s/l) × T + 0.078pH × C0 × T + 0.600r (s/l) × C0 × T | (9) |
To assess the significance of the effects, the Student's t-test was used with a significance threshold of 0.05. Critical test values were calculated based on the number of parameters of the model at a 95% confidence level. In this context, all Student's t values below 12.706 were considered not statistically significant. The detailed results of the tests are presented in Table 7.
| Terms | Effect | Estimate | Error standard | Value of ti | Value of p | Significant |
|---|---|---|---|---|---|---|
| Constante | 23.8962 | 0.3005 | 79.5099 | 0.0080 | Significant | |
| pH | −28.4656 | −14.2328 | 0.3005 | −47.3568 | 0.0134 | Significant |
| r (s/l) | 31.8075 | 15.9038 | 0.3005 | 52.9167 | 0.0120 | Significant |
| C0 | −7.9101 | −3.9551 | 0.3005 | −13.1597 | 0.0483 | Significant |
| T | −3.7464 | −1.8732 | 0.3005 | −6.2328 | 0.1013 | Not significant |
| pH × r (s/l) | −25.6274 | −12.8137 | 0.3005 | −42.6351 | 0.0149 | Significant |
| pH × C0 | −8.7402 | −4.3701 | 0.3005 | −14.5407 | 0.0437 | Significant |
| pH × T | 1.6877 | 0.8438 | 0.3005 | 2.8077 | 0.2178 | Not significant |
| r (s/l) × C0 | −10.1716 | −5.0858 | 0.3005 | −16.9220 | 0.0376 | Significant |
| r (s/l) × T | −2.3732 | −1.1866 | 0.3005 | −3.9481 | 0.1579 | Not significant |
| C0 × T | 1.3479 | 0.6739 | 0.3005 | 2.2424 | 0.2670 | Not significant |
| pH × r (s/l) × C0 | 6.5570 | 3.2785 | 0.3005 | 10.9085 | 0.0582 | Not significant |
| pH × r (s/l) × T | 1.3278 | 0.6639 | 0.3005 | 2.2090 | 0.2706 | Not significant |
| pH × C0 × T | 0.1564 | 0.0782 | 0.3005 | 0.2602 | 0.8380 | Not significant |
| r (s/l) × C0 × T | 1.2010 | 0.6005 | 0.3005 | 1.9980 | 0.2954 | Not significant |
Analysis of the results revealed that the coefficients associated with pH, S/L, and C0 were statistically significant (p < 0.05), while T was not significant (p > 0.05). Terms involving the squares of pH·R/L, pH·C0, and S/L·C0 were also significant (p < 0.05), while the pH·T, S/L·T, and C0·T interactions, as well as the values implicating the interactions of pH·S/L·C0, pH·R/L·T, pH·C0·T, and S/L·C0·T were non-significant (p > 0.05). In summary, the effect of temperature (T) was not significant, which indicates that the interactions involving temperature were not significant either. On the other hand, the other effects and interactions were significant, confirming the rejection of the null hypothesis and the presence of significant differences between averages. Considering these findings, the simplified regression equation becomes as follows:
| Uptake (%) = 23.896 − 14.233pH + 15.904R/L − 3.955C0 − 12.814pH × R/L − 4.370pH × C0 − 5.086R/L × C0 | (10) |
Validation of the linear model is of crucial importance, requiring the use of various measurements such as ANOVA, SCEL (corrected average quadratic error), SECR (residual average quadratic error), SCET (total average quadratic error), and the Fisher test. These ANOVA measurements, which allow for assessing the adjustment of the linear model and ensure the reliability of the results are summarized in Table 8. The results confirm the significance of the model, with a calculated F value (Fcalculated) of 551.9165, well above the critical value of F at the 5% threshold. In addition, the correlation coefficients R2, Radj.2 and Rprevu2 were significantly high, at 99.99%, 99.81% and 96.69% respectively. These high values indicate the adequacy of the experimental data for the proposed model.
| Source | ddl | Sum of squares | Mean square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 14 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 167.0081 167.0081 |
797.6434 | 551.9165 | 0.0334 |
| Linear | 4 | 7594.4591 | 1898.6148 | 1313.7160 | 0.0207 |
| pH | 1 | 3241.1587 | 3241.1587 | 2242.6676 | 0.0134 |
| r (s/l) | 1 | 4046.8778 | 4046.8778 | 2800.1720 | 0.0120 |
| C0 | 1 | 250.2795 | 250.2795 | 173.1769 | 0.0483 |
| T | 1 | 56.1432 | 56.1432 | 38.8474 | 0.1013 |
| 2-Factor interactions | 6 | 3387.6547 | 564.6091 | 390.6722 | 0.0387 |
| pH × r (s/l) | 1 | 2627.0571 | 2627.0571 | 1817.7499 | 0.0149 |
| pH × C0 | 1 | 305.5653 | 305.5653 | 211.4310 | 0.0437 |
| pH × T | 1 | 11.3928 | 11.3928 | 7.8831 | 0.2178 |
| r (s/l) × C0 | 1 | 413.8448 | 413.8448 | 286.3532 | 0.0376 |
| r (s/l) × T | 1 | 22.5276 | 22.5276 | 15.5876 | 0.1579 |
| C0 × T | 1 | 7.2672 | 7.2672 | 5.0284 | 0.2670 |
| 3-Factor interactions | 4 | 184.8942 | 46.2235 | 31.9836 | 0.1318 |
| pH × r (s/l) × C0 | 1 | 171.9750 | 171.9750 | 118.9954 | 0.0582 |
| pH × r (s/l) × T | 1 | 7.0521 | 7.0521 | 4.8796 | 0.2706 |
| pH × C0 × T | 1 | 0.0978 | 0.0978 | 0.0677 | 0.8380 |
| r (s/l) × C0 × T | 1 | 5.7692 | 5.7692 | 3.9919 | 0.2954 |
| Error | 1 | 1.4452 | 1.4452 | ||
| Total | 15 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 168.4533 168.4533 |
4.5. Pareto chart
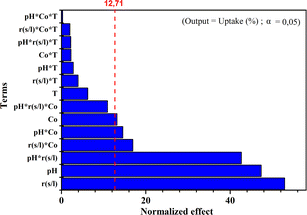
Fig. 6 presents the Pareto chart of the analysis of variances. This chart categorizes the variables and their interactions according to their increasing influence on the MB adsorption uptake (%) onto the NaX zeolite. The effects are standardized for better comparison. The standardized values in this figure are obtained by dividing the effect of each variable by the error on the estimated value of the corresponding variable. The higher the standardized effect, the more considered variable influences the adsorption uptake (%). Fig. 6 revealed a line that separates the significant effects from those that were not. The confidence interval chosen was 95%. All variables and interactions with an effect below the limit of significance (95% confidence interval) namely, variable4 (T), and all products containing this variable (interactions containing temperature), as well as the interaction pH × S/L × C0 were disregarded and not represented in the model. The corresponding Pareto chart shows that the coefficient of determination was approximately (R2 = 91.43%), which was highly satisfactory. The most dominant factor was S/L followed by pH.5. Conclusions
In this study, the hydrothermal synthesis of NaX zeolite was successfully carried out at 100 °C, 24 h and under autogenous pressure. The high frequency bands at 3650 cm−1 of hydroxyl groups (O–H), which facilitates MB adsorption, were highlighted during FTIR analysis. The observed high specific surface area (375 m2 g−1) and micropore volume (0.12 cm3 g−1) of the synthesized NaX facilitate its usage in the adsorption of organic molecules. The isotherm modelling study showed that MB adsorption onto NaX followed Langmuir isotherm based on the results of error functions R2, Adj. R2, RSS, MSE, χ2, RMSE and AIC and AICc criteria, while kinetic modelling results revealed the fitting of PSO kinetic model at low MB concentrations (5–30 mg L−1) and PFO kinetic model at high concentrations (50–120 mg L−1). However, the adsorption kinetic data followed PSO kinetic model at varying temperature, suggesting a rate limiting step and a chemisorption process. The thermodynamic study reveals that MB adsorption NaX was a spontaneous and an exothermic process. Using a full 2-level factorial design, we were able to identify the optimum conditions for the adsorption of MB onto NaX accurately and efficiently, minimising the number of trials required. The estimation study of the significant effects using Student's t-test revealed that the temperature was not significant, and the other interactions were significant. The regression equation with 16 factors was simplified to only 7. The resulting model was validated by an analysis of variance (ANOVA) confirming its relevance. Finally, the Pareto chart showed that the coefficient of determination (R2 = 91.43%) was highly satisfactory and the most influent variable in the adsorption of MB onto the NaX zeolite was S/L followed by pH.Data availability
The data supporting this article have been included as a part of ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
Moonis Ali Khan acknowledges the financial support through Researchers Supporting Project number (RSP2024R345), King Saud University, Riyadh. Saudi Arabia.References
- A. Aid, S. Amokrane, D. Nibou, E. Mekatel, M. Trari and V. Hulea, Water Sci. Technol., 2018, 77, 60–69, DOI:10.2166/wst.2017.509.
- S. F. Azha, M. Shahadat and S. Ismail, Dyes Pigm., 2017, 145, 550–560, DOI:10.1016/j.dyepig.2017.05.009.
- F. Kooli, Y. Liu, R. Al-Faze and A. AlSuhaimi, Appl. Clay Sci., 2015, 116, 23–30, DOI:10.1016/j.clay.2015.07.044.
- S. K. Pradhan, V. Pareek, J. Panwar and S. Gupta, J. Water Process Eng., 2019, 32, 100917, DOI:10.1016/j.jwpe.2019.100917.
- E. H. Mekatel, S. Amokrane, A. Aid, D. Nibou and M. Trari, C. R. Chim., 2015, 18(3), 336–344, DOI:10.1016/j.crci.2014.09.009.
- I. A. W. Tan, A. L. Ahmad and B. H. Hameed, Desalination, 2018, 225, 13–28, DOI:10.1016/j.desal.2007.07.005.
- R. I. Foster, J. T. Amphlett, K. W. Kim, T. Kerry, K. Lee and C. A. Sharrad, J. Ind. Eng. Chem., 2020, 81, 144–152, DOI:10.1016/j.jiec.2019.09.001.
- A. Kornilov, E. Piterkina, K. Shcherbakova, A. Makarov and O. Dmitrieva, Radiochemistry, 2020, 62(2), 173–176, DOI:10.1134/S1066362220020046.
- M. Hoyer, D. Zabelt, R. Steudtner, V. Brendler, R. Haseneder and J.-U. Repke, Sep. Purif. Technol., 2014, 132, 413–421, DOI:10.1016/j.seppur.2014.05.044.
- A. Akbari, J. Remigy and P. Aptel, Chem. Eng. Process., 2002, 41(7), 601–609, DOI:10.1016/S0255-2701(01)00181-7.
- H. Mekatel, S. Amokrane, B. Bellal, M. Trari and D. Nibou, Chem. Eng. J., 2012, 200, 611–618, DOI:10.1016/j.cej.2012.06.121.
- X. Yang, Z. Zhang, S. Kuang, H. Wei, Y. Li, G. Wu, A. Geng, Y. Li and W. Liao, Hydrometallurgy, 2020, 194, 105343, DOI:10.1016/j.hydromet.2020.105343.
- M. Goleij and H. Fakhraee, Iran. J. Chem. Chem. Eng., 2017, 36(5), 129–141, DOI:10.30492/IJCCE.2017.25481.
- S. Poorsadeghi, M. Z. Kassaee, H. Fakhri and M. Mirabedini, Iran. J. Chem. Chem. Eng., 2017, 36(4), 91–99, DOI:10.30492/IJCCE.2017.28714.
- M. A. Khan, A. A. Alqadami, S. M. Wabaidur and B. H. Jeon, Nanomaterials, 2023, 13(7), 1193, DOI:10.3390/nano13071193.
- A. A. Alqadami, S. M. Wabaidur, B. H. Jeon and M. A. Khan, Biomass Convers. Biorefin., 2023, 1–12, DOI:10.1007/s13399-022-03711-7.
- H. Majdoubi, A. A. Alqadami, R. E. K. Billah, M. Otero, B. H. Jeon, H. Hannache, Y. Tamraoui and M. A. Khan, Int. J. Environ. Res. Public Health, 2023, 20(1), 831, DOI:10.3390/ijerph20010831.
- S. M. Wabaidur, M. A. Khan, M. R. Siddiqui, M. Otero, B. H. Jeon, Z. A. Alothman and A. A. H. Hakami, J. Mol. Liq., 2020, 317, 113916, DOI:10.1016/j.molliq.2020.113916.
- E. T. Wahyuni, D. Rendo and S. Suherman, Global NEST J., 2021, 23, 119–126, DOI:10.30955/gnj.003249.
- M. Andrunik, M. Skalny, M. Gajewska, M. Marzec and T. Bajda, Heliyon, 2023, 9(10), E20572, DOI:10.1016/j.heliyon.2023.e20572.
- S. Amokrane, R. Rebiai and D. Nibou, J. Appl. Sci., 2007, 7, 1985–1988, DOI:10.3923/jas.2007.1985.1988.
- M. Senila and C. Oana, Heliyon, 2024, 10(3), E25303, DOI:10.1016/j.heliyon.2024.e25303.
- D. Nibou and S. Amokrane, J. Mol. Liq., 2021, 323, 114642, DOI:10.1016/j.molliq.2020.114642.
- G. Engelhardt, Introduction to Zeolite Science and Practice, ed. H. VanBekkum, E. M. Flanigen and J. C. Jansen, Elsevier Amesterdam, 1991 Search PubMed.
- E. H. Zouaoui, N. Djamel, W. A. Wan Ab Karim Ghani and A. Samira, Iran. J. Chem. Chem. Eng., 2021, 40(4), 1195–1215, DOI:10.30492/IJCCE.2020.40342.
- A. Dyer, An Introduction to Zeolite Molecular Sieve, John Wiley, London, 1988 Search PubMed.
- D. W. Breck, ZeoliteMolecularsieves-Structure Chemistry and Use, WileyInterscience, New York, 1974 Search PubMed.
- C. Baerlicher, W. M. Meier and D. H. Olson, Atlas of Zeolite Framework Types, Elsevier, Amesterdam, 5th revised edn, 2001 Search PubMed.
- Q. F. Lin, Z. R. Gao, C. Lin, S. Zhang, J. Chen, Z. Li, X. Liu, W. Fan, J. Li, X. Chen, M. A. Camblor and F. J. Chen, Science, 2021, 374(6575), 1605–1608, DOI:10.1126/science.abk3258.
- J. Li, Z. R. Gao, Q. F. Lin, C. Liu, F. Gao, C. Lin, S. Zhang, H. Deng, A. Mayoral, W. Fan, S. Luo, X. Chen, H. He, M. A. Camblor, F. J. Chen and J. Yu, Science, 2023, 379(6629), 283–287, DOI:10.1126/science.ade1771.
- Z. R. Gao, H. Yu, F. J. Chen, A. Mayoral, Z. Niu, Z. Niu, X. Li, H. Deng, C. Márquez-Álvarez, H. He, S. Xu, Y. Zhou, J. Xu, H. Xu, W. Fan, S. R. G. Balestra, C. Ma, J. Hao, J. Li, P. Wu, J. Yu and M. A. Camblor, Nature, 2024, 628(8006), 99–103, DOI:10.1038/s41586-024-07194-6.
- N. Y. Baouali, D. Nibou and S. Amokrane, Iran. J. Chem. Chem. Eng., 2022, 41(6), 1907–1920, DOI:10.30492/IJCCE.2021.128624.4168.
- S. Sivalingam and S. Sen, Appl. Surf. Sci., 2019, 463, 190–196, DOI:10.1016/j.apsusc.2018.08.019.
- Y.-P. Zhao, D.-X. Guo, S.-F. Li, J.-P. Cao and X.-Y. Wei, Desalin. Water Treat., 2020, 185, 355–363, DOI:10.5004/dwt.2020.25424.
- D. Nibou, H. Mekatel, S. Amokrane, M. Barkat and M. Trari, J. Hazard. Mater., 2010, 173(1–3), 637–646, DOI:10.1016/j.jhazmat.2009.08.132.
- R. S. AbdElkader, M. K. Mohamed, Y. A. Hasanien and E. M. Kandeel, J. Cluster Sci., 2023, 34, 3147–3163, DOI:10.1007/s10876-023-02454-3.
- M. Barkat, D. Nibou, S. Chegrouche and A. Mellah, Chem. Eng. Process. Process Intensif., 2009, 48(1), 38–47, DOI:10.1016/j.cep.2007.10.004.
- M. M. J. Treacy and J. B. Hugging, Collection of Simulated X Patterns for Zeolites, Elsevier, 4th revised edn, 2001 Search PubMed.
- S. K. Masoudian, S. Sadighi and A. Abbasi, Bull. Chem. React. Eng. Catal., 2013, 8(1), 54–60, DOI:10.9767/bcrec.8.1.4321.54-60.
- D. Ferhat, D. Nibou, E. Mekatel and S. Amokrane, Iran. J. Chem. Chem. Eng., 2019, 38(6), 63–81, DOI:10.30492/ijcce.2019.33252.
- D. Nibou, S. Khemaissia, S. Amokrane, M. Barkat, S. Chegrouche and A. Mellah, Chem. Eng. J., 2011, 172(1), 296–305, DOI:10.1016/j.cej.2011.05.113.
- Y. Kuang, X. Zhang and S. Zhou, Water, 2020, 12(2), 587, DOI:10.3390/w12020587.
- M. T. Yagub, T. K. Sen and H. M. Ang, Water, Air, Soil Pollut., 2012, 223, 5267–5282, DOI:10.1007/s11270-012-1277-3.
- M. T. Yagub, T. K. Sen, S. Afroze and H. M. Ang, Adv. Colloid Interface Sci., 2014, 209, 172–184, DOI:10.1016/j.cis.2014.04.002.
- B. K. Nandi, A. Goswami and M. K. Purkait, J. Hazard. Mater., 2009, 161(1), 387–395, DOI:10.1016/j.jhazmat.2008.03.110.
- B. K. Nandi, A. Goswami and M. K. Purkait, Appl. Clay Sci., 2009, 42(3–4), 583–590, DOI:10.1016/j.clay.2008.03.015.
- N. Hajnajafi, A. Khorshidi, A. G. Gilani and F. Verpoort, Removal of Methylene Blue from Aqueous Solution by Polydopamine@ Zeolitic Imidazolate-67, 2021, DOI:10.21203/rs.3.rs-1162284/v1.
- Y. Dehmani, B. B. Mohammed, R. Oukhrib, A. Dehbi, T. Lamhasni, Y. Brahmi, A. El-Kordy, D. S. Franco, J. Georgin, E. C. Lima and A. A. Alrashdi, Arabian J. Chem., 2024, 17(1), 105474, DOI:10.1016/j.arabjc.2023.105474.
- M. A. M. Lawrence, R. K. Kukkadapu and S. A. Boyd, Appl. Clay Sci., 1998, 13, 13–20, DOI:10.1016/S0169-1317(98)00009-X.
- A. Gürses, Ç. Doğar, M. Yalçın, M. Açıkyıldız, R. Bayrak and S. Karaca, J. Hazard. Mater., 2006, 131(1–3), 217–228, DOI:10.1016/j.jhazmat.2005.09.036.
- D. Nibou, S. Amokrane, H. Mekatel and N. Lebaili, Phys. Procedia, 2009, 2, 1433–1440, DOI:10.1016/j.phpro.2009.11.113.
- S. Bentahar, A. Dbik, M. El Khomri, N. El Messaoudi and A. Lacherai, J. Environ. Eng., 2017, 5(6), 5921–5932, DOI:10.1016/j.jece.2017.11.003.
- I. Langmuir, J. Am. Chem. Soc., 1916, 38(11), 2221–2295, DOI:10.1021/ja02268a002.
- H. Freundlich, Z. Phys. Chem., 1907, 57(1), 385–470, DOI:10.1515/zpch-1907-5723.
- M. I. Temkin, Zh. Fiz. Khim., 1941, 15, 296–332 CAS.
- S. Y. Elovich, O. G. Larinov, I. Akad, N. SSSR and O. Khim, Nauk, 1962, 2(2), 209–216 Search PubMed.
- A. Benmessaoud, D. Nibou, E. H. Mekatel and S. Amokrane, Iran. J. Chem. Chem. Eng., 2020, 39(4), 153–171, DOI:10.30492/ijcce.2019.35116.
- H. Xi, Z. Li, H. Zhang, X. Li and X. Hu, Sep. Purif. Technol., 2003, 31, 41–45, DOI:10.1016/S1383-5866(02)00150-8.
- N. Dahdouh, S. Amokrane, R. Murillo, E. Mekatel and D. Nibou, J. Polym. Environ., 2020, 28, 271–283, DOI:10.1007/s10924-019-01605-w.
- E. Mekatel, S. Amokrane, M. Trari, D. Nibou, N. Dahdouh and S. Ladjali, Arabian J. Sci. Eng., 2019, 44(6), 5311–5322, DOI:10.1007/s13369-018-3575-6.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra04483e |
| This journal is © The Royal Society of Chemistry 2024 |