DOI:
10.1039/D4RA04742G
(Paper)
RSC Adv., 2024,
14, 29526-29534
Structural, electronic and thermoelectric properties of boron phosphorous nitride B2PN via first principles study
Received
30th June 2024
, Accepted 26th August 2024
First published on 18th September 2024
Abstract
A theoretical study of monolayer boron phosphorous nitride (B2PN) is performed to explore its electronic and thermoelectric properties. The thermodynamic stability is determined by the formation energy of a monolayer. The dynamic stability is obtained from the phonon dispersion curve. We performed an AMID simulation to ensure the thermal stability and found that our material is thermally stable at 700 K. The system possesses direct band gaps of 0.25 eV and 0.4 eV with Perdew–Burke–Ernzerhof (PBE) and hybrid functional (HSE), respectively. The Seebeck coefficient is found to be the same in both directions, and the maximum value is 1.55 mV K−1. The relaxation time is found to be longer for the hole-doped system than the electron-doped system. It is observed that electrical conductivity is greater for hole-doped system in both directions, and a similar trend is observed for electronic thermal conductivity. We found that the lattice thermal conductivity of our systems is anisotropic. The lattice thermal conductivity along the Y-direction is greater than that in the X-direction. The calculation performed for the figure of merit (ZT) reveals that the system has a high ZT of 1.14 for a hole-doped system. The figure of merit makes the system a promising candidate for potential thermoelectric device applications.
Introduction
Thermoelectric materials are of great importance due to the increase in energy consumption. These materials are advantageous because they help to reduce global warming by converting heat into electrical power.1 The conversion of thermoelectricity by the Seebeck effect is calculated using the formula ΔV = SΔT, where S (Seebeck coefficient) is the thermoelectric power based on the voltage difference (ΔV) instead of the polarization of the electric potential.2 The figure of merit (ZT) indicates how efficient the material is for thermoelectric applications.3 Additional characteristics are also monitored for the selection of the thermoelectric materials, such as the lattice thermal conductivity, relaxation time and group velocity.
To make a real device, numerous techniques have been applied and attempted to obtain efficient materials with a high figure of merit. To this end, many bulk materials have been studied. For instance, well-known bulk-type Bi2Te3 and PbTe thermoelectric candidates exhibit very high ZT at high temperatures.3–7 Their ZT is found in the range of 1–2. However, the preservation of ZT under very limited conditions limits their use.
In addition to bulk materials, two-dimensional (2D) materials are also being explored owing to their potential as efficient thermoelectric materials. For instance, in 2D carbon materials, multiple topological structures are either predicted theoretically or synthesized empirically. These structures include penta-graphene, carbon eneyne,8 biphenylene,9 γ-graphyne,10 and various graphynes.11,12 In addition to adding new characteristics, doping with hetero atoms in carbon allotropes, most frequently nitrogen or boron atoms, can also result in the production of novel 2D systems, such as g-C3N4 and T-C3N.13,14 BN is a common dipole dopant used in 2D carbon systems. It is a synthetic III–V chemical compound with equal numbers of boron (B) and nitrogen (N) atoms.15,16 Within the lattice, B and N are covalently bonded, whereas the van der Waals force weakly binds the layers together. Out of the four prevalent phases, which are cubic (c-BN), wurtzite (w-BN), rhombohedral (r-BN), and hexagonal (h-BN), the most stable phase of boron nitride at room temperature is believed to be h-BN.17 Remarkably, the band gap in the graphyene-like BN monolayer structures may be partially modified by varying the B–N chain length.18 Niazian was able to assess the thermoelectric features through the use of a BN nanosheet structure simulation and figure of merit (ZT) calculations at 200, 300, and 600 K temperatures. At 200, 300, and 600 K, the ZT values of the BN nanosheet structure were 0.97, 1.03, and 1.70, respectively, indicating the strong thermoelectric performance of the nanosheets at high temperatures. The thermoelectric characteristics of a defective boron nitride (BN) nanosheet were also examined in this study, and it was shown that the ZT value of the defect-free BN nanosheet was much higher than the ZT value of a BN nanosheet with a single vacancy defect.19 Improving the thermoelectric appropriateness of materials is fairly challenging because all the internal parameters are intimately linked. However, the high performance of these materials may result in various applications in the future. This study presents the thermoelectric properties of 2D B2PN, driven by the potential applications of boron nitride (BN) systems highlighted in contemporary research. This study reveals that these materials are promising for thermoelectric applications. It is anticipated that this effort will enable researchers to explore this area more thoroughly and address future challenges.
Computational techniques
Herein, the structural, electronic and thermoelectric properties of monolayer B2PN are investigated using the Vienna Ab initio Simulation Package (VASP). The structure is fully relaxed with PBE potentials until the force becomes 0.001 eV A−1. The energy criteria of 10−6 are set up for the entire calculation. The K-mesh of 11 × 11 × 1 is considered to obtain an accurate result. A Z-direction vacuum of 20 A is created to prevent periodic interaction. After full relaxation of the structure, the band structure is computed with PBE and HSE potentials. The PHONOPY code is used to calculate the phonon dispersion curve. For the phonon dispersion curve, the supercell of 9 × 9 × 1 is taken with K-point 6 × 6 × 1. Using the BoltzTrap2 code, the thermoelectric features, such as the Seebeck coefficient, thermal conductivity and electrical conductivity, are computed. The thermoelectric features, such as electrical conductivity and electronic thermal conductivity, obtained from the BoltzTrap2 code, depend on the relaxation time. To make these features independent of the relaxation time, we calculated the relaxation time. For temperature and energy-dependent relaxation time calculation, we included the acoustic phonon scattering, ionized impurity scattering effects and optical phonon. The phono3py code is used to calculate the lattice thermal conductivity. For lattice thermal conductivity, the supercell of 3 × 3 × 1 is used. The energy criteria of 10−8, cutoff energy 550 eV and K-mesh of 2 × 2 × 1 are taken. In addition to these, a q-mesh of 90 × 70 × 1 is taken for accurate results.
Results and discussion
The top and side views of the B2NP monolayer structure are shown in Fig. 1(a) and (b). The orange, purple, and green spheres represent phosphorous, nitrogen, and boron, respectively. With lattice constants of a = 5.12 Å and b = 2.79 Å, the monolayer possesses an orthorhombic structure exhibiting Pmmm-47 symmetry. To verify thermodynamic stability, the monolayer formation energy (EF) is computed using the following relation:20| | |
EF = Edi-BPN − (2 EB + EN + EN),
| (1) |
where boron, phosphorous and nitrogen total energies are denoted by EB, EP and EN, respectively. Table 1 shows the formation energy for the system. Monolayer B2PN thermodynamic stability is confirmed by its negative formation energy value.21 Furthermore, we investigate the thermal stability using the ab initio molecular dynamic (AMID) simulations at 700 K. For MD simulations, we consider a 2 × 2 × 1 supercell to minimize the constraint of periodic boundary conditions. Fig. 1(c) shows the evolution of potential energy (eV) for the B2PN monolayer systems. The inset displays a snapshot of the atomic structure at five picoseconds (ps) at 700 K using the canonical (NVT) ensembles. The structural integrity is preserved even after 5 ps although some slight distortions can be observed in the structure, but the bonds between atoms are still present. This suggests that the B2PN monolayer systems are thermally stable at 700 K. To ensure dynamic stability, we calculated the phonon dispersion curve. The obtained phonon dispersion curves are presented in Fig. 2. There is no imaginary peak present in the dispersion curve, indicating the dynamic stability of the system. The band structures with PBE and HSE along a high symmetric path are calculated, as shown in Fig. 3(a) and (b). Direct band gaps of 0.25 eV and 0.4 eV were found for the B2NP with PBE and HSE.
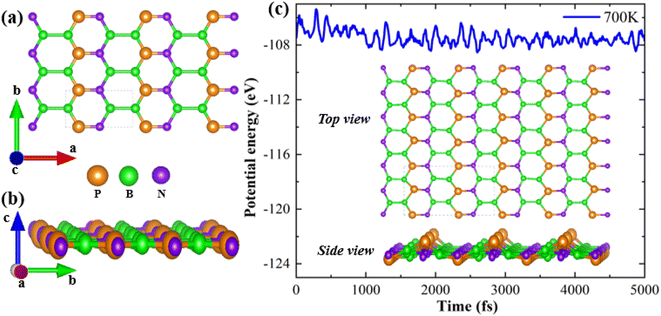 |
| | Fig. 1 (a) Top view and (b) side view of the optimized crystal structure of B2PN, and (c) evolution of potential energy with a simulation time for B2PN. The inset shows the top and side views of the structure with molecular dynamics at 700 K. | |
Table 1 The obtained lattice constant and formation energy of the monolayer
| Structure |
Lattice constant Å |
Formation energy eV per atom |
| Monolayer |
a = 5.12 Å, b = 2.79 Å |
−5.58 |
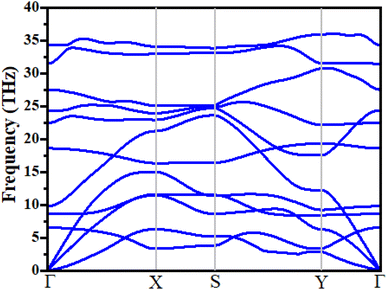 |
| | Fig. 2 Phonon spectrum of B2NP monolayer systems. | |
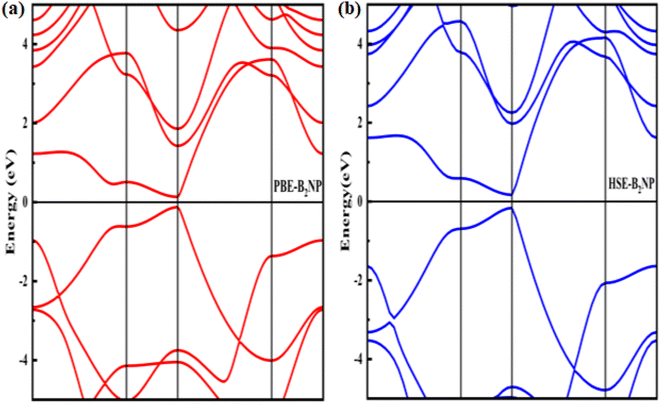 |
| | Fig. 3 Electronic band structures of (a) PBE-B2NP and (b) HSE-B2NP monolayer systems. | |
First, we explain the relationship between carrier concentration and chemical potential. Carrier concentration refers to the number of charge carriers (electrons or holes) per unit volume in a material, and it plays a crucial role in determining the electrical conductivity, Seebeck effect and thermal conductivity of thermoelectric materials. Doping introduces impurity states within the band gap, significantly altering the carrier concentration. N-type doping adds electrons, shifting the Fermi level closer to the conduction band and increasing the electron concentration. Conversely, p-type doping introduces holes, shifting the Fermi level closer to the valence band and increasing the hole concentration. Understanding the relationship between the carrier concentration and energy is essential for designing materials with enhanced thermoelectric efficiency. Fig. 4 illustrates the relationship between chemical potential and carrier concentration. Positive values of chemical potential correspond to n-type carriers, indicating an excess of electrons, while negative values signify p-type carriers, reflecting the abundance of holes.
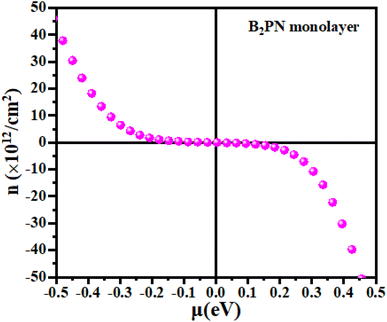 |
| | Fig. 4 The calculated carrier concentration as a function of the chemical potential of the B2NP monolayer system. | |
Now, we present an important thermoelectric parameter known as the Seebeck coefficient. The relationship shown below can be used to obtain the Seebeck coefficient.22
| |
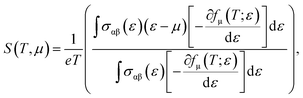 | (2) |
where the electron charge, conductivity tensor at a given electron energy (
ε), and temperature are represented by
e,
σαβ(
ε), and
T, respectively. The chemical potential and Fermi-Dirac distribution function are represented by
μ and
fμ.
23
The temperature-dependent Seebeck coefficient as a function of chemical potential is illustrated in Fig. 5(a) and (b). Charge carrier type dominance is shown by the sign of the Seebeck coefficient. As can be observed in the figure, the Seebeck coefficient in monolayer B2NP systems did not behave anisotropically because it exhibited almost the same trend in both the X- and Y-directions. In both hole- and electron-doped systems, the X- and Y-direction have almost the same Seebeck coefficient. For example, the maximum Seebeck coefficient in the X-direction at a chemical potential of 0.05 eV is 1.55 mV K−1, while in the Y-direction at 300 K, it is 1.55 mV K−1 at the same chemical potential. Additionally, the Seebeck coefficient decreases as the temperature increases.
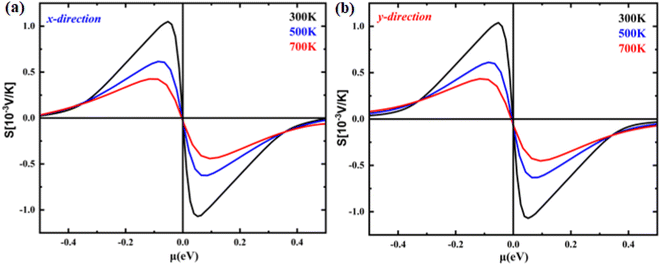 |
| | Fig. 5 The calculated Seebeck coefficient as a function of chemical potential at 300 K, 500 K and 700 K temperatures of (a) B2NP monolayer in the X-direction and (b) B2NP monolayer in the Y-direction. | |
Now, we present the relaxation time with respect to the chemical potential. However, it is worth noting that the relaxation time τ is in principle dependent on both temperature (T) and energy (E). This may greatly affect the electrical conductivity and electronic thermal conductivity. Therefore, we adopted the analytic formula to calculate the energy and temperature relaxation times.24 Here, the total relaxation time (τtot) is defined as follows:
| |
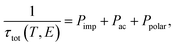 | (3) |
where the impurity scattering rate (
Pimp) was adopted from the Brooks–Herring formula
| |
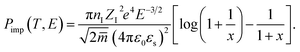 | (4) |
here,
nI,
ZI,
ε0,
εs, and
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif)
represent the ionized impurity concentration, impurity charge, vacuum permittivity, relative dielectric constant, and average effective mass, respectively. Note that
q0 is the Debye screening wavevector and
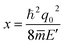
. Acoustic phonon scattering (
Pac) is treated within the deformation potential approach in a long wavelength acoustic phonon limit:
| |
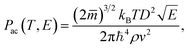 | (5) |
where
E and
D are the electron energy and deformation potential of the band energies calculated at the band extrema, respectively, while
ρ and
v are the mass density and average sound velocity, respectively. Optical polar scattering (
Ppolar) is defined using the Ridley model:
24| |
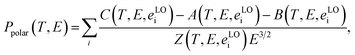 | (6) |
where the sum is overall longitudinal-optical phonons with energy
eLOi. More details about functions
A,
B,
C, and
Z can be found elsewhere.
25 The phenomenological parameters required in this expression were calculated using the first principle calculations. The effect of scattering can be estimated from the intrinsic parameters of the material, such as the dominant LO-phonon frequency (ℏ
ωLO), deformation potential (
D), effective mass (
m*), lattice (
εL) dielectric constants, average sound velocity (
v), high-frequency (
ε∞), and density of material (
ρ).
Table 2 illustrates all the parameters for the monolayer system in the
X- and
Y-direction. We computed the relaxation time for the monolayer system in the
X- and
Y-direction using these variables. The obtained results are presented in
Fig. 6(a) and (b). In both hole- and electron-doped systems, the relaxation time in the
Y-direction is longer than that in the
X-direction. Furthermore, for the monolayer system in both directions, the hole-doped system has a longer relaxation time than the electron-doped system because of its effective mass. Additionally, it is observed that the relaxation time becomes shorter as the doping concentration increases. This occurs because doping introduces more free charges (holes or electrons) into the materials, which leads to increased scattering events among charge carriers. Consequently, the average time between collisions, known as the relaxation time, decreases with higher doping concentrations. This increased scattering reduces the mobility of the charge carriers, impacting the overall electrical and thermal properties of the materials.
Table 2 Calculated effective mass ratio (m*/m), DP constant (D), high-frequency (ε∞) and lattice (εL) dielectric constants, average sound velocity (v), the dominant LO-phonon frequency (ℏωLO), and the density of material (ρ) of B2PN monolayer system
| System |
Direction |
Carrier type |
m*/m |
D (eV) |
ε∞ |
εL |
v (m s−1) |
ℏωLO (meV) |
ρ (kg m−3) |
| B2PN monolayer |
X |
e |
1.1 |
4.2 |
2.9 |
4.93 |
9579 |
141 |
4412 |
| h |
0.7 |
4.0 |
2.9 |
4.93 |
9579 |
141 |
4412 |
| YY |
e |
1.3 |
3.8 |
3.2 |
4.95 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 605 605 |
141 |
4412 |
| h |
0.2 |
3.5 |
3.2 |
4.95 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 605 605 |
141 |
4412 |
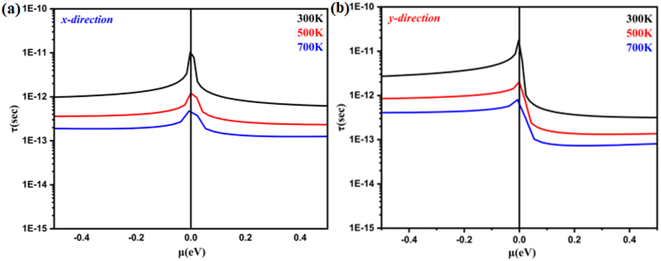 |
| | Fig. 6 Relaxation time as a function of the chemical potential of monolayer systems at 300 K, 500 K and 700 K in (a) the X-direction and (b) Y-direction. | |
Now, in Fig. 7(a) and (b), we compute the electrical conductivity using the Boltzmann method, which is incorporated into the Boltztrap2 code and may be written as follows:
| |
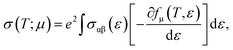 | (7) |
| |
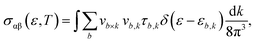 | (8) |
where the conductivity tensor is denoted by
σαβ (
ε), while
fμ and
e represent the Fermi distribution function and electron charge, respectively. The group velocity, cartesian indices, and carrier-dependent relaxation time are denoted by variables
vb,
k, and
τb,
k, respectively. Note that the electrical conductivity (
σ (
τ)) depends on the relaxation time.
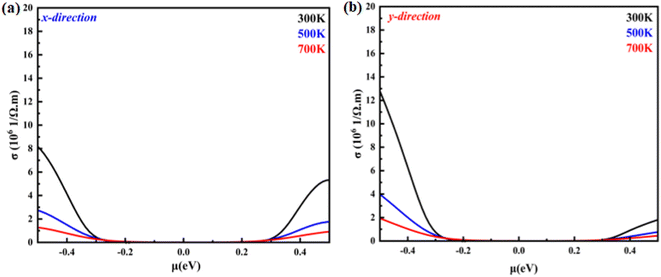 |
| | Fig. 7 Electrical conductivity as a function of the chemical potential of monolayer systems at 300 K, 500 K and 700 K in (a) the X-direction and (b) Y-direction. | |
Fig. 8(a) and (b) shows the temperature-dependent electrical conductivity of the monolayer system in the X- and Y-direction. The electrical conductivity of the hole-doped system is greater than that of the electron-doped system in the X- and Y-direction. This feature is attributed to the relaxation time. For the hole-doped system, its relaxation time is longer in the X- and Y-direction than that of the electron-doped system. For instance, the electrical conductivity in the X-direction for the hole-doped system is found to be 8 × 106 (Ω−1 m−1) with chemical potential values of 0.5 eV at 300 K, while in the Y-direction at the same temperature and same system, it is found to be 12.7 × 106 (Ω−1 m−1). It is observed that the electrical conductivity of the monolayer B2NP system is isotropic in both directions and developed nonlinearly with the chemical potential. Overall, the electrical conductivity in the Y-direction is greater than that in the X-direction.
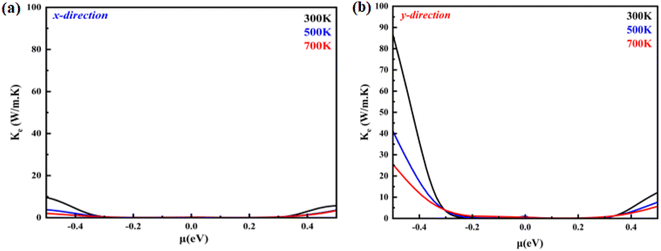 |
| | Fig. 8 Electronic thermal conductivity as a function of the chemical potential of monolayer systems at 300 K, 500 K and 700 K in (a) the X-direction and (b) Y-direction. | |
A material's thermal conductivity can be determined by measuring the heat conduction resulting from charge carrier movement and lattice vibration. The sum of the lattice thermal conductivity (κL) and electronic thermal conductivity (κe) can be used to express the total thermal conductivity (κ). The electronic thermal conductivity can be stated using the Boltzmann transport theory as follows:
| |
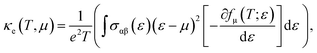 | (9) |
where
μ is the chemical potential,
σαβ(
ε) is the conductivity tensor,
e is the elementary charge,
T is temperature,
ε is the electron energy state and
fμ is the Fermi-Dirac distribution function. The electronic thermal conductivity of a monolayer system at temperatures of 300, 500, and 700 K is shown in the
X- and
Y-direction in
Fig. 8(a) and (b). We found that the B
2PN exhibited an isotropic behavior. The hole-doped system has higher electronic thermal conductivity than the electron-doped system in both directions. This is attributed to the relaxation time. It is further found that heat conductivity is greater in the
Y-direction than in the
X-direction. Conversely, lattice thermal conductivity can be written as follows:
| |
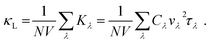 | (10) |
In this case, V and N denote the system's volume and unit cell. The phonon group velocity, phonon lifespan, and mode heat capacity are represented by vλ, τλ, and Cλ, respectively. The mode heat capacity is τλ = 1/2Γλ(ωλ), where Γ can be written as 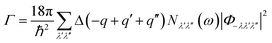 . Here, Φ−λλ′λ′′ is the phonon–phonon interaction strength among the three phonons λ, λ′, and λ′′. It can be computed from the second- and third-order force constants, while Nλ′λ′′(ω) = (nλ′ + nλ′′ + 1)δ(ω − ωλ′ − ωλ′′) + (nλ′ − nλ′′) × [δ(ω + ωλ′ − ωλ′′) – δ(ω − ωλ′ + ωλ′′)], where
. Here, Φ−λλ′λ′′ is the phonon–phonon interaction strength among the three phonons λ, λ′, and λ′′. It can be computed from the second- and third-order force constants, while Nλ′λ′′(ω) = (nλ′ + nλ′′ + 1)δ(ω − ωλ′ − ωλ′′) + (nλ′ − nλ′′) × [δ(ω + ωλ′ − ωλ′′) – δ(ω − ωλ′ + ωλ′′)], where 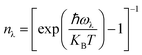 . Fig. 9 shows the lattice thermal conductivity of a monolayer system. The lattice thermal conductivity in the Y-direction is higher than that in the X-direction. For instance, at 300 K, the KL in the X-direction is found to be 8 (W m−1 K−1), while it is 17 (W m−1 K−1) in the Y-direction at the same temperature. Furthermore, it can be observed that as the temperature increases, the KL decreases. This behavior occurs because phonon–phonon scattering becomes more frequent at higher temperatures. Phonons, which are the main heat carriers in semiconductor solids, scatter more often as the temperature increases, leading to a reduction in the mean free path. Consequently, the lattice thermal conductivity decreases.26 Besides, we observed the anisotropic nature of lattice thermal conductivity. From the phonon dispersion curve, it can be observed that the propagation length of the acoustic modes in the Γ-X-direction is not the same as that of the Γ-Y-direction, indicating that its anisotropic nature is attributed to the crystal structure. From this behavior, we observe the anisotropic nature of lattice thermal conductivity in the X- and Y-direction.27
. Fig. 9 shows the lattice thermal conductivity of a monolayer system. The lattice thermal conductivity in the Y-direction is higher than that in the X-direction. For instance, at 300 K, the KL in the X-direction is found to be 8 (W m−1 K−1), while it is 17 (W m−1 K−1) in the Y-direction at the same temperature. Furthermore, it can be observed that as the temperature increases, the KL decreases. This behavior occurs because phonon–phonon scattering becomes more frequent at higher temperatures. Phonons, which are the main heat carriers in semiconductor solids, scatter more often as the temperature increases, leading to a reduction in the mean free path. Consequently, the lattice thermal conductivity decreases.26 Besides, we observed the anisotropic nature of lattice thermal conductivity. From the phonon dispersion curve, it can be observed that the propagation length of the acoustic modes in the Γ-X-direction is not the same as that of the Γ-Y-direction, indicating that its anisotropic nature is attributed to the crystal structure. From this behavior, we observe the anisotropic nature of lattice thermal conductivity in the X- and Y-direction.27
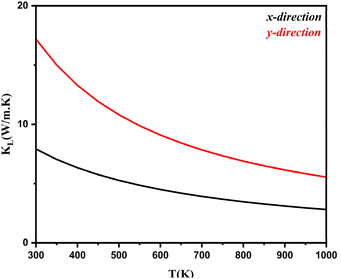 |
| | Fig. 9 Lattice thermal conductivity as a function of the chemical potential of monolayer systems at 300–1000 K in the X- and Y-direction. | |
Using all of the previously mentioned parameters, we determine the merit figure (ZT). The computed ZT values for the monolayer system in the X- and Y-direction are displayed in Fig. 10(a) and (b). The ZT values in both directions are greater for the hole-doped system than for the electron-doped system. This suggests that hole doping is more successful than electron doping. In addition, the ZT value is greater in the Y-direction than in the X-direction. For example, at 700 K, for p-type carriers, the value of ZT is 1.14, while in the X-direction, for p-type carriers, it becomes 0.4 at the same temperature. The maximum ZT is found at a carrier concentration of 4.5 × 1012 (cm−2) in the Y-direction, while in the X-direction, the maximum ZT is obtained at a carrier concentration of 9.4 × 1012 (cm−2). Furthermore, the obtained value of ZT is higher than the reported values for 2D hexagonal beryllium telluride (0.9 at 700 K) and Bi2Te3 (0.4).28,29 The obtained value is also greater from the reported Rb2NaTIZ6 (Z = Cl, Br and I) bulk material.30 Our results are in good agreement with previously studied thermoelectric materials, indicating their potential as promising candidates for further research.
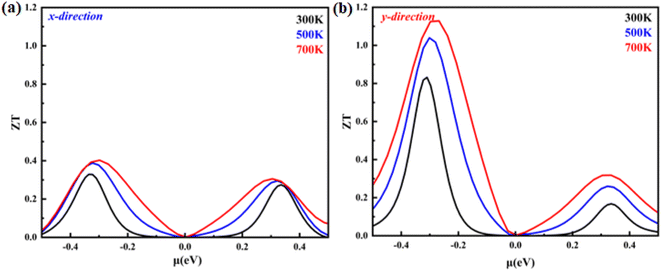 |
| | Fig. 10 Figure of merit (ZT) as a function of the chemical potential of monolayer systems at 300 K, 500 K and 700 K in (a) the X-direction and (b) Y-direction. | |
Conclusion
In this work, we investigated the electronic and thermoelectric properties of monolayer boron phosphorous nitride. The phonon dispersion curve indicates that these are dynamically stable. We performed an AMID simulation to ensure thermal stability and found that our material is thermally stable at 700 K. It was found that the band gap for the monolayer is 0.4 eV, indicating the semiconducting nature of the system. It is observed that the relaxation time is longer for the hole-doped system than for the electron-doped system. Besides, we investigated the Seebeck coefficient (S), electrical conductivity (σ), lattice thermal conductivity (κL), electronic thermal conductivity (κe) and figure of merit (ZT). The Seebeck coefficient has the same maximum value of 1.55 mV K−1 in both directions. The electrical conductivity is found to be greater for the hole-doped system than for the electron-doped system and is greater in the Y-direction than in the X-direction. The same trend is observed for electronic thermal conductivity. The lattice thermal conductivity has values of 8 (W m−1 K−1) and 17 (W m−1 K−1) in the X and Y-direction at 300 K, respectively. The figure of merit ZT is found to be greater in the Y-direction for the hole-doped system, and its value is 1.14, while in the X-direction, its value is 0.4 at 700 K. The results of the thermoelectric investigation indicate that these can be the best applicants for thermoelectric applications.
Data availability
The data will be made available on reasonable request.
Conflicts of interest
The authors declare no conflicting of interest.
Acknowledgements
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University Abha 61421, Asir, Kingdom of Saudi Arabia for funding this work through the Large Groups Project under the grant number RGP.2/545/44. Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2024R65), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
References
- F. Akhtar and M. H. Rehmani, Energy replenishment using renewable and traditional energy resources for sustainable wireless sensor networks: A review, Renewable Sustainable Energy Rev., 2015, 45(1), 769–784 CrossRef.
- V. Sharma, H. L. Kagdada, P. K. Jha, P. Śpiewak and K. J. Kurzydłowski, Thermal transport properties of boron nitride based materials: A review, Renewable Sustainable Energy Rev., 2020, 120(1), 109622 CrossRef CAS.
- S. I. Kim, K. H. Lee, H. A. Mun, H. S. Kim, S. W. Hwang, J. W. Roh, D. J. Yang, W. H. Shin, X. S. Li, Y. H. Lee and G. J. Snyder, Dense dislocation arrays embedded in grain boundaries for high-performance bulk thermoelectrics, Science, 2015, 348(6230), 109–114 CrossRef CAS PubMed.
- K. Biswas, J. He, I. D. Blum, C. I. Wu, T. P. Hogan, D. N. Seidman, V. P. Dravid and M. G. Kanatzidis, High-performance bulk thermoelectrics with all-scale hierarchical architectures, Nature, 2012, 489(7416), 414–418 CrossRef CAS PubMed.
- S. Cai, S. Hao, Z. Z. Luo, X. Li, I. Hadar, T. P. Bailey, X. Hu, C. Uher, Y. Y. Hu, C. Wolverton and V. P. Dravid, Discordant nature of Cd in PbSe: off-centering and core–shell nanoscale CdSe precipitates lead to high thermoelectric performance, Energy Environ. Sci., 2020, 13(1), 200–311 RSC.
- B. Poudel, Q. Hao, Y. Ma, Y. Lan, A. Minnich, B. Yu, X. Yan, D. Wang, A. Muto, D. Vashaee and X. Chen, High-thermoelectric performance of nanostructured bismuth antimony telluride bulk alloys, science, 2008, 320(5876), 634–638 CrossRef CAS.
- H. J. Wu, L. D. Zhao, F. S. Zheng, D. Wu, Y. L. Pei, X. Tong, M. G. Kanatzidis and J. Q. He, Broad temperature plateau for thermoelectric figure of merit ZT> 2 in phase-separated PbTe0. 7S0. 3, Nat. Commun., 2014, 5(1), 4515 CrossRef CAS PubMed.
- Z. Jia, Z. Zuo, Y. Yi, H. Liu, D. Li, Y. Li and Y. Li, Low temperature, atmospheric pressure for synthesis of a new carbon Ene-yne and application in Li storage, Nano Energy, 2017, 33, 343–349 CrossRef CAS.
- Q. Fan, L. Yan, M. W. Tripp, O. Krejčí, S. Dimosthenous, S. R. Kachel, M. Chen, A. S. Foster, U. Koert, P. Liljeroth and J. M. Gottfried, Biphenylene network: A nonbenzenoid carbon allotrope, Science, 2021, 372(6544), 852–856 CrossRef CAS PubMed.
- Q. Li, Y. Li, Y. Chen, L. Wu, C. Yang and X. Cui, Synthesis of γ-graphyne by mechanochemistry and its electronic structure, Carbon, 2018, 136, 248–254 CrossRef CAS.
- X. Li, H. Zhang and L. Chi, On-Surface Synthesis of Graphyne-Based Nanostructures, Adv. Mater., 2019, 31(42), 1804087 CrossRef CAS.
- C. Zheng, J. Zhu, C. Yang, C. Lu, Z. Chen and X. Zhuang, The art of two-dimensional soft nanomaterials, Sci. China: Chem., 2019, 62, 1145–1193 CrossRef CAS.
- W. J. Ong, L. L. Tan, Y. H. Ng, S. T. Yong and S. P. Chai, Graphitic carbon nitride (g-C3N4)-based photocatalysts for artificial photosynthesis and environmental remediation: are we a step closer to achieving sustainability?, Chem. Rev., 2016, 116(12), 7159–7329 CrossRef CAS PubMed.
- J. Q. Zhou, L. Li, C. Fu, J. Wang, P. Fu, C. P. Kong, F. Q. Bai, R. I. Eglitis, H. X. Zhang and R. Jia, A novel TC 3 N and seawater desalination, Nanoscale, 2020, 12(8), 5055–5066 RSC.
- X. Deng, M. Si and J. Dai, Communication: oscillated band gaps of B/N-codoped α-graphyne, J. Chem. Phys., 2012, 137(20), 201101 CrossRef PubMed.
- Z. L. Sun, Z. G. Shao, C. L. Wang and L. Yang, Electronic and optical properties of boron and nitrogen pair co-doped 6, 6, 12-graphyne nanosheet, Carbon, 2016, 110, 313–320 CrossRef CAS.
- A. Pakdel, Y. Bando and D. Golberg, Nano boron nitride flatland, Chem. Soc. Rev., 2014, 43(3), 934–959 RSC.
- X. D. Li and X. L. Cheng, Predicting the structural and electronic properties of two-dimensional single layer boron nitride sheets, Chem. Phys. Lett., 2018, 694, 102–106 CrossRef CAS.
- M. R. Niazian, Investigation of the thermoelectric properties of the perfect and defective (3, 7) boron nitride nanosheets by DFT, Pramana, 2023, 97(1), 15 CrossRef CAS.
- A. Algahtani, N. U. Khan, J. Iqbal, V. Tirth, S. Abdullaev, M. S. Refat, A. M. Alsuhaibani, A. M. Henaish, A. Zaman and H. Fetooh, Exploring the structural, opto-electronics and elastic properties of fluoro-perovskites KXF3 (X= Ir, Rh): A first-principles study, Inorg. Chem. Commun., 2023, 158, 111542 CrossRef CAS.
- U. A. Khan, N. U. Khan, A. H. Alghtani, V. Tirth, S. J. Ahmed, M. Sajjad, A. Algahtani, T. Shaheed and A. Zaman, First-principles investigation on the structural, electronic, mechanical and optical properties of silver based perovskite AgXCl3 (X= Ca, Sr), J. Mater. Res. Technol., 2022, 20, 3296–3305 CrossRef CAS.
- B. Marfoua and J. Hong, High thermoelectric performance in two dimensional chalcogenides systems: GaSe and GaTe, Nanotechnology, 2020, 32(11), 115702 CrossRef.
- G. K. Madsen, J. Carrete and M. J. Verstraete, BoltzTraP2, a program for interpolating band structures and calculating semi-classical transport coefficients, Comput. Phys. Commun., 2018, 231, 140–145 CrossRef CAS.
- G. Casu, A. Bosin and V. Fiorentini, Efficient thermoelectricity in Sr 2 Nb 2 O 7 with energy-dependent relaxation times, Phys. Rev. Mater., 2020, 4(7), 075404 CrossRef CAS.
- B. K. Ridley, Polar-optical-phonon and electron-electron scattering in large-bandgap semiconductors, J. Phys.: Condens. Matter, 1998, 10(30), 6717 CrossRef CAS.
- P. Govindaraj, K. Murugan and K. Venugopal, Role of lattice thermal conductivity in thermoelectric properties of chalcopyrite-type antimonides XSiSb2 (X= Mg, Be): A DFT insight, Mater. Chem. Phys., 2023, 295, 127190 CrossRef CAS.
- X. Gu and R. Yang, Phonon transport in single-layer transition metal dichalcogenides: A first-principles study, Appl. Phys. Lett., 2014, 105(13), 131903 CrossRef.
- A. Makavana, J. Gajjar, P. Kumar and D. R. Roy, Structural, Electronic, Thermoelectric and Optical properties of 2D hexagonal Beryllium Telluride under DFT Investigation, Comput. Condens. Matter, 2024, e00948 CrossRef.
- Q. Wang, Y. Tang, A. Miura, K. Miyazaki, Z. Horita and S. Iikubo, Improving thermoelectric properties of Bi2Te3 by straining under high pressure: Experiment and DFT calculation, Scr. Mater., 2024, 243, 115991 CrossRef CAS.
- S. H. Shah, T. Huang, S. Shakeel, S. Khan, M. W. Ashraf and G. Murtaza, Comprehensive study of structural, elastic, electronic, optical, and thermoelectric properties of Rb2NaTlZ6 (Z= Cl, Br, and I) by DFT, Mater. Sci. Semicond. Process., 2024, 178, 108400 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *o
*o

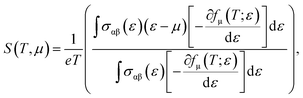
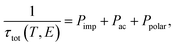
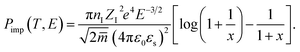
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) represent the ionized impurity concentration, impurity charge, vacuum permittivity, relative dielectric constant, and average effective mass, respectively. Note that q0 is the Debye screening wavevector and
represent the ionized impurity concentration, impurity charge, vacuum permittivity, relative dielectric constant, and average effective mass, respectively. Note that q0 is the Debye screening wavevector and 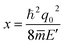 . Acoustic phonon scattering (Pac) is treated within the deformation potential approach in a long wavelength acoustic phonon limit:
. Acoustic phonon scattering (Pac) is treated within the deformation potential approach in a long wavelength acoustic phonon limit: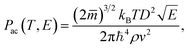
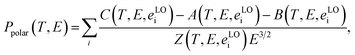
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 605
605![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 605
605
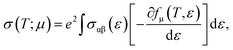
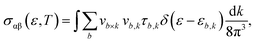


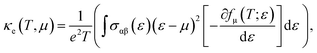
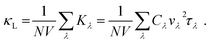
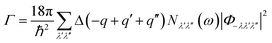 . Here, Φ−λλ′λ′′ is the phonon–phonon interaction strength among the three phonons λ, λ′, and λ′′. It can be computed from the second- and third-order force constants, while Nλ′λ′′(ω) = (nλ′ + nλ′′ + 1)δ(ω − ωλ′ − ωλ′′) + (nλ′ − nλ′′) × [δ(ω + ωλ′ − ωλ′′) – δ(ω − ωλ′ + ωλ′′)], where
. Here, Φ−λλ′λ′′ is the phonon–phonon interaction strength among the three phonons λ, λ′, and λ′′. It can be computed from the second- and third-order force constants, while Nλ′λ′′(ω) = (nλ′ + nλ′′ + 1)δ(ω − ωλ′ − ωλ′′) + (nλ′ − nλ′′) × [δ(ω + ωλ′ − ωλ′′) – δ(ω − ωλ′ + ωλ′′)], where 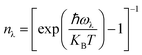 . Fig. 9 shows the lattice thermal conductivity of a monolayer system. The lattice thermal conductivity in the Y-direction is higher than that in the X-direction. For instance, at 300 K, the KL in the X-direction is found to be 8 (W m−1 K−1), while it is 17 (W m−1 K−1) in the Y-direction at the same temperature. Furthermore, it can be observed that as the temperature increases, the KL decreases. This behavior occurs because phonon–phonon scattering becomes more frequent at higher temperatures. Phonons, which are the main heat carriers in semiconductor solids, scatter more often as the temperature increases, leading to a reduction in the mean free path. Consequently, the lattice thermal conductivity decreases.26 Besides, we observed the anisotropic nature of lattice thermal conductivity. From the phonon dispersion curve, it can be observed that the propagation length of the acoustic modes in the Γ-X-direction is not the same as that of the Γ-Y-direction, indicating that its anisotropic nature is attributed to the crystal structure. From this behavior, we observe the anisotropic nature of lattice thermal conductivity in the X- and Y-direction.27
. Fig. 9 shows the lattice thermal conductivity of a monolayer system. The lattice thermal conductivity in the Y-direction is higher than that in the X-direction. For instance, at 300 K, the KL in the X-direction is found to be 8 (W m−1 K−1), while it is 17 (W m−1 K−1) in the Y-direction at the same temperature. Furthermore, it can be observed that as the temperature increases, the KL decreases. This behavior occurs because phonon–phonon scattering becomes more frequent at higher temperatures. Phonons, which are the main heat carriers in semiconductor solids, scatter more often as the temperature increases, leading to a reduction in the mean free path. Consequently, the lattice thermal conductivity decreases.26 Besides, we observed the anisotropic nature of lattice thermal conductivity. From the phonon dispersion curve, it can be observed that the propagation length of the acoustic modes in the Γ-X-direction is not the same as that of the Γ-Y-direction, indicating that its anisotropic nature is attributed to the crystal structure. From this behavior, we observe the anisotropic nature of lattice thermal conductivity in the X- and Y-direction.27





