DOI:
10.1039/D4RA04957H
(Paper)
RSC Adv., 2024,
14, 25599-25618
Pyrolysis study of a waste plastic mixture through different kinetic models using isothermal and nonisothermal mechanism†
Received
9th July 2024
, Accepted 31st July 2024
First published on 14th August 2024
Abstract
Pyrolysis can be a convenient way to produce oils and gases simultaneously, as well as hydrocarbons and even crude petrochemicals. It can also be used to produce energy from a waste plastic mixture (WPM). To ascertain the kinetics parameters at the heating rates of 5, 10, 20, and 50 °C min−1, various kinetic models, including (a) model-fitting and (b) model-free, which are further separated into isothermal and non-isothermal categories, have been selected. The apparent activation energy (Ea) and pre-exponential factor (Aa) were calculated using the Friedman (model-free isothermal), KAS, FWO (model-free non-isothermal), and Coats–Redfern (model-fitting non-isothermal) approaches. The activation energy (Ea), pre-exponential component (Aa), and overall reaction order (n) were also calculated using a multi-linear regression methodology. In addition, the solid fuel characterization of WPM has been compared with previous literature results, as have the physico-chemical characteristics of pyrolytic oil. Finally, a brief mention of WPM's kinetic process has been included in this work. However, the results indicated two stages of thermal degradation and volatilization of the WPM zone during pyrolysis (410–510 °C, 510–770 °C). In the temperature range of 410–510 °C, 510–770 °C, two-stage thermal degradation zones are used to analyze the kinetic parameters for WPM. The result showed the average activation values obtained by the KAS, FWO, and Friedmam methods were 297.61, 295.25, and 267.26 kJ mol−1. In the case of the Coats–Redfern methods, the lowest activation energy was obtained by the PT1 kinetic model at 22.56 kJ mol−1, and the highest activation energy was found in the D3 kinetic model at 418.80 kJ mol−1 in the temperature zone of 410–510 °C. The temperature zone with the lowest activation energy was found to be between 510 °C and 770 °C.
Introduction
From the early 1950s until the 1970s, very little plastic was produced globally. Plastic generation had been controlled during this time thanks to various recycling techniques. As time went on, however, its output tripled between the 1970s and the 1990s; in fact, every decade saw a corresponding increase in plastic manufacturing. The production of plastic waste increased dramatically after the year 2000, more so in a single decade than it had in the preceding fifty years.1 There are several ways that plastic waste is produced. For example, one million plastic bottles are bought worldwide every minute. Despite this, five trillion plastic bags are used annually, half of which are single-use items that are merely tossed away after usage. Approximately 400 to 450 million tonnes of plastic waste are produced annually in the modern period, and if preventive action is not taken today, it appears that eventually waste plastic will blanket the entire planet. According to UN reports, there are between 75 and 199 million tons of plastic waste in the world's oceans.1 The condition of aquatic ecosystems is terrible, and as a result, marine aquatic life is in jeopardy. It is true that plastic has some useful applications, particularly when it comes to single-use items. However, because plastic has a huge global market, some segments of our society are directly or indirectly dependent on the plastic industry or its manufacturing processes. Additionally, plastic has negative effects on the environment, society, economy, soil, and human health. Of all the contaminants found in our environment, microplastics appear to be particularly harmful to human health, food, polluted soil, and other areas. Approximately 36–40% of all plastics produced are used in food and beverage packaging, as well as single-use items, according to the UN Environment Program.1 The following are the most prevalent forms of waste plastic that are discovered in the environment: (a) water bottles, dispensing containers, cookie trays, and other items made of polyethylene terephthalate (PET); (b) shampoo bottles, milk bottles, freezer bags, and ice cream containers made of high-density polyethylene (HDPE); (c) food packaging film, trays, bags, containers, and other items made of low-density polyethylene (LDPE); (d) polypropylene (PP) used in single-use face masks, ice cream tubs, microwave plates, potato chip bags, bottle caps, etc.; (e) polystyrene (PS) plates, cups, silverware, etc.; (f) expanded polystyrene (EPS) used in hot beverage cups, protective packaging, etc. The world's worrying rise in pollution and global warming has led to the discovery of renewable energy sources that help to reduce environmental problems. Bio-oil, whether derived from plastic waste or agricultural residue, has a great deal of promise to soon replace fossil fuels. India, which is acknowledged as one of the world's agricultural nations, produces over 500 million tons of agricultural residues annually from various sources.2 Although there is a lack of trustworthy data available, India secretly created a significant amount of plastic waste annually. About 70% of all plastic wastes are polyolefins, or wastes made of polypropylene (PP), polyurethane (PE), low-density polyethylene (LDPE), and high-density polyethylene (HDPE). Other wastes made of plastic include polystyrene (PS), polyethylene terephthalate (PET), and polyvinyl chloride (PVC).3 Since pyrolysis yields valuable products like pyrolytic oil, non-condensable gases with a specific calorific value (CV), and char formed during slow pyrolysis, recovering plastic wastes requires more energy than pyrolysis itself. There were a lot of papers accessible about pyrolysis of plastic waste. A. Lopez et al.4 conducted research on how temperature and time affect product production. They discovered that 500 °C is the ideal temperature for product yield, conversion, and quality of items at their peak. Time also has minimal effect on this temperature. The pyrolysis of plastic wastes in tubular reactors was thoroughly examined by B. Csukas et al.5 utilizing an algorithm and a modeling methodology based on direct computer mapping. The ideal temperature range for this result was 465–545 °C, and the feeding rate was maintained between 6 and 20 g min−1. The model included a four-step breakdown mechanism for heavy oil, gas, naphtha, and middle distillate. Over the past few decades, a number of studies on the pyrolysis or recycling of plastic wastes have been published.6–14 The thermal plasma pyrolysis of waste rubber, including the characterization of its gaseous and solid products, was studied by Huang et al.15 The results indicated that the predominant gaseous compositions were H2, CO, C2H2, CH4, and C2H4. The gas's heating value needed to be between 5 and 9 MJ Nm−3. The solid carbons had a surface area of roughly 65 m2 g−1 and made up more than 80% of the elemental carbon. Under nonisothermal conditions, Y. S. Kim and co-authors16 investigated the thermodynamic parameters in the thermal breakdown of waste plastic and waste lubricant oil compound. The residence where polyethylene (PE), polypropylene (PP), polystyrene (PS), and polyethylene terephthalate (PET) were gathered is the source of the plastic waste used in this investigation. Using a semibatch bench-scale device, C. Ludlow-Palafox et al.17 investigated the pyrolysis of plastic derived from high density polyethylene and aluminum/polymer laminates using microwaves. Pyrolysis studies were conducted in the 500–700 °C range, and it was discovered that there was a relationship between temperature, the length of time the pyrolytic products were left in the reactor, and the chemical composition of the hydrocarbon fraction that was produced. An essay on producing valuable fuels from waste plastics through thermal and catalytic processes was reviewed by J. Aguado18 et al. Plastics undergo heat cracking, which mostly results in different hydrocarbon distributions that need to be processed further to produce useful products. Waste plastic oil (WPO), which is produced by pyrolyzing plastic waste and municipal solid waste, is a promising substitute fuel due to its physical and carbon chain similarities with diesel fuel. Naphtha, another ingredient in WPO, has a gasoline-like taste and might not be the best fit for a diesel engine. Distilled waste plastic oil (WPOD) is the end product of the process that technically should remove naphtha from WPO.19 The effects of various fuels burnt in a diesel engine on emissions from exhaust gases and combustion properties are being experimentally investigated in this work. Nitrogen oxide levels are higher in WPO and WPOD fuels than in diesel fuel. Their shorter carbon chains, however, result in a lower smoke index. Nonetheless, due to their high cetane index and calorific value, brake specific fuel consumption and brake thermal efficiency are advantageous. The amount of plastics consumed globally includes blends, alloys, high performance and specialty plastics, thermosetting plastics, and individual plastics like polythene (PE) (33.5%), polypropylene (PP) (19.5%), polyvinylchloride (PVC) (16.5%), polystyrene (PS) (8.5%), polyethylene terephthalate (PET) and polyurethane (PU) (5.5%), and styrene copolymers (3.5%).20 There are four different approaches to managing plastic waste: mechanical recycling, biological recycling, thermochemical recycling, and land filling. Additional primary product from separated/isolated plastic and secondary product from mixed plastic was categorized using mechanical recycling. Waste plastics are thermochemically converted through pyrolysis, also known as feedstock recycling, and thermal recycling, also known as incineration. Pyrolysis and burning both provide important fuels or chemicals and heat energy.21 Another investigation employed both natural and commercial Y-zeolite catalysts. The findings demonstrate that product yields and the quality of liquid and solid products are significantly impacted by the types of feedstock used. Waste HDPE yielded the largest liquid fraction. The gaseous fraction increased and the liquid fraction decreased in the presence of catalysts. Additionally, pyrolysis of municipal plastic wastes yielded solid products with a higher heating value than biomass and low rank coal.22 Another study looked into the use of low-cost, bentonite clay pellets that were free of binder and it also emphasizes how crucial it is to comprehend catalyst creation, electrochemical reaction systems, and reaction mechanisms.23,24 The suggested course uses gasification to turn plastic waste into methanol. Kinetic modeling of syngas treatments along with thermodynamic characterization of the feedstock is used to build and simulate the process. A polypropylene/polyethylene mixture containing varying amounts of polystyrene is used to assess how the process behaves when the feedstock is less hydrogen-rich. Plastic gasification, light hydrocarbon treatment, syngas conditioning, methanol synthesis, and methanol distillation are the steps in the process.25 Prior
studies have shown that the pyrolysis of individual plastics can recover more than 80 wt% of oil—a higher percentage than that of biomasses derived from wood.26 It was also investigated how different atmospheres (carbon dioxide and nitrogen) affected the pyrolysis properties of single and mixed polymers. Basically, during the pyrolysis of plastic waste, four distinct mechanisms could take place: chain stripping, random-chain scission, end-chain scission or depolymerization, and cross-linking.22,27 There has been a lot of research done on the pathways of plastic waste's value-adding due to the ongoing rise in waste production and the necessity to create more environmentally friendly waste management regulations.28 The dissolution/reprecipitation technique and pyrolysis are used to investigate the recycling of waste products and model polymers based on low-density polyethylene (LDPE), high-density polyethylene (HDPE), or polypropylene (PP). In every instance, the polymer recovery exceeded 90%. Pyrolysis produced an aliphatic composition primarily composed of hydrocarbons (alkanes and alkenes), according to analysis of the resulting gases and oils. This composition has a great deal of potential for recycling back into the petrochemical industry as a feedstock for the production of new plastics or refined fuels.29 Conventional pyrolysis of high density polyethylene (HDPE) typically yields substantial amounts of waxy compounds, or aliphatic hydrocarbons, that need further refining, but only tiny amounts of monomer (ethylene, C2H4). Cold plasma assisted pyrolysis of waste HDPE was used in this studies to achieve valorization. Up to 22–25 wt% of ethylene was recovered from HDPE waste with the use of cold plasma, which is up to 55 times more than what is obtained from the traditional pyrolysis of waste HDPE. With just 3–10 wt% of HZMS-5 or sulphated zirconia added, the gas (up to 41 wt%) and consequently the ethylene output at low temperatures were doubled, according to catalytic cold plasma pyrolysis.30 Apart from this electrochemical hydrogenation (ECH) is a novel technique for improving pyrolysis oil from biomass and plastic feedstocks and another effective way to break down polymers into oligomers and tiny oxidized compounds is through oxidative degradation.31,32 In order to create a kinetic model that accurately depicts the interactions between components, it is imperative to recognize the decomposition behavior of both individual and mixture components. Numerous studies have examined the kinetics of single MPW (Municipal Plastic Waste) mixed fractions33–38 or concentrated on basic binary and tertiary mixes.36,39 Kinetic research has produced erratic and dispersed results. The commercial grade (Ea) values for HDPE, LDPE, PP, and PS were reported by Sorum et al.33 to be 445.1 kJ mol−1, 340.8 kJ mol−1, 336.7 kJ mol−1, and 311.5 kJ mol−1, respectively. But according to Wu et al.,34 the figures for HDPE were 233–326 kJ mol−1, LDPE was 194–206 kJ mol−1, PP was 184–265 kJ mol−1, and PS was 172 kJ mol−1. Depending on the type of bottle and the method used, Saha and Ghoshal37 discovered that the (Ea) and pre-exponential values for various PET drinking bottles ranged from 2.83 × 1011 to 1.18 × 1025 and 162.15–338.98 kJ mol−1, respectively. Recycled plastic has been discovered to have 250 and 150 to 290 kJ mol−1, according to Encinar et al.40 The review also emphasizes the current difficulties in this area related to the industrial upscaling of these procedures.41 The full plastic life cycle and available solutions for managing plastic waste can help remove obstacles to the recycling of industrial chemicals and raise awareness of potential applications for these materials.42 One method that shows promise for the closed-loop recycling of plastic wastes is catalytic depolymerisation.43 The majority of WPM pyrolysis investigations assume a first order decomposition, which oversimplifies the mechanism of reaction and results in erroneous process projections. This could lead to significant problems when building WPM pyrolysers. With the use of thermogravimetric analysis (TGA), this work aimed to create a kinetic model for determining the actual reaction mechanism of WPM pyrolysis through experimental and numerical means. Because of the discrepancy between the apparent activation energy with conversion and the kinetic model with heating rate, the results demonstrated that a complex mechanism rather than simple first order happens during the breakdown. The outcomes of the linear model fitting process supported the theory that the WPM decomposition mechanism is a combination of series and parallel reactions, which also accorded well with experimental evidence. This paper's primary goal is to identify the likely reaction pathways that lead to the products' characterization in bio-oils. In order to comprehend the thermal degradation mechanism for waste plastic mixture (WPM) better, kinetic study was also conducted both isothermal and nonisothermal. Plastic wastes only created linear and low molecular weight hydrocarbons after pyrolysis. Thus, another goal of this work is to examine how the chemical composition of products depends on the raw materials that demonstrate unique characteristics in WPM.
Experimental section
Materials and methods
The waste made of plastic was collected from Mumbai, India's outskirts. Every major city in India has a scrap depositor where all debris, including plastic waste, is disposed of. Using an automatic proximate analyzer from Advance Research Instruments Company, New Delhi, India (APA 2), the proximate analysis of WPM materials (Table 2) was performed in accordance with ASTM methods (moisture: ASTM D3173; ash: ASTM D3174; volatile matter: ASTM D3175; and fixed carbon: by difference ASTM E1131-08). With a temperature control precision of ±5 °C, the furnace utilized for this purpose could measure temperatures between ambient temperature and 1000 °C. The analytical range was 0.2–100%, and the entire amount of time needed was almost 240 minutes. With an accuracy of 0.1 mg, the APA 2 electronic balance could measure up to 110 g. The ASTM D-2015 method was used to determine the calorific value in a Toshiba India digital bomb calorimeter, and a CHNS analyzer (vario MICRO cube) was used for the ultimate analysis. The temperatures of the combustion and reduction columns for the CHNS analyzer were 1150 °C and 850 °C, respectively. Sulphanilamide was the standard, and 1–3 mg of sample was needed. Helium gas served as the carrier gas and O2 as the oxidizing agent. The samples were put through TGA in Netzsch, TG209 F1, Libra, at 5, 10, 20, and 50 °C min−1, with a 50 mL min−1 nitrogen flow rate. The materials were dried for one hour at 110 °C. Between 35 °C and 1000 °C, the protective thermobalance was set at 20 mL min−1. The bio-oil was also characterized using GC-MS and the recovered pyrolytic oil was initially characterized using a Shimadzu GC MS-QP2010 gas chromatograph/mass spectrometer and A PerkinElmer Spectrum GX FT-IR analyzer was used to perform the FT-IR analysis. The experimental design and methodology were the same as those detailed in our earlier publication as shown in Fig. 1.49,50
Table 1 Most common and widely used mechanism of solid-state processes (Coats–Redfern methods) (ref. 58)
| Mechanism |
Symbol |
g(α) |
| Order of reaction |
| First order (Mapel unimolecular law) |
FO1 |
−ln(1 − α) |
| Second order |
FS2 |
−(1 − α)−1 − 1 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Exponential nucleation |
| Power law, n = 3/2 |
PL1 |
α3/2 |
| Power law, n = 1/2 |
PL2 |
α1/2 |
| Power law, n = 1/3 |
PL3 |
α1/3 |
| Power law, n = 1/4 |
PL4 |
α1/4 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Random nucleation and nuclei growth |
| Avrami-Erofe'ev, n = 1 |
AE1 |
[−ln(1 − α)]1/n |
| Avrami-Erofe'ev, n = 2 |
AE2 |
[−ln(1 − α)]1/n |
| Avrami-Erofe'ev, n = 3 |
AE3 |
[−ln(1 − α)]1/n |
| Avrami-Erofe'ev, n = 4 |
AE4 |
[−ln(1 − α)]1/n |
| Prout–Tompkins |
PT1 |
ln(α/(1 − α)) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Diffusion |
| One dimensional, 1D (Parabolic law) |
D1 |
α2 |
| Two dimensional, 2D (Valensi equation) |
D2 |
(1 − α)ln(1 − α) + α |
| Three dimensional, 3D (Jander equation) |
D3 |
[1 − (1 − α)1/3]2 |
| Three dimensional, 3D (Ginstling–Brounshtein equation) |
D4 |
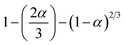 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Phase boundary controlled equation |
| Contracting area, cylindrical symmetry |
R2 |
1 − (1 − α)1/2 |
| Contracting volume, spherical symmetry |
R3 |
1 − (1 − α)1/3 |
Table 2 Proximate and ultimate analysis of WPM (solid)a
| Proximate analysis (wt%) |
| Type of feedstock |
Moisture (a.d.b) |
Volatile matters (a.d.b) |
Ash (a.d.b) |
Fixed carbon (a.d.b) |
HHV of plastic oil (MJ kg−1) |
Ref. |
| (a.d.b = air dried basis). |
| PP, PE, PVC |
0.82 |
87.2 |
4.17 |
7.81 |
33.3 |
44 |
| PP, PS |
0.32 |
99.13 |
— |
0.55 |
42.65 |
45 |
| PP waste |
— |
93.77 |
— |
1.62 |
45.20 |
46 |
| Tire particle |
0.93 |
63.67 |
8.97 |
26.67 |
37.32 |
47 |
| Waste plastic mixture (WPM) |
1.48 |
69.18 |
19.55 |
9.78 |
32.64 |
Present study |
| Ultimate analysis (wt% dried basis) |
| |
C |
H |
N |
S |
O |
Other (Cl) |
|
| PP, PE, PVC |
72.56 |
11.17 |
3.82 |
0.227 |
— |
12.22 |
44 |
| PP, PS |
81.81 |
5.68 |
0.15 |
0.11 |
— |
0.08 |
45 |
| PP waste |
83.65 |
14.27 |
0.67 |
0.1 |
0.15 |
1.16 |
46 |
| Tire particle |
80.5 |
7.33 |
0.33 |
1.57 |
10.27 |
— |
47 |
| PS, PE, PP, PET |
80.4 |
13 |
Trace |
0.0 |
6.6 |
— |
48 |
| Waste plastic mixture (WPM) |
64.49 |
9.93 |
1.14 |
— |
— |
— |
Present study |
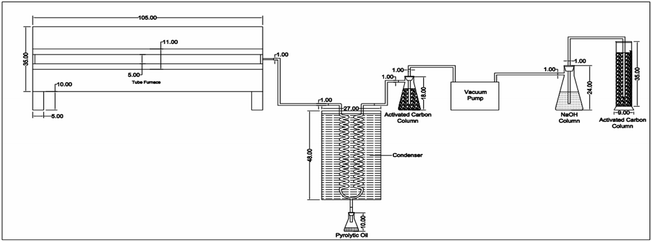 |
| | Fig. 1 Schematic diagram of pyrolytic oil set-up (ref. 50). | |
Kinetic modelling
WPM kinetic analysis yields the essential details regarding their thermal degradation, including the temperature at which pyrolysis should begin, its maximum rate, the temperature zone in which it should finish, and the rate at which it should heat up. The chemical composition of products and the makeup of bio-oils are greatly influenced by the aforementioned factors.
The Arrhenius approach and solving through multilinear regression. A solid-state material's rate of decomposition is temperature-dependent, and the conversion is best expressed by the following equation.:50–52| |
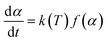 | (1) |
The weight loss from a degraded sample with rising temperature is known as conversion, or α.
| |
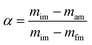 | (2) |
mim is the initial mass,
mam is the mass at time
t and
mfm is the final mass of the sample.
The Arrhenius equation provides the finest description of the temperature-dependent function, often known as the rate constant, or k(T) as follows:
| |
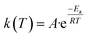 | (3) |
where
Ea is the apparent activation energy (kJ mol
−1),
T is the absolute temperature (K),
R is the gas constant (8.314 J mol
−1 K
−1) and
A is the pre-exponential factor (min
−1). Inserting
eqn (2) and
(3) into
eqn (1) gives the
eqn (4), which represents the equation for calculating the reaction kinetic parameters from the TGA results.
| |
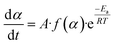 | (4) |
The function f(α) can be expressed as,
Here,
n is the reaction order, and substituting the value of
f(
α) in
eqn (4) gives the expression of the reaction rate as follows:
| |
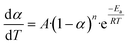 | (6) |
For a non-isothermal case, the linear heating rate is 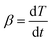 and the following equation can be applied:
and the following equation can be applied:
| |
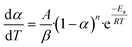 | (7) |
| |
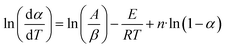 | (8) |
The above equation can be written in the following simplified form;
where
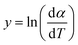
,
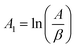
,
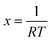
,
z = ln(1 −
α),
B1 = −
E and
C1 =
n| |
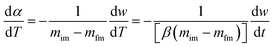 | (10) |
The data from the TGA and DTG curves may now be used to do multilinear regression and calculate A1, B1, and C1. Table 3 lists the kinetic characteristics of the pyrolysis of solid WPM at various heating rates.
The model-free isothermal Friedman method. For a given value of conversion (α), the apparent activation energy (Ea) can be determined from the slope of the plot of ln(βdα/dT) against 1/T at different heating rates using this approach,53 as well as in eqn (11).| |
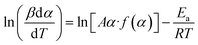 | (11) |
The model-free non-isothermal Flynn–Wall–Ozawa method. Using the FWO approach54,55 one can determine the apparent activation energy (Eaα) for a given conversion value at various heating rates by plotting the natural logarithm of the heating rates (ln(βj)) against 1000/Tαj, as in eqn (12).| |
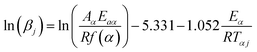 | (12) |
where f(α) is the value of conversion, and subscripts j and α indicate the values of the heating rate and conversion, respectively.
The Kissinger–Akahira–Sunose method. According to Akahira56 and Kissinger,57 the KAS technique yields the following expression:| |
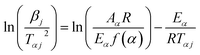 | (13) |
with the aforementioned calculation, the activation energy may be found from the slope −Eα/R, and the apparent activation energy can be computed from a plot of ln(βj/Tαj2) against 1000/Tαj for a given value of conversion, α.
Model fitting methods. This model fitting mainly involves Coats–Redfern (CR) methods, is most common and widely accepted proposed in 196458 which is defined as follows obtained from 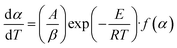 equation.
equation.| |
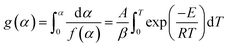 | (14) |
g(α) is represented as the form of integral reaction model. There are many such integral function g(α) is listed in literature and is summarized in Table 1.| |
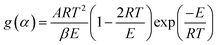 | (15) |
Now, above eqn (15) is rearranged and taking ‘log’ for the side provides logarithmic form as follows:
| |
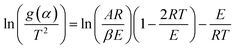 | (16) |
Since the value of
E lie in the range 100 to 400 kJ mol
−1, depending upon the samples, plastic wastes,
etc., so the term 2
RT/
E ≪ 1 can be neglected for further complications.
Eqn (16) can be rewritten as
| |
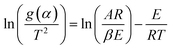 | (17) |
Putting different form of g(α) into eqn (17) and plotting 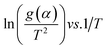 provides to a result in a straight line, the slope has been calculated from (−E/R) and the intercept respectively giving the values of E and A.
provides to a result in a straight line, the slope has been calculated from (−E/R) and the intercept respectively giving the values of E and A.
Result and discussion
Effect of physico-chemical properties of WPM
It was discovered that the moisture content, volatile matters and fixed carbon had an effect on the pyrolysis behavior of material during the pyrolysis of WPM. Greater moisture content in the materials led to the formation of oxygenated functional groups in pyrolytic oils, which often decreased the oil's calorific value. The conversion of condensable gases into bio-oil and the outflow of non-condensable gases from the system are the main effects of volatile matters on the production of oil.
Waste plastic has been the subject of several research studies, and an analysis of its oil qualities greatly depends on its physico-chemical characteristics. WPM has undergone both proximate and ultimate examination in order to accomplish this. The result indicates that the volatile matters are 69.18%, which is similar to the other result. Its value is low because of the high amount of ash (19.55%) identified in this study, which comprises pollutants that were collected from a Mumbai, India plastics dumpyard somewhere else.
With the use of proximate analysis, the calorific value was determined using the established correlations from the literature. The result demonstrates that the value ranges from the lowest 13.92 to the maximum 16.55 MJ kg−1, as indicated in Table 3. The correlations were used to calculate the CV of WPM (solid). Thus, it makes sense that liquid fuel should be produced from solid fuel since it is easier to carry. Equations for HHV (higher heating value) determination from proximate analysis are available in the literature.
Table 3 HHV calculated from the correlations as found in previous literature
| Ref. |
CV of solid wastes (WPM) |
| 44 |
45 |
46 |
47 |
WPM (kJ kg−1) |
Ref. |
| HHV = 76.56 − 1.3(VM + ash) + 7.03 × 10−3(VM + ash)2 |
16.46 |
16.77 |
16.47 |
16.46 |
16.55 |
59 |
| HHV = 354.3FC + 170.8VM (considering VM + FC + ASH = 100) |
17.66 |
17.12 |
17.66 |
16.58 |
15.11 |
60 |
| HHV = 0.196FC + 14.119 |
15.64 |
14.22 |
15.64 |
14.43 |
16.03 |
61 |
HHV = −10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 814.08 + 313.3T where, T = (FC + VM) 814.08 + 313.3T where, T = (FC + VM) |
18.95 |
20.41 |
18.95 |
19.07 |
13.92 |
62 |
TGA analysis
To investigate the pyrolysis behavior of WPM, a kinetic study of WPM was conducted at 5, 10, 20, and 50 °C min−1 in a nitrogen environment. The TGA and DTG trends at various heating rates are displayed in Fig. 2. The typical peaks of DTG curves (WPM) are somewhat pushed toward higher temperatures as the heating rate increases, and their values also slightly decrease. At four different heating rates, the first peak temperatures are 464, 478, 487, and 502 °C, respectively; the second peak temperatures are 621, 652, 668, and 720 °C, respectively. There are explanations for why pyrolysis peak temperatures rise as heating rate increases. The temperature differential between the sample and the crucible wall is directly impacted by the variation in the heat transfer rate from the exterior to the interior under different heating rates. Then, during the pyrolysis process, thermal hysteresis could happen. Since it will take the sample less time to reach the same temperature as the heating rate increases, the sample will react less strongly.63
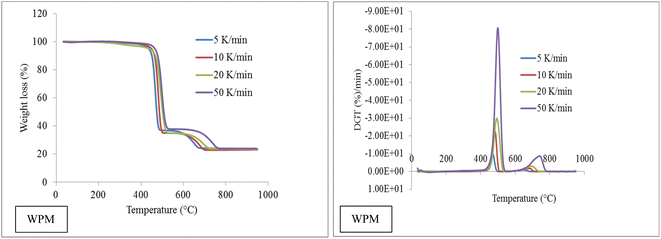 |
| | Fig. 2 Plots of TGA and DTG of WPM. | |
Table 4 displays the average degradation (%/min) and weight loss (%) of WPM across a variety of temperatures. In the case of WPM, it is evident that when the rate of heating increases, the average rate of degradation likewise rises in the corresponding temperature zones, which are 410–510 °C and 510–770 °C. There is little variation in the weight loss among temperature zones, but there is an overall downward tendency as heating rates rise; the corresponding percentages are 62.06%, 63.77%, 62.89%, and 50.21%. The cause must be that a higher heating rate gives the molecules less time to react, which results in less weight loss.
Table 4 Wt. loss (%) and ADR (average degradation rate) at temperature zones in each heating rates of WPM
| Temperature zones WPM |
| 5 °C/min |
10 °C/min |
20 °C/min |
50 °C/min |
| 410–510 °C |
510–770 °C |
410–510 °C |
510–770 °C |
410–770 °C |
510–770 °C |
410–510 °C |
510–770 °C |
| 62.06% |
29.69% |
63.77% |
21.48% |
62.89% |
28.36% |
59.21% |
22.50% |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| (ADR) (% min−1) |
| 3.44 |
0.927 |
7.08 |
1.43 |
11.42 |
3.14 |
26.84 |
7.41 |
The curves for biomass are relatively flatter at lower heating rates than they are at higher rates.51,64 However, WPM curves display comparatively sharper results across all heating rates; this could be due to effective heat transfer conduction. Because biomass is a poor heat conductor, there is a temperature gradient across its cross section. As long as enough time is allowed for heating, the outer surface and inner core of the biomass material reach the same temperature at a given period, allowing the temperature profile along the cross-section can be assumed to be linear at lower heating rates. However, there is a noticeable variation in the temperature profile across the biomass's cross-section at a higher heating rate. The kinetics of degradation prevents reaction completion at higher heating rates, which could explain the discrepancy between the overall degradation at a higher and lower heating rate. The necessary development of the volatile matters at lower temperature ranges is not given enough residence time. One such study using 5-, 10-, 15-, and 20-mm cubes and video recording of the procedure, the thermal behavior of waste tractor tire tread was examined. This experimental approach was unheard of in the literature. Empirical data indicates that the entire pyrolysis duration can be approximated by adding the local kinetic component and the heat-transfer component.65
Kinetic study analysis
For the kinetics parameters, a multi-linear regression technique and model-free methods (isothermal and non-isothermal) were used to produce the TGA study findings. Solid-state kinetics can be found using two different approaches: (a) model-fitting, and (b) model-free, which are further divided into isothermal and non-isothermal categories. This study's goal is to compare models and use both approaches to characterize the reaction kinetics at various heating rates. The FWO, KAS, Coats–Redfern (non-isothermal), and Friedman (isothermal) techniques were used to determine the apparent activation energy (Ea) and pre-exponential factor (Aa). In addition to these techniques, a multi-linear regression approach was used to determine the activation energy (Ea), pre-exponential component (Aa), and overall reaction order (n). Because model-fitting techniques may directly infer the kinetic parameters from a single TGA measurement, they have historically been widely employed for solid state reactions. The inability of these methods to identify the reaction model uniquely is one of their many drawbacks,66 particularly when dealing with non-isothermal data. While multiple models can be found to be statistically equivalent, choosing the right model can be challenging because the fitted kinetic parameters may differ by an order of magnitude. Higher values for the kinetic parameters are obtained when model-fitting techniques are applied to non-isothermal data. Isoconversional procedures have recently become more popular than this one. The benefit of the model-free analysis stems from its ease of use and the avoidance of mistakes associated with selecting a kinetic model.67 With the use of these techniques, one can estimate the activation energy (Ea) of an independent model at a certain conversion extent (αi). By repeating this process with various conversion values, we are able to obtain an activation energy profile as a function of αi. The fundamental premise is that, for a given reaction under various circumstances, the reaction model, f(αi), is the same for a given αi.68 These methods' drawback is that they require a series of measurements at various heating rates for the same sample mass and inert gas flow volume, and their variation can lead to mistakes. The FWO approach was used to determine the activation energy without taking the reaction mechanism into account. Thus, the WPM's response mechanism was discovered using the CR approach. Table 6 displays the sample's Ea values, which were determined using the slopes of ln[G(α)/T2] versus 1/T. By contrasting the calculated values of Ea from the FWO approach and the Coats–Redfern method, the most appropriate reaction mechanism for the sample was determined. After calculating the activation energy E and pre-exponential factor A for each zone at a heating rate of 10 °C min−1, the results are given in Table 6. After analyzing Table 6, it can be seen that only PL1, PL2, PL3, PL4, AE2, AE3, AE4, D1, and R2 have demonstrated a good coefficient of regression value close to one for each zone and heating rate according to the R2 fitting method. PL2, PL3, and PL4 have the highest regression values among them. The D3 model yields the highest values of pre-exponential component A and activation energy E. The activation energy likewise drops with increasing temperature. Table 5 illustrates how activation energy fluctuates during pyrolysis and is not constant throughout the processes. This suggests that the pyrolysis of this WPM involves many reaction mechanisms. With the highest coefficient of regression (R2) in each zone, ∼0.93 and 0.99, the most appropriate fitted model is PL2. With the exception of AE1 and AE2 at zone-2, the random nucleation mechanisms AE1–AE4 (Avrami–Erofe'ev) have discovered a modest coefficient of regression closer to 0.90. The activation energy value of the PL1 model (281.31 kJ mol−1) for Zone-1 is comparable to that found using iso-conversional methods (KAS method: 281.20 kJ mol−1 and FWO method: 279.42 kJ mol−1) for α = 0.7. In Zone-2, the activation energy value of the PL1 model does not resemble that of the iso-conversional approach. Conversely, the activation energy value of the FS2 model, which is 253.56 kJ mol−1, is comparable to that of the FWO method (255.70 kJ mol−1) and the KAS method (256.09 kJ mol−1) at α = 0.8. In models where temperature increases independently of R2, there is a corresponding drop in the value of pre-exponential component A. The pre-exponential factor pertains to transition states in solid state processes and is mostly dependent on temperature.69 Based on the findings, the Coats–Redfern method's PL (exponential nucleation, or power law) model is the most appropriate model to depict the pyrolysis of WPM at a heating rate of 10 °C min−1. The FWO, KAS (non-isothermal), and Friedman (isothermal) approaches were used to determine the apparent activation energy (Ea) and pre-exponential factor (Aa) and for the WPM, the plots of ln(β) versus 1000/T K−1, ln(β/T2) versus 1000/T K−1, and ln(β·dα/dT) versus 1000/T K−1 for a given value of conversion are shown in Fig. 3. In addition to these techniques, a multi-linear regression approach was used to determine the activation energy (Ea), pre-exponential component (Aa), and overall reaction order (n). For a specific conversion value (α), Table 5 displays the usual kinetic data of WPM for the KAS, FWO, and Friedman techniques. In KAS methods, the activation energy is 350.34 kJ mol−1 at α = 0.1 conversions, and it declines as conversion increases along with a simultaneous drop in the pre-exponential factor. This trend holds true for both Friedman and FWO approaches. It shows a very good regression coefficient in three different approaches. The phenomenon can be attributed to the high initial activation energy resulting from the breakage of the plastic waste molecule chain.
Table 5 Kinetic data of WPM at different values of conversion using different methods
| KAS method |
FWO method |
Friedman method |
| α |
Ea (kJ mol−1) |
Aα (min−1) |
R2 |
Ea (kJ mol−1) |
Aα (min−1) |
R2 |
Ea (kJ mol−1) |
Aα (min−1) |
R2 |
| 0.1 |
350.34 |
1.08 × 1024 |
0.92 |
345.28 |
5.10 × 1023 |
0.92 |
375.44 |
3.79 × 1026 |
0.95 |
| 0.2 |
347.80 |
5.41 × 1023 |
0.97 |
342.38 |
1.85 × 1023 |
0.97 |
321.21 |
3.43 × 1022 |
0.94 |
| 0.3 |
336.13 |
7.74 × 1022 |
0.97 |
331.36 |
4.12 × 1022 |
0.97 |
303.51 |
1.36 × 1021 |
0.94 |
| 0.4 |
322.99 |
8.88 × 1021 |
0.96 |
318.93 |
5.16 × 1021 |
0.96 |
283.80 |
3.97 × 1019 |
0.92 |
| 0.5 |
311.05 |
1.22 × 1021 |
0.95 |
307.65 |
7.73 × 1020 |
0.96 |
265.49 |
1.42 × 1018 |
0.89 |
| 0.6 |
297.00 |
1.16 × 1020 |
0.95 |
294.36 |
8.14 × 1019 |
0.95 |
248.62 |
6.05 × 1016 |
0.88 |
| 0.7 |
281.20 |
7.98 × 1018 |
0.94 |
279.42 |
6.30 × 1018 |
0.94 |
230.21 |
1.76 × 1015 |
0.90 |
| 0.8 |
256.09 |
1.05 × 1017 |
0.96 |
255.70 |
1.02 × 1017 |
0.97 |
180.87 |
2.07 × 1011 |
0.81 |
| 0.9 |
175.93 |
2.15 × 109 |
0.94 |
182.20 |
6.36 × 109 |
0.95 |
196.22 |
2.45 × 109 |
0.99 |
| Avg |
297.61 |
1.89 × 1023 |
|
295.25 |
8.24 × 1022 |
|
267.26 |
4.21 × 1025 |
|
Table 6 Arrhenius parameters for model-fitting non-isothermal decomposition of WPM at 10 °C min−1
| Kinetic model |
Zone-1 (410–510 °C) |
Zone-2 (510–770 °C) |
| Ea (kJ mol−1) |
A (min−1) |
R2 |
Ea (kJ mol−1) |
A (min−1) |
R2 |
| FO1 |
214.59 |
1.75 × 1014 |
0.9202 |
−0.82 |
−2.40 × 10−3 |
0.0097 |
| FS2 |
253.56 |
1.60 × 1017 |
0.8856 |
18.83 |
2.80 |
0.4180 |
| PL1 |
281.31 |
4.12 × 1018 |
0.9468 |
−8.63 |
−3.36 × 10−3 |
0.8977 |
| PL2 |
85.71 |
9.56 × 104 |
0.9376 |
−12.46 |
−3.28 × 10−3 |
0.9962 |
| PL3 |
53.11 |
3.85 × 102 |
0.9289 |
−13.10 |
−3.24 × 10−3 |
0.9990 |
| PL4 |
36.81 |
2.15 × 101 |
0.9184 |
−13.41 |
−3.21 × 10−3 |
0.9997 |
| AE1 |
214.59 |
1.75 × 1014 |
0.9202 |
−0.82 |
−2.40 × 10−3 |
0.0097 |
| AE2 |
101.25 |
1.60 × 106 |
0.9117 |
−7.60 |
−6.04 × 10−3 |
0.7822 |
| AE3 |
63.47 |
2.70 × 103 |
0.9018 |
−9.85 |
−5.09 × 10−3 |
0.9362 |
| AE4 |
44.58 |
9.85 × 101 |
0.8902 |
−10.98 |
−4.56 × 10−3 |
0.9722 |
| PT1 |
22.56 |
1.38 × 101 |
0.6814 |
1.96 |
7.82 × 10−3 |
0.0395 |
| D1 |
379.10 |
2.01 × 1025 |
0.9478 |
−6.72 |
−3.18 × 10−3 |
0.7395 |
| D2 |
397.40 |
2.40 × 1026 |
0.9414 |
−2.90 |
−1.87 × 10−3 |
0.1723 |
| D3 |
418.80 |
2.18 × 1027 |
0.9331 |
4.11 |
2.83 × 10−3 |
0.1217 |
| D4 |
404.48 |
1.82 × 1026 |
0.9387 |
−0.69 |
−1.64 × 10−4 |
0.0078 |
| R2 |
198.08 |
4.82 × 1012 |
0.9338 |
−6.85 |
−2.70 × 10−3 |
0.7254 |
| R3 |
203.36 |
8.14 × 1012 |
0.9296 |
−5.13 |
−1.98 × 10−3 |
0.4771 |
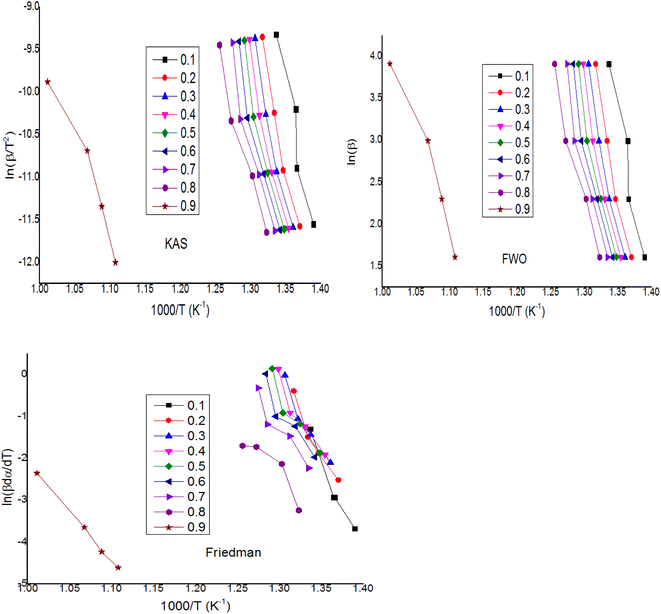 |
| | Fig. 3 Kissinger–Akahira–Sunose (KAS), FWO (Flynn–Wall–Ozawa) and Friedman plots of WPM at different values of conversion. | |
Table 7 displays the results of the multi-linear regression technique used to determine the kinetic data of WPM at 5, 20, and 50 °C min−1. With the exception of the 510–770 °C temperature zones, the regression coefficient shows great promise at rates of 20 and 50 °C min−1. According to research, the activation energy peaks in the 410–510 °C temperature range at 5 °C min−1 for WPM and subsequently falls as the heating rate increases. The temperature zones corresponding to this trend are 510–770 °C.
Table 7 Kinetic data of WPM (multi-linear regression technique)
| Rate of heating |
Kinetics parameters |
Temperature zone |
| WPM |
| 410–510 °C |
510–770 °C |
| 5 °C min−1 |
R2 |
0.94 |
0.99 |
| A (min−1) |
1.90 × 1025 |
2.25 × 1010 |
| E (kJ mol−1) |
365.61 |
197.46 |
| n |
0.99 |
0.25 |
| 20 °C min−1 |
R2 |
0.95 |
0.71 |
| A (min−1) |
2.82 × 1016 |
2.20 × 107 |
| E (kJ mol−1) |
244.56 |
146.13 |
| n |
0.58 |
0.21 |
| 50 °C min−1 |
R2 |
0.97 |
0.49 |
| A (min−1) |
6.01 × 1018 |
5.08 |
| E (kJ mol−1) |
274.42 |
120.44 |
| n |
0.49 |
0.17 |
Physico-chemical properties of WPM
A general formulation of the observed rate constant of each reaction as a function of pH and temperature could be quantified thanks to the fitting of these experimental data by a kinetic model. The crucial role of pH is expressly taken into consideration by the corresponding rate laws.70 So, physical characteristics of the bio-oil produced by pyrolyzing the WPM at 450 °C were measured, including pH, density, viscosity, and refractive index. At every working temperature, the extracted pyrolytic oil was found to have about the same GCV. Additionally, an elemental analysis was performed. The physical characteristics of the crude oil at 450 °C carbonization temperatures are listed in Table 8. The pyrolytic oil production process diagram for WPM is displayed in Fig. 4.
Table 8 Physio-chemical properties of pyrolytic oilsa
| Physico-chemical properties of bio-oils obtained at 450 °C |
Applied method |
Instrument name |
| Parameters |
WPM |
| a @ 50 °C, b @ 30 °C. |
| GCV (MJ Kg−1) |
32.64 |
ASTM D-2015 |
Toshiba India digital bomb calorimeter |
| Viscosity (cP) @ 50 °C |
1.6 |
ASTM |
Anton paar (RheolabQC) |
| Density (g ml−1) @ 30 °C |
1.11 |
ASTM |
|
| pH |
6.0 |
ASTM |
|
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
| Ultimate analysis of bio-oil |
|
|
|
| Elemental (wt%) |
|
|
|
| C |
59.33 |
ASTM standard |
Elementar vario MICRO cube and LECO CHNS-932 & RO-479 |
| H |
7.81 |
| S |
0.017 |
| N |
0.25 |
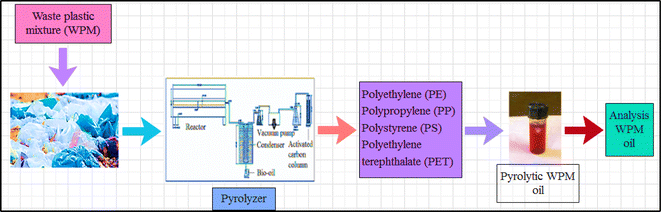 |
| | Fig. 4 Schematic diagram of the pyrolysis process set-up for slow pyrolysis. | |
Understanding the liquid fuel's carbon, hydrogen, and oxygen contents is crucial for biofuel characterisation. The usual chemical structure of WPM pyrolytic oil is displayed in Appendix (A.1).† However, WPM pyrolytic oil shows a lower CV than gasoline because each molecule lacks an oxygen atom, and it was discovered that carbon atoms C4 to C7 are connected to one or more oxygen atoms. There are no oxygen atoms in carbons C10 to C24. Last but not least, the carbons in gasoline are C7 through C12, and none of them include an oxygen atom.
FT-IR analysis
FT-IR was utilized to evaluate the chemical characteristics of a WPM oil sample by identifying the functional groups and chemical bonds present in the sample using an infrared absorption spectrum. Table 9 displays the functional groups that the FT-IR analysis of the oil revealed. The unique characteristics of obtained WPM oils—have been determined. The functional groups in WPM oils are made up of alkene, cyclic alkene, isocyanate, nitrile, and amine.
Table 9 FT-IR functional groups and indicated compounds of the pyrolytic oil
| Frequency range (cm−1) |
WPM oil |
WPM oil |
| Group |
Class of compound |
| 1000–900 |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C (bending) C (bending) |
Alkene |
| 1550–1350 |
N–O (stretching) |
Nitro compound |
| 1680–1600 |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C (stretching) C (stretching) |
Alkene, cyclic alkene |
| 2400–2000 |
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (stretching), C O (stretching), C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N (stretching), C N (stretching), C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C (stretching) C (stretching) |
Isocyanate, nitrile, alkyne |
| 3500–3400 |
N–H (stretching) |
Primary amine |
The chemical makeup of the original sources determines the functional group of pyrolytic oil. In comparison with biomass—which is mostly composed of carbon, hydrogen, oxygen, and a minor amount of nitrogen—produced chemicals related to oxygen that end up in the bio-oil mixture. Its calorific value has decreased due to the presence of oxygen, whereas WPM oil produced a high calorific value because of the absence of oxygen.
Fig. 5 illustrates the characteristic that sets WPM pyrolytic oil: only alkene (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, bending) is detected at a frequency in the 900–1000 cm−1 range in the case of WPM. WPM oil has been discovered to have an isocyanate, nitrile, and alkyne functional group in the frequency range of 2000–2400 cm−1.
C, bending) is detected at a frequency in the 900–1000 cm−1 range in the case of WPM. WPM oil has been discovered to have an isocyanate, nitrile, and alkyne functional group in the frequency range of 2000–2400 cm−1.
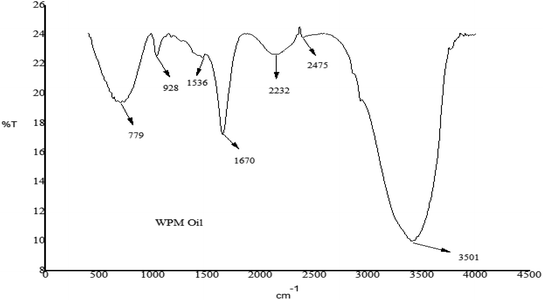 |
| | Fig. 5 FT-IR analysis of pyrolytic oil produced from WPM. | |
GC-MS analysis
GC-MS and FT-IR were used to evaluate the bio-oil produced at 450 °C temperatures in order to determine the various chemical components that were present. In essence, oil is a blend of various organic substances that typically result from the pyrolysis of WPM. It is commonly known that the pyrolysis of cellulose and hemicelluloses yields acids, aldehydes, alcohols, and ketones, and that lignin yields phenolics and cyclic oxygenates. In contrast, WPM exclusively yields hydrocarbons, such as alkene, isocyanate, alkyne, nitrile, and amine. Table 10, which is a complete display of the many types of compounds contained in the oils along with the percentage area occupied by each, is produced from the GC-MS data as shown in Fig. 6.
Table 10 Distribution and yield (area%) of pyrolytic oil compositions
| Type of organic compounds |
Area (%) |
Area (%) |
| WPM pyrolytic oil at 450 °C |
Gasoline |
| Aromatic hydrocarbons |
0.33 |
80.77 |
| Hydrocarbons (alkane + alkene) |
87.59 |
19.23 |
| Heterocyclic compounds |
1.35 |
0.0 |
| Nitrogen-containing organic compounds |
0 |
0 |
| Other organic compounds |
0 |
0 |
| Alcohols |
0 |
0 |
| Phenols |
0.91 |
0 |
| Ester |
4.68 |
0 |
| Ethers |
0 |
0 |
| Aldehydes |
0 |
0 |
| Ketones |
3.31 |
0 |
| Carboxylic acids and derivatives, etc. |
0.4 |
0 |
| Total |
98.57% |
100.0% |
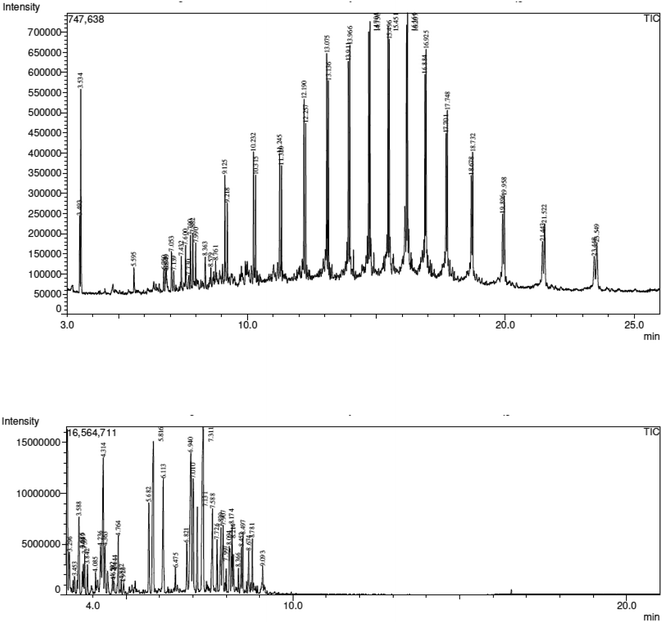 |
| | Fig. 6 (Top) GC-MS chromatogram of WPM pyrolytic oil, GC-MS chromatogram of gasoline (bottom). | |
Table 10 shows that the maximum value for ketone and its derivatives was 3.31% for WPM and the maximum value for gasoline was 0%. The existence of oxygenated molecules such O–H, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, and C–O is the cause of the low calorific value. Because there were very few or no oxygenated groups detected in WPM oil, 87.59% of the hydrocarbons, mostly alkane and alkene, exhibited a high calorific value. The same conclusion can be drawn for gasoline, as 80.77% of the aromatic hydrocarbons exhibited a very high calorific value. The chemical analysis of the pyrolytic oil obtained at 450 °C pyrolysis temperature is presented in Tables 11 and 12.
O, and C–O is the cause of the low calorific value. Because there were very few or no oxygenated groups detected in WPM oil, 87.59% of the hydrocarbons, mostly alkane and alkene, exhibited a high calorific value. The same conclusion can be drawn for gasoline, as 80.77% of the aromatic hydrocarbons exhibited a very high calorific value. The chemical analysis of the pyrolytic oil obtained at 450 °C pyrolysis temperature is presented in Tables 11 and 12.
Table 11 GC-MS data of the pyrolytic oil obtained from the pyrolysis of WPM at 450 °C
| Real time |
Compounds name |
Area% |
| 3.493 |
Propanoic acid, ethyl ester |
1.30 |
| 3.534 |
n-Propyl acetate |
3.38 |
| 5.595 |
2-Cyclopenten-1-one (CAS); cyclopentenone |
0.53 |
| 6.750 |
2-Cyclopenten-1-one, 2-methyl- |
0.32 |
| 6.819 |
5-Methyltetrahydrofuran-2-methanol, cis, trans |
0.28 |
| 6.849 |
2(3H)-furanone, dihydro- (CAS); butyrolactone |
0.22 |
| 7.053 |
2-Butanone, 3,4-epoxy-3-ethyl- (CAS); ethanone, 1-(2-ethyloxiranyl)- (CAS) |
0.95 |
| 7.139 |
2-Cyclohexen-1-one |
0.33 |
| 7.432 |
2(3H)-furanone, dihydro-5-methyl- |
0.50 |
| 7.600 |
2-Cyclopenten-1-one, 3-methyl- (CAS); 3-methyl-2-cyclopentenone |
0.60 |
| 7.730 |
Hexanoic acid |
0.40 |
| 7.790 |
Phenol |
0.91 |
| 7.882 |
1-Decene (CAS); dec-1-ene |
0.85 |
| 9.990 |
Decane |
0.55 |
| 8.363 |
3,6-Heptanedione |
0.64 |
| 8.579 |
2,3-Dimethyl-2-cyclopenten-1-one |
0.27 |
| 8.761 |
2(3H)-furanone, 5-ethyldihydro- (CAS); gamma-n-caprolactone |
0.35 |
| 9.125 |
1-Undecene |
1.43 |
| 9.218 |
Undecane |
1.09 |
| 10.232 |
1-Dodecene |
1.60 |
| 10.315 |
Dodecane (CAS); n-dodecane |
1.35 |
| 11.245 |
1-Tridecene (CAS); n-tridec-1-ene |
1.81 |
| 11.320 |
Tridecane |
1.73 |
| 12.190 |
1-Pentadecene (CAS); pentadec-1-ene |
2.46 |
| 12.257 |
Tetradecane |
2.18 |
| 13.075 |
1-Heptadecene (CAS); hexahydroaplotaxene |
4.52 |
| 13.136 |
Pentadecane |
3.06 |
| 13.911 |
1-Hexadecene (CAS); cetene |
4.71 |
| 13.966 |
Hexadecane (CAS); n-hexadecane |
5.40 |
| 14.701 |
1-Pentadecene |
4.54 |
| 14.750 |
Heptadecane (CAS); n-heptadecane |
5.93 |
| 15.451 |
1-Octadecene |
4.80 |
| 15.496 |
Octadecane |
4.69 |
| 16.166 |
1-Octadecene |
4.56 |
| 16.207 |
Octadecane |
4.94 |
| 16.884 |
1-Octadecene (CAS); alpha-octadecene |
2.90 |
| 16.925 |
Octadecane |
5.56 |
| 17.701 |
1-Nonadecene |
2.49 |
| 17.748 |
Tetracosane |
2.85 |
| 18.678 |
1-Octadecene (CAS); alpha-octadecene |
2.03 |
| 18.732 |
Tetracosane (CAS); n-tetracosane |
2.35 |
| 19.896 |
1-Nonadecene |
1.32 |
| 19.958 |
Tricosane (CAS) n-tricosane |
2.29 |
| 21.443 |
1-Tricosene |
1.31 |
| 21.522 |
Tetracosane |
1.59 |
| 23.448 |
1-Nonadecene |
0.84 |
| 23.549 |
Heneicosane |
1.29 |
Table 12 GC-MS data of gasoline
| Real time |
Compound name |
Area% |
| 3.296 |
2-Hexene, 3-methyl-, (Z)- |
1.46 |
| 3.453 |
Cyclopentene, 4,4-dimethyl- (CAS) 4,4-dimethylcyclopentene |
0.70 |
| 3.588 |
Cyclohexane, methyl- (CAS) methylcyclohexane |
3.60 |
| 3.685 |
Hexane, 2,5-dimethyl- (CAS) 2,5-dimethylhexane |
0.55 |
| 3.719 |
Hexane, 2,4-dimethyl- |
0.45 |
| 3.759 |
Cyclopentane, ethyl- |
1.14 |
| 3.842 |
Nonane, 3-methylene- |
0.99 |
| 4.085 |
Cyclobutane, (1-methylethylidene)- |
0.64 |
| 4.236 |
Heptane, 2-methyl- |
2.44 |
| 4.314 |
Toluene |
5.63 |
| 4.363 |
Heptane, 3-methyl- |
1.99 |
| 4.444 |
Cyclohexane, 1,2-dimethyl- (cis/trans) |
1.05 |
| 4.592 |
Cyclopentane, 1-ethyl-3-methyl- |
0.54 |
| 4.628 |
Cyclopentane, 1-ethyl-3-methyl-, cis- |
0.52 |
| 4.764 |
Octane |
1.77 |
| 4.852 |
Cyclohexane, 1,4-dimethyl-, cis- (CAS) 1-cis-4-dimethylcyclohexane |
0.35 |
| 4.926 |
Cyclohexene, 1,3-dimethyl- |
0.40 |
| 5.682 |
Ethylbenzene |
3.57 |
| 5.816 |
p-Xylene |
9.64 |
| 6.113 |
Benzene, 1,3-dimethyl- (CAS) m-xylene |
5.58 |
| 6.475 |
Benzene, (1-methylethyl)- (CAS) isopropylbenzene |
0.70 |
| 6.821 |
Benzene, propyl- (CAS) n-propylbenzene |
2.03 |
| 6.940 |
Benzene, 1-ethyl-3-methyl- (CAS) m-ethyltoluene |
9.36 |
| 7.010 |
Benzene, 1,2,4-trimethyl- (CAS) 1,2,4-trimethylbenzene |
4.22 |
| 7.131 |
Benzene, 1-ethyl-2-methyl- |
3.06 |
| 7.311 |
Benzene, 1,2,4-trimethyl- (CAS) 1,2,4-trimethylbenzene |
12.01 |
| 7.788 |
Benzene, 1,2,4-trimethyl- |
4.12 |
| 7.726 |
Indane |
1.55 |
| 7.839 |
Benzene, 1-methyl-3-propyl- (CAS) m-propyltoluene |
2.71 |
| 7.907 |
Benzene, 2-ethyl-1,4-dimethyl- (CAS) 1,4-dimethyl-2-ethylbenzene |
3.34 |
| 7.997 |
Benzene, 1-methyl-4-propyl- |
0.61 |
| 8.094 |
Benzene, 2-ethyl-1,4-dimethyl- (CAS) 1,4-dimethyl-2-ethylbenzene |
2.66 |
| 8.174 |
Benzene, 2-ethyl-1,4-dimethyl- (CAS) 1,4-dimethyl-2-ethylbenzene |
2.03 |
| 8.214 |
1H-Indene, 1-ethyl-2,3-dihydro-1-methyl- |
1.10 |
| 8.366 |
Benzene, 4-ethyl-1,2-dimethyl- |
0.71 |
| 8.452 |
Benzene, 1,2,4,5-tetramethyl- |
1.50 |
| 8.497 |
Benzene, 1,2,4,5-tetramethyl- |
1.76 |
| 8.674 |
Benzene, 1-methyl-2-(2-propenyl)- (CAS) o-allyltoluene |
1.63 |
| 8.781 |
2,4-Dimethylstyrene |
1.25 |
| 9.093 |
Azulene (CAS) cyclopentacycloheptene |
0.66 |
Kinetic mechanism of WPM
At temperatures greater than 200 °C, the pyrolysis of WPM is a liquid phase chain radical process. The regulating reactions in the decomposition process are bond fissions, hydrogen abstractions, β-decompositions, intramolecular abstractions, and terminations. In order to account for the diffusive limits, these corrections are also made to termination reactions, but they primarily only become meaningful for reactions with high activation energies, like initiation reactions. WPM breaks down via a straightforward depolymerization mechanism that only requires the chain backbone to be broken, with little to no reaction from the side groups. It is crucial to emphasize that the pyrolysis processes of the three distinct polymers are explained by the same reaction steps, or more accurately, the same reaction classes. To keep things simple, we can express the polymers using a simplified notation where the side chain (P) can be H, CH3, or phenyl for PE, PP, or PS, respectively. The following reaction classes aptly characterize the free chain radical reactions:
(1) Initial reactions, which result in the formation of radicals:
(1a) Random polymer backbone scission
(2) Responses of intermediate radicals to propagation:
(2a) Radicals undergo β-scission to produce smaller radicals and unsaturated compounds.
(2b) β-Scission in a particular position: reactions involving unzipping
(2c) Alkyl radical isomerization through H-transfers in (1, 4), (1, 5), and (1, 6)
(2d) End chain radicals cause the H-abstraction (metathesis) process on the polymer chain.
(2e) Mid chain radicals cause the H-abstraction (metathesis) process on the polymer chain.
(2f) H-abstraction (metathesis) response at a certain point
(3) Radical recombination reactions or termination:
The primary reaction classes are listed here, along with reports of basic reference reactions.71–74 For the purpose of completeness, termination reactions take place not just between radicals originating from initiation reactions but also between all of the propagating radicals generated during the degradation. Accurate identification of the model for the nucleophilic aromatic substitution, which has a well-known but intricate process, ensures a statistically precise determination of kinetic parameters. For the cracking reactions of hydrocarbon blends, lumped kinetic modeling has been the accepted modeling technique throughout the last few decades.75,76 Finally, waste plastic pyrolysis has drawn attention as a potential chemical recycling technique. We performed a life cycle assessment (LCA) and techno-economic analysis (TEA) of a hypothetical catalytic fast pyrolysis (CFP) facility that transforms 240 metric tons of mixed plastic waste per day in order to evaluate the viability of this method.77
Conclusion
This study has solely looked at WPM that can be utilized to create liquid fuel by thermochemical conversion. The advantages of converting solid waste into liquid fuels include their greater calorific value compared to solid waste and their ease of transportation. Hydrocarbons with a lower molecular weight have also been found to produce fewer pollutants than solid fuel. Proximate and ultimate analyses have been used in this study to incorporate solid fuel characteristics. According to the data, the carbon content and volatile matters of WPM are 64.49% and 69.1%. Owing to the high concentration of impurities in the WPM, it exhibits a high level of ash (19.55%), which has a major impact on volatile substances in the WPM. The values of the CV for these solid wastes, which were calculated using four different correlations, vary from 13.92 to 16.55 kJ kg−1 for WPM. Weight loss has been calculated in each of the following temperature ranges: 410–510 °C and 510–770 °C for WPM. For the purpose of constructing kinetics models (a) model-fitting and (b) model-free, which are further divided into isothermal and non-isothermal categories, TGA research has been conducted at various heating rates. The kinetic analyses are attributed using the following techniques: Friedman, KAS, FWO, Coats–Redfern, and multi-linear regression. The KAS, FWO, and Friedman methods yield average activation energies of 297.61, 295.25, and 267.26 kJ mol−1, respectively. The temperature zone (510–770 °C) with the lowest activation energy was found in this study. In kinetic models PL1 through PL4, the activation energies are 281.31, 85.71, 53.11, and 36.81 kJ mol−1; in D1 through D2, they are 379.10, 397.40, 418.80, and 404.48 kJ mol−1; and in AE1 through AE4, they are 214.59, 101.25, 63.47, and 44.58 kJ mol−1 (410–510 °C temperature zone). However, the results of the model-fitting non-isothermal decomposition (PL) of WPM at 10 °C min−1 using the Coats–Redfern approach revealed that the model's coefficient of regression for PL1 to PL4 in the range of 0.89 to 0.99 is the best among the results in zones 1 and 2. Aside from this, the D models (D1 through D4) of the Coats–Redfern technique show good agreement of the regression coefficient at zone 1, but not in zone 2. A decent regression coefficient at zone-1 is also demonstrated by models AE1 to AE4. The multi-linear regression technique yielded an overall reaction order of WPM that decreased in both temperature zones. The rationale for this is because whereas WPM is made up of just one monomer. The bio-oil's physico-chemical characteristics derived from WMP has been identified. The functional groups and chemical components of bio-oils have been determined using FT-IR and GC-MS studies. It was found that the WPM pyrolytic oil's CV has increased to 32.64 MJ kg−1 during pyrolysis. The poor calorific value of the oil can be attributed to its 3.31% ketone content (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) and its derivatives. It was discovered that gasoline has a higher calorific value than pyrolytic oil, which only contains 87.59% hydrocarbons, because gasoline includes more aromatic hydrocarbons (80.77%). In brief, the likely reaction mechanism of WPM has been described in terms of initiation, propagation that includes β-scission, H-transfers, H-abstraction, and termination.
O) and its derivatives. It was discovered that gasoline has a higher calorific value than pyrolytic oil, which only contains 87.59% hydrocarbons, because gasoline includes more aromatic hydrocarbons (80.77%). In brief, the likely reaction mechanism of WPM has been described in terms of initiation, propagation that includes β-scission, H-transfers, H-abstraction, and termination.
Data availability
The data supporting this article have been included as part of the ESI.†
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The research was conducted at the PDED of CSIR – Central Salt & Marine Chemicals Research Institute under the guidance of Dr Subarna Maiti. The author expresses gratitude to the AESD&CIF division of CSIR-CSMCRI for the extensive sample analysis. Thank you to NIMS University, Rajasthan, Jaipur – 303121 for covering the article processing charge (APC).
References
- https://www.unep.org/interactives/beat-plastic-pollution/?gclid=EAIaIQobChMIlNvD_pSLgAMV64NLBR1BuAyMEAAYASAAEgIEkfD_BwE.
- Biofuels Annual New Delhi Report, GAIN Publications, 2011, http://gain.fas.usda.gov/Recent%20GAIN%20Publications/Biofuels%20Annual_New%20Delhi_India_7-1-2011.pdf Search PubMed.
- L. Vivero, C. Barriocanal, R. Alvarez and M. A. Diez, Effects of plastic wastes on coal pyrolysis behaviour and the structure of semicokes, J. Anal. Appl. Pyrolysis, 2005, 74, 327–336, DOI:10.1016/j.jaap.2004.08.006.
- A. Lopez, I. de Marco, B. M. Caballero, M. F. Laresgoiti and A. Adrados, Influence of time and temperature on pyrolysis of plastic wastes in a semi-batch reactor, Chem. Eng. J., 2011, 173, 62–71, DOI:10.1016/j.cej.2011.07.037.
- B. Csukas, M. Varga, N. Miskolczi, S. Balogh, A. Angyal and L. Bartha, Simplified dynamic simulation model of plastic waste pyrolysis in laboratory and pilot scale tubular reactor, Fuel Process. Technol., 2013, 106, 186–200, DOI:10.1016/j.fuproc.2012.07.024.
- E. A. Williams and P. T. Williams, Analysis of products derived from the fast pyrolysis of plastic waste, J. Anal. Appl. Pyrolysis, 1997, 40(41), 347–363, DOI:10.1016/S0165-2370(97)00048-X.
- E. Kantarelis, P. Donaj, W. Yang and A. Zabaniotou, Sustainable valorization of plastic wastes for energy with environmental safety via High-Temperature Pyrolysis (HTP) and High-Temperature Steam Gasification (HTSG), J. Hazard. Mater., 2009, 167, 675–684, DOI:10.1016/j.jhazmat.2009.01.036.
- K. H. Lee and S. Cheon Oh, Kinetics of the thermal degradation of wax materials obtained from pyrolysis of mixed waste plastics, Korean J. Chem. Eng., 2010, 27(1), 139–143, DOI:10.1007/s11814-009-0305-5.
- J. K. Koo and S. W. Kim, Reaction kinetic model for optimum pyrolysis of plastic waste mixtures, Waste Manage. Res., 1993, 11, 515–529, DOI:10.1006/wmre.1993.1054.
- A. Lopez, I. de Marco, B. M. Caballero, A. Adrados and M. F. Laresgoiti, Deactivation and regeneration of ZSM-5 zeolite in catalytic pyrolysis of plastic wastes, Waste Manage., 2011, 31, 1852–1858, DOI:10.1016/j.wasman.2011.04.004.
- A. Adrados, I. de Marco, B. M. Caballero, A. Lopez, M. F. Laresgoiti and A. Torres, Pyrolysis of plastic packaging waste: A comparison of plastic residuals from material recovery facilities with simulated plastic waste, Waste Manage., 2012, 32, 826–832, DOI:10.1016/j.wasman.2011.06.016.
- A. Demirbas, Pyrolysis of municipal plastic wastes for recovery of gasoline-range hydrocarbons, J. Anal. Appl. Pyrolysis, 2004, 72, 97–102, DOI:10.1016/j.jaap.2004.03.001.
- T. Bhaskar, M. A. Uddin, K. Murai, J. Kaneko, J. K. Hamano, T. Kusaba, A. Muto and Y. Sakata, Comparison of thermal degradation products from real municipal waste plastics and model mixed plastics, J. Anal. Appl. Pyrolysis, 2003, 70, 579–587, DOI:10.1016/S0165-2370(03)00027-5.
- W. Kaminsky and J. S. Kim, Pyrolysis of mixed plastics into aromatics, J. Anal. Appl. Pyrolysis, 1999, 51, 127–134, DOI:10.1016/S0165-2370(99)00012-1.
- H. Huang, L. Tang and C. Z. Wu, Characterization of Gaseous and Solid Product from Thermal Plasma Pyrolysis of Waste Rubber, Environ. Sci. Technol., 2003, 37, 4463–4467, DOI:10.1021/es034193c.
- Y. S. Kim, Y. S. Kim and S. H. Kim, Investigation of Thermodynamic Parameters in the Thermal Decomposition of Plastic Waste-Waste Lube Oil Compounds, Environ. Sci. Technol., 2010, 44, 5313–5317, DOI:10.1021/es101163e.
- C. Ludlow-Palafox and H. A. Chase, Microwave-Induced Pyrolysis of Plastic Wastes, Ind. Eng. Chem. Res., 2001, 40, 4749–4756, DOI:10.1021/ie010202j.
- J. Aguado, D. P. Serrano and J. M. Escola, Fuels from Waste Plastics by Thermal and Catalytic Processes: A Review, Ind. Eng. Chem. Res., 2008, 47, 7982–7992, DOI:10.1021/ie800393w.
- W. Arjharn, P. Liplap, S. Maithomklang, K. Thammakul, S. Chuepeng and E. Sukjit, Distilled Waste Plastic Oil as Fuel for a Diesel Engine: Fuel Production, Combustion Characteristics, and Exhaust Gas Emissions, ACS Omega, 2022, 7, 9720–9729, DOI:10.1021/acsomega.1c07257.
- C. Cleetus, S. Thomas and S. Varghese, Synthesis of Petroleum-Based Fuel from Waste Plastics and Performance Analysis in a CI Engine, J. Energy, 2013, 608797, DOI:10.1155/2013/608797.
- A. K. Panda, R. K. Singh and D. K. Mishra, Thermolysis of waste plastics to liquid fuel A suitable method for plastic waste management and manufacture of value added products—A world prospective, Renewable Sustainable Energy Rev., 2010, 14, 233–248, DOI:10.1016/j.rser.2009.07.005.
- M. Syamsiro, H. Saptoadi, T. Norsujianto, P. Noviasri, S. Cheng, Z. Alimuddinc and K. Yoshikawa, Fuel Oil Production from Municipal Plastic Wastes in Sequential Pyrolysis and Catalytic Reforming Reactors, Energy Procedia, 2014, 47, 180–188, DOI:10.1016/j.egypro.2014.01.212.
- S. Budsaereechai, A. J. Hunt and Y. Ngernyen, Catalytic pyrolysis of plastic waste for the production of liquid fuels for engines, RSC Adv., 2019, 9, 5844–5857, 10.1039/c8ra10058f.
- J. Cho, B. Kim, T. Kwon, K. Lee and S. Choi, Electrocatalytic upcycling of plastic waste, Green Chem., 2023, 25, 8444–8458, 10.1039/d3gc03337f.
- K. Prifti, A. Galeazzi and F. Manenti, Design and Simulation of a Plastic Waste to Methanol Process: Yields and Economics, Ind. Eng. Chem. Res., 2023, 62, 5083–5096, DOI:10.1021/acs.iecr.2c03929.
- S. Bezergianni, A. Dimitriadis, G. Faussone and D. Karonis, Alternative Diesel from Waste Plastics, Energies, 2017, 10, 1–2, DOI:10.3390/en10111750.
- T. Shan, H. Bian, K. Wang, Z. Li, J. Qiu, D. Zhu, C. Wang and X. Tian, Study on pyrolysis characteristics and kinetics of mixed waste plastics under different atmospheres, Thermochi, Acta, 2023, 722, 179467, DOI:10.1016/j.tca.2023.179467.
- G. Lopez, M. Artetxe, M. Amutio, J. Bilbao and M. Olazar, Thermochemical routes for the valorization of waste polyolefinic plastics to produce fuels and chemicals-A review, Renewable Sustainable Energy Rev., 2017, 73, 346–368, DOI:10.1016/j.rser.2017.01.142.
- D. S. Achilias, C. Roupakias, P. Megalokonomosa, A. A. Lappas and E. V. Antonakou, Chemical recycling of plastic wastes made from polyethylene (LDPE and HDPE) and polypropylene (PP), J. Hazard. Mater., 2007, 149, 536–542, DOI:10.1016/j.jhazmat.2007.06.076.
- L. S. Diaz-Silvarrey, K. Zhang and A. N. Phan, Monomer recovery through advanced pyrolysis of waste high density polyethylene (HDPE), Green Chem., 2018, 20, 1813, 10.1039/C7GC03662K.
- C. Catizane, Y. Jiang and J. Sumner, Improving plastic pyrolysis oil quality via an electrochemical process for polymer recycling:a review, Energy Adv., 2024, 3, 366–388, 10.1039/d3ya00389b.
- S. Oh and E. E. Stache, Recent advances in oxidative degradation of plastics, Chem. Soc. Rev., 2024, 53, 7309–7327, 10.1039/d4cs00407h.
- L. Sorum, M. G. Gronli and J. E. Hustad, Pyrolysis characteristics and kinetics of municipal solid wastes, Fuel, 2001, 80, 1217–1227, DOI:10.1016/S0016-2361(00)00218-0.
- C. H. Wu, C. Y. Chang, J. L. Hor, S. M. Shih, L. W. Chen and F. W. Chang, On the thermal treatment of plastic mixtures of MSW: pyrolysis kinetics, Waste Manage., 1993, 13, 221–235, DOI:10.1016/0956-053X(93)90046-Y.
- R. W. J. Westerhout, J. Waanders, J. A. M. Kuipers and W. P. M. Van Swaaij, Kinetics of the low-temperature pyrolysis of polyethene, polypropene, and polystyrene modeling, experimental determination, and comparison with literature models and data, Ind.
Eng. Chem. Res., 1997, 36, 1955–1964, DOI:10.1021/ie960501m.
- U. Hujuri, A. K. Ghoshal and S. Gumma, Modelling pyrolysis kinetics of plastic mixtures, Polym. Degrad. Stab., 2008, 1832–1837, DOI:10.1016/j.polymdegradstab.2008.07.006.
- B. Saha and A. K. Ghoshal, Thermal degradation kinetics of poly (ethylene terephthalate) from waste soft drinks bottles, Chem. Eng. J., 2005, 111(1), 39–43 CrossRef CAS.
- S. M. Al-Salem and P. Lettieri, Kinetic study of high density polyethylene (HDPE) pyrolysis, Chem. Eng. Res. Des., 2010, 88, 1599–1606, DOI:10.1016/j.cej.2005.04.018.
- A. N. Garcia, A. Marcilla and R. Font R, Thermogravimetric kinetic study of the pyrolysis of municipal solid waste, Thermochim. Acta, 1995, 254, 277–304, DOI:10.1016/0040-6031(94)02002-6.
- J. M. Encinar and J. F. González, Pyrolysis of synthetic polymers and plastic wastes. kinetic study, Fuel Process. Technol., 2008, 89, 678–686, DOI:10.1016/j.fuproc.2007.12.011.
- K. Ghosal and C. Nayak, Recent advances in chemical recycling of polyethylene terephthalate waste into value added products for sustainable coating solutions – hope vs. hype, Mater. Adv., 2022, 3, 1974, 10.1039/d1ma01112j.
- H. Li and H. A. Aguirre-Villegas, et al., Expanding plastics recycling technologies:chemical aspects, technology status and challenges, Green Chem., 2022, 24, 8899, 10.1039/d2gc02588d.
- S. Zhang and Y. Xue, et al., PET recycling under mild conditions via substituent-modulated intramolecular hydrolysis, Chem. Sci., 2023, 14, 6558, 10.1039/d3sc01161e.
- S. B. Rasul, U. Som, M. S. Hossain and M. W. Rahman, Liquid fuel oil produced from plastic based medical wastes by thermal cracking, Sci. Rep., 2021, 11, 17048, DOI:10.1038/s41598-021-96424-2.
- L. Qin, et al, Thermal degradation of medical plastic waste by in situ FTIR, TG-MS and TG-GC/MS coupled analyses, J. Anal. Appl. Pyrolysis, 2018, 136, 132–145, DOI:10.1016/j.jaap.2018.10.012.
- I. G. Hakeem, F. Aberuagba and U. Musa, Catalytic pyrolysis of waste polypropylene using Ahoko kaolin from Nigeria, Appl. Petrochem. Res., 2018, 8, 203–210, DOI:10.1007/s13203-018-0207-8.
- J. A. Conesa, R. Font and A. Marcilla, Comparison between the Pyrolysis of Two Types of Polyethylenes in a Fludized Bed Reactor, Energy Fuels, 1997, 11, 126–136, DOI:10.1021/ef960098w.
- H. Almohamadi, M. Alamoudi, U. Ahmed, R. Shamsuddin and K. Smith, Producing hydrocarbon fuel from the plastic waste: Techno-economic analysis, Korean J. Chem. Eng., 2021, 38(11), 2208–2216, DOI:10.1007/s11814-021-0876-3.
- P. Das, S. Charola, M. Dinda, H. Patel and S. Maiti, Hydrogen from empty cotton boll agro-waste via thermochemical route and feasibility study of operating an IC engine in continuous mode, Int. J. Hydrogen Energy, 2017, 42, 14471–14484, DOI:10.1016/j.ijhydene.2017.04.041.
- P. Das, M. Dinda, N. Gosai and S. Maiti, High Energy Density Bio-oil via Slow Pyrolysis of Jatropha curcas Shells, Energy Fuels, 2015, 29, 4311–4320, DOI:10.1021/acs.energyfuels.5b00160.
- S. Maiti, S. Purakayastha and B. Ghosh, Thermal characterization of mustard straw and stalk in nitrogen at different heating rates, Fuel, 2007, 86, 1513–1518, DOI:10.1016/j.fuel.2006.11.016.
- L. Gasparovic, Z. Korenova and L. Jelemensky, Kinetic study of wood chips decomposition by TGA, Chem. Pap., 2010, 64(2), 174–181, DOI:10.2478/s11696-009-0109-4.
- H. L. Friedman, Kinetics of thermal degradation of char-forming plastics from thermogravimetry. Application to a phenolic plastic, J. Polym. Sci., Part C: Polym. Symp., 1964, 6, 183–195, DOI:10.1002/polc.5070060121.
- J. H. Flynn and L. A. Wall, A quick, direct method for the determination of activation energy from thermogravimetric data, J. Polym. Sci., Part B: Polym. Lett., 1966, 4, 323–328, DOI:10.1002/pol.1966.110040504.
- T. Ozawa, A new method of analyzing thermogravimetric data, Bulletin Chem. Soc. Jpn, 1965, 38, 1881–1886, DOI:10.1246/bcsj.38.1881.
- T. Akahira and T. Sunose, Joint convention of four electrical institutes, Sci. Technol., 1971, 16, 22–31 Search PubMed.
- H. E. Kissinger, Variation of peak temperature with heating rate in differential thermal analysis, J. Res. Natl. Bur. Stand., 1956, 57, 217–221, DOI:10.6028/jres.057.026.
- A. W. Coats and J. P. Redfern, Kinetic parameters from thermogravimetric data, Nature, 1964, 20, 68–69, DOI:10.1038/201068a0.
- S. Kucukbayrak, B. Durus, A. E. Mericboyu and E. Kadioglu, Estimation of calorific values of Turkish lignites, Fuel, 1991, 70, 979–981, DOI:10.1016/0016-2361(91)90054-E.
- T. Cordero, F. Marquez, J. Rodriquez-Mirasol and J. J. Rodriguez, Predicting heating values of lignocellulosic and carbonaceous materials from proximate analysis, Fuel, 2001, 80, 1567–1571, DOI:10.1016/S0016-2361(01)00034-5.
- A. Demirbas, Calculation of higher heating values of biomass fuels, Fuel, 1997, 76(5), 431–434, DOI:10.1016/S0016-2361(97)85520-2.
- L. Jimenez and F. Gonzalez, Study of the physical and chemical properties of lignocellulosic residues with a view to the production of fuels, Fuel, 1991, 70, 947–950, DOI:10.1016/0016-2361(91)90049-G.
- H. Liu, C. Wang, J. Zhang, W. Zhao and M. Fan, Pyrolysis Kinetics and Thermodynamics of Typical Plastic Waste, Energy Fuels, 2020, 34, 2385–2390, DOI:10.1021/acs.energyfuels.9b04152.
- H. Haykiri-Acma, S. Yaman and S. Kucukbayrak, Effect of heating rate on the pyrolysis yields of rapeseed, Renewable Energy, 2006, 31, 803–810, DOI:10.1016/j.renene.2005.03.013.
- A. A. Jansen, J. S. Gama, I. J. van der Walt and P. L. Crouse, Pyrolysis and gasification of 5–20 mm tyre rubber cubes under carbon dioxide flow, React. Chem. Eng., 2024, 9, 2180–2196, 10.1039/d3re00577a.
- A. Khawam and D. R. Flanagan, Complementary use of model-free and modelistic methods in the analysis of solid-state kinetics, J. Phys. Chem. B, 2005, 109, 10073–10080, DOI:10.1021/jp050589u.
- J. R. Opfermann, E. Kaisersberger and H. J. Flammersheim, Model-free analysis of thermoanalytical data-advantages and limitations, Thermochim. Acta, 2002, 391, 119–127, DOI:10.1016/S0040-6031(02)00169-7.
- D. Zhou, E. Schmitt, G. Zhang, D. Law, S. Vyazovkin and C. Wight, et al, Crystallization kinetics of amorphous nifedipine studied by model-fitting and model-free approaches, J. Pharm. Sci., 2003, 92, 1779–1792, DOI:10.1002/jps.10425.
- Y. Pang, D. Sun, Q. Gu, K. C. Chou, X. Wang and Q. Li, Comprehensive determination of kinetic parameters in solid–state phase transitions: An extended Jonhson-Mehl-Avrami-Kolmogorov model with analytical solutions, Cryst. Growth Des., 2016, 16, 2404–2415, DOI:10.1021/acs.cgd.6b00187.
- F. Tollini, A. Occhetta, F. Broglia, V. Calemma, S. Carminati, G. Storti, M. Sponchioni and D. Moscatelli, Influence of pH on the kinetics of hydrolysis reactions: the case of epichlorohydrin and glycidol, React. Chem. Eng., 2022, 7, 2211–2223, 10.1039/d2re00191h.
- A. Marongiu, T. Faravelli and E. Ranzi, Detailed kinetic modeling of the thermal degradation of vinyl polymers, J. Anal. Appl. Pyrolysis, 2007, 78, 343–362, DOI:10.1016/j.jaap.2006.09.008.
- T. M. Kruse, H. W. Wong and L. J. Broadbelt, Mechanistic Modeling of Polymer Pyrolysis: Polypropylene, Macromolecules, 2003, 36, 9594–9607, DOI:10.1021/ma030322y.
- T. M. Kruse, O. S. Woo, H. W. Wong, S. S. Khan and L. J. Broadbelt, Mechanistic Modeling of Polymer Degradation: A Comprehensive Study of Polystyrene, Macromolecules, 2002, 35, 7830–7844, DOI:10.1021/ma020490a.
- T. M. Kruse, H. W. Wong and L. J. Broadbelt, Modeling the Evolution of the Full Polystyrene Molecular Weight Distribution during Polystyrene Pyrolysis, Ind. Eng. Chem. Res., 2003, 42, 2722–2735, DOI:10.1021/ie020657o.
- E. Agunloye, P. Petsagkourakis, M. Yusuf, R. Labes, T. Chamberlain, F. L. Muller, R. A. Bourne and F. Galvanin, Automated kinetic model identification via cloud services using model-based design of experiments, React. Chem. Eng., 2024, 9, 1859–1876, 10.1039/D4RE00047A.
- S.-M. Lorbach, A. E. Lechleitner, T. Schubert and M. Lehner, A sequential lumped kinetic modelling approach for the co-pyrolysis of plastic mixtures with a heavy refinery intermediate product in a tubular reactor, React. Chem. Eng., 2024, 9, 1883–1895, 10.1039/D4RE00075G.
- G. Yadav, A. Singh and A. Dutta, et al., Techno-economic analysis and life cycle assessment for catalytic fast pyrolysis of mixed plastic waste, Energy Environ. Sci., 2023, 16, 3638–3653, 10.1039/d3ee00749a.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article

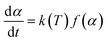
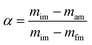
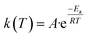
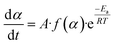
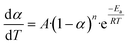
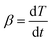 and the following equation can be applied:
and the following equation can be applied: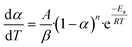
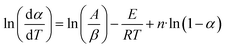
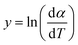 ,
, 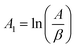 ,
, 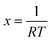 , z = ln(1 − α), B1 = −E and C1 = n
, z = ln(1 − α), B1 = −E and C1 = n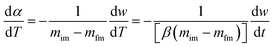
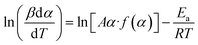
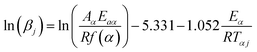
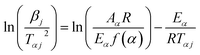
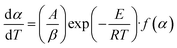 equation.
equation.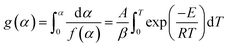
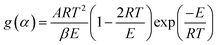
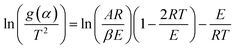
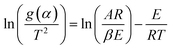
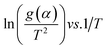 provides to a result in a straight line, the slope has been calculated from (−E/R) and the intercept respectively giving the values of E and A.
provides to a result in a straight line, the slope has been calculated from (−E/R) and the intercept respectively giving the values of E and A.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 814.08 + 313.3T where, T = (FC + VM)
814.08 + 313.3T where, T = (FC + VM)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C (bending)
C (bending)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C (stretching)
C (stretching)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (stretching), C
O (stretching), C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N (stretching), C
N (stretching), C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C (stretching)
C (stretching)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, bending) is detected at a frequency in the 900–1000 cm−1 range in the case of WPM. WPM oil has been discovered to have an isocyanate, nitrile, and alkyne functional group in the frequency range of 2000–2400 cm−1.
C, bending) is detected at a frequency in the 900–1000 cm−1 range in the case of WPM. WPM oil has been discovered to have an isocyanate, nitrile, and alkyne functional group in the frequency range of 2000–2400 cm−1.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, and C–O is the cause of the low calorific value. Because there were very few or no oxygenated groups detected in WPM oil, 87.59% of the hydrocarbons, mostly alkane and alkene, exhibited a high calorific value. The same conclusion can be drawn for gasoline, as 80.77% of the aromatic hydrocarbons exhibited a very high calorific value. The chemical analysis of the pyrolytic oil obtained at 450 °C pyrolysis temperature is presented in Tables 11 and 12.
O, and C–O is the cause of the low calorific value. Because there were very few or no oxygenated groups detected in WPM oil, 87.59% of the hydrocarbons, mostly alkane and alkene, exhibited a high calorific value. The same conclusion can be drawn for gasoline, as 80.77% of the aromatic hydrocarbons exhibited a very high calorific value. The chemical analysis of the pyrolytic oil obtained at 450 °C pyrolysis temperature is presented in Tables 11 and 12.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) and its derivatives. It was discovered that gasoline has a higher calorific value than pyrolytic oil, which only contains 87.59% hydrocarbons, because gasoline includes more aromatic hydrocarbons (80.77%). In brief, the likely reaction mechanism of WPM has been described in terms of initiation, propagation that includes β-scission, H-transfers, H-abstraction, and termination.
O) and its derivatives. It was discovered that gasoline has a higher calorific value than pyrolytic oil, which only contains 87.59% hydrocarbons, because gasoline includes more aromatic hydrocarbons (80.77%). In brief, the likely reaction mechanism of WPM has been described in terms of initiation, propagation that includes β-scission, H-transfers, H-abstraction, and termination.