Chalcophosphate metasurfaces with multipolar resonances and electro-optic tuning

Abstract

We computationally analyze the electro-optic response of metasurfaces consisting of interconnected nanoantennas with multipolar resonances using a chalcophosphate, Sn₂P₂S₆, as the active material. Sn₂P₂S₆ has large electro-optic coefficients and relatively low Curie temperature (<70 °C), allowing for strong changes in the refractive index of the material under moderate electric fields if the temperature can be finely controlled in proximity of the Curie point. Through numerical simulations, we show that metasurfaces designed with this nanostructured material demonstrate a significant shift of multipolar resonances upon biasing, despite moderate refractive-index values of the chalcophosphate and reduced mode localization due to this. The magnetic octupolar resonance of a dense array provides the strongest shift of spectral features upon changes in the refractive index, and we attribute it to the high mode localization of this higher-order multipole. We numerically demonstrate that narrow lattice resonances of collective nature do not provide an advantage in shifting the spectral features because of the nonlocal and delocalized nature of the modes, which are spread in the nanoantenna surrounding rather than confined inside nanoantennas. Both in-plane and out-of-plane biasing of the chalcophosphate crystals are similarly efficient with suitable electrode design, choice of electrode material, and crystal orientation within the nanoantennas. These designs exhibit optical properties similar to those of metasurfaces with isolated nanoantennas in the dense array.

---

1 Introduction

Nanostructures, including metasurfaces and photonic crystals, are engineered structures with rationally designed building blocks that enable devices with distinct responses to light, acoustic waves, and heat flows that are not attainable with naturally available materials. Optical nanostructures, with their reduced dimensions, enable the downsizing of traditional refractive optics to flat structures. These nanostructures possess remarkable capabilities in manipulating light, showing an unusually high optical density of states, and enhancing the light–matter interaction.^1–4 For example, the magnetic response of an antenna is essential for efficiently controlling the light it scatters. This has been the subject of active research for a long time because of the virtual absence of magnetic materials in the visible and infrared spectra, and the approximation μ(ω) ≈ 1 (where μ(ω) is the relative magnetic permeability) remains valid in the optical range. This planar photonic technology is anticipated to enable novel physics and devices with functionalities that differ significantly from those observed in three-dimensional bulk counterparts.

The Pockels effect, or linear electro-optic (EO) effect, is a nonlinear optical phenomenon observed in non-centrosymmetric materials, where an applied electric field modifies the refractive index of the material. This change can be exploited to control the amplitude and polarization of light that passes through the material, which is crucial in various optical devices such as modulators and switches.⁵

An impressive number of EO nanophotonic applications have already been realized using conventional EO materials at the nanoscale.^6–12 Metasurfaces enable the excitation of multiple resonant modes, which interact through near-field coupling and constructive or destructive interference, resulting in Fano resonances characterized by asymmetric line shapes and linewidths tunable through precise control of the coupling strength and resonance detuning.^13–16 Several designs involving EO metasurfaces and exploiting the Pockels effect have been demonstrated in recent years, including those based on thin-film layers (often called “etchless”)^17–31 and patterned layers of EO crystals.^32–43 Some of the designs involve both patterned and unpatterned EO layers underneath the patterned part,^34,35 as well as other innovative approaches with patterning and structuring of an EO material with the aim of placing it in the region of the highest field of the mode.^44,45 The most common EO crystals used are lithium niobate,^{9,10,17–26,31–38,42–46} barium titanate,^{8,27,39–41,47} and bismuth ferrite.^28–30 Other designs involve EO sol–gel synthesis, nanoparticles, and nanocrystals of barium titanate,^47–51 as well as EO polymers.^52–58 Typically, large electric fields are needed to induce refractive index changes large enough for practical applications. The thin-film designs provide an advantage in nanofabrication because they do not involve etching and patterning of the EO crystals, and the metasurface elements (gratings or nanoantennas) are placed on top of the EO layer. Such designs often benefit from utilizing resonant waveguide mode excitation and controlling the spectral position of this resonance.^18,23,24 Pronounced nonlocal properties can be achieved by the interplay of incident light and widely spread modes propagating across surface structures (that is, the metasurface elements). In contrast, the fabrication of nanoantennas and gratings of EO material requires etching, which complicates the process and makes it less practical. However, on the positive side, this nanostructuring results in a tighter mode localization and stronger EO response. Because of the higher optical field in proximity to the patterned part, the response to the change in refractive index results in a stronger shift of the spectral features. Patterned and unpatterned EO crystals have been shown to be particularly promising for wavefront shaping and beam steering.^26,37

Although metasurfaces and other nanophotonic designs help to enhance mode localization within or near the EO material, the reported spectral shifts of the resonant features remain relatively small for realistic biasing because of the inherently weak EO response of the material. Practical limits to the driving fields are imposed by considering the energy consumption and the breakdown strength of the materials and nanostructure. Other limitations are related to the transparency range of conventional materials. To address the upcoming challenges of future nanophotonic and optoelectronic technology, it is critical to develop novel materials with an enhanced EO response that can be chip-integrated. These materials are expected to provide novel, innovative technologies and enable nanophotonic devices with higher performance, reduced size and cost, and new functionalities. At the same time, the investigation of nanostructures is far from complete, and new behavior could emerge from exploring the vast parameter space of their geometry and inner structure. The present work proposes an approach to achieve efficient EO light manipulation with the current generation of EO materials.

Chalcophosphates are a family of materials with a general structure M₂P₂S₆, where M is a divalent metal, many of which are known to be ferroelectric and piezoelectric. They also typically have small bandgaps and low melting points. Within this family of materials, Sn₂P₂S₆ is one of the most widely studied compositions,^59–63 and it is known to exhibit EO properties,⁶¹ photorefraction,^64,65 and enhanced second-harmonic generation^62,66 due to its non-centrosymmetric crystal structure.

In addition, Sn₂P₂S₆ has a Curie temperature (transition from ferroelectric to paraelectric phase) of only 64–66 °C.^61,67,68 The proximity of this transition to room temperature, coupled with its large EO coefficient, presents a promising avenue for inducing substantial changes in the refractive index of the material under driving conditions that can be implemented relatively easily. In fact, the EO coefficient is known to increase significantly when the temperature approaches the Curie temperature from below,^61,69 but for most traditional EO materials, such as lithium niobate, the Curie temperature is too high to make this regime useable in practice.

Recent work⁷⁰ has reported on the outstanding properties of a related material, SnP₂S₆, whose EO coefficient is superior to well-established EO materials, such as lithium niobate. Thus, chalcophosphates^70–74 offer promise in frequency conversion and as active infrared EO materials for applications that require significant modulation of the refractive index in everyday settings and/or over small pathlength. The potential of these materials has not yet been explored, and this class of chalcophosphates has not yet been incorporated in functional metastructures.

In this work, we start to investigate this area by simulating numerically the optical properties of chalcophosphate-based metasurfaces with higher-order multipolar resonances excited in interconnected nanoantennas. We aim to develop the structure and enhance the EO response beyond what bulk and conventional materials offer. The large and temperature-controllable EO effect in the chalcophosphate metasurfaces can provide a means to induce significant variations in the refractive index. The corresponding tuning of the metasurface resonances is expected to be larger with chalcophosphates than with conventional EO materials, thus yielding increased efficiency or tailorability to the resulting devices.

Based on earlier studies of high-refractive-index nanostructures and the similarity of nanoantenna modes, we anticipate that an electric quadrupole mode couples to other even modes and can cause a resonant magnetic response of an antenna because of wave reflections from its boundaries. We computationally show that the proposed metasurfaces exhibit a notable shift of multipolar resonances when the refractive index is changed as a result of the EO effect, using a realistic bias near the Curie temperature. This is despite the moderate refractive index of the chalcophosphate and the reduced nanoantenna mode localization in comparison to conventional high-refractive-index materials, such as silicon. The simulations also show that the magnetic octupolar resonance exhibits the most pronounced shift in spectral features (peaks and dips), a phenomenon that we ascribe to the strongest localization of higher-order multipolar modes. This increased mode confinement contributes significantly to the observed spectral changes. In contrast, lattice resonances, which are based on nonlocal properties of the array and collective effects, provide relatively weak shifts of spectral features. We engineer metasurfaces with both in-plane and out-of-plane biasing by introducing bridges connecting the nanoantennas and thin conductive layers surrounding the EO material. The bridges and conductive layers have only a small effect on the multipolar modes, and the magnetic octupolar resonance remains the most beneficial for shifting the spectral features.

2 Multipolar resonances of EO metasurfaces

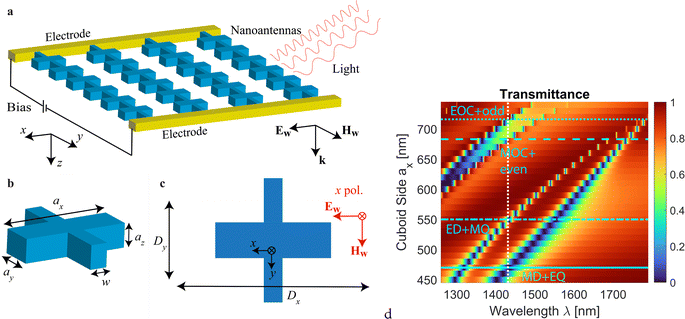
In nanoantennas made of high-refractive-index materials, such as silicon and III–V compounds, strong resonances are enabled by a high reflection from the nanoantenna boundaries and strong mode localization associated with them. However, the refractive indices of EO crystals, such as Sn₂P₂S₆ (n = 2.7–2.8 (ref. 63)), lithium niobate (n = 2.2–2.3 (ref. 75)), barium titanate, strontium titanate, and others, are considered moderate in the near-infrared range. Nanoantennas with moderate refractive index support relatively weak resonances, making the field localization not as strong as in high-refractive-index nanoantennas. Furthermore, realistic metasurfaces need to be placed on low-refractive-index substrates, resulting in lower reflection from the nanoantenna boundaries and even lower mode localization. These restrictions coming from the material response broaden the metasurface resonances, and nanoantennas need to be selected with larger dimensions to support the same variety of multipolar resonances (electric and magnetic dipole, quadrupole, etc.) as in the high-refractive-index nanoantennas.

To start with, we consider a periodic array of cuboid nanoantennas made of EO materials with properties similar to Sn₂P₂S₆ (Fig. 1a–c). The nanoantennas are connected in the y-direction. The bridge width w = 80 nm is fixed throughout the work. Similar designs of interconnected nanoantennas have been explored in earlier works^76–79 and have been shown to be beneficial when an electric field needs to be applied to the entire nanoantenna array. EO properties of finite-size lithium niobate arrays of ∼20–25 μm in characteristic dimensions have also been characterized.³⁴

Fig. 1 Schematic of the structure and its transmittance. (a–c) Interconnected nanoantennas made of an EO crystal (light blue color) and arranged in an array, forming a metasurface. (a) Schematic 3D view of the metasurface and the electrodes connecting the nanoantennas on each end (yellow color). The surrounding medium in all directions (below, above, and around) is silica. (b) 3D view of one nanoantenna with the bridge. (c) Top view of the unit cell and orientation of the electric and magnetic fields of the light wave relative to the nanoantenna. (d) Transmittance of the metasurface for D_x = D_y = 750 nm and varied cuboid side a_x = a_y = a_z. The white dashed vertical line corresponds to a wavelength of approximately 1430 nm, which is chosen for subsequent analysis. The solid, dot-dashed, dashed, and dotted horizontal cyan lines correspond to the side values of 470, 550, 683, and 716 nm, respectively, which are considered in more detail later. This set of parameters results in four resonances manifested as dips in the transmission spectrum with near-zero transmittance. The labels and assignment of the various resonance types are described and justified later in the text.

The dimensions of the nanoantennas a_x, a_y, and a_z are varied, keeping a_x = a_y = a_z. Several periods of the array, D_x and D_y, are considered. We analyze these nanoantennas with an assumption of n = 2.7, and we consider an extended near-infrared and telecommunication range of 1300–1800 nm. We assume that the refractive index of the nanoantenna n is isotropic (a discussion of the effect of anisotropy is included later in Section 3).

To account for realistic aspects of the design, we consider nanoantennas placed on a substrate with a refractive index of n_s = 1.47, surrounded by the same material, and covered with a superstrate matching the refractive index of the substrate. The general schematic includes electrodes on both sides of the interconnected nanoantennas along the y-direction. A large number of nanoantennas are assumed between the electrodes in the simulations, but, for simplicity only a relatively small number of nanoantennas are shown in Fig. 1a. This schematic corresponds to the case where the biasing (the static electric field) is applied in the y-direction. The light is incident normal to the metasurface (z-axis propagation direction) with x-polarization. It should be noted that the schematic does not show the surrounding medium, as, apart from the electrodes, the antennas are fully embedded by it and thus would not be visible.

Unless stated otherwise, the optical properties of the EO nanoantennas are computed using the commercial software CST Studio Suite. The calculated transmittance for a dense array as a function of the antenna dimension is shown in Fig. 1d. For D_x = D_y = 750 nm and a varied cuboid side a_x = a_y = a_z, the metasurface supports four resonances manifested as dips in the transmittance spectra, with near-zero transmittance. These spectral features shift to the red upon an increase in the cuboid side. In the subsequent analysis, we focus on the wavelength ∼1430 nm (vertical dashed line in the figure) as we observe all four resonances in this range. The nanoantenna dimensions and array period can be scaled to obtain resonances in other ranges of the infrared spectrum.

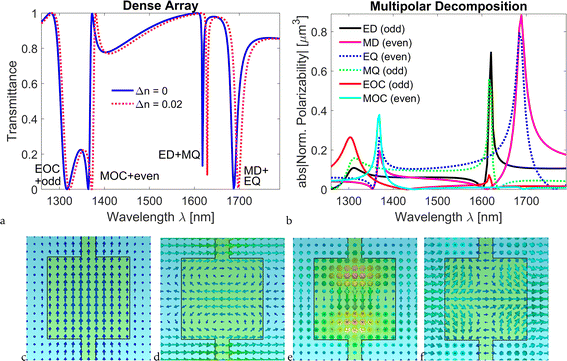
We present the transmittance spectra for D_x = D_y = 750 nm and a_x = a_y = a_z = 650 nm in Fig. 2a for two values of the refractive index. One can see that the spectral features – peaks and dips – are very narrow, and upon a change in the refractive index of the EO crystal by Δn = 0.02, which is obtainable, for example, by application of an appropriate electric field, the features shift drastically, as this spectral shift is comparable to the width of the transmittance feature in most cases. Such a drastic shift gives an opportunity to effectively control the signal and tune the metasurface response. For comparison, for a uniform thin film – continuous flat layer – with the same thickness of 650 nm and refractive index as the cuboid nanoantenna, the transmission spectrum does not show any sharp features, only exhibiting broad Fabry–Perot oscillations (see Fig. S1 of the ESI†). Additionally, the change in transmittance for the uniform film at any given wavelength when the refractive index is changed is much smaller than for the nanoantenna array.

Fig. 2 (a) Transmittance of the dense nanoantenna array with D_x = D_y = 750 nm and a_x = a_y = a_z = 650 nm. The solid line corresponds to the unbiased crystal (n = 2.7, Δn = 0). The dashed line shows the results for the biased crystal corresponding to an isotropic change in refractive index Δn = 0.02. Four multipolar modes result in the dips in the transmittance, and the dips are shifted upon biasing the crystal. (b) Multipolar decomposition for the case of an unbiased crystal: absolute value of the normalized effective polarizabilities. Here, “E” and “M” stand for electric and magnetic, and “D”, “Q”, and “OC” stand for dipole, quadrupole, and octupole, respectively. The electric dipole term includes a toroidal component. (c–f) Field distributions corresponding to the four resonances with different modes: (c) MD + EQ, (d) ED + MQ, (e) MOC + even, and (f) EOC + odd for D_x = D_y = 750 nm and a_x = a_y = a_z = 470 nm. The magnetic field H is shown in panels (c) and (e), which correspond to predominantly magnetic modes. The electric field E is shown in panels (d) and (f), which correspond to predominantly electric modes. The arrow lengths correspond to the relative field normalized to the magnitude of the incident field.

With the period dimensions D_x = D_y = 750 nm and the surrounding medium refractive index n_s = 1.47, the Rayleigh anomaly (RA) at the longest wavelength is λ_RA = n_sD_x = 1102.5 nm. This is much shorter than the wavelength at which the nanoantenna dipole resonances are excited, and thus the array can be considered dense. In such a dense array, the spectral positions of the nanoantenna resonances are close to those of the isolated nanoantenna. In contrast, in a nanoantenna array where the RA is spectrally close to the nanoantenna resonances, diffractive and collective phenomena play a crucial role, and we consider one of such cases later in this section.

A multipolar decomposition is performed for nanoantennas with the same parameters as in Fig. 2a, and the results are shown in Fig. 2b. This is carried out considering the scattered electromagnetic waves of local polarization sources and analyzing them using multipoles as the fundamental components (see ESI† for details on multipolar expressions). The procedure involves conducting full-wave numerical simulations, extracting the electric field distribution across the numerical domain at the specific spectral points, and integrating these fields to derive the corresponding multipolar contributions.⁸⁰ It accounts for all characteristics included in the numerical simulations (nanoantenna shape, metasurface surrounding, interconnection of nanoantennas by the bridge, etc.). Multipolar decomposition is a highly accurate method for determining multipolar components, offering a more precise and quantitative analysis compared to relying on field distribution alone, which is inherently qualitative.

The effective polarizabilities of each multipole are normalized based on the coefficients used in the calculations of reflection and transmission,⁸¹ reflecting the respective contributions to the overall array response. Multipoles can be even or odd, and they couple strongly within their group, resulting in the resonances of other multipoles within the group. The first mode in the metasurface transmittance spectrum (following the convention, we count starting with the longest wavelength) originates from the resonances of a magnetic dipole (MD) and an electric quadrupole (EQ), both of which are even multipoles. The second mode originates from the resonances of an electric dipole (ED) and a magnetic quadrupole (MQ), both of which are odd multipoles. The next higher-order modes are magnetic octupole (MOC) with other even multipoles and electric octupole (EOC) with other odd multiples. Throughout this work, we assign labels to the spectral features according to the nature of the resonances we identify in this multipolar decomposition (this is the meaning of the labels used earlier in Fig. 1d).

In addition to performing the multipolar decomposition, we present the electric and magnetic field profiles of the resonances, directly correlating them with specific multipolar modes at the wavelengths corresponding to each resonance. These distributions show the mode structure, helping to understand their contributions to scattering. In Fig. 2c–f, we show the field distributions corresponding to the MD + EQ, ED + MQ, MOC + even, and EOC + odd modes, respectively. In panels (c) and (d), one can clearly see dipolar field distributions. However, higher-order modes in panels (e) and (f) are less clear, as they include different even and odd components dominated by octupoles.

Lattice modes can be important in metasurfaces with varying periodicities, as they can significantly affect the tunable response of the structure. In our study, while the primary focus is on the optical properties induced by multipolar resonances, lattice modes can also play a critical role, especially in contributing to collective effects and modifying the resonance conditions. To address this and to provide a more comprehensive understanding of their impact on the metasurface EO tuning performance, we conduct an analysis of lattice modes and their change with refractive index.

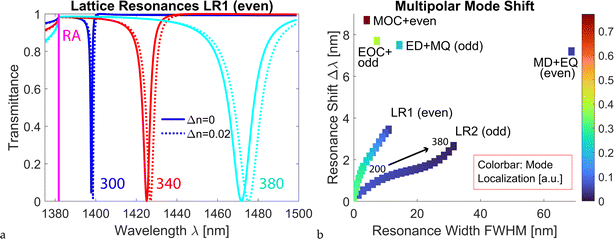
Nonlocal, collective effects have been known to result in narrow resonances. These spectral features are excited in proximity to the RA, as the latter corresponds to the emergence of new diffraction orders. Thus, lattice resonances can be controlled by the array periods D_x and D_y. They are also affected by the dimensions of the nanoantennas. We utilize this property to design an array of interconnected nanoantennas with lattice resonances. In Fig. 3a, we show these resonances for the case of D_x = 940 nm and D_y = 750 nm and the change in their position for different dimensions of the nanoantenna. In this case, the wavelength of RA at the longest wavelength is λ_RA = n_sD_x = 1381.8 nm. These lattice resonances are based on even multipoles (MD, EQ, and MOC) and thus referred to as ‘LR1 (even)’. In Fig. 3a, we see that the resonance is narrower for nanoantennas with the cuboid side of 300 nm than for the side of 380 nm. For the smaller nanoantennas, the resonance is excited closer to the RA and is narrower in bandwidth, which is consistent with the properties of lattice resonances.^4,82 Fig. 3a also shows that the lattice resonances of smaller nanoantennas experience smaller spectral shifts with a change in refractive index (Δn = 0.02 in the figure) than the lattice resonances for larger nanoantennas.

Fig. 3 (a) Transmittance spectra of the nanoantenna arrays supporting lattice resonances. Here, D_x = 940 nm and D_y = 750 nm. The wavelength of the Rayleigh anomaly (RA) λ_RA = n_sD_x is denoted as a vertical magenta line. Three sets of nanoantennas are considered: 300, 340, and 380 nm in dimensions a_x = a_y = a_z. The solid and dashed lines show the spectral features for the unbiased (Δn = 0) and biased (Δn = 0.02) crystal. (b) Summary of resonance shifts for different multipoles: four modes of the dense array and two lattice resonances are considered. The shift is determined for Δn = 0.02. MD + EQ mode is analyzed for a_x = a_y = a_z = 470 nm, ED + MQ for 550 nm, MOC + odd for 683 nm, and EOC + even for 716 nm. Different dimensions of the nanoantennas are considered to shift their resonances to the same spectral position of ∼1430 nm. D_x = D_y = 750 nm for all calculations of the dense array. Branches ‘LR1’ and ‘LR2’ corresponding to lattice resonances of even and odd multipoles are calculated by varying the nanoantenna dimensions. Branch ‘LR1 (even)’ is for D_x = 940 nm and D_y = 750 nm, and branch ‘LR2 (odd)’ is for D_x = 750 nm and D_y = 940 nm. For both branches ‘LR1 (even)’ and ‘LR2 (odd)’, the nanoantenna dimensions a_x = a_y = a_z range from 200 to 380 nm. The resonances for the sparse arrays form branches rather than one point, as in the case of a dense array.

Having identified multipolar resonances in the dense array and lattice resonances in the same spectral range, we next analyze how far the resonance can be shifted upon a change in the refractive index of the EO crystal (Fig. 3b). We choose again Δn = 0.02, and we calculate the shift of all the resonances we identified earlier. We adjust the dimensions of the nanoantennas so that the resonances are excited approximately at the same wavelength ∼1430 nm. Mode localization is calculated by introducing a very small absorption of the nanoantenna material and calculating the absorption in the nanoantennas. The resonance width is calculated as the full width at half maximum (FWHM), that is, the width of a spectral feature at half of its maximum amplitude.

One can observe that higher-order multipolar resonances in the dense array, such as EOC and MOC, exhibit resonance shifts larger than lower-order multipolar resonances, such as dipoles and quadrupoles. One can also see that the resonance width of the higher-order multiples is narrower and that the mode localization is higher (dark red and greenish colors on the colorbar as opposed to blue and light blue). These observations are consistent with the properties of higher-order multipolar modes in single nanoantennas.

It can also be seen that, compared to the lattice resonances in the sparse arrays, the multipolar resonances of the dense array exhibit larger shifts in general, even for comparable resonance widths. Mode ‘LR1 (even)’ exhibits slightly better performance than ‘LR2 (odd)’, resulting in a marginally larger shift of the resonance and higher mode localization. The mode localization of the field in branch ‘LR1 (even)’ can be as high as one in the EOC resonance of the dense array (the same greenish color in the colorbar). For nanoantenna dimensions ≥ 300 nm, LR1 and LR2 have widths comparable to or broader than multipolar resonances in the dense array. Smaller nanoantennas result in resonances that are very narrow.

Collective resonances occur because of the coherent scattering of the multipoles in the periodic lattice close to the diffractive regime. Lattice resonances have been extensively analyzed with respect to the change in the refractive index of the surrounding medium, especially in regard to sensing applications.^4,83–85 The lattice resonances have been shown to be very responsive to a change in the refractive index of the surrounding medium. However, the resonance response to the change in the refractive index of the nanoantenna has not received the same attention. Our analysis shows that the lattice resonances are relatively robust to changes in the refractive index of the nanoantenna, yielding only a very small shift in resonance position when the refractive index of the nanoantenna is changed. Because of this, these lattice resonances do not provide a particularly useful handle if a tunable structure is sought. The main reason for these properties is the delocalized nature of the lattice mode. In the next section, we focus on the analysis of the four modes that correspond to the dense array with D_x = D_y = 750 nm, as these modes demonstrated the largest shifts with respect to the change in refractive index.

3 Chalcophosphate metasurfaces with in-plane bias

As mentioned in the Introduction, the current selection of commercial infrared EO materials is rather limited, especially for operation in the mid- and far-infrared range (2.5–20 μm), and the magnitude of the EO coefficients for most is such that very large fields or long pathlengths are needed to achieve refractive index changes of practical use. Other material limitations are related to the tendency for layered growth, low laser-induced damage thresholds, absorption losses, and toxicity.

One promising material in the chalcophosphate family is tin thiohypodiphosphate, Sn₂P₂S₆, which is ferroelectric at room temperature but has a low Curie temperature (64.7 °C),⁶¹ has substantial EO coefficients,⁶¹ and has an extensive transparency range (from λ = 0.53 μm to λ = 8 μm).⁶² The EO coefficients for this material are already relatively large at room temperature (the largest reported component, r₁₁₁, is +174 ± 10 pm V⁻¹ at 633 nm and room temperature⁶¹) and larger than lithium niobate. Since the EO coefficients increase with increasing temperature up to the Curie point, significantly larger r_ijk values than at room temperature could be achieved by judicious control of the temperature, at least for some of the tensor components, thus offering the potential for considerable changes in the refractive index under manageable conditions. This is illustrated in Fig. 4a, where the blue line in the main graph shows the value of r₁₁₁ as a function of temperature, according to the parameters reported in ref. 61. r₁₁₁ values as high as 3000 pm V⁻¹ are possible in the vicinity of T_C.

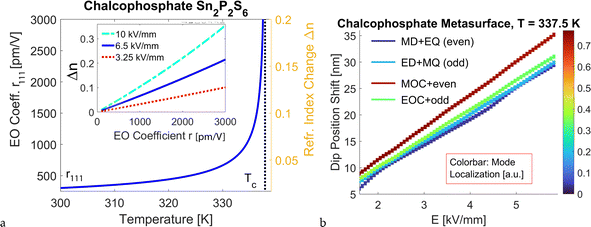Fig. 4 (a) EO coefficient r₁₁₁ for Sn₂P₂S₆ as a function of temperature (left ordinate axis). T_C = 64.7 °C is shown by the vertical black dotted line. Data are taken from ref. 61. The corresponding induced changes in the refractive index for E = 6.5 kV mm⁻¹ are shown on the right ordinate axis. Inset: The absolute change in refractive index as a function of the value of r for three different magnitudes of the electric field E. (b) Shift of the dip position for four modes of the dense arrays with respect to the bias field E. Calculations are performed for r₂₂₁ (room temperature value, 92 pm V⁻¹, and temperature dependence from ref. 61), T = 337.5 K (64.35 °C), and D_x = D_y = 750 nm. Similarly to Fig. 3, MD + EQ mode is analyzed for a_x = a_y = a_z = 470 nm, ED + MQ for 550 nm, MOC + odd for 683 nm, and EOC + even for 716 nm. The colorbar indicates the mode localization defined in the same way as in Fig. 3.

The inset shows the variation in the absolute value of the refractive index, |Δn| = (1/2)n³rE, achievable as a function of r for three values of the applied electric field. It can be seen that for a bias of 6.5 kV mm⁻¹, a change in the refractive index as high as Δn = 0.2 could be realized. To our knowledge, the breakdown field for Sn₂P₂S₆ has not been reported in the literature. For reference, the breakdown field for lithium niobate has been reported to be E = 70–80 kV mm⁻¹,⁸⁶ and we can assume that 6.5 kV mm⁻¹ is safely below the breakdown for the chalcophosphate of interest. The absolute refractive index changes achievable as a function of temperature for this applied voltage are shown on the right ordinate axis of the main graph in the same figure. An even higher |Δn| can be achieved with larger biases (see the cyan line in the inset of Fig. 4a). Complementing the results presented here, Fig. S4 of the ESI† shows the induced change in the refractive index Δn that can be achieved for different biases E and temperatures close to T_C (T = 336, 337, and 337.5 K). One can see that a substantial change in the refractive index Δn = 0.5 can be achieved for realistic bias values up to 12 kV mm⁻¹, provided the crystal temperature can be stabilized with sufficiently small fluctuations just below the Curie temperature. Thus, Sn₂P₂S₆ is a promising candidate for applications requiring significant changes in the refractive index.

It should be noted that Sn₂P₂S₆ is anisotropic (with n_i − n_j ∼ 0.1 or slightly higher, as shown in Fig. S2a†) and that more than one component of the refractive index matrix could be changed (and to a different extent) by various combinations of electric field and polarization directions. Furthermore, off-diagonal components of the refractive index can be non-zero or become non-zero when the field is applied, resulting in changes in the polarization eigenmodes. Here, we consider this to be a minor effect and neglect it, assuming that only diagonal components of the refractive index matrix are changed by the applied field and that all diagonal elements are changed to the same extent. This is justified by the following observations: (1) it was tested that the dispersion of the refractive index for Sn₂P₂S₆ (Fig. S2a†) affects the spectral profiles of the array only very weakly (Fig. S2b†). (2) If a weak refractive index anisotropy was introduced in the absence of bias, it was found not to cause excitation of any additional modes in the nanoantennas and only shift their position with respect to the isotropic material (Fig. S3†). As a consequence, one could expect that an anisotropic change of refractive index Δn would not significantly affect the spectral features in comparison to the isotropic case. Even nanoantennas made of the highly anisotropic van der Waals material MoS₂, with drastically different (but positive) in-plane and out-of-plane permittivity components, support resonance excitations similar to those in silicon nanoantennas (see ref. 87). Thus, the general conclusions about the type of modes and their behavior reached in the approximation of an isotropic refractive index of the EO nanoantennas should also hold for a more realistic – anisotropic – material. In this way, our calculations are the estimates of the largest possible resonance shift. A more complete accounting of anisotropy effects on nanoantenna resonances and EO-induced shifts will be considered in the follow-up work.

The considerations above are based on r₁₁₁, which is the largest component of the EO tensor for Sn₂P₂S₆. However, it requires the applied bias field to be parallel to the polarization direction, that is, the applied field and polarization are along the y-axis, which is not the case here. Instead, it is possible to orient the Sn₂P₂S₆ crystal before patterning it in the nanoantennas such that the active component of the EO tensor is r₂₂₁, as described below. Let us use capital letters to refer to the crystal frame of reference to avoid confusion with the laboratory frame x, y, z in Fig. 1a, and the same axes convention for a single crystal of Sn₂P₂S₆ as in ref. 61. To realize a structure like the one shown in Fig. 1a, we could envision nanoantennas made from Sn₂P₂S₆ oriented as follows: the Z axis of the crystal aligns with the propagation direction z of light through the structure, X is parallel to y (and thus E), and Y is parallel to x, the polarization direction considered in this work. No change in the orientation of the index ellipsoid is induced by an electric field applied along y = X (it should be noted, however, that the index ellipsoid is rotated relative to the X, Y, Z-frame for the zero field).

We then perform numerical simulations of the metasurface when the refractive index is tuned by the field E at a temperature close to T_C, and we track the shift of the dip position for four modes of the dense array (Fig. 4b). For these calculations, a value of r₂₂₁ = 92 pm V⁻¹ is used (ref. 61, neglecting the small wavelength dispersion from the visible to the near-infrared range).

One can see that for all modes, the dip position shift increases with a higher electric field. The mode ‘MOC + even’ experiences the fastest shift even though the mode localization is slightly reduced for the larger bias value. The other three modes demonstrate a comparable shift, with ‘EOC + odd’ having a slightly larger shift than the other modes. Depending on the mode, a shift of 28–35 nm can be achieved for a bias of E = 6 kV mm⁻¹. The dip position can also be changed with temperature while maintaining a fixed electric field (as shown in Fig. S5 of the ESI†).

In the calculations, we assume a positive change in the refractive index Δn (that is, Δn > 0). In practice, the sign of the index change can be controlled by the direction of the applied bias, allowing to obtain positive and negative Δn. An EO device operating based on the variation from −Δn to +Δn has improved performance. In our analysis, we observe a near-linear shift in the spectral positions of the features, and we do not expect any particularly different effects for Δn < 0. These results demonstrate the great potential of the chalcophosphate metasurface for EO applications since a significant shift of the spectral features can be obtained with reasonable bias.

4 Chalcophosphate metasurfaces with out-of-plane bias

The metasurface design considered above assumes interconnected nanoantennas and electrodes on both sides of the nanoantenna array. This design implies that an electric field (bias) is applied along the chain of interconnected nanoantennas (in the plane of the nanostructures), which have an approximate length of tens of micrometers. Achieving a bias of up to several kV mm⁻¹ would require relatively high voltages, which, in turn, could lead to higher chances of leakage and breakdown, especially around the defects of the metasurface.

To mitigate this challenge, an alternative approach is to apply the bias perpendicular to the metasurface (Fig. 5a). We refer to this configuration as out-of-plane biasing. Once again, the orientation of the Sn₂P₂S₆ crystal in the nanoantennas determines which component of the EO tensor is active in the target configuration. The out-of-plane biasing configuration can be realized by orienting the Sn₂P₂S₆ in the nanoantennas in one of two ways (using the same crystal frame of reference as in Section 3): (i) the crystal's X-axis is parallel to z of the device (and thus to E), Y is parallel to y, and Z is parallel to x (polarization direction of light). This selection exploits the r₃₃₁ component of the EO coefficient, which has been reported to be 140 pm V⁻¹ at 633 nm and larger than r₂₂₁.⁶¹ (ii) An alternative selection is again with X parallel to z, but with the reverse role of the other two crystal axes (i.e., Y parallel to x, and Z parallel to y) and exploiting the r₂₂₁ component. The latter selection is used for the simulation.

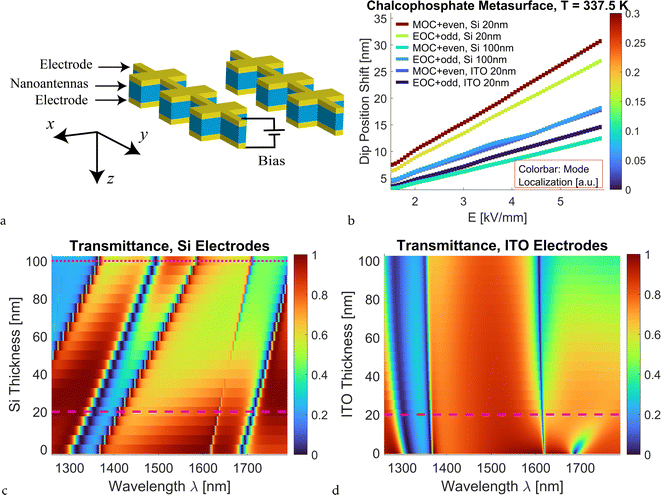Fig. 5 Metasurface for out-of-plane biasing, with thin electrode layers of silicon or ITO. (a) Schematic of the layout with conductive layers (yellow) above and below the chalcophosphate nanoantennas (blue). The upper and lower electrodes have the same thickness. (b) Shift of the dip position for MOC + even and EOC + odd modes in the chalcophosphate metasurface with electrodes as a function of the electric field. Calculations are conducted for r₂₂₁ and for T = 337.5 K (parameters from ref. 61). The colorbar indicates the mode localization defined in the same way as in Fig. 3. Results are shown for silicon electrodes with thicknesses of 20 and 100 nm and ITO electrodes of 20 nm. Other dimensions of the metasurface are the same as those used above. (c) Transmittance of the metasurface with silicon layers of varying thickness for the unbiased crystal (Δn = 0). The 20 nm and 100 nm cases are shown with dashed and dotted horizontal lines, respectively. Chalcophosphate cuboids have a_x = a_y = a_z = 650 nm. The resonances experience redshift with increasing thickness of the silicon layer, but all four resonances remain clearly visible even for thicker silicon layers. (d) Transmittance of the metasurface with ITO layers of varying thickness and an unbiased crystal (Δn = 0). Chalcophosphate cuboids have a_x = a_y = a_z = 650 nm. The 20 nm case is shown with the dashed horizontal line.

From a practical point of view, the out-of-plane bias configuration requires a layer of conductive material on the top and bottom of the nanoantennas (yellow-colored layers in Fig. 5a). Examples of materials that can be used as electrodes are doped silicon and indium tin oxide (ITO). The layers of silicon or ITO could be etched in the same fabrication step as the etching of the chalcophosphate crystal. The design with an active layer sandwiched between the electrodes is very common in general, as it is proven to be useful for enhancing field localization in the core part of a multilayer structure as well as biasing an active material in the out-of-plane direction.^14,37,77,88

We perform simulations of the periodic array of interconnected nanoantennas with top and bottom conductive layers and surrounded by silica, and we analyze the shift of the spectral features as a function of the electric field (Fig. 5b) and the effect of electrode thickness on the transmittance spectra of unbiased nanoantenna arrays (Fig. 5c and d). In panels b-d, the array is dense, and D_x = D_y = 750 nm. When we consider electrode layers made of silicon, we use the permittivity data for amorphous silicon, taking into account dispersion but assuming negligible losses. The permittivity data are taken from the refractiveindex.info database referring to ref. 89. Doping levels up to 10¹⁹ cm⁻³ do not cause high material losses and should provide sufficiently high conductivity and small resistance for use in the nanoantenna device. From the simulation results, one can see that changing the thickness of the silicon layer does not result in a significant alteration of the nanoantenna modes (Fig. 5c). The nanoantennas with electrodes exhibit the same four modes as those observed earlier for nanoantennas without the electrode layers. Thicker layers of silicon result in a redshift of the modes. An additional broad dip originating from the two resonances emerges for thicker silicon (>60 nm) and also experiences a redshift with increasing Si thickness. When a bias is applied, 20 nm silicon layers result in a dip position shift only slightly smaller than for nanoantennas with in-plane bias (compare Fig. 5b to 4b). 100 nm silicon layers result in a field-induced shift smaller by about a factor of two than the one for 20 nm-thick silicon layers. One can observe that the trend changes with the film thickness, and the shift of the MOC mode is not as drastic as that of the EOC one because modes corresponding to the different multipoles have a different response to the adjacent material.

The alternative conductive electrode material we consider is ITO (Fig. 5d). We take the ITO permittivity parameters from ref. 90 for the case of ITO annealed for 10 hours. This procedure has been shown to result in ITO with significantly reduced absorption losses compared to as-deposited ITO reported in the same source or ITO data reported in other sources, e.g., in ref. 91. It is found that the MD + EQ mode is not present for the metasurfaces with ITO layers. The other nanoantenna resonances are present and experience a slight blueshift with increasing ITO thickness. The significant decrease in transmittance and the disappearance of the spectral feature as the ITO thickness increases are caused by absorption losses in ITO. ITO layers of 20–40 nm have resistance ∼100 Ω,⁹² so we select 20 nm for the analysis of the change in spectral characteristic as a function of the applied electric field (Fig. 5b). Simulation results for ITO show that the mode shifts are very similar to those for 100 nm silicon and around half of the shift possible for the nanoantennas without electrodes or with 20 nm-thick silicon electrodes.

5 Discussion

It is interesting to compare our design with other theoretical proposals of EO metasurfaces. For lithium niobate with Δn ∼ 0.01 and bias voltage in both directions (effectively doubling the effect), the shift in the spectral feature (dip in transmittance) has been reported to be up to 8 nm.¹⁸ This is comparable to the values we obtain for higher-order multipolar resonances, presented in Fig. 2a and 3 for a slightly longer wavelength range. However, such a shift for the lithium niobate case requires a bias close to the electrical breakdown of the material. This does not leave room for further enhancement of the effect and could increase the chance of device failure. In contrast, Sn₂P₂S₆ and other chalcophosphates allow for a substantial increase in Δn, and a shift of the spectral feature as large as 35 nm can be observed at substantially lower applied voltages, as shown in Fig. 4. Experimental measurements on the lithium niobate metasurface have demonstrated a 3 nm spectral shift of the reflection dip upon bias variation of ±25 V and have been in good agreement with numerical predictions for the same metasurface design.¹⁷ Theoretical analysis of silicon-on-lithium niobate metasurfaces for EO wavefront shaping and high quality factor has demonstrated a 0.1 nm shift of the reflectance dip with a ±10 V bias.³⁷ Thus, chalcophosphates are promising for EO metasurfaces because of their significant Pockels effect at room temperature and its enhancement approaching T_C, enabling efficient electric-field-induced modulation of optical properties, and have the potential to provide modulation much larger than that of metasurfaces with lithium niobate.

Nanofabrication of metasurfaces made from crystalline materials, such as lithium niobate, silicon, or III–V compound, typically begins with crystal growth or bonding of a thin crystal layer onto a substrate (for example, silicon dioxide). The crystal layer thickness is then carefully reduced to the desired amount through processes such as polishing or chemical etching. Following this, an electron-beam resist is spin-coated onto the crystal surface, exposed with an electron beam lithographic write, and subsequently developed to create the desired pattern. A hard mask, often composed of a metal like chromium, is then deposited over the patterned resist, typically with an electron-beam evaporator in the case of a metal mask. The resist is lifted off, leaving the hard mask to protect specific areas during the subsequent etching process, which sculpts the crystalline material into the desired metasurface structure. Finally, a separate step is undertaken to fabricate electrical contacts, if required, for the metasurface or EO device based on it.

For the out-of-plane biasing configuration, the electrodes can be made of two-dimensional materials, such as graphene or transition metal dichalcogenides. Because of the ultra-thin layers, these materials should provide high conductivity and not significantly affect the metasurface optical response. However, from a fabrication point of view, they are still challenging to realize consistently and require difficult nanofabrication steps. Other possible designs include a bulk layer of chalcophosphate crystal with a pattern of holes, which, could support photonic-crystal-type modes.

6 Conclusions

We reported on theoretical results on high-performance EO chalcophosphate metasurfaces with interconnected nanoantennas supporting higher-order multipolar resonances. We computationally showed that this type of nanostructure is promising for realizing efficient subwavelength scatterers with tunable characteristics. We observed that a nanoantenna made out of Sn₂P₂S₆ possesses several multipolar resonances enabled by the support of internal modes and their reflection from the antenna boundaries. By exploring different antenna dimensions and designs, a full range of multipolar resonances (electric and magnetic dipoles, quadrupoles, octupoles, and higher-order multipoles) can be achieved.

Localized nanoantenna resonances in the dense array are shown to be more efficient than collective lattice resonances supported by the same nanoantennas in the same spectral range, even though the collective resonances are narrower. Tight mode localization in the nanoantennas and low Curie temperature of the chalcophosphate materials allow for a significant shift of resonant spectral features (tens of nm's) with realistic bias due to the enhancement of the EO coefficient when approaching T_C. Bridge interconnects and thin electrodes surrounding the nanoantennas facilitate biasing and have been shown to not diminish the EO characteristics of the metasurface. EO chalcophosphate metasurfaces can potentially revolutionize nanophotonic device concepts for various applications, such as modulators, sensors, and beam steerers, among others, operable in the infrared region.

Abbreviations

ED	Electric dipole
EO	Electro-optic
EOC	Electric octupole
EQ	Electric quadrupole
FWHM	Full width at half maximum
ITO	Indium tin oxide
LR	Lattice resonance
MD	Magnetic dipole
MOC	Magnetic octupole
MQ	Magnetic quadrupole
RA	Rayleigh anomaly

Data availability

This study was carried out using commercial software CST Studio Suite and COMSOL Multiphysics. CST Studio Suite can be contacted at the Simulia website https://www.3ds.com. The version of the code employed for this study is 2024. COMSOL Multiphysics can be contacted at https://www.comsol.com. The version of the code employed for this study is 5.6. The data supporting this article have also been included as part of the ESI.†

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

This research was supported in part by the Air Force Research Laboratory's Materials and Manufacturing Directorate, through the Air Force Office of Scientific Research Summer Faculty Fellowship Program®, Contract Numbers FA8750-15-3-6003, FA9550-15-0001, and FA9550-20-F-0005. V. E. B. also acknowledges support from the National Science Foundation under Grant No. 2418519.

References

1. M. Brongersma, Engineering optical nanoantennas, Nat. Photonics, 2008, 2, 270–272,  DOI:10.1038/nphoton.2008.60.
2. A. B. Evlyukhin, S. M. Novikov, U. Zywietz, R. Lynge Eriksen, C. Reinhardt, S. I. Bozhevolnyi and B. N. Chichkov, Demonstration of magnetic dipole resonances of dielectric nanospheres in the visible region, Nano Lett., 2012, 12(7), 3749–3755,  DOI:10.1021/nl301594s.
3. A. Alù and N. Engheta, Theory, modeling and features of optical nanoantennas, IEEE Trans. Antennas Propag., 2013, 61(4), 1508–1517,  DOI:10.1109/TAP.2013.2241718.
4. V. G. Kravets, A. V. Kabashin, W. L. Barnes and A. N. Grigorenko, Plasmonic surface lattice resonances: A review of properties and applications, Chem. Rev., 2018, 118(12), 5912–5951,  DOI:10.1021/acs.chemrev.8b00243.
5. V. E. Babicheva and M. Rumi, Tunable electro-optic resonant metasurfaces, in Plasmonics: Design, Materials, Fabrication, Characterization, and Applications XXII, ed. T. Tanaka and Y.-J. Lu, International Society for Optics and Photonics, SPIE, 2024, vol. 13111, p. 1311102,  DOI:10.1117/12.3027865.
6. L. R. Dalton, J. Leuthold, B. H. Robinson, C. Haffner, D. L. Elder, L. E. Johnson, S. R. Hammond, W. Heni, C. Hosessbacher, B. Baeuerle, E. De Leo, U. Koch, P. Habegger, Y. Fedoryshyn, D. Moor and P. Ma, Perspective: Nanophotonic electro-optics enabling THz bandwidths, exceptional modulation and energy efficiencies, and compact device footprints, APL Mater., 2023, 11(5), 050901,  DOI:10.1063/5.0145212.
7. P. Thureja, R. Sokhoyan, C. U. Hail, J. Sisler, M. Foley, M. Y. Grajower and H. A. Atwater, Toward a universal metasurface for optical imaging, communication, and computation, Nanophotonics, 2022, 11(17), 3745–3768,  DOI:10.1515/nanoph-2022-0155.
8. A. Karvounis, F. Timpu, V. V. Vogler-Neuling, R. Savo and R. Grange, Barium titanate nanostructures and thin films for photonics, Adv. Opt. Mater., 2020, 8(24), 2001249,  DOI:10.1002/adom.202001249.
9. G. Chen, N. Li, J. D. Ng, H.-L. Lin, Y. Zhou, Y. Hsing Fu, L. Y. T. Lee, Y. Yu, Ai-Q. Liu and A. J. Danner, Advances in lithium niobate photonics: development status and perspectives, Adv. Photonics, 2022, 4(3), 034003,  DOI:10.1117/1.AP.4.3.034003.
10. A. Fedotova, L. Carletti, A. Zilli, F. Setzpfandt, I. Staude, A. Toma, M. Finazzi, C. De Angelis, T. Pertsch, D. N. Neshev and M. Celebrano, Lithium niobate meta-optics, ACS Photonics, 2022, 9(12), 3745–3763,  DOI:10.1021/acsphotonics.2c00835.
11. N. Sun, D. Sun, D. Wu, Y. Guo, Y. Fan, F. Zou, M. Pu and X. Luo, Lowering the bit-energy of electro-optic modulators via polarization-phase modulation in thin-film batio3 ferroelectric crystal waveguide, Laser Photonics Rev., 2024, 18(3), 2300937,  DOI:10.1002/lpor.202300937.
12. D. Kang, H. Heo, Y. Yang, J. Seong, H. Kim, J. Kim and J. Rho, Liquid crystal-integrated metasurfaces for an active photonic platform, Opto-Electron. Adv., 2024, 7(6), 230216,  DOI:10.29026/oea.2024.230216.
13. V. E. Babicheva and A. B. Evlyukhin, Mie-resonant metaphotonics, Adv. Opt. Photonics, 2024, 16(3), 539–658,  DOI:10.1364/AOP.510826.
14. S. Mallick and D. Roy Chowdhury, Broadside-coupling-enabled insulator-to-metal transition in a terahertz metasurface, Europhys. Lett., 2022, 138(5), 55001,  DOI:10.1209/0295-5075/ac6e82.
15. J. Fan, Z. Li, Z. Xue, H. Xing, D. Lu, G. Xu, J. Gu, J. Han and L. Cong, Hybrid bound states in the continuum in terahertz metasurfaces, Opto-Electron. Sci., 2023, 2(4), 230006,  DOI:10.29026/oes.2023.230006.
16. Z. Jiang, Y. Liu and L. Wang, Applications of optically and electrically driven nanoscale bowtie antennas, Opto-Electron. Sci., 2022, 1(4), 210004,  DOI:10.29026/oes.2022.210004.
17. A. Weiss, C. Frydendahl, J. Bar-David, R. Zektzer, E. Edrei, J. Engelberg, N. Mazurski, B. Desiatov and U. Levy, Tunable metasurface using thin-film lithium niobate in the telecom regime, ACS Photonics, 2022, 9(2), 605–612,  DOI:10.1021/acsphotonics.1c01582.
18. L. Wang and I. Shadrivov, Electro-optic metasurfaces, Opt. Express, 2022, 30(20), 35361–35368,  DOI:10.1364/OE.469647.
19. C. Damgaard-Carstensen, M. Thomaschewski and S. I. Bozhevolnyi, Electro-optic metasurface-based free-space modulators, Nanoscale, 2022, 14, 11407–11414,  10.1039/D2NR02979K.
20. G. Liu, S. Zong, X. Liu, J. Chen and Z. Liu, High-performance etchless lithium niobate layer electro-optic modulator enabled by quasi-bics, Opt. Lett., 2024, 49(1), 113–116,  DOI:10.1364/OL.505351.
21. Y. Ju, H. Zhou, Y. Huang, Z. Yin, X. Deng, Z. Yang, F. Wang, Q. Gu, G. Deng and H. Zuo, The electro-optic spatial light modulator of lithium niobate metasurface based on plasmonic quasi-bound states in the continuum, Nanoscale, 2023, 15, 13965–13970,  10.1039/D3NR02278A.
22. X. Chen, R. Leng, K. Liu, C. Guo, Z. Zhu, S. Qin and J. Zhang, High quality factor resonant metasurface with etchless lithium niobate, Opt Laser. Technol., 2023, 161, 109163,  DOI:10.1016/j.optlastec.2023.109163.
23. C. Damgaard-Carstensen and S. I. Bozhevolnyi, Nonlocal electro-optic metasurfaces for free-space light modulation, Nanophotonics, 2023, 12(14), 2953–2962,  DOI:10.1515/nanoph-2023-0042.
24. M. Qi, X. Chen, W. Xu, Z. Zhu, X. Yuan and J. Zhang, High q resonant Sb₂S₃-lithium niobate metasurface for active nanophotonics, Nanomaterials, 2021, 11(9), 2373,  DOI:10.3390/nano11092373.
25. X. Chen, M. Qi, W. Xu, J. Zhang, Z. Zhu and S. Qin, Electrically tunable absorber based on a graphene integrated lithium niobate resonant metasurface, Opt. Express, 2021, 29(21), 32796–32803,  DOI:10.1364/OE.433890.
26. D. Barton III, M. Lawrence and J. Dionne, Wavefront shaping and modulation with resonant electro-optic phase gradient metasurfaces, Appl. Phys. Lett., 2021, 118(7), 071104,  DOI:10.1063/5.0039873.
27. M. J. Dicken, L. A. Sweatlock, D. Pacifici, H. J. Lezec, K. Bhattacharya and H. A. Atwater, Electrooptic modulation in thin film barium titanate plasmonic interferometers, Nano Lett., 2008, 8(11), 4048–4052,  DOI:10.1021/nl802981q.
28. S. H. Chu, D. J. Singh, J. Wang, E.-P. Li and K. P. Ong, High optical performance and practicality of active plasmonic devices based on rhombohedral BiFeO₃, Laser Photonics Rev., 2012, 6(5), 684–689,  DOI:10.1002/lpor.201280022.
29. T. Qu, Y. Song, K. Yang, Y. Huang, S. Wu, Z. Tan, and X. Long, High performance electro-optic modulator employing a thin BiFeO₃ film on au with absorption resonance, in Optical Interference Coatings, Optica Publishing Group, 2013, p. MB.6,  DOI:10.1364/OIC.2013.MB.6.
30. M. Zhu, Z. Du, Q. Liu, B. Chen, S. H. Tsang and E. H. T. Teo, Ferroelectric BiFeO₃ thin-film optical modulators, Appl. Phys. Lett., 2016, 108(23), 233502,  DOI:10.1063/1.4953201.
31. L. Bibbò, K. Khan, Q. Liu, M. Lin, Q. Wang and Z. Ouyang, Tunable narrowband antireflection optical filter with a metasurface, Photonics Res., 2017, 5(5), 500–506,  DOI:10.1364/PRJ.5.000500.
32. L. Wang, F. Setzpfandt and I. Shadrivov, Tunable anisotropic electro-optic metasurfaces, Opt. Mater. Express, 2023, 13(11), 3376–3383,  DOI:10.1364/OME.499704.
33. Y. Ju, H. Zhou, Y. Zhao, F. Wang, Z. Yang, X. Deng, Z. Wu, D. Guoliang and H. Zuo, Hybrid resonance metasurface for a lithium niobate electro-optical modulator, Opt. Lett., 2022, 47(22), 5905–5908,  DOI:10.1364/OL.474784.
34. H. Weigand, V. V. Vogler-Neuling, M. Reig Escala, D. Pohl, F. U. Richter, A. Karvounis, F. Timpu and R. Grange, Enhanced electro-optic modulation in resonant metasurfaces of lithium niobate, ACS Photonics, 2021, 8(10), 3004–3009,  DOI:10.1021/acsphotonics.1c00935.
35. Y. Ju, W. Zhang, Y. Zhao, X. Deng and H. Zuo, Polarization independent lithium niobate electro-optic modulator based on guided mode resonance, Opt. Mater., 2024, 148, 114928,  DOI:10.1016/j.optmat.2024.114928.
36. B. Gao, M. Ren and W. Wu, et al., Electro-optic lithium niobate metasurfaces, Sci. China: Phys., Mech. Astron., 2021, 64, 240362.
37. E. Klopfer, S. Dagli, D. I. I. I. Barton, M. Lawrence and J. A. Dionne, High-quality-factor silicon-on-lithium niobate metasurfaces for electro-optically reconfigurable wavefront shaping, Nano Lett., 2022, 22(4), 1703–1709,  DOI:10.1021/acs.nanolett.1c04723.
38. H. Xia, Z. Li and C. Chen, Toroidal dipole fano resonances driven by bound states in the continuum of lithium niobate metasurface for efficient electro-optic modulation, Opt. Commun., 2024, 554, 130178,  DOI:10.1016/j.optcom.2023.130178.
39. T. Naeem, H. Saad Khaliq, M. Zubair, T. Tauqeer and M. Q. Mehmood, Engineering tunability through electro-optic effects to manifest a multifunctional metadevice, RSC Adv., 2021, 11, 13220–13228,  10.1039/D1RA00901J.
40. N. Xu, H. Yuan, K. Jie, S. Qin, H. Huang, L. Chen, H. Liu, J. Guo, H. Meng, F. Wang, X. Yang and Z. Wei, Electrically-driven zoom metalens based on dynamically controlling the phase of barium titanate (BTO) column antennas, Nanomaterials, 2021, 11(3), 729,  DOI:10.3390/nano11030729.
41. K. Jie, H. Huang, S. Qin, J. Guo, H. Liu, H. Meng, F. Wang, X. Yang and Z. Wei, Electronically controlled time-domain integral average depolarizer based on a barium titanate (BTO) metasurface, Nanomaterials, 2022, 12(7), 1228,  DOI:10.3390/nano12071228.
42. R. Kanyang, C. Fang, Q. Yang, Y. Shao, G. Han, Y. Liu and Y. Hao, Electro-optical modulation in high q metasurface enhanced with liquid crystal integration, Nanomaterials, 2022, 12(18), 3179,  DOI:10.3390/nano12183179.
43. Y. Hou, Y. Xu, B. Du, Y. Zhang and L. Zhang, Electrically tunable dual polarization states of light using lithium niobate-based nanograting, Opt. Lett., 2024, 49(3), 470–473,  DOI:10.1364/OL.511314.
44. A. Hoblos, N. Courjal, M. P. Bernal and F. I. Baida, Low driving voltage lithium niobate metasurface electro-optical modulator operating in free space, Opt. Express, 2022, 30(26), 48103–48111,  DOI:10.1364/OE.478938.
45. X. Liu, G. Fu, S. Song, Y. Huang, M. Liu, G. Liu and Z. Liu, Tunability-selective lithium niobate light modulators via high-q resonant metasurface, Opt. Lett., 2024, 49(6), 1536–1539,  DOI:10.1364/OL.513631.
46. F. Timpu, J. Sendra, C. Renaut, L. Lang, M. Timofeeva, M. T. Buscaglia, V. Buscaglia and R. Grange, Lithium niobate nanocubes as linear and nonlinear ultraviolet mie resonators, ACS Photonics, 2019, 6(2), 545–552,  DOI:10.1021/acsphotonics.8b01594.
47. H. C. Weigand, U.-L. Talts, A.-L. Vieli, V. V. Vogler-Neuling, A. Nardi and R. Grange, Nanoimprinting solution-derived barium titanate for electro-optic metasurfaces, Nano Lett., 2024, 24(18), 5536–5542,  DOI:10.1021/acs.nanolett.4c00711.
48. A. Karvounis, V. V. Vogler-Neuling, F. U. Richter, E. Danervaud, M. Timofeeva and R. Grange, Electro-optic metasurfaces based on barium titanate nanoparticle films, Adv. Opt. Mater., 2020, 8(17), 2000623,  DOI:10.1002/adom.202000623.
49. A. Karvounis and R. Grange, Electro-mechanical to optical conversion by plasmonic-ferroelectric nanostructures, Nanophotonics, 2022, 11(17), 3993–4000,  DOI:10.1515/nanoph-2022-0105.
50. V. Valentina Vogler-Neuling, A. Karvounis, A. Morandi, H. Weigand, E. Danervaud and R. Grange, Photonic assemblies of randomly oriented nanocrystals for engineered nonlinear and electro-optic effects, ACS Photonics, 2022, 9(7), 2193–2203,  DOI:10.1021/acsphotonics.2c00081.
51. E.-L. Talts, H. C. Weigand, G. Saerens, P. Benedek, J. Winiger, V. Wood, J. Leuthold, V. Vogler-Neuling and R. Grange, Sol-gel barium titanate nanohole array as a nonlinear metasurface and a photonic crystal, Small, 2023, 19(50), 2304355,  DOI:10.1002/smll.202304355.
52. X. Sun, H. Yu, N. Deng, D. Ban, G. Liu and F. Qiu, Electro-optic polymer and silicon nitride hybrid spatial light modulators based on a metasurface, Opt. Express, 2021, 29(16), 25543–25551,  DOI:10.1364/OE.434480.
53. J. Zhang, Y. Kosugi, A. Otomo, Y. Nakano and T. Tanemura, Active metasurface modulator with electro-optic polymer using bimodal plasmonic resonance, Opt. Express, 2017, 25(24), 30304–30311,  DOI:10.1364/OE.25.030304.
54. J. Zhang, Y. Kosugi, A. Otomo, Y.-L. Ho, J.-J. Delaunay, Y. Nakano and T. Tanemura, Electrical tuning of metal-insulator-metal metasurface with electro-optic polymer, Appl. Phys. Lett., 2018, 113(23), 231102–12,  DOI:10.1063/1.5054964.
55. I. C. Benea-Chelmus, M. L. Meretska and D. L. Elder, et al., Electro-optic spatial light modulator from an engineered organic layer, Nat. Commun., 2021, 12, 5928.
56. X. Sun and F. Qiu, Polarization independent high-speed spatial modulators based on an electro-optic polymer and silicon hybrid metasurface, Photonics Res., 2022, 10(12), 2893–2900,  DOI:10.1364/PRJ.476688.
57. T. Zheng, Y. Gu and H. Kwon, et al., Dynamic light manipulation via silicon-organic slot metasurfaces, Nat. Commun., 2024, 15, 1557,  DOI:10.1038/s41467-024-45544-0.
58. I. C. Benea-Chelmus, S. Mason and M. L. Meretska, et al., Gigahertz free-space electro-optic modulators based on mie resonances, Nat. Commun., 2022, 13, 3170,  DOI:10.1038/s41467-022-30451-z.
59. M. M. Maior, Dielectric properties of Sn₂P₂S₆ crystals as a function of their growth conditions, Phys. Solid State, 1999, 41, 1333–1337.
60. A. A. Grabar Jan Kroupa, Y. I. Tyagur and Y. M. Vysochanskii, Electro-optic properties of Sn₂P₂S₆, Ferroelectrics, 1999, 223(1), 421–430,  DOI:10.1080/00150199908260598.
61. D. Haertle, G. Caimi, A. Haldi, G. Montemezzani, P. Günter, A. A. Grabar, I. M. Stoika and Y. M. Vysochanskii, Electro-optical properties of Sn₂P₂S₆, Opt. Commun., 2003, 215(4), 333–343,  DOI:10.1016/S0030-4018(02)02251-4.
62. D. Haertle, M. Jazbinšek, G. Montemezzani and P. Günter, Nonlinear optical coefficients and phase-matching conditions in Sn₂P₂S₆, Opt. Express, 2005, 13(10), 3765–3776,  DOI:10.1364/OPEX.13.003765.
63. D. Haertle, A. Guarino, J. Hajfler, G. Montemezzani and P. Günter, Refractive indices of Sn₂P₂S₆ at visible and infrared wavelengths, Opt. Express, 2005, 13(6), 2047–2057,  DOI:10.1364/OPEX.13.002047.
64. O. M. Shumelyuk, A. Y. Volkov, Y. M. Skrypka, L. E. Halliburton, N. C. Giles, C. A. Lenyk, S. A. Basun, A. A. Grabar, Y. M. Vysochansky, S. G. Odoulov and D. R. Evans, Near-infrared-sensitive photorefractive Sn₂P₂S₆ crystals grown by the Bridgman method, J. Appl. Phys., 2020, 127(10), 103103,  DOI:10.1063/1.5143204.
65. S. G. Odoulov, A. N. Shumelyuk, U. Hellwig, R. A. Rupp, A. A. Grabar and I. M. Stoyka, Photorefraction in tin hypothiodiphosphate in the near infrared, J. Opt. Soc. Am. B, 1996, 13(10), 2352–2360,  DOI:10.1364/JOSAB.13.002352.
66. G. Sevison, P. Halasyamani, J. Slagle and M. Rumi, Temperature Dependence of the Second Harmonic Generation Efficiency in Sn₂P₂(S_1-xSe_x)₆ Powders, in CLEO 2024, Technical Digest Series, Optica Publishing Group, 2024, paper JTh2A.3,  DOI:10.1364/CLEO_AT.2024.JTh2A.3.
67. C. D. Carpentier and R. Nitsche, Ferroelectricity in Sn₂P₂S₆, Mater. Res. Bull., 1974, 9(8), 1097–1100,  DOI:10.1016/0025-5408(74)90023-3.
68. K. Moriya, K. Iwauchi, M. Ushida, A. Nakagawa, K. Watanabe, S. Yano, S. Motojima and Y. Akagi, Dielectric studies of ferroelectric phase transitions in Pb_2xSn_2(1−x)P₂S₆ single crystals, J. Phys. Soc. Jpn., 1995, 64, 1775–1784.
69. P. Bernasconi, M. Zgonik and P. Gunter, Temperature dependence and dispersion of electro-optic and elasto-optic effect in perovskite crystals, J. Appl. Phys., 1995, 78(4), 2651–2658,  DOI:10.1063/1.360126.
70. J. He, S. H. Lee, F. Naccarato, G. Brunin, R. Zu, Y. Wang, L. Miao, H. Wang, N. Alem, G. Hautier, G.-M. Rignanese, Z. Mao and V. Gopalan, SnP₂S₆: A promising infrared nonlinear optical crystal with strong nonresonant second harmonic generation and phase-matchability, ACS Photonics, 2022, 9(5), 1724–1732,  DOI:10.1021/acsphotonics.2c00131.
71. Z. Li, J. Yao and Y. Wu, Chalcophosphates: A treasure house of infrared nonlinear optical materials, Cryst. Growth Des., 2020, 20(11), 7550–7564,  DOI:10.1021/acs.cgd.0c01234.
72. Zi-X. Chen, W. Liu and S.-P. Guo, A review of structures and physical properties of rare earth chalcophosphates, Coord. Chem. Rev., 2023, 474, 214870,  DOI:10.1016/j.ccr.2022.214870.
73. M.-M. Chen, S.-H. Zhou, W. Wei, M.-Y. Ran, B. Li, X.-T. Wu, H. Lin and Q.-L. Zhu, RbBiP₂S₆: A promising ir nonlinear optical material with a giant second-harmonic generation response designed by aliovalent substitution, ACS Mater. Lett., 2022, 4(7), 1264–1269,  DOI:10.1021/acsmaterialslett.2c00409.
74. E. I. Gerzanich, Optical properties of A₂B₂C₆ ferroelectrics-semiconductors: the effect of temperature and hydrostatic pressure, Ukr. J. Phys. Opt., 2008, 9(3), 129–163.
75. D. E. Zelmon, D. L. Small and D. Jundt, Infrared corrected sellmeier coefficients for congruently grown lithium niobate and 5 mol.% magnesium oxide–doped lithium niobate, J. Opt. Soc. Am. B, 1997, 14(12), 3319–3322,  DOI:10.1364/JOSAB.14.003319.
76. W. Wang, A. Klots, D. Prasai, Y. Yang, K. I. Bolotin and J. Valentine, Hot electron-based near-infrared photodetection using bilayer MoS₂, Nano Lett., 2015, 15(11), 7440–7444,  DOI:10.1021/acs.nanolett.5b02866.
77. A. Forouzmand, M. M. Salary, G. Kafaie Shirmanesh, R. Sokhoyan, H. A. Atwater and H. Mosallaei, Tunable all-dielectric metasurface for phase modulation of the reflected and transmitted light via permittivity tuning of indium tin oxide, Nanophotonics, 2019, 8(3), 415–427,  DOI:10.1515/nanoph-2018-0176.
78. V. Karimi and V. E. Babicheva, Multipole mie resonances in MXene-antenna arrays, J. Phys. Chem. C, 2023, 127(36), 17791–17801,  DOI:10.1021/acs.jpcc.3c02031.
79. V. Karimi and V. E. Babicheva, MXene-antenna electrode with collective multipole resonances, Nanoscale, 2024, 16, 4656–4667,  10.1039/D3NR03828A.
80. A. Han, J. V. Moloney and V. E. Babicheva, Applicability of multipole decomposition to plasmonic- and dielectric-lattice resonances, J. Chem. Phys., 2022, 156(11), 114104,  DOI:10.1063/5.0082005.
81. V. E. Babicheva and A. B. Evlyukhin, Analytical model of resonant electromagnetic dipole-quadrupole coupling in nanoparticle arrays, Phys. Rev. B, 2019, 99, 195444,  DOI:10.1103/PhysRevB.99.195444.
82. A. B. Evlyukhin, C. Reinhardt, U. Zywietz and B. N. Chichkov, Collective resonances in metal nanoparticle arrays with dipole-quadrupole interactions, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 245411,  DOI:10.1103/PhysRevB.85.245411.
83. P. Offermans, M. C. Schaafsma, S. R. K. Rodriguez, Y. Zhang, M. Crego-Calama, S. H. Brongersma and J. G. Rivas, Universal scaling of the figure of merit of plasmonic sensors, ACS Nano, 2011, 5(6), 5151–5157,  DOI:10.1021/nn201227b.
84. A. Danilov, V. G. Kravets, G. Tselikov, A. V. Grigorenko and A. V. Kabashin, Phase-sensitive plasmonics biosensors: from bulk to nanoscale architectures and novel functionalities, in Synthesis and Photonics of Nanoscale Materials XIII, ed. A. V. Kabashin, D. B. Geohegan, and J. J. Dubowski, International Society for Optics and Photonics, SPIE, 2016, vol. 9737, p. 97370D,  DOI:10.1117/12.2214883.
85. A. Yang, T. Hoang and M. Dridi, et al., Real-time tunable lasing from plasmonic nanocavity arrays, Nat. Commun., 2015, 6, 6939,  DOI:10.1038/ncomms7939.
86. M. Luennemann, U. Hartwig and G. Panotopoulos, et al., Electrooptic properties of lithium niobate crystals for extremely high external electric fields, Appl. Phys. B: Lasers Opt., 2003, 76, 403–406,  DOI:10.1007/s00340-003-1123-9.
87. A. V. Prokhorov, P. D. Terekhov, M. Y. Gubin, A. V. Shesterikov, X. Ni, V. R. Tuz and A. B. Evlyukhin, Resonant light trapping via lattice-induced multipole coupling in symmetrical metasurfaces, ACS Photonics, 2022, 9(12), 3869–3875,  DOI:10.1021/acsphotonics.2c01066.
88. F. Ding, Y. Yang, R. A. Deshpande and S. I. Bozhevolnyi, A review of gap-surface plasmon metasurfaces: fundamentals and applications, Nanophotonics, 2018, 7(6), 1129–1156,  DOI:10.1515/nanoph-2017-0125.
89. D. T. Pierce and W. E. Spicer, Electronic structure of amorphous si from photoemission and optical studies, Phys. Rev. B: Solid State, 1972, 5, 3017–3029,  DOI:10.1103/PhysRevB.5.3017.
90. R. Abraham Maniyara, C. Graham, B. Paulillo, Y. Bi, Y. Chen, G. Herranz, D. E. Baker, P. Mazumder, G. Konstantatos and V. Pruneri, Highly transparent and conductive ITO substrates for near infrared applications, APL Mater., 2021, 9(2), 021121,  DOI:10.1063/5.0040864.
91. A. Minenkov, S. Hollweger, J. Duchoslav, O. Erdene-Ochir, M. Weise, E. Ermilova, A. Hertwig and M. Schiek, Monitoring the electrochemical failure of indium tin oxide electrodes via operando ellipsometry complemented by electron microscopy and spectroscopy, ACS Appl. Mater. Interfaces, 2024, 16(7), 9517–9531,  DOI:10.1021/acsami.3c17923.
92. ITO Coatings, https://coloconcept.com/services/ito-coatings/, 2024, accessed: April 26, 2024.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ra05149a

---